河南省高考数学模拟试卷(理科)(4月份)A卷
- 格式:doc
- 大小:236.50 KB
- 文档页数:11

高考数学模拟试卷(理科)(一)(4月份)题号一二三总分得分一、选择题(本大题共12小题,共60.0分)1.已知x,y∈R,集合A={2,log3x},集合B={x,y},若A∩B={0},则x+y=( )A. B. 0 C. 1 D. 32.若复数z1=1+i,z2=1-i,则下列结论错误的是( )A. z1•z2是实数B. 是纯虚数C. |z|=2|z2|2D. z=4i3.已知=(-1,3),=(m,m-4),=(2m,3),若,则( )A. -7B. -2C. 5D. 84.如图,是以正方形的边AD为直径的半圆,向正方形内随机投入一点,则该点落在阴影区域内的概率为( )A.B.C.D.5.已知双曲线C:(a>0,b>0)的一个焦点坐标为(4,0),且双曲线的两条渐近线互相垂直,则该双曲线的方程为( )A. =1B.C. =1D. =1或=16.已知某几何体的三视图如图所示,则该几何体的表面积为( )A. 8π+6B. 6π+6C. 8π+12D. 6π+127.设x,y满足约束条件,则z=2x+y的取值范围是( )A. [-2,2]B. [-4,4]C. [0,4]D. [0,2]8.已知△ABC中,sin A,sin B,sin C成等比数列,则的取值范围是( )A. B. C. D.9.在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人--宰相宰相西萨•班•达依尔.国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍.请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!”国王觉得这要求太容易满足了,就命令给他这些麦粒.当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求.那么,宰相要求得到的麦粒到底有多少粒?下面是四位同学为了计算上面这个问题而设计的程序框图,其中正确的是( )A. B. C. D.10.若过点P(a,a)与曲线f(x)=x lnx相切的直线有两条,则实数a的取值范围是( )A. (-∞,e)B. (e,+∞)C. (0,)D. (1,+∞)11.已知菱形ABCD的边长为2,∠BAD=60°,沿对角线BD将菱形ABCD折起,使得二面角A-BD-C的余弦值为,则该四面体ABCD外接球的体积为( )A. B. 8π C. D. 36π12.已知函数f(x)=e x-ln(x+3),则下面对函数f(x)的描述正确的是( )A. ∀x∈(-3,+∞),f(x)≥B. ∀x∈(-3,+∞),f(x)C. ∃x0∈(-3,+∞),f(x0)=-1D. f(x)min∈(0,1)二、填空题(本大题共4小题,共20.0分)13.将函数f(x)=2sin(2x+φ)(φ<0)的图象向左平移个单位长度,得到偶函数g(x)的图象,则φ的最大值是______.14.已知a>0,b>0,(ax+)6展开式的常数项为,则a+2b的最小值为______.15.已知函数f(x)=,若f(x)-(m+2)x≥0,则实数m的取值范围是______.16.设过抛物线y2=2px(p>0)上任意一点P(异于原点O)的直线与抛物线y2=8px(p>0)交于A,B两点,直线OP与抛物线y2=8px(p>0)的另一个交点为Q,则=______.三、解答题(本大题共7小题,共82.0分)17.若数列{a n}是公差为2的等差数列,数列{b n}满足b1=1,b2=2,且a n b n+b n=nb n+1.(Ⅰ)求数列{a n}、{b n}的通项公式;(Ⅱ)设数列{c n}满足c n=,数列{c n}的前n项和为T n,若不等式(-1)nλ<T n+对一切n∈N*,求实数λ的取值范围.18.如图,在五面体ABCDEF中,四边形EDCF是正方形,AD=DE,∠ADE=90°,∠ADC=∠DCB=120°.(1)证明:平面ABCD⊥平面EDCF;(2)求直线AF与平面BDF所成角的正弦值.19.经销商第一年购买某工厂商品的单价为a(单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如表:上一年度[0,100)[100,200)[200,300)[300,400)[400,500)[500,+∞)销售额/万元商品单价a0.9a0.85a0.8a0.75a0.7a /元为了研究该商品购买单价的情况,为此调查并整理了50个经销商一年的销售额,得到下面的柱状图.已知某经销商下一年购买该商品的单价为X(单位:元),且以经销商在各段销售额的频率作为概率.(1)求X的平均估计值.(2)该工厂针对此次的调查制定了如下奖励方案:经销商购买单价不高于平均估计单价的获得两次抽奖活动,高于平均估计单价的获得一次抽奖活动.每次获奖的金额和对应的概率为获奖金额/元500010000概率记Y(单位:元)表示某经销商参加这次活动获得的奖金,求Y的分布列及数学期望..20.如图,已知椭圆的离心率为,E的左顶点为A、上顶点为B,点P在椭圆上,且△PF1F2的周长为.(I)求椭圆的方程;(II)设C,D是椭圆E上两不同点,CD∥AB,直线CD与x轴、y轴分别交于M,N两点,且的取值范围.21.已知f′(x)为函数f(x)的导函数,f(x)=e2x+2f(0)e x-f′(0)x.(1)求f(x)的单调区间;(2)当x>0时,af(x)<e x-x恒成立,求a的取值范围.22.在直角坐标系xOy中,直线l的参数方程为(t为参数),圆C的标准方程为(x-3)2+(y-3)2=4.以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(1)求直线l和圆C的极坐标方程;(2)若射线θ=与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB 的中点,求a的值.23.已知f(x)=|mx+3|-|2x+n|.(1)当m=2,n=-1时,求不等式f(x)<2的解集;(2)当m=1,n<0时,f(x)的图象与x轴围成的三角形面积大于24,求n的取值范围.答案和解析1.【答案】C【解析】解:A∩B={0};∴0∈A,0∈B;∴log3x=0;∴x=1,y=0;∴x+y=1.故选:C.根据A∩B={0}即可得出0∈A,0∈B,这样即可求出x,y的值,从而求出x+y的值.考查列举法表示集合的概念,交集的概念及运算,以及元素与集合的关系.2.【答案】D【解析】【分析】本题考查复数代数形式的乘除运算,考查复数模的求法,是基础题.直接利用复数代数形式的乘除运算及复数模的求法逐一判断得答案.【解答】解:∵z1=1+i,z2=1-i,∴z1•z2=1-i2=2,故A正确;,故B正确;,,故C正确;,故D错误.故选:D.3.【答案】A【解析】解:=(-1,3),=(m,m-4),=(2m,3),若,则-1×(m-4)-3×m=0;解得m=1;∴=(1,-3)=(2,3);=1×2+(-3)×3=-7.故选:A.根据平面向量的坐标运算与共线定理、数量积运算法则,计算即可.本题考查了平面向量的坐标运算与共线定理、数量积运算问题,是基础题.4.【答案】D【解析】解:连结AE,结合图象可知弓形①与弓形②面积相等,将弓形①移动到②的位置,则阴影部分将构成一个直角三角形,则阴影部分的面积为正方形面积的,则向正方形内随机投入一点,则该点落在阴影区域内的概率P=,故选:D.根据图象的关系,求出阴影部分的面积,结合几何概型的概率公式进行求解即可.本题主要考查几何概型的概率公式的应用,求出阴影部分的面积是解决本题的关键.5.【答案】A【解析】【分析】本题考查双曲线的方程和性质,主要是渐近线方程的运用,以及两直线垂直的条件:斜率之积为-1,考查方程思想和运算能力,属于基础题.由题意可得c=4,由双曲线的渐近线方程和两直线垂直的条件:斜率之积为-1,可得a=b,解方程可得a,b的值,即可得到所求双曲线的方程.【解答】解:双曲线C:(a>0,b>0)的一个焦点坐标为(4,0),可得c=4,即有a2+b2=c2=16,双曲线的两条渐近线互相垂直,即直线y=x和直线y=-x垂直,可得a=b,解方程可得a=b=2,则双曲线的方程为-=1.故选A.6.【答案】B【解析】解:几何体是组合体,上部是半圆柱,下部是半球,圆柱的底面半径与球的半径相同为1,圆柱的高为3,几何体的表面积为:2π×12+12×π+2×3+3π=6+6π.故选:B.由题意判断几何体的形状,然后求解几何体的表面积即可.本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.7.【答案】B【解析】解:作出约束条件所对应的可行域,(如图中阴影部分所示),变形目标函数z=2x+y,可得y=-2x+z,平移直线y=-2x可知,当直线经过点A(-2,0)时,目标函数取最小值-4,当直线经过点B(2,0)时,目标函数取最大值4,故z=-2x+y的取值范围为[-4,4].故选:B.作出约束条件所对应的可行域,变形目标函数,平移直线y=2x可得结论.本题考查简单线性规划,准确作图是解决问题的关键,属于中档题.8.【答案】B【解析】解:∵在△ABC中,sin A、sin B、sin C依次成等比数列,∴sin2B=sin A sin C,利用正弦定理化简得:b2=ac,由余弦定理得:cos B===(+)-≥2-=(当且仅当a=c时取等号),∴cos B≥,∴B的范围为(0,],设y==,设sin B+cos B=t,则2sin B cosB=t2-1,由于t=sin B+cos B=sin(B+),B∈(0,],知t∈(1,],故y===t-,t∈(1,],∵y=t-,在(1,]上是增函数,∴y∈(0,],故选:B.由sin A、sin B、sin C依次成等比数列,利用等比数列的性质列出关系式,利用正弦定理化简,再利用余弦定理表示出cos B,把得出关系式代入并利用基本不等式求出cos B的范围,再设sin B+cos B=t,可得y=t-,在(1,]上是增函数,即可求出.本题考查了解三角形,辅助角公式与函数值域综合,考查了转化与化归思想,属于中档题.9.【答案】C【解析】【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,可得答案.本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.【解答】解:由已知中程序的功能,可得循环变量的初值为1,终值为64,由于四个答案均为直到条件不满足时退出循环,故循环条件应为n≤64,而每次累加量构造一个以1为首项,以2为公式的等比数列,由S n=2n-1得:S n+1=2n+1-1=2S n+1,故循环体内S=1+2S,故选:C.10.【答案】B【解析】【分析】本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查函数方程的转化思想,以及运算能力,属于中档题.设切点为(m,m lnm),求出导数,求得切线的斜率,由两点的斜率公式可得=,设g(m)=,求出导数和单调区间,可得最大值,由题意可得0<<,解不等式即可得到所求范围.【解答】解:设切点为(m,m lnm),f(x)=x lnx的导数为f′(x)=1+ln x,可得切线的斜率为1+ln m,由切线经过点P(a,a),可得1+ln m=,化简可得=,(*),由题意可得方程(*)有两解,设g(m)=,可得g′(m)=,当m>e时,g′(m)<0,g(m)递减;当0<m<e时,g′(m)>0,g(m)递增.可得g(m)在m=e处取得最大值,即有0<<,此时有两个解,解得a>e.故选:B.11.【答案】B【解析】【分析】本题考查四面体的外接球的体积的求法,考查四面体、球等基础知识,考查运用求解能力、空间想象能力、探索能力、转化与化归思想,是中档题.正确作出图形,利用勾股定理建立方程,求出四面体的外接球的半径,即可求出四面体的外接球的体积.【解答】解:如图所示,取BD中点F,连结AF、CF,则AF⊥BD,CF⊥BD,∴∠AFC是二面角A-BD-C的平面角,过A作AE⊥平面BCD,交CF延长线于E,∴cos∠AFC=-,cos,AF=CF==3,∴AE=2,EF=1,设O为球心,过O作OO′⊥CF,交CF于O′,作OG⊥AE,交AE于G,设OO′=x,∵O′B=CF=2,O′F==1,设外接球的半径为R,则,∴由勾股定理得R2=O′B2+OO'2=4+x2=OG2+AG2=(1+1)2+(2-x)2,解得x=,∴R2=6,即R=,∴四面体的外接球的体积为V=πR3==8π.故选B.12.【答案】B【解析】解:因为函数f(x)=e x-ln(x+3),定义域为(-3,+∞),所以f′(x)=e x-,易知导函数f′(x)在定义域(-3,+∞)上是单调递增函数,又f′(-1)<0,f′(-)>0,所以f′(x)=0在(-3,+∞)上有唯一的实根,不妨将其设为x0,且x0∈(-1,-),则x=x0为f(x)的最小值点,且f′(x0)=0,即=,两边取以e为底的对数,得x0=-ln(x0+3)故f(x)≥f(x0)=-ln(x0+3)=-ln(x0+3)=+x0,因为x0∈(-1,-),所以2<x0+3,故f(x)≥f(x0)=>2+=-,即对∀x∈(-3,+∞),都有f(x)>-.故选:B.本题首先要对函数f(x)=e x-ln(x+3)进行求导,确定f′(x)在定义域上的单调性为单调递增函数,然后再利用当x∈(a,b)时,利用f′(a)f′(b)<0确定导函数的极值点x0∈(-1,-)从而.得到x=x0时是函数f(x)的最小值点.本题表面考查命题的真假判断,实际上是考查函数的求导,求最值问题,准确计算是基础,熟练运用知识点解决问题是关键.13.【答案】【解析】解:函数f(x)=2sin(2x+φ)(φ<0)的图象向左平移个单位长度,得f(x+)=2sin[2(x+)+φ]=2sin(2x+φ+)的图象,∴g(x)=2sin(2x++φ);又g(x)是偶函数,∴+φ=+kπ,k∈Z;∴φ=-+kπ,k∈Z;又φ<0,∴φ的最大值是-.故答案为:-.根据三角函数图象平移法则,结合函数的奇偶性求出φ的最大值.本题考查了三角函数的图象与性质的应用问题,是基础题.14.【答案】2【解析】解:(ax+)6展开式的通项为x6-2r,由6-2r=0,得r=3.∴,即.∴a+2b,当且仅当a=2b,即a=1,b=时,取“=”.∴a+2b的最小值为2.故答案为:2.写出二项展开式的通项,由x的指数为0求得r值,可得ab=,再由基本不等式求a+2b的最小值.本题考查二项式定理的应用,考查二项式系数的性质,训练了利用基本不等式求最值,是基础题.15.【答案】[-2,1]【解析】解:若f(x)-(m+2)x≥0,即有f(x)≥(m+2)x,分别作出函数f(x)和直线y=(m+2)x的图象,由直线与曲线相切于原点时,(x2+3x)′=2x+3,则m+2=3,解得m=1,由直线绕着原点从x轴旋转到与曲线相切,满足条件.即有0≤m+2≤3,解得-2≤m≤1.故答案为:[-2,1].由题意可得f(x)≥(m+2)x,分别作出函数f(x)和直线y=(m+2)x的图象,由直线与曲线相切于原点时,求出m=1,通过图象观察,即可得到所求m的范围.本题考查函数恒成立问题的解法,注意运用数形结合的思想方法,考查运算能力,属于中档题16.【答案】3【解析】【分析】本题考查了抛物线的性质,属于中档题.解:设直线OP方程为y=kx(k≠0),联立方程组求出P,Q的坐标,计算OP,PQ的比值得出结论.【解答】解:如图所示:联立方程组,解得P(,),联立方程组,解得Q(,),∴|OP|==,|PQ|==,∴==3.故答案为:3.17.【答案】解:(Ⅰ)∵数列{b n}满足b1=1,b2=2,且a n b n+b n=nb n+1,∴a1+1=2,解得a1=1,又数列{a n}是公差为2的等差数列,∴a n=1+2(n-1)=2n-1,∴2nb n=nb n+1,即2b n=b n+1,∴数列{b n}是等比数列,首项为1,公比为2,∴b n=2n-1;(Ⅱ)设数列{c n}满足c n===,数列{c n}的前n项和为T n=1++…+,∴=+…++,作差得=1+++…+-=-=2-,∴T n=4-,不等式(-1)nλ<T n+,化为(-1)nλ<4-,当n=2k(k∈N*)时,λ<4-恒成立,∵y=4-在n≥2时单调递增,∴y的最小值为3,∴λ<3;当n=2k-1(k∈N*)时,λ>-4+恒成立,∵y=-4+在n≥1时单调递减,∴y的最大值为-2,∴λ>-2.综上可得:实数λ的取值范围是(-2,3).【解析】本题考查了等差数列与等比数列的通项公式与求和公式、数列的单调性、数列递推关系、“错位相减法”,属于中档题.(Ⅰ)数列{b n}满足b1=1,b2=2,且a n b n+b n=nb n+1,利用等差数列的通项公式可得a n.可得2nb n=nb n+1,利用等比数列的通项公式可得b n;(Ⅱ)设数列{c n}满足c n===,利用“错位相减法”可得数列{c n}的前n项和为T n,再利用数列的单调性与分类讨论即可得出.18.【答案】证明:(1)因为AD⊥DE,DC⊥DE,AD、CD⊂平面ABCD,且AD∩CD=D ,所以DE⊥平面ABCD.又DE⊂平面EDCF,故平面ABCD⊥平面EDCF.解:(2)由已知DC∥EF,平面ABFE,平面ABFE,所以DC∥平面ABFE.又平面ABCD∩平面ABFE=AB,故AB∥CD.又因为∠ADC=∠DCB=120°,所以四边形ABCD为等腰梯形.又AD=DE,所以AD=CD=BC,又∠DCB=120°,则∠CDB=∠CBD=30°,所以∠ADB=∠ADC-∠CDB=90°,即AD⊥BD,令AD=1,如图,以D为原点,以DA为x轴,建立空间直角坐标系D-xyz,则D(0,0,0),A(1,0,0),F(-,,1),B(0,,0),∴=(,-,-1),=(0,,0),=(-,,1).设平面BDF的法向量为=(x,y,z),则,取x=2,可得y=0,z=1,得=(2,0,1),cos<,>=,设直线与平面BDF所成的角为θ,则sinθ=.所以直线AF与平面BDF所成角的正弦值为.【解析】本题考查面面垂直的证明,考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.(1)推导出AD⊥DE,DC⊥DE,从而DE⊥平面ABCD.由此能证明平面ABCD⊥平面EDCF.(2)以D为原点,以DA为x轴,建立空间直角坐标系D-xyz,利用向量法能求出直线AF与平面BDF所成角的正弦值.19.【答案】解:(1)由题可知:商品单价/a0.9a0.85a0.8a0.75a0.7a元频率0.20.30.240.120.10.04X的平均估计值为:a×0.2+0.9a×0.36+0.85a×0.24+0.8a×0.12+0.75a×0.1+0.7a×0.04=0.873a.(2)购买单价不高于平均估计单价的概率为0.24+0.12+0.04=0.5=.Y的取值为5000,10000,15000,20000.P(Y=5000)=,P(Y=10000)==,P(Y=15000)==,P(Y=20000)==.∴Y的分布列为:Y 5000 10000 15000 20000PE(Y)=+20000×=9375(元).【解析】(1)由统计表和柱状图能得到X的平均估计值.(2)购买单价不高于平均估计单价的概率为0.24+0.12+0.04=0.5=.Y的取值为5000,10000,15000,20000.分别求出相应的概率,由此能求出Y的分布列和E(Y).本题考查学生对频率分布直方图的理解以及分布列的相关知识,考查运算求解能力、数据处理能力、应用意识,考查分类与整合思想、必然与或然思想、化归与转化思想.20.【答案】解:(I)由题意知:,∴a2=4,b2=1,∴椭圆方程为.(II)∵A(-2,0),B(0,1),∴.由CD∥AB,设直线CD的方程为,由已知,得M(-2m,0),N(0,m),设C(x1,y1),D(x2,y2),由,得x2+2mx+2m2-2=0,△=(2m)2-4(2m2-2)>0,∴m2<2,∴x1+x2=-2m,x1x2=2m2-2,由得(x1+2m,y1)=λ(-x1,m-y1),∴x1+2m=-λx1,即,同理,由,得,∴=,由m2<2,得,∴λ+μ∈(-∞,-2]∪(2,+∞).【解析】(I)由题意知:,由此能求出椭圆方程.(II)由A(-2,0),B(0,1),知.由CD∥AB,设直线CD的方程为,由已知,得M(-2m,0),N(0,m),设C(x1,y1),D(x2,y2),由,得x2+2mx+2m2-2=0,再由根的判别式和韦达定理知,同理,,由此能求出λ+μ∈(-∞,-2]∪(2,+∞).本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.21.【答案】解:(1)由f(0)=1+2f(0),得f(0)=-1.因为f′(x)=2e2x-2e x-f′(0),所以f′(0)=2-2-f′(0),解得f′(0)=0.所以f(x)=e2x-2e x,f′(x)=2e x(e x-1),当x∈(-∞,0)时,f′(x)<0,则函数f(x)在(-∞,0)上单调递减;当x∈(0,+∞)时,f′(x)>0,则函数f(x)在(0,+∞)上单调递增.(2)令g(x)=af(x)-e x+x=ae2x-(2a+1)e x+x,根据题意,当x∈(0,+∞)时,g(x)<0恒成立.g′(x)=(2ae x-1)(e x-1).①当0<a<,x∈(-ln2a,+∞)时,g′(x)>0恒成立,所以g(x)在(-ln2a,+∞)上是增函数,且g(x)∈(g(-ln2a),+∞),所以不符合题意;②当a≥,x∈(0,+∞)时,g′(x)>0恒成立,所以g(x)在(0,+∞)上是增函数,且g(x)∈(g(0),+∞),所以不符合题意;③当a≤0时,因为x∈(0,+∞),所有恒有g′(x)<0,故g(x)在(0,+∞)上是减函数,于是“g(x)<0对任意x∈(0,+∞)都成立”的充要条件是g(0)≤0,即a-(2a+1)≤0,解得:a≥-1,故-1≤a≤0.综上,a的取值范围是[-1,0].【解析】(1)求出函数的导数,计算f(0),求出f′(0)的值,求出函数的单调区间即可;(2)令g(x)=af(x)-e x+x,求出函数的导数,通过讨论a的范围,求出函数的最值,从而确定a的范围即可.本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.22.【答案】解:(1)∵直线l的参数方程为(t为参数),∴在直线l的参数方程中消去t可得直线l的普通方程为x-y-=0,将x=ρcosθ,y=ρsinθ代入以上方程中,得到直线l的极坐标方程为ρcosθ-ρsinθ-=0.∵圆C的标准方程为(x-3)2+(y-3)2=4,∴圆C的极坐标方程为ρ2-6ρcosθ-6ρsinθ+14=0.(2)在极坐标系中,由已知可设M(),A(),B(ρ3,).联立,得,∴ρ2+ρ3=3+3.∵点M恰好为AB的中点,∴,即M(,).把M(,)代入,得×-=0,解得a=.【解析】本题考查直线和圆的极坐标方程的求法,考查实数值的求法,考查极坐标方程、直角坐标方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.(1)直线l的参数方程消去t可得直线l的普通方程,将x=ρcosθ,y=ρsinθ代入,能求出直线l的极坐标方程.由圆的标准方程能求出圆C的极坐标方程.(2)设M(),A(),B(ρ3,).联立,得,从而ρ2+ρ3=3+3,进而M(,).把M(,)代入,能求出a的值.23.【答案】解:(1)当m=2,n=-1时,f(x)=|2x+3|-|2x-1|,不等式f(x)<2等价于或或,解得:x<-或-≤x<0,即x<0.所以不等式f(x)<2的解集是(-∞,0).(2)由题设可得,f(x)=|x+3|-|2x+n|=,所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为:A(-,0),B(3-n,0),C(-,3-),所以三角形ABC的面积为(3-n+)(3-)=,由>24,解得:n>18或n<-6.∵n<0,∴n<-6.故n的取值范围是.【解析】本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道综合题.(1)代入m,n的值,分类讨论得到关于x的不等式组,解出即可;(2)求出A,B,C的坐标,表示出三角形的面积,得到关于n的不等式,解出即可.。


2020年河南省、广东省等五岳联考高考数学模拟试卷(理科)(4月份)一、单选题(本大题共12小题,共60.0分)1. 设集合M ={x|x 2−2x −3<0,x ∈Z},则集合M 的真子集个数为( )A. 8B. 7C. 4D. 32. 已知i 是虚数单位,则化简(1+i1−i )2020的结果为( )A. iB. −iC. −1D. 13. 若干年前,某教师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图该教师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该教师的月退休金为( )A. 4500元B. 5000元C. 5500元D. 6000元4. 将包括甲、乙、丙在内的8人平均分成两组参加文明交通”志愿者活动,其中一组指挥交通,一组分发宣传资料,则甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率为( )A. 27B. 37C. 17D. 3145. 已知抛物线y 2=4x 的焦点为F ,过点F 和抛物线上一点M(3,2√3)的直线l 交抛物线于另一点N ,则|NF|:|NM|等于( )A. 1:2B. 1:3C. 1:4D. 1:√36. 在所有棱长都相等的直三棱柱ABC −A 1B 1C 1中,D ,E 分别为棱CC 1,AC 的中点,则直线AB 与平面B 1DE 所成角的余弦值为( )A. √3010B. √3020C. √13020D. √70107. 已知点A(4,3),点B 为不等式组{y ≥0x −y ≤0x +2y −6≤0所表示平面区域上的任意一点,则|AB|的最小值为( )A. 5B. 4√55C. √5D. 2√558. 给出下列说法①定义在[a,b]上的偶函数f(x)=x 2−(a +4)x +b 的最大值为20; ②“x =π4”是“tanx =1”的充分不必要条件;③命题“∃x 0∈(0,+∞),x 0+1x 0≥2”的否定形式是“∀x ∈(0,+∞),x +1x <2”其中正确说法的个数为( )A. 0B. 1C. 2D. 39. 已知log m 3>0,a =m log 42,b =m log 32,c =m 20.5,则a ,b ,c 间的大小关系为( )A. a <b <cB. b <a <cC. c <a <bD. b <c <a10. 元代数学家朱世杰在《算学启蒙》中提及如下问题:今有银一秤一斤十两(1秤=15斤,1斤=16两),令甲、乙、丙从上作折半差分之,问:各得几何?其意思是:现有银一秤一斤十两,现将银分给甲、乙、丙三人,他们三人每一个人所得是前一个人所得的一半.若银的数量不变,按此法将银依次分给7个人,则得银最少的一个人得银( )A. 9两B. 266127两C.26663两 D. 250127两11. 在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,若acosB −bcosA =c3,则acosBacosA+bcosB的最大值为( )A. √2B. √22 C. √32 D. 2√3312. 已知f(x)为奇函数,g(x)为偶函数,且f(x)+g(x)=log 3(3x +1),不等式3g(x)−f(x)−t ≥0对x ∈R 恒成立,则t 的最大值为( )A. 1B. 3−2log 32C. 2D. 32log 32−1二、单空题(本大题共4小题,共20.0分)13. 已知向量a ⃗ =(2,−√5),b ⃗ =(1,2√5),则b ⃗ 在a ⃗ 方向上的投影等于______. 14. 在△ABC 中,∠B =2π3,A 、B 是双曲线E 的左、右焦点,点C 在E 上,且BC =12AB ,则E 的离心率为______.15. 已知函数f(x)=cos(ωx +φ)(ω>0,0≤φ≤π)是奇函数,且在[−π6,π4]上单调递减,则ω的最大值是 .16. 已知三棱锥A −BCD 中,平面ABD ⊥平面BCD ,BC ⊥CD ,BC =CD =2,AB =AD =√6,则三棱锥A −BCD 的外接球的体积为______.三、解答题(本大题共7小题,共82.0分)17.已知数列{a n}的前n项和为S n,且S n=12na n+a n−1.(1)求数列{a n}的通项公式;(2)若数列{2a n2}的前n项和为T n,证明:T n<32.18.如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABEF为正方形,AF⊥DF,AF=2√2FD,∠DFE=∠CEF=45.(1)证明:DC//FE;(2)求二面角D−BE−C的平面角的余弦值.19.已知点P在圆O:x2+y2=9上运动,点P在x轴上的投影为Q,动点M满足4PQ⃗⃗⃗⃗⃗ = 3√2MQ⃗⃗⃗⃗⃗⃗⃗ .(1)求动点M的轨迹E的方程;(2)设G(−3,0),H(3,0),过点F(1,0)的动直线l与曲线E交于A、B两点.问:直线AG与BH的斜率之比是否为定值?若为定值,求出该定值;若不为定值,试说明理由.20.某县为了帮助农户脱贫致富,鼓励农户利用荒地山坡种植果树,某农户考察了三种不同的果树苗A、B、C.经过引种实验发现,引种树苗A的自然成活率为0.7,引种树苗B、C的自然成活率均为p(0.6≤p≤0.8).(1)任取树苗A、B、C各一棵,估计自然成活的棵数为X,求X的分布列及其数学期望;(2)将(1)中的数学期望取得最大值时p的值作为B种树苗自然成活的概率,该农户决定引种n棵B种树苗,引种后没有自然成活的树苗有75%的树苗可经过人栽培技术处理,处理后成活的概率为0.8,其余的树苗不能成活.①求一棵B种树苗最终成活的概率;②若每棵树苗引种最终成活可获利400元,不成活的每棵亏损80元该农户为了获利期望不低于10万元,问至少要引种种树苗多少棵?21.已知函数f(x)=(a−1)x+xlnx的图象在点A(e2,f(e2))(e为自然对数的底数)处的切线斜率为4.(1)求实数a的值;(2)若m∈Z,且m(x−1)<f(x)+1对任意x>1恒成立,求m的最大值.22.以坐标原点为极点,以x轴的非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=√2(θ∈[−π2,π2]),直线l的参数方程为{x=−2+tcosαy=−4+tssinα(t为参数).(1)点A在曲线C上,且曲线C在点A处的切线与直线:x+2y+1=0垂直,求点A的直角坐标;(2)设直线l与曲线C有且只有一个公共点,求直线l的斜率的取值范围.23.设函数f(x)=|x−1|+2|x+1|,x∈R.(1)求不等式f(x)<5的解集;(2)若关于x的不等式f(x)+2<|2t−1|在实数范围内解集为空集,求实数t的取值范围.答案和解析1.【答案】B【解析】解:集合M={x|x|x2−2x−3<0,x∈Z}={x|−1<x<3,x∈Z}={0,1,2},所以集合M的真子集个数为:23−1=7个.故选:B.由列举法得到集合A中的元素个数,再由结论:含有n个元素的集合的真子集数共有:2n−1个,即得答案本题主要考查了集合的子集,一般地,含有n个元素的集合的真子集数共有:2n−1个.2.【答案】D【解析】解:∵1+i1−i =(1+i)2(1−i)(1+i)=i,∴(1+i1−i)2020=i2020=i4×505=1.故选:D.利用复数代数形式的乘除运算化简1+i1−i,再由虚数单位i的运算性质得答案.本题考查复数的代数形式的乘除运算,考查虚数单位i的运算性质,是基础题.3.【答案】B【解析】解:设目前该教师的月退休金为x元,则有10%x=4000×15%−100,解之得x=5000,故选:B.根据题中目前的月就医费比刚退休时少100元可列等式,求出即可.本题考查对条形图,折线图的数据整合能力,属于基础题.4.【答案】B【解析】解:①甲指挥交通,乙不指挥交通,是丙不能指挥交通,故有C52=10种方法,②乙指挥交通,甲不指挥交通,则丙必须指挥交通,故有C52=10种方法,③甲、乙都指挥交通,则丙不能指挥交通,故有C52=10种方法,∴甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率为: p =3C 52C 84=37.故选:B .①甲指挥交通,乙不指挥交通,是丙不能指挥交通,故有C 52=10种方法,乙指挥交通,甲不指挥交通,则丙必须指挥交通,故有C 52=10种方法,甲、乙都指挥交通,则丙不能指挥交通,故有C 52=10种方法,由此能求出甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率.本题考查概率的求法,考查分类讨论思想、列举法等基础知识,考查运算求解能力,是基础题.5.【答案】C【解析】解:抛物线y 2=4x 的焦点为F(1,0),所以k FM =2√33−1=√3,由{y 2=4x y =√3(x −1),可得3x 2−10x +3=0,所以x 1=3,x 2=13, 所以|FN||MN|=x 2+p2x 1+x 2+p=13+13+13+2=14.故选:C .求出抛物线的焦点坐标,通过直线与抛物线方程联立,求出MN 的坐标,然后转化求解|NF|:|NM|即可.本题考查抛物线的焦点弦,抛物线的简单性质以及数形结合的思想的应用,是中档题.6.【答案】C【解析】 【分析】本题考查了利用空间向量求线面角的问题,属于中档题.根据题意,建立空间直角坐标系,将所求的角转化为直线AB 与平面B 1DE 的法向量的夹角来求即可. 【解答】解:因为是所有棱长都相等的直三棱柱ABC −A 1B 1C 1. ∴该棱柱的上下底面是正三角形,侧面都是正方形,设各棱长均为2,取AB 的中点为原点,直线OC ,OB 分为x ,y 轴建立如图所示的空间直角坐标系.则O(0,0,0),B(0,1,0),E(√32,−12,0),D(√3,0,1),B 1(0,1,2). ∴ED⃗⃗⃗⃗⃗ =(√32,12,1),EB 1⃗⃗⃗⃗⃗⃗⃗ =(−√32,32,2), 设平面B 1DE 的法向量m ⃗⃗⃗ =(x,y,z), ∴{m ⃗⃗⃗ ⋅ED⃗⃗⃗⃗⃗ =0m ⃗⃗⃗ ⋅EB 1⃗⃗⃗⃗⃗⃗⃗ =0,∴{√32x +12y +z =0−√32x +32y +2z =0,令x =2,得m ⃗⃗⃗ =(2,6√3,−4√3).∵OB ⃗⃗⃗⃗⃗⃗ =(0,1,0)且AB ⃗⃗⃗⃗⃗ //OB ⃗⃗⃗⃗⃗⃗ . 设所求角为θ,则sinθ=|m⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |OB⃗⃗⃗⃗⃗⃗ |=3√3020, ∴cosθ=√13020. 故选:C .7.【答案】C【解析】解:不等式组{y ≥0x −y ≤0x +2y −6≤0的可行域如图:则|AB|的最小值为A 到B 的距离. 由{x −y =0x +2y −6=0解得B(2,2), |AB|的最小值:√(4−2)2+(3−2)2=√5, 故选:C .画出约束条件的可行域,利用已知条件求解距离的最小值即可.本题考查线性规划的简单应用,是基本知识的考查,考查数形结合以及点到直线的距离公式的应用.8.【答案】D【解析】解:①定义在[a,b]上的偶函数f(x)=x2−(a+4)x+b,所以有f(−x)=f(x),即a=−4,定义域为[a,b],所以b=4,所以函数f(x)在x=±4时取得最大值为20,正确;②由充要条件的定义“x=π4”能推出“tanx=1”成立,而“tanx=1”不能推出“x=π4”成立,所以“x=π4”是“tanx=1”的充分不必要条件正确;③由特称量词命题的否定定义可得命题“∃x0∈(0,+∞),x0+1x0≥2”的否定形式是“∀x∈(0,+∞),x+1x<2”正确;其中正确说法的个数为①②③三个,故选:D.①利用函数的奇偶性和最值可得答案,②由充要条件定义可判断,③由命题的否定定义可判断,从而可得结论.本题考查命题真假判断及充要条件,函数的奇偶性和最值,命题的否定,属基础题.9.【答案】A【解析】【分析】本题考查对数函数和指数函数的性质,属于基础题.利用对数函数和指数函数的性质求解.【解答】解:∵log m3>0,∴m>1,∵0<log42<log32<1,20.5>1,∴a<b<c,故选:A.10.【答案】B【解析】解:由题意共有银:16×16+10=266两,设分银最少的为a两,则7人的分银量构成以a为首项,2为公比的等比数列,则a(1−27)1−2=266,解得a=266127.故选:B.共有银:16×16+10=266两,设分银最少的为a两,则7人的分银量构成以a为首项,2为公比的等比数列,由此利用等比数列前n项和公式能求出结果.本题考查等比数列的首项的求法,考查等比数列的性质等基础知识,考查运算求解能力,是基础题.11.【答案】B【解析】解:因为acosB−bcosA=c3,由正弦定理可得,sinAcosB−sinBcosA=13sinC=13(sinAcosB+sinBcosA),化简可得,tanA=2tanB,则acosBacosA+bcosB=sinAcosBsinAcosA+sinBcosB=1cosAcosB+sinBsinA≤2√sinAcosB,当且仅当cosAcosB=sinBsinA时取等号,=2√tanBtanA =√22,即最大值√22,故选:B.由已知结合正弦定理及和差角公式化简可得tanA=2tanB,然后对所求式子进行化简,结合基本不等式即可求解.本题主要考查了正弦定理及三角恒等变形在求解三角形中的应用,还考查了基本不等式求解最值的应用,属于中档试题.12.【答案】B【解析】解:f(x)为奇函数,g(x)为偶函数,可得f(−x)=−f(x),g(−x)=g(x),由f(x)+g(x)=log3(3x+1),①可得f(−x)+g(−x)=log3(3−x+1),即为−f(x)+g(x)=log3(3−x+1),②联立①②可得f(x)=12x,g(x)=log3(3x+1)−12x,由不等式3g(x)−f(x)−t≥0对x∈R恒成立,可得t ≤3g(x)−f(x)=3log 3(3x+1)−2x =log 3(3x +1)332x恒成立,设ℎ(x)=(3x +1)332x,ℎ′(x)=ln3⋅32x (1+3x )2(3x −2)34x,当x >log 32时,ℎ′(x)>0,ℎ(x)递增,当x <log 32时,ℎ′(x)<0,ℎ(x)递减, 可得x =log 32处ℎ(x)取得极小值,且为最小值3−2log 32, 则t ≤3−2log 32, 故选:B .运用奇偶性的定义,将x 换为−x ,联立两个方程求得f(x),g(x),由题意可得t ≤3g(x)−f(x)的最小值,构造函数ℎ(x),求得导数和单调性、极值和最小值,可得所求范围. 本题考查函数的奇偶性的定义和函数恒成立问题解法,注意运用参数分离和构造函数法,运用导数求得单调性和最值,考查化简运算能力和推理能力,属于中档题.13.【答案】−83【解析】解:向量a ⃗ =(2,−√5),b ⃗ =(1,2√5), 则b ⃗ 在a⃗ 方向上的投影为|b ⃗|cosθ=a ⃗ ⋅b ⃗ |a ⃗ |=√5×2√5√22+(−√5)2=−83.故答案为:−83.根据平面向量投影的定义,计算即可.本题考查了平面向量投影的定义与计算问题,也考查了平面向量的坐标运算问题,是基础题.14.【答案】√7+13【解析】解:由题得,AB =2c ,BC =c ,∠B =23π, 则根据余弦定理可得AC =√AB 2+BC 2−2AB ⋅BC ⋅cosB =√4c 2+c 2−2×2c ×(−12)=√7c ,所以√7c −c =2a ,解得e =√7+13,故答案为√7+13.根据余弦定理可得AC =√7c ,结合双曲线定义,则有√7c −c =2a ,即可解出e .本题考查双曲线离心率的求法,考查余弦定理的应用,属于中档题.15.【答案】2【解析】【分析】本题考查了奇函数的定义,奇函数在原点有定义时,原点处的函数值为0,三角函数的诱导公式,正弦型函数的单调性,考查了计算能力.根据f(x)是奇函数即可得出φ=π2,进而得出f(x)=−sinωx,然后根据题意即可得出[−π6,π4]⊆[−π2ω,π2ω],然后即可得出0<ω≤2,从而得出ω的最大值.【解答】解:∵f(x)是R上的奇函数,∴f(0)=cosφ=0,且0≤φ≤π,∴φ=π2,∴f(x)=cos(ωx+π2)=−sinωx,且ω>0,f(x)在[−π6,π4]上单调递减,∴[−π6,π4]⊆[−π2ω,π2ω],∴π2ω≥π4且−π2ω⩽−π6,解得0<ω≤2,∴ω的最大值是2.故答案为:2.16.【答案】9π2【解析】解:∵AB=AD,取BD中点E,则AE⊥BD ∵平面ABD⊥平面BCD,则AE⊥BD,故AE⊥平面BCD,则球心O在AE上,且BD=2√2,EB=√2,AE=√AD2−BE2=2,设外接球的半径R,则OB2=OE2+EB2,∴R2=2+(2−R)2,解可得,R=32,V=4πR33=43×(32)3=9π2.根据四棱锥的性质可先求出球心的位置,然后根据勾股定理可求半径R,然后代入球的体积公式可求.本题主要通过空间几何体的外接球问题,考查了考生的空间想象能力,推理论证能力,属于中档试题.17.【答案】解:(1)当n=1时,S1=12a1+a1−1=a1,得a1=2,当n≥2时,由S n=12na n+a n−1得,S n−1=12(n−1)a n−1+a n−1−1,作差得,a n=12na n+a n−1−12a n−1−a n−1+1,化简得,na n=(n+1)a n−1,即a na n−1=n+1n,由a n=a na n−1⋅a n−1a n−2…a2a1⋅a1=n+1n⋅nn−1…32⋅2=n+1,综上,a n=n+1(n∈N∗);(2)证明:根据(1)得,当n=1时,2a12=12,当n≥2时,2a n2=2(n+1)2<2n(n+1)=2(1n−1n+1),所以T n=222+232+242+⋯+2(n+1)2<12+2(12−13+13−14+⋯+1n−1n+1)=12+1−2n+1<32,故命题成立.【解析】(1)当n=1时,S1=12a1+a1−1=a1,得a1=2,当n≥2时,由S n=12na n+a n−1得,S n−1=12(n−1)a n−1+a n−1−1,作差化简求出a n的通项公式;(2)根据(1)得,当n=1时,2a12=12,当n≥2时,2a n2=2(n+1)2<2n(n+1)=2(1n−1n+1),根据裂项相消法和放缩法,证明结论成立.本题考查了数列递推式求数列的通项公式和前n项和公式,考查运算能力,中档题.18.【答案】解:(1)证明:∵四边形ABEF 为正方形,∴AB//FE ,∵AB ⊄平面EFDC ,FE ⊂平面EFDC ,∴AB//平面EFDC , ∵AB ⊂平面ABCD ,平面ABCD ∩平面EFDC =DC , ∴DC//AB ,∴DC//FE .(2)解:∵AF ⊥EF ,AF ⊥DF ,∴AF ⊥平面EFDC , ∴平面ABEF ⊥平面EFDC ,作DG ⊥EF ,垂足为G ,则DG ⊥平面ABEF ,∴以G 为原点,GF 为x 轴,在平面ABEF 中,过G 作EF 的垂线为y 轴,GD 为z 轴,建立空间直角坐标系,则题意得∠DFG =∠CEF =45°,设AB =4, 则D(0,0,1),E(−3,0,0),C(−2,0,1),B(−3,4,0),BD ⃗⃗⃗⃗⃗⃗ =(3,−4,1),ED ⃗⃗⃗⃗⃗ =(3,0,1),BC ⃗⃗⃗⃗⃗ =(1,−4,1),EC ⃗⃗⃗⃗⃗ =(1,0,1), 设平面DBE 的法向量m⃗⃗⃗ =(x,y,z), 则{m ⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ =3x −4y +z =0m ⃗⃗⃗ ⋅ED ⃗⃗⃗⃗⃗ =3x +z =0,取x =1,得m⃗⃗⃗ =(1,0,−3), 设平面BEC 的法向量n⃗ =(a,b,c), 则{n ⃗ ⋅BC ⃗⃗⃗⃗⃗ =a −4b +c =0n ⃗ ⋅EC ⃗⃗⃗⃗⃗ =a +c =0,取a =1,得n ⃗ =(1,0,−1), 设二面角D −BE −C 的平面角为θ, 则二面角D −BE −C 的平面角的余弦值为: cosθ=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=1√10⋅√2=2√55.【解析】(1)推导出AB//FE ,从而AB//平面EFDC ,进而DC//AB ,由此能证明DC//FE . (2)由AF ⊥EF ,AF ⊥DF ,得AF ⊥平面EFDC ,从而平面ABEF ⊥平面EFDC ,作DG ⊥EF ,垂足为G ,则DG ⊥平面ABEF ,以G 为原点,GF 为x 轴,在平面ABEF 中,过G 作EF 的垂线为y 轴,GD 为z 轴,建立空间直角坐标系,利用向量法能证明二面角D −BE −C 的平面角的余弦值.本题考查线线平行的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.19.【答案】解:(1)设M(x,y),P(x 0,y 0),Q(x 0,0), 则由4PQ ⃗⃗⃗⃗⃗ =3√2MQ ⃗⃗⃗⃗⃗⃗⃗ ,得 4(0,−y 0)=3√2(x 0−x,−y),∴x 0=x ,y 03√24y ,代入圆O :x 2+y 2=9,可得x 29+y 28=1.∴动点M 的轨迹E 的方程为x 29+y 28=1;(2)直线AG 与BH 的斜率之比为定值12. 证明如下:设直线l 为x =my +1,A(x 1,y 1),B(x 2,y 2).联立{x =my +1x 29+y 28=1,得(8m 2+9)y 2+16my −64=0.则y 1+y 2=−16m 8m 2+9,y 1y 2=−648m 2+9. ∴my 1y 2=4(y 1+y 2), 则k AGk BH=y 1x 1+3⋅x 2−3y 2=y 1(my 2−2)(my 1+4)y 2=my 1y 2−2y 1my 1y 2+4y 2=4(y 1+y 2)−2y 14(y 1+y 2)+4y 2=2y 1+4y 24y 1+8y 2=12.【解析】(1)设M(x,y),P(x 0,y 0),Q(x 0,0),则由4PQ ⃗⃗⃗⃗⃗ =3√2MQ⃗⃗⃗⃗⃗⃗⃗ ,得x 0=x ,y 03√24y ,代入圆O :x 2+y 2=9,可得动点M 的轨迹E 的方程;(2)设直线l 为x =my +1,A(x 1,y 1),B(x 2,y 2),联立直线方程与椭圆方程,利用根与系数的关系即可求得直线AG 与BH 的斜率之比为定值12.本题考查轨迹方程的求法,考查直线与椭圆的位置关系,考查计算能力,属于中档题.20.【答案】解:(1)X 的所有可能取值为0,1,2,3,则P(X =0)=0.3(1−p)2=0.3−0.6p +0.3p 2,P(X =1)=0.7(1−p)2+0.3×2p(1−p)=0.1p 2−0.8p +0.7, P(X =2)=2×0.7p(1−p)+0.3p 2=−1.1p 2+1.4p , P(X =3)=0.7p 2, 所以X 的分布列为所以E(X)=1×0.1p 2−0.8p +0.7+2×−1.1p 2+1.4p +3×0.7p 2=2p +0.7. (2)因为0.6≤p ≤0.8,由(1)可知,当p =0.8时,E(X)取得最大值, ①一棵B 种树苗最终成活的概率为0.8+(1−0.8)×0.75×0.8=0.92, ②记Y 为n 棵树苗的成活棵数,则Y ~B(n,0.92),E (Y)=0.92n , ∴(0.92×400−0.08×80)n ≥100000, 解得n ≥100000361.6≈276.55,∴n ≥277,∴该农户至少要种植277棵树苗,才可获利不低于10万元.【解析】(1)X 的所有可能取值为0,1,2,3,然后用p 分别表示出每个X 的取值所对应的概率即可得分布列和数学期望;(2)先结合p 的取值范围和(1)中的结论确定p 的取值,然后就能得到一颗B 种树苗成活的概率;记Y 为n 棵树苗的成活棵数,则Y ~B(n,0.92),再结合二项分布的性质,列出关于n 的不等式,解之并取整即可.本题考查了随机变量的分布列、数学期望等基础知识点,考查了学生数学建模的能力,即把实际问题转化为数学问题,再运算求解的能力,对于考生的综合分析能力提出较高要求,属于中档题.21.【答案】解:(1)∵f(x)=(a −1)x +xlnx ,∴f′(x)=a +lnx ,∵函数f(x)=(a −1)x +xlnx 的图象在点A(e 2,f(e 2))处的切线斜率为4, ∴f′(e 2)=a +lne 2=4,∴a =2.(2)由(1)知f(x)=x +xlnx ,∵m(x −1)<f(x)+1对任意x >1恒成立,∴m <f(x)+1x−1对任意x >1恒成立, 令g(x)=f(x)+1x−1,则g′(x)=(lnx+2)(x−1)−(x+xlnx+1)(x−1)2=x−lnx−3(x−1)2.令μ(x)=x −lnx −3,则μ′(x)=1−1x ,∵x >1,∴μ′(x)>0,∴μ(x)=x −lnx −3在(1,+∞)为增函数. ∵μ(4)=1−ln4<0,μ(5)=2−ln5>0, ∴∃x 0∈(4,5),使得μ(x 0)=x 0−lnx 0−3=0,∴x ∈(1,x 0)时,g′(x)<0,g(x)单调递减,x ∈(x 0,+∞)时,g′(x)>0,g(x)单调递增, ∴g(x)min =g(x 0)=x 0+x 0lnx 0+1x 0−1=x 0+x 0(x 0−3)+1x 0−1=x 0−1,故有m <x 0−1对x >1都成立,∵x 0∈(4,5),x 0−1∈(3,4),∴m 的最大值为3.【解析】(1)f(x)=(a −1)x +xlnx ⇒f′(x)=a +lnx ,依题意,f′(e 2)=a +lne 2=4,可求得a 的值;(2)由(1)知f(x)=x +xlnx ,∀x >1,m(x −1)<f(x)+1⇔m <f(x)+1x−1对任意x >1恒成立,构造函数g(x)=f(x)+1x−1,求g′(x)=x−lnx−3(x−1)2,再令μ(x)=x −lnx −3,分析得到∃x 0∈(4,5),使得μ(x 0)=x 0−lnx 0−3=0,g(x)min =g(x 0)=x 0−1∈(3,4),从而可求得m 的最大值.本题第(1)问考查切线问题,第(2)问考查恒成立问题,通过分离参数后,构造函数,利用导数解决问题,考查转化思想与运算能力,对学生要求较高,属于难题.22.【答案】解:(1)已知曲线C 的极坐标方程为ρ=√2(θ∈[−π2,π2]),转换为直角坐标方程为x 2+y 2=2(x ≥0),A 在曲线C 上,且曲线C 在点A 处的切线与直线:x +2y +1=0垂直, 所以{x 2+y 2=2y =−12xx ≥0,解得{x =2√105y =−√105,即A(2√105,−√105). (2)直线l 的直角坐标方程为y =−4+k(x +2)与半圆x 2+y 2=2(x ≥0)有且只有一个交点, 故√1+k 2=√2,整理得k 2−8k +7=0,解得k =1或7,由于B(0,√2),C(0,−√2)P(−2,−4), 所以k PB =4+√22,k PC =4−√22, 所以直线l 的斜率的范围为(4−√22,4−√22]∪{1}.【解析】(1)直接利用参数方程极坐标方程和直角坐标方程之间的转换的应用求出结果. (2)利用直线和曲线的位置关系的应用建立等量关系,进一步求出范围的值. 本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,点到直线的距离公式的应用,三角函数关系式的恒等变换,正弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.23.【答案】解:(1)函数f(x)={−3x −1,x <−1x +3,−1≤x ≤13x +1,x >1,则{x <−1−3x −1<5或{x >13x +1<5或{−1≤x ≤1x +3<5, 解得−2<x <−1或1<x <43或−1≤x ≤1, 则原不等式的解集为(−2,43);(2)关于x 的不等式f(x)+2<|2t −1|在实数范围内解集为空集, 等价为(f(x)+2)min ≥|2t −1|, 由(1)可得f(x)的最小值为f(−1)=2,则2+f(x)的最小值为4,则|2t −1|≤4,解得−32≤t ≤52, 则t 的取值范围是[−32,52].【解析】(1)将f(x)写成分段函数的形式,f(x)<5等价为一次不等式组,解不等式,求并集,可得所求解集;(2)由题意可得(f(x)+2)min ≥|2t −1|,由f(x)的解析式可得f(−1)为最小值,再由绝对值不等式的解法可得所求范围.本题考查绝对值不等式的解法和不等式恒成立问题解法,注意运用转化思想和分类讨论思想,考查化简运算能力和推理能力,属于中档题.。
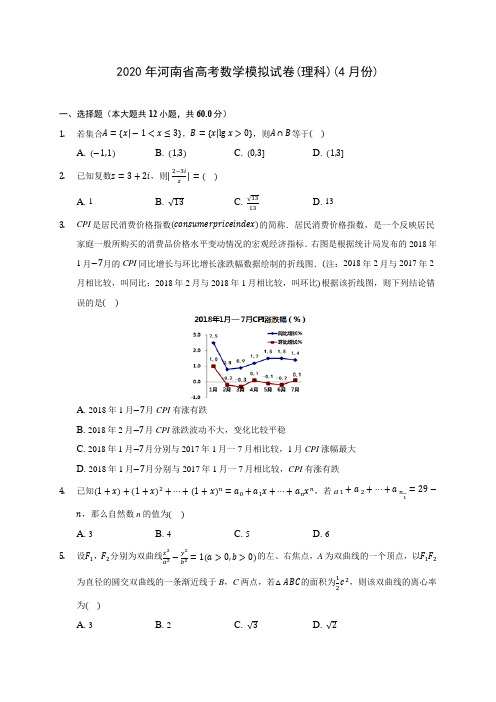
2020年河南省高考数学模拟试卷(理科)(4月份)一、选择题(本大题共12小题,共60.0分)1.若集合A={x|−1<x≤3},B={x|lg x>0},则A∩B等于()A. (−1,1)B. (1,3)C. (0,3]D. (1,3]2.已知复数z=3+2i,则|2−3iz|=()A. 1B. √13C. √1313D. 133.CPI是居民消费价格指数(consumerpriceindex)的简称.居民消费价格指数,是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.右图是根据统计局发布的2018年1月−7月的CPI同比增长与环比增长涨跌幅数据绘制的折线图.(注:2018年2月与2017年2月相比较,叫同比;2018年2月与2018年1月相比较,叫环比)根据该折线图,则下列结论错误的是()A. 2018年1月−7月CPI有涨有跌B. 2018年2月−7月CPI涨跌波动不大,变化比较平稳C. 2018年1月−7月分别与2017年1月一7月相比较,1月CPI涨幅最大D. 2018年1月−7月分别与2017年1月一7月相比较,CPI有涨有跌4.已知(1+x)+(1+x)2+⋯+(1+x)n=a0+a1x+⋯+a n x n,若a 1+a 2+⋯+a n−1=29−n,那么自然数n的值为()A. 3B. 4C. 5D. 65.设F1,F2分别为双曲线x2a2−y2b2=1(a>0,b>0)的左、右焦点,A为双曲线的一个顶点,以F1F2为直径的圆交双曲线的一条渐近线于B,C两点,若△ABC的面积为12c2,则该双曲线的离心率为()A. 3B. 2C. √3D. √26. 已知在数列{a n }中,a 1=2,a n+1=nn+1a n ,则a 2020的值为( )A. 12020B. 12019C. 11010D. 110097. 已知一个几何体的三视图如图所示,它的表面积是( )A. 2+2√2B. 2+√2C. 3+√2D. 3+2√28. 已知函数f(x)=2sin (ωx +π4)在区间(0,π8)上单调递增,则ω的最大值为( )A. 12B. 1C. 2D. 49. 已知菱形ABCD 的对角线AC =2,对角线AC ,BD 相交于点E ,则AE ⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =( ) A. 1 B. √2 C. 2 D. 2√210. 如图所示的平面图形是由正方形和其内切圆及另外4个四分之一圆弧构成,若在正方形内随机取一点,用A 表示事件“点落在正方形的内切圆内”,B 表示事件“点落在阴影内”,则P(B|A)=( )A. π4 B. 1−π4 C. π−24D.π−2π11. 对于定义在R 上的奇函数f(x),满足f(−x)+f(3+x)=0,若f(−1)=1,则f(1)+f(2)+f(3)+⋯+f(2015)=( )A. −1B. 0C. 1D. 212. 已知正四棱锥的底面边长为2,侧棱长为√5,则该正四棱锥的体积为( )A. 43B. 23C. 4√3D. 4√33二、填空题(本大题共4小题,共20.0分)13. 函数f(x)=(x +1)lnx −4(x −1)在(1,f(1))处的切线方程为______ .14.等差数列{a n}中,a4=10且a3,a6,a10成等比数列,数列{a n}前20项的和S20=______.15.有四张卡片,分别写有数字11,22,33,44,甲、乙、丙、丁四人各取走一张,甲看了丙的卡片后说:“我卡片上的数字大于丙卡片上的数字,但不是最大的”,乙看了丙的卡片后说:“我卡片上的数字比丙卡片上的数字大22”,丁说:“我卡片上的数字不是最小的”,则甲卡片上的数字是_______.16.设椭圆C:x2a2+y2b2=1(a>b>0)的左右焦点为F1,F2,过F2作x轴的垂线与C交于A,B两点,F1B与y轴交于点D,若AD⊥F1B,则椭圆C的离心率等于________.三、解答题(本大题共7小题,共82.0分)17.如图,在三棱柱ABC−A1B1C1中,AC⊥平面BCC1B1,AC=1,BC=√3,BB1=2,∠B1BC=30°.(1)证明:B1C⊥平面ABC.(2)求二面角B1−A1C−C1的余弦值.18.在△ABC中,AB=1,∠BAC=120°,△ABC的面积为√34.(1)求BC的长;(2)若D是边BC上一点,且2DC=DA,求sin∠ADC.19. 已知点A(4,0),B(1,0),若动点T 满足AB⃗⃗⃗⃗⃗ ⋅AT ⃗⃗⃗⃗⃗ =6|BT ⃗⃗⃗⃗⃗ |. (1)求动点T 的轨迹Γ;(2)在x 轴正半轴上是否存在一点P ,过该点的直线l(不与x 轴重合)与曲线Γ交于两点M ,N ,使得1|PM|2+1|PN|2为定值,若有求出P 点坐标和定值,若不存在,说明理由.20. 已知函数f(x)=12x 2+mcosx ,m >0,f′(x)是f(x)的导函数,g(x)=f′(x)+1.(1)当m =2时,判断函数g(x)在(0,π)上是否存在零点,并说明理由; (2)若f(x)在(0,π)上存在最小值,求m 的取值范围.21. 如图是一旅游景区供游客行走的路线图,假设从进口A 开始到出口B ,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共4名游客结伴到旅游景区游玩,他们从进口A 的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口B 中,设点C是其中的一个交叉路口点.(1)求甲经过点C的概率;(2)设这4名游客中恰有X名游客都是经过点C,求随机变量X的概率分布列和数学期望.22.在直角坐标系xOy中,曲线C的参数方程是{x=14+12cosα,y=√34+12sinα(α是参数),以原点为极点,x轴的正半轴为极轴建立极坐标系.(1)求曲线C的极坐标方程;(2)在曲线C上取一点M,直线OM绕原点O逆时针旋转π3,交曲线C于点N,求|OM|·|ON|的最大值.23.设f(x)=50xx2+1(1)求f(x)在[0,+∞)的最大值(2)求f(x)在[2,+∞)上的最大值-------- 答案与解析 --------1.答案:D解析:考查描述法、区间的定义,对数函数的单调性,以及交集的运算.可求出集合B,然后进行交集的运算即可.解:B={x|x>1};∴A∩B=(1,3].故选:D.2.答案:A解析:把复数z=3+2i代入|2−3iz|,再由商的模等于模的商求解.本题考查复数模的求法,是基础的计算题.解:∵z=3+2i,∴|2−3iz |=|2−3i3+2i|=|2−3i||3+2i|=1.故选:A.3.答案:D解析:解:对于A:2018年1月−7月CPI有4,7月涨有2,3,5,6,跌,故A正确;对于B:2018年2月−7月CPI涨跌波动不大,变化比较平稳,涨跌幅均在±0.1,0.2,故B正确;对于C:2018年1月−7月分别与2017年1月一7月相比较,1月涨幅2.5,其值最大,故C正确;对于D:2018年1月−7月分别与2017年1月一7月相比较,CPI全部上涨,故D错误.故选:D.根据同比和环比的概念逐项分析可得.本题考查统计图的应用,属中档题.4.答案:B解析:本题考查在解决二项展开式的系数和问题时常用的方法是赋值法、考查解决展开式的特定项问题是常用的方法是利用二项展开式的通项公式.令等式中的x=1求出展开式的各项系数和,令x=0求出展开式的常数项;利用二项展开式的通项公式求出a n;列出方程求出n.解:令x=1得2+22+23+⋯+2n=a0+a1+a2+⋯+a n即2−2n+11−2═a0+a1+a2 +⋯+a n即2n+1−2═a0+a1+a2+⋯+a n令x=0得a0=1+1+1+⋯+1=n∵a n=1∴a1+a2+⋯+a n−1=2n+1−n−3∴2n+1−n−3=29−n解得n=4故选B.5.答案:D解析:本题考查双曲线的离心率,考查三角形面积的计算,同时考查点到直线的距离公式的运用,属于中档题.利用△ABC的面积为12c2,求出双曲线的渐近线的方程,运用点到直线的距离公式,解方程可得c=√2a,即可求出该双曲线的离心率.解:设双曲线的一条渐近线方程为y=bax,即为bx−ay=0,则A(a,0)到渐近线的距离为d=√a2+b2=abc,由题意,△ABC的面积为12c2,则12⋅2c⋅abc=12c2,即为4a2b2=c4,即有4a2(c2−a2)=c4,即有c2=2a2,即c=√2a,则e=ca=√2.故选:D.6.答案:C解析:本题考查的知识要点:数列的通项公式,数列的递推关系式,主要考查学生的运算能力和转换能力及思维能力,属于基础题.直接利用递推关系式的应用求出数列的通项公式,进一步求出结果.解:数列{a n}中,a1=2,a n+1=nn+1a n,所以(n+1)a n+1−na n=0,所以na n=1×a1=2,所以a n=2n,故a2020=22020=11010.故选C.7.答案:C解析:三视图复原的几何体是直三棱柱,高为1,底面是等腰直角三角形,根据三视图数据求出表面积.本题考查由三视图求表面积,考查计算能力,是基础题.解:由三视图可知此几何体为一底面为等腰直角三角形的直三棱柱.底面直角边为1,高为1的直三棱柱,所以:S表=S侧+2S底=(1+1+√2)×1+2×12×1×1=3+√2.故选C.8.答案:C解析:本题考查函数y =Asin(ωx +φ)的图象与性质,求出ωx +π4的范围,然后利用正弦函数的单调性求解即可.解: 当x ∈(0,π8)时,ωx +π4∈(π4,π8ω+π4), 则由题意可得π8ω+π4⩽π2,解得ω⩽2, 即ω的最大值为2. 故选C .9.答案:C解析:本题考查了向量的数量积,直接根据菱形的性质,并结合数量积运算,即可求解. 解:由向量数量积的几何意义可知AE ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AE ⃗⃗⃗⃗⃗ ||AC ⃗⃗⃗⃗⃗ |=12|AC ⃗⃗⃗⃗⃗ |2=2, 故选C .10.答案:D解析:本题主要考查了条件概率,属于基础题.假设正方形的边长为2,则其面积为4,分别求出正方形和内切圆内阴影部分的面积,利用条件概率求解出P(B|A)即可.解:假设正方形的边长为2,则其面积为4, 正方形内切圆的面积为12×π=π, 所以P(A)=π4.内切圆内阴影部分的面积为[14×π×12−(1×1−14π×12)]×2=π−2, 所以P(AB)=π−24,P(B|A)=P(AB)P(A)=π−2π.故选D.11.答案:B解析:解:定义在R上的奇函数f(x),满足f(−x)+f(3+x)=0,可得f(x)=f(3+x),所以函数的周期为3.定义在R上的奇函数f(x),可知f(0)=0,又f(−1)=1,∴f(2)=f(−1)=1,f(1)=−f(−1)=−1.f(1)+f(2)+f(3)=−1+1+0=0;∴f(1)+f(2)+f(3)+⋯+f(2015)=671(f(1)+f(2)+f(3))+f(1)+f(2)=0−1+1=0.故选:B.利用函数的奇偶性,以及函数的关系式,求出函数的周期,然后求解函数值即可.本题考查抽象函数的应用,函数的周期以及函数的奇偶性的应用,考查计算能力.12.答案:D解析:本题考查正四棱锥的体积的求法,考查数据处理能力、运算求解能力以及应用意识,考查数形结合思想等,是基础题.先求出正四棱锥的高,再利用正四棱锥的体积即可求解.解:如图,正四棱锥P−ABCD中,AB=2,PA= √5,设正四棱锥的高为PO,连结AO,AC=√ 2,则AO= 12在直角三角形POA中,PO= √PA2−AO2 = √5−2 =√3.所以V P−ABCD=13⋅S ABCD⋅PO=13×4×√3= 4√33.故选D.13.答案:2x+y−2=0解析:解:函数f(x)=(x+1)lnx−4(x−1)的导数为f′(x)=lnx+x+1x−4,可得在(1,f(1))处的切线斜率为k=f′(1)=ln1+2−4=−2,切点为(1,0),则在(1,f(1))处的切线方程为y−0=−2(x−1),即为2x+y−2=0.故答案为:2x+y−2=0.求出函数的导数,可得切线的斜率和切点,运用点斜式方程可得切线方程.本题考查函数导数的运用:求切线方程,考查导数的几何意义,正确求得导数和运用导数的几何意义是解题的关键,属于基础题.14.答案:200或330解析:本题考查等差数列的性质以及等差数列求和,属于基础题.设等差数列{a n}的公差为d,由已知列式求得公差,进一步分类求得首项,再由等差数列的前n项和公式求解.解:设等差数列{a n}的公差为d,由a4=10且a3,a6,a10成等比数列,得(10+2d)2=(10−d)(10+6d),解得d=0或d=1.当d=0时,a1=10,则S20=200;当d=1时,a1=a4−3d=10−3=7,则S20=20×7+20×192×1=330.故答案为200或330.15.答案:22解析:本题考查简单的合情推理,属于基础题.根据题意假设,排除不可能的,即可得解.解:由题意可知乙、丙卡片上的数字只可能分别是44和22或33和11,又因为甲卡片上的数字大于丙卡片上的数字,但不是最大的,故甲卡片上的数字只可能是33或22,若甲卡片上的数字是33,则丁卡片上的数字只能是11,这与丁卡片上的数字不是最小的矛盾,故甲卡片上的数字只能是22,故答案为22.16.答案:√33解析:本题主要考查椭圆离心率的求解,属基础题.利用中垂线的性质判定AF1=AB=2AF2,,进而利用椭圆的定义求得离心率.解:因为OD平行于F2B,所以D为F1B中点,又AD⊥F1B,所以AF1=AB=2AF2,设AF2=m,则AF1=2m,F1F2=√3m,因此e=ca =2c2a=F1F2AF1+AF2=√3m2m+m=√33.故答案为√33.17.答案:(1)证明:因为BC =√3,BB 1=2,∠B 1BC =30°,所以B 1C =√3+4−2×√3×2cos30°=1,所以BC 2+B 1C 2=BB 12,则B 1C ⊥BC .因为AC ⊥平面BCC 1B 1,且B 1C ⊂平面BCC 1B 1, 所以AC ⊥B 1C ,因为BC ∩AC =C ,所以B 1C ⊥平面ABC .(2)解:由(1)可知CA ,CB ,CB 1两两垂直,故以C 为原点,CB 1⃗⃗⃗⃗⃗⃗⃗ ,CB ⃗⃗⃗⃗⃗ ,CA ⃗⃗⃗⃗⃗ 的方向分别为x ,y ,z 轴的正方向建立空间坐标系C −xyz .则A 1(1,−√3,1),B 1(1,0,0),C(0,0,0),C 1(1,−√3,0), 故CA 1⃗⃗⃗⃗⃗⃗⃗ =(1,−√3,1),CB 1⃗⃗⃗⃗⃗⃗⃗ =(1,0,0),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,0,−1). 设平面A 1B 1C 的法向量m⃗⃗⃗ =(x 1,y 1,z 1), 则{m ⃗⃗⃗ ⋅CA 1⃗⃗⃗⃗⃗⃗⃗ =x 1−√3y 1+z 1=0,m ⃗⃗⃗ ⋅CB 1⃗⃗⃗⃗⃗⃗⃗ =x 1=0,令y 1=1,则m ⃗⃗⃗ =(0,1,√3).设平面A 1C 1C 的法向量n⃗ =(x 2,y 2,z 2), 则{n ⃗ ⋅A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =−z 2=0,n ⃗ ⋅CA 1⃗⃗⃗⃗⃗⃗⃗ =x 2−√3y 2+z 2=0, 令y 2=1,则n ⃗ =(√3,1,0) 则cos〈m ⃗⃗⃗ ,n ⃗ 〉=m ⃗⃗⃗ ⋅n ⃗⃗|m ⃗⃗⃗ |⋅|n ⃗⃗ |=12×2=14. 设二面角B 1−A 1C −C 1为θ, 由图可知θ为锐角,则cosθ=14.解析:(1)通过勾股定理计算证明B 1C ⊥BC.推出AC ⊥B 1C ,然后证明B 1C ⊥平面ABC .(2)以C 为原点,CB 1⃗⃗⃗⃗⃗⃗⃗ ,CB ⃗⃗⃗⃗⃗ ,CA ⃗⃗⃗⃗⃗ 的方向分别为x ,y ,z 轴的正方向建立空间坐标系C −xyz.求出平面A 1B 1C 的法向量,平面A 1C 1C 的法向量,设二面角B 1−A 1C −C 1为θ,利用空间向量的数量积求解即可. 本题考查直线与平面垂直的判断定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力,是中档题.18.答案:解:(1)∵△ABC 的面积为√34. ∴12AB ⋅AC ⋅sin∠BAC =√34,即12AC ⋅sin120°=√34,解得AC =1.由余弦定理可得BC =√AB 2+AC 2−2AB ⋅AC ⋅cos∠BAC =√1+1+2×1×1×12=√3;(2)依题意,△ABC 为等腰三角形,∠BAC =120°,∴∠ACB =30°, 在△ACD 中,由正弦定理可得ADsin∠ACD =CDsin∠CAD , ∵2DC =DA ,∴sin∠CAD =14. ∴cos∠CAD =√154, ∴sin∠ADC =sin[π−(∠ACD +∠CAD)]=sin(∠ACD +∠CAD)=12×√154+√32×14=√15+√38.解析:(1)由三角形面积公式结合已知条件即可求出AC ,再由余弦定理求解可得BC 的长; (2)由正弦定理可得sin∠CAD ,再由三角函数的诱导公式化简求值即可. 本题考查了三角形面积公式,考查了正弦定理以及余弦定理的应用,是中档题.19.答案:解:(1)设动点T(x,y),∵A(4,0),B(1,0),∴AT ⃗⃗⃗⃗⃗ =(x −4,y),AB ⃗⃗⃗⃗⃗ =(−3,0),BT ⃗⃗⃗⃗⃗ =(x −1,y), 代入AB ⃗⃗⃗⃗⃗ ⋅AT ⃗⃗⃗⃗⃗ =6|BT ⃗⃗⃗⃗⃗ |,整理得:x 24+y 23=1; (2)假设存在定点P(m,0)(m >0),使得1|PM|2+1|PN|2为定值. 设M(x 1,y 1),N(x 2,y 2),直线l :x =ty +m ,则|PM|2=(x 1−m)2+y 12=(t 2+1)y 12,|PN|2=(t 2+1)y 22. ∴1|PM|2+1|PN|2=1(t 2+1)(1y 12+1y 22)=1(t 2+1)y 12+y 22y 12y 22=1(t 2+1)(y 1+y 2)2−2y 1y 2y 12y 22 (1)联立x =ty +m 与x 24+y 23=1,整理得:(3t 2+4)y 2+6tmy +3m 2−12=0.∴y 1+y 2=−6tm3t 2+4,y 1y 2=3m 2−123t 2+4,代入(1)式得:1|PM|2+1|PN|2=1(t 2+1)⋅(−6tm 3t 2+4)2−2⋅3m 2−123t 2+4(3m 2−123t 2+4)2=t 2(18m 2+72)+96−24m 2t 2(3m 2−12)2+(3m 2−12)2.要使得上式为定值,须18m 2+72=96−24m 2,解得m =2√77, 此时1|PM|2+1|PN|2取到定值79. ∴当P 为(2√77,0)时,1|PM|2+1|PN|2取到定值79.解析:(1)设出动点坐标,得到向量AT ⃗⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗⃗ ,BT ⃗⃗⃗⃗⃗ 的坐标,代入AB ⃗⃗⃗⃗⃗ ⋅AT ⃗⃗⃗⃗⃗ =6|BT ⃗⃗⃗⃗⃗ |整理得到动点T 的轨迹Γ;(2)假设存在定点P(m,0)(m >0),使得1|PM|2+1|PN|2为定值,设出M ,N 的坐标及直线l 的方程x =ty +m ,把1|PM|2+1|PN|2用M ,N 的坐标及t 表示,再把直线和椭圆方程联立后利用根与系数关系得到M ,N 的纵坐标的关系,代入1|PM|2+1|PN|2整理得到关于m 的表达式,然后由分子的系数关系求得m 的值,则答案可求.本题考查轨迹方程,考查了向量在解题中的应用,体现了设而不求的解题思想方法,考查了学生的综合运算能力,是压轴题.20.答案: 解:(1)m =2时,g(x)=x −2sinx +1,g′(x)=1−2cosx ,令g′(x)=0,即cosx =12,x ∈(0,π),得x =π3, 当x 变化时,g′(x),g(x)变化如下:∴函数g(x)的单调递减区间为(0,π3),单调递增区间为(π3,π). ∴g(x)的极小值为g(π3)=π3+1−√3>0. ∴函数g(x)在(0,π)上不存在零点. (2)因为f(x)=12x 2+mcosx ,所以, 令,则.①当0<m ≤1时,1−mcosx ≥0,即ℎ′(x)⩾0,在(0,π)单调递增,∴x ∈(0,π)时,ℎ(x)>ℎ(0)=0,∴f(x)在(0,π)单调递增,∴f(x)在(0,π)不存在最小值, ②当m >1时,1m ∈(0,1), 所以,即cosx =1m 在(0,π)内有唯一解x 0, 当x ∈(0,x 0)时,,当x ∈(x 0,π)时,,所以ℎ(x)在(0,x 0)上单调递减,在(x 0,π)上单调递增. 所以ℎ(x 0)<ℎ(0)=0,又因为ℎ(π)=π>0,所以ℎ(x)=x −msinx 在(x 0,π)⊆(0,π)内有唯一零点x 1, 当x ∈(0,x 1)时,ℎ(x)<0即,当x ∈(x 1,π)时,ℎ(x)>0即,所以f(x)在(0,x 1)上单调递减,在(x 1,π)上单调递增.所以函数f(x)在x =x 1处取得最小值, 即m >1时,函数f(x)在(0,π)上存在最小值.解析:本题主要考查利用导数研究闭区间上函数的最值,零点的问题,属于较难题. (1)m =2时,g(x)=x −2sinx +1令g ′(x)=0,即cosx =12,x ∈(0,π),得x =π3,利用函数的单调区间,极值即可得到结论; (2)因为f(x)=12x 2+mcosx ,所以f ′(x)=x −msinx ,根据函数的单调区间分类讨论即可求解.21.答案:解:(1)设甲从进口A 开始到出口B 经过C 为事件M ,甲选中间的路的概率为13,在前面从岔路到达点C 的概率为12,所以选从中间一条路走到C 的概率为P 1=12×13=16, 同理选择从最右边的路走到点C 的概率为P 2=12×13=16, 因为选择从中间或最右边到达点C 的两个事件是彼此互斥的, 所以P (M )=P 1+P 2=13;(2)随机变量的可能取值为X =0,1,2,3,4,P (X =0)=C 40(13)0(23)4=1681, P (X =1)=C 41(13)1(23)3=3281,P (X =2)=C 42(13)2(23)2=2481=827,P (X =3)=C 43(13)3(23)1=881, P (X =4)=C 44(13)4(23)0=181,所以X 的概率分布列为数学期望为E (X )=0×1681+1×3281+2×2481+3×881+4×181=43.解析:本题考查概率的求解及离散型随机变量的分布列与期望的计算,属于一般题. (1)利用古典概型及互斥事件概率公式求概率即可; (2)根据离散型随机变量的性质求解即可得结果.22.答案:解:(1)由曲线C 的参数方程是{x =14+12cosα,y =√34+12sinα(α是参数), 消去α得曲线C 的普通方程为x 2+y 2−12x −√32y =0,所以C 的极坐标方程为ρ=√32sinθ+12cosθ,即ρ=sin(θ+π6).(2)不妨设M(ρ1,θ),N(ρ2,θ+π3),θ∈[0,2π],则|OM|⋅|ON|=sin(θ+π6)sin(θ+π6+π3)=cosθ(√32sinθ+12cosθ)=√34sin2θ+14cos2θ+14=12sin(2θ+π6)+14,当,即当θ=π6时,取得最大值,最大值为34.解析:本题考查参数方程极坐标方程和直角坐标方程之间的转换,三角函数关系式的恒等变换,正弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间的进行转换.(2)利用极径的应用和三角函数关系式的恒等变换和正弦型函数性质的应用求出结果.23.答案:解:(1)当x>0时,有x+1x≥2,∴f(x)=50xx2+1=50x+1x≤25,当且仅当x=1x,即x=1时等号成立,∴f(x)在[0,+∞)上的最大值是25.(2)∵函数y=x+1x在[2,+∞)上是增函数且恒为正,∴f(x)=50x2+1=50x+1x在[2,+∞)上是减函数,且f(2)=20,故f(x)在[2,+∞)上的最大值为20.解析:本题是一道求函数最值的题目,需结合基本不等式以及函数的增减性进行解答.(1)当x>0时,由基本不等式可得x+1x ≥2,则f(x)=50xx2+1=50x+1x≤25,据此可得f(x)在[0,+∞)上的最大值;(2)函数f(x)=50x2+1=50x+1x在[2,+∞)上是减函数,据此可得f(x)在[2,+∞)上的最大值.。

高考数学模拟试卷(理科)(4月份)一、选择题(本大题共12小题,共60.0分)1. 集合U ={0,1,2,3,4,5},A ={1,2},B ={x ∈N |x 2-3x ≤0},则∁U (A ∪B )=( )A. {0,1,2,3}B. {0,4,5}C. {1,2,4}D. {4,5} 2. i 为虚数单位,若复数z +=i ,则=( )A. 1-iB. -1+iC. -1-iD. 1+i3. 我国古代学者庄子在《庄子·天下篇》中提到:“一尺之棰,日取其半,万世不竭”,指一尺长的木棒,今天取其一半,明天取剩下的一半,后天再取剩下的一半,永远也取不尽.现有尺长的线段,每天取走它的,天后剩下的线段长度不超过尺,则的最小值为( )A.B. C.D. 4. 已知椭圆的一个焦点为,则的值为( )A.B.C. D.5. 已知向量,的夹角为60°,且||=2,|2-|=,则||可能为( )A. 3B.C. 2D. 46. 设公差为-3的等差数列{a n }的前n 项和为S n ,若S 2019=2019,则a 3+a 6+a 9+…+a 2019=()A.B. C. 673 D. 1346 7. 若函数y =f (x )具有下列两个性质:①在区间[-]上单调递增,②其图象关于直线x =对称,则f (x )的解析式可以是( )A. f (x )=sin (-2x )B. f (x )=cos (2x +)C. f (x )=sin (2x +)D. f (x )=cos (-2x )8. 某几何体的三视图如图所示,则该几何体的体积为( )A.B.C. π+1D.9.已知命题p:f(x)=sin x+≥4(0<x<),命题q:若x2-x+m>0对x∈R恒成立,则m>0.则下列选项中真命题为()B. C. D.A.10.已知函数f(x)是定义在R上的偶函数,且当x<0时,f(x)=,若实数a满足f(3-|a+1|)>f(-),则a的取值范围是()A. (-,-)B. (-)∪(-,+∞)C. (-,-)D. (-)∪(-,+∞)11.已知区域内的点满足不等式组,在区域内任取一点,则函数有零点的概率为( )A. B. C. D.12.在正方体ABCD-A1B1CD1中,点M在线段AD1上,若直线A1M与平面A1B1C1D1内的动直线所成角的最小值,则AM:MD1=()A.B.C.D.二、填空题(本大题共4小题,共20.0分)13.(x-)10的展开式中所有项的系数之和为______.14.若执行如图所示的程序框图,输入,则输出的值为_______.15.已知l为曲线y=在(1,a)处的切线,当直线l与坐标轴围成的三角形面积为,实数a的值为______16.在平面直角坐标系xOy中,离心率为的双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线上一点,且PF1⊥x轴,过点P作双曲线C的两条渐近线的平行线,分别交两条渐近线于A,B两点,若四边形PAOB的面积为2,则△PF1F2的面积为______.三、解答题(本大题共7小题,共82.0分)17.在△ABC中,内角A,B,C的对边分别为a,b,c,若向量=(2cos2,cos),=(,cos),•=.(1)求tan A tan B的值;(2)求的最小值.18.某市政府为减轻汽车尾气对大气的污染,保卫蓝天,鼓励广大市民使用电动交通工具出行,决定为电动车(含电动自行车和电动汽车)免费提供电池检测服务现从全市已挂牌照的电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图:(1)采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,再从这9辆中随机抽取2辆,求至少有一辆为电动汽车的概率;(2)为进一步提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:电动自行车每辆补助300元;电动汽车每辆补助500元;对电池需要更换的电动车每辆额外补助400元.用样本频率替代概率估计总体.①现从全市已挂牌照的电动车中随机抽取3辆,记这3辆电动车电池性能为良好的辆数为X,试求X的分布列;②估算平均每辆电动车享受的政府补贴金额.19.如图,斜三棱柱ABC-AB1C1的底面△ABC为正三角形,AB=AA1,∠A1AB=∠A1AC,AA1与底面ABC所成的角为30°.(1)证明:BB1⊥BC;(2)求二面角A-BB1-C1的余弦值.20.已知抛物线C1:y2=2px(p>0),圆C2:x2+y2=r2(r>0),直线l:y=kx+m与抛物线C1相切于点A,且与圆C2相切于点B.(1)当k=2时,请分别写出p,r关于m的表达式;(2)设F为抛物线C1的焦点,△FAB,△FOB的面积分别为S1,S2,若S1=6S2,求实数k的值.21.已知函数f(x)=x2-(a+1)x+a ln x.(1)讨论函数f(x)的单调性;(2)对任意的a∈[3,5],x1,x2∈[1,3](x1≠x2),恒有|f(x1)-f(x2)|<λ|-|,求实数λ的取值范围.22.在平面直角坐标系xOy中,已知曲线C1的参数方程为(t为参数),曲线C2的参数方程为,(θ为参数)(1)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,当α=时,求曲线C1,C2的极坐标方程;(2)若曲线C1与曲线C2交于A,B两点(不重合),求|OA|+|OB|的取值范围.23.已知函数f(x)=|2x-a|+a.(1)当a=2时,求不等式f(x)≤6的解集;(2)设函数g(x)=|2x-1|,当x∈R时,f(x)+g(x)≥3,求a的取值范围.答案和解析1.【答案】D【解析】解:B={x∈N|0≤x≤3}={0,1,2,3},则A∪B={0,1,2,3},则∁U(A∪B)={4,5},故选:D.求出集合B的等价条件,结合补集并集的定义进行计算即可.本题主要考查集合的基本运算,结合补集并集的定义是解决本题的关键.2.【答案】B【解析】解:由z+=i,得z===-1-2i+i=-1-i,∴.故选:B.把已知等式变形,再由复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.【答案】C【解析】【分析】读懂题意,列出不等式求解即可.本题难度较小,主要考查等比数列的概念及通项公式的应用.【解答】解:由题意可知,m天后剩下的线段的长度为,则,解得m≥10,所以m的最小值为10.故选C.4.【答案】C【解析】解:方程变形为,∵椭圆的焦点在y轴上,∴a2=2m,b2=6,又c=2且a2-b2=c2,∴2m-6=22,∴m=5.故选:C.依题意,将椭圆的方程标准化,利用其焦点在y轴上,利用椭圆的性质即可求得m的值.本题考查椭圆的简单性质,将椭圆的方程标准化是打开思维的关键,考查分析、运算能力,属于中档题.5.【答案】A【解析】解:已知|2-|=,则有:即:向量,的夹角为60°,且||=2∴,即•=2cos60°||解得:即:或则||可能为3故选:A.运用向量的平方即为模的平方等到,的等式,在带入向量,的数量积和||=2,再由向量的夹角公式,计算只含的模的方程即可得到.本题主要考查向量夹角,向量的平方即为模的平方求解,根据向量数量积的应用是解决本题的关键是基础题.6.【答案】B【解析】【分析】本题考查等差数列的前n项和的求法,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.由S2019==2019,得a1+a2019=2,再由a3+a6+a9+…+a2019=(a1+a2019-6),能求出结果.【解答】解:公差为-3的等差数列{a n}的前n项和为S n,S2019=2019,∴S2019==2019,解得a1+a2019=2,∴a3+a6+a9+…+a2019=(a1+a2019-6)=-1346.故选B.7.【答案】D【解析】解:(1)对A,f()=sin()=,不符合条件②,故A错;(2)对B,f()=cos=-1符合条件②,由f(x)=cos(2x+)知,f(x)在[-]上递减,不符合条件①,故B错;(3)对C,f()=sin()=,不符合条件②,故C错;(4)对D,f()=cos(0)=1符合条件②,由知,f(x)在[-]上递增,符合条件①,故D对.故选:D.首先检验各选项是否符合条件②,排查一些选项后再看是否符合条件①即可.本题考查了正弦函数与余弦函数的单调性和对称性,属基础题.8.【答案】A【解析】解:由三视图还原原几何体如图,该几何体可看作两个几何体的组合体,左侧是四分之一圆锥,右侧是四棱锥,圆锥的底面半径为1,高为1,棱锥的底面是边长为1的正方形,一条侧棱垂直于底面,且长度为1.∴该几何体的体积为.故选:A.由三视图还原原几何体,该几何体可看作两个几何体的组合体,左侧是四分之一圆锥,右侧是四棱锥,圆锥的底面半径为1,高为1,棱锥的底面是边长为1的正方形,一条侧棱垂直于底面,且长度为1.再由锥体的体积公式求解.本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.9.【答案】D【解析】【分析】此题考查了命题的真假,难度不大.利用“对号”函数容易求得f(x)>5,可确定p为真命题;利用判别式小于0,可求得m,故命题q也是真命题.【解答】解:∵,∴0<sin x<1,∴f(x)=sin x+∈(5,+∞),∴命题p为真命题;∵x2-x+m>0对x∈R恒成立,∴=1-4m<0,∴,∴命题q为真命题,故选:D.10.【答案】B【解析】解;根据题意,当x<0时,f(x)=,其导数f′(x)=>0,则f(x)在区间(-∞,0)上为增函数,又由f(x)是定义在R上的偶函数,则f(x)在区间(0,+∞)上为减函数,f(3-|a+1|)>f(-)⇒f(3-|a+1|)>f()⇒3-|a+1|<⇒|a+1|>,解可得:a<-或a>-,即a的取值范围为()∪(-,+∞);故选:B.根据题意,由函数的解析式求出其导数,分析可得f(x)在区间(-∞,0)上为增函数,结合函数的奇偶性可得f(x)在区间(0,+∞)上为减函数,据此可得f(3-|a+1|)>f(-)⇒f(3-|a+1|)>f()⇒3-|a+1|<⇒|a+1|>,解可得a的取值范围,即可得答案.本题考查函数奇偶性与单调性的综合应用,涉及不等式的计算,属于基础题.11.【答案】A【解析】解:作出不等式组表示的平面区域,如图△ABC部分;由,得A(0,2);由,得B(0,-4);由,得C(2,0);则△ABC的面积为S△ABC=×6×2=6,函数f(x)=x2+2ax+b有零点,则△=4a2-4b≥0,化为b≤a2,即y≤x2;由,得D(1,1);且x2=x3=,S△CDE=×1×1=,S△OBC=×2×4=4,所以满足函数f(x)=x2+2ax+b有零点时对应点的面积为S′=++4=,利用几何概型的概率公式,计算所求的概率为P==.故选:A.作出不等式组表示的平面区域,求出满足函数f(x)有零点时对应点的面积,计算对应区域的面积比即可.本题考查了几何概型的概率计算问题,也考查了简单的线性规划应用问题,属于中档题.12.【答案】C【解析】解:∵A1D1为A1M在平面A1B1C1D1的射影,∴直线A1M与平面A1B1C1D1内的动直线所成角的最小值为∠D1A1M,即∠D1A1M==60°,∴∠A1MD1=75°,设A1D1=a,在△A1D1M中,由正弦定理可得=,∴D1M==a,故AM=a-a=a,∴==•=.故选:C.设正方体棱长为a,根据∠D1A1M=计算D1M,AM,得出答案.本题考查了空间直线所成角的计算,属于中档题.13.【答案】1【解析】解:令x=1,可得(x-)10的展开式中所有项的系数之和为1,故答案为:1.令x=1,可得(x-)10的展开式中所有项的系数之和.本题主要考查二项式定理的应用,通过给二项式的x赋值,求得展开式中所有项的系数之和,属于基础题.14.【答案】【解析】【分析】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S=++…+的值,利用裂项法可得答案.【解答】解:由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S=++…+的值,可得:S=++…+=(1-)+()+…+(-)=1-=.故答案为:.15.【答案】0或【解析】解:求导数可得y′=,所以在点(1,a)处的切线斜率为:1-a,切线方程为:y-a=(1-a)(x-1),令x=0,得y=2a-1;令y=0,得x=.所以切线与两坐标轴围成的三角形的面积为×|(2a-1)×|=,解得a=0或a=故答案为:0或.求出函数的导数,求得在点(1,1)处的切线斜率,再由点斜式方程可得切线方程,再分别令x=0,y=0,再由三角形的面积公式,即可得到.本题考查导数的几何意义,考查学生的计算能力,确定切线方程是关键.16.【答案】4【解析】解:e==,可得a=b,可得双曲线的渐近线方程为y=±x,设P为第二象限上的点,可得P(-c,a),由题意可得四边形PAOB为矩形,由P到直线y=-x的距离为d=,P到直线y=x的距离为d'=,即有dd'==2,即2a2-a2=4,可得a=2,c=2,△PF1F2的面积为•2c•a=4.故答案为:4.由离心率公式可得a=b,可得双曲线的渐近线方程为y=±x,设P为第二象限上的点,可得P(-c,a),由题意可得四边形PAOB为矩形,由矩形的面积公式,可得a,c,即可得到所求三角形的面积.本题考查双曲线的方程和性质,主要是离心率的求法,考查化简运算能力,属于中档题.17.【答案】解:(1)因为向量=(2cos2,cos),=(,cos),•=.所以•=2cos2×+cos cos=,所以4cos(A-B)=5cos(A+B),所以9sin A sin B=cos A cos B,所以tan A tan B=;(2)=-==≥=,当且仅当A=B时取等号,故的最小值为:.【解析】(1)利用两个向量的数量积公式以及半角公式,求的tan A tan B即可;(2)利用余弦定理将式子,再应用基本不等式求出式子的最小值即可,本题考查了两个向量的数量积公式,余弦定理等,关键是基本不等式的应用,属中档题.18.【答案】解:(1)由电池性能统计图得:电池性能较好的电动车有45辆,其中电动自动车20辆,电动汽车25辆,采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,其中,抽到电动自行车9×=4辆,抽到电动汽车9×=5辆,再从这9辆中随机抽取2辆,基本事件总数n==36,至少有一辆为电动汽车包含的基本事件个数m==30,∴至少有一辆为电动汽车的概率p==.(2)①随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能为需要更换、尚能使用、较好、良好四个等级的电动车分别为9辆,26辆,45辆,20辆,现从全市已挂牌照的电动车中随机抽取3辆,记这3辆电动车电池性能为良好的辆数为X,则X的可能取值为0,1,2,3,P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,∴X的分布列为:②估算平均每辆电动车享受的政府补贴金额为:=[300(8+22+20+10)+500(1+4+25+10)+400×9]=416.【解析】(1)电池性能较好的电动车有45辆,其中电动自动车20辆,电动汽车25辆,采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,抽到电动自行车9×=4辆,抽到电动汽车9×=5辆,再从这9辆中随机抽取2辆,基本事件总数n==36,至少有一辆为电动汽车包含的基本事件个数m==30,由此能求出至少有一辆为电动汽车的概率.(2)①电池性能为需要更换、尚能使用、较好、良好四个等级的电动车分别为9辆,26辆,45辆,20辆,现从全市已挂牌照的电动车中随机抽取3辆,记这3辆电动车电池性能为良好的辆数为X,则X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列.②由频率分布直方图能估算平均每辆电动车享受的政府补贴金额.本题考查概率、离散型随机变量的分布列、平均数的求法,考查古典概型、排列组合、频率分布直方图等基础知识,考查运算求解能力,是基础题.19.【答案】证明:(1)取BC的中点D,连接AD,∵△ABC为正三角形,∴BC⊥AD,∵∠A1AB=∠A1AC,∴A1在平面ABC上的射影O在AD上,∵A1O⊥平面ABC,∴A1O⊥BC,又AD∩A1O=O,∴BC⊥平面A1AD,∴BC⊥AA1,又AA1∥BB1,∴BB1⊥BC.(2)由(1)可知∠A1AO为AA1与底面ABC所成的角,即∠A1AO=30°,∴OA=AA1,又AD=AB,AB=AA1,故OA=AD,于是O与D点重合.以D为原点,以DA,DB,DA1为x轴,y轴,z轴建立空间直角坐标系D-xyz,设AB=AA1=2,则A(,0,0),B(0,1,0),B1(-,1,1),C(0,-1,0),∴=(-,0,1),=(-,1,0),=(0,2,0),设平面ABB1的法向量为=(x,y,z),则,即,令x=1可得y=,z=,即=(1,,),设平面BB1C1C的法向量为=(x,y,z),则,即,令x=1可得y=0,z=,即=(1,0,),∴cos<>===.∴二面角A-BB1-C1的余弦值为.【解析】(1)取BC的中点D,证明BC⊥平面A1AD,可得BC⊥AA1,故而BC⊥BB1;(2)证明A1D⊥平面ABC,以D为原点建立空间坐标系,求出平面ABB1和平面BB1C1C 的法向量,计算法向量的夹角得出二面角的大小.本题考查了线面垂直的判定,考查空间向量与二面角的计算,属于中档题.20.【答案】解:(1)直线l:y=2x+m,联立抛物线方程可得4x2+(4m-2p)x+m2=0,由△=0,即(4m-2p)2-16m2=0,解得p=4m;由直线与圆C2:x2+y2=r2(r>0)相切,可得=r,即r=|m|;(2)F(,0),由y=kx+m和抛物线方程联立,可得k2x2+(2km-2p)x+m2=0,由△=0,即(2km-2p)2-4k2m2=0,解得p=2km;此时切点A(,),直线y=kx+和圆相切,可得=r,再由直线y=kx+,联立圆方程x2+y2=,解得x=-,y=,即B(-,),|AB|==,F到AB的距离d=,即有S1=••=•,p2,S2=••||=•,由S1=6S2,可得2k4-3k2+1=0,解得k=±1或k=±.【解析】(1)联立直线y=2x+m和抛物线方程,运用判别式为0,可得p与m的关系;再由直线和圆相切的条件:d=r,可得r与m的关系;(2)求得抛物线的焦点坐标,联立直线和抛物线方程,由判别式为0,解得切点A;由直线和圆方程联立,求得切点B,求得AB的长,以及F到直线AB的距离,运用三角形的面积公式,化简整理,解方程可得所求值.本题考查直线与抛物线的相切的条件,以及直线与圆相切的条件,考查三角形的面积公式的运用,考查方程思想和运算能力,属于难题.21.【答案】解:(1)f′(x)=x-(a+1)+=,(x∈(0,+∞)).a≤0时,x-a>0,可得:函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.0<a<1时,可得:函数f(x)在(0,a)上单调递增,在(a,1)上单调递减,在(1,+∞)上单调递增.a=1时,f′(x)≥0,可得:函数f(x)在(0,+∞)上单调递增.1<a时,可得:函数f(x)在(0,1)上单调递增,在(1,a)上单调递减,在(a,+∞)上单调递增.(2)不妨设0<x1<x2,由(1)可得:a∈[3,5]时,函数f(x)在x∈[1,3]单调递减,∵x1,x2∈[1,3](x1≠x2),恒有|f(x1)-f(x2)|<λ|-|,∴f(x1)-f(x2)<λ(-),化为:f(x1)-<f(x2)-,令g(x)=f(x)-=x2-(a+1)x+a ln x-,a∈[3,5],x∈[1,3],则函数g(x)在x∈[1,3]上单调递增,a∈[3,5],∴g′(x)=x-(a+1)++≥0,在x∈[1,3]上恒成立,a∈[3,5],化为:λ≥-x3+(a+1)x2-ax=h(x),x∈[1,3],a∈[3,5],h′(x)=-3x2+2(a+1)x-a=u(x)u′(x)=-6x+2(a+1),在x∈[1,3]上单调递减.u′(1)=2a-4>0,u′(3)=2a-16<0.∴存在唯一x0∈(1,3),使得u′(x0)=-6x0+2(a+1)=0,解得x0=∈.h′(1)=2a-1>0,h′(3)=6a-24<0.∴函数h(x)在[1,x0)上单调递增,在(x0,3]上单调递减.∴x=x0时,函数h(x)取得极大值即最大值,h(x0)=-+(a+1)-ax0=-+(a+1)-a=.∴λ≥.a∈[3,5],∴实数λ的取值范围是[,+∞).a∈[3,5].【解析】(1)f′(x)=x-(a+1)+=,(x∈(0,+∞)).对a分类讨论,即可得出单调性.(2)不妨设0<x1<x2,由(1)可得:a∈[3,5]时,函数f(x)在x∈[1,3]单调递减,根据x1,x2∈[1,3](x1≠x2),恒有|f(x1)-f(x2)|<λ|-|,f(x1)-f(x2)<λ(-),化为:f(x1)-<f(x2)-,令g(x)=f(x)-=x2-(a+1)x+a ln x-,a∈[3,5],x∈[1,3],可得函数g(x)在x∈[1,3]上单调递增,a∈[3,5],可得g′(x)=x-(a+1)++≥0,在x∈[1,3]上恒成立,a∈[3,5],化为:λ≥-x3+(a+1)x2-ax=h(x),x∈[1,3],a∈[3,5],利用导数研究函数的单调性极值与最值即可得出.本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、分类讨论方法、等价转化方法,考查了推理能力与计算能力,属于难题.22.【答案】解:(1)α=时,曲线C1的极坐标方程为:θ=;由得(x-)2+(y-1)2=1,即x2+y2-2-2y+3=0,将x=ρcosθ,y=ρsinθ代入得曲线C2的极坐标方程为:ρ2-2ρcosθ-2ρsinθ+3=0(2)将θ=α代入C2的极坐标方程得:ρ2-ρ(2cosα+2sinα)+3=0,由△=(2cosα+2sinα)2-12>0,得|4sin(α+)|∈(2,4],设A,B对应的极径为ρ1,ρ2,则ρ1+ρ2=2cosα+2sinα,ρ1ρ2=3,∴|OA|+|OB|=|ρ1|+|ρ2|=|ρ1+ρ2|=|2cosα+2sinα|=|4sin(α+)|∈(2,4].【解析】(1))α=时,曲线C1的极坐标方程为:θ=;由cos2θ+sin2θ=1可得C2的普通方程,再由x=ρcosθ,y=ρsinθ可得C2的极坐标方程;(2)将θ=α代入C2的极坐标方程得:ρ2-ρ(2cosα+2sinα)+3=0,再根据△>0以及韦达定理、极径的几何意义可得.本题考查了直角坐标方程化极坐标方程、参数方程化普通方程、韦达定理、极径的几何意义,属中档题.23.【答案】解:(1)当a=2时,f(x)=|2x-2|+2,∵f(x)≤6,∴|2x-2|+2≤6,|2x-2|≤4,|x-1|≤2,∴-2≤x-1≤2,解得-1≤x≤3,∴不等式f(x)≤6的解集为{x|-1≤x≤3};(2)∵g(x)=|2x-1|,∴f(x)+g(x)=|2x-1|+|2x-a|+a≥3,2|x-|+2|x-|+a≥3,|x-|+|x-|≥,当a≥3时,成立,当a<3时,|x-|+|x-|≥|a-1|≥>0,∴(a-1)2≥(3-a)2,解得2≤a<3,∴a的取值范围是[2,+∞).【解析】本题考查含绝对值不等式的解法及绝对值不等式的三角不等式,同时考查不等式恒成立问题,是中档题,解题时要认真审题,注意不等式性质的合理运用.(1)当a=2时,由已知得|2x-2|+2≤6,由此能求出不等式f(x)≤6的解集.(2)由f(x)+g(x)=|2x-1|+|2x-a|+a≥3,得|x-|+|x-|≥,由此能求出a的取值范围.。

2024年河南名校高三数学4月模拟检测试卷(考试时间:120分钟试卷满分:150分)2024.04注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若2i23ia +-为纯虚数,R a ∈,则=a ()A .3B .4C .-3D .-42.设集合{}{}1,,0,3,38A a B a a =-=--,若A B ⊆,则=a ()A .0B .1C .2D .33.已知圆锥的底面圆的半径为1,其侧面展开图是一个圆心角为π2的扇形,则该圆锥的母线长为()A .52B .3C .72D .44.已知函数()ππ2sin 2cos 233f x x x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭,则下列结论正确的是()A .()f x 的最小正周期为πB .()f x 在ππ,84⎛⎫- ⎪⎝⎭上单调递增C .()f x '为偶函数D .()f x 的最小值为325.已知点(),P m n 是圆C 22:8x y +=上的任意一点,则()()22114m n m n ⎡⎤-++⎢⎥⎣⎦的最大值为()A .25B .24C .23D .226.过双曲线22:14x C y -=的左焦点1F 作倾斜角为θ的直线l 交C 于,M N 两点.若113MF F N = ,则cos θ=()A 10B 310C 255D 557.将8个数学竞赛名额全部分给4个不同的班,其中甲、乙两班至少各有1个名额,则不同的分配方案种数为()A .56B .84C .126D .2108.已知函数()f x 的定义域为R ,对于任意实数x ,y 满足()()()()21f x y f x y f x f y ++-=+,且()02f =,则下列结论错误的是()A .()11f =B .()f x 为偶函数C .()f x 是周期函数D .()110512f =二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.2023年7月31日国家统计局发布了制造业采购经理指数(PMI ),如下图所示:下列说法正确的是()A .从2023年1月到2023年7月,这7个月的制造业采购经理指数(PMI )的第75百分位数为51.9%B .从2023年1月到2023年7月,这7个月的制造业采购经理指数(PMI )的极差为38%.C .从2022年7月到2023年7月制造业采购经理指数(PMI )呈下降趋势D .PMI 大于50%表示经济处于扩张活跃的状态;PMI 小于50%表示经济处于低迷萎缩的状态,则2023年1月到2023年3月,经济处于扩张活跃的状态10.已知抛物线Γ:216y x =,过点()6,0N 作直线12,l l ,直线1l 与Γ交于A ,C 两点,A 在x 轴上方,直线2l 与Γ交于B ,D 两点,D 在x 轴上方,连接,,,AB CD AD BC ,若直线AB 过点()2,0M ,则下列结论正确的是()A .若直线AB 的斜率为1,则直线CD 的斜率为13B .直线CD 过定点()18,0C .直线AD 与直线BC 的交点在直线4x =-上D .ABN 与CDN △的面积之和的最小值为11.已知定义在R 上的奇函数()f x 连续,函数()f x 的导函数为()f x '.当0x >时,()()()cos sin e f x x f x x f x '>+⋅',其中e 为自然对数的底数,则()A .()f x 在R 上为减函数B .当0x >时,()0f x <C .π3π22f f ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭D .()f x 在R 上有且只有1个零点三、填空题:本题共3小题,每小题5分,共15分.12.已知数列{}n a 的前n 项和为n S ,若101,21n a n a λ=+=,则λ=,9S =.13.太极图被称为“中华第一图”,其形状如阴阳两鱼互抱在一起,因而又被称为“阴阳鱼太极图”.如图所示的图形是由半径为2的大圆O 和两个对称的半圆弧组成的,线段MN 过点O 且两端点,M N 分别在两个半圆弧上,P 是大圆上一动点,则PM PN ⋅的最小值为.14.已知正四棱台1111ABCD A B C D -的内切球半径11222r AB A B ==,则异面直线11A B 与1DD 所成角的余弦值为四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC 中,内角,,A B C 的对边分别为,,,1cos a b c a A A ==-.(1)求cos A ;(2)若AD 为ABC 的中线,且AD =,求ABC 的面积S .16.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,且π3ABC ∠=,平面PAC ⊥平面ABCD .F 为PA 的中点,且,4,2,,,CF PF PC BC PB PD M N ====分别为,PB PD 的中点.(1)证明:BD AC ⊥.(2)设DM 交平面NAC 于点H ,求平面ABC 与平面ABH 夹角的余弦值.17.某市共有教师1000名,为了解老师们的寒假研修情况,评选研修先进个人,现随机抽取了10名教师利用“学习APP”学习的时长(单位:小时):35,43,90,83,50,45,82,75,62,35,时长不低于80小时的教师评为“研修先进个人”.(1)现从该样本中随机抽取3名教师的学习时长,求这3名教师中恰有2名教师是研修先进个人的概率.(2)若该市所有教师的学习时长X 近似地服从正态分布()2,N μσ,其中10,σμ=为抽取的10名教师学习时长的样本平均数,利用所得正态分布模型解决以下问题:①试估计学习时长不低于50小时的教师的人数(结果四舍五人到整数);②若从该市随机抽取的n 名教师中恰有ξ名教师的学习时长在[]50,70内,则n 为何值时,()10P ξ=的值最大?附:若随机变量X 服从正态分布()2,N μσ,则()0.6827P X μσμσ-≤≤+≈,()220.9545P X μσμσ-≤≤+≈,()330.9973P X μσμσ-≤≤+≈.18.如图所示,在圆锥内放入两个球12,O O ,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且这两个球都与平面α相切,切点分别为12,F F ,数学家丹德林利用这个模型证明了平面α与圆锥侧面的交线为椭圆,记为Γ,12,F F 为椭圆Γ的两个焦点.设直线12F F 分别与该圆锥的母线交于A ,B 两点,过点A的母线分别与球12,O O 相切于C ,D 两点,已知22AC AD ==以直线12F F 为x 轴,在平面α内,以线段12F F 的中垂线为y 轴,建立平面直角坐标系.(1)求椭圆Γ的标准方程.(2)点T 在直线4x =上,过点T 作椭圆Γ的两条切线,切点分别为M ,N ,A ,B 分别是椭圆Γ的左、右顶点,连接,AM BN ,设直线AM 与BN 交于点P .证明:点P 在直线4x =上.19.已知0b >,函数()()()ln f x x a x b =++的图象在点()()1,1f 处的切线方程为ln 2ln 20x y --=.(1)求a ,b 的值;(2)若方程()1e f x =(e 为自然对数的底数)有两个实数根12,x x ,且12x x <,证明:21111e eln2x x -<++1.A【分析】由复数除法运算化简复数,结合复数是纯虚数列方程解出参数a 即可.【详解】因为()()()2i 23i 2634i2i 23i 1313a a a a ++-+++==-为纯虚数,所以260340a a -=⎧⎨+≠⎩,解得3a =.故选:A.2.C【分析】根据题意,得到0a -=或38a a -=-,求得a 的值,结合集合的包含关系,即可求解.【详解】由集合{}{}1,,0,3,38A a B a a =-=--,因为A B ⊆,所以0a -=或38a a -=-,解得0a =或2a =,当0a =时,{}1,0,{0,3,8}A B ==-,不符合题意;当2a =时,{}{}1,2,0,1,2A B =-=-,符合题意.故选:C .3.D【分析】设母线长为l ,根据题意得到π2π12l =⨯,即可求解.【详解】设母线长为l ,由题意,可得π2π12l =⨯,解得4l =,即圆锥的母线长为4.故选:D.4.C【分析】由积化和差公式化简,根据周期公式判断A ,根据正弦函数的最值判断D ,根据正弦型函数的单调性判断B ,根据导数判断C.【详解】因为()ππ2sin 2cos 2sin433f x x x x ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭2ππ42=,其最小值为1-A 错误,D 错误;因为ππ84x -<<,所以π4π2x -<<,可知()f x 在ππ,84⎛⎫- ⎪⎝⎭上不单调,B 错误;又()4cos4f x x =',所以()f x '为偶函数,C 正确.故选:C 5.A【分析】设m n αα⎧=⎪⎨=⎪⎩,,代入算式中由倍角公式化简,利用基本不等式求积的最大值.【详解】点(),P m n 是圆C 22:8x y +=上的任意一点,设m n αα⎧=⎪⎨=⎪⎩,,则()()()()2222118cos sin 2cos sin 14m n m n αααα⎡⎤⎡⎤-++=-++⎢⎥⎣⎦⎣⎦()()222sin232sin281sin232sin24252αααα-++⎛⎫=-+≤= ⎪⎝⎭,当且仅当1sin24α=-时,等号成立.()()22114m n m n ⎡⎤-++⎢⎥⎣⎦的最大值为25.故选:A 6.D【分析】根据双曲线的定义,结合焦点三角形以及余弦定理即可求解.【详解】设双曲线的右焦点为F ,连接,MF NF ,由题意可得2,1,a b c ===设1133,2343,24,MF F N x MF a x x FN a x x ===+=+=+=+由余弦定理可得2222221111111111cos cos 022F N F F NF F M F F MFNF F MF F F N F F F M F F+-+-∠+∠=+=⋅⋅,即()()222222449443022232x c x x c xx cx c+-++-++=⋅⋅⋅⋅,解得13x =,所以()22211441cos MF F +-+∠==cos θ=.故选:D7.B【分析】将问题等价转换为将10个数学竞赛名额全部分给4个不同的班,每个班至少有1个名额的分法,利用隔板法即可求解.【详解】将8个数学竞赛名额全部分给4个不同的班,其中甲、乙两班至少各有1个名额的分法,等价于将10个数学竞赛名额全部分给4个不同的班,每个班至少有1个名额的分法.用3个隔板插入10个小球中间的空隙中,将球分成4堆,由于10个小球中间共有9个空隙,因此共有39C 84=种不同的分法.故选:B.8.C【分析】对于A ,令0x y ==,结合()02f =即可判断;对于B ,令0x =结合偶函数的性质即可判断;对于C ,令0y =即可判断;对于D ,得出递推关系()112nf n ⎛⎫+= ⎪⎝⎭,由此即可验算.【详解】令0x y ==,得()()()20201f f f =,因为()02f =,所以()11f =,A 正确;令0x =,则()()()()()212f y f y f f y f y +-==,所以()()f y f y =-,则()f x 为偶函数,B 正确;令0y =,得()()()()221041f x f x f f x =+=+,即()()112f x f x +=,所以()f x 不是周期函数,C 错误;当x 取正整数n 时,()()()11111222nnf n f n f ⎛⎫⎛⎫+==== ⎪ ⎪⎝⎭⎝⎭ ,则()911102512f ⎛⎫== ⎪⎝⎭,D 正确.故选:C.【点睛】关键点点睛:判断D 选项的关键是得出()112nf n ⎛⎫+= ⎪⎝⎭,由此即可顺利得解.9.ABD【分析】根据折线图中的数据,结合极差、平均数、百分位数定义与计算方法逐一判断即可.【详解】由图知,从2023年1月到2023年7月,这7个月的制造业采购经理指数(PMI )从小到大的顺序为48.8%,49.0%,49.2%,49.3%,50.1%,51.9%,52.6%,因为775% 5.25⨯=,所以第75百分位数为第6个数,即为51.9%,故A 正确;从2023年1月到2023年7月,这7个月的制造业采购经理指数(PMI )的最大值为52.6%,最小值为48.8%,所以极差为52.6%48.8% 3.8%-=,故B 正确;由图易知制造业采购经理指数(PMI )有升有降,故C 错误;由图知2023年1月到2023年3月PMI 均大于50%,所以经济处于扩张活跃的状态,故D 正确.故选:ABD.10.ABD【分析】分别联立曲线与直线1,,,AB BD l CD 方程,表示出韦达定理,解方程组可得B 正确;由斜率的定义结合选项B 可得A 正确;当1l x ⊥轴时,求出,,,A B C D 四点坐标,得到两直线方程,求出交点横坐标可判断C 错误;由三角形的面积公式结合选项B 和基本不等式可得D 正确.【详解】设()()()()11223344,,,,,,,A x y B x y C x y D x y ,设直线CD 交x 轴于点(),0t ,0t >,直线1l 的方程为:16x m y =+,联立12616x m y y x=+⎧⎨=⎩,消去x 可得2116960y m y --=,()21Δ164960m =+⨯>,所以1396y y =-,同理2496y y =-,设直线:2AB x my =+,联立2216x my y x=+⎧⎨=⎩,消去x 可得216320y my --=,()2Δ164320m =+⨯>,所以1232y y =-,设直线:CD x ny t =+,联立216x ny t y x=+⎧⎨=⎩,消去x 可得216160y ny t --=,()2Δ164160n t =+⨯>,所以3416y y t =-,联立方程组1213243432969616y y y y y y y y t=-⎧⎪=-⎪⎨=-⎪⎪=-⎩,可得18t =,故B 正确;对于A ,由B 可得122212123412121234341212122233443416969696961616316321616AB CDy y y y y y y y k x x y y y y y y y y k y y y y y y y y y y x x -----+-+--=======--++-+--,所以当1AB k =时,有13CD k =,故A 正确;当1l x ⊥轴时,可知(((6,,6,,A C D -,2,3B ⎛ ⎝⎭,求得直线AD的方程为18x =-,直线BC20y ++=,将这两方程联立方程组,解得6x =-,故C 错误;设ABN 与CDN △的面积分别为12,S S ,则()()()()()()121243124311621862622S S y y y y y y y y +=⨯-⨯-+⨯-⨯-=-+-,又12143414321618y y y y y y y y ⨯-=+≥-=+≥,又12S S +≥14y y ==D 正确.故选:ABD.11.BCD【分析】根据题意,令()()()cos e g x f x x =-,利用导数求得()g x 在()0,∞+上单调递增,结合π3π22g g ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,得到π3π22f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,可判定C 正确;再由0x >时,()()0g x g >,可判定B 正确;根据()f x 是定义在R 上的奇函数,结合单调性和零点的定义,可判定D 正确.根据()f x 的单调性无法判断,可判定A 错误.【详解】由()()()cos sin e f x x f x x f x '>+⋅',可得()()()cos e sin 0f x x f x x -->'.令()()()cos e g x f x x =-,则当0x >时,()()()()cos e sin 0g x f x x f x x =--'>',所以()g x 在()0,∞+上单调递增,所以π3π22g g ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,即ππ3π3πcos e cos e 2222f f ⎛⎫⎛⎫⎛⎫⎛⎫-<- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭,可得()()π3πe e 22f f ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭,所以π3π22f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,所以C 正确;因为()()()001e 0g f =-=,所以当0x >时,()()00g x g >=,又因为cos e 0x -<,所以当0x >时,()0f x <,所以B 正确;由()f x 是定义在R 上的奇函数,故当0x <时,()()0f x f x =-->,又因为()00f =,所以()f x 在R 上有且只有1个零点,所以D 正确.因为()f x 的单调性无法判断,所以A 错误.故选:BCD.12.299【分析】利用给定条件,直接求出λ,再判断数列特征求出9S .【详解】由101,21n a n a λ=+=,得10121λ+=,解得2λ=;则21n a n =+,显然{}n a 是等差数列,所以19959()9911992a a S a +===⨯=.故答案为:2;9913.0【分析】先根据向量运算表示出PM PN ⋅,结合OM 的最值可得答案.【详解】连接PO ,可得()()2224PM PN PO OM PO OM PO OM OM ⋅=+⋅-=-=- ,显然当2OM 最大,即OM 取得最大值2时,PM PN ⋅ 取得最小值0.故答案为:0.14.10【分析】作正四棱台的轴截面,设1124AB A B a ==,由几何关系得出,3KG a FK FG a ===,结合勾股定理可得12a =,进一步延长侧棱11,DD CC ,设它们相交于点P ,从而只需分别求出1,2CD PD 即可.【详解】由题设知正四棱台1111ABCD A B C D -的高h 设1124AB A B a ==,作正四棱台的轴截面,如图所示,其中I ,J ,L 分别为圆O 与四边形EFGH 的切点,FK GH ⊥,K 为垂足,从而有IF FL a ==,2JG GL a ==,所以,3KG a FK FG a ===,由2229a a -=,解得1.2a =延长侧棱11,DD CC ,设它们相交于点P,则异面直线11A B 与1DD 所成的角为11PD C ∠.因为112AB A B =,所以1111PG BC ABFG B C A B ==,所以11111263,212PG FG a HD AD A D A B EF a =========,所以PC PD ==从而11cos .1102cos P CDPDC DD P C =∠∠=故答案为:1010.【点睛】关键点点睛:关键是得出1122AB A B ==,进一步得出,PG PD 的长度,由此即可顺利得解.15.(1)2cos 3A =【分析】(1sin 22A A =,结合22sincos 122A A +=,求得25cos 26A =,结合余弦的倍角公式,即可求解;(2)由(1)得到sin A =2AB AC AD += ,求得224123b c bc ++=,再由由余弦定理得到22443b c bc +-=,求得3bc =,结合三角形的面积公式,即可求解.【详解】(1)解:由51cos 5A A =-,可得225cos 2sin 5222A A A =,因为0πA <<,可知sin 02A ≠sin 22A A=,又因为22sincos 122A A +=,联立方程组得25cos 26A =,所以22cos 2cos 123A A =-=.(2)解:由(1)知2cos 3A =,可得5sin 3A ==,因为AD 为ABC 的中线,且AD =2AB AC AD +=,两边平方得224123b c bc ++=,又由余弦定理得2222cos 4b c bc A a +-==,即22443b c bc +-=,两式相减,可得3bc =,所以11sin 322S bc A ==⨯⨯16.(1)证明见解析(2)312943【分析】(1)设BD 与AC 交于点O ,根据题意,证得PO BD ⊥和PC BD ⊥,结合线面垂直的判定定理,证得BD ⊥平面PAC ,进而证得BD AC ⊥.(2)由(1)知PC ⊥平面ABCD ,得到OF ⊥平面ABCD ,以O 为坐标原点,建立空间直角坐标系,求得平面ABH 和平面ABC的法向量(m =和()0,0,1n = ,结合向量的夹角公式,即可求解.【详解】(1)证明:如图所示,设BD 与AC 交于点O ,连接PO ,因为底面ABCD 是平行四边形,所以O 为,BD AC 的中点,又因为PB PD =,所以PO BD ⊥,因为CF FP FA ==,且F 为PA 的中点,所以PC AC ⊥,又因为PC ⊂平面PAC ,且平面PAC ⊥平面ABCD ,平面PAC 平面ABCD AC =,所以PC ⊥平面ABCD ,因为BD ⊂平面ABCD ,所以PC BD ⊥,又因为PO PC P = ,且,PO PC ⊂平面PAC ,所以BD ⊥平面PAC ,因为AC ⊂平面PAC ,所以BD AC ⊥.(2)解:如图所示,连接ON ,因为ON 为PBD △的中位线,所以//ON PB ,因为平面PBD 平面,ACH OH BM ON ==且H ON ∈,所以OH MB ∥,且12OH MB =,由,O F 分别为,AC AP 的中点,看到的//OF PC ,由(1)知PC ⊥平面ABCD ,所以OF ⊥平面ABCD .以O 为坐标原点,以,,OA OB OF 所在直线分别为,,x y z 轴,建立空间直角坐标系,如图所示,则()()()()()0,0,0,0,0,2,1,0,0,1,0,0,1,0,4O F A C B P --,所以11,44OH BP ⎛⎫==-- ⎪ ⎪⎝⎭,则()5,,4AB AH ⎛⎫=-=-- ⎪ ⎪⎝⎭,设(),,m x y z = 为平面ABH的法向量,则05044m AB x m AH x y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩,取2y =,可得x z ==(m =,又由平面ABC 的一个法向量为()0,0,1n =,设平面ABC 与平面ABH 的夹角为θ,可得cos 43m n m n θ⋅== .即平面ABC 与平面ABH的夹角余弦值为43.17.(1)740(2)①841;②14【分析】(1)根据题意利用古典概型即可计算;(2)①由样本数计算μ,进而利用()0.6827P X μσμσ-≤≤+≈求解即可;②首先求在[]50,70内的概率,再由题意可知(),0.6827B n ξ~,然后设()()101010C 0.68270.317310n n f n n -=⨯⨯≥,最后利用()()1f n f n +可求使得()()1f n f n +<的最小n 的值,从而得到使()10P ξ=最大的n 的值.【详解】(1)设事件“抽取的3名教师中恰有2名教师是研修先进个人”为A .由题知样本中学习时长不低于80小时的人数为3,时长低于80小时的人数为7,则()2137310C C 7C 40P A ==,所以这3名教师中恰有2名教师是研修先进个人的概率为740.(2)①由样本数据知,3543908350458275623560,1010μσ+++++++++===.因为()()()1500.8413522P X P X P X μσμσμσ-≤≤+≥=≥-=+≈,所以0.841351000841⨯≈,所以,学习时长不低于50小时的教师人数为841.②每名教师的学习时长在[]50,70内的概率为()0.6827P X μσμσ-≤≤+≈,由题意可知(),0.6827B n ξ~,则()10101010C 0.68270.3173n n P ξ-==⨯⨯,设()()101010C 0.68270.317310n nf n n -=⨯⨯≥,则()()1010911010101C 0.68270.31730.31730.3173C 0.68270.31739n n n n f n n f n n -+-+⨯⨯+==⨯⨯-.令0.31730.317319n n +>-,得9317344221368276827n <=,所以当13n ≤时,()()1f n f n +>,令0.31730.317319n n +<-,得4422136827n >,所以当14n ≥时,()()1f n f n +<,所以当14n =时,()f n 最大,即使()10P ξ=最大的n 的值为14.18.(1)2214x y +=(2)证明见解析【分析】(1)根据切线长定理可得12,AF AC AF AD ==,可得1224AF AF a +==,2AD AC c -==,从而可求解.(2)根据题意设出直线()()12:2,:2PA y k x PB y k x =+=-,分别与椭圆方程联立,再结合根与系数的关系从而可求解.【详解】(1)设椭圆Γ的标准方程为()222210,0x y a b a b+=>>,由切线长定理知12,AF AC AF AD ==,则1224AF AF AC AD a +=+==,解得2a =.由2AD AC c -==,解得1c b ==.所以椭圆Γ的标准方程为22 1.4x y +=(2)设()()()()001122,,,,,,4,P x y M x y N x y T t ,已知()()2,0,2,0A B -,设()()12:2,:2PA y k x PB y k x =+=-,联立方程组()221142x y y k x ⎧+=⎪⎨⎪=+⎩,消去y 得()222211114161640k x k x k +++-=,显然()()422111Δ256641641160k k k =--+=>,由21121164214k x k --=+,可得211212814k x k -=+,21111221128421414k k y k k k ⎛⎫-=+= ⎪++⎝⎭,所以2112211284,1414k k M k k ⎛⎫- ⎪++⎝⎭,联立方程组()222142x y y k x ⎧+=⎪⎨⎪=-⎩,消去y 得()222222214161640k x k x k +-+-=,显然()()422222Δ256641641160k k k =--+=>,由22222164214k x k -=+,可得222222814k x k -=-+,22222222228421414k k y k k k ⎛⎫--=--= ⎪++⎝⎭,同理2222222824,.1414k k N k k ⎛⎫-- ⎪++⎝⎭因为M ,N 是切点,且()4,T t ,所以直线MN 的方程为414xty +=,即1x ty +=,显然直线MN 过定点()1,0D ,即M ,D ,N 三点共线,则122212221222124414142882111414k k k k k k k k -++=----++,解得213k k =或1241k k =-(舍去),联立方程组()()01002022y k x y k x ⎧=+⎪⎨=-⎪⎩,解得()1202124k k x k k +==-,即点P 在直线4x =上.【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()()1122,,,x y x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,注意∆的判断;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.19.(1)1,1a b =-=(2)证明见解析【分析】(1)求导得()()ln x af x x b x b+=+++',结合()1ln2f '=,()10f =可列出方程组求解;(2)由题意得10201x x x <<<<,构造函数证明不等式()()()1ln 11ln 2x x x -+≥-⋅,当且仅当1x =时,等号成立;()()1ln 1x x x -+≥-,当且仅当0x =时,等号成立;从而可分别得到2211eln2x x '=+>,111ex x =-'<,由此即可得证.【详解】(1)因为()()ln x a f x x b x b +=+++',所以()()11ln 1ln21af b b+=++=+',由题意知()10f =,所以()()()11ln 10f a b =++=,联立方程组()()()1ln 101ln 1ln21a b a b b⎧++=⎪⎨+++=⎪+⎩,解得1,1a b =-=.(2)由(1)可知()()()1ln 1,1f x x x x =-+>-,()()00,10f f ==,()()21ln 11f x x x =-+++',设()()f x u x '=,()()221011u x x x '=+>++,所以()u x 即()f x '在()1,-+∞上单调递增.又()()010,1ln 20f f ''=-<=>,所以存在()00,1x ∈,使得()00f x '=,故()f x 在()01,x -上单调递减,在()0,x +∞上单调递增,设()()1ln 2h x x =-⋅,令()()()()()()1ln 11ln 2F x f x h x x x x =-=-+--⋅,则()()()12ln 1ln2ln 11ln211x F x x x x x -=++'-=+-+-++,因为()f x '在()1,-+∞上单调递增,所以()F x '在()1,-+∞上单调递增.又()10F '=,所以当11x -<<时,()0F x '<,当1x >时,()0F x '>.所以()F x 在()1,1-上单调递减,在()1,+∞上单调递增.故()()10F x F ≥=,即()()()1ln 11ln 2x x x -+≥-⋅,当且仅当1x =时,等号成立.因为方程()1ef x =有两个实数根12,x x ,且12x x <,也就是()()()()211100ef x f x f f ==>==,且注意到()f x 在()1,+∞上单调递增,所以10201x x x <<<<,所以()()()2221ln 11ln2x x x -+>-,即()()22f x h x >.设()1e h x =的根为:2x ',则211eln2x ='+,又()h x 在()1,-+∞上单调递增,所以()()()222h x f x h x '=>,故22x x '>①.易知()f x 的图象在坐标原点处的切线方程为()g x x =-,令()()()()()1ln 1T x f x g x x x x =-=-++,则()()()22ln 12ln 111x T x x x x x ='++=-++++,因为()f x '在()1,-+∞上单调递增,所以()T x '在()1,-+∞上单调递增.又()00T '=,所以当10x -<<时,()0T x '<,当0x >时,()0T x '>,所以()T x 在()1,0-上单调递减,在()0,∞+上单调递增.所以()()00T x T ≥=,()()1ln 1x x x -+≥-,当且仅当0x =时,等号成立.因为10x <,所以()()1211ln 1x x x -+>-,即()()11f x g x >.设()1e g x =的根为1x ',则11ex '=-,又()g x 在()1,-+∞上单调递减,所以()()()111g x f x g x '=>,所以11x x '<,从而11x x '->-②.由①②可知:2121111eln2ex x x x ''-<-=++.【点睛】关键点点睛:第二问的关键是构造适当的函数分别得到分别得到2211eln2x x '=+>,111ex x =-'<,由此即可顺利得解.。

河南省高三四月调考数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2016高三上·闽侯期中) 复数﹣的实部与虚部的和为()A . ﹣B . 1C .D .【考点】2. (2分) (2017高三上·古县开学考) 设集合M={x| },函数f(x)=ln(1﹣)的定义域为N,则M∩N为()A . [ ,1]B . [ ,1)C . (0, ]D . (0,)【考点】3. (2分) (2020高三上·天津期中) 设等差数列的前项之和为,已知,则()A . 12B . 20C . 40D . 100【考点】4. (2分) (2015高三上·孟津期末) 设 F1F2分别为双曲线x2﹣y2=1的左,右焦点,P是双曲线上在x轴上方的点,∠F1PF2为直角,则sin∠PF1F2的所有可能取值之和为()A .B . 2C .D .【考点】5. (2分) (2019高二下·延边月考) 若,则的值为()A .B .C .D .【考点】6. (2分) (2020高二下·宁波月考) 一个长方形塑料箱子中装有20个大小相同的乒乓球,其中标有数字0的有10个,标有数字的有个(). 现从该长方形塑料箱子中任取一球,其中表示所取球的标号. 若,则()A . 0B . 1C . 2D . 3【考点】7. (2分)若命题“p或q”为真,“非p”为真,则()A . p真q真B . p假q真C . p真q假D . p假q假【考点】8. (2分) (2018高一下·金华期末) 在同一坐标系中,函数与函数的图象可能是()A .B .C .D .【考点】9. (2分) (2018高二下·中山月考) 阅读如图所示的程序框图,为使输出的数据为31,则①处应填的自然数为()A . 4B . 5C . 6D . 7【考点】10. (2分)一个空间几何体的三视图如图所示,则该几何体的的体积为【考点】11. (2分) (2019高二下·合肥期中) 直线与曲线相交,则满足的条件是()A .B .C .D . 且【考点】12. (2分)“”是“直线与圆相切”的()A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件【考点】二、填空题 (共4题;共4分)13. (1分) (2017高二上·安平期末) 如图所示,在棱长为4的正方体ABCD﹣A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是________.【考点】14. (1分)已知数列{an}为等差数列,a1=1,公差d≠0,a1、a2、a5成等比数列,则a2014的值为________【考点】15. (1分)设变量,满足约束条件则z=1﹣2x﹣3y的最小值为________.【考点】16. (1分) (2019高二下·蛟河期中) 点是曲线上的点,则的最大值和最小值的差是________.【考点】三、解答题 (共7题;共60分)17. (10分) (2019高一下·哈尔滨期中) 在中,角所对的边是,若(1)求的值;(2)若点为的中点,且,求的面积【考点】18. (10分)(2017·菏泽模拟) 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.(1)求证:BF∥平面ADP;(2)求二面角B﹣DF﹣P的余弦值.【考点】19. (15分) (2017高三上·赣州期末) 传统文化就是文明演化而汇集成的一种反映民族特质和风貌的民族文化,是民族历史上各种思想文化、观念形态的总体表征.教育部考试中心确定了2017年普通高考部分学科更注重传统文化考核.某校为了了解高二年级中国数学传统文化选修课的教学效果,进行了一次阶段检测,并从中随机抽取80名同学的成绩,然后就其成绩分为A、B、C、D、E五个等级进行数据统计如下:成绩人数A9B12C31D22E6根据以上抽样调查数据,视频率为概率.(1)若该校高二年级共有1000名学生,试估算该校高二年级学生获得成绩为B的人数;(2)若等级A、B、C、D、E分别对应100分、80分、60分、40分、20分,学校要求“平均分达60分以上”为“教学达标”,请问该校高二年级此阶段教学是否达标?(3)为更深入了解教学情况,将成绩等级为A、B的学生中,按分层抽样抽取7人,再从中任意抽取3名,求抽到成绩为A的人数X的分布列与数学期望.【考点】20. (10分)(2017·晋中模拟) 已知椭圆C:的右焦点在直线l: x﹣y﹣3=0上,且椭圆上任意两个关于原点对称的点与椭圆上任意一点的连线的斜率之积为﹣.(1)求椭圆C的方程;(2)若直线t经过点P(1,0),且与椭圆C有两个交点A,B,是否存在直线l0:x=x0(其中x0>2)使得A,B到l0的距离dA , dB满足恒成立?若存在,求出x0的值,若不存在,请说明理由.【考点】21. (5分)(2017·潮南模拟) 设函数f(x)=x2+aln(x+1)(a为常数)(Ⅰ)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;(Ⅱ)若函数y=f(x)有两个极值点x1 , x2 ,且x1<x2 ,求证:.【考点】22. (5分) (2016高二上·吉安期中) 已知圆C和y轴相切,圆心在直线x﹣3y=0上,且被直线y=x截得的弦长为,求圆C的方程.【考点】23. (5分)已知a,b是实数,函数f(x)=x|x﹣a|+b.(1)当a=2时,求函数f(x)的单调区间;(2)当a>0时,求函数f(x)在区间[1,2]上的最大值;(3)若存在a∈[﹣3,0],使得函数f(x)在[﹣4,5]上恒有三个零点,求b的取值范围.【考点】参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共7题;共60分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、答案:19-3、考点:解析:答案:20-1、答案:20-2、考点:解析:考点:解析:答案:22-1、考点:解析:答案:23-1、考点:解析:。

2020届河南省高考理科数学4月模拟试题一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x≥0},B={x|y=lg(x2﹣x)},则A∩B=()A.[0,+∞)B.(1,+∞)C.{0}∪[1,+∞)D.(﹣∞,0]∪(1,+∞)2.(5分)已知复数z=(i为复数单位),则|z|=()A.B.C.D.3.(5分)2019年,河南省郑州市的房价依旧是郑州市民关心的话题.总体来说,二手房房价有所下降,相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计郑州市某新房销售人员一年的工资情况的结果如图所示,若近几年来该销售人员每年的工资总体情况基本稳定,则下列说法正确的是()A.月工资增长率最高的为8月份B.该销售人员一年有6个月的工资超过4000元C.由此图可以估计,该销售人员2020年6,7,8月的平均工资将会超过5000元D.该销售人员这一年中的最低月工资为1900元4.(5分)已知(x+1)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a2+a4的值为()A.7B.8C.15D.165.(5分)已知双曲线的一个焦点为F,过F作x轴的垂线分别交双曲线的两渐近线于A,B两点,若△AOB的面积为2b2,则双曲线C的离心率为()A.B.C.D.6.(5分)九连环是我国古代至今广为流传的一种益智游戏,它由九个铁丝圆环相连成串,按一定规则移动圆环的次数,决定解开圆环的个数.在某种玩法中,用a n表示解下n(n ≤9,n∈N*)个圆环所需的多少移动次数,数列{a n}满足a1=1,且,则解下5个环所需的最少移动次数为()A.7B.10C.16D.227.(5分)已知某个几何体的三视图如图所示,根据图中标出的数据,可得出这个几何体的表面积是()A.6B.C.D.8.(5分)已知函数在区间上单调递增,则ω的取值范围是()A.B.C.D.9.(5分)已知平行四边形ABCD中,AB=AD=2,∠DAB=60°,对角线AC与BD相交于点O,点M是线段BC上一点,则•的最小值为()A.﹣B.C.﹣D.10.(5分)已知ABCD为正方形,其内切圆I与各边分别切于E,F,G,H,连接EF,FG,GH,HE.现向正方形ABCD内随机抛掷一枚豆子,记事件A:豆子落在圆I内,事件B:豆子落在四边形EFGH外,则P(B|A)=()A.B.C.D.11.(5分)已知定义在R上的奇函数f(x),对任意实数x,恒有f(x+3)=﹣f(x),且当时,f(x)=x2﹣6x+8,则f(0)+f(1)+f(2)+…+f(2020)=()A.6B.3C.0D.﹣312.(5分)如图,在四棱锥P﹣ABCD中,P A=PB=PC=PD=2,底面ABCD是边长为的正方形.点E是PC的中点,过点A,E作棱锥的截面,分别与侧棱PB,PD交于M,N两点,则四棱锥P﹣AMEN体积的最小值为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分.13.(5分)已知函数f(x)=(x﹣2)lnx,则函数f(x)在x=1处的切线方程为.14.(5分)已知数列{a n}为公差不为零的等差数列,其前n项和为S n,且a1,a2,a4成等比数列,S5=15,则a4=.15.(5分)现有灰色与白色的卡片各八张.分别写有数字1到8.甲、乙.丙、丁四个人每人面前摆放四张,并按从小到大的顺序自左向右排列(当灰色卡片和白色卡片数字相同时,白色卡片摆在灰色卡片的右侧).如图,甲面面的四张卡片已经翻开,则写有数字4的灰色卡片是(填写字母).16.(5分)设F1,F2是椭圆的两个焦点,过F1,F2分别作直线l1,l2.且l1∥l2,若l1与椭圆C交于A,B两点,l2与椭圆C交于C,D两点(点A,D在x轴上方),则四边形ABCD面积的最大值为.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必.考题,每个试题考生都必须作答.第22、23题为选考题考生根据要求作答.(一)必考题:共60分.17.(12分)如图,在三棱柱ABC﹣﹣﹣A1B1C1中,△BCC1为正三角形,AC⊥BC,AC=AA 1=2,,点P在线段BB1上,且A1P⊥AA1.(1)证明:AA1⊥C1P;(2)求BC1和平面A1CP所成角的正弦值.18.(12分)如图,在梯形ABCD中,AB∥CD,CD=3AB=3.(1)若CA=CD,且,求△ABC的面积S;(2)若,,求BD的长.19.(12分)已知O为坐标原点,点F(0,1),M为坐标平面内的动点,且2,||,成等差数列.(1)求动点M的轨迹方程;(2)设点M的轨迹为曲线T,过点N(0,2)作直线l交曲线T于C,D两点,试问在y轴上是否存在定点Q,使得为定值?若存在,求出定点Q的坐标,若不存在,说明理由.20.(12分)已知函数f(x)=axe x+(x+1)sin x+cos x.(1)若a=1,,求函数f(x)的最小值;(2)函数,,若函数g(x)的导函数g'(x)存在零点,求实数a的取值范围.21.(12分)某中医药研究所研制出一种新型抗癌药物,服用后需要检验血液是否为阳性,现有n(n∈N*)份血液样本,每个样本取到的可能性均等,有以下两种检验方式:(1)逐份检验,则需要检验n次;(2)混合检验,将其中k(k∈N*,2≤k≤n)份血液样本分别取样混合在一起检验,若结果为阴性,则这k份的血液全为阴性,因而这k份血液样本只需检验一次就够了:若检验结果为阳性,为了明确这k份血液究竟哪份为阳性,就需要对这k份再逐份检验,此时这k份血液的检验次数总共为k+1次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是相互独立的,且每份样本是阳性的概率为p(0<p<1).(1)假设有6份血液样本,其中只有两份样本为阳性,若采取逐份检验的方式,求恰好经过两次检验就能把阳性样本全部检验出采的概率.(2)现取其中的k(k∈N*,2≤k≤n)份血液样本,记采用逐份检验的方式,样本需要检验的次数为ξ1;采用混合检验的方式,样本需要检验的总次数为ξ2.(ⅰ)若Eξ1=Eξ2,试运用概率与统计的知识,求p关于k的函数关系p=f(k);(ⅱ)若,采用混合检验的方式需要检验的总次数的期望比逐份检验的总次数的期望少,求k的最大值.(ln4=1.386,ln5=1.609,ln6=1.792,ln7=1.946,ln8=2.079,ln9=2.197)(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.(10分)已知在平面直角坐标系内,曲线C的参数方程为(θ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为.(1)把曲线C和直线l化为直角坐标方程;(2)过原点O引一条射线分别交曲线C和直线l于A,B两点,射线上另有一点M满足|OA|2=|OM|•|OB|,求点M的轨迹方程(写成直角坐标形式的普通方程).[选修4-5:不等式选讲]23.已知函数f(x)=2|x+2|﹣3|x﹣1|.(1)求函数f(x)的最大值M;(2)已知a>0,b>0,a+4b=M,求的最大值.。

2024年新高考数学模拟卷A 卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}2468M =,,,,{}2|280N x x x =--≤,则M N ⋂=()A .{}2,4B .{}2,4,6C .{}2,4,6,8D .[]24,【答案】A【详解】由题意{}2|280{|24}N x x x x x =--≤=-≤≤,∴{2,4}M N ⋂=.故选:A .2.复数2(2)i z i-=i 为虚数单位,则A .25B .C .5D .【答案】C【详解】()()()223443,1i i i z i i--⨯-===--()()2243 5.z -+-=3.已知()1,3a =-,()2,1b =- ,且()()2//a b ka b +-,则实数k =()A .2-B .2C .12D .12-【答案】D【详解】 (1,3)=- a ,()2,1b =- ,(1ka b k ∴-= ,3)(2---,1)(2k =+,13)k --,2(3,1)a b +=--,()//(2)ka b a b +-,(2)3(13)k k ∴-+=---,∴解得:12k =-.故选:D .4.已知函数2,(1)()4,(1)x a x ax x f x a x ⎧-++<⎪=⎨⎪≥⎩,若()y f x =在(),-∞+∞上单调递增,则实数a 的取值范围是()A .[]2,4B .()2,4C .()2,+∞D .[)2,+∞【答案】A【详解】()f x 在(),-∞+∞上单调递增;∴2112211414aa a a a a a a⎧≥⎪≥⎧⎪⎪>⇒>⎨⎨⎪⎪≤⎩⎪-++≤⎩,解得24a ≤≤;所以实数a 的取值范围为[]2,4.故选:A .5.若椭圆X :()22211x y a a +=>与双曲线H :2213x y -=的离心率之和为736,则=a ()A .2B 3C 2D .1【答案】A【详解】椭圆X :()22210x y aa +=>H :2213x y -==,=2a=.故选:A.6.设过点(0,P 与圆22:410C x y x +--=相切的两条直线的夹角为α,则cos α=()A .19BC .19-D .【答案】A【详解】解法1:如图,圆22410x yx +--=,即22(2)5x y -+=,则圆心(2,0)C ,半径r ,过点(0,P 作圆C 的切线,切点为,A B ,连接AB .因为3PC =,则2PA PB ==,得2sin 3APC APC ∠∠=,则221cos cos sin 09APB APC APC∠=∠-∠=-<,即APB ∠为钝角,且α为锐角,所以1cos cos(π)9APB α=-∠=.故选A.解法2:如图,圆22410x y x +--=,即22(2)5x y -+=,则圆心(2,0)C ,半径r =,过点(0,P 作圆C 的切线,切点为,A B ,连接AB .因为3PC =,则2PA PB ==,因为22222cos 2cos PA PB PA PB APB CA CB CA CB ACB+-⋅∠=+-⋅∠,且πACB APB ∠=-∠,则448cos 5510cos APB ACB +-∠=+-∠,即44cos 55cos APB ACB -∠=-∠,解得1cos 09APB ∠=-<,即APB ∠为钝角,且α为锐角,则1cos cos(π)9APB α=-∠=.故选:A.解法3:圆22410x y x +--=,即22(2)5x y -+=,则圆心(2,0)C ,半径r =线方程为0x=,则圆心到切点的距离2d r =<,不合题意;若切线斜率存在,则设切线方程为y kx =,即0kx y -=,则圆心到切线的距离d =120,k k ==-1212sin tan 1cos k k k k ααα-==+,又α为锐角,由22sin cos 1αα+=解得1cos 9α=.故选:A.7.若数列{}n a 满足212n na p a +=(p 为常数,n ∈N ,1n ≥),则称{}n a 为“等方比数列”.甲:数列{}n a 是等方比数列;乙:数列{}n a 是等比数列,则().A .甲是乙的充分非必要条件B .甲是乙的必要非充分条件C .甲是乙的充要条件D .甲是乙的既非充分也非必要条件【答案】B【详解】若{}n a 为等比数列,设其公比为q ,则()222112n n n n a a q p a a ++⎛⎫=== ⎪⎝⎭,p 为常数,所以{}2n a 成等比数列,即{}n a 是等方比数列,故必要性满足.若{}n a 是等方比数列,即{}2n a 成等比数列,则{}n a 不一定为等比数列,例如23452,2,2,2,2,...--,有()221224n na a +=±=,满足{}n a 是等方比数列,但{}n a 不是等比数列,充分性不满足.故选:B8.若ππ2sin sin sin 44βααβ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭,则()tan αβ+=()A .-1B .1C .-2D .2【答案】A【详解】解法一:由题得()()2sin sin cos 2222βαααβαβ⎫-=-+-⎪⎪⎝⎭,所以2sin sin 2cos sin sin cos cos sin cos cos sin sin αβαβαβαβαβαβ-=-++,即sin cos cos sin cos cos sin sin 0αβαβαβαβ++-=,即()()sin cos 0αβαβ+++=,显然()cos 0αβ+≠,故()tan 1αβ+=-.解法二:令π4αθ-=,则π4αθ=+,所以ππ2sin sin sin 44βααβ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭可化为π2sin sin sin 2βθθβ⎛⎫=-+ ⎪⎝⎭,即()2sin sin cos βθθβ=-,所以2sin sin cos cos sin sin βθθβθβ=+,即cos cos sin sin 0θβθβ-=,所以()cos 0θβ+=,则ππ2k θβ+=+,k ∈Z ,所以()πππ3πtan tan tan πtan 14424k αβθβ⎛⎫⎛⎫+=++=++==- ⎪ ⎪⎝⎭⎝⎭,k ∈Z .故选:A.二、多选题:本题共3小题,每小题6分,共18分。

2020年河南省高考数学模拟试卷(理科) (4月份)第1页(共23页)一项是符合题目要求的.价有所下降,相比二手房而言, 新房市场依然强劲,价格持续升高.已知销售人员主要靠售 房提成领取工资.现统计郑州市某新房销售人员一年的工资情况的结果如图所示, 若近几年 来该销售人员每年的工资总体情况基本稳定,则下列说法正确的是 ( )A .月工资增长率最高的为 8月份B .该销售人员一年有 6个月的工资超过4000元C .由此图可以估计,该销售人员 2020年6, 7, 8月的平均工资将会超过 5000元D .该销售人员这一年中的最低月工资为 1900元6. (5分)九连环是我国古代至今广为流传的一种益智游戏,它由九个铁丝圆环相连成串,、选择题:本题共 12小题,每小题5分,共60分.在每小题给出的四个选项中,只有1. (5分)已知集合 {x|x ・・0} , B {x|y lg(x 2 x)},则 A |2.3. A . [0 , ) (5分)已知复数 (5 分)2019 年, B . (1,) C . {0}U [1, (,0】U (1,) — (i 为复数单位) (i 1) B . 2 ,则 |z| ( ) 河南省郑州市总体来说,二手房房 54. ( 5分)已知(x 1) 2 a 0 a 1 x a 2x 3 a 3X 4 5 a 4X a 5X ,贝U a 2 a 4的值为 C . 15 D . 165. ( 5分)已知双曲线 2 2 C:a 話 1(a 0,b 0)的一个焦点为F ,过F 作x 轴的垂线分别 交双曲线的两渐近线于 A , B 两点,若 AOB的面积为2b 2,则双曲线C 的离心率为( )按一定规则移动圆环的次数,决定解开圆环的个数.在某种玩法中,用 则解下5个环所需的最少移动次数为 ( )7. (5分)已知某个几何体的三视图如图所示,根据图中标出的数据,可得出这个几何体的表面积是( ) uuiur uuuu于点O ,点M 是线段BC 上一点,则 OM gDM 的最小值为(10 . ( 5分)已知ABCD 为正方形,其内切圆I 与各边分别切于事件B :豆子落在四边形 EFGH 夕卜,则P (B|A )( )n (n, 9,n N *)个圆环所需的多少移动次数,数列{a n }满足a i 1,且a n2a n i 1,n 为偶数2a n i 2,n 为奇数 a n 表示解下B . 10C . 16D . 22B . 8 4.6C . 426D . 4.6(5分)已知函y sin( 0)在区间( 齐)上单调递增,则 的取值范围是( 1A . (0,—] 2 1 [-,1] 2 1 2 (-,一] 3 3 2[-,2] 3(5分)已知平行四边形 ABCD 中, AB AD 2, DAB 60 对角线AC 与,G , H ,连接 EF ,FG , GH , HE .现向正方形 ABCD 内随机抛掷一枚豆子, 记事件 A :豆子落在圆I 内,C. 1 -11. (5分)已知定义在R上的奇函数f (x),对任意实数x,恒有f(x 3) f (x),且当3 2x (0,㊁]时,f(x) x 6x 8,贝U f (0) f (1) f ( 2) f (2020)(C.12. (5分)如图,在四棱锥P ABCD中, PA PB PC PD 2 ,底面ABCD是边长为2E作棱锥的截面, 分别与侧棱PB , PD交于M , 的正方形.点E是PC的中点,过点A ,( )A .辽3B .二3二、填空题:本题共4小题,每小题5分,共20 分.13. (5分)已知函数f (x) (x 2) lnx,则函数f (x)在x 1处的切线方程为14. (5分)已知数列{a n}为公差不为零的等差数列,其前n项和为£,且印,a2 , a4成等比数列,S515,则a415. (5分)现有灰色与白色的卡片各八张.分别写有数字1至U &甲、乙.丙、丁四个人每人面前摆放四张,并按从小到大的顺序自左向右排列(当灰色卡片和白色卡片数字相同时,白色卡片摆在灰色卡片的右侧)卡片是(填写字母)..如图,甲面面的四张卡片已经翻开,则写有数字4的灰色X216. (5分)设F , F2是椭圆C:—4y2 1的两个焦点,过F! , F2分别作直线h , I2 .且h //I2 ,。

一、单选题二、多选题1. 如图所示,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E 是棱DD 1的中点,F 是侧面CDD 1C 1上的动点,且B 1F ∥平面A 1BE ,则F 在侧面CDD 1C 1上的轨迹的长度是()A .aB.C.D.2. ( )A.B.C.D.3.方程的解集为( )A.B.C.D.4. 已知各项均为正数的等比数列的前项和为,若,,则( )A .27B .32C .64D .815. 关于函数,的性质,以下说法正确的是( )A .函数的周期是B .函数在上有极值C .函数在单调递减D .函数在内有最小值6. 如图ABCDEF 为五面体,其中四边形ABCD 为矩形,,,和都是正三角形,则该五面体的体积为()A.B.C.D.7. 函数的最小正周期是( )A .B.C.D.8. 已知函数有两个极值点,若,则关于的方程的不同实根个数为( )A .2B .3C .4D .59. 已知数列对任意的整数,都有,则下列说法中正确的有( )A .若,则B.若,,则C .数列可以是等差数列D .数列可以是等比数列河南省(豫北重点高中)2021-2022学年高三下学期4月份模拟考试理科数学试题(高频考点版)河南省(豫北重点高中)2021-2022学年高三下学期4月份模拟考试理科数学试题(高频考点版)三、填空题四、解答题10. 已知平面直角坐标系中,,,动点满足,其轨迹为一条连续的封闭曲线.则( )A.曲线关于轴对称B .曲线与轴交点为和C .面积的最大值为6D.的取值范围为11.数列各项均为正数,其前n 项和,且满足,下列四个结论中正确的是( )A .为等比数列B .为递减数列C .中存在大于3的项D .中存在小于的项12. 已知抛物线,为坐标原点,点为直线上一点,过点作抛物线的两条切线,切点分别为,,则( )A.抛物线的准线方程为B .直线一定过抛物线的焦点C .线段长的最小值为D.13. 已知圆,直线.若,过点可作两条与圆分别相切于,且,则实数的取值范围为________.14. 某小区要建一座八边形的休闲公园,它的主体造型的平面图是由两个相同的矩形和构成的面积为的十字型地域,计划在正方形上建一座花坛,造价为4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元,再在四个空角(图中四个三角形)上铺草坪,造价为80元.设总造价为(单位:元),长为(单位:).的最小值是___________,此时的值是___________.15. 已知中,D在线段上,的长分别为2、3、6,则长为_______,的面积为________.16.如图,四棱锥中,侧面底面,,,,,,点在棱上,且,点在棱上,且平面.(1)求证:平面;(2)求二面角的余弦值.17. 已知中心在原点,焦点在轴上的椭圆的离心率为,椭圆上异于长轴顶点的任意点与左右两焦点、构成的三角形中面积的最大值为.(1)求椭圆的标准方程;(2)已知点,连接与椭圆的另一交点记为,若与椭圆相切则视为、重合,连接与椭圆的另一交点记为,求的取值范围.18. 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别,,,,(单位:克)中,经统计频率分布直方图如图所示.(1)估计这组数据的平均数;(2)在样本中,按分层抽样从质量在,中的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中共有芒果大约10000个,经销商提出以下两种收购方案:方案①:所有芒果以10元/千克收购;方案②:对质量低于350克的芒果以3元/个收购,对质量高于或等于350克的芒果以5元/个收购.请通过计算确定种植园选择哪种方案获利更多?19. 已知函数.(1)当时,求的单调区间;(2)当且时,讨论在上的零点个数.20. 已知,证明:;并讨论为何值时等号成立.21. 某高校组织自主招生考试,共有2000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名学生的成绩进行统计,将统计的结果按如下方式分成八组:第一组,第二组,……,第八组.如图是按上述分组方法得到的频率分布直方图:(1)求值并估计这2000名学生的平均分;(2)若计划按成绩取1000名学生进入面试环节,试估计应将分数线定为多少?。

一、单选题二、多选题三、填空题1.已知函数,其中表示不超过的最大整数,下列关于说法正确的是( )①函数为偶函数;②的值域为;③为周期函数,且周期; ④与的图象恰有一个公共点.A .①③B .②③C .③④D .①④2.已知等差数列公差,数列为正项等比数列,已知,则下列结论中正确的是( )A.B.C.D.3. 已知幂函数的图象经过点,下面给出的四个结论:①;②为奇函数;③在R 上单调递增;④,其中所有正确命题的序号为( )A .①④B .②③C .②④D .①②③4. 古印度数学家婆什迦罗在《莉拉沃蒂》一书中提出如下问题:某人给一个人布施,初日4德拉玛(古印度货币单位),其后日增5德拉玛.朋友啊,请马上告诉我,半个月中,他总共布施多少德拉玛?在这个问题中,这人15天的最后7天布施的德拉玛总数为( )A .413B .427C .308D .1335. 圆锥中,为圆锥顶点,为底面圆的圆心,底面圆半径为3,侧面展开图面积为,底面圆周上有两动点,则面积的最大值为( )A .4B.C.D .66. 为落实“五育并举”的全面培养的教育体系,某校开设了中华传统文化美德讲习、地方特色美食烹饪、本区域民族体育项目及汉文化礼仪四门选修校本课,该校某班级有6名同学分别选修其中的一门课程,每门课程至少有一位同学选修,则恰有2名同学选修本区域民族体育项目的概率为( )A.B.C.D.7. 已知为非零实数,且,则下列结论正确的是( )A.B.C.D.8. 筒车亦称为“水转筒车”,一种以流水为动力,取水灌田的工具,筒车发明于隋而盛于唐,距今已有1000多年的历史.如图,假设在水流量稳定的情况下,一个半径为3米的筒车按逆时针方向做每6分钟转一圈的匀速圆周运动,筒车的轴心距离水面的高度为1.5米,设筒车上的某个盛水筒的初始位置为点(水面与筒车右侧的交点),从此处开始计时,下列结论正确的是()A .分钟时,以射线为始边,为终边的角为B .分钟时,该盛水筒距水面距离为米C .1分钟时该盛水筒距水面距离与3分钟时该盛水筒距水面距离相等D .1个小时内有20分钟该盛水筒距水面距离不小于3米河南省(豫北重点高中)2021-2022学年高三下学期4月份模拟考试理科数学试题(2)河南省(豫北重点高中)2021-2022学年高三下学期4月份模拟考试理科数学试题(2)四、解答题9.,,且,若对于任意的x ,y 不等式恒成立,则实数k 的取值范围为______.10. 已知集合若则___________.11.已知是以为周期的奇函数,且时,,则当时,的解析式为______________12. 去掉正整数中被4整除以及被4除余1的数,剩下的正整数按自小到大的顺序排成数列,再将数列中第项去掉,中剩余的项按自小到大的顺序排成数列,则的值为__________.13. 计算:(1);(2).14.如图,在四棱柱中,平面,底面满足,且,.(1)求证:平面;(2)求直线与平面所成角的正弦值.15. 已知,(1)求的值;(2)求的值.16.(1)请用文字语言叙述异面直线的判定定理;(2)把(1)中的定理写成“已知:...,求证:...”的形式,并用反证法证明.。
河南省高考数学模拟试卷(理科)(4月份)A卷
姓名:________ 班级:________ 成绩:________
一、选择题 (共12题;共24分)
1. (2分) (2018高三上·杭州月考) 已知全集,设集合,,则
()
A .
B .
C .
D .
2. (2分)复数,则复数在复平面上对应的点位于()
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
3. (2分) (2018高二下·辽宁期中) 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:)可得这个几何体的体积是()
A .
B .
C .
D .
4. (2分)已知函数,下面结论错误的是()
A . 函数的最小正周期为
B . 函数在区间上是增函数
C . 函数的图象关于直线x=0对称
D . 函数是奇函数
5. (2分)执行如图所示的程序框图,输出的a值为()
A . 3
B . 5
C . 7
D . 9
6. (2分)已知数列的通项公式,则数列的前项和取得最小值时的值为()
A .
B .
C .
D .
7. (2分)定义:若函数f(x)的图象经过变换T后所得图象对应函数的值域与f(x)的值域相同,则称变换T是f(x)的同值变换.下面给出四个函数及其对应的变换T,其中T不属于f(x)的同值变换的是()
A . f(x)=, T将函数f(x)的图象关于y轴对称
B . f(x)=, T将函数f(x)的图象关于x轴对称
C . f(x)=2x+3,T将函数f(x)的图象关于点(﹣1,1)对称
D . , T将函数f(x)的图象关于点(﹣1,0)对称
8. (2分) (2016高二下·珠海期末) 5名学生4名老师站成一排合影,5名学生站一起的排法种数为()
A .
B .
C .
D .
9. (2分)如图所示,在正方体ABCDA1B1C1D1中,E , F分别是AB , AD的中点,则异面直线B1C与EF 所成的角的大小为()
A . 30°
B . 45°
C . 60°
D . 90°
10. (2分) (2019高一下·哈尔滨月考) 已知,为三角形所在平面上的一点,且点满足:
,则点为三角形的()
A . 外心
B . 垂心
C . 重心
D . 内心
11. (2分) (2015高三下·武邑期中) 已知双曲线,它的一个顶点到较近焦点的距
离为1,焦点到渐近线的距离是,则双曲线C的方程为()
A . x2﹣ =1
B . ﹣y2=1
C . ﹣y2=1
D . x2﹣ =1
12. (2分) (2019高二上·烟台期中) 若函数在区间内是增函数,则实数的取值范围是()
A .
B .
C .
D .
二、填空题 (共4题;共4分)
13. (1分)若x,y满足约束条件,则目标函数z=﹣2x+y的最小值为________
14. (1分)(2017·广元模拟) 若 + +…+ =256,则的展开式中含x5项的系数为________.(用数字作答)
15. (1分) (2015高二上·东莞期末) 已知数列{an}的前n项和,则an=________.
16. (1分) (2017高一上·深圳期末) 在函数①y=2x;②y=2﹣2x;③f(x)=x+x﹣1;④f(x)=x﹣x﹣3中,存在零点且为奇函数的序号是________.
三、解答题 (共7题;共70分)
17. (10分) (2018高三上·双鸭山月考) 在中,角所对的边分别为,且满足
, .
(1)求的面积;
(2)若、的值.
18. (15分) (2016高二下·南城期中) 心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如表:(单位:人)
几何题代数题总计
男同学22830
女同学81220
总计302050
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5﹣7分钟,乙每次解答一道几何题所用的时间在6﹣8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式:
P(K2≥k)0.150.100.050.0250.0100.0050.001
k 2.072 2.706 3.841 5.024 6.6357.87910.828
K2= .
19. (10分)(2016·运城模拟) 如图,四棱猪ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E为棱AA1的中点.
(1)
证明:B1C1⊥CE;
(2)
求二面角B1﹣CE﹣C1的余弦值.
20. (10分) (2015高二上·安阳期末) 已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个短轴端点是(0,2 ).
(1)求椭圆C的方程;
(2) P(2,3)、Q(2,﹣3)是椭圆上两点,A、B是椭圆位于直线PQ两侧的两动点,
①若直线AB的斜率为,求四边形APBQ面积的最大值;
②当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
21. (10分)已知,设函数
(1)若,求函数在上的最小值;
(2)讨论函数的单调性.
22. (10分) (2015高三上·务川期中) 已知直线l的方程为ρsin(θ+ )= ,圆C的方程为
(θ为参数).
(1)把直线l和圆C的方程化为普通方程;
(2)求圆C上的点到直线l距离的最大值.
23. (5分) (2019高一上·浙江期中) 经市场调查,某种小家电在过去天的销售量(台)和价格(元)均为销售时间 (天)的函数,且销售量近似地满足 .前天价格为
;后天价格为 .
(Ⅰ)写出该种商品的日销售额 (元)与时间的函数关系;
(Ⅱ)求日销售额 (元)的最大值.
参考答案一、选择题 (共12题;共24分)
1-1、
2-1、答案:略
3-1、
4-1、
5-1、答案:略
6-1、
7-1、答案:略
8-1、答案:略
9-1、
10-1、
11-1、
12-1、
二、填空题 (共4题;共4分)
13-1、
14-1、
15-1、
16-1、
三、解答题 (共7题;共70分) 17-1、答案:略
17-2、答案:略
18-1、答案:略
18-2、答案:略
18-3、答案:略
19-1、答案:略
19-2、答案:略
20-1、答案:略
20-2、答案:略
21-1、答案:略
21-2、答案:略
22-1、答案:略
22-2、答案:略
23-1、
第11 页共11 页。