正态分布测试题

利用正态分布求概率练习题正态分布是概率论与统计学中的一种重要分布，也被称为高斯分布。

利用正态分布求概率是统计学中常见的问题，下面将通过一些练习题来演示如何利用正态分布求解概率。

1. 练习题一：假设某城市成年男性的身高服从均值为175厘米，标准差为6厘米的正态分布。

现在我们想要计算这个城市成年男性身高在160厘米到170厘米之间的概率。

解答：首先，我们需要将身高标准化为标准正态分布。

标准化的方法是计算出以下z分数：z = (x - μ) / σ其中，x代表某个具体的身高数值，μ代表均值，σ代表标准差。

将x=160代入计算：z1 = (160 - 175) / 6 = -2.5将x=170代入计算：z2 = (170 - 175) / 6 = -0.83然后，我们需要查找标准正态分布表来获得对应z值的概率。

查表可知，z1对应的概率为0.0062，z2对应的概率为0.2031。

因此，成年男性身高在160厘米到170厘米之间的概率为：P(160 ≤ x ≤ 170) = P(-2.5 ≤ z ≤ -0.83) = P(z ≤ -0.83) - P(z ≤ -2.5) ≈0.2031 - 0.0062 ≈ 0.1969，约为0.197。

2. 练习题二：某汽车厂商生产的轮胎的寿命服从均值为40000公里，标准差为2000公里的正态分布。

现在要求计算这种轮胎的寿命超过43000公里的概率。

解答：同样地，我们需要将寿命标准化为标准正态分布。

标准化的公式为：z = (x - μ) / σ将x=43000代入计算：z = (43000 - 40000) / 2000 = 1.5我们需要查找标准正态分布表来获得对应z值的概率。

查表可知，z=1.5对应的概率为0.9332。

因此，这种轮胎的寿命超过43000公里的概率为：P(x > 43000) = P(z > 1.5) = 1 - P(z ≤ 1.5) = 1 - 0.9332 = 0.0668，约为0.067。

高中数学:二项分布、正态分布及其应用练习1．设X ～N (μ1,σ21),Y ～N (μ2,σ22),这两个正态分布密度曲线如图所示．下列结论中正确的是( C )A ．P (Y ≥μ2)≥P (Y ≥μ1)B ．P (X ≤σ2)≤P (X ≤σ1)C ．对任意正数t ,P (X ≤t )≥P (Y ≤t )D ．对任意正数t ,P (X ≥t )≥P (Y ≥t ) 解析:由题图可知μ1<0<μ2,σ1<σ2, ∴P (Y ≥μ2)<P (Y ≥μ1),故A 错 ； P (X ≥σ2)>P (X ≤σ1),故B 错； 当t 为任意正数时,由题图可知 P (X ≤t )≥P (Y ≤t ),而P (X ≤t )＝1－P (X ≥t ),P (Y ≤t )＝1－P (Y ≥t ), ∴P (X ≥t )≤P (Y ≥t ),故C 正确,D 错．2．(福建厦门模拟)袋中装有2个红球,3个黄球,有放回地抽取3次,每次抽取1球,则3次中恰有2次抽到黄球的概率是( D )A.25B.35C.18125D.54125解析:袋中装有2个红球,3个黄球,有放回地抽取3次,每次抽取1球,每次取到黄球的概率P 1＝35,∴3次中恰有2次抽到黄球的概率是P ＝C 23⎝ ⎛⎭⎪⎫352⎝ ⎛⎭⎪⎫1－35＝54125. 3．(河北唐山模拟)甲乙等4人参加4×100米接力赛,在甲不跑第一棒的条件下,乙不跑第二棒的概率是( D )A.29 B.49C.23 D.79解析:甲不跑第一棒共有A13·A33＝18种情况,甲不跑第一棒且乙不跑第二棒共有两类:(1)乙跑第一棒,共有A33＝6种情况；(2)乙不跑第一棒,共有A12·A12·A22＝8种情况,∴甲不跑第一棒的条件下,乙不跑第二棒的概率为6＋818＝79.故选D.4．(山东淄博一模)设每天从甲地去乙地的旅客人数为随机变量X,且X～N(800,502)．则一天中从甲地去乙地的旅客人数不超过900的概率为(A)(参考数据:若X～N(μ,σ2),有P(μ－σ<X≤μ＋σ)＝0.682 6,P(μ－2σ<X≤μ＋2σ)＝0.954 4,P(μ－3σ<X≤μ＋3σ)＝0.997 4)A．0.977 2 B．0.682 6C．0.997 4 D．0.954 4解析:∵X～N(800,502),∴P(700≤X≤900)＝0.954 4,∴P(X>900)＝1－0.954 42＝0.022 8,∴P(X≤900)＝1－0.022 8＝0.977 2.故选A.5．甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分)．甲组:76,90,84,86,81,87,86,82,85,83乙组:82,84,85,89,79,80,91,89,79,74现从这20名学生中随机抽取一人,将“抽出的学生为甲组学生”记为事件A；“抽出的学生的英语口语测试成绩不低于85分”记为事件B,则P(AB),P(A|B)的值分别是(A)A.14,59 B.14,49C.15,59 D.15,49解析:由题意知,P(AB)＝1020×510＝14,根据条件概率的计算公式得P(A|B)＝P(AB)P(B)＝14920＝59.6．为向国际化大都市目标迈进,某市今年新建三大类重点工程,它们分别是30项基础设施类工程、20项民生类工程和10项产业建设类工程．现有3名民工相互独立地从这60个项目中任选一个项目参与建设,则这3名民工选择的项目所属类别互异的概率是( D )A.12B.13C.14D.16解析:记第i 名民工选择的项目属于基础设施类、民生类、产业建设类分别为事件A i ,B i ,C i ,i ＝1,2,3.由题意,事件A i ,B i ,C i (i ＝1,2,3)相互独立,则P (A i )＝3060＝12,P (B i )＝2060＝13,P (C i )＝1060＝16,i ＝1,2,3,故这3名民工选择的项目所属类别互异的概率是P ＝A 33P (A i B i C i )＝6×12×13×16＝16.7．位于坐标原点的一个质点P 按下述规则移动:质点每次移动一个单位,移动的方向为向上或向右,并且向上、向右移动的概率都是12.质点P 移动五次后位于点(2,3)的概率是516.解析:由于质点每次移动一个单位,移动的方向为向上或向右,移动五次后位于点(2,3),所以质点P 必须向右移动两次,向上移动三次,故其概率为C 35⎝ ⎛⎭⎪⎫123·⎝ ⎛⎭⎪⎫122＝C 35⎝ ⎛⎭⎪⎫125＝C 25⎝ ⎛⎭⎪⎫125＝516. 8．(江西南昌模拟)口袋中装有大小形状相同的红球2个,白球3个,黄球1个,甲从中不放回地逐一取球,已知第一次取得红球,则第二次取得白球的概率为35.解析:口袋中装有大小形状相同的红球2个,白球3个,黄球1个,甲从中不放回地逐一取球,设事件A 表示“第一次取得红球”,事件B 表示“第二次取得白球”,则P (A )＝26＝13,P (AB )＝26×35＝15,∴第一次取得红球后,第二次取得白球的概率为P (B |A )＝P (AB )P (A )＝1513＝35.9.如图,四边形EFGH 是以O 为圆心,半径为1的圆的内接正方形．将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则P (B |A )＝14.解析:由题意可得,事件A发生的概率P(A)＝S正方形EFGHS圆O＝2×2π×12＝2π.事件AB表示“豆子落在△EOH内”,则P(AB)＝S△EOHS圆O＝12×12π×12＝12π,故P(B|A)＝P(AB)P(A)＝12π2π＝14.10．某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作．设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1 000小时的概率为3 8.解析:设元件1,2,3的使用寿命超过1 000小时的事件分别记为A,B,C,显然P(A)＝P(B)＝P(C)＝12,∴该部件的使用寿命超过1 000小时的事件为(A B＋A B＋AB)C,∴该部件的使用寿命超过1 000小时的概率P＝⎝⎛⎭⎪⎫12×12＋12×12＋12×12×12＝38.11．(2014·新课标Ⅰ)从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:(1)求这500件产品质量指标值的样本平均数x和样本方差s2(同一组中的数据用该组区间的中点值作代表)；(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数x,σ2近似为样本方差s2.(ⅰ)利用该正态分布,求P(187.8＜Z＜212.2)；(ⅱ)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数．利用(ⅰ)的结果,求E(X)．附:150≈12.2.若Z～N(μ,σ2),则P(μ－σ＜Z＜μ＋σ)＝0.682 6,P(μ－2σ＜Z＜μ＋2σ)＝0.954 4.解:(1)抽取产品的质量指标值的样本平均数x和样本方差s2分别为x＝170×0.02＋180×0.09＋190×0.22＋200×0.33＋210×0.24＋220×0.08＋230×0.02＝200,s2＝(－30)2×0.02＋(－20)2×0.09＋(－10)2×0.22＋0×0.33＋102×0.24＋202×0.08＋302×0.02＝150.(2)(ⅰ)由(1)知,Z～N(200,150),从而P(187.8<Z<212.2)＝P(200－12.2<Z<200＋12.2)＝0.682 6.(ⅱ)由(ⅰ)知,一件产品的质量指标值位于区间(187.8,212.2)的概率为0.682 6,依题意知X～B(100,0.682 6),所以E(X)＝100×0.682 6＝68.26.12．(广东顺德一模)某市市民用水拟实行阶梯水价,每人月用水量不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了100位市民,获得了他们某月的用水量数据,整理得到如下频率分布直方图,并且前四组频数成等差数列．(1)求a ,b ,c 的值及居民月用水量在2～2.5内的频数；(2)根据此次调查,为使80%以上居民月用水价格为4元/立方米,应将w 定为多少？(精确到小数点后2位)(3)若将频率视为概率,现从该市随机调查3名居民的月用水量,将月用水量不超过2.5立方米的人数记为X ,求其分布列及均值．解:(1)∵前四组频数成等差数列, ∴所对应的频率组距也成等差数列,设a ＝0.2＋d ,b ＝0.2＋2d ,c ＝0.2＋3d ,∴0.5(0.2＋0.2＋d ＋0.2＋2d ＋0.2＋3d ＋0.2＋d ＋0.1＋0.1＋0.1)＝1, 解得d ＝0.1,∴a ＝0.3,b ＝0.4,c ＝0.5.居民月用水量在2～2.5内的频率为0.5×0.5＝0.25. 居民月用水量在2～2.5内的频数为0.25×100＝25. (2)由题图及(1)可知,居民月用水量小于2.5的频率为0.7<0.8, ∴为使80%以上居民月用水价格为4元/立方米, 应规定w ＝2.5＋0.10.15×0.5≈2.83.(3)将频率视为概率,设A (单位:立方米)代表居民月用水量, 可知P (A ≤2.5)＝0.7, 由题意,X ～B (3,0.7),P (X ＝0)＝C 03×0.33＝0.027, P (X ＝1)＝C 13×0.32×0.7＝0.189, P (X ＝2)＝C 23×0.3×0.72＝0.441, P (X ＝3)＝C 33×0.73＝0.343.∴X 的分布列为X12 3P 0.0270.1890.4410.343∵X～B(3,0.7),∴E(X)＝np＝2.1.13．(广东茂名一模)设X～N(1,1),其正态分布密度曲线如图所示,那么向正方形ABCD中随机投掷10 000个点,则落入阴影部分的点的个数的估计值是(D)(注:若X～N(μ,σ2),则P(μ－σ<X<μ＋σ)＝68.26%,P(μ－2σ<X<μ＋2σ)＝95.44%)A．7 539 B．6 038C．7 028 D．6 587解析:∵X～N(1,1),∴μ＝1,σ＝1.∵P(μ－σ<X<μ＋σ)＝68.26%,∴P(0<X<2)＝68.26%,则P(1<X<2)＝34.13%,∴阴影部分的面积为1－0.341 3＝0.658 7.∴向正方形ABCD中随机投掷10 000个点,则落入阴影部分的点的个数的估计值是10 000×0.658 7＝6 587.故选D.14．(金华一中模拟)春节放假,甲回老家过节的概率为13,乙、丙回老家过节的概率分别为14,15.假定三人的行动相互之间没有影响,那么这段时间内至少1人回老家过节的概率为(B)A.5960 B.35C.12 D.160解析:“甲、乙、丙回老家过节”分别记为事件A,B,C,则P(A)＝13,P(B)＝14,P(C)＝15,所以P(A)＝23,P(B)＝34,P(C)＝45.由题知A,B,C为相互独立事件,所以三人都不回老家过节的概率P(A B C)＝P(A)P(B)P(C)＝23×34×45＝25,所以至少有一人回老家过节的概率P＝1－25＝35.15．甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球．先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示由甲罐取出的球是红球,白球和黑球的事件；再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是②④.(写出所有正确结论的序号)①P(B)＝2 5；②P(B|A1)＝5 11；③事件B与事件A1相互独立；④A1,A2,A3是两两互斥的事件；⑤P(B)的值不能确定,它与A1,A2,A3中哪一个发生都有关．解析:由题意知A1,A2,A3是两两互斥的事件,P(A1)＝510＝12,P(A2)＝210＝15,P(A3)＝310,P(B|A1)＝12×51112＝511,由此知,②正确；P(B|A2)＝411,P(B|A3)＝411,而P(B)＝P(A1B)＋P(A2B)＋P(A3B)＝P(A1)P(B|A1)＋P(A2)P(B|A2)＋P(A3)P(B|A3)＝12×511＋15×411＋310×411＝922.由此知①③⑤不正确；A1,A2,A3是两两互斥事件,④正确,故答案为②④.16．(河北石家庄新华模拟)“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标值,所得频率分布直方图如下:(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数x(同一组中的数据用该组区间的中点值作代表)；(2)①由直方图可以认为,速冻水饺的该项质量指标值Z 服从正态分布N (μ,σ2),利用该正态分布,求Z 落在(14.55,38.45)内的概率；②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于(10,30)内的包数为X ,求X 的分布列和数学期望．附:计算得所抽查的这100包速冻水饺的质量指标值的标准差为σ＝142.75≈11.95； 若ξ～N (μ,σ2),则P (μ－σ<ξ≤μ＋σ)＝0.682 6,P (μ－2σ<ξ≤μ＋2σ)＝0.954 4.解:(1)所抽取的100包速冻水饺该项质量指标值的平均数x ＝5×0.1＋15×0.2＋25×0.3＋35×0.25＋45×0.15＝26.5.(2)①∵Z 服从正态分布N (μ,σ2),且μ＝26.5,σ≈11.95,∴P (14.55<Z <38.45)＝P (26.5－11.95<Z <26.5＋11.95)＝0.682 6, ∴Z 落在(14.55,38.45)内的概率是0.682 6. ②根据题意得X ～B ⎝ ⎛⎭⎪⎫4，12,P (X ＝0)＝C 04⎝ ⎛⎭⎪⎫124＝116； P (X ＝1)＝C 14⎝ ⎛⎭⎪⎫124＝14； P (X ＝2)＝C 24⎝ ⎛⎭⎪⎫124＝38； P (X ＝3)＝C 34⎝ ⎛⎭⎪⎫124＝14； P (X ＝4)＝C 44⎝ ⎛⎭⎪⎫124＝116. ∴X 的分布列为X 0 1 2 3 4 P116143814116∴E (X )＝4×12＝2.。

正态分布一、选择题（本大题共8小题，共40.0分）1.某地市高三理科学生有30000名，在一次调研测试中，数学成绩，已知，若按分层抽样的方式取200份试卷进行成绩分析，则应从120分以上的试卷中抽取A. 5份B. 10份C. 15份D. 20份2.设两个正态分布和曲线如图所示，则有A. B.C. D.3.设随机变量服从正态分布，若，则a的值为A. B. C. 5 D. 34.已知随机变量，且，，则A. B. C. D.5.已知：，且，，则A. B. C. D.6.已知随机变量服从正态分布，则A. 4B. 6C. 8D. 117.设随机变量服从正态分布，则函数不存在零点的概率A. B. C. D.8.某一部件由三个电子元件按如图所示方式连接而成，元件1或元件2正常工作，则部件正常工作：设三个电子元件的使用寿命单位：小时均服从正态分布，若每个元件使用寿命超过1200小时的概率为，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过800小时的概率为A. B. C. D.二、填空题（本大题共5小题，共25.0分）9.随机变量X服从正态分布，，，则的最小值为______．10.若随机变量，则，已知随机变量，则______．11.若随机变量服从正态分布，，，设，且，在平面直角坐标系xOy中，若圆上有四个点到直线的距离为1，则实数c的取值范围是______12.下列说法中错误的有_________________残差图中残差点所在的水平带状区域越宽，则回归方程的预报精确度越高．两个模型中残差平方和越小的模型拟合的效果越好。

设随机变量X服从正态分布，若则根据下表提供的数据，线性回归方程为，那么表中13.某县10000名学生的某次数学考试成绩X服从正态分布，其密度函数曲线如图，则成绩X位于区间的人数大约是______ ．，，．三、解答题（本大题共3小题，共36.0分）14.“过大年，吃水饺”是我国不少地方过春节的一大习俗，2018年春节前夕，A市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标．求所抽取的100包速冻水饺该项质量指标值的样本平均数同一组中的数据用该组区间的中点值作代表；由直方图可以认为，速冻水饺的该项质量指标值Z服从正态分布，利用该正态分布，求Z落在内的概率；将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺，记这4包速冻水饺中这种质量指标值位于内的包数为X，求X的分布列和数学期望．附：计算得所抽查的这100包速冻水饺的质量指标的标准差为；若，则，．15.十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康．经过不懈的奋力拼搏，新农村建设取得巨大进步，农民收入也逐年增加．为了更好的制定2019年关于加快提升农民年收入力争早日脱贫的工作计划，该地扶贫办统计了2018年50位农民的年收入并制成如下频率分布直方图：根据频率分布直方图估计50位农民的年平均收入单位：千元同一组数据用该组数据区间的中点值表示；由频率分布直方图可以认为该贫困地区农民年收入X服从正态分布，其中近似为年平均收入，近似为样本方差，经计算得；，利用该正态分布，求：在2019年脱贫攻坚工作中，若使该地区约有占总农民人数的的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入大约为多少千元？为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1000位农民．若每个农民的年收人相互独立，问：这1000位农民中的年收入不少于千元的人数最有可能是多少？附：参考数据与公式，若，则；；；16.第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行，赛期10天，共设置射击、游泳、田径、篮球等27个大项，329个小项，共有来自100多个国家的近万名现役军人同台竞技．前期为迎接军运会顺利召开，武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动，努力让大家更多的了解军运会的相关知识，并倡议大家做文明公民，武汉市体育局为了解广大民众对军运会知识的知晓情况，在全市开展了网上问卷调查，民众参与度极高，现从大批参与者中随机抽取200名幸运参与者，他们得分满分100分数据，统计结果如下：若此次问卷调查得分总体服从正态分布，用样本估计总体，设，分别为这200人得分的平均值和标准差同一组数据用该区间的中点值作为代表，求，的值的值四舍五入取整数，并计算．在的条件下，为感谢大家参与这次活动，市体育局还对参加问卷调查的幸运市民制定如下奖励方案：得分低于的可以获得1次抽奖机会，得分不低于的可获得2次抽奖机会，在一次抽奖中，抽中价值15元的纪念品A的概率为，抽中价值为30元的纪念品B的概率为现有市民张先生参加了此次问卷调查并成为幸运参与者，记Y为他参加活动获得纪念品的总价值，求Y的分布列和数学期望，并估算此次纪念品所需要的总金额．参考数据：；；。

正态分布测试题及答案1. 正态分布是一种连续概率分布，其形状呈钟形曲线，也称为高斯分布。

以下哪个选项描述了正态分布的特征？A. 对称性B. 所有数据都集中在均值附近C. 曲线下的总面积等于1D. 所有选项都正确答案：D2. 如果一个随机变量X服从标准正态分布，那么它的均值μ和标准差σ分别是多少？A. μ=0，σ=1B. μ=1，σ=0C. μ=0，σ=0D. μ=1，σ=1答案：A3. 在正态分布中，68-95-99.7经验法则描述了数据的分布情况。

根据这个法则，以下哪个比例的数据落在均值的两个标准差之内？A. 68%B. 95%C. 99.7%D. 100%答案：B4. 假设一个正态分布的总体均值为100，标准差为15，随机抽取一个样本，样本容量为100。

根据中心极限定理，样本均值的分布情况如何？A. 样本均值服从均值为100，标准差为15的正态分布B. 样本均值服从均值为100，标准差为1.5的正态分布C. 样本均值服从均值为100，标准差为0.15的正态分布D. 样本均值服从均值为100，标准差为0.015的正态分布答案：B5. 正态分布的概率密度函数（PDF）表达式为f(x)=1/(σ√(2π)) *e^(-(x-μ)²/(2σ²))，其中μ和σ分别代表什么？A. μ代表均值，σ代表方差B. μ代表方差，σ代表均值C. μ代表均值，σ代表标准差D. μ代表标准差，σ代表方差答案：C结束语：以上是关于正态分布的一些基本测试题及答案，希望能够帮助大家更好地理解和掌握正态分布的相关知识。

高三数学正态分布试题1.（2011•湖北）已知随机变量ξ服从正态分布N（2，a2），且P（ξ＜4）=0.8，则P（0＜ξ＜2）=（）A．0.6B．0.4C．0.3D．0.2【答案】C【解析】∵随机变量X服从正态分布N（2，σ2），μ=2，得对称轴是x=2．P（ξ＜4）=0.8∴P（ξ≥4）=P（ξ＜0）=0.2，∴P（0＜ξ＜4）=0.6∴P（0＜ξ＜2）=0.3．故选C．2.设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-1<X<0)=()A．p B．1-2pC．-p D．p-【答案】C【解析】∵X～N(0,1),∴对称轴为x=0,∴P(X>1)=p,∴P(X<-1)=p,∴P(-1<X<0)=P(-1<X<1)==-p.3.已知随机变量X服从正态分布N(2，σ2)，且P(X<4)＝0.8，则P(0<X<2)＝________．【答案】0.3【解析】P(X<4)＝0.8，则P(X>4)＝0.2，又因为分布图像关于直线x＝2对称，则P(X<0)＝P(X>4)＝0.2，则P(0<X<4)＝0.6，P(0<X<2)＝0.3.4.设随机变量ξ服从正态分布N(μ，σ2)，函数f(x)＝x2＋4x＋ξ没有零点的概率是，则μ＝()．A．1B．4C．2D．不能确定【答案】B【解析】据题意函数f(x)＝x2＋4x＋ξ没有零点时，Δ＝16－4ξ<0，即ξ>4，根据正态密度曲线的对称性，当函数f(x)＝x2＋4x＋ξ没有零点的概率是时，μ＝4.5.已知随机变量服从正态分布= 。

【答案】0.1587【解析】随机变量服从正态分布，所以对称轴为【考点】正态分布点评：正态分布的对称轴，6.已知随机变量，若，则等于．【答案】0.3；【解析】正态分布曲线的对称轴是x=0，而，所以等于0.5-0.2=0.3.【考点】本题主要考查正态分布的概念及其性质。

1.已知随机变量X服从正态分布N(1，σ2)，且P(0＜X≤1)＝0.4，则且P(X＞2)＝()．A.0.4B.0.1C.0.6D.0.2【答案】B随机变量ξ服从正态分布，∴曲线关于对称，∵，∴.2.某校高考数学成绩ξ近似地服从正态分布N（100，52），且P（ξ＜110）=0.96，则P（90＜ξ＜100）的值为（）A.0.49B.0.48C.0.47D.0.46【答案】D∵ξ近似地服从正态分布N（100，52），∴P（ξ＜100）=0.5，∴P（100＜ξ＜110）=P（ξ＜110）-P（ξ＜100）=0.96-0.5=0.46，∴P（90＜ξ＜100）=P（100＜ξ＜110）=0.46．3.经统计，某市高三学生期末数学成绩X-N（85，σ2），且P（80＜X＜90）=0.3，则从该市任选一名高三学生，其成绩不低于90分的概率是（）A.0.35B.0.65C.0.7D.0.85【答案】A∵学生成绩X服从正态分布N（85，σ2），且P（80＜X＜90）=0.3，∵P（X≥90）=[1-P（80＜X＜90）]=，2.4正态分布∴从该市任选一名高三学生，其成绩不低于90分的概率是0.35．4.某校有1200人参加某次模拟考试，其中数学考试成绩近似服从正态分布N（105，σ2）（σ＞0），试卷满分150分，统计结果量示数学成绩优秀（高于120分）的人数占总人数的，则此次数学考试成绩在90分到105分之间的人数约为（）A.180B.240C.360D.480【答案】C∵P（X≤90）=P（X≥120）=0.2，∴P（90≤X≤120）=1-0.4=0.6，∴P（90≤X≤105）=P（90≤X≤120）=0.3，∴此次数学考试成绩在90分到105分之间的人数约为1200×0.3=360．5.某住宅小区有1500名户，各户每月的用电量近似服从正态分布N（200，100），则月用电量在220度以上的户数估计约为（）（参考数据：若随机变量X服从正态分布N（μ，σ2），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974）A.17B.23C.34D.46【答案】C由题意，μ=200，σ=10，在区间（180，220）的概率为0.9544，∴用电量在220度以上的概率为=0.0228，∴用电量在220度以上的户数估计约为1500×0.0228≈34，6.已知随机变量X服从正态分布N(a,4)，且P(X≤1)＝0.5，则实数a的值为________.【答案】1∵X服从正态分布N(a,4)，∴正态曲线关于直线x＝a对称，又P(X≤1)＝0.5，故a＝1.7.某班有50名同学，一次数学考试的成绩ξ服从正态分布N(110，102)，已知P(100≤ξ≤110)＝0．34，估计该班学生数学成绩在120分以上的有________人．【答案】8∵考试的成绩ξ服从正态分布N（110，102）．∴考试的成绩ξ关于ξ=110对称，∵P（100≤ξ≤110）=0.34，∴P（ξ≥120）=P（ξ≤100）=（1-0.34×2）=0.16，∴该班数学成绩在120分以上的人数为0.16×50=8．8.已知随机变量ξ，且ξ～N{μ，σ2），若P（﹣3＜ξ＜﹣1）＝P（3＜ξ＜5），则μ＝________【答案】1依题意，P（-3＜ξ＜-1）=P（3＜ξ＜5），又区间（-3，-1）和（3，5）关于x=1对称，结合正态分布的知识，关于x=μ对称的区域所对应的概率相等，所以μ=19.为了了解某地区高三男生的身体发育状况，抽查了该地区1000名年龄在17.5岁至19岁的高三男生的体重情况，抽查结果表明他们的体重X(kg)服从正态分布N(μ，22)，且正态分布密度曲线如图所示，若体重大于58.5kg小于62.5kg属于正常情况，则这1000名男生中属于正常情况的人数约为________.(参考数据：P（μ-σ＜X＜μ+σ）=0.683，P（μ-2σ＜X＜μ+2σ）=0.954，P（μ-3σ＜X＜μ+3σ）=0.997）【答案】683依题意可知，μ＝60.5，σ＝2，故P(58.5<X<62.5)＝P(μ－σ<X<μ＋σ)＝0.683，从而属于正常情况的人数约为1000×0.683＝683.10.某市对所有高校学生进行普通话水平测试，发现成绩服从正态分布N（μ，σ2），下表用茎叶图列举出来抽样出的10名学生的成绩．（1）计算这10名学生的成绩的均值和方差；（2））给出正态分布的数据：P（μ-σ＜X＜μ+σ）=0.6826，P（μ-2σ＜X＜μ+2σ）=0.9544．由（1）估计从全市随机抽取一名学生的成绩在（76，97）的概率．【答案】解：（1）=90，S2==49．（2）由（1）可估计，μ=90，σ=7．P（76＜x＜97）=P（μ-2σ＜x＜μ）+P（μ＜x＜μ+σ）=+=0.8185．11.下列说法中正确的是设随机变量X服从二项分布，则已知随机变量X服从正态分布且，则小赵、小钱、小孙、小李到4个景点旅游，每人只去一个景点，设事件“4个人去的景点互不相同”，事件“小赵独自去一个景点”，则；；．A. B. C. D.【答案】A设随机变量X服从二项分布，则，正确；服从正态分布，正态曲线的对称轴是．，，，正确；设事件“4个人去的景点不相同”，事件“小赵独自去一个景点”，则，所以，正确；，，故不正确．12.已知三个正态分布密度函数（x∈R，i=1，2，3）的图象如图所示，则（）A.μ1＜μ2=μ3，σ1=σ2＞σ3B.μ1＞μ2=μ3，σ1=σ2＜σ3C.μ1=μ2＜μ3，σ1＜σ2=σ3D.μ1＜μ2=μ3，σ1=σ2＜σ3【答案】D∵正态曲线关于x=μ对称，且μ越大图象越靠近右边，∴第一个曲线的均值比第二和第三和图象的均值小，且二，三两个的均值相等，只能从A，D两个答案中选一个，∵σ越小图象越瘦长，得到第二个图象的σ比第三个的σ要小13.设随机变量ξ服从正态分布N（2，σ2），则函数f（x）=2x2-4x+ξ不存在零点的概率（）A. B. C. D.【答案】A∵函数f（x）=2x2-4x+ξ不存在零点，∴△=16-8ξ＜0，∴ξ＞2．∵随机变量ξ服从正态分布N（2，σ2），∴曲线关于直线x=2对称，∴P（ξ＞2）=．14.已知随机变量X服从正态分布N（3，σ2），若P（1＜X＜5）=3P（X≥5），则P（X≤1）等于()A.0.2B.0.25C.0.3D.0.4【答案】A∵随机变量X服从正态分布N（3，σ2），∴对称轴是x=3，∴P（X≥5）=P（X≤1），∵P（1＜X＜5）=3P（X≥5），∴5P（X≤1）=1，解得P（X≤1）=0.2.15.(1)若（1+2x）5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a0+a2+a4=______．(2)7个人站成一排，若甲，乙，丙三人互不相邻的排法共有______种．(3)随机变量ξ服从正态分布N（1，σ2），已知P（ξ＜0）=0.3，则P（ξ＜2）=______．(4)已知随机变量X服从二项分布B（n，p），若E（X）=30，D（X）=20，则P=______．【答案】（1）121（2）1440（3）0.7（4）（1）令x=1，则；再令x=-1，则a0-a1+a2-a3+a4-a5=-1，∴，（2）∵7个人站成一排，若甲、乙、丙彼此不相邻，∴采用插空法来解，先排列甲、乙、丙之外的4人，有A44种结果，再在排列好的4人的5个空里，排列甲、乙、丙，有A53种结果，根据分步计数原理知共有A44A53=1440种结果，（3）随机变量ξ服从正态分布N（1，σ2），∴曲线关于x=1对称，∴P（ξ＜0）=P（ξ＞2）=0.3，∴P（ξ＜2）=1-0.3=0.7，（4）随机变量X服从二项分布B（n，p），若E（X）=30，D（X）=20，可得np=30，npq=20，q=，则p=，16“过大年，吃水饺”是我国不少地方过春节的一大习俗．2018年春节前夕，A市某质检部门随机抽取了100包某种品牌的速冻水饺，检测其某项质量指标，求所抽取的100包速冻水饺该项质量指标值的样本平均数（同一组中的数据用该组区间的中点值作代表；由直方图可以认为，速冻水饺的该项质量指标值Z服从正态分布，利用该正态分布，求Z落在（14.55，38.45）内的概率；将频率视为概率，若某人从某超市购买了4包这种品牌的速冻水饺这4包速冻水饺中这种质量指标值位于（10，30）内的包数为X，求X的分布列和数学期望．附：计算得所抽查的这100包速冻水饺的质量指标的标准差为；若Z~，则，．【答案】所抽取的100包速冻水饺该项质量指标值的样本平均数为：．(2)服从正态分布，且，，，落在内的概率是．根据题意得，；；；；的分布列为：X01234P．。

正态散布一、选择题1.已知随机变量听从正态散布 N ( 2,9) ，若 P( c 1) P( c 1) ，则 c 等于（）2.已知随机变量听从正态分 N ( 2, 2 ) ，且 P( 4) 0.8 ，则 P(0 2) 等于（）3.已知随机变量听从正态散布 N ( 2, 2 ) ， P( ≤ 4) 0.84 ，则 P( ≤ 0) 等于（）4.已知随机变量X 听从正态散布N (2,2)，P(0 X 4) 0.8 ，则 P( X 4) 等于（）A ．5.已知随机变量听从正态散布 N ( 3, 2 ) ，且 P( 2) 0.3 ，则 P(2 4) 等于（）6.已知随机变量听从正态散布 N ( 3, 2 ) ， P( ≤ 4) 0.842 ，则 P( ≤ 2) 等于（）7.已知随机变量X 听从正态散布N (3,1)，且P(2 X 4) 0.6826 ，则 P( X 4) 等于（）8.已知随机变量X 听从正态散布N (0, 2 ) ，若 P( X 2) 0.023 ，则 P( 2 ≤ X ≤ 2) 等于（）9.在某次联考数学测试中，学生成绩听从正态散布(100, 2 ) ( 0) ，若在（ 80,120）内的概率为，则落在（ 0,80）内的概率为（）10. 已知随机变量X 服从正态分布 N ( , 2 ) ，且 P( 2 X 2 ) 0.9544 ，P( X ) 0.6826 ，若4, 1 ,则 P(5 X 6) （）11.某商场经营的一种袋装的大米的质量听从正态散布2 )（单位 kg）,任选一袋这类大米，其质量在9.8~10.2kg 的概率为（）12.一批电池的使用时间 X （单位：小时）听从正态散布N ( 36,42 ) ，在这批灯泡中任取一个“使用时间不小于 40 小时”的概率是（）第 1 页共2页二、填空题13. 某校在本学期期中考试中，理科数学考试成绩~ N ( 90,2 ),统计结果显示P(60 120) ，该校参加此次考试的理科学生共420 人，试预计该校成绩高于120 分的理科学生数为 __________.14. 某班有50 名学生，一次考试的成绩服从正态分布 N (100, 2 ) , 已知P(90 100) ,预计该班数学成绩在110分以上的人数为 __________.15.某中学 200 名考生的高考数学成绩近似听从正态散布N (120,102)，则此校数学成绩在140 分以上的考生人数约为 __________.16.某市高二理科学生数学考试的成绩 x 听从正态散布，其密度曲线如图，已知该市理科学生总数是 10000 人，则成绩位于(65,85]的人数约 __________.17. 在某项丈量中，丈量结果听从正态散布N (1, 2 ) (0) ，若在(0,1)内取值的概率为，则在(0,2)内取值的概率为__________.18.假定每日从甲地去乙地的游客人数 X 是听从正态散布N (800,502)的随机变量．记一天中从甲地去乙地的游客人数不超出900 的概率为 __________.19.一批电阻的阻值 X 听从正态散布N (1000,52) (单位 ).今从甲乙两箱成品中各随机抽取一个电阻，测得阻值分别为1011和982，能够以为__________. (填写正确序号)①甲乙两箱电阻均可出厂；②甲乙两箱电阻均不行出厂；③甲箱电阻可出厂，乙箱电阻不行出厂；④甲箱电阻不行出厂，乙箱电阻可出厂.20. 某一零件由三个电子元件按下列图方式连结而成，元件 1 或元件 2 正常工作，且元件 3正常工作，则零件正常工作．设三个电子元件的使用寿命(单位：小时 )均听从正态散布N (1000,502 ) ，且各个元件可否正常工作互相独立，那么该零件的使用寿命超出1000 小时的概率为 __________.15 2O75x20 题图16题图第 2 页共2页。

（1）正态曲线下、横轴上，从均数到∞+的面积为( )。

A ．95%B ．50%C ．%D ．不能确定 答案：B 。

解析：由正态曲线的特点知。

（2）某班有48名同学，一次考试后的数学成绩服从正态分布，平均分为80，标准差为10，理论上说在80分到90分的人数是 （ ）A 32B 16C 8D 20 答案：B 。

解析:数学成绩是X —N(80,102)，80809080(8090)(01)0.3413,480.3413161010P X P Z P Z --⎛⎫≤≤=≤≤=≤≤≈⨯≈ ⎪⎝⎭（31为)(1,1x σμϕ，2为)(22x σμϕ， 则1μ 2μ，1σ 2σ答案：＜，＞。

解析：由正态密度曲线图象的特征知。

例2：甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格.求甲、乙两人至少有一人考试合格的概率.答案：设甲、乙两人考试合格的事件分别为A 、B ，则P (A )=310361426C C C C +=321202060=+，P (B )=15141205656310381228=+=+C C C C . 因为事件A 、B 相互独立， 方法一：∴甲、乙两人考试均不合格的概率为 ()()()45115141321=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=⋅=⋅B P A P B A P∴甲、乙两人至少有一人考试合格的概率为 ()454445111=-=⋅-=B A P P 答：甲、乙两人至少有一人考试合格的概率为4544．方法二：∴甲、乙两人至少有一个考试合格的概率为()()()454415143215143115132=⨯+⨯+⨯=⋅+⋅+⋅=B A P B A P B A P P答：甲、乙两人至少有一人考试合格的概率为4544.1．标准正态分布的均数与标准差分别为( )。

A ．0与1 B ．1与0 C ．0与0 D ．1与1 答案：A 。

正态分布题型正态分布是统计学中常见的一种概率分布，也被称为高斯分布或钟形曲线。

它是一种连续分布，其图像是一个钟形曲线，左右对称。

根据正态分布的性质，在平均数附近的数据点出现的次数更多，随着距离平均值的增加，数据点的出现次数变得越来越少。

正态分布经常被用来描述许多现实世界中的现象，例如人口身高、体重、智力测试得分等。

在统计学中，我们在处理数据时，通常会使用一些常见的正态分布题型来推断未知数据的参数和分布。

以下是一些常见的正态分布题型：1. 求标准正态分布下的概率：这种题型通常会给出一个标准正态分布下的Z值，要求计算对应的概率。

例如，我们可以得到这样一道题目："一个人的智商测试得分为130，假设智力测试得分以正态分布进行，而平均值为100，标准差为15，请问此人智商测试得分高于平均值的概率是多少？"解决这个问题，我们可以将Z值计算为(130-100) / 15 = 2。

根据标准正态分布表格， Z得分为2相应的累计概率为0.9772。

这意味着，此人智力测试得分高于平均值的概率为0.9772或97.72%。

2. 求任意正态分布下的概率：这种题型会给出一个任意正态分布下的数值和分布参数，要求计算对应的概率。

与前面的例子类似，我们可以举一个例子："一批产品的质量以正态分布进行，平均质量值为800g，标准差为20g，在800g和840g之间质量合格的概率是多少？"解决这个问题，我们首先需要标准化这个问题所涉及的质量数值，对于840g，我们可以计算它处于均值的Z值为(840-800) / 20 = 2。

同样的，对于800g，我们可以计算它处于均值的Z值为(800-800) / 20 = 0。

我们可以使用标准正态分布表格来计算Z值得到的概率，即(0.9772 - 0.5) * 2 = 0.9544。

这意味着，在800g和840g之间质量合格的概率为0.9544或95.44%。

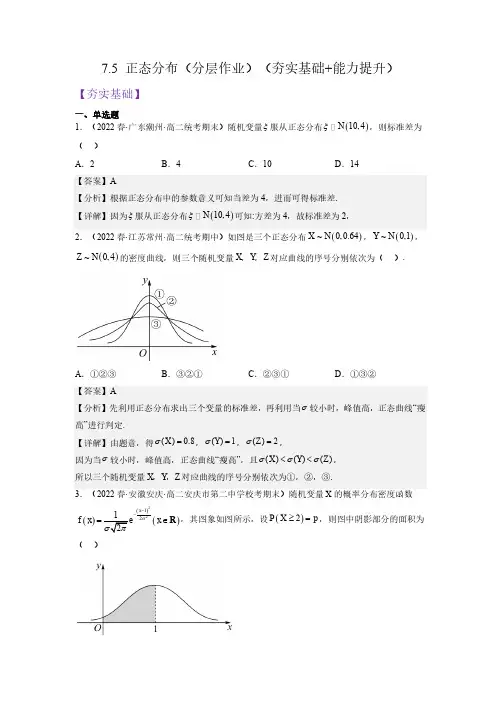
7.5 正态分布（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题 1．（2022春·广东潮州·高二统考期末）随机变量ξ服从正态分布()10,4N ξ，则标准差为（ ） A ．2 B ．4C ．10D ．14【答案】A【分析】根据正态分布中的参数意义可知当差为4，进而可得标准差. 【详解】因为ξ服从正态分布()10,4N ξ可知:方差为4，故标准差为2，2．（2022春·江苏常州·高二统考期中）如图是三个正态分布()~0,0.64X N ，()~0,1Y N ，()~0,4Z N 的密度曲线，则三个随机变量X ，Y ，Z 对应曲线的序号分别依次为（ ）.A ．①②③B ．③②①C ．②③①D ．①③②【答案】A【分析】先利用正态分布求出三个变量的标准差，再利用当σ较小时，峰值高，正态曲线“瘦高”进行判定.【详解】由题意，得()0.8X σ=，()1Y σ=，()2Z σ=，因为当σ较小时，峰值高，正态曲线“瘦高”，且()()()X Y Z σσσ<<， 所以三个随机变量X ，Y ，Z 对应曲线的序号分别依次为①，②，③.3．（2022春·安徽安庆·高二安庆市第二中学校考期末）随机变量X 的概率分布密度函数()()()2212x f x x σ--=∈R ，其图象如图所示，设()2P X p ≥=，则图中阴影部分的面积为（ ）A ．pB ．2pC ．12p -D ．12p -A ．两个随机变量的线性相关性越强，则相关系数r 的绝对值越接近于0B ．若X 是随机变量，则()()()()2121,2141E X E X D X D X +=++=+.C ．已知随机变量()0,1N ξ，若(1)P p ξ>=，则(1)12P p ξ>-=-D ．设随机变量ξ表示发生概率为p 的事件在一次随机实验中发生的次数，则()14D ξ≤某中学参加网课的100名同学每天的学习时间（小时）服从正态分布()29,1N ，则这些同学中每天学习时间超过10小时的人数估计为（ ）. 附：随机变量ξ服从正态分布()2,N μσ，则()0.6826P μσξμσ-<<+=，()220.9544P μσξμσ-<<+=. A ．12 B ．16C ．30D ．32所以每天学习时间超过10小时的人数为1000.158716⨯≈，6．（2023秋·辽宁营口·高二统考期末）正常情况下，某厂生产的零件尺寸X 服从正态分布()22,N σ（单位：m ），()1.90.1P X <=，则()2.1P X <=（ ）A ．0.1B ．0.4C ．0.5D ．0.9【答案】D【分析】根据正态分布概率的对称性求解. 【详解】因为()()1.9 2.10.1P X P X <=>=， 所以()1.9 2.110.10.10.8P X <<=--=，所以()()()2.1 1.9 2.1 1.90.9P X P X P X <=<<+<=，7．（2022·高二课时练习）4月23日为世界读书日，已知某高校学生每周阅读时间（单位：h ）()8,4XN ，则下列说法错误的是（ ）A ．该校学生每周平均阅读时间为8hB ．该校学生每周阅读时间的标准差为2C ．若该校有10000名学生，则每周阅读时间在46h 的人数约为2718D ．该校学生每周阅读时间低于4h 的人数约占2.28% ()8,4N 知)100.6826≤≈46h 的人数约占(62P X -≤，所以C 错误；0.95442.28%=从N （90，2σ），若()90950.3P c ≤≤=，则可估计该班体能测试成绩低于85分的人数为（ ）A ．5B ．10C ．15D ．30则可估计该班体能测试成绩低于85分的人数为500.210⨯=人， 9．（2022春·山西忻州·高二统考期末）随机变量X 服从正态分布()2,N μσ，且(1)(5)P X P X >-=<，则下列说法一定正确的是（ ）A ．3μ=B ．2μ=C ．3σ=D ．2σ=分）服从正态分布()285,N σ，且(8387)0.3,(7883)0.26P P ξξ<≤=<≤=，则(78)P ξ≤=（ ）A ．0.03B ．0.05C ．0.07D ．0.0911．（2022春·江苏苏州·高二校考期末）在网课期间，为了掌握学生们的学习状态，某省级示范学校对高二一段时间的教学成果进行测试．高二有1 000名学生，某学科的期中考试成绩(百分制且卷面成绩均为整数)Z 服从正态分布()282.5,5.4N ，则(人数保留整数) （ ）参考数据：若20.682 7220.954 5()()()Z N P Z P Z μσμσμσμσμσ<≤≈<≤≈～，，则－＋，－＋，330.997 3()P Z μσμσ<≤≈－＋．A ．年级平均成绩为82.5分B ．成绩在95分以上(含95分)人数和70分以下(含70分)人数相等C ．成绩不超过77分的人数少于150D ．超过98分的人数为1 【答案】ABD【分析】根据正态分布的概念可知A 对，根据对称性可知B 对，根据3σ原则和曲线的对称性即可求解C,D.【详解】由()282.5,5.4N Z ～，可知82.5, 5.4μσ==，所以平均分为82.5μ=，故A 对.12．（2022春·重庆沙坪坝·高二重庆八中校考期末）已知121,X N σ~，220,Y N σ~，则下列结论中正确的是（ ）A ．若12σσ=，则()()10P X P Y >>>B ．若12σσ=，则()()101P X P Y >+>=C ．若12σσ>，则()()0211P X P Y ≤≤<-≤≤D ．若12σσ>，则()()0101P X P Y ≤≤>≤≤13．（2022春·云南昭通·高二校联考期末）设随机变量()2,X N μσ，X 的正态密度函数为()22x f x -，则μ=______.14．（2023秋·河南南阳·高二统考期末）已知随机变量ξ服从正态分布()210,N σ，若()310.5P a ξ≤+=，则实数=a ______．【答案】3【分析】由正态分布曲线的特点可知，得正态曲线关于10x =对称，且100.5PX ≤=（），结合题意得到a 的值．【详解】随机变量ξ服从正态分布()210,N σ，正态曲线关于10x =对称，且100.5PX ≤=（）， 由()310.5P a ξ≤+=，可知3110a +=，解得3a =．15．（2022春·重庆·高二校联考阶段练习）已知随机变量X 服从正态分布()2,N μσ，若()260.6P X <<=，()60.2P X ≥=，则μ=______． 【答案】4【分析】先求出()2P X ≤的概率，然后根据正态分布的特征求解即可. 【详解】解：由题意得：∵()()()()2162610.60.20.26P X P X P X P X ≤=-≥-<<=--==≥ ∴2与6关于x μ=对称 ∴4μ=．16．（2023秋·安徽宿州·高二安徽省泗县第一中学校考期末）某学校高二年级有1500名同学，一次数学考试的成绩X 服从正态分布()2110,10N ．已知(100110)0.34P X <≤=，估计高二年级学生数学成绩在120分以上的有__________人．17．（2023秋·辽宁葫芦岛·高二葫芦岛第一高级中学校考期末）随机变量X 服从正态分布，即()10,9X N ~，随机变量23Y X =-，则()E Y =__________，()D Y =__________． 【答案】 17 36【分析】首先根据正态分布的知识得()(),E X D X ，然后可得答案. 【详解】因为()10,9X N ~，所以()()10,9E X D X ==，因为23Y X =-，所以()()2320317E Y E X =-=-=，()()436D Y D X ==， 五、解答题18．（2023秋·河南南阳·高二统考期末）某车间生产一批零件，现从中随机抽取10个，测量其内径的数据如下（单位：mm ）：192，192，193，197，200，202，203，204，208，209．设这10个数据的均值为μ，标准差为σ． (1)求μ和σ；(2)已知这批零件的内径X （单位：mm ）服从正态分布()2,N μσ，若该车间又新购一台设备，安装调试后，试生产了5个零件，测量其内径（单位：mm ）分别为：181，190，198，204，213，如果你是该车间的负责人，以原设备生产性能为标准，试根据3σ原则判断这台设备是否需要进一步调试？并说明你的理由． 参考数据：若()2,XN μσ，则：()0.6826P X μσμσ-<≤+≈，()220.9544P X μσμσ-<≤+≈，()330.9974P X μσμσ-<≤+≈，40.99740.99≈． (200,36N )200180.9974+≈所以五个零件的内径中恰有1态分布()2N 500,5（单位：g ）．(1)求正常情况下，任意抽取一包白糖，质量小于485g 的概率约为多少？。

正态分布练习题一、选择题1. 正态分布的数学表达式为：A. N(μ, σ^2)B. N(σ, μ^2)C. N(μ, σ)D. N(μ^2, σ)2. 正态分布的均值μ和标准差σ分别代表：A. 位置参数和形状参数B. 形状参数和位置参数C. 形状参数和尺度参数D. 尺度参数和形状参数3. 标准正态分布的均值和标准差分别是：A. 0和1B. 1和0C. 1和1D. 0和04. 68-95-99.7规则描述的是：A. 正态分布的对称性B. 正态分布的均值和标准差C. 正态分布的密度函数D. 正态分布数据的分布范围5. 正态分布曲线下，从均值到一个标准差之外的区域所占的面积比例是：A. 68%B. 95%C. 99.7%D. 34%二、填空题6. 正态分布的密度函数为 \(f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)，其中\(\sigma\)代表______，\(\mu\)代表______。

7. 如果一个正态分布的均值为100，标准差为15，则该分布的3σ原则表示数据落在65到135之间的概率为______。

8. 标准正态分布的密度函数是 \(f(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}\)，其中\(z\)代表______。

9. 假设某次考试的成绩服从正态分布，均分为75分，标准差为10分。

如果一个学生的成绩是85分，那么他的Z分数是______。

10. 正态分布的对称性意味着对于任意的正数a，有P(X < a) =______。

三、简答题11. 解释正态分布的三个特征，并给出每个特征在实际应用中的意义。

12. 描述68-95-99.7规则，并解释其在数据分析中的重要性。

13. 如果你有一个正态分布的数据集，如何计算其均值和标准差？14. 为什么标准正态分布是数据分析中的一个重要工具？15. 给出一个实际例子，说明正态分布如何应用于解决实际问题。

专题 正态分布一、单选题1．设随机变量()~01X N ，，则()0P X ≤= A ．0 B ．1 C ． 12D ．1 42．已知随机变量ξ～N (3，22)，若ξ＝2η＋3，则D (η)等于 A ．0 B ．1 C ．2D ．43．已知随机变量ζ服从正态分布N (3， 2a )，则P (3)ζ<＝A ．15 B ．14C ．13D ．124．若随机变量()23,X N σ，且()50.2P X ≥=，则()15P X ≤≤等于A ．0.6B ．0.5C ．0.4D ．0.35．已知随机变量()20,X N σ，若()010.4P X <<=，则()1P X >的值为A ．0.1B ．0.2C ．0.3D ．0.66．已知随机变量ξ服从正态分布()5,9N ，若(2)(2)p c p c ξξ>+=<−，则c 的值为 A ．4 B ．5 C ．6D ．77．已知随机变量X 服从正态分布N (3，1)，且P (2≤X ≤4)＝0.682 7，则P (X >4)＝ A ．0.158 8 B ．0.158 65 C ．0.158 6D ．0.158 58．若随机变量ξ服从正态分布()22020,σN ，则()2020ξ<=PA ．12B ．11010C ．14D ．120209．某校有1000人参加某次模拟考试，其中数学考试成绩近似服从正态分布()2105,(0)X N σσ~>，试卷满分150分，统计结果显示数学成绩优秀（高于或等于120分）的人数占总人数的110，则此次数学考试成绩在90分到105分之间的人数约为 A ．100 B ．200 C ．300D ．40010．设随机变量()2,N ξμσ，函数()22f x x x ξ=−+有零点的概率是0.5，则μ等于A ．1B ．2C ．3D ．不确定11．设随机变量~(1,9)X N ，且(0)(1)P X P X a ≤=≥−，则实数a 的值为 A ．2 B ．3 C ．4D ．512.已知某批零件的长度误差（单位：毫米）服从正态分布()203N ，，从中随机取一件，其长度误差落在区间()36，内的概率为( ). （附：若随机变量ξ服从正态分布()2Nμσ，，则()68.26%P μσξμσ−<<+=， ()2295.44%P μσξμσ−<<+=）A.4.56%B ．13.59%C ．27.18%D ．31.74%13．已知随机变量()2~2,(0)X N σσ>，若(4)0.7P X <=，则(02)P X <<=A ．0.2B ．0.3C ．0.5D ．0.714．以Φ(x )表示标准正态总体在区间(－∞，x )内取值的概率，若随机变量ξ服从正态分布N (μ，σ2)，则概率P (|ξ－μ|＜σ)等于 A ．Φ(μ＋σ)－Φ(μ－σ) B ．Φ（1）－Φ(－1) C ．Φ1()μσ−D ．2Φ(μ＋σ)15．在某次学科知识竞赛中（总分100分），若参赛学生成绩ξ服从2(80,)N σ(σ>0)，若ξ在(70，90)内的概率为0.7，则落在[90，100]内的概率为A ．0.2B ．0.15C ．0.1D ．0.0516．某小区有1000户居民，各户每月的用电量（单位：度）近似服从正态分布(200,100)N ，则用电量在210度以上的居民户数约为 （参考数据：若随机变量服从正态分布()2,N μσ，则()0.6827P μσξμσ−<≤+≈，()220.9545P μσξμσ−<+≈≤，(33)0.9973P μσξμσ−<≤+≈） A ．17 B ．23 C ．90D ．15917．在某次联考数学测试中，学生成绩ξ服从正态分布2(100,)σ，(0)σ>，若ξ在(80,120)内的概率为0.8，则ξ落在(0,80)内的概率为 A ．0.05 B ．0.1 C ．0.15D ．0.218．在某区2020年5月份的高二期中质量检测考试中，学生的数学成绩服从正态分布()98,100XN ．已知参加本次考试的学生约有9450人，如果某学生在这次考试中数学成绩为108分，那么他的数学成绩大约排在该区的名次是 附：若()2,XN μσ，则()0.6826P X μσμσ−<<+=，()220.9544P X μσμσ−<<+=．A ．1500B ．1700C ．4500D ．800019．已知()24,X N σ～，且()20.3P X ≤=，则(6)P X ≤=A ．0.3B ．0.4C ．0.85D ．0.720．已知随机变量()2~1,X N σ，()00.8P X ≥=，则()2P X >=A ．0.2B ．0.4C ．0.6D ．0.821．设随机变量()25,X N σ~，若()100.4P X a >−=，则()P X a >=A ．0.6B ．0.4C ．0.3D ．0.222．已知随机变量X 服从二项分布()4,B p ，其期望()3E X =，随机变量Y 服从正态分布()1,2N ，若()0P Y p >=，则()02P Y <<=A ．23 B ．34C ．14D ．1223．如图分别是甲、乙、丙三种品牌手表日走时误差分布的正态分布密度曲线，则下列说法不正确的是A ．三种品牌的手表日走时误差的均值相等B ．三种品牌的手表日走时误差的均值从大到小依次为甲、乙、丙C ．三种品牌的手表日走时误差的方差从小到大依次为甲、乙、丙D ．三种品牌手表中甲品牌的质量最好24．在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C 为正态分布()2,4N −的密度曲线）的点的个数的估计值为（附：()2,XN μσ，则()0.6827P X μσμσ−<≤+=，()220.9545P X μσμσ−<≤+=）A ．2718B ．1359C ．340D ．90625．设X~N (1，σ2)，其正态分布密度曲线如图所示，且P (X ≥3)=0.022 8，那么向正方形OABC中随机投掷20 000个点，则落入阴影部分的点的个数的估计值为[附：随机变量ξ服从正态分布N (1，σ2)，则P (μ-σ<ξ<μ+σ)=0.682 6，P (μ-2σ<ξ<μ+2σ)=0.954 4]A ．12 076B ．13 174C ．14 056D ．7 53926．某种芯片的良品率X 服从正态分布()20.95,0.01N ，公司对科技改造团队的奖励方案如下：若芯片的良品率不超过95%，不予奖励；若芯片的良品率超过95%但不超过96%，每张芯片奖励100元；若芯片的良品率超过96%，每张芯片奖励200元．则每张芯片获得奖励的数学期望为元附：随机变量ξ服从正态分布()2,N μσ，则()0.6826P μσξμσ−<<+=，(22)0.9544P μσξμσ−<<+=， (33)0.9974P μσξμσ−<<+=．A ．52.28B ．65.87C ．50.13D ．131.7427．某市为弘扬我国优秀的传统文化，组织全市10万中小学生参加网络古诗词知识答题比赛，总分100分，经过分析比赛成绩，发现成绩X 服从正态分布()82,16N ，请估计比赛成绩不小于90分的学生人数约为参考数据：()0.683P X μσμσ−<≤+=，()220.954P X μσμσ−<≤+=，()330.997P X μσμσ−<≤+=A ．2300B ．3170C ．3415D ．46028．在某次数学测试中，学生成绩ξ服从正态分布()2100,(0)σσ>，若ξ在(80,120)内的概率为0.6，则任意选取两名学生的成绩，恰有一名学生成绩不高于80的概率为 A ．0.16 B ．0.24 C ．0.32D ．0.4829．王先生朝九晚五上班，上班通常乘坐公交加步行或乘坐地铁加步行．赵先生从家到公交站或地铁站都要步行5分钟．公交车多且路程近一些，但乘坐公交路上经常拥堵，所需时间（单位：分钟）服从正态分布(33N ，24)，下车后从公交站步行到单位要12分钟；乘坐地铁畅通，但路线长且乘客多，所需时间（单位：分钟）服从正态分布(44N ，22)，下地铁后从地铁站步行到单位要5分钟．给出下列说法：从统计的角度认为所有合理的说法的序号是（1）若8:00出门，则乘坐公交上班不会迟到；（2）若8:02出门，则乘坐地铁上班不迟到的可能性更大； （3）若8:06出门，则乘坐公交上班不迟到的可能性更大；（4）若8:12出门．则乘坐地铁上班几乎不可能不迟到． 参考数据：2~(,)Z N μσ，则()0.6827P Z μσμσ−<+≈…，(22)0.9545P Z μσμσ−<+≈…，(33)0.9973P Z μσμσ−<+≈…A ．（1）（2）（3）（4）B ．（2）（4）C ．（3）（4）D ．（4）30．某市开展一次考试，考试后统计的数学成绩X 服从正态分布，且~(80,100)X N ，则下列命题不正确的是A ．该市这次考试的数学平均成绩为80分B ．分数在120分以上的人数与分数在60分以下的人数相同C ．分数在110分以上的人数与分数在50分以下的人数相同D ．该市这次考试的数学标准差为1031．某校高一年级数学检测，经抽样分析，成绩ξ占近似服从正态分布()295,N σ，且(9195)0.25P ξ<≤=．若该校有700人参加此次检测，估计该校此次检测数学成绩不低于99分的人数为 A ．100 B ．125 C ．150D ．17532．设随机变量(),1N ξμ，函数()22f x x x ξ=+−没有零点的概率是0.5，则()01P ξ<≤=附：若()2,N ξμσ，则()0.6826P X μσμσ−<≤+≈，()220.9544P X μσμσ−<≤+≈．A ．0.1587B ．0.1359C ．0.2718D ．0.3413二、多选题1．已知三个正态分布密度函数()()()222,1,2,3i i x i f x x R i μσ−−=∈=的图象如图所示，则下列结论正确的是A ．123σσσ==B ．123σσσ=<C ．123μμμ=>D ．123μμμ<=2．4月23日为世界读书日，已知某高校学生每周阅读时间X 服从正态分布()~9,4X N ，则（附：()2~,X N μσ，()0.683P X μσμσ−<<+=，()220.955P X μσμσ−<<+=，()330.997P X μσμσ−<<+=．）A ．该校学生每周平均阅读时间为9小时B ．该校学生每周阅读时间的标准差为4C ．该校学生每周阅读时间不超过3小时的人数占0.3%D ．若该校有10000名学生，则每周阅读时间在3-5小时的人数约为2103．某水稻种植研究所调查某地水稻的株高，得出株高（单位：cm ）服从正态分布，其密度函数为2(100)200(),(,)x x x ϕ−−=∈−∞+∞，则下列说法正确的是A ．该地水稻的平均株高为100cmB ．该地水稻株高的方差为10C ．该地水稻株高在120cm 以上的数量和株高在80cm 以下的数量一样多D ．随机测量一株水稻，其株高在(80,90)和在(100,110)（单位：cm ）的概率一样大 4．甲、乙两类水果的质量(单位：kg)分别服从正态分布N (μ1，21δ)，N (μ2，22δ)，其正态分布的密度曲线如图所示，则下列说法正确的是A ．甲类水果的平均质量μ1=0.4 kgB ．甲类水果的质量比乙类水果的质量更集中于平均值左右C ．甲类水果的平均质量比乙类水果的质量小D ．乙类水果的质量服从正态分布的参数δ2=1．995．甲､乙两类水果的质量(单位：kg )分别服从正态分布221122(,),(,)N N μσμσ，其正态分布的密度曲线22()2(),,x f x x μσ−−=∈R 如图所示，则下列说法正确的是A ．甲类水果的平均质量10.4kg μ=B ．甲类水果的质量比乙类水果的质量更集中于平均值左右C ．甲类水果的平均质量比乙类水果的平均质量小D ．乙类水果的质量服从的正态分布的参数2=1.99σ6．已知某校高三年级有1000人参加一次数学模拟考试，现把这次考试的分数转换为标准分，标准分的分数转换区间为(]60,300，若使标准分X 服从正态分布N ()180,900，则下列说法正确的有参考数据：①()0.6827P X μσμσ−<≤+=；②(22)0.9545P X μσμσ−<≤+=；③3309().973P X μσμσ−<≤+= A ．这次考试标准分超过180分的约有450人 B ．这次考试标准分在(]90,270内的人数约为997C ．甲、乙、丙三人恰有2人的标准分超过180分的概率为38D ．()2402700.0428P X <≤=7．已知在数学测验中，某校学生的成绩服从正态分布()110,81N ，其中90分为及格线，则下列结论中正确的有（附：随机变量ξ服从正态分布()2,N μσ，则()220.9545P μσξμσ−<<+=）A ．该校学生成绩的期望为110B ．该校学生成绩的标准差为9C ．该校学生成绩的标准差为81D ．该校学生成绩及格率超过95%三、填空题1．设随机变量ξ服从正态分布()21,N σ，若()20.8ξ<=P ，则()02P ξ<<=________． 2．已知随机变量X 服从正态分布()2,N μσ，若45P X P ⎛⎫>= ⎪⎝⎭(0)X <，则μ=________． 3．已知X ～N (μ，σ2)，且P (X >0)＋P (X ≥－4)＝1，则μ＝________． 4．已知随机变量ξ服从正态分布()21,N σ，若()40.9P ξ<=，则()21P ξ−<<=________．5．某超市经营的某种包装优质东北大米的质量X (单位：千克)服从正态分布N (25，0.22)，任意选取一袋这种大米，质量在24.8～25.4 千克的概率为________．(附：若Z ～N (μ，σ2)，则P (|Z －μ|＜σ)＝0.682 6，P (|Z －μ|＜2σ)＝0.954 4，P (|Z －μ|＜3σ)＝0.997 4)6．某校对全市的英语成绩进行统计，发现英语成绩的频率分布直方图形状与正态分布2(95,8)N 的密度曲线非常拟合．据此估计：在全市随机抽取的4名高三同学中，恰有2名同学的英语成绩超过95分的概率是________．7．随机变量~(2)X B p ，，2~(2)Y N σ，，若(1)0.64P X ≥=，(02)P Y p <<=，则(4)P Y >=________．8．小张驾车从家到学校上班所需的时间X (单位：min )服从正态分布(2025)N ，，则王老师从家到学校所需时间在(3035]，内的概率为________．(若2~()X N μσ，，则()0.6827P X μσμσ−<≤+=，(22)0.9545P X μσμσ+<≤+=， 3309().973P X μσμσ−<≤+=)．9．设()25,X N σ~，若()5,9X ∈的概率为0.45，则()1,X ∈+∞的概率为________．10．已知随机变量ξ服从正态分布()23,N σ，且(1)1(5)9P P ξξ<=<，则(35)P ξ<<=________． 11．为了解高三复习备考情况，某校组织了一次阶段考试，若高三全体考生的数学成绩近似服从正态分布()2100,17.5N ，已知成绩117以上（含117）的学生有80人，则此次参加考试的学生成绩不超过82的概率为________，如果成绩大于135分的为特别优秀，那么本次考试数学成绩特别优秀的大约有________人．参考数据：()0.68P x μσμσ−<<+=，(22)0.96P x μσμσ−<<+=12．在某市高二的联考中，这些学生的数学成绩ξ服从正态分布()100,100N ，随机抽取10位学生的成绩，记X 表示抽取的10位学生成绩在()80,120之外的人数，则()1P X ≥=________，X 的数学期望EX =________． 附：若随机变量Z 服从正态分布()2,N μσ，则(22)0.9544P Z μσμσ−<<+=，(33)0.9974P Z μσμσ−<<+=，取100.95440.6271=，100.99740.9743=．13．已知某批零件的长度误差X 服从正态分布()2,N μσ，其密度函数()()222,x x μσμσϕ−−=的曲线如图所示，则σ=________；从中随机取一件，其长度误差落在()3,6内的概率为________．（附：若随机变量ξ服从正态分布()2,N μσ，则()0.6826P μσξμσ−<≤+=，()220.9544P μσξμσ−<≤+=，()330.9974P μσξμσ−<≤+=．）五、解答题1．在某校举行的数学竞赛中，全体参赛学生的竞赛成绩ξ近似服从正态分布()70,100N ．已知成绩在90分以上（含90分）的学生有12名． （1）此次参赛的学生总数约为多少人?（2）若该校计划奖励竞赛成绩排在前50名的学生，则设奖的分数线约为多少分? 说明：对任何一个正态分布()2~,X N μσ来说，通过1X Z μσ−=转化为标准正态分布()~0,1Z N ，从而查标准正态分布表得到()()1P X X Z <=Φ． 参考数据：可供查阅的（部分）标准正态分布表()Z Φ2．2020年某市教育主管部门为了解近期举行的数学竞赛的情况，随机抽取500名参赛考生的数学竞赛成绩进行分析，并制成如下的频率分布直方图：（1）求这500名考生的本次数学竞赛的平均成绩x (精确到整数)； （2）由频率分布直方图可认为这次竞赛成绩X 服从正态分布()2,N μσ，其中μ近似等于样本的平均数x ，σ近似等于样本的标准差s ，并已求得18s ≈．用该样本的频率估计总体的概率，现从该市所有考生中随机抽取10名学生，记这次数学竞赛成绩在(86,140]之外的人数为Y ，求(2)P Y =的值(精确到0.001)． 附：（1）当()2,XN μσ时，()0.6827,(22)0.9545P X P X μσμσμσμσ−<+=−<+=剟；（2）820.81860.18140.0066⨯≈．3.为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ．（1）假设生产状态正常，记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ−+之外的零件数，求(1)P X ≥及X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(3,3)μσμσ−+之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性； （ⅱ）下面是检验员在一天内抽取的16个零件的尺寸： 9.9510.12 9.969.9610.01 9.929.9810.0410.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95经计算得16119.9716i i x x ===∑，0.212s ==≈，其中i x 为抽取的第i 个零件的尺寸，1,2,,16i =⋅⋅⋅．用样本平均数x 作为μ的估计值ˆμ，用样本标准差s 作为σ的估计值ˆσ，利用估计值判断是否需对当天的生产过程进行检查？剔除ˆˆˆˆ(3,3)μσμσ−+之外的数据，用剩下的数据估计μ和σ（精确到0.01）．附：若随机变量Z 服从正态分布2(,)N μσ，则(33)0.997 4P Z μσμσ−<<+=，160.997 40.959 2≈0.09≈．4．某市教育局为调查诗文朗诵活动开展的效果，对全市参加过经典诗文诵读活动的学生进行了测试，并从中抽取了1000份试卷，根据这1000份试卷的成绩(单位：分，满分100分)得到如下频数分布表．（1）求这1000份试卷成绩的平均数x (同一组中的数据用该组区间的中点值为代表)． （2）假设此次测试的成绩X 服从正态分布()2,N μσ，其中μ近似为样本平均数，2σ近似为样本方差2s ，已知s 的近似值为6.61，以样本估计总体，假设有84.14%的学生的测试成绩高于市教育局预期的平均成绩，则市教育局预期的平均成绩大约为多少(结果保留一位小数)？（3）该市教育局准备从成绩在[]90,100内的120份试卷中用分层抽样的方法抽取6份，再从这6份试卷中随机抽取3份进行进一步分析，记Y 为抽取的3份试卷中测试成绩在[]95,100内的份数，求Y 的分布列和数学期望．参考数据：若()2,XN μσ，则()0.6827P X μσμσ−<≤+≈，()220.9545P X μσμσ−<≤+≈，()330.9973P X μσμσ−<≤+≈．。

第48讲 正态分布一、单选题1．（2021·全国高二课时练习）在某市2020年3月份的高三线上质量检测考试中，学生的数学成绩服从正态分布N (98，100)．已知参加本次考试的全市学生有9 455人，如果某学生在这次考试中的数学成绩是108分，那么他的数学成绩大约排在全市第（ ） A ．1 500名 B ．1 700名 C ．4 500名 D ．8 000名【答案】A 【详解】因为学生的数学成绩X 服从正态分布N (98，100)，则P (X >108)=12[1-P (88≤X ≤108)]=12[1-P (μ-σ≤X ≤μ+σ)]≈12×(1-0.6827)=0.15865， 而0.15865×9455≈1500，所以该学生的数学成绩大约排在全市第1500名. 故选：A2．（2021·全国高二课时练习）关于正态分布N (μ，2σ)，下列说法正确的是（ ） A ．随机变量落在区间长度为3σ的区间之外是一个小概率事件 B ．随机变量落在区间长度为6σ的区间之外是一个小概率事件 C ．随机变量落在[－3σ，3σ]之外是一个小概率事件 D ．随机变量落在[μ－3σ，μ＋3σ]之外是一个小概率事件 【答案】D 【详解】由正态分布中的3σ原则，可得3309().973P X μσμσ-≤≤+≈，所以(3P X μσ>-或3)1(33)10.99730.0027X P X μσμσμσ<+=--≤≤+=-≈， 所以随机变量X 落在[]33μσμσ-+，之外是一个小概率事件. 故选：D.3．（2021·全国高二课时练习）设有一正态总体，它的正态曲线是函数f (x )的图象，且()2(10)8x f x --，则这个正态总体的均值与标准差分别是（ ） A ．10与8 B ．10与2 C ．8与10 D ．2与10【答案】B 【详解】由正态密度函数的定义和解析式可知，总体的均值10μ=，方差24σ=，即2σ=. 故选：B.4．（2021·全国高二课时练习）已知X ～N (0，1)，则X 在区间(－∞，－2)内取值的概率约为（ ） A ．0.954 B ．0.046 C ．0.977 D ．0.023【答案】D 【详解】由题意知，正态曲线的对称轴为x ＝0，所以P (X ＜－2)＝0.5－12P (－2≤X ≤2)＝0.5－0.95442＝0.022 8. 故选：D.5．（2021·全国高二课时练习）正态分布N (0，1)在区间(－2，－1)和(1，2)上取值的概率为P 1，P 2，则二者大小关系为（ ） A ．P 1＝P 2 B ．P 1＜P 2C ．P 1＞P 2D ．不确定【答案】A 【详解】根据正态曲线的特点，图象关于x ＝0对称，可得在区间(－2，－1)和(1,2)上取值的概率P 1，P 2相等． 故选：A6．（2021·河北邢台·高三月考）已知随机变量ξ服从正态分布N （3，4），若(21)(21)P c P c ξξ>+=<-，则c 的值为（ ） A ．32B ．2C ．1D ．12【答案】A 【详解】由正态分布的对称性知，(21)33(21)c c +-=--，得32c =. 故选：A7．（2021·河北沧州·）某杂交水稻种植研究所调查某地水稻的株高X （单位：cm ）的情况，得出()2100,10X N ~，随机测量一株水稻，其株高在()110,120（单位：cm ）范围内的概率为（ ）（附：若随机变量()2,X N μσ，则()0.6826P X μσμσ-<<+=，()220.9544P X μσμσ-<<+=）A ．0.0456B ．0.1359C ．0.2718D ．0.3174【答案】B 【详解】由题意得()901100.6826P X <<=，()801200.9544P X <<=，所以()0.95440.68261101200.13592P X -<<==，故选：B8．（2021·全国高二专题练习）正态分布概念是由德国数学家和天文学家Moivre 在1733年首先提出，由于德国数学家高斯率先把其应用于天文学研究，故我们把正态分布又称作高斯分布，早期的天文学家通过长期对某一天体的观测收集到大量数据；对这些数据进行分析发现这些数据变量,X 近似服从()29,N σ，若()100.91P X <=，则()8P X ≤= A ．0.09 B ．0.41C ．0.59D ．0.91【答案】A 【详解】()()()8101100.09P X P X P X ≤=≥=-<=，故选：A . 二、多选题9．（2021·全国高二课时练习）下面给出的关于正态曲线的4个叙述中，正确的有（ ） A ．曲线在x 轴上方，且与x 轴不相交B ．当x >μ时，曲线下降，当x <μ时，曲线上升C ．当μ一定时，σ越小，总体分布越分散，σ越大，总体分布越集中D ．曲线关于直线x ＝μ对称，且当x ＝μ时，位于最高点 【答案】ABD 【详解】由正态密度曲线的几何特点可知：（1）曲线在x 轴上方，且与x 轴不相交；故A 正确.（2）曲线关于直线对称，当x μ=时，曲线处于最高点，当向左右远离时，曲线不断降低，呈现出“中间高、两边低”的钟形曲线；故D 正确.（3）当x μ<时，曲线上升，当x μ>时，曲线下降，并且当曲线向左向右无限延伸时，以x 轴为渐近线，向x 轴无限靠近；故B 正确.（4）当μ一定时，曲线的形状由σ确定；σ越小，曲线越“瘦高”，总体分布越集中，σ越大，曲线越“矮胖”，总体分布越分散；故C 错误. 故选：ABD.10．（2021·全国高二专题练习）如图分别是甲、乙、丙三种品牌手表日走时误差分布的正态分布密度曲线，则下列说法正确的是（ ）A ．三种品牌的手表日走时误差的均值相等B ．三种品牌的手表日走时误差的均值从大到小依次为甲、乙、丙C ．三种品牌的手表日走时误差的方差从小到大依次为甲、乙、丙D ．三种品牌手表中甲品牌的质量最好 【答案】ACD 【详解】由题中图象可知三种品牌的手表日走时误差的平均数（均值）相等，由正态密度曲线的性质，可知σ越大，正态曲线越扁平，σ越小，正态曲线越瘦高，故三种手表日走时误差的标准差（或方差2σ）从小到大依次为甲、乙、丙，甲品牌的质量最好. 故选：ACD.11．（2021·阳江市第一中学高二月考）已知()2~,X N μσ，()()021P X P X ≥+≥-=，且()20.3P X ≤-=，则（ ）A ．1μ=-B ．2μ=-C ．()200.4P X -≤≤=D ．()200.3P X -≤≤=【答案】AC 【详解】因为()()021P X P X ≥+≥-=，所以()()02P X P X ≥=≤-，所以1μ=-. 故()2010.320.4P X -≤≤=-⨯=. 故选：AC12．（2021·福建三明·高二期末）若随机变量()()()~0,2,N x P x ξφξ=≤，其中0x >，则下列等式成立的有（ ） A ．()()1x x φφ-=- B ．()()22x x φφ= C ．()()21P x x ξφ<=- D ．()()22P x x ξφ>=-【答案】ACD 【详解】因为()~0,2N ξ，所以其正态曲线关于直线0x =对称，因为()()x P x φξ=≤，0x >，所以()()()1x P x x φξφ-=≤-=-，A 正确；因为()()()(),2222P x P x x x φξφξ==≤≤，所以()()22x x φφ=不一定成立，B 不正确； 因为()()()()1221P x P x x x x ξξφφ<=-<<=--=-，C 正确；因为()(P x P x ξξ>=>或)x ξ<-()()()122x x x φφφ=-+-=-，D 正确； 故选：ACD.三、填空题13．（2021·全国高二单元测试）设随机变量ξ服从正态分布()43N ，，若()()51P a P a ξξ<-=>+，则实数a =______. 【答案】6 【详解】由题意，随机变量ξ服从正态分布()4,3N ，可得24,3μσ==， 又由()()51P a P a ξξ<-=>+，可得5x a =-和1x a =+关于4x =， 所以518a a -++=，解得6a =. 故答案为：6.14．（2021·福建福州三中高三月考）已知随机变量ξ服从正态分布()2,N μσ，若()()24P m P m ξξ≥-=≤+()m ∈R ，则μ=______． 【答案】3 【详解】 依题意可知()()2432m m μ-++==．故答案为：3.15．（2021·全国高二单元测试）已知随机变量X 服从正态分布N (3，1)，且P (X <2c +2)=P (X >c +4)，则c =__．【答案】0 【详解】因随机变量X 服从正态分布N (3，1)，则它对应的正态密度曲线对称轴为x =3，又P (X <2c +2)=P (X >c +4)， 则由正态分布的对称性可得2c +2+c +4=6，解得c =0， 所以c =0. 故答案为：016．（2021·浙江丽水·高二课时练习）如果随机变量ξ服从N (μ，σ)，且E (ξ)＝3，D (ξ)＝1，那么μ＝________，σ＝________.【答案】3 1 【详解】()~,,N ξμσ()()23,1,E D ξμξσ∴====1σ∴=，故答案为3,1.四、解答题17．（2021·福建三明·高三模拟预测）为促进物资流通，改善出行条件，驻某县扶贫工作组引入资金新建了一条从该县到市区的快速道路.该县脱贫后，工作组为了解该快速道路的交通通行状况，调查了行经该道路的各种类别的机动车共1000辆，对行车速度进行统计后，得到如图所示的频率分布直方图：（1）试根据频率分布直方图，求样本中的这1000辆机动车的平均车速(同一组中的数据用该组区间的中点值代替)；（2）设该公路上机动车的行车速度v 服从正态分布()2,N μσ，其中μ，2σ分别取自该调查样本中机动车的平均车速和车速的方差2s (经计算2210.25s =).（i ）请估计该公路上10000辆机动车中车速不低于85千米/时的车辆数(精确到个位)：（ii ）现从经过该公路的机动车中随机抽取10辆，设车速低于85千米/时的车辆数为X ，求X 的数学期望.附注：若()2~,N ξμσ，则()0.6827P μσξμσ-<≤+=，()220.9545P μσξμσ-<≤+=，()330.9973P μσξμσ-<≤+=.参考数据：229841=.【答案】（1）70.5千米/时；（2）（i ）1587辆，（ii ）()8.4135E X =. 【详解】（1）由图知：(450.01550.015650.02750.03850.015950.01)1070.5v =⨯+⨯+⨯+⨯+⨯+⨯⨯=千米/时. ∴这1000辆机动车的平均车速为70.5千米/时.（2）由（1）及题设知：(70.5,210.25)v N ，则70.5,14.5μσ==， （i ）1()(85)()0.158652P v P v P v μσμσμσ--≤≤+≥=≥+==，∴10000辆机动车中车速不低于85千米/时的车辆数100000.158651587⨯≈辆. （ii ）由（2）知：车速低于85千米/时的概率为10.158650.84135P =-=，故(10,0.84135),X B∴()100.841358.4135E X =⨯=.18．（2021·重庆市清华中学校高三月考）国家发展改革委、住房城乡建设部于2017年发布了《生活垃圾分类制度实施方案》，规定46个城市在2020年底实施生活垃圾强制分类，垃圾回收、利用率要达35%以上.截至2019年底，这46个重点城市生活垃圾分类的居民小区覆盖率已经接近70%.武汉市在实施垃圾分类之前，从本市人口数量在两万人左右的320个社区中随机抽取50个社区，对这50个社区某天产生的垃圾量（单位：吨）进行了调查，得到如下频数分布表，并将人口数量在两万人左右的社区垃圾数量超过28吨/天的确定为“超标”社区：（2）若该市人口数量在两万人左右的社区这一天的垃圾量大致服从正态分布()2,N μσ，其中μ近似为（1）中的样本平均值x ，2σ近似为样本方差2s ，经计算得 5.2s =.请利用正态分布知识估计这320个社区中“超标”社区的个数.（参考数据：()0.6827P X μσμσ-<≤+≈；()220.9545P X μσμσ-<≤+≈；()330.9974P X μσμσ-<≤+≈）【答案】（1）22.8吨；（2）51. 【详解】（1）由频数分布表得： 1451762092312268296322.7622.8542x ⨯+⨯+⨯+⨯+⨯=+≈⨯⨯=+，所以这50个社区这一天垃圾量的平均值为22.8吨；（2）由（1）知22.8μ=， 5.2s =， 5.2s σ∴==，则28μσ=+， ()()()110.6827280.1586522P X P X P X μσμσμσ--<≤+-∴>=>+===，3200.1586550.76851⨯=≈，所以这320个社区中“超标”社区的个数为51.19．（2021·全国高二单元测试）设从某地前往火车站，可乘公共汽车，也可乘地铁，若乘公共汽车所需时间（单位：min ）X ～N （50，102），乘地铁所需时间Y ～N （60，42），则 （1）若有70min 可用，则乘公共汽车好还是乘地铁好？（2）由于时间紧迫，决定做出租车去火车站，此时使用手机中打车软件甲，甲软件定位了A 公司2辆出租车，B 公司4辆出租车，每车被叫中的概率相等，甲软件能叫来两辆车，求A 公司出租车被叫来的辆数ξ的分布列和数学期望E （ξ）.（已知P （μ﹣3σ＜X ≤μ+3σ）＝0.9974，P （μ﹣2σ＜X ≤μ+2σ）＝0.9544）【答案】（1）乘地铁；（2）分布列见解析，23.【详解】解：（1）乘公共汽车及时赶到的概率为()()10.9544070170192.772P X P X ≤=->-=-= 乘地铁及时赶到的概率为()()()7068168110.95440.97722P Y P Y P Y ≤>≤=->==-- 因此在这种情况下应乘地铁. （2）ξ的取值为0，1，2.则P （ξ＝0）＝2426C C ＝25，P （ξ＝1）＝112426C C C ＝815，P （ξ＝2）＝2226C C ＝115，ξ的分布列E ξ＝0×5+1×15+2×15＝3. 20．（2021·河南（理））市教育局举办了全市高中生关于创建文明城市的知识竞赛（满分120分），规定竞赛成绩不低于90分的为优秀，低于90分的为非优秀.为了解竞赛成绩与学生课外阅读量之间的关系，某研究机构随机抽取了参加竞赛的60名高中生，通过问卷调查，得到以下数据：（2）若参加这次竞赛的高中生共有20000名，参赛学生的竞赛成绩()~90,100N ξ，试估计竞赛成绩大于110分的学生大约有多少人？参考公式及数据：()()()()()22n ad bc K a b c d a c b d -=++++，其中na b c d =+++.~,N ξμσ时， 0.6826P μσξμσ-<≤+=，220.9544P μσξμσ-<≤+=.【答案】（1）有99.5%的把握认为课外阅读量与本次竞赛的成绩优秀有关；（2）456人. 【详解】（1）∵()()()()()()2226022208101359.6437.8793030322814n ad bc K a b c d a c b d -⨯-⨯===≈>++++⨯⨯⨯， ∴有99.5%的把握认为课外阅读量与本次竞赛的成绩优秀有关.（2）由()~90,100N ξ，知：90μ=，10σ=. ∴()()()111021220.02282P P P ξξμσμσξμσ>=>+=--<≤+=⎡⎤⎣⎦，故竞赛成绩大于110分的学生约有200000.0228456⨯=，∴估计竞赛成绩大于110分的学生大约有456人.。

正态分布应用练习题正态分布（也称为高斯分布）是统计学中一种常见的概率分布。

它是以数学家卡尔·弗里德里希·高斯命名的，因为他在研究测量误差时首先提出了这个分布。

正态分布在实际问题中的应用非常广泛，包括经济学、自然科学、社会科学等领域。

在本文中，我们将通过一些练习题来应用正态分布。

练习题一：考试成绩假设一门考试的平均分为80分，标准差为10分，试求该门考试的成绩分布情况。

解答：根据正态分布理论，我们可以利用正态分布的概率密度函数来计算某个分数的概率。

设考试成绩为X，则X服从正态分布N(80, 10^2)。

现假设有一名学生的考试成绩为90分，我们可以计算该成绩在整个考试成绩中的排名。

根据正态分布的概率密度函数，我们可以得到：P(X ≤ 90) = Φ((90-80)/10)其中，Φ表示标准正态分布的累积分布函数。

查找标准正态分布表可得Φ(1) ≈ 0.8413。

因此，P(X ≤ 90) ≈ 0.8413，也就是说，该学生的考试成绩在所有考试成绩中排名约为84.13%。

练习题二：产品质量控制某公司生产的产品每天的重量符合正态分布，平均重量为500克，标准差为10克。

该公司规定产品的合格范围在490克到510克之间。

现在，我们要求计算该公司生产的产品中，重量符合规定范围的比例。

解答：设产品重量为X，X服从正态分布N(500, 10^2)。

我们可以计算该产品的重量在规定范围内的概率。

P(490 ≤ X ≤ 510) = Φ((510-500)/10) - Φ((490-500)/10)通过查找标准正态分布表，我们可以得到Φ(1) ≈ 0.8413 和Φ(-1) ≈ 0.1587。

因此，P(490 ≤ X ≤ 510) ≈ 0.8413 - 0.1587 ≈ 0.6826。

即该公司生产的产品中，重量在490克到510克之间的比例约为68.26%。

练习题三：房屋租金某城市的房屋租金符合正态分布，平均租金为5000元，标准差为1000元。

1，已知随机事件ξ服从正态分布()2σμ，N ，且()8.04=<ξP ，则()=<<40ξPA ．6.0B ．4.0 C. 3.0 D ．2.02，已知随机事件ξ服从正态分布()13，N ，且()6826.040=<<ξP ，则()=<4ξP A ．1588.0 B ．1587.0 C. 1586.0 D ．1585.03，从中5,4,3,2,1任取两个不同的数，事件A ：取到的两个数之和为偶数；事件B ：取到的两个数都是偶数。

则()=A B P /A ．81B ．41 C. 52 D ．21 4，若随机变量个概率分布密度函数为()()82,2221+-=x e x πϕσμ，则()=-12x E _________5，设随机变量⎪⎭⎫ ⎝⎛21,6~B X ，则==)3(X P A ．165 B ．163 C. 85 D ．83 6，小王通过英语测试的概率是31，他连续测试三次，那么其中恰有一次通过的概率为 A ．94 B ．92 C. 274 D ．272 7，国庆节放假，甲去北京旅游的概率为31，乙、丙去北京旅游的概率分别为5141，，假定三人的行动相互之间没有影响，那么期间至少一人去北京旅游的概率为A ．6059B ．53 C. 21 D ．6018，设554432110,1010=≤<<<≤x x x x x ，随机变量1ξ的取值54321,x x x x x ，，，的概率均为2.0，随机变量2ξ取值222221554433221x x x x x x x x x x +++++，，，，的概率也均为2.0，若记21,ξξD D 分别为1ξ，2ξ的方差，则A ．21ξξD D >B ．21ξξD D = C. 21ξξD D < D ．无法确定 9，若()p n B X ,~，且3,6==DX EX ，则()1=X P 的值为（ ）A ．2-23⋅B ．4-2 C. -1023⋅ D ．8-210，签盒中有编号为6,54,3,2,1，的六只签，从中任意取出3支签，设X 为这三支签中号码最大的一个，则X 的数学期望为（ ）A ．5B ．25.5 C. 8.5 D ．6.411，设随机变量的概率分布规律为()()()()R a n n n a n X P ∈=+==4,3,2,11，则⎪⎭⎫ ⎝⎛<<2521X P 的值为 A ．32 B ．43 C. 54 D ．65。

正态分布应用题
正态分布是一个非常重要的统计分布，在各个领域都有广泛的应用。

本文将通过几个具体的应用题，来展示正态分布在实际问题中的运用。

一、考试成绩分布
某次考试全班100名学生的成绩分布呈正态分布，平均分为75分，标准差为8分。

请计算以下几个问题：
1. 有多少学生的成绩高于85分？
2. 高于60分的学生占总人数的比例是多少？
3. 如果成绩低于60分的学生需要补考，那么有多少学生需要补考？
二、身高分布
某地区的成年男性的身高呈正态分布，均值为170厘米，标准差为
5厘米。

请回答以下问题：
1. 身高在160厘米到180厘米之间的男性占总人数的比例是多少？
2. 身高超过175厘米的男性占总人数的比例是多少？
3. 如果要选拔身高在前10%的男性进行篮球比赛，身高需要达到多
少厘米以上？
三、生产质量控制
某工厂的产品重量符合正态分布，平均重量为100克，标准差为2克。

工厂规定，产品的重量在正负3标准差范围内属于正常。

请计算
以下问题：
1. 产品重量在94克到106克之间的产品占比是多少？
2. 超过106克重量的产品占比是多少？
3。

如果要保证95%的产品符合标准，产品的重量不能超过多少克？
通过以上几个实际问题的计算，我们可以看到正态分布在不同领域
的广泛应用。

掌握正态分布的特点和计算方法，可以帮助我们更好地
理解和解决实际问题。

希望本文能够对您有所帮助。