下载文档原格式
投入产出表[1]投入产出表(部门联系平衡表)，是指以产品部门分类为基础的棋盘式平衡表，用于反映国民经济各部门的投入和产出、投入的来源和产出的去向，以及部门与部门之间相互提供、相互消耗产品的错综复杂的技术经济关系。
[编辑]投入产出表的产生投入产出表在二十世纪三十年代产生于美国，它是由美国经济学家、哈佛大学教授瓦西里·列昂惕夫（W.Leontief）在前人关于经济活动相互依存性的研究基础上首先提出并研究和编制的。
列昂惕夫从1931年开始研究投入产出技术，编制投入产出表，目的是研究美国的经济结构。
1936年他撰写的“美国经济制度中投入产出数量关系”在《经济学和统计学评论》上发表。
它是世界上有关投入产出技术的第一篇论文，标志着投入产出技术的诞生。
1953年列昂惕夫与他人合作，出版了《美国经济结构研究》一书。
通过这些论著，列昂惕夫提出了投入产出表的概念及其编制方法，阐述了投入产出技术的基本原理，创立了投入产出技术这一科学理论。
正是在投入产出技术方面的卓越贡献，列昂惕夫于1973年获得了第五届诺贝尔经济学奖。
[编辑]投入产出表的发展投入产出技术从诞生到现在的七十多年里，无论是在理论方面，还是在实践方面都得到了很大的发展，取得了丰硕成果。
早期的投入产出模型，只是静态的投入产出模型。
后来，随着研究的深入，开发了动态投入产出模型，投入产出技术由静态扩展到动态。
近期，随着投入产出技术与数量经济方法等经济分析方法日益融合，投入产出分析应用领域不断扩大。
五十年代末六十年代初，我国经济理论界和一些高等院校的少数同志开始研究投入产出技术，某些高等院校还开设了投入产出技术课程。
“文革”期间，此项工作几乎中断。
1974年8月，为研究宏观经济发展情况的需要，在国家统计局和国家计委的组织下，由国家统计局、国家计委、中国科学院、中国人民大学、原北京经济学院等单位联合编制了1973年全国61种产品的实物型投入产出表。
利用该表开展的应用工作，在制定投资计划和产品生产计划等方面发挥了积极的作用。
一．投入产出的涵义（一）投入产出分析的理论基础里昂惕夫在从事美国经济结构分析的工作过程中，对瓦尔拉斯的“一般均衡理论”进行了简化：（1）将经济主体的活动以生产工艺的相似性为依据，归纳为若干产业部门以及集合为家庭和其他非生产部门。
（2）突出诸部门之间在生产活动中的结构性相互关系，将通过中间产品的交易形成的相互关联。
从投入和产出两个方面以生产技术系数（投入系数）的形式固定下来。
（3）与此同时，将生产方面的这种关系同支出方面即最终需求在各个产业的结构，以及分配方面的附加价值在各产业内的分布连接起来，形成了供求平衡、收支平衡为轴心的体系。
通过简化，里昂惕夫的模型和瓦尔拉斯的模型出现了两点较大的区别：（1）在瓦尔拉斯的模型中生产要素间存在可替代性，而在里昂惕夫的模型中生产要素失去了可替代性，形成了一些固定的系数，因此生产系统就能以线形关系来表示了。
（2）里昂惕夫模型中省略了瓦尔拉斯一般均衡理论模型的一个核心思想，即价格对主体在追求最佳化时必然发生影响的思想。
（二）投入产出的涵义投入产出作为一种科学的分析方法和理论，在国内外曾有过各种名称，如投入产出分析、投入产出技术、产业关联分析方法、部门联系平衡法等。
作为一种方法，它是研究国民经济体系中或区域经济体系中各个产业部门间投入与产出的相互依存关系的数量分析方法，然而它不仅仅局限于分析产业间联系，还可以利用产业间投入与产出的有关数量比例去研究国民经济中的其他方面的问题。
投入产出的“投入”是指产品生产出来后所分配的去向、流向，即使用方向和数量，又叫流量，例如用于生产消费、生活消费和积累。
投入产出法是投入产出理论的具体应用，是“把一个复杂经济体系中各部门之间的相互依存关系系统地数量化的方法”。
它借助投入产出表，对各产业间在生产、交换和分配上的关联关系进行分析，然后利用产业间关联关系的特点，为经济预测和经济计划服务。
二．投入产出表投入产出表也称里昂惕夫表或产业联系表。
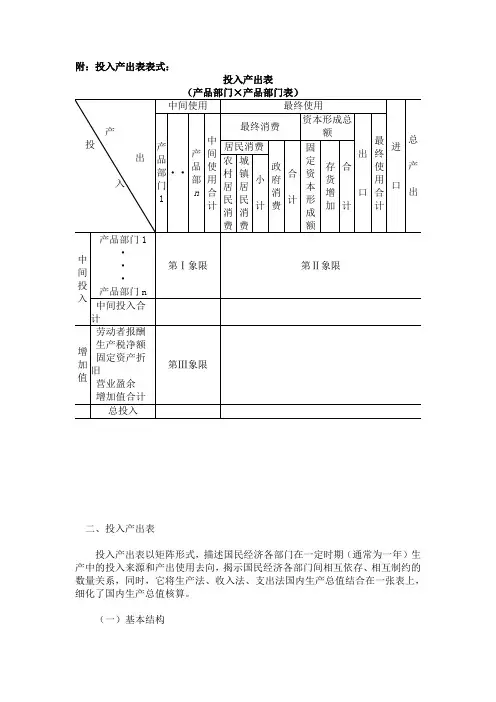
附：投入产出表表式：投入产出表二、投入产出表投入产出表以矩阵形式，描述国民经济各部门在一定时期（通常为一年）生产中的投入来源和产出使用去向，揭示国民经济各部门间相互依存、相互制约的数量关系，同时，它将生产法、收入法、支出法国内生产总值结合在一张表上，细化了国内生产总值核算。
（一）基本结构投入产出表由供给表、使用表和产品部门×产品部门表组成。
供给表又称产出表，主栏为n个产品部门，宾栏为m个产业部门，沿行方向看，反映属于某一产品部门的货物或服务是由哪些产业部门生产的，合计为属于该产品部门的货物或服务的总产出；沿列方向看，反映某一产业部门生产各产品部门货物或服务的价值量，合计为该产业部门总产出。
全部产业部门总产出等于全部产品部门总产出。
通常产品部门个数多于产业部门个数。
按生产者价格计算的总供给等于按生产者价格计算的总产出与进口之和；按购买者价格计算的总供给等于按生产者价格计算的总供给与商业和运输费用之和。
使用表又称投入表，通常由三部分组成，第一部分的主栏包括n个产品部门，宾栏包括m个产业部门。
沿行方向看，表明各产品部门生产的货物或服务提供给各产业部门使用的价值量，沿列方向看，表明各产业部门从事生产活动所消耗各产品部门生产的货物或服务的价值量；第二部分是第一部分在水平方向上的延伸，其主栏与第一部分相同，也是n个产品部门，其宾栏由最终消费、资本形成总额、出口等最终使用项组成，它反映各产品部门生产的货物或服务用于最终使用的价值量及其构成；第三部分是第一部分在垂直方向上的延伸，其主栏由劳动者报酬、生产税净额、固定资产折旧和营业盈余等增加值项组成，宾栏与第一部分的宾栏一致，也是m个产业部门，它反映各产业部门增加值的构成情况。
产品部门×产品部门表，形式上与使用表相似，也是由三部分组成，第一部分是由名称相同、排列次序相同、数目一致的n个产品部门纵横交叉而成的，其主栏为中间投入、宾栏为中间使用，它充分揭示了国民经济各产品部门之间相互依存、相互制约的技术经济联系，反映了国民经济各部门之间相互依赖、相互提供劳动对象供生产和消耗的过程。
产业结构与产业关联-------基于投入产出表的分析摘要本文利用某地区投入产出表计来分析该地区的产业关联效应，计算并运用影响力系数、感应系数、直接消耗系数、完全消耗系数等指标来描述来分析该地区产业关联和产业结构，在此基础上得出各产业关系及各产业的优势劣势。
关键词：产业关联，产业结构，直接消耗系数，完全消耗系数，影响力系数，感应系数引言：地区经济是一个复杂的整体，各个产业部门之间存在着既广泛又密切的技术经济联系，因而某一个产业部门在生产过程中的任何变化，都将通过产业关联关系对其他产业部门产生一定的波及作用。
利用投入产出的分析方法，可以定量地分析一定时期内国民经济各产业部门在社会再生产过程中所形成的直接和间接的相互依存、相互制约的技术经济联系。
产业关联是指国民经济各部门在社会再生产过程中所形成的直接和间接的相互依存、相互制约的经济联系。
它是国民经济中一个产业与其他产业之间的技术经济联系。
关联度是对关联关系的量化，指一个产业投入产出关系的变动对其它产业投入产出水平的波及程度和影响程度。
一产业关联的分析基本工具投入产出表和投入产出模型是产业关联分析的基本工具，包括实物型和价值型两种类型，使用最广泛地是价值型分析工具。
如下两张表：本文基于的投入产出表为附表1表行向表示该产业的分配或者是去向，即产出部门的产品或者是服务提供给投入部门的作为中间需求和最终需求的量。
列向表示产品的价值组成，即在投入过程中消耗的产出部门的产品或者服务的量。
在投入产出表中,总投入等于总产出。
中间投入等于中间使用,从而最初投入部分等于最终需求部分, 按照上述分类,投入产出表水平方向和竖直方向纵横交错,构成相互联系投入产出的相关理论的三个部分:中间需求部分、最终需求部分和增加值部分。
中间需求部分是投入产出表的核心部分,它反映了一定时期内几个经济系统在生产过程中各个部门之间的投入产出关系。
横向的数据表示某一产业向包括本部门在内的所有部门提供其产出的中间产品的状况,纵向的数据表示某一部门在生产中所有部门购进中间产品的状况。
§2.3 投入产出表的平衡与修正一、问题的提出价值型投入产出表按列收集数据汇总后，肯定会发现，每一行加总不一定等于事先确定的总产出，每一列加总也不一定等于已知的总投入。
这是完全可以理解的：如此庞大的工程，最后列入表中的每一个数据都是由成千上万个数据汇总得到的，不可能没有误差。
但从理论上讲，它们应该是平衡的，最后公布的投入产出表也必须是平衡的。
因此就要用机械的方法将数据由不平衡调正到平衡。
这就是投入产出表的平衡。
如果应用U-V 表方法，U 表和V 表本身就是需要调整平衡的。
前面已经提及，编制投入产出表费时费力，人们并不希望经常编表，希望编出一张表能多用几年；但人们又希望能把投入产出表及时加以修正以满足应用要求。
于是就提出了投入产出表的修正方法问题。
用于平衡和修正投入产出表的较成熟的方法是R.A.S 方法。
二、R.A.S 方法原理1. 一个简单的例子 先从一个简单的例子出发介绍R.A.S 方法的原理。
假设有一张数据表如表2-3-1中(1)所示，该表按行相加应该等于u ，但现收集到的数据按行加总结果为u 1；按列加总应该等于v ，但收集到的数据却为v 1。
因为确认u 与v 是正确的，那么表中数据则是不准确的，需要进行调整，使其按行、列加总等于u 与v 。
这里u 和v 分别称为行控制数和列控制数。
先求出每行中u 与u 1的比例数11/u u r =。
用该比例数分别乘每行中每个数据，即用0.873乘第1行元素，用1.184乘第2行元素，用0.9111乘第3行元素，得到新的数据表(2)。
该表每行加总肯定等于行控制数，但按列加总为v 2，仍不等于列控制数v 。
表2-3-1 R.A.S 方法(1) (2)甲 乙 丙 u 1u r 1甲 乙 丙 u u 2=甲 160 0.873 甲乙 150 1.184 乙 丙 120 0.911 丙 v 1 100 266.7 75 2v 97.3 256.2 76.5v100250802s1.027 0.976 1.046(3) (4)甲 乙 丙 u 3 r 3 甲 乙 丙 u u i =甲 1.01 甲 乙 0.996 乙 丙0.992丙v 3v i =再求出每列v 与v 2的比例数2s ,22/v v s =。
