当前位置：文档之家 › 工程力学应力状态与应力状态分析样本

工程力学应力状态与应力状态分析样本

  • 格式：doc
  • 大小：1.10 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

工程力学---应力状态分析

工程力学---应力状态分析

τα =
ห้องสมุดไป่ตู้
2
sin2α +τ xcos2α
上述关系建立在静力学基础上， 上述关系建立在静力学基础上，故所得结 论既适用于各向同性与线弹性情况， 论既适用于各向同性与线弹性情况，也适 用于各向异性、 用于各向异性、非线弹性与非弹性问题
单辉祖：工程力学 12
应力圆
应力圆原理
σα = σ x +σ y σ x −σ y
17
例 2-2 利用应力圆求截面 m-m 上的应力
解： ：
σ m = −115 MPa
τ m = 35 MPa
18
单辉祖：工程力学
例 2-2 利用应力圆求截面 m-m 上的应力
解： 1. 画应力圆 ： A点对应截面 x, B点对应截面 y 点对应截面 点对应截面 τ 2. 由应力圆求 σm 与 m 顺时针转60 由A点（截面 x ）顺时针转 。至D点（截面 y ） 点 点
解： σ x = −100 MPa τ x = −60 MPa σ y = 50 MPa α = −30o ：
σm =
σ x + σ y σ x −σ y
2 +
τm =
单辉祖：工程力学
σ x −σ y
2
2
cos2α −τ xsin2α = −114.5MPa
sin2α +τ xcos2α = 35.0MPa
(τ ydAsinα)sinα + (σ ydAsinα)cosα = 0
σα = σ xcos2α +σ ysin2α − (τ x +τ y )sinα cosα
τα = (σ x −σ y )sinα cosα +τ xcos2α −τ ysin2α

《工程力学》实验应力分析

《工程力学》实验应力分析

r 1 2 3 4 2(1 )M
上下表面
M
r 2(1 )
E M
E r 2(1 )
R3 R4
R2 t2
R1
B
R1
R2
A
C
R4
R3
D
21
13.3 测量电桥的接法及其应用
例2 通过应变测量(1)求偏心载荷F;(2) 求e.试确定
布片、接桥方案。截面bh
y
e
y
解：(1)测F
z x
F Fe F 分析：
Me
Me
25
13.4 二向应力状态下主应力方向已知时的应力测定
1
3
B
R1
R2
A
C
R4
R3
D
解: 应力分析
1 3
沿与轴线成450方向为主方向,
故沿主应力方向布片.
采用全桥接法.
r 1 2 3 4 41
1
r
4
26
13.4 二向应力状态下主应力方向已知时的应力测定
1
3
B
R1
R2
A
C
R4
工程力学
第13章 实 验 应 力 分 析
1
第13章 实验应力分析
§13.1 概述 §13.2 电测应力分析的基本原理 §13.3 测量电桥的接法及应用 §13.4 二向应力状态下主应力已知时
的应力测定 §13.5 二向应力状态下主应力未知时
的应力测定
2
13.1 概 述
一. 为什么要进行实验应力分析
例1 已知E， , 测定max, 试确定布片、接桥方案。
M
R1
M
解：第一方案，
R2

工程力学7第七章应力状态和应变状态分析

工程力学7第七章应力状态和应变状态分析

x y x y cos 2 x sin 2 2 2 x y sin 2 x cos 2 2
0
x y
2
(
x y
2
)
2
2
2 x
y
y
y
2
090
0
x y
2
(
x y
2
2、为什么要研究一点的应力状态 单向应力状态和纯剪切应力状态的强度计算
σmax≤ [σ] τ
max≤[τ
]
梁截面上的任意点的强度如何计算？
分析材料破坏机理
F F F F T
T
3、怎么研究一点的应力状态
单元体
•各面上的应力均匀分布





• 相互平行的一对面上 应力大小相等、符号相同
满足：力的平衡条件 切应力互等定理
§7-2 平面应力状态分析
一、解析法:
1.任意斜面上的应力 y

y

y
y
y
n
y

x
a
x

e
d
x

x
x
bz
x
x

x
e
x
x




y


f
yy
x
x

b


c
y

y

y
f t
应力的符号规定同前 α角以从x轴正向逆时针 转到斜面的法线为正
(设ef的面积为dA)
x y x y cos 2 x sin 2 2 2 x y sin 2 x cos 2 2

工程力学-应力状态与应力状态分析

工程力学-应力状态与应力状态分析

8 应力状态与应变状态分析1、应力状态的概念，2、平面应力状态下的应力分析，3、主平面是切应力为零的平面，主应力是作用于主平面上的正应力。

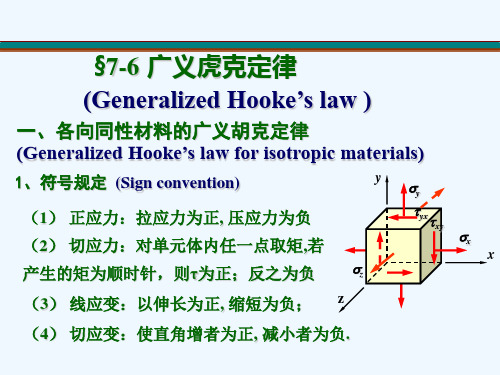
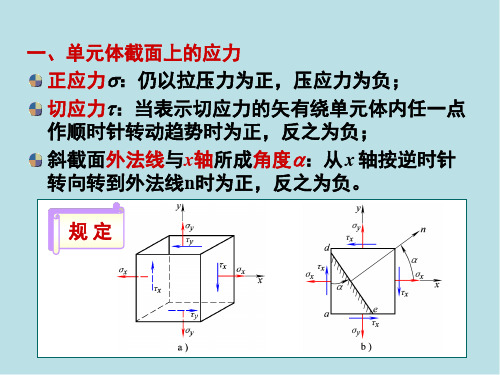
（1）过一点总存在三对相互垂直的主平面，对应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=（2）任斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=（3) 主应力的大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面的方位y x xytg σστα--=2204、主应变122122x y x y xy xyx y()()tg εεεεεεγγϕεε⎡=+±-+⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1x z y y E σσμσε+-=)]([1y x z z E σσμσε+-=G zxzx τγ=G yzyz τγ=，G xyxy τγ=6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。

”8.1 试画出下图8.1(a)所示简支梁A 点处的原始单元体。

图8.1[解]（1）原始单元体要求其六个截面上的应力应已知或可利用公式直接计算，因此应选取如下三对平面：A 点左右侧的横截面，此对截面上的应力可直接计算得到；与梁xy 平面平行的一对平面，其中靠前的平面是自由表面，所以该对平面应力均为零。

再取A 点偏上和偏下的一对与xz 平行的平面。

截取出的单元体如图8.1(d)所示。

(2)分析单元体各面上的应力:A 点偏右横截面的正应力和切应力如图8.1(b)、(c)所示，将A 点的坐标x 、y 代入正应力和切应力公式得A 点单元体左右侧面的应力为：z M y I σ=bI QS z z*=τ由切应力互等定律知,单元体的上下面有切应力τ ；前后边面为自由表面，应力为零。

工程力学24373

工程力学24373

方向面的取向(方向角q)有关。因而有可能存在某种方向面，其上
之切应力xy＝0，这种方向面称为主平面（principal plane），其
方向角用qp表示。
tan2qp＝
－2τ xy x y
主平面上的正应力称为主应力（principal stress）。主平面法线方
向即主应力作用线方向，称为主方向（principal directions）.主方
1. 问题的提出 2. 应力的三个重要概念 3. 一点应力状态的描述
第10章 应力状态分析
1. 问题的提出
请看下列实验现象：
低碳钢和铸铁的拉伸实验 低碳钢和铸铁的扭转实验
第10章 应力状态分析
铸铁拉伸实验
低碳钢拉伸实验
韧性材料拉伸时为什么会出现滑移线？
第10章 应力状态分析
低碳钢扭转实验
铸铁扭转实验
与前几章中所采用的平衡方法不同的是，平衡对象既 不是整体杆或某一段杆，也不是微段杆或其一部分，而是 三个方向尺度均为小量的微元局部。解析公式。
此外，本章中还将采用与平衡解析式相比拟的方法， 作为分析和思考问题的一种手段，快速而有效地处理一些 较为复杂的问题，从而避免死背硬记繁琐的解析公式。
第10章 应力状态分析
qqqq q q y x x s i n c o s y s i n c o s x y s i n 2 y x c o s 2
上述结果表明，一点处的应力状态，在不同的坐标系中有不 同的表达形式，即对于同一点，可以用不同取向的微元表示其应 力状态。这相当于将微元连同其坐标轴旋转了一个角度，或者说
x'y'
x'
xy
x'y'
x'

工程力学-应力状态

工程力学-应力状态
σ 30 100 50 2 100 50 2
sy
n
例1 已知 sx= –100MPa、sy =50MPa 、tx = – 60MPa，a = –30º
cos[2 ( 30)] ( 60)sin[2 ( 30)]
114.5MPa
τ 30
上海应用技术学院
τ T WP
此时不适用基本变形下的强度条件，应同时考虑s 、t 的影响。 又如：受内压容器筒壁
上海应用技术学院
sy
A 筒壁某点A处应力： sx 、sy，为双向受拉状态。 又如：火车车轮与铁轨接触处表层
4
sx
s s
A
s
A点应力：为三向受压状态。 此外：在通过A点不同斜截面上的应力是不同的，将影响到构 件的破坏形式。
s
OC CFcos2 α DFsin2 α σx σy σx σy cos2 α τ x sin2 α σ α 2 2
上海应用技术学院
证明： H点横坐标： OM 纵坐标： MH CD与s 轴夹角为2a0
OM σx σy 2 σx σy 2 cos2 α τ x sin2 α σ α
ty
e
cos2 α τ x sin2 α
b
sy
切线方向上： Σ F 0 τ
τ α d A (σ x d A cos α )sin α ( τ x d A cos α )cos α (σ y d A sin α )cos α ( τ y d A sin α )sin α 0
∴ τ α σ x sin α cos α σ y sin α cos α τ x cos2 α τ y sin 2 α
上海应用技术学院

工程力学-材料力学之应力应变状态分析

工程力学-材料力学之应力应变状态分析
泊松比 = 0.3 , F1=100KN ， F2=100KN。
求：（1）A点处的主应变 1， 2 ， 3
（2）A点处的线应变 x ， y ， z
F1 b A F2 z b=50mm h=100mm
Hale Waihona Puke 19F2al
解：梁为拉伸与弯曲的组合变形. A点有拉伸引起的正应力
和弯曲引起的切应力.
铜块横截面上的压应力mpa3010300analysiessst155mpa铜块的主应力为mpampa30最大切应力mpa2510951010034analysiessst例题11一直径d20mm的实心圆轴在轴的的两端加力矩m126n45方向的应变analysiessstanalysiessst外径d60mm的薄壁圆筒在表面上k点与其轴线成45y两方向分别贴上应变片然后在圆筒两端作用矩为的扭转力偶如图所示已知圆筒材料的弹性常数为若该圆筒的变形在弹性范围内且analysiessst从圆筒表面k点处取出单元体其各面上的应力分量如图所示可求得mpa80maxmpa80maxanalysiessstmaxmaxmax10拉应变圆筒表面上k点处沿径向z轴的应变和圆筒中任一点该点到圆筒横截面中心的距离为maxmax因此该圆筒变形后的厚度并无变化仍然为t10mmanalysiessstb50mmh100mm例题13已知矩形外伸梁受力f作用
在任意形式的应力状态下, 各向同性材料内一点处的体
积应变与通过该点的任意三个相互垂直的平面上的正应力之
和成正比, 而与切应力无关.
11
例题10 边长 a = 0.1m 的铜立方块，无间隙地放入体积较大， 变形可略去
不计的钢凹槽中, 如图所示. 已知铜的弹性模量 E=100GPa，泊松比 =0.34， 当受到F=300kN 的均布压力作用时，求该铜块的主应力、体积应变以及最

工程力学第2节 二向应力状态分析

工程力学第2节 二向应力状态分析

例12-1 已知构件内某点处的应力单元体如图所示，
试求斜截面上的正应力 和切应力 。
解：按正负号规定则有：
x 60 MPa x 120 MPa y 80 MPa 300
代入公式得：


x
y
2
x
y
2
cos2
x
sin 2
78.9MPa
低碳钢试件扭转破坏是被剪断的，且其抗剪能力
低于其抗拉能力。
铸铁试件扭转破坏是被拉断的，且其抗拉能力低 于其抗剪能力。
例12-3 图示单元体，x=100MPa，x= –20MPa，
y=30MPa。试求：1） = 40º的斜截面上的 和 ； 2）确定A点处的max、max和它们所在的位置。


x
y
2
sin 2
x
cos2

121MPa
二、主应力和极限切应力
1、主应力和主平面


x
y
2
x
y
2
cos2
x
sin 2


x
y
2
sin 2
x
cos2
将公式 对 求一阶导数、并令其为0：
d d


x

2
y
(2 sin
由切应力互等定理有x=y，并利用三角关系：
sin2 1 cos2 、 cos2 1 cos2 及
2
2
ቤተ መጻሕፍቲ ባይዱ
2sin cos sin 2 对以上二式进行整理得到：


x
y
2

x
y
2

工程力 第10章 应力状态分析

工程力 第10章 应力状态分析

xy
yx
y y
一点处应力状态描述及其分 类
平面（二向）
应力状态
x
( Plane State of
Stresses )
y
yx xy
x
y
一点处应力状态描述及其分 类
y
x
x
y
yx
xy
x
单向应力状态
( One Dimensional State of Stresses )
纯剪应力状态
( Shearing State of Stresses )
x'y' x'
x'y' x'
xy
yx
x
微元平衡分析结果表明：即使同一点不同方向面 上的应力也是各不相同的，此即应力的面的概念。
第10章 应力状态分析
应力
哪一个面上？ 哪一点？
指明
哪一点？ 哪个方向面？
过一点不同方向面上应力的集合，称之为这一
点的应力状态（State of the Stresses of a Given Point）。
为什么脆性材料扭转时沿45º螺旋面断开？
第10章 应力状态分析
根据微元的局部平衡
y' xx'来自x'y'
x'
x 拉中有切
x
第10章 应力状态分析
根据微元的局部平衡
y'
yx
x'
x'y' x'
xy
xy
yx
切中有拉
第10章 应力状态分析
重要结论
不仅横截面上存在应力，斜截面上也 存在应力；不仅要研究横截面上的应力， 而且也要研究斜截面上的应力。

工程力学-应力状态与应力状态分析

工程力学-应力状态与应力状态分析

8 应力状态与应变状态分析1、应力状态的概念，2、平面应力状态下的应力分析，3、主平面是切应力为零的平面，主应力是作用于主平面上的正应力。

（1）过一点总存在三对相互垂直的主平面，对应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=（2）任斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=（3) 主应力的大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面的方位y x xytg σστα--=2204、主应变12122x y xyx y()tg εεεεγϕεε⎡=+±⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1x z y y E σσμσε+-=)]([1y x z z E σσμσε+-=G zxzx τγ=G yzyz τγ=，G xyxy τγ=6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。

”8.1 试画出下图8.1(a)所示简支梁A 点处的原始单元体。

图8.1[解]（1）原始单元体要求其六个截面上的应力应已知或可利用公式直接计算，因此应选取如下三对平面：A 点左右侧的横截面，此对截面上的应力可直接计算得到；与梁xy 平面平行的一对平面，其中靠前的平面是自由表面，所以该对平面应力均为零。

再取A 点偏上和偏下的一对与xz 平行的平面。

截取出的单元体如图8.1(d)所示。

(2)分析单元体各面上的应力:A 点偏右横截面的正应力和切应力如图8.1(b)、(c)所示，将A 点的坐标x 、y 代入正应力和切应力公式得A 点单元体左右侧面的应力为：z M y I σ=bI QS z z*=τ由切应力互等定律知,单元体的上下面有切应力τ ；前后边面为自由表面，应力为零。

工程力学材料力学之应力应变状态分析

工程力学材料力学之应力应变状态分析
工程力学材料力学之应力应变状态分 析
二、材料破坏的两种类型（常温、静载荷） (Two failure types for materials in normal temperature and static loads)
1. 断裂失效(Fracture failure) （1）脆性断裂 : 无明显的变形下突然断裂. （2）韧性断裂 : 产生大量塑性变形后断裂.
剪切
扭转
工程力学材料力学之应力应变状态分 析
上述强度条件具有如下特点： (1)危险点处于单向应力状态或纯剪切应力状态； (2)材料的许用应力 ，是通过拉(压)试验或纯剪试验测定试 件在破坏时其横截面上的极限应力,以此极限应力作为强度指 标,除以适当的安全系数而得，即根据相应的试验结果建立的 强度条件.
胡克（1635-1703）
波义耳（1627-1691）
惠更斯（1629-1695）工程力学材料力学牛析之顿应力（应1变64状3态-分1727）
复杂应力状态的应变能密度
三向应力状态
体积改变能密度 畸变能密度
工程力学材料力学之应力应变状态分 析
§7-8 强度理论(The failure criteria)
构件每单位体积的体积变化, 称为体积应变用θ表示.
各向同性材料在三向应力状态下的体应变
如图所示的单元体，三个边长为 a1 , a2 , a3 变形后的边长分别为
a1(1+，a2(1+2 ，a3(1+3
变形后单元体的体积为
2
a2
1
3
a1
a3
V1=a1(1+·a2(1+2 ·a3(1+3
工程力学材料力学之应力应变状态分 析
二向应力状态下(In plane stress-state) 设 3= 0

工程力学第13章应力状态分析和强度理论

工程力学第13章应力状态分析和强度理论

max
m in

x
y
2


(
x

2
y
)2


2 xy
——主应力的大小
3)、 切应力 的极值及所在截面
由


x
y
2
sin 2
xy cos 2 ,
令 d
0
d 1
tan
21


x 2 xy
y
(1 ; 1 1 900 )
——最大切应力 所在的位置
z
x
y y
x
z x
2
I 3 1
(1)求平行于σ1的方向面的应力σα 、 τα ,其上之应力与σ1 无关.
1
3
II 2
(2)求平行于σ2的方向面的应力σα、 τα ,其上之应力与σ2 无关.
2
III 1 3
2
(3)求平行于σ3的方向面的应力σα 、 τα ,其上之应力与σ3 无关.
例2、槽形刚体内放置一边长为a = 10 cm 正方形钢块，试求钢 块的三个主应力。F = 8 kN，E = 200 GPa, μ = 0.3。
Fy
解：1) 研究对象ຫໍສະໝຸດ 正方形钢块y F 80 MPa, A
x
?,
z 0.
x 0, y ?, z ? .
y
x b
a
c x x
y
b x


x

a y
c
y t
n 单元体各面面积
x bc : dA
ab: dAcos ac : dAsin
设：斜截面面积为ｄA，由分离体平衡得：

工程力学 应力状态

工程力学 应力状态
x y sin 2 x cos2 2
d 令 0 d
x y tg 2 2 x
可解出两个相差 的极值平面，一 2 个面上为极大值，另一个面上为极小值。
23
1 1 x y 将 tg 2 2 x
代入(7-2)式，可得：
60.8MPa
26
x y 60 sin 120 x cos120 2
70 sin 120 50 cos 120 2
55.3MPa
② 求主应力
2 x 2 50 tg 2 0 1.429 x y 70


A
B



横截面
横截面 外轮廓线
7
① 材料单元体上相对坐标面上的 应力大小相等、方向相反。 ② 材料单元体上任意方向面上的 应力视作均匀分布。
8
§7-2 平面应力状态分析
一、解析法求斜截面的应力
应力状态分析：已知材料单元体坐标平面的应
力，求任意方向面上的应力。
9
最常见的情况：有一对方向面上的应力为 零，单元体上所有的应力 在同一平面内，称为二向
(1) (2)
(1)2 (2)2 得：
x y 2 x y 2 ( ) ( cos 2 x sin 2 ) 2 2 2 x y ( sin 2 x cos2 ) 2 2
30
整理可得： x y 2 x y 2 2 2 ( ) ( ) x
(7-1)记忆
同理，利用
F
t
0 ，可得：
x y sin 2 x cos 2 2
(7-2)记忆
13

应力、应力状态分析(习题解答)

应力、应力状态分析(习题解答)

8-9 矩形截面梁如图所示，绘出1、2、3、4点的应力单元体，并写出各点的应力计算式。

解：(1)求支反力R A =,R B = (2)画内力图如图所示。

xPl(-)(+)PlMkN ·m)PPy(-)(-)(+)VkN)题8-9图(3) 求梁各点的正应力、剪应力：(4)画各点的应力单元体如图所示。

9-1 试用单元体表示图示构件的A 、B 的应力单元体。

（a ）解：（1）圆轴发生扭转变形，扭矩如图所示。

111max 222222333333max 442330,22(')[()]448114()121200(0,0)16ZZZ ZzV pA b hh h hP P b M V S Pl hy I I bb h b h b M SM PlW b h σττστστστ==-=-⋅=-⋅⋅-⋅⨯⨯-⋅=⋅=⋅==⋅⨯⨯⨯⨯⋅=====-=-=⨯⨯80A-+16080T (kN ·m )（2）绘制A 、B 两点的应力单元体：A 、B 两点均在圆轴最前面的母线上，横截面上应力沿铅垂方向单元体如图所示：331601020.21680510.216A A t bB t T Pa kPa W T Pa kPaW τπτπ===⨯===-⨯（b ）解：（1）梁发生弯曲变形，剪力、弯矩图如图所示。

-+120VkN)40MkN ·m)+120402060题9-1（b ）（2）绘制A 、B 两点的应力单元体：A 点所在截面剪力为正，A 点横截面的剪力为顺时针，同时A 点所在截弯矩为正下拉，而A 点是压缩区的点。

B 点所在截面剪力为负，B 点横截面的剪力为逆时针，同时B 点所在截弯矩为正下拉，而B 点是拉伸区的点。

单元体如图所示：333.3333.60100.0537.50.1200.21212010(0.1200.050.075) 5.6250.1200.20.1201220100.0512.50.1200.2124010(0.1200.05A A A tA z A A tB B B t B z B B t M y Pa MPaI V S Pa MPaI b M y Pa MPaI V S I bστστ⨯=-⋅=-⨯=-⨯⋅⨯⨯⨯⨯=⋅==⋅⨯⨯⨯=⋅=⨯=⨯⋅-⨯⨯⨯⨯=⋅=⋅g g 30.075) 1.8750.1200.20.12012Pa MPa=-⨯⨯9-2（c解：(1)由题意知：30,20.5030ox x y MP MPa MP στσα==-==，，。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

8 应力状态与应变状态分析1、应力状态概念，2、平面应力状态下应力分析，3、主平面是切应力为零平面，主应力是作用于主平面上正应力。

（1）过一点总存在三对互相垂直主平面，相应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=（2）任斜截面上应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=（3) 主应力大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面方位yx xytg σστα--=2204、主应变122122x y x y xy xyx y()()tg εεεεεεγγϕεε⎡=+±-+⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1x z y y E σσμσε+-=)]([1y x z z E σσμσε+-=G zxzx τγ=G yzyz τγ=，G xyxy τγ=6、应力圆与单元体之间相应关系可总结为“点面相应、转向相似、夹角两倍。

”8.1 试画出下图8.1(a)所示简支梁A 点处原始单元体。

图8.1[解]（1）原始单元体规定其六个截面上应力应已知或可运用公式直接计算，因而应选用如下三对平面：A 点左右侧横截面，此对截面上应力可直接计算得到；与梁xy 平面平行一对平面，其中靠前平面是自由表面，因此该对平面应力均为零。

再取A 点偏上和偏下一对与xz 平行平面。

截取出单元体如图8.1(d)所示。

(2)分析单元体各面上应力:A 点偏右横截面正应力和切应力如图8.1(b)、(c)所示，将A 点坐标x 、y 代入正应力和切应力公式得A 点单元体左右侧面应力为：zMy I σ=b I QS z z *=τ解题范例由切应力互等定律知,单元体上下面有切应力τ ；先后边面为自由表面，应力为零。

在单元体各面上画上应力，得到A 点单元体如图8.1(d)。

8.2 图8.2(a)所示单元体,试求（1）图示斜截面上应力;（2）主方向和主应力，画出主单元体;（3）主切应力作用平面位置及该平面上正应力，并画出该单元体。

[解]（1）求斜截面上正应力︒30－σ和切应力︒30－τ图8.2由公式MPa 5.64)60sin()60()60cos(21005021005030-=︒---︒---++-=︒-σMPa95.34)60cos()60()60sin(21005030=︒--+︒---=︒-τ（2）求主方向及主应力8.01005012022tan -=----=--=y x x σστα ︒-=66.382α︒=︒-=67.7033.1921αα最大主应力在第一象限中，相应角度为070.67α=︒，主应力大小为15010050100cos(270.67)(60)sin(270.67)121.0MPa 22σ=⨯︒--⨯︒=－＋－－＋由yx σσσσαα+＝＋21可解出21(50)100(121.0)71.0MPax y ασσσσ=+=-+-=-－因有一种为零主应力，因而)33.19(MPa0.7133︒--＝第三主方向＝ασ画出主单元体如图8.2(b)。

（3）主切应力作用面法线方向25.1120100502tan =---='α ︒='34.512α︒='︒='67.11567.2521αα主切应力为'2'1MPa 04.96)34.51cos()60()34.51sin(210050ααττ-=-=︒-+︒--=此两截面上正应力为MPa 0.25)34.51sin()60()34.51cos(2100502100501=︒--︒--++-='ασMPa 0.25)34.231sin()60()34.231cos(2100502100502=︒--︒--++-='ασ主切应力单元体如图8.2（c ）所示。

由yx MPa σσσσαα+==+=+''500.250.2521，可以验证上述成果对的性。

8.3 试用图形解析法，重解例8.2。

[解] （1）画应力圆建立比例尺，画坐标轴τσ、。

对图8.2(a)所示单元体，在τσ-平面上画出代表x x τσ、点A(-50,-60)和代表yy τσ、点B(100,60)。

连接A 、B ，与水平轴σ交于C 点，以C 点为圆心，CB （或CA ）为半径，作应力圆如图8.3所示.图8.3(2) 斜截面上应力在应力圆上自A 点顺时针转过︒60，到达G 点。

G 点在τσ、坐标系内坐标即为该斜截面上应力，从应力圆上可直接用比例尺测量或计算得到G 点水平和垂直坐标值：64.5ασ=-MPaτα=34.95MPa(3)主方向、主应力及主单元体图8.3所示应力圆图上H 点横坐标OH 为第一主应力，即1121.04MPa OH σ==K 点横坐标OK 为第三主应力，即371.04MPa OK σ==-由应力圆图上可以看出，由B 点顺时针转过02α为第一主方向，在单元体上则为由y轴顺时针转0α，且00238.66,19.33αα=︒=︒应力圆图上由A 顺时针转到K 点(︒=∠66.38ACK )，则在单元体上由x 轴顺时针转过︒33.19为第三主方向,画出主单元体仍如图8.2(b)所示。

（4）主切应力作用面位置及其上应力图8.3所示应力圆上N 、P 点分别表达主切应力作用面相对方位及其上应力。

在应力圆上由B 到N ，逆时针转过︒34.51，单元体上max τ作用面外法线方向为由y轴逆时针转过︒67.25，且MPa 04.96min max==-=CB ττmin max ττ和作用面上正应力均为25MPa,主切应力作用面单元体仍如图8.2(c)所示。

8.4 如图8.4所示两端封闭薄壁筒同步承受内压强p 和外力矩m 作用。

在圆筒表面a 点用应变仪测出与x 轴分别成正负45︒方向两个微小线段ab 和ac 应变ε45︒＝629.4×10–6，ε–45︒＝－66.9×10–6，试求压强P 和外力矩m 。

已知薄壁筒平均直径d ＝200mm ，厚度t ＝10mm ， E ＝200GPa ，泊松比μ＝0.25。

图8.4[解] （1）a 点为平面应力状态,在a 点取出如图8.4(c)所示原始单元体，其上应力：22,,42x y x pd pd mt t d t σστπ===-（2）求图8.4(c)斜单元体efgh 各面上正应力：24524532283228x yx x y x pd mt d t pd m t d t σσστπσσστπ-+=-=++=+=-（3）运用胡克定律，列出应变ε45︒、ε–45︒表达式()()()()()()2454545245454511321181132118pd m E E t d t pd m E E t d t εσμσμμπεσμσμμπ---⎡⎤=-=-++⎢⎥⎣⎦⎡⎤-=-+⎢⎥⎣⎦＝-将给定数据代入上式6 63213200210629.4100.75 1.252001081020010p mπ-⎛⎫⨯⨯⨯=⨯⨯+⨯⎪⨯⨯⨯⎝⎭66321320021066.9100.75 1.252001081020010p mπ-⎛⎫⨯⨯-⨯=⨯⨯-⨯⎪⨯⨯⨯⎝⎭得内压强和外力矩p＝10MPa， m＝35kNm8.5矩形截面简支梁如图8.5所示，已知梁横截面面积为A，截面惯性矩为I，材料弹性模量为E，泊松比为μ,梁外表面中性层上A点45°方向线应变为ε450。

请选取荷载F.图 8.5(A)AEμε-︒145（B）AE145-︒με(C)AE)1(4945με-︒（D）AE)1(9445με-︒答案:(A)8.1单元体最大正应力面上切应力恒等于零吗?[解]对的。

由于在主平面上正应力σ1是单元体内各截面上正应力极值（可觉得最大值），而主平面上切应力为零。

8.2 单元体最大切应力面上正应力恒等于零,对吗?[解] 不对的。

三向应力状态下单元体有3个主应力，而最大切应力由31σσ决定，即：231maxσστ-=习题解析8.3 若一单元体中两个面上切应力数值相等 ，符号相反 ，则该两平面必然互相垂直 ，这种说法对吗?[解] 对的。

由切应力双生互等定理知,若切应力数值上21ττ=，符号相反时，该两平面必然互相垂直。

图 8.68.4 直径 d=20mm 、L=2m 圆截面杆,受力如图 8.7 。

试绘杆件中 A 点和 B 点单元体受力图,算出单元体上应力数值,并拟定这些点与否为危险点。

[解] 如下图8.8为图8.7各单元体受力图：1τ2τ1τ2τxσσyσyσ（c ） 图 8.7(a) （b ） （d ）图 8.8 应力计算: 图（a ）A 点 ：a N63.69MP A σ==-图（b ）A 点：a38050.96MP d 16τ==π 图（c ）A 点：a N127.38MP A σ==B 点：aN127.38MP A σ== ，a 38050.96MP d 16τ==π点A 点A 点A )(a )(c )(b 点B )(d 点B τττ图（d ）中A 点(压应力):3a33z M 201025.48MP1W 3.14(2010)32-⨯σ===⨯⨯⨯ B 点：*z az QS 4Q 0.17MP I b 3A τ===(b ）中A 为危险点，（c ）中A 、B 为危险点，（d ）中A ，B 点均为危险点,相比之下A 点应力较大。

8.5 已知应力状态如图 8.9 所示(应力单位:MPa)。

试用图解法求: (1)(a)、(b)中指定斜截面上应力;并用解析法校核之;(2) (c)、(d) 、(e)上主应力大小与方向,在单元体上画出主平面位置 ,求最大切应力。

(a)300斜截面单元本;(b)450斜截面单元体;(c) 纯切应力单元体;(d) 压拉切单元体 (e) 拉压切单元体。

图 8.9[解](a) 按比例画出应力圆如下图,可得α=300斜截面正应力和切应力为E 点坐标为30a45MP ︒σ=30a8.5MP ︒τ=解析法校核：x y x yx ax y x a30505030cos 2sin 2cos6045MP 222250303sin 2cos 2538.5MP 222αασ+σσ-σ+-σ=+α-τα=+=σ-σ-τ=α+τα=⋅== (b) 用比例画出应力圆,E 点坐标为45a5MP ︒σ=45a25MP ︒τ=解析法校核：x y x yx a x yx a 5050cos 2sin 2cos 9020sin 905MP 222250sin 2cos 2sin 9025MP 22αασ+σσ-σσ=+α-τα=+-=σ-στ=α+τα=⋅=(c ）应力圆如下图,与σ轴交点即为主应力相应点，从应力圆上可按比例直接量得两个主应力之值分别为：σCEXO τY2α11a 232aOA 50MP ,0,OA50MP σ==σ=σ==-主平面方位可由应力圆上量得,因112D OA 90ϕ=∠=-最大主应力作用面与x 平面之夹角为(从D1到A1是顺时针转):45ϕ=-13max a50MP 2σ-στ==最大切力；(d ）应力圆与σ轴交点即为主应力得应点，从应力图上可按比例直接量得两个主应力之值分别为：11a22a 3OA 70MP OA 30MP ,0σ==σ==σ= 最大主应力作用面与x 平面之夹角为(可由应力圆上得):12FCA 9045ϕ=∠=-ϕ=-max aCF 20MP τ==最大切力(e ）应力圆与σ轴交点即为主应力相应点，从应力圆上可按比例直接量得两个主应力之值分别为11a 32aOA 44.7MP OA 44.7MP σ==σ==-主平面方位，可由应力圆上量得：226.513.2ϕ=-ϕ=-（相应于主应力σ1所在主平面）max a40MP τ=最大切力8.6 图 8.10 示单元体 ( 单位为 MPa)，问分别属于什么应力状态。