高中物理动量定理专题(问题详解)-word

高中物理高考物理动量定理解题技巧讲解及练习题(含答案)一、高考物理精讲专题动量定理1．如图甲所示，物块A、B的质量分别是m A＝4.0kg和m B＝3.0kg。

用轻弹簧拴接，放在光滑的水平地面上，物块B右侧与竖直墙壁相接触。

另有一物块C从t＝0时以一定速度向右运动，在t＝4s时与物块A相碰，并立即与A粘在一起不再分开，C的v－t图象如图乙所示。

求：（1）C的质量m C；（2）t＝8s时弹簧具有的弹性势能E p1，4~12s内墙壁对物块B的冲量大小I；（3）B离开墙后的运动过程中弹簧具有的最大弹性势能E p2。

【答案】（1）2kg ；（2）27J，36N·S；（3）9J【解析】【详解】（1）由题图乙知，C与A碰前速度为v1＝9m/s，碰后速度大小为v2＝3m/s，C与A碰撞过程动量守恒m C v1＝(m A＋m C)v2解得C的质量m C＝2kg。

（2）t＝8s时弹簧具有的弹性势能E p1＝12(m A＋m C)v22=27J取水平向左为正方向，根据动量定理，4~12s内墙壁对物块B的冲量大小I=(m A＋m C)v3-(m A＋m C)（-v2）=36N·S（3）由题图可知，12s时B离开墙壁，此时A、C的速度大小v3＝3m/s，之后A、B、C及弹簧组成的系统动量和机械能守恒，且当A、C与B的速度相等时，弹簧弹性势能最大(m A＋m C)v3＝(m A＋m B＋m C)v41 2(m A＋m C)23v＝12(m A＋m B＋m C)24v＋E p2解得B离开墙后的运动过程中弹簧具有的最大弹性势能E p2＝9J。

2．蹦床运动是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。

一个质量为60kg的运动员，从离水平网面3.2m高处自由下落，着网后沿竖直方向蹦回离水平网面5.0m高处。

已知运动员与网接触的时间为1.2s，若把这段时间内网对运动员的作用力当作恒力来处理，求此力的大小和方向。

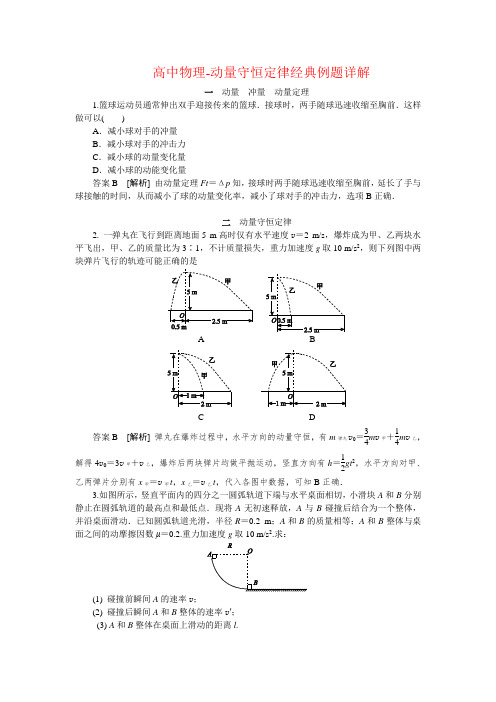
高中物理-动量守恒定律经典例题详解一 动量 冲量 动量定理1.篮球运动员通常伸出双手迎接传来的篮球．接球时，两手随球迅速收缩至胸前．这样做可以( )A ．减小球对手的冲量B ．减小球对手的冲击力C ．减小球的动量变化量D ．减小球的动能变化量答案B [解析] 由动量定理Ft ＝Δp 知，接球时两手随球迅速收缩至胸前，延长了手与球接触的时间，从而减小了球的动量变化率，减小了球对手的冲击力，选项B 正确．二 动量守恒定律2. 一弹丸在飞行到距离地面5 m 高时仅有水平速度v ＝2 m/s ，爆炸成为甲、乙两块水平飞出，甲、乙的质量比为3∶1，不计质量损失，重力加速度g 取10 m/s 2，则下列图中两块弹片飞行的轨迹可能正确的是A BC D答案B [解析] 弹丸在爆炸过程中，水平方向的动量守恒，有m 弹丸v 0＝34m v 甲＋14m v 乙，解得4v 0＝3v 甲＋v 乙，爆炸后两块弹片均做平抛运动，竖直方向有h ＝12gt 2，水平方向对甲、乙两弹片分别有x 甲＝v 甲t ，x 乙＝v 乙t ，代入各图中数据，可知B 正确．3.如图所示，竖直平面内的四分之一圆弧轨道下端与水平桌面相切，小滑块A 和B 分别静止在圆弧轨道的最高点和最低点．现将A 无初速释放，A 与B 碰撞后结合为一个整体，并沿桌面滑动．已知圆弧轨道光滑，半径R ＝0.2 m ；A 和B 的质量相等；A 和B 整体与桌面之间的动摩擦因数μ＝0.2.重力加速度g 取10 m/s 2.求：(1) 碰撞前瞬间A 的速率v ；(2) 碰撞后瞬间A 和B 整体的速率v ′； (3) A 和B 整体在桌面上滑动的距离l .[答案] (1)2 m/s (2)1 m/s (3)0.25 m [解析] 设滑块的质量为m . (1)根据机械能守恒定律有mgR ＝12m v 2解得碰撞前瞬间A 的速率有v ＝2gR ＝2 m/s.(2)根据动量守恒定律有m v ＝2m v ′解得碰撞后瞬间A 和B 整体的速率v ′＝12v ＝1 m/s.(3)根据动能定理有12(2m )v ′2＝μ(2m )gl 解得A 和B 整体沿水平桌面滑动的距离l ＝v ′22μg＝0.25 m ． 4.质量为2 kg 的小车以2 m/s 的速度沿光滑的水平面向右运动，若将质量为0 .5 kg 的砂袋以3 m/s 的水平速度迎面扔上小车，则砂袋与小车一起运动的速度的大小和方向是( )A ．1.0 m/s ，向右B ．1.0 m/s ，向左C ．2.2 m/s ，向右D ．2.2 m/s ，向左答案D [解析] 忽略空气阻力和分离前后系统质量的变化，卫星和箭体整体分离前后动量守恒，则有(m 1＋m 2)v 0＝m 1v 1＋m 2v 2，整理可得v 1＝v 0＋m 2m 1(v 0－v 2)，故D 项正确． 5.冰壶运动深受观众喜爱，图X29­1甲为2014年2月第22届索契冬奥会上中国队员投掷冰壶的镜头．在某次投掷中，冰壶甲运动一段时间后与对方静止的冰壶乙发生正碰，如图乙．若两冰壶质量相等，则碰后两冰壶最终停止的位置，可能是图丙中的哪幅图( )图X29­1答案B [解析] 两个质量相等的冰壶发生正碰，碰撞前后都在同一直线上，选项A 错误；碰后冰壶A 在冰壶B 的左边，选项C 错误；碰撞过程中系统的动能可能减小，也可能不变，但不能增大，所以选项B 正确，选项D 错误．6.下图X29­2是“牛顿摆”装置，5个完全相同的小钢球用轻绳悬挂在水平支架上，5根轻绳互相平行，5个钢球彼此紧密排列，球心等高．用1、2、3、4、5分别标记5个小钢球．当把小球1向左拉起一定高度，如图甲所示，然后由静止释放，在极短时间内经过小球间的相互碰撞，可观察到球5向右摆起，且达到的最大高度与球1的释放高度相同，如图乙所示．关于此实验，下列说法中正确的是()图X29­2A．上述实验过程中，5个小球组成的系统机械能守恒，动量守恒B．上述实验过程中，5个小球组成的系统机械能不守恒，动量不守恒C．如果同时向左拉起小球1、2、3到相同高度(如图丙所示)，同时由静止释放，经碰撞后，小球4、5一起向右摆起，且上升的最大高度高于小球1、2、3的释放高度D．如果同时向左拉起小球1、2、3到相同高度(如图丙所示)，同时由静止释放，经碰撞后，小球3、4、5一起向右摆起，且上升的最大高度与小球1、2、3的释放高度相同答案D[解析] 5个小球组成的系统发生的是弹性正碰，系统的机械能守恒，系统在水平方向的动量守恒，总动量并不守恒，选项A、B错误；同时向左拉起小球1、2、3到相同的高度，同时由静止释放并与4、5碰撞后，由机械能守恒和水平方向的动量守恒知，小球3、4、5一起向右摆起，且上升的最大高度与小球1、2、3的释放高度相同，选项C错误，选项D正确．三动量综合问题7. 如图所示，水平地面上静止放置一辆小车A，质量m A＝4 kg，上表面光滑，小车与地面间的摩擦力极小，可以忽略不计．可视为质点的物块B置于A的最右端，B的质量m B ＝2 kg.现对A施加一个水平向右的恒力F＝10 N，A运动一段时间后，小车左端固定的挡板与B发生碰撞，碰撞时间极短，碰后A、B粘合在一起，共同在F的作用下继续运动，碰撞后经时间t＝0.6 s，二者的速度达到v t＝2 m/s.求：(1)A开始运动时加速度a的大小；(2)A、B碰撞后瞬间的共同速度v的大小；(3)A的上表面长度l.答案(1)2.5 m/s2(2)1 m/s(3)0.45 m[解析] (1)以A为研究对象，由牛顿第二定律有F＝m A a①代入数据解得a＝2.5 m/s2②(2)对A、B碰撞后共同运动t＝0.6 s的过程，由动量定理得Ft＝(m A＋m B)v t－(m A＋m B)v③代入数据解得v ＝1 m/s ④(3)设A 、B 发生碰撞前，A 的速度为v A ，对A 、B 发生碰撞的过程，由动量守恒定律有m A v A ＝(m A ＋m B )v ⑤A 从开始运动到与B 发生碰撞前，由动能定理有Fl ＝12m A v 2A ⑥ 由④⑤⑥式，代入数据解得l ＝0.45 m ⑦8.如图所示，质量分别为m A 、m B 的两个弹性小球A 、B 静止在地面上，B 球距地面的高度h ＝0.8 m ，A 球在B 球的正上方，先将B 球释放，经过一段时间后再将A 球释放，当A 球下落t ＝0.3 s 时，刚好与B 球在地面上方的P 点处相碰，碰撞时间极短，碰后瞬间A 球的速度恰为零，已知m B ＝3m A ，重力加速度大小g 取10 m/s 2，忽略空气阻力及碰撞中的动能损失．求：(1)B 球第一次到过地面时的速度； (2)P 点距离地面的高度．答案解：(ⅰ)设B 球第一次到达地面时的速度大小为v B ，由运动学公式有v B ＝2gh ①将h ＝0.8 m 代入上式，得v 1＝4 m/s.②(ⅱ)设两球相碰前后，A 球的速度大小分别为v 1和v ′1(v ′1＝0)，B 球的速度分别为v 2和v ′2，由运动学规律可得v 1＝gt ③由于碰撞时间极短，重力的作用可以忽略，两球相碰前后的动量守恒，总动能保持不变，规定向下的方向为正，有m A v 1＋m B v 2＝m B v ′2④12m A v 21＋12m B v 22＝12m v ′22⑤ 设B 球与地面相碰后速度大小为v ′B ，由运动学及碰撞的规律可得v ′B ＝v B ⑥设P 点距地面的高度为h ′，由运动学规律可得h ′＝v ′2B －v 222g⑦联立②③④⑤⑥⑦式，并代入已知条件可得h ′＝0.75 m ．⑧9. 一中子与一质量数为A (A >1)的原子核发生弹性正碰．若碰前原子核静止，则碰撞前与碰撞后中子的速率之比为( )A.A ＋1A －1B.A －1A ＋1C.4A（A ＋1）2 D.（A ＋1）2（A －1）2答案A [解析] 本题考查完全弹性碰撞中的动量守恒、动能守恒．设碰撞前后中子的速率分别为v 1，v ′1，碰撞后原子核的速率为v 2，中子的质量为m 1，原子核的质量为m 2，则m 2＝Am 1.根据完全弹性碰撞规律可得m 1v 1＝m 2v 2＋m 1v ′1，12m 1v 21＝12m 2v 22＋12m 1v ′21，解得碰后中子的速率v ′1＝⎪⎪⎪⎪⎪⎪m 1－m 2m 1＋m 2v 1＝A －1A ＋1v 1，因此碰撞前后中子速率之比v 1v ′1＝A ＋1A －1，A 正确．10.如图X29­6所示，竖直平面内的光滑水平轨道的左边与墙壁对接，右边与一个足够高的14光滑圆弧轨道平滑相连，木块A 、 B 静置于光滑水平轨道上，A 、B 的质量分别为1.5kg 和0.5 kg.现让A 以6 m/s 的速度水平向左运动，之后与墙壁碰撞，碰撞的时间为0.3 s ，碰后的速度大小变为4 m/s.当A 与B 碰撞后会立即粘在一起运动，g 取10 m/s 2，求：(1)在A 与墙壁碰撞的过程中，墙壁对A 的平均作用力的大小； (2)A 、B 滑上圆弧轨道的最大高度．图X29­6答案(1)50 N (2)0.45 m[解析] (1)设水平向右为正方向，当A 与墙壁碰撞时根据动量定理有 Ft ＝m A v ′1－m A ·(－v 1) 解得F ＝50 N.(2)设碰撞后A 、B 的共同速度为v ，根据动量守恒定律有 m A v ′1＝(m A ＋m B )vA 、B 在光滑圆形轨道上滑动时，机械能守恒，由机械能守恒定律得 12(m A ＋m B )v 2＝(m A ＋m B )gh 解得h ＝0.45 m.四 力学观点的综合应用11.如图的水平轨道中，AC 段的中点B 的正上方有一探测器，C 处有一竖直挡板，物体P 1沿轨道向右以速度v 1与静止在A 点的物体P 2碰撞，并接合成复合体P ，以此碰撞时刻为计时零点，探测器只在t 1＝2 s 至t 2＝4 s 内工作．已知P 1、P 2的质量都为m ＝1 kg ，P 与AC 间的动摩擦因数为μ＝0.1，AB 段长L ＝4 m ，g 取10 m/s 2，P 1、P 2和P 均视为质点，P 与挡板的碰撞为弹性碰撞．(1)若v 1＝6 m/s ，求P 1、P 2碰后瞬间的速度大小v 和碰撞损失的动能ΔE ；(2)若P 与挡板碰后，能在探测器的工作时间内通过B 点，求v 1的取值范围和P 向左经过A 点时的最大动能E .答案(1)3 m/s 9 J (2)10 m/s ≤v 1≤14 m/s 17 J [解析] (1)P 1、P 2碰撞过程动量守恒，有m v 1＝2m v解得v ＝v 12＝3 m/s碰撞过程中损失的动能为ΔE ＝12m v 21－12(2m )v 2解得ΔE ＝9 J.(2)由于P 与挡板的碰撞为弹性碰撞．故P 在AC 间等效为匀减速运动，设P 在AC 段加速度大小为a ，碰后经过B 点的速度为v 2 ，由牛顿第二定律和运动学规律，得μ(2m )g ＝2ma3L ＝v t －12at 2v 2＝v －at解得v 1＝2v ＝6L ＋μgt 2t v 2＝6L －μgt 22t由于2 s ≤t ≤4 s 所以解得v 1的取值范围10 m/s ≤v 1≤14 m/sv 2的取值范围1 m/s ≤v 2≤5 m/s所以当v 2＝5 m/s 时，P 向左经过A 点时有最大速度 v 3＝v 22－2μgL则P 向左经过A 点时有最大动能E ＝12(2m )v 23＝17 J. 12. 冰球运动员甲的质量为80.0 kg.当他以5.0 m/s 的速度向前运动时，与另一质量为100 kg 、速度为3.0 m/s 的迎面而来的运动员乙相撞．碰后甲恰好静止．假设碰撞时间极短，求：(1 )碰后乙的速度的大小； (2)碰撞中总机械能的损失． [答案] (1)1.0 m/s (2)1400 J[解析] (1)设运动员甲、乙的质量分别为m 、M ，碰前速度大小分别为v 、V ，碰后乙的速度大小为V ′.由动量守恒定律有m v －MV ＝MV ′①代入数据得V ′＝1.0 m/s ②(2)设碰撞过程中总机械能的损失为ΔE ，应有12m v 2＋12MV 2＝12MV ′2＋ΔE ③ 联立②③式，代入数据得ΔE ＝1400 J ④。

动量定理题型及例题讲解动量定理是物理学中的一个重要定理，它描述了力、质量和时间之间的关系。

动量定理指出，在一个惯性系中，外力的冲量等于物体动量的增量。

下面我将介绍动量定理的题型和例题讲解。

一、动量定理题型动量定理题型一般可分为以下三种:1. 动量守恒定律应用题动量守恒定律是指在一个系统内，若不存在外力作用，则系统的总动量保持不变。

在这类题型中，考生需要根据动量守恒定律，计算出系统的总动量，然后根据动量定理，求解外力对系统的作用。

2. 动量定理公式应用题在这类题型中，考生需要根据动量定理，计算出物体的动量增量，然后根据动量守恒定律，求解外力对物体的作用。

3. 碰撞问题应用题碰撞问题是物理学中的一个重要问题，它涉及到动量守恒定律和动量定理。

在这类题型中，考生需要根据动量守恒定律和动量定理，计算出碰撞前后物体的动量变化，然后根据碰撞原理，求解外力对物体的作用。

二、动量定理例题讲解下面我们来看几个动量定理的例题:1. 动量守恒定律应用题例题：一个质量为 2 千克的物体，以 5 米/秒的速度沿水平面滑行，如果在物体表面放置一个弹簧，求弹簧的弹力。

解析：根据动量守恒定律，由于物体的速度不变，系统的总动量守恒。

因此，外力的冲量等于物体的动量增量。

即:I = m * v其中，I 为外力的冲量，m 为物体的质量，v 为物体的速度。

根据题意，可知:I = m * v = 2 * 5 = 10 J因此，外力对物体的作用为:F = I / a = 10 / 1 = 10 N。

2. 动量定理公式应用题例题：一个质量为 2 千克的物体，以 5 米/秒的速度沿水平面滑行，如果在物体表面放置一个弹簧，求弹簧的弹力。

解析：根据动量定理，在外力作用期间，物体的动量增量为:p = m * v"其中，p 为物体的动量，m 为物体的质量，v"为物体的速度。

根据题意，可知:v" = v - at其中，a 为物体的水平加速度，t 为物体滑行的时间。

高考物理动量定理解题技巧及经典题型及练习题(含答案)及解析一、高考物理精讲专题动量定理1．如图所示，静置于水平地面上的二辆手推车沿一直线排列，质量均为m ，人在极短的时间内给第一辆车一水平冲量使其运动，当车运动了距离L 时与第二辆车相碰，两车以共同速度继续运动了距离L 时停。

车运动时受到的摩擦阻力恒为车所受重力的k 倍，重力加速度为g ，若车与车之间仅在碰撞时发生相互作用，碰撞吋间很短，忽咯空气阻力，求： (1)整个过程中摩擦阻力所做的总功； (2)人给第一辆车水平冲量的大小。

【答案】(1)-3kmgL ；(2)10m kgL 【解析】 【分析】 【详解】(1)设运动过程中摩擦阻力做的总功为W ，则W =-kmgL -2kmgL =-3kmgL即整个过程中摩擦阻力所做的总功为-3kmgL 。

(2)设第一辆车的初速度为v 0，第一次碰前速度为v 1，碰后共同速度为v 2，则由动量守恒得mv 1=2mv 222101122kmgL mv mv -=- 221(2)0(2)2k m gL m v -=-由以上各式得010v kgL =所以人给第一辆车水平冲量的大小010I mv m kgL ==2．如图1所示，水平面内的直角坐标系的第一象限有磁场分布，方向垂直于水平面向下，磁感应强度沿y 轴方向没有变化，与横坐标x 的关系如图2所示，图线是双曲线（坐标是渐近线）；顶角θ=53°的光滑金属长导轨MON 固定在水平面内，ON 与x 轴重合，一根与ON 垂直的长导体棒在水平向右的外力作用下沿导轨MON 向右滑动，导体棒在滑动过程中始终保持与导轨良好接触，已知t =0时，导体棒位于顶角O 处；导体棒的质量为m =4kg ；OM 、ON 接触处O 点的接触电阻为R =0．5Ω，其余电阻不计，回路电动势E 与时间t 的关系如图3所示，图线是过原点的直线，求：（1）t =2s 时流过导体棒的电流强度的大小； （2）在1~2s 时间内导体棒所受安培力的冲量大小；（3）导体棒滑动过程中水平外力F （单位：N ）与横坐标x （单位：m ）的关系式． 【答案】（1）8A （2）8N s ⋅（3）32639F x =+【解析】 【分析】 【详解】（1）根据E-t 图象中的图线是过原点的直线特点，可得到t =2s 时金属棒产生的感应电动势为4V E =由欧姆定律得24A 8A 0.5E I R === （2）由图2可知，1(T m)x B =⋅ 由图3可知，E 与时间成正比，有E =2t （V ）4EI t R== 因θ=53°，可知任意t 时刻回路中导体棒有效切割长度43x L = 又由F BIL =安所以163F t 安=即安培力跟时间成正比所以在1~2s 时间内导体棒所受安培力的平均值163233N 8N2F +==故8N s I F t =∆=⋅安（3）因为43vE BLv Bx ==⋅所以1.5(m/s)v t =可知导体棒的运动时匀加速直线运动，加速度21.5m/s a =又212x at =，联立解得 32639F x =+【名师点睛】本题的关键首先要正确理解两个图象的数学意义，运用数学知识写出电流与时间的关系，要掌握牛顿运动定律、闭合电路殴姆定律，安培力公式、感应电动势公式．3．图甲为光滑金属导轨制成的斜面，导轨的间距为1m l =，左侧斜面的倾角37θ=︒，右侧斜面的中间用阻值为2R =Ω的电阻连接。

高中物理动量定理解题技巧讲解及练习题(含答案)及解析一、高考物理精讲专题动量定理1．如图所示，一个质量为m 的物体，初速度为v 0，在水平合外力F （恒力）的作用下，经过一段时间t 后，速度变为v t 。

(1)请根据上述情境，利用牛顿第二定律推导动量定理，并写出动量定理表达式中等号两边物理量的物理意义。

(2)快递公司用密封性好、充满气体的塑料袋包裹易碎品，如图所示。

请运用所学物理知识分析说明这样做的道理。

【答案】详情见解析 【解析】 【详解】(1)根据牛顿第二定律F ma =,加速度定义0i v v a t-=解得 0=-i Ft mv mv即动量定理, Ft 表示物体所受合力的冲量，mv t -mv 0表示物体动量的变化 (2)快递物品在运送途中难免出现磕碰现象，根据动量定理0=-i Ft mv mv在动量变化相等的情况下，作用时间越长，作用力越小。

充满气体的塑料袋富有弹性，在碰撞时，容易发生形变，延缓作用过程，延长作用时间，减小作用力，从而能更好的保护快递物品。

2．一质量为0.5kg 的小物块放在水平地面上的A 点，距离A 点5 m 的位置B 处是一面墙，如图所示.物块以v 0＝8m/s 的初速度从A 点沿AB 方向运动，在与墙壁碰撞前瞬间的速度为7m/s ，碰后以5m/s 的速度反向运动直至静止.g 取10 m/s 2.(1)求物块与地面间的动摩擦因数μ；(2)若碰撞时间为0.05s ，求碰撞过程中墙面对物块平均作用力的大小F ； (3)求物块在反向运动过程中克服摩擦力所做的功W . 【答案】（1）0.32μ=（2）130F N =（3）9W J = 【解析】（1）由动能定理，有：2201122mgs mv mv μ-=-可得0.32μ=．（2）由动量定理，有'F t mv mv ∆=-可得130F N =． （3）'2192W mv J ==． 【考点定位】本题考查动能定理、动量定理、做功等知识3．如图所示，真空中有平行正对金属板A 、B ，它们分别接在输出电压恒为U =91V 的电源两端，金属板长L =10cm 、两金属板间的距离d =3.2cm ，A 、B 两板间的电场可以视为匀强电场。

高考物理：动量定理的五种应用及例题详解！动量定理是力对时间的积累效应，使物体的动量发生改变，适用的范围很广，它的研究对象可以是单个物体，也可以是物体系；它不仅适用于恒力情形，而且也适用于变力情形，尤其在解决作用时间短、作用力大小随时间变化的打击、碰撞等问题时，动量定理要比牛顿定律方便得多。

一、用动量定理解释生活中的现象【例1】竖立放置的粉笔压在纸条的一端.要想把纸条从粉笔下抽出，又要保证粉笔不倒，应该缓缓、小心地将纸条抽出，还是快速将纸条抽出？说明理由。

【解析】纸条从粉笔下抽出，粉笔受到纸条对它的滑动摩擦力μmg作用，方向沿着纸条抽出的方向。

不论纸条是快速抽出，还是缓缓抽出，粉笔在水平方向受到的摩擦力的大小不变。

在纸条抽出过程中，粉笔受到摩擦力的作用时间用t表示，粉笔受到摩擦力的冲量为μmgt，粉笔原来静止，初动量为零，粉笔的末动量用mv表示.根据动量定理有：μmgt=mv。

如果缓慢抽出纸条，纸条对粉笔的作用时间比较长，粉笔受到纸条对它摩擦力的冲量就比较大，粉笔动量的改变也比较大，粉笔的底端就获得了一定的速度.由于惯性，粉笔上端还没有来得及运动，粉笔就倒了。

如果在极短的时间内把纸条抽出，纸条对粉笔的摩擦力冲量极小，粉笔的动量几乎不变.粉笔的动量改变得极小，粉笔几乎不动，粉笔也不会倒下。

二、用动量定理解曲线运动问题【例2】以速度v0水平抛出一个质量为1kg的物体，若在抛出后5s未落地且未与其它物体相碰，求它在5s内的动量的变化.(g=10m/s2)。

【解析】此题若求出末动量，再求它与初动量的矢量差，则极为繁琐.由于平抛出去的物体只受重力且为恒力，故所求动量的变化等于重力的冲量.则Δp=Ft=mgt=1×10×5=50 kg·m/s。

注：① 运用Δp=mv-mv0求Δp时，初、末速度必须在同一直线上，若不在同一直线，需考虑运用矢量法则或动量定理Δp=Ft求解Δp.②用I=F·t求冲量，F必须是恒力，若F是变力，需用动量定理I=Δp求解I。

物理动量定理专项及解析一、高考物理精讲专题动量定理1．如图所示，粗糙的水平面连接一个竖直平面内的半圆形光滑轨道，其半径为R =0.1 m ，半圆形轨道的底端放置一个质量为m =0.1 kg 的小球B ，水平面上有一个质量为M =0.3 kg 的小球A 以初速度v 0=4.0 m / s 开始向着木块B 滑动，经过时间t =0.80 s 与B 发生弹性碰撞．设两小球均可以看作质点，它们的碰撞时间极短，且已知木块A 与桌面间的动摩擦因数μ=0.25，求：（1）两小球碰前A 的速度； （2）球碰撞后B ,C 的速度大小；（3）小球B 运动到最高点C 时对轨道的压力；【答案】（1）2m/s （2）v A ＝1m /s ，v B ＝3m /s （3）4N ，方向竖直向上 【解析】 【分析】 【详解】（1）选向右为正，碰前对小球A 的运动由动量定理可得： –μ Mg t ＝M v – M v 0 解得：v ＝2m /s（2）对A 、B 两球组成系统碰撞前后动量守恒，动能守恒：A B Mv Mv mv =+222111222A B Mv Mv mv =+ 解得：v A ＝1m /s v B ＝3m /s（3）由于轨道光滑，B 球在轨道由最低点运动到C 点过程中机械能守恒：2211222B Cmv mv mg R '=+ 在最高点C 对小球B 受力分析，由牛顿第二定律有： 2CN v mg F m R'+= 解得：F N ＝4N由牛顿第三定律知，F N '＝F N ＝4N小球对轨道的压力的大小为3N ，方向竖直向上．2．质量为m 的小球，从沙坑上方自由下落，经过时间t 1到达沙坑表面，又经过时间t 2停在沙坑里．求：⑴沙对小球的平均阻力F ；⑵小球在沙坑里下落过程所受的总冲量I ．【答案】(1)122()mg t t t + (2)1mgt 【解析】试题分析：设刚开始下落的位置为A ，刚好接触沙的位置为B ，在沙中到达的最低点为C.⑴在下落的全过程对小球用动量定理：重力作用时间为t 1+t 2，而阻力作用时间仅为t 2，以竖直向下为正方向，有： mg(t 1+t 2)-Ft 2=0, 解得：方向竖直向上⑵仍然在下落的全过程对小球用动量定理：在t 1时间内只有重力的冲量，在t 2时间内只有总冲量（已包括重力冲量在内），以竖直向下为正方向，有： mgt 1-I=0,∴I=mgt 1方向竖直向上 考点：冲量定理点评：本题考查了利用冲量定理计算物体所受力的方法．3．如图甲所示，平面直角坐标系中，0≤x ≤l 、0≤y ≤2l 的矩形区域中存在交变匀强磁场，规定磁场垂直于纸面向里的方向为正方向，其变化规律如图乙所示，其中B 0和T 0均未知。

高中物理动量定理题20套(带答案)含解析一、高考物理精讲专题动量定理1．如图所示，一质量m 1=0.45kg 的平顶小车静止在光滑的水平轨道上．车顶右端放一质量m 2=0.4 kg 的小物体，小物体可视为质点．现有一质量m 0=0.05 kg 的子弹以水平速度v 0=100 m/s 射中小车左端，并留在车中，已知子弹与车相互作用时间极短，小物体与车间的动摩擦因数为μ=0.5，最终小物体以5 m/s 的速度离开小车．g 取10 m/s 2．求：（1）子弹从射入小车到相对小车静止的过程中对小车的冲量大小．（2）小车的长度．【答案】（1）4.5N s ⋅ （2）5.5m【解析】①子弹进入小车的过程中，子弹与小车组成的系统动量守恒，有：0011()o m v m m v =+，可解得110/v m s =；对子弹由动量定理有：10I mv mv -=-， 4.5I N s =⋅ (或kgm/s)；②三物体组成的系统动量守恒，由动量守恒定律有：0110122()()m m v m m v m v +=++；设小车长为L ，由能量守恒有：22220110122111()()222m gL m m v m m v m v μ=+-+- 联立并代入数值得L ＝5.5m ；点睛：子弹击中小车过程子弹与小车组成的系统动量守恒，由动量守恒定律可以求出小车的速度，根据动量定理可求子弹对小车的冲量；对子弹、物块、小车组成的系统动量守恒，对系统应用动量守恒定律与能量守恒定律可以求出小车的长度．2．一质量为0.5kg 的小物块放在水平地面上的A 点，距离A 点5m 的位置B 处是一面墙，如图所示，物块以v 0=9m/s 的初速度从A 点沿AB 方向运动，在与墙壁碰撞前瞬间的速度为7m/s ，碰后以6m/s 的速度反向运动直至静止．g 取10m/s 2．(1)求物块与地面间的动摩擦因数μ；(2)若碰撞时间为0.05s ，求碰撞过程中墙面对物块平均作用力的大小F ．【答案】（1）0.32μ= （2）F =130N【解析】试题分析：（1）对A 到墙壁过程，运用动能定理得：，代入数据解得：μ=0.32．（2）规定向左为正方向，对碰墙的过程运用动量定理得：F △t=mv′﹣mv ，代入数据解得：F=130N ．3．滑冰是青少年喜爱的一项体育运动。

高考物理动量定理解题技巧及经典题型及练习题( 含答案 ) 含解析一、高考物理精讲专题动量定理1．质量为 m 的小球，从沙坑上方自由下落，经过时间t1到达沙坑表面，又经过时间t2停在沙坑里．求：⑴沙对小球的平均阻力F；⑵小球在沙坑里下落过程所受的总冲量I．【答案】(1) mg(t1t2t 2 )(2) mgt1【解析】试题分析：设刚开始下落的位置为A，刚好接触沙的位置为B，在沙中到达的最低点为C.⑴在下落的全过程对小球用动量定理：重力作用时间为t1 +t2，而阻力作用时间仅为t2，以竖直向下为正方向，有：mg(t +t )-Ft =0, 解得：方向竖直向上1 2 2⑵仍然在下落的全过程对小球用动量定理：在t1时间内只有重力的冲量，在t2时间内只有总冲量（已包括重力冲量在内），以竖直向下为正方向，有：mgt 1-I=0,∴I=mgt1方向竖直向上考点：冲量定理点评：本题考查了利用冲量定理计算物体所受力的方法．2．如图所示，长为L 的轻质细绳一端固定在地高度为 H。

现将细绳拉至与水平方向成30 O 点，另一端系一质量为m ，由静止释放小球，经过时间的小球， O 点离t 小球到达最低点，细绳刚好被拉断，小球水平抛出。

若忽略空气阻力，重力加速度为g。

(1)求细绳的最大承受力；(2)求从小球释放到最低点的过程中，细绳对小球的冲量大小；(3)小明同学认为细绳的长度越长，小球抛的越远；小刚同学则认为细绳的长度越短，小球抛的越远。

请通过计算，说明你的观点。

2 m2 gL ；（3）当L H【答案】（ 1） F=2mg ；（ 2）I F mgt 时小球抛的最远2【解析】【分析】【详解】(1)小球从释放到最低点的过程中，由动能定理得mgLsin 30 1 m v022小球在最低点时，由牛顿第二定律和向心力公式得2mv0F mgL解得：F=2mg(2)小球从释放到最低点的过程中，重力的冲量I G=mgt动量变化量p mv0由三角形定则得，绳对小球的冲量I F mgt 2m2gL(3)平抛的水平位移x v0t ，竖直位移H L 1 gt22解得x 2L( H L)当 L H时小球抛的最远23．如图所示，质量M=1.0kg 的木板静止在光滑水平面上，质量m=0.495kg 的物块（可视为质点）放在的木板左端，物块与木板间的动摩擦因数μ=0.4。

高中物理动量定理解题技巧及经典题型及练习题( 含答案 ) 及解析一、高考物理精讲专题动量定理1．观赏“烟火”表演是某地每年“春节”庆祝活动的压轴大餐。

某型“礼花”底座仅0.2s 的发射时间，就能将质量为 m=5kg 的礼花弹竖直抛上 180m 的高空。

（忽略发射底座高度，不计空气阻力， g 取 10m/s 2）(1)“礼花”发射时燃烧的火药对礼花弹的平均作用力是多少？（已知该平均作用力远大于礼花弹自身重力）(2)某次试射，当礼花弹到达最高点时爆炸成沿水平方向运动的两块（爆炸时炸药质量忽略不计），测得前后两块质量之比为1： 4，且炸裂时有大小为E=9000J 的化学能全部转化为了动能，则两块落地点间的距离是多少？【答案】 (1)1550N； (2)900m【解析】【分析】【详解】(1)设发射时燃烧的火药对礼花弹的平均作用力为F，设礼花弹上升时间为t，则：h 1gt 2 2解得t 6s对礼花弹从发射到抛到最高点，由动量定理Ft 0mg(t t0 )0其中t00.2s解得F 1550N(2)设在最高点爆炸后两块质量分别为m1、 m2，对应的水平速度大小分别为v1、 v2，则：在最高点爆炸，由动量守恒定律得m1v1m2 v2由能量守恒定律得E 1m1v121m2v22 22其中m11m24 m m1m2联立解得v1120m/sv230m/s 之后两物块做平抛运动，则竖直方向有h 1gt 2 2水平方向有s v1t v2t由以上各式联立解得s=900m2．质量为 m 的小球，从沙坑上方自由下落，经过时间t1到达沙坑表面，又经过时间t2停在沙坑里．求：⑴沙对小球的平均阻力F；⑵小球在沙坑里下落过程所受的总冲量I．mg(t1t 2 )【答案】 (1)(2) mgt1t2【解析】试题分析：设刚开始下落的位置为A，刚好接触沙的位置为B，在沙中到达的最低点为C.⑴在下落的全过程对小球用动量定理：重力作用时间为t1 +t2，而阻力作用时间仅为t2，以竖直向下为正方向，有：mg(t 1+t2)-Ft2=0, 解得：方向竖直向上⑵仍然在下落的全过程对小球用动量定理：在t1时间内只有重力的冲量，在t2时间内只有总冲量（已包括重力冲量在内），以竖直向下为正方向，有：mgt 1-I=0,∴I=mgt1方向竖直向上考点：冲量定理点评：本题考查了利用冲量定理计算物体所受力的方法．3．如图所示，足够长的木板端， A、 B、C 的质量分别为A 和物块m、2m 和C置于同一光滑水平轨道上，物块 B 置于 A 的左3m，已知 A、 B 一起以 v0的速度向右运动，滑块C向左运动，A、C 碰后连成一体，最终A、B、 C 都静止，求：（i） C 与 A 碰撞前的速度大小（i i ）A、 C 碰撞过程中 C 对 A 到冲量的大小．【答案】（ 1） C 与 A 碰撞前的速度大小是v0；（2） A、 C 碰撞过程中 C 对 A 的冲量的大小是3mv0．2【解析】【分析】【详解】试题分析：①设 C 与 A 碰前速度大小为v1,以A碰前速度方向为正方向，对A、 B、 C 从碰前至最终都静止程由动量守恒定律得：(m 2m) v0－3mv1 ?0解得： v1v0．②设 C 与 A 碰后共同速度大小为v2，对A、C在碰撞过程由动量守恒定律得：mv0－3mv1( m 3m)v2在 A、 C 碰撞过程中对 A 由动量定理得：I CA mv2－ mv0解得： I CA 3mv0 2即A、 C 碰过程中 C 对 A 的冲量大小为3mv0．方向为负．2考点：动量守恒定律【名师点睛】本题考查了求木板、木块速度问题，分析清楚运动过程、正确选择研究对象与运动过程是解题的前提与关键，应用动量守恒定律即可正确解题；解题时要注意正方向的选择．4．如图所示，在倾角θ=37°的足够长的固定光滑斜面的底端，有一质量m=1.0kg、可视为质点的物体，以 v0=6.0m/s 的初速度沿斜面上滑。

高中物理动量守恒定律试题(有答案和解析)含解析一、高考物理精讲专题动量守恒定律1．如图所示，质量为M=1kg 上表面为一段圆弧的大滑块放在水平面上，圆弧面的最底端刚好与水平面相切于水平面上的B 点，B 点左侧水平面粗糙、右侧水平面光滑，质量为m=0.5kg 的小物块放在水平而上的A 点，现给小物块一个向右的水平初速度v 0=4m/s ，小物块刚好能滑到圆弧面上最高点C 点，已知圆弧所对的圆心角为53°，A 、B 两点间的距离为L=1m ，小物块与水平面间的动摩擦因数为μ=0.2，重力加速度为g=10m/s 2．求： (1)圆弧所对圆的半径R ；(2)若AB 间水平面光滑，将大滑块固定，小物块仍以v 0=4m/s 的初速度向右运动，则小物块从C 点抛出后，经多长时间落地?【答案】（1）1m （2）428225t s = 【解析】 【分析】根据动能定理得小物块在B 点时的速度大小；物块从B 点滑到圆弧面上最高点C 点的过程，小物块与大滑块组成的系统水平方向动量守恒，根据动量守恒和系统机械能守恒求出圆弧所对圆的半径；，根据机械能守恒求出物块冲上圆弧面的速度，物块从C 抛出后，根据运动的合成与分解求落地时间； 【详解】解：(1)设小物块在B 点时的速度大小为1v ，根据动能定理得：22011122mgL mv mv μ=- 设小物块在B 点时的速度大小为2v ，物块从B 点滑到圆弧面上最高点C 点的过程，小物块与大滑块组成的系统水平方向动量守恒，根据动量守恒则有：12()mv m M v =+ 根据系统机械能守恒有：2201211()(cos53)22mv m M v mg R R =++- 联立解得：1R m =(2)若整个水平面光滑，物块以0v 的速度冲上圆弧面，根据机械能守恒有：2200311(cos53)22mv mv mg R R =+- 解得：322/v m s =物块从C 抛出后，在竖直方向的分速度为：38sin 532/5y v v m s =︒= 这时离体面的高度为：cos530.4h R R m =-︒=212y h v t gt -=-解得：4282t s +=2．如图所示，质量为M =2kg 的小车静止在光滑的水平地面上，其AB 部分为半径R =0.3m的光滑14圆孤，BC 部分水平粗糙，BC 长为L =0.6m 。

物理动量定理专项含解析一、高考物理精讲专题动量定理1．2022年将在我国举办第二十四届冬奥会，跳台滑雪是其中最具观赏性的项目之一．某滑道示意图如下，长直助滑道AB 与弯曲滑道BC 平滑衔接，滑道BC 高h =10 m ，C 是半径R =20 m 圆弧的最低点，质量m =60 kg 的运动员从A 处由静止开始匀加速下滑，加速度a =4.5 m/s 2，到达B 点时速度v B =30 m/s ．取重力加速度g =10 m/s 2． （1）求长直助滑道AB 的长度L ；（2）求运动员在AB 段所受合外力的冲量的I 大小；（3）若不计BC 段的阻力，画出运动员经过C 点时的受力图，并求其所受支持力F N 的大小．【答案】（1）100m （2）1800N s ⋅（3）3 900 N 【解析】（1）已知AB 段的初末速度，则利用运动学公式可以求解斜面的长度，即2202v v aL -=可解得:221002v v L m a-==（2）根据动量定理可知合外力的冲量等于动量的该变量所以01800B I mv N s =-=⋅（3）小球在最低点的受力如图所示由牛顿第二定律可得：2Cv N mg m R-= 从B 运动到C 由动能定理可知：221122C B mgh mv mv =-解得;3900N N =故本题答案是：（1）100L m = （2）1800I N s =⋅ （3）3900N N =点睛：本题考查了动能定理和圆周运动，会利用动能定理求解最低点的速度，并利用牛顿第二定律求解最低点受到的支持力大小．2．如图1所示，水平面内的直角坐标系的第一象限有磁场分布，方向垂直于水平面向下，磁感应强度沿y 轴方向没有变化，与横坐标x 的关系如图2所示，图线是双曲线（坐标是渐近线）；顶角θ=53°的光滑金属长导轨MON 固定在水平面内，ON 与x 轴重合，一根与ON 垂直的长导体棒在水平向右的外力作用下沿导轨MON 向右滑动，导体棒在滑动过程中始终保持与导轨良好接触，已知t =0时，导体棒位于顶角O 处；导体棒的质量为m =4kg ；OM 、ON 接触处O 点的接触电阻为R =0．5Ω，其余电阻不计，回路电动势E 与时间t 的关系如图3所示，图线是过原点的直线，求：（1）t =2s 时流过导体棒的电流强度的大小； （2）在1~2s 时间内导体棒所受安培力的冲量大小；（3）导体棒滑动过程中水平外力F （单位：N ）与横坐标x （单位：m ）的关系式． 【答案】（1）8A （2）8N s ⋅（3）32639F x =+【解析】 【分析】 【详解】（1）根据E-t 图象中的图线是过原点的直线特点，可得到t =2s 时金属棒产生的感应电动势为4V E =由欧姆定律得24A 8A 0.5E I R === （2）由图2可知，1(T m)x B =⋅ 由图3可知，E 与时间成正比，有E =2t （V ）4EI t R== 因θ=53°，可知任意t 时刻回路中导体棒有效切割长度43x L =又由F BIL =安所以163F t 安=即安培力跟时间成正比所以在1~2s 时间内导体棒所受安培力的平均值163233N 8N2F +==故8N s I F t =∆=⋅安（3）因为43vE BLv Bx ==⋅所以1.5(m/s)v t =可知导体棒的运动时匀加速直线运动，加速度21.5m/s a =又212x at =，联立解得6F =+【名师点睛】本题的关键首先要正确理解两个图象的数学意义，运用数学知识写出电流与时间的关系，要掌握牛顿运动定律、闭合电路殴姆定律，安培力公式、感应电动势公式．3．如图甲所示，平面直角坐标系中，0≤x ≤l 、0≤y ≤2l 的矩形区域中存在交变匀强磁场，规定磁场垂直于纸面向里的方向为正方向，其变化规律如图乙所示，其中B 0和T 0均未知。

⾼中物理总复习--动量定理含解析⾼中物理总复习--动量定理含解析⼀、⾼考物理精讲专题动量定理1．质量为m 的⼩球，从沙坑上⽅⾃由下落，经过时间t 1到达沙坑表⾯，⼜经过时间t 2停在沙坑⾥．求：⑴沙对⼩球的平均阻⼒F ；⑵⼩球在沙坑⾥下落过程所受的总冲量I ．【答案】(1)122()mg t t t (2)1mgt 【解析】试题分析：设刚开始下落的位置为A ，刚好接触沙的位置为B ，在沙中到达的最低点为C.⑴在下落的全过程对⼩球⽤动量定理：重⼒作⽤时间为t 1+t 2，⽽阻⼒作⽤时间仅为t 2，以竖直向下为正⽅向，有： mg(t 1+t 2)-Ft 2=0, 解得：⽅向竖直向上⑵仍然在下落的全过程对⼩球⽤动量定理：在t 1时间内只有重⼒的冲量，在t 2时间内只有总冲量（已包括重⼒冲量在内），以竖直向下为正⽅向，有： mgt 1-I=0,∴I=mgt 1⽅向竖直向上考点：冲量定理点评：本题考查了利⽤冲量定理计算物体所受⼒的⽅法．2．如图所⽰，⾜够长的⽊板A 和物块C 置于同⼀光滑⽔平轨道上，物块B 置于A 的左端，A 、B 、C 的质量分别为m 、2m 和3m ，已知A 、B ⼀起以v 0的速度向右运动，滑块C 向左运动，A 、C 碰后连成⼀体，最终A 、B 、C 都静⽌，求：（i ）C 与A 碰撞前的速度⼤⼩（ii ）A 、C 碰撞过程中C 对A 到冲量的⼤⼩．【答案】（1）C 与A 碰撞前的速度⼤⼩是v 0；（2）A 、C 碰撞过程中C 对A 的冲量的⼤⼩是32mv 0．【解析】【分析】【详解】试题分析：①设C 与A 碰前速度⼤⼩为1v ,以A 碰前速度⽅向为正⽅向，对A 、B 、C 从碰前⾄最终都静⽌程由动量守恒定律得：01(2)3?0m m v mv －+= 解得：10v v =．②设C 与A 碰后共同速度⼤⼩为2v ，对A 、C 在碰撞过程由动量守恒定律得：012 3(3)mv mv m m v =+－在A 、C 碰撞过程中对A 由动量定理得：20CA I mv mv =－解得：032CA I mv =-即A 、C 碰过程中C 对A 的冲量⼤⼩为032mv ．⽅向为负．考点：动量守恒定律【名师点睛】本题考查了求⽊板、⽊块速度问题，分析清楚运动过程、正确选择研究对象与运动过程是解题的前提与关键，应⽤动量守恒定律即可正确解题；解题时要注意正⽅向的选择．3．⼀个质量为60千克的蹦床运动员从距离⽔平蹦床⽹⾯上3.2⽶的⾼处⾃由下落，触⽹后沿竖直⽅向蹦回到离⽔平⽹⾯5⽶⾼处.已知运动员与⽹接触的时候为1.2秒。

高中物理专题汇编物理动量定理(一)含解析一、高考物理精讲专题动量定理1．如图所示，一光滑水平轨道上静止一质量为M ＝3kg 的小球B ．一质量为m ＝1kg 的小球A 以速度v 0＝2m/s 向右运动与B 球发生弹性正碰，取重力加速度g ＝10m/s 2．求：（1）碰撞结束时A 球的速度大小及方向； （2）碰撞过程A 对B 的冲量大小及方向．【答案】（1）－1m/s ，方向水平向左（2）3N·s ，方向水平向右 【解析】【分析】A 与B 球发生弹性正碰，根据动量守恒及能量守恒求出碰撞结束时A 球的速度大小及方向；碰撞过程对B 应用动量定理求出碰撞过程A 对B 的冲量； 解：（1）碰撞过程根据动量守恒及能量守恒得：0A B mv mv Mv =+2220111222A B mv mv Mv =+ 联立可解得：1m/s B v =，1m/s A v =- 负号表示方向水平向左 （2）碰撞过程对B 应用动量定理可得：0B I Mv =- 可解得：3I N s =⋅ 方向水平向右2．如图所示，一个质量为m 的物体，初速度为v 0，在水平合外力F （恒力）的作用下，经过一段时间t 后，速度变为v t 。

(1)请根据上述情境，利用牛顿第二定律推导动量定理，并写出动量定理表达式中等号两边物理量的物理意义。

(2)快递公司用密封性好、充满气体的塑料袋包裹易碎品，如图所示。

请运用所学物理知识分析说明这样做的道理。

【答案】详情见解析 【解析】 【详解】(1)根据牛顿第二定律F ma =,加速度定义0i v v a t-=解得 0=-i Ft mv mv即动量定理, Ft 表示物体所受合力的冲量，mv t -mv 0表示物体动量的变化 (2)快递物品在运送途中难免出现磕碰现象，根据动量定理0=-i Ft mv mv在动量变化相等的情况下，作用时间越长，作用力越小。

充满气体的塑料袋富有弹性，在碰撞时，容易发生形变，延缓作用过程，延长作用时间，减小作用力，从而能更好的保护快递物品。

高中物理动量定理常见题型及答题技巧及练习题(含答案)含解析一、高考物理精讲专题动量定理1．蹦床运动是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。

一个质量为60kg 的运动员，从离水平网面3.2m 高处自由下落，着网后沿竖直方向蹦回离水平网面5.0m 高处。

已知运动员与网接触的时间为1.2s ，若把这段时间内网对运动员的作用力当作恒力来处理，求此力的大小和方向。

（g 取10m/s 2）【答案】1.5×103N ；方向向上【解析】【详解】设运动员从h 1处下落，刚触网的速度为1128m /s v gh ==运动员反弹到达高度h 2,，网时速度为22210m /s v gh ==在接触网的过程中,运动员受到向上的弹力F 和向下的重力mg ，设向上方向为正，由动量定理有()21()F mg t mv mv -=--得F =1.5×103N方向向上2．如图所示，光滑水平面上有一轻质弹簧，弹簧左端固定在墙壁上，滑块A 以v 0＝12 m/s 的水平速度撞上静止的滑块B 并粘在一起向左运动，与弹簧作用后原速率弹回，已知A 、B 的质量分别为m 1＝0.5 kg 、m 2＝1.5 kg 。

求：①A 与B 撞击结束时的速度大小v ；②在整个过程中，弹簧对A 、B 系统的冲量大小I 。

【答案】①3m/s ； ②12N •s【解析】【详解】①A 、B 碰撞过程系统动量守恒，以向左为正方向由动量守恒定律得m 1v 0=（m 1+m 2）v代入数据解得v =3m/s②以向左为正方向，A 、B 与弹簧作用过程由动量定理得I =（m 1+m 2）（-v ）-（m 1+m 2）v代入数据解得I =-12N •s负号表示冲量方向向右。

3．如图所示，在倾角θ=37°的足够长的固定光滑斜面的底端，有一质量m =1.0kg 、可视为质点的物体，以v 0=6.0m/s 的初速度沿斜面上滑。