四象限分析1

四象限脉冲整流器的一种控制方法与仿真No.O1.2011北京电力高等专科学校BeijingElectricPowerCollege电子,通信与自动控制固四象限脉冲整流器的一种控制方法与仿真朱闻名贺升学(西南交通大学电气工程学院,四川成都610031)摘要:本文主要简述两重四象限整流技术的特点,主电路拓扑结构及数学模型.通过采用瞬态电流控制方法来减少整流器网侧谐波量提高交流侧电压电流的功率因数,输出稳定的直流电压,并通过仿真进行验证关键词:两重四象限整流器;瞬态电流控制;仿真中图分类号:TM92'文献标识码:A一,两重四象限整流器的工作原理与数学模型两重四象限整流技术就是将两个两电平四象限整流器并联起来共同给直流负载供电的技术.两重四象限整流技术是2个4QC并联为直流负载供电,中间电容部分存储能量,输出平滑的直流电压,当其中一个整流器出现故障时,另一个仍可以继续工作,这大大提高了系统直流供电质量与可靠性.'(一)四象限整流器的结构与原理图1为四象限整流器电路图….其中LN与RN为折合到二次侧的牵引变压器的漏感和电阻,L与C为二次滤波回路,cd为支撑电容.通过对开关进行导通与关断对直流侧电压进行调制,这样在变流器的输入端生成一个与电网电压同步的脉宽调制波,由四象限整流器等效图,可以得出等效的平衡式:N:jmLNINRNINUs当一定,的幅值和相位由的幅值及其与的相位差来决定,脉冲整流器可以工作在牵引与再生制动两种工况.由公式看出:只要控制了的幅值和相位,就控制了的幅值和相位.二,整流器的控制方法对于四象限电压型整流器,控制方法有间接电流控制和直接电流控制.间接电流控制没有电流反馈回路,结构虽然简单,但是不能很好的使电流跟踪电压,效果不是很理想.直接电流控制应用比较多,尤其瞬态电流控制方法目前广泛应用在动车组变流器,效果优势明显,控制结构相对简单.(一)瞬态电流控制的原理瞬态电流控制公式如下:,M=(乙一Ua)+I/T一I:iJd}UNIN=1+I(,)=o'._(,v风sinta+oosca)sinca-6Xt)其中K1和T为调节器参数;K为比例放大系数;Ia,u一分别为中间直流环节电流和中间直流环节电压;u(t),U为二次侧电压瞬时值和有效值;U为中间直流环节电压的给定值.(二)瞬态电流控制框图图2为瞬态电流的控制框图,通过比较运算后最终输出参考电压,并与三角载波比较生成P_lI『M信号驱动开关.8图2为瞬态电流控制框图三,仿真分析(一)仿真模型根据整流结构搭建MATLAB/SIMULINK仿真模型,模型包括变压器二术.文章编号:1009-0118(2011)一O1—0008一O1次侧漏感和电阻,单相两点平整流模块,滤波电路,支撑电容,阻性负载及瞬态电流控制模块.(三)仿真结果分析通过使用瞬态电流控制策略对两重四象限整流器进行仿真,主要对交流侧功率因数,整流器输入电压及直流侧电压和电流等进行仿真分析.直流电压给定值为3000V,交流输入电流为2500V,采用离散方式,两个整流器的控制模块中,采用三角载波,将两载波的相位差调整为90度.l,交流侧电压与电流交济洌电流具有稳定值,且能稳定迅速地跟随电压,保持着高的功率因数. 2,整流器输入端电压输入端电压在短时间内呈现为一系列的正弦脉冲波,且幅值基本稳定,基本符合整流器电压输入要求.3,直流侧电压与电流西3为直流负载电流～一～,图4为直流侧负载电压从图3,图4看出,直流侧电压与电流能迅速稳定,直流侧直流电压给定值为3000V,从图4看出,直流电压值保持在3000V左右,为逆变器与电机提供了稳定的电源.四,结束语本文主要讲述了动车组两重四象限整流器的结构,原理,并通过使用瞬态电流控制法对整流器进行了仿真控制.从仿真结果看对整流器的控制效果比较满意,功率因数接近1,直流侧电压稳定在额定值,是两重四象限整流器一种理想的控制方法.目前,两重四象限整流技术已经用于高速列车变流器中,但是本文将逆变与电机部分理想等效为了电阻负载,与实际的控制效果还有一定的差距,还需要更接近实际的仿真研究.参考文献:f1]李伟,张黎.交一直一交传动系统网侧变流器预测电流控制方法的计算机仿真及实现中国铁道科学,2002,23,(6).f2]邹仁.四象限变流器瞬态电流控制的仿真研究Ⅱ].机车电传动,2003,(6).[31章志兵,张志学.单相三电平整流器控制方法及中点平衡的研究Ⅱ】.机车电传,2008,(4).[4]宋文胜,刘志敏,冯晓云.四象限变流器控制策略研究与仿真Ⅱ】.电力机车与城轨车辆,2007,30,(2].作者简介:朱闻名(1984一),男,汉族,湖南常德人,西南交通大学电气工程学院硕士,电力电子与电力传动专业,研究方向:电力电子变流技..。

时间管理之每日四象限工作计划模板篇一：时间管理四象限表来自：百度百科时间“四象限”法是美国的管理学家科维提出的一个时间管理的理论，把工作按照重要和紧急两个不同的程度进行了划分，基本上可以分为四个“象限”：既紧急又重要(如客户投诉、即将到期的任务、财务危机等)、重要但不紧急(如建立人际关系、人员培训、制订防范措施等)、紧急但不重要(如电话铃声、不速之客、部门会议等)、既不紧急也不重要(如上网、闲谈、邮件、写博客等)。

按处理顺序划分：先是既紧急又重要的，接着是重要但不紧急的，再到紧急但不重要的，最后才是既不紧急也不重要的。

“四象限”法的关键在于第二和第三类的顺序问题，必须非常小心区分。

另外，也要注意划分好第一和第三类事，都是紧急的，分别就在于前者能带来价值，实现某种重要目标，而后者不能。

以下是四个象限的具体说明：1、第一象限是重要又急迫的事。

举例：诸如应付难缠的客户、准时完成工作、住院开刀等等。

这是考验我们的经验、判断力的时刻，也是可以用心耕耘的园地。

如果荒废了，我们很会可能变成行尸走肉。

但我们也不能忘记，很多重要的事都是因为一拖再拖或事前准备不足，而变成迫在眉睫。

该象限的本质是缺乏有效的工作计划导致本处于“重要但不紧急”第二象限的事情转变过来的，这也是传统思维状态下的管理者的通常状况，就是“忙”。

2、第二象限是重要但不紧急的事。

案例：主要是与生活品质有关，包括长期的规划、问题的发掘与预防、参加培训、向上级提出问题处理的建议等等事项。

荒废这个领域将使第一象限日益扩大，使我们陷入更大的压力，在危机中疲于应付。

反之，多投入一些时间在这个领域有利于提高实践能力，缩小第一象限的范围。

做好事先的规划、准备与预防措施，很多急事将无从产生。

这个领域的事情不会对我们造成催促力量，所以必须主动去做，这是发挥个人领导力的领域。

这更是传统低效管理者与高效卓越管理者的重要区别标志，建议管理者要把80%的精力投入到该象限的工作，以使第一象限的“急”事无限变少，不再瞎“忙”。

1.X理论Y理论和超Y理论：X理论假设：一般人的本性是懒惰的，工作越少越好，可能的话会逃避工作。

大部分人对集体（公司，机构，单位或组织等）的目标不关心，因此管理者需要以强迫，威胁处罚，指导，金钱利益等诱因激发人们的工作源动力。

一般人缺少进取心，只有在指导下才愿意接受工作，因此管理者需要对他们施加压力。

Y理论假设：人们在工作上体力和脑力的投入就跟在娱乐和休闲上的投入一样，工作是很自然的事——大部分人并不抗拒工作。

即使没有外界的压力和处罚的威胁，他们一样会努力工作以期达到目的——人们具有自我调节和自我监督的能力。

人们愿意为集体的目标而努力，在工作上会尽最大的努力，以发挥创造力，才智——人们希望在工作上获得认同感，会自觉遵守规定。

在适当的条件下，人们不仅愿意接受工作上的责任，并会寻求更大的责任。

许多人具有相当高的创新能力去解决问题。

在大多数的机构里面，人们的才智并没有充分发挥。

超Y理论：该理论认为，没有什么一成不变的、普遍适用的最佳的管理方式，必须根据组织内外环境自变量和管理思想及管理技术等因变量之间的函数关系，灵活地采取相应的管理措施，管理方式要适合于工作性质、成员素质等。

2.工作分析:现代管理学将工作分析定义为一种确定完成各项工作所需技能、责任和知识的系统过程。

工作分析是人力资源管理工作的基础，其分析质量对其他人力资源管理模块具有举足轻重的影响。

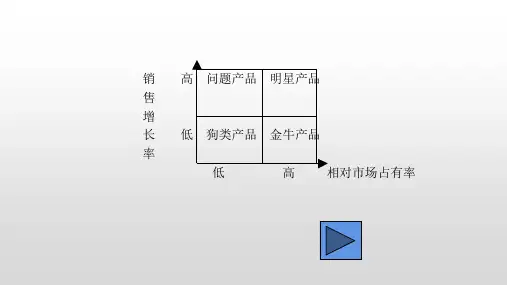
3.波士顿矩阵（四象限分析法）：波士顿矩阵认为一般决定产品结构的基本因素有两个：即市场引力与企业实力。

市场引力包括企业销售量（额）增长率、目标市场容量、竞争对手强弱及利润高低等。

其中最主要的是反映市场引力的综合指标——销售增长率，这是决定企业产品结构是否合理的外在因素。

4.德尔菲法：德尔菲法（Delphi method），是采用背对背的通信方式征询专家小组成员的预测意见，经过几轮征询，使专家小组的预测意见趋于集中，最后做出符合市场未来发展趋势的预测结论。

5.企业内部银行：企业内部银行，是引进商业银行的信贷与结算职能和方式于企业内部，来充实和完善企业内部经济核算的办法。

2014-2015九年级第一学期期中知识点梳理一、考试范围：第二十三章到第二十四章，内容分别是：数据分析、一元二次方程、图形的相似、解直角三角形、反比例函数。

二、知识点梳理（按章节进行详细梳理）'第二十三章：数据分析 1、加权平均数=权之和权数据权数据⋯⋯+⨯+⨯=⋯⋯⋯⋯总总 (作用：综合考量整组数据) 2、中位数：将数据按大小排列后，处于中间位置的一个数，或处于中间位置的两个数的平均值 （作用：确定某个数据所处位置（中上或中下））3、众数：出现次数最多的数 （作用：确定某种型号或品种最受欢迎）4、极差：一组数据中的最大值减去最小值 ￥5、方差：])(...)()[(1222212x x x x x x nSn -++-+-=（极差、方差作用：确定数据的稳定性和波动性）第二十四章：一元二次方程 第一节、 一元二次方程在一个等式中，只含有一个未知数，且未知数的最高次数是2次的整式方程叫做一元二次方程。

: 一元二次方程有四个特点：(1)只含有一个未知数；(2)且未知数次数最高次数是2；(3)是整式方程．要判断一个方程是否为一元二次方程，先看它是否为整式方程，若是，再对它进行整理．如果能整理为 02=++c bx ax (a ≠0)的形式，则这个方程就为一元二次方程；（4）将方程化为一般形式：02=++c bx ax 时，应满足（a ≠0）第二节、解一元二次方程解一元二次方程的基本思想方法是通过“降次”将它化为两个一元一次方程。

一元二次方程有四种解法：（1）、直接开平方法：用直接开平方法解形如 (n ≥0)的方程，其解为x=± m. 直接开平方法就是平方的逆运算.通常用根号表示其运算结果. ￥ （2）、配方法通过配成完全平方式的方法，得到一元二次方程的根的方法。

这种解一元二次方程的方法称为配方法，配方的依据是完全平方公式。

①.转化： 将此一元二次方程化为ax^2+bx+c=0的形式(即一元二次方程的一般形式）②.系数化1： 将二次项系数化为1 ③.移项： 将常数项移到等号右侧 \④.配方： 等号左右两边同时加上一次项系数一半的平方⑤.变形： 将等号左边的代数式写成完全平方形式 ⑥.开方： 左右同时开平方⑦.求解： 整理即可得到原方程的根 （3）、公式法(4)、因式分解法：把方程变形为一边是零，把另一边的二次三项式分解成两个一次因式的积的形式，让两个一次因式分别等于零，得到两个一元一次方程，解这两个一元一次方程所得到的根，就是原方程的两个根。

四象限原理首先，我们来看看第一个象限——重要且紧急。

这个象限中的事务通常是需要立即解决的，它们对个人或组织的利益有直接影响，如果不及时处理，可能会带来严重的后果。

比如突发的客户投诉、重要项目的紧急变动、突发疾病等。

在面对这些事务时，我们需要立刻采取行动，投入足够的时间和精力，以确保问题得到及时解决，避免进一步的损失。

其次，重要不紧急的事务属于第二个象限。

这些事务可能并不需要立即处理，但它们对个人或组织的长远发展具有重要意义。

比如制定长期规划、学习新技能、建立人际关系等。

尽管这些事务看起来不紧急，但我们不能因为它们不紧急就忽视它们的重要性。

在处理紧急事务之余，我们也要留出时间和精力来处理这些重要的但不紧急的事务，以确保个人和组织的长期发展。

第三个象限是紧急不重要的事务。

这些事务通常是一些琐碎的、无关紧要的事情，但它们需要立即处理，往往会让人感到焦虑和压力。

比如一些无关紧要的会议、琐碎的邮件、他人的紧急请求等。

在面对这些事务时，我们需要审慎判断，避免过度投入时间和精力，以免影响重要事务的处理。

最后，第四个象限是既不重要又不紧急的事务。

这些事务对个人或组织的发展没有实质性影响，通常是一些琐碎的、无关紧要的事情。

比如社交媒体上的无关评论、无意义的时间浪费、无关紧要的琐事等。

在处理这些事务时，我们需要学会拒绝、合理安排时间，避免被这些事务所占据，以免影响重要事务的处理。

总的来说，四象限原理提醒我们在处理问题和做决策时要有条不紊，合理分配时间和精力。

重要且紧急的事务需要立即处理，重要不紧急的事务需要长期规划，紧急不重要的事务需要审慎处理，既不重要又不紧急的事务需要避免。

只有合理处理四象限中的事务，才能提高工作效率，提升生活质量，实现个人和组织的长期发展目标。

四象限原理不仅适用于个人，也适用于组织，它是管理学中的一种重要思维模式，对于提高管理效率和决策水平具有重要意义。

时间管理四象限中第一象限什么是时间管理四象限？时间管理四象限是一种帮助我们有效地管理时间和任务的方法。

这个概念最早由美国管理学专家斯蒂芬·R·柯维提出，他将所有的任务和活动划分为四个象限，根据紧急性和重要性进行分类。

四个象限如下：1.第一象限：紧急且重要2.第二象限：不紧急但重要3.第三象限：紧急但不重要4.第四象限：不紧急且不重要在这篇文章中，我们将重点关注时间管理四象限中的第一象限：紧急且重要。

第一象限的特点第一象限包括那些紧急且重要的任务和活动。

这些任务通常会对我们的生活和工作产生直接的影响，如果不及时处理，可能导致重大问题或损失。

以下是一些常见的第一象限任务的例子：•重要的工作任务和项目•紧急的客户问题和投诉•紧急的健康问题或突发事件•重要的家庭事务，如支付账单和处理紧急事情等如何有效管理第一象限任务管理第一象限任务非常关键，因为它们对我们的生活和工作至关重要。

以下是一些方法，可以帮助我们有效地管理第一象限中的任务：1.优先级管理：首先，我们需要确定哪些任务是最重要和最紧急的。

通过制定并遵守优先级列表，我们可以确保我们在紧急情况下能够专注于最重要的任务。

2.时间规划：为第一象限任务设定明确的截止日期和时间，并确保它们能够得到及时处理。

这可以通过制定详细的时间表、使用提醒工具或日历应用程序来实现。

3.集中精力：在处理第一象限任务时，确保将注意力集中在当前任务上。

避免分散注意力，以及不相关的干扰因素，这样可以提高工作效率和准确性。

4.委派任务：如果可能的话，将一些任务委托给他人，特别是一些不需要你个人处理的事务。

合理利用团队成员的能力，可以节省时间并确保任务得到高效处理。

5.反馈和调整：定期回顾和评估第一象限任务的进展，及时进行反馈和调整。

如果有必要，重新安排任务的优先级，并确保你的时间和资源得到有效利用。

第一象限的重要性第一象限的任务之所以如此重要，是因为它们直接关系到我们的生活和工作的成败。

第九章静电场及其应用9.3电场电场强度（一）第1课时电场强度一、单选题：1.有关电场强度的理解，下述说法正确的是()A．由E＝Fq可知，电场强度E跟放入的电荷q所受的电场力成正比B．在电场中某点放入试探电荷q，该点的场强为E＝Fq，取走q后，该点场强不变C．由E＝k qr2可知，在离点电荷很近，r接近于零时，电场强度无穷大D．以点电荷Q为中心、r为半径的球面上各处的场强E相同答案B解析电场强度由电场本身决定，与试探电荷的电荷量以及所受的电场力无关，由E＝Fq可知，电场强度E等于电荷q所受的电场力F与电荷量q的比值，选项A错误；在电场中某点放入试探电荷q，该点的场强为E＝Fq，取走q后，该点场强不变，选项B正确；在离点电荷很近，r接近于零时，电场强度的公式E＝k qr2不再适用，选项C错误；以点电荷Q为中心的球面上各点场强大小相等，方向不同，D错误．2.如图所示的是在一个电场中A、B、C、D四点分别引入试探电荷时，测得的试探电荷的电荷量跟它所受静电力的函数关系图象，那么下列叙述正确的是()A．A、B、C、D四点电场强度大小相等B．A、B、C、D四点的电场强度大小关系是E D>E A>E B>E CC ．A 、B 、C 、D 四点的电场强度大小关系是E A >E B >E D >E CD ．无法确定这四个点的电场强度大小关系【答案】B 【解析】题图中给出了A 、B 、C 、D 四个位置上电荷量和它所受静电力大小的变化关系，由电场强度的定义式E ＝F q可知，F －q 图象的斜率代表电场强度．斜率大的电场强度大，斜率小的电场强度小．故选项B 正确，选项A 、C 、D 错误．3.关于电场中某点的场强大小和方向的描述，下列说法正确的是()A ．由E ＝F q知，若q 减半，则该处电场强度为原来的2倍B ．由E ＝k Q r2知，E 与Q 成正比，与r 2成反比C ．由E ＝k Q r2知，在以Q 为球心，r 为半径的球面上，各处场强均相同D ．电场中某点的场强方向就是该点所放电荷受到的电场力方向【答案】B 【解析】E ＝F q为场强的定义式，而电场中某点的场强只由电场本身决定，与是否引入试探电荷q 及q 的大小、正负无关，选项A 错误；E ＝k Q r 2是点电荷Q 产生的电场中各点场强的决定式，故E ∝Q r2，选项B 正确；因场强为矢量，E 相同意味着大小、方向都相同，而在球面上各处场强方向不同，选项C 错误；因所放电荷电性不知道，若为正电荷，则E 与＋q 受力方向相同，否则相反，故选项D 错误．4.如图所示,真空中O 点有一点电荷,在它产生的电场中有A 、B 两点,A 点的电场强度大小为E A ,方向与AB 连线成60°角,B 点的电场强度大小为E B ,方向与AB 连线成30°角。

专题强化二十一带电粒子在组合场中的运动目标要求 1.掌握带电粒子在组合场中的运动规律和分析思路.2.学会处理磁场和磁场组合场、电场和磁场组合场中带电粒子的运动问题．1．组合场：电场与磁场各位于一定的区域内，并不重叠，或在同一区域，电场、磁场交替出现．2．分析思路(1)划分过程：将粒子运动的过程划分为几个不同的阶段，对不同的阶段选取不同的规律处理．(2)找关键点：确定带电粒子在场区边界的速度(包括大小和方向)是解决该类问题的关键．(3)画运动轨迹：根据受力分析和运动分析，大致画出粒子的运动轨迹图，有利于形象、直观地解决问题．3．常见粒子的运动及解题方法题型一磁场与磁场的组合磁场与磁场的组合问题实质就是两个有界磁场中的圆周运动问题，带电粒子在两个磁场中的速度大小相同，但轨迹半径和运动周期往往不同．解题时要充分利用两段圆弧轨迹的衔接点与两圆心共线的特点，进一步寻找边角关系．例1(2020·江苏卷·16)空间存在两个垂直于Oxy平面的匀强磁场，y轴为两磁场的边界，磁感应强度分别为2B0、3B0.甲、乙两种比荷不同的粒子同时从原点O沿x轴正向射入磁场，速度均为v.甲第1次、第2次经过y轴的位置分别为P、Q，其轨迹如图所示．甲经过Q时，乙也恰好同时经过该点．已知甲的质量为m，电荷量为q.不考虑粒子间的相互作用和重力影响．求：(1)Q 到O 的距离d ；(2)甲两次经过P 点的时间间隔Δt ； (3)乙的比荷q ′m ′可能的最小值．答案 (1)m v 3qB 0 (2)2πm qB 0 (3)2qm解析 (1)甲粒子先后在两磁场中做匀速圆周运动，设半径分别为r 1、r 2 由q v B ＝m v 2r 可知r ＝m vqB ，故r 1＝m v 2qB 0，r 2＝m v3qB 0且d ＝2r 1－2r 2 解得d ＝m v 3qB 0(2)甲粒子先后在两磁场中做匀速圆周运动，设运动时间分别 t 1、t 2 由T ＝2πr v ＝2πm qB 得t 1＝πm 2qB 0，t 2＝πm 3qB 0且Δt ＝2t 1＋3t 2 解得Δt ＝2πmqB 0(3)乙粒子周期性地先后在两磁场中做匀速圆周运动 若经过两磁场的次数均为n (n ＝1,2,3，…) 相遇时，有n m ′v 3q ′B 0＝d ，n 5πm ′6q ′B 0＝t 1＋t 2解得q ′m ′＝n qm根据题意，n ＝1舍去．当n ＝2时，q ′m ′有最小值，(q ′m ′)min ＝2qm若先后经过右侧、左侧磁场的次数分别为(n ＋1)、n (n ＝0,1,2,3，…)，经分析不可能相遇． 综上分析，乙的比荷的最小值为2qm.题型二 电场与磁场的组合考向1 先电场后磁场1．带电粒子先在匀强电场中做匀加速直线运动，然后垂直进入匀强磁场做匀速圆周运动，如图甲．2．带电粒子先在匀强电场中做类平抛运动，然后垂直进入磁场做匀速圆周运动，如图乙．例2 (2018·全国卷Ⅰ·25)如图，在y >0的区域存在方向沿y 轴负方向的匀强电场，场强大小为E ；在y <0的区域存在方向垂直于xOy 平面向外的匀强磁场．一个氕核11H 和一个氘核21H先后从y 轴上y ＝h 点以相同的动能射出，速度方向沿x 轴正方向．已知11H 进入磁场时，速度方向与x 轴正方向的夹角为60°，并从坐标原点O 处第一次射出磁场.11H 的质量为m ，电荷量为q .不计重力．求：(1)11H 第一次进入磁场的位置到原点O 的距离； (2)磁场的磁感应强度大小；(3)21H 第一次离开磁场的位置到原点O 的距离． 答案 (1)233h (2)6mE qh (3)233(2－1)h 解析 (1)11H 在电场中做类平抛运动，在磁场中做匀速圆周运动，运动轨迹如图所示．设11H 在电场中的加速度大小为a 1，初速度大小为v 1，它在电场中的运动时间为t 1，第一次进入磁场的位置到原点O 的距离为s 1，由运动学公式有s 1＝v 1t 1① h ＝12a 1t 12② 由题给条件，11H 进入磁场时速度的方向与x 轴正方向夹角θ1＝60°.11H 进入磁场时速度沿y 轴方向的分量的大小为 a 1t 1＝v 1tan θ1③ 联立以上各式得 s 1＝233h ④(2)11H 在电场中运动时，由牛顿第二定律有 qE ＝ma 1⑤设11H 进入磁场时速度的大小为v 1′，由速度合成法则有 v 1′＝v 12＋(a 1t 1)2⑥设磁感应强度大小为B ，11H 在磁场中运动的圆轨道半径为R 1，由洛伦兹力公式和牛顿第二定律有q v 1′B ＝m v 1′2R 1⑦由几何关系得 s 1＝2R 1sin θ1⑧ 联立以上各式得 B ＝6mEqh⑨ (3)设21H 在电场中沿x 轴正方向射出的速度大小为v 2，在电场中的加速度大小为a 2，由题给条件得12(2m )v 22＝12m v 12⑩ 由牛顿第二定律有 qE ＝2ma 2⑪设21H 第一次射入磁场时的速度大小为v 2′，速度的方向与x 轴正方向夹角为θ2，入射点到原点的距离为s 2，在电场中运动的时间为t 2.由运动学公式有 s 2＝v 2t 2⑫ h ＝12a 2t 22⑬ v 2′＝v 22＋(a 2t 2)2⑭ sin θ2＝a 2t 2v 2′⑮ 联立以上各式得s 2＝s 1，θ2＝θ1，v 2′＝22v 1′⑯ 设21H 在磁场中做圆周运动的半径为R 2，由⑦⑯式及粒子在匀强磁场中做圆周运动的半径公式得R 2＝2m v 2′qB＝2R 1⑰所以出射点在原点左侧．设21H 进入磁场的入射点到第一次离开磁场的出射点的距离为s 2′，由几何关系有 s 2′＝2R 2sin θ2⑱联立④⑧⑯⑰⑱式得，21H 第一次离开磁场时的位置到原点O 的距离为s 2′－s 2＝233(2－1)h .考向2 先磁场后电场1．进入电场时粒子速度方向与电场方向相同或相反(如图甲所示)． 2．进入电场时粒子速度方向与电场方向垂直(如图乙所示)．例3 如图所示的xOy 坐标系中，第一象限存在与xOy 平面平行的匀强电场E ，且与y 轴负方向的夹角θ＝30°，第二象限存在垂直平面向外的匀强磁场，磁感应强度大小为B .一带正电粒子自O 点射入第二象限，速度v 与x 轴负方向的夹角θ＝30°，粒子经磁场偏转后从y 轴上的P 点进入第一象限，并由x 轴上的M 点(未画出)离开电场．已知OM 距离为3L ，粒子的比荷为vBL，不计粒子重力．(1)求OP 两点的距离；(2)求粒子在磁场中运动的时间；(3)当该粒子经过P 点的同时，在电场中的N 点由静止释放另一个完全相同的带电粒子，若两粒子在离开电场前相遇且所需时间最长，求N 点的坐标． 答案 (1)3L (2)2πL 3v (3)(32L ，332L )解析 (1)带电粒子在第二象限内做匀速圆周运动，轨迹如图，圆心为C由牛顿第二定律，得q v B ＝m v 2R解得R ＝L由几何关系得∠OCP ＝120°则OP ＝3L(2)粒子在磁场中的运动周期T ＝2πRv 粒子偏转120°，即在磁场中运动时间t ＝T3解得t ＝2πL3v(3)带电粒子进入第一象限时速度与y 轴正方向成60°角，与电场方向垂直，故粒子在第一象限内做类平抛运动，轨迹如图．由于两粒子完全相同，所以只需在带电粒子进入电场时速度方向的直线上PN 范围内任一点释放粒子，均可保证两粒子在电场中相遇，且两粒子在M 点相遇所需时间最长，即在图中N 点由静止释放粒子即可．设N 点的横坐标为x ，纵坐标为y ，根据几何知识可得PN ＝QM ＝3L 又x ＝PN cos 30° y ＝OP ＋PN sin 30° 解得x ＝32L ，y ＝332L考向3 粒子多次进出电场、磁场的运动例4 (2021·广东卷·14)如图是一种花瓣形电子加速器简化示意图，空间有三个同心圆a 、b 、c 围成的区域，圆a 内为无场区，圆a 与圆b 之间存在辐射状电场，圆b 与圆c 之间有三个圆心角均略小于90°的扇环形匀强磁场区Ⅰ、Ⅱ和Ⅲ.各区磁感应强度恒定，大小不同，方向均垂直纸面向外．电子以初动能E k0从圆b 上P 点沿径向进入电场，电场可以反向，保证电子每次进入电场即被全程加速，已知圆a 与圆b 之间电势差为U ，圆b 半径为R ，圆c 半径为3R ，电子质量为m ，电荷量为e ，忽略相对论效应，取tan 22.5°＝0.4.(1)当E k0＝0时，电子加速后均沿各磁场区边缘进入磁场，且在电场内相邻运动轨迹的夹角θ均为45°，最终从Q 点出射，运动轨迹如图中带箭头实线所示，求Ⅰ区的磁感应强度大小、电子在Ⅰ区磁场中的运动时间及在Q 点出射时的动能；(2)已知电子只要不与Ⅰ区磁场外边界相碰，就能从出射区域出射．当E k0＝keU 时，要保证电子从出射区域出射，求k 的最大值． 答案 (1)5eUm eR πR meU 4eU 8eU (2)136解析 (1)电子在电场中加速有2eU ＝12m v 2在Ⅰ区磁场中，由几何关系可得r ＝R tan 22.5°＝0.4R 根据洛伦兹力提供向心力有B 1e v ＝m v 2r联立解得B 1＝5eUmeR电子在Ⅰ区磁场中的运动周期为T ＝2πrv由几何关系可得，电子在Ⅰ区磁场中运动的圆心角为 φ＝54π电子在Ⅰ区磁场中的运动时间为t ＝φ2πT联立解得t ＝πR meU4eU电子从P 到Q 在电场中共加速8次，故在Q 点出射时的动能为E k ＝8eU(2)设电子在Ⅰ区磁场中做匀速圆周运动的最大半径为r m ，此时圆周的轨迹与Ⅰ区磁场边界相切，由几何关系可得()3R －r m 2＝R 2＋r m 2解得r m ＝33R 根据洛伦兹力提供向心力有B 1e v m ＝m v m 2r m2eU ＝12m v m 2－keU联立解得k ＝136.例5 如图，直角坐标系xOy 中，在第一象限内有沿y 轴负方向的匀强电场；在第三、第四象限内分别有方向垂直于坐标平面向里和向外的匀强磁场．一质量为m 、电荷量为q (q >0)的粒子从y 轴上P 点(0，h )以初速度v 0垂直于y 轴射入电场，再经x 轴上的Q 点沿与x 轴正方向成45°角进入磁场．粒子重力不计．(1)求匀强电场的场强大小E ；(2)要使粒子能够进入第三象限，求第四象限内磁感应强度B 的大小范围； (3)若第四象限内磁感应强度大小为m v 0qh ，第三象限内磁感应强度大小为2m v 0qh，且第三、第四象限的磁场在y ＝－L (L >2h )处存在一条与x 轴平行的下边界MN (图中未画出)，则要使粒子能够垂直边界MN 飞出磁场，求L 的可能取值．答案 (1)m v 022qh (2)B <(1＋2)m v 02qh(3)L ＝⎝⎛⎭⎫1＋32n h (n ＝1,2,3…) 解析 (1)在第一象限内，粒子在静电力作用下做类平抛运动，由运动学规律有v y 2＝2ah ，v y ＝v 0tan 45°由牛顿第二定律有：qE ＝ma 联立解得E ＝m v 022qh(2)粒子在Q 点的速率v ＝v 0cos 45°＝2v 0，h ＝12v y t ，x ＝v 0t 可得OQ 的距离为x ＝2h粒子进入第四象限后做匀速圆周运动，如图甲所示，轨迹恰与y 轴相切时，对应恰能够进入第三象限的磁感应强度最大值由牛顿第二定律有q v B max ＝m v 2R min由几何关系有x ＝R min ()1＋cos 45° 联立以上各式解得B max ＝(1＋2)m v 02qh故B 的大小范围为B <(1＋2)m v 02qh(3)由洛伦兹力提供向心力可知q v B ＝m v 2R粒子在第四、第三象限的轨道半径分别为 R 1＝2h ，R 2＝2h 2易知：粒子由Q 点进入第四象限后运动半周进入第三象限，作出粒子在第四、第三象限的可能运动轨迹如图乙所示要让粒子垂直边界MN 飞出磁场，则L 满足的条件为 R 1sin 45°＋n ()R 1＋R 2sin 45°＝L (n ＝0,1,2,3…) 结合题意L >2h解得L ＝⎝⎛⎭⎫1＋32n h (n ＝1,2,3…)． 课时精练1．平面直角坐标系xOy 中，第二象限存在沿y 轴负方向的匀强电场，场强大小为E ，第三、四象限存在垂直坐标平面向里的匀强磁场，如图所示．一质量为m ，带电荷量为q 的正粒子从坐标为(－L ，L )的P 点沿y 轴负向进入电场，初速度大小为v 0＝2EqLm，粒子第二次到达x 轴的位置为坐标原点．不计粒子的重力．(1)求匀强磁场的磁感应强度B 的大小；(2)若粒子由P 点沿x 轴正方向入射，初速度仍为v 0＝2EqLm，求粒子第二次到达x 轴时与坐标原点的距离． 答案 (1)4mEqL (2)6＋24L 解析 (1)由动能定理得EqL ＝12m v 2－12m v 02粒子进入磁场时速度大小为v ＝4EqLm在磁场中L ＝2R q v B ＝m v 2R可得B ＝4mE qL(2)假设粒子由y 轴离开电场，运动轨迹如图所示L ＝v 0t ， y 1＝12at 2，Eq ＝ma解得y 1＝L4<L ，假设成立v y ＝at速度偏转角tan θ＝v yv 0第一次到达x 轴的坐标x 1＝L －y 1tan θ＝32L在磁场中R ′＝m v ′qBx 2＝2R ′sin θ＝2m v ′qB sin θ＝2m v y qB ＝24L粒子第二次到达x 轴的位置与坐标原点的距离 x ＝x 1＋x 2＝6＋24L .2.如图所示，在x 轴上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外；在x 轴下方存在匀强电场，电场方向与xOy 平面平行，且与x 轴成45°夹角．一质量为m 、电荷量为q (q >0)的粒子以初速度v 0从y 轴上的P 点沿y 轴正方向射出，一段时间后进入电场，进入电场时的速度方向与电场方向相反；又经过一段时间T 0，磁场的方向变为垂直于纸面向里，大小不变．不计重力．(1)求粒子从P 点出发至第一次到达x 轴时所需时间； (2)若要使粒子能够回到P 点，求电场强度的最大值． 答案 (1)5πm 4qB (2)2m v 0qT 0解析 (1)带电粒子在匀强磁场中做匀速圆周运动，运动轨迹如图所示．设运动半径为R ，运动周期为T ，根据洛伦兹力提供向心力，有q v 0B ＝m v 02RT ＝2πR v 0联立解得T ＝2πmBq依题意，粒子第一次到达x 轴时，转过的角度为54π所需时间为t 1＝θ2πT ＝58T解得t 1＝5πm4qB.(2)粒子进入电场后，先做匀减速直线运动，直到速度减小为0，然后沿原路返回做匀加速直线运动，到达x 轴时速度大小仍为v 0，设粒子在电场中运动的总时间为t 2，加速度大小为a ，有qE ＝ma v 0＝a ·t 22解得t 2＝2m v 0qE根据题意，要使粒子能够回到P 点，必须满足 t 2≥T 0解得电场强度最大值E max ＝2m v 0qT 0. 3．如图所示，xOy 平面内，OP 与x 轴夹角为θ＝53°，在 xOP 范围内(含边界)存在垂直于坐标平面向里的匀强磁场，磁感应强度大小为B ＝0.1 T ．第二象限有平行于 y 轴向下的匀强电场，场强大小为E ＝8340×105 V/m.一带电微粒以速度 v 0 ＝5×106 m/s 从 x 轴上 a (L,0)点平行于OP 射入磁场，并从OP 上的b 点垂直于OP 离开磁场，与y 轴交于c 点，最后回到x 轴上的点d ，图中点b 、d 未标出．已知L ＝54 m ，sin 53°＝45，cos 53°＝35，不计微粒的重力，求：(1)微粒的比荷qm ；(2)d 点与O 点的距离l;(3)仅改变磁场强弱而其他条件不变，当磁感应强度B x 大小满足什么条件时，微粒能到达第四象限．答案 (1)5×107 C/kg (2)4 m (3)B x ≥0.2 T解析 (1)微粒在磁场中做匀速圆周运动，由几何关系得： r ＝L sin 53°由牛顿第二定律得q v 0B ＝m v 02r解得qm＝5×107 C/kg(2)粒子进入电场后做类斜抛运动．由几何关系得 y Oc ＝L cos 53°＋r sin 53°在y 轴方向 y Oc ＝－v 0t cos 53°＋12qE mt 2在x 轴方向 l ＝ v 0t sin 53° 解得l ＝4 m(3)微粒在磁场中做匀速圆周运动的轨迹与边界OP 相切时，恰好能到达第四象限． 由几何关系知R ＝12L sin 53°由牛顿第二定律得q v 0B 1＝m v 02R解得B 1 ＝ 0.2 T故当磁感应强度B x ≥0.2 T 时，微粒能到达第四象限．4．(2022·湖北宜昌市联考)如图所示，在矩形区域ABCD 内存在竖直向上的匀强电场，在BC 右侧Ⅰ、Ⅱ两区域存在匀强磁场，L 1、L 2、L 3是磁场的边界(BC 与L 1重合)，宽度相同，方向如图所示，区域Ⅰ的磁感应强度大小为B 1.一电荷量为＋q 、质量为m 的粒子(重力不计)从AD 边中点以初速度v 0沿水平向右方向进入电场，粒子恰好从B 点进入磁场，经区域Ⅰ后又恰好从与B 点同一水平高度处进入区域Ⅱ.已知AB 长度是BC 长度的3倍．(1)求带电粒子到达B 点时的速度大小； (2)求区域Ⅰ磁场的宽度L ；(3)要使带电粒子在整个磁场中运动的时间最长，求区域Ⅱ的磁感应强度B 2的最小值． 答案 (1)23v 03 (2)23m v 03qB 1(3)1.5B 1解析 (1)设带电粒子进入磁场时的速度大小为v ，与水平方向成θ角，粒子在匀强电场中做类平抛运动，由类平抛运动的速度方向与位移方向的关系有：tan θ＝L BC L AB ＝33，则θ＝30°根据速度关系有：v ＝v 0cos θ＝23v 03；(2)设带电粒子在区域Ⅰ中的轨道半径为r 1，由牛顿第二定律得：q v B 1＝m v 2r 1，轨迹如图甲所示：由几何关系得：L ＝r 1 解得：L ＝23m v 03qB 1；(3)当带电粒子不从区域Ⅱ右边界离开磁场时，在磁场中运动的时间最长．设区域Ⅱ中最小磁感应强度为B 2m ，此时粒子恰好不从区域Ⅱ右边界离开磁场，对应的轨迹半径为r 2，轨迹如图乙所示：可得：q v B 2m ＝m v 2r 2根据几何关系有：L ＝r 2(1＋sin θ) 解得：B 2m ＝1.5B 1.。

CDA LEVEL1 第六章业务数据分析考试占比：业务数据分析（30%）a.数据驱动型业务管理方法（占比 3%）b.指标的应用与设计（占比 12%）c.业务分析方法（占比 15%）客户分析商品分析流量、转化分析行为效果分析业务分析模型业务分析方法考试内容：总体要求理解业务数据分析方法、掌握业务数据分析流程、能够使用及设计创建业务指标、能够结合业务模型及业务分析方法正确理解业务问题，找到问题原因，并能够提出解决问题建议◆ 1、数据驱动型业务管理方法【熟知】熟知数据从业务中来到业务中去的全过程熟知数据驱动型业务管理的价值意义熟知数据驱动型业务管理流程熟知数据驱动型业务管理思维方式【应用】能够通过数据驱动型业务管理流程找到业务分析与业务管理需求的结合点，能够正确理解数据的出处及产生逻辑，能够正确的运用数据为业务管理提供有价值的数据分析结果◆ 2、指标的应用与设计【领会】指标的作用【熟知】熟知从指标结果出发到业务行为落地的思维过程及分析方法熟知指标与透视计算间的关系熟知常用指标：流量相关指标、转化相关指标、营运、销售相关指标、库存类指标常用财务指标、绩效类指标、客户相关指标、熟知拆解业务需求设计指标方法【应用】能够根据指标结果洞察业务问题及影响能够根据业务场景选择恰当的指标进行观测能够根据业务需求设计新指标，完善指标体系◆ 3、业务分析方法【领会】不同业务分析方法各自的作用【熟知】熟知以下业务分析方法：客户分析：客户来源分析、客户价值分析、客户生命周期分析、客户行为分析商品分析：商品进销存分析、商品渠道分析、商品耗损分析、商品价格分析流量、转化分析：流量转化分析、流量渠道分析行为效果分析：活动效果分析、销售分析、其他行为效果分析业务分析模型：漏斗模型、RFM 模型、客户价值模型业务分析方法：树状结构分析法、二八分析法、四象限分析法、同期群分析法【应用】能够应用恰当分析方法解决业务问题能够将数据处理分析技能融入到业务分析方法中，为数据驱动型业务管理提供正确、全面、客观的数据依据知识点：1.业务指标分析是发现业务问题的核心方法。

1+X数字营销技术应用题库1+X数字营销技术应用（中级题库）一、单选题1.为了向用户展示意义较为完整的描述，搜索引擎会在限制的范围内对描述内容进行适当的增删。

（对）2.关键词词库清洗包括清除掉不必要的重复数据、处理缺失的数据、删除无意义与违规关键词（对）。

3.包邮、特价、正品、活动促销等都属于营销关键词。

（对）4.可以利用搜索引擎为网店提供的数据分析工具获取关键词，例如搜索下拉框、相关关键词等。

（对）5.关键词挖掘是指利用关键词扩展工具，对目标词库进行相关数据指标分析，以得出最优关键词。

（对）6.Intitle结果数是指标题中包含某关键词的网页数量（对）。

7.对于网站而言，权威性体现在该网站在XXX有CP 备案号（对）。

8.网站PV代表网站页面的阅读量，是衡量一个网站或页面的用户拜访量（对）。

9.兴趣分布是基于搜索目标受众行为数据以及画像库，刻画出关注某兴趣的人群分布情况（对）。

10.均匀访问页面数也叫访问深度，是指每个受众在一次浏览网站的过程中，均匀访问的页面数量（对）。

12.在进行搜索排名优化时，可以在搜索引擎中搜索核心关键词及相关关键词，查看不同核心关键词下网页的排名位置（对）。

13.分析竞争对手的搜索竞价营销策略时可以通过搜索重点关键词记录排名的形式收集不同时间段内对手的调整动向（对）。

14.相关词是指与某关键词具有一定相关性的关键词，一般而言，相关词的数量和搜索指数越大，关键词的竞争程度也就越大（对）。

15.添加通配符能够增加创意飘红的概率（对）。

16.在排名不变的情形下，进步关键词的质量分，出价会响应下降。

（对）17.在搜索竞价营销过程中，采用CPM出价方式出价，只要展现了广告主的广告内容，广告主就为此付费（对）。

18.推广账户的实际消费不会大于每日预算，可以根据推广情况随时修改预算。

（对）19.企业推广账户的关键词，质量度得分越高代表体系认为企业的推广成效和着陆对于看到推广成效的目标受众来说更具有相干性（对）。

四象限知识点总结一、四象限的定义四象限是指平面直角坐标系中，以原点为中心，x轴和y轴为边界所划分出的四个部分。

这四个部分分别被称为第一象限、第二象限、第三象限和第四象限。

1. 第一象限：x轴和y轴都是正数。

x轴的右边是正数，y轴的上边是正数。

坐标为(x, y)，x和y都大于0。

2. 第二象限：x轴负，y轴正。

x轴的左边是负数，y轴的上边是正数。

坐标为(-x, y)，x为负，y为正。

3. 第三象限：x轴负，y轴负。

x轴的左边是负数，y轴的下边是负数。

坐标为(-x, -y)，x和y都小于0。

4. 第四象限：x轴正，y轴负。

x轴的右边是正数，y轴的下边是负数。

坐标为(x, -y)，x为正，y为负。

二、四象限的特点1. 第一象限：所有的坐标都是正数。

这个象限中的点都是正数点，是正的都在这个象限中。

2. 第二象限：x轴为负数，y轴为正数。

这个象限中的点的x坐标都是负数，y坐标都是正数。

3. 第三象限：x轴为负数，y轴为负数。

这个象限中的点的x坐标都是负数，y坐标都是负数。

4. 第四象限：x轴为正数，y轴为负数。

这个象限中的点的x坐标都是正数，y坐标都是负数。

三、四象限的应用四象限在数学中的应用非常广泛，尤其是在平面几何和代数中。

下面我们就来介绍一些四象限的应用。

1. 计算坐标在四象限中，我们可以根据点的位置来判断其坐标的正负，从而方便进行计算和分析。

例如，对于一个坐标为(-3, 5)的点，我们可以知道它位于第二象限，即x轴为负，y轴为正。

2. 图形的位置在平面几何中，我们经常需要判断各个点的位置以及图形的位置。

通过四象限，我们可以轻松地判断点所在的象限，从而确定图形的位置和性质。

3. 函数图像在代数中，我们经常需要画函数的图像。

通过四象限，我们可以清晰地表现出函数的定义域和值域，从而更好地理解函数的性质和特点。

四、四象限的运算在四象限中，我们经常需要进行各种运算和分析。

下面我们来介绍一些常见的四象限运算。

专题7.1 平面直角坐标系【八大题型】【人教版】【题型1 判断点所在的象限】 (1)【题型2 坐标轴上点的坐标特征】 (3)【题型3 点到坐标轴的距离】 (4)【题型4 平行与坐标轴点的坐标特征】 (6)【题型5 坐标确定位置】 (8)【题型6 点在坐标系中的平移】 (11)【题型7 图形在坐标系中的平移】 (13)【题型8 图形在格点中的平移变换】 (15)【题型1 判断点所在的象限】【例1】（2022春•洪山区期末）已知点P（x，y）在第四象限，则点Q（﹣x﹣3，﹣y）在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据第四象限的横纵坐标范围，可求得x，y的取值范围，再确定Q点横纵坐标的取值范围即可解答．【解答】解：点P（x，y）在第四象限，∴x＞0，y＜0，∴﹣x﹣3＜0，﹣y＞0，∴点Q（﹣x﹣3，﹣y）在第二象限．故选：B．【变式1-1】（2022春•长沙期末）已知点P（﹣a，b），ab＞0，a+b＜0，则点P在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据有理数的乘法、有理数的加法，可得a、b的符号，根据第一象限内点的横坐标大于零，纵坐标大于零，可得答案．【解答】解：因为ab＞0，a+b＜0，所以a＜0，b＜0，所以﹣a＞0，所以点P（﹣a，b）在第四象限，故选：D．【变式1-2】（2022春•青山区期末）已知，点A的坐标为（m﹣1，2m﹣3），则点A一定不会在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据每个象限点的坐标的符号特征列出不等式组，解不等式组，不等式组无解的选项符合题意．【解答】解：A选项，{m―1＞02m―3＞0，解得：m＞32，故该选项不符合题意；B选项，{m―1＜02m―3＞0，不等式组无解，故该选项符合题意；C选项，{m―1＜02m―3＜0，解得：m＜1，故该选项不符合题意；D选项，{m―1＞02m―3＜0，解得：1＜m＜32，故该选项不符合题意；故选：B．【变式1-3】（2022春•晋州市期中）对任意实数x，点P（x，x2+3x）一定不在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【分析】利用各象限内点的坐标性质分析得出答案．【解答】解：当x＞0，则x2+3x＞0，故点P（x，x2+3x）可能在第一象限；当x＜0，则x2+3x＞0或x2+3x＜0，故点P（x，x2+3x）可能在第二、三象限；当x＝0时，点P（x，x2+3x）在原点．故点P（x，x2+3x）一定不在第四象限．故选：D．均为0.【题型2 坐标轴上点的坐标特征】【例2】（2022春•陇县期中）在平面直角坐标系中，点M（m﹣3，m+1）在x轴上，则点P （m﹣1，1﹣m）在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据x轴上的点纵坐标为0，可得m+1＝0，从而求出m的值，进而求出点P的坐标，最后根据平面直角坐标系中每一象限点的坐标特征，即可解答．【解答】解：由题意得：m+1＝0，∴m＝﹣1，当m＝﹣1时，m﹣1＝﹣2，1﹣m＝2，∴点P（﹣2，2）在第二象限，故选：B．【变式2-1】（2022春•海淀区校级期中）在平面直角坐标系中，点P的坐标为（2m﹣4，m+1），若点P在y轴上，则m的值为（ ）A．﹣1B．1C．2D．3【分析】根据y轴上的点横坐标为0，可得2m﹣4＝0，然后进行计算即可解答．【解答】解：由题意得：2m﹣4＝0，解得：m＝2，故选：C．【变式2-2】（2022春•仓山区校级期中）已知点A（﹣3，2m+3）在x轴上，点B（n﹣4，4）在y轴上，则点C（m，n）在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【分析】直接利用x轴以及y轴上点的坐标得出m，n的值，进而得出答案．【解答】解：∵点A（﹣3，2m+3）在x轴上，点B（n﹣4，4）在y轴上，∴2m+3＝0，n﹣4＝0，解得：m=―32，n＝4，则点C（m，n）在第二象限．故选：B．【变式2-3】（2022春•东莞市期中）已知点P（2a﹣4，a+1），若点P在坐标轴上，则点P 的坐标为 ．【分析】分两种情况：当点P在x轴上，当点P在y轴上，分别进行计算即可解答．【解答】解：分两种情况：当点P在x轴上，a+1＝0，∴a＝﹣1，当a＝﹣1时，2a﹣4＝﹣6，∴点P的坐标为：（﹣6，0），当点P在y轴上，2a﹣4＝0，∴a＝2，当a＝2时，a+1＝3，∴点P的坐标为：（0，3），综上所述，点P的坐标为：（﹣6，0）或（0，3），故答案为：（﹣6，0）或（0，3）．【题型3 点到坐标轴的距离】【例3】（2022春•巴南区期末）已知点P在x轴的下方，若点P到x轴的距离是3，到y 轴的距离是4，则点P的横坐标与纵坐标的和为 ．【分析】根据题意可得点P在第三象限或第四象限，再根据点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值解答．【解答】解：∵点P在x轴下方，点P到x轴的距离是3，到y轴的距离是4，∴点P的横坐标为±4，纵坐标为﹣3，∴点P的坐标为（4，﹣3）或（﹣4，﹣3），点P的横坐标与纵坐标的和为4﹣3＝1或﹣4﹣3＝﹣7．故答案为：1或﹣7．【变式3-1】（2021秋•城固县期末）已知点M（a，b）在第一象限，点M到x轴的距离等于它到y轴距离的2倍，且点M到两坐标轴的距离之和为6，则点M的坐标为 ．【分析】根据点到x轴的距离是纵坐标的绝对值，点到y轴的距离是点的横坐标的绝对值，可得答案．【解答】解：因为点M（a，b）在第一象限，所以a＞0，b＞0，又因为点M（a，b）在第一象限，点M到x轴的距离等于它到y轴距离的2倍，且点M 到两坐标轴的距离之和为6，所以{b=2aa+b=6，解得{a=2b=4，所以点M的坐标为（2，4）．故答案为：（2，4）．【变式3-2】（2022春•云阳县期中）坐标平面内有一点A（x，y），且点A到x轴的距离为3，到y轴的距离恰为到x轴距离的2倍．若xy＜0，则点A的坐标为（ ）A．（6，﹣3）B．（﹣6，3）C．（3，﹣6）或（﹣3，6）D．（6，﹣3）或（﹣6，3）【分析】根据题意可得x，y异号，然后再利用点到x的距离等于纵坐标的绝对值，点到y 的距离等于横坐标的绝对值，即可解答．【解答】解：∵xy＜0，∴x，y异号，∵点A到x轴的距离为3，到y轴的距离恰为到x轴距离的2倍，∴点A（6，﹣3）或（﹣6，3），故选：D．【变式3-3】（2021秋•阳山县期末）在平面直角坐标系中，点A的坐标是（3a﹣5，a+1）．若点A到x轴的距离与到y轴的距离相等，且点A在y轴的右侧，则a的值为（ ）A．1B．2C．3D．1 或3【分析】根据点A到x轴的距离与到y轴的距离相等可得3a﹣5＝a+1或3a﹣5＝﹣（a+1），解出a的值，再由点A在y轴的右侧可得3a﹣5＞0，进而可确定a的值．【解答】解：∵点A到x轴的距离与到y轴的距离相等，∴3a﹣5＝a+1或3a﹣5＝﹣（a+1），解得：a＝3或1，∵点A在y轴的右侧，∴点A的横坐标为正数，∴3a﹣5＞0，∴a＞5 3，∴a＝3．故选：C．【题型4 平行与坐标轴点的坐标特征】【例4】（2022春•东莞市期末）在平面直角坐标系中，点A的坐标为（3，2），AB平行于x轴，若AB＝4，则点B的坐标为（ ）A．（7，2）B．（1，5）C．（1，5）或（1，﹣1）D．（7，2）或（﹣1，2）【分析】线段AB∥x轴，A、B两点纵坐标相等，又AB＝4，B点可能在A点左边或者右边，根据距离确定B点坐标．【解答】解：∵AB∥x轴，∴A、B两点纵坐标都为2，又∵AB＝4，∴当B点在A点左边时，B（﹣1，2），当B点在A点右边时，B（7，2）；故选：D．【变式4-1】（2022春•延津县期中）在平面直角坐标系中，点A（﹣2，1），B（2，3），C （a，b），若BC∥x轴，AC∥y轴，则点C的坐标为（ ）A．（﹣2，1）B．（2，﹣3）C．（2，1）D．（﹣2，3）【分析】根据已知条件即可得到结论．【解答】解：∵点A（﹣2，1），B（2，3），C（a，b），BC∥x轴，AC∥y轴，∴b＝3，a＝﹣2，∴点C的坐标为（﹣2，3），故选：D．【变式4-2】（2022春•涪陵区期末）在平面直角坐标系中，若点P和点Q的坐标分别为P （﹣2，m），Q（﹣2，1），点P在点Q的上方，线段PQ＝5，则m的值为（ ）A．6B．5C．4D．7【分析】借助图形，采用数形结合的思想求解．【解答】解：∵P（﹣2，m），Q（﹣2，1），点P在点Q的上方，线段PQ＝5，∴m＝1+5＝6．故选：A．【变式4-3】（2022春•硚口区期中）如图，已知点A（4，0），B（0，2），C（﹣5，0），CD∥AB交y轴于点D．点P（m，n）为线段CD上（端点除外）一点，则m与n满足的等量关系式是（ ）A．m+2n＝﹣5B．2m+n＝﹣10C．m﹣n＝﹣5D．2m﹣n＝﹣6【分析】利用平移的性质可得点B与C对应时，点A的对应点为（﹣1，﹣2），由此可确定点P满足的等量关系式．【解答】解：∵AB∥CD，A（4，0），B（0，2），C（﹣5，0），当B与C对应时，点A平移后对应的点是（﹣1，﹣2），∵点P（m，n）为线段CD上（端点除外）一点，将点C（﹣5，0）和（﹣1，﹣2）分别代入m+2n＝﹣5，2m+n＝﹣10，m﹣n＝﹣5，2m﹣n＝﹣6中，只有m+2n＝﹣5满足条件．故选：A．【题型5 坐标确定位置】【例5】（2022春•中山市期中）中国象棋具有悠久的历史，战国时期，就有了关于象棋的正式记载，如图是中国象棋棋局的一部分，如果用（2，﹣1）表示“炮”的位置，（﹣2，0）表示“士”的位置，那么“将”的位置应表示为（ ）A．（﹣2，3）B．（0，﹣5）C．（﹣3，1）D．（﹣4，2）【分析】直接利用已知点坐标建立平面直角坐标系，进而得出答案．【解答】解：如图所示：“将”的位置应表示为（﹣3，1）．故选：C．【变式5-1】（2021秋•渠县校级期中）在大型爱国主义电影《长津湖》中，我军缴获了敌人防御工程的坐标地图碎片（如图），若一号暗堡坐标为（1，2），四号暗堡坐标为（﹣3，2），指挥部坐标为（0，0），则敌人指挥部可能在（ ）A．A处B．B处C．C处D．D处【分析】根据一号暗堡和四号暗堡的横纵坐标分别确定x轴和y轴的大致位置，然后画出直角坐标系即可得到答案．【解答】解：∵一号暗堡的坐标为（1，2），四号暗堡的坐标为（﹣3，2），∴它们的连线平行于x轴，∵一号暗堡和四号暗堡的纵坐标为正数，四号暗堡离y轴要远，如图，∴B点可能为坐标原点，∴敌军指挥部的位置大约是B处．故选：B．【变式5-2】（2022春•朝阳区期末）为更好的开展古树名木的系统保护工作，某公园对园内的6棵百年古树都利用坐标确定了位置，并且定期巡视．（1）在如图所示的正方形网格中建立平面直角坐标系xOy，使得古树A、B的位置分别表示为A（1，2），B（0，﹣1）；（2）在（1）建立的平面直角坐标系xOy中，①表示古树C的位置的坐标为 ；②标出另外三棵古树D（﹣1，﹣2），E（1，0），F（1，1）的位置；③如果“（﹣2，﹣2）→（﹣2，﹣1）→（﹣2，0）→（﹣2，1）→（﹣1，2）→（0，2）→（1，2）→（1，1）→（1，0）→（1，﹣1）→（0，﹣1）→（0，﹣2）→（﹣1，﹣2）”表示园林工人巡视古树的一种路线，请你用这种形式画出园林工人从原点O出发巡视6棵古树的路线（画出一条即可）．【分析】（1）根据A（1，2），B（0，﹣1）建立坐标系即可；（2）①根据坐标系中C的位置即可求得；②直接根据点的坐标描出各点；③根据6棵古树的位置得出运动路线即可．【解答】解：（1）如图：（2）①古树C的位置的坐标为（﹣1，2）；故答案为：（﹣1，2）；②标出D（﹣1，﹣2），E（1，0），F（1，1）的位置如上图；③园林工人从原点O出发巡视6棵古树的路线：（0，0）→（1，0）→（1，1）→（1，3）→（﹣1，2）→（﹣1，2）→（0，1）．【变式5-3】（2022春•海淀区校级期中）如图1，将射线OX按逆时针方向旋转β角（0°≤β＜360°），得到射线OY，如果点P为射线OY上的一点，且OP＝m，那么我们规定用（m，β）表示点P在平面内的位置，并记为P（m，β）．例如，图2中，如果OM＝5，∠XOM＝110，那么点M在平面内的位置，记为M（5，110°），根据图形，解答下列问题：（1）如图3，点N在平面内的位置记为N（6，30°），那么ON＝ ，∠XON＝ ．（2）如果点A、B在平面内的位置分别记为A（4，30°），B（3，210°），则A、B 两点间的距离为 ．【分析】（1）由题意得第一个坐标表示此点距离原点的距离，第二个坐标表示此点与原点的连线与x 轴所夹的角的度数；（2）根据相应的度数判断出AB 是一条线段，从而得出AB 的长为4+3＝7．【解答】解：（1）根据点N 在平面内的位置记为N （6，30°）可知，ON ＝6，∠XON ＝30°．故答案为：6，30°；（2）如图所示：∵A （4，30°），B （3，210°），∴∠AOX ＝30°，∠BOX ＝210°，∴∠AOB ＝180°，∵OA ＝4，OB ＝3，∴AB ＝4+3＝7．故答案为：7．） 【例6】（2022春•洪湖市期中）在平面直角坐标系中，将点（1，﹣4）平移到点（﹣3，﹣2），经过的平移变换为（ ）A ．先向左平移4个单位长度，再向下平移6个单位长度B ．先向右平移4个单位长度，再向上平移6个单位长度C ．先向左平移4个单位长度，再向上平移2个单位长度）向左平移a 个单位再向上平移b 个单向下平移b 个单位D．先向右平移4个单位长度，再向下平移2个单位长度【分析】根据点向左平移，纵坐标不变的特点即可求解．【解答】解：∵点（1，﹣4）平移到点（﹣3，﹣2），∴﹣3﹣1＝﹣4，∴﹣2﹣（﹣4）＝2，∴先向左平移4个单位长度，再向上平移2个单位长度故选：C．【变式6-1】（2022春•武侯区期末）在平面直角坐标系中，将点M（3m﹣1，m﹣3）向上平移2个单位长度得到点M'，若点M'在x轴上，则点M的坐标是（ ）A．（2，﹣2）B．（14，2）C．（﹣2，―103）D．（8，0）【分析】让点M的纵坐标加2后等于0，求得m的值，进而得到点M的坐标．【解答】解：∵将点M（3m﹣1，m﹣3）向上平移2个单位长度得到点M'，若点M'在x 轴上，∴m﹣3+2＝0，解得：m＝1，∴3m﹣1＝2，m﹣3＝﹣2，∴M（2，﹣2）．故选：A．【变式6-2】（2022春•碑林区校级期中）在平面直角坐标系中，将点P（a，b）向右平移3个单位，再向下平移2个单位，得到点Q．若点Q位于第四象限，则a，b的取值范围是（ ）A．a＞0，b＜0B．a＞1，b＜2C．a＞1，b＜0D．a＞﹣3，b＜2【分析】利用平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减求解即可．【解答】解：P（a，b）向右平移3个单位，再向下平移2个单位得到（a+3，b﹣2），∵Q位于第四象限，∴a+3＞0，b﹣2＜0，∴a＞﹣3，b＜2．故选D．【变式6-3】（2021秋•苏州期末）在平面直角坐标系中，把点P（a﹣1，5）向左平移3个单位得到点Q（2﹣2b，5），则2a+4b+3的值为　．【分析】根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得答案．【解答】解：将点P（a﹣1，5）向左平移3个单位，得到点Q，点Q的坐标为（2﹣2b，5），∴a﹣1﹣3＝2﹣2b，∴a+2b＝6，∴2a+4b+3＝2（a+2b）+3＝2×6+3＝15，故答案为：15．【例7】（2022春•胶州市期末）如图，△ABC的顶点坐标A（2，3），B（1，1），C（4，2），将△ABC先向左平移3个单位，再向下平移1个单位，得到△A'B'C'，则BC边上一点D（m，n）的对应点D'的坐标是（ ）A．（m+3，n+1）B．（m﹣3，n﹣1）C．（﹣1，2）D．（3﹣m，1﹣n）【分析】根据坐标平移规律解答即可．【解答】解：∵将△ABC先向左平移3个单位，再向下平移1个单位，得到△A'B'C'，∴BC边上一点D（m，n）的对应点D'的坐标是（m﹣3，n﹣1）．故选：B．【变式7-1】（2022•青岛二模）如图，线段AB经过平移得到线段A'B'，其中点A，B的对应点分别为点A'，B'，这四个点都在格点上．若线段A'B'有一个点P'（a，b），则点P'在AB上的对应点P的坐标为（ ）A．（a﹣2，b+3）B．（a﹣2，b﹣3）C．（a+2，b+3）D．（a+2，b﹣3）【分析】先利用点A它的对应点A′的坐标特征得到线段AB先向右平移2个单位，再向下平移3个单位得到线段A′B′，然后利用点平移的坐标规律写出点P（a，b）平移后的对应点P′的坐标．【解答】解：由图知，线段A'B'向右平移2个单位，再向下平移3个单位即可得到线段AB，所以点P'（a，b）在AB上的对应点P的坐标为（a+2，b﹣3），故选：D．【变式7-2】（2022春•滨城区期中）如图，第一象限内有两点P（m﹣4，n），Q（m，n﹣3），将线段PQ平移，使点P、Q分别落在两条坐标轴上，则点P平移后的对应点的坐标是（ ）A．（﹣2，0）B．（0，3）C．（0，3）或（﹣4，0）D．（0，3）或（﹣2，0）【分析】设平移后点P、Q的对应点分别是P′、Q′．分两种情况进行讨论：①P′在y 轴上，Q′在x轴上；②P′在x轴上，Q′在y轴上．【解答】解：设平移后点P、Q的对应点分别是P′、Q′．分两种情况：①P′在y轴上，Q′在x轴上，则P′横坐标为0，Q′纵坐标为0，∵0﹣（n﹣3）＝﹣n+3，∴n﹣n+3＝3，∴点P平移后的对应点的坐标是（0，3）；②P′在x轴上，Q′在y轴上，则P′纵坐标为0，Q′横坐标为0，∵0﹣m＝﹣m，∴m﹣4﹣m＝﹣4，∴点P平移后的对应点的坐标是（﹣4，0）；综上可知，点P平移后的对应点的坐标是（0，3）或（﹣4，0）．故选：C．【变式7-3】（2022春•如东县期中）三角形ABC在经过某次平移后，顶点A（﹣1，m+2）的对应点为A（2，m﹣3），若此三角形内任意一点P（a，b）经过此次平移后对应点P1（c，d）．则a+b﹣c﹣d的值为（ ）A．8+m B．﹣8+m C．2D．﹣2【分析】由A（﹣1，2+m）在经过此次平移后对应点A1（3，m﹣3），可得△ABC的平移规律为：向右平移3个单位，向下平移5个单位，由此得到结论．【解答】解：∵A（﹣1，2+m）在经过此次平移后对应点A1（2，m﹣3），∴△ABC的平移规律为：向右平移3个单位，向下平移5个单位，∵点P（a，b）经过平移后对应点P1（c，d），∴a+3＝c，b﹣5＝d，∴a﹣c＝﹣3，b﹣d＝5，∴a+b﹣c﹣d＝﹣3+5＝2，故选：C．【题型8 图形在格点中的平移变换】【例8】（2021春•抚远市期末）在平面直角坐标系xOy中，点A的坐标为（0，4），线段MN的位置如图所示，其中点M的坐标为（﹣3，﹣1），点N的坐标为（3，﹣2）．（1）将线段MN平移得到线段AB，其中点M的对应点为A，点N的对应点为B．①点M平移到点A的过程可以是：先向 平移　个单位长度，再向 平移 个单位长度；②点B的坐标为 ；（2）在（1）的条件下，若点C的坐标为（4，0），连接AC，BC，求△ABC的面积．【分析】（1）由点M及其对应点的A的坐标可得平移的方向和距离，据此可得点N的对应点B的坐标；（2）割补法求解可得．【解答】解：（1）如图，①点M平移到点A的过程可以是：先向右平移3个单位长度，再向上平移5个单位长度；②点B的坐标为（6，3），故答案为：右、3、上、5、（6，3）；（2）如图，S△ABC＝6×4―12×4×4―12×2×3―12×6×1＝10．【变式8-1】（2022春•长沙期末）如图，△ABC的顶点A（﹣1，4），B（﹣4，﹣1），C （1，1）．若△ABC向右平移4个单位长度，再向下平移3个单位长度得到△A'B'C'，且点C的对应点坐标是C'．（1）画出△A'B'C'，并直接写出点C'的坐标；（2）若△ABC内有一点P（a，b）经过以上平移后的对应点为P'，直接写出点P'的坐标；（3）求△ABC的面积．【分析】（1）首先确定A、B、C三点平移后的对应点位置，然后再连接即可；（2）由平移的性质可求解；（3）利用面积的和差关系可求解．【解答】解：（1）如图所示：∴点C（5，﹣2）；（2）∵△ABC向右平移4个单位长度，再向下平移3个单位长度得到△A'B'C'，∴点P'（a+4，b﹣3）；（3）S△ABC＝5×5―12×3×5―12×2×3―12×5×2＝25﹣7.5﹣3﹣5＝9.5．【变式8-2】（2022春•江岸区校级月考）如图，三角形A′B′C′是由三角形ABC经过某种平移得到的，点A与点A′，点B与点B′，点C与点C′分别对应，且这六个点都在格点上，观察各点以及各点坐标之间的关系，解答下列问题：（1）分别写出点B和点B′的坐标，并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的；（2）连接BC′，直接写出∠CBC′与∠B′C′O之间的数量关系 ；（3）若点M（a﹣1，2b﹣5）是三角形ABC内一点，它随三角形ABC按（1）中方式平移后得到的对应点为点N（2a﹣7，4﹣b），求a和b的值．【分析】（1）由图形可得出点的坐标和平移方向及距离；（2）根据平移的性质和平角的定义和平行线的性质即可求解；（3）根据以上所得平移方式，利用“横坐标，右移加，左移减；纵坐标，上移加，下移减”的规律列出关于a、b的方程，解之求得a、b的值．【解答】解：（1）由图知，B（2，1），B′（﹣1，﹣2），三角形A′B′C′是由三角形ABC向左平移3个单位，向下平移3个单位得到的；（2）∠CBC′与∠B′C′O之间的数量关系∠CBC′﹣∠B′C′O＝90°．故答案为：∠CBC′﹣∠B′C′O＝90°；（3）由（1）中的平移变换得a﹣1﹣3＝2a﹣7，2b﹣5﹣3＝4﹣b，解得a＝3，b＝4．故a的值是3，b的值是4．【变式8-3】（2021春•安阳县期中）在平面直角坐标系中，三角形ABC经过平移得到三角形A'B'C'，位置如图所示．（1）分别写出点A，A'的坐标：A ，A' ．（2）请说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的．（3）若点M（m，4﹣n）是三角形ABC内部一点，则平移后对应点M'的坐标为（2m﹣8，n﹣4），求m和n的值．【分析】（1）根据已知图形可得答案；（2）由A（1，0）的对应点A′（﹣4，4）得平移规律，即可得到答案；（3）由（2）平移规律得出m、n的方程．【解答】解：（1）由图知A（1，0），A'（﹣4，4），故答案为：（1，0），（﹣4，4）；（2）A（1，0）对应点的对应点A′（﹣4，4）得A向左平移5个单位，向上平移4个单位得到A′，三角形A'B'C'是由三角形ABC向左平移5个单位，向上平移4个单位得到．（3）△ABC内M（m，4﹣n）平移后对应点M'的坐标为（m﹣5，4﹣n+4），∵M'的坐标为（2m﹣8，n﹣4），∴m﹣5＝2m﹣8，4﹣n+4＝n﹣4，∴m＝3，n＝6．。

第五章三角函数5．1任意角和弧度制5．1.1任意角［目标] 1.理解任意角的概念，能区分各类角的概念;2.掌握象限角的概念，并会用集合表示象限角；3。

理解终边相同的角的含义及其表示，并能解决有关问题．[重点] 用集合的形式表示终边相同的角．［难点］会判断角的终边所在的象限．知识点一角的概念的推广和分类［填一填］1．任意角的概念角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．2．正角、负角和零角我们规定，一条射线绕其端点按逆时针方向旋转形成的角叫做正角，按顺时针方向旋转形成的角叫做负角．如果一条射线没有做任何旋转，我们称它形成了一个零角．这样,零角的始边与终边重合．如果α是零角，那么α＝0°.1．根据角的新的定义，角的范围有什么变化？提示：角的范围不再是以前学的锐角、直角以及钝角，而是任意的角．2．如图所示，图(1)中,角α的度数为330°，图（2）中，角β的度数为－150°，角γ的度数为570°。

解析：题图(1）中，α＝360°－30°＝330°；题图(2）中，β＝－360°＋60°＋150°＝－150°；γ＝360°＋60°＋（－β）＝360°＋60°＋150°＝570°.知识点二象限角[填一填］为了讨论问题的方便，我们在直角坐标系内使角的顶点与原点重合，角的始边与x轴的非负半轴重合．那么，角的终边在第几象限，我们就说这个角是第几象限角．如果角的终边在坐标轴上，就认为这个角不属于任何一个象限，称它为轴线角（或称为象限界角)．3．把角的顶点放在平面直角坐标系的原点，角的始边与x 轴的非负半轴重合,旋转该角，则其终边（除端点外）可能落在什么位置?提示：坐标轴上或四个象限内．4．“锐角”、“第一象限角"、“小于90°的角”三者有何不同？提示：锐角是第一象限角也是小于90°的角,而第一象限角可以是锐角，也可以大于360°，还可能是负角,小于90°的角可以是锐角,也可以是零角或负角．知识点三终边相同的角[填一填］所有与角α终边相同的角,连同角α在内，可构成一个集合S ＝｛β｜β＝α＋k·360°，k∈Z}，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．［答一答]5．终边相同的角相等吗？相等的角终边相同吗？提示：终边相同的角不一定相等，它们相差360°的整数倍；相等的角，终边相同．6．与－2 014°角终边相同的最小正角是146°。

专题1.2 二次函数的图象【六大题型】【浙教版】【题型1 二次函数的配方法】 (1)【题型2 二次函数的五点绘图法】 (4)【题型3 二次函数的图象与各系数之间的关系】 (9)【题型4 二次函数图象的平移变换】 (12)【题型5 二次函数图象的对称变换】 (14)【题型6 利用对称轴、顶点坐标公式求值】 (16)【题型1 二次函数的配方法】【例1】（2022秋•饶平县校级期末）用配方法将下列函数化成y＝a（x+h）2+k的形式，并指出抛物线的开口方向，对称轴和顶点坐标．（1）y=12x2﹣2x+3；（2）y＝（1﹣x）（1+2x）．【分析】（1）利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式；（2）化为一般式后，利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．【解答】解：（1）y=12x2﹣2x+3=12（x﹣2）2+1，开口向上，对称轴是直线x＝2，顶点坐标（2，1）；（2）y＝（1﹣x）（1+2x）＝﹣2x2+x+1＝﹣2（x―14）2+98，开口向下，对称轴是直线x=14，顶点坐标（14，98）．【变式1-1】（2022•西华县校级月考）用配方法确定下列二次函数图象的对称轴与顶点坐标．（1）y＝2x2﹣8x+7；（2）y＝﹣3x2﹣6x+7；（3）y＝2x2﹣12x+8；（4）y＝﹣3（x+3）（x﹣5）．【分析】（1）利用配方法表示解析式配成顶点式，然后根据二次函数的性质写出抛物线的对称轴、顶点坐标；（2）利用配方法表示解析式配成顶点式，然后根据二次函数的性质写出抛物线的对称轴、顶点坐标；（3）利用配方法表示解析式配成顶点式，然后根据二次函数的性质写出抛物线的对称轴、顶点坐标；（4）利用配方法表示解析式配成顶点式，然后根据二次函数的性质写出抛物线的对称轴、顶点坐标．【解答】解：（1）y＝2（x2﹣4x）+7＝2（x2﹣4x+4﹣4）+7＝2（x﹣2）2﹣1，对称轴为x＝2，顶点坐标为（2，﹣1）；（2）y＝﹣3（x2+2x）+7＝﹣3（x2+2x+1﹣1）+7＝﹣3（x+1）2+10，对称轴为x＝﹣1，顶点坐标为（﹣1，10）；（3）y＝2x2﹣12x+8＝2（x2﹣6x+9﹣9）+8＝2（x﹣3）2﹣10，对称轴为x＝3，顶点坐标为（3，﹣10）；（4）y＝﹣3（x+3）（x﹣5）＝﹣3（x2﹣2x﹣15）＝﹣3（x2﹣2x+1﹣1﹣15）＝﹣3（x﹣1）2+16 3，对称轴为x＝1，顶点坐标为（1，163）．【变式1-2】（2021•邵阳县月考）把下列二次函数化成顶点式，即y＝a（x+m）2+k的形式，并写出他们顶点坐标及最大值或最小值．（1）y＝﹣2x﹣3+1 2 x2（2）y＝﹣2x2﹣5x+7（3）y＝ax2+bx+c（a≠0）【分析】利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，可把一般式转化为顶点式，从而求出函数图象的顶点坐标及最值．【解答】解：（1）y＝﹣2x﹣3+1 2 x2=12（x2﹣4x+4）﹣2﹣3=12（x﹣2）2﹣5，顶点坐标是（2，﹣5），最小值是﹣5；（2）y＝﹣2x2﹣5x+7＝﹣2（x2+52x+2516）+258+7＝﹣2（x+54）2+818，顶点坐标是（―54，818），最大值是818；（3）y＝ax2+bx+c＝a（x2+bax+b24a2）―b24a+c＝a（x+b2a）2+4ac b24a，顶点坐标是（―b2a，4ac b24a），当a＜0时，最大值是4ac b24a；当a＞0时，最小值是4ac b24a．【变式1-3】（2022•监利市期末）用配方法可以解一元二次方程，还可以用它来解决很多问题例如：因为5a2≥0，所以5a2+1≥1，即：当a＝0时，5a2+1有最小值1．同样，因为﹣5（a2+1）≤0，所以﹣5（a2+1）+6≤6有最大值1，即当a＝1时，﹣5（a2+1）+6有最大值6．（1）当x＝　2　时，代数式﹣3（x﹣2）2+4有最　大　（填写大或小）值为　4　．（2）当x＝　2　时，代数式﹣x2+4x+4有最　大　（填写大或小）值为　8　．（3）矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是14m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少？【分析】（1）由完全平方式的最小值为0，得到x＝2时，代数式的最大值为4；（2）将代数式前两项提取﹣1，配方为完全平方式，根据完全平方式的最小值为0，即可得到代数式的最大值及此时x的值；（3）设垂直于墙的一边长为xm，根据总长度为14m，表示出平行于墙的一边为（14﹣2x）m，表示出花园的面积，整理后配方，利用完全平方式的最小值为0，即可得到面积的最大值及此时x的值．【解答】解：（1）∵（x﹣2）2≥0，∴当x＝2时，（x﹣2）2的最小值为0，则当x＝2时，代数式﹣3（x﹣2）2+4的最小值为4；（2）代数式﹣x2+4x+4＝﹣（x﹣2）2+8，则当x＝2时，代数式﹣x2+4x+4的最大值为8；（3）设垂直于墙的一边为xm，则平行于墙的一边为（14﹣2x）m，∴花园的面积为x（14﹣2x）＝﹣2x2+14x＝﹣2（x2﹣7x+494）+492=―2（x―72）2+492，则当边长为3.5米时，花园面积最大为492m2．故答案为：（1）2，大，4；（2）2，大，8；【题型2 二次函数的五点绘图法】【例2】（2022•东莞市模拟）已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如下表：x…01234…y…52125…（1）求该二次函数的表达式；（2）当x＝6时，求y的值；（3）在所给坐标系中画出该二次函数的图象．【分析】（1）由表格可知抛物线顶点坐标（2，1），设抛物线解析式为y＝a（x﹣2）2+1，利用待定系数法即可解决问题．（2）把x＝6代入（1）中的解析式即可．（3）利用描点法画出图象即可．【解答】解：（1）由表格可知抛物线顶点坐标（2，1），设抛物线解析式为y＝a（x﹣2）2+1，∵x＝0时，y＝5，∴5＝4a+1，∴a＝1，∴二次函数解析式为y＝（x﹣2）2+1即y＝x2﹣4x+5．（2）当x＝6时，y＝（6﹣2）2+1＝17．（3）函数图象如图所示，．【变式2-1】（2022•竞秀区一模）已知抛物线y＝x2﹣2x﹣3（1）求出该抛物线顶点坐标．（2）选取适当的数据填入表格，并在直角坐标系内描点画出该抛物线的图象．x……y……【分析】（1）直接利用配方法求出二次函数的顶点坐标即可；（2）利用描点法画出二次函数的图象．【解答】解：（1）y＝x2﹣2x﹣3＝（x﹣1）2﹣4，故该抛物线顶点坐标为：（1，﹣4）；（2）如图所示：x…﹣10123…y…0﹣3﹣4﹣30…．【变式2-2】已知二次函数y＝ax2﹣2的图象经过（﹣1，1）．（1）求出这个函数的表达式；（2）画出该函数的图象；（3）写出此函数的开口方向、顶点坐标、对称轴．【分析】（1）直接把（﹣1，1）代入y＝ax2﹣2中求出a的值即可得到抛物线解析式；（2）利用描点法画函数图象；（2）根据二次函数的性质求解．【解答】解：（1）把（﹣1，1）代入y＝ax2﹣2得a﹣2＝1，解得a＝3，所以抛物线解析式为y＝3x2﹣2；（2）如图：（3）抛物线的开口向上，顶点坐标为（0，﹣2），对称轴为y轴．【变式2-3】（2022•越秀区模拟如图，已知二次函数y=―12x2+bx+c的图象经过A（2，0）、B（0，﹣6）两点．（1）求这个二次函数的解析式；（2）求该二次函数图象的顶点坐标、对称轴以及二次函数图象与x 轴的另一个交点；（3）在右图的直角坐标系内描点画出该二次函数的图象及对称轴．【分析】（1）根据图象经过A （2，0）、B （0，﹣6）两点，把两点代入即可求出b 和c ，（2）把二次函数写成顶点坐标式，据此写出顶点坐标，对称轴等，（3）在坐标轴中画出图象即可．【解答】解：（1）∵的图象经过A （2，0）、B （0，﹣6）两点，∴―2+2b +c =0c =―6，解得b ＝4，c ＝﹣6，∴这个二次函数的解析式为y =―12x 2+4x ―6，（2）y =―12x 2+4x ―6=―12（x 2﹣8x +16）+8﹣6=―12（x ﹣4）2+2，∴二次函数图象的顶点坐标为（4，2）、对称轴为x ＝4、二次函数图象与x 轴相交时：0=―12（x ﹣4）2+2，解得：x ＝6或2，∴另一个交点为：（6，0），（3）作图如下．【题型3 二次函数的图象与各系数之间的关系】【例3】（2022春•玉山县月考）函数y＝ax2﹣a与y＝ax+a（a≠0）在同一坐标系中的图象可能是（ ）A．B．C．D．【分析】根据题目中的函数解析式、二次函数的性质和一次函数的性质，利用分类讨论的方法可以得到函数y＝ax2﹣a与y＝ax+a（a≠0）在同一坐标系中的图象可能是哪个选项中的图象．【解答】解：当a＞0时，函数y＝ax2﹣a的图象开口向上，顶点坐标为（0，﹣a），y＝ax+a（a≠0）的图象经过第一、二、三象限，故选项A、D错误；当a＜0时，函数y＝ax2﹣a的图象开口向下，顶点坐标为（0，﹣a），y＝ax+a（a≠0）的图象经过第二、三、四象限，故选项B错误，选项C正确；故选：C．【变式3-1】（2022•邵阳县模拟）二次函数y＝ax2+b的图象如图所示，则一次函数y＝ax+b的图象可能是（ ）A．B．C．D．【分析】直接利用二次函数图象得出a，b的符号，进而利用一次函数的图象性质得出答案．【解答】解：如图所示：抛物线开口向下，交y轴的正半轴，则a＜0，b＞0，故一次函数y＝ax+b的图象经过第一、二、四象限．故选：C．【变式3-2】（2022•凤翔县一模）一次函数y＝kx+k与二次函数y＝ax2的图象如图所示，那么二次函数y＝ax2﹣kx﹣k的图象可能为（ ）A．B．C．D．【分析】由二次函数y＝ax2的图象知：开口向上，a＞0，一次函数y＝kx+k图象可知k＞0，然后根据二次函数的性质即可得到结论．【解答】解：由二次函数y＝ax2的图象知：开口向上，a＞0，一次函数y＝kx+k图象可知k＞0，∴二次函数y＝ax2﹣kx﹣k的图象开口向上，对称轴x=―k2a在y轴的右侧，交y轴的负半轴，∴B选项正确，故选：B．【变式3-3】（2022•澄城县三模）已知m，n是常数，且n＜0，二次函数y＝mx2+nx+m2﹣4的图象是如图中三个图象之一，则m的值为（ ）A．2B．±2C．﹣3D．﹣2【分析】可根据函数的对称轴，以及当x＝0时，y的值来确定符合题意的函数式，进而确定m的值．【解答】解：∵y＝mx2+nx+m2﹣4，∴x=―n2m，因为n＜0，所以对称轴不可能是x＝0，所以第一个图不正确．二，三两个图都过原点，∴m2﹣4＝0，m＝±2．第二个图中m＞0，开口才能向上．对称轴为：x=―n2m＞0，所以m可以为2．第三个图，m＜0，开口才能向下，x=―n2m＜0，而从图上可看出对称轴大于0，从而m＝﹣2不符合题意．故选：A．【题型4 二次函数图象的平移变换】【例4】（2022•绍兴县模拟）把抛物线y＝ax2+bx+c的图象先向右平移2个单位，再向上平移2个单位，所得的图象的解析式是y＝（x﹣3）2+5，则a+b+c＝　3　．【分析】先得到抛物线y＝（x﹣3）2+5的顶点坐标为（3，5），通过点（3，5）先向左平移2个单位再向下平移2个单位得到点的坐标为（1，3），然后利用顶点式写出平移后的抛物线解析式，再把解析式化为一般式即可得到a、b和c的值．【解答】解：∵y＝（x﹣3）2+5，∴顶点坐标为（3，5），把点（3，5）先向左平移2个单位再向下平移2个单位得到点的坐标为（1，3），∴原抛物线解析式为y＝（x﹣1）2+3＝x2﹣2x+4，∴a＝1，b＝﹣2，c＝4．∴a+b+c＝3，故答案为3．【变式4-1】（2022•澄城县二模）要得到函数y＝﹣（x﹣2）2+3的图象，可以将函数y＝﹣（x﹣3）2的图象（ ）A．向右平移1个单位，再向上平移3个单位B．向右平移1个单位，再向下平移3个单位C．向左平移1个单位，再向上平移3个单位D．向左平移1个单位，再向下平移3个单位【分析】根据抛物线顶点的变换规律得到正确的选项．【解答】解：抛物线y＝﹣（x﹣3）2的顶点坐标是（3，0），抛物线y＝﹣（x﹣2）2+3的顶点坐标是（2，3），所以将顶点（3，0）向左平移1个单位，再向上平移3个单位得到顶点（2，3），即将函数y＝﹣（x﹣3）2的图象向左平移1个单位，再向上平移3个单位得到函数y＝﹣（x﹣2）2+3的图象．故选：C．【变式4-2】（2022秋•滨江区期末）将抛物线y＝ax2+bx﹣1向上平移3个单位长度后，经过点（﹣2，5），则4a﹣2b﹣1的值是　2　．【分析】根据二次函数的平移得出平移后的表达式，再将点（﹣2，5）代入，得到4a﹣2b＝3，最后整体代入求值即可．【解答】解：将抛物线y＝ax2+bx﹣1向上平移3个单位长度后，表达式为：y＝ax2+bx+2，∵经过点（﹣2，5），代入得：4a﹣2b＝3，则4a﹣2b﹣1＝3﹣1＝2．故答案为：2．【变式4-3】（2022•澄城县二模）二次函数y＝（x﹣1）（x﹣a）（a为常数）图象的对称轴为直线x＝2，将该二次函数的图象沿y轴向下平移k个单位，使其经过点（0，﹣1），则k的值为（ ）A．3B．4C．2D．6【分析】根据抛物线解析式得到抛物线与x轴的交点横坐标，结合抛物线的轴对称性质求得a的值，结合抛物线解析式求平移后图象所对应的二次函数的表达式，利用待定系数法求得k的值．【解答】解：由二次函数y＝（x﹣1）（x﹣a）（a为常数）知，该抛物线与x轴的交点坐标是（1，0）和（a，0）．∵对称轴为直线x＝2，∴1a2=2．解得a＝3．则该抛物线解析式是：y＝x2﹣4x+3．∴抛物线向下平移k个单位后经过（0，﹣1），∴﹣1＝3﹣k．∴k＝4．故选：B．【题型5 二次函数图象的对称变换】【例5】（2022•绍兴县模拟）在同一平面直角坐标系中，若抛物线y＝x2+（2a﹣b）x+b+1与y＝﹣x2+（a+b）x+a﹣4关于x轴对称，则a+b的值为（ ）A．﹣5B．3C．5D．15【分析】根据关于x轴对称，函数y是互为相反数即可求得．【解答】解：∵抛物线y＝x2+（2a﹣b）x+b+1与y＝﹣x2+（a+b）x+a﹣4关于x轴对称，∴﹣y＝﹣x2﹣（2a﹣b）x﹣b﹣1，∴―(2a―b)=a+b ―b―1=a―4，解得a＝0，b＝3，∴a+b＝3，故选：B．【变式5-1】（2022•苍溪县模拟）抛物线y＝﹣（x+2）2关于y轴对称的抛物线的表达式为　y＝﹣（x﹣2）2　．【分析】写出顶点关于y轴对称的点，把它作为所求抛物线的顶点，这样就可确定对称后抛物线的解析式．【解答】解：抛物线y＝﹣（x+2）2顶点坐标为（﹣2，0），其关于y轴对称的点的坐标为（2，0），∵两抛物线关于y轴对称时形状不变，∴抛物线y＝﹣（x+2）2关于y轴对称的抛物线的表达式为y＝﹣（x﹣2）2．故答案是：y＝﹣（x﹣2）2．【变式5-2】（2022•蜀山区校级二模）在平面直角坐标系中，将抛物线y＝x2+2x+3绕着原点旋转180°，所得抛物线的解析式是（ ）A．y＝﹣（x﹣1）2﹣2B．y＝﹣（x+1）2﹣2C．y＝﹣（x﹣1）2+2D．y＝﹣（x+1）2+2【分析】先利用配方法得到抛物线y＝x2+2x+3的顶点坐标为（﹣1，2），再写出点（﹣1，2）关于原点的对称点为（1，﹣2），由于旋转180°，抛物线开口相反，于是得到抛物线y＝x2+2x+3绕着原点旋转180°，所得抛物线的解析式是y＝﹣（x﹣1）2﹣2．【解答】解：y＝x2+2x+3＝（x+1）2+2，抛物线y＝x2+2x+3的顶点坐标为（﹣1，2），点（﹣1，2）关于原点的对称点为（1，﹣2），所以抛物线y＝x2+2x+3绕着原点旋转180°，所得抛物线的解析式是y＝﹣（x﹣1）2﹣2．故选：A．【变式5-3】（2022春•仓山区校级期末）在平面直角坐标系中，已知抛物线L1：y＝kx2+4kx+8（k≠0）与抛物线L2关于x轴对称，且它们的顶点相距8个单位长度，则k的值是（ ）A．﹣1或3B．1或﹣2C．1或3D．1或2【分析】先求出抛物线L1的顶点坐标，再根据顶点相距8个单位长度列方程即可解得答案．【解答】解：∵y＝kx2+4kx+8＝k（x+2）2+8﹣4k，∴抛物线L1：y＝kx2+4kx+8顶点为（﹣2，8﹣4k），∵抛物线L1：y＝kx2+4kx+8（k≠0）与抛物线L2关于x轴对称，它们的顶点相距8个单位长度，∴8﹣4k=82或8﹣4k=―82，解得k＝1或k＝3，故选：C．【题型6 利用对称轴、顶点坐标公式求值】【例6】（2022•苍溪县模拟）已知二次函数y＝（a﹣1）x2﹣x+a2﹣1图象经过原点，则a的取值为（ ）A．a＝±1B．a＝1C．a＝﹣1D．a＝0【分析】把（0，0）代入函数解析式求出a的值，再由a﹣1≠0求解．【解答】解：把（0，0）代入y＝（a﹣1）x2﹣x+a2﹣1得0＝a2﹣1，解得a＝1或a＝﹣1，∵a﹣1≠0，∴a＝﹣1，故选：C．【变式6-1】（2022•合肥模拟）如果抛物线y＝x2﹣6x+c﹣2的顶点到x轴的距离是4，则c的值等于　7或15　．【分析】根据抛物线y＝x2﹣6x+c﹣2的顶点到x轴的距离是4，可知顶点的纵坐标的绝对值是4，然后计算即可．【解答】解：∵抛物线y＝x2﹣6x+c﹣2的顶点到x轴的距离是4，∴|4×1×(c2)(6)24×1|＝4，解得c1＝7，c2＝15，故答案为：7或15．【变式6-2】（2022•襄城区模拟）已知二次函数y＝x2+bx+c的顶点在x轴上，点A（m﹣1，n）和点B （m+3，n）均在二次函数图象上，求n的值为　4　．【分析】根据题意得出b＝﹣2（m+1），c＝（m+1）2，即可得出y＝x2﹣2（m+1）x+（m+1）2，把A 的坐标代入即可求得n的值．【解答】解：∵点A（m﹣1，n）和点B（m+3，n）均在二次函数y＝x2+bx+c图象上，∴―b2=m1m32，∴b＝﹣2（m+1），∵二次函数y＝x2+bx+c的顶点在x轴上，∴b2﹣4c＝0，∴[﹣2（m +1）]2﹣4c ＝0，∴c ＝（m +1）2，∴y ＝x 2﹣2（m +1）x +（m +1）2，把A 的坐标代入得，n ＝（m ﹣1）2﹣2（m +1）（m ﹣1）+（m +1）2＝4，故答案为：4．【变式6-3】（2022•公安县期中）已知二次函数y ＝x 2+mx +m ﹣1，根据下列条件求m 的值．（1）图象的顶点在y 轴上．（2）图象的顶点在x 轴上．（3）二次函数的最小值是﹣1．【分析】（1）将二次函数配方成顶点式y ＝（x +m 2）2―m 24m 44，由图象的顶点在y 轴上可得―m 2=0，即m ＝0；（2）由图象的顶点在x 轴上可得m 24m 44=0，解之即可；（3）由二次函数的最小值是﹣1可得―m 24m 44=―1，解之即可．【解答】解：（1）y ＝x 2+mx +m ﹣1＝x 2+mx +m 24―m 24+m ﹣1＝（x +m 2）2―m 24m 44，∴抛物线的顶点坐标为（―m 2，―m 24m 44）∵图象的顶点在y 轴上，∴―m 2=0，即m ＝0；（2）∵图象的顶点在x 轴上，∴m 24m 44=0，解得m ＝2；（3）∵二次函数的最小值是﹣1，∴―m 24m 44=―1，解得：m ＝0或m ＝4．。