偏心荷载作用下刚性独立基础基底压力的简化计算

二、基底压力的简化计算（一）竖直中心荷载作用下当竖直荷载作用于基础中轴线时，基底压力呈均匀分布(图3-19)，其值按下式计算：对于矩形基础式中：p--基底压力(kPa)；P--作用于基础底面的竖直荷载(kN)；F--上部结构荷载设计值 (kN) ；G--基础自重设计值和基础台阶上回填土重力之和（kN），G=γ·A·D；γ--基础材料和回填土平均重度，一般取20kN/m3；A--基底面积 (m2 )；A=BL，B和L分别为矩形基础的宽度和长度 (m)；D--基础埋置深度 (m)。

对于条形基础，在长度方向上取1m计算，故有：式中：p--沿基础长度方向1m内相应的荷载值kN/m；其余意义同上。

（二）单向偏心荷载作用下矩形基础受偏心荷载作用时，基底压力可按材料力学偏心受压柱计算。

如果基础只受单向偏心荷载作用时，基底两端的压力为：式中：e--竖直荷载的偏心矩(m)；其余意义同上。

按式(3-16)计算，基底压力分布有下列三种情况：（1）当e<B/6时，p min为正值，基底压力为梯形分布(图3-20a)；（2）当e=B/6时，p min=0，基底压力按三角形分布(图3-20b)；（3）当e>B/6 时，p min为负值，表示基础底面与地基之间一部分出现拉应力。

但实际上，在地基土与基础之间不可能存在拉力，因此基础底面下的压力将重新分布(图3-20c)。

这时，可根据力的平衡原理确定基础底面的受压宽度和应力大小(图3-20c)，有基础受压宽度：基础底面最大应力：式中：K=B/2-e，符号意义同前。

若条形基础受偏心荷载作用，同样可取长度方向上的一延米进行计算，则基底宽度方向两端的压力为：基底压力的具体求解方法参见例题3-4。

【例题3-4】柱基础底面尺寸为1.2×1.0m2，作用在基础底面的偏心荷载F+G=150kN，如下图所示。

如果偏心距分别为0.1m、0.2m、0.3m。

地基承载力计算5.2.1 基础底面的压力，应符合下列规定：1. 当轴心荷载作用时p k≤ƒa (5.2.1-1)式中：p k——相应于作用的标准组合时，基础底面处的平均压力值(kPa)；ƒa——修正后的地基承载力特征值(kPa)。

2. 当偏心荷载作用时，除符合式(5.2.1-1)要求外，尚应符合下式规定：p kmax≤1.2ƒa (5.2.1-2)式中：p kmax——相应于作用的标准组合时，基础底面边缘的最大压力值(kPa)。

5.2.2 基础底面的压力，可按下列公式确定：1. 当轴心荷载作用时p k＝(F k＋G k)/A (5.2.2-1)式中：F k——相应于作用的标准组合时，上部结构传至基础顶面的竖向力值(kN)；G k——基础自重和基础上的土重(kN)；A——基础底面面积(m2)。

2. 当偏心荷载作用时p kmax＝[(F k＋G k)/A]＋(M k/W) (5. 2.2-2)p kmin＝[(F k＋G k)/A]－(M k/W) (5. 2.2-3)式中：M k——相应于作用的标准组合时，作用于基础底面的力矩值(kN·m)；W——基础底面的抵抗矩(m3)；p kmin——相应于作用的标准组合时,基础底面边缘的最小压力值(kPa)。

3. 当基础底面形状为矩形且偏心距e＞b/6时(图5.2.2)，p kmax应按下式计算：p kmax＝[2（F k＋G k)]/3la (5. 2.2-4)式中：l——垂直于力矩作用方向的基础底面边长(m)；a——合力作用点至基础底面最大压力边缘的距离(m)。

图5.2.2 偏心荷载(e＞b/6)下基底压力计算示意b-力矩作用方向基础底面边长5.2.3 地基承载力特征值可由载荷试验或其他原位测试、公式计算，并结合工程实践经验等方法综合确定。

5.2.4 当基础宽度大于3m或埋置深度大于0.5m时，从载荷试验或其他原位测试、经验值等方法确定的地基承载力特征值，尚应按下式修正：ƒa＝ƒak＋ηbγ(b－3)＋ηdγm(d－0.5) (5.2.4)式中：ƒa——修正后的地基承载力特征值(kPa)；ƒak——地基承载力特征值(kPa)，按本规范第5. 2.3条的原则确定；ηb、ηd——基础宽度和埋置深度的地基承载力修正系数，按基底下土的类别查表5.2.4取值；γ——基础底面以下土的重度(kN/m3)，地下水位以下取浮重度；b—基础底面宽度(m)，当基础底面宽度小于3m时按3m取值，大于6m时按6m取值；γm——基础底面以上土的加权平均重度(kN/m3)，位于地下水位以下的土层取有效重度；d——基础埋置深度(m)，宜自室外地面标高算起。

偏心荷载作用下刚性独立基础基底压力的简化计算偏心荷载指的是荷载的作用点与结构物的几何中心不重合，因此会产生偏心力。

当偏心荷载作用于刚性独立基础上时，会产生基底的压力。

本文将介绍偏心荷载作用下刚性独立基础基底压力的简化计算方法。

1.分析法刚性独立基础基底压力的计算通常会使用一些假设和简化方法。

其中最常用的方法是考虑独立基础的弹性模量，假设基底的应力分布近似为圆形，以及假设荷载作用下的基底应力分布为均匀。

基于上述假设，我们可以按照以下步骤进行刚性独立基础基底压力的简化计算：1.通过结构设计或分析得到作用在基础上的偏心荷载P和偏心距e。

2.计算基底的半径R：R=(P/σ）^0.5，其中σ为基底允许应力。

3.计算基底面积A：A=πR^24. 计算基底的平均应力σ_avg：σ_avg = P / A。

5. 计算基底的最大应力σ_max：σ_max = σ_avg × 1.5，一般约定为1.5倍基底平均应力。

6.检查计算结果是否符合结构设计和允许应力的要求。

以上是偏心荷载作用下刚性独立基础基底压力的简化计算方法，该方法适用于一些较为简单的情况。

在实际工程中，由于不同的结构和土壤条件的差异，可能会有其他的计算方法和公式。

因此，在进行具体计算时，应根据实际情况和相关规范指导进行计算。

2.试验法除了分析法，试验法也是一种常用的计算刚性独立基础基底压力的方法。

该方法通过在实际工程中进行模型试验，测量偏心荷载作用下基底的压力，从而得到准确的结果。

试验法的优点是可以考虑更多的影响因素，并且对真实工程有更好的适用性。

在试验法中，可以使用静力加载试验、动力加载试验等方法进行基底压力的测量。

然后根据实验结果，可以对刚性独立基础基底压力进行分析和计算。

综上所述，上述为偏心荷载作用下刚性独立基础基底压力的简化计算方法。

在实际工程中，应结合具体情况选择合适的计算方法，并注意考虑不同假设和简化方法的适用条件。

最后，为确保工程安全和合理性，应遵循相关规范和设计要求进行计算和验证。

偏心荷载作用下刚性独立基础基底压力的简化计算摘要：偏心荷载作用下，刚性独立基础的基底压力运用材料力学叠加法计算更加便于记忆。

关键词：偏心荷载刚性独立基础材料力学叠加法柱下钢筋混凝土独立基础（简称“柱下独立基础”）作为常见的一类扩展基础，在各种工业和民用建筑基础设计中得到广泛的应用[1]。

在现有的大量与基础工程有关的教材中[2，3，4，5]，刚性独立基础基底压力的计算都根据规范[6]中的公式列出。

现在基础工程[8]的基础上结合材料力学[7]叠加法对该方法进行改进。

一、叠加法的涵义在微小变形条件下，其弯矩与荷载成线性关系。

而在线弹性范围内，挠曲线的曲率与弯矩成正比，当挠度很小时，曲率与挠度间呈线性关系。

因而，梁的挠度和转角均与作用在梁上的荷载成线性关系。

在这种情况下，梁在几项荷载（如集中力、集中力偶或分布力）同时作用下该截面的挠度或转角的叠加。

次为叠加原理。

由几个外力共同作用下，引起的某一参数（内力、位移等）的变化等于每一外力单独作用时引起的该参数变化值的代数和的方法，称为叠加法。

二、叠加法的条件1、服从胡克定律[7]对于工程中常用的材料，如低碳钢、合金钢所制成的拉杆，由一系列实验证明：当杆内的应力不超过材料的某一极限值，即比例极限时，杆的伸长量与其所受外力、杆的原长成正比，而与其横截面面积成反比，即有，引进比例常数，则有，由于，故上式可写为。

此关系式称为胡克定律。

2、服从小变形假设[9]假定物体内各点在荷载作用下所产生的位移远小于物体原来的尺寸，因而应变分量和转角都远小于1.应用这一假设，可使问题大为简化。

例如，在研究物体受力平衡时，可以不考虑由于变形引起的物体尺寸和方位的变化，即按变形前的几何尺寸及荷载状态进行计算。

又如，在研究物体的变形和位移时，可以略去应变和转角的二次幂或二次乘积及其以上的项。

三、计算实例（一）基本资料：1.基底荷载：2.偏心矩：3.条形基础，基础宽，计算时取基础截面尺寸：（二）基底压力的叠加算法1.在基底荷载的作用下：基底受均布荷载作用，基底压力为：2.在偏心矩的作用下：弯曲截面系数：基础底面离中点最远处的基底压力：3.承载力叠加基础底面最小的基底压力为：基础底面最大的基底压力为：四、一般情况下承载力类型讨论当时：承载力为梯形荷载当时：承载力为三角形荷载当时：承载力一边出现负值的三角形荷载参考文献：[1]张卓然.浅谈柱下独立基础底板的抗弯计算.广东土木与建筑，2006[2]凌治平，易经武主编.基础工程.人民交通出版社，2008[3]莫海鸿，杨小平主编.基础工程.中国建筑工业出版社，2003[4]周景星，王洪瑾，虞石民，李广信主编.基础工程.清华大学出版社，2007[5]李亮，魏丽敏主编.基础工程.中南大学出版社，2005[6]《建筑地基基础设计规范GB50007-2002》[7]孙训方，方孝淑，关泰来主编.材料力学（I）第五版.高等教育出版社，2005[8]李亮，魏丽敏主编.基础工程.中南大学出版社，2009[9]王光钦主编.弹性力学.中国铁道出版社，2008年·北京。

土力学（西安交通大学）智慧树知到课后章节答案2023年下西安交通大学西安交通大学绪论单元测试1.通常把在土木工程建设中涉及岩石、土、地下水中的部分也称为岩土工程。

A:对 B:错答案:对2.下列哪些工程问题与岩土工程密切相关（）A:钢结构设计 B:公路路基 C:基坑开挖 D:浇筑楼层答案:公路路基;基坑开挖3.土力学是土木工程本科阶段的一门专业基础课，也是基础设施建设密切相关的学科的核心课程。

A:对 B:错答案:对4.土是由岩石风化后，经过剥蚀、自然力搬运，在新的环境下堆积或沉积下来的颗粒状松散物质。

A:对 B:错答案:对5.滑坡是与岩土工程有关的地质灾害。

A:错 B:对答案:对第一章测试1.土颗粒的大小及其级配，通常是用粒径级配曲线表示的，若某土样的粒径级配曲线越平缓，则说明( )A:土颗粒大小较均匀，级配不良 B:土颗粒大小不均匀，级配良好 C:土颗粒大小不均匀，级配不良 D:土颗粒大小较均匀，级配良好答案:土颗粒大小不均匀，级配良好2.通常同一土样的饱和重度γsat大于浮重度γ’A:对 B:错答案:对3.下列关于土的物理性质三相比例指标说法正确的是（）A:土的孔隙率是土中孔隙的体积占总体积的百分比 B:土的含水量是指土中水的质量与总质量的比值 C:土的孔隙比始终不会大于1 D:土的天然含水量、孔隙比是可以直接测定的基本指标答案:土的孔隙率是土中孔隙的体积占总体积的百分比4.通常砂土的结构属于（）A:蜂窝状结构 B:其余选项均可 C:絮凝状结构 D:单粒结构答案:单粒结构5.完全饱和土的孔隙体积等于水的体积。

A:对 B:错答案:对6.黏性土的塑性指数越大，说明土硬度越大。

A:错 B:对答案:错7.黏性土由半固态转入可塑态的界限为（）A:液性指数 B:塑限 C:液限 D:塑性指数答案:塑限8.通过土的击实试验可以测定土的最优含水量（）A:错 B:对答案:对第二章测试1.由于毛细凝聚力的存在，在海滨地区可以建造一些砂雕艺术品。

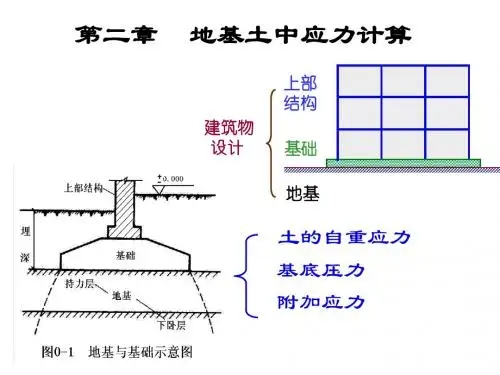
二、基底压力的简化计算（一）竖直中心荷载作用下当竖直荷载作用于基础中轴线时，基底压力呈均匀分布(图3-19)，其值按下式计算：对于矩形基础式中：p--基底压力(kPa)；P--作用于基础底面的竖直荷载(kN)；F--上部结构荷载设计值 (kN) ；G--基础自重设计值和基础台阶上回填土重力之和（kN），G=γ·A·D；γ--基础材料和回填土平均重度，一般取20kN/m3；A--基底面积 (m2 )；A=BL，B和L分别为矩形基础的宽度和长度 (m)；D--基础埋置深度 (m)。

对于条形基础，在长度方向上取1m计算，故有：式中：p--沿基础长度方向1m内相应的荷载值kN/m；其余意义同上。

（二）单向偏心荷载作用下矩形基础受偏心荷载作用时，基底压力可按材料力学偏心受压柱计算。

如果基础只受单向偏心荷载作用时，基底两端的压力为：式中：e--竖直荷载的偏心矩(m)；其余意义同上。

按式(3-16)计算，基底压力分布有下列三种情况：（1）当e<B/6时，p min为正值，基底压力为梯形分布(图3-20a)；（2）当e=B/6时，p min=0，基底压力按三角形分布(图3-20b)；（3）当e>B/6 时，p min为负值，表示基础底面与地基之间一部分出现拉应力。

但实际上，在地基土与基础之间不可能存在拉力，因此基础底面下的压力将重新分布(图3-20c)。

这时，可根据力的平衡原理确定基础底面的受压宽度和应力大小(图3-20c)，有基础受压宽度：基础底面最大应力：式中：K=B/2-e，符号意义同前。

若条形基础受偏心荷载作用，同样可取长度方向上的一延米进行计算，则基底宽度方向两端的压力为：基底压力的具体求解方法参见例题3-4。

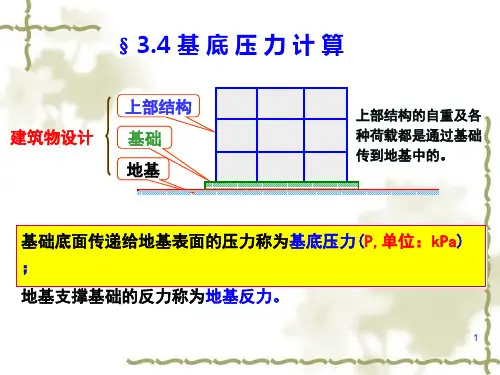
【例题3-4】柱基础底面尺寸为1.2×1.0m2，作用在基础底面的偏心荷载F+G=150kN，如下图所示。

如果偏心距分别为0.1m、0.2m、0.3m。

第一章1.土的组成：土是由固体颗粒及其颗粒间孔隙中的水和气体组成。

2.土的三相组成：固体颗粒,液态水,气体.3.粒组:工程上将土颗粒按其大小分为若干粒经范围,每一区段范围为一组。

4.粒径级配曲线陡表示粒径大小相差不多，土粒均匀；曲线缓表示粒径大小相差悬殊，土粒不均匀，称为土的级配良好。

5.C u称土的不均匀系数○1工程上把C u ≤5的土看成均粒土，属级配不良；C u>5时称为不均颗粒; C u>10的土级配良好○2当级配良好时, C u=1~3;因此当C u＜1或C u>3时,均表示级配线不连续，这种土一般认为是级配不良的土。

6.土的物理性指标可分两类：○1是必须通过试验测定的，如含水量,密度和土粒相对密度;○2是根据试验测定的指标换算的,如孔隙比,孔隙率和饱和度等。

7.砂土的松密程度还可以用土体相对密度来评价8.Dr=e max−ee max−emine max——最大孔隙比e min——最小孔隙比e——天然孔隙比9.砂土按土体相对密度分类：0＜D r≤0.33 疏松0.33＜D r≤0.66 中密0.66＜D r≤1 密实10.流态：含有大量自由水塑态：含水较固态为大，大量弱结合水和部分自由水固态：○1（半固体状）大量强结合水，部分弱结合水○2（固体状）强结合水11.黏性土的液性指数（相对稠度）：天然含水量与塑限的差值和液限与塑限差值之比，其大小能反映土的软硬程度I L=ω−ωP ωL−ωP注：ω——天然含水量；ωL——液限含水量ωP——塑限含水量12.塑性指数：I P=ωL−ωP13.塑性指数表示黏性土具有可塑性的含水量变化范围，塑性指数数值越大，意味着黏性土处于可塑态的含水量变化范围越大。

14.s t=q uq0S t——黏性土的灵敏度q u——原状土的无侧限抗压强度q0——与原状土密度，含水量相同，结构完全破坏的重塑土的无侧限抗压强度①灵敏度（St）反映黏性土结构性的强弱②灵敏度越高的土，其结构性越高，受扰动后土的强度降低就越多15.三相比例指标16.用质量63.5kg重锤，76cm落距自由下落，计入贯入器贯入土层30cm的锤击数，称为标准贯入数N63.5第二章（土的应力）1.基底压力的分布与基础的大小、刚度、形状、埋深、地基土的性质及作用在基础上荷载的大小和分布等因素有关2.基底压力的简化计算:中心荷载下的基底压力：P=F+GA（G=r G Ad; r G=20）偏心荷载下的基底压力：{Pmax=F+GA+MWPmin=F+GA−MW（将W=16b²l;e=MF+G带入）e<b/6(梯形分布)；e=b/6（三角形分布）；e>b/6（P min<0）3.基底附加压力：作用在基础面的压力与基础底面处原来的土中自重应力之差：P0=P-γ0d4、发生向上渗流时，孔隙水压力增加了r w△h有效应力减少了r w△h；向下渗流时，反之5、矩形荷载下的地基附加应力：n=lb ，m =zb（l为长边，b为短边，z为深度）第三章（土的压缩变形）1、室内侧线压缩试验（固结试验）（实验仪器：压缩仪）是研究土的压缩性的最基本方法2、由于金属环刀和刚性护环的限制，土样在压力作用下只可能发生竖向压缩，而无侧向变形3、压缩性指标（简答题）（1）压缩系数a=e1−e2p2−p1（曲线越陡，随着压力的增加，孔隙比的减小越显著，压缩性越高）（2）压缩指数Cc=（e1-e2）log P1P2（值越大压缩性越高）（3）压缩模量Es=σzεz =1+e1a（侧线压缩模量）（越小土的压缩性越高）4、测定土的压缩性指标，除从室内压缩试验测定外，还可以通过现场原位测试取得5、土的变形模量是指土体在无侧限条件下的应力与应变的比值，用E0表示6、沉降计算方法：弹性理论方法、分层法总和法、应力面积法7、单向压缩层总和法：此深度称为沉降计算深度Zn，按应力比法确定，即在沉降计算深度处，一般土σz=0.2σc;若该深度下有高压缩性土，应继续向下计算至σz=0.1σc深度处8、如果将其与目前土层所受的自重压力P1相比较，天然土层按其固结状态可分为正常固结土、超固结土和欠固结土第四章1.达西定律：是指水在土中的渗透速度与水头梯度成正比，即v=kI q=kIA式中v—渗透速度（m/s）I—水头梯度，即沿着水流方向单位长度上的水头差，a、b两点的水头梯度I=（H1-H2）/l k—渗透系数（m/s）q—渗透流量（m3/s）,即单位时间内流过面积A的水量。

2-8单元1-1、砂类土和粘性土各有那些典型的形成作用？ 【答】土在其形成过程中有各种风化作用共同参与，它们同时进行。

砂类土主要是由于温度变化、波浪冲击、地震引起的物理力使岩体崩解、破碎形成。

粘性土主要是岩体与空气、水和各种水溶液相互作用形成。

2-2、有一饱和的原状土样切满于容积为21.7cm 3的环刀内，称得总质量为72.49g ，经105℃烘干至恒重为61.28g ，已知环刀质量为32.54g ，土粒比重为2.74，试求该土样的湿密度、含水量、干密度及孔隙比（要求汇出土的三相比例示意图，按三相比例指标的定义求解）。

解：3/84.17.2154.3249.72cm g V m =-==ρ%3954.3228.6128.6149.72=--==S W m m ω 3/32.17.2154.3228.61cm g V m S d =-==ρ 069.149.1021.11===S V V V e 2-3、某原状土样的密度为1.85g/cm 3，含水量为34%，土粒相对密度为2.71，试求该土样的饱和密度、有效密度和有效重度（先推导公式然后求解）。

解：（1）VV m WV s sat ρρ⋅+=W S m m m += SW m m =ω 设1=S m ρω+=∴1VW S S S V m d ρ=WS W S S S d d m V ρρ⋅=⋅=∴1()()()()()()3W S S WS SW W satcm /87g .1171.20.341171.285.1d 11d 11d 111d 11111=+⨯+-⨯=++-=+++⎪⎪⎭⎫ ⎝⎛-=+-++=+⎪⎪⎭⎫ ⎝⎛⋅-++=∴ρωρωρωρωρρωρρωρρρωρW S d 有（2）()3'/87.0187.1cm g VV V V V V V m V V m W sat W V Ssat WV W V W S S W S S =-=-=+-=-+-=-=ρρρρρρρρρ （3）3''/7.81087.0cm kN g =⨯=⋅=ργ 或3'3/7.8107.18/7.181087.1cmkN cm kN g W sat sat sat =-=-==⨯=⋅=γγγργ2-4、某砂土土样的密度为1.77g/cm 3，含水量9.8%，土粒相对密度为2.67，烘干后测定最小孔隙比为0.461，最大孔隙比为0.943，试求孔隙比e 和相对密实度Dr ，并评定该砂土的密实度。

第一章：土的物理性质及工程分类（一）单项选择题1、一种土的容重γ、饱和容重sat γ、浮容重γ'和干容重d γ的大小顺序为。

A ．sat γ>γ'>d γ>γB ．γ>γ'>d γ>sat γC ．sat γ>γ>d γ>γ'D ．sat γ> d γ>γ>γ'2、土的三个基本物理指标为土的容重、土的含水量及 。

A ．孔隙比B ．饱和度C ．土粒比D ．孔隙度3、有一完全饱和土样切满环刀内，称得总重量为克，经105°C 烘干至恒温为克，已知环刀质量为克，土的相对密度为，其天然孔隙比为 。

A. B. C. D.4、某砂土试样的天然密度为3m t ，含水量为20%，土粒相对密度为，最大干密度为3m t ,最小干密度为3m t ，其相对密实度及密实程度为。

A.28.0=r D 松散状态B.35.0=r D 中密状态C.25.0=r D 松散状态D.68.0=r D 密实状态5、标准贯入试验时，使用的穿心锤重与穿心锤落距分别是 。

A. 锤重Kg 10，落距cm 50B. 锤重Kg 5.63，落距cm 76C ．锤重Kg 5.63，落距cm 50 D. 锤重Kg 10，落距cm 766、一般土中的粘粒含量越高，土的分散程度也越大，土中亲水矿物含量增加。

则 也相应增加。

A ．液限1ωB ．塑限p ωC ．液性指数1I D. 塑性指数p I7、土的三个基本物理指标为土的容重、土的含水量及 。

A ．孔隙比B ．饱和度C ．土粒比D ．孔隙度8、对饱和土的固结过程中的物理性质指标进行定性分析，液性指数减小，孔隙比 ，含水量 ，饱和度 ，土变 。

A ．增大B ．减小C ．不变D ．软E 。

硬9、 由某土的粒径级配曲线获得5.1260=d 、03.010=d ，则该土的不均匀系数为 。

A ． B. C. 3104.2-⨯ D.10、对无粘性土的工程性质影响最大的因素是 。

双向偏心受压矩形基础基底压力的计算摘要:受双向偏心荷载作用基础,当基础底面出现零应力区时,传统的设计方法难以计算其基底压力,本文给出了矩形基础底面出现零应力区时,基底压力的计算公式,编制了计算表格并应用于工程实际。

分析表明,采用新的允出现零应力区的设计方法,双向偏心受压基础的安全性和经济性均有较大提高。

关键词:矩形基础双向偏心竖向力基底压力1 引言在石油工程设计中,设备基础受力情况复杂,多为双向偏心受压(见图1),且常出现偏心距较大的情况。

设计时,按双向偏心荷载作用计算更为合理。

在现行的《建筑地基基础设计规范》GB50007-2002[1]中,并未给出双向偏心荷载作用下的基底压力值计算公式。

传统计算方法按不允许基底出现零应力区设计。

这种方法过于保守,因此准确计算出基础在双向偏心荷载作用下的基底压力具有实际价值。

2 基底不出现零应力区时基底压力的计算2.1计算假定1基础底面压力为平面分布基础底面压力为平面分布2基础底面与地基之间只能传递压力不可能传递拉力。

这样一来,就以零压力线为界,将基础底面划分为两个区域,零压力线以外部分为零压力区,该区域基础底面压力为零;另一部分为基础底面的压力区。

基础顶面上的竖向力F全部经由压力区传至地基。

3基础为矩形刚性基础,在受力过程中没有变形,基础满足抗弯、抗剪、抗冲切要求。

基底出现零应力区时,矩形基础基底压力的计算同样应符合上述假定。

2.2计算模型Ⅰ通常的计算方法根据基础底面压力为平面分布的基本假定,认为基底不出现拉力,基础全截面受压,基底应力如图2所示,公式如下:通过公式(1)可以求出基底最大压应力P1,最小压应力P3。

2.3适用条件使用上式计算基底应力时,必须满足计算得出的最小压力Pmin≥0的条件,即基础底面不能出现拉力。

此时偏心距满足:。

实际工程中,当作用在基础上的竖向力F较小,弯矩M较大时,偏心距往往大于上述计算要求,要想满足Pmin≥0的条件,势必要选用较大的基础底面。