计算电磁学

计算电磁学就业方向
计算电磁学是电磁学的一个分支，它应用电磁场理论和数学方法来解决电磁场问题。

在当今科技日新月异的时代，计算电磁学已经成为各个领域中不可或缺的一部分。

因此，计算电磁学也是一个广阔的就业方向。

一、电子行业
随着电子行业的发展，计算电磁学在电子行业中的应用越来越广泛。

比如，在芯片设计中，计算电磁学可以用来模拟和分析电磁场的分布，从而帮助设计师优化芯片性能。

另外，在电子产品的生产和测试中，计算电磁学也可以用来预测设备的电磁兼容性和电磁干扰，从而提高产品的质量和可靠性。

因此，在电子行业中，计算电磁学的就业前景非常良好。

二、通信行业
计算电磁学在通信行业中也有着广泛的应用。

比如，在无线通信系统中，计算电磁学可以用来模拟和分析信号传输的路径和衰减情况，从而优化通信系统的性能。

此外，在雷达和卫星通信系统中，计算电磁学也可以用来模拟和分析电磁波的传播和反射情况，从而帮助设计师提高系统的信号强度和覆盖范围。

因此，在通信行业中，掌握计算电磁学技能的人才非常有市场竞争力。

三、能源行业
在能源行业中，计算电磁学可以用来模拟和分析电磁场对电力设备的影响，从而预测电力设备的损耗情况和寿命。

此外，在电力系统
的设计和维护中，计算电磁学也可以用来优化电力设备的布局和参数设置，从而提高电力系统的效率和可靠性。

因此，在能源行业中，掌握计算电磁学技能的人才也非常受欢迎。

总之，计算电磁学是一个非常有前途的学科，在各个领域中都有广泛的应用。

因此，如果有志于从事科技研发和工程技术的人们，可以选择学习和掌握计算电磁学技能，以此来开拓自己的职业发展前景。

计算电磁学计算电磁学是指对一定物质和环境中的电磁场相互作用的建模过程，通常包括麦克斯韦方程计算上的有效近似。

计算电磁学被用来计算天线性能，电磁兼容，雷达散射截面和非自由空间的电波传播等问题。

计算电磁学的主要思想有，基于积分方程的方法，基于微分（差分）方程的方法，及其他模拟方法。

1.基于积分方程的方法1.1 离散偶极子近似（discrete dipole approximation，DDA） DDA是一种计算电磁波在任意几何形状物体上散射和吸收的方法，其表达式基于麦克斯韦方程的积分形式。

DDA用有限阵列的可极化点来近似连续形式的物体。

每个点通过对局部电场的响应获得对应的偶极子矩量，然后这些偶极子通过各自的电场相互作用。

因此，DDA 有时也被认为是耦合偶极子近似。

这种线性方程的计算一般采用共轭梯度迭代法。

由于离散矩阵的对称性，就可能在迭代中使用FFT计算矩阵的向量乘法。

1.2 矩量法（Method of Moments，MoM ），边界元法（Boundary Element Method，BEM ）MoM和BEM是求解积分形式（边界积分形式）的线性偏微分方程的数值计算方法，已被应用于如流体力学，声学，电磁学等诸多科技领域。

自从上世纪八十年代以来，该方法越来越流行。

由于只计算边界值，而不是方程定义的整个空间的数值，该方法是计算小表面（体积）问题的有效办法。

从概念上讲，它们在建模后的表面建立网格。

然而对于很多问题，此方法的效率较基于体积离散的方法（FEM，FDTD）低很多。

原因是，稠密矩阵的生成将意味着存储需求和计算时间会以矩阵维数的平方律增长。

相反的，有限元矩阵的存储需求和计算时间只会按维数的大小线性增长。

即使可以采用矩阵压缩技术加以改善，计算成功率和因此增加的计算复杂性仍强烈依赖问题的本质。

BEM可用在能计算出格林函数的场合，如在线性均匀媒质中的场。

为了能使用BEM，需要对问题有很多限制，使用上不方便。

电磁学：电磁学是研究电磁现象的规律和应用的物理学分支学科，起源于18世纪。

广义的电磁学可以说是包含电学和磁学，但狭义来说是一门探讨电性与磁性交互关系的学科。

主要研究电磁波、电磁场以及有关电荷、带电物体的动力学等等。

计算电磁学：《计算电磁学》是2002年03月科学出版社出版的图书，作者是王秉中。

内容简介：本书在论述计算电磁学的产生背景、现状和发展趋势的基础上，系统地介绍了电磁仿真中的有限差分法、人工神经网络在电磁建模中的应用，遗传算法在电磁优化中的应用等。

图书目录：第一章绪论1.1 计算电磁学的产生背景1.1.1 高性能计算技术1.1.2 计算电磁学的重要性1.1.3 计算电磁学的研究特点1.2 电磁场问题求解方法分类1.2.1 解析法1.2.2 数值法1.2.3 半解析数值法1.3 当前计算电磁学中的几种重要方法1.3.1 有限元法1.3.2 时域有限差分法1.3.3 矩量法1.4 电磁场工程专家系统1.4.1 复杂系统的电磁特性仿真1.4.2 面向CAD 的复杂系统电磁特性建模1.4.3 电磁场工程专家系统第一篇电磁仿真中的有限差分法第二章有限差分法2.1 差分运算的基本概念2.2 二维电磁场泊松方程的差分格式2.2.1 差分格式的建立2.2.2 不同介质分界面上边界条件的离散方法2.2.3 第一类边界条件的处理2.2.4 第二类和第三类边界条件的处理2.3 差分方程组的求解2.3.1 差分方程组的特性2.3.2 差分方程组的解法2.4 工程应用举例2.5 标量时域有限差分法2.5.1 瞬态场标量波动方程2.5.2 稳定性分析2.5.3 网格色散误差2.5.4 举例第三章时域有限差分法I——差分格式及解的稳定性3.1 FDTD 基本原理3.1.1 Yee 的差分算法3.1.2 环路积分解释3.2 解的稳定性及数值色散3.2.1 解的稳定条件3.2.2 数值色散3.3 非均匀网格及共形网格3.3.1 渐变非均匀网格3.3.2 局部细网格3.3.3 共形网格3.4 三角形网格及平面型广义Yee 网格3.4.1 三角形网格离散化3.4.2 数值解的稳定性3.4.3 平面型广义Yee 网格3.5 半解析数值模型3.5.1 细导线问题3.5.2 增强细槽缝公式3.5.3 小孔耦合问题3.5.4 薄层介质问题3.6 良导体中的差分格式第四章时域有限差分法Ⅱ——吸收边界条件4.1 Bayliss-Turkel 吸收边界条件4.1.1 球坐标系4.1.2 圆柱坐标系4.2 Engquist-Majda 吸收边界条件4.2.1 单向波方程的泰勒级数近似4.2.2 Mur 的差分格式4.2.3 Trefethen-Halpern 近似展开4.2.4 Higdon 算子4.3 廖氏吸收边界条件4.4 梅-方超吸收边界条件4.5 Berenger 完全匹配层（PML）4.5.1 PML 媒质的定义4.5.2 PML 媒质中平面波的传播4.5.3 PML-PML 媒质分界面处波的传播4.5.4 用于FDTD的PML4.5.5 三维情况下的PML4.5.6 PML 的参数选择4.5.7 减小反射误差的措施4.6 Gedney 完全匹配层4.6.1 完全匹配单轴媒质4.6.2 FDTD 差分格式4.6.3 交角区域的差分格式4.6.4 PML 的参数选取第五章时域有限差分法Ⅲ——若干实用技术5.1 激励源技术5.1.1 强迫激励源5.1.2 总场/散射场体系5.2 集总参数电路元件的模拟5.2.1 扩展FDTD方程5.2.2 集总参数电路元件举例5.3 近区场到远区场的变换5.4 数字信号处理技术5.4.1 极点展开模型与Prony算法5.4.2 线性及非线性信号预测器模型5.4.3 系统识别方法及数字滤波器模型5.5 应用举例5.5.1 均匀三线互连系统5.5.2 同轴线馈电天线5.5.3 多体问题5.5.4 同轴-波导转换器5.5.5 波导元件的高效分析5.5.6 传输线问题的降维处理第六章基于交变隐式差分方向方法的时域有限差分法——ADI-FDTD 方法6.1 ADI-FDTD 基本原理6.1.1 ADI-FDTD 差分格式I6.1.2 ADI-FDTD 差分格式Ⅱ6.2 解的稳定性与数值色散6.2.1 二维问题的稳定性6.2.2 三维问题的稳定性6.2.3 增长矩阵6.3 吸收边界条件6.3.1 Gedney的PML媒质中的ADI-FDTD格式6.3.2 Berenger的PML媒质中的ADI-FDTD格式6.4 应用举例6.4.1 有耗平行板传输线6.4.2 有耗平行板传输线——降维处理6.4.3 用混合网格二维FDTD算法分析传输线第二篇人工神经网络在电磁建模中的应用第七章人工神经网络模型7.1 生物神经元7.2 人工神经元模型7.2.1 单端口输入神经元7.2.2 活化函数7.2.3 多端口输入神经元7.3 多层感知器神经网络7.3.1 单层前传网络7.3.2 多层前传网络7.4 多层感知器的映射能力7.5 多样本输入并行处理第八章用回传算法训练多层感知器8.1 神经网络的学习能力8.1.1 受控学习方式8.1.2 误差校正算法8.2 误差回传算法8.2.1 初始化8.2.2 delta法则8.2.3 计算的两个过程8.3 训练模式8.4 回传算法的改进8.4.1 带矩量修正的广义delta法则8.4.2 学习速率参数自适应算法“指南”8.4.3 delta-delta 学习规则8.4.4 delta-bar-delta 学习规则8.4.5 Matlab 中的学习参数自适应算法8.5 将受控学习看做函数最优化问题8.5.1 共轭梯度法8.5.2 牛顿法8.5.3 Levenberg-Marquardt 近似8.6 网络推广8.6.1 训练集合大小的确定8.6.2 网络结构的优化第九章神经网络与电磁建模9.1 正交试验设计9.1.1 全组合正交试验设计9.1.2 方螺旋电感的神经网络模型9.1.3 微带协同馈电系统的神经网络模型9.1.4 带状线间隙不连续性的神经网络模型9.1.5 部分组合正交试验设计9.2 中心组合试验设计9.2.1 中心组合试验设计9.2.2 单层间互连结构的神经网络模型9.2.3 带状线双层间互连结构的神经网络模型9.2.4 同轴-波导转换器的神经网络模型9.3 随机组合试验设计9.3.1 高速互连结构的神经网络模型9.3.2 例子第十章知识人工神经网络模型10.1 外挂式知识人工神经网络模型10.1.1 差值模型和PKI 模型10.1.2 输入参数空间映射模型10.1.3 主要元素项分析10.1.4 稳健的知识人工神经网络模型10.2 嵌入式知识人工神经网络模型10.2.1 知识人工神经元10.2.2 知识人工神经元三层感知器10.2.3 应用实例第三篇遗传算法在电磁优化中的应用第十一章遗传算法基本原理11.1 基本的遗传算法11.1.1 基本遗传算法的描述11.1.2 应用遗传算法的准备工作11.1.3 遗传操作11.2 遗传算法的特点及数学机理11.2.1 遗传算法的特点11.2.2 遗传算法的数学机理第十二章遗传算法在电磁优化中的应用12.1 天线及天线阵的优化设计12.1.1 天线的优化设计12.1.2 微带天线的优化设计12.1.3 天线阵的优化设计12.2 平面型带状结构的优化设计12.2.1 稀疏化带状栅的优化设计12.2.2 带状电阻栅加载导体带的优化设计12.2.3 多层周期性导体带状栅的优化设计参考文献。

电磁学的数值计算方法电磁学是研究电场和磁场相互作用的学科，它在日常生活和科学研究中起着重要的作用。

随着计算机技术的快速发展，数值计算方法在电磁学中的应用也越来越广泛。

本文将介绍几种常用的电磁学数值计算方法，并探讨其原理和应用。

一、有限差分法（Finite Difference Method）有限差分法是一种基于离散化空间和时间的数值计算方法，常用于求解求解具有边值条件的偏微分方程。

在电磁学中，有限差分法可以用来求解电磁场的静电场、静磁场以及时变电磁场等问题。

该方法通过将空间和时间进行网格离散化，将偏微分方程转化为差分方程，并用迭代方法求解得到数值解。

二、有限元法（Finite Element Method）有限元法是一种广泛应用于各种物理问题求解的数值计算方法，电磁学也不例外。

该方法通过将求解区域划分为有限的小元素，并在局部内部逼近真实场量的变化。

在电磁学中，有限元法可以用来求解电场、磁场以及电磁波传播等问题。

通过选择合适的元素类型和插值函数，以及建立元素之间的边界条件，可以得到电磁场的数值解。

三、时域积分法（Time Domain Integral Method）时域积分法是一种基于格林函数的数值计算方法，通过积分形式表示电磁场的边界条件和过渡条件，进而求解电磁场。

时域积分法广泛应用于求解电磁波的辐射和散射问题，如天线辐射和散射、电磁波在介质中的传播等。

该方法通过离散化电磁场的源和观测点，并利用格林函数的性质进行数值积分，得到电磁场的数值解。

四、有限时域差分法（Finite-Difference Time-Domain Method）有限时域差分法是一种基于电磁场的离散化网格和时间的有限差分法，是求解各种电磁问题最常用的数值计算方法之一。

有限时域差分法通过离散化时空域，将麦克斯韦方程组转化为差分方程组，并通过时间步进的方式求解得到电磁场的数值解。

该方法适用于求解各种电磁波传播、辐射和散射等问题。

介绍计算电磁学基础知识及数值方法汇总计算电磁学是研究电磁场与电磁波的产生、传播和相互作用规律的一门学科。

它在现代科学和工程领域中具有广泛的应用，包括电子、通信、雷达、天气预报和医学成像等领域。

为了解决电磁学中的复杂问题，人们发展了许多数值方法来模拟和分析电磁场。

电磁学基础知识包括静电学、静磁学和电磁波学。

静电学研究静止电荷与电场之间的关系，电场的产生和性质。

其中包括库仑定律、高斯定律和电势等基本概念。

静磁学研究静止电流和磁场之间的关系，包括安培定律、毕奥-萨伐尔定律和洛伦兹定律等内容。

电磁波学研究电磁场的传播和相互作用，包括法拉第电磁感应定律、麦克斯韦方程组和电磁辐射等内容。

在研究和应用电磁学问题时，数值方法起到了重要的作用。

数值方法是指使用计算机计算和模拟电磁场的技术手段。

其中最常用的数值方法包括有限差分法（Finite Difference Method，FDM）、有限元法（Finite Element Method，FEM）和边界元法（Boundary Element Method，BEM）。

有限差分法是一种基于离散化方法的数值方法，它将电磁场方程中的微分方程转化为离散的代数方程。

通过在空间上取离散的点和在时间上取离散的时间步长，可以逐步求解方程组，得到电磁场的数值解。

有限差分法适用于各种电磁场问题，特别是在二维和三维空间中。

有限元法是一种将连续问题离散化为有限个简单子区域的数值方法。

它通过将电磁场区域划分为有限个单元，利用单元的形状函数和节点的数值解，近似求解电磁场方程。

有限元法可以处理任意形状的几何体，适用于复杂的电磁学问题。

边界元法是一种基于边界条件的数值方法。

它将电磁边界上的边界积分方程转化为离散的代数方程，通过求解边界上的电荷密度或矢量势，得到电磁场的数值解。

边界元法适用于边界形式简单的电磁问题，例如无限大平面和球面问题。

除了这些传统的数值方法，还有一些其他的数值方法被广泛应用于电磁学中，例如有限时域差分法（Finite Difference Time Domain，FDTD）和有限元时域法（Finite Element Time Domain，FETD）。

计算电磁学就业方向电磁学是物理学的一个重要分支，研究电荷、电流和电磁场之间的相互作用。

在现代科学和技术的发展中，电磁学扮演着重要的角色。

计算电磁学作为电磁学的一个分支，运用计算机技术来模拟和解析电磁现象，为现代科学技术的发展提供了强有力的支持。

在计算电磁学领域，有许多就业方向值得我们关注。

一、电磁场模拟与仿真工程师电磁场模拟与仿真工程师是计算电磁学领域中的重要岗位之一。

他们利用计算机软件，进行电磁场分析和模拟，为各个行业提供解决方案和技术支持。

比如，在电子工程领域，他们可以模拟电子器件的电磁场分布，优化电路设计，提高电子设备的性能。

在通信工程领域，他们可以模拟无线信号的传播特性，优化天线设计，提高通信系统的覆盖范围和传输质量。

在电力工程领域，他们可以模拟电力系统中的电磁场分布，评估电力设备的安全性和稳定性。

二、电磁兼容性工程师电磁兼容性工程师是计算电磁学领域中的另一个重要岗位。

他们主要负责评估和改善电子设备之间的电磁兼容性，确保各种设备能够在同一环境下正常工作，而不会相互干扰。

电磁兼容性工程师需要运用计算电磁学的方法，对设备的辐射和敏感性进行分析和模拟，通过优化设备的结构和电磁屏蔽措施，降低设备之间的电磁干扰。

三、电磁波传播和天线工程师电磁波传播和天线工程师是计算电磁学领域中的另一个重要岗位。

他们主要研究电磁波在不同介质中的传播特性，设计和优化天线系统，提高无线通信的覆盖范围和传输质量。

电磁波传播和天线工程师需要利用计算电磁学的方法，模拟和分析电磁波在不同环境中的传播路径和衰减情况，通过优化天线的结构和布局，提高天线的增益和方向性，提高通信系统的性能。

四、电磁辐射安全工程师电磁辐射安全工程师是计算电磁学领域中的另一个重要岗位。

他们主要负责评估和控制电磁辐射对人体健康的影响，设计和优化电磁辐射防护措施。

电磁辐射安全工程师需要利用计算电磁学的方法，模拟和分析电磁辐射的分布和强度，评估辐射对人体的影响，通过优化设备的结构和工作方式，减少电磁辐射对人体的影响。

各种计算电磁学方法比较和仿真软件计算电磁学方法是基于电磁理论和数值计算方法的电磁场分析方法，广泛应用于电磁设备的设计和分析中。

在电磁场计算中，常见的方法包括有限差分法(Finite Difference Method, FDM)、有限元法(Finite Element Method, FEM)、边界元法(Boundary Element Method, BEM)和时域积分方程法(Time Domain Integral Equation Method, TDIE)等，每种方法都有其特点和适用范围。

有限差分法是一种有限差商逼近的数值求解方法，将连续域中的偏微分方程转化为差分方程，然后通过离散化求解得到电磁场分布。

有限差分法具有简单、易于理解和实现的优点，适用于处理规则的几何体和均匀介质的场问题。

然而，当处理复杂几何体和非均匀介质问题时，有限差分法的计算效率较低。

有限元法是一种通过分割计算域为有限个简单形状单元，并在每个单元上采用多项式近似的方法。

有限元法可以较好地处理任意形状的几何体和非均匀介质问题，并且对于大型复杂结构也具有较好的可扩展性。

有限元法在电磁场计算中广泛应用，例如在电感、电容和波导等领域。

边界元法是一种基于位势-势流理论的计算方法，将电磁场分析问题转化为求解边界上的积分方程。

边界元法可以处理复杂几何边界的问题，并且相对于有限元法，边界元法中的待求解变量的数目较少，计算量较小。

边界元法在电磁场计算中常用于处理表面波和边界散射等问题。

时域积分方程法是一种基于麦克斯韦方程组的数值计算方法，通过将时间导数和空间导数分开进行求解，可以用来描述电磁波在时域中的传播。

时域积分方程法可以处理电磁散射、辐射和天线等问题，并且对于时间反演分析也具有优势。

除了上述传统的计算电磁学方法，现代仿真软件也广泛用于电磁场计算和设计。

一些常见的电磁场仿真软件包括Ansys、COMSOL Multiphysics、CST Microwave Studio、FEKO和HFSS等。

计算电磁学(1) 时域方法与谱域方法电磁学的数值计算方法可以分为时域方法(Time Domain或TD)和频域方法(Frequeney Domain或FD)两大类。

时域方法对Maxwell方程按时间步进后求解有关场量。

最著名的时域方法是时域有限差分法(Finite Difference Time Domain或FDTD)。

这种方法通常适用于求解在外界激励下场的瞬态变化过程。

若使用脉冲激励源，一次求解可以得到一个很宽频带范围内的响应。

时域方法具有可靠的精度，更快的计算速度，并能够真实地反应电磁现象的本质，特别是在诸如短脉冲雷达目标识别、时域测量、宽带无线电通讯等研究领域更是具有不可估量的作用。

频域方法是基于时谐微分、积分方程，通过对N个均匀频率采样值的傅立叶逆变换得到所需的脉冲响应，即研究时谐(Time Harmonic)激励条件下经过无限长时间后的稳态场分布的情况，使用这种方法，每次计算只能求得一个频率点上的响应。

过去这种方法被大量使用，多半是因为信号、雷达一般工作在窄带。

当要获取复杂结构时域超宽带响应时，如果采用频域方法，则需要在很大带宽内的不同频率点上的进行多次计算，然后利用傅立叶变换来获得时域响应数据，计算量较大；如果直接采用时域方法，则可以一次性获得时域超宽带响应数据，大大提高计算效率。

特别是时域方法还能直接处理非线性媒质和时变媒质问题，具有很大的优越性。

时域方法使电磁场的理论与计算从处理稳态问题发展到能够处理瞬态问题，使人们处理电磁现象的范围得到了极大的扩展。

频域方法可以分成基于射线的方法(Ray-based)和基于电流的方法(Current-based)。

前者包括几何光学法(GO)、几何绕射理论(GTD)和一致性绕射理论(UTD)等等。

后者主要包括矩量法(MoM)和物理光学法(PO)等等。

基于射线的方法通常用光的传播方式来近似电磁波的行为，考虑射向平面后的反射、经过边缘、尖劈和曲面后的绕射。

计算电磁学笔记电磁学是物理学的一个分支，研究电场和磁场的相互作用及其对物质的影响。

以下是一些电磁学中常用的计算公式和笔记：1. 库仑定律：两个点电荷间的电力与它们的电荷量和它们之间的距离成正比，与它们之间的相对位置无关。

公式为 F = k * (q1 * q2) / r^2，其中F为电力，k为电力常数，q1和q2为两个电荷的电荷量，r为它们之间的距离。

2. 电场强度：电场强度E指的是单位正电荷所受的电力的大小，公式为 E = F / q，其中E为电场强度，F为电力，q为单位正电荷的电荷量。

3. 电场的叠加：当有多个电荷体系同时存在时，它们产生的电场相互叠加。

可以使用叠加原理来计算总的电场强度。

4. 高斯定律：电场通过任何闭合曲面的总通量等于该闭合曲面包围的所有电荷的代数和的1/ε0（ε0为真空介电常数）。

公式为∮E·dA = Q_in / ε0，其中∮E·dA为电场E通过曲面的通量，Q_in为曲面内的电荷量。

5. 安培定律：通过一段闭合回路的磁场总通量等于该闭合回路内部的电流的代数和的μ0（μ0为真空磁导率）。

公式为∮B·ds = μ0 * I_in，其中∮B·ds为磁场B通过回路的通量，I_in为回路内的电流。

6. 洛伦兹力：电荷在电场和磁场中受到的合力称为洛伦兹力。

公式为 F = q * (E + v × B)，其中F为洛伦兹力，q为电荷量，E为电场强度，v为电荷的速度，B为磁场强度。

这些仅仅是电磁学中一些常用的计算公式和笔记，电磁学的内容非常广泛，涉及到电磁波、电磁感应、电磁场的变化等领域。

在学习电磁学时，还需要深入理解这些公式的推导和应用，以及与其他物理学分支的关联。

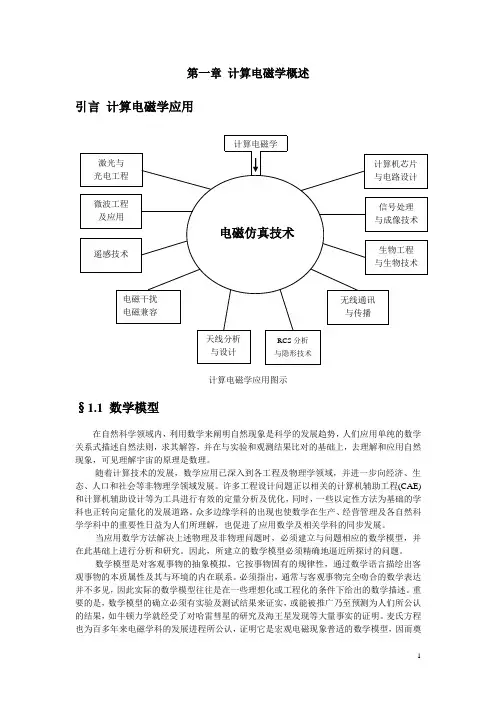
第一章计算电磁学概述引言计算电磁学应用计算电磁学应用图示§1.1 数学模型在自然科学领域内，利用数学来阐明自然现象是科学的发展趋势，人们应用单纯的数学关系式描述自然法则，求其解答，并在与实验和观测结果比对的基础上，去理解和应用自然现象，可见理解宇宙的原理是数理。

随着计算技术的发展，数学应用已深入到各工程及物理学领域，并进一步向经济、生态、人口和社会等非物理学领域发展。

许多工程设计问题正以相关的计算机辅助工程(CAE)和计算机辅助设计等为工具进行有效的定量分析及优化，同时，一些以定性方法为基础的学科也正转向定量化的发展道路。

众多边缘学科的出现也使数学在生产、经营管理及各自然科学学科中的重要性日益为人们所理解，也促进了应用数学及相关学科的同步发展。

当应用数学方法解决上述物理及非物理问题时，必须建立与问题相应的数学模型，并在此基础上进行分析和研究。

因此，所建立的数学模型必须精确地逼近所探讨的问题。

数学模型是对客观事物的抽象模拟，它按事物固有的规律性，通过数学语言描绘出客观事物的本质属性及其与环境的内在联系。

必须指出，通常与客观事物完全吻合的数学表达并不多见，因此实际的数学模型往往是在一些理想化或工程化的条件下给出的数学描述。

重要的是，数学模型的确立必须有实验及测试结果来证实，或能被推广乃至预测为人们所公认的结果，如牛顿力学就经受了对哈雷彗星的研究及海王星发现等大量事实的证明。

麦氏方程也为百多年来电磁学科的发展进程所公认，证明它是宏观电磁现象普适的数学模型，因而奠定了经典电磁理论的基础。

根据数学建模的方法分类，模型可分为微分方程模型、积分方程模型、优化模型和控制论模型等。

按实际问题中变量特征分类，数学模型又可分为确定性模型和随机模型，而由变化情况分类，则可分为连续型模型和离散型模型，此外，线性模型与非线性模型；静态模型与动态模型等这里就不一一赘述。

必须指出数学模型的分类并不具有特殊意义，但物理概念的引入要便于理解，模型的建立应有助于综合利用各种数学工具，从各个侧面分析出客观事物的本质。

计算电磁学就业方向
电磁学是物理学的一个重要分支，它研究电荷、电流和电场、磁场之间的相互作用关系，是现代科技领域中不可或缺的一部分。

计算电磁学是电磁学的一个分支，它主要研究电磁场的数值计算方法和模拟技术，广泛应用于电子工程、通信工程、电力系统、航空航天等领域。

那么，计算电磁学的就业方向有哪些呢
1. 电子工程
计算电磁学在电子工程中的应用非常广泛，例如在集成电路设计中，可以利用计算电磁学的方法对电路中的电磁干扰进行分析和优化，提高电路的性能和稳定性；在电磁兼容性设计中，可以利用计算电磁学的方法对电磁干扰和电磁辐射进行模拟和分析，从而设计出符合标准的电子产品。

2. 通信工程
计算电磁学在通信工程中的应用也非常广泛，例如在天线设计中，可以利用计算电磁学的方法对天线的辐射特性进行分析和优化，提高天线的性能和覆盖范围；在电磁波传播模拟中，可以利用计算电磁学的方法对电磁波在不同环境下的传播特性进行模拟和分析，从而优化通信系统的设计和部署。

3. 电力系统
计算电磁学在电力系统中的应用也非常广泛，例如在变压器设计中，可以利用计算电磁学的方法对变压器中的电磁场进行分析和优化，提高变压器的效率和稳定性；在输电线路设计中，可以利用计算电磁学的方法对输电线路中的电磁场进行分析和优化，提高输电线路的安全性和稳定性。

4. 航空航天
计算电磁学在航空航天领域中的应用也非常广泛，例如在飞机设计中，可以利用计算电磁学的方法对飞机中的电磁干扰进行分析和优化，提高飞机的性能和安全性；在卫星设计中，可以利用计算电磁学的方法对卫星中的电磁场进行分析和优化，提高卫星的通信和导航性能。

总之，计算电磁学的就业方向非常广泛，涉及到电子工程、通信工程、电力系统、航空航天等多个领域，具有广泛的应用前景和发展空间。

计算电磁学
计算电磁学是电磁学的实验和计算分支领域，在传统的电磁理论的基础上增加了计算的要求。

计算电磁学研究了电磁学中科学实验和算法对物理系统的影响，以提高精确性。

计算电磁学有着悠久的发展历史，这门学科着重研究电磁学中科学实验和算法，让精确度大大提高，在20世纪50年代中期迅速发展，在几乎所有电磁学和电子学领域都有应用，展示了它的强大性。

计算电磁学涉及到多个学科，包括电子学、计算机科学、物理学和数学。

电磁学的基本物理原理可以通过线性和非线性的数学方程描述，包括磁谱法、电子学理论、量子力学和拓扑学等。

它的基本方法包括离散有限元法（FEM）、谱元分析法（Spectral Element Method）、有限体系（Finite System）、混合有限元法（Mixed Finite Element Method）等。

这些方法被广泛应用于物理反弹实验、钳子形实验、电磁共振实验、量子力学理论模拟、电性质调控、电磁测量、通信系统、辐射安全和核电等领域。

研究工作主要集中在实验技术、算法和计算方法上，由于这些方法的优势，计算电磁学在数值计算上具有众多优势。

计算电磁学的发展受益于现代计算能力的不断提高，例如实验重构、可视化等技术，它们有助于把计算电磁学应用到实际问题中。

计算电磁学在工程实践中有着广泛的应用前景，同时也为探索电磁学的实验和理论相关性提供了更深入的研究机会。

因此，计算电磁学将继续成为一个具有挑战性的领域，并为未来的电磁学研究提供广阔的发展空间。

总之，计算电磁学是一门有趣且具有发展前景的学科。

正因为这门学科的重要性，计算电磁学的研究也会不断发展，在改变我们对现代电磁学的理解和实践方面发挥重要作用。

计算电磁学摘要：作为一门交叉学科，计算电磁学结合了计算机技术、数值计算学和电磁学等相关学科的知识，正经历着日新月异的发展。

各种各样的计算方法层出不穷，由此诞生的各种商业DEA软件如HFSS、CST、FECO、ADS等在工程领域中得到了广泛的应用，为解决各种复杂的工程问题提供了有力的帮助，极大地缩短了研究周期，降低了成本和提高了稳定性。

计算电磁学是指对一定物质和环境中的电磁场相互作用的建模过程，通常包括麦克斯韦方程计算上的有效近似。

计算电磁学被用来计算天线性能，电磁兼容，雷达散射截面和非自由空间的电波传播等问题。

计算电磁学的主要思想有，基于积分方程的方法，基于微分（差分）方程的方法，及其他模拟方法。

关键词：计算电磁学，麦克斯韦方程，雷达散射截面Computational ElectromagneticsAbstract: As an interdisciplinary, computational electromagnetics combines the knowledge of computer technology, numerical calculus and electromagnetics and other related disciplines, is experiencing the ever-changing development. A variety of computing methods emerge in an endless stream, the birth of a variety of commercial DEA software such as HFSS, CST, FECO, ADS, etc. in the field of engineering has been widely used to solve a variety of complex engineering problems provide a strong help , Greatly shortening the research cycle, reducing costs and improving stability. Computational electromagnetism is the modeling process for the interaction of electromagnetic fields in a given substance and environment, usually including the effective approximation of the Maxwell equation. Computational electromagnetism is used to calculate antenna performance, electromagnetic compatibility, radar cross section and non-free space radio propagation problems. The main ideas of computational electromagnetics are based on the integral equation method, the method based on differential (differential) equation, and other simulation methods.Key word: computational electromagnetics, Maxwell equation, radar cross section第一章引言1864年Maxwell在前人的理论（高斯定律、安培定律、法拉第定律和自由磁极不存在）和实验的基础上建立了统一的电磁场理论，并用数学模型揭示了自然界一切宏观电磁现象所遵循的普遍规律，这就是著名的Maxwell方程。

数学的计算电磁学在现代科学领域中，数学与电磁学的结合产生了一门强大而重要的学科，被称为计算电磁学。

计算电磁学通过数学模型和计算方法来研究电磁场的性质和行为，为我们理解和应用电磁现象提供了巨大的便利和深入的洞察力。

一、电磁学的基础知识在深入探讨计算电磁学之前，我们首先需要了解一些电磁学的基础知识。

电磁学研究电荷和电流之间相互作用的物理学分支，描述了电磁场的性质和行为。

其中，麦克斯韦方程组是电磁学的基石，通过这些方程，我们可以描述电荷和电流如何影响电磁场，并且由此推导出诸如电磁波、静电场和磁场等重要现象。

二、数学在电磁学中的应用数学在电磁学中扮演着至关重要的角色，通过数学工具和方法，我们可以对电磁现象进行精确的描述和计算。

在计算电磁学中，最常用的数学工具是矢量分析和偏微分方程。

1. 矢量分析矢量分析是研究矢量场的分析和计算方法。

在电磁学中，矢量场的描述是非常重要的，比如电场和磁场就是矢量场。

我们可以使用矢量分析的工具，如散度、旋度和梯度等来描述和计算电磁场的性质。

2. 偏微分方程偏微分方程是研究变量之间关系的方程，它们在描述电磁现象的数学模型中起着关键作用。

对于麦克斯韦方程组来说，它们本身就是一组偏微分方程，描述了电荷和电流如何产生电磁场，通过求解这些方程，我们可以得到有关电磁场的详细信息。

三、计算电磁学的应用领域计算电磁学广泛应用于不同的领域，下面将介绍其中的几个重要应用。

1. 电磁场仿真计算电磁学通过建立电磁场的数学模型，可以对电场和磁场进行仿真计算。

这对于研究电磁场的分布、传播和相互作用非常有用。

电磁场仿真在无线通信、电磁兼容性和天线设计等领域有着广泛的应用。

2. 电磁波传播计算电磁学可以帮助我们研究电磁波在不同介质中的传播行为。

通过计算和模拟，我们可以了解电磁波的传播路径、衰减程度和反射、折射现象等。

这对于无线通信、雷达系统和光纤通信等技术的设计和优化至关重要。

3. 电磁相互作用计算电磁学还可以帮助我们研究物体与电磁场的相互作用。

CEM（计算电磁学）是研发过程中最复杂的物理领域，比CFD和计算材料科学要难得多。

计算电磁学的复杂性主要表现在物理场的抽象，计算的大规模和众多的求解方法上，涉及大量的基础技术知识。

要求解的偏微分方程是麦克斯韦方程。

麦克斯韦根据以前的实验（例如Oster和Ferrari），通过数学推理获得了完整的方程组。

在方程的理论支持下，电磁学得到了迅速发展。

这些方程式完全描述了电，磁，材料，频率和时间之间的关系。

溶液电磁学可分为三类：分析方法，数值方法以及半分析和半数值方法。

（1）时域法和频谱域法电磁学的数值计算方法可以分为两类：时域或TD和频率域或FD。

迈入时间后，通过时域方法求解麦克斯韦方程。

最著名的时域方法是有限差分时域（FDTD）。

该方法通常适合解决外部激励下的瞬态过程。

如果使用脉冲激励源，则可以通过一次性解决方案获得较宽的频率响应。

时域方法具有可靠的准确性，更快的计算速度，并且可以真实地反映电磁现象的本质，特别是在短脉冲雷达目标识别，时域测量，宽带无线电通信等研究领域。

频域方法基于时间谐波微分方程和积分方程，通过对n个均匀频率样本进行傅立叶逆变换获得所需的脉冲响应，即研究时间谐波激励下无限时间后的稳态场分布。

使用这种方法，在每次计算中只能获得一个频率点的响应。

在过去，这种方法得到了广泛的应用，主要是因为信号和雷达通常在窄带中工作。

当要获得复杂结构的时域超宽带响应时，如果采用频域方法，则需要在大带宽内的不同频率点进行多次计算，然后使用傅立叶变换获得时间。

域响应数据，需要大量计算；如果直接使用时域方法，可以一次获取时域UWB响应数据，大大提高了计算效率。

特别地，时域方法可以直接处理非线性介质和时变介质的问题，具有很大的优势。

时域方法使电磁场的理论和计算从处理稳态问题发展到处理瞬态问题，大大扩展了处理电磁现象的范围。

频域方法可以分为基于射线的方法和基于电流的方法。

前者包括几何光学（GO），几何衍射理论（GTD），均匀衍射理论（UTD）等。

电磁学问题的计算方法及其应用电磁学是一门物理学科，主要研究电和磁的相互作用和规律。

在现代科技领域，电磁学的应用涉及到电信、嵌入式系统、无线通信、雷达、电子元器件等领域。

而对于电磁学问题的计算方法，下面将从两方面进行探讨。

一、计算方法1. 马克思威尔方程组马克思威尔方程组是电磁场的基础方程组。

它包括了电荷守恒方程、电场的高斯定理、磁场的安法定理和电磁感应定律。

利用这些方程，可以对电磁场进行完整的数学描述。

电荷守恒方程描述了电荷的守恒性质。

即电荷在任何时刻都会保持不变。

电场的高斯定理则是指出了电荷之间的相互作用，在物体表面遇到电场会受到压力的影响。

磁场的安法定理描述了磁场的传输和扩散。

最后，电磁感应定律描述了电场和磁场之间的相互影响。

2. 有限元法有限元法是近年来计算电磁问题的常规方法。

它的计算步骤主要分为几个步骤，即预处理、建模、求解、求解后处理和结果验证。

通过这些步骤，可以模拟电磁场在不同条件下的运行情况。

在实际应用中，有限元法主要用于电场、磁场和电磁波问题的计算。

应用有限元法可有效地避免一些电路设计中可能存在的问题，如电感和电容等元件的临界频率。

3. 有限差分法有限差分法是一种常见的电磁问题计算方法，它将电磁场的连续性转化为差分形式，并通过计算机进行离散化处理。

有限差分法的优势在于可以掌握计算的实时过程，方便进行迭代计算。

有限差分法可以直接用于计算静态电场、静态磁场和电磁波传播等问题。

但是当问题的计算规模越来越大时，有限差分法往往会变得相对耗时。

二、应用领域1. 电子器件设计电子器件设计需要考虑不同物理现象间的相互作用。

如电磁场、电流、电压等因素在电子器件设计中都会扮演重要的角色。

通过计算模拟这些物理现象，设计师可以大量节省实际制造时间、测试成本和成本。

电子器件设计领域中，经常会使用计算机辅助设计（CAD）软件，它能够以更快的速度和更高的准确性计算出电磁场分布和其它参数，并辅助进一步的优化电路设计。

计算电磁学摘要：作为一门交叉学科，计算电磁学结合了计算机技术、数值计算学和电磁学等相关学科的知识，正经历着日新月异的发展。

各种各样的计算方法层出不穷，由此诞生的各种商业DEA软件如HFSS、CST、FECO、ADS等在工程领域中得到了广泛的应用，为解决各种复杂的工程问题提供了有力的帮助，极大地缩短了研究周期，降低了成本和提高了稳定性。

计算电磁学是指对一定物质和环境中的电磁场相互作用的建模过程，通常包括麦克斯韦方程计算上的有效近似。

计算电磁学被用来计算天线性能，电磁兼容，雷达散射截面和非自由空间的电波传播等问题。

计算电磁学的主要思想有，基于积分方程的方法，基于微分（差分）方程的方法，及其他模拟方法。

关键词：计算电磁学，麦克斯韦方程，雷达散射截面Computational ElectromagneticsAbstract: As an interdisciplinary, computational electromagnetics combines the knowledge of computer technology, numerical calculus and electromagnetics and other related disciplines, is experiencing the ever-changing development. A variety of computing methods emerge in an endless stream, the birth of a variety of commercial DEA software such as HFSS, CST, FECO, ADS, etc. in the field of engineering has been widely used to solve a variety of complex engineering problems provide a strong help , Greatly shortening the research cycle, reducing costs and improving stability. Computational electromagnetism is the modeling process for the interaction of electromagnetic fields in a given substance and environment, usually including the effective approximation of the Maxwell equation. Computational electromagnetism is used to calculate antenna performance, electromagnetic compatibility, radar cross section and non-free space radio propagation problems. The main ideas of computational electromagnetics are based on the integral equation method, the method based on differential (differential) equation, and other simulation methods.Key word: computational electromagnetics, Maxwell equation, radar cross section第一章引言1864年Maxwell在前人的理论（高斯定律、安培定律、法拉第定律和自由磁极不存在）和实验的基础上建立了统一的电磁场理论，并用数学模型揭示了自然界一切宏观电磁现象所遵循的普遍规律，这就是著名的Maxwell方程。