“电路原理”第1-6章作业参考
- 格式:doc
- 大小:806.50 KB
- 文档页数:17

第一章 电路模型和电路定律电路理论主要研究电路中发生的电磁现象,用电流i 、电压u 和功率p 等物理量来描述其中的过程。
因为电路是由电路元件构成的,因而整个电路的表现如何既要看元件的联接方式,又要看每个元件的特性,这就决定了电路中各支路电流、电压要受到两种基本规律的约束,即:(1)电路元件性质的约束。
也称电路元件的伏安关系(VCR ),它仅与元件性质有关,与元件在电路中的联接方式无关。
(2)电路联接方式的约束(亦称拓扑约束)。
这种约束关系则与构成电路的元件性质无关。
基尔霍夫电流定律(KCL )和基尔霍夫电压定律(KVL )是概括这种约束关系的基本定律。
掌握电路的基本规律是分析电路的基础。
1-1 说明图(a ),(b )中,(1),u i 的参考方向是否关联(2)ui 乘积表示什么功率(3)如果在图(a )中0,0<>i u ;图(b )中0,0u i <>,元件实际发出还是吸收功率解:(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端,即电流的参考方向与元件两端电压降落的方向一致,称电压和电流的参考方向关联。
所以(a )图中i u ,的参考方向是关联的;(b )图中i u ,的参考方向为非关联。
(2)当取元件的i u ,参考方向为关联参考方向时,定义ui p =为元件吸收的功率;当取元件的i u ,参考方向为非关联时,定义ui p =为元件发出的功率。
所以(a )图中的ui 乘积表示元件吸收的功率;(b )图中的ui 乘积表示元件发出的功率。
(3)在电压、电流参考方向关联的条件下,带入i u ,数值,经计算,若0>=ui p ,表示元件确实吸收了功率;若0<p ,表示元件吸收负功率,实际是发出功率。
(a )图中,若0,0<>i u ,则0<=ui p ,表示元件实际发出功率。
在i u ,参考方向非关联的条件下,带入i u ,数值,经计算,若0>=ui p ,为正值,表示元件确实发出功率;若0<p ,为负值,表示元件发出负功率,实际是吸收功率。
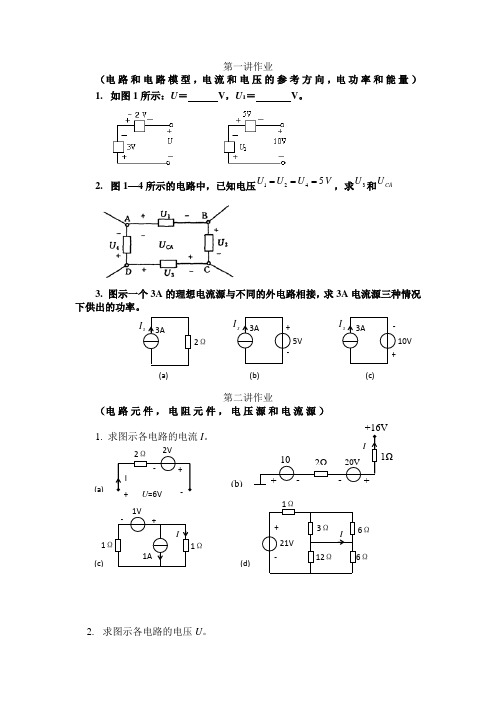
第一讲作业(电路和电路模型,电流和电压的参考方向,电功率和能量) 1. 如图1所示:U = V ,U 1= V 。
2. 图1—4所示的电路中,已知电压1245U U U V===,求3U 和CAU3. 图示一个3A 的理想电流源与不同的外电路相接,求3A 电流源三种情况第二讲作业(电路元件,电阻元件,电压源和电流源)I 。
2. 求图示各电路的电压U 。
3. 图示各电路,求:(1) 图(a)中电流源S I 产生功率S P 。
(2) 图(b)中电流源S U 产生功率S P第三讲作业(受控电源,电路基本定律(VAR 、K CL 、K VL ))1. 图示某电路的部分电路,各已知的电流及元件值已标出在图中,求I 、s U 、R 。
2. 图示电路中的电流I = ( )。
3. 图示含受控源电路,求:(1) 图(a)中电压u 。
(2) 图(b)中2Ω电阻上消耗的功率R P 。
第四讲作业(电路的等效变换,电阻的串联和并联,电阻的Y形联结和△形连结的等效变换)1.图示电路中的acb支路用图支路替代,而不会影响电路其他部分的电流和电压。
2.电路如图,电阻单位为Ω,则R ab=_________。
3. 求图示各电路中的电流I 。
第五讲作业(电压源和电流源的串联和并联,实际电源的两种模型及其等效变换,输入电阻)1. 求图示电路中的电流I 和电压U ab 。
2. 用等效变换求图示电路中的电流I 。
.3. 求图示各电路ab 端的等效电阻ab R 。
第三章作业3-1、某电路有n 结点,b 支路,其树枝数为 ,连枝数为 ,基本回路数为 ;独立的KCL 方程有 个,独立的KVL 方程有 个,独立的KCL 和KVL 方程数为 。
3-2、电路的图如图,以2、3、4为树枝,请写出其基本回路组。
3-3、电路如图,用支路电流法列方程。
3-4、电路见图,用网孔分析法求I 。
3-5、用网孔电流法(或回路电流法)求解图2电路中电流I及电压U 。

第一章电路模型和电路定律电路理论主要研究电路中发生的电磁现象,用电流、电压和功率等物理量来描述其中的过程。
因为电路是由电路元件构成的,因而整个电路的表现如何既要看元件的联接方式,又要看每个元件的特性,这就决定了电路中各支路电流、电压要受到两种基本规律的约束,即:(1)电路元件性质的约束。
也称电路元件的伏安关系(VCR),它仅与元件性质有关,与元件在电路中的联接方式无关。
(2)电路联接方式的约束(亦称拓扑约束)。
这种约束关系则与构成电路的元件性质无关。
基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)是概括这种约束关系的基本定律。
掌握电路的基本规律是分析电路的基础。
1-1说明图(a),(b)中,(1)的参考方向是否关联?(2)乘积表示什么功率?(3)如果在图(a)中;图(b)中,元件实际发出还是吸收功率?解:(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端,即电流的参考方向与元件两端电压降落的方向一致,称电压和电流的参考方向关联。
所以(a)图中的参考方向是关联的;(b)图中的参考方向为非关联。
(2)当取元件的参考方向为关联参考方向时,定义为元件吸收的功率;当取元件的参考方向为非关联时,定义为元件发出的功率。
所以(a)图中的乘积表示元件吸收的功率;(b)图中的乘积表示元件发出的功率。
(3)在电压、电流参考方向关联的条件下,带入数值,经计算,若,表示元件确实吸收了功率;若,表示元件吸收负功率,实际是发出功率。
(a)图中,若,则,表示元件实际发出功率。
在参考方向非关联的条件下,带入数值,经计算,若,为正值,表示元件确实发出功率;若,为负值,表示元件发出负功率,实际是吸收功率。
所以(b)图中当,有,表示元件实际发出功率。
1-2 若某元件端子上的电压和电流取关联参考方向,而,,求:(1)该元件吸收功率的最大值;(2)该元件发出功率的最大值。
解:(1)当时,,元件吸收功率;当时,元件吸收最大功率:(2)当时,,元件实际发出功率;当时,元件发出最大功率:1-3 试校核图中电路所得解答是否满足功率平衡。

第一章电路模型和电路定律电路理论主要研究电路中发生的电磁现象,用电流i、电压u和功率p等物理量来描述其中的过程。
因为电路是由电路元件构成的,因而整个电路的表现如何既要看元件的联接方式,又要看每个元件的特性,这就决定了电路中各支路电流、电压要受到两种基本规律的约束,即:(1)电路元件性质的约束。
也称电路元件的伏安关系(VCR),它仅与元件性质有关,与元件在电路中的联接方式无关。
(2)电路联接方式的约束(亦称拓扑约束)。
这种约束关系则与构成电路的元件性质无关。
基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)是概括这种约束关系的基本定律。
掌握电路的基本规律是分析电路的基础。
1-1说明图(a),(b)中,(1)u,i的参考方向是否关联?(2)ui乘积表示什么功率?(3)如果在图(a)中u0,i0;图(b)中u0,i0,元件实际发出还是吸收功率?解:(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端,即电流的参考方向与元件两端电压降落的方向一致,称电压和电流的参考方向关联。
所以(a)图中u,i的参考方向是关联的;(b)图中u,i的参考方向为非关联。
(2)当取元件的u,i 参考方向为关联参考方向时,定义pui为元件吸收的功率;当取元件的u,i参考方向为非关联时,定义p ui为元件发出的功率。
所以(a)图中的ui乘积表示元件吸收的功率;(b)图中的ui乘积表示元件发出的功率。
(3)在电压、电流参考方向关联的条件下,带入u,i数值,经计算,若p ui0,表示元件确实吸收了功率;若p0,表示元件吸收负功率,实际是发出功率。
(a)图中,若u0,i0,则p ui0,表示元件实际发出功率。
在u,i参考方向非关联的条件下,带入u,i数值,经计算,若pui0,为正值,表示元件确实发出功率;若p0,为负值,表示元件发出负功率,实际是吸收功率。
所以(b)图中当u0,i0,有pui0,表示元件实际发出功率。



电路理论教程希有答案第二版第一章本章的内容主要是运用电路理论,结合一些常见案例和公式进行讲解,希望能给同学们一些帮助。
本章涉及到以下哪些问题?对于数字电路的学习可以用到一元二次方程,其解析如下:A.用二极管串联一颗三极管作为调制器时,由单极或双极组成的一元二次方程。
B.电路元件中一个电阻为5Ω,两个引脚为1Ω和0Ω。
C.如果三极管的电压大于零,则表示电路的漏电电流大于零,因此两级串联电阻之和就等于零。
一、基本电路原理1.常见的三极管包括栅极电阻R4、栅极电压R5、栅极电流R6。
2.基本电路元件是三极管。
3.常见三极管的导通电阻R3、R4由二极管串联而成,分别连接两个两端,用于控制电路工作状态。
4.常见电路元件如图 b所示。
其中,栅极电阻R4是用来调节芯片通断电流,其值是R3值。
二、电路特性1.电路特性的描述(A.定义);2.电路的极性;3.串联电阻的影响;4.互补性;5.电路的特性方程(C.; D.);6.短路的判定。
三、公式说明1.原理分析:利用电阻的不同特性,可以计算出电路的电阻,但要考虑电阻的电流密度和损耗情况,因此一定要有准确的计算方法。
使用欧姆定律和电容定律来计算电阻两端与元件间的电阻电流:将电阻两端的电流设为零,可以得到两个等值电阻电容 F,两个等值电容 A之间产生的漏电电流也为零。
在一定数值下根据公式,可以计算出任意数量电阻的阻值,并根据计算结果选择电阻。
四、例题讲解例1:图中 V、V0分别为V1、C2两端的电压, v为三极管的漏电电流, E、 F分别为三极管开通时和关断时的电流。
说明图中V1和V0端分别有5Ω电阻和0Ω电阻,则图中 V、 V点上的电压分别应是()Ω?由题意可知: A与 B点组成负载输入,输出相同的电压,说明电路两个两端串联电阻之和即为()。
在电路中 C点上有2个负载电压; C、 F分别对应两个漏电电流,如图所示:解析: A点与 C点之间在电路中没有设置稳压或者稳流器,因此这一等效电路只能用来补偿输入端对输出端的漏电流,不能用来作为电源。

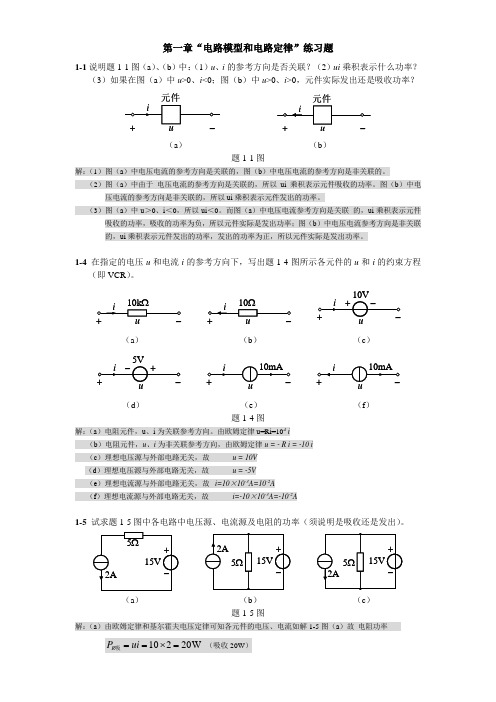
第一章“电路模型和电路定律”练习题1-1说明题1-1图(a )、(b )中:(1)u 、i 的参考方向是否关联?(2)ui 乘积表示什么功率?(3)如果在图(a )中u >0、i <0;图(b )中u >0、i >0,元件实际发出还是吸收功率?(a ) (b )题1-1图解:(1)图(a )中电压电流的参考方向是关联的,图(b )中电压电流的参考方向是非关联的。
(2)图(a )中由于 电压电流的参考方向是关联的,所以ui 乘积表示元件吸收的功率。
图(b )中电压电流的参考方向是非关联的,所以ui 乘积表示元件发出的功率。
(3)图(a )中u >0、i <0,所以ui <0。
而图(a )中电压电流参考方向是关联 的,ui 乘积表示元件吸收的功率,吸收的功率为负,所以元件实际是发出功率;图(b )中电压电流参考方向是非关联的,ui 乘积表示元件发出的功率,发出的功率为正,所以元件实际是发出功率。
1-4 在指定的电压u 和电流i 的参考方向下,写出题1-4图所示各元件的u 和i 的约束方程(即VCR )。
(a ) (b ) (c )(d ) (e ) (f )题1-4图解:(a )电阻元件,u 、i 为关联参考方向。
由欧姆定律u=Ri=104 i (b )电阻元件,u 、i 为非关联参考方向,由欧姆定律u = - R i = -10 i (c )理想电压源与外部电路无关,故 u = 10V (d )理想电压源与外部电路无关,故 u = -5V(e )理想电流源与外部电路无关,故 i=10×10-3A=10-2A(f )理想电流源与外部电路无关,故i=-10×10-3A=-10-2A1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a ) (b ) (c )题1-5图解:(a )由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1-5图(a )故 电阻功率10220WR P u i ==⨯=吸(吸收20W )电流源功率 I 5210WP ui ==⨯=吸(吸收10W ) 电压源功率U 15230WP ui ==⨯=发(发出30W )(b )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b )故 电阻功率12345WR P =⨯=吸(吸收45W ) 电流源功率 I 15230WP =⨯=发(发出30W ) 电压源功率U 15115WP =⨯=发(发出15W )(c )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(c )故 电阻功率15345WR P =⨯=吸(吸收45W )电流源功率 I 15230WP =⨯=吸(吸收30W ) 电压源功率U 15575WP =⨯=发(发出75W )1-16 电路如题1-16图所示,试求每个元件发出或吸收的功率。



电路原理课后答案电路原理是电子工程专业的一门重要课程,它涉及到电路的基本概念、分析方法和设计技术。
通过学习电路原理,我们可以掌握电路的基本工作原理,为日后的电子电路设计和实际应用打下坚实的基础。
下面是一些电路原理课后习题的答案,希望能够帮助大家更好地理解和掌握这门课程。
1. 电路原理中,最基本的电路元件是什么?答,最基本的电路元件是电阻、电容和电感。
2. 什么是欧姆定律?它的数学表达式是什么?答,欧姆定律是指在恒定温度下,电流与电压成正比,即I=U/R,其中I为电流,U为电压,R为电阻。
3. 什么是串联电路?并写出串联电路的等效电阻公式。
答,串联电路是指电路中的电阻依次连接在一起,电流依次通过每一个电阻。
串联电路的等效电阻公式为R=R1+R2+...+Rn。
4. 什么是并联电路?并写出并联电路的等效电阻公式。
答,并联电路是指电路中的电阻同时连接在一起,电流分别通过每一个电阻。
并联电路的等效电阻公式为1/R=1/R1+1/R2+...+1/Rn。
5. 什么是电压分压原理?并写出电压分压电路的计算公式。
答,电压分压原理是指在串联电路中,电压与电阻成正比,即U=IR。
电压分压电路的计算公式为U1=U(R1/(R1+R2)),U2=U(R2/(R1+R2))。
6. 什么是电流合流原理?并写出电流合流电路的计算公式。
答,电流合流原理是指在并联电路中,电流与电阻成反比,即I=U/R。
电流合流电路的计算公式为I=I1+I2。
通过以上习题的答案,我们可以更好地理解电路原理中的基本概念和计算方法。
希望大家能够通过认真学习和练习,掌握好这门课程,为将来的学习和工作打下坚实的基础。


第一章 电路模型和电路定律电路理论主要研究电路中发生的电磁现象,用电流i 、电压u 和功率p 等物理量来描述其中的过程。
因为电路是由电路元件构成的,因而整个电路的表现如何既要看元件的联接方式,又要看每个元件的特性,这就决定了电路中各支路电流、电压要受到两种基本规律的约束,即:(1)电路元件性质的约束。
也称电路元件的伏安关系(VCR ),它仅与元件性质有关,与元件在电路中的联接方式无关。
(2)电路联接方式的约束(亦称拓扑约束)。
这种约束关系则与构成电路的元件性质无关。
基尔霍夫电流定律(KCL )和基尔霍夫电压定律(KVL )是概括这种约束关系的基本定律。
掌握电路的基本规律是分析电路的基础。
1-1 说明图(a ),(b )中,(1),u i 的参考方向是否关联?(2)ui 乘积表示什么功率?(3)如果在图(a )中0,0<>i u ;图(b )中0,0u i <>,元件实际发出还是吸收功率?解:(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端,即电流的参考方向与元件两端电压降落的方向一致,称电压和电流的参考方向关联。
所以(a )图中i u ,的参考方向是关联的;(b )图中i u ,的参考方向为非关联。
(2)当取元件的i u ,参考方向为关联参考方向时,定义ui p =为元件吸收的功率;当取元件的i u ,参考方向为非关联时,定义ui p =为元件发出的功率。
所以(a )图中的ui 乘积表示元件吸收的功率;(b )图中的ui 乘积表示元件发出的功率。
(3)在电压、电流参考方向关联的条件下,带入i u ,数值,经计算,若0>=ui p ,表示元件确实吸收了功率;若0<p ,表示元件吸收负功率,实际是发出功率。
(a )图中,若0,0<>i u ,则0<=ui p ,表示元件实际发出功率。
在i u ,参考方向非关联的条件下,带入i u ,数值,经计算,若0>=ui p ,为正值,表示元件确实发出功率;若0<p ,为负值,表示元件发出负功率,实际是吸收功率。

《电工原理——(电工基础)》课程学习指导资料编写:舒朝君适用专业:电气工程及其自动化适用层次:专科(业余)四川大学网络教育学院2003年11月《电工基础》课程学习指导资料编写:舒朝君审稿(签字):审批(主管教学负责人签字):本课程学习指导资料根据该课程教学大纲的要求,参照现行采用教材《电工基础》(白乃平主编,西安电子科技大学出版社,2002年)以及课程学习光盘,并结合远程网络业余教育的教学特点和教学规律进行编写,适用于工科类专业专科学生。
第一部分课程的学习目的及总体要求一、课程的学习目的《电工基础》是高等工业学校专科电类专业必修的一门技术基础课程。
它的主要任务是为今后学习专业知识和从事工程技术工作打好电工技术的理论基础,并受到必要的基本技能的训练。
二、课程学习的总体要求本课程包括电路的基本概念与基本定律,直流电阻电路的分析方法,电感元件与电容元件,正弦交流电路,三相交流电路,负感电路,线性电路的过渡过程,磁路和铁心线圈电路。
电路部分学习重在基本概念、基本定律和基本方法的掌握,避免繁琐的公式推导和数学运算。
本课程先续课程是高等数学,大学物理,后续课程是模电、数电等。
第二部分课程学习的基本要求及重点难点内容分析第一章.电路的基本概念与基本定律1.1.电路和电路模型1.2.电路的基本物理量及其参考方向1.3.电功率和电能1.4.欧姆定律1.5.电压源和电流源1.6.基尔霍夫定律。
熟悉电路的工作状态、电路模型和额定值的意义;掌握电流、电压、电位及其参考方向;掌握电压源、电流源概念,电功率和电能的概念及计算。
熟悉掌握欧姆定律和基尔霍夫定律的应用计算。
本章的重点:电功率,电压源和电流源,基尔霍夫定律本章的难点:电流、电压、电位的参考方向,基尔霍夫定律的应用计算重点例题:例1。
1,例1。
4本章应要求学生完成的作业:1。
1;1。
4;1。
7;1。
8;1。
13重点题形:例:I1=5A,I2=3A,求I3=?.解:第二章.直流电阻电路的分析方法2.1.电阻串并联等效变换2.2.电阻的星形连接与三角形连接的等效变换2.3.两种电源的等效变换2.4.支路电流法2. 5. 网孔法2.6.节点电压法2.7.迭加原理2.8.戴维南定理2.9.受控电源介绍熟悉:节点电压法,电阻的星形连接与三角形连接的等效变换掌握:电路的基本分析方法熟悉掌握:迭加定理,支路电流法,戴维南定理,两种电源的等效变换方法。
第一章“电路模型和电路定律”练习题1-1说明题1-1图(a )、(b )中:(1)u 、i 的参考方向是否关联?(2)ui 乘积表示什么功率?(3)如果在图(a )中u >0、i <0;图(b )中u >0、i >0,元件实际发出还是吸收功率?元件(a ) (b )题1-1图答:(1)1-1图(a )中u 、i 在元件上为关联参考方向:1-1图(b )中u 、i 在元件上为非关联参考方向。
(2)1-1图(a )中P=ui 表示元件吸收的功率;1-1图(b )中P=ui 表示元件发出的功率。
(3)1-1图(a )中P=ui <0表示元件吸收负功率,实际发出功率:1-1图(b )中P=ui >0 元件实际发出功率。
1-4 在指定的电压u 和电流i 的参考方向下,写出题1-4图所示各元件的u 和i 的约束方程(即VCR )。
(a ) (b ) (c )(d ) (e ) (f )题1-4图答:1-4图(a )中u 、i 为非关联参考方向,u=10×103i 。
1-4图(b )中u 、i 为非关联参考方向,u=-10i 。
1-4图(c )中u 与电压源的激励电压方向相同u= 10V. 1-4图(d )中u 与电压源的激励电压方向相反u= -5V. 1-4图(e )中i 与电流源的激励电流方向相同i=10×10-3A 1-4图(f )中i 与电流源的激励电流方向相反i=-10×10-3A1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
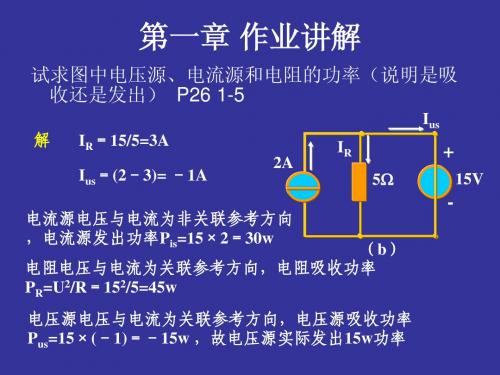
(a ) (b ) (c )题1-5图答:题1-5图(a)中流过15V电压源的2A电流与激励电压15V为非关联参考方向,因此,电压源发出功率P U发=15×2W=30W; 2A电流源的端电压为U A=(-5×2+15)V=5V, 此电压与激励电流为关联参考方向,因此,电流源吸收功率P I吸=5×2W=10W;电阻消耗功率P R=I2R=22×5W=20W电路中P U发=P I吸+P R功率平衡。
1-5图(b)中电压源中的电流I US=(2-5/15)A=-1A,其方向与激励电压关联,15V的电压源吸收功率P US吸=15×(-1A)=-15W电压源实际发出功率15W。
2A电流源两端的电压为15V,与激励电流2A为非关联参考方向,2A电流源发出功率P IS发=2×15=30W。
、电阻消耗功率P R=152/5=45W,电路中P US+P R=P IS发功率平衡。
1-5图(c)中电压源折中的电流I US=(2+15/5)A=5A方向与15V激励电压非关联,电压源发出功率P US发=5×15=75W。
电流源两端的电压为15V,与激励电流2A为关联参考方向,电流源吸收功率P IS吸=2×15=30W,电阻消耗功率P R=152/5=45W,电路中P US发=P IS吸+P R功率平衡。
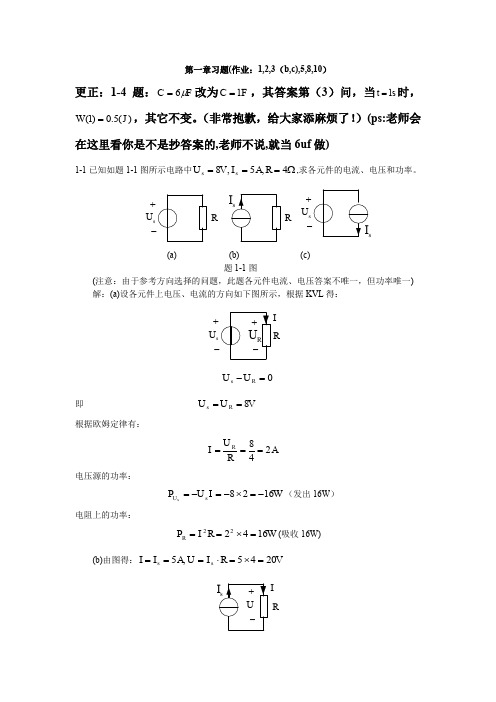
1-16 电路如题1-16图所示,试求每个元件发出或吸收的功率。
I1(a)(b)题1-16图答:题1-16图(a)中,应用KVL可得方程:-U+2×0.5+2U=0得U=-1V,电流源电压U与激励电流方向为非关联,因此电流源发出功率P IS发=-1×0.5=-0.5W(实际吸收功率)。
电阻功率P R=0.52×2=0.5W VCVS两端的电压2U与流入电流方向关联,故吸收功率P US吸=2U×0.5=-1W(实际发出功率)。
P IS发=P US吸+P R题1-16图(b)中,在结点A应用KCL可得:I2=I1+2I1-3I1再在左侧回路应用KVL可得:2I1+3I1=2得I1=0.4A根据各电流、电压方向的关联关系,可知,电压源发出功率为P US发=2I1=0.8WCCCS发出功率为P CS发=3I1×2I1=3×0.4×2×0.4=0.96W2Ω电阻消耗功率P R1=I12×2=0.32W2Ω电阻消耗功率P R2=(3I1)2×1=1.44WP US发+P CS发=P R1+P R21-20 试求题1-20图所示电路中控制量u1及电压u。
u1题1-20图答:先将电流i写为控制量u1的表达式,即i=(2-u1)/1×103再在回路中列写KVL 方程可得u 1=10×103×(2 -u 1)/1×103+10 u 得u 1=20V u=10 u 1=200V第二章“电阻电路的等效变换”练习题2-1电路如题2-1图所示,已知u S =100V ,R 1=2k Ω,R 2=8k Ω。
试求以下3种情况下的电压u 2和电流i 2、i 3:(1)R 3=8k Ω;(2)R 3=∞(R 3处开路);(3)R 3=0(R 3处短路)。
题2-1图答:答:(1)当R 3=8k Ω时,R 2// R 3=8×8/(8+8)=4 k Ω,因此u 2=4×103×100/(2×103+4×103)=66.67V i 2= i 3= u 2/8×103=8.333mA(2) 当R 3=∞时,按分压公式8×103×1×00V/(2×103+8×103)=80Vi 2 = u 2/ R 2=80/8×103A=10 mA i 3=0(3)当R 3=0时u 2=0,i 2,0得i 3=u S / R 1=100/2×103A=50 mA2-5用△—Y 等效变换法求题2-5图中a 、b 端的等效电阻:(1)将结点①、②、③之间的三个9Ω电阻构成的△形变换为Y 形;(2)将结点①、③、④与作为内部公共结点的②之间的三个9Ω电阻构成的Y 形变换为△形。
ab③题2-5图答:答:(1)变换后R ab =3+〔(3+9)×(3+3)〕/〔(3+9)+(3+3)〕=7Ω(2)连接成Y 型的3个9Ω电阻经变换成3个连接成△型的27Ω电阻。
变换后有: 1/(1/27+1/〔(9×27)/(9+27)+(3×27/(3+37)〕=7Ω2-11 利用电源的等效变换,求题2-11图所示电路的电流i 。
10V4Ω题2-11图答:将并联的电压源支路变换为等效电流源,串联的电流源支路变换为电压源,如图(a )所示,并联的各电流源合并为一个电流源后再变换为电压源。
二个电压源串联后成为图(b )(c)所示的等效电路。
从图(c)可得:I 1=2.5/(5+5)=0.25A 而i =0.5 I 1=0.125A2-13 题2-13图所示电路中431R R R ==,122R R =,CCVS 的电压11c 4i R u =,利用电源的等效变换求电压10u 。
u SR 4题2-13图答:将受控电压源支路变换为受控电流源如图所示可得:10u =(i 1+2 i 1)〔2R 1//(R 1+R 1)〕=3R 1 i 1 由KVL 可得:R 1 i 1=u S -10u 得 10u /3= u S -10u u S =0.75 uS2-14试求题2-14图(a )、(b )的输入电阻ab R 。
1(a ) (b )题2-14图答:(1)2-14图(a )中VCVS 的控制量u1=R 1i 1, i 即为流过受控源本身的电流,故VCVS可看为一个电阻,阻值-uR1,故从a 、b 端看如的电阻为: Rab=R2+(-uR1)+R1= R1(1-u)+ R2(2)2-14图(b )中可直接写出u a b 与i 1的关系为第三章“电阻电路的一般分析”练习题3-1 在以下两种情况下,画出题3-1图所示电路的图,并说明其结点数和支路数:(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
(a ) (b )题3-1图答:将每个元件作为一个支路时,题3-1图(a )、(b )分别如图(a1)、(b1)所示。
图(a1)中结点数n=6,支路数b=11; 图(b 1)中结点数n=7,支路数b=12(2)将电压源电阻串联组合、电流源电阻并联组合均分别看为一个支路时,题3-1图(a )、(b )分别如图(a2)、(b2)所示。
图(a2)中结点数n=4,支路数b=8;图(b 2)中结点数n=5,支路数b=93-2 指出题3-1中两种情况下,KCL 、KVL 独立方程各为多少? 答:题3-1图(a1)中,KCL 独立方程数为:n-1=6-1=5 KVL 独立方程数为:b- n+1=11-6+1=6题3-1图(b 1)中,KCL 独立方程数为:n-1=7-1=6 KVL 独立方程数为:b- n+1=12-7+1=6 题3-1图(a2)中,KCL 独立方程数为:n-1=4-1=3 KVL 独立方程数为:b- n+1=8-4+1=5 题3-1图(b 2)中,KCL 独立方程数为:n-1=5-1=4 KVL 独立方程数为:b- n+1=9-5+1=53-7题3-7图所示电路中Ω==1021R R ,Ω=43R ,Ω==854R R ,Ω=26R ,V 20S3=u ,V 40S6=u ,用支路电流法求解电流5i 。
u 题3-7图答:为减少变量数和方程数,将电压源和与其串联的电阻组合看为一个支路,本题中b=6,n=4。
3个独立回路和支路电流i1-i6的参考方向如图所示列出KCL 方程如:结点1 i1+i2+i6=0 结点2 i3+i4-i2=0 结点3 i5-i4-i6=0 列出KVL 方程,并代入元件参数值,可得:回路1: 2i6-8i4-10i2=-40 回路2: 10i2+4i3-10i1=-20 回路3:-4i3+8i4+8i5=40 着6个方程组成的联立方程可简化写为:可在MATLAB 上求解得5i=-0.956A 3-8 用网孔电流法求解题3-7图中电流5i 。
答:设网孔电流im1、im2、im3如题解3-8图所示,网孔方程为:20 im1-10 im2-8 im3=-40 -10 im1+24 im2-4im3=-20 -8im1-4im2+20 im3=20用克莱姆法则求解则3-11 用回路电流法求解题3-11图所示电路中电流I。
5V题3-11图答:题3-11图中有一个无伴电流源支路,选取回路电流时,使得仅有一个回路电流通过该无伴电流源,就可省略该回路的KVL方程,使计算量减少,现取题解3-11图所示的3个回路回路方程为:(5+5+30)I11+(5+5)I12-5I13=30(5+5+)I11+(5+5+20)I12-25I13=30-5I13=1整理后得到 40I11+10I12=35和10I11+30I12=50可得:I12=0.5A 即 I=0.5A3-12 用回路电流法求解题3-12图所示电路中电流a I 及电压o U 。