高中数学数形结合思想经典例题(含解析)
- 格式:doc
- 大小:530.01 KB
- 文档页数:16

高考数学运用数形结合的思想方法解题专项练习(含答案解析)一、单选题1.(2023春·江苏盐城·高三盐城中学校考)若直线():40l x m y +−=与曲线x =有两个交点,则实数m 的取值范围是( )A .0m <<B .0m ≤<C .0m <≤D .0m ≤【答案】B【解析】x =()0,0,半径为2的圆在y 轴以及右侧的部分,如图所示:直线():40l x m y +−=必过定点()0,4, 当直线l 与圆相切时,直线和圆恰有一个交点,2=,结合直线与半圆的相切可得m =当直l 的斜率不存在时,即0m =时,直线和曲线恰有两个交点, 所以要使直线和曲线有两个交点,则0m ≤故选:B.2.(2023春·湖北随州·高三随州市曾都区第一中学校考阶段练习)已知x ,y 是实数,且22410x y x +−+=,则21y x ++的最大值是( )A B .116C .336D 【答案】D【解析】方程可化为()223x y −+=,表示以()2,021y x ++的几何意义是圆上一点与点A ()1,2−−连线的斜率,设21k y x =++,即()21y k x +=+,当此直线与圆相切时,斜率最大或最小,当切线位于切线AB 时斜率最大.=k =,所以21y x ++故选:D .3.(2023春·陕西渭南·高一统考)已知函数()f x 是定义在R 上的偶函数,当[)0,x ∈+∞时,()24f x x x =−.若函数()()()R g x f x m m =+∈,则函数()g x 的零点个数不可能是( )A .1B .2C .3D .4【答案】A【解析】函数()f x 是定义在R 上的偶函数,当[)0,x ∈+∞时,()224(2)4f x x x x =−=−−,作出()f x 的图像如图:,故当0m =时,()()g x f x =有3个零点;当0m <或4m =时,()()g x f x m =+的图像与x 轴有两个交点,则函数有2个零点; 当04m <<时,()()g x f x m =+的图像与x 轴有4个交点,则函数有4个零点;由于()()g x f x m =+也为偶函数,结合()f x 图像可知,()()g x f x m =+不可能有1个零点, 故选:A4.(2023春·陕西西安·高三统考期末)已知函数()e ,03,0x x f x x x ⎧≥=⎨−<⎩, 若函数()()()g x f x f x =−−,则函数()g x 的零点个数为( ) A .1 B .3 C .4 D .5【答案】D【解析】当0x >时,0x −<,()3f x x −=当0x <时,0x −>,()e xf x −−=()()()3e ,00,0e 3,0x x x x g x f x f x x x x −⎧−>⎪∴=−−==⎨⎪+<⎩,()()()()g x f x f x g x −=−−=−,且定义域为R ,关于原点对称,故()g x 为奇函数,所以我们求出0x >时零点个数即可,(0,)3e x g x x x =−>,()3e 0x g x '=−>,令()3e 0x g x '=−>,解得0ln3x <<,故()g x 在()0,ln 3上单调递增,在(ln3,)+∞单调递减,且(ln3)3ln330g =−>,而()226e 0g =−<,故()g x 在(ln 3,2)有1零点,1311e 03g ⎛⎫=−< ⎪⎝⎭,故()g x 在1(,ln 3)3上有1零点,图像大致如图所示:故()g x 在()0,∞+上有2个零点,又因为其为奇函数,则其在(),0∞−上也有2个零点,且()00g =,故()g x 共5个零点, 故选:D.5.(2023春·黑龙江哈尔滨·高一哈尔滨三中校考阶段练习)若函数()f x 的定义域为(),1f x −R 为偶函数,当1x ≥−时,()31xf x −=−,则函数()()12g x f x =−的零点个数为( )A .0B .1C .2D .4【答案】D【解析】令310x −−≥解得0x ≤,令310x −−<解得0x >, 所以当1x ≥−时,()11,1033111,03xxxx f x x −⎧⎛⎫−−≤≤⎪ ⎪⎪⎝⎭=−=⎨⎛⎫⎪−+> ⎪⎪⎝⎭⎩, ()1f x −为偶函数,所以()1f x −的图像关于y 轴对称,所以()f x 的图像关于直线=1x −轴对称, 故作出()f x 的图像如下,令()()102g x f x =−=,即()12f x =, 由图像可知,()f x 的图像与12y =的图像共有四个交点, 所以函数()()12g x f x =−的零点个数为4个.故选:D.6.(2023·山东潍坊·统考模拟预测)已知函数()f x 是定义域为R 的偶函数,且(1)f x −是奇函数,当01x 剟时,有()f x =()(2021)y f x k x =−−的零点个数为5,则实数k 取值范围是( ) A .15<2<1kB .16<3<1kC k k =D .k <k 【答案】C【解析】∵偶函数()f x ,()()f x f x ∴−=,(1)f x −是奇函数,得(1)(1)f x f x −=−−−,即 ()(2)f x f x =−−−,(2)()f x f x −−−=−,得4T =,()(2021)0f x k x −−=,即()y f x =与(2021)y k x =−的图像交点的个数,因为4T =,即为()y f x =与(1)y k x =−的图像交点的个数,因为()f x =k 应该在1k 与2k 之间或为3k ,213k k k ==k k =故选:C.7.(2023·全国·高三专题练习)已知函数()()ln2,01ln 2ln 2,12xx f x x x ⎧<<⎪=⎨−+≤<⎪⎩,若存在02a b c <<<<使得()()()f a f b f c ==,则111ab bc ca++的取值范围是( ) A .20,93⎛⎫⎪⎝⎭B .20,3⎛⎫+∞ ⎪⎝⎭C .∞⎫+⎪⎪⎣⎭ D .⎫⎪⎪⎣⎭【答案】A【解析】∵()()ln 2ln2ln 22x x ⎡⎤−+=−⎣⎦,∴ln 2y x =与()ln 2ln2y x =−+的图像关于直线1x =对称,作出()f x 的大致图像如图所示,易知2b c +=,由ln2ln2a b =,即ln 2ln 2a b −=,ln 40ab =,得14ab =, ∵112b <<,∴11124a<<,得1142a <<,∴()()421621112181244a a a a b c a c ab bc ca abc a a+++++++====−−. 设81t a =−, 则()1,3t ∈,111117184t ab bc ca t ⎛⎫++=++ ⎪⎝⎭. 17t t+≥=t 故当()1,3t ∈时,令()1718h t t t +=+,()h t 单减,()()80136,33h h ==, 故1172018,943t t ⎛⎫⎛⎫++∈ ⎪ ⎪⎝⎭⎝⎭. 故选:A 二、多选题8.(2023·全国·高三专题练习)已知1F ,2F 是双曲线()2222:10,0x yE a b a b−=>>的左、右焦点,过1F 作倾斜角为30的直线分别交y 轴与双曲线右支于点,M P ,1PM MF =,下列判断正确的是( )A .2160PF F ∠=,B .2112MF PF =C .ED .E的渐近线方程为y =【答案】BCD【解析】如下图所示,因为1PM MF =,即M 为1PF 中点,O 为12F F 中点,所以2//OM PF ,因为12OM F F ⊥,所以212PF F F ⊥,所以212PF F π∠=,2112MF PF =,A 错误,B 正确; 由212PF F F ⊥知:22b PF a=,又122F F c =,1230PF F ∠=,2c =)222c a ac −=220e −,解得:e =C 正确;所以==c e a 223c a =,所以22222b c a a =−=,所以ba= 所以E 的渐近线方程为y =,D 正确.故选:BCD .9.(2023·全国·高三专题练习)已知直线l 过抛物线2:8C y x =的焦点F l 与抛物线交于,P Q 两点(P 在第一象限),以,PF QF 为直径的圆分别与y 轴相切于,A B 两点,则下列结论正确的是( ) A .32||3PQ =B .AB =C .若M 为抛物线C 上的动点,(2,1)N ,则min (||||)4MF MN +=D .若0(,M x 为抛物线C 上的点,则9MF = 【答案】ABC【解析】设直线PQ 的方程为:y x ﹣2),与28y x =联立整理可得:3x 2﹣20x +12=0,解得:x 23=或6,则P (6,,Q (23,;所以|PQ |=623++4323=,选项A 正确;因为F (2,0),所以PF ,QF 的中点分别为:(4,,(43,,所以A (0,,B (0,,所以|AB =, 选项B 正确;如图M 在抛物线上,ME 垂直于准线交于E ,可得|MF |=|ME |, 所以|MF |+|MN |=|ME |+|MN |≥NE =2+2=4,当N ,M ,E 三点共线时, |MF |+|MN |最小,且最小值为4,选项C 正确;对于选项D ,若0(M x 为抛物线C 上的点,则05x =,又4p =, 所以072pMF x =+=,选项D 错误. 故选:ABC.10.(2023春·河南·高三校联考)在三棱锥A BCD −中,平面ABD ⊥平面BCD ,BD CD ⊥,2BD CD ==,ABD △为等边三角形,E 是棱AC 的中点,F 是棱AD 上一点,若异面直线DE与BF AF 的值可能为( ) A .23B .1C .43D .53【答案】AC【解析】由ABD △为等边三角形,取BD 的中点O ,连接AO ,则AO BD ⊥ 又平面ABD ⊥平面BCD ,且平面ABD ⋂平面BCD BD = 所以AO ⊥平面BCD ,由BD CD ⊥过O 作与CD 平行的直线为y 轴,分别以,OB OA 为,x z 轴建立如图所示的空间直角坐标系,因为2BD CD ==,则()1,0,0B ,()()(1,0,0,1,2,0,D C A −−,所以12E ⎛− ⎝⎭.设()F a ,则12DE ⎛= ⎝⎭,()BF a =−,则28=13a =−或23a =−, 故1233AF AD ==或2433AF AD ==.故选:AC11.(2023秋·福建三明·高一福建省宁化第一中学校考阶段练习)已知G 为ABC 的重心,60BAC ∠=︒,2AB AC ⋅=,则||AG uuu r的可能取值为( )A .23B .1CD .32【答案】CD【解析】如图,G 是ABC 的重心,记,,AB c AC b AB a ===, 则2211()()3323AG AD AB AC AB AC ==⨯+=+, 222222111()(2)(4)999AG AB AC AB AB AC AC b c =+=+⋅+=++,又1cos6022AB AC bc bc ⋅=︒==,即4bc =,所以2228b c bc +≥=,当且仅当2b c ==时等号成立,所以214(84)93AG ≥⨯+=.即233AG ≥CD 满足. 故选:CD .12.(2023春·湖北黄冈·高三校考开学考试)已知ABC 的重心为G ,过G 点的直线与边AB ,AC 的交点分别为M ,N ,若AM MB λ=,且AMN 与ABC 的面积之比为920,则λ的可能取值为( )A .43B .32C .53D .3【答案】BD【解析】如图,()AM MB AB AM λλ==−,1AM AB λλ∴=+,即1AB AM λλ+=,设AC t AN =,则11()333tAG AB AC AM AN λλ+=+=+, M G N 、、三点共线,1=133t λλ+∴+,12t λ∴=−, 所以12AC AN λ⎛⎫=− ⎪⎝⎭,AMN ∴与ABC 的面积之比为920,191sin sin 2202AM AN A AB AC A ∴=⨯⨯, 即112029λλλ+⎛⎫⎛⎫−=⎪⎪⎝⎭⎝⎭,化简得22990λλ−+=,解得32λ=或3. 故选:BD13.(2023春·湖南长沙·高三长沙一中校联考)在三维空间中,定义向量的外积:a b ⨯叫做向量a 与b 的外积,它是一个向量,满足下列两个条件:①()a a b ⊥⨯,()b a b ⊥⨯,且a ,b 和a b ⨯构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图所示);②a b ⨯的模sin ,a b a b a b ⨯=,(,a b 表示向量a ,b 的夹角). 在正方体1111ABCD A B C D −中,有以下四个结论,正确的有( )A .11AB AC AD DB ⨯=⨯ B .111AC A D ⨯与1BD 共线C .AB AD AD AB ⨯=⨯ D .6BC AC ⨯与正方体表面积的数值相等【答案】ABD【解析】对于A ,设正方体的棱长为1,在正方体中1,60AB AC =︒,则111sin ,2AB AC AB AC AB AC ⨯===, 因为11//BD B D ,且1160AD B ∠=︒,所以1,120AD DB =︒,所以111sin ,2AD DB AD DB AD DB ⨯=== 所以11AB AC AD DB ⨯=⨯,所以A 正确;对于B ,1111AC B D ⊥,111AC BB ⊥,1111B B B D B ⋂=,111,B B B D ⊂平面11BB D D ,11AC ⊥平面11BB D D ,因为1BD ⊂平面11BB D D ,所以111BD AC ⊥,同理可证11BD A D ⊥, 再由右手系知,111AC A D ⨯与1BD 同向,所以B 正确;对于C ,由a ,b 和a b ⨯构成右手系知,a b ⨯与b a ⨯方向相反, 又由a b ⨯模的定义知,sin ,sin ,a b a b a b b a a b b a ⨯===⨯, 所以a b ba ⨯=−⨯,则AB AD AD AB ⨯=−⨯,所以C 错误; 对于D ,正方体棱长为a ,266sin 456BC AC BC AC a a ⨯=⋅︒=⨯, 正方体表面积为26a ,所以D 对. 故选:ABD .三、填空题14.(2023·全国·高三专题练习)已知函数243,0()41,01x x x f x x x ⎧++≤⎪=⎨−>⎪+⎩.若关于x 的方程()()()2[]2110f x m f x m +−−+=有6个不同的实数根,则m 的取值范围___________.【答案】7,5⎛− ⎝⎭【解析】因为243,0()41,01x x x f x x x ⎧++≤⎪=⎨−>⎪+⎩,所以当0x ≤时,()243f x x x =++开口向上,对称轴为2x =−,()()min 21f x f =−=−,两零点为1,3x x =−=−;当0x >时,()411f x x =−+,则()f x 在()0,∞+上单调递减,零点为3x =,且()1f x >−; 由此作出()f x 的图像如图,.令()t f x =,则当13t −<<时,()t f x =有三个实数根,因为()()()2[]2110f x m f x m +−−+=有6个不同的实数根,所以()22110t m t m +−−+=必须有两个不等实根12,t t ,且()21,1,3t t ∈−,令()()2211g t t m t m =+−−+,则()()103021132Δ0g g m ⎧−>⎪>⎪⎪⎨−−<−<⎪⎪>⎪⎩,即()()()()212110932110621221410m m m m m m m ⎧−−−+>⎪+−−+>⎪⎨−<−<⎪⎪−−−+>⎩,解得75m −<<7,5m ⎛∈− ⎝⎭.故答案为:7,5⎛− ⎝⎭. 15.(2023春·全国·高一期末)已知函数241,1()log 3,1xx f x x x ⎧−⎪=⎨+>⎪⎩…集合21()2()02M x f x t f x t ⎧⎫⎛⎫=−++=⎨⎬ ⎪⎝⎭⎩⎭∣,若集合M 中有3个元素,则实数t 的取值范围为________.【答案】{|0t t =或1}2t ≥【解析】令()f x m =,记21()(2)2g m m t m t =−++的零点为12,m m ,因为集合M 中有3个元素,所以()f x 的图像与直线12,y m y m ==共有三个交点,则,12001m m =⎧⎨<<⎩或12101m m =⎧⎨<<⎩或12001m m >⎧⎨<<⎩当10m =时,得0=t ,212m =,满足题意; 当11m =时,得12t =,212m =,满足题意;当12001m m >⎧⎨<<⎩时,(0)01(1)1202g t g t t =>⎧⎪⎨=−−+<⎪⎩,解得12t >. 综上,t 的取值范围为{|0t t =或1}2t ≥.故答案为:{|0t t =或1}2t ≥16.(2023秋·黑龙江绥化·高一校考期末)ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知30,12=︒=A b ,若ABC 有两解,写出a 的一个可能的值为__________.【答案】7(满足(612)a ∈,均可,答案不唯一) 【解析】由于满足条件的ABC 有两个,则sin b A a b <<,即612a <<.故答案为:7(满足(612)a ∈,均可,答案不唯一).17.(2023·海南·统考模拟预测)已知函数()314f x x m π⎛⎫=++− ⎪⎝⎭在3,04π⎡⎤−⎢⎥⎣⎦上有3个零点1x ,2x ,3x ,其中123x x x <<,则1232x x x ++=______. 【答案】53π−【解析】令()0f x =314x m π⎛⎫++= ⎪⎝⎭,故()314f x x m π⎛⎫++− ⎪⎝⎭的零点为函数()314g x x π⎛⎫++ ⎪⎝⎭与函数y =m 交点的横坐标,作出函数g (x )在3,04π⎡⎤−⎢⎥⎣⎦上的大致图像:令3()42x k k πππ+=+∈Z ,解得()123k x k ππ=+∈Z , 令1k =−,得4x π=−,则由图知2322=4x x ππ⎛⎫+=⨯−− ⎪⎝⎭,令2k =−,得712x π=−,则由图知12772=126x x ππ⎛⎫+=⨯−− ⎪⎝⎭, 故123752263x x x πππ++=−−=−. 故答案为:53π−﹒18.(2023春·辽宁沈阳·高三沈阳市第一二〇中学校考阶段练习)已知双曲线22:14x y C m −=与直线2y x =无交点,则m 的取值范围是_____. 【答案】(]0,16【解析】依题意,由22:14x y C m −=可得0m >,双曲线C 的渐近线方程为y =,因为双曲线C 与直线2y x =无交点,所以直线2y x =应在两条渐近线上下两部分之间,2≤,解得016m <≤,即(]0,16m ∈. 故答案为:(]0,16..。
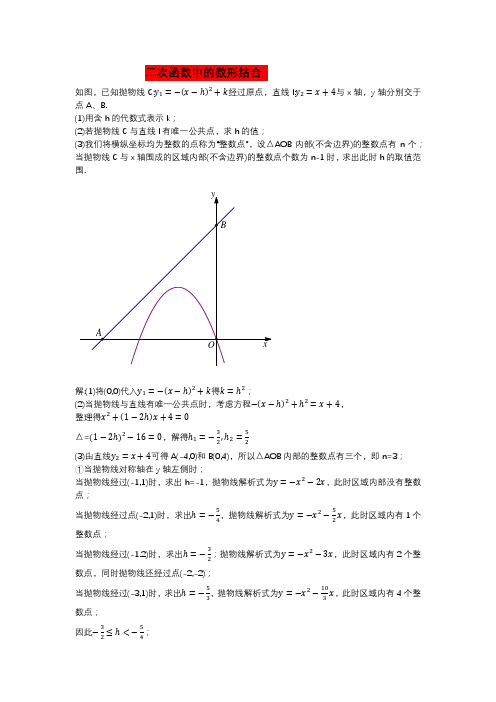
二次函数中的数形结合如图,已知抛物线C:y 1=−(x −ℎ)2+k 经过原点,直线l:y 2=x +4与x 轴,y 轴分别交于点A 、B.(1)用含h 的代数式表示k ;(2)若抛物线C 与直线l 有唯一公共点,求h 的值;(3)我们将横纵坐标均为整数的点称为“整数点”,设△AOB 内部(不含边界)的整数点有n 个;当抛物线C 与x 轴围成的区域内部(不含边界)的整数点个数为n-1时,求出此时h 的取值范围.解:(1)将(0,0)代入y 1=−(x −ℎ)2+k 得k =ℎ2;(2)当抛物线与直线有唯一公共点时,考虑方程−(x −ℎ)2+ℎ2=x +4,整理得x 2+(1−2ℎ)x +4=0△=(1−2ℎ)2−16=0,解得ℎ1=−32,ℎ2=52(3)由直线y 2=x +4可得A(-4,0)和B(0,4),所以△AOB 内部的整数点有三个,即n=3; ①当抛物线对称轴在y 轴左侧时;当抛物线经过(-1,1)时,求出h=-1,抛物线解析式为y =−x 2−2x ,此时区域内部没有整数点;当抛物线经过点(-2,1)时,求出ℎ=−54,抛物线解析式为y =−x 2−52x ,此时区域内有1个整数点;当抛物线经过(-1.2)时,求出ℎ=−32;抛物线解析式为y =−x 2−3x ,此时区域内有2个整数点,同时抛物线还经过点(-2,-2);当抛物线经过(-3,1)时,求出ℎ=−53,抛物线解析式为y =−x 2−103x ,此时区域内有4个整数点;因此−32≤ℎ<−54;②抛物线对称轴在y 轴右侧时当抛物线经过(1,1)时,求出h=1,抛物线解析式为y =−x 2+2x ,此时区域内部没有整数点; 当抛物线经过点(2,1)时,求出ℎ=54,抛物线解析式为y =−x 2+52x ,此时区域内有1个整数点;当抛物线经过(1.2)时,求出ℎ=32;抛物线解析式为y =−x 2+3x ,此时区域内有2个整数点,同时抛物线还经过点(2,2);当抛物线经过(3,1)时,求出ℎ=53,抛物线解析式为y =−x 2+103x ,此时区域内有4个整数点;因此54<ℎ≤32; (也可由抛物线对称性得到)综上所述,−32≤ℎ<−54;54<ℎ≤32。

第五十二讲数形联合A组一、选择题1. 已知函数 f(x)= x2+ e x-1(x<0) 与 g(x)= x2+ ln( x+ a)的图象上存在对于y 轴对称的点,则 a 2的取值范围是 ()A.-∞,1-∞,e) C.-1, eD.- e,1e B.(e e答案: B分析:由题意可得,当x>0 时, y= f(- x)与 y= g(x)的图象有交点,即g(x)= f(- x)有正解,即 x2+ln( x+ a) = (-x)2+ e-x-12有正解,即 e-x- ln(x+ a)-12= 0 有正解,令 F(x)= e-x- ln(x1-x-1-x1+a)-,则 F′(x)=- e<0,故函数 F(x)= e- ln(x+ a)-在 (0,+∞)上是单一递减2x+ a2的,要使方程g(x)= f(- x)有正解,则存在正数 x 使得 F(x) ≥0,即 e-x-ln( x+ a)-1≥0,所以2e x1 e x1x 在(0,+∞)上单一递减,所以e 011a≤e2x ,又y= e2a< e20= e2,选B.2. 函数 f(x)= 1 x 2 (| x |1),假如方程 f(x)=a 有且只有一个实根,那么 a 知足 ( )| x |(| x |1)A. a<0B.0≤ a<1C.a=1D.a>1答案: C分析:由图知 a=1 时,图象只有一个交点,应选 C.3.已知圆 C:( x-3)2+( y-4)2=1和两点 A(-m,0),B( m,0)( m>0),若圆 C上存在点 P,使得∠ APB=90°,则 m的最大值为()A.7B.6C.5D.4答案: B分析 . 依据题意,画出表示图,以下图,则圆心 C 的坐标为 (3,4) ,半径 r = 1,且 | AB | =2m .1因为∠ APB = 90°,连结 OP ,易知 | OP |= 2| AB | =m .要求 m 的最大值,即求圆 C 上的点 P 到原点 O 的最大距离 .22因为 | OC | = 3 + 4 = 5,所以 | OP |max = | OC | + r = 6,1224. 设平面点集 A = {( x ,y )|( y - x ) · ( y -x ) ≥ 0} , B = {( x , y )|( x - 1) +( y - 1) ≤1} ,则 A∩B 所表示的平面图形的面积为 ( ) 334πA. 4πB.5πC.7πD.21答案: D 分析:因为对于会合A , ( y - x ) y - x ≥ 0,y - x ≥0,y - x ≤0,所以1或1其表示的平面地区如图 .y -x ≥ 0y - x ≤ 0,对于会合 B , ( x - 1) 2+ ( y -1) 2≤ 1 表示以 (1,1) 为圆心, 1 为半径的圆及其内部地区,其面积为π .12由题意意知 A ∩ B 所表示的平面图形为图中暗影部分,曲线y = x 与直线 y =x 将圆 ( x -1) +( - 1) 2=1 分红1, 2, 3,4四部分 . 因为圆 ( x - 1)2+( y- 1) 2=1 与 y = 1 的图象都对于直ySSSSx线 y = x 对称,进而 S =S , S = S ,而 S + S + S + S =π,所以 S=S +S = π暗影 2.1234123424二、填空题5. 已知函数 y = f ( x )( x ∈ R) ,对函数 y = g ( x )( x ∈ I ) ,定义 g ( x ) 对于 f ( x ) 的“对称函数” 为函数 y= h( x)( x∈ I ),y= h( x)知足:对随意x∈ I ,两个点( x,h( x)),( x,g( x))对于点( x,f ( x))对称.若 h( x)是 g( x)=4-x2对于f ( x) = 3x+b的“对称函数” ,且h( x)> g( x) 恒成立,则实数 b的取值范围是 ________.答案: (210,+∞ )分析由已知得h x+ 4-x2) = 6+ 2- 4-x 2(x)> ()=3+,所以 (.2x b h x x b h g x恒成立,即 6x +2- 4-2> 4-x2,3 +> 4-x2恒成立 .b x x b在同一坐标系内,画出直线y=3x+ b 及半圆 y=2如图所4-x(b示) ,可得>2,即b>2 10,故答案为 (2 10,+∞ ). 10x2y26.椭圆a2+b2= 1( a>b>0) 的左、右极点分别是A,B,左、右焦点分别是 F1,F2,若| AF1|,| F1F2 | , | F1B| 成等比数列,则此椭圆的离心率为________.【分析】1121122∵ | AF| =a-c,|FF|= 2c, | F B| =a+c,且三者成等比数列,则| FF|11222c5=| AF| · | F B| ,即 4c=( a-c) · ( a+c) ,得a= 5c,∴ e=a=5.【答案】5 5三、解答题7. 已知函数f (x) = 2lnx-x2+( ∈R).ax a(1) 当=2时,求f (x) 的图象在x= 1处的切线方程;a(2) 若函数g( x)= f (x)-ax+ m在1, e上有两个零点,务实数m的取值范围.e22解: (1)当 a=2时, f( x) = 2ln x-x+ 2x,f′ ( x) =x- 2x+2,切点坐标为 (1 , 1),切线的斜率k= f ′(1)=2,则切线方程为y-1=2( x-1),即 y=2x-1.(2)g( x)=2ln x- x2+ m,2- 2(x+ 1)(x- 1)则 g′( x)=x-2x=x.1∵ x∈e,e,∴当 g′( x)=0时, x=1.1当 <x<1 时,g′( x)>0 ;e当 1<x<e 时,g′ ( x)<0.故 g ( x ) 在 x = 1 处获得极大值 g (1) = m - 1.112121 1又 g e = m - 2- e 2, g (e) = m + 2- e , g (e) - g e = 4- e + e 2<0,则 g (e)< g e ,1∴ g ( x ) 在 , e 上的最小值是 g (e) . e1g ( x ) 在, e 上有两个零点的条件是eg ( 1)= m - 1>0,11 g e = m - 2-e 2≤ 0,1解得 1<m ≤ 2+e 2 ,1∴实数 m 的取值范围是1,2+ e 2 .8. 已知函数 f(x)的图象是由函数g(x)=cos x 的图象经以下变换获得:先将g(x)图象上全部点π的纵坐标伸长到本来的2 倍 (横坐标不变 ),再将所获得的图象向右平移2个单位长度 .(1) 求函数 f(x)的分析式,并求其图象的对称轴方程;(2) 已知对于 x 的方程 f( x) +g( x)=m 在 [0,2 π)内有两个不一样的解α, β.2m 2 ①务实数m 的取值范围;②证明: cos(α- β)=- 1.5解 法一 (1) 将 g(x)= cos x 的图象上全部点的纵坐标伸长到本来的2 倍(横坐标不变 )获得 y=2cos x 的图象,再将 y =2cos x 的图象向右平移π y = 2cos x -π 个单位长度后获得的图象,22故 f(x)= 2sin x.进而函数 f(x)= 2sin x 图象的对称轴方程为πx = k π+(k ∈ Z ).2(2) ① f(x)+g(x)= 2sin x + cos x = 52sin x + 1cos x = 5sin(x + φ)55此中 sin φ= 1, cos φ=255.依题意, sin(x + φ)= m在 [0,2π)内有两个不一样的解α, β,当且仅当m< 1,故 m 的取值55范围是 (- 5, 5).②证明 因为 α, β是方程5sin( x + φ)=m 在 [0,2π)内的两个不一样的解。

专题复习三数形结合I、专题精讲:数学家华罗庚说得好:“数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离".几何图形的形象直观,便于理解,代数方法的一般性,解题过程的机械化,可操作性强,便于把握,因此数形结合思想是数学中重要的思想方法.所谓数形结合就是根据数学问题的题设和结论之间的在联系,既分析其数量关系,又揭示其几何意义使数量关系和几何图形巧妙地结合起来,并充分地利用这种结合,探求解决问题的思路,使问题得以解决的思考方法.II、典型例题剖析例1.某公司推销一种产品,设X(件)是推销产品的数量,y (元)是推销费,图3—3—1巳表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:(1)求Y1与Y2的函数解析式;(2)解释图中表示的两种方案是如何付推销费的?(3)如果你是推销员,应如何选择付费方案?Y<兀)Y1 Y2-。
2。
」600500400300200100解:(1) y1=20x,y2=10x+300. 图3-3-1(2) Y1是不推销产品没有推销费,每推销10件产品得推销费200元,Y2是保底工资300元,每推销10件产品再提成100元.(3)若业务能力强,平均每月保证推销多于30件时,就选择Yi的付费方案;否则,选择Y2的付费方案.点拨:图象在上方的说明它的函数值较大,反之较小,当然,两图象相交时,说明在交点处的函数值是相等的.例2.某农场种植一种蔬菜,销售员平根据往年的销售t每于克销售价(元)情况,对今年这种蔬菜的销售价格进行了预测,预测 5情况如图3—3—2,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系,观察图象,你能得到关于这种蔬菜销售情况的哪些信息?答题要求:(1)请提供四条信息;(2)不必求函数的解析.解:(1) 2月份每千克销售价是3.5元;7对月份每千克销售价是0.5元;(3) 1月到7月的销售价逐月下降;(4) 7月到12月的销售价逐月上升;4321o I 1 2 3 4 5 6 7 s 9 10 11 12月份图3-3-2(5) 2月与7月的销售差价是每千克3元;(6) 7月份销售价最低,1月份销售价最高;(7) 6月与8月、5月与9月、4月与10月、3月与11月,2月与12月的销售价分别相同.点拨:可以运用二次函数的性质:增减性、对称性.最大(小)值等,得出多个结论.例3.某报社为了解读者对本社一种报纸四个版面的喜欢情况,对读者作了一次问卷调查,要求读者选出自己最喜欢的一个版面,将所得数据整理后绘制成了如图3—3—3所示的条形统计图:个单位:人2000(1)请写出从条形统计图中获得的一条信息;(2)请根据条形统计图中的数据补全如图3—3—4所示的扇形统计图(要求:第二版与第三版相邻,并说明这两福统计图各有什么特点?图3-3-3(3)请你根据上述数据,对该报社提出一条合理的建议。

要点考向1:利用数学概念或数学式的几何意义解题例1:实系数一元二次方程x2+ax+2b=0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,求:(1)点(a,b)对应的区域的面积;(2)的取值范围;(3)(a-1)2+(b-2)2的值域.思路精析:列出a,b满足的条件→画出点(a,b)对应的区域→求面积→根据的几何意义求范围→根据(a-1)2+(b-2)2的几何意义求值域.解析:方程x2+ax+2b=0的两根在区间(0,1)和(1,2)上的几何意义分别是:函数y=f(x)= x2+ax+2b 与x轴的两个交点的横坐标分别在区间(0,1)和(1,2)内,由此可得不等式组由,解得A(-3,1).由,解得C(-1,0).∴在如图所示的aOb坐标平面内,满足条件的点(a,b)对应的平面区域为△ABC(不包括边界).(1)△ABC的面积为(h为A到Oa轴的距离).(2)几何意义是点(a,b)和点D(1,2)边线的斜率.由图可知(3)∵(a-1)2+(b-2)2表示的区域内的点(a,b)与定点(1,2)之间距离的平方,注:如果等式、代数式的结构蕴含着明显的几何特征,就要考虑用数形结合的思想方法来解题,即所谓的几何法求解,比较常见的对应有:(1)连线的斜率;(2)之间的距离;(3)为直角三角形的三边;(4)图象的对称轴为x=.只要具有一定的观察能力,再掌握常见的数与形的对应类型,就一定能得心应手地运用数形结合的思想方法.要点考向2:用数形结合求方程根的个数,解决与不等式有关的问题例2:(1)已知:函数f(x)满足下面关系:①f(x+1)=f(x-1);②当x∈[-1,1]时,f(x)=x2,则方程f(x)=lgx 解的个数是()(A)5 (B)7 (C)9 (D)10(2)设有函数f(x)=a+ 和g(x)= ,已知x∈[-4,0]时,恒有f(x)≤g(x),求实数a的范围.思路精析:(1)画出f(x)的图象→画出y=lgx的图象→数出交点个数.(2)f(x)≤g(x)变形为→画出的图象→画出的图象→寻找成立的位置解析:(1)选C.由题间可知,f(x)是以2为周期,值域为[0,1]的函数.又f(x) =lgx,则x∈(0,10],画出两函数图象,则交点个数即为解的个数.由图象可知共9个交点.(2)f(x)≤g(x),即,变形得,令…………①,………………②①变形得,即表示以(-2,0)为圆心,2为半径的圆的上半圆;②表示斜率为,纵截距为1-a的平行直线系.设与圆相切的直线为AT,其倾斜角为 ,则有tanα=,,要使f(x)≤g(x)在x∈[-4,0]时恒成立,则②成立所表示的直线应在直线AT的上方或与它重合,故有1-a≥6,∴a≤-5.注:(1)用函数的图象讨论方程(特别是含参数的指数、对数、根式、三角等复杂方程)的解的个数是一种重要的思想方法,其基本思想是先把方程两边的代数式看作是两个熟悉函数的表达式(不熟悉时,需要作适当变形转化为两熟悉的函数),然后在同一坐标系中作出两个函数的图象,图象的交点个数即为方程解的个数.(2)解不等式问题经常联系函数的图象,根据不等式中量的特点,选择适当的两个(或多个)函数,利用两个函数图象的上、下位置关系转化数量关系来解决不等式的解的问题,往往可以避免繁琐的运算,获得简捷的解答.(3)函数的单调性经常联系函数图象的升、降;奇偶性经常联系函数图象的对称性;最值(值域)经常联系函数图象的最高、最低点的纵坐标.要点考向2:数形结合在解析几何中的应用例3:已知椭圆C的中心在原点,一个焦点F.(Ⅰ)求椭圆C的方程;(Ⅱ)若椭圆C在第一象限的一点P的横坐标为1,过点P作倾斜角互补的两条不同的直线PA,PB分别交椭圆C于另外两点A,B,求证:直线AB的斜率为定值;(Ⅲ)求PAB∆面积的最大值.解析:(Ⅰ)设椭圆C的方程为22221(0)y xa ba b+=>>.由题意222,:a b ca bc⎧=+⎪⎪=⎨⎪=⎪⎩………………………………………………2分解得24a=,22b=.所以椭圆C 的方程为22142y x +=.………………………………………………4分(Ⅱ)由题意知,两直线PA ,PB 的斜率必存在,设PB 的斜率为k ,则PB的直线方程为(1)y k x =-.由22(1),1.42y k x y x ⎧-=-⎪⎨+=⎪⎩得222(2)2))40k x k k x k +++-=.……6分设(,)A A A x y ,(,)B B B x y,则22212B B k x x k --=⋅=+,同理可得2222A k x k +-=+,则22A Bx x k -=+,28(1)(1)2A B A B k y y k x k x k -=----=+. 所以直线AB的斜率A BAB A By y k x x -==-为定值. ……………………………………8分(Ⅲ)设AB的直线方程为y m =+.由22,1.42y m y x ⎧=+⎪⎨+=⎪⎩得22440x m ++-=.由22)16(4)0m ∆=-->,得28m <.……………………………………10分此时2A B x x +=-,244A B m x x -⋅=. P 到AB的距离为d =,AB ==则12PABS AB d ∆==2282m m -+==因为24m =使判别式大于零,所以当且仅当2m =±时取等号,[所以PAB ∆13分注:1.数形结合思想中一个非常重要的方面是以数辅形,通过方程等代数的方法来研究几何问题,也就是解析法,解析法与几何法结合来解题,会有更大的功效.2.此类题目的求解要结合该类图形的几何性质,将条件信息或结论信息结合在一起,观察图形特征,转化为代数语言,即方程(组)或不等式(组),从而将问题解决.要点考向2:数形结合在立体几何中的应用例4:如图1,在直角梯形ABCD 中,90ADC ∠=︒,//CD AB ,4,2AB AD CD ===, M 为线段AB 的中点.将ADC ∆沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示.(Ⅰ) 求证:BC ⊥平面ACD ; (Ⅱ) 求二面角A CD M --的余弦值.解析:(Ⅰ)在图1中,可得AC BC ==从而222AC BC AB +=,故AC BC ⊥.取AC 中点O 连结DO ,则DO AC ⊥,又面ADC ⊥面ABC , 面ADC面ABC AC =,DO ⊂面ACD ,从而OD ⊥平面ABC . …………………4分∴OD BC ⊥,又AC BC ⊥,AC OD O =.∴BC ⊥平面ACD . ………………………………………………6分(Ⅱ)建立空间直角坐标系O xyz -如图所示,则M ,(C ,D(2,CM =,(2,0,CD =. ………………………………………………8分设1(,,)n x y z =为面CDM 的法向量,则1100n CM n CD ⎧⋅=⎪⎨⋅=⎪⎩即00+=+=,解得y x z x =-⎧⎨=-⎩. 令1x =-,可得1(1,1,1)n =-.又2(0,1,0)n =为面ACD的一个法向量,∴121212cos ,3||||3n n n n n n ⋅<>===.∴二面角A CD M --的余弦值为3.注:1.应用空间向量可以解决的常见问题有空间角中的异面直线所成的角、线面角、二面角;位置关系中的平行、垂直及点的空间位置.其一般思路是:尽量建立空间直角坐标系,将要证、要求的问题转化为坐标运算.2.立体几何问题的求解往往将题目所给信息先转换成几何图形性质,结合该类图形的几何性质,将条件信息和结论信息结合在一起,观察图形特征,为代数法求解找到突破口.【跟踪模拟训练】一、选择题(每小题6分,共36分)1.方程lgx=sinx 的根的个数( )(A)1个 (B)2个 (C)3个 (D)4个2.已知全集U=R ,集合A={x|x2-3x-10<0},B={x|x>3},则右图中阴影部分表示的集合为( )A .(3,5)B .(-2,+∞)C .(-2,5)D .(5,+ ∞)3.在平面直角坐标系xOy 中,已知平面区域A={(x,y)|x+y ≤1,且x ≥0,y ≥0},则平面区域B={(x+y,x-y)|(x,y)∈A}的面积为( ) (A)2 (B)1 (C)12 (D) 144.函数32()f x x bx cx d =+++图象如图,则函数 2233cy x bx =++的单调递增区间为( ) A .]2,(--∞ B .),3[+∞ C .]3,2[-D .),21[+∞5.不等式组2142x a x a⎧->⎨-<⎩有解,则实数a 的取值范围是( )A .(1,3)-B .(,1)(3,)-∞-+∞C .(3,1)-D .(,3)(1,)-∞-+∞6.已知f(x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,那么不等式f(x)·cosx<0的解集是 ( )二、填空题(每小题6分,共18分)7.复数(x-2)+yi ,其中x 、y 均为实数,当此虚数的模为1时,的取值范围是8.已知关于x 的方程x 2-4|x|+5=m 有四个不相等的实根,则实数m 的范围是_______. 9.设A={(x,y)|x 2+(y-1)2=1},B={(x,y)|x+y+m ≥0},则使A B 成立的实数m 的取值范围是______.三、解答题(10、11题每题15分,12题16分,共46分)10.如图,已知四棱锥P ABCD -的底面是正方形,PA ⊥底面ABCD ,且2PA AD ==,点M 、N 分别在侧棱PD 、PC 上,且PM MD = (Ⅰ)求证:AM ⊥平面PCD ;(Ⅱ)若12PN NC =,求平面AMN 与平面PAB 的所成锐二面角的大小11.如图,1l ,2l 是通过某市开发区中心0的两条南北和东西走向的道路,连接M 、N 两地的铁路是一段抛物线弧,它所在的抛物线关于直线L1对称.M 到L1、L2的距离分别是2 km 、4km ,N 到L1、L2的距离分别是3 km 、9 kin .(1)建立适当的坐标系,求抛物线弧MN的方程;(Ⅱ)该市拟在点0的正北方向建设一座工厂,考虑到环境问题,要求厂址到点0的距离大于5km而不超过8km,并且铁路上任意一点到工厂的距离不能小于6km.求此厂离点0的最近距离.(注:工厂视为一个点)12.已知函数f(x)=-x2+8x,g(x)=6lnx+m.(1)求f(x)在区间[t,t+1]上的最大值h(t);(2)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由.参考答案1.【解析】选C.在同一坐标系中作出y=lgx与y=sinx的图象,如图.其交点数为3.2.答案:B3.作出不等式组表示的平面区域B,如图所示,根据图形可知该区域为等腰直角三角形,可求出面积,所以平面区域B的面积为1.4.答案:D5.答案:A6.【解析】选B.根据对称性画出f(x)在(-3,0)上的图象如图,结合y=cosx在(-3,0), (0,3)上函数值的正负,易知不等式f(x)cosx<0的解集是【解析】由题意知,设,则k为过圆(x-2)2+y2=17.上的点及原点的直线斜率,作图如下:又由对称性,可得答案:答案:8.【解析】令f(x)=x2-4|x|+5=(|x|-2)2+1,其图象如图.画直线y=m,由图象知当1<m<5时,方程有四个不相等的实根.答案:(1,5)9.【解析】由于集合A,B都是点的集合,故可结合图形进行分析、求解.集合A是一个圆x2+(y-1)2=1上的点的集合,集合B是一个不等式x+y+m≥0表示的平面区域内的点的集合, 要使A B,则应使圆被平面区域所包含(如图),即直线x+y+m=0应与圆相切或相离(在圆的下方),而当直线与圆相切时有故m 的取值范围是m ≥-1.答案:m ≥-110.解:(Ⅰ)建立如图所示的空间直角坐标系,xyz A -又 PA=AD=2,则有P (0,0,2),D (0,2,0) (0,1,1),(2,2,0).M C (2,2,2).PC ∴=-(0,1,1)AM =……3分(Ⅰ)0,0,AM CD AM PC AM CD AM PC ==∴⊥⊥又,.PC CD C AM PCD =∴⊥平面……………7分(Ⅱ)设1(,,),,2N x y z PN NC =则有120(2),.23x x x -=-∴= 同理可得24,.33y z ==即得224(,,).333N ………………9分 由4480,.333PC AN PC AN ⋅=+-=∴⊥(2,2,2).AMN PC ∴=-平面的法向量为而平面PAB 的法向量可为(0,2,0),AD =cos ,12PC AD PC AD PC AD⋅∴<>===⋅故所求平面AMN 与PAB 所成锐二面角的大小为.33arccos…………12分11.解析:(1)分别以1l 、2l为x 轴、y 轴建立如图所示的平面直角坐标系,则M (2,4),N (3,9)设MN 所在抛物线的方程为c ax y +=2,则有⎩⎨⎧+=+=c a c a 9944,解得⎩⎨⎧==01c a∴所求方程为2x y =(2≤x ≤3)5分(说明:若建系后直接射抛物线方程为)0(22>=p py x ,代入一个点坐标求对方程,本问扣2分)(2)设抛物线弧上任意一点P (x ,2x )(2≤x ≤3) 厂址为点A (0,t )(5<t ≤8),由题意得222)(||t x x PA -+=≥6∴)6()21(224-+-+t x t x ≥0 7分令2x u =,∵2≤x ≤3,∴4≤u ≤9∴对于任意的]9,4[∈u ,不等式)6()21(22-+-+t u t u ≥0恒成立(*) 8分设)6()21()(22-+-+=t u t u u f ,∵t <5≤8∴22129t --<≤215.要使(*)恒成立,需△≤0,即)6(4)12(22---t t ≤010分解得t ≥425,∴t 的最小值为425所以,该厂距离点O 的最近距离为6.25km12分12.【解析】(1)f(x)=-x 2+8x=-(x-4)2+16.①当t+1<4即t<3时,f(x)在[t,t+1]上单调递增(如图①).h(t)=f(t+1)=-(t+1)2+8(t+1)=-t 2+6t+7.②当t ≤4≤t+1即3≤t ≤4时,f(x)的最大值为h(t)=f(4)=16(如图②) ③当t>4时,f(x)在[t,t+1]上单调递减(如图③),h(t)=f(t)=-t 2+8t.(2)函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点,即函数φ(x)=g(x)-f(x)的图象与x轴的正半轴有且只有三个不同的交点.∵φ(x)=x2-8x+6lnx+m,[当x∈(0,1)时φ′(x)>0,φ(x)是增函数;当x∈(1,3)时,φ′(x)<0,φ(x)是减函数;当x∈(3,+∞)时,φ′(x)>0,φ(x)是增函数;当x=1或x=3时,φ′(x)=0.∴φ(x)极大值=φ(1)=m-7,φ(x)极小值=φ(3)=m+6ln3-15.∵当x充分接近0时,φ(x)<0,当x充分大时,φ(x)>0,∴要使φ(x)的图象与x轴正半轴有三个不同的交点,即7<m<15-6ln3.所以存在实数m,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3). 【备课资源】4.已知函数f(x)=|x2+2x|,若关于x的方程f2(x)+bf(x)+c=0有7个不同的实数根,则b,c的大小关系是( )(A)b>c (B)b≥c或b≤c中至少有一个正确 (C)b<c (D)不能确定【解析】选C.f(x)=|x2+2x|的图象如图.要使关于x的方程f2(x)+bf(x)+c=0有7个不同的实数根,则关于f(x)的一元二次方程f2(x)+bf(x)+c=0有两个不同的根.且一个根在(0,1)内,另一个根为1.∴b<c.5.若直线y=kx-1与曲线y=有公共点,则k的取值范围是________.【解析】∵曲线y=的定义域为[1,3],且其图象为圆(x-2)2+y2=1的下半圆,如图所示,则直线y=kx-1要与曲线有公共点,则直线只能处于l1,l2之间,且可与l1、l2重合,则k的取值范围是[0,1].答案:[0,1]6.已知有向线段PQ的起点P与终点Q的坐标分别为P(-1,1),Q(2,2).若直线l:x+my+m=0与有向线段PQ延长线相交,求实数m的取值范围.8.集合A={x|-1<x<1},B={x|x<a},(1)若A∩B=,求a的取值范围;(2)若A∪B={x|x<1},求a的取值范围.【解析】(1)如图所示:A={x|-1<x<1}B={x|x<a},且A∩B=,∴数轴上点x=a在x=-1左侧,∴a≤-1.(2)如图所示:A={x|-1<x<1},B={x|x<a}且A∪B={x|x<1},∴数轴上点x=a在x=-1和x=1之间,∴-1<a≤1.9.如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l1上,C在l2上,AM=MB=MN.(1)证明AC⊥NB;(2)若∠ACB=60°,求NB与平面ABC所成角的余弦值.【解析】如图,建立空间直角坐标系M-xyz.令MN=1,则有A(-1,0,0),B(1,0,0),N(0,1,0).(1)∵MN是l1、l2的公垂线,l1⊥l2,∴l2⊥平面ABN,∴l2平行于z轴.故可设C(0,1,m).于是。
![[全]高中数学-数形结合六大应用及例题详解](https://img.taocdn.com/s1/m/6296e9febb68a98270fefa5a.png)
[全]高中数学-数形结合六大应用及例题详解数形结合是数学中的一种非常重要的思想方法,它包含了“以形助数”和“以数辅形”两个方面。
一、什么是数形结合?1、借助形的生动性和直观性来阐明数之间的联系。
例如应用函数的图象来直观的说明函数的性质;2、借助于数的精确性和规范性来阐明形的某些属性。
如应用曲线的方程来精确的阐明曲线的几何性质。
概括的说,就是在解决数学问题时,将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,实现抽象概念与具体形象的联系与转化二、数形结合应用的三个原则1、等价性原则在数形结合时,代数性质和几何性质转换必须是等价的,否则解题将会出现漏洞。
有时,由于图形的局限性,不能完整的表现数的一般性,这时图形的性质只能是一种直观而浅显的说明,要注意其带来的负面效应。
2、双方性原则既要进行几何直观分析,又要进行相应的代数抽象探求,仅对代数进行几何分析容易出错。
3、简单性原则不要为了“数形结合”而数形结合。
具体运用时,一要考虑是否可行和是否有利;二要选择好突破口,恰当设参、用参、建立关系、做好转化;三要挖掘隐含条件,准确界定参变量的取值范围,特别是运用函数图象时应设法选择动直线与二次曲线。
三、如何运用数形结合思想解答数学题1、要彻底明白一些概念和运算的几何意义以及曲线的代数特征;2、要恰当设参,合理用参,建立关系,做好转化;3、要正确确定参数的取值范围,以防重复和遗漏;4、精心联想“数”与“形”,使一些较难解决的代数问题几何化,几何问题代数化,以便于问题求解。
很多数学概念都具有明显的几何意义,善于利用这些几何意义,往往能收到事半功倍的效果。
数学中的知识,有的本身就可以看作是数形的结合。
如:锐角三角函数的定义是借助于直角三角形来定义的;任意角的三角函数是借助于直角坐标系或单位圆来定义的。
四、应用方式和例题详解(一)数形结合思想在解决方程的根、不等式解集问题中的应用解析:方法说明:(1)用函数的图象讨论方程(特别是含参数的指数、对数、根式、三角等复杂方程)的解得个数是一种重要的思想方法,其根本思想是先把方程两边的代数式看作是两个熟悉函数表达式(不熟悉时,需要作适当变形转化为两个熟悉的函数),然后在同一坐标系中作出两个函数的图象,图象的交点个数即为方程解得个数。
方法技巧专题32 数形结合 解析篇【一】函数图象数形结合法1.例题【例1】设定义在R 上的函数)(x f 是最小正周期为2π的偶函数,)(x f '是)(x f 的导函数.当x ∈[0,π]时,0≤f (x )≤1;当x ∈(0,π)且x ≠π2时,0)(2>'-x f x )(π.则函数y =f (x )-sin x 在[-3π,3π]上的零点个数为( ) A .4 B .5C .6D .8【解析】∵当x ∈[0,π]时,0≤f (x )≤1,f (x )是最小正周期为2π的偶函数,∴当x ∈[-3π,3π]时,0≤f (x )≤1. ∵当x ∈(0,π)且x ≠π2时,⎝⎛⎭⎫x -π2f ′(x )>0,∴当x ∈⎣⎡⎦⎤0,π2时,f (x )为单调减函数; 当x ∈⎣⎡⎦⎤π2,π时,f (x )为单调增函数, ∵当x ∈[0,π]时,0≤f (x )≤1,定义在R 上的函数f (x )是最小正周期为2π的偶函数,在同一坐标系中作出y =sin x 和y =f (x )的草图如图,由图知y =f (x )-sin x 在[-3π,3π]上的零点个数为6,故选C.【例2】在R 上定义的函数()f x 是偶函数,且()(2)f x f x =-,若()f x 在区间[12],上是减函数,则()f xA.在区间[21]--,上是增函数,在区间[34],上是增函数 B.在区间[21]--,上是增函数,在区间[34],上是减函数 C.在区间[21]--,上是减函数,在区间[34],上是增函数 D.在区间[21]--,上是减函数,在区间[34],上是减函数 【解析】 f (x )= f (-x )= f (2-x ),故f (x )的草图如图:由图可知,B 正确。
2.巩固提升综合练习【练习1】已知函数f (x )是定义在R 上的偶函数,且f (-x -1)=f (x -1),当x ∈[-1,0]时,f (x )=-x 3,则关于x 的方程f (x )=|cos πx |在⎣⎡⎦⎤-52,12上的所有实数解之和为( ) A .-7 B .-6 C .-3 D .-1答案 A【解析】因为函数f (x )为偶函数,所以f (-x -1)=f (x +1)=f (x -1),所以函数f (x )的周期为2,如图,在同一平面直角坐标系内作出函数y =f (x )与y =|cos πx |的图象,由图知关于x 的方程f (x )=|cos πx |在⎣⎡⎦⎤-52,12上的实数解有7个.不妨设7个解中x 1<x 2<x 3<x 4<x 5<x 6<x 7,则由图得x 1+x 2=-4,x 3+x 5=-2,x 4=-1,x 6+x 7=0,所以方程f (x )=|cos πx |在⎣⎡⎦⎤-52,12上的所有实数解的和为-4-2-1+0=-7,故选A.【练习2】已知函数f(x)=⎩⎪⎨⎪⎧2-x -1(x ≤0),f (x -1)(x >0),若方程f(x)=x +a 有且只有两个不相等的实数根,则实数a的取值范围为( )A .(-∞,0]B .[0,1)C .(-∞,1)D .[0,+∞)答案 C【解析】函数f(x)=⎩⎪⎨⎪⎧2-x -1(x ≤0),f (x -1)(x >0)的图象如图所示,当a<1时,函数y =f(x)的图象与函数y =x +a 的图象有两个交点,即方程f(x)=x +a 有且只有两个不相等的实数根.【二】几何意义数形结合法—线性规划问题1.例题【例1】如果实数x ,y 满足(x -2)2+y 2=3,则yx 的最大值为( )A.12B.33C.32D.3【解析】方程(x -2)2+y 2=3的几何意义为坐标平面上的一个圆,圆心为M (2,0),半径为r =3(如图),而yx =y -0x -0则表示圆M 上的点A (x ,y )与坐标原点O (0,0)的连线的斜率.所以该问题可转化为动点A 在以M (2,0)为圆心,以3为半径的圆上移动,求直线OA 的斜率的最大值. 由图可知当∠OAM 在第一象限,且直线OA 与圆M 相切时,OA 的斜率最大, 此时OM =2,AM =3,OA ⊥AM ,则OA =OM 2-AM 2=1,tan ∠AOM =AMOA =3,故yx 的最大值为3,故选D. 答案 D【例2】已知实数x ,y 满足不等式组2435y x x y x y -≤⎧⎪+≥⎨⎪-≤⎩,若目标函数z=y ﹣mx 取得最大值时有唯一的最优解(1,3),则实数m 的取值范围是( ) A .m <﹣1 B .0<m <1 C .m >1 D .m≥1【答案】C【解析】作出不等式组对应的平面区域如图,由z=y -mx ,得y=mx+z ,即直线的截距最大,z 也最大 当m=0,此时y=z ,不滴足条件;当m>0,直线y=mx+z 的斜率k=m>0,要使目标函数最大时有唯一的最优解(1,3), 则直线y=mx+z 的斜率m>1当m<0,目标函数y=mx+z 的斜率k=m<0,不滿足題意. 综上,m>1.故选:C.:2.【练习1】设点P (x ,y )满足⎪⎪⎩⎪⎪⎨⎧≥≥≥+-≤-+110103y x y x y x ,则y x -x y的取值范围是( )A.⎣⎡⎭⎫32,+∞B.⎣⎡⎦⎤-32,32C.⎣⎡⎦⎤-32,1 D .[-1,1] 答案 B【解析】作出不等式组⎩⎪⎨⎪⎧x +y -3≤0,x -y +1≥0,x ≥1,y ≥1所表示的可行域,如图阴影部分所示(包括边界),其中A (2,1),B (1,2),令t =y x ,f (t )=t -1t ,根据t 的几何意义可知,t 为可行域内的点与坐标原点连线的斜率,连接OA ,OB ,显然OA 的斜率12最小,OB 的斜率2最大,即12≤t ≤2.由于函数f (t )=t -1t 在⎣⎡⎦⎤12,2上单调递增,故-32≤f (t )≤32,即y x -xy的取值范围是⎣⎡⎦⎤-32,32.【练习2】若函数f (x )=x 2+ax+2b 在区间(0,1)和(1,2)内各有一个零点,则31a b a +--的取值范围是 A .(14,1) B .(34,32) C .(14,54) D .(54,2) 【答案】D【解析】∵函数f (x )=x 2+ax+2b 在区间(0,1)和(1,2)内各有一个零点,∴(0)20(1)120(2)4220f b f a b f a b =>⎧⎪=++<⎨⎪=++>⎩,求得012020b a b a b >⎧⎪++<⎨⎪++>⎩, 它所表示的区域为△ABC 内的部分,【三】圆锥曲线数形结合法1.例题【例1】已知点P 在抛物线y 2=4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点的距离之和取得最小值时,点P 的坐标为( ) A.⎝⎛⎭⎫14,-1B.⎝⎛⎭⎫14,1 C .(1,2) D .(1,-2)【解析】点P 到抛物线焦点的距离等于点P 到抛物线准线的距离,如图所示,设焦点为F ,过点P 作准线的垂线,垂足为S ,则|PF |+|PQ |=|PS |+|PQ |,故当S ,P ,Q 三点共线时取得最小值,此时P ,Q 的纵坐标都是-1,设点P 的横坐标为x 0,代入y 2=4x 得x 0=14,故点P 的坐标为⎝⎛⎭⎫14,-1,故选A. 1.圆锥曲线数形结合法:是根据圆锥曲线中许多对应的长度、数式等都具有一定的几何意义,挖掘题目中隐含的几何意义,采用数形结合思想,快速解决某些相应的问题.破解此类题的关键点: ①画出图形,画出满足题设条件的圆锥曲线的图形,以及相应的线段、直线等;②数形求解,通过数形结合,利用圆锥曲线的定义、性质、直线与圆锥曲线的位置关系、圆与圆锥曲线的位置关系等进行分析与求解;③得出结论,结合题目条件进行分析,得出所要求解的结论.2.破解圆锥曲线问题的关键是画出相应的图形,注意数和形的相互渗透,并从相关的图形中挖掘对应的信息进行研究.直线与圆锥曲线的位置关系的转化有两种: ①通过数形结合建立相应的关系式;②通过代数形式转化为二元二次方程组的解的问题进行讨论.答案 A【例2】设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右顶点分别为A 1,A 2,左、右焦点分别为F 1,F 2,以F 1F 2为直径的圆与双曲线左支的一个交点为P .若以A 1A 2为直径的圆与直线PF 2相切,则双曲线C 的离心率为( )A. 2B. 3C.2D.5 答案 D【解析】如图所示,设以A 1A 2为直径的圆与直线PF 2的切点为Q ,连接OQ ,则OQ ⊥PF 2.又PF 1⊥PF 2,O 为F 1F 2的中点, 所以|PF 1|=2|OQ |=2a .又|PF 2|-|PF 1|=2a ,所以|PF 2|=4a .在Rt △F 1PF 2中,由|PF 1|2+|PF 2|2=|F 1F 2|2,得4a 2+16a 2=20a 2=4c 2,即e =ca = 5.2.巩固提升综合练习【练习1】已知抛物线的方程为x 2=8y ,F 是其焦点,点A (-2,4),在此抛物线上求一点P ,使△APF 的周长最小,此时点P 的坐标为________. 答案 ⎝⎛⎭⎫-2,12 【解析】因为(-2)2<8×4,所以点A (-2,4)在抛物线x 2=8y 的内部,如图所示,设抛物线的准线为l ,过点P 作PQ ⊥l 于点Q ,过点A 作AB ⊥l 于点B ,连接AQ ,由抛物线的定义可知,△APF 的周长为|PF |+|P A |+|AF |=|PQ |+|P A |+|AF |≥|AQ |+|AF |≥|AB |+|AF |,当且仅当P ,B ,A 三点共线时,△APF 的周长取得最小值,即|AB |+|AF |.因为A (-2,4),所以不妨设△APF 的周长最小时,点P 的坐标为(-2,y 0),代入x 2=8y ,得y 0=12,故使△APF 的周长最小的点P 的坐标为⎝⎛⎭⎫-2,12.【练习2】如图,点是抛物线的焦点,点,分别在抛物线和圆的实线部分上运动,且总是平行于轴,则周长的取值范围是( )A .B .C .D .【答案】B【解析】抛物线x 2=4y 的焦点为(0,1),准线方程为y =﹣1,圆(y ﹣1)2+x 2=4的圆心为(0,1),与抛物线的焦点重合,且半径r =2, ∴|FB |=2,|AF |=y A +1,|AB |=y B ﹣y A , ∴三角形ABF 的周长=2+y A +1+y B ﹣y A =y B +3,∵1<y B <3,∴三角形ABF 的周长的取值范围是(4,6).【四】数形结合思想在解方程或函数零点问题中的应用1.例题【例1】函数f (x )=2x -1x 的零点个数为( ) A.0 B.1 C.2 D.3 答案 B【解析】在同一平面直角坐标系下,作出函数y 1=2x 和y 2=1x 的图象,如图所示.函数f (x )=2x -1x 的零点个数等价于2x =1x 的根的个数, 等价于函数y 1=2x 和y 2=1x 图象的交点个数. 由图可知只有一个交点,所以有一个零点.故选B. 【例2】方程lgx = sinx 的实根的个数为 ( ) A. 1个B. 2个C. 3个D. 4个【解析】画出y = lgx 和y = sinx 在同一坐标系中的图象,如图所示,两函数图象有3个交点,选C.2.巩固提升综合练习【练习1】若关于x 的方程||x x +4=kx 2有四个不同的实数解,则k 的取值范围为________.答案 ⎝⎛⎭⎫14,+∞由图可得0<1k <4, 解得k >14.所以k 的取值范围为⎝⎛⎭⎫14,+∞. 【练习2】已知函数f (x )⎩⎪⎨⎪⎧x 4+1,x ≤1,ln x ,x >1,则方程f (x )=ax 恰有两个不同的实根时,实数a 的取值范围是________.答案 ⎣⎡⎭⎫14,1e【解析】画出函数f (x )的图象如图所示,由图可知,要使直线y =ax 与函数f (x )有两个交点,当y =ax 与y=x 4+1平行时,显然有两个交点,此时a=14.当a >14时,只需求出当直线y =ax 和曲线y =ln x 相切时的斜率即可.由于相切时交点只有1个,故结合图象知,实数a 的取值范围是⎣⎡⎭⎫14,1e .【五】数形结合思想在求解不等式或参数范围中的应用1.例题【例1】设函数f (x )=⎩⎪⎨⎪⎧2-x ,x ≤0,1,x >0,则满足f (x +1)<f (2x )的x 的取值范围是( )A.(-∞,-1]B.(0,+∞)C.(-1,0)D.(-∞,0) 答案 D④当⎩⎪⎨⎪⎧x +1>0,2x >0,即x >0时,f (x +1)=1,f (2x )=1,不合题意.综上,不等式f (x +1)<f (2x )的解集为(-∞,0). 故选D.方法二 ∵f (x )=⎩⎪⎨⎪⎧2-x ,x ≤0,1,x >0,∴函数f (x )的图象如图所示.由图可知,当x +1≤0且2x ≤0时,函数f (x )为减函数,故f (x +1)<f (2x )转化为x +1>2x . 此时x ≤-1.当2x <0且x +1>0时,f (2x )>1,f (x +1)=1,满足f (x +1)<f (2x ). 此时-1<x <0.综上,不等式f (x +1)<f (2x )的解集为(-∞,-1]∪(-1,0)=(-∞,0).故选D. 【例2】若不等式|x -2a |≥12x +a -1对x ∈R 恒成立,则实数a 的取值范围是________. 答案 ⎝⎛⎦⎤-∞,12解析 作出y 1=|x -2a |和y 2=12x +a -1的简图,如图所示.依题意得⎩⎪⎨⎪⎧2a ≤2-2a ,a -1<0,故a ≤12.2.【练习1】设A ={(x ,y )|x 2+(y -1)2=1},B ={(x ,y )|x +y +m ≥0},则使A ⊆B 成立的实数m 的取值范围是________.答案 [2-1,+∞)【解析】集合A 是圆x 2+(y -1)2=1上的点的集合,集合B 是不等式x +y +m ≥0表示的平面区域内的点的集合,要使A ⊆B ,则应使圆被平面区域所包含(如图),即直线x +y +m =0应与圆相切或相离(在圆的左下方),而当直线与圆相切时,有|m +1|2=1,又m >0,所以m =2-1,故m 的取值范围是[2-1,+∞).【练习2】已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2ax ,x ≥1,2ax -1,x <1,若存在两个不相等的实数x 1,x 2,使得f (x 1)=f (x 2),则实数a的取值范围为________. 答案 [0,+∞)解析 根据题意知f (x )是一个分段函数,当x ≥1时,是一个开口向下的二次函数,对称轴方程为x =a ;当x <1时,是一个一次函数.当a >1时,如图(1)所示,符合题意;当0≤a ≤1时,如图(2)所示,符合题意;当a <0时,如图(3)所示,此时函数在R 上单调递减,不满足题意.综上所述,可得a ≥0.【六】数形结合思想在圆与直线问题中的应用1.例题【例1】已知实数x、y满足x2+y2=3(0y≥),求(1)13ymx+=+,(2)b=2x+y的取值范围。
高中数学数形结合思想经典例题(含解析)高中数学数形结合思想经典例题一、选择题1.已知函数f (x )=3x ,x≤0,log 2x ,x>0,下列结论正确的是( )A .函数f (x )为奇函数B .f (f (14))=19C .函数f (x )的图象关于直线y =x 对称D .函数f (x )在R 上是增函数2.已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为( ) A .(-∞,-1)∪(0,+∞) B .(-∞,0)∪(1,+∞) C .(-1,0)D .(0,1)3.函数f (x )=ln|x +cos x |的图象为( )4.设奇函数f (x )在(0,+∞)上为增函数,且f (2)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-2,0)∩(2,+∞)B .(-∞,-2)∪(0,2)C .(-∞,-2)∪(2,+∞)D .(-2,0)∪(0,2)5.实数x ,y 满足不等式组x -y +2≥0,2x -y -5≤0,x +y -4≥0,则z =|x +2y -4|的最大值为( )A.2155B .21C .20D .256.已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根,则实数k 的取值范围是( ) A .(0,12)B .(12,1)C .(1,2)D .(2,+∞)7.若实数x ,y 满足|x -3|≤y ≤1,则z =2x +yx +y 的最小值为( )A.53 B .2 C.35D.128.设方程10x =|lg(-x )|的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1D .0<1<="" bdsfid="103" p="">9.已知函数y =f (x )在(0,1)内的一段图象是如图所示的一段曲线,若0<x 1<x 2<1,则( )A.f (x 1)x 1<f (x 2)x 2B.f (x 1)x 1=f (x 2)x 2C.f (x 1)x 1>f (x 2)x 2D .不能确定10.设关于x ,y 的不等式组2x -y +2>0,x +m<0,y -m>0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2,求m 的取值范围是( ) A .(-∞,43)B .(-∞,13)C .(-∞,-23)D .(-∞,-53)11.在△AB C 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF →=( ) A.89 B.109 C.259D.26912.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤45成立,则实数a的值为( ) A.15 B.25 C.12D .113.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( ) A.72 B.52 C .3D .214.已知双曲线C :x 2a 2-4y 2=1(a >0)的右顶点到其一条渐近线的距离等于34,抛物线E :y 2=2px 的焦点与双曲线C 的右焦点重合,则抛物线E 上的动点M 到直线l 1:4x -3y +6=0和l 2:x =-1的距离之和的最小值为( )A .1B .2C .3D .4二、填空题15.已知函数y =|x 2-1|x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是__________.16.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x .那么,不等式f (x +2)<5的解集是________.17.已知变量x ,y 满足约束条件x +2y -3≤0,x +3y -3≥0,y -1≤0,则F (x ,y )=log 2(y +1)+log 12(x +1)的最小值为________.18.已知直线y =x -2与圆x 2+y 2-4x +3=0及抛物线y 2=8x 的四个交点从上面依次为A ,B ,C ,D 四点,则|AB |+|CD |=________.19.已知函数f (x )=?-x 2+2x ,x≤0,ln (x +1),x>0.若|f (x )|≥ax ,则a 的取值范围是______.20.已知函数f (x )=?|x|,x≤m ,x 2-2mx +4m ,x>m ,其中m >0.若存在实数b ,使得关于x 的方程f (x )=b有三个不同的根,则m 的取值范围是________.高中数学数形结合思想经典例题解析一、选择题1.已知函数f (x )=?3x ,x≤0,log 2x ,x>0,下列结论正确的是( )A .函数f (x )为奇函数B .f (f (14))=19C .函数f (x )的图象关于直线y =x 对称D .函数f (x )在R 上是增函数【答案】 B【解析】作出函数f (x )的图象,如图所示,可知A ,C ,D 均错.f (f (14))=3log 214=3-2=19,故B 正确.2.已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为( ) A .(-∞,-1)∪(0,+∞) B .(-∞,0)∪(1,+∞) C .(-1,0) D .(0,1)【答案】 C【解析】∵f (x )=ax 2-(a +2)x +1,Δ=(a +2)2-4a =a 2+4>0,∴函数f (x )=ax 2-(a +2)x +1必有两个不同的零点.又∵f (x )在(-2,-1)上有一个零点,则f (-2)f (-1)<0,∴(6a +5)(2a +3)<0,解得-32<-5<="" bdsfid="173" p=""><-5<="" bdsfid="175" p="">6.<-5<="" bdsfid="177" p="">又∵a ∈Z ,∴a =-1.<-5<="" bdsfid="179" p="">不等式f (x )>1,即-x 2-x >0.解得-1<="" )=ln|x="" 3.函数f=""<-5<="" bdsfid="182" p=""><-5<="" bdsfid="184" p="">【答案】 A<-5<="" bdsfid="186" p="">【解析】因为f (0)=ln|cos0|=0,故排除C ,D ;又f (1)=ln|1+cos1|>ln 1=0,故排除B ,选A.<-5<="" bdsfid="188" p="">4.设奇函数f (x )在(0,+∞)上为增函数,且f (2)=0,则不等式f (x )-f (-x )<-5<="" bdsfid="190" p="">x <0的解集为( )<-5<="" bdsfid="192" p="">A .(-2,0)∩(2,+∞)<-5<="" bdsfid="194" p="">B .(-∞,-2)∪(0,2)<-5<="" bdsfid="196" p="">C .(-∞,-2)∪(2,+∞)<-5<="" bdsfid="198" p="">D .(-2,0)∪(0,2)<-5<="" bdsfid="200" p="">【答案】 D<-5<="" bdsfid="202" p="">【解析】由已知条件可以画出函数f (x )的草图,如图所示.由函数f (x )为奇函数可化简不等式f (x )-f (-x )x <0为2f (x )<-5<="" bdsfid="204" p="">x <0.若x >0,则需<-5<="" bdsfid="206" p="">有f (x )<0,结合图象可知00,结合图象可知<-5<="" bdsfid="209" p="">-2<0.综上可知,不等式的解集为(-2,0)∪(0,2).<="" bdsfid="210" p=""><-5<="" bdsfid="212" p="">5.实数x ,y 满足不等式组<-5<="" bdsfid="214" p="">?x -y +2≥0,2x -y -5≤0,x +y -4≥0,则z =|x +2y -4|的最大值为( )<-5<="" bdsfid="216" p="">A.215<-5<="" bdsfid="218" p="">5<-5<="" bdsfid="220" p="">B .21<-5<="" bdsfid="222" p="">C .20<-5<="" bdsfid="224" p="">D .25<-5<="" bdsfid="226" p="">【答案】 B<-5<="" bdsfid="228" p="">【解析】作出不等式组表示的平面区域,如下图中阴影部分所示.z =|x +2y -4|=|x +2y -4| <-5<="" bdsfid="230" p="">5<-5<="" bdsfid="232" p="">·5,即其几何含义为阴影区域内的点到直线x +2y -4=0的距离的5倍.<-5<="" bdsfid="234" p="">由?<-5<="" bdsfid="236" p="">x -y +2=0,2x -y -5=0,得B 点坐标为(7,9),显然点B 到直线x +2y -4=0的距离最大,此时z max<-5<="" bdsfid="238" p="">=21.<-5<="" bdsfid="240" p="">6.已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根,则实数k 的取值范围是( ) A .(0,12)<-5<="" bdsfid="242" p="">B .(1<-5<="" bdsfid="244" p="">2,1)<-5<="" bdsfid="246" p="">C .(1,2)<-5<="" bdsfid="248" p="">D .(2,+∞)<-5<="" bdsfid="250" p="">【答案】 B<-5<="" bdsfid="252" p="">【解析】在同一坐标系中分别画出函数f (x ),g (x )的图象如图所示,方程f (x )=g (x )有两个不相等的实根等价于两个函数的图象有两个不同的交点,结合图象可知,当直线y =kx 的斜率大于坐标原点与点(2,1)连线的斜率且小于直线y =x -1的斜率时符合题意,故1<-5<="" bdsfid="254" p="">2<-5<="" bdsfid="256" p=""><1.<="" bdsfid="257" p=""> <-5<="" bdsfid="259" p=""><-5<="" bdsfid="261" p="">7.若实数x ,y 满足|x -3|≤y ≤1,则z =2x +y<-5<="" bdsfid="263" p="">x +y 的最小值为( )<-5<="" bdsfid="265" p="">A.53 B .2 C.35<-5<="" bdsfid="267" p="">D.12<-5<="" bdsfid="269" p="">【答案】 A<-5<="" bdsfid="271" p="">【解析】依题意,得实数x ,y 满足<-5<="" bdsfid="273" p="">?x +y -3≥0,x -y -3≤0,0≤y≤1,画出可行域如图阴<-5<="" bdsfid="275" p="">影部分所示,其中A (3,0),C (2,1),z =2+y<-5<="" bdsfid="277" p="">x 1+y x =1+11+y x ∈[5<-5<="" bdsfid="279" p="">3,2],故<-5<="" bdsfid="281" p="">选A.<-5<="" bdsfid="283" p="">8.设方程10x =|lg(-x )|的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1 D .0<="" p="" 【答案】=""><-5<="" bdsfid="286" p="">【解析】本题考查函数的性质.在同一坐标系下,画出函数y =10x 与y =|lg(-x )|的图象,结合图象不难看出,它们的两个交点中,其中一个交点横坐标属于<-5<="" bdsfid="288" p="">(-∞,-1),另一个交点横坐标属于(-1,0),即在x 1,x 2中,其中一个属于(-∞,-1),另一个属于(-1,0),不妨设x 1∈(-∞,-1),x 2∈(-1,0),则有10x 1=|lg(-x 1)|=lg(-x 1),10x 2=|lg(-x 2)|=-lg(-x 2),10x 1-10x 2=lg(-x 1)+lg(-x 2)=lg(x 1x 2)<0,0<="" )在(0,1)内的一段图象是如图所示的一段曲线,若0<x="" 1x="" 1<x="" 2 <-5<="" bdsfid="291" p=""><-5<="" bdsfid="293" p="">A.f (x 1)x 1<f (x 2)x 2<-5<="" bdsfid="295" p="">B.f (x 1)x 1=f (x 2)<-5<="" bdsfid="297" p="">x 2<-5<="" bdsfid="299" p="">C.f (x 1)x 1>f (x 2)x 2<-5<="" bdsfid="301" p="">D .不能确定<-5<="" bdsfid="303" p="">【答案】 C<-5<="" bdsfid="305" p="">【解析】如图,设曲线上两点P 1(x 1,f (x 1)),P 2(x 2,f (x 2)),kOP 1=<-5<="" bdsfid="307" p="">f (x 1)-0x 1-0=f (x 1)x 1,kOP 2=f (x 2)-0x 2-0<-5<="" bdsfid="309" p="">=f (x 2)<-5<="" bdsfid="311" p="">x 2,由于0<x 1<-5<="" bdsfid="313" p=""><x 2<1,根据斜率与倾斜角之间的关系,显然有kOP 1>kOP 2,即f (x 1)x 1>f (x 2)<-5<="" bdsfid="315" p="">x 2<-5<="" bdsfid="317" p="">,故选C. 10.设关于x ,y 的不等式组<-5<="" bdsfid="319" p="">?2x -y +2>0,x +m<0,y -m>0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0 <-5<="" bdsfid="321" p="">=2,求m 的取值范围是( ) A .(-∞,4<-5<="" bdsfid="323" p="">3)<-5<="" bdsfid="325" p="">B .(-∞,1<-5<="" bdsfid="327" p="">3)<-5<="" bdsfid="329" p="">C .(-∞,-2<-5<="" bdsfid="331" p="">3)<-5<="" bdsfid="333" p="">D .(-∞,-5<-5<="" bdsfid="335" p="">3<-5<="" bdsfid="337" p="">)<-5<="" bdsfid="339" p="">【答案】 C<-5<="" bdsfid="341" p="">【解析】作出不等式组所表示的平面区域,根据题设条件分析求解.当m ≥0时,若平面区域存在,则平面区域内的点在第二象限,平面区域内不可能存在点P (x 0,y 0)满足x 0-2y 0=2,因此m <0. 如图所示的阴影部分为不等式组表示的平面区域.<-5<="" bdsfid="343" p="">要使可行域内包含y =1<-5<="" bdsfid="345" p="">2<-5<="" bdsfid="347" p="">x -1上的点,只需可行域边界点(-m ,m )在直线y =<-5<="" bdsfid="349" p="">12x -1的下方即可,即m <-12m -1,解得m <-23<-5<="" bdsfid="351" p="">. 11.在△AB C 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF →=( ) A.89 B.109 C.259 D.269<-5<="" bdsfid="353" p="">【答案】 B<-5<="" bdsfid="355" p="">【解析】由|AB →+AC →|=|AB →-AC →|,化简得AB →·AC →<-5<="" bdsfid="357" p="">=0,又因为AB 和AC 为三角形的两条边,不可能为0,所以AB →与AC →垂直,所以△ABC 为直角三角形.以AC 为x 轴,以AB 为y 轴建立平面直角坐标系,如图所示,则A (0,0),B (0,2),C (1,0),由E ,F 为BC 的三等分点知E (23,23),F (13,4<-5<="" bdsfid="359" p="">3),所以AE →=(23,<-5<="" bdsfid="361" p="">23),AF →=(13,4<-5<="" bdsfid="363" p="">3),所以AE →·AF →=23×13+23×43=109<-5<="" bdsfid="365" p="">. 12.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤4 <-5<="" bdsfid="367" p="">5成立,则实数a<-5<="" bdsfid="369" p="">的值为( ) A.15 B.2<-5<="" bdsfid="371" p="">5 C.12<-5<="" bdsfid="373" p="">D .1 【答案】 A<-5<="" bdsfid="375" p="">【解析】(x -a )2+(ln x 2-2a )2表示点P (x ,ln x 2)与点Q (a ,2a )距离的平方.而点P 在曲线g (x )=2ln x 上,点Q (a ,2a )在直线y =2x 上.<-5<="" bdsfid="377" p="">因为g ′(x )=2x ,且y =2x 表示斜率为2的直线,所以由2<-5<="" bdsfid="379" p="">x<-5<="" bdsfid="381" p="">=2,解得x =1.<-5<="" bdsfid="383" p="">从而曲线g (x )=2ln x 在x =1处的切线方程为y =2(x -1),又直线y =2(x -1)与直线y =2x 平行,且它们间的距离为<-5<="" bdsfid="385" p="">222+(-1)2<-5<="" bdsfid="387" p="">=25<-5<="" bdsfid="389" p="">5,如图所示.<-5<="" bdsfid="391" p=""><-5<="" bdsfid="393" p="">故|PQ |的最小值为25<-5<="" bdsfid="395" p="">5<-5<="" bdsfid="397" p="">,<-5<="" bdsfid="399" p="">即f (x )=(x -a )2+(ln x 2-2a )2的最小值为(255)2=4<-5<="" bdsfid="401" p="">5,当|PQ |最小时,P 点的坐标为(1,0),所以<-5<="" bdsfid="403" p="">2a -0a -1<-5<="" bdsfid="405" p="">×2=-1,解得a =1<-5<="" bdsfid="407" p="">5.<-5<="" bdsfid="409" p="">13.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →<-5<="" bdsfid="411" p="">,则|QF |=( ) A.72 B.52 C .3 D .2<-5<="" bdsfid="413" p="">【答案】 C<-5<="" bdsfid="415" p="">【解析】利用FP →=4FQ →<-5<="" bdsfid="417" p="">转化长度关系,再利用抛物线定义求解.∵FP →=4FQ →,∴|FP →|=4|FQ →|. ∴<-5<="" bdsfid="419" p="">|PQ||PF|=3<-5<="" bdsfid="421" p="">4<-5<="" bdsfid="423" p="">.如图,过Q 作QQ ′⊥l ,垂足为Q ′,设l 与x 轴的交点为A ,则|AF |=4. ∴<-5<="" bdsfid="425" p="">|PQ||PF|=|QQ′||AF|=3<-5<="" bdsfid="427" p="">4<-5<="" bdsfid="429" p="">.∴|QQ ′|=3. 根据抛物线定义可知|QQ ′|=|QF |=3,故选C.<-5<="" bdsfid="431" p="">14.已知双曲线C :x 2a 2-4y 2=1(a >0)的右顶点到其一条渐近线的距离等于3<-5<="" bdsfid="433" p="">4,抛物线E :y 2=<-5<="" bdsfid="435" p="">2px 的焦点与双曲线C 的右焦点重合,则抛物线E 上的动点M 到直线l 1:4x -3y +6=0和l 2:<-5<="" bdsfid="437" p="">x =-1的距离之和的最小值为( ) A .1 B .2 C .3 D .4<-5<="" bdsfid="439" p="">【答案】 B<-5<="" bdsfid="441" p="">【解析】 x 2<-5<="" bdsfid="443" p="">a 2-4y 2=1的右顶点坐标为(a ,0),一条渐近线为<-5<="" bdsfid="445" p="">x -2ay =0.由点到直线的距离公式得d =<-5<="" bdsfid="447" p="">|a|12+4a 2=34<-5<="" bdsfid="449" p="">,解得a =<-5<="" bdsfid="451" p="">3<-5<="" bdsfid="453" p="">2或a =-32(舍去),故双曲线的方程为4x 2<-5<="" bdsfid="455" p="">3<-5<="" bdsfid="457" p="">-4y 2=1.因为c =<-5<="" bdsfid="459" p="">34+14<-5<="" bdsfid="461" p="">=1,故双曲线的右焦点为(1,0),即抛物线的焦点为(1,0),所以p =2,x =-1是抛物线的准线,如图,作MA ⊥l 1于点A ,MB ⊥l 2于<-5<="" bdsfid="463" p="">点B ,设抛物线的焦点为F ,连接MF ,则由抛物线的定义知|MB |=|MF |,当M ,A ,F 三点共线时,距离之和最小,其最小值是点F 到l 1的距离,由点到直线的距离公式可得d 1=|4+6|<-5<="" bdsfid="465" p="">(-3)2+42=10<-5<="" bdsfid="467" p="">5=2,即距离之和的最小值为2,选B.<-5<="" bdsfid="469" p="">二、填空题<-5<="" bdsfid="471" p="">15.已知函数y =|x 2-1|<-5<="" bdsfid="473" p="">x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是<-5<="" bdsfid="475" p="">__________.<-5<="" bdsfid="477" p="">【答案】 (0,1)∪(1,4) 【解析】根据绝对值的意义,<-5<="" bdsfid="479" p="">y =|x 2-1|x -1=<-5<="" bdsfid="481" p="">x +1,x>1或x<-1,-x -1,-1≤x<1.<-5<="" bdsfid="483" p=""><-5<="" bdsfid="485" p="">在直角坐标系中作出该函数的图象,如下图中实线所示.根据图象可知,当0<1或1<4时有两个交点.<="" bdsfid="486" p=""><-5<="" bdsfid="488" p=""><-5<="" bdsfid="490" p="">16.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x .那么,不等式f (x +2)<5的解集是________.【答案】 (-7,3)<-5<="" bdsfid="492" p="">【解析】当x ≥0时,f (x )=x 2-4x <5的解集为[0,5),又f (x )为偶函数,所以f (x )<5的解集为(-5,5).所以f (x +2)<5的解集为(-7,3).<-5<="" bdsfid="494" p="">17.已知变量x ,y 满足约束条件<-5<="" bdsfid="496" p="">?x +2y -3≤0,x +3y -3≥0,y -1≤0,则F (x ,y )=log 2(y +1)+log 12(x +1)的最小值<-5<="" bdsfid="498" p="">为________.【答案】-2<-5<="" bdsfid="500" p="">【解析】 F (x ,y )=log 2(y +1)+log 12(x +1)=log 2(y +1)-log 2(x +1)=log 2y +1x +1,令k =y +1<-5<="" bdsfid="502" p="">x +1<-5<="" bdsfid="504" p="">=<-5<="" bdsfid="506" p="">y -(-1)<-5<="" bdsfid="508" p="">x -(-1)<-5<="" bdsfid="510" p="">,则k 表示可行域内(如图所示)的点与P (-1,-1)所在直线的斜率.<-5<="" bdsfid="512" p=""><-5<="" bdsfid="514" p="">18.已知直线y =x -2与圆x 2+y 2-4x +3=0及抛物线y 2=8x 的四个交点从上面依次为A ,B ,C ,D 四点,则|AB |+|CD |=________.【答案】 14<-5<="" bdsfid="516" p="">【解析】如图所示,圆的方程可化为(x -2)2+y 2=1,抛物线的焦点F (2,0),准线x =-2.<-5<="" bdsfid="518" p=""><-5<="" bdsfid="520" p="">由y =x -2,y 2=8x ,<-5<="" bdsfid="522" p="">得x 2-12x +4=0,设直线与抛物线交于A (x A ,y A ),D (x D ,y D ),则x A +x D =12. |AB |+|CD |=(|AF |-|BF |)+(|DF |-|CF |)=(|AF |-1)+(|DF |-1)=|AF |+|DF |-2,由抛物线的定义得|AF |=x A +2,|DF |=x D +2,故|AB |+|CD |=(|AF |+|DF |)-2=x A +x D +2=14.<-5<="" bdsfid="524" p="">19.已知函数f (x )=?<-5<="" bdsfid="526" p="">-x 2+2x ,x≤0,ln (x +1),x>0.若|f (x )|≥ax ,则a 的取值范围是______.<-5<="" bdsfid="528" p="">【答案】 [-2,0]<-5<="" bdsfid="530" p="">【解析】画出函数|f (x )|的图象,数形结合求解.<-5<="" bdsfid="532" p=""><-5<="" bdsfid="534" p="">作出函数y =|f (x )|的图象,如图,当|f (x )|≥ax 时,必有k ≤a ≤0,<-5<="" bdsfid="536" p="">其中k 是y =x 2-2x (x ≤0)在原点处的切线斜率,显然,k =-2. ∴a 的取值范围是[-2,0].<-5<="" bdsfid="538" p="">20.已知函数f (x )=?<-5<="" bdsfid="540" p="">|x|,x≤m ,<-5<="" bdsfid="542" p="">x 2-2mx +4m ,x>m ,其中m >0.若存在实数b ,使得关于x 的方程f (x )=b<-5<="" bdsfid="544" p="">有三个不同的根,则m 的取值范围是________.【答案】 (3,+∞)<-5<="" bdsfid="546" p="">【解析】 f (x )=?<-5<="" bdsfid="548" p="">|x|,x≤m ,<-5<="" bdsfid="550" p="">x 2-2mx +4m ,x>m ,当x >m 时,f (x )=x 2-2mx +4m =(x -m )2+4m -m 2,<-5<="" bdsfid="552" p="">其顶点为(m ,4m -m 2);当x ≤m 时,函数f (x )的图象与直线x<-5<="" bdsfid="554" p="">=m 的交点为Q (m ,m ).①当m>0,<-5<="" bdsfid="556" p="">4m -m 2≥m ,<-5<="" bdsfid="558" p="">即0<="" bdsfid="559" p="" ≤3时,函数f=""><-5<="" bdsfid="561" p="">直线y =b 与函数f (x ) 的图象有一个或两个不同的交点,不符合题意;②当?<-5<="" bdsfid="563" p="">4m -m 2<=""><-5<="" bdsfid="566" p="">m>0,即<-5<="" bdsfid="568" p="">m >3时,函数f (x )的图象如图2所示,则存在实数b 满足4m -m 2<-5<="" bdsfid="571" p=""><-5<="" bdsfid="573" p="">。
高中数学数形结合思想经典例题一、选择题1.已知函数f (x )=⎩⎪⎨⎪⎧3x ,x≤0,log 2x ,x>0,下列结论正确的是( )A .函数f (x )为奇函数B .f (f (14))=19C .函数f (x )的图象关于直线y =x 对称D .函数f (x )在R 上是增函数2.已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为( ) A .(-∞,-1)∪(0,+∞) B .(-∞,0)∪(1,+∞) C .(-1,0)D .(0,1)3.函数f (x )=ln|x +cos x |的图象为( )4.设奇函数f (x )在(0,+∞)上为增函数,且f (2)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-2,0)∩(2,+∞)B .(-∞,-2)∪(0,2)C .(-∞,-2)∪(2,+∞)D .(-2,0)∪(0,2)5.实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +2≥0,2x -y -5≤0,x +y -4≥0,则z =|x +2y -4|的最大值为( )A.2155B .21C .20D .256.已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根, 则实数k 的取值范围是( ) A .(0,12)B .(12,1)C .(1,2)D .(2,+∞)7.若实数x ,y 满足|x -3|≤y ≤1,则z =2x +yx +y 的最小值为( )A.53 B .2 C.35D.128.设方程10x =|lg(-x )|的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1D .0<x 1x 2<19.已知函数y =f (x )在(0,1)内的一段图象是如图所示的一段曲线,若0<x 1<x 2<1,则( )A.f (x 1)x 1<f (x 2)x 2B.f (x 1)x 1=f (x 2)x 2C.f (x 1)x 1>f (x 2)x 2D .不能确定10.设关于x ,y 的不等式组⎩⎪⎨⎪⎧2x -y +2>0,x +m<0,y -m>0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2,求m 的取值范围是( ) A .(-∞,43)B .(-∞,13)C .(-∞,-23)D .(-∞,-53)11.在△AB C 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF →=( ) A.89 B.109 C.259D.26912.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤45成立,则实数a的值为( )A.15B.25C.12D .113.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( ) A.72 B.52 C .3D .214.已知双曲线C :x 2a 2-4y 2=1(a >0)的右顶点到其一条渐近线的距离等于34,抛物线E :y 2=2px 的焦点与双曲线C 的右焦点重合,则抛物线E 上的动点M 到直线l 1:4x -3y +6=0和l 2:x =-1的距离之和的最小值为( ) A .1 B .2 C .3 D .4二、填空题15.已知函数y =|x 2-1|x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是__________.16.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x .那么,不等式f (x +2)<5的解集是________.17.已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -3≤0,x +3y -3≥0,y -1≤0,则F (x ,y )=log 2(y +1)+log 12(x +1)的最小值为________.18.已知直线y =x -2与圆x 2+y 2-4x +3=0及抛物线y 2=8x 的四个交点从上面依次为A ,B ,C ,D 四点,则|AB |+|CD |=________.19.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x≤0,ln (x +1),x>0.若|f (x )|≥ax ,则a 的取值范围是______.20.已知函数f (x )=⎩⎪⎨⎪⎧|x|,x≤m ,x 2-2mx +4m ,x>m ,其中m >0.若存在实数b ,使得关于x 的方程f (x )=b有三个不同的根,则m 的取值范围是________.高中数学数形结合思想经典例题解析一、选择题1.已知函数f (x )=⎩⎪⎨⎪⎧3x ,x≤0,log 2x ,x>0,下列结论正确的是( )A .函数f (x )为奇函数B .f (f (14))=19C .函数f (x )的图象关于直线y =x 对称D .函数f (x )在R 上是增函数【答案】 B【解析】 作出函数f (x )的图象,如图所示,可知A ,C ,D 均错.f (f (14))=3log 214=3-2=19,故B 正确.2.已知二次函数f (x )=ax 2-(a +2)x +1(a ∈Z ),且函数f (x )在(-2,-1)上恰有一个零点,则不等式f (x )>1的解集为( ) A .(-∞,-1)∪(0,+∞) B .(-∞,0)∪(1,+∞) C .(-1,0) D .(0,1)【答案】 C【解析】 ∵f (x )=ax 2-(a +2)x +1,Δ=(a +2)2-4a =a 2+4>0, ∴函数f (x )=ax 2-(a +2)x +1必有两个不同的零点. 又∵f (x )在(-2,-1)上有一个零点,则f (-2)f (-1)<0, ∴(6a +5)(2a +3)<0,解得-32<a <-56.又∵a ∈Z ,∴a =-1.不等式f (x )>1,即-x 2-x >0.解得-1<x <0. 3.函数f (x )=ln|x +cos x |的图象为( )【答案】 A【解析】 因为f (0)=ln|cos0|=0,故排除C ,D ;又f (1)=ln|1+cos1|>ln 1=0,故排 除B ,选A.4.设奇函数f (x )在(0,+∞)上为增函数,且f (2)=0,则不等式f (x )-f (-x )x <0的解集为( )A .(-2,0)∩(2,+∞)B .(-∞,-2)∪(0,2)C .(-∞,-2)∪(2,+∞)D .(-2,0)∪(0,2)【答案】 D【解析】 由已知条件可以画出函数f (x )的草图,如图所示.由函数f (x )为奇函数可化简不等式f (x )-f (-x )x <0为2f (x )x <0.若x >0,则需有f (x )<0,结合图象可知0<x <2;若x <0,则需有f (x )>0,结合图象可知-2<x <0.综上可知,不等式的解集为(-2,0)∪(0,2).5.实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +2≥0,2x -y -5≤0,x +y -4≥0,则z =|x +2y -4|的最大值为( )A.2155B .21C .20D .25【答案】 B【解析】 作出不等式组表示的平面区域,如下图中阴影部分所示.z =|x +2y -4|=|x +2y -4|5·5,即其几何含义为阴影区域内的点到直线x +2y -4=0的距离的5倍.由⎩⎪⎨⎪⎧x -y +2=0,2x -y -5=0,得B 点坐标为(7,9),显然点B 到直线x +2y -4=0的距离最大,此时z max=21.6.已知函数f (x )=|x -2|+1,g (x )=kx .若方程f (x )=g (x )有两个不相等的实根, 则实数k 的取值范围是( ) A .(0,12)B .(12,1)C .(1,2)D .(2,+∞)【答案】 B【解析】 在同一坐标系中分别画出函数f (x ),g (x )的图象如图所示,方程f (x )=g (x )有两个不相等的实根等价于两个函数的图象有两个不同的交点,结合图象可知,当直线y =kx 的斜率大于坐标原点与点(2,1)连线的斜率且小于直线y =x -1的斜率时符合题意,故12<k <1.7.若实数x ,y 满足|x -3|≤y ≤1,则z =2x +yx +y 的最小值为( )A.53 B .2 C.35D.12【答案】 A【解析】 依题意,得实数x ,y 满足⎩⎪⎨⎪⎧x +y -3≥0,x -y -3≤0,0≤y≤1,画出可行域如图阴影部分所示,其中A (3,0),C (2,1),z =2+yx 1+y x =1+11+y x ∈[53,2],故选A.8.设方程10x =|lg(-x )|的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1 D .0<x 1x 2<1【答案】 D【解析】 本题考查函数的性质.在同一坐标系下,画出函数y =10x 与y =|lg(-x )|的图象,结合图象不难看出,它们的两个交点中,其中一个交点横坐标属于(-∞,-1),另一个交点横坐标属于(-1,0),即在x 1,x 2中,其中一个属于(-∞,-1),另一个属于(-1,0),不妨设x 1∈(-∞,-1),x 2∈(-1,0),则有10x 1=|lg(-x 1)|=lg(-x 1),10x 2=|lg(-x 2)|=-lg(-x 2),10x 1-10x 2=lg(-x 1)+lg(-x 2)=lg(x 1x 2)<0,0<x 1x 2<1,故选D. 9.已知函数y =f (x )在(0,1)内的一段图象是如图所示的一段曲线,若0<x 1<x 2<1,则( )A.f (x 1)x 1<f (x 2)x 2B.f (x 1)x 1=f (x 2)x 2C.f (x 1)x 1>f (x 2)x 2D .不能确定【答案】 C【解析】 如图,设曲线上两点P 1(x 1,f (x 1)),P 2(x 2,f (x 2)),kOP 1=f (x 1)-0x 1-0=f (x 1)x 1,kOP 2=f (x 2)-0x 2-0=f (x 2)x 2,由于0<x 1<x 2<1,根据斜率与倾斜角之间的关系,显然有kOP 1>kOP 2,即f (x 1)x 1>f (x 2)x 2,故选C. 10.设关于x ,y 的不等式组⎩⎪⎨⎪⎧2x -y +2>0,x +m<0,y -m>0表示的平面区域内存在点P (x 0,y 0),满足x 0-2y 0=2,求m 的取值范围是( ) A .(-∞,43)B .(-∞,13)C .(-∞,-23)D .(-∞,-53)【答案】 C【解析】 作出不等式组所表示的平面区域,根据题设条件分析求解. 当m ≥0时,若平面区域存在,则平面区域内的点在第二象限,平面区域内不可能存在点P (x 0,y 0)满足x 0-2y 0=2,因此m <0. 如图所示的阴影部分为不等式组表示的平面区域.要使可行域内包含y =12x -1上的点,只需可行域边界点(-m ,m )在直线y =12x -1的下方即可,即m <-12m -1,解得m <-23. 11.在△AB C 中,|AB →+AC →|=|AB →-AC →|,AB =2,AC =1,E ,F 为BC 的三等分点,则AE →·AF→=( ) A.89 B.109 C.259 D.269【答案】 B【解析】 由|AB →+AC →|=|AB →-AC →|,化简得AB →·AC →=0,又因为AB 和AC 为三角形的两条边,不可能为0,所以AB →与AC →垂直,所以△ABC 为直角三角形.以AC 为x 轴,以AB 为y 轴建立平面直角坐标系,如图所示,则A (0,0),B (0,2),C (1,0),由E ,F 为BC 的三等分点知E (23,23),F (13,43),所以AE →=(23,23),AF →=(13,43),所以AE →·AF →=23×13+23×43=109. 12.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤45成立,则实数a的值为( ) A.15 B.25 C.12D .1 【答案】 A【解析】 (x -a )2+(ln x 2-2a )2表示点P (x ,ln x 2)与点Q (a ,2a )距离的平方. 而点P 在曲线g (x )=2ln x 上,点Q (a ,2a )在直线y =2x 上.因为g ′(x )=2x ,且y =2x 表示斜率为2的直线,所以由2x=2,解得x =1.从而曲线g (x )=2ln x 在x =1处的切线方程为y =2(x -1),又直线y =2(x -1)与直线y =2x 平行,且它们间的距离为222+(-1)2=255,如图所示.故|PQ |的最小值为255,即f (x )=(x -a )2+(ln x 2-2a )2的最小值为(255)2=45,当|PQ |最小时,P 点的坐标为(1,0),所以2a -0a -1×2=-1,解得a =15.13.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( ) A.72 B.52 C .3 D .2【答案】 C【解析】 利用FP →=4FQ →转化长度关系,再利用抛物线定义求解. ∵FP →=4FQ →, ∴|FP →|=4|FQ →|. ∴|PQ||PF|=34.如图,过Q 作QQ ′⊥l ,垂足为Q ′,设l 与x 轴的交点为A ,则|AF |=4. ∴|PQ||PF|=|QQ′||AF|=34.∴|QQ ′|=3. 根据抛物线定义可知|QQ ′|=|QF |=3,故选C.14.已知双曲线C :x 2a 2-4y 2=1(a >0)的右顶点到其一条渐近线的距离等于34,抛物线E :y 2=2px 的焦点与双曲线C 的右焦点重合,则抛物线E 上的动点M 到直线l 1:4x -3y +6=0和l 2:x =-1的距离之和的最小值为( ) A .1 B .2 C .3 D .4【答案】 B【解析】 x 2a 2-4y 2=1的右顶点坐标为(a ,0),一条渐近线为x -2ay =0.由点到直线的距离公式得d =|a|12+4a 2=34,解得a =32或a =-32(舍去),故双曲线的方程为4x 23-4y 2=1.因为c =34+14=1,故双曲线的右焦点为(1,0),即抛物线的焦点为(1,0),所以p =2,x =-1是抛物线的准线,如图,作MA ⊥l 1于点A ,MB ⊥l 2于点B ,设抛物线的焦点为F ,连接MF ,则由抛物线的定义知|MB |=|MF |,当M ,A ,F 三点共线时,距离之和最小,其最小值是点F 到l 1的距离,由点到直线的距离公式可得d 1=|4+6|(-3)2+42=105=2,即距离之和的最小值为2,选B.二、填空题15.已知函数y =|x 2-1|x -1的图象与函数y =kx -2的图象恰有两个交点,则实数k 的取值范围是__________.【答案】 (0,1)∪(1,4) 【解析】 根据绝对值的意义,y =|x 2-1|x -1=⎩⎪⎨⎪⎧x +1,x>1或x<-1,-x -1,-1≤x<1.在直角坐标系中作出该函数的图象,如下图中实线所示.根据图象可知,当0<k <1或1<k <4时有两个交点.16.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x .那么,不等式f (x +2)<5的解集是________. 【答案】 (-7,3)【解析】 当x ≥0时,f (x )=x 2-4x <5的解集为[0,5),又f (x )为偶函数,所以f (x )<5的解集为(-5,5).所以f (x +2)<5的解集为(-7,3).17.已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y -3≤0,x +3y -3≥0,y -1≤0,则F (x ,y )=log 2(y +1)+log 12(x +1)的最小值为________. 【答案】 -2【解析】 F (x ,y )=log 2(y +1)+log 12(x +1)=log 2(y +1)-log 2(x +1)=log 2y +1x +1,令k =y +1x +1=y -(-1)x -(-1),则k 表示可行域内(如图所示)的点与P (-1,-1)所在直线的斜率.18.已知直线y =x -2与圆x 2+y 2-4x +3=0及抛物线y 2=8x 的四个交点从上面依次为A ,B ,。