工程力学第六章答案梁的变形
- 格式:doc
- 大小:626.50 KB
- 文档页数:16
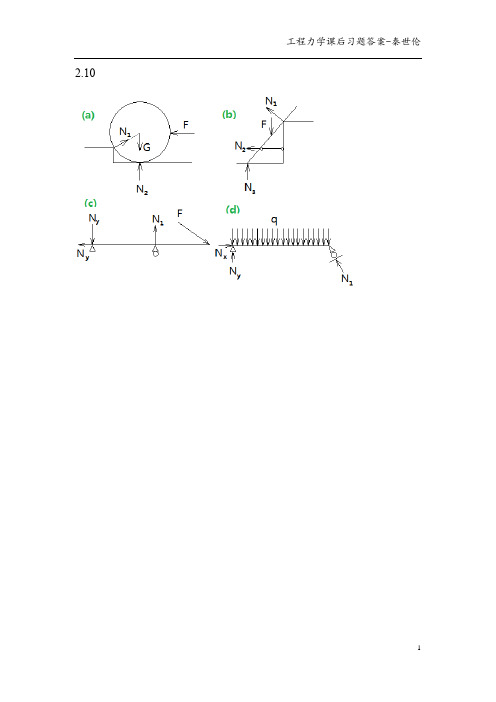
3.3 图3.3所示钢架的点B 作用一个水平力F ,钢架重量忽略不计。
求支座A 、D 的约束力。
解:由图3.3可以确定D 点受力的方向,这里将A 点的力分解为x 、y 方向,如图3.3.1 根据力与矩平衡有)2(:)(0:)(0:)(=-=-=-∑∑∑FL L F A M F F y F F F x F Dy Dx (1)解上面三个方程得到 )(2),(2),(↑=↓=←=F F F F F F D y x3.5如图3.5铰链四杆机构ABCD 的CD 边固定,在铰链A 、B 处有力F1、F2作用,如图所示。
该机构在图示位置平衡,杆重忽略不计。
求力F1和力F2的关系。
解:(1)对A 点分析,如图3.5.1,设AB 杆的内力为T ,则将力投影到垂直于AC 方向的AM 上有0)15cos()30cos(:)(1=︒-︒∑T F AM F ①图3.5(2)对B 点分析,如图3.5.2,将力投影到垂直于BD 方向的BN 有 0)30cos()60cos(:)B N (2=︒-︒∑T F F ②由①、②可得 22108593790.64395055332F F F ≈+=3.8如图3.8有5根杆件组成的结构在A 、B 点受力,且CA 平行于DB ,CA DE BE DB ===。
F=20kN,P=12kN 。
求BE 杆的受力。
解:(1)对A 点受力分析,将力投影到垂直于AC 方向的AN 上有060sin :)(=-︒∑F FAN F AB①(2)对B 点受力分析,如图3.8.2.将力投影到垂直于BD 方向的BM 上有060cos 60sin 30cos :)B M (=︒-︒-︒∑P F FF BE AB②由①、②可得373095kN 16.1658075kN 328≈=BE F (方向斜向上)3.9如图(见书上)所示3根杆均长2.5m ,其上端铰结于K 处,下端A 、B 、C 分别与地基铰结,且分布在半径r=1.5m 的圆周上,A 、B 、C 的相对位置如图所示。

工程力学习题答案6廖明成第六章 杆类构件的内力分析习 题6.1 试求图示结构1-1和2-2截面上的内力,指出AB 和CD 两杆的变形属于哪类基本变形,并说明依据。
(a )(b )题6.1图解:(a )应用截面法:对题的图取截面2-2以下部分为研究对象,受力图如图一所示:BM图一图二由平衡条件得:0,AM=∑6320N F ⨯-⨯=解得:NF =9KNCD 杆的变形属于拉伸变形。
应用截面法,取题所示截面1-1以右及2-2以下部分作为研究对象,其受力图如图二所示,由平衡条件有: 0,OM =∑ 6210NF M ⨯-⨯-= (1)0,yF =∑ 60NSF F --=(2)将NF =9KN 代入(1)-(2)式,得:M=3 kN·mSF =3 KNAB 杆属于弯曲变形。
(b )应用截面法 ,取1-1以上部分作为研究对象,受力图如图三所示,由平衡条件有:0,Fx =∑20NF -=图三F NMNF =2KN0,DM =∑ 210M -⨯=M=2KNAB 杆属于弯曲变形6.2 求图示结构中拉杆AB 的轴力。
设由AB 连接的1和2两部分均为刚体。
题6.2图解:首先根据刚体系的平衡条件,求出AB杆的内力。
刚体1的受力图如图一所示D图一 图二平衡条件为:0,CM=∑104840D N F F ⨯-⨯-⨯=(1)刚体2受力图如图二所示,平衡条件为:0,EM =∑ 240NDF F ⨯-⨯=(2)解以上两式有AB 杆内的轴力为:NF =5KN6.3 试求图示各杆件1-1、2-2和3-3截面上的轴力,并做轴力图。
(a )C(b )(c )(d )题6.3图解:(a ) 如图所示,解除约束,代之以约束反力,做受力图,如图1a 所示。
利用静力平衡条件,确定约束反力的大小和方向,并标示在图1a 中,作杆左端面的外法线n ,将受力图中各力标以正负号,轴力图是平行于杆轴线的直线,轴力图线在有轴向力作用处要发生突变,突变量等于该处总用力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,轴力图如2a 所示,截面1和截面2上的轴力分别为1N F =-2KN2N F =-8KN ,(a )nkN(a 1)(2)C(b )CBkNb 1)(b 2)((b )解题步骤和(a )相同,杆的受力图和轴力图如(1b )(2b )所示,截面1和截面2上的轴力分别为1N F =4KN 2N F =6KN(c )解题步骤和(a )相同,杆的受力图和轴力图如(1c )(2c )所示,截面1,截面2和截面3上的轴力分别为1N F =3F 2N F =4F ,3NF =4FB C(c )4F(c 1)(c 2)(d)A D(d 1)(d 2)(d )解题步骤和(a )相同,杆的受力图和轴力图如(1d )(2d )所示,截面1和截面2上的轴力分别为1N F =2KN 2N F =2KN6.4 求图示各轴1-1、2-2截面上的扭矩,并做各轴的扭矩图。

一、单选题1、研究梁的变形的目的是()。
A.进行梁的正应力计算B.进行梁的刚度计算C.进行梁的稳定性计算D.进行梁的剪应力计算正确答案:B2、图示圆截面悬臂梁,若直径d增大1倍(其它条件不变),则梁的最大正应力、最大挠度分别降至原来的()。
A.1/2 1/4B.1/4 1/8C.1/8 1/8D.1/8 1/16正确答案:D3、下面关于梁、挠度和转角的讨论中,正确的结论是()。
A.挠度最大的截面转角为零B.挠度最大的截面转角最大C.转角为零的截面挠度最大D.挠度的一阶导数等于转角正确答案:D4、已知两悬臂梁的抗弯截面刚度EI相同,长度分别为l和2l,在自由端各作用F1和F2,若二者自由端的挠度相等,则F1/F2=()。
A.2B.4C.6D.8正确答案:D5、梁上弯矩为零处()。
A.梁的转角一定为零B.梁的挠度一定为零C.挠度一定为零,转角不一定为零D.梁的挠曲线的曲率一定为零正确答案:D6、已知等直梁在某段上的挠曲轴方程w(x)=–Cx4,C为常量,则在该段梁上()。
A.分布载荷是x的一次函数B.分布载荷是x的二次函数C.无分布载荷作用D.有均匀分布载荷作用正确答案:D7、在等直梁弯曲变形中,挠曲线曲率最大值发生在()。
A.剪力最大处B.转角最大处C.弯矩最大处D.挠度最大处正确答案:C8、材料相同的(a)悬臂梁和(b)悬臂梁,长度也相同,在自由端各作用2P和P,截面形状分别是b(宽)×2b(高)、b×b。
关于它们的最大挠度正确的是()。
A.(a)梁最大挠度是(b)梁的1/4倍B.(a)梁最大挠度是(b)梁的1/2倍C.(a)梁最大挠度与(b)梁的相等D.(a)梁最大挠度是(b)梁的2倍正确答案:A9、已知简支梁的EI为常数,在梁的左端和右端分别作用一力偶m1和m2今欲使梁的挠曲线在x=l/3处出现一拐点,则比值m1/m2为()。
A.2B.3C.1/2D.1/3正确答案:C10、两根梁尺寸,受力和支承情况完全相同,但材料不同,弹性模量分别为E1和E2,且E1=7E2,则两根梁的挠度之比y1/y2为()。


工程力学知到章节测试答案智慧树2023年最新重庆大学第一章测试1.变形固体的基本假设是()。
参考答案:连续、均匀性假设和各向同性假设;2.要使构件安全、正常地工作,必须满足()。
参考答案:强度要求、刚度要求、稳定性要求第二章测试1.平衡是指物体相对于惯性参考系保持静止或作匀速转动的状态。
()参考答案:错2.根据力的平行四边形法,作用于同一物体上的两个力都可以合成为一个合力。
()参考答案:错3.变形体在两个大小相等、方向相反、作用线沿同一直线的力作用下不一定能维持平衡。
()参考答案:对4.受力图中各约束反力的作用线方位及指向(除柔索和光滑接触面约束外)一般自己假定。
()参考答案:对5.下列关于刚体的描述,不正确的是()。
参考答案:变形极小的物体就可视为刚体6.下列关于约束反力的表述中,不正确的是()。
参考答案:约束反力的大小和方向由约束构造特点确定7.如题图所示体系,构件自重不计,则支座A处约束反力作用线方位正确的是()。
参考答案:沿AE8.如题图所示体系,构件自重不计,则受力分析图不正确的是()。
参考答案:第三章测试1.在任何坐标系中,力都可以用其在坐标轴上的投影解析表示。
()参考答案:错2.力对某轴之矩等于力对轴上任一点之矩在该轴上的投影。
()参考答案:对3.只要保持力偶矩不变,力偶可在其作用面内任意移动和转动,都不会改变原力偶对物体的作用效应。
()参考答案:错4.力系向某点简化,其主矢和主矩都不为零,且主矢和主矩正交,则该力系可以继续简化为一合力。
()参考答案:错5.作用在一个刚体上的两力,满足的条件,则该二力可能是()。
参考答案:一对平衡的力或一个力偶6.某平面力系向其平面内A点简化的结果为:,则该力系向其平面内任选的另一点B简化的结果为()。
参考答案:7.下列关于力平移的表述中,正确的是()。
参考答案:作用在刚体上的力可以沿其作用线平移到该刚体上任一点,其作用效应不变8.各力作用位置如图所示的平面力系中,已:F1=4kN,F2=3kN,q=2kN/m,M1=100N·m,M2=200N·m。


工程力学试题及答案(六)-2012一、填空题(每空1分,共44分)1.在分析两个或多个构件之间互相作用时,要注意________力与________力的关系。
2.作用于平面内A点的力F=10kN,如图示,向距A点为100cm的O点平移后,得到主矢量的大小为________和主矩大小为________。
3.设有一个力F,当力F与________轴________但________时有力F在X轴上的投影F X=0,力F对x轴之矩m x(F)≠0。
4.由平面假设所得到的轴向变形时,截面上的计算公式σ=N/A中的σ是________,这个公式不仅适用于________变形,而且也适用于________变形。
5.已知主动轮A输入功率为80马力,从动轮B和C输出功率为30马力和50马力,传动轴的转速n=1400转/分,那么,各轮上的外力偶矩的大小分别为m A=____ ,m B=______, m C=______。
6.图示结构中固定端A的反力为________、________、________。
7.图示各结构是静定还是静不定,及其静不定次数。
图(a)是________,(b)是________,(c)是________。
8.力的可传原理只适用于________体,而不适用于________体,因此不适用于研究力对物体的________效应。
9.若截面对于y轴和z轴的惯性积I yz=0,则此对轴称为________轴,若此对轴又通过形心,则称此对轴为________轴。
对称图形中含有对称轴的一对坐标轴必为________轴。
10.图示是梁的左段,A点力2P为反力,B点作用力P,C点作用力偶Pa,此时截面C的剪力Q C=________,弯矩M C=________。
11.矩形截面弯曲剪应力公式为τ=SI bZZ*,其中S*z是所求剪应力的点,画平行于中性轴的横线________截面面积对中性轴的面积矩,因此S*z是________量,截面上的最大剪应力发生在________。

1-1五个力作用于一点O,如图示。
图中方格的边长为10mm 。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =669.5N , ∠(F R,i )=34.901-2如图示平面上的三个力F1=100N,F2=50N,F3=50N,三力作用线均过A点,尺寸如图。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =161.2N , ∠(F R,F i)=29.701-3试计算下列各图中的力F对点O之矩。
解题思路:各小题均由式(1-16)求力矩。
答案:略1-4如图所示的挡土墙重G 1=75 kN ,铅直土压力G 2=120 kN ,水平土压力F p =90 kN 。
试求三力对前趾A 点之矩的和,并判断挡土墙是否会倾倒。
解题思路:(1)由式(1-16)求三力对前趾A 点之矩的代数和; (2)若其值为负(顺时针转),则挡土墙不会翻倒。
答案:∑M A =-180kN.m ,不会倾倒。
1-5如图所示,边长为a 的正六面体上沿对角线AH 作用一力F 。
试求力F 在三个坐标轴上的投影,力F 对三个坐标轴之矩以及对点O 之矩矢。
解题思路:(1)由式(1-13)、(1-14)、(1-15)求合力的大小和方向; (2)由式(1-25)求力对三个坐标轴之矩; (3)由式(1-26)求力对坐标原点之矩。
答案:M x =0,Fa M y 33=,Fa M 33z =-, k Fa j Fa M O 3333-=1-7试画出下列各图中物体A ,构件AB 的受力图。
未画重力的物体重量不计,所有接触面均为光滑接触。
解题思路:(1)画出研究对象的轮廓形状; (2)画出已知的主动力;(3)在解除约束处按约束的性质画出约束力。

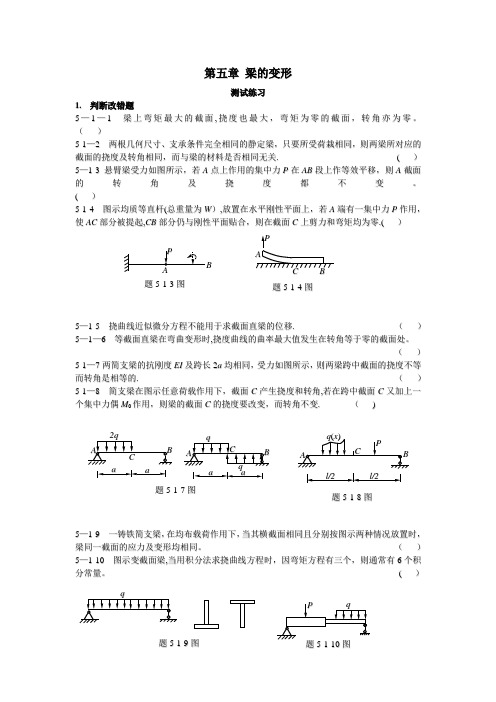
第五章 梁的变形测试练习1. 判断改错题5—1—1 梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零。
( )5-1—2 两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关. ( ) 5—1-3 悬臂梁受力如图所示,若A 点上作用的集中力P 在A B 段上作等效平移,则A 截面的转角及挠度都不变。
( )5-1-4 图示均质等直杆(总重量为W ),放置在水平刚性平面上,若A 端有一集中力P 作用,使A C 部分被提起,C B 部分仍与刚性平面贴合,则在截面C 上剪力和弯矩均为零.( )5—1-5 挠曲线近似微分方程不能用于求截面直梁的位移. ( ) 5—1—6 等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
( ) 5-1—7两简支梁的抗刚度E I 及跨长2a 均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的. ( ) 5-1—8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁的截面C 的挠度要改变,而转角不变. ( )5—1-9 一铸铁简支梁,在均布载荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力及变形均相同。
( ) 5—1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量。
( )题5-1-3图题5-1-4图题5-1-8图题5-1-7图题5-1-9图2.填空题5-2—1 挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在和。
5—2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则=21P P 。
5-2-3 应用叠加原理求梁的变形时应满足的条件是:。
5-2—4 在梁的变形中挠度和转角之间的关系是。
5—2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是,连续条件是.5—2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是,连续条件是。

第8章 弯曲变形本章要点【概念】平面弯曲,剪力、弯矩符号规定,纯弯曲,中性轴,曲率,挠度,转角。
剪力、弯矩与荷载集度的关系;弯曲正应力的适用条件;提高梁的弯曲强度的措施;运用叠加法求弯曲变形的前提条件;截面上正应力分布规律、切应力分布规律。
【公式】 1. 弯曲正应力 变形几何关系:yερ=物理关系:Ey σρ=静力关系:0N AF dA σ==⎰,0y AM z dA σ==⎰,2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率:1MEIρ=弯曲正应力应力:,My Iσ=,max max z M W σ=弯曲变形的正应力强度条件:[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力:bI S F y z z S ⋅⋅=*)(τ,A F bh F S S 2323max ==τ工字形梁弯曲切应力:dI S F y z z S ⋅⋅=*)(τ,A F dh F S S ==max τ圆形截面梁弯曲切应力:bI S F y z z S ⋅⋅=*)(τ,A F S 34max =τ弯曲切应力强度条件:[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程:()''EIw M x =-梁的转角方程:1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程:12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、 建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有()。
查看答案A 、平衡关系,物理关系,变形几何关系B 、变形几何关系,物理关系,静力关系;C 、变形几何关系,平衡关系,静力关系D 、平衡关系, 物理关系,静力关系;2、 利用积分法求梁的变形,不需要用到下面那类条件()来确定积分常数。
查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、 在图1悬臂梁的AC 段上,各个截面上的()。

工程力学习题答案第一章 静力学基础知识思考题:1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1.根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在A 、B 、C 三处受力作用。
由于力和的作用线交于点O 。
如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
(b )同上。
由于力和的作用线 交于O 点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
2.不计杆重,画出下列各图中AB 杆的受力图。
解:(a )取杆AB 为研究对象,杆除受力外,在B 处受绳索作用的拉力,在A 和E 两处还受光滑接触面约束。
约束力和的方向分别沿其接触表面的公法线,并指向杆。
其中力与杆垂直,力通过半圆槽的圆心O 。
AB 杆受力图见下图(a )。
(b)由于不计杆重,曲杆BC 只在两端受铰销B 和C 对它作用的约束力和,故曲杆BC 是二力构件或二力体,此两力的作用线必须通过B 、C 两点的连线,且=。
研究杆AB ,杆在A 、B 两点受到约束反力和,以及力偶m 的作用而平衡。
根据力偶的性质,和必组成一力偶。
(d)由于不计杆重,杆AB 在A 、C 两处受绳索作用的拉力和,在B 点受到支座反力。
和相交于O 点,根据三力平衡汇交定理,可以判断必沿通过pB RpB Rp B T A N E N E N A N B N C N BN CN A N B N A N B N A T C T B N A T C TB NB、O两点的连线。
见图(d).第二章 力系的简化与平衡思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1. 平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm ,求此力系向O 点简化的结果,并确定其合力位置。
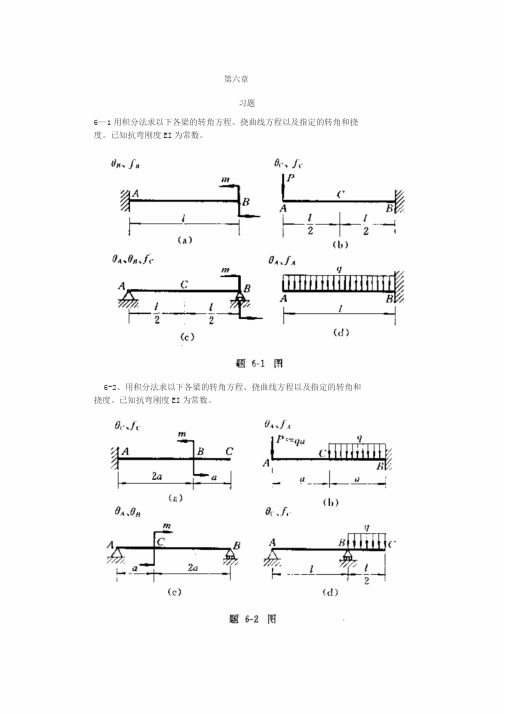
第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。

大学工程力学试题及答案一、选择题(每题2分,共20分)1. 以下哪项不是材料力学中的基本假设?A. 均匀性假设B. 连续性假设C. 各向同性假设D. 各向异性假设答案:D2. 梁的弯曲应力公式为:A. σ = (M/I) * (y/R)B. σ = (M/I) * (R/y)C. σ = (M/I) * (y/R)D. σ = (M/I) * (R/y)答案:C3. 弹性模量E的单位是:A. N/mB. N/m²C. PaD. J/m³答案:C4. 以下哪种材料不属于脆性材料?A. 玻璃B. 陶瓷C. 橡胶D. 混凝土答案:C5. 根据能量守恒定律,以下说法不正确的是:A. 机械能守恒B. 能量可以无中生有C. 能量可以转化为其他形式D. 能量守恒定律适用于所有物理过程答案:B6. 静定结构与超静定结构的主要区别在于:A. 材料种类B. 受力情况C. 几何形状D. 约束数量答案:D7. 以下哪种情况不属于平面力系的平衡条件?A. 合力为零B. 合力矩为零C. 合外力为零D. 合外力矩为零答案:C8. 梁的剪力图和弯矩图可以用来确定:A. 梁的变形B. 梁的内力C. 梁的自重D. 梁的外力答案:B9. 梁的挠度与弯矩之间的关系是:A. 线性关系B. 非线性关系C. 没有关系D. 反比关系答案:B10. 以下哪种方法不适用于解决超静定结构问题?A. 弯矩分配法B. 力法C. 位移法D. 能量法答案:A二、填空题(每题2分,共20分)1. 材料的弹性模量E与泊松比μ之间的关系是E = _______。
答案:2G(1+μ)2. 梁在纯弯矩作用下,其横截面上的应力分布为_______。
答案:线性分布3. 在静力平衡状态下,一个物体的合力为_______。
答案:零4. 材料力学中的胡克定律表明,在弹性范围内,材料的应力与应变之间存在_______关系。
答案:线性5. 梁的弯矩与截面的惯性矩I成_______关系。


面试工程力学试题库及答案填空1.所谓平衡,是指物体相对于地球处于静止或作___的状态。
答案:匀速直线运动题型:填空题2.对空间平面一般力系,可列的独立方程数目为6个;对平面一般力系,可列的独立方程数目为________;对平面汇交力系,可列的独立方程数目为___。
答案:3个|2个题型:填空题3.梁的三种类型为___、___和___。
答案:简支梁|悬臂梁|外伸梁4.构件的承载能力主要包括构件的强度、___、和___ 三方面的要求。
答案:刚度|稳定性题型:填空题5.梁的变形用挠度和___来量度。
答案:挠度题型:填空题6.材料力学里的的五个假设分别是___ 假设、___ 假设、___假设、___ 假设、___ 假设。
答案:连续性|均匀性|各向同性|小变形|完全弹性题型:填空题7、应力状态的分类为___ 、___ 和___ 。
答案:三向应力状态|二向应力状态|单向应力状态题型:填空题8、四种常见的强度理论是___、___、_________和______ 。
答案:最大拉应力理论|最大拉应变理论|最大切应力理论|畸变能理论题型:填空题9.力系平衡的充分与必要条件是:该力系的___ 和对同一点的___ 都等于零。
答案:主矢|主矩题型:填空题10. 对空间平面一般力系,可列的独立方程数目为___个;对平面一般力系,可列的独立方程数目为___ ;对平面汇交力系,可列的独立方程数目为___。
答案:6个|3个|2个题型:填空题11.处理组合变形的四个步骤是:外力分析、___ 、___ 和___ 。
答案:内力分析|应力分析|强度计算题型:填空题12.轴向拉伸和压缩时,斜截面上正应力和切应力的公式是:___ 、___ 。
答案:σα=σ.cos2α|τα=\frac{1}{2}21σsin2α题型:填空题13.低碳钢在整个拉伸过程中可分为四个阶段,分别是___ 、___ 、___ 、和___。
答案:弹性阶段|屈服阶段|强化阶段|局部变形阶段题型:填空题14.利用强度条件,可以解决三种类型的强度计算问题,它们是___ 、___ 和______。

工程力学[单项选择题]1、力对点之矩和力偶对点之矩,与矩心位置的关系是()。
A.都与矩心的位置无关B.都与矩心的位置有关C.力对点之矩与矩心的位置有关,力偶对点之矩与矩心的位置无关D.无法确定参考答案:C[单项选择题]2、已知构件受力如图所示,不计自重,支座A的约束力方向是()。
A.沿AB的连线B.沿AC的连线C.沿AD的连线D.无法确定方向参考答案:B[单项选择题]3、铰接三杆机构OABO1在图示位置平衡,各杆自重不计。
已知OA=40cm,O1B=60cm,作用在OA上的力偶矩M=1N.M。
力偶矩M2的大小是()。
1A.1N.MB.2N.MC.3N.MD.5N.M参考答案:C[单项选择题]4、力偶对物体的作用效应决定于()。
A.力偶矩的大小B.力偶的转向C.力偶的作用平面D.力偶矩的大小、力偶的转向、力偶的作用平面参考答案:D[单项选择题]5、已知梁上作用一力偶M,梁长为l,梁重不计,支座A和B的约束力为()。
A.AB.BC.CD.D参考答案:B[单项选择题]6、曲柄连杆活塞机构的活塞上受力F=400N。
如不计所有构件的重量,在曲柄上应加多大的力偶矩M是()才能使机构在图示位置平衡。
A.AB.BC.CD.D参考答案:C[单项选择题]7、两个共点力可合成一个力,一个力也可分解为两个相交的力。
一个力分解为两个相交的力可以有()个解。
A.1B.2C.3D.无穷参考答案:D[单项选择题]8、水平梁受三角形载荷作用,分布载荷的最大值为qkN/m,梁长为1,与之等效合力的大小和位置分别是()。
A.AB.BC.CD.D参考答案:B[单项选择题]9、图所示重为P=100N的物体放在水平面上,静摩擦系数F=0.3,动摩擦系数F=0.25,水平推力P=10N,则摩擦力等于()。
A.0NB.10NC.25ND.30N参考答案:B[单项选择题]10、已知某平面力系简化的最后结果为一合力,若将此平面力系向作用面内其它任一点0简化,则主矢FR 和主矩M()。

第六章 杆类构件的内力分析6.1。
(a )(b )题6.1图解:(a )应用截面法:对题的图取截面2-2以下部分为研究对象,受力图如图一所示:BM图一图二由平衡条件得:0,AM=∑6320N F ⨯-⨯=解得: N F =9KN CD 杆的变形属于拉伸变形。
应用截面法,取题所示截面1-1以右及2-2以下部分作为研究对象,其受力图如图二所示,由平衡条件有:0,OM=∑6210N F M ⨯-⨯-=(1)0,yF=∑60N S F F --=(2)将N F =9KN 代入(1)-(2)式,得: M =3 kN·m S F =3 KN AB 杆属于弯曲变形。
(b )应用截面法 ,取1-1以上部分作为研究对象,受力图如图三所示,由平衡条件有:0,Fx =∑20NF-=图三MNF =2KN0,DM=∑210M -⨯= M =2KNAB 杆属于弯曲变形 6.2题6.2图解:首先根据刚体系的平衡条件,求出AB 杆的内力。
刚体1的受力图如图一所示D2m图一图二平衡条件为:0,CM=∑104840D N F F ⨯-⨯-⨯=(1) 刚体2受力图如图二所示,平衡条件为:0,EM=∑240N D F F ⨯-⨯= (2)解以上两式有AB 杆内的轴力为:N F =5KN6.3(a )(c )题6.3图解:(a ) 如图所示,解除约束,代之以约束反力,做受力图,如图1a 所示。
利用静力平衡条件,确定约束反力的大小和方向,并标示在图1a 中,作杆左端面的外法线n ,将受力图中各力标以正负号,轴力图是平行于杆轴线的直线,轴力图线在有轴向力作用处要发生突变,突变量等于该处总用力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,轴力图如2a 所示,截面1和截面2上的轴力分别为1N F =-2KN 2N F =-8KN ,n (b 2 (面N F题6.4图解(a )如图所示,分别沿1-1,2-2截面将杆截开,受力图如1a 所示,用右手螺旋法则,并用平衡条件可分别求得:1T =16 kN·m 2T =-20 kN·m ,根据杆各段扭矩值做出扭矩图如2a 所示。

工程力学知到章节测试答案智慧树2023年最新贵州理工学院第一章测试1.力对物体的作用效应取决于力的三要素,分别是()。
参考答案:力的大小;力的方向;力的作用点2.作用于刚体上的力,可以沿其作用线移至刚体内任意一点,而不改变它对刚体的作用效应。
()参考答案:对3.受力后几何形状和尺寸均保持不变的物体称为()。
参考答案:刚体4.两物体间相互作用的力总是同时存在,并且两力等值、反向共线,作用在同个物体上。
()参考答案:错5.柔体约束特点是限制物体沿绳索伸长方向的运动,只能给物体提供拉力。
()参考答案:对第二章测试1.指出以下力的多边形中,合力为零的有()。
参考答案:;2.F1、F2、F3及F4是作用在刚体上的平面汇交力系,其力矢之间的关系如图,这个汇交力系的合力FR为()。
参考答案:3.平面汇交力系有()个独立平衡方程。
参考答案:24.刚架ABCD,不计自重,仅受力F作用,铰链A反力F的作用线必定()。
参考答案:通过C点5.作用在物体上的多个力,如果各个力的作用线汇交于一点,这样的力系就称为平面汇交力系。
()错第三章测试1.力偶无合力,且力偶只能用力偶来等效。
()参考答案:对2.扳手所受力如图,已知,力F对O点之矩为()。
0.69kN·m3.关于力偶性质的下列说法中,正确的是()。
参考答案:力偶对其作用面上任意点之矩均相等,与矩心位置无关;力偶无合力;若力偶矩的大小和转动方向不变,可同时改变力的大小和力偶臂的长度,作用效果不变4.力偶对物体有移动效应。
()参考答案:错5.力的作用线通过矩心时,力矩为零。
()参考答案:对第四章测试1.司机操纵方向盘驾驶汽车时,可用双手对方向盘施加一个力偶,也可用单手对方向盘施加一个力,这两种方式能取得相同的效果,说明一个力与一个力偶可以等效。
()参考答案:错2.力线平移定理认为,作用在刚体上的力F可以平行移到刚体内任一点,但必须同时附加一个力偶,其力偶矩等于原力F对平移点的矩。

工程力学_浙江大学中国大学mooc课后章节答案期末考试题库2023年1.关于磁悬浮列车减小摩擦的方法,正确的说法是参考答案:使摩擦面脱离接触2.材料不同的两物块A和B叠放在水平面上,其中物块A放在物块B上,物块B放在地面上。
在物块B上作用一力,已知物块A重0.5kN,物块B重0.2kN,物块A、B间的摩擦系数f1=0.25,物块B与地面间的摩擦系数f2=0.2,拉动B物块所需要的最小力为参考答案:0.14kN3.一物块重600N,放在不光滑的平面上,静摩擦因数fs=0.3,动摩擦因数f=0.2,在左侧有一推力150N,物块有向右滑动的趋势。
则其此时所受的摩擦力以及最大静摩擦力分别是多少参考答案:150N、180N4.零杆不受力,所以它是桁架中不需要的杆,可以撤除参考答案:错误5.用10N的力拉着木箱在水平面上运动时,木箱受到的摩擦力是10N参考答案:错误6.用50N的力推桌子没有推动,是因为推力小于摩擦力参考答案:错误7.重心和形心是否重合取决于材料是否匀质参考答案:正确8.物体越重受到的摩擦力就越大参考答案:错误9.材料经过冷作硬化后,其比例极限和塑性分别参考答案:提高,下降10.假设一拉伸杆件的弹性模量E=300GPa,比例极限为 sp=300MPa,杆件受一沿轴线的拉力,测得轴向应变为e=0.0015,则该拉应力s的大小为参考答案:300MPa£s£450MPa11.受轴向拉伸的杆件,其最大切应力与轴线的角度为4512.一等直拉杆在两端承受拉力作用,若其一段为钢,另一段为铝,则两段的参考答案:应力相同,变形不同13.脆性材料与塑性材料相比,其拉伸性能的最大特点是参考答案:没有明显的屈服阶段和塑性变形14.现有一两端固定、材料相同的阶梯杆,其大径与小径的横截面积之比为4:1,杆的大径与小径长度相同,在大径与小径交界处施加一轴向力P,则杆的大径与小径所受轴力之比为参考答案:4:115.在低碳钢的拉伸实验中,材料的应力变化不大而变形显著增加的是参考答案:屈服阶段16.下列结论中哪些是正确的?①若压杆中的实际应力不大于该压杆的临界应力,则杆件不会失稳;②受压杆件的破坏均由失稳引起;③压杆临界应力的大小可以反映压杆稳定性的好坏;④若压杆中的实际应力大于scr=πE2/λ2,则压杆必定破坏。
第五章 梁的变形测试练习1. 判断改错题5-1-1 梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零. ( )5-1-2 两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
( ) 5-1-3 悬臂梁受力如图所示,若A 点上作用的集中力P 在A B 段上作等效平移,则A 截面的转角及挠度都不变。
( ) 5-1-4 图示均质等直杆(总重量为W ),放置在水平刚性平面上,若A 端有一集中力P 作用,使A C 部分被提起,C B 部分仍与刚性平面贴合矩均为零。
( )5-1-5挠曲线近似微分方程不能用于求截面直梁的位移。
( ) 5-1-6 等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
( ) 5-1-7两简支梁的抗刚度E I 及跨长2a 均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的。
( ) 5-1-8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁的截面C 的挠度要改变,而转角不变。
( )题5-1-3图 B 题5-1-4图 C 2 2 题5-1-8图题5-1-7图5-1-9 一铸铁简支梁,在均布载荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力及变形均相同。
( ) 5-1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量。
( )2.填空题5-2-1 挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在 和 。
5-2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则=21P P 。
5-2-3 应用叠加原理求梁的变形时应满足的条件是: 。
5-2-4 在梁的变形中挠度和转角之间的关系是 。
5-2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是 ,连续条件是 。
5-2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是 ,连续条件是 。
5-2-7 图示结构为 次超静定梁。
题5-1-9图题5-1-10图题5-2-2图题5-2-7图C 题5-2-6图2 x 题5-2-5图C5-2-8 纯弯曲梁段变形后的曲率与外力偶矩M 的关系为 ,其变形曲线为 曲线。
5-2-9 两根E I 值相同、跨度之比为1:2的简支梁,当承受相同的均布荷载q 作用时,它们的挠度之比为 。
5-2-10 当梁上作用有均布荷载时,其挠曲线方程是x 的 次方程。
梁上作用有集中力时,挠曲线方程是x 的 次方程。
梁上作用有力偶矩时,挠曲线方程是x 的 次方程。
5-2-11 图示外伸梁,若A B 段作用有均布荷载,B C 段上无荷载,则A B 段挠曲线方程是x 的 次方程;B C 段挠曲线方程是x 的 次方程。
5-2-12 减小梁变形的主要途径有: , , 。
5-2-13 已知梁的挠度曲线方程为)3(6)(2x l EIPx x y -=,则该梁的弯矩方程为 。
5-2-14 梁的变形中,挠度和截面弯矩M 的关系是 ,挠度和截面剪力Q 的关系是 。
5-2-15 为使图示A B 段的挠曲线为一直线,则x = 。
5-2-16 要使图示简支梁的挠曲线的拐点位于距A 端l /3处,则M 1:M 2= 。
5-2-17 图示静定梁,其B D 上无荷载作用,若已知B 截面的挠度y B ,则C 截面的挠度y C = ,D 截面的转角θD = 。
题5-2-11图A题5-2-17图2 32题5-2-16图题5-2-15图3.选择题5-3-1 简支梁长为l ,跨度中点作用有集中力P ,则梁的最大挠度f =( ) (E I =常量)A .EI Pl 483B .EI Pl 484C .EI Pl 38455D .EIPl 335-3-2 悬臂梁长为l ,梁上作用有均布荷载q ,则自由端截面的挠度为。
( )A .EI ql 64B .EI ql 63C .EI ql 84D .EIql 835-3-3 两梁尺寸及材料均相同,而受力如图示,则两梁的 A . 弯矩相同,挠曲线形状不相同 B . 弯矩相同,挠曲线形状相同 C . 弯矩不相同,挠曲线形状不相同 D . 弯矩不相同,挠曲线形状相同5-3-4 图示(a )、(b )两梁,长度、截面尺寸及约束均相同,图(a )梁的外力偶矩作用在C 截面,图(b )梁的外力偶矩作用在B 支座的右作侧,则两梁A B 段的内力和弯曲变形的比较是 ( )。
A 。
内力相同,变形不相同B .内力及变形均相同C .内力及变形均不相同D .内力不相同,变形相同5-3-5 当用积分法求图示梁的挠度曲线方程时,在确定积分常量的四个条件中,除x =0,θA =0;x =0,y A =0外,另两个条件是 ( ) 。
题5-3-4图C 0(a ) (b )P 题5-3-3图A .(y c )左= (y c )右,(θC )左=(θC )右B .(y c )左= (y c )右,y B =0C .y C =0,y B =0D .y B =0,θC =05-3-6 图示简支梁在分布荷载q (x )=f (x )作用下,梁的挠度曲线方程为⎰⎰++-=,)()(D Cx dxdx x M x EIy ,其中,积分常量 ( )。
A .0,0==D C B .0,0≠=D CC .0,0≠≠D C D .0,0=≠D C5-3-7 挠曲线方程中的积分常梁主要反映了 A . 对近似微分方程误差的修正 B . 剪力对变形的影响 C . 约束条件对变形的影响 D . 梁的轴向位移对变形的影响5-3-8 图示悬臂梁在B 、C 两截面上各承受一个力偶矩作用,两力偶矩大小相等,转向相反,使梁产生弯曲变形。
B 截面的变形为 ( )。
A .0,0≠=θy B . 0,0=≠θy C .0,0≠≠θy D 。
0,0==θy5-3-9 图示简支梁受集中力作用,其最大挠度f 发生在( )。
A .集中力作用处 B 。
跨中截面 C .转角为零处 D 。
转角最大处5-3-10 两简支梁E I 及l 均相同,作用荷载如图所示。
跨中截面C 分别产生挠度y C 和转角A 题5-3-5图q (x )题5-3-6图题5-3-8图θC ,则两梁C 点的挠度及两梁C 点的转角有 ( )。
A .θC 相等,y C 不相等B 。
θC 不相等,y C 相等 C .θC 和 都不相等D 。
θC 和y C 都相等4.计算题5-4-1 试画出图示各梁挠曲线的大致形状。
5-4-2 一简支梁承受图示分布荷载q =K x 22(K 为已知),试求此梁的挠曲线方程(设E I =常量)。
5-4-3 已知图示梁的带积分常量的挠曲线方程为)2()2(2412163)210(12163)(2222423222221111312121l x lD x C l x q x ql x ql EIy x D x C x ql x ql x EIy ≤≤++-+-=≤≤++-=试求方程中的积分常量。
5-4-4 试用叠加法求图示梁B 点的挠度和转角。
(E I =常量)题5-3-10图2 2(a )3 33(c )2 2(f )(b(d )22(e )题5-4-1图22 题5-4-4图A2 2题5-4-3图 x5-4-5 外伸梁受图示荷载作用,试求C 截面的挠度和A 截面的转角。
(E I =常量。
) 5-4-6 矩形截面梁A B 的抗弯刚度为E I ,受力如图示。
试问B 端支座向上抬高Δ为多少时,梁的A 截面的弯矩和C 截面的弯矩绝对值相等。
(材料的抗拉与抗压性能相同)5-4-7 图示弯曲的钢板梁A B ,截面为矩形,宽度为b ,高度为h ,钢板放在刚硬地面上时原有曲率半径为ρ,在两端受力P 作用使其平直,则将有均布压力作用于刚硬地面C -C 上。
已知刚梁E (弹性模量),试求所需的P 力及其在压平时梁内的最大正应力。
5-4-8 长度为l 、抗弯刚度为E I 的悬臂梁A B ,受均布荷载q 作用而弯曲时,与半径为r 的刚性圆柱面接触,如图所示。
试求当梁上某一段A C 与刚性圆柱面在C 点接触(假设C 点与梁左端A 的距离为x )时,B 点的挠度。
5-4-9 单位长度重量为q 、抗弯刚度为E I 的矩形截面钢条,放置在水平刚性面上,刚条的一端伸出水平面一小段C D ,如图所示。
若伸出长度为a ,试求刚条翘起而不与水平面接触的C D 段的长度b 。
5-4-10 超静定梁如图所示,AB 段内作用有均布荷载q ,当C 支座向下沉陷EIql 964=∆时,试求梁的反力。
5-4-11 矩形截面悬臂梁如图所示,梁长为l ,在沿其截面高度h 承受非均匀加热,设梁顶2 2题5-4-6图 题5-4-5图 题5-4-7图C 2题5-4-10图题5-4-9图部温度改变为t 1,底部温度改变为t 2,且t 2>t 1。
温度沿截面高度呈线形改变。
材料的线膨胀系数为a ,弹性模量为E ,由于不均匀受热而使梁发生弯曲变形,当梁的悬臂端施加偶矩M 0时,能使梁展直。
问应施加多大的外力偶矩5-4-12 悬臂梁A B 和C D 的自由端处用拉杆B C 相连,受力如图所示,若A B 梁和C D 梁的抗弯刚度E I 相等,试求在下列两种情况下C 点的挠度. (1) 当B C 杆为刚性杆,即E A = 时; (2) 当B C 杆长为2l ,2lEIEI 时。
5-4-13 A B 与B C 两梁铰接于B ,如图所示。
已知两梁的抗弯度相等,P =40k N /m ,,试求B 点的约束力。
5-4-14 悬臂梁和简支梁材料和截面均相同。
已知E 及未受力前A B 梁B 点与C D 梁中点之间的间隙Δ(垂直距离),如图所示,当受P 力后A B 梁在B 点的挠度大于Δ,试求各梁的支座反力。
5-4-15 具有初始挠度的A B 梁如图所示,梁的E I 和l 均为已知。
当梁上作用有三角形分布荷载时(q 0已知),梁便呈直线形状。
试求梁的初始挠曲线方程。
8题5-4-11图/2题5-4-12图/2Aq 0AxA5-4-16 试根据对称性求图示梁的挠曲线方程。
E I =常量5-4-17 两端固定的等截面梁,梁上作用一外力偶矩M 0 ,如图所示。
欲使在固定端A 的反力偶矩M A 为零,则力偶矩M 0应作用在梁上何位置(即x =)测试练习解答1. 判断改错题5-1-1 ×。
挠度和转角不仅与弯矩有关,而且与边界位移条件也有关,例如,当悬臂梁自由端作用有集中力P 时,自由端的M =0,但挠度和转角都是最大值。