工程力学材料力学答案-第十一章
- 格式:doc
- 大小:290.50 KB
- 文档页数:8

工程力学第十一章习题解答题目:一物体质量为10kg,在水平地面上以10m/s的初速度开始运动,若物体受到一个恒力F=20N的作用,且与运动方向相反,求物体在力作用下停止前所经过的距离。
解答过程:一、问题分析根据牛顿第二定律,力等于质量乘以加速度,即F=ma。
本题中,物体受到一个恒力F=20N的作用,且与运动方向相反,因此加速度a为负值。
我们需要求解物体在力作用下停止前所经过的距离。
二、解题步骤1. 求加速度a根据牛顿第二定律,F=ma,代入已知数据,得到加速度a:a = F/m = -20N / 10kg = -2m/s²2. 求物体停止前所经过的时间t由于物体初速度v0=10m/s,加速度a=-2m/s²,根据速度-时间关系式v=v0+at,我们可以求解物体停止前的时间t:0 = 10m/s - 2m/s² tt = 10m/s / 2m/s² = 5s3. 求物体在力作用下停止前所经过的距离s根据位移-时间关系式s=v0t + 1/2at²,代入已知数据,求解物体在力作用下停止前所经过的距离s:s = 10m/s 5s + 1/2 (-2m/s²) (5s)²s = 50m - 25ms = 25m三、答案验证根据动能定理,物体在运动过程中,动能的变化等于外力做的功。
物体从初始速度10m/s减速到0,动能变化为:ΔK = 1/2 m (v² - v0²) = 1/2 10kg (0 - 100m²/s²) = -500J外力做的功为:W = F s = 20N 25m = 500J由于动能变化等于外力做的功,所以我们的答案是正确的。
四、总结本题主要考查了牛顿第二定律、速度-时间关系式、位移-时间关系式和动能定理的应用。
通过求解加速度、时间和距离,我们得到了物体在力作用下停止前所经过的距离为25m。


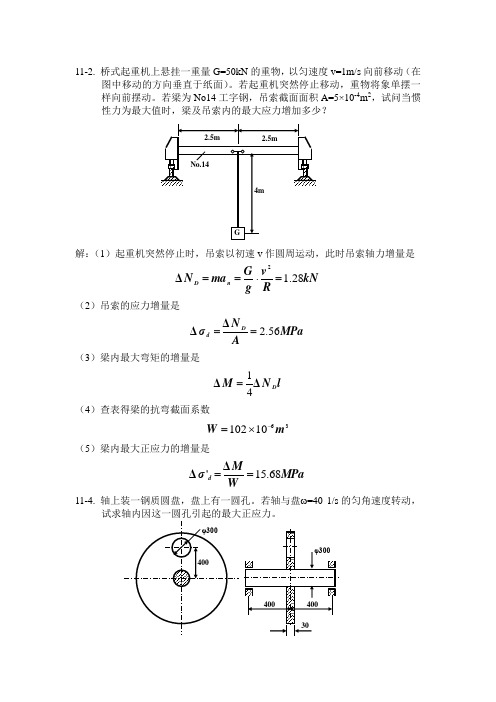
11-2. 桥式起重机上悬挂一重量G=50kN 的重物,以匀速度v=1m/s 向前移动(在图中移动的方向垂直于纸面)。
若起重机突然停止移动,重物将象单摆一样向前摆动。
若梁为No14工字钢,吊索截面面积A=5×10-4m 2,试问当惯性力为最大值时,梁及吊索内的最大应力增加多少?解:(1)起重机突然停止时,吊索以初速v 作圆周运动,此时吊索轴力增量是kN Rv g G ma N n D 28.12=⋅==Δ(2)吊索的应力增量是MPa AN σDd 56.2==ΔΔ (3)梁内最大弯矩的增量是l N M D ΔΔ41=(4)查表得梁的抗弯截面系数3610102m W -⨯=(5)梁内最大正应力的增量是MPa WM σd 68.15'==ΔΔ11-4. 轴上装一钢质圆盘,盘上有一圆孔。
若轴与盘ω=40 1/s 的匀角速度转动,试求轴内因这一圆孔引起的最大正应力。
解:(1)假设挖空圆盘和圆孔部分的质量分别是M 和m ,它们的质心距轴线的距离分别为R 的r ,则有mr MR =(2)挖空圆盘的惯性力是kN ωr gVγωmr ωMR Ma F n n 64.10222=⋅==== 上式中钢的密度取3/8.76m kN γ=(3)轴内的最大正应力增量是MPa WlF W M σnd 5.1241max max ===Δ11-5. 在直径为100mm 的轴上装有转动惯量I=0.5kN ⋅m ⋅s2的飞轮,轴的转速为300r/min 。
制动器开始作用后,在20转内将飞轮刹住,试求轴内最大剪应力。
设在制动器作用前,轴已与驱动装置脱开,且轴承的磨擦力矩可以不计。
解:(1)飞轮作匀减速转动2220/25.120/42.3130s rad φωωεωs rad πn ωt t -=-=∴=== (2)惯性力距是kNm εI m d 96.1=-=(3)轴在飞轮和制动器之间发生扭转变形MPa d πTW T τm T t d 10163max ===∴= 11-6. 钢轴AB 的直径为80mm ,轴上有一直径为80mm 钢质圆杆CD ,CD 垂直于AB 。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的点B 系另一绳BE ,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB 段铅直;DE 段与水平线、CB 段与铅直线成等角α=0.1rad (弧度)(当α很小时,tan α≈α)。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
题2-4图作BD 两节点的受力图 联合解得:kN F F F A 80100tan 2=≈=α2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,,机构在图示位置平衡。
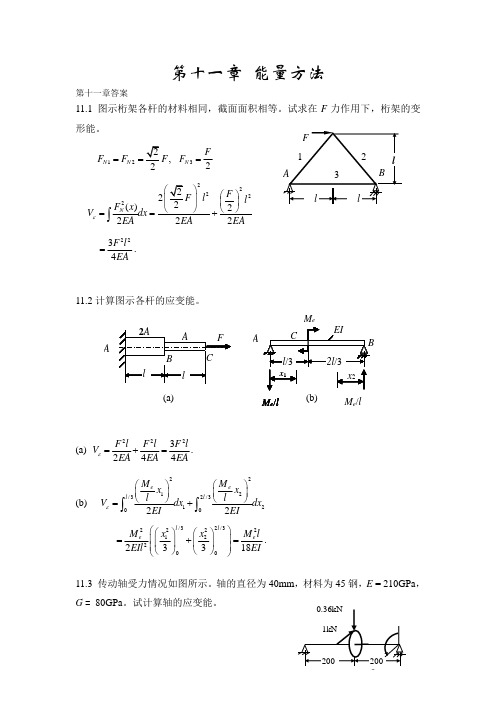
第十一章 能量方法第十一章答案11.1 图示桁架各杆的材料相同,截面面积相等。
试求在F 力作用下,桁架的变形能。
12,2N N F F F ==32N F F =222222()2222N F F l l F x V dx EA EA EAε⎫⎛⎫⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=.11.2计算图示各杆的应变能。
(a) 2223244F l F l F l V EA EA EAε=+=. (b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l e e M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.11.3 传动轴受力情况如图所示。
轴的直径为40mm ,材料为45钢,E = 210GPa,G = 80GPa 。
试计算轴的应变能。
51 / 6由扭转引起的应变能:20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能:20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=.11.4 计算图示梁的应变能,并说明是否满足叠加原理及其原因。
2230()26lFl Fx F l V dx EI EIε-==⎰而22310()22lFl F lV dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰.不满足叠加原理,因为应变能与内力的关系不是线性的。
11.5在外伸梁的自由端作用力偶矩e ,试用互等定理,并借助于附录E ,求跨度中点C 的挠度w c 。
(见课本下册p40例12-4)11.6 图示刚架的各杆的EI 皆相等,试求截面AC 的转角。
CM eA l /2 l /2B D a EIMe=FlFlx(a) A 点:在A 点加一个向下的单位力。
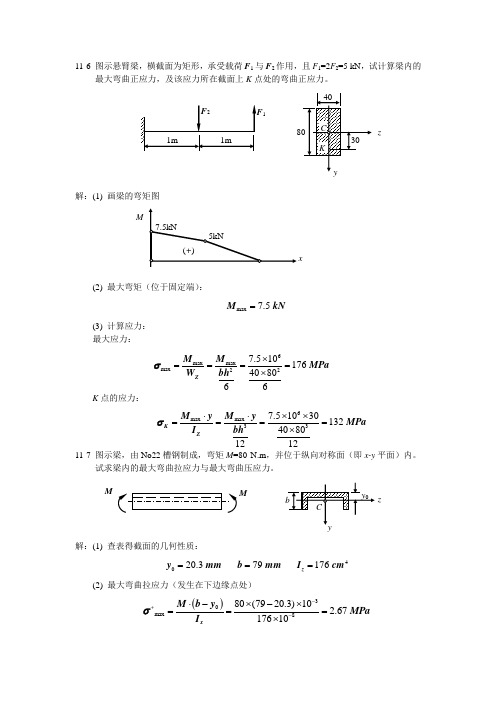
11-6 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图(2) 最大弯矩(位于固定端):max 7.5 M kN =(3) 计算应力: 最大应力:K 点的应力:11-7 图示梁,由No22槽钢制成,弯矩M =80 N.m ,并位于纵向对称面(即x-y 平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解:(1) 查表得截面的几何性质:4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力(发生在下边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力(发生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁,由No28工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa ,a =1 m 。
解:(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为:49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为:2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力:2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁,F =10 kN ,M e =70 kNm ,许用拉应力[σ+]=35 MPa ,许用压应力[σ-]=120 MPa ,试校核梁的强度。
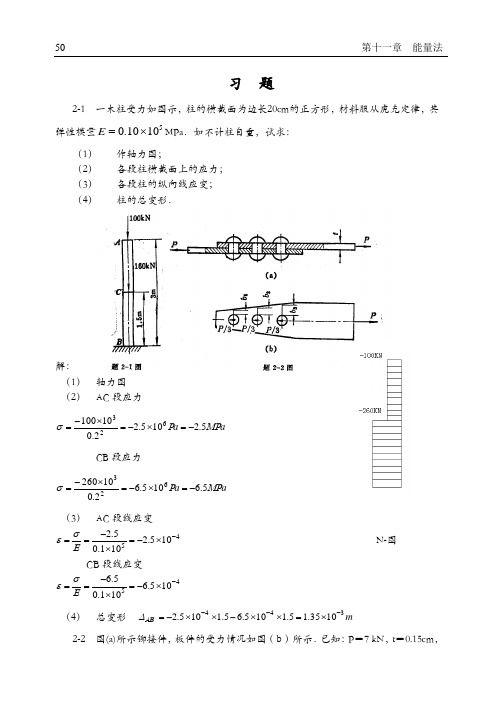
习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1)作轴力图; (2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-=CB 段应力a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变45105.2101.05.2-⨯-=⨯-==E σε N-图 CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε (4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=- a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=-a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max ==2-3 直径为1cm 的圆杆,在拉力P =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
解:(1) 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- (2)︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒ 2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
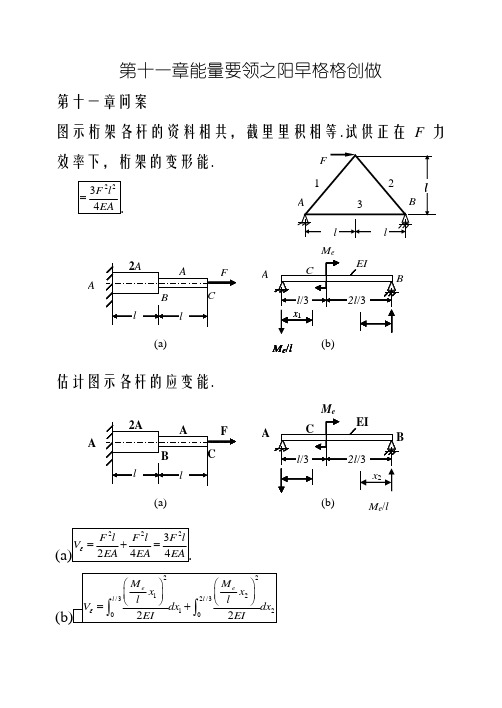
第十一章能量要领之阳早格格创做第十一章问案图示桁架各杆的资料相共,截里里积相等.试供正在F 力效率下,桁架的变形能.估计图示各杆的应变能.传动轴受力情况如图所示.轴的直径为40mm ,资料为45钢,E = 210GPa ,G = 80GPa.由扭转引起的应变能: 由蜿蜒引起的应变能:估计图示梁的应变能,并证明是可谦脚叠加本理及其本果.而没有谦脚叠加本理,果为应变能取内力的闭系没有是线性的.借帮于附录E ,供跨度中面(睹课本下册p40例12-4)11.6 图示刚刚架的各杆的EI 皆相等,试供截里A 、B 的位移战截里C 的转角.(a)A 面:正在A 面加一个背下的单位力.M (x 1)=0, M (x 2)=Fx 2, M (x 3)=FbC 面:正在C 加一个顺时针的力奇矩为1的单位力奇(b) A 面:正在A面加一个背下的单位力B 面:正在B 面加一个背左的单位力图示桁架各杆的资料相共,截里里积相等C 处的火仄位移战笔直位移.CF BAR火仄位移:(122) 3.828Fl FlEA EA +=-=-.笔直位移:Fl EA ∆=-.2,E 索 = 177GPa.F = 20kN ,(a)假设横梁ABCD 为刚刚体,供C 面的笔直位移.(2)若没有把ABCD 假设为刚刚体,且已知其抗直刚刚度为EI 2,试再供C 面的笔直位移.(1)42110.87.891033F EA -⎛⎫∆=⨯=⨯ ⎪⎝⎭m.(2)20.44047.89102Fx dx EI -∆=⨯+⎰4447.8910 1.48109.3710---=⨯+⨯=⨯m.11.9 等截里直杆BC 的轴线为四分之三的圆周.若AB 杆可视为刚刚性杆,试供正在F 力效率下,截里B 的火仄位移及笔直位移.火仄位移:M ()=FR cos, ()sin M R θθ=33320sin cos 2FR FRd EI EI πθθθ∆==⎰.D CFAB60 ° 60 ° 800 400400RFO B BF ORA F笔直位移:()(1cos )M R θθ=--33.36FR EI =.11.10 图示圆弧形小直率杆,仄衡半径为R .力F笔直于圆环中线地圆的仄里.试供二个F 力效率面的相对于线位移.M ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=-333pFR FR EI GI ππ=+.11.11图示圆弧形小直率杆,仄衡半径为R .正在横截里A 取B 处受一对于集结力F 效率.力F 正在圆环中线地圆的仄里内.试供二个F 力效率面的相对于线位移. M ()=FR sin,()sin M R θθ=32320sin FR FRd EI EI πθπθ∆==⎰.11.12图示轴线为火仄里内四分之一圆周的直杆,正在自由端B 效率笔直荷载F ,设EI 战GI P 为已知,试供正在F 力效率下端里B 的笔直位移.F O O Rθ B F AM ()=FR sin, ()sin M R θθ= T ()=FR (1-cos), ()(1cos )T R θθ=- 33(38)44pFR FR EI GI ππ-=+.。

11-6 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图(2) 最大弯矩(位于固定端):max 7.5 M kN =(3) 计算应力: 最大应力:K 点的应力:11-7 图示梁,由No22槽钢制成,弯矩M =80 N.m ,并位于纵向对称面(即x-y 平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解:(1) 查表得截面的几何性质:4020.3 79 176 z y mm b mm I cm ===(2) 最大弯曲拉应力(发生在下边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPa I σ-+-⋅-⨯-⨯===⨯6max max max227.510176 408066ZM M MPa bh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯x M1zM M z(3) 最大弯曲压应力(发生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯ 11-8 图示简支梁,由No28工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa ,a =1 m 。
解:(1) 求支反力31 44A B R qa R qa ==(2) 画内力图(3) 由胡克定律求得截面C 下边缘点的拉应力为:49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=也可以表达为:2max4C C z zqa MW W σ+== (4) 梁内的最大弯曲正应力:2maxmax max 993267.5 8C zz qa M MPa W W σσ+====qxxF SM11-14 图示槽形截面悬臂梁,F =10 kN ,M e =70 kNm ,许用拉应力[σ+]=35 MPa ,许用压应力[σ-]=120 MPa ,试校核梁的强度。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的点B 系另一绳BE ,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB 段铅直;DE 段与水平线、CB 段与铅直线成等角α=0.1rad (弧度)(当α很小时,tanα≈α)。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
题2-4图 作BD 两节点的受力图 联合解得:kN F F F A80100tan 2=≈=α 2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,,机构在图示位置平衡。


第十一章 能量方法第十一章答案11、1 图示桁架各杆的材料相同,截面面积相等。
试求在F 力作用下,桁架的变形能。
12,2N N F F F ==32N F F = 2222222()2222N F F l l F x V dx EA EA EA ε⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=、11、2计算图示各杆的应变能。
(a) 2223244F l F l F l V EA EA EAε=+=、 (b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l e e M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、11、3 传动轴受力情况如图所示。
轴的直径为40mm ,材料为45钢,E = 210GPa ,G = 80GPa 。
试计算轴的应变能。
由扭转引起的应变能:20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能:20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=、11、4 计算图示梁的应变能,并说明就是否满足叠加原理及其原因。
2230()26lFl Fx F lV dx EI EIε-==⎰而22310()22l Fl F lV dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰、不满足叠加原理,因为应变能与内力的关系不就是线性的。
、0、36kN(b)1kN200200 EIMe=FlFlx11、5在外伸梁的自由端作用力偶矩中点C 的挠度w c 。
(见课本下册p40例12-4)11、6 图示刚架的各杆的EI 皆相等,试求截面A 、B 的位移与截面C 的转角。
(a) A 点:在A 点加一个向下的单位力。
M (x 1)=0, M (x 2)=Fx 2, M (x 3)=Fb11()M x x =,22()M x Fx =,3()0M x = 3330()()h M x M x Fabhdx EI EI∆==-⎰、C 点:在C 加一个逆时针的力偶矩为1的单位力偶。


材料力学答案第十一章仅供学习与交流,如有侵权请联系网站删除 谢谢50第十一章 能量方法第十一章答案11.1 图示桁架各杆的材料相同,截面面积相等。
试求在F 力作用下,桁架的变形能。
12,2N N F F F == 32N F F = 222222()2222N F F l l F x V dx EA EA EA ε⎫⎛⎫⎪ ⎪⎝⎭⎝⎭==+⎰2234F l EA=.11.2计算图示各杆的应变能。
(a)仅供学习与交流,如有侵权请联系网站删除 谢谢512223244F l F l F l V EA EA EAε=+=.(b) 2212/32/3120022e e l l M M x x l l V dx dx EI EIε⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎰⎰ /32/322221220023318l l ee M M l x x EIl EI ⎛⎫⎛⎫⎛⎫ ⎪=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.11.3 传动轴受力情况如图所示。
轴的直径为40mm ,材料为45钢,E = 210GPa ,G = 80GPa 。
试计算轴的应变能。
由扭转引起的应变能:20.220800.0322pV dx GI ε==⎰由弯曲引起的应变能:20.210(531.4)20.0292x V dx EIε==⎰120.061J V V V εεε=+=.11.4 计算图示梁的应变能,并说明是否满足叠加原理及其原因。
2230()26lFl Fx F l V dx EI EIε-==⎰0.08kN· 0.36kN (b) 1kN 2000200EIMe=FlFlx仅供学习与交流,如有侵权请联系网站删除 谢谢52而22310()22lFl F l V dx EI EIε==⎰22320()26lFx F l V dx EI EIε-==⎰.不满足叠加原理,因为应变能与内力的关系不是线性的。
11.5在外伸梁的自由端作用力偶矩M跨度中点C 的挠度w c 。
11-6 图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2F 2=5 kN ,试计算梁内的
最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1) 画梁的弯矩图
(2) 最大弯矩(位于固定端):
max 7.5 M kN =
(3) 计算应力: 最大应力:
K 点的应力:
11-7 图示梁,由No22槽钢制成,弯矩M =80 N.m ,并位于纵向对称面(即x-y 平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
解:(1) 查表得截面的几何性质:
4020.3 79 176 z y mm b mm I cm ===
(2) 最大弯曲拉应力(发生在下边缘点处)
()30max
8
80(7920.3)10 2.67 17610x M b y MPa I σ
-+-⋅-⨯-⨯===⨯
6max max max
22
7.510176 408066
Z
M M MPa bh W σ⨯====⨯6max max 33
7.51030
132 ********
K Z
M y M y MPa bh I σ⋅⋅⨯⨯====⨯
x M
1
z
M M z
(3) 最大弯曲压应力(发生在上边缘点处)
30max
8
8020.3100.92 17610
x M y MPa I σ
---⋅⨯⨯===⨯ 11-8 图示简支梁,由No28工字钢制成,在集度为q 的均布载荷作用下,测得横截面C 底
边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力,已知钢的弹性模量E =200 Gpa ,a =1 m 。
解:(1) 求支反力
31 44
A B R qa R qa ==
(2) 画内力图
(3) 由胡克定律求得截面C 下边缘点的拉应力为:
49max 3.010******* C E MPa σε+-=⋅=⨯⨯⨯=
也可以表达为:
2
max
4C C z z
qa M
W W σ+== (4) 梁内的最大弯曲正应力:
2
max
max max 993267.5 8
C z
z qa M MPa W W σσ+
=
===
q
x
x
F S
M
11-14 图示槽形截面悬臂梁,F =10 kN ,M e =70 kNm ,许用拉应力[σ+]=35 MPa ,许用压应力
[σ-]=120 MPa ,试校核梁的强度。
解:(1) 截面形心位置及惯性矩:
112212(150250)125(100200)150
96 (150250)(100200)
C A y A y y mm A A ⋅+⋅⨯⋅+-⨯⋅=
==+⨯+-⨯
332
284
1505025200(15050)(25)2(25200)(150)12121.0210 zC
C C I y y mm ⎡⎤⨯⨯=+⨯⋅-++⨯⋅-⎢⎥
⎣⎦=⨯ (2) 画出梁的弯矩图
(3) 计算应力
A +截面下边缘点处的拉应力及上边缘点处的压应力分别为:
68
(250)
4010(25096)60.4 1.0210C A A zC
M y MPa I σ
++
+⋅-⨯-=
==⨯ 68
40109637.61.0210
C
A A zC
M y MPa I σ-
++
⋅⨯⨯=
==⨯ A -截面下边缘点处的压应力为
68
(250)
3010(25096)45.3 1.0210
C A A zC
M y MPa I σ
--
-⋅-⨯-=
==⨯ 可见梁内最大拉应力超过许用拉应力,梁不安全。
11-15 图示矩形截面钢梁,承受集中载荷F 与集度为q 的均布载荷作用,试确定截面尺寸b 。
已知载荷F =10 kN ,q =5 N/mm ,许用应力[σ] =160 Mpa 。
C
B
x
解:(1) 求约束力:
3.75 11.25 A B R kNm R kNm ==
(2) 画出弯矩图:
(3) 依据强度条件确定截面尺寸
[]66max max
23
3.7510 3.7510160 466
z
M MPa bh b W σσ⨯⨯===≤= 解得:
32.7 b mm ≥
11-17 图示外伸梁,承受载荷F 作用。
已知载荷F =20KN ,许用应力[σ]=160 Mpa ,试选择
工字钢型号。
解:(1) 求约束力:
5 25 A B R kNm R kNm ==
(2) 画弯矩图:
(3) 依据强度条件选择工字钢型号
[]6max max
2010160 M MPa W W
σσ⨯==≤=
解得:
3125 W cm ≥
查表,选取No16工字钢
F
x
M
x
M
11-20 当载荷F 直接作用在简支梁AB 的跨度中点时,梁内最大弯曲正应力超过许用应力
30%。
为了消除此种过载,配置一辅助梁CD ,试求辅助梁的最小长度a 。
解:(1) 当F 力直接作用在梁上时,弯矩图为:
此时梁内最大弯曲正应力为:
[]max,1max,13/2
30%M F W
W
σσ=
=
= 解得:
[]20%F
W
σ=..............① (2) 配置辅助梁后,弯矩图为:
依据弯曲正应力强度条件:
[]max,2max,2324F Fa
M W
W
σσ-=
=
= 将①式代入上式,解得:
1.385 a m =
11-22 图示悬臂梁,承受载荷F 1与F 2作用,已知F 1=800 N ,F 2=1.6 kN ,l =1 m ,许用应力[σ]
=160 MPa,试分别在下列两种情况下确定截面尺寸。
(1) 截面为矩形,h =2b ; (2) 截面为圆形。
B
x
x
1
解:(1) 画弯矩图
固定端截面为危险截面
(2) 当横截面为矩形时,依据弯曲正应力强度条件:
[]3621max
2233
2800102 1.610160 26633
z x x z
M M F l F l MPa b h h b b b W W σσ⋅⋅⨯⨯⨯=+=+=+≤=⋅⋅ 解得:
35.6 71.2 b mm h mm ==
(3) 当横截面为圆形时,依据弯曲正应力强度条件:
[]max max 32
160 32
M W
MPa
σσ=
==
=
≤=
解得:
52.4 d mm =
11-25 图示矩形截面钢杆,用应变片测得其上、下表面的轴向正应变分别为εa =1.0×10-3与
εb =0.4×10-3,材料的弹性模量E =210Gpa 。
试绘横截面上的正应力分布图。
并求拉力F 及偏心距e 的数值。
解:(1) 杆件发生拉弯组合变形,依据胡克定律知:
333
3
1.010******** 0.4102101084 a a b b E MPa E MPa
σεσε--=⋅=⨯⨯⨯==⋅=⨯⨯
⨯=
横截面上正应力分布如图:
y
y
(M x (M
z
b a
(2) 上下表面的正应力还可表达为:
22
210 6
846
a b M N F e F MPa b h W A b h
M N F e F MPa b h W A b h σσ⋅=
+=+=⋅⋅⋅=-+=-+=⋅⋅
将b 、h 数值代入上面二式,求得:
18.38 1.785 F mm e mm ==
11-27 图示板件,载荷F =12 kN ,许用应力[σ] =100 MPa ,试求板边切口的允许深度x 。
(δ=5
mm )
解:(1) 切口截面偏心距和抗弯截面模量:
()2
40 26
x x
e W δ-==
(2) 切口截面上发生拉弯组合变形;
33max
21210121021005(40)5(40)
6
x
Fe F MPa x W A x σ⨯⨯
⨯=+=+=⨯-⨯- 解得:
5.2 x mm =
e。