八年级数学华师大圆的对称性垂径定理应用PPT优秀课件
- 格式：ppt
- 大小：305.50 KB
- 文档页数：13
下载文档原格式
合集下载
垂径定理公开课ppt课件
D
A OM B
C 1题图
2题图
C 3题M图
精品课件
9
针对训练（二）
4. 如图是一圆柱形输水管的横截面，阴影部分为
有水部分，如果水面AB宽为8cm，水面最深地方的
高度为2cm，则该输水管的半径为 5cm
.
解：作OC ⊥AB并延长交弧AB与点M，连接OB，
则CM=2， BC=
1 2
1
AB= 2
×8=4,
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
O
设半径为R, OC=R-2，在Rt△OCB中， C
O2C BC 2O2B ,即 (R2)242R2
M
解得：R=5 构造直角三角形，运用垂径定理和勾股定理
列方程求解.
精品课件
10
【知识点】
三、课堂小结
1.圆的轴对称性 圆是轴对称图形，每一条直径所在的直线都
是它的对称轴，圆的对称轴有无数条 2.垂径定理
垂直于弦的直径平分这条弦，并且平分弦所对 的两条弧
条件的实质是：（1）过圆心（2）垂直于弦
精品课件
11
【解题方法】 构造直角三角形，运用垂径定理和勾股定理
解决圆中弦、弦心距、半径问题
【数学思想】
方程思想
精品课件
12
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
精品课件
8
针对训练（二）
1.如图，在⊙O中，AB为直径，弦CD⊥AB于点M, AB=20， OM=6，则CD= 16 . 2. 绍兴是著名的桥乡，如图，石拱桥的桥顶到水面的距离 CD为8m，桥拱半径OC为5m，则水面宽AB为 8m . 3.如图，⊙O是水平放置的输油管道的横截面，其直径为2m， 油面的宽度AB=1.2m，则点O到油面的距离是 0.8m ，油 面的最大深度为 0.2m .
A OM B
C 1题图
2题图
C 3题M图
精品课件
9
针对训练（二）
4. 如图是一圆柱形输水管的横截面，阴影部分为
有水部分，如果水面AB宽为8cm，水面最深地方的
高度为2cm，则该输水管的半径为 5cm
.
解：作OC ⊥AB并延长交弧AB与点M，连接OB，
则CM=2， BC=
1 2
1
AB= 2
×8=4,
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
O
设半径为R, OC=R-2，在Rt△OCB中， C
O2C BC 2O2B ,即 (R2)242R2
M
解得：R=5 构造直角三角形，运用垂径定理和勾股定理
列方程求解.
精品课件
10
【知识点】
三、课堂小结
1.圆的轴对称性 圆是轴对称图形，每一条直径所在的直线都
是它的对称轴，圆的对称轴有无数条 2.垂径定理
垂直于弦的直径平分这条弦，并且平分弦所对 的两条弧
条件的实质是：（1）过圆心（2）垂直于弦
精品课件
11
【解题方法】 构造直角三角形，运用垂径定理和勾股定理
解决圆中弦、弦心距、半径问题
【数学思想】
方程思想
精品课件
12
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
精品课件
8
针对训练（二）
1.如图，在⊙O中，AB为直径，弦CD⊥AB于点M, AB=20， OM=6，则CD= 16 . 2. 绍兴是著名的桥乡，如图，石拱桥的桥顶到水面的距离 CD为8m，桥拱半径OC为5m，则水面宽AB为 8m . 3.如图，⊙O是水平放置的输油管道的横截面，其直径为2m， 油面的宽度AB=1.2m，则点O到油面的距离是 0.8m ，油 面的最大深度为 0.2m .
《圆的垂径定理》课件
第四步
综合第二步和第三步的结论， 得出垂径定理。
定理的应用
01
02
03
计算弦长
已知圆的半径和弦所对的 圆心角，利用垂径定理可 以计算出弦的长度。
计算弧长
已知圆的半径和弧所对的 圆心角，利用垂径定理可 以计算出弧的长度。
计算圆心角
已知圆的半径和弦长，利 用垂径定理可以计算出圆 心角的度数。
03
垂径定理的应用
02
垂径定理在解析几何中可以用于 解决一些实际应用问题，例如计 算桥梁的承重能力、设计圆形工 件等。
垂径定理在实际问题中的应用
在实际生活中，垂径定理的应用非常 广泛，例如在建筑设计、机械制造、 航空航天等领域中，垂径定理都发挥 着重要的作用。
垂径定理在物理学中也有应用，例如 在研究光的反射和折射、地球的重力 场等。
垂径定理在几何问题中的应用
垂径定理在证明圆的性质时发挥了重要作用，例如证明圆周角定 理、圆内接四边形的性质等。
垂径定理是解决几何问题中关于圆的问题的基础，例如求圆的面 积、周长、圆心角等。
垂径定理在解析几何中的应用
01
在解析几何中，垂径定理可以与 其他数学知识结合使用，例如与 三角函数、坐标系等结合，解决 更复杂的几何问题。
详细描述
弦切角定理指出，在圆中，连接弦与切线的交点的线段与弦所夹的角等于该弦 所对应的圆心角。这个定理在解决与弦、切线和圆心角相关的问题时非常有用 。
切线长定理
总结词
切线长定理是关于圆的切线长度的重 要定理。
详细描述
切线长定理指出，过圆外一点向圆作 两条切线，则该点到两切点的线段长 度相等。这个定理在解决与圆的切线 和相关长度相关的问题时非常有用。
定理的应用
华师大圆的对称性垂径定理应用PPT教学课件
解释下列句中红色的字。
①朝服衣冠 （
）
② 吾妻之美我者，私我也 （
）
③能面刺寡人之过者。 （
）
④ 闻寡人之耳者（
）
⑤宫妇左右莫不私王（
）
⑥邹忌讽齐王纳谏 （
）
⑦能谤讥于市朝（
）
⑧今齐地方千里 （
）
解释下列句中红色的字。(答案)
①朝服衣冠（在早晨 ）
② 吾妻之美我者，私我也 （以……为美
）
③能面刺寡人之过者.（当面 ）
A
60D0
B
O
O ø650
A
┌E
B
D
600
C
船能过拱桥吗
驶向胜利 的彼岸
2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶 高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并 高出水面2米的货船要经过这里,此货船能顺利通过这 座拱桥吗？
相信自己能独 立完成解答.
船能过拱桥吗
驶向胜利 的彼岸
间（jià n）进 期（jī）年
重点词句解释：
美我：
认为我美
私：
动词，偏爱
诚知： 确实知道
皆以美于徐公：都认为比徐公美
地方： 土地方圆
左右： 身边
重点词句解释：
昳丽：
光艳美丽
服：
名词用作动词，穿戴
窥镜：
照镜子
旦日：
第二天
不若：
不如
孰视之：
仔细地看
暮寝而思之： 晚上躺着想这件事
蔽甚矣： 蒙蔽很深了
“ ——
《 古 文 观 止 》
语 破 之 ， 快 哉 ！ ”
关 头 ， 从 闺 房 小
臣 谄 君 蔽 ， 兴 亡
圆对称性垂径定理逆定理.ppt
DA源自600BO ø650
C
挑战自我画一画
2、已知：如图，⊙O 中， AB为 弦， OC⊥AB, AB = 6cm ，CD = 1cm.
求⊙O 的半径OA.
⌒
C
A
D
B
O
做一做 9
挑战自我画一画
2、已知：如图，⊙O 中， AB为 弦，D 为 AB 的中点，OC交A⌒B 于C ，AB = 6cm ，
⌒⌒ AD=BD.
能运用自如.
做一做P92 3
垂径定理的逆定理
AB是⊙O的一条弦,且AM=BM.
过点M作直径CD.
左图是轴对称图形吗?如果是,其对称轴是什么?
你能发现图中有哪些等量关系(位置关系)? 与同伴说说你的想法和理由.
C
小明发现图中有:
A
┗●
B
M
●O
由 ① CD是直径 ③ AM=BM
A
●O
B
A
B
●O
C
D
C
D
垂径定理的推论 圆的两条平行弦所夹的弧相等.
试一试 5
挑战自我填一填
1、判断：
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两
条弧.
（）
⑵平分弦所对的一条弧的直径一定平分这条弦所对的
另一条弧.
（）
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷圆的两条弦所夹的弧相等，则这两条弦平行（ )
①③ ②④⑤ 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
①④ ②③⑤ 平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的 ①⑤ ②③④ 另一条弧.
②③ ②④ ②⑤
①④⑤ 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
C
挑战自我画一画
2、已知：如图，⊙O 中， AB为 弦， OC⊥AB, AB = 6cm ，CD = 1cm.
求⊙O 的半径OA.
⌒
C
A
D
B
O
做一做 9
挑战自我画一画
2、已知：如图，⊙O 中， AB为 弦，D 为 AB 的中点，OC交A⌒B 于C ，AB = 6cm ，
⌒⌒ AD=BD.
能运用自如.
做一做P92 3
垂径定理的逆定理
AB是⊙O的一条弦,且AM=BM.
过点M作直径CD.
左图是轴对称图形吗?如果是,其对称轴是什么?
你能发现图中有哪些等量关系(位置关系)? 与同伴说说你的想法和理由.
C
小明发现图中有:
A
┗●
B
M
●O
由 ① CD是直径 ③ AM=BM
A
●O
B
A
B
●O
C
D
C
D
垂径定理的推论 圆的两条平行弦所夹的弧相等.
试一试 5
挑战自我填一填
1、判断：
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两
条弧.
（）
⑵平分弦所对的一条弧的直径一定平分这条弦所对的
另一条弧.
（）
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷圆的两条弦所夹的弧相等，则这两条弦平行（ )
①③ ②④⑤ 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
①④ ②③⑤ 平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的 ①⑤ ②③④ 另一条弧.
②③ ②④ ②⑤
①④⑤ 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
圆的对称性—垂径定理 Microsoft PowerPoint 演示文稿
h d O
⑴d + h = r
a 2 ⑵ r =d +( ) 2
2 2
作业评讲 ：
（1） 如图，在⊙O中，CD是直径，AB是 如图， CD是直径 AB是 是直径， CD⊥AB，已知CD 20， 4， AB。 弦，且CD⊥AB，已知CD = 20，CM = 4，求AB。 C 连接OA 解：连接 M B A ∵ CD = 20 ∴ AO = CO = 10 ∴ OM = OC – CM = 10 – 4 = 6 O 在⊙O中，直径 ⊥弦AB，由垂径 中 直径CD⊥ ， 定理得 ∴ AB =2AM △OMA是Rt △ 是 D 在Rt △OMA中，AO = 10，OM = 6 中 ，
圆的对称性
——垂径定理
活动一
探讨圆的对称性
（1）圆是轴对称图形吗？ 圆是轴对称图形吗？ 如果是,它的对称轴是什么? 如果是,它的对称轴是什么?你能找到多少条 对称轴？ 对称轴？ 你是用什么方法解决上述问题的? 你是用什么方法解决上述问题的?
●
O
• 圆是轴对称图形. 圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无 圆的对称轴是任意一条经过圆心的直线, 任意一条经过圆心的直线 数条对称轴. 数条对称轴. 可利用折叠的方法即可解决上述问题. 可利用折叠的方法即可解决上述问题.
O
F E G
B D
延伸提高
1.过⊙O内一点 的最长弦为 ㎝，最短弦为 ㎝，则 过 内一点A的最长弦为 内一点 的最长弦为10㎝ 最短弦为8㎝ OA= ㎝ 2.已知：如图，⊙O的直径 和CD相交于点 。已 已知： 的直径AB和 相交于点 相交于点E。 已知 如图， 的直径 知AE=1㎝，EB=5㎝，∠DEB=60，求CD的长 ㎝ ㎝ ， 的长 3. 如图，一条公路的转弯处是一段圆弧 即图中弧 如图，一条公路的转弯处是一段圆弧(即图中弧 即图中弧CD, 是弧CD的圆心 其中CD=600m,E为弧 上的一 为弧CD上的一 点O是弧 的圆心 其中 是弧 的圆心),其中 为弧 垂足为F,EF=90m.求这段弯路的半径 求这段弯路的半径. 点,且OE⊥CD垂足为 且 ⊥ 垂足为 求这段弯路的半径 C
【初中数学课件】华师大版圆的对称性第二课时ppt课件
2
CH 1 CD8 2
• ∴Rt△AOG中， O GO2A A2G ，8
• Rt△COH中， O HO2C C2 H 6 ．
• ∴GH＝OG＋OH＝14．
• (2)当弦AB与CD位于圆心O的同侧时，如图 23-1-8②所示．
• 2G020/H7/21＝OG－OH＝8－6＝2．
2020/7/21
根据自学提示检查自学效果
2020/7/21
教师点评
• 1. 圆也是轴对称图形，任意一条直径所 在的直线都是它的对称轴。
• 2.垂径定理： 注意： (1)此性质必须具备两个条件：直径；此直 径垂直于弦，两者缺一不可． (2)常用此知识点进行一类计算题：在弦长、 弦心距、半径三个量中，只需知道其中任意 两个，都可求出第三个，此时需构造Rt△， 利用勾股定理求解．
2020/7/21
当堂训练
• Ｐ４９练习１、２
2020/7/21
1.如图所示，直径为10cm的圆中解：连结OA．
∵OM⊥AB，
∴ AM 1 AB
∵
OA
1
2
105，OM＝4，
2
AM O2 A OM 23
∴AB＝2AM＝6(cm)．
2. 在 ⊙O半径为10，弦AB＝12，CD＝ 16，且AB∥CD．求AB与CD之间的离．
分析：本题目属于 “图形不明确型”题 目，应分类求解． (如右图)
• (1)当弦AB与CD在圆心O的两侧时，如图 23-1-8①所示．
• 作OG⊥AB，垂足为G，延长GO交CD于H ，连结OA、OC．
• ∵AB∥CD，GH⊥AB，∴GH⊥CD．
• •
∵OG⊥AB，AB＝12， ∴． AG 1AB6 同理．
CH 1 CD8 2
• ∴Rt△AOG中， O GO2A A2G ，8
• Rt△COH中， O HO2C C2 H 6 ．
• ∴GH＝OG＋OH＝14．
• (2)当弦AB与CD位于圆心O的同侧时，如图 23-1-8②所示．
• 2G020/H7/21＝OG－OH＝8－6＝2．
2020/7/21
根据自学提示检查自学效果
2020/7/21
教师点评
• 1. 圆也是轴对称图形，任意一条直径所 在的直线都是它的对称轴。
• 2.垂径定理： 注意： (1)此性质必须具备两个条件：直径；此直 径垂直于弦，两者缺一不可． (2)常用此知识点进行一类计算题：在弦长、 弦心距、半径三个量中，只需知道其中任意 两个，都可求出第三个，此时需构造Rt△， 利用勾股定理求解．
2020/7/21
当堂训练
• Ｐ４９练习１、２
2020/7/21
1.如图所示，直径为10cm的圆中解：连结OA．
∵OM⊥AB，
∴ AM 1 AB
∵
OA
1
2
105，OM＝4，
2
AM O2 A OM 23
∴AB＝2AM＝6(cm)．
2. 在 ⊙O半径为10，弦AB＝12，CD＝ 16，且AB∥CD．求AB与CD之间的离．
分析：本题目属于 “图形不明确型”题 目，应分类求解． (如右图)
• (1)当弦AB与CD在圆心O的两侧时，如图 23-1-8①所示．
• 作OG⊥AB，垂足为G，延长GO交CD于H ，连结OA、OC．
• ∵AB∥CD，GH⊥AB，∴GH⊥CD．
• •
∵OG⊥AB，AB＝12， ∴． AG 1AB6 同理．
华师大版圆的对称性第二课时PPT优选课件
汇报人：XXX 日期：20XX年XX月XX日
2020/10/18
3
根据自学提示检查自学效果
2020/10/18
4
教师点评
❖ 1. 圆也是轴对称图形，任意一条直径所 在的直线都是它的对称轴。
❖ 2.垂径定理： 注意：
ቤተ መጻሕፍቲ ባይዱ
(1)此性质必须具备两个条件：直径；此直
径垂直于弦，两者缺一不可．
(2)常用此知识点进行一类计算题：在弦长、
弦心距、半径三个量中，只需知道其中任意
两个，都可求出第三个，此时需构造Rt△，
利2020用/10/1勾8 股定理求解．
5
当堂训练
Ｐ４９练习１、２
2020/10/18
6
1.如图所示，直径为10cm的圆中，圆心 到弦AB的距离为4cm．求弦AB的长．
解：连结OA． ∵OM⊥AB， ∴ AM1AB
∵ OA 11052，OM＝4， 2
A M O2A O2M 3
23.1圆的对称性
(第二课时)
2020/10/18
1
学习目标
理解并掌握垂径定理：垂直于弦 的直径平分这条弦，并且平分这 条弦所对的两条弧。
2020/10/18
2
自学指导
认真阅读P48例1后到P49页练习前的 内容.并思考下列问题：
1. 圆是轴对称图形吗?如果是,它的对 称轴是什么?
2. 通过完成P48页的试一试,你得到的 结论是什么?
∴AB＝2AM＝6(cm)．
2. 在 ⊙O半径为10，弦AB＝12，CD＝ 16，且AB∥CD．求AB与CD之间的离．
分析：本题目属于 “图形不明确型”题 目，应分类求解． (如右图)
谢谢您的聆听与观看
THANK YOU FOR YOUR GUIDANCE.
2020/10/18
3
根据自学提示检查自学效果
2020/10/18
4
教师点评
❖ 1. 圆也是轴对称图形，任意一条直径所 在的直线都是它的对称轴。
❖ 2.垂径定理： 注意：
ቤተ መጻሕፍቲ ባይዱ
(1)此性质必须具备两个条件：直径；此直
径垂直于弦，两者缺一不可．
(2)常用此知识点进行一类计算题：在弦长、
弦心距、半径三个量中，只需知道其中任意
两个，都可求出第三个，此时需构造Rt△，
利2020用/10/1勾8 股定理求解．
5
当堂训练
Ｐ４９练习１、２
2020/10/18
6
1.如图所示，直径为10cm的圆中，圆心 到弦AB的距离为4cm．求弦AB的长．
解：连结OA． ∵OM⊥AB， ∴ AM1AB
∵ OA 11052，OM＝4， 2
A M O2A O2M 3
23.1圆的对称性
(第二课时)
2020/10/18
1
学习目标
理解并掌握垂径定理：垂直于弦 的直径平分这条弦，并且平分这 条弦所对的两条弧。
2020/10/18
2
自学指导
认真阅读P48例1后到P49页练习前的 内容.并思考下列问题：
1. 圆是轴对称图形吗?如果是,它的对 称轴是什么?
2. 通过完成P48页的试一试,你得到的 结论是什么?
∴AB＝2AM＝6(cm)．
2. 在 ⊙O半径为10，弦AB＝12，CD＝ 16，且AB∥CD．求AB与CD之间的离．
分析：本题目属于 “图形不明确型”题 目，应分类求解． (如右图)
谢谢您的聆听与观看
THANK YOU FOR YOUR GUIDANCE.
部优：《圆的轴对称性—垂径定理》课件
证明推理
请大家利用所学知识证明垂径定理的推论： 平分弦（非直径）的直径垂直于弦，并且平分弦所对的两条弧.
（1）需要将用文字语言描述的定理转化为图形语言和符号语言. 如图，在⊙O中，AB为⊙O的条非直径的弦，直径CD平分AB交 AB于P，即AP=BP， 求证：CD⊥AB，
（2）可以从圆的轴对称性质出发证明，只要证明A和B为关于直线CD的对称点即可. （3）此处强调非直径的弦，因为圆的所有直径都是互相平分的，但不一定垂直.
探究归纳
请大家利用所学知识证明垂径定理：垂直于弦的直径平分弦并且平分弦 所对的两条弧.
（1）需要将用文字语言描述的定理转化为图形语言和符号语言. 如图，在⊙O中，AB为⊙O的一条弦，直径CD⊥AB交AB于P， 求证：AP=BP，
（2）可以从圆的轴对称性质出发证明，只要证明A和B是关于直 线CD的对称点即可.连接OA，OB，通过证明△OAP与△OBP全 等，得到AP=BP，说明DC所在直线为线段AB的对称轴 ， 根 据 圆的轴对称性得到：
垂径定理还有别的推论吗？
解决问题
问 题 1：对于活动1提出的问题，你现在有思路了吗？请大家小组讨论， 给出问题的计算过程.
如图，赵州桥的桥拱呈圆弧形，C为 的中点，且CD⊥AB， 已知CD=7.23 m，AB=37 m，求该圆的半径．
解决问题
根据垂径定理的推论，可知CD的延长线必定过O点，且AD=BD．
4. 如图，AB为⊙O的直径，P为OB的中点，∠APC=30°. 若AB=16，求CD的长.
达标检测
5.如图，AB，CD是⊙O的弦，M，N分别为AB，CD的中点，且∠AMN=∠CNM. 求证：AB=CD.
6.某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形 截面的半径.如图是水平放置的破裂管道有水部分的截面，若这个输水管道此时的水面 宽为16cm，且水最深高度为4cm，求这个圆形截面的半径.
圆的对称性圆PPT课件
O
P
A
B
C
D
若把上题改为：P是⊙O内一点，直线APB，CPD分别交⊙O于A、B和C、D，已知AB=CD，
结论还成立吗？
F
E
E
1.连结AB;
作法:
平分弦所对的弧
C
D
A
B
Ｍ
F
G
错在哪里？
1．作AB的垂直平分线CD
2．作AT、BT的垂直平分线EF、GH
Ｔ
Ｅ
Ｎ
Ｈ
Ｐ
强调：等分弧时一定要作弧所对的弦的垂直平分线．
作图依据：
拓展延伸：船能过拱桥吗
如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.由题设得
5
8
4
3
2、在⊙O中，OC平分弦AB，AB = 16，OA = 10，则∠OCA = °，OC = 。
16
10
90
6
课堂练习：
7、已知：如图，⊙O中，AB为弦，OC⊥AB，OC交AB于D ，AB=6cm ，CD=1cm. 求⊙O的半径.
课堂小结： 本节课探索发现了垂径定理的推论1和推论2,并且运用推论1等分弧。 ●要分清推论1的题设和结论,即已知什么条件,可推出什么结论. 这是正确理解应用推论1的关键; ●例3是基本几何作图,会通过作弧所夹弦的垂直平分线来等分弧.能够体会转化思想在这里的运用.
初中数学垂径定理(1)精品ppt课件
A
O d
．
C
r
B
例2：一条排水管的截面如图所示。已知排水管的半径
OB=10，水面宽AB=16。求截面圆心O到水面的距离。
想一想:排水管中水最深多少? 解:作OC⊥AB于C, 由垂径定理得: AC=BC=1/2AB=0.5×16=8 由勾股定理得:
10 C 8
2
8
OC OB BC 10 8 6
D
条件
CD为直径
CD⊥AB
例1 已知AB，如图，用直尺和圆规求作这 条弧的中点．
⌒
作法： ⒈ 连结AB. ⒉作AB的垂直平分线 CD， 交弧AB于点E.
E A D B C
点E就是所求弧AB的中点．
变式一： 求弧AB的四等分点．
C
m
F
E G
n
A
B
D
变式一： 求弧AB的四等分点．
Ｅ
C
Ｍ
G
Ｐ
强调：等分弧时一定 要作弧所对的弦的垂 直平分线．
A
3
C D
1
3
B
O
1、已知⊙O的半径为10cm，点P是⊙O内一点，且OP=8，
则过点P的所有弦中，最短的弦是（ D ）
(A)6cm (B)8cm (C)10cm (D)12cm
O
10 8 6
P
2． 已知⊙O的半径为10，弦AB∥CD，AB=12， CD=16，则AB和CD的距离为 2或14 ．
六、总结回顾
Ｎ
A
Ｔ
B
F
D
Ｈ
3、已知：如图在⊙O中，弦AB//CD。
AC=BD 求证： ⌒ ⌒
O A C B D
圆心到圆的一条弦的距离叫做弦心距．
O d
．
C
r
B
例2：一条排水管的截面如图所示。已知排水管的半径
OB=10，水面宽AB=16。求截面圆心O到水面的距离。
想一想:排水管中水最深多少? 解:作OC⊥AB于C, 由垂径定理得: AC=BC=1/2AB=0.5×16=8 由勾股定理得:
10 C 8
2
8
OC OB BC 10 8 6
D
条件
CD为直径
CD⊥AB
例1 已知AB，如图，用直尺和圆规求作这 条弧的中点．
⌒
作法： ⒈ 连结AB. ⒉作AB的垂直平分线 CD， 交弧AB于点E.
E A D B C
点E就是所求弧AB的中点．
变式一： 求弧AB的四等分点．
C
m
F
E G
n
A
B
D
变式一： 求弧AB的四等分点．
Ｅ
C
Ｍ
G
Ｐ
强调：等分弧时一定 要作弧所对的弦的垂 直平分线．
A
3
C D
1
3
B
O
1、已知⊙O的半径为10cm，点P是⊙O内一点，且OP=8，
则过点P的所有弦中，最短的弦是（ D ）
(A)6cm (B)8cm (C)10cm (D)12cm
O
10 8 6
P
2． 已知⊙O的半径为10，弦AB∥CD，AB=12， CD=16，则AB和CD的距离为 2或14 ．
六、总结回顾
Ｎ
A
Ｔ
B
F
D
Ｈ
3、已知：如图在⊙O中，弦AB//CD。
AC=BD 求证： ⌒ ⌒
O A C B D
圆心到圆的一条弦的距离叫做弦心距．
圆的轴对称性与垂径定理PPT课件
有什么关系？
如图：
A
AOB= COD
B
☺
o
C
D
2020年10月2日
20
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
?
AOB= COD
B
o
C
D
2020年10月2日
21
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
2020年10月2日
22
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
o
C
D
2020年10月2日
23
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
B
☺
o
C
D
2020年10月2日
24
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如图：
A
AOB= COD
17
把圆O的半径ON绕圆心O旋转任意一个角度，
由此可以看出，点N'仍落在圆上。
N' N
O
结论：把圆绕圆心旋转任意一个角度后，
2020年10月2日
仍与原来的圆重合。
18 继续
圆心角：顶点在圆心的角叫圆心角。
N' N
O
如图中所示， NO N '就是一个圆心角。
2020年10月2日
点此继续 19
下面我们一起来观察一下圆心角与它所对的弦、弧
B
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AB是⊙O的一条弦,且AM=BM.
过点M作直径CD.
右图是轴对称图形吗?如果是,其对称轴是什么?
C
你能发现图中有哪些等量关系?与同伴说 说你的想法和理由.
A
┗●
B 我们发现图中有:
M
●O
由 ① CD是直径 ③ AM=BM
可推得
②CD⊥AB,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
D
垂径定理的逆定理
F
OE CD , D C F 1 C D 1 6 030 (0 m )0 .
的三角形 的特点.
O
22 根据勾股定理 ,得 O2C C2F O2,F 即
R 2 32 0 R 0 92 .0
解这个,方 得R程 54.5 这段弯路的半径5约45为 m.
赵州石拱桥
驶向胜利 的彼岸
1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥 拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高 (弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半 径(精确到0.1m).
圆的对称性
●O
驶向胜利 的彼岸
AB是⊙O的一条弦.
作直径CD,使CD⊥AB,垂足为M.
右图是轴对称图形吗?如果是,其对称轴是什么?
C
A M└ ●O
D
你能发现图中有哪些等量关系?与同伴说
说你的想法和理由.
B 我们发现图中有:
由 ① CD是直径 ② CD⊥AB
可推得
③AM=BM,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
赵州石拱桥
驶向胜利 的彼岸
解：如图，用 AB 表示桥拱，AB 所在圆的圆心为O，半径为Rm，
经过圆心O作弦AB的垂线OD，D为垂足，与 AB 相交于点C.根
据垂径定理，D是AB的中点，C是AB 的中点，CD就是拱高.
由题设 A B 3.4 ,7 C D 7 .2 ,
37.4
11
C
AD AB 3.741.87, 22
驶向胜利 的彼岸
如图,在下列五个条件中:
① CD是直径, ② CD⊥AB, ③ AM具备其中两个条件,就可推出其余三个结论.
C
A M└
B
●O
你可以写出相应的结论吗?
D
挑战自我画一画
驶向胜利 的彼岸
如图,M为⊙O内的一点,利用尺规作一条弦AB, 使AB过点M.并且AM=BM.
A
60D0
B
O
O ø650
A
┌E
B
D
600
C
船能过拱桥吗
驶向胜利 的彼岸
2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶 高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并 高出水面2米的货船要经过这里,此货船能顺利通过这 座拱桥吗？
相信自己能独 立完成解答.
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
O D O C D C R7.2.
7.2
A
D
B
在Rt△OAD中，由勾股定理，得
O2A A2 D O2D , 即 R 2 1 .7 2 8 (R 7 .2 )2 .
解得 R≈27.9（m）.
R
O
答：赵州石拱桥的桥拱半径约为27.9m.
垂径定理的应用
驶向胜利 的彼岸
在直径为650mm的圆柱形油槽内装入一些油后，截面 如图所示.若油面宽AB = 600mm，求油的最大深度.
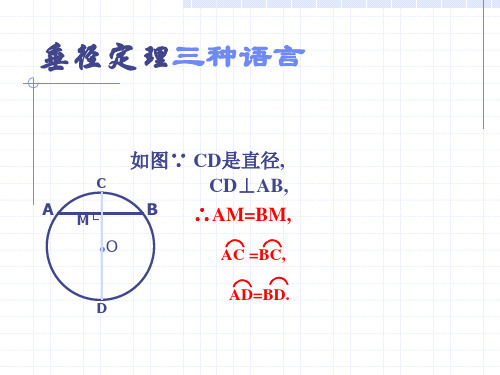
垂径定理
驶向胜利 的彼岸
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
C
A M└ ●O
D
如图∵ CD是直径,
B
CD⊥AB,
∴AM=BM,
A⌒C =B⌒C,
A⌒D=B⌒D.
提示:
垂径定理是
圆中一个重 要的结论,三
种语言要相 互转化,形成 整体,才能运 用自如.
垂径定理的逆定理: 平分弦（不是直径） 的直径垂直于弦,并且平 分弦所对的两条 弧.
垂径定理的应用
驶向胜利 的彼岸
例1 如图，一条公路的转变处是一段圆弧(即图中弧
CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一
点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
C
解:连接OC.
老师提示: 注意闪烁 ●
E 设弯路的 R半 m ,则 O 径F 为 (R90 )m.
●M ●O
试一试P93 12
挑战自我填一填
驶向胜利 的彼岸
1、判断：
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条
弧.
（）
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另
一条弧.
（）
⑶经过弦的中点的直径一定垂直于弦.（
）
⑷圆的两条弦所夹的弧相等，则这两条弦平行. （ ）
⑸弦的垂直平分线一定平分这条弦所对的弧. （ ）