涵洞八字墙工程量计算公式
- 格式:xls
- 大小:35.00 KB
- 文档页数:4

八字墙翼墙(墙身)砼用量精确通用计算公式推导
八字墙翼墙(墙身)砼用量精确通用计算公式
推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将 (4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。

路斜交涵洞斜八字式洞口布置图及尺寸表进行分析整理: 已知:γ—涵洞轴线与路线前进方向的夹角(右侧顺时针方向)θ—水流扩散角,即八字墙与涵洞轴线的夹角a —涵洞斜度,即涵轴线的法线方向与路线的夹角(锐角) H —接涵洞洞身部位八字墙墙身高度(等于涵洞墙身高度+板厚) h —接出口部位八字墙墙身高度(根据实际可不同,常取0.2) m —路基边坡坡比n —八字墙墙身正背坡(常取4.0) α—八字墙顶面垂直宽度(常取0.4) e —八字墙基础襟边宽度(常取0.1或0.2) d —八字墙基础厚度正翼墙(常称大八字墙): 反翼墙(常称小八字墙):а+= βθ正 а-= βθ反正βαcos /c =正 反反βαcos /c =γsin /m m =0 γsin /m m =0()正正正ββcos m /sin n n 0+= ()反反反ββcos m /sin n n 0-=八字墙墙身体积:()()3300220h H n 6m c h H m 21V -+-=正身正 ()()3300220h H n 6m c h H m 21V -+-=反身反八字墙墙身体积计算示意图()正正正0mn /1tan arctan δ-=β ()反反反0mn /1tan arctan δ+=β正正βcos /e e 1= 反反βcos /e e 1= 正正δcos /e e 2= 反反δcos /e e 2=()正正正ββcos /sin 1e e 3 -= ()反反反δcos /δsin 1e e 3 -= 八字墙基础体积:()()()()edn h c 21e e e d h H n 2m d h H e e c m V 03122200210 ⎥⎦⎤⎢⎣⎡+++++-+-++=正正正正正正正正正正()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 0312******* ⎥⎦⎤⎢⎣⎡+++++-+-++=反反反反反反反反反反 附图:精品文档。

路斜交涵洞斜八字式洞口布置图及尺寸表进行分析整理: 已知:γ—涵洞轴线与路线前进方向的夹角(右侧顺时针方向)θ—水流扩散角,即八字墙与涵洞轴线的夹角a —涵洞斜度,即涵轴线的法线方向与路线的夹角(锐角) H —接涵洞洞身部位八字墙墙身高度(等于涵洞墙身高度+板厚) h —接出口部位八字墙墙身高度(根据实际可不同,常取0.2) m —路基边坡坡比n —八字墙墙身正背坡(常取4.0) α—八字墙顶面垂直宽度(常取0.4) e —八字墙基础襟边宽度(常取0.1或0.2) d —八字墙基础厚度正翼墙(常称大八字墙): 反翼墙(常称小八字墙):а+= βθ正 а-= βθ反 正βαcos /c =正 反反βαcos /c =γsin /m m =0 γsin /m m =0()正正正ββcos m /sin n n 0+= ()反反反ββcos m /sin n n 0-=八字墙墙身体积:()()3300220h H n 6m c h H m 21V -+-=正身正 ()()3300220h H n 6m c h H m 21V -+-=反身反八字墙墙身体积计算示意图()正正正0mn /1tan arctan δ-=β ()反反反0mn /1tan arctan δ+=β 正正βcos /e e 1= 反反βcos /e e 1= 正正δcos /e e 2= 反反δcos /e e 2=()正正正ββcos /sin 1e e 3 -= ()反反反δc o s /δs i n 1e e 3 -= 八字墙基础体积:()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 0312******* ⎥⎦⎤⎢⎣⎡+++++-+-++=正正正正正正正正正正 ()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 03122200210 ⎥⎦⎤⎢⎣⎡+++++-+-++=反反反反反反反反反反附图:涵洞八字墙墙身计算方法参考某涵洞八字墙墙身设计如下(见下图:涵洞右侧洞口前方冀墙):涵洞与路线右交角为120°(α=90°-120°=-30°),路基边坡m=1.5(即1:1.5),冀墙正截面背侧坡比n0=4(即4:1),正截面顶宽c0=40cm,洞口截面高H=479cm,冀尾截面高h=70cm,正侧面线转到涵洞轴线转角β=-20°(绕O点逆时针取负),涵洞轴线流水坡度i=2%。

八字墙墙身的计算公式涵洞与路线右交角为120°(α=90°-120°=-30°),路基边坡m0=1.5(即1:1.5),冀墙正截面背侧坡比n0=4(即4:1),正截面顶宽c0=40cm,洞口截面高H=479cm,冀尾截面高h=70cm,正侧面线转到涵洞轴线转角β=-20°(绕O点逆时针取负),涵洞轴线流水坡度i=2%。
相关计算如下:1.墙身计算考虑流水坡度i合成:m=m0/(1±m0i/cosα),在上游取正,在下游取负,m=1.5/(1+1.5*2%/cos30°)=1.4498;2.涵洞轴线冀长:L=(H-h)m/cosα=(4.79-0.7)*1.4498/cos30°=6.847m;3.洞口截面墙顶宽:c= c0/cos(β-α)=0.40/cos(-20°+30°)=0.406m;4.洞口截面墙背侧坡比: n=[n0+signβsin(β-α)/m]cos(β-α),sign为取符号函数signβ=sign(-20°)=-1,n=[4-sin(-20°+30°)/1.4498]cos(-20°+30°)=3.8213忽略流水坡度i影响, n’=[4-sin(-20°+30°)/1.5]cos(-20°+30°)=3.82525.洞口截面底宽:a=c+H/n=0.406+4.79/3.8213=1.660m,(n’→1.658m);6.冀尾截面底宽:b=c+h/n=0.406+0.70/3.8213=0.589m,(n’→0.588m);7.墙身体积计算(任取与洞口截面平行的一超薄dz段分析,如立面图阴影部分),其体积为: dV≈[(c+x) y /2]dz,其中x=c+y/n,dz =mdy代入得:dV≈ [y2/2/n+ cy]mdy,对y从h~H积分并整理得:V=0.5[(H3-h3)/3/n+c(H2-h2)]mV=0.5*[(4.793-0.73)/3/3.8213+0.406*(4.792-0.72)]*1.4498=13.536m3 (n’→V=13.529m3)令(H-h)m=Lcosα代入得:V=0.5[(H2+Hh+h2)/3/n+c(H+h)]Lcosα八字墙墙身计算公式设八字墙顺水流长度为L,两个截面积为a和b(即靠洞口的截面和离洞口最远的截面,这两个截面都是梯形,内坡是0,外坡是3:1),体积=(a+b)*L/2(一边八字)。

涵洞⼋字墙体积计算公式
注:红⾊为所要填得数,蓝⾊为⾃动⽣成的数字。
注:
β——翼墙与垂直于端墙⽅向的夹⾓n0——翼墙平⾏于端墙⽅向的背坡系数
a——翼墙垂直顶宽c——翼墙平⾏于端墙⽅向的顶宽
m——路基边坡坡度系数c0——翼墙后墙平⾏于端墙⽅向放坡长
n——翼墙垂直断⾯的背坡系数c1——翼墙后墙平⾏于端墙⽅向的底宽
e——基础襟边垂直宽度c2——翼墙前墙平⾏于端墙⽅向的底宽
h——翼墙前墙⾼度 e1——内侧基础襟边平⾏于端墙⽅向宽
H——翼墙后墙⾼度 e2——外侧基础襟边平⾏于端墙⽅向宽
d——基础厚度
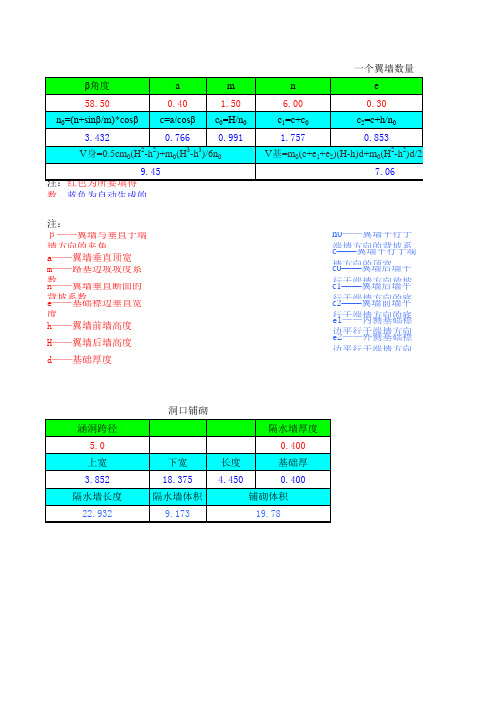
洞⼝铺砌
⼀个翼墙数量
0+(e 1+e 2+c+h/n 0)
墙平⾏于端墙⽅向的背坡系数平⾏于端墙⽅向的顶宽
墙后墙平⾏于端墙⽅向放坡长度墙后墙平⾏于端墙⽅向的底宽墙前墙平⾏于端墙⽅向的底宽边平⾏于端墙⽅向宽度侧基础襟边平⾏于端墙⽅向宽度
量m0(H2-h2。

涵洞八字墙工程量计算公式推导时间:2021.03.02 创作:欧阳数
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为H,X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82三、基础体积计算公式
将(4)式脱出积分公式整理得
其实八字墙基础是底面为梯形的一个棱柱体
基础体积=梯形面积乘以高
四、基础体积计算例
上图中T=1.5、J=1.18、H=0.6 、X=3.821=2.82。

八字墙翼墙(墙身)砼用量精确通用计算公式推导
因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H, X 变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),
墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将(4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。

路斜交涵洞斜八字式洞口布置图及尺寸表进行分析整理: 已知:γ—涵洞轴线与路线前进方向的夹角(右侧顺时针方向)θ—水流扩散角,即八字墙与涵洞轴线的夹角a —涵洞斜度,即涵轴线的法线方向与路线的夹角(锐角) H —接涵洞洞身部位八字墙墙身高度(等于涵洞墙身高度+板厚) h —接出口部位八字墙墙身高度(根据实际可不同,常取0.2) m —路基边坡坡比n —八字墙墙身正背坡(常取4.0) α—八字墙顶面垂直宽度(常取0.4) e —八字墙基础襟边宽度(常取0.1或0.2) d —八字墙基础厚度正翼墙(常称大八字墙): 反翼墙(常称小八字墙):а+= βθ正 а-= βθ反正βαcos /c =正 反反βαcos /c = γsin /m m =0 γsin /m m =0()正正正ββcos m /sin n n 0+= ()反反反ββcos m /sin n n 0-=八字墙墙身体积:()()3300220h H n 6m c h H m 21V -+-=正身正 ()()3300220h H n 6m c h H m 21V -+-=反身反八字墙墙身体积计算示意图()正正正0mn /1tan arctan δ-=β ()反反反0mn /1tan arctan δ+=β 正正βcos /e e 1= 反反βcos /e e 1= 正正δcos /e e 2= 反反δcos /e e 2=()正正正ββcos /sin 1e e 3 -= ()反反反δcos /δsin 1e e 3 -=八字墙基础体积:()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 0312******* ⎥⎦⎤⎢⎣⎡+++++-+-++=正正正正正正正正正正 ()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 03122200210 ⎥⎦⎤⎢⎣⎡+++++-+-++=反反反反反反反反反反附图:。

路斜交涵洞斜八字式洞口布置图及尺寸表进行分析整理: 已知:γ—涵洞轴线与路线前进方向的夹角(右侧顺时针方向)θ—水流扩散角,即八字墙与涵洞轴线的夹角a —涵洞斜度,即涵轴线的法线方向与路线的夹角(锐角) H —接涵洞洞身部位八字墙墙身高度(等于涵洞墙身高度+板厚) h —接出口部位八字墙墙身高度(根据实际可不同,常取0.2) m —路基边坡坡比n —八字墙墙身正背坡(常取4.0) α—八字墙顶面垂直宽度(常取0.4) e —八字墙基础襟边宽度(常取0.1或0.2) d —八字墙基础厚度正翼墙(常称大八字墙): 反翼墙(常称小八字墙):а+= βθ正 а-= βθ反 正βαcos /c =正 反反βαcos /c =γsin /m m =0 γsin /m m =0()正正正ββcos m /sin n n 0+= ()反反反ββcos m /sin n n 0-=八字墙墙身体积:()()3300220h H n 6m c h H m 21V -+-=正身正 ()()3300220h H n 6m c h H m 21V -+-=反身反八字墙墙身体积计算示意图()正正正0mn /1tan arctan δ-=β ()反反反0mn /1tan arctan δ+=β 正正βcos /e e 1= 反反βcos /e e 1= 正正δcos /e e 2= 反反δcos /e e 2=()正正正ββcos /sin 1e e 3 -= ()反反反δcos /δsin 1e e 3 -= 八字墙基础体积:()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 0312******* ⎥⎦⎤⎢⎣⎡+++++-+-++=正正正正正正正正正正 ()()()()ed n h c 21e e e d h H n 2m d h H e e c m V 03122200210 ⎥⎦⎤⎢⎣⎡+++++-+-++=反反反反反反反反反反附图:涵洞八字墙墙身计算方法参考某涵洞八字墙墙身设计如下(见下图:涵洞右侧洞口前方冀墙):涵洞与路线右交角为120°(α=90°-120°=-30°),路基边坡m=1.5(即1:1.5),冀墙正截面背侧坡比n0=4(即4:1),正截面顶宽c0=40cm,洞口截面高H=479cm,冀尾截面高h=70cm,正侧面线转到涵洞轴线转角β=-20°(绕O点逆时针取负),涵洞轴线流水坡度i=2%。

涵洞八字墙工程量计算公式推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
、低令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X
高)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼的一端为X
低
墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X 低=1、X 高=3.82
339.875
.36182.35.12182.346.05.113322=⨯-⨯+-⨯⨯=)()(、体积 339.875
.36182.35.1246.023.4182.3233=⨯-⨯+⨯⨯+=)()(、体积 三、基础体积计算公式
)()(基础体积低高40dx X x x B
TH TJH ⎰+=- 将 (4)式脱出积分公式整理得
其实八字墙基础是底面为梯形的一个棱柱体
基础体积=梯形面积乘以高
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82
949.382.275
.326.05.182.26.018.15.112=⨯⨯⨯+⨯⨯⨯=、基础体积 947.36.02
23.418.193.12=⨯⨯+=)(、基础体积。
![[yf]涵洞八字墙项目量计算公式推导083](https://img.taocdn.com/s1/m/69937511ed630b1c59eeb5b0.png)
涵洞八字墙工程量计算公式推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X
高、低的一端为X
低
)、
翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T相关,它随墙高增高而增长。
.
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将 (4)式脱出积分公式整理得
其实八字墙基础是底面为梯形的一个棱柱体
基础体积=梯形面积乘以高
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。
八字墙翼墙(墙身)砼用量精确通用计算公式推导
*注:因为常用平均面积法、切分法、棱台算法等计算法计算翼墙体积(砼用量),在长大翼墙计算过程中会随着长度增长误差也随着增长,若求精确故不可采用。
以下计算公式,均能精确到0.01m3左右。
一、墙身体积计算公式
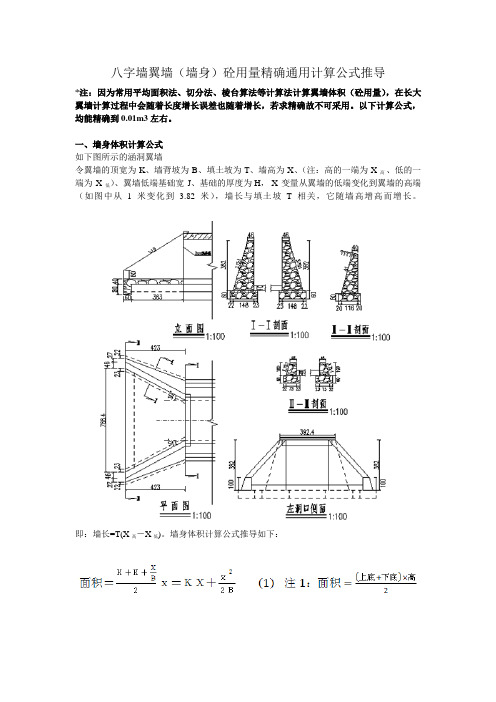
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为 H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到 3.82米),墙长与填土坡T相关,它随墙高增高而增长。
即:墙长=T(X高-X低)。
墙身体积计算公式推导如下:
将(2)式脱出积分公式整理得
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
三、基础体积计算公式
将 (4)式脱出积分公式整理得
四、基础体积计算例
上图中 T=1.5、J=1.18、H=0.6 、X=3.82-1=2.82。

八字墙翼墙(墙身)砼用量精确通用计算公式推导
一、墙身体积计算公式
如下图所示的涵洞翼墙
令翼墙的顶宽为K、墙背坡为B、填土坡为T、墙高为X、(注:高的一端为X高、低的一端为X低)、翼墙低端基础宽J、基础的厚度为H, X变量从翼墙的低端变化到翼墙的高端(如图中从1米变化到3.82米),墙长与填土坡T 相关,它随墙高增高而增长。
即:墙长二T(X高—X低)。
墙身体积计算公式推导如下:
面积=—(1)注1:面积=〔上軒严咼体积可::(TKX+^X2)弘⑵.
将(2)式脱出积分公式整理得
体积=斗+呼
二、墙身体积计算例
上图中K=0.46、B=3.75、T=1.5、X低=1、X高=3.82
体积
=1.5 X 0.46八3.8—1巧*讣八3竺7引
=8
.
339
二、基础体积计算公式
体积二严v(TJH+¥£血⑴ 将(4)式脱出积分公式整理得TH
体积=TJHX + —X2(5)
四、基础体积计算例
上图中T=1.5、J=1.18、H=0.6、X=3.82-仁2.82
亠心L 1*5 X 0.6 r
体积=lJx 1.13x0.6x2.82十一X 2.823 = 3.949
2 X 3.75
6 X 3.75。