离散数学平面图及图的着色

离散数学中的着色问题研究离散数学是数学的一个分支，主要研究集合、函数、关系、图论等离散结构及其应用。

在离散数学中，着色问题是一个经典的研究方向。

着色问题是指在给定的图或图的某个特定部分上，给每个顶点或每条边分配一个颜色，使得相邻的顶点或边颜色不相同的一类问题。

着色问题最早可以追溯到1852年，当时英国著名数学家弗朗西斯·格思欧提出了“四色猜想”，即地图着色问题的一个特例。

他猜测，任意平面图都可以用四种颜色进行着色，使得任意两个相邻区域颜色不同。

虽然直到1976年才由凯尼思·阿普尔、沃尔夫冈·赫登和约翰·哈姆顿等人证明了这个猜想的正确性，但这个问题奠定了着色问题研究的基础。

在着色问题的研究中，最为著名的是顶点着色问题和图的边着色问题。

顶点着色问题是指对于给定的图，为图的每个顶点分配一个颜色，并且相邻的顶点颜色不能相同。

而图的边着色问题是指为图的每条边分配一个颜色，要求相邻的边颜色不相同。

这两个问题都是在给定一定的约束条件下，寻找合理的颜色分配方案，是离散数学中的基础问题。

着色问题在实际应用中有着广泛的意义和应用。

例如，在地图着色中，不同颜色的区域表示不同的行政区域或国家，通过合理的着色可以方便地进行区分。

此外，在调度问题中，着色问题也具有重要作用。

例如，在一条生产线上的任务安排，可以通过着色问题来确定每个任务在不同时间段的执行顺序，从而实现资源的优化分配。

在着色问题的研究中，有很多经典的算法和策略。

其中最著名的算法是所谓的贪心算法，即每次选择未被染色的顶点或边中与已染色顶点或边相邻且颜色不同的进行染色，直到所有顶点或边都被染色。

贪心算法是一种简单而有效的算法，但并不总是能够找到最优解。

其他的算法包括回溯算法、深度优先搜索算法等，它们在着色问题的求解中各有特点，可以根据具体情况进行选择和应用。

此外，在着色问题的研究中，还涉及到很多扩展和变种。

例如多重集着色问题，指的是允许相邻的顶点或边可以有相同的颜色；带权着色问题，指的是为每个颜色分配一个权重，并寻找使总权重最大的颜色分配方案等。

图是离散数学中的重要概念，而平面图和平面图的着色是图论中的两个关键概念。

平面图是指在平面上绘制的图形，使得图中的边不会相交。

平面图的着色是指对平面图中的顶点进行染色，且相邻的顶点不会被染成相同的颜色。

平面图的概念最早由欧拉在1736年提出。

他发现，如果一个图是可以在平面上绘制而不会边相交的，那么这个图是一个平面图。

欧拉还引入了一个重要的公式，即欧拉定理，它描述了平面图中的顶点、边和面的关系：V - E + F = 2，其中V代表顶点数，E代表边数，F代表面数。

对于平面图的着色问题，四色定理是一个非常重要的结果。

四色定理指出，任何一个平面图，在不考虑多重边和自环的情况下，最多只需要使用四种颜色就能够对图的顶点进行染色，使得相邻的顶点不会有相同的颜色。

这个定理在1976年被由英国数学家Tomás Oliveira e Silva使用计算机辅助证明，被认为是图论史上的一大突破。

对于平面图的着色，有一种特殊的染色方法叫做四色标号。

四色标号是指对于任意一个平面图，都可以给图中的每个顶点赋予一个自然数，使得相邻的顶点之间的差值不超过3。

这种染色方法保证了相邻的顶点不会被染成相同的颜色，同时最多只需要使用四种颜色。

平面图的着色不仅在图论中有着重要的应用，同时在现实生活中也有很多实际的应用。

比如，考虑地图上的城市，如果我们希望将城市标记成不同的颜色，以表示它们的关系，那么可以利用平面图的着色来实现。

另外，平面图的着色还有很多其他的实际应用，比如在工程规划中用于规划电路的布线、在计算机科学中用于处理图像等等。

总之，离散数学中的图的平面图与平面图的着色是图论中的两个重要概念。

平面图是指在平面上绘制的图形，使得边不会相交；平面图的着色是指对平面图中的顶点进行染色，且相邻的顶点不会被染成相同的颜色。

四色定理是平面图着色的重要结果，它指出任意一个平面图可以使用最多四种颜色进行着色。

平面图的着色在现实生活中有着广泛的应用，是离散数学中的一个重要研究领域。

离散数学是研究离散结构和离散运算的数学分支，它在计算机科学、信息技术、密码学等领域中具有重要的应用价值。

而图论作为离散数学的一个重要分支，在实际应用中扮演着重要的角色。

图是由节点和连接节点的边组成的抽象表示，可以用来描述许多现实生活中的问题，如交通网络、社交网络等。

而图的着色问题，即如何给图的节点上色，是图论中一个重要的课题。

在离散数学中，图的颜色数是指给图的每个节点赋予的不同颜色的数量。

解决图的着色问题，即求解最小的颜色数，是离散数学中的一个经典问题。

根据图的邻接关系，我们可以将图分为不相邻的节点集合，或称为独立点集。

而在每个独立点集中，节点之间不存在连接，即没有边相连。

因此，在同一个独立点集中的节点可以赋予相同的颜色。

而对于连接的节点，我们需要确保相邻的节点颜色不同。

基于这样的思想，我们可以使用贪心算法来给图的节点进行着色。

贪心算法的基本思路是从一个初始节点开始，每次选择一个尚未被上色的节点，并且给它赋予不同于相邻节点的颜色。

重复这个过程，直到所有的节点都被着色。

但是，通过贪心算法所得到的着色结果并不一定是最优解。

这引出了著名的四色定理。

四色定理是图论中一个重要的定理，指出任何平面图都可以使用不超过四种颜色进行着色，使得相邻节点的颜色不同。

该定理是由基姆和罗伯特森等人在1976年通过计算机模拟方法得到的，随后在1997年由托马斯·韦伦斯顿等人通过使用图论方法进行证明。

证明四色定理的过程非常复杂，但基本思想是从数学的角度证明了四色定理的逻辑正确性。

简单来说，四色定理的证明过程是通过构造方法，将平面图转化为一种特殊的图结构，即棋盘染色问题。

然后通过分析棋盘染色问题的特征和规律，进行推理和证明。

四色定理的证明不仅仅具有理论意义，也具有重要的实际应用。

例如，在地图着色中，四色定理可以用于保证地图上相邻地区的颜色不同。

此外，在计算机图像处理中，也可以采用四色定理的方法，有效地减少图像的颜色数量，从而节省存储空间和运算时间。

离散数学中的染色问题研究离散数学是数学的一个分支领域，研究的是不连续的、离散的结构和对象。

其中一个重要的研究方向就是染色问题，它在多个领域有着广泛的应用。

本文将介绍离散数学中染色问题的基本概念、解决方法以及实际应用。

一、概述染色问题是一类涉及给定对象赋予各种颜色的数学问题。

常见的染色问题有图的顶点着色问题和平面地图着色问题。

图的顶点着色问题要求给定无向图的各个顶点赋予不同的颜色，使得相邻的顶点不能有相同颜色。

平面地图着色问题是指给定一个地图上的区域，要求相邻的区域之间不能有相同的颜色。

二、解决方法对于染色问题的解决方法，有多种不同的算法和策略。

下面将介绍其中较常用的几种方法。

1. 贪心算法贪心算法是一种简单而高效的解决染色问题的方法。

它的基本思想是每次选择一个合适的颜色给节点染色，并尽量避免相邻节点具有相同颜色。

贪心算法通常通过对节点顺序的选择和颜色的分配来实现。

2. 回溯算法回溯算法是一种递归的解决方法，它通过穷举所有可能的情况来求解染色问题。

具体实现时，从图的第一个节点开始遍历并进行颜色的选择，当发现无法进行下一步时就回溯到上一个节点进行其他尝试。

3. 图的染色多项式图的染色多项式是一种数学表示方法，用于描述染色问题的解决情况。

它能够准确计算出各种染色方案的数量，并通过多项式的形式抽象出问题的共性和规律。

三、实际应用染色问题在实际中具有广泛的应用，下面将介绍其中几个重要的应用领域。

1. 地图着色染色问题最早被应用于地图着色，目的是要求相邻的区域之间不能有相同的颜色。

这在地理学和地图制作中非常重要，能够帮助人们更清晰地理解地理空间。

2. 时间表编排染色问题在课程表、员工排班等时间表编排中也有广泛应用。

通过合理的染色方案，可以保证时间表的合理性和可行性，避免冲突和混乱。

3. 无线频道分配在无线通信领域，染色问题被应用于无线频道的分配。

通过给不同区域或设备分配不同的频道，可以减少干扰和信号冲突，提高通信效率。

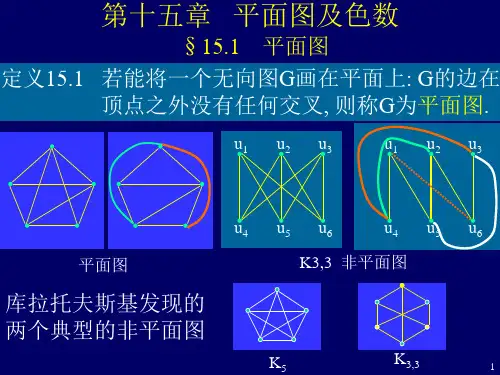
§5.6 平面图与图地着色 习题5.61． 假定一个连通平面图有8个顶点,每个顶点地度数都为3。

请问,这个图地平面嵌入将平面分成多少个面？解 根据条件有8=p ,122/83=⨯=q ,从而根据欧拉定理有62=+-=p q f 。

2．设G 是具有k 个连通分图地)(q p ，平面图地一个平面嵌入,其面数为f ,证明：1+=+-k f g p解 下面用数学归纳法证明如下：（1）1=k 时即为欧拉公式,所以成立。

（2）假设m k ≤时公式成立。

（3）当1+=m 时,将图G 看成两个图1G 与2G 地并,其中1G 为一个连通分图, 2G 为其余m 个连通分图地并,根据上面地假设,对图1G 与2G 有：11111+=+-f q p ,1222+=+-m f q p ,将上两式相加得： 1)1()1()()(212121++=-+++-+m f f q q p p注意到图1G 与2G 共用一个外部面,我们即得1+=+-k f g p 。

3.假定一个)(q p ，图是连通地平面二部图,且p ≥3,则q ≤42-p 。

证;由于二部图中每个回路地长度都是偶数。

当p ≥3时,即每个面地围数至少是4。

据定理,2q ≥4f=4(2-p+q) 从而q ≤42-p 。

4．图5.42地4个图是平面图吗？如果是,给出一个平面嵌入;如果不是,找出与5K 或K 3,3同胚地子图。

图5.42 习题4地图解 图（1）,（2）,（4）改画如下：从而知图（1）,（2）是可平面图,图（4）是5阶完全图5K ,从而是非可平面图。

图（3）也是一个非可平面图,可用库拉托斯基定理证明如下：5．一个简单图地交叉数是指在平面里画这个图且不允许任何三条边在同一点交叉时,各边交叉地最少次数。

求以下非平面图地交叉数：3,3K , 5K , 6K , 7K , 4,3K , 4,4K , 5,5K解：3,3K 地交叉次数是15K 地交叉次数是56K 地交叉次数是107K 地交叉次数是184,3K 地交叉次数是84,4K 地交叉次数是115,5K 地交叉次数是166．下面地算法可以用来为简单图点着色。

离散数学中的图着色问题研究与算法设计离散数学是数学的一个分支，研究离散的结构和对象。

在离散数学中，图论是一个重要的研究领域。

图着色问题是图论中的一个经典问题，其研究和算法设计具有重要的理论和实际意义。

图着色问题是指如何用有限种颜色对图中的顶点进行着色，使得相邻的顶点颜色不相同。

这里的相邻顶点是指在图中有一条边连接的顶点。

图着色问题最早由英国数学家弗朗西斯·格斯顿于1852年提出，被称为“四色定理”。

四色定理是图着色问题的一个重要结果。

它指出，任何平面图都可以用至多四种颜色进行着色，使得相邻顶点颜色不相同。

这个定理的证明非常复杂，涉及到大量的数学理论和计算机算法。

直到1976年，美国数学家肯尼思·阿普尔和沃尔夫冈·哈肯提出了一个基于计算机的证明，才最终解决了这个问题。

除了四色定理，图着色问题还有许多其他的研究和算法设计。

其中一个经典的问题是最小顶点着色问题。

最小顶点着色问题是指找到一个最小的颜色数，使得图中的每个顶点都能被染上一种颜色，并且相邻顶点颜色不相同。

这个问题在实际中有着广泛的应用，比如任务调度、频率分配等领域。

解决最小顶点着色问题的算法有许多种。

其中一种常用的算法是贪心算法。

贪心算法的基本思想是每次选择一个顶点，将其染上一个未被使用的颜色，然后继续选择下一个顶点。

如果某个顶点的颜色与相邻顶点相同，则选择另一种颜色进行染色。

通过不断迭代，直到所有的顶点都被染色为止。

贪心算法的时间复杂度较低，但是并不一定能够找到最优解。

除了贪心算法，还有其他的算法可以解决最小顶点着色问题，比如回溯算法、分支定界算法等。

这些算法的时间复杂度较高，但是可以找到最优解。

然而，由于图着色问题是一个NP完全问题，即不存在多项式时间内的算法可以解决该问题。

因此，对于大规模的图着色问题，通常采用近似算法或者启发式算法来求解。

近似算法是一种在多项式时间内找到一个接近最优解的算法。

其中一个常用的近似算法是基于最大度数的着色算法。