《相交线与平行线》单元测试题及答案
- 格式:doc
- 大小:112.50 KB
- 文档页数:9

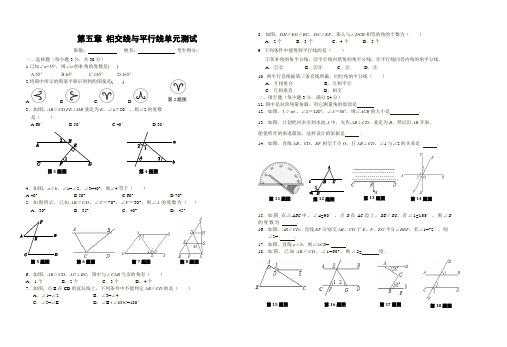
B E DA CF87654321DCBA第五章 相交线与平行线测试题一、选择题(每题3分,共30分)1、如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )A .50°B .60°C .140°D .160°图1 图2 图3 2、如图2,已知AB ∥CD ,∠A =70°,则∠1的度数是( )A .70°B .100°C .110°D .130°3、已知:如图3,AB CD ⊥,垂足为O ,EF 为过点O 的一条直线,则1∠ 与2∠的关系一定成立的是( )A .相等B .互余C .互补D .互为对顶角4、如图4,AB DE ∥,65E ∠=,则B C ∠+∠=( )A .135B .115C .36D .65图4 图5 图65、如图5,小明从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20方向行走至C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )A .右转80°B .左转80°C .右转100°D .左转100° 6、如图6,如果AB ∥CD ,那么下面说法错误的是( )A .∠3=∠7;B .∠2=∠6C 、∠3+∠4+∠5+∠6=1800D 、∠4=∠87、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30,那么这两个角是( )A . 42138、;B . 都是10;C . 42138、或4210、;D . 以上都不对8、下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )A .①、②是正确的命题;B .②、③是正确命题;C .①、③是正确命题 ;D .以上结论皆错DB A C1ab1 2OABCD EF 2 1Oa b M P N 1 2 3A B C a b1 23 B E9、下列语句错误的是( )A .连接两点的线段的长度叫做两点间的距离;B .两条直线平行,同旁内角互补C .若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角D .平移变换中,各组对应点连成两线段平行且相等10、如图7,a b ∥,M N ,分别在a b ,上,P 为两平行线间一点,那么123∠+∠+∠=( )A .180B .270C .360D .540二、填空题(每题3分,共18分)11、如图8,直线a b ∥,直线c 与a b ,相交.若170∠=,则2_____∠=.图7 图8 图9 图1012、如图9,已知170,270,360,∠=︒∠=︒∠=︒则4∠=______︒.13、如图10,已知AB ∥CD ,BE 平分∠ABC ,∠CDE =150°,则∠C =______14、如图11,已知a b ∥,170∠=,240∠=,则3∠ 图11 1315、如图12的一个条件 .16、如图13,已知AB CD //,∠α=____________ 三、解答题(共52分)17、推理填空:(每空1分,共12分)如图: ① 若∠1=∠2,则 ∥ ( ) 若∠DAB+∠ABC=1800,则∥ ()②当 ∥ 时,∠ C+∠ABC=1800 ( ) 当 ∥ 时,∠3=∠C ( )18、如图,∠1=30°,AB ⊥CD ,垂足为O ,EF 经过点O .求∠2、∠3的度数. (8分)12 bac b ac d1 2 3 4 A BCDE 321DCBAABCDO123EF19、已知:如图AB ∥CD ,EF 交AB 于G ,交CD 于F ,FH 平分∠EFD ,交AB 于H ,∠AGE=500,求:∠BHF 的度数.(8分)20、(10分(1)如图a ,图中共有___对对顶角;(2)如图b ,图中共有___对对顶角; (3)如图c ,图中共有___对对顶角.(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n 条直线相交于一点,则可形成多少对对顶角?(5)若有2008条直线相交于一点,则可形成 多少对对顶角?21、(6分)如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B =30º,求∠EAD ,∠DAC ,∠C 的度数。

相交线与平行线一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,共24分)1.在下面各图中,∠1与∠2是对顶角的是()A.B.C.D.2.如图,直线a、b相交于点O,若∠1=30°,则∠2等于()A.60°B.30°C.140°D.150°3.如图,直线a,b相交于点O,若∠1=40°,则∠2=()A.40°B.50°C.60°D.140°4.如图,点P在直线l外,点A,B在直线l上,PA=3,PB=7,点P到直线l的距离可能是()A.2 B.4 C.7 D.85.如图,直线a∥b,∠1=50°,则∠2的度数为()A.40°B.50°C.55°D.60°6.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是()A.连接直线外一点与直线上各点的所有线段中,垂线段最短B.在同一平面内,垂直于同一条直线的两条直线互相平行C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D.经过直线外一点,有且只有一条直线与这条直线平行7.如图,已知ON丄a,OM丄a,所以OM与ON重合的理由是()A.两点确定一条直线B.经过一点有且只有一条线段垂直于己知直线C.过一点只能作一条垂线D.垂线段最短8.如图,直线AB∥CD,∠A=70°,∠E=30°,则∠C等于()A.30°B.40°C.60°D.70°二、填空题(本大题共6小题,每小题3分,共18分)9.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:.10.如图,已知O是直线AB上一点,∠1=30°,OD平分∠BOC,则∠2=.11.如图,直线AB、CD相交于点O,EO⊥AB,∠AOC=25°。

人教版七年级下册数学第五章《相交线与平行线》单元练习题(含答案)一、单选题1.如图,AB CD ∥ ,点E 在CA 的延长线上若50BAE ∠=︒,则ACD ∠的大小为( )A .100°B .120°C .130°D .110°2.如图,要修建一条公路,从A 村沿北偏东75°方向到B 村,从B 村沿北偏西25°方向到C 村.若要保持公路CE 与从A 村到B 村的方向一致,则应顺时针转动的度数为( )A .50°B .75°C .100°D .105°3.如图,直线AB ∥CD ,如果∠1=70°,那么∠BOF 的度数是( )A .70°B .100°C .110°D .120°4.具有下列关系的两角:①互为补角;②同位角;③对顶角;④内错角;⑤邻补角;⑥同旁内角.其中一定有公共顶点的两角的对数为( )A .1对B .2对C .3对D .4对5.如图,将三角板与直尺贴在一起,使三角板的直角顶点C (∠ACB =90°)在直尺的一边上,若∠2=65°,则∠1的度数是( )A .15°B .25°C .35°D .65°6.下列命题中,真命题是( )A .一条直线截另外两条直线所得到的同位角相等B .两个无理数的和仍是无理数C .有公共顶点且相等的两个角是对顶角D .等角的余角相等7.如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C=70°,则∠AED=( )A .55°B .125°C .135°D .140°8.如图,12l l //,点O 在直线1l 上,若90AOB ︒∠=,135︒∠=,则2∠的度数为()A .65°B .55°C .45°D .35°9.下列命题是真命题的是( )A .如果一个数的相反数等于这个数本身,那么这个数一定是0B .如果一个数的倒数等于这个数本身,那么这个数一定是1C .如果一个数的平方等于这个数本身,那么这个数一定是0D .如果一个数的算术平方根等于这个数本身,那么这个数一定是010.如图,直线AB ∥ CD ,∠ B=50°,∠ C=40°,则∠E 等于( )A .70°B .80°C .90°D .100°二、填空题 11.如图,AD ∥BC ,EF ∥BC ,BD 平分∠ABC ,图中与∠ADO 相等的角有_______ 个,分别是___________.因为AB ∥CD ,EF ∥AB ,根据_____________________________,所以_____________.12.如图,在正方形网格中,三角形DEF 是由三角形ABC 平移得到的,则点C 移动了________格.13.如图,在ABC ∆中,4AB =,6BC =,60B ∠=︒,将ABC ∆沿射线BC 的方向平移2个单位后,得到A B C '''∆,连结A C ',则A B C ∆''的周长为______.14.下面三个命题: ①若是方程组的解,则或; ②函数通过配方可化为; ③最小角等于的三角形是锐角三角形. 其中正确命题的序号为 .15.设圆上有n 个不同的点,连接任两点所得线段,将圆分成若干个互不重合的区域,记()f n 为区域数的最大值,则(5)_________f =,(6)________f =.16.如图,已知AB ∥ED,∠ABC=300,∠EDC=400,则∠BCD 的度数是 .17.点M ,N 在线段AB 上,且MB =6cm ,NB =9cm ,且N 是AM 的中点,则AB =___cm ,AN =____cm .18.把命题“三个角都相等的三角形是等边三角形”改写成“如果……,那么……”的形式是_____;该命题的条件是_____,结论是_____.三、解答题19.如图,已知点A 是射线OP 上一点.(1)过点A 画OQ 的垂线,垂足为B ;过点B 画OP 的平行线BC ;(2)若50POQ ∠=,求ABC ∠的度数.20.(1)问题背景:已知:如图①-1,//AB CD ,点P 的位置如图所示,连结,PA PC ,试探究APC ∠与PAB ∠、PCD ∠之间有什么数量关系,并说明理由.(将下面的解答过程补充完整,括号内写上相应理由或数学式)解:(1)APC ∠与PAB ∠、PCD ∠之间的数量关系是:360APC PAB PCD ∠+∠+∠=︒(或360()APC PAB PCD ∠=︒∠+∠只要关系式形式正确即可)理由:如图①-2,过点P 作//PE AB .∵//PE AB (作图),∴180PAB APE ∠+∠=︒( ),∴//AB CD (已知)//PE AB (作图),∴//PE _______( ),∴CPE PCD ∠+∠=_______( ),∴180180360PAB APE CPE PCD ∠+∠+∠+∠=+︒=︒(等量代换)又∵APE CPE APC ∠+∠=∠(角的和差),∴360APC PAB PCD ∠+∠+∠=︒(等量代换)总结反思:本题通过添加适当的辅助线,从而利用平行线的性质,使问题得以解决.(2)类比探究:如图②,//AB CD ,点P 的位置如图所示,连结PA 、PC ,请同学们类比(1)的解答过程,试探究APC ∠与PAB ∠、PCD ∠之间有什么数量关系,并说明理由.(3)拓展延伸:如图③,//AB CD ,ABP ∠与CDP ∠的平分线相交于点1P ,若128P ∠=︒,求P ∠的度数,请直接写出结果,不说明理由.21.如图,抛物线y =ax 2+bx ﹣3与x 轴交于A (﹣1,0),B (3,0),与y 轴交于点C ,顶点为D .(1)求抛物线的解析式及点D的坐标.(2)在线段BC下方的抛物线上,是否存在异于点D的点E,使S△BCE=S△BCD?若存在,求出点E的坐标;若不存在,请说明理由.(3)点M3,2m⎛⎫- ⎪⎝⎭在抛物线上,点P为y轴上一动点,求2MP+2PC的最小值.22.如图,在96⨯网格中,已知△ABC,请按下列要求画格点三角形A' B' C'(三角形的三个顶点都是小正方形的顶点).(1)在图①中,将△ABC平移,使点O落在△ABC的边AB(不包括点A和点B)上;(2)在图②中,将△ABC平移,使点O落在△ABC的内部.23.如图.一次函数y=12x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.(1)求点A与点B的坐标;(2)求△ABC的面积.24.在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.(1)过B作AC的平行线BD.(2)作出表示B到AC的距离的线段BE.(3)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).(4)△ABC的面积为.25.如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.解:∵∠1=∠2(已知)∠2=∠DGF∴∠1=∠DGF(____________)∴BD∥CE∴∠3+∠C=180°( )又∵∠3=∠4(已知)∴∠4+∠C=180°∴∥(同旁内角互补,两直线平行)∴∠A=∠F( ).26.如图,所有小正方形的边长都为1,A、B、C都在格点上.(1)过点C画直线AB的平行线(不写画法,下同);(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.(3)线段_____的长度是点A到直线BC的距离;(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.27.如图,AB∥CD,∠1=∠2,求证:AM∥CN参考答案1.C2.C3.C4.B5.B6.D7.B8.B9.A10.C11.4 ∠DOF、∠EOB、∠ABD、∠DBC平行于同一直线的两条直线平行CD∥EF 12.513.1214.②③15.16;3116.70°17. 12 318.如果一个三角形的三个角都相等,那么这个三角形是等边三角形一个三角形的三个角都相等这个三角形是等边三角形19.(2)40°20.(1)∠APC+∠PAB+∠PCD=360°,理由见解析;两直线平行,同旁内角互补;CD,如果两条直线都和第三条直线平行,那么这两条直线也互相平行;180°,两直线平行,同旁内角互补;(2)∠APC=∠PAB+∠PCD,(3)∠P=56°.21.(1)y=x2﹣2x﹣3,D的坐标为(1,﹣4);(2)存在异于点D的点E,使S△BCE=S△BCD,点E的坐标为(2,﹣3);(3)最小值为23.(1)A(0,1),B(3,0);(2)5 324. (3) <;(4) 9 26.(3)AG;(4)<.。

人教版七年级数学下册第5章《相交线与平行线》单元测试卷一.选择题1.下列说法,正确的是( )A. 若ac=bc,则a=bB. 两点之间的所有连线中,线段最短C. 相等的角是对顶角D. 若AC=BC,则C是线段AB的中点【答案】B【解析】【分析】根据等式的性质可判断A的正误;根据线段的性质判断B的正误;根据对顶角的性质判断C的正误;根据中点的性质判断D的正误.【详解】解:A、若ac=bc(c≠0),则a=b,故此选项错误,B、两点之间的所有连线中,线段最短,说法正确,故此选项正确,C、相等的角是对顶角,说法错误,应是对顶角相等,故此选项错误,D、若AC=BC,则点C是线段AB的中点,说法错误,应是若AC=BC=AB,则点C是线段AB的中点,故此选项错误,故选:B.【点睛】此题主要考查了等式的性质、对顶角的性质、线段的性质、中点,关键是熟练掌握课本基础知识,牢固掌握定理.2.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )A. 50°B. 55°C. 60°D. 70°【答案】D【解析】【分析】先根据平行线的性质求出∠C的度数,再由三角形外角的性质即可得出结论.【详解】∵AB∥CD,∠1=40°,∠2=30°,∴∠C=40°.∵∠3是△CDE的外角,∴∠3=∠C+∠2=40°+30°=70°.故答案选D.【点睛】本题考查的知识点是平行线的性质,解题的关键是熟练的掌握平行线的性质.3.如图,将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上,已知∠A=30°,∠1=40°,则∠2的度数为( )A. 55°B. 60°C. 65°D. 70°【答案】D【解析】【分析】根据平行线的性质求出∠3=∠1=40°,根据三角形的外角性质求出∠2=∠3+∠A,代入求出即可.【详解】∵EF∥MN,∠1=40°,∴∠1=∠3=40°.∵∠A=30°,∴∠2=∠A+∠3=70°.故选D.【点睛】本题考查了平行线的性质,三角形外角性质的应用,能求出∠3的度数是解答此题的关键,注意:两直线平行,内错角相等.4.图中的∠1、∠2可以是对顶角的是( )A. B.C. D.【答案】C【解析】【分析】根据对顶角的定义,具有公共顶点且角的两边互为反向延长线对各图形分析判断后进行解答.【详解】解:A、∠1与∠2不是对顶角,B、∠1与∠2不是对顶角,C、∠1与∠2是对顶角,D、∠1与∠2不是对顶角,故选:C.【点睛】本题主要考查了对顶角的定义,熟练掌握定义是解题关键.5.如图,若AB,CD相交于点O,∠AOE=90°,则下列结论不正确的是( )A. ∠EOC与∠BOC互为余角B. ∠EOC与∠AOD互为余角C. ∠AOE与∠EOC互为补角D. ∠AOE与∠EOB互为补角【答案】C【解析】【分析】直接利用垂直的定义结合互余以及互补的定义分析得出答案.【详解】解:∵∠AOE=90°,∴∠BOE=90°,∵∠AOD=∠BOC,∴∠EOC+∠BOC=90°,∠EOC+∠AOD=90°,∠AOE+∠EOB=180°,故A、B、D选项正确,C错误.故选:C.【点睛】此题主要考查了垂直的定义、互余以及互补的定义,正确把握相关定义是解题关键.6.已知:如图,直线BO⊥AO于点O,OB平分∠COD,∠BOD=22°.则∠AOC的度数是( )A. 22°B. 46°C. 68°D. 78°【答案】C【解析】【分析】由垂直的定义可知∠AOB=90°,由角平分线的定义可知∠BOC=∠BOD=22°,从而求得∠AOC的度数. 【详解】解:∵BO⊥AO,∴∠AOB=90°,∵OB平分∠COD,∴∠BOC=∠BOD=22°,∴∠AOC=90°-22°=68°.故选C.【点睛】本题考查了垂直的定义,角平分线的定义.7.如图,∠1=68°,直线a平移后得到直线b,则∠2﹣∠3的度数为( )A. 78°B. 132°C. 118°D. 112°【答案】D【解析】【分析】根据补角的性质、对角的性质,再进行代换可以求出∠2-∠3的度数.【详解】延长直线c与b相交,令∠2的补角是∠4,则∠4=180º-∠2,令∠3的对顶角是∠5,则∠3=∠5,∵a∥b,∴∠6=∠1=68°.又∠4+∠5=∠6.∴(180º-∠2)+∠3=68°即:∠2-∠3= 112°【点睛】本题考查了补角的性质、对角的性质等知识点,熟练掌握是本题的解题关键.8.如图,下列条件中,能判断AB∥CD的是( )A. ∠FEC=∠EFBB. ∠BFC+∠C=180°C. ∠BEF=∠EFCD. ∠C=∠BFD【答案】C【解析】【分析】根据平行线的判定定理对各选项进行逐一判断即可.【详解】A.由∠FEC=∠EFB,可得CE∥BF,故本选项错误;B.由∠BFC+∠C=180°,可得CE∥BF,故本选项错误;C.由∠BEF=∠EFC,可得AB∥CD,故本选项正确;D.由∠C=∠BFD,可得CE∥BF,故本选项错误.故选C.【点睛】本题考查了平行线的判定,解题时注意:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.9.如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB 最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )A. ②③B. ①②③C. ③④D. ①②③④【答案】A【解析】【分析】根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”;“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”进行判断,即可解答.【详解】①线段AP是点A到直线PC的距离,错误;②线段BP的长是点P到直线l的距离,正确;③P A,PB,PC三条线段中,PB最短,正确;④线段PC的长是点P到直线l的距离,错误.故选A.【点睛】本题考查了垂线的两条性质:①从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.②从直线外一点到这条直线上各点所连的线段中,垂线段最短.10.将长方形ABCD纸片沿AE折叠,得到如图所示的图形,已知∠CED′=70°,则∠AED的大小是( )A. 60°B. 50°C. 75°D. 55°【答案】D【解析】【分析】根据折叠的性质得到∠AED=∠AED′,由平角的定义得到∠AED+∠AED′+∠CED′=180°,而∠CED′=60°,则2∠DEA=180°-70°=110°,即可得到∠AED的度数.【详解】解:∵长方形ABCD沿AE折叠得到△AED′,∴∠AED=∠AED′,而∠AED+∠AED′+∠CED′=180°,∠CED′=70°,∴2∠DEA=180°-70°=110°,∴∠AED=55°.故选:D.【点睛】本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应边相等.二.填空题11.如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.【答案】105【解析】【分析】直接利用平移的性质结合三角形外角的性质得出答案.【详解】由题意可得:m∥n,则∠CAD+∠1=180°.∵∠3=∠4,∴∠4+∠CAD=∠2,∴∠2﹣∠3=∠CAD+∠3﹣∠3=∠CAD=180°﹣∠1=180°﹣75°=105°.故答案为:105.【点睛】本题考查了平移的性质、三角形外角的性质以及平行线的性质,正确转化角的关系是解题的关键.12.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有_____.【答案】①④【解析】【分析】根据垂直定义可得∠BCA=90°,∠ADC=∠BDC=∠ACF=90°,然后再根据余角定义和补角定义进行分析即可.【详解】∵AC⊥BF,∴∠BCA=90°,∴∠ACD+∠1=90°,∴∠1是∠ACD的余角,故①正确;∵CD⊥BE,∴∠ADC=∠CDB=90°,∴∠B+∠BCD=90°,∠ACD+∠DAC=90°.∵∠BCA=90°,∴∠B+∠BAC=90°,∠1+∠ACD=90°,∴图中互余的角共有4对,故②错误;∵∠1+∠DCF=180°,∴∠1的补角是∠DCF.∵∠1+∠DCA=90°,∠DAC+∠DCA=90°,∴∠1=∠DAC.∵∠DAC+∠CAE=180°,∴∠1+∠CAE=180°,∴∠1的补角有∠CAE,故③说法错误;∵∠ACB=90°,∠ACF=90°,∠ADC=∠BDC=90°,∴∠BDC,∠ACB,∠ACF和∠ADC互补,故④说法正确.正确的是①④.故答案为:①④.【点睛】本题考查了余角和补角,关键是掌握两角之和为90°时,这两个角互余,两角之和为180°时,这两个角互补.13.如图,射线OA⊥OC,射线OB⊥OD,若∠AOB=40°,则∠COD=____°.【答案】40【解析】【分析】根据OA⊥OC,OB⊥OD,可得∠AOC=90°,∠BOD=90°,然后得到∠AOB与∠BOC互余,∠COD与∠BOC互余,根据同角的余角相等,继而可求解即可.【详解】解:∵OA⊥OC,OB⊥OD,∴∠AOC=90°,∠BOD=90°,∴∠AOB与∠BOC互余,∠COD与∠BOC互余,∴∠AOB=∠COD =40°,故答案为:40°.【点睛】本题考查了余角的知识,关键发现∠AOB、∠COD都是∠BOC余角,根据同角的余角相等解答.14.点P是直线l外一点,点A,B,C,D是直线l上的点,连接PA,PB,PC,PD.其中只有PA与l垂直,若PA=7,PB=8,PC=10,PD=14,则点P到直线l的距离是_____.【答案】7【解析】【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.【详解】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短.∵P A与l垂直, P A=7,∴点P到直线l的距离=PA,即点P到直线l的距离=7故答案为:7.【点睛】本题主要考查了垂线段最短的性质,熟记性质是解题的关键.15.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.【答案】55°【解析】【分析】过点E作EF∥AB,则EF∥CD,可得∠ABE=∠BEF, ∠DEF=∠CDE.先根据角平分线的定义,得出∠ABE =∠CBE=20°,∠ADE=∠CDE=35°,进而求得∠E的度数.【详解】过点E作EF∥AB,则EF∥CD,∴∠ABE=∠BEF, ∠DEF=∠CDE.∵AB∥CD,∴∠BCD=∠ABC=40°,∠BAD=∠ADC=70°,∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠CBE=∠ABC=20°,∠ADE=∠CDE=∠ADC=35°,∴∠BED=∠BEF+∠DEF=20°+35°=55°.故答案为:55°.【点睛】此题考查了平行线的性质,角平分线的定义,正确做出辅助线是解题的关键.本题也考查了数形结合的数学思想.16.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是_____.【答案】40°【解析】【分析】由EF⊥BD,∠1=50°,结合三角形内角和为180°,即可求出∠D的度数,再由“两直线平行,同位角相等”即可得出结论.【详解】解:在△DEF中,∠1=50°,∠DEF=90°,∴∠D=180°-∠DEF-∠1=40°.∵AB∥CD,∴∠2=∠D=40°.故答案为:40°.【点睛】本题考查平行线的性质以及三角形内角和为180°,解题关键是求出∠D=40°.解决该题型题目时,根据平行线的性质,找出相等或互补的角是解题技巧.三.解答题17.如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.(1)求证:DC∥EF;(2)若EF⊥AB,∠1=55°,求∠ADG的度数.【答案】(1)见解析(2)35°【解析】【分析】(1)由知∠1=∠DCF,则∠2=∠DCF,即可证明;(2)由得∠B=90°-∠2=35°,再根据(1)可知的度数.【详解】∵∴∠1=∠DCF,∵∴∠2=∠DCF,∴;(2)∵,∴∠BEF=90°,∴∠B=90°-∠2=35°,又∵∴=∠B=35°.【点睛】此题主要考察平行线的性质与判定.18.如图,直线AB,CD相交于点O.OF平分∠AOE,OF⊥CD于点O.(1)请直接写出图中所有与∠AOC相等的角:______.(2)若∠AOD=150°,求∠AOE的度数.【答案】(1)∠BOD,∠DOE;(2)∠AOE=120°.【解析】【分析】(1)根据邻补角的定义确定出∠AOC和∠BOD,再根据角平分线的定义可得∠AOF=∠EOF,根据垂直的定义可得∠COF=∠DOF=90°,然后根据等角的余角相等求出∠DOE=∠AOC,从而最后得解;(2)根据垂直的定义得到∠DOF,根据角平分线的定义求出即可得到结论.【详解】解:(1)∵直线AB,CD相交于点O,∴∠AOC=∠BOD,∵OF平分∠AOE,∴∠AOF=∠EOF,∵OF⊥CD,∴∠COF=∠DOF=90°,∴∠DOE=∠AOC,∴与∠AOD相等的角有∠BOD,∠DOE,故答案为:∠BOD,∠DOE.(2)∵OF⊥CD,∴∠DOF=90°,∵∠AOD=150°,∴∠AOF=60°,∵OF平分∠AOE,∴∠AOE=2∠AOF=120°.【点睛】本题考查了垂线,余角和补角,对顶角相等的性质,角平分线的定义.19.如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).理由:∵∠1=∠C,(已知)∴_______∥______,(_______)∴∠2=______.(______)又∵∠2+∠3=180°,(已知)∴∠3+_____=180°.(等量代换)∴______∥______,(______)∴∠ADC=∠EFC.(______)∵EF⊥BC,(已知)∴∠EFC=90°,∴∠ADC=90°,∴______⊥_____.【答案】略【解析】【分析】结合图形,根据平行线的判定和性质逐一进行填空即可.【详解】∵∠1=∠C,(已知)∴GD∥AC,(同位角相等,两直线平行)∴∠2=∠DAC.(两直线平行,内错角相等)又∵∠2+∠3=180°,(已知)∴∠3+∠DAC=180°.(等量代换)∴AD∥EF,(同旁内角互补,两直线平行)∴∠ADC=∠EFC.(两直线平行,同位角相等)∵EF⊥BC,(已知)∴∠EFC=90°,∴∠ADC=90°,∴AD⊥BC.故答案为:GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.【点睛】本题考查平行线的判定和性质,已经垂线的定义,解题关键是注意平行线的性质和判定定理的综合运用.20.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.(1)求证:∠DAF=∠F;(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.【答案】(1)证明见解析;(2)与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.【解析】【分析】(1)依据AB⊥BC于点B,DC⊥BC于点C,即可得到AB∥CF,进而得出∠BAF+∠F=180°,再根据∠BAF =∠EDF,即可得出ED∥AF,依据三角形外角性质以及角平分线的定义,即可得到∠DAF=∠F;(2)结合图形,根据余角的概念,即可得到所有与∠CED互余的角.【详解】解:(1)∵AB⊥BC于点B,DC⊥BC于点C,∴∠B+∠C=180°,∴AB∥CF,∴∠BAF+∠F=180°,又∵∠BAF=∠EDF,∴∠EDF+∠F=180°,∴ED∥AF,∴∠ADE=∠DAF,∠EDC=∠F,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠DAF=∠F;(2)∵∠C=90°,∴∠CED+∠CDE=90°,∴∠CED与∠CDE互余,又∵∠ADE=∠DAF=∠EDC=∠F,∴与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.【点睛】本题主要考查了平行线的判定与性质、余角的概念,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.21.【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.(2)若∠AFH+∠CHF=100°,求∠FOH的度数.【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)【答案】【探究】(1)30,125;(2)∠FOH=130°;【拓展】∠FOH=90°﹣α.【解析】【分析】(1)先根据角平分线的定义求出∠OFH,∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;(2)先根据角平分线的定义求出∠OFH+∠FHO的度数,再根据三角形的内角和定理求出∠FOH的度数;(拓展)先根据角平分线的定义求出∠OFH=∠AFH,∠OHI=∠CHI=(180°-∠CHF),再根据两直线平行内错角相等得∠FOH=∠OHI﹣∠OFH即可。

人教版2022年七年级下册第5章《相交线与平行线》单元检测卷满分120分时间100分钟一.选择题(共8小题,满分24分,每小题3分)1.下面各图中,能够通过右图平移得到的是()A.B.C.D.2.下列图中,∠1与∠2属于对顶角的是()A.B.C.D.3.直线l外有一点P,直线l上有三点A、B、C,若P A=4cm,PB=2cm,PC=3cm,那么点P到直线l的距离()A.不小于2cm B.大于2cm C.不大于2cm D.小于2cm4.命题“同角的补角相等”改写成“如果……,那么……”的形式是()A.如果是同角的补角,那么相等B.如果两个角是同角的补角,那么这两个角相等C.如果两个角互补,那么这两个角相等D.如果两个角是同角,那么这两个角是补角5.在同一平面内,将两个完全相同的三角板如图所示摆放(直角边重合),可以画出两条互相平行的直线a,b.这样操作的依据是()A.内错角相等,两直线平行B.同位角相等,两直线平行C.两直线平行,内错角相等D.两直线平行,同位角相等A.24°B.26°C.34°D.44°7.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于()A.116°B.118°C.120°D.124°8.如图,将△ABC沿BC所在直线向右平移2cm得到△DEF,连结AD.若△ABC的周长为10cm,则四边形ABFD 的周长为()A.10cm B.12cm C.14cm D.20cm二.填空题(共8小题,满分32分,每小题4分)9.如图,射线BD,CE相交于点A,则∠B的内错角是.10.在乡村振兴活动中,某村通过铺设水管将河水引到村庄C处,为节省材料,他们过点C向河岸作垂线,垂足为点D,于是确定沿CD铺设水管,这样做的数学道理是.11.“平行于同一条直线的两条直线平行”是命题.(填“真”或“假”)12.如图所示方式摆放纸杯测量角的基本原理是.13.如图所示,添加一个条件使得AB∥CD.14.将一副三角板按如图放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则:①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=30°,则有AC∥DE;④如果∠2=45°,则有BC∥AD.上述结论中正确的是(填写序号).15.已知AB∥CD,∠ACD=60°,∠BAE:∠CAE=2:3,∠FCD=4∠FCE,若∠AEC=78°,则∠AFC=.16.如图,在一块长8米,宽6米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,则这块草地的绿地面积为米2.三.解答题(共9小题,满分64分)17.(5分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点),请画出△ABC向右平移2单位再向下平移3个单位的△A1B1C1.18.(5分)如图所示,已知∠1+∠2=180°,∠4=110°,求∠3的度数.19.(6分)如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?观察下面的解答过程,补充必要的依据或结论.解∵∠1=60°(已知),∠ABC=∠1 (),∴∠ABC=60°(等量代换).又∵∠2=120°(已知),∴()+∠2=180°(等式的性质),∴AB∥CD().又∵∠2+∠BCD=(°),∴∠BCD=60°(等式的性质).∵∠D=60°(已知),∴∠BCD=∠D(),∴BC∥DE().20.(6分)如图,若∠ADE=∠ABC,BE⊥AC于E,MN⊥AC于N,求证:∠1=∠2.21.(7分)如图所示,已知∠1=115°,∠2=65°,∠3=100°.(1)图中所有角中(包含没有标数字的角),共有几对内错角?(2)求∠4的大小.22.(8分)如图所示、已知直线AB、CD交于点O、OE⊥CD.(1)若∠AOC=42°,求∠BOE的度数;(2)若∠BOD:∠BOC=2:7,OF平分∠AOD,求∠EOF的度数.23.(9分)如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.(1)求证:EF∥BC;(2)若FP⊥AC,∠2+∠C=90°,求证:∠1=∠B;(3)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.24.(9分)如图,直线AB,CD相交于点O,OE平分∠BOC.【基础尝试】(1)如图1,若∠AOC=40°,求∠DOE的度数;【画图探究】(2)作射线OF⊥OC,设∠AOC=x°,请你利用图2画出图形,探究∠AOC与∠EOF之间的关系,结果用含x 的代数式表示∠EOF.【拓展运用】(3)在第(2)题中,∠EOF可能和∠DOE互补吗?请你作出判断并说明理由.25.(9分)问题探究:如图①,已知AB∥CD,我们发现∠E=∠B+∠D.我们怎么证明这个结论呢?张山同学:如图②,过点E作EF∥AB,把∠BED分成∠BEF与∠DEF的和,然后分别证明∠BEF=∠B,∠DEF =∠D.李思同学:如图③,过点B作BF∥DE,则∠E=∠EBF,再证明∠ABF=∠D.问题解答:(1)请按张山同学的思路,写出证明过程;(2)请按李思同学的思路,写出证明过程;问题迁移:(3)如图④,已知AB∥CD,EF平分∠AEC,FD平分∠EDC.若∠CED=3∠F,请直接写出∠F的度数.参考答案一.选择题(共8小题,满分24分,每小题3分)1.【解答】解:A、图形比原图少房顶的炊烟,形状发生改变,故错误;B、图形的形状和大小没有改变,符合平移的性质,故正确;C、屋顶里面的窗子与原图不同,形状发生改变,故错误;D、图形比原图少房顶的炊烟,屋顶里面的窗子与原图不同,形状发生改变,故错误.故选:B.2.【解答】解:由对顶角的定义可得B选项中的∠1与∠2是对顶角.故选:B.3.【解答】解:∵P A=4cm,PB=2cm,PC=3cm,∴PB最短,∵直线外一点与直线上点的连线中,垂线段最短,∴P到直线l的距离不大于2cm,故选:C.4.【解答】解:命题“同角的补角相等”改写成“如果……,那么……”的形式是:如果两个角是同角的补角,那么这两个角相等,故选:B.5.【解答】解:如图:∵两个完全相同的三角板,∴∠1=∠2,而∠1、∠2是一对内错角,∴a∥b,故选:A.6.【解答】解:∵EF⊥AB于E,∠CEF=56°,∴∠AEC=90°﹣∠CEF=90°﹣56°=34°,∴∠BED=∠AEC=34°.故选:C.7.【解答】解:∵AB∥CD,∴∠1=∠3,∵∠2+∠3=180°,∴∠1+∠2=180°,∵∠2=2∠1﹣6°,∴∠1+2∠1﹣6=180°,解得∠1=62°,∴∠2=2×62﹣6=118°,故选:B.8.【解答】解:∵△ABC沿BC方向平移2cm得到△DEF,∴AD=CF=2cm,AC=DF,∴四边形ABFD的周长=AB+(BC+CF)+DF+AD=AB+BC+AC+AD+CF,∵△ABC的周长=10cm,∴AB+BC+AC=10cm,∴四边形ABFD的周长=10+2+2=14(cm).故选:C.二.填空题(共8小题,满分32分,每小题4分)9.【解答】解:由内错角的意义可得,∠B与∠EAB是内错角,故答案为:∠EAB.10.【解答】解:这样做的数学道理是:垂线段最短,故答案为:垂线段最短.11.【解答】解:“平行于同一条直线的两条直线平行”是真命题.故答案为:真.12.【解答】解:图中的测量角的原理是:对顶角相等.故答案为:对顶角相等.13.【解答】解:∠A=∠ECD或∠A+∠ACD=180°,理由如下:∵∠A=∠ECD,∴AB∥CD(同位角相等,两直线平行);∵∠A+∠ACD=180°,故答案为:∠A=∠ECD或∠A+∠ACD=180°.14.【解答】解:①∵∠BAC=∠DAE=90°,∴∠1+∠2=∠2+∠3=90°,∴∠1=∠3,故①正确;②∵∠1+∠2+∠2+∠3=180°,∴∠CAD+∠2=180°,故②正确;③∵∠2=30°,∴∠1=∠E=60°,∴AC∥DE,故③正确;④∵∠2=45°,∴∠3=∠B=45°,∴BC∥AD,故④正确.故答案为:①②③④.15.【解答】解:∵AB∥CD,∴∠CAB=180°﹣∠ACD=180°﹣60°=120°,∵∠BAE:∠CAE=2:3,∴∠CAE=120×=72°,∵∠AEC=78°,∴∠ACE=180°﹣∠AEC﹣∠CAE=180°﹣78°﹣72°=30°,设∠FCE=x,则∠FCD=4x,∴∠ACF=∠ACD﹣∠FCD=60°﹣4x,∴∠ACE=∠ACF+∠ECF=60°﹣3x,∴60°﹣3x=30°,∴x=10°,∴∠ACF=60°﹣40°=20°,∴∠AFC=180°﹣∠ACF﹣∠CAE=180°﹣20°﹣72°=88°,故答案是:88°.(8﹣1)×6=7×6=42(平方米),所以:这块草地的绿地面积为42平方米,故答案为:42.三.解答题(共9小题,满分64分)17.【解答】解:如图,△A1B1C1即为所求.18.【解答】解:∵∠1+∠2=180°,∠2=∠5,∴∠1+∠5=180°,∴CD∥EF,∴∠3=∠4,∵∠4=110°,∴∠3=110°.19.【解答】解∵∠1=60°(已知),∠ABC=∠1 (对顶角相等),∴∠ABC=60°(等量代换).又∵∠2=120°(已知),∴∠ABC+∠2=180°(等式的性质),∴AB∥CD(同旁内角互补,两直线平行).又∵∠2+∠BCD=180°,∴∠BCD=60°(等式的性质).∵∠D=60°(已知),∴∠BCD=∠D(等量代换),∴BC∥DE(内错角相等,两直线平行).故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.20.【解答】证明:∵∠ADE=∠ABC,∵BE⊥AC,MN⊥AC,∴BE∥MN,∴∠2=∠EBC,∴∠1=∠2.21.【解答】解:如图所示:(1)直线c和d被直线b所截,有两对内错角,即∠2和∠6,∠5和∠7,同理还有六对内错角,共有8对内错角;(2)∵∠2+∠5=180°,∠2=65°,∴∠5=180°﹣65°=115°,∵∠1=115°,∴∠1=∠5,∴a∥b,∴∠3=∠6,又∵∠3=100°,∴∠6=100°,∴∠4=∠6=100°.22.【解答】解:(1)∵∠AOC=42°,OE⊥CD.∴∠DOE=90°,∠BOD=42°,∴∠BOE=90°﹣∠BOD=48°;(2)∵∠BOD:∠BOC=2:7,∴∠BOD=180°×=40°,∴∠BOC=180°﹣40°=140°,∵∠BOC=∠AOD=140°,∵OF平分∠AOD,∴∠DOF==°=70°,∵∠EOF=∠EOD+∠DOF,∴∠EOF=90°+70°=160°.23.【解答】(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,∴∠E=∠BQM,∴EF∥BC;(2)证明:∵FP⊥AC,∴∠PGC=90°,∵EF∥BC,∴∠EAC+∠C=180°,∵∠2+∠C=90°,∴∠BAC=∠PGC=90°,∴AB∥FP,∴∠1=∠B;(3)解:∵∠3+∠4=180°,∠4=∠MNF,∴∠3+∠MNF=180°,∴AB∥FP,∴∠F+∠BAF=180°,∵∠BAF=3∠F﹣20°,∴∠F+3∠F﹣20°=180°,解得∠F=50°,∵AB∥FP,EF∥BC,∴∠B=∠1,∠1=∠F,∴∠B=∠F=50°.24.【解答】解:(1)∵∠AOC+∠BOC=180°,∠AOC=40°,∴∠BOC=180°﹣40°=140°,∵OE平分∠BOC,∴∠COE=∠BOC=70°,∵∠DOE+∠COE=180°,∴∠DOE=180°﹣70°=110°;(2)∠EOF=∠AOC或∠EOF=180°+∠AOC.当OF在∠BOC内部时,如图,∵∠AOC+∠BOC=180°,∠AOC=x°,∴∠BOC=(180﹣x)°,∵OE平分∠BOC,∴∠COE=∠BOC=(90﹣x)°,∵OF⊥OC,∴∠COF=90°,∴∠EOF=90°﹣∠COE=90°﹣(90﹣x)°=x°,即∠EOF=∠AOC;当OF在∠AOD内部时,如图,∵∠AOC+∠BOC=180°,∠AOC=x°,∴∠BOC=(180﹣x)°,∵OE平分∠BOC,∴∠COE=∠BOC=(90﹣x)°,∵OF⊥OC,∴∠COF=90°,∴∠EOF=90°+∠COE=90°+(90﹣x)°=(180+x)°,即∠EOF=180°+∠AOC.综上所述:∠EOF=∠AOC或∠EOF=180°+∠AOC;(3)∠EOF可能和∠DOE互补.当AB⊥CD,且OF与OB重合时,∠BOC=∠BOD=90°,∵OE平分∠BOC,∴∠BOE=BOC=45°,即∠EOF=45°,∴∠DOE=∠BOD+∠BOE=90°+45°=135°,∴∠EOF+∠DOE=180°,即∠EOF和∠DOE互补.25.【解答】解:(1)如图②中,过点E作EF∥AB,∵AB∥CD,EF∥AB,∴AB∥EF∥CD,∴∠B=∠BEF,∠D=∠CEF,∴∠BED=∠BEF+∠DEF=∠B+∠D.(2)如图③中,过点B作BF∥DE交CD的延长线于G.∵DE∥FG,∴∠EDC=∠G,∠DEB=∠EBF,∵AB∥CG,∴∠G=∠ABF,∴∠EDC=∠ABF,∴∠DEB=∠EBF=∠ABE+∠ABF=∠ABE+∠EDC.(3)如图④中,∵EF平分∠AEC,FD平分∠EDC,∴∠AEF=∠CEF,∠CDF=∠EDF,设∠AEF=∠CEF=x,∠CDF=∠EDF=y,则∠F=x+y,∵∠CED=3∠F,∴∠CED=3x+3y,∵AB∥CD,∴∠BED=∠CDE=2y,∵∠AEC+∠CED+∠DEB=180°,∴5x+5y=180°,∴x+y=36°,∴∠F=36°.。

相交线与平行线》单元测试题及答案初一下学期数学相交线与平行线单元质量检测姓名。
学号:本次考试为90分钟,共100分。
一、填空题:(每小题3分,共30分)1、空间内两条直线的位置关系可能是相交或平行。
2、“两直线平行,同位角相等”的题设是前提条件,结论是同位角相等。
3、已知∠A和∠B是邻补角,且∠A比∠B大20,则∠A=110度,∠B=70度。
4、如图1,O是直线AB上的点,OD是∠COB的平分线,若∠AOC=40,则∠BOD=70度。
5、如图2,如果AB∥CD,那么∠B+∠F+∠E+∠D=360度。
6、如图3,图中ABCD-A B C D是一个正方体,则图中与BC所在的直线平行的直线有3条,与A B所在的直线成异面直线的直线有2条。
7、如图4,直线a∥b,且∠1=28度,∠2=50度,则∠ACB=102度。
8、如图5,若A是直线DE上一点,且BC∥DE,则∠2+∠4+∠5=180度。
9、在同一平面内,如果直线l1∥l2,l2∥l3,则l1与l3的位置关系是平行。
10、如图6,∠ABC=120度,∠BCD=85度,AB∥ED,则∠CDE=15度。
二、选择题:(每小题3分,共30分)11、已知:如图7,∠1=60度,∠2=120度,∠3=70度,则∠4的度数是(B)A、70 B、60 C、50 D、4012、已知:如图8,下列条件中,不能判断直线l1∥l2的是(E)A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180 E、无法判断13、如图9,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40度,那么∠EHI=(D)A、40 B、45 C、50 D、5514、一个角的两边分别平行于另一个角的两边,则这两个角(B)A、相等 B、相等或互补 C、互补 D、不能确定15、在正方体的六个面中,和其中一条棱平行的面有(B)A、5个B、4个C、3个D、2个16、两条直线被第三条直线所截,则(B)A、同位角相等 B、内错角相等 C、同旁内角互补 D、以上结论都不对17、如图10,AB∥CD,则∠ACD=∠BDC。

七年级数学下册《相交线与平行线》单元测试卷(附答案)一、选择题(每题3分,共30分)1.如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是()A.垂线段最短B.两点确定一条直线C.两点之间,线段最短D.平行于同一条直线的两条直线平行2.如图,将一个含有30°角的直角三角尺放置在两条平行线a,b上.若∠1=135°,则∠2的度数为()A.95°B.110°C.105°D.115°3.如图,将△ABC沿BC方向平移1个单位得△DEF,若△ABC的周长等于10,则四边形ABFD 的周长为()A.12 B.10 C.9 D.84.下面四个图案中,能由如图经过平移得到的是()A.B. C. D.5.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为()A.16cm B.18cm C.20cm D.22cm6.如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是()A.垂直B.相等C.平分D.平分且垂直7.如图,下列说法错误的是()A.∠A与∠3是同位角B.∠4与∠B是同旁内角C.∠A与∠C是内错角D.∠1与∠2是同旁内角8.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于()A.4 B.5 C.6 D.以上都不对9.甲、乙、丙3人从图书馆各借了一本书(如下表所示),他们相约在每个星期天相互交换读完的书,经过数次交换后,他们都读完了这3本书.已知甲读的第三本书是乙读的第二本书,则丙读的第二本书是()甲乙丙书A书B书C A.书A B.书B C.书C D.无法确定10.下列各项正确的是()A.直线外一点到已知直线的垂线段叫做这点到直线的距离B.过一点有且只有一条直线与已知直线垂直C.同一平面内,两条直线的位置关系只有相交和平行两种D.有公共顶点且相等的两个角是对顶角二、填空题(每题3分,共24分)11.如图,已知∠1+∠2=180°,则图中与∠1相等的角共有_____个.12.如图,在图中标注的∠1、∠3、∠4、∠5中,当∠2 =∠_______时,AE∥BF.13.如图,已知a∥b,∠1=45°,则∠2=_________.14.“互补的两个角一定是同旁内角”是命题(填“真”或“假”).15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为.16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有个交点.17.如图所示,l1∥l2,点A,E,D在直线l1上,点B,C在直线l2上,满足BD平分∠ABC,BD⊥CD,CE平分∠DCB,若∠BAD=128°,那么∠AEC=.18.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E 交AF于点G,若∠CEF=70°,则∠GFD′=°.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.如图,直线AB与CD相交于点O,OE平分∠BOC,∠AOD=110°,求∠AOE的度数.20.已知,如图a∥b,c∥d,∠1=73°,求∠2和∠3的度数.21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.(1)写出两个不同的条件;(2)从(1)中选择一个来证明.22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.(1)试判断DE与BC的位置关系,并说明理由.(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.23.完成下列画图(1)如图,将△ABC向右平移4个单位,再向上平移2个单位长度,得到△A′B′C′,线段AB 与A′B′位置及数量关系是.(2)如图,一辆汽车在笔直的公路AB上由A向B行驶,M、是位于公路AB一侧的村庄.设汽车行驶到点P时,离村庄M的距离最小,请在图中公路AB上画出点P的位置,并说明数学原理.24.在ABC 中,D 是BC 边上一点,且CDA CAB ∠=∠,MN 是经过点D 的一条直线.(1)若直线MN AC ⊥,垂足为点E . ①依题意补全图1.②若70,CAB ︒∠=20DAB ︒∠=,则CAD ∠=________,CDE ∠=________. (2)如图2,若直线MN 交AC 边于点F ,且CDF CAD ∠=∠,求证:FD AB ∥.参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 CCABCDAAAC二、填空题:11.312.413.45°. 解析:∵a∥b,∠1=45°,∴∠2=∠1=45°.14.解:如图,∠1=∠2=90°,∵∠1+∠2=180°,∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,∴“互补的两个角一定是同旁内角”是假命题,故答案为:假.15.解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵GH∥EF,∴∠AEC=∠2=24°,∴∠1=∠ABC﹣∠AEC=36°.故答案为:36°.16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,∴8条直线两两相交,交点的个数最多为=28.故答案为:28.17.【分析】根据平行线的性质和角平分线的性质,可以得到∠AEC的度数,本题得以解决.【解答】解:∵l1∥l2,∴∠BAD+∠ABC=180°,∵∠BAD=128°,∴∠ABC=52°,∵BD平分∠ABC,∴∠DBC=26°,∵BD⊥CD,∴∠BDC=90°,∴∠BCD=64°,∵CE平分∠DCB,∴∠ECB=32°,∵l1∥l2,∴∠AEC+∠ECB=180°,∴∠AEC=148°,故答案为:148°.【点评】本题考查平行线的性质、角平分线的性质、垂线,解答本题的关键是明确题意,利用数形结合的思想解答.18.【分析】由AD∥BC可得∠AFE=∠CEF,∠CEF+∠DFE=180°,由翻折可得∠D'FE=∠DFE,进而求解.【解答】解:∵AD∥BC,∴∠AFE=∠CEF=70°,∵∠CEF+∠DFE=180°,∴∠DFE=180°﹣∠CEF=110°,由翻折可得∠D'FE=∠DFE=110°,∴∠GFD'=∠D'FE﹣∠AFE=110°﹣70°=40°,故答案为:40.【点评】本题考查角的相关计算,解题关键是掌握平行线的性质.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.【答案】解:∵∠AOD=110°,∴∠COB=110°,∠AOC=70°,∵OE平分∠BOC,∴∠COE=55°,∴∠AOE=70°+55°=125°.故答案为:∠AOE=125°.20.【答案】解:∵a∥b,∴∠1=∠2=73°,∵c∥d,∴∠3=180°-73°=107°.21.解:此题答案不唯一,合理即可.(1)添加∠FCB=∠CBE或CF∥BE.(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.证明:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠CBE,∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.22.解:(1)DE∥BC,理由如下:∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠5,∵∠3=∠B,∴∠5=∠B,∴DE∥BC,(2)∵DE平分∠ADC,∴∠5=∠6,∵DE∥BC,∴∠5=∠B,∵∠2=3∠B ,∴∠2+∠5+∠6=3∠B +∠B +∠B =180°, ∴∠B =36°, ∴∠2=108°, ∵∠1+∠2=180°, ∴∠1=72°.23.(1)解:如图,△A ′B ′C ′即为所求作;线段AB 与A ′B ′位置及数量关系分别是平行且相等, 故答案为:平行且相等. (2)解:如图,点P 即为所求.数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短, 24.(1)①如图所示.②70,CAB ︒∠=20DAB ︒∠=,50CAD ︒∴∠=.70CDA CAB ︒∠=∠=,18060C CAD CDA ︒︒∴∠=-∠-∠=.DE AC ⊥,第 11 页 共 11 页 9030CDE C ︒︒∴∠=-∠=. 故答案为50,︒30︒.(2)CDA CAB ∠=∠, 且,CDA CDF ADF ∠=∠+∠CAB CAD BAD ∠=∠+∠, CDF ADF CAD BAD ∴∠+∠=∠+∠. ,CDF CAD ∠=∠,ADF BAD ∴∠=∠FD AB ∴∥.。

相交线与平行线单元测试题含答案相交线与平行线单元测试题一、选择题1、下列说法正确的是() A. 相交的两条直线一定有一个交点 B. 同位角相等 C. 两直线平行,对角线一定相等 D. 相等的两个角一定是对顶角2、以下不能说明直线AB与CD平行的是() A. AB//CD,A与B在同一方向,C与D在同一方向 B. $\angle 3 = \angle 4$ C. $\angle A = \angle C$ D. $\angle A + \angle B = 180^{\circ}$,$\angleC + \angleD = 180^{\circ}$3、下列说法正确的是() A. 过一点有且只有一条直线与已知直线平行 B. 两直线平行,同位角相等 C. 内错角相等,两直线平行 D. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行4、下列说法正确的是() A. 两条直线被第三条直线所截,同位角相等 B. 相等的两个角是对顶角 C. 两直线平行,同旁内角互补 D. 互补的两个角不一定是邻补角5、下列说法正确的是() A. 同位角相等 B. 互补的角是邻补角 C. 两直线平行,同旁内角相等 D. 两直线平行,内错角相等二、填空题1、同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相________,简述为________.2、两直线平行,同位角________;两直线平行,内错角________;两直线平行,同旁内角________.3、两条直线的位置关系有________、________.4、若三条直线两两相交,则共有________个交点.5、在同一平面内,若两直线都垂直于第三条直线,那么这两条直线________.6、如图所示,若$\angle A + \angle B = 180^{\circ}$,$\angle A = \angle D$,则$\angle B =$________.7、如图所示,若$\angle A = \angle B$,则$\angle C =$________.8、如图所示,若$\angle A + \angle B = 90^{\circ}$,$\angle B + \angle C = 90^{\circ}$,则$\angle A =$________.9、若一个角的两边分别和另一个角的两边分别平行,则这两个角的关系是________.10、如图所示,若AB//CD,则$\angle A + \angle B + \angle C=$________.三、解答题1、已知两条平行线被第三条直线所截,则形成的同位角的数量是多少?这些同位角还具有什么性质?2、利用所给图形探究规律。

七年级数学下册第五章《相交线与平行线》单元测试题-人教版(含答案)一、单选题1.在下图中,1∠和2∠是同位角的是( )A .(1)、(2)B .(1)、(3)C .(2)、(3)D .(2)、(4) 2.如图,直线AB 与CD 相交于点O ,75AOC ∠=︒,125∠=︒,则2∠的度数是( )A .25°B .30°C .40°D .50° 3.如图,直线1l 与2l 相交于点O ,1OM l ⊥,若4418α=︒',则β的度数是( )A .5542'︒B .4542'︒C .'4552︒D .4642'︒ 4.如图,两条直线交于点O ,若1280∠+∠=︒,则3∠的度数为( )A .40︒B .80︒C .100D .140︒ 5.如图,,AB CD BC EF ∥∥.若158∠=︒,则2∠的大小为( )A .120︒B .122︒C .132︒D .148︒ 6.如图,直线a ∥b ,将三角尺直角顶点放在直线b 上,若∠1=50°,则∠2的度数是( )A .20°B .30°C .40°D .50° 7.如图,将一副三角板按如图放置,则下列结论:∠13∠=∠;∠2180CAD ∠+∠=︒;∠如果235∠=︒,则有BC AD ∥;∠4275∠+∠=︒.其中正确的序号是( )A .∠∠∠∠B .∠∠∠C .∠∠∠D .∠∠∠ 8.如图,点E 在BC 的延长线上,下列条件中不能判定//AB CD 的是( )A .3=4∠∠B .12∠=∠C .B DCE ∠=∠D .13180D ∠+∠+∠=︒9.下列语句是命题的是( )A .画出两个相等的角B .所有的直角都相等吗C .延长线段AB 到C ,使得BC BA =D .两直线平行,内错角相等10.如图,下列条件中能判定AB CE ∥的是( )A .∠B =∠ACE B .∠B =∠ACBC .∠A =∠ECD D .∠A =∠ACE=180°;∠∠7=∠5.其中能够说明a ∥b 的条件为( )A .∠∠B .∠∠C .∠∠D .∠∠ 12.如图,直线AB ,CD 相交于点E ,EF AB ⊥于点E ,若20FEC AEC ∠-∠=︒,那么AED ∠的度数为( )A .125°B .135°C .140°D .145°二、填空题 13.已知如图,三条直线1l 、2l 、3l 交于一点,则∠1+∠2+∠3=_________.14.如图,要把池水引到C 处,可作CD AB ⊥于点D ,然后沿CD 开渠,可使所开渠道最短,依据是______.15.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西16.如图,AB CD ∥,若40A ∠=︒,26C ∠=︒,则∠E =______.17.如图,将∠ABE 向右平移2cm 得到∠DCF ,如果∠ABE 的周长是16cm ,那么四边形ABFD 的周长是_____.18.如图,在四边形ABCD 中.点E 为AB 延长线上一点,点F 为CD 延长线上一点,连接EF ,交BC 于点G ,交AD 于点H ,若12∠=∠,A C ∠=∠,求证:E F ∠=∠.证明:13∠=∠( ),12∠=∠(已知). ∠ = (等量代换).∴AD BC ∥( )4180A ∴∠+∠=( ), A C ∠=∠(已知),4180C ∴∠+∠=(等量代换). ∠ ∥ (同旁内角互补,两直线平行).19.如图直线AD 与直线BC 相交于点O ,OE 平分AOB ∠,130∠=︒,则EOD ∠的度数为___________°.三、解答题20.如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,OF 平分∠COE .(1)若∠AOC =76°,求∠BOF 的度数;(2)若∠BOF =36°,求∠AOC 的度数;21.如图,已知AD BC ⊥,EF BC ⊥,12∠=∠.(1)求证:EF AD ∥;(2)求证:180BAC AGD ∠+∠=︒.22.如图,直线AB 和CD 相交于O 点,OE CD ⊥,142EOF ∠=︒,13BOD BOF ∠∠=::,求AOF ∠的度数.23.如图,两直线AB ,CD 相交于点O ,OE 平分∠BOD ,∠AOC :∠AOD =7:11.(1)求∠COE 的度数;(2)若OF ∠OE ,求∠COF 的度数.24.如图,直线CD 、EF 交于点O ,OA ,OB 分别平分COE ∠和DOE ∠,已知1290∠+∠=︒,且2:32:5∠∠=.(1)求BOF ∠的度数;(2)试说明AB CD 的理由.参考答案1.B2.D解:由题可知75BOD AOC ∠=∠=︒,125∠=︒,217525BOD ∴∠=∠-∠=︒-︒=50︒.3.B解:由题意得90180αβ++︒=︒,∠180904542βα'=︒-︒-=︒,4.D解:12∠=∠,1280∠+∠=︒,140∴∠=︒,13180∠+∠=︒,31801140∴∠=︒-∠=︒.5.B解:设CD 与EF 交于G ,∠AB ∠CD∠∠1=∠C =58°∠BC ∠FE ,∠∠C +∠CGE =180°,∠∠CGE =180°-58°=122°,∠∠2=∠CGE =122°,6.C解:如图,由题意得:∠3=180°-90°-∠1=40°,∠a ∥b ,∠∠2=∠3=40°,7.B解:∠1290CAB ∠=∠+∠=︒,3290EAD ∠=∠+∠=︒,∠13∠=∠,故∠正确;∠212329090180CAD ∠+∠=∠+∠+∠+∠=︒+︒=︒故∠正确;∠235∠=︒,∠3902903565∠=︒-∠=︒-︒=︒,1(18090)452B ∠=︒-︒=︒, ∠BC 与AD 不平行,故∠错误;∠43CBA EDA ∠+∠=∠+∠,即445330∠+︒=∠+︒,又∠2+3=90∠∠︒,∠44590230∠+︒=︒∠+︒-42=75∠+∠︒,故∠正确;综上,∠∠∠正确,8.A解:A 、∠3=4∠∠,∠//AD BC ,故选项A 不能判定//AB CD ,符合题意;B 、∠12∠=∠,∠//AB CD ,故选项B 能判定//AB CD ,不符合题意;C 、∠B DCE ∠=∠,∠//AB CD ,故选项C 能判定//AB CD ,不符合题意;D 、∠13180D ∠+∠+∠=︒,即180D DAB ∠+∠︒=,∠//AB CD ,故选项D 能判定//AB CD ,不符合题意;9.D解:A 、画出两个相等的角,没有做错判断,不是命题;B 、所有的直角都相等吗,没有做错判断,不是命题;C 、延长线段AB 到C ,使得BC BA =,没有做错判断,不是命题;D 、两直线平行,内错角相等,是命题;10.DA . ∠B =∠ACE ,不是同位角,内错角,不能判定AB CE ∥,不符合题意;B . ∠B =∠ACB ,不是同位角,内错角,不能判定AB CE ∥,不符合题意;C . ∠A =∠ECD ,不是同位角,内错角,不能判定AB CE ∥,不符合题意; D . ∠A =∠ACE ,内错角相等,两直线平行,能判定AB CE ∥,符合题意;11.A∠∠∠1=∠5,∠a ∥b ,故正确;∠∠∠5=∠7,∠1=∠7,∠∠1=∠5,∠a ∥b ,故正确;∠∠2+∠3=180°,∠2和∠3是邻补角,不能说明任何一组直线平行,故错误; ∠∠7=∠5,∠7和∠5是对顶角,不能说明任何一组直线平行,故错误.12.D设AEC ∠为x ,则+20FEC x ∠=︒,∠EF AB ⊥,∠90AEF ∠=︒,∠90AEC FEC ∠+∠=︒,∠2090x x ++︒=︒,解得35x =︒,即35AEC ∠=︒,∠18035145AED ∠=︒-︒=︒.13.180°解:如图,14∠=∠,123423180∴∠+∠+∠=∠+∠+∠=︒.故答案为:180︒.14.垂线段最短15.48°先根据题意画出图形,利用平行线的性质解答即可.解:如图,∠AC∠BD ,∠1=48°,∠∠2=∠1=48°,根据方向角的概念可知,乙地所修公路的走向是南偏西48°.16.66︒解:如图所示,过点E 作EF AB ∥,∠EF AB AB CD ∥,∥,∠AB CD EF ∥∥,∠4026AEF A CEF C ==︒==︒∠∠,∠∠,∠66AEC AEF CEF =+=︒∠∠∠,故答案为:66︒.17.20cm解:∠∠ABE 向右平移2cm 得到∠DCF ,∠DF =AE ,∠四边形ABFD 的周长=AB +BE +DF +AD +EF ,=AB +BE +AE +AD +EF ,=∠ABE 的周长+AD +EF ,∠平移距离为2cm ,∠AD =EF =2cm ,∠∠ABE 的周长是16cm ,∠四边形ABFD 的周长=16+2+2=20cm .故答案为:20cm .18.对顶角相等;23∠∠,;同位角相等,两直线平行;两直线平行,同旁内角互补;CF ,EA ;两直线平行,内错角相等.证明:13∠=∠(对顶角相等),12∠=∠(已知), 23∴∠=∠(等量代换),∴AD BC ∥(同位角相等,两直线平行),4180A ∴∠+∠=(两直线平行,同旁内角互补), A C ∠=∠(已知),4180C ∴∠+∠=(等量代换), ∴CF EA ∥(同旁内角互补,两直线平行),E F ∴∠=∠(两直线平行,内错角相等); 故答案为:对顶角相等;23∠∠,;同位角相等,两直线平行;两直线平行,同旁内角互补;CF ,EA ;两直线平行,内错角相等.19.105解:∠130∠=︒,∠180118030150AOB ∠=︒-∠=︒-︒=︒,∠OE 平分AOB ∠, ∠111507522BOE AOB ∠=∠=⨯︒=︒, ∠2130∠=∠=︒,∠27530105EOD BOE ∠=∠+∠=︒+︒=︒故答案为:10520.(1)∠BOF =33°(2)∠AOC =72°(1)∠∠AOC 、∠BOD 是对顶角,∠∠BOD=∠AOC=76°,∠OE 平分∠BOD , ∠∠DOE=∠BOE=12∠BOD=38°∠∠COE=142°,∠OF 平分∠COE . ∠∠EOF=12∠COE=71°,又∠BOE+∠BOF=∠EOF ,∠∠BOF=∠EOF−∠BOE=71°−38°=33°,(2)∠OE 平分∠BOD ,OF 平分∠COE ,∠BOE EOD COF FOE ∠=∠∠=∠,,∠设BOE x ∠=,则EOD x ∠=,故2COA x ∠=,36EOF COF x ∠=∠=+︒, 则23636180AOC COF BOF x x ∠+∠+∠=++︒+︒=︒, 解得36x =︒,故∠AOC =72°.21.(1)见解析(2)见解析(1)证明:∠AD BC ⊥,EF BC ⊥, ∠90EFB ∠=︒,90ADB ∠=︒(垂直的定义), ∠∠=∠EFB ADB (等量代换),∠EF AD ∥(同位角相等,两直线平行); (2)证明:∠EF AD ∥,∠1BAD ∠=∠(两直线平行,同位角相等), 又12∠=∠(已知),∠2BAD ∠=∠(等量代换),∠DG BA ∥(内错角相等,两直线平行), ∠180BAC AGD ∠+∠=︒(两直线平行,同旁内角互补). 22.102AOF ∠=︒解:∠OE CD ⊥,∠90EOD ∠=︒,∠142EOF ∠=︒,∠1429052DOF ∠=︒-︒=︒,∠13BOD BOF ∠∠=::, ∠1262BOD DOF ∠=∠=︒, ∠78BOF BOD DOF ∠=∠+∠=︒,∠180AOF BOF ∠+∠=︒,∠180********AOF BOF ∠=︒-∠=︒-︒=︒. ∠102AOF ∠=︒.23.(1)145︒(2)125︒1)解:∠711180AOC AOD AOC AOD ∠∠=∠+∠=︒::,, ∠∠AOC =71818070⨯︒=︒, ∠∠DOB =∠AOC =70°,又∠OE 平分∠BOD ,∠DOE ∠=12DOB ∠=127035⨯︒=︒,∠180********COE DOE ∠=︒-∠=︒-︒=︒, (2)∠OF OE ⊥,∠90EOF ∠=︒,∠90903555FOD DOE ∠=︒-∠=︒-︒=︒, ∠180********COF FOD ∠=︒-∠=︒-︒=︒. 24.(1)BOF ∠的度数为140︒(2)见解析(1)解:∠OA ,OB 分别平分COE ∠和DOE ∠, ∠12AOE AOC COE ∠=∠=∠,122BOE DOE ∠=∠=∠, ∠180COE DOE ∠+∠=°,∠290AOC ∠+∠=︒,∠3COE ∠=∠, ∠132AOC ∠=∠, ∠123902∠+∠=︒,∠2:32:5∠∠=, ∠5322∠=∠, ∠15229022∠+⨯∠=︒,∠240∠=︒,∠3100∠=︒,∠23140BOF ∠=∠+∠=︒;(2)解:1290∠+∠=︒,290AOC ∠+∠=︒, ∠1AOC ∠=∠,∠AB CD .。

相交线与平行线测试题及答案doc一、选择题(每题5分,共20分)1. 在同一平面内,两条直线的位置关系有几种?A. 一种B. 两种C. 三种D. 四种答案:B2. 下列说法中,正确的是:A. 同一平面内,两条直线不相交,则它们一定平行B. 同一平面内,两条直线相交,则它们一定垂直C. 同一平面内,两条直线平行,则它们永不相交D. 同一平面内,两条直线相交,则它们一定平行答案:C3. 如果两条直线都与第三条直线平行,那么这两条直线的关系是:A. 相交B. 平行C. 垂直D. 无法确定答案:B4. 两条直线相交,交点处的夹角为90°,那么这两条直线的关系是:A. 相交B. 平行C. 垂直D. 重合答案:C二、填空题(每题5分,共20分)1. 如果两条直线都与第三条直线相交,且交角相等,则这两条直线____。
答案:平行2. 在同一平面内,两条直线不相交,则它们是____。
答案:平行3. 垂直于同一直线的两条直线一定是____。
答案:平行4. 两条平行线被第三条直线所截,同位角相等,内错角互补,同旁内角和为____。
答案:180°三、解答题(每题10分,共20分)1. 已知直线AB与直线CD相交于点O,且∠AOB=∠COD=90°,求证:AB∥CD。
证明:因为∠AOB=∠COD=90°,所以AB⊥OB,CD⊥OD。
根据垂直于同一条直线的两条直线平行,所以AB∥CD。
2. 已知直线l1与直线l2相交于点P,且l1∥l3,l2∥l4,求证:l3与l4相交。
证明:因为l1∥l3,l2∥l4,所以∠l1P=∠l3P,∠l2P=∠l4P。
根据同位角相等,两直线平行,所以l3∥l1,l4∥l2。
又因为l1与l2相交,所以l3与l4相交。
四、计算题(每题10分,共40分)1. 在同一平面内,直线m与直线n相交,交点为O。
已知∠1=45°,求∠2的度数。
答案:∠2=180°-45°=135°2. 已知直线a与直线b平行,直线c与直线a相交于点A,且∠BAC=60°,求∠ABC的度数。

第五章相交线与平行线一、选择题1.a、b、c是同一平面内的任意三条直线,其交点有()A. 1或2个B. 1或2或3个C. 0或1或3个D. 0或1或2或3个【答案】D【解析】由题意画出图形,如图所示:2.如图,在高为3米,水平距离为4米楼梯的表面铺地毯,地毯的长度至少需多少米()A. 4B. 5C. 6D. 72.【答案】D【解析】地毯长度至少需3+4=7米.故选D.3.下列语句中,是对顶角的语句为()A.有公共顶点并且相等的两个角B.两条直线相交,有公共顶点的两个角C.顶点相对的两个角D.两条直线相交,有公共顶点没有公共边的两个角【答案】D【解析】A.有公共顶点并且两边分别都在同一条直线上的两个角是对顶角,故本选项错误;B.两条直线相交所成的角是对顶角或邻补角,故本选项错误;C.顶点相对的两个角的两边不一定在同一条直线上,不一定是对顶角,故本选项错误;D.两条直线相交,有公共顶点没有公共边的两个角的两边在同一条直线上,是对顶角,故本选项正确;故选D.4.如图,能判定EC∥AB的条件是()A.∠B=∠ACBB.∠B=∠ACEC.∠A=∠ACED.∠A=∠ECD【答案】C【解析】根据∠B=∠ACB,不能得到EC∥AB,故A错误;根据∠B=∠ACE,不能得到EC∥AB,故B错误;根据∠A=∠ACE,能判定EC∥AB,故C正确;根据∠A=∠ECD不能得到EC∥AB,故D错误;故选C.5.有下列说法:①△ABC在平移的过程中,对应线段一定相等.②△ABC在平移的过程中,对应线段一定平行.③△ABC在平移的过程中,周长不变.④△ABC在平移的过程中,面积不变.其中正确的有()A.①②③B.①②④C.①③④D.②③④【答案】C【解析】①∵平移不改变图形的大小,∴△ABC在平移过程中,对应线段一定相等,故正确;②∵经过平移,对应线段所在的直线共线或平行,∴对应线段一定平行错误;③∵平移不改变图形的形状和大小,∴△ABC在平移过程中,周长不变,故正确;④∵平移不改变图形的大小和形状,∴△ABC在平移过程中,面积不变,正确;∴①、③、④都符合平移的基本性质,都正确.故选C.6.如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是()A. 25°B. 35°C. 45°D. 50°【答案】D【解析】∵CD∥EF,∠C=∠CFE=25°,∵FC平分∠AFE,∴∠AFE=2∠CFE=50°,又∵AB∥EF,∴∠A=∠AFE=50°,故选D.7.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是()①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平面内垂直于同一直线的两条直线平行.A.①②③B.①②④C.①③④D.①③答案】C【解析】由图可知,用角尺画木板边缘的两条垂线,这样画的理由:①同位角相等,两直线平行;③同旁内角互补,两直线平行;④平面内垂直于同一直线的两条直线平行.故选C.8.两条直线相交所构成的四个角中:①有三个角都相等;②有一对对顶角互补;③有一个角是直角;④有一对邻补角相等.其中能判定这两条直线垂直的有()A. 1个B. 2个C. 3个D. 4个【答案】D【解析】①有三个角都相等,能判定互相垂直;②有一对对顶角互补,可计算出夹角是90°,可以判定垂直;③有一个角是直角,可以判定垂直;④有一对邻补角相等,可以判定垂直.故选D.二、填空题9.已知,如图,AD∥BE,∠1=20°,∠DCE=45°,则∠2的度数为______.【答案】25°【解析】∵AD∥BE,∠DCE=45°,∴∠DCE=∠ADC=45°.∵∠1=20°,∴∠2=∠ADC-∠1=45°-20°=25°.故答案为25°10.如图,已知点A、B、C、F在同一条直线上,AD∥EF,∠D=40°,∠F=30°,那么∠ACD的度数是________.【答案】110°【解析】∵AD∥EF,∴∠A=∠F=30°,∵∠D=40°,∴∠ACD=180°-30°-40°=110°.故答案为110°.11.如图∠1=(3x-40)°,∠2=(220-3x)°,那么AB与CD的位置关系是________.【答案】平行【解析】因为∠2=(220-3x)°,所以∠3=180°-∠2=(3x-40)°,可得:∠1=∠3,所以AB与CD平行,故答案为平行.12.把下列命题改写成“如果…那么…“的形式:(1)互补的两个角不可能都是锐角:________________________________________.(2)垂直于同一条直线的两条直线平行:________________________________________.(3)对顶角相等:____________________________________________________.【答案】如果两个角互补,那么这两个角不可能都是锐角如果两直线都垂直于第三条直线,那么这两直线平行如果两个角为对顶角,那么这两个角相等【解析】(1)如果两个角互补,那么这两个角不可能都是锐角;(2)如果两直线都垂直于第三条直线,那么这两直线平行;(3)如果两个角为对顶角,那么这两个角相等.故答案为:如果两个角互补,那么这两个角不可能都是锐角;如果两直线都垂直于第三条直线,那么这两直线平行;如果两个角为对顶角,那么这两个角相等.13.如图,与∠2互为同旁内角的是________;与∠3互为同位角的是________;∠6与∠9是______,它们是直线________与______被直线______所截得的;∠3与∠5是直线______与直线______被直线______所截得的;与∠1是同位角的有______,在标有数字的九个角中,大小一定相等的角有__________________.【答案】∠1和∠3∠4和∠5内错角AC DE BE AC BC BE∠7和∠8∠2=∠6,∠5=∠7【解析】由图可得,∠1,∠3与∠2互为同旁内角;∠4,∠5与∠3互为同位角;∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;∠3与∠5是直线AC与直线BC被直线BE所截得的同位角;∠7,∠8与∠1是同位角;根据对顶角相等可得,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.故答案为:∠1,∠3;∠4,∠5;内错角,AC,DE,BE;AC,BC,BE;∠7,∠8;∠2=∠6,∠5=∠7.14.如图,请你添加一个条件________,使AB∥CD.【答案】∠1=∠5【解析】添加∠1=∠5.∵∠1=∠5,∴AB∥CD.故答案为∠1=∠5.15.如图,直线a∥b,∠2=∠3,若∠1=45°,则∠4=______.【答案】45°【解析】延长DC交a于E,如图,∵∠2=∠3,∴AB∥DE,∴∠4=∠5,∵a∥b,∴∠1=∠5=45°,∴∠4=∠5=45°.故答案为45°.16.如图,∠1和∠3是直线______、______被直线______所截得到的______角;∠3和∠2是直线______、______被直线______所截得到的______角.【答案】a b c同旁内a c b内错【解析】如题图,∠1和∠3是直线a、b被直线c所截得到的同旁内角;∠3和∠2是直线a、c被直线b所截得到的内错角.故答案为:a,b,c,同旁内;a,c,b,内错角.17.如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠DON为________度.【答案】35【解析】∵∠BOC=110°,∴∠BOD=70°,∵ON为∠BOD平分线,∴∠DON=35°.故答案为35.18.如图,一张三角形纸片ABC,∠B=45°,现将纸片的一角向内折叠,折痕ED∥BC,则∠AEB的度数为________.【答案】90°【解析】∵ED∥BC,∴∠FED=∠B=45°,由折叠可得∠AEF=2∠FED=90°,∴∠AEB=180°-90°=90°,故答案为90°.三、解答题19.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.【答案】证明∵BE⊥FD,∴∠EGD=90°,∴∠1+∠D=90°,又∠2和∠D互余,即∠2+∠D=90°,∴∠1=∠2,又已知∠C=∠1,∴∠C=∠2,∴AB∥CD.【解析】首先由BE⊥FD,得∠1和∠D互余,再由已知,∠C=∠1,∠2和∠D互余,所以得∠C =∠2,从而证得AB∥CD.20.(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积.(3)如图④,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽为1 m,求这块菜地的面积.20.【答案】(1)如图:(2)三个图形中除去阴影部分后剩余部分的面积:①ab-b;②ab-b;③ab-b;(3)40×10-10×1=390(m2).答:这块菜地的面积是390m2.【解析】(1)根据两个折点,可得小路是三个平行四边形;(2)根据路的形状是矩形,可得路的面积,根据面积的和差,可得答案;(3)根据等底等高的面积相等,可得路的面积,根据面积的和差,可得答案.21.直线a∥b,b∥c,直线d与a相交于点A.(1)判断a与c的位置关系,并说明理由;(2)判断c与d的位置关系,并说明理由.【答案】(1)a与c的位置关系是平行,理由是:∵直线a∥b,b∥c,∴a∥c;(2)c与d的位置关系是相交,理由是:∵c∥a,直线d与a相交于点A,∴c与d的位置关系是相交.【解析】(1)根据平行公理得出即可;(2)根据c∥a和直线d与a相交推出即可.22.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°,求∠AOC的度数.【答案】(1)∵∠AOC=68°,∴∠BOD=68°,∵OE平分∠BOD,∴∠BOE=∠DOE=34°,∵∠DOF=90°,∴∠EOF=∠DOF-∠DOE=90°-34°=56°;(2)∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x.∴∠BOE=∠FOE-∠BOF=x-15°.又∵∠BOE+∠AOE=180°,∴x-15°+x=180°,解得x=130°,∴∠AOC=2∠BOE=2×=100°.【解析】(1)根据角平分线的定义结合∠AOC=68°即可求出∠BOE=∠DOE=34°,再由∠EOF与∠DOE互余即可求出∠EOF的度数;(2)由角平分线的定义可得出∠BOE=∠DOE,根据∠BOE+∠AOE=180°、∠COE+∠DOE=180°即可找出∠AOE=∠COE=x,再根据角平分线的定义可知∠FOE=x.23.如图,给出下列论断:①∠1=∠E;②∠4=∠B;③∠2+∠B=180°;④∠3+∠E=180°;⑤∠A+∠E=180°;⑥AB∥CD;⑦AB∥EF;⑧CD∥EF.请你从中选出一个论断作为题设,一个论断作为结论,组成一个真命题,至少写出三个.(格式:如果…,那么…)23.【答案】如果①∠1=∠E;那么⑧CD∥EF;如果②∠4=∠B;那么⑥AB∥CD;如果③∠2+∠B=180°;那么⑥AB∥CD.【解析】根据平行线的性质与判定,结合所给条件即可作出答案.24.如图,在Rt△ABC中,∠C=90°,AC=4 cm,BC=3 cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8 cm,DB=2 cm.(1)求△ABC向右平移的距离AD的长;(2)求四边形AEFC的周长.【答案】(1)∵△ABC沿AB方向向右平移得到△DEF,∴AD=BE=CF,BC=EF=3 cm,∵AE=8 cm,DB=2 cm,∴AD=BE=CF==3 cm;(2)四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18 cm.【解析】(1)根据平移的性质可得AD=BE=CF,BC=EF=3 cm,然后根据AE、BD的长度求解即可;(2)根据平移的性质可得EF=BC,CF=AD,然后根据四边形的周长的定义列式计算即可得解.。
第五章 相交线与平行线单元测试班级: 姓名: 考生得分:一、选择题(每小题3分,共30分) 1.已知∠α=35°,则∠α的补角的度数是( ) A.55° B.65° C.145° D.165° 2.将图中所示的图案平移后得到的图案是( )A. B. C. D.3.如图,AB ∥CD ,FE ⊥DB ,垂足为E ,∠1=50°,则∠2的度数 是( )A.60°B.50°C.40°D.30°4.如图,a ∥b ,∠1=∠2,∠3=40°,则∠4等于( ) A.40° B.50° C.60° D.70° 5.如图所示,已知AB ∥CD ,∠C =70°,∠F =30°,则∠A 的度数为( ) A .30° B .35° C .40° D .45°6.如图,AB ∥CD ,AC ⊥BC ,图中与∠CAB 互余的角有( ) A .1个 B .2个 C .3个 D .4个7.如图,点E 在CD 的延长线上,下列条件中不能判定AB ∥CD 的是( ) A .∠1=∠2 B .∠3=∠4 C .∠5=∠B D .∠B +∠BDC =180°8.如图,DH ∥EG ∥BC ,DC ∥EF ,那么与∠DCB 相等的角的个数为( ) A .2个 B .3个 C .4个 D .5个 9. 下列条件中能得到平行线的是( )①邻补角的角平分线;②平行线内错角的角平分线;③平行线同旁内角的角平分线. A .①② B .②③ C .② D .③10. 两平行直线被第三条直线所截,同位角的平分线( ) A .互相重合 B .互相平行 C .互相垂直 D .相交二、填空题(每小题3分,满分24分) 11.图中是对顶角量角器,用它测量角的原理是 .12.如图,l ∥m ,∠1=120°,∠A =55°,则∠ACB 的大小是 . 13.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠, 能使所开的渠道最短,这样设计的依据是 .14.如图,直线AB ,CD ,EF 相交于点O ,且AB ⊥CD ,∠1与∠2的关系是 .15.如图,在△ABC 中,∠A =90°,点D 在AC 边上,DE ∥BC ,若∠1=155°,则∠B 的度数为 .16.如图,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF ,若∠1=72°,则∠2= .1718第2题图第6题图 第7题图 第8题图第11题图第13题图 第14题图 第15题图 第16题图 第17题图第18题图第3题图三、解答题(共46分)19.(7分)读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.20.(7分)如图,方格中有一条美丽可爱的小金鱼.(1)若方格的边长为1,则小鱼的面积为;(2)画出小鱼向左平移3格后的图形.(不要求写作图步骤和过程)21.(8分)已知:如图,∠BAP+∠APD =180°,∠1 =∠2.求证:∠E =∠F.22.(8分)已知:如图,∠1 =∠2,∠3 =∠4,∠5 =∠6.求证:ED∥FB.23.(8分)如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.24.(9分)如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.25.(10分)如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?第19题图第五章相交线与平行线检测题参考答案1.C 解析:∵∠α=35°,∴∠α的补角的度数为180°35°=145°,故选C.2. C 解析:根据平移的性质可知C正确.3. C 解析:因为FE⊥DB,所以∠FED=90°,由∠1=50°可得∠FDE=90°-50°=40°.因为AB∥CD,由两直线平行,同位角相等,可得∠2=∠FDE=40°.4. D 解析:因为a∥b,所以∠2=∠4.又∠2=∠1,所以∠1=∠4.因为∠3=40°,所以∠1=∠4==70°.5. C 解析:由AB∥CD可得,∠FEB=∠C=70°,∵∠F=30°,又∵∠FEB=∠F+∠A,∴∠A=∠FEB∠F=70°30°=40°.故选项C是正确的.6. C 解析:∵AB∥CD,∴∠ABC=∠BCD.设∠ABC的对顶角为∠1,则∠ABC=∠1.又∵AC⊥BC,∴∠ACB=90°,∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°,因此与∠CAB互余的角为∠ABC,∠BCD,∠1.故选C.7. A 解析:选项B中,∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),故正确;选项C中,∵∠5=∠B,∴AB∥CD(内错角相等,两直线平行),故正确;选项D中,∵∠B+∠BDC=180°,∴AB∥CD(同旁内角互补,两直线平行),故正确;而选项A中,∠1与∠2是直线AC、BD被直线AD所截形成的内错角,∵∠1=∠2,∴AC∥BD,故A错误.选A.8. D 解析:如题图所示,∵DC∥EF,∴∠DCB=∠EFB.∵DH∥EG∥BC,∴∠GEF=∠EFB,∠DCB=∠HDC,∠DCB=∠CMG=∠DME,故与∠DCB相等的角共有5个.故选D.9. C 解析:结合已知条件,利用平行线的判定定理依次推理判断.10. B 解析:∵两条平行直线被第三条直线所截,同位角相等,∴它们角的平分线形成的同位角相等,∴同位角相等的平分线平行.故选B.11.对顶角相等解析:根据图形可知量角器测量角的原理是:对顶角相等.12. 65°解析:∵l∥m,∴∠ABC=180°-∠1=180°-120°=60°.在△ABC中,∠ACB=180°-∠ABC-∠A=180°-60°-55°=65°.13. 垂线段定理:直线外一点与直线上所有点的连线中,垂线段最短解析:根据垂线段定理,直线外一点与直线上所有点的连线中,垂线段最短,∴沿AB开渠,能使所开的渠道最短.14. ∠1+∠2=90°解析:∵直线AB、EF相交于O点,∴∠1=∠DOF.又∵AB⊥CD,∴∠2+∠DOF=90°,∴∠1+∠2=90°.15. 65°解析:∵∠1=155°,∴∠EDC=180°-155°=25°.∵DE∥BC,∴∠C=∠EDC=25°.∵在△ABC中,∠A=90°,∠C=25°,∴∠B=180°-90°-25°=65°.故答案为65°.16. 54°解析:∵AB∥CD,∴∠BEF=180°∠1=180°72°=108°,∠2=∠BEG.又∵EG平分∠BEF,∴∠BEG=∠BEF=×108°=54°,故∠2=∠BEG=54°.17. 78°解析:延长BC与直线a相交于点D,∵a∥b,∴∠ADC=∠DBE=50°. ∴∠ACB=∠ADC +28°=50°+28°=78°.故应填78°.18. 120 解析:∵AB∥CD,∴∠1=∠3,而∠1=60°,∴∠3=60°.又∵∠2+∠3=180°,∴∠2=180°-60°=120°.故答案为120.19.解:(1)(2)如图所示.第19题答图(3)∠PQC=60°.理由:∵PQ∥CD,∴∠DCB+∠PQC=180°.∵∠DCB=120°,∴∠PQC=180°120°=60°.20. 解:(1)小鱼的面积为7×621×5×621×2×521×4×221××121×21×11=16.(2)将每个关键点向左平移3个单位,连接即可.第20题答图21.证明:∵ ∠BAP +∠APD = 180°,∴ AB ∥CD .∴ ∠BAP =∠APC . 又∵ ∠1 =∠2,∴ ∠BAP −∠1 =∠APC −∠2.即∠EAP =∠APF .∴ AE ∥FP .∴ ∠E =∠F .22.证明:∵ ∠3 =∠4,∴ AC ∥BD .∴ ∠6+∠2+∠3 = 180°. ∵ ∠6 =∠5,∠2 =∠1,∴ ∠5+∠1+∠3 = 180°. ∴ ED ∥FB .23. 解:∵ DE ∥BC ,∠AED =80°,∴ ∠EDC =∠BCD ,∠ACB=∠AED=80°.∵ CD 平分∠ACB ,∴ ∠BCD = 21∠ACB =40°,∴ ∠EDC =∠BCD =40°.24. 解:∵ AB ∥CD ,∴ ∠B +∠BCE =180°(两直线平行,同旁内角互补).∵ ∠B =65°,∴ ∠BCE =115°.∵ CM 平分∠BCE ,∴ ∠ECM =21∠BCE =57.5°. ∵ ∠ECM +∠MCN +∠NCD =180°,∠MCN =90°,∴ ∠NCD =180°-∠ECM -∠MCN =180°-57.5°-90°=32.5°.25、解:(1)∵∠AOE +∠AOF =180°(互为补角),∠AOE =40°,∴∠AOF =140°; 又∵OC 平分∠AOF ,∴∠FOC =∠AOF =70°,∴∠EOD =∠FOC =70°(对顶角相等);而∠BOE =∠AOB ﹣∠AOE =50°,∴∠BOD =∠EOD ﹣∠BOE =20°; (2)(3)略。

人教版七年级数学下册第五章相交线与平行线单元卷附解析一、选择题(共12题;共36分)1.直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于()A. 58°B. 70°C. 110°D. 116°2.如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是()A. ∠AOC=40°B. ∠COE=130°C. ∠EOD=40°D. ∠BOE=90°3.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于()时,AB∥CD.A. 50°B. 40°C. 30°D. 60°4.如图,a∥b,∠1=70°,则∠2等于()A. 20°B. 35°C. 70D. 110°5.下列说法正确的是()A. 若两条直线被第三条直线所截,则同旁内角互补B. 相等的角是对顶角C. 有一条公共边并且和为180°的两个角互为邻补角D. 若三条直线两两相交,则共有6对对顶角6.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A. 同位角相等,两直线平行B. 内错角相等,两直线平行C. 两直线平行,同位角相等D. 两直线平行,内错角相等7.下列说法错误的是()A. 无数条直线可交于一点B. 直线的垂线有无数条,但过一点与直线垂直的直线只有一条C. 直线的平行线有无数条,但过直线外一点的平行线只有一条D. 互为邻补角的两个角一个是钝角,一个是锐角8.下列四个命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等.其中真命题的个数是( )A. 1个B. 2个C. 3个D. 4个9.一个角的两边分别垂直于另一个角的两边,那么这两个角之间的关系是( ).A. 相等B. 互补C. 相等或互补D. 无法确定10.如图,已知AB⊥BD,CB⊥CD,AD=14 cm,BC=10 cm,若线段BD的长度为偶数,则线段BD的长度为( )A. 8 cmB. 10 cmC. 12 cmD. 14 cm11.如图,已知直线a∥b,AC⊥AB,AC交直线b于点C,如果∠1=62°,则∠2的度数是()A. 36°B. 32°C. 30°D. 28°12.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人。

相交线与平行线测试题及答案难一、选择题1. 在同一平面内,两条直线的位置关系是()。
A. 相交或平行B. 相交或重合C. 平行或重合D. 相交、平行或重合答案:D2. 如果两条直线都与第三条直线平行,那么这两条直线的关系是()。
A. 相交B. 平行C. 重合D. 不确定答案:B3. 两条直线相交成90度角,这两条直线是()。
A. 相交线B. 垂直线C. 平行线D. 异面直线答案:B二、填空题4. 如果两条直线都与第三条直线相交,且交角相等,则这两条直线()。
答案:平行5. 在平面几何中,如果两条直线不相交,则它们被称为()。
答案:平行线三、判断题6. 两条平行线被第三条直线所截,同位角相等。
()答案:正确7. 垂直于同一直线的两条直线一定平行。
()答案:错误四、解答题8. 已知直线AB与直线CD相交于点O,且∠AOB=90°,求证:AB⊥CD。
证明:因为∠AOB=90°,所以AB与CD相交成直角,根据垂直的定义,AB⊥C D。
9. 若直线m平行于直线n,直线n平行于直线p,求证:直线m平行于直线p。
证明:根据平行公理,如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
因此,直线m平行于直线p。
五、综合题10. 在平面直角坐标系中,直线l1的方程为y=2x+3,直线l2的方程为y=-x+5,求证:l1与l2相交。
证明:首先,我们可以将两个方程联立求解。
\begin{cases}y = 2x + 3 \\y = -x + 5\end{cases}将第一个方程中的y代入第二个方程,得到:2x + 3 = -x + 5解得:x = 1将x=1代入任意一个方程求得y,例如第一个方程:y = 2(1) + 3 = 5因此,l1与l2的交点为(1,5),所以l1与l2相交。
11. 已知直线l1平行于直线l2,直线l2平行于直线l3,求证:直线l1平行于直线l3。
证明:根据平行公理,如果两条直线都与第三条直线平行,那么这两条直线也互相平行。

平行线与相交线测试题及答案第一篇:平行线与相交线测试题及答案一、选择题1、一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是()A.第一次右拐50°,第二次左拐130°C.第一次左拐50°,第二次左拐130°B.第一次左拐50°,第二次右拐50°D.第一次右拐50°,第二次右拐50°2、如图3,AB∥CD,那么∠A,∠P,∠C的数量关系是()A.∠A+∠P+∠C=90°B.∠A+∠P+∠C=180°C.∠A+∠P+∠C=360°D.∠P+∠C=∠A3、一个人从点A点出发向北偏东60°方向走到B点,再从B点出发向南偏西15°方向走到C点,那么∠ABC等于()A.75°B.105°C.45°D.135°ABABBACFEDCCD图3D图4 图54、如图5所示,已知∠3=∠4,若要使∠1=∠2,则需()A.∠1=∠3B.∠2=∠3C.∠1=∠4D.AB∥CD5、下列说法正确的个数是()①同位角相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;;④三条直线两两相交,总有三个交点;⑤若a∥b,b∥c,则a∥c.A.1个B.2个C.3个D.4个6、如图6,O是正六边形ABCDEF的中心,下列图形:△OCD,△ODE,△OEF,△OAF,•△OAB,其中可由△OBC平移得到的有()A.1个B.2个C.3个D.4个二、填空题7、命题“垂直于同一直线的两直线平行”的题设是是.8、三条直线两两相交,有个交点.EDBDAC43BADCACB图7图8图99、如图8,已知AB∥CD,∠1=70°则∠2=_______,∠3=______,∠4=_______.10、如图10所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=______,∠AOC=_______,∠BOC=________.11、如图11所示,四边形ABCD中,∠1=∠2,∠D=72°,则∠BCD=_______.12、如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是_________,那么这两个角分别是度.三、作图题13、如图,(1)画AE⊥BC于E,AF⊥DC于F.(2)画DG∥AC交BC 的延长线于G.(3)经过平移,将△ABC的AC边移到DG,请作出平移后的△DGH.AD四、解答题BC14、已知:AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求∠P的度数15、如图,E在直线DF上,B为直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.16、已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想∠BDE与∠C有怎样的大小关系?试说明理由.参考答案:一、1.B2.C3.C4.D5.B6.B二、7.两条直线都和同一条直线垂直,这两条直线平行;8.1,3;9.70°,70°,110°;10.65°,65°,115°;11.108°;12.相等或互补;三、13.如下图:FADBE14.如图,过点P作AB的平行线交EF于点G。

第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1。
如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D。
对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为( )A.40°B.35° C。
50°D。
45°31 2 3。
如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC。
∠B+∠ECB=180° D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为( )A。
向右平移1格再向下 B。
向右平移3格再向下C.向右平移2格再向下D.以上答案均可5。
如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D。
垂直于同一直线的两直线平行6。
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )A.40°B.70°C.80° D。
140°7。
同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是( )A。
a∥d B。
a⊥c C。
a⊥d D。
b⊥d8。
如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )A.120 ° B。
130° C.140° D。
150°9。
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )A。
30° B.60° C。
80° D。
《相交线与平行线》单元测试题(时间:90分钟 满分:100分)学校 班别 姓名 座号 成绩一、填空题:(每小题3分,共30分)把每小题的正确答案填在各题对应的横线上。
1、空间内两条直线的位置关系可能是 或 、 。
2、“两直线平行,同位角相等”的题设是 ,结论是 。
3、∠A 和∠B 是邻补角,且∠A 比∠B 大200,则∠A = 度,∠B = 度。
4、如图1,O 是直线AB 上的点,OD 是∠COB 的平分线,若∠AOC =400,则∠BOD =。
5、如图2,如果AB ∥CD ,那么∠B +∠F +∠E +∠D = 0。
6、如图3,图中ABCD-D C B A ''''是一个正方体,则图中与BC 所在的直线平行的直线有 条,与B A ''所在的直线成异面直线的直线有 条。
图1O DCB A FE 图2DC BA A 'B 'C 'D '图3D CB Aba12C图4BA7、如图4,直线a ∥b ,且∠1=280,∠2=500,则∠ACB = 0。
8、如图5,若A 是直线DE 上一点,且BC ∥DE ,则∠2+∠4+∠5= 0。
9、在同一平面内,如果直线1l ∥2l ,2l ∥3l ,则1l 与3l 的位置关系是 。
10、如图6,∠ABC =1200,∠BCD =850,AB ∥ED ,则∠CDE 0。
二、选择题:各小题只有唯一一个正确答案,请将正确答案的代号填在题后的括号内(每小题3分,共30分)11、已知:如图7,∠1=600,∠2=1200,∠3=700,则∠4的度数是( )A 、700B 、600C 、500D 、40012、已知:如图8,下列条件中,不能判断直线1l ∥2l 的是( )A 、∠1=∠3B 、∠2=∠3C 、∠4=∠5D 、∠2+∠4=180054321A BCDE图5A B CDE 图6 2l 1l 4321图72l 1l 54321图813、如图9,已知AB ∥CD ,HI ∥FG ,EF ⊥CD 于F ,∠1=400,那么∠EHI =( )A 、400B 、450C 、500D 、55014、一个角的两边分别平行于另一个角的两边,则这两个角( )A 、相等B 、相等或互补C 、互补D 、不能确定 15、在正方体的六个面中,和其中一条棱平行的面有( )A 、5个B 、4个C 、3个D 、2个 16、两条直线被第三条直线所截,则( )A 、同位角相等B 、内错角相等C 、同旁内角互补D 、以上结论都不对 17、如图10,AB ∥CD ,则( )A 、∠BAD +∠BCD =1800B 、∠ABC +∠BAD =180C 、∠ABC +∠BCD =1800 D 、∠ABC +∠ADC =18001IHGE DCBA 图9A BC D图10CB AD图1154321图1218、如图11,∠ABC =900,BD ⊥AC ,下列关系式中不一定成立的是( ) A 、AB >AD B 、AC >BC C 、BD +CD >BC D 、CD >BD 19、下列语句中,是假命题的个数是( )①过点P 作直线BC 的垂线;②延长线段MN ;③直线没有延长线;④射线有延长线。
A 、0个 B 、1个 C 、2个 D 、3个20、如图12,下面给出四个判断:①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角。
其中错误的是( )A 、①②B 、①②③C 、②④D 、③④ 三、完成下面的证明推理过程,并在括号里填上根据(每空1分,本题共12分)21、已知,如图13,CD 平分∠ACB ,DE ∥BC ,∠AED =820。
求∠EDC 的度数。
证明:∵DE ∥BC (已知)∴∠ACB =∠AED ( )∠EDC =∠DCB ( ) 又∵CD 平分∠ACB (已知)∴∠DCB =21∠ACB ( )又∵∠AED =820(已知)∴∠ACB =820( ) ∴∠DCB =08221=410( ) ∴∠EDC =410( )22、如图14,已知AOB 为直线,OC 平分∠BOD ,EO ⊥OC 于O 。
求证:OE 平分∠AOD 。
证明:∵AOB 是直线(已知)∴∠BOC +∠COD +∠DOE +∠EOA =1800( ) 又∵EO ⊥OC 于O (已知)ED CBA图13∴∠COD +∠DOE =900( )∴∠BOC +∠EOA =900( )又∵OC 平分∠BOD (已知)∴∠BOC =∠COD ( ) ∴∠DOE =∠EOA ( ) ∴OE 平分∠AOD ( )四、计算与证明:(每小题5分,共20分)23、已知,如图15,∠ACB =600,∠ABC =500,BO 、CO 分别平分∠ABC 、∠ACB ,EF 是经过点O 且平行于BC 的直线,求∠BOC 的度数。
F OE CBA图1524、已知,如图16,AB ∥CD ,GH 是相交于直线AB 、EF 的直线,且∠1+∠2=1800。
求证:CD ∥EF 。
HG321D F EC BA 图1625、如图17:AB ∥CD ,∠CEA =3∠A ,∠BFD =3∠D 。
求证:CE ∥BF 。
O E D CB A 图14DF ECBA图1726、如图18,已知AB ∥CD ,∠A =600,∠ECD =1200。
求∠ECA 的度数。
DEC BA图18五、探索题(第27、28题各4分,本大题共8分)27、如图19,已知AB ∥DE ,∠ABC =800,∠CDE =1400。
请你探索出一种(只须一种)添加辅助线求出∠BCD 度数的方法,并求出∠BCD 的度数。
14080D ECBA图1928、阅读下面的材料,并完成后面提出的问题。
(1)已知,如图20,AB ∥DF ,请你探究一下∠BCF 与∠B 、∠F 的数量有何关系,并说明理由。
(2)在图20中,当点C 向左移动到图21所示的位置时,∠BCF 与∠B 、∠F 又有怎样的数量关系呢?(3)在图20中,当点C 向上移动到图22所示的位置时,∠BCF 与∠B 、∠F 又有怎样的数量关系呢?(4)在图20中,当点C 向下移动到图23所示的位置时,∠BCF 与∠B 、∠F 又有怎样的数量关系呢?21FDE CB A图2021FDECBA图21FDCBA图22图分析与探究的过程如下: 在图20中,过点C 作CE ∥AB∵CE ∥AB (作图) AB ∥DF (已知)∴AB ∥EC ∥DF (平行于同一条直线的两条直线平行)∴∠B +∠1=∠F +∠2=1800(两直线平行,同旁内角互补)∴∠B+∠1+∠2+∠F=3600(等式的性质)即∠BCF+∠B+∠F=3600在图21中,过点C作CE∥AB∵CE∥AB(作图)AB∥DF(已知)∴AB∥EC∥DF(平行于同一条直线的两条直线平行)∴∠B=∠1,∠F=∠2(两直线平行,内错角相等)∴∠B+∠F=∠1+∠2(等式的性质)即∠BCF=∠B+∠F直接写出第(3)小题的结论:(不须证明)。
由上面的探索过程可知,点C的位置不同,∠BCF与∠B、∠F的数量关系就不同,请你仿照前面的推理证明过程,自己完成第(4)小题的推理证明过程。
图参考答案一、填空题:1、平行、相交、异面;2、两直线平行,同位角相等;3、1000、800;4、700;5、5400;6、3条、8条;7、780;8、1800;9、平行;10、250二、选择题:三、完成下面的证明过程,在后面的括号里填上根据(本题共6分) 21、证明:∵∠DE ∥BC (已知)∴∠ACB =∠AED (两直线平行,同位角相等) ∠EDC =∠DCB (两直线平行,内错角相等) 又∵CD 平分∠ACB (已知) ∴∠DCB =21∠ACB (角平分线定义) 又∵∠AED =820(已知)∴∠ACB =820(等量代换) ∴∠DCB =08221⨯=410(等量代换) ∴∠EDC =410(等量代换) 22、证明:∵AOB 是直线(已知)∴∠BOC +∠COD +∠DOE +∠EOA =1800(平角的定义) 又∵EO ⊥OC 于O (已知)∴∠COD +∠DOE =900(垂直的定义)∴∠BOC +∠EOA =900(等量代换)又∵OC 平分∠BOD (已知)∴∠BOC =∠COD (角平分线定义) ∴∠DOE =∠EOA (等角的余角相等) ∴OE 平分∠AOD (角平分线定义)23、证明:∵BO 平分∠ABC (已知) ∴∠OBC =21∠ABC (角平分线的定义) 又∵∠ABC =500(已知) ∴∠OBC =05021⨯=250(等量代换) 又∵EF ∥BC (已知)∴∠EOB =∠OBC (两直线平行,内错角相等)∴∠EOB =250(等量代换)同理∠FOC =300EDCBA图13O E DC BA 图14又∵∠BOC =1800-∠EOB -∠FOC (平角的定义)∴∠BOC =1800-250-300=1250(等量代换)24、证明:∵∠1+∠2=1800(已知) ∠1=∠3(对顶角相等)∴∠2+∠3=1800(等量代换)∴AB ∥EF (同旁内角互补,两直线平行) 又∵AB ∥CD (已知)∴CD ∥EF (平行于同一条直线的两条直线平行) 25、证明:∵AB ∥CD (已知)∴∠A =∠D (两直线平行,内错角相等) 又∵∠CEA =3∠A ,∠BFD =3∠D (已知) ∴∠CEA =∠BFD (等量代换)∴∠CED =∠BFA (等角的补角相等)∴CE ∥BF (内错角相等,两直线平行)26、解:∵AB ∥CD (已知)∴∠A +∠ACD =1800(两直线平行,同旁内角互补)又∵∠A =600(已知)∴∠ACD =1200(等量代换)又∵∠ECA =3600-∠ECD -∠ACD (周角的意义)∠ECD =1200(已知)∴∠ECA =1200(等量代换) 五、探索题:27、过C 作CF ∥DE∵CF ∥DE (作图) AB ∥DE (已知)∴AB ∥DE ∥CF (平行于同一条直线的两条直线平行)∴∠BCF =∠B =800(两直线平行,内错角相等)∠DCF +∠D =1800(两直线平行,同旁内角互补)又∵∠D =1400(已知)∴∠DCF =400(等量代换)又∵∠BCD =∠BCF -∠DCF (角的和差定义)∴∠BCD =800-400(等量代换)即∠BCD =40014080FD ECBA图19图28、第(3)小题的结论为:∠BCF =∠F -∠B证明:在图23中,过点C作CE∥AB∵CE∥AB(作图)AB∥DF(已知)∴CE∥AB∥DF(平行于同一条直线的两条直线平行)∴∠F=∠ECF,∠B=∠ECB(两直线平行,内错角相等)∴∠B-∠F=∠ECB-∠ECF(等式的性质)又∵∠BCF=∠ECB-∠ECF(角的和差定义)∴∠BCF=∠B-∠F(等量代换)。