势函数

热力学基础中的热力学势函数热力学势函数是热力学研究中的重要工具，它通过数学表达方式来描述系统的性质和变化规律。

在热力学基础中，热力学势函数的概念与使用方法是必须掌握的。

本文将介绍热力学势函数的定义、特点以及常见的势函数类型。

一、热力学势函数的定义热力学势函数是描述热力学体系平衡状态的函数，它与系统的状态变量有关。

根据热力学第一定律，系统的内能是一个重要的状态量，因此，内能的变化可以作为定义热力学势函数的出发点。

二、热力学势函数的特点1. 对于闭系，热力学势函数是一个关于系统内能和其他状态变量的函数。

2. 对于恒温恒容系统，热力学势函数是一个关于熵和体积的函数。

3. 对于恒温恒压系统，热力学势函数是一个关于焓和熵的函数。

4. 热力学势函数是一个广延量，它与系统的大小有关。

三、常见的热力学势函数类型1. 内能（U）：内能是最基本的热力学势函数，它与系统的温度、体积以及组分数相关。

2. 焓（H）：焓是在恒压条件下的热力学势函数，它与系统的温度、压力、体积以及组分数相关。

3. 自由能（F）：自由能是在恒温恒容条件下的热力学势函数，它与系统的温度、体积以及组分数相关。

4. 吉布斯自由能（G）：吉布斯自由能是在恒温恒压条件下的热力学势函数，它与系统的温度、压力、体积以及组分数相关。

四、热力学势函数的应用1. 研究平衡条件：通过分析热力学势函数的极值，可以确定系统的平衡状态以及平衡条件。

2. 计算热力学性质：通过对热力学势函数的微分关系，可以计算得到系统的热力学性质，如熵变、焓变等。

3. 预测化学反应的方向：根据热力学势函数的变化趋势，可以判断化学反应的方向和可逆性。

4. 优化工业过程：利用热力学势函数的最小值原理，可以优化工业过程中的能量转化和利用。

五、结语热力学势函数是热力学基础中的重要概念和工具，在研究和应用中有着广泛的应用。

通过对热力学势函数的定义、特点和应用进行了解，可以更好地理解和分析热力学体系的平衡状态和性质。

eam势函数
eam势函数作为分子动力学模拟中常见的能量函数，通常被用于表尔逊(Buckingham)相互作用之间分子的模拟计算。

这是因为它能够有效地反映各种原子间的不同相互作用。

其原理很简单，是通过对原子或原子对之间的距离和原子类型进行描述，然后用势函数来表示能量。

注意，只有当势函数的参数是通过实验测定的，才能够准确地反映实际原子间的作用。

eam势函数的基本形式可以表示为：
E =ijσ(rij) +ijρ(rij) +ijε(rij)
其中，σ，ρ，ε分别表示两个原子间的形状相似性，数量相似性和能量相似性。

rij是两个原子间的距离，假设它们之间的距离在一定的范围内。

同时，ε的参数值受原子之间的相互作用影响，并且会根据其特性进行识别。

eam势函数可以用来模拟电荷迁移、结构形成和溶剂作用等结构变化过程，以及材料本质性质及性能参数的研究。

它也可以用来研究分子电荷和能量之间的联系，进而研究离子溶解过程中的化学反应机理。

此外，eam势函数也可以用于金属表面形貌研究、结构识别等技术领域，进一步提高分析精度。

eam势函数有许多优点，它可以非常容易的分离出复杂的能量函数，从而节省计算时间，提高计算效率，减少计算误差。

此外，eam 势函数也可以实现多尺度模拟，从而更好的研究分子间的相互作用。

此外，eam势函数的参数也很容易取得，使得它可以更快的收敛。

总的来说，eam势函数是一个非常有用的工具，可以应用于很多领域。

它有着更少的参数，更快的收敛，更低的误差，更好的精度，能更好地模拟原子间的相互作用，以及多尺度模拟的能力，使得它在分子动力学模拟中得到了普遍的应用。

热力学的热力学势函数热力学是研究物质的宏观性质和状态变化规律的学科，而热力学势函数是热力学理论中的重要概念之一。

本文将对热力学势函数进行详细介绍，包括它的定义、性质和应用。

一、热力学势函数的定义热力学势函数是描述热力学系统平衡态的宏观性质的函数。

在热力学中，常用的热力学势函数有内能（U）、焓（H）、自由能（F）和吉布斯函数（G）。

1. 内能（U）：内能是描述系统总能量的函数，它包括系统的热能和势能。

内能的变化可以通过热量传递和做功来表征。

2. 焓（H）：焓是内能和压力的乘积，它描述了在等压条件下系统的热能变化。

3. 自由能（F）：自由能是系统做非功的最大可能能量，它等于系统的内能减去温度与熵的乘积。

4. 吉布斯函数（G）：吉布斯函数是系统能够做非功和无位移的最大可能能量，它等于系统的内能减去温度与熵的乘积，再加上对外界所做的功。

二、热力学势函数的性质热力学势函数具有一些重要的性质，这些性质使其在热力学理论中起到了重要的作用。

1. 可微性：热力学势函数是可微的，可以根据系统的状态变化求取其微分。

2. 可加性：热力学势函数具有可加性，即多个系统的热力学势函数之和等于总系统的热力学势函数。

3. 极值性：热力学势函数在平衡态时取极值，这使得热力学势函数可以作为热力学过程中的判据。

4. 上凸性：热力学势函数具有上凸性，即它的二阶导数大于等于零，这对于热力学稳定性的判断是重要的。

三、热力学势函数的应用热力学势函数在实际应用中具有广泛的用途，其主要应用如下：1. 判据函数：通过判断热力学势函数的变化可以判断系统的平衡态和稳定性。

2. 热力学关系：热力学势函数之间存在一系列的关系，如吉布斯-亥姆霍兹方程、亥姆霍兹方程等，可以用于热力学计算。

3. 热力学过程分析：根据热力学势函数的变化可以分析热力学过程中的能量转化和熵增减。

4. 工程应用：热力学势函数在工程领域有广泛的应用，如在能源系统中的热力学性能分析、化学反应动力学等方面。

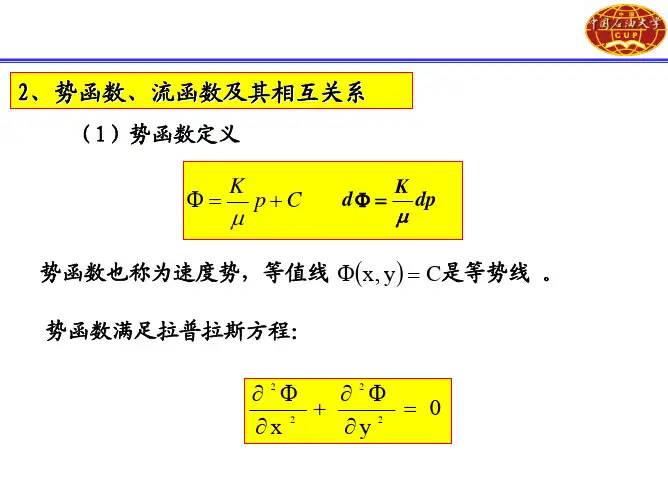
流函数和势函数公式流体力学中的流函数可以用来描述流体的速度场。

速度场表示流体在空间中各点的速度分布情况。

对于无旋的流动，可以引入流函数，流函数可以唯一地确定流线。

流线是流体在给定时刻通过各点的轨迹线。

在无旋的流动中，速度场可以通过流函数的梯度得到。

流函数可以按照如下公式定义：ψ=ψ(x,y,z)其中，ψ是流函数，表示速度场在其中一截面上的流函数值，(x,y,z)是该截面上的坐标。

流函数满足拉普拉斯方程：∇²ψ=0其中，∇²是拉普拉斯算子，表示流函数对坐标的二阶混合偏导数的和，等于零表示流函数满足拉普拉斯方程。

流函数的物理意义是流线沿着这个函数的等值线的方向运动。

通过给定流函数值，可以确定流线的轨迹。

势函数是流体力学中另一个重要的数学工具。

势函数用来描述无旋的流动场中的速度场。

对于无旋的流动，速度场可以通过势函数的梯度得到。

势函数可以按照如下公式定义：φ=φ(x,y,z)其中，φ是势函数，表示速度场在其中一截面上的势函数值，(x,y,z)是该截面上的坐标。

势函数满足亥姆霍兹方程：∇²φ=0势函数的物理意义是速度场是势函数的梯度。

通过给定势函数值，可以确定速度场的分布情况。

流函数和势函数是流体力学中流动的描述工具。

通过流函数和势函数，可以方便地描述流体的流动和速度场。

流函数适用于无旋流动，通过流函数的梯度可以得到速度场。

势函数适用于无旋流动，通过势函数的梯度可以得到速度场。

流函数和势函数是相互对偶的工具，二者之间有一个互逆的关系。

在实际应用中，流函数和势函数在求解流体问题中起着重要的作用。

通过流函数和势函数，可以方便地计算速度场和流线，从而解决各种涉及流体流动的问题。

总结起来，流函数和势函数是流体力学中用来描述流动的两个重要的数学工具。

流函数用来描述无旋流动的速度场，势函数用来描述无旋流动场中的速度场。

二者分别满足拉普拉斯方程和亥姆霍兹方程。

流函数和势函数在解决流体流动问题中具有重要的作用。

势函数法势函数主要⽤于确定分类⾯，其思想来源于物理。

1 势函数法基本思想假设要划分属于两种类别\omega_1和\omega_2的模式样本，这些样本可看成是分布在n维模式空间中的点x_k。

把属于\omega_1的点⽐拟为某种能源点，在点上，电位达到峰值。

随着与该点距离的增⼤，电位分布迅速减⼩，即把样本x_k附近空间x点上的电位分布，看成是⼀个势函数K(x, x_k)。

对于属于\omega_1的样本集群，其附近空间会形成⼀个"⾼地"，这些样本点所处的位置就是"⼭头"。

同理，⽤电位的⼏何分布来看待属于\omega_2的模式样本，在其附近空间就形成"凹地"。

只要在两类电位分布之间选择合适的等⾼线，就可以认为是模式分类的判别函数。

2. 判别函数的产⽣模式分类的判别函数可由分布在模式空间中的许多样本向量\{x_k,k=1,2,\cdots \text{且},x_k\in \omega_1\cup w_2\}的势函数产⽣。

任意⼀个样本所产⽣的势函数以K(x,x_k)表征，则判别函数d(x)可由势函数序列K(x, x_1),K(x,x_2),\cdots来构成，序列中的这些势函数相应于在训练过程中输⼊机器的训练模式样本x_1,x_2,\cdots。

在训练状态，模式样本逐个输⼊分类器，分类器就连续计算相应的势函数，在第k步迭代时的积累位势决定于在该步前所有的单独势函数的累加。

以K(x)表⽰积累位势函数，若加⼊的训练样本x_{k+1}是错误分类，则积累函数需要修改，若是正确分类，则不变。

3.判别函数产⽣逐步分析设初始势函数K_0(x) = 0第⼀步：加⼊第⼀个训练样本x_1，则有{K_1}(x) = \left\{ {\begin{array}{*{20}{c}} {K(x,{x_1})}&{{\rm{if}}\;{x_1} \in {\omega _1}}\\ { - K(x,{x_1})}&{{\rm{if}}\;{x_1} \in {\omega _2}}\end{array}} \right.这⾥第⼀步积累势函数K_1(x)描述了加⼊第⼀个样本时的边界划分。

kim势函数
Kim势函数是一种用于描述分子间相互作用的函数，它可以用来计算分子间的相互作用能。

Kim势函数的形式为：
V(r) = A exp(-r/ρ) - B exp(-r/λ) - C/r^6
其中，r是分子间距离，A、B、C、ρ和λ是参数。

Kim势函数的优点在于它可以描述分子间的各种相互作用，包括范德华力、氢键、静电相互作用等。

此外，Kim势函数还可以用于模拟分子间的相互作用，例如在分子动力学模拟中。

Kim势函数的参数可以通过实验或计算得到。

例如，可以通过测量分子间距离和相互作用能来确定参数。

此外，还可以使用量子化学计算方法来计算参数。

Kim势函数在化学、物理、材料科学等领域都有广泛的应用。

例如，在材料科学中，Kim势函数可以用来研究材料的力学性质、热力学性质等。

在化学中，Kim势函数可以用来研究分子间的相互作用、反应动力学等。

总之，Kim势函数是一种非常有用的函数，它可以用来描述分子间的相互作用，并且在化学、物理、材料科学等领域都有广泛的应用。

势函数的名词解释势函数（also known as potential function）是应用领域中常用的数学概念，广泛用于描述物理问题中的能量分布和力的作用。

它是一个数学函数，描述了某一系统的势能随空间位置的变化规律。

一、势函数的定义和基本原理势函数一般是一个多元函数，输入是系统的各个位置坐标，输出是对应位置的势能大小。

在物理学中，势函数被用来描述某个物体或系统所受的力的作用，并通过对势能的计算得到力的大小。

势函数的基本原理是根据能量守恒定律，将系统的总能量（包括动能和势能）表示为势函数的形式。

根据这个函数，我们可以推导出各个位置上的力，并通过这些力来分析物体或系统的行为。

二、势函数的应用领域1. 力学中的应用在经典力学中，势函数被广泛应用于描述物体在力的作用下的运动规律。

通过势函数，我们可以计算物体所受的力，并推导出加速度、速度和位移的变化规律。

例如，引力势函数被用来描述天体之间的相互作用，从而解释行星运动的规律。

2. 电磁学中的应用在电磁学中，势函数被用来描述电场和磁场对电荷和电流的作用。

通过对电势函数和矢量势函数的计算，可以得到电场强度和磁场强度的大小和方向。

这些物理量对于电磁场中的粒子运动和电磁波的传播等方面都具有重要意义。

3. 量子力学中的应用在量子力学中，势函数被用来描述微观粒子的运动规律。

波函数是量子力学中的势函数，描述了粒子在空间中的分布，可以通过对波函数的计算得到粒子的能量、动量等物理量。

势函数在量子力学的薛定谔方程中起着重要的作用。

三、势函数的特性和解析性质1. 势函数的导数和偏导数势函数通常具有足够的可导性，其导数和偏导数在物理学中有重要的物理意义。

例如，对于标量势函数来说，其梯度的方向和大小可以指示力的作用方向和大小。

而对于矢量势函数来说，其旋度表示了力的转动效应。

2. 势函数的等值面和力线势函数的等值面表示了势函数取相同数值的位置所构成的曲面，在物理学中常用来表示等势面。

brenner 1990势函数1. 研究背景brenner 1990势函数是指由David W. Brenner于1990年提出的一种全局有效的分子力学势函数。

分子力学势函数是用来描述分子结构和相互作用能的数学模型，常用于分子模拟、蛋白质结构预测等领域。

brenner 1990势函数是对碳原子之间相互作用的势函数，具有较好的描述碳纳米材料力学性质的能力。

2. 势函数原理brenner 1990势函数主要基于核心-壳模型，将碳原子视为一个核心和周围的壳组成。

势函数的形式为：V(r) = ∑[A_ij * exp(-B_ij * r_ij)]其中，r_ij为原子i和原子j之间的间距，A_ij和B_ij为相互作用参数。

该势函数包含了三种相互作用：键（σ）、角（∠）和二面角（φ），能够较准确地描述碳原子之间的相互作用能。

3. 势函数特点brenner 1990势函数在描述碳原子之间相互作用时具有以下特点：- 准确性高：该势函数能够较准确地描述碳原子的结构和力学性质，尤其在纳米材料的模拟中表现良好。

- 全局有效：与一些经验势函数相比，brenner 1990势函数是一种全局有效的势函数，适用范围广泛。

- 可扩展性：该势函数的形式简洁，可以较容易地扩展到描述其他材料的相互作用。

4. 应用领域brenner 1990势函数在碳纳米材料力学性质预测、纳米材料模拟等领域得到了广泛的应用：- 碳纳米管模拟：brenner 1990势函数在碳纳米管的结构优化、拉伸模拟等方面表现突出，为理解碳纳米管的力学性质提供了重要的理论基础。

- 石墨烯模拟：作为一种碳纳米材料，石墨烯的力学性质对其应用具有重要意义。

brenner 1990势函数在描述石墨烯层间相互作用、弯曲等方面具有一定优势。

- 碳纳米材料设计：利用brenner 1990势函数，可以对碳纳米材料的力学性质进行预测，为新材料设计提供理论支持。

5. 研究展望尽管brenner 1990势函数在描述碳原子相互作用方面表现良好，但也存在一些局限性。

求势函数定积分势函数在物理学中是一个重要的概念，它用来描述力场的性质和作用。

常见的物理量如重力、电场和磁场都可以通过势函数进行描述。

势函数是向量场的标量函数，它满足一些向量场的梯度。

在本文中，我们将介绍势函数的定义、性质、定积分和一些实际应用。

我们将从最基本的势函数的定义开始，然后讨论势函数的梯度和定积分的概念。

首先，我们定义一个向量场F(x,y,z)在点P(x0,y0,z0)的势函数为一个标量函数U(x,y,z)，使得梯度∇U(x0,y0,z0)等于向量场F(x,y,z)在点P(x0,y0,z0)的值。

换句话说，势函数U(x,y,z)的所有偏导数都等于向量场F(x,y,z)的对应分量。

表示为∇U(x0,y0,z0)=F(x0,y0,z0)。

势函数的梯度可以理解为向量场的变化率，它指示了在一些点附近向量场的方向和速率。

梯度表示为一个向量，其方向为最大变化的方向，其大小为变化率的大小。

定积分是对一个函数在一定区间上的求和操作，可以用来计算势函数在一个区域上的总变化量。

定积分可以理解为将一个函数在一段区间上的曲线下面的面积求和。

根据势函数的定义，我们可以将向量场的定积分转化为势函数的定积分。

具体来说，考虑一个平面区域S，用参数方程描述为x=f(u,v)和y=g(u,v)，其中(u,v)属于一个有限区域D。

假设向量场F(x,y)在这个区域上是连续的，并且有势函数U(x,y)。

那么，我们可以将向量场的定积分转化为势函数的定积分，如下所示：∬S F(x, y)·dS = ∬D ∇U(f(u, v), g(u, v))·(f'(u, v), g'(u, v))·dudv其中，dS是面积元素，dudv是区域D上的面积元素，f'(u, v)和g'(u, v)是参数方程的偏导数。

通过定积分我们可以计算势函数在区域S上的总变化量。

如果势函数为标量场，我们还可以计算在闭合曲线C上的总变化量，称为线积分。

morse势函数
Morse势函数是一种通用固体物理理论，它可以用来研究大多数物质的微观结构与数学特性。

它是由美国著名物理学家理查德莫尔斯（Richard M. Morse）在1929年提出的，他的思想是建立一个可以用来描述各种原子和分子的简易模型，而Morse势函数就是实现这一思想的最有效方法之一。

Morse势函数用来描述原子或分子的微观结构，它的形式为：V=D(1-exp(-μ(r-r0)))2，其中V代表势函数值，D代表曲率、μ代表势函数平移量，r代表原子或分子中心之间的距离，r0代表势函数最小点处的距离，它可以把原子和分子之间的位置、结构以及形态等信息表示出来。

Morse势函数可以用来研究固体物理问题，它可以运用多种结构模型来研究原子或分子运动的结构以及分子间的相互作用。

Morse势函数拓展了物理学家将物质描述为特定形状的模型波函数的概念，它的谱带宽度和势函数的形状都可以从Morse势函数中得到，使得研究物质的性质更加容易。

Morse势函数在固体物理研究有着重要意义，它可以用来解释多原子分子的性质如弹性、热容量等，由于它的简单性，它也可以用来研究复杂的大分子物质的性质，特别是用于小分子物质的研究。

如今，Morse势函数也在其他领域被广泛使用，例如核物理、分子动力学、化学反应等。

它可以用来描述量子力学中的受力，并研究量子效应对物质的影响，也可以用来计算化合物的结构和特性。

Morse势函数有着广泛的应用，它能够有效地解释非常多的物理和化学现象，其最大的优势在于它可以用于多种物理和化学模型的研究，因此，它在各个领域都得到了广泛的应用。

Morse势函数不仅能够有效地描述大多数物质的微观结构，而且它还能够在多种物理和化学模型中得到广泛的应用。

势函数的定义
势函数的定义
势函数是数学中的一种函数，它是描述物理力场的一种工具。

势函数的定义来源于能量的守恒定律，也就是说，在任何物理场中，物体所受的力都可以看作受到一个质点的力作用于这些物体上，并且与质点的位置有关。

而这个位置，则可以用势函数来表示。

势函数的具体定义是：在一定的物理场中，某个物体所处的位置的势能，是它和其他物体之间的相互作用能量的总和。

这个能量是一个标量，以单位体积的形式表示，通常表示为J/m3（焦耳/立方米）。

在对势函数进行定义时，需要考虑到相互作用的物体之间的距离、场强和作用方向等因素。

这些因素的组合，最终构成了各种不同的势函数。

例如，如果考虑重力场的情况，每个质点都会受到地球所产生的作用力。

根据重力势能的定义，每个质点处的势能可以表示为其本身的质量和离开地球表面的高度之间的关系。

因此，我们可以用地球的引力场来描述这个势函数。

同样地，如果考虑电场的情况，每个质点都会受到周围电荷所产生的作用力。

这时，我们可以通过电场强度来描述质点的势函数。

电场强度也是一个矢量值，表示质点受到的电场力的大小和方向。

此外，势函数的定义也可以延伸到更加复杂的情况，例如磁场和引力波等。

在这些情况下，我们需要使用更多的数学方法和模型来描述势函数的变化和演化。

总之，势函数是描述物理场的一种重要数学工具。

它可以帮助我们更好地理解和掌握各种力场的特性和变化规律，从而更好地预测和解决实际的物理问题。

势函数假设检验势函数是一个描述自变量和因变量之间关系的函数，其中自变量是随机变量，因变量就是一个实数，自变量和因变量的变化规律用数学表达式表示就是： f(x)＝|| x1－ x2||。

目前，对势函数的研究已经渗透到了社会的各个方面，也是本人想要深入学习的。

因为当时生病所以在学校完成了这门实验课程的学习，在这次课程上，由于没有好好听讲导致做错了很多题，受到老师的批评，但是作为我来说确实值得。

由于我们在这门课程上不能够及时的跟踪实验进度，这次的实验可以说是一次很好的机会去巩固理论知识。

通过这次暑假的实习，使我体会到了“纸上得来终觉浅”，只有把从书本上学到的理论知识应用于实践中，才能真正掌握这门知识。

所以这次实习给了我一次将所学知识运用到实际的机会，提供了锻炼自己和检验自己学习成果的场所。

为我们今后工作打下基础。

我还记得在学校里实习，科学技术老师给我们讲了很多注意事项，还要求我们严格按照实验室的规则去操作，老师特别强调了这些重点内容，以防我们不小心而造成实验失败，影响实验进程，所以我特别谨慎，努力地去听，仔细地去记。

认真阅读了每一个注意事项，然后仔细观察老师的操作步骤，实验内容，并做了详细的笔记，然后根据操作步骤亲自动手，熟练掌握操作流程。

来到这里才知道，原来当个科学家真的很不容易，要考虑那么多问题，要掌握那么多知识，光靠一个人的力量是不行的，还需要集体的智慧和力量。

我们要学会互相帮助，团结协作，让我感觉最深的就是在做实验的时候，要注意相互配合，否则会影响效率，影响实验的质量。

第二天就开始正式进行实验了，首先，我们要学会如何接待客户。

给他介绍了科室里的几位医生，有哪些主要的研究方向。

然后就耐心地等待顾客的咨询。

当第一位顾客走进来的时候，我非常紧张，担心顾客会因为不满意而离开，同时又担心耽误了顾客的宝贵时间，所以就在那里呆呆地站着。

在这个时候，老师让我去招呼一下顾客。

我连忙回到座位上，迅速准备好要说的话。