高中物理—光的折射与全反射(一)测试

光的折射和反射测试题光是一种电磁波，能够在真空和透明介质中传播。

当光遇到边界表面时，可能会发生折射和反射现象。

在这篇文章中，我们将对光的折射和反射进行测试题，以检验对这些现象的理解。

题目1：光的反射请简要解释什么是光的反射，并举一个日常生活中的例子。

题目2：光的折射定律请解释什么是光的折射定律，并给出一个例子说明。

题目3：折射角的计算光在空气中以30°的角度入射到水中，假设水的折射率为1.33，请计算光在水中的折射角。

题目4：全反射当光从光密介质射向光疏介质时，折射角可以超过90°吗？请解释原因。

题目5：总反射角的计算当光从水中射向空气时，光的入射角为45°，水的折射率为1.33，请计算光的总反射角。

题目6：折射率的意义光在真空中的速度为3.0 × 10^8 m/s，而在玻璃中的速度为2.0 ×10^8 m/s。

请计算玻璃的折射率，并解释折射率的意义。

题目7：折射和颜色光在经过折射后，有可能发生色散现象。

请解释为什么光在折射后会产生颜色。

题目8：菲涅尔反射请解释什么是菲涅尔反射，并简要说明其在光学设备中的应用。

题目9：反光衣的原理请解释反光衣的原理，并说明反光衣的作用。

题目10：实际应用中的折射和反射请列举三个实际生活中应用到折射和反射原理的例子，并简要说明其原理。

答案：1. 光的反射是指当光遇到边界表面时，一部分光返回原来的介质。

一个日常生活中的例子是镜子反射出的影像。

2. 光的折射定律是指光从一种介质进入另一种介质时，折射角、入射角和两种介质的折射率之间存在一个关系。

例如，当光从空气射入水中时，根据折射定律，入射角和折射角满足sin(入射角)/sin(折射角) = 折射率。

3. 光在水中的折射角可以通过折射定律计算。

根据题目条件，光在空气中的入射角为30°，而水的折射率为1.33。

利用折射定律，我们可以计算出光在水中的折射角为arcsin(sin(30°)/1.33) ≈ 22.48°。

高中物理光的反射、折射、全反射(提纲、例题、练习、解析)(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中物理光的反射、折射、全反射(提纲、例题、练习、解析)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中物理光的反射、折射、全反射(提纲、例题、练习、解析)(word版可编辑修改)的全部内容。

光的反射、折射、全反射【学习目标】1．通过实例分析掌握光的反射定律与光的折射定律．2．理解折射率的定义及其与光速的关系．3．学会用光的折射、反射定律来处理有关问题．4．知道光疏介质、光密介质、全反射、临界角的概念．5．能判定是否发生全反射，并能分析解决有关问题．6．了解全反射棱镜和光导纤维．7．明确测定玻璃砖的折射率的原理．8．知道测定玻璃砖的折射率的操作步骤．9．会进行实验数据的处理和误差分析．【要点梳理】要点一、光的反射和折射1．光的反射现象和折射现象如图所示，当光线入射AO到两种介质的分界面上时，一部分光被反射回原来的介质，即反射光线OB，这种现象叫做光的反射．另一部分光进入第二种介质,并改变了原来的传播方向，即光线OC，这种现象叫做光的折射现象,光线OC称为折射光线．折射光线与法线的夹角称为 ）．折射角（22．反射定律反射光线与入射光线、法线处在同一平面内，反射光线与入射光线分别位于法线的两侧；反射角等于入射角．3．折射定律(1)内容:折射光线跟入射光线和法线在同一平面内，折射光线和入射光线分别位于法线的两侧．入射角的正弦跟折射角的正弦成正比．即12sin sin θθ=常数．如图所示．也可以用sin sin in r=的数学公式表达，n 为比例常数．这就是光的折射定律． (2）对折射定律的理解：①注意光线偏折的方向：如果光线从折射率（1n ）小的介质射向折射率（2n )大的介质，折射光线向法线偏折，入射角大于折射角，并且随着入射角的增大(减小）折射角也会增大（减小）;如果光线从折射率大的介质射向折射率小的介质，折射光线偏离法线，入射角小于折射角，并且随着入射角的增大（减小）折射角也会增大（减小）．②折射光路是可逆的，如果让光线逆着原来的折射光线射到界面上，光线就会逆着原来的人射光线发生折射，定律中的公式就变为12sin 1sin nθθ=,式中1θ、2θ分别为此时的入射角和折射角．4．折射率-—公式中的n （1）定义．实验表明，光线在不同的介质界面发生折射时．相同入射角的情况下．折射角不同．这意味着定律中的n 值是与介质有关的，表格中的数据，是在光线从真空中射向介质时所测得的n 值,可以看到不同介质的n 值不同，表明n 值与介质的光学性质有关,人们把这种性质称为介质的折射率．实际运用中我们把光从真空斜射人某种介质发生折射时，入射角1θ的正弦跟折射角2θ的正弦之比。

A．光束Ⅰ仍为复色光、光束Ⅱ、Ⅲ为单色光
B．光束Ⅱ在玻璃中的传播速度比光束Ⅲ小
C．增大α角且α<90°、光束Ⅱ、Ⅲ会远离光束Ⅰ
D．改变α角且α<90°、光束Ⅱ、Ⅲ一定与光束Ⅰ平行
E．减小α角且α>0、光束Ⅲ可能会在上表面发生全反射ABD[由题意画出如图所示的光路图、可知光束Ⅰ是反射光线、所以仍是复色光、而光束Ⅱ、Ⅲ由于折射率的不同导致偏折分离、所以光束Ⅱ、Ⅲ是单色光、故A正确；由于光束Ⅱ的偏折程度大于光束Ⅲ、所以玻璃对光束Ⅱ的折
射率大于对光束Ⅲ的折射率、根据v＝c
n
可知、光束Ⅱ在玻璃中的传播速度比光
束Ⅲ小、故B正确；当增大α角且α<90°、即入射角减小时、光束Ⅱ、Ⅲ会靠近光束Ⅰ、故C错误；因为厚玻璃平面镜的上下表面是平行的、根据光的入射角与反射角相等以及光的可逆性、可知改变α角且α<90°、光束Ⅱ、Ⅲ一定与光束Ⅰ平行、故D正确；减小α角且α>0、根据折射定律、光的折射角增大、根据光的可逆性知、光束Ⅲ不可能在上表面发生全反射、故E错误。

]。

1．(2009年高考广东单科)在阳光照射下，充满雾气的瀑布上方常常会出现美丽的彩虹．彩虹是太阳光射入球形水珠经折射、内反射，再折射后形成的．光的折射发生在两种不同介质的________上，不同的单色光在同种均匀介质中__________不同．【答案】 界面 传播速度2．一个大游泳池，池底是水平面，池中水深1.2 m ，有一直杆竖直立于池底，浸入水中部分BC 恰为杆长AC 的1/2.太阳光以与水平方向成37°角射在水面上，如右图所示，测得杆在池底的影长是2.5 m ．求水的折射率．(sin 37°＝0.6，cos 37°＝0.8)【解析】 作出光路图如右图所示，由图可知：x ＝h cot 37°＝1.2×43m ＝1.6 m 因为x ＋x ′＝2.5 m ，所以x ′＝2.5 m －1.6 m ＝0.9 m又tan r ＝x ′h ＝34，所以r ＝37°，所以 n ＝sin i sin r ＝sin 53°sin 37°＝0.80.6≈1.33. 【答案】 1.333．光线以60°的入射角从空气射入玻璃中，折射光线与反射光线恰好垂直．(真空中的光速c ＝3.0×108 m/s)(1)求出玻璃的折射率和光在玻璃中的传播速度；(2)当入射角变为45°时，折射角变为多大？(3)当入射角增大或减小时折射率是否发生变化？请说明理由．【解析】 (1)由题意知，此时折射角为30°，折射率n ＝sin 60°sin 30°＝ 3 光在介质中的传播速度v ＝c n ＝3.0×1083m/s ＝1.7×108 m/s. (2)设此时折射角为γ2，则：sin γ2＝sin 45°n ＝sin 45°3＝66 即γ2＝arcsin 66. (3)折射率不会发生变化．因为折射率由介质和入射光的频率决定，而跟入射角的大小无关．【答案】 (1)3 1.7×108 m/s (2)arcsin 66(3)不会4．(2009年高考山东理综)一束单色光由左侧射入盛有清水的薄壁圆柱形玻璃杯，右图为过轴线的截面图，调整入射角α，光线恰好在水和空气的界面上发生全反射．已知水的折射率为43，求sin α的值． 【解析】 当光线在水面发生全反射时有sin C ＝1n当光线从左侧射入时，由折射定律有sin αsin ⎝⎛⎭⎫π2－C ＝n 联立这两式代入数据可得sin α＝73 【答案】 735. 如右图所示，置于空气中的一不透明容器内盛满某种透明液体．容器底部靠近器壁处有一竖直放置的 6.0 cm 长的线光源．靠近线光源一侧的液面上盖有一遮光板，另一侧有一水平放置的与液面等高的望远镜，用来观察线光源．开始时通过望远镜不能看到线光源的任何一部分．将线光源沿容器底向望远镜一侧平移至某处时，通过望远镜刚好可以看到线光源底端．再将线光源沿同一方向移动8.0 cm ，刚好可以看到其顶端．求此液体的折射率n.【解析】 若线光源底端在A 点时，望远镜内刚好可看到线光源的底端，则有：∠AOO ′＝α其中α为此液体到空气的全反射临界角．由折射定律得：sin α＝1n同理，线光源顶端在B 1点时，望远镜内刚好可看到线光源的顶端，则∠B 1OO ′＝α由图中几何关系得：sin α＝AB AB 1解得：n ＝ (AB 2)＋ (BB 21)AB由题给的条件可知AB ＝8.0 cm ，BB 1＝6.0 cm代入上式得n ＝1.25.【答案】 1.256．一台激光器，它的功率为P ，如果它发射出的单色光在空气中的波长为λ，(1)它在时间t 内辐射的光能为________，如果已知这束单色光在某介质中的传播速度为v ，那么这束单色光从该介质射向真空发生全反射的临界角为________．(2)由于激光是亮度高、平行度好、单色性好的相干光，所以光导纤维中用激光作为信息高速传输的载体．要使射到粗细均匀的圆形光导纤维一个端面上的激光束都能从另一个端面射出，而不会从侧壁“泄漏”出来，光导纤维所用材料的折射率至少应为多大？【解析】 (1)激光器t 时间内发出的能W ＝Pt由n ＝c v ，sin C ＝1n，则 C ＝arcsin v c. (2)设激光束在光导纤维端面的入射角为i ，折射角为r ，折射光线射向侧面时的入射角为i ′，折射角为r ′，如上图所示．由折射定律：n ＝sin i sin r， 由几何关系：r ＋i ′＝90°，sin r ＝cos i ′.由全反射临界角的公式：sin i ′＝1n ，cos i ′＝1－1n2， 要保证从端面射入的任何光线都能发生全反射，应有i ＝r ′＝90°，sin r ′＝1.故 n ＝sin i sin r ＝sin i cos i ′＝11－1n 2， 解得n ＝2，故光导纤维的折射率应为n ≥ 2.【答案】 (1)Pt arcsin v c(2) 2 7．(2009年高考海南单科)如图，一透明半圆柱体折射率为n ＝2，半径为R 、长为L ，一平行光束从半圆柱体的矩形表面垂直射入，从部分柱面有光线射出．求该部分柱面的面积S【解析】 半圆柱体的横截面如下图所示，OO ′为半径．设从A 点入射的光线在B 点处恰好满足全反射条件，由折射定律有sin θ＝1n式中，θ为全反射临界角．由几何关系得∠O ′OB ＝θS ＝2RL ·∠O ′OB代入题所给条件得S ＝π3RL . 【答案】 π3RL8.右图所示，为用某种透明材料制成的一块柱体形棱镜的水平截面图，CD 为14圆周，圆心为O .光线从AB 面入射，入射角i＝60°，它射入棱镜后射在BC 面上的O 点并恰好不从BC 面射出．(1)画出光路图；(2)试求该棱镜的折射率n 和光线在棱镜中传播的速度大小v .(光在真空中的速度c ＝3.0×108 m/s)【解析】 (1)光路图如右图所示．(2)设光线在AB 面的折射角为r ，则n ＝sin isin r 由题意，光线在BC 面恰好发生全反射，sin c ＝1n由图r ＋c ＝90°联立以上各式得n ＝1.3(或72)又n ＝cv故v ＝2.3×108 m/s(或6 77×108 m/s)．【答案】 (1)见解析 (2)n ＝1.3(或 72)v ＝2.3×108 m/s(或6 77×108 m/s)。

《第4章光的折射和全反射》试卷(答案在后面)一、单项选择题（本大题有7小题，每小题4分，共28分）1、一束光线从空气射入水中时，下列说法正确的是：A、入射角等于折射角B、折射光线一定比入射光线偏离法线C、折射角大于入射角D、折射光线和入射光线分居法线两侧2、一束光线从水中射入空气时，下列说法正确的是：A、入射角大于折射角B、折射光线与入射光线在同一直线上C、折射光线一定偏离法线D、折射光线和入射光线分居法线两侧3、一束光线从空气（折射率为1.00）射入水（折射率为1.33），当入射角为45°时，折射角为多少度？A. 30°B. 40°C. 53.1°D. 78.7°4、当光从一种介质射入另一种介质时，如果反射光和折射光之间的夹角某一数值会等于90°，此时的入射角称为临界角。

当入射光的折射角为90°时，对应的入射角称为：A. 临界角B. 平行角C. 漫反射角D. 全反射角5、光从空气斜射入水中时（水和空气的折射率分别为n₁和n₂，且n₁ > n₂），下列关于折射现象的描述正确的是（）A. 折射光线与入射光线分居法线两侧B. 折射光线、入射光线和法线都在同一平面内C. 折射角小于入射角D. 折射光线、入射光线、法线都与光线方向相垂直6、一束单色光从水中斜射入空气时，下面的哪种情形会导致观察者看到光的路径出现一定的弯折？（）A. 增加入射水面的粗糙程度B. 提高观察者与入射水面的距离C. 小心调整观察者与法线的距离D. 旋转入射光线7、一束光线从空气射入水中，入射角为30°，已知水的折射率为1.33，则折射角最接近于：A. 22°B. 25°C. 30°D. 40°二、多项选择题（本大题有3小题，每小题6分，共18分）1、下列关于光的折射现象的描述，正确的是：A、光从空气进入水中时，传播速度变慢，折射角大于入射角。

《光的折射全反射》典型题1．(多选)已知介质对某单色光的临界角为θ，则( )A．该介质对此单色光的折射率为1 sin θB．此单色光在该介质中传播速度为c sin θ(c为真空中光速) C．此单色光在该介质中的波长是真空中波长的sin θ倍D．此单色光在该介质中的频率是真空中的1 sin θ2．如图，一束光经玻璃三棱镜折射后分为两束单色光a、b，波长分别为λa、λb，该玻璃对单色光a、b的折射率分别为n a、n b，则( )A．λa＜λb，n a＞n bB．λa＞λb，n a＜n bC．λa＜λb，n a＜n bD．λa＞λb，n a＞n b3．某同学通过实验测定半圆形玻璃砖的折射率n.如图甲所示，O是圆心，MN是法线，AO、BO分别表示某次测量时光线在空气和玻璃砖中的传播路径．该同学测得多组入射角i和折射角r，作出sin i－sin r图象如图乙所示．则( )A．光由A经O到B，n＝1.5B．光由B经O到A，n＝1.5C．光由A经O到B，n＝0.67D．光由B经O到A，n＝0.674．光纤通信中信号传播的主要载体是光导纤维，它的结构如图所示，其内芯和外套材料不同，光在内芯中传播．下列关于光导纤维的说法中正确的是( )A．内芯的折射率比外套的大，光传播时在内芯与外套的界面上发生全反射B．内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生全反射C．波长越短的光在光纤中传播的速度越大D．频率越大的光在光纤中传播的速度越大5．打磨某剖面如图所示的宝石时，必须将OP、OQ边与轴线的夹角θ切磨在θ1<θ<θ2的范围内，才能使从MN边垂直入射的光线，在OP边和OQ边都发生全反射(仅考虑如图所示的光线第一次射到OP边并反射到OQ边后射向MN 边的情况)，则下列判断正确的是( )A．若θ>θ2，光线一定在OP边发生全反射B．若θ>θ2，光线会从OQ边射出C．若θ<θ1，光线会从OP边射出D．若θ<θ1，光线会在OP边发生全反射6．某研究性学习小组利用插针法测量半圆形玻璃砖的折射率．实验探究方案如下：在白纸上作一直线MN，并作出它的一条垂线AB，将半圆形玻璃砖(底面的圆心为O)放在白纸上，它的直径与直线MN重合，在垂线AB上插两枚大头针P1和P2，然后在半圆形玻璃砖的右侧插上适量的大头针，可以确定光线P1P2通过玻璃砖后的光路，从而求出玻璃砖的折射率．实验中提供的器材除了半圆形玻璃砖、木板和大头针外，还有量角器等．(1)某同学用上述方法测量玻璃砖的折射率，他在画出的垂线AB上竖直插上了P1、P2两枚大头针，但在半圆形玻璃砖的右侧区域内，不管眼睛在何处，都无法透过玻璃砖同时看到P1、P2的像，原因是________________________.为同时看到P1、P2的像，他应采取的措施是_______________________.(2)在采取相应措施后，请在半圆形玻璃砖的右侧画出所插大头针的可能位置，并用“×”表示，作出光路图．(3)为计算折射率，将应测量的物理量标注在光路图上，并由此得出折射率的计算公式为n＝________.7．如图所示，AOB是截面为扇形的玻璃砖的横截面图，其顶角θ＝76°，今有一细束单色光在横截面内从OA边上的点E沿垂直于OA的方向射入玻璃砖，光线直接到达AB面且恰好未从AB面射出．已知OE＝35OA，cos 53°＝0.6，试求：(1)玻璃砖的折射率n；(2)光线第一次从OB射出时折射角的正弦值．8．如图所示，直角三角形ABC是一玻璃砖的横截面，AB＝L，∠C＝90°，∠A＝60°.一束单色光PD从AB边上的D点射入玻璃砖，入射角为45°，DB＝L 4，折射光DE恰好射到玻璃砖BC边的中点E，已知光在真空中的传播速度为c.求：(1)玻璃砖的折射率；(2)该光束从AB边上的D点射入玻璃砖到第一次射出玻璃砖所需的时间．9．半径为R的固定半圆玻璃砖的横截面如图所示，O点为圆心，OO′与直径AB垂直，足够大的光屏CD紧靠在玻璃砖的左侧且与AB垂直，一光束沿半径方向与OO′成θ＝30°射向O点，光屏CD区域出现两个光斑，已知玻璃的折射率为 2.求：(1)当θ变为多大时，两光斑恰好变为一个；(2)当光束沿半径方向与OO′成θ＝30°射向O点时，光屏CD区域两个光斑的距离．10．一玻璃立方体中心有一点状光源．今在立方体的部分表面镀上不透明薄膜，以致从光源发出的光线只经过一次折射不能透出立方体．已知该玻璃的折射率为2，求镀膜的面积与立方体表面积之比的最小值．《光的折射全反射》典型题1．(多选)解析：选ABC.介质对该单色光的临界角为θ，它的折射率n ＝1sin θ，A 正确；此单色光在介质中的传播速度v ＝cn ＝c sin θ，B 正确；波长λ＝v f ＝c sin θc /λ0＝λ0sin θ，C 正确；光的频率是由光源决定的，与介质无关，D 错误．2．解析：选B.由题图可知，在入射角相同的情况下，光线a 的偏折程度小于光线b 的偏折程度，因此光线a 的折射率小于光线b 的折射率，故选项A 、D 错误；由于折射率越大频率越高，因此光线a 的频率小于光线b 的频率，由c ＝λν可知光线a 的波长大于光线b 的波长，选项B 正确．3．解析：选 B.光线从空气斜射入介质时，入射角大于折射角，从题图可以看出对应的折射角比入射角大，故光是从介质射入空气中，即光由B 经O 到A ，由sin i －sin r 图象的斜率表示折射率的倒数，可得n ＝0.90.6＝1.5，选项B 正确．4．解析：选A.光纤内芯比外套折射率大，在内芯与外套的界面上发生全反射，A 对，B 错；频率大的光，波长短，折射率大，在光纤中传播速度小，C 、D 错．5．解析：选 D.光线发生全反射的条件是光从光密介质进入光疏介质时，入射角i 大于临界角C .光线从图示位置入射，到达OP 边时入射角i 1＝π2－θ，θ越小，i 1越大，发生全发射的可能性越大，根据题意，要在OP 边上发生全反射，应满足θ＜θ2，A 、B 错误．若光线在OP 上发生全反射后到达OQ 边，入射角i 2＝3θ－π2，θ越大，i 2越大， 发生全反射的可能性越大，根据题意，要在OQ 边上发生全反射，应满足θ＞θ1，C 错误、D 正确．6．解析：(1)在半圆形玻璃砖的右侧区域内，不管眼睛在何处，都无法透过玻璃砖同时看到P 1、P 2的像，原因是入射光线AB 离圆心较远，在半圆形面发生了全反射；为同时看到P 1、P 2的像，他应采取的措施是：沿着MN 方向，向M 点方向平移玻璃砖． (2)光路如右图所示．(3)折射率的计算公式为n ＝sin isin r .答案：(1)入射光线AB 离圆心较远，在半圆形面发生了全反射 沿着MN 方向向M 点方向平移玻璃砖 (2)见解析 (3)见解析 sin isin r7．解析：(1)因OE ＝35OA ，由数学知识知光线在AB 面的入射角等于37°，光线恰好未从AB 面射出，所以AB 面入射角等于临界角，则临界角为C ＝37°.由sin C ＝1n 得n ＝53.(2)据几何知识得β＝θ＝76°，则OB 面入射角为 α＝180°－2C －β＝30°.设光线第一次从OB 射出的折射角为r ，由sin r sin α＝n 得sin r ＝56. 答案：(1)53 (2)56 8．解析：(1)作出光路图，如图所示，过E 点的法线是三角形的中位线，由几何关系可知△DEB 为等腰三角形，故DE ＝DB ＝L4.由几何知识知光在AB 边折射时折射角为30°，所以 n ＝sin 45°sin 30°＝ 2.(2)设临界角为θ，有sin θ＝1n ，可解得θ＝45°，由光路图及几何知识可判断，光在BC 边发生全反射，在AC 边第一次射出玻璃砖．根据几何知识可知EF ＝L2，则光束从AB 边射入玻璃砖到第一次射出玻璃砖所需要的时间t ＝DE ＋EF v .代入v ＝c n 可解得t ＝3 2L4c .答案：(1) 2 (2)3 2L4c . 9．解析：(1)光屏上的两个光斑恰好变为一个，说明光线恰好在AB 面发生全反射，n ＝sin 90°sin θ代入数据可得θ＝45°(2)当θ＝30°时，如图所示光线在AB面同时发生反射和折射，反射光线沿半径射出到P点，α＝θ＝30°可得AP＝R cot α＝3R在AB面发生折射，由n＝sin βsin 30°解得sin β＝22，β＝45°可得AQ＝R则两光斑间距离PQ＝AP＋AQ＝(3＋1)R答案：(1)45°(2)(3＋1)R10．解析：光源发出的光线只经过一次折射不能透出立方体，表示光线第一次到达表面时发生全反射的区域不需要镀膜，发生非全反射的区域需要镀膜．考虑从玻璃立方体中心O点发出一条光线，假设它斜射到玻璃立方体上表面发生折射，由折射定律可知n sin θ＝sin α①式中，n为折射率，θ为入射角，α为折射角．现假设A点是上表面面积最小的不透明薄膜边缘上的一点．由题意，在A点恰好发生全反射，故αA＝π2②。

光的折射、全反射练习题（一）1.现在高速公路上的标志牌都用“回归反光膜”制成，夜间行车时，它能把车灯射出的光逆向返回，标志牌上的字特别醒目。

这种“回归反光膜”是用球体反射元件制成的，如图所示，反光膜内均匀分布着直径为10μm的细玻璃珠，所用玻璃的折射率为3，为使入射的车灯光线经玻璃珠折射→反射→再折射后恰好和入射光线平行，那么第一次入射的入射角应是( )A．15° B．30°C．45° D．60°2.三种介质I、II、III的折射率分别为n1、n2和n3，且n1＞n2＞n3，则（）A．光线由介质I入射II有可能发生全反射B．光线由介质I入射III有可能发生全反射C．光线由介质III入射I有可能发生全反射D．光线由介质II入射I有可能发生全反射3.一条光线在三种介质的平行界面上反射或折射的情况如图所示，若光在 I、II、III三种介质中的速度分别为v1、v2和v3，则( )A．v1＞v2＞v3 B．v1＜v2＜v3C．v1＞v3＞v2 D．v1＜v3＜v24．一束光穿过介质1、2、3时，光路如图所示，则 ( )A．介质1的折射率最大B．介质2是光密介质C．光在介质2中的速度最大D．当入射角由45°逐渐增大时，在1、2分界面上可能发生全反射5.如图，MN是一条通过透明球体球心的直线．一单色细光束AB平行于MN射向球体，B为入射点，若出射光线CD与MN的交点P到球心O的距离是球半径的3倍，且与MN所成的角α＝30°.求：透明球体的折射率．6. 一半径为R的1/4球体放置在水平桌面上，球体由折射率为3的透明材料制成．现有一束位于过球心O的竖直平面内的光线，平行于桌面射到球体表面上，折射入球体后再从竖直表面射出，如图所示．已知入射光线与桌面的距离为3R/2，求出射角θⅡⅢ7.折射率为3的玻璃球，被一束光照射.若入射角i为60°，则在入射点O处反射光和折射光的夹角为________.(如图甲所示)图甲图乙8.如图乙所示，一束波长为0.40 μm的紫光，从空气中垂直三棱镜的AB面入射，从AC面射出方向如图所示，则玻璃对紫光的折射率n=_______，紫光在玻璃中的传播速度v=_______m/s，紫光在玻璃中的波长λ=________ m.9. 半径为R的玻璃半圆柱体，横截面积如图所示，圆心为O，两条平行单色红光，沿截面积射向圆柱面，方向与底面垂直，光线1的入射点A为圆柱面的顶点，光线2的入射点为B，∠AOB=60°，已知该玻璃对红光折射率n。

高中物理【光的折射全反射】典型题1．(多选)已知介质对某单色光的临界角为θ，则()A．该介质对此单色光的折射率为1sin θB．此单色光在该介质中传播速度为c sin θ(c为真空中光速)C．此单色光在该介质中的波长是真空中波长的sin θ倍D．此单色光在该介质中的频率是真空中的1sin θ解析：选ABC．介质对该单色光的临界角为θ，它的折射率n＝1sin θ，A正确；此单色光在介质中的传播速度v＝cn＝c sinθ，B正确；波长λ＝vf＝c sin θcλ0＝λ0sin θ，C正确；光的频率是由光源决定的，与介质无关，D错误．2．光纤通信中信号传播的主要载体是光导纤维，它的结构如图所示，其内芯和外套材料不同，光在内芯中传播．下列关于光导纤维的说法中正确的是()A．内芯的折射率比外套的大，光传播时在内芯与外套的界面上发生全反射B．内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生全反射C．波长越短的光在光纤中传播的速度越大D．频率越大的光在光纤中传播的速度越大解析：选A．光纤内芯比外套折射率大，在内芯与外套的界面上发生全反射，A对，B 错；频率大的光，波长短，折射率大，在光纤中传播速度小，C、D错．3．如图所示，一束光经玻璃三棱镜折射后分为两束单色光a、b，波长分别为λa、λb，该玻璃对单色光a、b的折射率分别为n a、n b，则()A．λa<λb，n a>n b B．λa>λb，n a<n bC．λa<λb，n a<n b D．λa>λb，n a>n b解析：选B ．一束光经过三棱镜折射后，折射率小的光偏折较小，而折射率小的光波长较长．所以λa >λb ，n a <n b .故选项B 正确．4．如图，△ABC 为一玻璃三棱镜的横截面，∠A ＝30°，一束红光垂直AB 边射入，从AC 边上的D 点射出，其折射角为60°，则玻璃对红光的折射率为________．若改用蓝光沿同一路径入射，则光线在D 点射出时的折射角________(选填“小于”“等于”或“大于”)60°.解析：根据题述和图示可知，i ＝60°，γ＝30°，由折射定律，玻璃对红光的折射率n ＝sin isin γ＝ 3.若改用蓝光沿同一路径入射，由于玻璃对蓝光的折射率大于玻璃对红光的折射率，则光线在D 点射出时的折射角大于60°.答案：3 大于5．如图所示，由某种透明介质制成的长直细圆柱体置于真空中．某种单色光在介质中传输，经过多次全反射后从右端射出．若以全反射临界角传输的光线刚好从右端以张角2θ出射，则此介质的折射率为( )A ．1＋sin 2θB ．1＋cos 2θC ．1＋cos 2θD ．1＋sin 2θ解析：选D ．设介质中发生全反射的临界角为α，如图．则由全反射临界角与α的关系可知：sin α＝1n.由图，经多次全反射后从右端射出时，入射角和反射角满足关系：n ＝sin θsin ⎝⎛⎭⎫π2－a .联立两式可得n ＝ 1＋sin 2 θ.6.如图，一半径为R 的玻璃半球，O 点是半球的球心，虚线OO ′表示光轴(过球心O 与半球底面垂直的直线)．已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上，有些光线能从球面射出(不考虑被半球的内表面反射后的光线)．求：(1)从球面射出的光线对应的入射光线到光轴距离的最大值；(2)距光轴R 3的入射光线经球面折射后与光轴的交点到O 点的距离． 解析： (1)如图，从底面上A 处射入的光线，在球面上发生折射时的入射角为i ，当i 等于全反射临界角i c 时，对应入射光线到光轴的距离最大，设最大距离为l .i ＝i c ①设n 是玻璃的折射率，由全反射临界角的定义有n sin i c ＝1②由几何关系有sin i ＝l R③ 联立①②③式并利用题给条件，得l ＝23R .④ (2)设与光轴相距R 3的光线在球面B 点发生折射时的入射角和折射角分别为i 1和γ1，由折射定律有n sin i 1＝sin γ1⑤设折射光线与光轴的交点为C ，在△OBC 中，由正弦定理有sin ∠C R ＝sin(180°－γ1)OC⑥ 由几何关系有∠C ＝γ1－i 1⑦sin i 1＝13⑧ 联立⑤⑥⑦⑧式及题给条件得OC ＝3(22＋3)5R ≈2.74R .⑨ 答案：(1)23R (2)2.74R7．(多选)如图所示，O1O2是半圆形玻璃砖过圆心的法线，a、b是关于O1O2对称的两束平行单色光束，两光束从玻璃砖右方射出后的光路图如图所示，则下列说法正确的是()A．该玻璃砖对a光的折射率比对b光的折射率小B．有可能a是绿光，b是红光C．两光束从空气进入玻璃的过程中各自的频率均不变D．在真空中，a光的波长比b光的波长长解析：选ACD．由题图可知，b光偏离原来的传播方向较多，玻璃对b光的折射率大，故A正确；玻璃对b光的折射率大，b光的频率高，故B错误；光在不同介质中传播，频率不变，故C正确；根据真空中波速c＝λν，b光频率高，波长短，故D正确．8．如图所示，光液面传感器有一个像试管模样的玻璃管，中央插一块两面反光的玻璃板，入射光线在玻璃管内壁与反光板之间来回发生反射，进入到玻璃管底部，然后在另一侧反射而出(与光纤原理相同)．当透明液体的折射率大于玻璃管壁的折射率时，就可以通过光液面传感器监测出射光的强弱来判定玻璃管是否被液体包住了，从而了解液面的高度．以下说法正确的是()A．玻璃管被液体包住之后，出射光强度增强B．玻璃管被液体包住之后，出射光消失C．玻璃管被液体包住之后，出射光强度减弱D．玻璃管被液体包住之后，出射光强度不变解析：选C．玻璃管被液体包住之前，由于玻璃管之外是光疏介质空气，光线发生全反射，没有光线从玻璃管壁中射出．当玻璃管被透明液体包住之后，液体的折射率大于玻璃管壁的折射率时，光线不再发生全反射，有一部分光线进入液体，反射光的强度会减弱，故C 正确．9．(多选)如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射入E点，并偏折到F点，已知入射方向与边AB的夹角为θ＝30°，E、F分别为边AB、BC的中点，则下列说法正确的是( )A ．该棱镜的折射率为 3B ．光在F 点发生全反射C ．光从空气进入棱镜，波长变短D ．光从空气进入棱镜，波速变小解析：选ACD ．在E 点作出法线可知入射角为60°，折射角为30°，由n ＝sin 60°sin 30°可得折射率为3，故A 正确；由几何关系可知，在BC 边上的入射角小于临界角，不会发生全反射，B 错；由公式v ＝c n可知，光从空气进入棱镜，波速变小，又v ＝λf ，光从空气进入棱镜，波长变短，故C 、D 正确．10.如图，一玻璃工件的上半部是半径为R 的半球体，O 点为球心；下半部是半径为R 、高为2R 的圆柱体，圆柱体底面镀有反射膜．有一平行于中心轴OC 的光线从半球面射入，该光线与OC 之间的距离为0.6R .已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)．求该玻璃的折射率．解析：如图，根据光路的对称性和光路可逆性，与入射光线相对于OC 轴对称的出射光线一定与入射光线平行．这样，从半球面射入的折射光线，将从圆柱体底面中心C 点反射．设光线在半球面的入射角为i ，折射角为γ.由折射定律有sin i ＝n sin γ①由正弦定理有sin γ2R ＝sin(i －γ)R ② 由几何关系，入射点的法线与OC 的夹角为i .由题设条件和几何关系有sin i ＝L R③ 式中L 是入射光线与OC 的距离，L ＝0.6R .由②③式和题给数据得sin γ＝6205④ 由①③④式和题给数据得n ＝ 2.05≈1.43答案： 2.05(或1.43)11．如图所示，在注满水的游泳池的池底有一点光源A ，它到池边的水平距离为3.0 m ．从点光源A 射向池边的光线AB 与竖直方向的夹角恰好等于全反射的临界角，水的折射率为43.(1)求池内的水深；(2)一救生员坐在离池边不远处的高凳上，他的眼睛到池面的高度为2.0 m ．当他看到正前下方的点光源A 时，他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字)．解析：(1)光由A 射向B 恰好发生全反射，光路如图甲所示．甲则sin θ＝1n ，得sin θ＝34又|AO |＝3 m ，由几何关系可得：|AB |＝4 m ，|BO |＝7 m ，所以水深7 m.(2)光由A 点射入救生员眼中光路图如图乙所示．乙由折射定律n ＝sin 45°sin α可知sin α＝328tan α＝323＝32323 设|BE |＝x ，由几何关系得tan α＝|AQ ||QE |＝3 m －x 7 m代入数据得x ＝⎝⎛⎭⎫3－316123 m ≈1.3 m ， 由几何关系得，救生员到池边的水平距离为 |BC |＝2 m －x ≈0.7 m答案：(1)7 m (2)0.7 m。

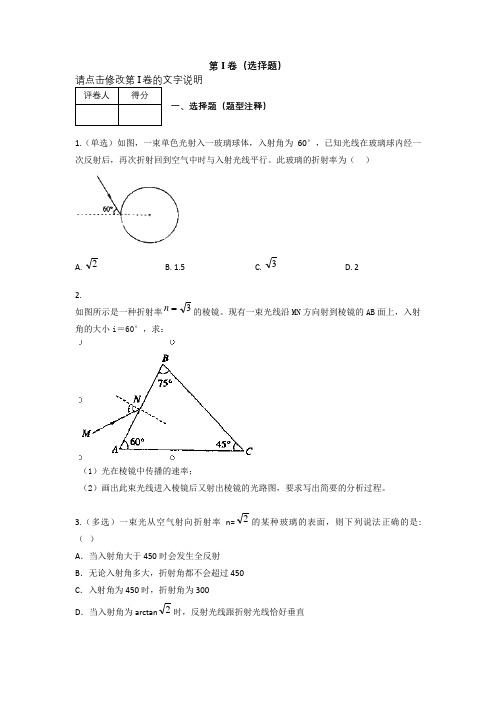
第I卷（选择题）请点击修改第I卷的文字说明评卷人得分一、选择题（题型注释）1.（单选）如图，一束单色光射入一玻璃球体，入射角为60°，已知光线在玻璃球内经一次反射后，再次折射回到空气中时与入射光线平行。

此玻璃的折射率为（）A. 2B. 1.5C. 3D. 22.如图所示是一种折射率3n的棱镜。

现有一束光线沿MN方向射到棱镜的AB面上，入射角的大小i＝60°，求：（1）光在棱镜中传播的速率；（2）画出此束光线进入棱镜后又射出棱镜的光路图，要求写出简要的分析过程。

3.（多选）一束光从空气射向折射率n=2的某种玻璃的表面，则下列说法正确的是:（）A．当入射角大于450时会发生全反射B．无论入射角多大，折射角都不会超过450C．入射角为450时，折射角为300D．当入射角为arctan2时，反射光线跟折射光线恰好垂直第II卷（非选择题）请点击修改第II卷的文字说明评卷人得分二、填空题（题型注释）4.直角玻璃三棱镜的截面如图所示，一条光线从AB面入射，ab为其折射光线，ab与AB 面的夹角α= 60°．已知这种玻璃的折射率n =2，则：①这条光线在AB面上的的入射角为；②图中光线ab （填“能”或“不能”）从AC面折射出去．5.如图所示，一个用透明材料制成的截面为直角三角形的三棱镜ABC．现在有一束单色光从空气中以θ=45°的入射角自直角边AB射入，折射时的偏转角为15°，然后光线射到AC 面而刚好发生了全反射，则这种透明材料的折射率为________，全反射的临界角为_________，角∠A=________.6.如图所示，用某种透光物制成的直角三棱镜ABC；在垂直于AC面的直线MN上插两枚大头针P1、P2，在AB面的左侧透过棱镜观察大头针P1、P2的像，调整视线方向，直到P1的像__________________，再在观察的这一侧先后插上两枚大头针P3、P4，使P3________，P4________.记下P3、P4的位置，移去大头针和三棱镜，过P3、P4的位置作直线与AB面相交于D，量出该直线与AB面的夹角为45°.则该透光物质的折射率n＝________，并在图中画出正确完整的光路图．评卷人得分三、实验题（题型注释）评卷人得分四、计算题（题型注释）7.如图所示，一束光从空气垂直射到直角棱镜的AB面上，已知棱镜材料的折射率为1.4，画出这束光进入棱镜后的光路图（要求必须有计算步骤）8.知光线自空气射入甲介质中，入射角为60°，折射角为30°；光线从乙介质射入空气，入射角为45°，折射角为60°，求：（1）甲、乙两种介质的折射率之比n甲∶n乙；（2）光在甲、乙两种介质中的光速之比v甲∶v乙9.如图所示，真空中有一个半径为R，折射率为n＝2的透明玻璃球．一束光沿与直径成θ0＝45°角的方向从P点射入玻璃球，并从Q点射出，求光线在玻璃球中的传播时间．10.如图所示，真空中有一个半径为R，折射率为n＝2的透明玻璃球．一束光沿与直径成θ0＝45°角的方向从P点射入玻璃球，并从Q点射出，求光线在玻璃球中的传播时间．11.一棱镜的截面为直角三角形ABC ，∠A=30o ，斜边AB=a 。

光的折射 全反射1．(多选)如图所示的是在四川景区九寨沟拍摄的一张风景照片，湖水清澈见底，近处湖面水下的树枝和池底都看得很清楚，而远处则只看到对岸山峰和绿树的倒影，水面下的景物则根本看不到。

下列说法正确的是( )A ．远处山峰的倒影非常清晰，是因为来自山峰的光线在水面上发生了全反射B ．光从空气射入水中，光的波速变小，波长变小C ．远处水面下景物的光线到水面处，入射角较大，可能发生了全反射，所以看不见D ．来自近处水面下景物的光射到水面处，入射角较小，反射光强而折射光弱，因此有较多的能量射出水面而进入人的眼睛中解析：BC 远处山峰的倒影非常清晰，是因为山峰的光线在水面上发生了反射，但不是全反射，因为全反射只有光从光密介质射入光疏介质时才可能发生，故A 错误。

光线由空气射入水中，光的波速变小，频率不变，由波速公式v ＝λf 知波长变小，故B 正确。

远处水面下景物的光线射到水面处，入射角很大，当入射角大于或等于全反射临界角时能发生全反射，光线不能射出水面，因而看不见，故C 正确。

近处水面下景物的光线到水面处，入射角越小，反射光越弱而折射光越强，射出水面而进入人眼睛中的能量越多，故D 错误。

2．如图所示，一小孩在河水清澈的河面上以1 m/s 的速度游泳，t ＝0时刻他看到自己正下方的河底有一小石块，t ＝3 s 时他恰好看不到小石块了，河水的折射率n ＝43，下列说法正确的是( )A ．3 s 后，小孩会再次看到河底的石块B ．前3 s 内，小孩看到的石块越来越明亮C ．这条河的深度为7 mD ．t ＝0时小孩看到的石块深度为473m 解析：C t ＝3 s 时他恰好看不到小石块了，说明在此位置从小石块射到水面的光发生了全反射，则3 s 后的位置从小石块射到水面的光仍发生全反射，则小孩仍不会看到河底的石块，选项A 错误；前3 s 内，从小石子上射向水面的光折射光线逐渐减弱，反射光逐渐增强，可知小孩看到的石块越来越暗，选项B 错误；由于sin C ＝1n ＝34，则tan 37°＝377，可知水深h ＝v t tan C ＝3377m ＝7 m ，选项C 正确；t ＝0时小孩看到的石块深度为h ′＝h n ＝374m ，选项D 错误。

B 光的折射及全反射1.一束光从空气射向折射率n=2的某种玻璃的表面，如图所示，i 表示入射角，则（ ）A ．无论入射角i 有多大，折射角r 都不会超过45B ．欲使折射角r ＝300，应以i ＝450的角度入射 C ．当入射角i ＝arctan 2时，反射光线与折射光线恰好互相垂直D ．以上结论都不正确2.h m 深处，向上观察水面，能看到的天穹和周围的景物都出现在水面上 的一个圆形面积为S 的区域内，关于圆面积S 和深度h 的关系正确的是（ ）A 、S 与水深h 成正比B 、S 与水深h 成反比C 、S 与水深h 的平方成正比D 、S 与水深h 的平方成反比3.发出白光的细线光源ab ，长度为l 0，竖直放置，上端a 恰好在水面以下，如图。

现考虑线光源a b 发出的靠近水面法线（图中的虚线）的细光束经水面折射后所成的像，由于水对光有色散作用，若以l 1表示红光成的像的长度，l 2表示蓝光成的像的长度，则（ ）A ． l 1< l 2<l 0B ．l 1> l 2>l 0C ．l 2> l 1>l 0D ．l 2< l 1<l 04.公园里灯光喷泉的水池中有处于同一深度若干彩灯，在晚上观察不同颜色彩灯的深度和水面上被照亮的面积，下列说法正确的是 （ ）A ．红灯看起来较浅，红灯照亮的水面面积较小B ．红灯看起来较深，红灯照亮的水面面积较小C ．红灯看起来较浅，红灯照亮的水面面积较大D ．红灯看起来较深，红灯照亮的水面面积较大5.如图5所示，红色细光束a 射到折射率为2的透明球表面，入射角为45°，在球的内壁经过一次反射后，从球面射出的光线为b ，则入射光线a 与出射光线b 之间的夹角α为 ( )A ．30°B ．45°C ．60°D ．75°6、一玻璃砖横截面如图所示，其中ABC 为直角三角形（AC 边末画出），AB 为直角边∠ABC=45°；ADC 为一圆弧，其圆心在BC 边的中点。

选修1高中物理《全反射》测试题(含答案)一、全反射选择题1．如图所示，一束光从空气中射向折射率为n＝2的某种玻璃的表面，θ1表示入射角，则下列说法中正确的是()A．当θ1>45°时会发生全反射现象B．只有当θ1＝90°时才会发生全反射C．无论入射角θ1是多大，折射角θ2都不会超过45°D．欲使折射角θ2＝30°，应以θ1＝45°的角度入射E.当入射角的正切tan θ1＝2时，反射光线和折射光线恰好互相垂直2．如图所示，在等边三棱镜截面ABC内，有一束单色光从空气射向其边界上的E点，已知该单色光入射方向与三棱镜边界AB的夹角为θ=30º，该三棱镜对该单色光的折射率为3，则下列说法中正确的是（）A．该单色光在AB边界发生全反射B．该单色光从空气进入棱镜，波长变长C．该单色光在三棱镜中的传播光线与底边BC平行D．该单色光在AC边界发生全反射3．如图，半圆形玻璃砖置于光屏PQ的左下方．一束白光沿半径方向从A点射入玻璃砖，在O点发生反射和折射，折射光在白光屏上呈现七色光带．若入射点由A向B缓慢移动，并保持白光沿半径方向入射到O点，观察到各色光在光屏上陆续消失．在光带未完全消失之前，反射光的强度变化以及光屏上最先消失的光分别是（）A．减弱，紫光B．减弱，红光C．增强，紫光D．增强,红光4．如图所示两细束单色光平行射到同一个三棱镜上，经折射后交于光屏上的同一个点M。

则下列说法中正确的是（）A．如果a为蓝色光，则b可能为红色光B．在该三棱镜中b色光的传播速率比a光的传播速率小C．棱镜射向空气中a色光的临界角比b色光的临界角大D．a光的折射率小于b光折射率5．如图所示，口径较大、充满水的薄壁圆柱形浅玻璃缸底有一发光小球，则（）A．小球必须位于缸底中心才能从侧面看到小球B．小球所发的光能从水面任何区域射出C．小球所发的光从水中进入空气后频率变大D．小球所发的光从水中进入空气后传播速度变大6．如图所示，空气中有一折射率为2的玻璃柱体，其横截而是圆心角为90o、半径为R 的扇形OAB、一束平行光平行于横截面，以45o入射角射到OA上，OB不透光，若考虑首次入射到圆弧AB上的光，则AB上有光透出的部分的弧长为（）A．16RπB．14RπC．13RπD．512Rπ7．中国古人对许多自然现象有深刻认识，唐人张志和在《玄真子．涛之灵》中写道：“雨色映日而为虹”，从物理学的角度看，虹时太阳光经过雨滴的两次折射和一次反射形成的，右图是彩虹成因的简化示意图，其中a、b时两种不同频率的单色光，则两光A．在同种玻璃种传播，a光的传播速度一定大于b光B ．以相同角度斜射到同一玻璃板透过平行表面后，b 光侧移量大C ．分别照射同一光电管，若b 光能引起光电效应，a 光一定也能D ．以相同的入射角从水中射入空气，在空气张只能看到一种光时，一定是a 光 8．如图所示，将透明长方体放在空气中，矩形ABCD 是它的一个截面，将a 、b 两种单色细光束射入到P 点，入射角为45θ︒=，12AP AD =，若a 光折射后恰好射至AD 面上，b 光从CD 面射出，则（ ）A ．在介质中b 光比a 光速度大B ．a 光在介质中的折射率52n =C ．若要a 光束在AD 面上发生全反射，角θ的范围应满足42ππθ<≤D ．改变入射角θ的大小，b 光一定可以从AD 面射出9．如图所示是一个用折射率n=2.4的透明介质做成的四棱柱的镜截面图。

第一讲 光的折射和全反射➢ 知识梳理一、光的折射定律 折射率 1．折射定律(1)内容：如图所示，折射光线与入射光线、法线处在同一平面内，折射光线与入射光线分别位于法线的两侧；入射角的正弦与折射角的正弦成正比。

(2)表达式：sin θ1sin θ2＝n 12。

(3)在光的折射现象中，光路是可逆的。

2．折射率(1)折射率是一个反映介质的光学性质的物理量。

(2)定义式：n ＝sin θ1sin θ2。

(3)计算公式：n ＝cv，因为v ＜c ，所以任何介质的折射率都大于1。

(4)当光从真空(或空气)斜射入某种介质时，入射角大于折射角；当光由介质斜射入真空(或空气)时，入射角小于折射角。

二、全反射 光导纤维1．定义：光从光密介质射入光疏介质，当入射角增大到某一角度时，折射光线将全部消失，只剩下反射光线的现象叫作全反射。

2．条件(1)光从光密介质射入光疏介质。

(2)入射角大于或等于临界角。

3．临界角：折射角等于90°时的入射角。

若光从光密介质(折射率为n )射向真空或空气时，发生全反射的临界角为C ，则sin C ＝1n 。

介质的折射率越大，发生全反射的临界角越小。

4．光导纤维光导纤维的原理是利用光的全反射，如图所示。

考点一、折射定律及折射率的理解与应用1．对折射率的理解(1)折射率的大小不仅反映了介质对光的折射本领，也反映了光在该介质中传播速度的大小v ＝cn.(2)折射率的大小不仅与介质本身有关，还与光的频率有关．①同一种介质中，频率越大的光折射率越大，传播速度越小．②同一种光，在不同介质中虽然波速、波长不同，但频率相同．2．光路的可逆性在光的折射现象中，光路是可逆的．如果让光线逆着原来的折射光线射到界面上，光线就会逆着原来的入射光线发生折射．3．平行玻璃砖、三棱镜和圆柱体(球)对光路的控制特点平行玻璃砖三棱镜圆柱体(球)对光线的作用通过平行玻璃砖的光线不改变传播方向，但要发生侧移通过三棱镜的光线经两次折射后，出射光线向棱镜底面偏折圆界面的法线是过圆心的直线，光线经过两次折射后向圆心偏折例1、(2021·浙江6月选考·12)用激光笔照射透明塑料制成的光盘边缘时观察到的现象如图所示．入射点O 和两出射点P、Q恰好位于光盘边缘等间隔的三点处，空气中的四条细光束分别为入射光束a、反射光束b、出射光束c和d、已知光束a和b间的夹角为90°，则()A．光盘材料的折射率n＝2B．光在光盘内的速度为真空中光速的三分之二C．光束b、c和d的强度之和等于光束a的强度D．光束c的强度小于O点处折射光束OP的强度例2、(2019·全国卷Ⅰ)如图，一艘帆船静止在湖面上，帆船的竖直桅杆顶端高出水面3 m 。

专题14光的折射、全反射【母题来源一】2016年全国新课标Ⅰ卷【母题原题】如图，在注满水的游泳池的池底有一点光源A，它到池边的水平距离为3.0 m。

从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角，水的折射率为。

（i）求池内的水深；（ii）一救生员坐在离池边不远处的高凳上，他的眼睛到地面的高度为2.0 m。

当他看到正前下方的点光源A时，他的眼睛所接受的光线与竖直方向的夹角恰好为45°。

求救生员的眼睛到池边的水平距离（结果保留1位有效数字）。

【答案】（i）7m≈2.6 m（ii）0.7 mn sin i=sin θ①由几何关系有sin i22l h式中，l=3 m，h是池内水的深度。

联立①②式并代入题给数据得h7m≈2.6 m③（ii ）设此时救生员的眼睛到池边的距离为x 。

依题意，救生员的视线与竖直方向的夹角为θ'=45°。

由折射定律有n sin i'=sin θ' ④式中，i'是光线在水面的入射角。

设池底点光源A 到水面入射点的水平距离为a 。

由几何关系有sin i'=22a h +⑤x +l =a +h' ⑥式中h'=2 m 。

联立③④⑤⑥式得x =(3723–1)m≈0.7 m⑦ 【考点定位】光的折射定律【名师点睛】本题主要考查了光的折射定律的应用；解题关键是根据题意画出完整的光路图，然后根据光的折射定律结合几何关系列出方程求解；此题意在考查考生应用数学处理物理问题的能力。

【母题来源二】2016年全国新课标Ⅲ卷【母题原题】如图，玻璃球冠的折射率为3，其底面镀银，底面的半径是球半径的3倍；在过球心O 且垂直于底面的平面（纸面）内，有一与底面垂直的光线射到玻璃球冠上的M 点，该光线的延长线恰好过底面边缘上的A 点。

求该光线从球面射出的方向相对于其初始入射方向的偏角。

【答案】180150ENO β=-∠=设图中N 点为光线在球冠内底面上的反射点，所考虑的光线的光路图如图所示，设光线在M点的入射角为i ，折射角为r ，在N 点的入射角为i '，反射角为i ''，玻璃折射率为n ，由于OAM △为等边三角形，有i =60°【考点定位】光的折射定律 【方法技巧】解决光学问题的关键要掌握全反射的条件、折射定律sin sin i n r =、临界角公式1sin C n =、光速公式cv n =，运用几何知识结合解决这类问题。

第3课时 光的折射 全反射折射定律与折射率的理解和应用1、如图所示，光线以入射角θ1从空气射向折射率n ＝2的玻璃表面．(1)当入射角θ1＝45°时，求反射光线与折射光线间的夹角θ. (2)当入射角θ1为何值时，反射光线与折射光线间的夹角θ＝90°？答案 (1)105° (2)arctan 2解析 (1)设折射角为θ2，由折射定律sin θ1sin θ2＝n 得sin θ2＝sin θ1n＝sin 45°2＝12，所以，θ2＝30°. 因为θ1′＝θ1＝45°，所以θ＝180°－45°－30°＝105°.(2)因为θ1′＋θ2＝90°，所以，sin θ2＝sin (90°－θ1′)＝cos θ1′＝cos θ1 由折射定律得tan θ1＝2，θ1＝arctan 2. 2、已知介质对某单色光的临界角为θ，则( )A ．该介质对此单色光的折射率等于1sin θB ．此单色光在该介质中的传播速度等于c ·sin θ(c 为真空中的光速)C ．此单色光在该介质中的波长是在真空中波长的sin θ倍D ．此单色光在该介质中的频率是真空中的1sin θ答案 ABC解析 介质对该单色光的临界角为θ，它的折射率n ＝1sin θ，A 项正确；此单色光在介质中的传播速度和波长分别为v ＝c n ＝c sin θ，B 正确；λ＝v ν＝c ·sin θc /λ0＝λ0sin θ，所以λ∶λ0＝sin θ∶1，故C 项正确；而光的频率是由光源决定的，与介质无关，故D 项错误． 3、如图所示是一种折射率n ＝1.5的棱镜，现有一束光线沿MN 的方向射到棱镜的AB 界面上，入射角的正弦值为sin i ＝0.75.求： (1)光在棱镜中传播的速率；(2)通过计算说明此束光线射出棱镜后的方向并画出光路图(不考虑返回到AB 面上的光线)． 答案 见解析解析 (1)由n ＝c v 得v ＝cn＝2×108 m/s(2)设光线进入棱镜后的折射角为r ，由sin i sin r ＝n ，得sin r ＝sin in ＝0.5，r ＝30°，光线射到BC 界面时的入射角i 1＝90°－45°＝45°由于sin 45°>1n ，所以光线在BC 边发生全反射，光线沿DE 方向射出棱镜后的方向与AC边垂直，光路图如图所示．4、 如图所示，ABCD 为一直角梯形棱镜的截面，∠C ＝60°，P 为垂直于直线BC 的光屏，现用一宽度等于AB 边的单色平行光束垂直射向AB 面，经棱镜折射后在屏P 上形成宽度等于23AB 的一条光带，求棱镜的折射率．解析 光路图如图所示，根据题意有 θ1＝θ2＝30°，FC ＝23AB则EF ＝13AB根据几何关系有DE ＝CE tan 30°＝AB tan 30°＝33AB 在△DEF 中，tan θ3＝EF DE＝33，解得θ3＝30° 由折射定律可得n ＝sin (θ2＋θ3)sin θ1，解得n ＝ 3答案35、如图所示，在坐标系的第一象限内有一横截面为四分之一圆周的柱状玻璃体OPQ ，OP ＝OQ ＝R ，一束单色光垂直OP 面射入玻璃体，在OP 面上的入射点为A ，OA ＝R2，此单色光通过玻璃体后沿BD 方向射出，且与x 轴交于D 点，OD ＝3R ，求该玻璃的折射率．答案3解析 作光路图如图所示．在PQ 面上的入射角 sin θ1＝OA OB ＝12，θ1＝30° 由几何关系可得θ2＝60° 折射率n ＝sin θ2sin θ1＝ 36、如图所示为用某种透明材料制成的一块柱形棱镜的截面图，圆弧CD 为半径为R 的四分之一的圆周，圆心为O ，光线从AB 面上的某点入射，入射角θ1＝45°，它进入棱镜后恰好以临界角射在BC 面上的O 点． (1)画出光线由AB 面进入棱镜且从CD 弧面射出的光路图； (2)求该棱镜的折射率n ；(3)求光线在该棱镜中传播的速度大小v (已知光在空气中的传播速度c ＝3.0×108 m/s)． 解析 (1)光路图如图所示．(2)光线在BC 面上恰好发生全反射，入射角等于临界角C sin C ＝1n ，cos C ＝n 2－1n.光线在AB 界面上发生折射，折射角θ2＝90°－C ，由几何关系得sin θ2＝cos C ， 由折射定律得n ＝sin θ1sin θ2由以上几式联立解得n ＝62(3)光速v ＝cn ＝6×108 m/s答案 (1)见解析图 (2)62(3)6×108 m/s7、为测量一块等腰直角三棱镜ABD 的折射率，用一束激光沿平行于BD 边的方向射向直角边AB 边，如图8所示．激光束进入棱镜后射到另一直角边AD 边时，刚好能发生全反射．该棱镜的折射率为多少？图8答案62解析 作出法线如图所示n ＝sin 45°sin r ，n ＝1sin C ，C ＋r ＝90°即sin 45°cos C ＝1sin C解得tan C ＝2，sin C ＝63，n ＝62. 8、如图所示，MNPQ 是一块截面为正方形的玻璃砖，正方形的边长为30 cm ，有一束很强的细光束AB 射到玻璃砖的MQ 面上，入射点为B ，该光束从B 点进入玻璃砖后再经QP 面反射沿DC 方向射出．其中B 为MQ 的中点，∠ABM ＝30°，PD ＝7.5 cm ，∠CDN ＝30°.试在原图上准确画出该光束在玻璃砖内的光路图，并求出该玻璃砖的折射率．解析 找出B 点关于界面QP 的对称点E ，连接ED 交QP 于F 点，即光束在F 点发生反射，所以其光路图如图所示． 由几何关系得DE ＝302＋(15＋7.5)2 cm ＝37.5 cm sin θ2＝DP ＋QEDE＝0.6 由折射定律得n ＝sin θ1sin θ2＝1.44.答案 见解析图 1.44对全反射的考查9、 如图是透明圆柱介质的横截面，C 、D 为圆上两点．一束单色光沿BC 方向入射，从D点射出．已知∠COD ＝90°，∠BCO ＝120°.(1)求介质的折射率； (2)改变∠BCO 的大小，能否在介质的内表面发生全反射？答案 (1)62(2)不能解析 (1)作出光路图如图，由几何关系知α＝60°，β＝45°；折射率n ＝sin αsin β＝62.(2)由光路可逆可知，光不可能在介质内表面发生全反射．10、(2009·浙江理综·18)如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射向E 点，并偏折到F 点．已知入射方向与边AB 的夹角为θ＝30°， E 、F 分别为边AB 、BC 的中点，则 ( )A ．该棱镜的折射率为 3B ．光在F 点发生全反射C ．光从空气进入棱镜，波长变小D ．从F 点出射的光束与入射到E 点的光束平行 答案 AC解析 由几何关系可得入射角θ1＝60°，折射角θ2＝30°，由n ＝sin θ1sin θ2＝3，A 对；由sinC ＝1n ，临界角C >30°，故在F 点不发生全反射，B 错；由n ＝c v ＝λ0λ知光进入棱镜波长变小，C 对；F 点出射的光束与BC 边的夹角为30°，与入射光线不平行，D 错；故选A 、 C.11、 如图所示，扇形AOB 为透明柱状介质的横截面，圆心角∠AOB＝60°.一束平行于角平分线OM 的单色光由OA 射入介质，经OA 折射的光线恰平行于OB ，以下对介质的折射率值及折射光线中恰好射到M 点的光线能不能发生全反射的说法正确的是( ) A.3，不能发生全反射B.3，能发生全反射C.233，不能发生全反射D.233，能发生全反射答案 A解析 画出光路图，并根据几何关系标出角度，如图所示．由图可知，介质的折射率n ＝sin 60°sin 30°＝3；因为sin 30°＝12<33＝1n＝sin C ，所以折射光线中恰好射到M 点的光线不能发生全反射，选项A 正确． 12、如图所示，直角三角形ABC 为一三棱镜的横截面，∠A ＝30°.一束单色光从空气射向BC 上的E 点，并偏折到AB 上的F 点，光线EF 平行于底边AC .已知入射光与BC 边的夹角为θ＝30°.试通过计算判断光在F 点能否发生全反射． 答案 能解析 由几何关系知，光线在BC 界面的入射角θ1＝60°，折射角θ2＝30° 根据折射定律得n ＝sin θ1sin θ2＝sin 60°sin 30°＝ 3由几何关系知，光线在AB 界面的入射角为θ3＝60°而棱镜对空气的临界角C 的正弦值sin C ＝1n ＝33<sin θ3，则光线在AB 界面的入射角θ3>C ，所以光线在F 点能发生全反射．。

高中物理选择性必修一单元测试题《光的折射和全反射》（最新试题含答案）一、单选题（本大题共12小题，共48分）1.关于光的折射现象，下列说法中正确的是A. 折射角一定小于入射角B. 折射率跟折射角的正弦值成反比C. 折射率大的介质，光在其中的传播速度小D. 折射角增大为原来的2倍，入射角也增大为原来的2倍2.下列关于光学现象的说法正确的是A. 海市蜃楼是因为光的色散B. 雨后的彩虹是由于七色光对水滴的折射率不同发生了光的色散的结果C. 红光进入水中，其频率和传播速度都会变小D. 用于传输信号的光纤利用了光的全反射，且内芯的折射率要小于外套的折射率3.红、黄、绿三种单色光以相同的入射角到达某介质和空气的界面时，若黄光恰好发生全反射，则A. 绿光一定能发生全反射B. 红光一定能发生全反射C. 三种单色光相比，红光在介质中的传播速率最小D. 红光在介质中的波长比它在空气中的波长长4.如图所示，光在真空和某介质的界面MN上发生折射，则介质的折射率为( )A. B. C. D.5.如图是光由空气射入半圆形玻璃砖，再由玻璃砖射入空气的光路图，O点是半圆形玻璃砖的圆心。

下列情况可能发生的是A. B. C. D.6.如图，一束复色光从空气中沿半圆玻璃砖半径方向射入，从玻璃砖射出后分成a、b两束单色光，则A. 玻璃砖对a光的折射率为1.5B. 玻璃砖对a光的折射率为C. b光在玻璃中的传播速度比a光大D. b光在玻璃中发生全反射的临界角比a光小7.华裔科学家高锟获得2009年诺贝尔物理奖，他被誉为“光纤通讯之父”光纤通讯中信号传播的主要载体是光导纤维，它的结构如图所示，其内芯和外套材料不同，光在内芯中传播．下列关于光导纤维的说法中正确的是．A. 波长越短的光在光纤中传播的速度越大B. 频率越大的光在光纤中传播的速度越大C. 内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生全反射D. 内芯的折射率比外套的大，光传播时在内芯与外套的界面上发生全反射8.如图所示，圆心为O、半径为R的半圆形玻璃砖置于水平桌面上，光线从P点垂直界面入射后，恰好在玻璃砖圆形表面发生全反射；当入射角时，光线从玻璃砖圆形表面出射后恰好与入射光平行。