一元函数微分学知识点
- 格式:doc
- 大小:37.00 KB
- 文档页数:2

第二章讲义2007:36分2008:21分2009:32分2010:42分2011:29分一、导数的概念1、导数的概念左右导数的概念2、可导与连续的关系二、导数的计算导函数导函数基本结果求导法则复合函数的导数隐函数的导数对数求导法参数方程表示的函数的导数高阶导数三、导数的几何意义四、导数的应用1、中值定理1-1中值定理1-2中值定理推论2、单调性、极值与最值2-1单调性及其应用2-2极值2-3最值3、凹凸性、拐点4、洛必达法则5、渐近线一、导数的概念1、导数的概念1.讨论函数()⎪⎩⎪⎨⎧=≠=.0,0,0,1sin 23x x xx x f 在0=x 处的可导性. 2.设函数()x f 可导,且()()011lim12x f f x x→--=-,则()1f '=( ) A .2 B .1- C .1 D .2-3.设()x f 在1=x 处可导,且()11='f ,则()()=+--→hh f h f h 121lim 0( ) A .1- B .2- C .3- D .4- 4.设函数()f x 在0x =处满足,()()()03f x f x x α=-+,且()lim0x x xα→=,则()0f '=( )A .1-B .1C .3-D .3 5.函数()x f 在点0x x =处可导,且()10-='x f ,则()()=+-→hh x f x f h 23lim000A .32B .32-C .23- D .236.设()1='x f ,则()()=--+→hh x f h x f h 32lim 0( ) A .4 B .5 C .2 D .17.设()x f 为奇函数,则()30='x f 时,()=-'0x f ________.左右导数的概念2、可导与连续的关系1.函数在某点处连续是其在该点处可导的A .必要条件B .充分条件C .充要条件D .无关条件二、导数的计算导函数导函数基本结果 求导法则复合函数的导数1.设函数5sin 212π--=x y ,则='yA .5cos 212π--x x B .21xx--C .212x x - D . 5cos 52122π---x x2.已知lnsin(12)y x =-,求.dy dx隐函数的导数1.设由方程22e xy e y =- 确定的函数为()x y y =,求.|0=x dx dy2.设 ()y f x =是由方程ln sin 2xy e y y x +=确定的隐函数,求dy dx. 3.由1=++xy y x ①所确定的隐函数()x y y =在1=x 处导数为________. 对数求导法1.已知y x =,求.dx dy2.若函数()()()ln 1xf x x x =>,则()f x '=( ) A . ()1ln x x - B .()()1ln ln ln(ln )x xx x x -+C .()ln ln(ln )xx x D .()ln xx x参数方程表示的函数的导数1.曲线231,21,x t y t t =+⎧⎨=-+⎩则1|t dydx ==________.1. x y sin =的三阶导数是( )A .x sinB .x sin -C .x cosD .x cos -2.设函数()x f 具有四阶导数,且()f x ''=()()4f x =( )A .B C .1 D .3214x --3.设函数()()()()()4321--++=x x x x x f ,则()()=x f 4________. 4.已知()21x f x e -=,则()()20070f =_______.5.若()()x f x f =-,在区间()+∞,0内,()()0,0>''>'x f x f ,则()x f 在 区间()0,∞-内A .()()0,0<''<'x f x fB .()()0,0>''>'x f x fC .()()0,0<''>'x f x fD .()()0,0>''<'x f x f6.设参数方程⎩⎨⎧-=+=.13,122t y t x 所确定的函数为()x y y =,则=22dx yd _______. 7.设函数()y y x =由参数方程33cos ,sin x t y t ⎧=⎨=⎩确定,则224|t d ydx π==( )A .2-B .1-C .D 三、导数的几何意义1.函数31xy x=+在(2,2)点处的切线方程为________. 2.曲线x x y ln =平行于直线01=+-y x 的切线方程是 A .1-=x y B .()1+-=x y C .1+-=x y D .()()11ln -+=x x y 3.曲线x y ln =上点)0,1(处的切线方程为________.4.曲线22y x x =+-在点M 处的切线平行于直线51y x =-,则点M 的坐标为5.过曲线arctan x y x e =+上的点()0,1处的法线方程为( ) A .210x y -+= B .220x y -+= C .210x y --= D .220x y +-=6.曲线sin 2,cos ,x t y t =⎧⎨=⎩在4t π=对应点处的切线方程为( )A .2x =B .1y =C .1y x =+D .1y x =- 四、导数的应用 1、中值定理1-1中值定理1.下列函数中,在区间[]1,1-上满足罗尔定理条件的是( )A . x y e =B .ln ||y x =C .21y x =-D .21y x =2.函数()22f x x x =--在区间[]0,2上使用拉格朗日中值定理时,结论中的ξ= _______.3.判断:()f x 在[],a b 上连续,在(),a b 内可导,且()()f a f b ≠,一定不存在(),a b ξ∈,使得()0.f ξ'=( )4.设()x f 在[],a b 上连续,且不是常数函数,若()()f a f b =,则在(),a b 内( ) A .必有最大值或最小值 B .既有最大值又有最小值C .既有极大值又有极小值D .至少存在一点ξ,使得()0.f ξ'= 5.设()f x '在[],a b 上连续,存在,m M 两个常数,且满足12a x x b ≤<≤,证明: ()()()()212121m x x f x f x M x x -≤-≤-.6.设函数()x f 在闭区间 [ 0 , 1 ] 上连续,在开区间 ( 0 , 1 )内可导,且()().21,00==f f 证明:在 ( 0 , 1 ) 内至少存在一点x ,使得().12+='ξξf1-2中值定理推论1.设[]1,1-∈x ,则=+x x arccos arcsin ( ) A .2π B .4πC .0D .1 2.已知()x xd e f x e dx -⎡⎤=⎣⎦,且()00f =,则()f x =( ) A .2x x e e + B .2x x e e - C .2x x e e -+ D .2x x e e --2、单调性、极值与最值2-1单调性及其应用1.函数()f x x =_______. 2.方程01sin =-+x x 在区间()1,0内根的个数是( ) A .0 B .1 C .2 D .32-2极值1.若函数()2f x ax bx =+在1x =处取得极值2,则a =_______,b =_______.2.下列说法正确的是( )A . 函数的极值点一定是函数的驻点B .函数的驻点一定是函数的极值点C .二阶导数非零的驻点一定是极值点D .以上说法都不对3.若函数()x f 在区间()b a ,内连续,在点0x x =处不可导,()b a x ,0∈ ,则 A .0x 是()x f 的极大值点 B .0x 是()x f 的极小值点 C .0x 不是()x f 的极值点 D .0x 可能是()x f 的极值点 4. 若()()0,000>''='x f x f ,则下述表述正确的是( )A .0x 是()x f 的极大值点B .0x 是()x f 的极小值点C .0x 不是()x f 的极值点D .无法确定0x 是否为()x f 的极值点 2-3最值1.靠一堵充分长的墙边,增加三面墙围成一矩形场地,在限定场地面积为642m 的条件下,问增加的三面墙各长多少时,其总长最小2.要做一个容积为V 的圆柱形带盖容器,问它的高与底面半径的比值是多少时 用料最省?3.求点()1,0P 到抛物线2x y =上点的距离的平方的最小值.3、凹凸性、拐点1.设()x f 在区间()b a ,内有()()0,0<''>'x f x f ,则()x f 在区间()b a ,内( ) A .单调减少且凹的 B .单调增加且凸的 C .单调减少且凸的 D .单调增加且凹的2.曲线31x y +=的拐点为( )A .()1,0B .()0,1C .()0,0D .()1,1 3.曲线352y x x =+-的拐点是( )A . 0x =B .()0,2-C .无拐点D .0,2x y ==-4.函数sin y x x =-在区间()0,2π内单调________,其曲线在区间0,2π⎛⎫⎪⎝⎭内的凸凹性为________的.5.曲线42246y x x x =-+的凸区间为( )A .()2,2-B .(),0-∞C .()0,+∞D .(),-∞+∞ 6.曲线x xe y -= 的拐点为A .1=xB .2=xC . ⎪⎭⎫⎝⎛22,2e D .⎪⎭⎫⎝⎛e 1,11,4、洛必达法则1.312cos limsin()3x x x ππ→-=-A .1B .0 CD.2.求011lim .1x x x e →⎛⎫- ⎪-⎝⎭3.计算sin 0lim x x x +→4.sin lim sin x x x x x →∞+-(洛必达法则)1cos sin limlim 11cos sin x x x xx x→∞→∞+-===--.()5、渐近线1.曲线2232xx y -=的水平渐近线为( ) A .32=y B .32-=y C .31=y D .31-=y 2.曲线1|1|y x =-( ) A .只有水平渐进线;B .既有水平渐进线,又有垂直渐近线;C .只有垂直渐近线;D .既无水平渐进线,又无垂直渐近线.3.曲线xe y x=( )A .仅有水平渐进线B .既有水平渐进线,又有垂直渐近线C .仅有垂直渐近线D .既无水平渐进线,又无垂直渐近线4.曲线35arctan 2+=xxy A .仅有水平渐近线 B .仅有垂直渐近线C .既有水平渐近线,又有垂直渐近线D .既无水平渐近线,又无垂直渐近线5.方程xy 1arcsin = 所表示的曲线( )A .仅有水平渐近线B .仅有垂直渐近线C .既有水平渐近线,又有垂直渐近线D .既无水平渐近线,又无垂直渐近线。


第二章 一元函数的导数和微分微分学是微积分的重要组成部分,它的基本概念是导数与微分,其中导数反映出函数相对于自变量的变化而变化的快慢程度,而微分则指明当自变量有微小变化时,函数值变化的近似值.第一节 导数的概念在科学研究和工程技术中,常常遇到求变量的变化率的问题。
例如,物体作匀速直线运动时,其速度为物体在时刻t 0到t 的位移差s (t )-s (t 0) 与相应的时间差t -t 0的商00()()--s t s t v =t t .如果物体作变速直线运动,则上面的公式就不能用来求物体在某一时刻的瞬时速度了.不过,我们可先求出物体从时刻t 0到t 的平均速度,然后假定t →t 0,求平均速度的极限00()()lim→--t t s t s t t t ,并以此极限作为物体在t 0时刻的瞬时速度.从数学角度来看,00()()--f x f x x x 叫做函数y =f (x )在x 0与x 的差商,而把x →x 0时,该差商的极限值(如果存在的话)叫做函数f (x )在x 0处的导数.一般说来,工程技术中一个变量相对于另一个变量的变化率问题,可以化成求导数的问题进行处理.一、导数的定义定义 设函数y =f (x )在U (x 0)内有定义.如果极限00()()lim→--x x f x f x x x存在,则称该极限值为f (x )在点x 0处的导数,记为000()()()lim→-'=-x x f x f x f x x x , (2-3-1)此时也称函数f (x )在点x 0可导.函数f (x )在点x 0处的导数还可记为0d d =y x x x ;0d ()d =f x x x x ;0'=y x x .导数f ′(x 0)可以表示为下面的增量形式00000()()()limlim ∆→∆→+∆-∆'==∆∆x x f x x f x yf x x x. (2-3-2)如果(2-3-1)式和式(2-3-2)中右边的极限不存在,则称f (x )在点x 0不可导.当00()()lim→--x x f x f x x x = ∞时,我们通常说函数y = f (x )在点x 0处的导数为无穷大.如果函数y =f (x )在开区间(a ,b )内的每一点处都可导,则称f (x )在此开区间(a ,b )内可导.这时,∀x ∈(a ,b ),对应着f (x )的一个确定的导数值,这是一个新的函数关系,称该函数为原来函数f (x )的导函数,记为f ′(x ),y ′,d ()d f x x ,d d yx等,此时 0()()()lim ∆→+∆-'=∆x f x x f x f x x, x ∈(a ,b ).显然,f (x )在点x 0∈(a ,b )的导数f ′(x 0)就是导函数f ′(x )在点x =x 0处的函数值:00()()''==f x f x x x .为方便起见,我们简称函数的导函数为导数.由函数y =f (x )在点x 0处的导数f ′(x 0)的定义可知,它是一种极限:000()()()lim→-'=-x x f x f x f x x x ,而极限存在的充要条件是左、右极限都存在且相等.因此f ′(x 0)存在(即f (x )在点x 0可导)的充要条件应是下面的左、右极限00()()lim -→--x x f x f x x x ,000()()lim +→--x x f x f x x x 都存在且相等.我们将这两个极限分别称为函数f (x )在x 0处的左导数和右导数,记为f ′-(x 0)和f ′+(x 0),即000()()()lim --→-'=-x x f x f x f x x x ,000()()()lim ++→-'=-x x f x f x f x x x或写成增量形式:0000()()()lim --∆→+∆-'=∆x f x x f x f x x,0000()()()lim ++∆→+∆-'=∆x f x x f x f x x.定理1 函数y =f (x )在点x 0可导的充要条件是f ′-(x 0)及f ′+(x 0)存在且相等.该定理实际上是第一章第四节中定理2的推论. 例1 函数f (x )=|x |在点x =0处是否可导? 解 因为(0)(0)sgn()∆-+∆-==∆∆∆x f x f x x x,所以0(0)lim sgn()1++∆→'=∆=x f x ,0(0)lim sgn()1--∆→'=∆=-x f x ,由于f ′+(0)≠f ′-(0),因此f (x )=|x |在x =0处不可导.例2 研究函数,0,()ln(1),0<⎧=⎨+≥⎩x x f x x x 在点x =0处的可导性.解 易知f (x )在点x =0处连续,而0()(0)(0)lim ++→-'=x f x f f x0ln(1)0lim +→+-=x x x1lim ln(1)1+→=+=xx x , 00()(0)0(0)lim lim 1---→→--'===x x f x f x f x x, 由于f ′+(0)=f ′-(0)=1,故f (x )在点x =0处可导,且f ′(0)=1.例3 求函数f (x )=C ,x ∈(-∞,+∞)的导数,其中C 为常数.解 00()()()limlim 0∆→∆→+∆--'===∆∆x x f x x f x C Cf x x x, 即(C )′=0.通常说成:常数的导数等于零.例4 设y =x n ,n 为正整数,求y ′.解 0()lim ∆→+∆-'∆n nx x x x y =x12210lim(C ()())---∆→+∆++∆ n n n n x =nxxx x 1-=n nx ,即 (x n )′=nx n -1.特别地,n =1时,有(x )′=1. 例5 设y =sin x ,求y ′.解 0sin()sin limx x x xy x∆→+∆-'=∆022cos sin22limx x x x x∆→+∆=∆ 022cos 22lim cos x x x x x x∆→∆+∆⋅==∆即 (sin x )′=cos x .例6 设y =cos x ,x ∈(-∞,+∞),求y ′.解 0cos()cos limx x x xy x∆→+∆-'=∆02sin()sin 22limx x x x x∆→∆∆-+=∆ 02sin()22limsin x x x x x x∆→∆∆-⋅+==-∆, 即 (cos x )′=-sin x .例7 设y =a x ,x ∈(-∞,+∞),a >0,求y ′. 解 注意到u →0时,e u -1~u ,从而00(1)lim lim x x x x x x x a a a a y x x+∆∆∆→∆→--'==∆∆ln 00e 1ln limlim ln x a xx x x x x aa a a a x x∆∆→∆→-∆===∆∆, 即(a x )′=a x ln a (a >0).特别地 (e x )′=e x . 例8 设y =log a x ,x ∈(0,+∞),a >0且a ≠1,求y ′.解 00log (1)log ()log limlima a a x x xx x xx y xx∆→∆→∆++∆-'==∆∆00111lim log (1)lim log e =ln x x a a x x x x x x x a∆∆→∆→∆=+=,即 (log a x )′=1ln x a. 特别地 1(ln )x x'=.例9 设y =x 3,求y ′|x =2.解 因为 y ′=(x 3)′=3x 3-1=3x 2, 所以 y ′|x =2 =3x 2|x =2 =3×22=12.下面我们讨论可导与连续的关系.定理2 若y =f (x )在点x 0可导,则f (x )在点x 0必连续. 证 因为f (x )在点x 0可导,即000()()lim()x x f x f x f x x x →-'=-存在.由无穷小量与函数极限的关系得000()()()f x f x f x x x α-'=+-,其中α→0(x →x 0),于是0000()()()()()f x f x f x x x x x α'-=-+-故 [][]00000lim ()()lim ()()()0x x x x f x f x f x x x x x α→→'-=-+-=.即f (x )在点x 0连续.例10 研究函数1sin ,0,()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩ 在点x =0处的连续性和可导性.解 因为1lim ()lim sin0(0)x x f x x f x→→===, 所以f (x )在点x =0处连续,但是0001sin 0()(0)1lim lim limsin 0x x x x f x f x x x x→→→--==- 不存在,故f (x )在点x =0处不可导.此例说明“连续不一定可导”,连续只是可导的必要条件. 二、导数的几何意义连续函数y =f (x )的图形在直角坐标系中表示一条曲线,如图2-1所示.设曲线y =f (x )上某一点A 的坐标是(x 0,y 0),当自变量由x 0变到x 0+Δx 时,点A 沿曲线移动到点B (x 0+Δx ,y 0+Δy ),直线AB 是曲线y =f (x )的割线,它的倾角记作β.从图形可知,在直角三角形AB C 中,tan CB y AC x β∆==∆,所以yx∆∆的几何意义是表示割线AB 的斜率.图2-1当Δx →0时,B 点沿着曲线趋向于A 点,这时割线AB 将绕着A 点转动,它的极限位置为直线AT ,这条直线AT 就是曲线在A 点的切线,它的倾角记作α.当Δx →0时,既然割线趋近于切线,所以割线的斜率yx∆∆=tan β必然趋近于切线的斜率tan α,即 00()lim tan x yf x xα∆→∆'==∆.由此可知,函数y =f (x )在x 0处的导数f ′(x 0)的几何意义就是曲线y =f (x )在对应点A (x 0,y 0)处的切线的斜率.曲线y =f (x )在点A (x 0,y 0)的切线方程可写成:(1) f ′(x 0)存在,切线方程为y -f (x 0)= f ′(x 0)(x -x 0);(2) f (x )在点x 0处连续,f ′(x 0)=∞,则切线方程为x =x 0.例11 求过点(2,0)且与曲线y =1x 相切的直线方程. 解 显然点(2,0)不在曲线y =1x上.由导数的几何意义可知,若设切点为(x 0,y 0),则y 0=1x ,且所求切线的斜率k 为 02011()x x k xx ='==-, 故所求切线方程为020011(2)y x x x -=--. 又切线过点(2,0),所以有020011(2)x x x -=--. 于是得x 0=1,y 0=1,从而所求切线方程为y -1= -(x -1),即y =2-x .例12 在曲线32y x =上求一点,使该点处的曲线的切线与直线y =3x -1平行. 解 在32y x =上的任一点M (x ,y )处切线的斜率k 为32()k y x ''===而已知直线y =3x -1的斜率k 1=3.令k =k 13=,解之得x =4,代入曲线方程得 3248y ==.故所求点为(4,8).三、函数四则运算的求导法定理3设函数u =u (x ),v =v (x )在点x 处可导,k 1,k 2为常数,则下列各等式成立: (1) [k 1u (x )+k 2v (x )]′=k 1u ′(x )+k 2v ′(x ); (2) [(u (x )v (x )]′=u ′(x )v (x )+u (x )v ′(x );(3) 2()()()()()()()u x u x v x u x v x v x v x '''⎡⎤-=⎢⎥⎣⎦[v (x )≠0]. 证 仅以(3)为例进行证明.记g (x )=()()u x v x ,且v (x )≠0,则01()()()lim()()x u x x u x g x x v x x v x ∆→⎡⎤+∆'=-⎢⎥∆+∆⎣⎦ 01()()()()lim()()()()x u x x u x v x x v x v x u x v x v x x x x ∆→+∆-+∆-⎡⎤=-⎢⎥+∆∆∆⎣⎦ 0001()()()()lim()lim ()lim ()()x x x u x x u x v x x v x v x u x v x v x x x x ∆→∆→∆→+∆-+∆-⎡⎤=-⎢⎥+∆∆∆⎣⎦ 2()()()()()u x v x u x v x v x ''-=.定理中的(1)式和(2)式均可推广至有限多个函数的情形.读者不难自行完成. 例13 设52434y x x =-+,求y ′.解 52(434)y x x ''=-+52(4)(3)(4)x x '''=-+4206x x =-.例14 设y =x 3cos x sin x ,求y ′.解 3(c o s s i n )y x x x''= 333()cos sin (cos )sin cos (sin )x x x x x x x x x '''=++232323cos sin sin cos x x x x x x x =-+.例15 设y =tan x ,求y ′.解 sin (tan )()cos xy x x'''== 2(sin )cos sin (cos )cos x x x x x''-=2222cos sin 1cos cos x x x x+==,即 (tan x )′=21cos x=sec 2x =1+tan 2x . 类似可得2221(cot )csc (1cot )sin x x x x'=-=-=-+. 例16 设y =sec x ,求y ′.解 在定理3的(3)中,取u (x )≡1,则有21()()()v x v x v x ''⎛⎫=- ⎪⎝⎭. 于是y ′=(sec x )′=21(cos )cos cos x x x ''⎛⎫=- ⎪⎝⎭2sin sec tan cos xx x x==,即 (sec x )′=sec x tan x .类似可得 (csc x )′=-csc x cot x .第二节 求导法则一、复合函数求导法定理1(链导法) 若u =φ(x )在点x 处可导,而y =f (u )在相应点u =φ(x )处可导,则复合函数y =f (φ(x ))在点x 处可导,且d d d d d d y y u x u x=⋅,或记为 [f (φ(x ))]′=f ′(φ(x ))·φ′(x ). (2-2-1)证 因为y =f (u )在u 的导数0()limu yf u x∆→∆'=∆存在,所以()yf u xα∆'=+∆,其中α→0(Δu →0), 故 ()y f u x x α'∆=∆+∆,从而 00limlim ()x x y u u f u x x x α∆→∆→∆∆∆⎛⎫'=+ ⎪∆∆∆⎝⎭000()limlim lim x x x u uf u x xα∆→∆→∆→∆∆'=+∆∆.又u =φ(x )在点x 处可导,故φ(x )必在点x 处连续,因此Δx →0时必有Δu →0.于是000lim()()lim lim x u x y uf u x x xϕα∆→∆→∆→∆∆''=+∆∆()()(())()f u x f x x ϕϕϕ''''==,而[]0lim(())x yf x xϕ∆→∆'=∆,定理证毕.例1 设f (x )=x μ,μ ∈R ,x >0,求f ′(x ). 解 由于x μ=e μln x ,x >0.令u =μln x ,则x μ系由y =e u 及u =μln x 复合而成.d(e )d(ln )()d d u x f x u xμ'=⋅ln 11e e u x x x xμμμμμ-===, 即 (x μ)′=μx μ-1,μ∈R ,x >0.例2 设y =e -x ,求y ′.解 令u = -x ,则y =e u ,从而d d d d(e )d()d d d d d u y y u x x u x u x-=⋅=⋅ e (1)e u x -=-=-.即 (e -x )′= -e -x .对复合函数的分解熟练后,就不必再写出中间变量,而可按下列各题的方式进行计算.例3 设1sin1y x=+,求y ′. 解 21111cos()cos 11(1)1y x x x x''==++++. 例4设y =y ′.解2)x y '''==22(e )x x '=222e ()x x x '=⋅22e 2x x x =⋅22x x=.例5设ln(y x =,求y ′. 解ln(y x x '⎡⎤''==+⎣⎦21⎡⎤'==⎢⎢⎣=.二、反函数求导法定理2 设函数y =f (x )与x =φ(y )互为反函数,f (x )在点x 可导,φ(y )在相应点y 处可导,且d ()0d xy yϕ'=≠,则 d 1d d d x y yx=,或1()()f x y ϕ'='. 简单地说成:反函数的导数是其直接函数导数的倒数.证 由x =φ(y )=φ(f (x ))及y =f (x ),x =φ(y )的可导性,利用复合函数的求导法,得1=φ′(f (x ))f ′(x )=φ′(y )f ′(x ),故 1(),()0()f x y y ϕϕ''=≠'. 例6 设y =arcsin x ,求y ′. 解 由定理2及x =sin y 可知11(sin )cos y y y y '====' 这里记号(sin )y y '表示求导是对变量y 进行的.由上式得(arcsin )x '=.同理可得:(arccos )x '=,21(arctan )1x x '=+,21(arccot )1x x-'=+. 三、参数方程求导法若方程x =φ(t )和y =ψ(t )确定y 与x 间的函数关系,则称此函数关系所表达的函数为由参数方程(),(),x t y t ϕψ=⎧⎨=⎩t ∈(α,β) (2-2-2) 所确定的函数.下面我们来讨论由参数方程所确定的函数的导数.设t =φ-1(x )为x =φ(t )的反函数,在t ∈(α,β)中,函数x =φ(t ),y =ψ(t )均可导,这时由复合函数的导数和反函数的导数公式,有111d (())(())(())d y x x x x ψϕψϕϕ---'''⎡⎤==⎣⎦ 11()(())()()t x t t ψψϕϕϕ-''=='' (φ′(t )≠0). 于是由参数方程(2-2-2)所确定的函数y =y (x )的导数为d d ()d d d ()d yy t t x x t tψϕ'=='(φ′(t )≠0). (2-2-3) 例7 设33cos ,sin ,x a t y a t ⎧=⎨=⎩求d d yx .解 3232(cos )d 3sin cos tan d (sin )3cos (sin )t t a t y a t tt x a t a t t '===-'-(2n t π≠,n 为整数).例8 设2223,13,1at x t aty t ⎧=⎪⎪+⎨⎪=⎪+⎩ -∞<t <+∞,求d d yx.解 222222223()d 6(1)6213d 3(1)61()1t taty at t at tt at x a t at t t '+-+===+--'+ (t ≠±1).例9 求极坐标方程r =e a θ(0<θ<π/4,a >1)所确定的函数y =y (x )的导数.解 由极坐标与直角坐标的关系,得cos e cos ,sin e sin ,a a x r y r θθθθθθ⎧==⎨==⎩故 (e cos )d e sin +e cos sin cos d (e sin )e cos e sin cos sin a a a a a a y a a x a a θθθθθθθθθθθθθθθθθθ'+==='--.例10 求椭圆cos ,sin x a t y bt =⎧⎨=⎩在t =π/4处的切线方程和法线方程.解 d (sin )cot d (cos )yb t bt x a t a '==-',所以在椭圆上对应于t =π/4的点处的切线和法线的斜率为4d cot d 4t=ybbk x a a ππ==-=-切,a kb =法.切线方程和法线方程分别为bx +ay =和ax -by =a 2-b 2).四、隐函数求导法如果在含变量x 和y 的关系式F (x ,y )= 0中,当x 取某区间I 内的任一值时,相应地总有满足该方程的惟一的y 值与之对应,那么就说方程F (x ,y )=0在该区间内确定了一个隐函数y =y (x ).这时y (x )不一定都能用关于x 的表达式表示.例如方程e y +xy -e -x =0和y =cos(x +y )都能确定隐函数y =y (x ).如果F (x ,y )=0确定的隐函数y =y (x )能用关于x 的表达式表示,则称该隐函数可显化.例如x 3+y 5-1=0,解出y =,就把隐函数化成了显函数.若方程F (x ,y )=0确定了隐函数y =y (x ),则将它代入方程中,得F (x ,y (x ))≡0.对上式两边关于x 求导(若可导),并注意运用复合函数求导法则,就可以求出y ′(x )来. 例11 求方程y =cos(x +y )所确定的隐函数y =y (x )的导数.解 将方程两边关于x 求导,注意y 是x 的函数,得y ′= -sin(x +y )(1+y ′),即 sin()1sin()x y y x y -+'=++ , 1+sin(x +y )≠0. 例12 求由方程e y +xy -e -x = 0所确定的隐函数y = y (x )的导数.解 将方程两边关于x 求导,得e y y ′+y +xy ′+e -x =0,故 e exy y y x -+'=-+ (x +e y ≠0). 在计算幂指函数的导数以及某些乘幂、连乘积、带根号函数的导数时,可以采用先取对数再求导的方法,简称对数求导法.它的运算过程如下:在y =f (x )(f (x )>0)的两边取对数,得ln y =ln f (x ).上式两边对x 求导,注意到y 是x 的函数,得y ′=y (ln f (x ))′.例13 求2242(2)(1)(1)x y x x +=+++的导数. 解 先在两边取对数,得242ln 2ln(2)ln(1)ln(1)y x x x =+-+-+.上式两边对x 求导,注意到y 是x 的函数,得3242442211y x x x y x x x '=--+++, 于是 3242442211x x x y y x x x ⎛⎫'=-- ⎪+++⎝⎭,即22342242(2)442(1)(1)211x x x x y x x x x x ⎛⎫+'=-- ⎪+++++⎝⎭.例14 设()()v x y u x =,u (x )>0,其中u (x ),v (x )均可导,求y ′.解 两边取对数得ln y =v (x )ln u (x ),两边对x 求导,得()()ln ()()()y u x v x u x v x y u x '''=+, 于是 ()()()()()ln ()()v x v x u x y u x v x u x u x '⎛⎫''=+ ⎪⎝⎭. 特别地,当()()u x v x x ==时,()(1ln )x x x x x '=+.例15 求y =x sin x (x >0)的导数.解 两边取对数得ln y =sin x ln x .两边对x 求导,得sin cos ln y x x x y x'=+. 于是 sin sin cos ln x x y x x x x ⎛⎫'=+ ⎪⎝⎭. 第三节 函数的微分一、微分的概念定义1 设函数y =f (x )在U (x 0)内有定义,若∃A ∈R ,使Δy =A Δx +o (Δx ) (2-3-1)成立,则称函数y =f (x )在点x 0处可微分(简称可微),线性部分A Δx 称为f (x )在x 0处的微分,记为d y =A Δx (其中Δx =x -x 0),A 称为微分系数.定义中的式(2-3-1)可写为0000000()()()()()lim lim 0x x x x f x f x A x x f x f x A x x x x →→⎛⎫----=-= ⎪--⎝⎭, (2-3-2) 即式(2-3-1)成立的充要条件为 000()()limx x f x f x A x x →-=-. 于是便有下面的定理.定理1 函数y =f (x )在点x 0可微的充要条件是函数y =f (x )在点x 0可导.当f (x )在点x 0处可微时,必有d y =f ′(x 0)Δx . 该定理说明函数的可微性与可导性是等价的.函数y =f (x )在任意点x 的微分,称为函数的微分,记为d y =f ′(x )Δx . (2-3-3)例1 设y =x ,求d y .解 因为y ′=(x )′=1,所以d y =1×Δx =Δx .为方便起见,我们规定:自变量的增量称为自变量的微分,记为d x =Δx .于是式(2-3-3)可记为d y =f ′(x )d x . (2-3-4)例2 求y =sin x 当x =π/4,d x =0.1时的微分.解 d y =(sin x )′d x =cos x d x .当x =π/4,d x =0.1时,有d cos 0.10.07074y π=⨯=≈. 在几何上,y =f (x )在x 0处的微分d y =f ′(x 0)d x 表示曲线y =f (x )在点M (x 0,f (x 0))处切线MT 的纵坐标相应于Δx 的改变量PQ (见图2-2),因此d y =Δx tan α.图2-2二、微分的运算公式1.函数四则运算的微分设u =u (x ),v =v (x )在点x 处均可微,则有d(Cu )=C d u (C 为常数),d(u +v )=d u +d v ,d(uv )=u d v +v d u ,2d()=,0u vdu udv v v v -≠. 这些公式由微分的定义及相应的求导公式立即可证得.2.复合函数的微分若y =f (u )及u =φ(x )均可导,则复合函数y =f (φ(x ))对x 的微分为d y =f ′(u )φ′(x )d x . (2-3-5)注意到d u =φ′(x )d x ,则函数y =f (u )对u 的微分为d y =f ′(u )d u . (2-3-6)将(2-3-6)式与(2-3-4)式比较可知,无论u 是自变量还是另一个变量的可微函数,微分形式d y =f ′(u )d u 保持不变.此性质称为一阶微分的形式不变性.由此性质,我们可以把导数记号d d y x ,d d y u等理解为两个变量的微分之商了,因此,导数有时也称微商.用微商来理解复合函数的导数以及求复合函数的导数就方便多了.例3 设y =d y .解 记u =a 2+x 2,则yd du y y u u '==.又 d u =u ′x d x =2x d x ,故d 2d y x x x ==.为了读者使用的方便,我们将一些基本初等函数的导数和微分对应列表如下.表2-1第四节 高阶导数与高阶微分一、高阶导数若函数y =f (x )在U (x )内可导,其导函数为f ′(x ),且极限0()()lim x f x x f x x∆→''+∆-∆ 存在,则称该极限值为函数f (x )在点x 处的二阶导数,记为f ″(x ), 22d d y x,y ″等. 函数y =f (x )的二阶导数f ″(x )仍是x 的函数,如果它可导,则f ″(x )的导数称为原函数f (x )的三阶导数,记为()f x ''',33d d y x,y '''等. 一般说来,函数y =f (x )的n -1阶导数仍是x 的函数,如果它可导,则它的导数称为原来函数f (x )的n 阶导数,记为()()n f x ,d d n n y x,()n y 等.通常四阶和四阶以上的导数都采用这套记号,而不用“′”.一阶、二阶和三阶导数则采用“′”的记号.由以上叙述可知,求一个函数的高阶导数,原则上是没有什么困难的,只需运用求一阶导数的法则按下列公式计算()(1)()n n y y -'= (n =1,2,…)或写成11d d d d d d n n-n n y y x x x -⎛⎫= ⎪⎝⎭,()(1)()(())n n f x f x -'=. 如果函数y =f (x )在区间I 上有直到n 阶的连续的导数,我们使用记号f (x )∈C n (I )来表示. 例1 设y =x n ,n 为正整数,求它的各阶导数.解 1()n n y x nx -''==,12()(1)n n y nx n n x --'''==-,……()(1)(1)k n k y n n n k x -=--+ ,……()(1)321!n y n n n =⨯-⨯⨯⨯⨯= ,(1)()()(!)0n n y y n +''===.显然,y =x n 的n +1阶以上的各阶导数均为0.例2 设y =sin x ,求它的n 阶导数()n y .解 cos sin()2y x x π'==+,()cos()sin(2)22y y x x ππ''''==+=+⨯,设 ()sin()2k y x k π=+⋅,则 (1)()()cos()sin (1)22k k y y x k x k +ππ⎡⎤'==+=++⎢⎥⎣⎦.由数学归纳法,知()(sin )sin()2n nx x =+π,n =1,2,….由此式我们可得到y =cos x 的高阶导数公式:()(1)1(cos )(sin )sin()cos()22n n n nx x x x --=-=-+π=+π,即 ()(cos )cos()2n nx x =+π,n =1,2,….例3 设y =ln(1+x ),求()n y .解 11y x '=+,211()()1(1)y y x x '''''===-++,2312()(1)(1)y y x x '⎡⎤''''''==-=⎢⎥++⎣⎦,运用数学归纳法可知()1(1)!(1)(1)n n n n y x --=-+,n =1,2,3,….例4 设y =a x (a >0),求()n y .解 ()ln x x y a a a ''==,2(ln )ln x x y a a a a '''==.设 ()ln k x k y a a =,则 ()(1)1ln ln k x k x k+y a a a a +'==.故 ()()ln x n x n a a a =, n =1,2,….特别地,有 ()(e )e x n x =, n =1,2,….对于高阶导数,有下面的运算法则:设函数u =u (x )和v =v (x )在点x 处都具有直到n 阶的导数, 则u (x )±v (x ),u (x )v (x )在点x 处也具有n 阶导数,且(u ±v )(n )=u (n )±v (n ), (2-4-1)()()(1)(2)(1)()2!n n n n n n u v u v n u v u v ---'''⋅=⋅+⋅⋅++ ()(1)(1)!n n n n k uv k --++ =()()0C n i n i i ni u v -=⋅⋅∑, (2-4-2) 其中u (0)=u ,v (0)= v ,(1)(1)C !i n n n n i i --+= .(2- 4-2)式称为莱布尼茨(Leibniz)公式,将它与二项展开式对比,就很容易记住. (2-4-1)式由数学归纳法易证.(2-4-2)式证明如下:当n =1时,由(uv )′=u ′v +uv ′知公式成立.设当n =k 时公式成立,即()()()()(1)(2)()(1)C 2!kk i k i i k k k k k i k k y u v u v ku v u v uv ---=-'''=⋅⋅=++++∑ .两边求导,得(1)(1)()()(1)k k k k k y u v u v k u v u v ++-''''⎡⎤⎡⎤=+++⎣⎦⎣⎦(1)(2)()(1)(1)2!k k k k k k u v u v u v uv --++''''''⎡⎤⎡⎤+++++⎣⎦⎣⎦1(1)()10C k i k i i k i u v ++-+==⋅⋅∑,即n =k +1时公式(2-4-2)也成立,从而(2-4-2)成立.例5 设y =x 2·e 2x ,求y (20).解 设u =e 2x ,v =x 2,则u (i )=2i ·e 2x (i =1,2,…,20),v ′=2x ,v ″=2,v (i )=0 (i =3,4,…,20).代入莱布尼茨公式,得y (20)=(x 2·e 2x )(20)202219218220192e 202e 22e 22!x x x x x ⋅=⋅⋅+⋅⋅⋅+⋅⋅⋅20222e (2095)x x x =⋅⋅++.例6 设e x +y -xy =1,求y ″(0).解 方程两边对x 求导,得(1+y ′)e x +y -y -xy ′=0.上式两边再对x 求导,得(1+y ′)2e x +y +y ″e x +y -2y ′-xy ″=0.令x =0,可得y =0,y ′(0)= -1,将这些值代入上式得y ″(0)= -2.例7已知cos,sin,x a ty b t=⎧⎨=⎩求22ddyx.解d(sin)coscot d(cos)siny b t b t bt x a t a t a'==-=-'.注意dcotdy btx a=-,x=a cos t仍是参数方程,所以仍须用参数方程求导法则,从而22d d cot()d d ddd(cos)dby ty at xxx a tt'⎛⎫- ⎪⎝⎭=='2321csc cscsinb bt ta a t a=⋅⋅=-⋅-.*二、高阶微分对于函数y=f(x),类似于高阶导数可以定义高阶微分.设f(x)有直至n阶的导数,自变量的增量仍为d x,则二阶微分定义为d2y=d(d y)=d(f′(x)d x)=d(f′(x))d x=f″(x)d x·d x=f″(x)d x2;三阶微分定义为d3y=d(d2y)=d(f″(x)d x2)=d(f″(x))d x2=f'''(x)d x d x2=f'''(x)d x3;一般地,定义n阶微分为d n y=d(d n-1y)=f(n)(x)d x n. (2-4-3) 以上公式中的x都是自变量,d x n表示n个d x的乘积(n=2,3,4,…).对于复合函数来说,二阶及二阶以上的微分已不再具有公式(2-4-3)的形式了.例如,设y=f(u),u=φ(x),且都具有相应的可微性,则d y=f′(u)d u,而d2y=d(f′(u)d u)=d(f′(u))d u+f′(u)d(d u)=f″(u)d u2+f′(u)d2u. (2-4-4)这是因为d u不再是固定的了,它依赖于自变量x,即d u=φ′(x)d x.(2-4-4)式说明高阶微分已不再具有形式不变性了.这是高阶微分与一阶微分的重要区别之一.例8 设y=x sin x,求d2y.解d y=(x sin x)′d x=(sin x+x cos x)d x;d2y=d(d y)=(sin x+x cos x)′d x2=(cos x+cos x-x sin x)d x2=(2cos x-x sin x)d x2.例9设u=u(x),v=v(x)均有二阶导数,y=u(x)v(x),求d2y.解d y=y′d x=[u(x)v(x)]′d x=[u′(x)v(x)+u(x)v′(x)]d xd 2y =d(d y )=d [(u ′(x )v (x )+u (x )v ′(x ))d x ]=[u ′(x )v (x )+u (x )v ′(x )]′d x 2=[u ″(x )v (x )+2u ′(x )v ′(x )+ u (x )v ″(x )]d x 2.第五节 微分中值定理本节介绍微分学中有重要应用的反映导数更深刻性质的微分中值定理.定理1 [罗尔(Ro lle)定理] 若f (x )∈C ([a ,b ]),f (x )在(a ,b )内可导,且f (a )=f (b ),则∃ξ∈(a ,b )使得f ′(ξ)=0.证 由f (x )∈C ([a ,b ])知f (x )在[a ,b ]上必取得最大值M 与最小值m .若M >m ,则M 与m 中至少有一个不等于f (x )在区间端点的值.不妨设M ≠f (a ).由最值定理,∃ξ∈(a ,b ),使f (ξ)=M .又0()()()lim 0x f x f f xξξξ++∆→+∆-'=≤∆,0()()()lim 0x f x f f x ξξξ--∆→+∆-'=≥∆, 故 f ′(ξ)=0.若M =m ,则f (x )在[a ,b ]上为常数,故(a ,b )内任一点都可成为ξ,使f ′(ξ)=0. 罗尔定理的几何意义是:若y =f (x )满足定理的条件,则其图像在[a ,b ]上对应的曲线弧AB 上一定存在一点具有水平切线,如图2-3所示.图2-3定理2[拉格朗日(L ag r ang e)中值定理] 若f (x )∈C ([a ,b ]),f (x )在(a ,b )内可导,则∃ξ∈(a ,b )使得f (b )-f (a )=f ′(ξ)(b -a ). (2-5-1)证 考虑辅助函数Φ(x )=f (x )-λx (其中λ待定),为了使Φ(x )满足定理1的条件,令Φ(a )=Φ(b )得 λ=()()f b f a b a--, 即 Φ(x )=f (x )-()()f b f a b a --x . 于是由定理1,∃ξ∈(a ,b ),使Φ′(ξ)=0,即f (b )-f (a )=f ′(ξ)(b -a ).如图2-4所示,连结曲线弧 AB 两端的弦AB ,其斜率为()()f b f a b a--.因此,定理的几何意义是:满足定理条件的曲线弧 AB 上一定存在一点具有平行于弦AB 的切线.图2-4显然,罗尔定理是拉格朗日中值定理的特殊情形.式(2-5-1)称为拉格朗日中值公式,显然,当b <a 时,式(2-5-1)也成立.设x 和x +Δx 是(a ,b )内的两点,其中Δx 可正可负,于是在以x 及x +Δx 为端点的闭区间上有f (x +Δx )-f (x )=f ′(ξ)Δx ,其中ξ为x 与x +Δx 之间的某值,记ξ = x +θΔx ,0<θ<1,则f (x +Δx )-f (x )=f ′(x +θΔx )Δx (0<θ<1). (2-5-2)(2-5-2) 式称为有限增量公式.推论1 若函数f (x )在区间I 上的导数恒为零,则f (x )在区间I 上为一常数. 证 x 1,x 2∈I ,x 1<x 2,在[x 1,x 2]上应用定理2,得f (x 2)-f (x 1) =f ′(ξ)(x 2-x 1),ξ∈(x 1,x 2).由于f ′(ξ)=0,故f (x 2)=f (x 1).由x 1,x 2的任意性可知,函数f (x )在区间I 上为一常数.在第一节我们知“常数的导数为零”,推论1就是其逆命题.由推论1立即可得以下结论. 推论2 若∀x ∈I ,f ′(x )=g ′(x ),则在I 上f (x )=g (x )+C (C 为常数).例1 求证arcsin x +arccos x =π2,x ∈[-1,1]. 证 令f (x )=arcsin x +arccos x ,则f ′(x )=,x ∈(-1,1).由推论1得f (x )=C ,x ∈(-1,1).又 因f (0)=π2,且f (±1)= π2. 故 f (x )=arcsin x +arccos x =π2,x ∈[-1,1].例2 证明不等式arc tan x 2-arc tan x 1≤x 2-x 1(其中x 1<x 2).证 设f (x )=arc tan x ,在[x 1,x 2]上利用拉格朗日中值定理, 得 arc tan x 2-arc tan x 1=211ξ+(x 2-x 1),x 1<ξ<x 2. 因为211ξ+≤1,所以 arc tan x 2-arc tan x 1≤x 2-x 1.例3 设函数f (x )=x (x -2)(x -4)(x -6),说明方程f ′(x )=0在(-∞,+∞)内有几个实根,并指出它们所属区间.解 因为f ′(x )是三次多项式,所以方程f ′(x )=0在(-∞,+∞)内最多有3个实根.又由于f (0)=f (2)=f (4)=f (6)=0,f (x )在区间[0,2],[2,4],[4,6]上满足罗尔定理的条件.故 ξ1∈(0,2),ξ2∈(2,4),ξ3∈(4,6),使f ′(ξ1)=0,f ′(ξ2)=0,f ′(ξ3)=0.即方程f ′(x )=0在(-∞,+∞)内有3个实根,分别属于区间(0,2),(2,4),(4,6).例4 若f (x )>0在[a ,b ]上连续,在(a ,b )内可导,则∃ξ∈(a ,b ),使得()()ln()()()f b f b a f a f ξξ'=-. 证 原式即()ln ()ln ()()()f f b f a b a f ξξ'-=-. 令φ(x )=ln f (x ),有 φ′(x )=()()f x f x '.显然φ(x )在[a ,b ]上满足拉格朗日中值定理的条件,在[a ,b ]上应用定理可得所证. 下面再考虑由参数方程x =g (t ),y =f (t ),t ∈[a ,b ]给出的曲线段,其两端点分别为A (g (a ),f (a )),B (g (b ),f (b )).连结A ,B 的弦AB 的斜率为()()()()f b f ag b g a -- (见图2-5),而曲线上任何一点处的切线斜率为d ()d ()x f t y g t '='.图2-5若曲线上存在一点C [对应参数t =ξ∈(a ,b )],在该点曲线的切线与弦AB 平行,则可得()()()()()()f b f a fg b g a g ξξ'-='-.定理3[柯西(CaUchy )中值定理] 若f (x ),g (x )∈C ([a ,b ])均在(a ,b )内可导,且g ′(x )≠0,则∃ξ∈(a ,b )使得()()()()()()f b f a fg b g a g ξξ'-='-.证 由g ′(x )≠0和拉格朗日中值定理得g (b )-g (a )=g ′(η)(b -a )≠0, η∈(a ,b ).由此有g (b )≠g (a ),考虑辅助函数Φ(x )=f (x )-λg (x )(λ待定).为使Φ(x )满足罗尔中值定理的条件,令Φ(a )=Φ(b ),得λ=()()()()f b f ag b g a --.取λ的值如上,由罗尔定理知∃ξ∈(a ,b ),使Φ′(ξ)=0,即()()()()0()()f b f a fg g b g a ξξ-''-=-,即()()()()()()f b f a fg b g a g ξξ'-='-. 由此定理得证.显而易见,若取g (x )≡x ,则定理3成为定理2,因此定理3是定理1,2的推广,它是这三个中值定理中最一般的形式.例5 设函数f (x )在[x 1,x 2]上连续,在(a ,b )内可导,且x 1·x 2>0,证明∃ξ∈(x 1,x 2),使112212()()()()x f x x f x f f x x ξξξ-'=--.证 原式可写成122121()()()()11f x f x x x f f x x ξξξ-'=--. 令φ(x )=()f x x ,ψ(x )=1x.它们在[x 1,x 2]上满足柯西中值定理的条件,且有 ()()x x ϕψ''=f (x )-xf ′(x ). 应用柯西中值定理即得所证.第六节 泰勒公式在本章前面已知道,如果f (x )在点x 0处可微,则f (x )=f (x 0)+f ′(x 0)(x -x 0)+o (x -x 0).此式表明:对于任何在x 0处有一阶导数的函数,在U (x 0)内能用关于(x -x 0)的一个一次多项式来近似表示它,多项式的系数就是该函数在x 0处的函数值和一阶导数值,这种近似表示的误差是比(x -x 0)高阶的无穷小.于是,人们猜想:如果函数f (x )在点x 0处有n 阶导数,则可以用一个关于(x -x 0)的n 次多项式来近似表示f (x ),该多项式的系数仅与函数f (x )在点x 0的函数值和各阶导数值有关,这种近似表示的误差是比(x -x 0)n 高阶的无穷小.泰勒(Tayl o r)对这个猜想进行了研究,并得到了下面的结论.定理1(泰勒中值定理) 若f (x )在U (x 0)内具有n +1阶导数,则∀x ∈U (x 0),有f (x )=()000()()()!k nk n k f x x x R x k =-+∑, (2-6-1) 其中R n (x )=o ((x -x 0)n ),且(1)1000(())()()(1)!n n n f x x x R x x x n θ+++-=-+, 0<θ<1. (2-6-2)公式(2-6-1)称为f (x )在点x 0的n 阶泰勒公式,式中R n (x )称为余项.式(2-6-2)表示的余项称为拉格朗日余项,而R n (x )=o ((x -x 0)n )称为皮亚诺(Peano)余项.()000()()()!k nk n k f x P x x x k ==-∑称为n 阶泰勒多项式.运用泰勒多项式近似表示函数f (x )的误差可由余项进行估计.例如,若∀x ∈U (x 0),有|f (n +1)(x )|≤M ,则可得误差估计式10()()()(1)!n n n M R x f x P x x x n +=-≤-+.特别地,当公式(2-6-1)中的x 0=0时,通常称为麦克劳林(MaclaUrin)公式,即f (x )=∑nk =0f (k )(0)k !xk +Rn (x ), (2-6-3)其中 (1)1()()(1)!n n n f x R x x n θ++=+,0<θ<1.很显然,拉格朗日中值公式是带拉格朗日余项的零阶泰勒公式,泰勒中值定理也是拉格朗日中值定理的推广.例1 求f (x )=e x 的n 阶麦克劳林公式.解 f (k )(x )=e x ,f (k )(0)=1(k =0,1,2,…).e x=21()2!!nn x x x o x n +++++. 其拉格朗日余项为1e ()(1)!xn n R x x n θ+=+,θ∈(0,1).例2 求f (x )=sin x 的n 阶麦克劳林公式.解 f (k )(x )=πsin()2x k +⋅ (k =0,1,2,…),故()0,2(0)(1),21k jk jf k j =⎧=⎨-=+⎩ (j=0,1,2,…). 取n =2m ,得sin x =352112(1)()3!5!(21)!m m m x x x x o x m ---+-+-+- .其拉格朗日余项为212(21)πsin 2()(21)!m m m x R x x m θ++⎡⎤+⎢⎥⎣⎦=+21cos (1)(21)!mm x xm θ+=-+, θ∈(0,1). 类似地有cos x =242211(1)()2!4!(2)!mm m x x x o x m +-+-+-+ , 其拉格朗日余项为12221cos ()(1)(22)!m m m x R x x m θ+++=-+, θ∈(0,1).例3 求f (x )=ln(1+x )的n 阶麦克劳林展开式. 解 ()1(1)!()(1)(1)k k kk fx x --=-+ ,(k =1,2,…), 故f (k )(0)=(-1)k -1(k -1)! (k =1,2,…,n ).又 f (0)=0,f (n +1)(ξ)1!(1)(1)n n ξ+=-+, 其中,ξ在0与x 之间.于是,当x ∈(-1,+∞)时,ln(1+x )=234111(1)(1)2!3!4!(1)(1)nn n nn x x x x x x n n ξ+-+-+-++-+-++ , 其中ξ在0与x 之间.利用泰勒公式可以求极限.例4 求极限2240cos e limx x x x -→-.解 利用泰勒公式,有cos x =2441()2!4!x x o x -++, 2222421e1()2!2!2!x x x o x -⎛⎫⎛⎫=+-+-+ ⎪ ⎪⎝⎭⎝⎭,于是 24421cos e ()12x x x o x --=-+. 所以244244001()cos e 112limlim 12x x x x o x x x x -→→-+-==-. 第七节 洛必达法则本节我们将利用微分中值定理来考虑某些重要类型的极限.由第二章我们知道在某一极限过程中,f (x )和g (x )都是无穷小量或都是无穷大量时,f (x )/g (x )的极限可能存在,也可能不存在.通常称这种极限为不定式(或待定型),并分别简记为00或∞∞. 洛必达(L’H ospital)法则是处理不定式极限的重要工具,是计算00型、∞∞型极限的简单而有效的法则.该法则的理论依据是柯西中值定理.一、型不定式 定理1设f (x ),g (x )满足: (1) 0lim x x →f (x )=0,0lim x x →g (x )=0;(2)在U ︒(x 0)内可导,且g ′(x )≠0; (3) 0limx x →()()f xg x ''存在(或为∞), 则 0limx x →()()f xg x = 0lim x x →()()f x g x ''. 证 由于极限0limx x →()()f xg x 与f (x )和g (x )在x =x 0处有无定义没有关系,不妨设f (x 0)=g (x 0)=0.这样,由条件(1)、(2)知f (x )及g (x )在U (x 0)连续.设x ∈U (x 0),则在[x ,x 0]或[x 0,x ]上,柯西中值定理的条件得到满足,于是有00()()()()()()()()f x f x f x fg x g x g x g ξξ'-=='-, 其中ξ在x 与x 0之间.令x →x 0(从而ξ→x 0),上式两端取极限,再由条件(3)就得到limx x →()()f x g x =0lim x ξ→()()f g ξξ''= 0lim x x →()()f xg x '', 对于当x →∞时的型不定式,洛必达法则也成立. 推论1 f (x ),g (x )满足 (1)lim x →∞f (x )=0,lim x →∞g (x )=0;(2) 当|x |>X 时可导,且g ′(x )≠0; (3) limx →∞()()f xg x ''存在(或为∞), 则 ()()limlim()()x x f x f x g x g x →∞→∞'='. 证 令t =1x,则x →∞时t →0,从而 01lim ()lim ()0t x f f x t →→∞==,1lim ()lim ()0x x g g x t→∞→∞==. 由定理1,得2002111()()()()()lim lim lim lim 111()()()()()x t t x f f f x f x t t t g x g x g g t t t→∞→→→∞'-'===''-. 显然,若lim ()()f xg x ''仍为00型不定式,且f ′(x ),g ′(x )满足定理条件,则可继续使用洛必达法则而得到()()()limlim lim ()()()f x f x f xg x g x g x '''==''',且仍然可以依此类推.例1 求33221216lim 248x x x x x x →-+--+.解 32322222121631263lim lim lim 248344642x x x x x x x x x x x x x →→→-+-===--+---.例2 求πarctan 2lim x x x→+∞-. 解 2221πa r c t a n 12l i m l i m l i m 1111x x x x xx x x x→+∞→+∞→+∞--+===+-. 二、∞∞型不定式定理2设f (x ),g (x )满足 (1) 0lim x x →f (x )=∞,0lim x x →g (x )=∞;(2) 在U ︒(x 0)内可导,且g ′(x )≠0;(3) 0limx x →()()f xg x ''存在(或为∞), 则 00()()limlim()()x x x x f x f x g x g x →→'='. 该定理也是应用柯西中值定理来证明的,因过程较繁,故略. 推论2若f (x ),g (x )满足 (1) lim x →∞f (x )=∞,lim x →∞g (x )=∞;(2) 当|x |>X 时可导,且g ′(x )≠0; (3) limx →∞()()f xg x ''存在(或为∞), 则 ()()limlim ()()x x f x f x g x g x →∞→∞'='. 例3 求ln limax xx →+∞ (α>0).解 11l n 1l i m l i m l i m 0a a a x x xxx x a x a x-→+∞→+∞→+∞===. 例4 求lim eax x x →+∞ (α>0).解 1lim lim e e a a x xx x x ax -→+∞→+∞=.若0<α≤1,则上式右端极限为0;若α>1,则上式右端仍是∞∞型不定式,这时总存在自然数n 使n -1<α≤n ,逐次应用洛必达法则直到第n 次有1lim lim e ea a x x x x x ax -→+∞→+∞== (1)(1)lim 0e a nxx a a a n x n -→+∞--+= (次). 故 lim 0eax x x →+∞= (α>0).例5 求π2tan limtan 3x xx →.。

数学基本知识:一元函数的微分对于某一个函数F(x),下面引入一个相关函数来观察其函数极限g(x) = (F(x0 + x) - F(x0))/ x上式中的x0暂视为一个常数。
将上式改写为:g(x,x0) = (F(x0 + x) - F(x0))/ x其中g(x,x0)表示此函数含有参数x0(暂视为常数)。
显然,如果F(x)在x=x0点上连续,则g(x,x0)在x=0这个点上是个待定型0/0。
若g(x,x0)的x=0点是个可去间断点(即其在此点上的左右极限存在且相等),通过重新定义g(0,x0)使其等于g(x,x0)在此点上的极限,则可得到唯一的值g(0,x0) = lim[x→0] g(x,x0)现在,换一种形式表示上式f(x) = g(0,x) = lim[∆x→0] g(∆x,x) = lim[∆x→0] [(F(x + ∆x) - F(x))/ ∆x]其中,将原x换成∆x(表示x的一个小的差分量),将x0换成x (视原x0为变量且用x代之)。
即f(x) = lim[∆x→0] [(F(x + ∆x) - F(x))/ ∆x]这就是通常所用的导函数定义形式。
记为f(x) = d/dx F(x)(或dF(x)/dx、F'(x))如前所述,这是个一元实函数集上的映射。
如果将导函数的定义写成如下形式f(x) = lim[x'→x] [(F(x') - F(x)) / (x' - x)]则可以看出导函数f(x)其实就是与函数F(x)交点为(x,F(x))和(x',F(x'))的割线之斜率在x'→x时的极限,即过点(x,F(x))的切线斜率。
这就是导函数的几何意义。
我们已经知道,导函数可表示成f(x) = dF(x)/dx。
其中dF(x)/dx 原本只是个“符号”,是映射d/dx F(x)的另一种表示。
如果考虑函数F(x)过点(x,F(x))的切线上的点,其切线上任意两点的差分商∆y/∆x都等于f(x),换种写法为∆y = f(x)∆x (= F'(x)∆x)令差分无限小,且用dy和dx代之,便有dy = f(x)dx (= F'(x)dx)这就是所谓的微分形式(简称微分)。

一元函数微分学内容概要总结
一元函数微分学是微积分的重要内容之一,主要研究函数的变化率、斜率、极值、凹凸性等性质。
以下是一元函数微分学的内容概要总结:
1. 导数与微分,导数是函数在某一点的变化率,表示函数曲线在该点的切线斜率,常用符号表示为f'(x)或者dy/dx。
微分是函数在某一点附近的线性近似,常用符号表示为dy。
2. 函数的求导,通过求导可以得到函数在某一点的导数,可以通过极限的定义或者导数的运算法则进行求导。
3. 导数的应用,导数可以用来求函数的极值,判断函数的增减性和凹凸性,求曲线的渐近线,解决最优化问题等。
4. 微分方程,微分方程是关于未知函数及其导数的方程,是自然科学和工程技术中描述变化规律的重要数学工具。
5. 泰勒公式,泰勒公式是函数在某点附近的多项式逼近公式,可以用来近似计算函数的值。
6. 函数的高阶导数,除了一阶导数外,函数还可以有二阶导数、三阶导数等高阶导数,可以描述函数的曲率、加速度等性质。
7. 微分学与积分学的关系,微分学和积分学是微积分的两大分支,它们之间通过微积分基本定理建立了联系,即导数与原函数的
关系。
以上是一元函数微分学的内容概要总结,涵盖了导数与微分、
函数的求导、导数的应用、微分方程、泰勒公式、高阶导数以及微
分学与积分学的关系等内容。
希望能对你有所帮助。

第二章一元函数微分学一.先回顾导数的定义:设函数在内有定义,如果极限存在,则称在处可导,称为函数的可导点,且称上述极限值为函数在处的导数,记为:或;或简记为.注意导数的本质是瞬时变化率,它还有另外两种常见的等价定义:1.=;2.;要特别关注处的导数有特殊形式:(更特别地,要知道两个重要的结论:1.可导必连续;2。
函数在处可导的充要条件是对于分段函数在分段点处的可导性,一定从要考察其左、右导出发.例1.已知=A,试求下列极限的值(1)(2)。
例2.研究函数在处的可导性.解:因为同理,可求得.由于,所以在处不可导。
(记住这个结论)练习:设在处可导,求的值.解:(一)因为在处可导,从而在处也连续.所以,即(二)由得.例3.已知,试求在处的导数.解:因为,所以,由此例可见,在导数存在的情况下,求导问题就归结为求一个型的极限.故求导就是求极限,不必多举例,今后很少针对具体函数计算在一点处的导数值.如把函数在一点处可导的概念推广到一个区间,则可得到导函数的概念.大家要牢记基本导数表(共十五、六条)。
这里的每一条都是根据导数的定义推出来的,请大家在下面自己试着也推推.如:,求.二.导数的几何意义关于导数的几何意义,主要考察的题型有两种。
一种题型是选择题或判断题。
比如:若函数在处可导,则曲线在处必有切线;(√);反之,若曲线在处有切线,则在处必可导,则(×).另一种题型是根据几何意义找切线.例4.求曲线与直线垂直的切线.解:设切点.切线斜率由题意,即故切线方程为下面举一个复杂点的,把前面的知识点窜起来.例5.设为连续函数,且求曲线在点处的切线方程。
(08年研究生考试题)解:由于,且故(前面已讲过理由)而,所以,切线方程为三.导数的四则运算四则求导法则非常简单,但不注意的话,容易犯错误。
下面举几个小例子.例6.求的导数.注意:部分同学可能会犯下面的错误:.例7.设求此题应先化简再求导:注意:个别同学容易把幂函数求导与指数函数求导的公式搞混.例8.求的导数.解:.四.反函数求导法则若函数,其反函数为.若在的某邻域内连续、严格单调且,则在点可导,且.例9.求的导数.解:设原函数,则其反函数为.根据反函数求导法则.有.五.复合求导法则大家可能还有印象,复合函数的导数是.(与直接套用基本导数表相比,这个2从何而来?)如果记,则,故此题恰好满足等式:(*)这是否是巧合的?我们说不是.事实上,(*)式正揭示出了复合函数的求导法则.定理:若函数在可导,而函数在对应的处也可导,则复合函数在处也可导,且或(或.注意:复合函数的链式求导法则可推广至复合两次以上的情形,如:对函数,如记,则各变量间的关系是:有上式可通过连续使用两次链式法则得到。

第四部分 一元函数微积分第11章 函数极限与连续[内容提要]一、函数:(138-141页)1、函数的定义:对应法则、定义域的确定、函数值计算、简单函数图形描绘。
2、函数分类:基本初等函数(幂函数、指数函数、对数函数、三角函数、反三角函数的统称);复合函数([()]y f x ϕ=);初等函数(由常数和基本初等函数构成的,且只能用一个式子表达的函数);分段函数;隐函数;幂指函数(()()g x y f x =);反函数。
3、函数的特性:奇偶性;单调性;周期性;有界性.二、极限:1、极限的概念:(141-142页)定义1:(数列极限)给定数列{}n x ,如果当n 无限增大时,其通项n x 无限趋向于某一个常数a ,即a x n -无限趋近于零,则称数列{}n x 以a 的极限,或称数列{}n x 收敛于a ,记为a x n n =∞→lim ,若{}n x 没有极限,则称数列{}n x 发散。
定义2:(0x x →时函数)(x f 的极限)设函数)(x f 在点0x 的某一去心邻域0(,)U x δo内有定义,当x 无限趋向于0x (0x x ≠)时,函数)(x f 的值无限趋向于A ,则称0x x →时, )(x f 以A 为极限,记作A x f x x =→)(lim 0。
左极限:设函数)(x f 在点0x 的左邻域00(,)x x δ-内有定义,当0x x <且无限趋向于0x 时,函数)(x f 的值无限趋向于常数A ,则称0x x →时,)(x f 的左极限为A ,记作00(0)lim ()x x f x f x A -→-==。
右极限:设函数)(x f 在点0x 的右邻域00(,)x x δ+内有定义,当0x x >且无限趋向于0x 时,函数)(x f 的值无限趋向于常数A ,则称0x x →时,)(x f 的右极限为A ,记作00(0)lim ()x x f x f x A +→+==。
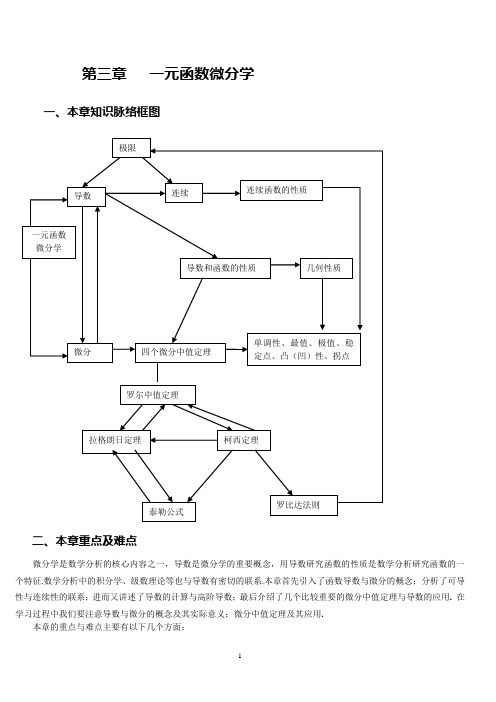
第三章一元函数微分学一、本章知识脉络框图二、本章重点及难点微分学是数学分析的核心内容之一,导数是微分学的重要概念,用导数研究函数的性质是数学分析研究函数的一个特征.数学分析中的积分学、级数理论等也与导数有密切的联系.本章首先引入了函数导数与微分的概念;分析了可导性与连续性的联系;进而又讲述了导数的计算与高阶导数;最后介绍了几个比较重要的微分中值定理与导数的应用. 在学习过程中我们要注意导数与微分的概念及其实际意义;微分中值定理及其应用.本章的重点与难点主要有以下几个方面:● 函数导数的概念、可导性与连续性的关系;费马定理、导函数的介值定理;导数的运算(复合函数、反函数的求导法则);掌握参变量方程所确定的函数的导数;高阶导数的概念及其求法.● 微分(含高阶微分)概念的理解及其运算法则;函数连续性、可导性、可微性之间的关系.● 拉格朗日定理、柯西中值定理、泰勒定理及它们定理的应用推广;极值的三个充分条件及其证明过程;对函数凸性概念的理解及相关命题的证明;函数图象性态的列表表示法.三、本章的基本知识要点(一)导数与微分1. 设函数)(x f y =在点0x 的某邻域内有定义,若极限)()(lim00x x x f x f x x --→存在,则称函数f 在点0x 处可导,并称该极限为函数f 在点0x 处的导数,记作)(0x f ' 类似的,定义函数f 在点0x 处的左导数与右导数:x x f x x f x f x ∆-∆+='-→∆-)()(lim )(0000,)(0x f +'xx f x x f x ∆-∆+=+→∆)()(lim 000右导数和左导数统称为单侧导数.2. 设函数()x f y =定义在点0x 的某邻域()0x U 内.当给0x 一个增量x ∆,()00x U x x ∈∆+时,相应地得到函数的增量为()()00x f x x f y -∆+=∆.如果存在常数A ,使得y ∆能表示成()x x A y ∆+∆=∆则称函数f 在点0x 可微,并称()1式中的第一项x A ∆为f 在点0x 的微分,记作x A dy x x ∆==0或 ()x A x df x x ∆==0.由定义可见,函数的微分与增量仅相差一个关于x ∆的高阶无穷小量,由于dy 是x ∆的线性函数,所以当0≠A 时,也说微分dy 是增量y ∆的线性主部.容易看出,函数f 在点0x 可导和可微是等价的. 3. 导数与微分的基本性质.(1)(有限增量公式)若f 在点0x 可导,则()()x x x f y ∆+∆'=∆ 0(0→∆x );(2)(可导的充要条件)若函数)(x f y =在点0x 的某邻域内有定义,则)(0x f '存在⇔)(0x f +'与)(0x f -'都存在,且)(0x f +'=)(0x f -'; (3)(可导与可微的关系)函数f 在点0x 可导和可微是等价的;(4)(可微与连续性的关系)若f 在点0x 可微,则f 在点0x 必连续(反之不真);(5)(导数的几何意义)导数的几何意义解释是曲线的斜率,即函数f 在点0x 的导数)(0x f '是曲线)(x f y =在点)(0,0y x 的切线斜率若α表示这条切线与x 轴正向的夹角,则)(0x f '.tan α=从而0)(0>'x f 意味着切线与x 轴正向的夹角为锐角;0)(0<'x f 意味着切线与x 轴正向的夹角为钝角;0)(0='x f 示切线与x 轴平行;(6)(费马定理)设函数f 在点0x 的某邻域内有定义,且在点0x 可导.若点0x 为f 的极值点,则必有.0)(0='x f我们称满足方程)(x f '的点为稳定点.(7)(达布定理)若函数f 在],[b a 上可导,且)()(b f a f -+'≠',k 为介于)(a f +',)(b f -'之间任一实数,则至少存在一点),(b a ∈ξ,使得k f =')(ξ.4.求导(微分)法则.(1)(线性法则)'')'(g f g f βαβα±=±(其中βα,为常数); (2)(乘积法则)'')'(g f g f g f +=; (3)(商法则)22')'1(,'')'(g g g g fg g f g f -=-=(其中0≠g ); (4)(复合函数求导法则))())(()))(((x g x g f x g f ''='(也称链式法则);(5)(反函数求导法则)dxdydx dy 1=; (6)(莱布尼茨法则)()(),)(0)(k k n kn nk n g f C g f -=∑= 其中)!(!!k n k n C k n -=是组合系数.5. 若函数f 的导函数'f ,在点0x 可导,则称'f ,在点0x 的导数为f 在点0x 的二阶导数,记作()0''x f,即()()()0''00''0limx f x x x f x f x x =--→同时称f 在点0x 为二阶可导.利用数学归纳法可由f 的1-n 阶导函数定义f 的n 阶导函数(或简称n 阶导数),二阶以及二阶以上的导数都称为高阶导数,函数f 在点0x 处的n 阶导数记作 ()()()00||,0x x n n x x n n dxyd yx f==或 相应地,n 阶导函数记作: ()()n n n n dx y d y f或,.这里n n dx y d 亦写作为y dxd n n.6. 一阶微分形式不变性:不管u 是自变量还是中间量,f 的一阶微分始终具有()du u f u df '=)(的形式.7.基本初等函数的求导公式 (1)0)'(=c (c 为常数); (2)1)'(-=αααxx (α为任意实数);(3)x x x x sin )'(cos ,cos )'(sin -==; (4)x x x x 22csc )'(cot ,sec )'(tan -== x x x x x x c o t c s c )'(csc ,tan sec )'(sec -== (5)xxxxe e a a a ==)'(,ln )'(;(6)).1(ln ,ln 1)'(log xx a x x a == (二)微分中值定理1.罗尔中值定理 若函数f 满足如下条件:(i)f 在闭区间[]b a ,上连续;(ii)f 在开区间()b a ,内可导;(iii)()()b f a f =,则在()b a ,内至少存在一点ξ,使得()0='ξf .罗尔定理的几何意义是说:在每一点都可导的一段连续曲线上,如果曲线的两端点高度相等,则至少存在一条水平切线.注 定理中的三个条件缺少任何一个,结论将不一定成立.2. 拉格朗日(Lagrange )中值定理 若函数满足如下条件:()fi 在闭区间[]b a ,上连续;()f ii 在开区间()b a ,内可导, 则在()b a ,内至少存在一点ξ,使得()()()ab a f b f f --='ξ. 显然,特别当()()b f a f =时,本定理的结论即为罗尔定理的结论,这表明罗尔定理是拉格朗日定理的一个特殊情形.拉格郎日中值定理的几何意义是:在满足定理条件的曲线)(x f y =上至少存在一点))(,(ξξf P ,该曲线在该点出的切线平行于曲线俩短点的连线,我们在证明中引入的辅助线函数)(x F ,正是曲线=y )(x f 与直线ab a f b f a f y AB --+=)()()(()(a x -)之差.定理的结论称为拉格朗日公式。

一元函数微分学知识点一元函数微分学是微积分中的重要内容,它主要研究函数的变化率和极值问题。
微分学中的主要概念包括导数、微分以及一些常见函数的微分法则。
下面将依次介绍这些知识点。
一、导数导数是描述函数变化率的重要工具。
给定一个函数f(x),在某一点x 处的导数表示函数在该点的变化速率。
导数可以用极限来定义,即导数等于函数在该点处的极限值。
导数的记号常用f'(x)或者dy/dx 表示。
导数有几个重要的性质,包括线性性、乘积法则、商法则和链式法则。
线性性表示导数运算具有线性性质,即对于任意常数a和b,有(a*f(x) + b*g(x))' = a*f'(x) + b*g'(x)。
乘积法则描述了两个函数相乘的导数计算方法,即(f(x)*g(x))' = f'(x)*g(x) + f(x)*g'(x)。
商法则是用来计算两个函数相除的导数,即(f(x)/g(x))' = (f'(x)*g(x) - f(x)*g'(x))/g(x)^2。
链式法则适用于复合函数,即若有一个函数h(x) = f(g(x)),则h'(x) = f'(g(x))*g'(x)。
二、微分微分是导数的一种应用,它可以用来近似计算函数在某一点的值。
微分的记号常用dx表示,它表示函数在某一点的微小变化。
微分的计算公式是dy = f'(x)*dx,其中dy表示函数在x处的微小变化,dx表示自变量的微小变化。
微分和导数之间有一个重要的关系,即导数是微分的极限形式。
当自变量的微小变化趋于0时,微分就变成了导数。
因此,导数可以用微分来近似计算。
三、常见函数的微分法则在微分学中,有一些常见函数的微分法则被广泛应用。
这些函数包括常数函数、幂函数、指数函数、对数函数和三角函数。
对于常数函数f(x) = C,其中C为常数,它的导数为f'(x) = 0。

一元函数微分学公式微分学是数学中的一个重要分支,研究函数的微小变化。
在微分学中,一元函数的微分公式是非常基础且重要的知识点。
本文将介绍一元函数微分学公式的相关内容,帮助读者更好地理解和应用微分学知识。
一元函数微分学公式主要包括导数的定义、常见函数的导数公式、导数运算法则以及高阶导数等内容。
下面我们逐一介绍这些内容。
1. 导数的定义导数是一元函数微分学的核心概念,它描述了函数在某一点上的变化率。
设函数f(x)在点x=a处可导,则导数f'(a)的定义为:f'(a) = lim┬(x→a)〖(f(x)-f(a))/(x-a)〗其中lim表示极限,x→a表示x趋近于a的过程,(f(x)-f(a))/(x-a)表示函数的增量与自变量增量的比值。
导数可以理解为函数在该点上的瞬时变化率。
2. 常见函数的导数公式对于一些常见的函数,我们可以通过求导公式来快速计算它们的导数。
以下是一些常见函数的导数公式:- 幂函数:(x^n)' = nx^(n-1),其中n为常数;- 指数函数:(a^x)' = a^x * ln(a),其中a为常数;- 对数函数:(logₐx)' = 1/(x * ln(a)),其中a为底数;- 三角函数:(sinx)' = cosx,(cosx)' = -sinx,(tanx)' = sec^2(x),其中x为弧度;- 反三角函数:(arcsinx)' = 1/√(1-x^2),(arccosx)' = -1/√(1-x^2),(arctanx)' = 1/(1+x^2),其中x在定义域内。
通过这些导数公式,我们可以快速求解常见函数的导数,为后续的微分计算提供便利。
3. 导数运算法则在微分学中,导数具有一些基本的运算法则,可以帮助我们简化复杂函数的导数计算。
- 常数倍法则:(cu)' = cu',其中c为常数;- 和差法则:(f(x)±g(x))' = f'(x)±g'(x);- 积法则:(f(x)g(x))' = f'(x)g(x)+f(x)g'(x);- 商法则:(f(x)/g(x))' = (f'(x)g(x)-f(x)g'(x))/[g(x)]^2,其中g(x)≠0。

一、一元函数微分学一元函数微分学由导数和微分组成。
导数:样本量随自变量的变化而变化的快慢程度;微分:曲线的切线上的纵坐标的增量。
二、常数和基本初等函数求导公式 (1) 0)(='C(2) 1)(-='μμμx x(3) x x cos )(sin =' (4) x x sin )(cos -=' (5) x x 2sec )(tan =' (6) x x 2csc )(cot -=' (7) x x x tan sec )(sec ='(8) x x x cot csc )(csc -=' (9) a a a x x ln )(='(10) (e )e x x '=(11) a x x a ln 1)(log ='(12) x x 1)(ln =',(13) 211)(arcsin x x -='(14) 211)(arccos x x --='(15)21(arctan )1x x '=+(16)21(arccot )1x x '=-+三、函数的和、差、积、商的求导法则 设)(x u u =,)(x v v =都可导,则 (1) v u v u '±'='±)((2) u C Cu '=')((C 是常数)(3)v u v u uv '+'=')((4)2v v u v u v u '-'='⎪⎭⎫ ⎝⎛四、反函数求导法则若函数)(y x ϕ=在某区间y I 内可导、单调且0)(≠'y ϕ,则它的反函数)(x f y =在对应区间x I 内也可导,且)(1)(y x f ϕ'='或dydxdx dy 1=五、复合函数求导法则 设)(u f y =,而)(x u ϕ=且)(u f 及)(x ϕ都可导,则复合函数)]([x f y ϕ=的导数为dy dy du dx du dx =或()()y f u x ϕ'''=六、高阶导数的莱布尼兹公式七、隐函数的导数一般地,如果变量x ,y 之间的函数关系是由某一个方程()0,=y x F 所确定,那么这种函数就叫做由方程所确定的隐函数.对数求导法根据隐函数的求导法,我们还可以得到一个简化求导运算的方法.它适合由几个因子通过乘、除、乘方、开方所构成的比较复杂的函数(包括幂指函数)的求导.这个方法是先取对数,化乘、除为加、减,化乘方、开方为乘积,然后利用隐函数求导法求导,22234241433339tt t t t e d dt e e e dx dt dx e dt--⎛⎫=-⋅=-== ⎪-⎝⎭22223t d y d dy d e dx dx dx dx ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭因此称为对数求导法.幂指函数的一般形式为()0v y u u =>,其中,u v 是x 的函数.八、由参数方程所确定的函数的导数一般地,如果参数方程()()x t y t ϕψ=⎧⎪⎨=⎪⎩,(t 为参数) 确定y 与x 之间的函数关系,则称此函数关系所表示的函数为由参数方程所确定的函数.如果函数()t x ϕ=,()t y ψ=都可导,且()0≠'t ϕ,又()t x ϕ=具有单调连续的反函数()x t 1-=ϕ,则由参数方程所确定的函数可以看成()t y ψ=与()x t 1-=ϕ复合而成的函数()[]x y 1-=ϕψ,根据复合函数与反函数的求导法则,有()()t t dtdx dt dy dx dt dt dy dx dy ϕψ''=⋅=⋅=1,即()()t t dx dy ϕψ''= , 也可写成 dtdxdtdy dx dy=.求方程32ttx ey e-⎧=⎪⎨=⎪⎩所确定的函数的二阶导数22d ydx.解 ()()tt t t t e ee e e dx dy 2323232-=-=''=--,注意二阶导的求法。

一元函数微积分学知识点总结
学习数学能使人们更合乎逻辑、更有条理、更严密、更精确、更深入地思考和解决问题,能增强人们的好奇心、想象力和创造性。
一、定义
导数
微分
不定积分
定积分
变限积分
反常积分
二、计算
求导数
1.复合函数求导
2.分段函数求导
3.隐函数求导
4.高阶导数求导
求积分
1.凑积分法
2.换元法
3.分部积分法
4.有理函数积分法
5.运用牛顿-莱布尼茨公式
三、应用
几何应用(数一、数二、数三)
1.导数的几何应用:“三点两性一线”(极值点、最值点、拐点、单调性、凹凸性、渐近线)
2.积分的几何应用:利用定积分计算平面图形的面积、旋转体的体积和函数的平均值
物理应用(数一、数二)
1.变化率问题
2.静水压力
3.抽水作功
4.质点引力
经济应用(数三)
1.边际
2.弹性
3.积分的简单经济应用
四、逻辑推理证明
中值定理的证明
求方程的根
不等式的证明
等式的证明
【注】整个高数上册就是在讲一元函数微积分,复习这部分要整体把握,先把整个知识框架了熟于心,在复习过程中多总结知识点
之间的联系。
由于最近五一集训营和真题大全解的事情比较忙,知识点精讲一直没有更新,真题出来之后五月份我会重点多讲解知识点,把整个一元函数部分每个知识点梳理一遍,希望同学们多多体谅!。

880题一元函数微分学26题解析一、引言在高等数学中,一元函数微分学是的重要组成部分,它既有理论价值,又有实际应用。
为了帮助大家更好地掌握一元函数微分学的知识点,本文将对880题一元函数微分学26题进行解析,以供大家学习和参考。
二、一元函数微分学基本概念回顾1.导数与微分的定义导数和微分是描述函数在某一点变化率的数学概念。
导数表示函数在某一点的变化率,微分则表示函数在某一点附近的增量。
它们分别为:f"(x) = lim(h→0) [(f(x + h) - f(x))/h]f(x) = f(x0) + ∫[f"(μ)dμ](从x0到x的积分)2.导数与微分的性质(1)线性性质:f"(c) = (f(x) - f(c))/(x - c)(2)可积性:若f"(x)可积,则f(x)在[a, b]上可积。
(3)泰勒公式:f(x) = f(x0) + f"(x0)(x - x0) + o(x - x0)3.常见函数的导数与微分对于常见的基本函数,如幂函数、指数函数、对数函数、三角函数等,我们可以通过公式或表格查询它们的导数与微分。
三、题型解析1.求导题(1)常见函数的求导对于幂函数、指数函数、对数函数等,我们可以直接应用它们的导数公式进行求导。
(2)复合函数、反函数的求导复合函数的导数遵循链式法则,即f"(g(x)) = f"(g) * g"(x)。
反函数的求导可以通过交换f(x)和x的位置,然后求导。
(3)隐函数的求导隐函数的求导方法是将隐函数表示为显函数,然后利用求导公式进行求导。
(4)高阶导数的求解高阶导数的求解方法是将函数表示为幂级数,然后逐阶求导。
2.微分题(1)常见函数的微分对于幂函数、指数函数、对数函数等,我们可以直接应用它们的微分公式进行计算。
(2)微分在实际问题中的应用微分在实际问题中的应用主要包括求极值、最值问题、曲率等。

n 一元函数微分学1、数列极限若数列 {x }及常数a ,0,ε∀>N ∃正数,当n N >时,有n x a ε-<,则称该数列{}n x 的极限为a ,记作lim n n x a →∞=或()n x a n →→∞。
此时也称数列收敛,否则称数列发散。
数列极限的四则运算:若lim ,lim ,n n n n x A y B →∞→∞==则:1)lim()n n n x y A B →∞±=±;2)lim n n n x y AB →∞=;高 数一元函数微分学知识点速记3)0时,limn n x n =Ay →∞y B当n ≠0且B ≠lim n n n y z =a 夹逼准则:设lim n →∞→∞=,且当n >N 时,有y n n n≤x ≤z ,则lim n n x →∞=a 。
2、函数极限lim x f (x )=A →+∞⇔∀ε>0,∃X >0,当x >X 时,有f (x )-A <εlim x f (x )=A →-∞⇔∀ε>0,∃X >0,当x <-X 时,有f (x )-A <ε●左极限:000(x )lim 00,x )(x )x →x f f (x )=A x ∈(x f εδε--=⇔∀>∃δ>--A <,当时,有●右极限:000(x )lim 0(x ,(x )x →x f f (x )=A x ∈x f εδε++=⇔∀>0,∃δ>-A <当+)时,有x →x 0x →x 0x →x 0lim f (x )A f (x f (x )=Alim +)lim -=⇔=3、几个重要极限1)lim sin x =1x →0x2)0lim 1(+)1x x x e→=3))=1a >o n 4)1n =5)lim e x =0x →-∞6)lim x e x →+∞=∞7)x →0lim +x 1x =4、无穷小量无穷小量:若(x )0lim x →x f =0,则称函数f (x )是当0x →x 时的无穷小量。



第一章 函数与极限
1. 函数 会求函数的定义域,对应法则;
几种特殊的函数(复合函数、初等函数等);
函数的几种特性(有界性、单调性、周期性、奇偶性)
2. 极限
(1)概念 无穷小与无穷大的概念及性质;
无穷小的比较方法;(高阶、低阶、同阶、等价) 函数的连续与间断点的判断
(2)计算 函数的极限计算方法(对照极限计算例题,熟悉每个方法的应用条件)
极限的四则运算法则
利用无穷小与无穷大互为倒数的关系;
利用无穷小与有界函数的乘积仍为无穷小的性质;
消去零因子法;
无穷小因子分出法;
根式转移法;
利用左右极限求分段函数极限;
利用等价无穷小代换(熟记常用的等价无穷小);
利用连续函数的性质;
洛必达法则(掌握洛必达法则的应用条件及方法);
∞
∞或00型,)()(lim )()(lim x g x f x g x f ''= 两个重要极限(理解两个重要极限的特点);1sin lim
0=→x x x ,1)()(sin lim 0)(=ϕϕ→ϕx x x e x x x =+→10)1(lim ,e x
x x =+∞→)11(lim , 一般地,0)(lim =ϕx ,∞=ψ)(lim x ,)()(lim )())(1lim(x x x e x ψϕψ=ϕ+
3 函数的连续
连续性的判断、间断点及其分类
第二章 导数与微分
1 导数
(1)导数的概念:增量比的极限;导数定义式的多样性,会据此求一些函数的极限。
导数的几何意义:曲线上某点的切线的斜率
(2)导数的计算:
基本初等函数求导公式;
导数的四则运算法则;(注意函数积、商的求导法则)
复合函数求导法则(注意复合函数一层层的复合结构,不能漏层)
隐函数求导法则(a :两边对x 求导,注意y 是x 的函数;b :两边同时求微分;) 高阶导数
2 微分 函数微分的定义,dx x f dy x x )(00'==
第三章 导数的应用
洛必达法则(函数极限的计算)
函数的单调性与极值,最值、凹凸性与拐点的求法。