必修三 2.3 变量间的相关关系

课题§2.3 变量间的相关关系课型新课教学目标（1）利用散点图判断线性相关关系，了解最小二乘法的思想及2回归方程系数公式的推导过程，利用电子表格求出回归直线的方程并对实际问题进行分析和预测，通过实例加强对回归直线方程含义的理解。

（2）通过自主探究体会数形结合、类比、及最小二乘法的数学思想方法。

（3）通过动手操作培养学生观察、分析、比较和归纳能力，引出利用计算机等现代化教学工具的必要性。

教学过程教学内容备注一、自主学习阅读教材P84—P91，请思考下列问题：（1）变量之间的相关关系（2）散点图（3）回归直线（4）回归方程二、质疑提问1. 函数是研究两个变量之间的依存关系的一种数量形式.对于两个变量，如果当一个变量的取值一定时，另一个变量的取值被惟一确定，则这两个变量之间的关系就是一个函数关系.2. 在中学校园里，有这样一种说法：“如果你的数学成绩好，那么你的物理学习就不会有什么大问题.”按照这种说法，似乎学生的物理成绩与数学成绩之间存在着某种关系，我们把数学成绩和物理成绩看成是两个变量，那么这两个变量之间的关系是函数关系吗？3. 这两个变量是有一定关系的，它们之间是一种不确定性的关系.类似于这样的两个变量之间的关系，有必要从理论上作些探讨，如果能通过数学成绩对物理成绩进行合理估计，将有着非常重要的现实意义.三、问题知识探究（一）：变量之间的相关关系思考1：考察下列问题中两个变量之间的关系，想一想这些问题中两个变量之间的关系是函数关系吗？（1）商品销售收入与广告支出经费；（2）粮食产量与施肥量；（3）人体内的脂肪含量与年龄.思考2：“名师出高徒”可以解释为教师的水平越高，学生的水平就越高，那么学生的学业成绩与教师的教学水平之间的关系是函数关系吗？你能举出类似的描述生活中两个变量之间的这种关系的成语吗？思考3：上述两个变量之间的关系是一种非确定性关系，称之为相关关系，那么探究相关关系的含义如何？自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系，叫做相关关系.思考4：函数关系与相关关系之间的区别与联系.函数关系中的两个变量间是一种确定性关系；相关关系是一种非确定性关系.函数关系是一种因果关系而相关关系不一定是因果关系，也可能是伴随关系.3. 函数关系与相关关系之间有着密切联系，在一定条件下可以互相转化.例1 在下列两个变量的关系中，哪些是相关关系？①正方形边长与面积之间的关系；②作文水平与课外阅读量之间的关系；③人的身高与年龄之间的关系；④降雪量与交通事故的发生率之间的关系.知识探究（二）：散点图 【问题】在一次对人体脂肪含量和年龄关系的研究中，研究人员获得了一组样本数据：其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.思考1：观察上表中的数据，大体上看，随着年龄的增加，人体脂肪含量怎样变化？思考2：以x 轴表示年龄，y 轴表示脂肪含量，你能在直角坐标系中描出样本数据对应的图形吗？ 思考3：上图叫做散点图，你能描述一下散点图的含义吗？ 在平面直角坐标系中，表示具有相关关系的两个变量的一组数据图形，称为散点图.思考4：观察散点图的大致趋势，人的年龄的与人体脂肪含量具有什么相关关系？思考5：在上面的散点图中，这些点散布在从左下角到右上角的区域，对于两个变量的这种相关关系，我们将它称为正相关.一般地，如果两个变量成正相关，那么这两个变量的变化趋势如何？思考6：如果两个变量成负相关，从整体上看这两个变量的变化趋势如何？其散点图有什么特点？ 一个变量随另一个变量的变大而变小，散点图中的点散布在从左上角到右下角的区域思考7：你能列举一些生活中的变量成正相关或负相关的实例吗?例2 以下是某地搜集到的新房屋的销售价格和房屋的面积的数据：画出数据对应的散点图，并指出销售价格与房屋面积这两个变量是正相关还是负相关. 问题提出1. 两个变量之间的相关关系的含义如何？成正相关和负相关的两个相关变50494541392723年龄28.226.327.525.921.217.89.5脂肪61605857565453年龄34.635.233.530.831.430.229.6脂肪思考6：利用计算器或计算机可求得年龄和人体脂肪含量的样本数据的回归方程为，由此我们可以根据一个人个年龄预测其体内脂肪含量的百分比的回归值.若某人37岁，则其体内脂肪含量的百分比约为多少？20.9%四、课堂检测练习 1.已知下列变量，它们之间的关系是函数关系的有①，是相关关系的有②③.①已知二次函数y=ax2+bx+c，其中a、c是已知常数，取b为自变量，因变量是这个函数的判别式△=b2－4ac;②光照时间和果树亩产量；③每亩施用肥料量和粮食产量.练习2. 今有一组试验数据如下表所示：现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是( C )A. y=log2xB. y=2xC. y=(x2－1)/2D. y=2x－2练习 3.F表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y(吨标准煤)的几组对照数据x 3 4 5 6y 2.5 3 4 4.5(1)请画出上表数据的散点图；(2)请根据上表提供的数据，崩最小二乘法求出Y关于x的线性回归方程Y=bx+a；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性同归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值：3×2．5+4×3+5×4+6×4．5=66.5)解：（1）如图48.0577.0-=xy1.99 6.125.14.03.0x1.518.01127.54.04y（2）由对照数据，计算得：4166.5i ii X Y ==∑4222221345686ii X==+++=∑4.5X =266.54 4.5 3.566.563ˆ0.7864 4.58681b-⨯⨯-===-⨯- ;ˆˆ 3.50.7 4.50.35aY bX =-=-⨯= 所求的回归方程为 0.70.35y x =+(3) 100x =, 1000.70.3570.35y =⨯+=吨,预测生产100吨甲产品的生产能耗比技改前降低9070.3519.65-=(吨)五、 小结评价1. 求样本数据的线性回归方程，可按下列步骤进行： 第一步，计算平均数；，y x第二步，求和；，∑∑==ni in i ii xy x 121第三步，计算;)())((1221121x b y a xn xy x n yx x xy y x xb ni ini ii ni ini i i-=--=---=∑∑∑∑====，第四步，写出回归方程 .a bx y +=∧2. 回归方程被样本数据惟一确定，各样本点大致分布在回归直线附近.对同一个总体，不同的样本数据对应不同的回归直线，所以回归直线也具有随机。

高中数学 2.3变量间的相关关系讲解 新人教A 版必修3一、相关关系：自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系，叫做相关关系。

【说明】函数关系是一种非常确定的关系，而相关关系是一种非确定性关系。

思考探究：1、有关法律规定，香烟盒上必须印上“吸烟有害健康”的警示语。

吸烟是否一定会引起健康问题？你认为“健康问题不一定是由吸烟引起的，所以可以吸烟”的说法对吗？2、某地区的环境条件适合天鹅栖息繁衍，有人经统计发现了一个有趣的现象，如果村庄附近栖息的天鹅多，那么这个村庄的婴儿出生率也高，天鹅少的地方婴儿出生率低，于是他得出了一个结论：天鹅能够带来孩子。

你认为这样的结论可靠吗？如何证明这个问题的可靠性？分析：（1）吸烟只是影响健康的一个因素，对健康的影响还有其他的一些因素，两者之间非函数关系即非因果关系；（2）不对，这也是相关关系而不是函数关系。

上面提到了很多相关关系，那它们之间的相关关系强还是弱？我们下面来研究一下。

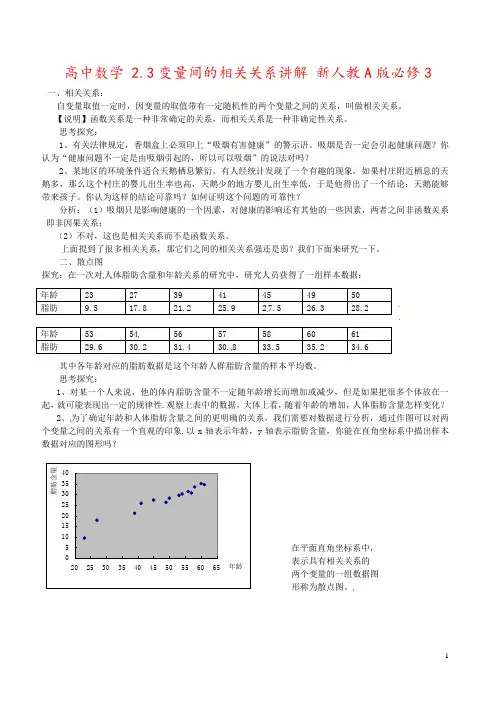
二、散点图探究：在一次对人体脂肪含量和年龄关系的研究中，研究人员获得了一组样本数据：其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数。

思考探究：1、对某一个人来说，他的体内脂肪含量不一定随年龄增长而增加或减少，但是如果把很多个体放在一起，就可能表现出一定的规律性.观察上表中的数据，大体上看，随着年龄的增加，人体脂肪含量怎样变化？2、为了确定年龄和人体脂肪含量之间的更明确的关系，我们需要对数据进行分析，通过作图可以对两个变量之间的关系有一个直观的印象.以x 轴表示年龄，y 轴表示脂肪含量，你能在直角坐标系中描出样本数据对应的图形吗？在平面直角坐标系中， 表示具有相关关系的两个变量的一组数据图 形称为散点图。

年龄 23 27 39 41 45 49 50脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2年龄 53 54 56 57 58 60 61脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.651015202530354020253035404550556065年龄脂肪含量3、观察人的年龄的与人体脂肪含量散点图的大致趋势，有什么样的特点？阅读课本85~86P ，这种相关关系我们称为什么？还有没有其他的相关关系？它又有怎样的特点？三、线性相关、回归直线方程和最小二乘法在各种各样的散点图中，有些散点图中的点是杂乱分布的，有些散点图中的点的分布有一定的规律性，年龄和人体脂肪含量的样本数据的散点图中的点的分布有什么特点？如果散点图中的点的分布，从整体上看大致在一条直线附近，则称这两个变量之间具有线性相关关系，这条直线叫做回归直线。

2.3.1变量之间的相关关系教学目标：通过收集现实问题中两个有关联变量的数据作出散点图，并利用散点图直观认识变量间的相关关系。

教学重点：通过收集现实问题中两个有关联变量的数据作出散点图，并利用散点图直观认识变量间的相关关系。

教学过程：案例分析:一般说来，一个人的身高越高，他的人就越大，相应地，他的右手一拃长就越长，因此，人的身高与右手一拃长之间存在着一定的关系。

为了对这个问题进行调查，我们收集了北京市某中学2003年高三年级96名学生的身高与右手一拃长的数据如下表。

关系吗？（2）如果近似成线性关系，请画出一条直线来近似地表示这种线性关系。

（3）如果一个学生的身高是188cm ，你能估计他的一拃大概有多长吗？ 解：根据上表中的数据，制成的散点图如下。

它们之间是线性相关的。

那么，怎样确定这条直线呢？同学1：选择能反映直线变化的两个点，例如（153，16），（191，23）二点确定一条直线。

同学2：在图中放上一根细绳，使得上面和下面点的个数相同或基本相同。

同学3：多取几组点对，确定几条直线方程。

再分别算出各个直线方程斜率、截距的算术平均值，作为所求直线的斜率、截距。

同学4：我从左端点开始，取两条直线，如下图。

再取这两条直线的“中间位置”作一条直线。

同学5：我先求出相同身高同学右手一拃长的平均值，画出散点图，如下图，再画出近似的直线，使得在直线两侧的点数尽可能一样多。

1015202530150155160165170175180185190195同学6：我先将所有的点分成两部分，一部分是身高在170 cm 以下的，一部分是身高在170 cm 以上的；然后，每部分的点求一个“平均点”——身高的平均值作为平均身高、右手一拃的平均值作为平均右手一拃长，即（164，19），（177，21）；最后，将这两点连接成一条直线。

同学7：我先将所有的点按从小到大的顺序进行排列，尽可能地平均分成三等份；每部分的点按照同学3的方法求一个“平均点”，最小的点为（161.3，18.2），中间的点为（170.5，20.1），最大的点为（179.2，21.3）。