张伟江教授简介 - 上海交通大学数学系

视野•名师名校◄数学教育改革"先锋”----数学大师张奠宙◎上海市城市科技学校邵红能2018年12月20日，我国著名数学史家、数学教育家，华东师范大学数学科学学院教授张奠宙在上海逝世，享年85岁。

未来，乃是过去历史的继续。

不能正确地认识历史,吸取经验教训，也就找不到前进的方向。

辛亥革命以来，中国数学教育走过了100年。

早年，我国学习日本;后来,接受欧美国家的影响。

建国后的1950年代，全盘学习苏联。

经过“大跃进”年代和“文革”十年的波折，而今，中国数学教育取得了举世瞩目的成绩。

1986年，张奠宙所著的《20世纪数学史话》引起杨振宁、陈省身的重视。

在两位大师指点下，张奠宙陆续推出《中国现代数学的发展》、《20世纪数学经纬》、《陈省身传》等著作,成为中国现代数学史的奠基之作。

张奠宙(1933-2018.12.20),浙江省奉化人，华东师范大学教授、博导，张奠宙长期担任数学分析和函数论课程的教学，曾担任《数学教学》杂志主编和名誉主编。

在教学之余，从事数学教育和现代数学史研究，出版《20世纪数学史话》、《现代数学与中学数学》、《数学教育研究导引》、《数学方法论稿》、《中国数学双基教学沢《陈省身传》等著作20余种，发表文章近千篇。

张奠宙48青年教师在泛函分析研究领域对中国的数学发展做出了卓越的贡献。

在我国教育界，张奠宙被广大中小学教师所熟悉，被尊称为“中国数学教育界的泰斗”。

2013年6月，华东师范大学数学系举办了“未来十年中国数学教育展望”高层次的学术研讨会，时值张奠宙八十华诞，为他举办了庆祝典礼。

张奠宙的主要研究方向为泛函分析、数学教育、现代数学史，被人尊称为“三栖学者”。

他曾担任教育部全国教师教育课程资源专家委员会委员、教育部师范司高师教学改革指导委员会委员、《高中数学课程国家标准》研制组组长等。

其中，1995年至1998年,张奠宙任国际数学教育委员会执行委员，这是中国人第一次进入世界数学教育的领导机构。

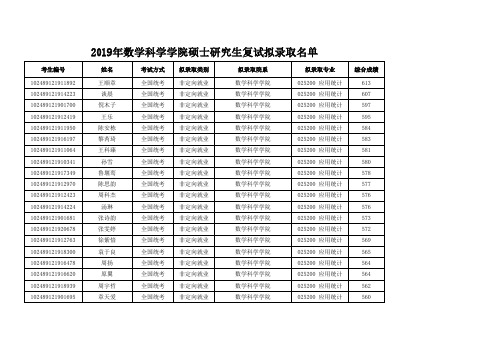
2019年上交数学科学学院数学考研复试时间复试内容复试流程复试资料及经验随着考研大军不断壮大，每年毕业的研究生也越来越多，竞争也越来越大。

对于准备复试的同学来说，其实还有很多小问题并不了解，例如复试考什么？复试怎么考？复试考察的是什么？复试什么时间？复试如何准备等等。

今天启道小编给大家整理了复试相关内容，让大家了解复试，减少一点对于复试的未知感以及恐惧感。

准备复试的小伙伴们一定要认真阅读，对你的复试很有帮助啊！院系简介上海交通大学数学系成立于1928年, 对中国近代数学的发展作出过重要贡献，中国第一次数学会就在上海交大召开。

1952年院系调整，数学系大部分师生被调整到复旦大学和华东师范大学。

1956年，交大西迁，副校长张鸿教授首次将交大教学传统归纳为“门槛高，基础厚，要求严”。

1978年9月，重新组建应用数学系；2001年冬恢复为数学系。

百年来交大数学系桃李芬芳，知名校友中有获得国家最高科技奖的吴文俊院士、胡和生院士及龚升等著名数学家，也有神华集团总裁凌文、红杉中国基金创始人沈南鹏等杰出企业家。

专业介绍数学（mathematics或maths，来自希腊语，“máthēma”；经常被缩写为“math”），是研究数量、结构、变化、空间以及信息等概念的一门学科，从某种角度看属于形式科学的一种。

数学家和哲学家对数学的确切范围和定义有一系列的看法。

复试时间英语 3.18体检 3月16 8：00-10：30 闵行校区校医院资格审查 3月16下午 14：00-15：30 上院311专业综合笔试 3月17上午 9：00-11：00 上院303专业英语笔试 3月17下午 14：00-15：00 上院303英语听力 3月19 12：00进场见研招网面试 3月20 9：00-18：00（8：30集合）上院420复试内容（科目）复试分数线政治英语业务课一业务课二总分数学 50 55 70 85 310应用统计 50 60 100 100 378复试流程1.专业测试学院组织专业课测试，建议以笔试为主。

2019年度广东省科学技术奖公示信息项目名称液体-气体两相流模型的适定性理论主要完成单位单位1：华南理工大学单位2：西北大学单位3：华中师范大学主要完成人（职称、完成单位、工作单位）1.朱长江（职称：教授、工作单位：华南理工大学、完成单位：华南理工大学、主要贡献：提出了完成本项目研究的主要思路，并实施了本项目所有创新点的主要科研工作。

10篇代表作全部都有他的署名并在研究中做出了决定性的贡献。

先后主持完成国家杰出青年科学基金项目和国家自然科学基金重点项目等项目。

）2.姚磊（职称：教授、工作单位：西北大学、完成单位：西北大学、主要贡献：参与本项目主要科研工作。

10篇代表作中有5篇都有他的署名并在研究中做出了重要贡献。

先后主持国家自然科学基金青年项目和面上项目。

基于本项目的主要研究工作，于2012年获全国百篇优秀博士学位论文奖）3.温焕尧（职称：教授、工作单位：华南理工大学、完成单位：华中师范大学、主要贡献：重要科学发现第二项的代表性论文2。

提出了梯度平方分解恒等式。

）项目简介刻画流体之间相互作用的液体-气体两相流模型是石油工业中描述管道和深井中油和气的生产和输运的常见数学模型。

该模型不仅具有深刻的物理意义，而且也具有重要的数学理论价值。

关于其研究是近二十多年来本领域的热点问题之一,有许多关于该模型及其相关模型的数值结果，但对于该模型的适定性理论，即存在性、唯一性和稳定性等结果却很少。

该项目系统地研究了液体-气体两相流模型的自由边界问题、初边值问题和Cauchy问题解的适定性等问题。

挪威应用数学家Steinar Evje 教授在其同一篇论文中提到了我们的其中1篇代表作11次并作为后续研究。

我们在研究爆破机制时提出了速度的梯度平方分解恒等式，从而代替了传统方法中的梯度平方分解不等式。

美国《数学评论》(MR3457694)对我们的一篇代表作进行了评论，认为是文章有趣且非常有技巧。

本项目第一完成人朱长江教授曾获国家杰出青年科学基金资助以及入选了万人计划“国家教学名师”，所领导的两相流模型研究团队被同行专家称为国内外该领域的两个团队之一“Zhu’s group” (具体请见[Lizhi Ruan, Proceedings of the Royal Society of Edinburgh, 144A,351-362, 2014]第352页)，另外一个团队为挪威应用数学家Steinar Evje教授团队。

上海交通大学致远学院2018年秋季学期《代数结构》课程教学说明一.课程基本信息1．开课学院（系）：致远学院2．课程名称：《代数结构》(Algebraic Structures英文名)3．学时/学分：48学时/ 3学分4．先修课程：离散数学，线性代数5．上课时间：星期二14:00-15:40（单周）&星期五10:00-11:406．上课地点：上院3187．任课教师：刘胜利slliu@8．办公室及电话：电院群楼3-429, 139********9．助教：崔男，cuinan913@10.Office hour：每周二上午9:30 - 12:00，电院群楼3-429二.课程主要内容（如何可以，请提供中英文）第一章群(1)基本概念及实例群、子群、循环群；对称即群：平面上的运动群、数域的对称，多项式的对称；置换群：置换群概念及实例。

(2)群的同构定理陪集、正规子群、商群；群的同态及分解定理；群的第一同构定理；群的第二同构定理；群的第三同构定理。

(3)群在集合上的作用，正规作用，共轭作用，左乘等。

Faithful作用, 传递作用。

Orbit-Stablizer定理、Orbit-Counting定理(Burside引理)，及串珠染色问题的解决。

Sylow-p群的定义和性质。

西罗定理：西罗第一定理(sylow p群的存在性)、西罗第二定理(sylow p群的个数)、西罗第三定理(sylow p群的关系)。

(4)群的直积：群的内直积、群的外直积、及其两者之间的关系(5)有限交换群的结构结构最简单的群：循环群的阶及其元素的级；有限p群的分解；有限交换群的直和分解。

第二章环(1) 基本概念及实例环、子环、整环、除环及域；环的特征及其性质；环上的广义分配律。

(2) 环的同构定理环同态、环同态的核、及其性质；理想，集合生成的理想、理想的性质；商环的定义、与环同态及其核间的关系；环的分解定理；环的第一同构定理；环的第二同构定理；环的第三同构定理。

2018年度中等职业教育质量年度报告黑龙江东亚学团职业高级中学2019年3月目录一、学校情况11.1学校概况 11.2学生情况 11.3教师队伍 21.4设施设备 2二、学生发展32.1学生素质 32.2在校体验 42.3资助情况 52.4就业质量 52.5职业发展 6三、质量保障措施63.1专业动态调整 63.2教育教学改革 73.3教师培养培训 83.4规范管理 83.5德育工作情况 133.6党建情况 16四、校企合作164.1校企合作开展情况和效果184.2学生实习情况 184.3集团化办学情况18五、社会贡献195.1技术技能人才培养 195.2社会服务 205.3对口支援 20六、举办者履责206.1经费保障 206.2政策措施 21七、特色创新221.加强心理健康教育22八、主要问题和改进措施222018年度黑龙江东亚学团职业高级中学质量报告1.学校情况1.1学校概况黑龙江东亚学团职业高级中学系原第一机床厂职业高级中学，成立于1980年, 学校的主要任务是为工厂培养技术工人。

1995年，齐齐哈尔第一机床厂经济效益开始滑坡，出现拖欠职工工资的情况。

1998年2月学校加入了齐齐哈尔工程学院（原齐齐哈尔职业学院）为龙头的民办教育集团——黑龙江东亚学团，学校易名为黑龙江东亚学团职业高级中学。

2008年8月20日，由齐齐哈尔市国有资产监督管理委员会、齐齐哈尔职业学院、齐齐哈尔市龙沙区人民政府和齐齐哈尔第一机床厂四家单位共同签署的文件《关于对东亚学团资产清查界定和处置的协议书》中，黑龙江东亚学团职业高中办学性质被界定为“国有公办，执行托管协议。

委托齐齐哈尔工程学院（原齐齐哈尔职业学院）进行管理”。

校园占地面积5864.64平方米，建筑面积（校舍面积）22841.32平方米，校园总面积39040.32平方米。

学校资产总额13718916.91元，固定资产7554957.64元。

1.2学生情况目前学校在籍学生257人，其中职高学籍为37人；开设计算机平面设计、计算机网络技术、航空服务、铁路客运服务、汽车运用与维修、数控技术应用、机械制造技术等专业，2018年招生人数比上一年有所减少。

上海交通大学研究生（非数学专业）数学基础课程《矩阵理论》教学大纲（附：选课指南）一．概况1．开课学院（系）和学科：理学院数学系2．课程代码：3．课程名称：矩阵理论4．学时/学分：51学时/3学分5．预修课程：线性代数（行列式，矩阵与线性方程组，线性空间F n，欧氏空间R n，特征值与矩阵的对角化，实对称矩阵与二次型）, 高等数学（一元微积分，空间解析几何，无穷级数，常微分方程）6．适合专业：全校的机、电、材、管理、生命和物理、力学诸大学科类，以及人文学科等需要的专业（另请参看选课指南）。

7．教材/教学参考书：《矩阵理论》，苏育才、姜翠波、张跃辉编，科学出版社，2006《矩阵分析》, R.A. Horn and C.R. Johnson, Cambridge Press (中译本)，杨奇译，机械工业出版社，2005。

《矩理阵论与应用》，陈公宁编，高等教育出版社，1990。

《特殊矩阵》，陈景良，陈向晖，清华大学出版社，2001。

《代数特征值问题》，JH.威尔金森著，石钟慈邓健新译，科学出版社，2001。

二、课程的性质和任务矩阵理论作为一种基本的数学工具，在数学学科与其他科学技术领域诸如数值分析、优化理论、微分方程、概率统计、系统工程等学科都有广泛应用。

电子计算机及计算技术的发展也为矩阵理论的应用开辟了更广阔的前景。

因此，学习和掌握矩阵的基本理论和方法，对于将来从事工程技术工作的工科研究生来说是必不可少的。

通过该门课程的学习，期望学生能深刻地理解矩阵理论的基本知识和数学思想，掌握有关的计算方法及技巧，提高学生的数学素质，提高科研能力，掌握矩阵理论在多元微积分、线性控制系统、微分方程、逼近理论、投入产出分析等领域的许多应用。

三、课程的教学内容和要求矩阵理论的教学内容分为十部分，对不同的内容提出不同的教学要求。

(数字表示供参考的相应的学时数)第一章矩阵代数（复习，2）1 矩阵的运算、矩阵的秩和初等变换、Hermite梯形阵、分块矩阵（2）要求：掌握矩阵的运算及性质，尤其是对矩阵乘法“左行右列”规则的深入理解和融会贯通；熟练掌握利用初等变换求矩阵的秩、Hermite梯形阵等的技巧；理解并掌握分块矩阵的运算技巧与要领。

金融数学12550261
任课教师：张寄洲（教授）
课程简介：
金融数学利用数学工具研究金融，进行数学建模、理论分析、数值计算等定量分析，以求找到金融学内在规律并用以指导实践。

金融数学也可以理解为现代数学与计算技术在金融领域的应用，因此，金融数学是一门新兴的交叉学科，发展很快，是目前十分活跃的前沿学科之一。

本课程系统地介绍了金融数学中的一些核心理论知识, 内容包括金融产品介绍、期权定价的离散模型-- 二叉树模型、随机积分与布朗运动、期权定价的连续模型--欧式期权定价的Black-Scholes
模型及其推广、数值计算与模拟--蒙特卡罗方法和有限差分方法、奇异期权的介绍和数值解法、利率与债券模型等。

教师简介：
张寄洲，博士后、教授，现在上海师范大学数理学院工作。

曾任中国数学学会理事、上海市数学学会常务理事、上海市工业与应用数学学会常务理事、中国运筹学会《智能计算》分会副理事长、现任《上海中学数学》主编、《数学教育学报》理事和编委。

于1996年在中国科学院数学研究所获理学博士学位，1996年至1998年在武汉大学做博士后研究工作。

2002年以来先后应邀访问了美国、加拿大、德国和日本等国家以及香港和台湾等地区十多所大学等。

参加完成了国家自然科学基金两项和上海市重大科技攻关项目两项，主持完成上海市自然科学基金项目和上海市教委科学基金等项目多项。

其研究成果与人合得2000年湖北省自然科学二等奖。

已独立和与人合作发表学术论文100多篇和编著翻译教材4部。

培养和在学各类研究生100多名。

致远学院课程教学大纲一、课程基本信息课程代码：MA131 课程名称（中文）：渐近分析课程名称（英文）：Asymptotic Analysis学分/学时：34/2 课程讨论时数(小时)：0课程实验数(小时)：0 开课时间：春课程类别：本科生学位课开课院系：理学院数学系任课教师（姓名/工号）：周栋焯/10696预修课程：数学分析，高等代数，复变函数，常微分方程，偏微分方程面向专业：理学院数学系、物理系以及“理工结合类”学生二、课程内容简介本课程是针对高年级的数学系或者物理系开设的，课程将重点强调如何运用数学方法（如渐近展开、扰动分析等）来解决实际物理问题，而不追求这些方法的严格性的证明，其内容包括如何利用拉普拉斯方法以及最速下降法近似求解指数型的积分以及如何理解伯格斯方程激波的产生；如何利用WKB方法近似得到常微分方程的高频解，以及中间需要用到的Airy函数的性质；如何利用稳相方法求解振荡型的积分以及如何分析线性色散波方程的解的长时间的行为；如何使用变分方法以及相关的哈密尔顿-雅可比理论；如何理解几何光学中的费马原理；如何利用奇异扰动理论来处理包含多个时间尺度的常微分方程以及相关的边界层理论，最后介绍一些多尺度分析的知识和技巧以及弱非线性波理论。

三、教学内容安排与学习要求第一部分基础知识介绍(4学时)1.1 “大O”与“小O”阶数1.2 渐近序列与超越所有阶1.3 渐近级数与渐近展开第二部分指数型积分的近似（10学时）2.1 指数型积分与Watson引理2.2 拉普拉斯方法与斯特林公式2.4 弱扩散伯格斯方程的极限解2.4 最速下降法与鞍点法2.5 Airy函数的渐近行为第三部分振荡型积分的近似（6学时）3.1 稳相方法3.2 线性色散波方程解的长时间行为3.3 几何光学第四部分常微分方程的扰动（8学时）4.1 级数解的渐近行为4.2 WKB理论4.3 奇异扰动理论与边界层第五部分多尺度分析（6学时）5.1变分方法5.2哈密尔顿-雅可比理论5.3共振与久期行为5.4弱非线性波理论四、课程考核要求1. 实验（上机）内容和基本要求本课程无实验和上机安排，但要求学生能对一些基本微分方程进行计算机模拟。

上海交通大学数学学科硕士研究生课程大纲《代数拓扑》（Algebraic Topology）(2005试行稿)一．概况1．开课学院（系）和学科：理学院数学系数学2．课程代码：3．课程名称：代数拓扑4．学时/学分： 54/35. 开课时间：春季6．预修课程：基础代数学7．教材: Allen Hatcher, Algebraic Topology, Cambridge University Press, 2002, available at: /~hatcher/AT/ATpage.html主要参考书：a. Jean Dieudonné, A History of Algebraic and Differential Topology 1900-1960.Birkhäuser, Boston - Basel, 1989.b. Albrecht Dold, Lectures on Algebraic Topology, Second Edition, Springer, 1980.c. Marvin J. Greenberg, John R. Harper, Algebraic Topology: A First Course, TheBenjamin/Cummings Publishing Company, Inc., 1981.d. Ioan Mackenzie James (editor), History of Topology, North-Holland, 1999.e. Jiří Matoušek, Using the Borsuk-Ulam Theorem: Lectures on Topological Methods inCombinatorics and Geometry, Springer, 2003.f. Tomasz Kaczynski, Konstantin Mischaikow, Marian Mrozek, Computational Homology,Springer, 2004.g. J. Peter May, A Concise Course in Algebraic Topology, University of Chicago Press,1999, available at: /~may/CONCISE/ConciseRevised.pdfh. James R. Munkres, Elements of Algebraic Topology, Addison-Wesley PublishingCompany, 1984.i. Hajime Sato, Algebraic Topology: An Intuitive Approach, American MathematicalSociety, 1999.j. 沈信耀，同调论：代数拓扑学之一，科学出版社，2002.k. 苏竞存，流形的拓扑学，武汉大学出版社，1992.二．课程简介本课程介绍同调与上同调的基本理论. 大致内容有: 奇异同调; 同调的计算与应用; 同调公理; 上同调群, 杯积; Poincaré对偶, 上同调的计算与应用。