与球有关的切接问题(全面)

微专题17球的切、接、截问题1.球的切接问题(1)长方体的外接球①球心：体对角线的交点；②半径：r＝a2＋b2＋c22(a，b，c为长方体的长、宽、高).(2)正方体的外接球、内切球及与各条棱相切的球(a为正方体的棱长)①外接球：球心是正方体中心，半径r＝32a，直径等于体对角线长；②内切球：球心是正方体中心，半径r＝a2，直径等于正方体棱长；③与各条棱都相切的球：球心是正方体中心，半径r＝22a，直径等于面对角线长.(3)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分，a为正四面体的棱长)①外接球：球心是正四面体的中心，半径r＝64a；②内切球：球心是正四面体的中心，半径r＝6 12a.2.平面截球平面截球面得圆.截面圆的圆心与球心的连线与截面圆圆面垂直且R2＝d2＋r2(R为球半径，r为截面圆半径，d为球心到截面圆的距离).类型一外接球问题考向1墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型，用构造法(构造长方体)解决，外接球的直径等于长方体的体对角线长.长方体同一顶点的三条棱长分别为a，b，c，外接球半径为R.则(2R)2＝a2＋b2＋c2，即2R＝a2＋b2＋c2.常见的有以下三种类型：例1 已知三棱锥P－ABC的四个顶点在球O的球面上，P A＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是P A，AB的中点，∠CEF＝90°，则球O的体积为()A.86πB.46πC.26πD.6π答案D解析因为点E，F分别为P A，AB的中点，所以EF∥PB.因为∠CEF＝90°，所以EF⊥CE，所以PB⊥CE.取AC的中点D，连接BD，PD，易证AC⊥平面BDP，所以PB⊥AC，又AC∩CE＝C，AC，CE⊂平面P AC，所以PB⊥平面P AC，所以PB⊥P A，PB⊥PC，因为P A＝PB＝PC，△ABC为正三角形，所以P A⊥PC，即P A，PB，PC两两垂直，将三棱锥P－ABC放在正方体中如图所示.因为AB＝2，所以该正方体的棱长为2，所以该正方体的体对角线长为6，所以三棱锥P－ABC的外接球的半径R＝62，所以球O的体积V＝43πR 3＝43π⎝⎛⎭⎪⎫623＝6π，故选D.考向2对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型，用构造法(构造长方体)解决，外接球的直径等于长方体的体对角线长，如图所示，(2R)2＝a2＋b2＋c2(长方体的长、宽高分别为a，b，c)，即R2＝18(x2＋y2＋z2)，如图.例2 在三棱锥A－BCD中，AB＝CD＝2，AD＝BC＝3，AC＝BD＝4，则三棱锥A－BCD外接球的表面积为________.答案29π2解析构造长方体，三个长度为三对面的对角线长，设长方体的长宽高分别为a，b，c，则a2＋b2＝9，b2＋c2＝4，c2＋a2＝16，所以2(a2＋b2＋c2)＝9＋4＋16＝29，即a2＋b2＋c2＝4R2＝292，则外接球的表面积为S＝4πR2＝29π2.考向3汉堡模型汉堡模型是直三棱柱、圆柱的外接球模型，模型如下，由对称性可知，球心O的位置是△ABC的外心O1与△A1B1C1的外心O2的连线的中点，算出小圆O1的半径AO1＝r，OO1＝h2，所以R2＝r2＋h24.例3 在三棱柱ABC－A1B1C1中，AB＝BC＝AC，侧棱AA1⊥底面ABC，若该三棱柱的所有顶点都在同一个球O的表面上，且球O的表面积的最小值为4π，则该三棱柱的侧面积为()A.6 3B.3 3C.3 2D.3答案B解析如图，设三棱柱上、下底面中心分别为O1，O2，则O1O2的中点为O，设球O的半径为R，则OA＝R，设AB＝BC＝AC＝a，AA1＝h，则OO 2＝12h ，O 2A ＝23×32AB ＝33a .在Rt △OO 2A 中，R 2＝OA 2＝OO 22＋O 2A 2＝14h 2＋13a 2≥2×12h ×33a ＝33ah ， 当且仅当h ＝233a 时，等号成立， 所以S 球＝4πR 2≥4π×33ah ， 所以43π3ah ＝4π， 所以ah ＝3，所以该三棱柱的侧面积为3ah ＝3 3. 考向4 垂面模型垂面模型是有一条侧棱垂直底面的棱锥模型，可补为直棱柱内接于球；如图所示，由对称性可知球心O 的位置是△CBD 的外心O 1与△AB 2D 2的外心O 2连线的中点，算出小圆O 1的半径CO 1＝r ，OO 1＝h2，则R ＝r 2＋h 24.例4 (2022·广州模拟)已知四棱锥S －ABCD 的所有顶点都在球O 的球面上，SD ⊥平面ABCD ，底面ABCD 是等腰梯形，AB ∥CD 且满足AB ＝2AD ＝2DC ＝2，且∠DAB ＝π3，SC ＝2，则球O 的表面积是( ) A.5π B.4π C.3π D.2π答案 A解析 依题意，得AB ＝2AD ＝2，∠DAB ＝π3，由余弦定理可得BD ＝3，则AD 2＋DB 2＝AB 2，则∠ADB ＝π2. 又四边形ABCD 是等腰梯形，故四边形ABCD 的外接圆直径为AB ，半径r ＝AB2＝1，设AB 的中点为O 1，球的半径为R ，因为SD ⊥平面ABCD ， 所以SD ＝SC 2－CD 2＝1，R 2＝12＋⎝ ⎛⎭⎪⎫SD 22＝54，则S ＝4πR 2＝5π. 考向5 切瓜模型切瓜模型是有一侧面垂直底面的棱锥模型，常见的是两个互相垂直的面都是特殊三角形，在三棱锥A －BCD 中，侧面ABC ⊥底面BCD ，设三棱锥的高为h ，外接球的半径为R ，球心为O ，△BCD 的外心为O 1，O 1到BC 的距离为d ，O 与O 1的距离为m ，△BCD 和△ABC 外接圆的半径分别为r 1，r 2，则⎩⎪⎨⎪⎧R 2＝r 21＋m 2，R 2＝d 2＋（h －m ）2，解得R ，可得R ＝r 21＋r 22－l 24(l 为两个面的交线段长).例5 (2022·济宁模拟)在边长为6的菱形ABCD 中，∠A ＝π3，现将△ABD 沿BD 折起，当三棱锥A－BCD的体积最大时，三棱锥A－BCD的外接球的表面积为________.答案60π解析边长为6的菱形ABCD，在折叠的过程中，当平面ABD⊥平面BCD时，三棱锥的体积最大；由于AB＝AD＝CD＝BC＝6，∠C＝∠A＝π3.所以△ABD和△CBD均为正三角形，设△ABD和△CBD的外接圆半径为r，则2r＝BDsin C，所以r＝2 3.△ABD和△CBD的交线段为BD，且BD＝6.所以三棱锥A－BCD的外接球的半径R＝（23）2＋（23）2－624＝15.故S球＝4·π(15)2＝60π.训练1 (1)(2022·青岛一模)设三棱柱的侧棱垂直于底面，所有棱的长都为1，顶点都在一个球面上，则该球的表面积为()A.5πB.πC.113π D.73π(2)在三棱锥P－ABC中，平面P AB⊥平面ABC，平面P AC⊥平面ABC，且P A＝4，底面△ABC的外接圆的半径为3，则三棱锥P－ABC的外接球的表面积为________.答案(1)D(2)52π解析(1)由三棱柱所有棱的长a＝1，可知底面为正三角形，底面三角形的外接圆直径2r＝1sin 60°＝233，所以r＝33，设外接球的半径为R ，则有R 2＝r 2＋⎝ ⎛⎭⎪⎫a 22＝13＋14＝712，所以该球的表面积S ＝4πR 2＝73π，故选D.(2)因为平面P AB ⊥平面ABC ，平面P AC ⊥平面ABC ， 所以P A ⊥平面ABC .设三棱锥P －ABC 的外接球的半径为R ，结合底面△ABC 的外接圆的半径r ＝3， 可得R 2＝⎝ ⎛⎭⎪⎫P A 22＋r 2＝22＋33＝13，所以三棱锥P －ABC 的外接球的表面积为S 表＝4πR 2＝52π. 类型二 内切球问题内切球问题的解法(以三棱锥为例)第一步：先求出四个表面的面积和整个锥体的体积；第二步：设内切球的半径为r ，建立等式V P －ABC ＝V O －ABC ＋V O －P AB ＋V O －P AC ＋ V O －PBC ⇒V P －ABC ＝13S △ABC ·r ＋13S △P AB ·r ＋13S △P AC ·r ＋13S PBC ·r ＝13(S △ABC ＋S △P AB ＋S △P AC ＋S △PBC )r ； 第三步：解出r ＝3V P －ABCS △ABC ＋S △P AB ＋S △P AC ＋S △PBC.例6 (1)(2022·成都石室中学三诊)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P －ABC 为鳖臑，P A ⊥平面ABC ，P A ＝BC ＝4，AB ＝3，AB ⊥BC ，若三棱锥P －ABC 有一个内切球O ，则球O 的体积为( ) A.9π2 B.9π4 C.9π16D.9π(2)在直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝6，BC ＝8，AC ＝10，则该三棱柱内能放置的最大球的表面积是( )A.16πB.24πC.36πD.64π答案 (1)C (2)A解析 (1)设球O 的半径为r ， 则三棱锥P －ABC 的体积V ＝13×12×3×4×4＝13×(12×3×4＋12×4×3＋12×5×4＋12×4×5)×r ， 解得r ＝34，所以球O 的体积V ＝43πr 3＝9π16，故选C.(2)由题意，球的半径为底面三角形内切圆的半径r ，因为底面三角形的边长分别为6，8，10，所以底面三角形为直角三角形， r ＝AB ＋BC －AC 2＝6＋8－102＝2.又因为AA 1＝6，2r ＝4<6，所以该三棱柱内能放置的最大球半径为2，此时S 表面积＝4πr 2＝4π×22＝16π. 训练2 已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________. 答案 23π解析 圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆.在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点， 则PD ＝22，△PEO ∽△PDB ，故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22， 故内切球的体积为43π⎝ ⎛⎭⎪⎫223＝23π.类型三 球的截面问题解决球的截面问题抓住以下几个方面：(1)球心到截面圆的距离；(2)截面圆的半径；(3)直角三角形(球心到截面圆的距离、截面圆的半径、球的半径构成的直角三角形).例7 (2022·杭州质检)在正三棱锥P －ABC 中，Q 为BC 中点，P A ＝2，AB ＝2，过点Q 的平面截三棱锥P －ABC 的外接球所得截面面积的取值范围为________. 答案 ⎣⎢⎡⎦⎥⎤π，3π2解析 因为正三棱锥P －ABC 中，PB ＝PC ＝P A ＝2，AC ＝BC ＝AB ＝2，所以PB 2＋P A 2＝AB 2，即PB ⊥P A ， 同理PB ⊥PC ，PC ⊥P A ，因此正三棱锥P －ABC 可看作正方体的一角，如图.记正方体的体对角线的中点为O ，由正方体结构特征可得，点O 即是正方体的外接球球心，所以点O 也是正三棱锥P －ABC 外接球的球心，记外接球半径为R ， 则R ＝122＋2＋2＝62，因为球的最大截面圆为过球心的圆，所以过点Q 的平面截三棱锥P －ABC 的外接球所得截面的面积最大为S max ＝πR 2＝3π2.又Q 为BC 中点，由正方体结构特征可得OQ ＝12P A ＝22；由球的结构特征可知，当OQ 垂直于过点Q 的截面时，截面圆半径最小为 r ＝R 2－OQ 2＝1，所以S min ＝πr 2＝π.因此，过Q 的平面截三棱锥P －ABC 的外接球所得截面面积的取值范围为⎣⎢⎡⎦⎥⎤π，3π2.训练3 (1)设球O 是棱长为4的正方体的外接球，过该正方体棱的中点作球O 的截面，则最小截面的面积为( ) A.3π B.4π C.5πD.6π(2)(2022·武汉质检)已知棱长为2的正方体ABCD －A 1B 1C 1D 1，球O 与该正方体的各个面相切，则平面ACB 1截此球所得的截面的面积为________. 答案 (1)B (2)2π3解析 (1)当球O 到截面圆心连线与截面圆垂直时，截面圆的面积最小， 由题意，正方体棱的中点与O 的距离为22，球的半径为23， ∴最小截面圆的半径为12－8＝2，∴最小截面面积为π·22＝4π.(2)∵正方体ABCD －A 1B 1C 1D 1的棱长为2，球O 与该正方体的各个面相切，则球O 的半径为1，设E ，F ，G 分别为球O 与平面ABCD 、平面BB 1C 1C 、平面AA 1B 1B 的切点，则等边三角形EFG 为平面ACB 1截此球所得的截面圆的内接三角形， 由已知可得EF ＝EG ＝GF ＝2， ∴平面ACB 1截此球所得的截面圆的半径 r ＝22sin 60°＝63，∴截面的面积为π×⎝ ⎛⎭⎪⎫632＝2π3.一、基本技能练1.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A.π B.3π4 C.π2 D.π4答案 B解析 如图画出圆柱的轴截面ABCD ，O 为球心.球的半径R ＝OA ＝1，球心到底面圆的距离为OM ＝12.∴底面圆半径r ＝OA 2－OM 2＝32故圆柱体积V ＝π·r 2·h ＝π·⎝ ⎛⎭⎪⎫322×1＝3π4. 2.若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为( ) A.12π B.24π C.36π D.144π答案 C解析由题意知球的直径2R＝（23）2＋（23）2＋（23）2＝6，∴R＝3，∴S球＝4πR2＝36π.故选C.3.一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为()A.3πB.4πC.33πD.6π答案A解析构造棱长为1的正方体，该四面体的外接球也是棱长为1的正方体的外接球，所以外接球半径R＝32，所以外接球表面积为S＝4πR2＝3π.4.已知直三棱柱ABC－A1B1C1的6个顶点都在球O的球面上，若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为()A.3172 B.210C.132 D.310答案C解析将直三棱柱补为长方体ABEC－A1B1E1C1，则球O是长方体ABEC－A1B1E1C1的外接球.∴体对角线BC1的长为球O的直径.因此2R＝32＋42＋122＝13，则R＝132.5.(2022·南阳二模)已知边长为2的等边三角形ABC，D为BC的中点，以AD为折痕进行折叠，使折后的∠BDC＝π2，则过A，B，C，D四点的球的表面积为()A.3πB.4πC.5πD.6π答案 C解析 折后的几何体构成以D 为顶点的三棱锥，且三条侧棱互相垂直，可构造长方体，其对角线即为球的直径，三条棱长分别为1，1，3，所以2R ＝1＋1＋3＝5，球的表面积S ＝4π⎝ ⎛⎭⎪⎫522＝5π.6.(2022·青岛模拟)如图是一个由6个正方形和8个正三角形围成的十四面体，其所有顶点都在球O 的球面上，若十四面体的棱长为1，则球O 的表面积为( )A.2πB.4πC.6πD.8π答案 B解析 根据图形可知，该十四面体是由一个正方体切去八个角得到的， 如图所示，十四面体的外接球球心与正方体的外接球球心相同，建立空间直角坐标系，∵该十四面体的棱长为1，故正方体的棱长为2， ∴该正方体的外接球球心的坐标为O ⎝ ⎛⎭⎪⎫22，22，22，设十四面体上一顶点为D ，则D ⎝ ⎛⎭⎪⎫2，22，0，所以十四面体的外接球半径 R ＝OD ＝⎝⎛⎭⎪⎫2－222＋⎝ ⎛⎭⎪⎫22－222＋⎝ ⎛⎭⎪⎫0－222＝1，故外接球的表面积为S ＝4πR 2＝4π.故选B.7.四面体ABCD 的四个顶点都在球O 上且AB ＝AC ＝BC ＝BD ＝CD ＝4，AD ＝26，则球O 的表面积为( ) A.70π3 B.80π3 C.30π D.40π答案 B解析 如图，取BC 的中点M ，连接AM ，DM ，由题意可知，△ABC 和△BCD 都是边长为4的等边三角形. ∵M 为BC 的中点，∴AM ⊥BC ，且AM ＝DM ＝23， 又∵AD ＝26，∴AM 2＋DM 2＝AD 2， ∴AM ⊥DM ，∵BC ∩DM ＝M ，BC ，DM ⊂平面BCD ， ∴AM ⊥平面BCD ，∵AM ⊂平面ABC ，∴平面ABC ⊥平面BCD ， △ABC 与△BCD 外接圆半径r ＝23DM ＝433， 又△ABC 与△BCD 的交线段BC ＝4. 所以四面体外接球半径R ＝⎝ ⎛⎭⎪⎫4332＋⎝ ⎛⎭⎪⎫4332－424＝2153， 四面体ABCD 的外接球的表面积为4π×R 2＝803π.8.已知三棱锥P －ABC 的棱AP ，AB ，AC 两两垂直，且长度都为3，以顶点P 为球心，2为半径作一个球，则球面与三棱锥的表面相交所得到的四段弧长之和等于( ) A.2π3 B.5π6 C.π D.3π2答案 D解析 如图，∠APC ＝π4，AP ＝3，AN ＝1，∠APN ＝π6，∠NPM ＝π12，MN ︵＝π12×2＝π6，同理GH ︵＝π6，HN ︵＝π2，GM ︵＝2π3， 故四段弧长之和为π6＋π6＋π2＋2π3＝3π2.9.(多选)(2022·石家庄调研)已知一个正方体的外接球和内切球上各有一个动点M 和N ，若线段MN 长的最小值为3－1，则( ) A.该正方体的外接球的表面积为12π B.该正方体的内切球的体积为π3 C.该正方体的棱长为1D.线段MN 长的最大值为3＋1 答案 AD解析设该正方体的棱长为a，则其外接球的半径R＝32a，内切球的半径R′＝a2，该正方体的外接球与内切球上各有一个动点M，N，由于两球球心相同，可得MN的最小值为3a2－a2＝3－1，解得a＝2，故C错误；所以外接球的半径R＝3，表面积为4π×3＝12π，故A正确；内切球的半径R′＝1，体积为43π，故B错误；MN的最大值为R＋R′＝3＋1，故D正确.故选AD.10.(多选)设圆锥的顶点为A，BC为圆锥底面圆O的直径，点P为圆O上的一点(异于B，C)，若BC＝43，三棱锥A－PBC的外接球表面积为64π，则圆锥的体积为()A.4πB.8πC.16πD.24π答案BD解析如图，设圆锥AO的外接球球心为M，半径为r，则M在直线AO上，4πr2＝64π，解得r＝4.由勾股定理得BM2＝OM2＋OB2，即42＝(23)2＋OM2，可得OM＝2，即OM＝|AO－r|＝|AO－4|＝2，解得AO＝6或AO＝2.当AO＝6时，圆锥AO的体积为V＝13π×(23)2×6＝24π；当AO＝2时，圆锥AO的体积为V＝13π×(23)2×2＝8π.故选BD.11.在三棱锥A－BCD中，△BCD和△ABD均是边长为1的等边三角形，AC＝2，则该三棱锥外接球的表面积为________.答案2π解析取AC的中点O，连接OB，OD，在△ABC中，AB＝BC＝1，AC＝2，所以∠ABC＝90°，所以OA＝OB＝OC＝22，同理得OD＝22，故点O为该三棱锥外接球的球心，所以球O的半径r＝22，S球＝4πr2＝2π.12.如图，已知球O是棱长为3的正方体ABCD－A1B1C1D1的内切球，则平面ACD1截球O的截面面积为________.答案3π2解析根据题意知，平面ACD1是边长为9＋9＝32的正三角形，且所求截面的面积是该正三角形的内切圆的面积，则由图得，△ACD1内切圆的半径r＝13（32）2－⎝⎛⎭⎪⎫3222＝62，所以平面ACD 1截球O 的截面面积为S ＝π×⎝ ⎛⎭⎪⎫622＝3π2.二、创新拓展练13.(多选)(2022·华大新高考联考)已知三棱锥S －ABC 中，SA ⊥平面ABC ，SA ＝AB ＝BC ＝2，AC ＝2，点E ，F 分别是线段AB ，BC 的中点，直线AF ，CE 相交于G ，则过点G 的平面α截三棱锥S －ABC 的外接球O 所得截面面积可以是( ) A.23π B.89π C.π D.32π答案 BCD解析 因为AB 2＋BC 2＝AC 2，故AB ⊥BC ， 故三棱锥S －ABC 的外接球O 的半径R ＝2＋2＋22＝62，取AC 的中点D ，连接BD 必过G ， 因为AB ＝BC ＝2，故DG ＝13BD ＝13，因为OD ＝22，故OG 2＝⎝ ⎛⎭⎪⎫222＋⎝ ⎛⎭⎪⎫132＝1118，则过点G 的平面截球O 所得截面圆的最小半径r 2＝⎝ ⎛⎭⎪⎫622－1118＝89，故截面面积的最小值为89π，最大值为πR 2＝32π，故选BCD.14.(多选)(2022·济南模拟)已知三棱锥P －ABC 的四个顶点都在球O 上，AB ＝BC ＝AC ＝1，∠APC ＝π6，平面P AC ⊥平面ABC ，则( ) A.直线OA 与直线BC 垂直B.点P 到平面ABC 的距离的最大值为1＋32C.球O 的表面积为13π3D.三棱锥O －ABC 的体积为18 答案 ACD解析 设△ABC 外接圆的圆心为O 1，连接OO 1，O 1A . 因为O 为三棱锥P －ABC 外接球的球心， 所以OO 1⊥平面ABC ，所以OO 1⊥BC ，因为AB ＝BC ＝AC ＝1， 所以O 1A ⊥BC ，所以BC ⊥平面OO 1A ， 所以OA ⊥BC ，故A 选项正确； 设△P AC 外接圆的圆心为O 2， AC 的中点为D ，连接O 2D ， 由于AC ＝1，∠APC ＝π6， 所以圆O 2的半径r 2＝12×1sin π6＝1，则易知O 2D ＝32，所以点P 到平面ABC 的距离的最大值为1＋32(此时P ，O 2，D 三点共线)，故B 选项错误；由于AB ＝BC ＝AC ＝1，平面P AC ⊥平面ABC ，平面P AC ∩平面ABC ＝AC ， 所以圆O 1的半径r 1＝12×1sin π3＝33，圆O 2的半径r 2＝1，△ABC 与△P AC 的交线段AC ＝1， 所以三棱锥P －ABC 外接球半径R 2＝⎝ ⎛⎭⎪⎫332＋12－14＝1312.故球O 的表面积S ＝4π×1312＝13π3，故C 选项正确；由于OO 1⊥平面ABC ，且OO 1＝O 2D ＝32，S △ABC ＝34，所以三棱锥O －ABC 的体积为13×OO 1×S △ABC ＝13×32×34＝18，故D 选项正确，故选ACD.15.在菱形ABCD 中，AB ＝23，∠ABC ＝60°，若将菱形ABCD 沿对角线AC 折成大小为60°的二面角B －AC －D ，则四面体DABC 的外接球球O 的体积为________. 答案 5239π27解析 如图，设M ，N 分别为△ABC ，△ACD 的外心，E 为AC 的中点，则EN ＝EM ＝13BE ＝1，在平面BDE 内过点M 作BE 的垂线与过点N 作DE 的垂线交于点O .∵BE ⊥AC ，DE ⊥AC ，BE ∩DE ＝E ，∴AC ⊥平面BDE .∵OM ⊂平面BDE ，∴OM ⊥AC ，∵OM ⊥BE ，BE ∩AC ＝E ，∴OM ⊥平面ABC ，同理可得ON ⊥平面ACD ，则O 为四面体DABC 的外接球的球心，连接OE ，∵EM ＝EN ，OE ＝OE ，∠OME ＝∠ONE ＝90°，∴△OME ≌△ONE ，∴∠OEM ＝30°，∴OE ＝EM cos 30°＝233.∵AC ⊥平面BDE ，OE ⊂平面BDE ，∴OE ⊥AC ，∴OA ＝OE 2＋AE 2＝393，即球O 的半径R ＝393.故球O 的体积V ＝43πR 3＝5239π27.16.(2022·湖南三湘名校联考)在直三棱柱ABC －A 1B 1C 1中，AB ⊥BC ，AB ＝BC ＝AA 1＝4，M 为棱AB 的中点，N 是棱BC 的中点，O 是三棱柱外接球的球心，则平面MNB 1截球O 所得截面的面积为________.答案 8π解析 如图1，将直三棱柱补形成正方体ABCD －A 1B 1C 1D 1， 连接BD 1，则直三棱柱的外接球也是正方体的外接球，球心O 是BD 1的中点，半径R ＝2 3.连接BD 交MN 于点E ，连接B 1E 交BD 1于点F ， 过点O 作OO 1⊥B 1E 于点O 1，连接B 1D 1，因为MN ∥AC ，AC ⊥平面BB 1D 1D ，所以MN ⊥平面BB 1D 1D ，所以OO 1⊥MN ，所以OO 1⊥平面MNB 1.如图2，在矩形BB 1D 1D 中，BF FD 1＝BE B 1D 1＝14，所以BF OF ＝23，过点B 作BG ⊥B 1E 于点G ， 则BG ＝BE ·BB 1B 1E ＝43， BG OO 1＝BF OF ＝23，所以OO 1＝2， 设截面圆的半径为r ， 则r 2＝R 2－OO 21＝(23)2－22＝8， 所以截面的面积为8π.。

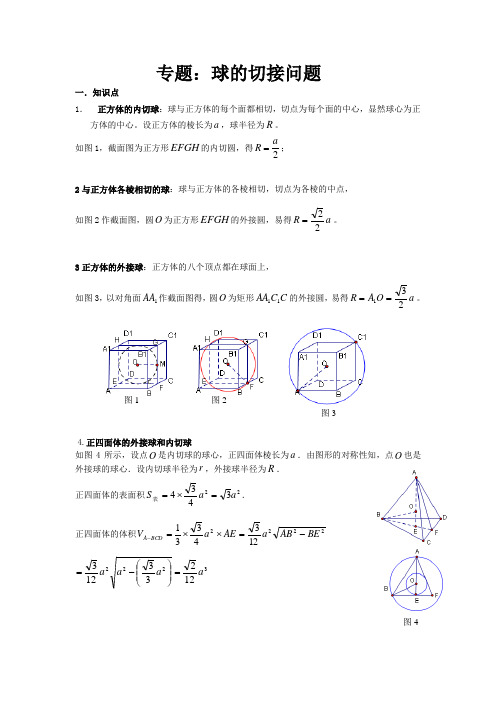
专题：球的切接问题 一．知识点1． 正方体的内切球：球与正方体的每个面都相切，切点为每个面的中心，显然球心为正方体的中心。

设正方体的棱长为a ，球半径为R 。

如图1，截面图为正方形EFGH 的内切圆，得2a R =；2与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点， 如图2作截面图，圆O 为正方形EFGH 的外接圆，易得a R 22=。

3正方体的外接球：正方体的八个顶点都在球面上，如图3，以对角面1AA 作截面图得，圆O 为矩形C C AA 11的外接圆，易得a O A R 231==。

4.正四面体的外接球和内切球如图4所示，设点O 是内切球的球心，正四面体棱长为a ．由图形的对称性知，点O 也是外接球的球心．设内切球半径为r ，外接球半径为R ． 正四面体的表面积223434a a S =⨯=表． 正四面体的体积22221234331BE AB a AE a V BCD A -=⨯⨯=- 322212233123a a a a =⎪⎪⎭⎫ ⎝⎛-= 图1 图2图3图4BCD A V r S -=⋅表31，a aaS V r BCD A 12631223323=⨯==∴-表在BEO Rt ∆中，222EO BE BO +=，即22233r a R +⎪⎪⎭⎫ ⎝⎛=，得a R 46=，得r R 3= 小结:正四面体内切球半径是高的14，外接球半径是高的345.长方体的外接球：即正方体的各顶点都在球面上。

设长方体的棱长分别为a ，b ，c 。

怎么作平面截图来反映半径和边长的关系？结论：由图形（4）我们可以发现外接球的半径2222c b a R ++=二、题型与方法归类 例1、（1）若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为________．本题主要考查简单的组合体和球的表面积．画出球的轴截面可得，球的直径是正方体的对角线，所以有球的半径R ＝332，则该球的表面积为S ＝4πR 2＝27π.故填27π (2) 求棱长为1的正四面体外接球的体积．设SO 1是正四面体S －ABC 的高，外接球的球心O 在SO 1上，设外接球半径为R ，AO 1＝r ， 则在△ABC 中，用解直角三角形知识得r ＝33， 从而SO 1＝SA 2－AO 21＝1－13＝23， 在Rt △AOO 1中，由勾股定理得R 2＝(23－R )2＋(33)2，解得R ＝64， ∴V 球＝43πR 3＝43π(64)3＝68π.变式练习:1已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积( C )A ．16πB ．20πC ．24πD ．32π2已知正方体外接球的体积是323π，那么正方体的棱长等于( D ) A ．2 2 B.233 C.423 D.433解析 由题意知V ＝43πR 3＝32π3，∴R ＝2，外接球直径为4，即正方体的体对角线，设棱长为a ，则体对角线l ＝3a ＝4，a ＝433.3.半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为________，体积为________．【解析】 外切圆柱的底面半径为R ，高为2R ，∴S 表＝S 侧＋2S 底＝2πR ·2R ＋2πR 2＝6πR 2，V 圆柱＝πR 2·2R ＝2πR 3. 【答案】 6πR 2；2πR 3例2、已知A 、B 、C 、D 是球O 面上的四个点，OA 、OB 、OC 两两垂直，且OA ＝1,OB ＝2,OC ＝3，求球的体积与表面积。

球的切接问题方法大全
解决球的切接问题主要有以下几种方法：
1. 补形法：将几何体补成长方体或立方体，这样更容易找到球心和外接球的半径。

2. 找球心法：找到几何体某两个面外接圆的圆心，从圆心作垂线，两垂线的交点即为球心。

通过构造直角三角形来解决。

3. 坐标法：将几何问题代数化，通过设立球心坐标，利用球心到球面上各顶点的距离都等于半径来求解问题。

4. 化“球”为“圆”法：球的轴截面是大圆，含有球的全部元素，因此可以通过作出球的一个大圆，化“球”为“圆”来解决问题，将空间问题转化为平面问题。

5. 内切问题：通过切割法来解决，通过体积自等来求内切球半径。

在处理球的切接问题时，应根据具体的情况选择合适的方法。

与球有关的切、接问题1．球的表面积公式：S ＝4πR 2；球的体积公式V ＝43πR 3 2．与球有关的切、接问题中常见的组合： (1)正四面体与球：如图，设正四面体的棱长为a ，内切球的半径为r ，外接球的半径为R ，取AB 的中点为D ，连接CD ，SE 为正四面体的高，在截面三角形SDC 内作一个与边SD 和DC 相切，圆心在高SE 上的圆．因为正四面体本身的对称性，内切球和外接球的球心同为O .此时，CO ＝OS ＝R ，OE ＝r ，SE ＝ 23a ，CE ＝33a ，则有R ＋r ＝ 23a ，R 2－r 2＝|CE |2＝a 23，解得R ＝64a ，r ＝612a . (2)正方体与球：①正方体的内切球：截面图为正方形EFHG 的内切圆，如图所示．设正方体的棱长为a ，则|OJ |＝r ＝a 2(r 为内切球半径)． ②与正方体各棱相切的球：截面图为正方形EFHG 的外接圆，则|GO |＝R ＝22a . ③正方体的外接球：截面图为正方形ACC 1A 1的外接圆，则|A 1O |＝R ′＝32a . (3)三条侧棱互相垂直的三棱锥的外接球：①如果三棱锥的三条侧棱互相垂直并且相等，则可以补形为一个正方体，正方体的外接球的球心就是三棱锥的外接球的球心．即三棱锥A 1-AB 1D 1的外接球的球心和正方体ABCD -A 1B 1C 1D 1的外接球的球心重合．如图，设AA 1＝a ，则R ＝32a . ②如果三棱锥的三条侧棱互相垂直但不相等，则可以补形为一个长方体，长方体的外接球的球心就是三棱锥的外接球的球心．R 2＝a 2＋b 2＋c 24＝l 24(l 为长方体的体对角线长)． 角度一：正四面体的内切球1．(2015·长春模拟)若一个正四面体的表面积为S 1，其内切球的表面积为S 2，则S 1S 2＝________.解析：设正四面体棱长为a ，则正四面体表面积为S 1＝4·34·a 2＝3a 2，其内切球半径为正四面体高的14，即r ＝14·63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2π6a 2＝63π. 角度二：直三棱柱的外接球2．(2015·唐山统考)如图，直三棱柱ABC -A 1B 1C 1的六个顶点都在半径为1的半球面上，AB ＝AC ，侧面BCC 1B 1是半球底面圆的内接正方形，则侧面ABB 1A 1的面积为( )A ．2B ．1 C. 2 D.22解析：选C 由题意知，球心在侧面BCC 1B 1的中心O 上，BC 为截面圆的直径，∴∠BAC ＝90°，△ABC 的外接圆圆心N 是BC 的中点，同理△A 1B 1C 1的外心M 是B 1C 1的中心．设正方形BCC 1B 1的边长为x ，Rt △OMC 1中，OM ＝x 2，MC 1＝x 2，OC 1＝R ＝1(R 为球的半径)，∴⎝⎛⎭⎫x 22＋⎝⎛⎭⎫x 22＝1，即x ＝2，则AB ＝AC ＝1，∴S 矩形ABB 1A 1＝2×1＝ 2.角度三：正方体的外接球3．一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形)，则该几何体外接球的体积为________．解析：依题意可知，新的几何体的外接球也就是原正方体的外接球，要求的直径就是正方体的体对角线；∴2R ＝23(R 为球的半径)，∴R ＝3，∴球的体积V ＝43πR 3＝43π. 答案：43π角度四：四棱锥的外接球4．(2014·大纲卷)正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9π D.27π4解析：选A 如图所示，设球半径为R ，底面中心为O ′且球心为O ，∵正四棱锥P -ABCD中AB ＝2，∴AO ′＝ 2.∵PO ′＝4，∴在Rt △AOO ′中，AO 2＝AO ′2＋OO ′2，∴R 2＝(2)2＋(4－R )2，解得R＝94，∴该球的表面积为4πR 2＝4π×⎝⎛⎭⎫942＝81π4，故选A. [类题通法]“切”“接”问题的处理规律1．“切”的处理解决与球的内切问题主要是指球内切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．2．“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．[牛刀小试]1．(2015·云南一检)如果一个空间几何体的正视图、侧视图、俯视图都是半径等于5的圆，那么这个空间几何体的表面积等于( )A ．100π B.100π3 C ．25π D.25π3解析：选A 易知该几何体为球，其半径为5，则表面积为S ＝4πR 2＝100π.2．(2014·陕西高考)已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为( )A.32π3 B ．4π C ．2π D.4π3解析：选D 因为该正四棱柱的外接球的半径是四棱柱体对角线的一半，所以半径r ＝1212＋12＋(2)2＝1，所以V 球＝4π3×13＝4π3.故选D. 3．已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的底面边长为6时，其高的值为( )A ．3 3 B.3 C ．2 6 D ．2 3解析：选D 设正六棱柱的高为h ，则可得(6)2＋h 24＝32，解得h ＝2 3. 4．(2015·山西四校联考)将长、宽分别为4和3的长方形ABCD 沿对角线AC 折起，得到四面体A -BCD ，则四面体A -BCD 的外接球的体积为________．解析：设AC 与BD 相交于O ，折起来后仍然有OA ＝OB ＝OC ＝OD ，∴外接球的半径r ＝32＋422＝52，从而体积V ＝4π3×⎝⎛⎭⎫523＝125π6. 5．一个圆锥过轴的截面为等边三角形，它的顶点和底面圆周在球O 的球面上，则该圆锥的体积与球O 的体积的比值为________．解析：设等边三角形的边长为2a ，则V 圆锥＝13·πa 2·3a ＝33πa 3；又R 2＝a 2＋(3a －R )2，所以R ＝233a ，故 V 球＝4π3·⎝⎛⎭⎫233a 3＝323π27a 3，则其体积比为932. [高考全国课标卷真题追踪]1．（15课标1理）已知,A B 是球O 的球面上两点，090AOB ∠=,C 为该球面上的动点，若O ABC -三棱锥体积的最大值为36，则球O 的表面积为（ C ）(A)36π (B)64π (C)144π (D)256π2.（13课标1理）如图，有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为( A )（A ）3cm 3500π （B ）3cm 3866π （C ）3cm 31372π （D ）3cm 32048π 3.（12课标理）已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为（ A ）(A)26 (B)36 (C)23 （D ）224.（12课标文）平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为 （ B ）（A ）6π （B ）43π （C ）46π （D ）63π5.（10新课标理）设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( B )(A) 2a π (B) 273a π (C) 2113a π (D) 25a π 6.（10新课标文）设长方体的长、宽、高分别为2,,a a a ,其顶点都在一个球面上,则该球的表面积为( B )（A ）23a π （B ）26a π （C ）212a π （D ）224a π 7．（07新课标文）已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,2AC r =,则球的体积与三棱锥体积之比是（Ｄ）Ａ.π Ｂ.2π Ｃ.3π Ｄ.4π8.（13新课标2文）已知正四棱锥O ABCD -的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为24π。

专题19 几何体中与球有关的切、接问题球的截面的性质(1)球的任何截面是圆面；(2)球心和截面(不过球心)圆心的连线垂直于截面；(3)球心到截面的距离d 与球的半径R 及截面的半径r 的关系为r ＝R 2－d 2几个与球有关的切、接常用结论(1)正方体的棱长为a ，球的半径为R ，①假设球为正方体的外接球，那么2R ＝3a ；②假设球为正方体的内切球，那么2R ＝a ；③假设球与正方体的各棱相切，那么2R ＝2a .(2)假设长方体的同一顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，那么2R ＝a 2＋b 2＋c 2. (3)正四面体的外接球与内切球的半径之比为3∶1. 一、题型选讲题型一 、几何体的外接球解决多面体的外接球问题，关键是确定球心的位置，方法是先选择多面体中的一面，确定此面外接圆的圆心，再过圆心作垂直此面的垂线，那么球心一定在此垂线上，最后根据其他顶点确定球心的准确位置．对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置．例1、【2021年高考全国Ⅰ卷理数】,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，假设⊙1O 的面积为4π，1AB BC AC OO ===，那么球O 的外表积为 A ．64π B ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意， 得24,2r r π=π=∴，ABC 为等边三角形，由正弦定理可得2sin60AB r =︒=1OO AB ∴==1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的外表积2464S R ππ==.应选：A.此题考查球的外表积，应用球的截面性质是解题的关键，考查计算求解能力，属于根底题.例2、【2021年高考天津】假设棱长为 A ．12π B ．24πC ．36πD ．144π【答案】C【解析】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即3R ==，所以，这个球的外表积为2244336S R πππ==⨯=. 应选：C ．此题考查正方体的外接球的外表积的求法，求出外接球的半径是此题的解题关键，属于根底题.求多面体的外接球的面积和体积问题，常用方法有：〔1〕三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；〔2〕直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；〔3〕如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心. 例3、〔2021届山东省潍坊市高三上学期统考〕边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，那么过A ，B ，C ，D 四点的球的外表积为〔 〕A ．3πB ．4πC ．5πD ．6π【答案】C【解析】边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，构成以D 为顶点的三棱锥，且三条侧棱互相垂直，可构造以其为长宽高的长方体，其对角线即为球的直径，三条棱长分别为1,12R ==24(52S ππ==，应选C.例4、〔2021届山东省日照市高三上期末联考〕四棱锥P ABCD -的体积是，底面ABCD 是正方形，PAB ∆是等边三角形，平面PAB ⊥平面ABCD ，那么四棱锥P ABCD -外接球体积为〔 〕A ．BCD ．【答案】A【解析】设AB 的中点为Q ，因为PAB ∆是等边三角形，所以PQ AB ⊥，而平面PAB ⊥平面ABCD ， 平面PAB ⋂平面ABCD AB =，所以PQ ⊥平面ABCD ，四棱锥P ABCD -的体积是，13AB AB PQ =⨯⨯⨯13AB AB AB =⨯⨯，所以边长6AB =，PQ =OH x =，OM x =，()(222222R OA OM AM x ==+=+，2222223R OP OH PH x ==+=+，x =2212321R =+=343V R π==球.应选：A.例5、〔2021届山东省德州市高三上期末〕中国古代数学经典?九章算术?系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，PA ⊥平面ABCE ，四边形ABCD 为正方形，AD =ED =，假设鳖臑P ADE -的外接球的体积为，那么阳马P ABCD -的外接球的外表积等于______.【答案】20π 【解析】四边形ABCD 是正方形，AD CD ∴⊥，即AD CE ⊥，且AD =ED ，所以，ADE ∆的外接圆半径为122AE r ===设鳖臑P ADE -的外接球的半径1R ，那么3143R π=，解得1R =.PA ⊥平面ADE ，1R ∴=，可得2PA ==PA ∴正方形ABCD 的外接圆直径为22r AC ==，2r ∴=PA ⊥平面ABCD ，所以，阳马P ABCD -的外接球半径2R ==因此，阳马P ABCD -的外接球的外表积为22420R ππ=. 故答案为：20π.题型二、几何体的内切球求解多面体的内切球的问题，一般是将多面体分割为以球心为顶点，多面体的各面为底面的棱锥，利用多面体的体积等于各棱锥的体积之和求内切球的半径．例6、【2021年高考全国Ⅲ卷理数】圆锥的底面半径为1，母线长为3，那么该圆锥内半径最大的球的体积为_________．【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如下图， 其中2,3BC AB AC ===，且点M 为BC 边上的中点， 设内切圆的圆心为O ，由于AM =122S =⨯⨯=△ABC 设内切圆半径为r ，那么：ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得：22r，其体积：3433V r =π=π.. 与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出适宜的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.例7、〔2021届山东省潍坊市高三上期中〕如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如下图粽子形状的六面体，那么该六面体的外表积为__________；假设该六面体内有一小球，那么小球的最大体积为___________．【答案】2 729【解析】〔1〕因为16(1222S =⨯⨯⨯=，所以该六面体的外表积为2. 〔2〕由图形的对称性得，小球的体积要到达最大，即球与六个面都相切时，2倍，所以六面体体积是6. 由于图像的对称性，内部的小球要是体积最大，就是球要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥，设球的半径为R ，所以16()63R R =⨯⇒=，所以球的体积3344()393297V R ππ===.故答案为：. 二、达标训练1、〔2021届山东省泰安市高三上期末〕正三棱锥S ABC -的侧棱长为6，那么该正三棱锥外接球的外表积是〔 〕 A ．16π B ．20πC ．32πD ．64π【答案】D【解析】如下图，因为正三棱锥S ABC -的侧棱长为6，那么263AE ==6SE ===, 又由球心O 到四个顶点的距离相等，在直角三角形AOE 中，,6AO R OE SE SO R ==-=-，又由222OA AE OE =+，即222(6)R R =+-，解得4R =， 所以球的外表积为2464S R ππ==， 应选D.2、【2021年高考全国II 卷理数】△ABC 的等边三角形，且其顶点都在球O 的球面上.假设球O的外表积为16π，那么O 到平面ABC 的距离为A B ．32C ．1D 【答案】C【解析】设球O 的半径为R ，那么2416R π=π，解得：2R =.设ABC △外接圆半径为r ，边长为a ，ABC △的等边三角形，212a ∴=，解得：3a =，2233r ∴==∴球心O 到平面ABC 的距离1d =.应选：C ．此题考查球的相关问题的求解，涉及到球的外表积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.3、【2021年高考全国Ⅰ卷理数】三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，那么球O 的体积为A ．B ．C ．D【答案】D 【解析】解法一：,PA PB PC ABC ==△为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CEAC C EF =∴⊥平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一局部，2R ==即344π33R V R =∴=π==，应选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴，又90CEF ∠=︒，12CE AE PA x ∴===， AEC △中，由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =，D 为AC 的中点，1cos 2AD EAC PA x ∠==，2243142x x x x+-+∴=，2212122x x x ∴+=∴==，，PA PB PC ∴=== 又===2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==，2R ∴=，344338V R ∴=π=π⨯=，应选D.此题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．4、【2021年高考全国Ⅰ卷理数】设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为 A． B ．C ．D ．【答案】B【解析】如下图，设点M 为三角形ABC 的重心，E 为AC 中点，当点D 在平面ABC 上的射影为M 时，三棱锥D ABC -的体积最大，此时，4OD OB R ===，2ABCS AB ==△，6AB ∴=,点M 为三角形ABC 的重心，23BM BE ∴==Rt OBM ∴△中，有2OM ==，426DM OD OM ∴=+=+=， ()max 163D ABC V -∴=⨯= B.5、【2021年新高考全国Ⅰ卷】直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 为半径的球面与侧面BCC 1B 1的交线长为________．【答案】2. 【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A BC D -的棱长均为2，所以△111D B C 为等边三角形，所以1D E=111D E B C ⊥，又四棱柱1111ABCD A BC D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥， 因为1111BB B C B =，所以1D E ⊥侧面11BC CB ，设P 为侧面11BC CB 与球面的交线上的点，那么1DE EP ⊥，1D E ，所以||EP ===所以侧面11BC CB 与球面的交线上的点到E因为||||EF EG ==11BC CB 与球面的交线是扇形EFG 的弧FG ， 因为114B EFC EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得2FG π==.故答案为：2. 6、〔2021届山东省滨州市三校高三上学期联考〕三棱锥S ABC -，SA ⊥平面ABC ，6ABC π∠=，3SA =，1BC =，直线SB 和平面ABC 所成的角大小为3π.假设三棱锥S ABC -的四个顶点都在同一球面上，那么该球的外表积为________.【答案】13π【解析】如图：SA ⊥平面ABC ，那么SBA ∠为直线SB 和平面ABC 所成的角，即3SBA π∠=在Rt SAB ∆中：tan 3SAAB π=== 如图，设O 为三棱锥S ABC -外接球的球心，G 为ABC ∆外接圆圆心，连结,,,,OA OB GA GB OG ，那么必有OG ⊥面ABC在ABC ∆，2222cos31216AC AB BC AB BC π=+-⋅⋅=+-=， 那么1AC = 其外接圆半径122,1sin sin 6AC r r ABC π====∠， 又1322OG SA ==， 所以三棱锥S ABC -外接球半径为R ===该球的外表积为21344134S R πππ==⨯=, 故答案为：13π.7、〔2021届山东省枣庄、滕州市高三上期末〕如图，在三棱锥P -ABC 中，,PA AB ⊥PC BC ⊥，,AB BC ⊥22,AB BC ==PC ，那么PA 与平面ABC 所成角的大小为________；三棱锥P -ABC外接球的外表积是________.【答案】45︒ 6π【解析】如图，作平行四边形ABCD ，连接PD ，由AB BC ⊥，那么平行四边形ABCD 是矩形．由BC CD ⊥，BC PC ⊥，PC CD C =，∴BC ⊥平面PCD ，而PD ⊂平面PCD ，∴BC PD ⊥，同理可得AB PD ⊥，又AB BC B ⋂=，∴PD ⊥平面ABCD ．,PD CD PD AD ⊥⊥，PAD ∠是PA 与平面ABC 所成角．由2,CD AB PC ===1PD =，又1AD BC ==，∴45PAD ∠=︒．∴PA 与平面ABC 所成角是45︒．由,PA AB ⊥PC BC ⊥知PB 的中点到,,,A B C P 的距离相等，PB 是三棱锥P -ABC 外接球的直径．由BC ⊥平面PCD 得BC PC ⊥，PB ===24()62PB S ππ==． 故答案为：45︒；6π．8、〔2021届山东省烟台市高三上期末〕三棱锥P ABC -的四个顶点都在球O 的外表上，PA ⊥平面ABC ，6PA =，AB =2AC =，4BC =，那么：〔1〕球O 的外表积为__________；〔2〕假设D 是BC 的中点，过点D 作球O 的截面，那么截面面积的最小值是__________．【答案】52π 4π【解析】〔1〕由题,根据勾股定理可得AC AB ⊥,那么可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,那么体对角线为外接球直径,即2r ==,那么r =,所以球的外表积为224452r πππ=⨯=；〔2〕由题,因为Rt ABC ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,那么外接圆半径为2,故截面面积为224ππ⨯=故答案为：〔1〕52π；〔2〕4π9、〔2021届山东省滨州市高三上期末〕在四面体S ABC -中，2SA SB ==，且SA SB ⊥，BC =，AC =________，该四面体外接球的外表积为________.8π【解析】因为2SA SB ==，且SA SB ⊥，BC ，AC =AB ==因此222BC AC AB +=，那么AC BC ⊥；取AB 中点为O ，连接OS ，OC ，那么OA OB OC OS ====所以该四面体的外接球的球心为O ，半径为OC =所以该四面体外接球的外表积为248S ππ=⋅=；又因为SA SB =，所以SO AB ⊥；因为底面三角形ABC 的面积为定值122AC BC ⋅=，SO因此，当SO ⊥平面ABC 时，四面体的体积最大，为13ABC V S SO =⋅=故答案为：(1). (2). 8π10、〔2021届山东省济宁市高三上期末〕下列图是两个腰长均为10cm 的等腰直角三角形拼成的一个四边形ABCD ，现将四边形ABCD 沿BD 折成直二面角A BD C --，那么三棱锥A BCD -的外接球的体积为__________3cm ．【答案】【解析】由题设可将该三棱锥拓展成如下图的正方体，那么该正方体的外接球就是三棱锥的外接球，由于正方体的对角线长为2l R ==即球的半径R =该球的体积343V R π==，应填答案．。