理论力学答案完整版(清华大学出版社)3

第5章 点的复合运动分析5－1 曲柄OA 在图示瞬时以ω0绕轴O 转动，并带动直角曲杆O 1BC 在图示平面内运动。

若d 为已知，试求曲杆O 1BC 的角速度。

解：1、运动分析：动点：A ，动系：曲杆O 1BC ，牵连运动：定轴转动，相对运动：直线，绝对运动：圆周运动。

2、速度分析：r e a v v v += 0a 2ωl v =；0e a 2ωl v v == 01e 1ωω==AO v BC O （顺时针）5－2 图示曲柄滑杆机构中、滑杆上有圆弧滑道，其半径cm 10=R ，圆心O 1在导杆BC 上。

曲柄长cm 10=OA ，以匀角速rad/s 4πω=绕O 轴30=φ。

求此时滑转动。

当机构在图示位置时，曲柄与水平线交角杆CB 的速度。

解：1、运动分析：动点：A ，动系：BC ，牵连运动：平移，相对运动：圆周运动，绝对运动：圆周运动。

2、速度分析：r e a v v v += πω401a =⋅=A O v cm/s ； 12640a e ====πv v v BC cm/s5－3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。

曲柄OA 的末端与滑块铰接，滑块可沿摇杆O 1B 上的滑道滑动。

已知曲柄OA 长r 并以等角速度ω转动，两轴间的距离是OO 1 = d 。

试求滑块滑道中的相对运动方程，以及摇杆的转动方程。

解：分析几何关系：A 点坐标 d t r x +=ωϕcos cos 1 （1） t r x ωϕsin sin 1= （2） （1）、（2）两式求平方，相加，再开方，得： 1．相对运动方程 将（1）、（2）式相除，得： 2．摇杆转动方程：5－4 曲柄摇杆机构如图所示。

已知：曲柄O 1A 以匀角速度ω1绕轴O 1转动，O 1A = R ，O 1O 2 =b ，O 2O = L 。

试求当O 1A 水平位置时，杆BC 的速度。

解：1、A 点：动点：A ，动系：杆O 2A ，牵连运动：定轴转动，相对运动：直线，绝对运动：圆周运动。

CA(a)ωO(a)第10章动能定理及其应用10－1计算图示各系统的动能：1．质量为m ，半径为r 的均质圆盘在其自身平面内作平面运动。

在图示位置时，若已知圆盘上A、B 两点的速度方向如图示，B 点的速度为v B ，θ =45º（图a ）。

2．图示质量为m 1的均质杆OA ，一端铰接在质量为m 2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为v （图b ）。

3．质量为m 的均质细圆环半径为R ，其上固结一个质量也为m 的质点A 。

细圆环在水平面上作纯滚动，图示瞬时角速度为ω（图c ）。

解：1．2222221632(2121)2(212121B B B C C C mv r v mr v m J mv T =⋅+=+=ω2．222122222214321(21212121vm v m r v r m v m v m T +=⋅++=3．22222222)2(212121ωωωωmR R m mR mR T =++=10－2图示滑块A 重力为1W ，可在滑道内滑动，与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。

现已知道滑块沿滑道的速度为1v ，杆AB 的角速度为1ω。

当杆与铅垂线的夹角为ϕ时，试求系统的动能。

解：图（a ）BA T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕω⋅⋅+⋅++++=l g W l l v l v l g W v g W ]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10－3重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。

齿轮II 通过匀质的曲柄OC 带动而运动。

曲柄的重力为Q F ，角速度为ω，齿轮可视为匀质圆盘。

试求行星齿轮机构的动能。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。

则其合力可以表示为。

①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。

试求动齿轮以圆心A 为基点的平面运动方程。

解：ϕc o s )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。

试以杆与铅垂线的夹角θ 表示杆的角速度。

解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。

作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。

则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。

试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。

解：RvR v A A ==ωR v R v B B 22==ωB A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。

设杆BC 在水平位置时，滚子的角速度ω＝12 rad/s ，θ＝30︒，ϕ＝60︒，BC ＝270mm 。

试求该瞬时杆BC 的角速度和点C 的速度。

目录第一章质点力学 (2)第二章质点组力学 (56)第三章刚体力学 (74)第四章转动参考系 (105)第五章分析力学 (115)第一章 质点力学1.1 由题可知示意图如题1.1.1图:{{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a . 则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得11021at t s v +=再由此式得()()2121122t t t t t t s a +-=证明完毕.1.2 解 由题可知,以灯塔为坐标原点建立直角坐标如题1.2.1图.题1.2.1图设A 船经过0t 小时向东经过灯塔,则向北行驶的B 船经过⎪⎭⎫ ⎝⎛+2110t 小时经过灯塔任意时刻A 船的坐标()t t x A 15150--=，0=A yB 船坐标0=B x ，⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛+-=t t y B 15211150则AB 船间距离的平方()()222B A B A y y x x d -+-=即()2021515t t d -=201521115⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛++t t()20202211225225675900450⎪⎭⎫ ⎝⎛++++-=t t tt t2d 对时间t 求导()()67590090002+-=t t dtd d AB 船相距最近，即()02=dtdd ，所以h t t 430=- 即午后45分钟时两船相距最近最近距离22min231543154315⎪⎭⎫ ⎝⎛⨯-⨯+⎪⎭⎫ ⎝⎛⨯=s km1.3 解 ()1如题1.3.2图第1.3题图y题1.3.2图由题分析可知，点C 的坐标为⎩⎨⎧=+=ψψϕsin cos cos a y a r x 又由于在∆AOB 中，有ϕψsin 2sin ar =（正弦定理）所以ry r a 2sin 2sin ==ψϕ联立以上各式运用1cos sin 22=+ϕϕ由此可得rya x r a x 22cos cos --=-=ψϕ得12422222222=---++r y a x y a x r y 得22222223y a x r a x y -=-++化简整理可得()()2222222234r a y x y a x -++=-此即为C 点的轨道方程.（2）要求C 点的速度，分别求导⎪⎪⎩⎪⎪⎨⎧=--=2cos sin cos 2cos sin ϕωψψϕωϕωr y r r x 其中ϕω = 又因为ψϕsin 2sin a r =对两边分别求导 故有ψϕωψcos 2cos a r =所以22y x V +=4cos sin cos 2cos sin 2222ϕωψψϕωϕωr r r +⎪⎪⎭⎫ ⎝⎛--= ()ψϕψϕϕψω++=sin cos sin 4cos cos 22r1.4 解 如题1.4.1图所示，A BOCLxθd 第1.4题图OL 绕O 点以匀角速度转动，C 在AB 上滑动，因此C 点有一个垂直杆的速度分量22x d OC v +=⨯=⊥ωωC 点速度dx d d v v v 222sec sec cos +====⊥⊥ωθωθθ 又因为ωθ= 所以C点加速度 θθθω ⋅⋅⋅⋅==tan sec sec 2d dt dv a ()2222222tan sec 2d x d x d +==ωθθω1.5 解 由题可知，变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin 1π 由加速度的微分形式我们可知dtdv a =代入得dtT t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫ ⎝⎛-=002sin 1π可得 ：D Ttc Tct v ++=2cos2ππ（D 为常数）代入初始条件：0=t 时，0=v ，故c TD π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos2T t T t c v ππ 又因为dtds v =所以=ds dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos2ππ 对等式两边同时积分，可得：⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=t T t T T t c s 2sin 22212πππ1.6 解 由题可知质点的位矢速度r λ=//v ①沿垂直于位矢速度μθ=⊥v又因为 r r λ== //v ， 即r rλ=μθθ==⊥r v 即rμθθ= ()()j i v a θ r dtd r dt d dt d +==（取位矢方向i ，垂直位矢方向j ） 所以()j i i i θ r rdtd r i dt r d r dt d +=+=()dtd r dt d r dt dr r dt d j j j j θθθθ ++=i j j 2r r r θθθ -+= 故()()j i a θθθ r r r r22++-= 即 沿位矢方向加速度()2θ r ra -= 垂直位矢方向加速度()θθr r a 2+=⊥ 对③求导r rr 2λλ== 对④求导θμμθθr rr +-=2⎪⎭⎫⎝⎛+=λμμθr 把③④⑦⑧代入⑤⑥式中可得rr a 222//θμλ-= ⎪⎭⎫ ⎝⎛+=⊥r a μλμθ1.7 解 由题可知⎩⎨⎧==θθsin cos r y r x ①②对①求导θθθ sin cos r r x-= ③ 对③求导2 ④对②求导θθθcos sin r r y+=⑤ 对⑤求导θθθθθθθsin cos cos 2sin 2 r r r ry -++=⑥ 对于加速度a ，我们有如下关系见题1.7.1图题1.7.1图即⎩⎨⎧+=+=θθθθθθcos sin sin cos a a y a a x r r⑦--⑧ 对⑦⑧俩式分别作如下处理：⑦θcos ⨯，⑧θsin ⨯ 即得⎩⎨⎧+=-=θθθθθθθθθθcos sin sin sin cos sin cos cos a a y a a x r r⑨--⑩ ⑨+⑩得θθsin cos yx a r += ⑾ 把④⑥代入 ⑾得2θr r a r -= 同理可得θθθ r r a 2+= 1.8解 以焦点F 为坐标原点，运动如题1.8.1图所示]题1.8.1图则M 点坐标⎩⎨⎧==θθsin cos r y r x 对y x ,两式分别求导⎪⎩⎪⎨⎧+=-=θθθθθθcos sin sin cos r r yr r x 故()()22222cos sin sin cos θθθθθθ r r r r y xv ++-=+=222ωr r+= 如图所示的椭圆的极坐标表示法为()θcos 112e e a r +-=对r 求导可得（利用ωθ= ）又因为()()221cos 111e a e e a r -+-=θ即()rer e a --=21cos θ 所以()()2222222221211cos 1sin e r e ar r e a --+--=-=θθ故有()2222224222sin 1ωθωr e a r e v +-=()2224221ea r e -=ω()()]1211[2222222e r e ar r ea --+--22ωr +()()⎥⎦⎤⎢⎣⎡--+-⋅-=2222222221121e e ar r r e e a r ω()r r a b r -=2222ω 即()r a r br v -=2ω（其中()b a e b ,1222-=为椭圆的半短轴）1.9证 质点作平面运动，设速度表达式为j i v y x v v +=令为位矢与轴正向的夹角，所以dt d v dt dv dt d v dt dv dt d y y x x j j i i v a +++==j i ⎪⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=θθ x y y x v dt dv v dt dv 所以[]j i a ⎪⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛-=θθ x yy x v dt dv v dt dv ()j i y x v v +⋅ θθ y x y y y x x x v v dt dv v v v dt dv v ++-=dtdv v dt dv v y yxx += 又因为速率保持为常数，即C C v v y x ,22=+为常数对等式两边求导022=+dtdv v dt dv v y y xx所以0=⋅v a即速度矢量与加速度矢量正交.1.10解 由题可知运动轨迹如题1.10.1图所示，题1.10.1图则质点切向加速度dtdv a t =法向加速度ρ2n v a =，而且有关系式ρ2v 2k dt dv -= ①又因为()232y 1y 1'+''=ρ②2px y 2=所以yp y =' ③ 32yp y -='' ④ 联立①②③④2322322y p 1y p 2kv dtdv⎪⎪⎭⎫ ⎝⎛+-= ⑤又dydv ydt dy dy dv dt dv =⋅=把2px y 2=两边对时间求导得pyy x= 又因为222y xv += 所以22221py v y+= ⑥ 把⑥代入⑤23223222122121⎪⎪⎭⎫ ⎝⎛+⋅-=⋅⎪⎪⎭⎫ ⎝⎛+y p y p kv dydvp y v既可化为222py dykp v dv +-= 对等式两边积分222py dykp v dv p p vu+-=⎰⎰- 所以πk ue v -=1.11解 由题可知速度和加速度有关系如图1.11.1所示题1.11.1图⎪⎪⎩⎪⎪⎨⎧====ααcos sin 2a dt dv a a r v a t n 两式相比得dtdvr v ⋅=ααcos 1sin 2 即2cot 1vdv dt r =α 对等式两边分别积分200cot 1v dv dt rv v t⎰⎰=α 即αcot 11rtv v -=此即质点的速度随时间而变化的规律.1.12证 由题1.11可知质点运动有关系式⎪⎪⎩⎪⎪⎨⎧==ααcos sin 2a dtdv a r v ①② 所以 ωθθθd dv dt d d dv dt dv =⋅=，联立①②，有ααωθcos sin 2r v d dv = 又因为r v ω=所以 θαd vdv cot =，对等式两边分别积分，利用初始条件0=t 时，0θθ=()αθθcot 00-=e v v1.13 证（a ）当00=v ，即空气相对地面上静止的，有牵相绝v v v +=.式中绝v 质点相对静止参考系的绝对速度， 相v 指向点运动参考系的速度， 牵v 指运动参考系相对静止参考系的速度.可知飞机相对地面参考系速度：绝v =v '，即飞机在舰作匀速直线运动.所以飞机来回飞行的总时间v l t '=20. （b ）假定空气速度向东，则当飞机向东飞行时速度01v v v +'=飞行时间1v v lt +'=当飞机向西飞行时速度0v v v v v -'=+=牵相飞行时间2v v lt -'=故来回飞行时间021v v l t t t +'=+=0v v l -'+222v v lv -''= 即2200220112v v t v v v lt '-='-'= 同理可证，当空气速度向西时，来回飞行时间2201v v t t '-=（c ）假定空气速度向北.由速度矢量关系如题1.13.1图v 题1.13.1图v v v '+=0绝202v v v -'= 所以来回飞行的总时间222vv l t -'=2200220112v vt v v v l '-='-'=同理可证空气速度向南时，来回飞行总时间仍为2201v v t t '-=1.14解 正方形如题1.14.1图。

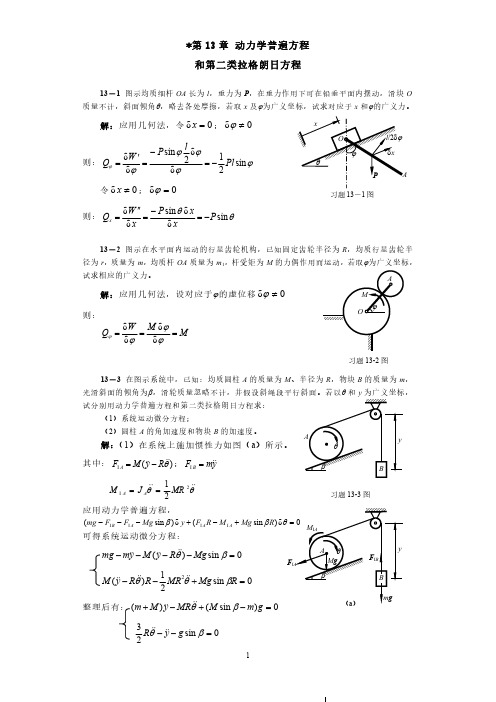
习题13－1图*第13章动力学普遍方程和第二类拉格朗日方程13－1图示均质细杆OA 长为l ，重力为P ，在重力作用下可在铅垂平面内摆动，滑块O 质量不计，斜面倾角θ，略去各处摩擦，若取x 及ϕ为广义坐标，试求对应于x 和ϕ的广义力。

解：应用几何法，令0δ=x ；0δ≠ϕ则：ϕϕϕϕϕϕsin 21δδ2sin δδPl lP W Q -=-='=令0δ≠x ；0δ=ϕ则：θθsin δδsin δδP xxP x W Q x -=-=''=13－2图示在水平面内运动的行星齿轮机构，已知固定齿轮半径为R ，均质行星齿轮半径为r ，质量为m ，均质杆OA 质量为m 1，杆受矩为M 的力偶作用而运动，若取ϕ为广义坐标，试求相应的广义力。

解：应用几何法，设对应于ϕ的虚位移0δ≠ϕ则：M M W Q ===ϕϕϕϕδδδδ13－3在图示系统中，已知：均质圆柱A 的质量为M 、半径为R ，物块B 的质量为m ，光滑斜面的倾角为β，滑轮质量忽略不计，并假设斜绳段平行斜面。

若以θ 和y 为广义坐标，试分别用动力学普遍方程和第二类拉格朗日方程求：（1）系统运动微分方程；（2）圆柱A 的角加速度和物块B 的加速度。

解：（1）在系统上施加惯性力如图（a ）所示。

其中：)(I θ R y M F A -=；y m F B=I θθ2I 21MR J M A A ==应用动力学普遍方程，δ)sin (δ)sin (I I I I +-+---θββR Mg M R F y Mg F F mg A A A B 可得系统运动微分方程：0sin )(=----βθMg R y M y m mg 0sin 21)(2=+--R Mg MR R R yM βθθ 整理后有：0)sin ()(=-+-+g m M MR yM m βθ 0sin 23=--βθg yR习题13-2图习题13-3图F应用第二类拉格朗日方程：2222)(21212121θθ R y M MR y m T -+⋅+=；)(sin θβR y Mg mgy V -+-==-=V T L 2222)(21212121θθ R y M MR y m -+⋅+)(sin θβR y Mg mgy --+)(d d θ R yM y m y L t -+=∂∂；βsin Mg mg y L -=∂∂0d d =∂∂-∂∂y L y L t ；0)sin ()(=-+-+g m M MR y M m βθ （a ）)(21d d 2θθθ R y RM MR L t --=∂∂；R Mg L βθsin =∂∂0d d =∂∂-∂∂θθL L t；0sin 23=--βθg y R （b ）（2）求圆柱A 的角加速度和物块B 的加速度。

理论力学教科书课后习题及解析第一章偶，大小是260Nm，转向是逆时针。

习题 4- 1．求图示平面力系的合成结果，长度单位为m。

习题 4－ 3．求下列各图中平行分布力的合力和对于 A 点之矩。

解： (1) 平行力系对 A 点的矩是：解： (1) 取 O 点为简化中心，求平面力系的主矢：取 B 点为简化中心，平行力系的主矢是：求平面力系对O 点的主矩：平行力系对 B 点的主矩是：(2)合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B，且：如图所示；向 A 点简化的结果是一个力R A和一个力偶M A，且：如图所示；将 R B向下平移一段距离d，使满足：最后简化为一个力R ，大小等于R B。

其几何意义是： R 的大小等于载荷分布的将 R A向右平移一段距离d，使满足：矩形面积，作用点通过矩形的形心。

(2)取 A 点为简化中心，平行力系的主矢是：最后简化为一个力R，大小等于R A。

其几何意义是：R 的大小等于载荷分布的三角形面积，作用点通过三角形的形心。

平行力系对 A 点的主矩是：列平衡方程：习题 4-4 ．求下列各梁和刚架的支座反力，长度单位为m。

解方程组：反力的实际方向如图示。

校核：解： (1) 研究 AB 杆，受力分析，画受力图：结果正确。

(2) 研究 AB 杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：(3) 研究 ABC ，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：列平衡方程：反力的实际方向如图示。

校核：解方程组：结果正确。

反力的实际方向如图示。

校核：结果正确。

习题 4-5 ．重物悬挂如图，已知G=1.8kN ，其他重量不计；求铰链 A 的约束反力和杆 BC 所受的力。

列平衡方程：解方程组：解： (1) 研究整体，受力分析（BC 是二力杆），画受力图：反力的实际方向如图示。

列平衡方程：习题 4-8 ．图示钻井架，G=177kN ，铅垂荷载P=1350kN ，风荷载 q=1.5kN/m ，水平力 F=50kN ；求支座 A 的约束反力和撑杆CD 所受的力。

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应，力是（ A ）。

A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示，作用在物体A 上的两个大小不等的力1F 和2F ，沿同一直线但方向相反，则其合力可表为（ C ）。

A.1F –2FB.2F - 1FC.1F +2F图1－18 图1－191-3 F =100N ，方向如图1-19所示。

若将F 沿图示x ，y 方向分解，则x 方向分力的大小x F = C N ，y 方向分力的大小y F = ___B __ N 。

A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。

A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。

A. 刚体；B. 变形体；C. 刚体和变形体。

1-6 如图1-20所示，已知一正方体，各边长a ，沿对角线BH 作用一个力F ，则该力在x 1轴上的投影为 A 。

A. 0B. F/2C. F/6D.－F/31-7如图1-20所示，已知F=100N ，则其在三个坐标轴上的投影分别为： Fx = －402N ，Fy = 302N ，Fz = 502 N 。

图1－20 图1－21第二章力系的简化2-1．通过A（3，0，0），B（0，4，5）两点（长度单位为米），且由A指向B的力F，在z轴上投影为，对z轴的矩的大小为。

答：F/2；62F/5。

2-2．已知力F的大小，角度φ和θ，以及长方体的边长a，b，c，则力F在轴z和y上的投影：Fz= ；Fy= ；F对轴x的矩M x(F)= 。

答：Fz=F·sinφ；Fy=－F·cosφ·cosφ；Mx（F）=F（b·sinφ+c·cosφ·cosθ）图2－40 图2－412-3．力通过A（3，4、0），B（0，4，4）两点（长度单位为米），若F=100N，则该力在x轴上的投影为，对x轴的矩为。

理论力学第三版课后习题答案【篇一：理论力学教程思考题答案第三版.doc】2r?.。

这表示质点的径向与横向运动在相互影响，它们一起才?2，a??rar??r??r?能完整地描述质点的运动变化情况1.3答：内禀方程中，an是由于速度方向的改变产生的，在空间曲线中，由于a恒位于密切面内，速度v总是沿轨迹的切线方向，而an垂直于v指向曲线凹陷一方，故an总是沿助法线方向。

质点沿空间曲线运动时，ab?0,fb?0z何与牛顿运动定律不矛盾。

因质点除受作用力f，还受到被动的约反作用力r，二者在副法线方向的分量成平衡力fb?rb?0，故ab?0符合牛顿运动率。

有人会问：约束反作用力靠谁施加，当然是与质点接触的周围其他物体由于受到质点的作用而对质点产生的反作用力。

有人也许还会问：某时刻若fb与rb大小不等，ab就不为零了？当然是这样，但此时刻质点受合力的方向与原来不同，质点的位置也在改变，副法线在空间中方位也不再是原来ab所在的方位，又有了新的副法线，在新的副法线上仍满足fb?rb?0即ab?0。

这反映了牛顿定律得瞬时性和矢量性，也反映了自然坐标系的方向虽质点的运动而变。

1.4答：质点在直线运动中只有a?而无an，质点的匀速曲线运动中只有an而无a?；质点作变速运动时即有at又有an。

1.5而dr即反应位矢r大小的改变又反映其方向的改变，是质点运动某时刻的速度矢量，dtdrdr?j而dr?r?i?r??。

在直线运动中，?r只表示r大小的改变。

如在极坐标系中，dtdtdt规定了直线的正方向后，drdrdrdr。

且的正负可表示的指向，二者都可表示质点dtdtdtdt的运动速度；在曲线运动中drdrdrdr?，且也表示不了的指向，二者完全不同。

dtdtdtdtdvdv表示质点运动速度的大小，方向的改变是加速度矢量，而只是质点运动速度大小dtdtdvdvaan,而?a?。

dtdt的改变。

在直线运动中规定了直线的正方向后，二者都可表示质点运动的加速度；在曲线运动中，二者不同，1.6答：不论人是静止投篮还是运动投篮，球对地的方向总应指向篮筐，其速度合成如题1.6v球对人v人对地题1-6图图所示，故人以速度v向球网前进时应向高于篮筐的方向投出。