清华大学高等数值分析 第一次实验作业

7、设y0=28，按递推公式y n=y n−1−1100√783，n=1,2,…计算y100，若取√783≈27.982，试问计算y100将有多大误差？答：y100=y99−1100√783=y98−2100√783=⋯=y0−100100√783=28−√783若取√783≈27.982，则y100≈28−27.982=0.018，只有2位有效数字，y100的最大误差位0.00110、设f(x)=ln⁡(x−√x2−1)，它等价于f(x)=−ln⁡(x+√x2−1)。

分别计算f(30)，开方和对数取6位有效数字。

试问哪一个公式计算结果可靠？为什么？答：√x2−1≈29.9833则对于f(x)=ln(x−√x2−1)，f(30)≈−4.09235对于f(x)=−ln(x+√x2−1)，f(30)≈−4.09407而f(30)=⁡ln⁡(30−√302−1)⁡，约为−4.09407，则f(x)=−ln⁡(x+√x2−1)计算结果更可靠。

这是因为在公式f(x)=ln⁡(x−√x2−1)中，存在两相近数相减（x−√x2−1）的情况，导致算法数值不稳定。

11、求方程x2+62x+1=0的两个根，使它们具有四位有效数字。

答：x12=−62±√622−42=−31±√312−1则x1=−31−√312−1≈−31−30.98=−61.98x2=−31+√312−1=131+√312−1≈−131+30.98≈−0.0161312.（1）、计算√101.1−√101，要求具有4位有效数字答：√101.1−√101=√101.1+√101≈0.110.05+10.05≈0.00497514、试导出计算积分I n=∫x n4x+1dx1的一个递推公式，并讨论所得公式是否计算稳定。

答：I n=∫x n4x+1dx1 0=∫14(4x+1)x n−1−14x n−14x+1dx=114∫x n−11dx−14∫x n−14x+1dx1=14n−14I n−1，n=1，2…I0=∫14x+1dx=ln541记εn为I n的误差，则由递推公式可得εn=−14εn−1=⋯=(−14)nε0当n增大时，εn是减小的，故递推公式是计算稳定的。

数值分析大作业一一、算法设计方案1、求λ1和λ501的值：思路：采用幂法求出按模最大特征值λmax，该值必为λ1或λ501，若λmax小于0，则λmax=λ1；否则λmax=λ501。

再经过原点平移，使用幂法迭代出矩阵A-λmax I的特征值，此时求出的按模最大特征值即为λ1和λ501的另一个值。

2、求λs的值：采用反幂法求出按模最小的特征值λmin即为λs，其中的方程组采用LU分解法进行求解。

3、求与μk最接近的特征值：对矩阵A采用带原点平移的反幂法求解最小特征值，其中平移量为：μk。

4、A的条件数cond(A)=| λmax/λmin|；5、A的行列式的值：先将A进行LU分解，再求U矩阵对角元素的乘积即为A 行列式的值。

二、源程序#include<iostream>#include<iomanip>#include<math.h>#define N 501#define E 1.0e-12 //定义精度常量#define r 2#define s 2using namespace std;double a[N];double cc[5][N];void init();double mifa();double fmifa();int max(int aa,int bb);int min(int aa,int bb);int max_3(int aa,int bb,int cc);void LU();void main(){double a1,a2,d1,d501=0,ds,det=1,miu[39],lamta,cond;int i,k;init();/*************求λ1和λ501********************/a1=mifa();if(a1<0)d1=a1; //若小于0则表示λ1的值elsed501=a1; //若大于0则表示λ501的值for(i=0;i<N;i++)a[i]=a[i]-a1;a2=mifa()+a1;if(a2<0)d1=a2; //若小于0则表示λ1的值elsed501=a2; //若大于0则表示λ501的值cout<<"λ1="<<setiosflags(ios::scientific)<<setprecision(12)<<d1<<"\t";cout<<"λ501="<<setiosflags(ios::scientific)<<setprecision(12)<<d501<<endl;/**************求λs*****************/init();ds=fmifa();cout<<"λs="<<setiosflags(ios::scientific)<<setprecision(12)<<ds<<endl;/**************求与μk最接近的特征值λik**************/cout<<"与μk最接近的特征值λik:"<<endl;for(k=0;k<39;k++){miu[k]=d1+(k+1)*(d501-d1)/40;init();for(i=0;i<N;i++)a[i]=a[i]-miu[k];lamta=fmifa()+miu[k];cout<<"λi"<<k+1<<"\t\t"<<setiosflags(ios::scientific)<<setprecision(12)<<lamta<<en dl;}/**************求A的条件数**************/cout<<"矩阵A的条件式";cond=abs(max(abs(d1),abs(d501))/ds);cout<<"cond="<<setiosflags(ios::scientific)<<setprecision(12)<<cond<<endl;/**************求A的行列式**************/cout<<"矩阵A的行列式";init();LU();for(i=0;i<N;i++){det*=cc[2][i];}cout<<"det="<<setiosflags(ios::scientific)<<setprecision(12)<<det<<endl;system("pause");}/**************初始化函数，给a[N]赋值*************/void init(){int i;for(i=1;i<=501;i++)a[i-1]=(1.64-0.024*i)*sin((double)(0.2*i))-0.64*exp((double)(0.1/i)); }/**************幂法求最大绝对特征值**************/double mifa(){int i,k=0;double u[N],y[N]={0},b=0.16,c=-0.064,Beta_=0,error;for(i=0;i<501;i++)u[i]=1; //令u[N]=1for(k=1;k<2000;k++) //控制最大迭代次数为2000{/***求y(k-1)***/double sum_u=0,gh_sum_u;for(i=0;i<N;i++){sum_u+=u[i]*u[i]; }gh_sum_u=sqrt(sum_u);for(i=0;i<N;i++){y[i]=u[i]/gh_sum_u;}/****求新的uk****/u[0]=a[0]*y[0]+b*y[1]+c*y[2];u[1]=b*y[0]+a[1]*y[1]+b*y[2]+c*y[3]; //前两列和最后两列单独拿出来求中D间的循环求for(i=2;i<N-2;i++){u[i]=c*y[i-2]+b*y[i-1]+a[i]*y[i]+b*y[i+1]+c*y[i+2];}u[N-2]=c*y[N-4]+b*y[N-3]+a[N-2]*y[N-2]+b*y[N-1];u[N-1]=c*y[N-3]+b*y[N-2]+a[N-1]*y[N-1];/***求beta***/double Beta=0;for(i=0;i<N;i++){Beta+=y[i]*u[i];}//cout<<"Beta"<<k<<"="<<Beta<<"\t"; 输出每次迭代的beta /***求误差***/error=abs(Beta-Beta_)/abs(Beta);if(error<=E) //若迭代误差在精度水平内则可以停止迭代{return Beta;} //控制显示位数Beta_=Beta; //第个eta的值都要保存下来，为了与后个值进行误差计算 }if(k==2000){cout<<"error"<<endl;return 0;} //若在最大迭代次数范围内都不能满足精度要求说明不收敛}/**************反幂法求最小绝对特¬征值**************/double fmifa(){int i,k,t;double u[N],y[N]={0},yy[N]={0},b=0.16,c=-0.064,Beta_=0,error;for(i=0;i<501;i++)u[i]=1; //令u[N]=1for(k=1;k<2000;k++){double sum_u=0,gh_sum_u;for(i=0;i<N;i++){sum_u+=u[i]*u[i]; }gh_sum_u=sqrt(sum_u);for(i=0;i<N;i++){y[i]=u[i]/gh_sum_u;yy[i]=y[i]; //用重新赋值，避免求解方程组的时候改变y的值}/****LU分解法解方程组Au=y，求新的***/LU();for(i=2;i<=N;i++){double temp_b=0;for(t=max(1,i-r);t<=i-1;t++)temp_b+=cc[i-t+s][t-1]*yy[t-1];yy[i-1]=yy[i-1]-temp_b;}u[N-1]=yy[N-1]/cc[s][N-1];for(i=N-1;i>=1;i--){double temp_u=0;for(t=i+1;t<=min(i+s,N);t++)temp_u+=cc[i-t+s][t-1]*u[t-1];u[i-1]=(yy[i-1]-temp_u)/cc[s][i-1];}double Beta=0;for(i=0;i<N;i++){Beta+=y[i]*u[i];}error=abs(Beta-Beta_)/abs(Beta);if(error<=E){return (1/Beta);}Beta_=Beta;}if(k==2000){cout<<"error"<<endl;return 0;} }/**************求两数最大值的子程序**************/int max(int aa,int bb){return(aa>bb?aa:bb);}/**************求两数最小值的子程序**************/int min(int aa,int bb){return(aa<bb?aa:bb);}/**************求三数最大值的子程序**************/int max_3(int aa,int bb,int cc){ int tt;if(aa>bb)tt=aa;else tt=bb;if(tt<cc) tt=cc;return(tt);}/**************LU分解**************/void LU(){int i,j,k,t;double b=0.16,c=-0.064;/**赋值压缩后矩阵cc[5][501]**/for(i=2;i<N;i++)cc[0][i]=c;for(i=1;i<N;i++)cc[1][i]=b;for(i=0;i<N;i++)cc[2][i]=a[i];for(i=0;i<N-1;i++)cc[3][i]=b;for(i=0;i<N-2;i++)cc[4][i]=c;for(k=1;k<=N;k++){for(j=k;j<=min(k+s,N);j++){double temp=0;for(t=max_3(1,k-r,j-s);t<=k-1;t++)temp+=cc[k-t+s][t-1]*cc[t-j+s][j-1];cc[k-j+s][j-1]=cc[k-j+s][j-1]-temp;}//if(k<500){for(i=k+1;i<=min(k+r,N);i++){double temp2=0;for(t=max_3(1,i-r,k-s);t<=k-1;t++)temp2+=cc[i-t+s][t-1]*cc[t-k+s][k-1];cc[i-k+s][k-1]=(cc[i-k+s][k-1]-temp2)/cc[s][k-1];}}}}三、程序结果。

问题1：20.给定数据如下表：试求三次样条插值S(x)，并满足条件 (1)S`(0.25)=1.0000，S`(0.53)=0.6868； （2）S ’’(0.25)=S ’’(0.53)=0。

分析：本问题是已知五个点，由这五个点求一三次样条插值函数。

边界条件有两种，（1）是已知一阶倒数，（2）是已知自然边界条件。

对于第一种边界(已知边界的一阶倒数值)，可写出下面的矩阵方程。

⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡432104321034322110d M M M M M 200020000020022d d d d λμμλμλμλ其中μj =j1-j 1-j h h h +，λi=j1-j j h h h +，dj=6f[x j-1,x j ,x j+1]， μn =1，λ0=1对于第一种边界条件d 0=0h 6（f[x 0,x 1]-f 0`），d n =1-n h 6（f`n-f `[x n-1,x n ]） 解：由matlab 计算得：由此得矩阵形式的线性方程组为：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡ 2.1150-2.4286-3.2667-4.3143-5.5200-M M M M M 25714.00001204286.000004000.026000.0006429.023571.0001243210解得 M 0=-2.0286;M 1=-1.4627;M 2= -1.0333; M 3= -0.8058; M 4=-0.6546S(x)=⎪⎪⎩⎪⎪⎨⎧∈-+-+-∈-+-+-∈-+-+-∈-+-+-]53.0,45.0[x 5.40x 9.1087x 35.03956.8.450-x 1.3637-x .5301.67881- ]45.0,39.0[x 9.30x 11.188x 54.010.418793.0-x 2.2384-x .450(2.87040-]39.0,30.0[x 03.0x 6.9544x 9.30 6.107503.0-x 1.9136-x .3902.708779-]30.0,25.0[x 5.20x 10.9662x 0.3010.01695.20-x 4.8758-x .3006.76209-33333333），（）（）（）（），（）（）（）），（）（）（）（），（）（）（）（Matlab 程序代码如下：function tgsanci(n,s,t) %n代表元素数，s,t代表端点的一阶导。

20130917题目求证：在矩阵的LU 分解中，111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明：在高斯消去过程中，假设0jj a ≠ ，若a=0，可以通过列变换使得前面的条件成立，这里不考虑这种情况。

对矩阵A 进行LU 分解，()()()()()1111111L M n M M M n ---=-=••-………… ，其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ，i e 、j e 为n 维线性空间的自然基。

()M j 是通过对单位阵进行初等变换得到，通过逆向的变换则可以得到单位阵，由此很容易得到()M j 的逆矩阵为1n T n ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。

故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换，从右向左乘，则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。

由于最初的矩阵为单位阵，变换从右向左展开，因而每一次变换不改变已经更新的数据，既该变换是从右向左一列一列更新数据，故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。

数学证明：1n Tij i j i j e e α=+⎛⎫ ⎪⎝⎭∑具有,000n j j A -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式，且有+1,-11,10000=000n j j n j n j A B --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式，因此： 1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问：能否用逐次householder 相似变换变实矩阵A 为上三角矩阵，为什么？解：不能用逐次householder 相似变换变A 为上三角矩阵，原因如下：A 记作：()12=,,n A a a a ……， ，存在householder 阵1H s.t. 1111H a e α= ，则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数，故无法通过householder 变换实现上三角化。

数值分析实验报告-清华大学--线性代数方程组的数值解法(总15页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--线性代数方程组的数值解法实验1. 主元的选取与算法的稳定性问题提出：Gauss 消去法是我们在线性代数中已经熟悉的。

但由于计算机的数值运算是在一个有限的浮点数集合上进行的，如何才能确保Gauss 消去法作为数值算法的稳定性呢？Gauss 消去法从理论算法到数值算法，其关键是主元的选择。

主元的选择从数学理论上看起来平凡，它却是数值分析中十分典型的问题。

实验内容：考虑线性方程组 n n n R b R A b Ax ∈∈=⨯,,编制一个能自动选取主元，又能手动选取主元的求解线性方程组的Gauss 消去过程。

实验要求：（1）取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157,6816816816 b A ，则方程有解T x )1,,1,1(* =。

取n=10计算矩阵的条件数。

让程序自动选取主元，结果如何？（2）现选择程序中手动选取主元的功能。

每步消去过程总选取按模最小或按模尽可能小的元素作为主元，观察并记录计算结果。

若每步消去过程总选取按模最大的元素作为主元，结果又如何？分析实验的结果。

（3）取矩阵阶数n=20或者更大，重复上述实验过程，观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异，说明主元素的选取在消去过程中的作用。

（4）选取其他你感兴趣的问题或者随机生成矩阵，计算其条件数。

重复上述实验，观察记录并分析实验结果。

程序清单n=input('矩阵A 的阶数:n=');A=6*diag(ones(1,n))+diag(ones(1,n-1),1)+8*diag(ones(1,n-1),-1); b=A*ones(n,1);p=input('计算条件数使用p-范数,p='); cond_A=cond(A,p) [m,n]=size(A);Ab=[A b];r=input('选主元方式(0:自动;1:手动)，r=');Abfor i=1:n-1switch rcase(0)[aii,ip]=max(abs(Ab(i:n,i)));ip=ip+i-1;case (1)ip=input(['第',num2str(i),'步消元，请输入第',num2str(i),'列所选元素所处的行数：']);end;Ab([i ip],:)=Ab([ip i],:);aii=Ab(i,i);for k=i+1:nAb(k,i:n+1)=Ab(k,i:n+1)-(Ab(k,i)/aii)*Ab(i,i:n+1);end;if r==1Abendend;x=zeros(n,1);x(n)=Ab(n,n+1)/Ab(n,n);for i=n-1:-1:1x(i)=(Ab(i,n+1)-Ab(i,i+1:n)*x(i+1:n))/Ab(i,i);endx运行结果(1)n=10，矩阵的条件数及自动选主元Cond(A,1) =×103Cond(A,2) = ×103Cond(A,inf) =×103程序自动选择主元（列主元）a.输入数据矩阵A的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动)，r=0b.计算结果x=[1，1，1，1，1，1，1，1，1，1]T(2)n=10，手动选主元a. 每步消去过程总选取按模最小或按模尽可能小的元素作为主元矩阵A 的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动)，r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元，请输入第1列所选元素所处的行数：1(2)(2) 6.0000 1.00007.00004.6667 1.0000 5.66678.0000 6.000015.0000[]8.00001.000015.00006.0000 1.00008.0000 6.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元，请输入第2列所选元素所处的行数：2…（实际选择时，第k 步选择主元处于第k 行） 最终计算得x=[, , , , , , , , , ]Tb. 每步消去过程总选取按模最大的元素作为主元 矩阵A 的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动)，r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元，请输入第1列所选元素所处的行数：2(2)(2)8.0000 6.0000 1.000015.0000-3.50000.7500-4.250008.0000 6.0000 1.000015.0000[]8.0000 6.000015.00008.0000 1.00006.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元，请输入第2列所选元素所处的行数：3…（实际选择时，第k 步选择主元处于第k+1行） 最终计算得x=[1，1，1，1，1，1，1，1，1，1]T(3)n=20，手动选主元a. 每步消去过程总选取按模最小或按模尽可能小的元素作为主元 矩阵A 的阶数:n=20计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动)，r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元，请输入第1列所选元素所处的行数：1(2)(2) 6.0000 1.00007.00004.6667 1.0000 5.66678.0000 6.000015.0000[]8.00001.000015.00006.0000 1.00008.0000 6.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元，请输入第2列所选元素所处的行数：2…（实际选择时，第k 步选择主元处于第k 行） 最终计算得x=[，，，，，，，，，，，，，，，，，，，]T b. 每步消去过程总选取按模最大的元素作为主元 矩阵A 的阶数:n=20计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动)，r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元，请输入第1列所选元素所处的行数：2(2)(2)8.0000 6.0000 1.000015.0000-3.50000.7500-4.250008.0000 6.0000 1.000015.0000[]8.0000 6.000015.00008.0000 1.00006.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元，请输入第2列所选元素所处的行数：3…（实际选择时，第k步选择主元处于第k+1行）最终计算得x=[1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1，1]T(4)A分别为幻方矩阵，Hilbert矩阵，pascal矩阵和随机矩阵简要分析计算(1)表明：对于同一矩阵，不同范数定义的条件数是不同的；Gauss消去法在消去过程中选择模最大的主元能够得到比较精确的解。

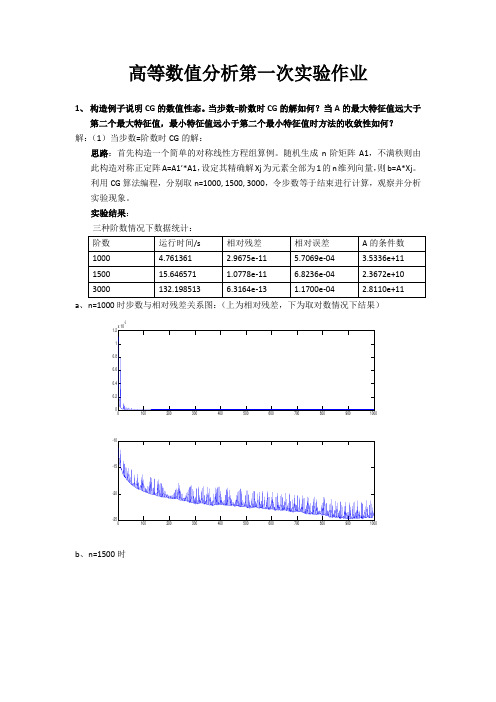
《数值分析》课程设计—作业实验一1.1 水手、猴子和椰子问题：五个水手带了一只猴子来到南太平洋的一个荒岛上，发现那里有一大堆椰子。

由于旅途的颠簸，大家都很疲惫，很快就入睡了。

第一个水手醒来后，把椰子平分成五堆，将多余的一只给了猴子，他私藏了一堆后便又去睡了。

第二、第三、第四、第五个水手也陆续起来，和第一个水手一样，把椰子分成五堆，恰多一只猴子，私藏一堆，再去入睡，天亮以后，大家把余下的椰子重新等分成五堆，每人分一堆，正好余一只再给猴子，试问原先共有几只椰子？试分析椰子数目的变化规律，利用逆向递推的方法求解这一问题。

解：一、问题分析：对于本题，比较简单，我们只需要判断原来椰子的个数及每个人私藏了一份之后剩下的是否能被5除余1，直到最后分完。

二、问题求解：通过matlab 建立M 文件，有如下程序：或者对于第一个程序，n 取2000；对于第二个程序，n 取20001，就能得到我们想要的结果，即原先一共有15621个椰子，最终平均每人得4092个椰子。

n=input('input n:');forx=1:n p=5*x+1;for k=1:5 p=5*p/4+1;end if p==fix(p) break ; end enddisp([x,p]) input n:20001023 15621function fentao(n)a=cat(1,7);for j=n:-1:1 a(1)=j;i=1; while i<7a(i+1)=4*(a(i)-1)/5; i=i+1;endif a(7)==fix(a(7)) a, end end end>> fentao(20001) a =15621 12496 9996 7996 6396 5116 4092（本文档内的有些运行结果，限于篇幅，使文档结构更和谐、紧凑，已做相关的改动，程序代码没变）1.2 当0,1,2,,100n = 时，选择稳定的算法计算积分1d 10n xn xe I x e--=+⎰.解：一、问题分析：由1d 10n xn xe I x e--=+⎰知： 110101==+⎰dx I I以及： )1(110101011)1(1nnxxnxxn n n endx edx ee eI I ----+-+-==++=+⎰⎰得递推关系：⎪⎩⎪⎨⎧--=-=-+n n n I e n I I I 10)1(1101101，但是通过仔细观察就能知道上述递推公式每一步都将误差放大十倍，即使初始误差很小，但是误差的传播会逐步扩大，也就是说用它构造的算法是不稳定的，因此我们改进上述递推公式（算法）如下：⎪⎪⎩⎪⎪⎨⎧--=-=+-))1(1(101)1(101110n n n I e n I I I通过比较不难得出该误差是逐步缩小的，即算法是稳定的。

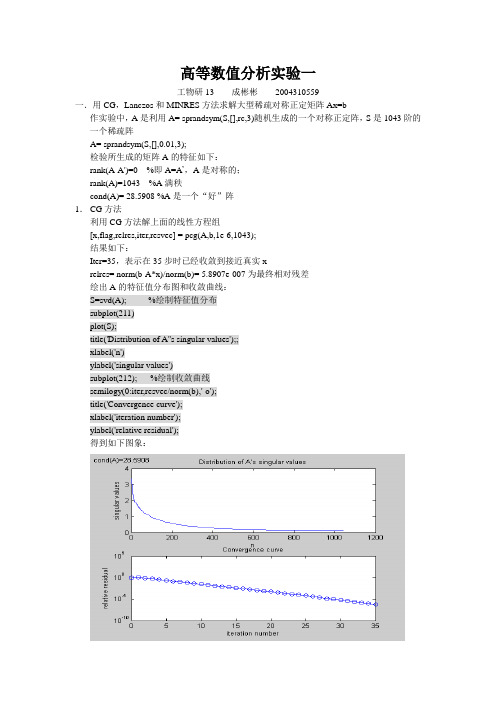
高等数值分析实验一工物研13 成彬彬2004310559一．用CG，Lanczos和MINRES方法求解大型稀疏对称正定矩阵Ax=b作实验中，A是利用A= sprandsym(S,[],rc,3)随机生成的一个对称正定阵，S是1043阶的一个稀疏阵A= sprandsym(S,[],0.01,3);检验所生成的矩阵A的特征如下：rank(A-A')=0 %即A=A’，A是对称的；rank(A)=1043 %A满秩cond(A)= 28.5908 %A是一个“好”阵1．CG方法利用CG方法解上面的线性方程组[x,flag,relres,iter,resvec] = pcg(A,b,1e-6,1043);结果如下：Iter=35，表示在35步时已经收敛到接近真实xrelres= norm(b-A*x)/norm(b)= 5.8907e-007为最终相对残差绘出A的特征值分布图和收敛曲线：S=svd(A); %绘制特征值分布subplot(211)plot(S);title('Distribution of A''s singular values');;xlabel('n')ylabel('singular values')subplot(212); %绘制收敛曲线semilogy(0:iter,resvec/norm(b),'-o');title('Convergence curve');xlabel('iteration number');ylabel('relative residual');得到如下图象：为了观察CG方法的收敛速度和A的特征值分布的关系，需要改变A的特征值：(1).研究A的最大最小特征值的变化对收敛速度的影响在A的构造过程中，通过改变A= sprandsym(S,[],rc,3)中的参数rc(1/rc为A的条件数)，可以达到改变A的特征值分布的目的：通过改变rc=0.1，0.0001得到如下两幅图以上三种情况下，由收敛定理2.2.2计算得到的至多叠代次数分别为：48，14和486，由于上实验结果可以看出实际叠代次数都比上限值要小较多。

数值分析实验课第一次作业1207410003周萍萍 12级数学师范2班1：矩阵1032006705012 3 4 2 A ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭计算2,34,235.c A A =+1001 0000B ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭将A 的第1和2列拼接在B 的右侧得到D.将D 的3,4行拼接在B 的转置的下面得到E.使用size 函数给出矩阵E 的维数.解：>> A=[1,0,3,2;0,0,6,7;0,5,0,1;2,3,4,3];>> C=3*A(2,3)+5*A(4,2)C =33>> B=[1,0;0,1;0,0;0,0];>> D=[B,A(:,1:2)] 矩阵的拼接D =1 0 1 00 1 0 00 0 0 50 0 2 3>> E=[B';D(3:4,:)]E =1 0 0 00 1 0 00 0 0 50 0 2 3>> size(E) 矩阵函数计算ans4 4第2题：将0到1是10等分，记为a 。

e 是维数和a 相同的全2数组，计算a./b 和b.\a解：>> a=linspace(0,1,10); 数组的输入>> b=[2,2,2,2,2,2,2,2,2,2];>> a./bans =0 0.0556 0.1111 0.1667 0.2222 0.2778 0.3333 0.3889 0.4444 0.5000>> b.\aans =0 0.0556 0.1111 0.1667 0.2222 0.2778 0.3333 0.3889 0.4444 0.5000第3题：a=‘You ’ ,b=‘are ’, c=‘a ’,d=‘student ’请拼接出一个 You are a student ！的字符串解:>> a='You';b='are';c='a';d='student';>> >> s=[a,' ',b,' ',c,' ',d,'!']s =You are a student! 字符串运算第4题： 使用不同颜色和线形绘制出 [0,2]π 上的 sin 22x x y = 曲线和1cos cos 77,[0,2].1sin sin 77x y θθθπθθ⎧=+⎪⎪∈⎨⎪=-⎪⎩曲线若在区间上均匀取31个点，用‘o ’标出曲线上的点，标出坐标系的x ，y 坐标轴，要求坐标系中x 方向和y 方向单位长度相同。

《数值分析》计算实习报告第一题院系：机械工程及自动化学院_学号： _____姓名： _ ______2017年11月7日一、算法设计方案1、求λ1，λ501和λs 的值1)利用幂法计算出矩阵A 按模最大的特征值，设其为λm 。

2)令矩阵B =A −λm I （I 为单位矩阵），同样利用幂法计算出矩阵B 按模最大的特征值λm ′。

3)令λm ′′=λm ′+λm 。

由计算过程可知λm 和λm ′′分别为矩阵A 所有特征值按大小排序后，序列两端的值。

即，λ1=min⁡{λm ,λm ′′}，λ501=max⁡{λm ,λm ′′}。

4) 利用反幂法计算λs 。

其中，反幂法每迭代一次都要求解线性方程组1k k Au y -=，由于矩阵A 为带状矩阵，故可用三角分解法解带状线性方程组的方法求解得到k u 。

2、求A 的与数μk =λ1+k λ501−λ140最接近的特征值λi k (k =1,2, (39)1) 令矩阵D k =A −μk I ，利用反幂法计算出矩阵D k 按模最小的特征值λi k ′,则λi k =λi k ′+μk 。

3、求A 的（谱范数）条件数cond(A )2和行列式det A1) cond(A)2=|λm λs |，前文已算出m λ和s λ，直接带入即可。

2) 反幂法计算λs 时，已经对矩阵A 进行过Doolittle 分解，得到A=LU 。

而L 为对角线上元素全为1的下三角矩阵，U 为上三角矩阵，可知det 1L =，5011det ii i U u ==∏，即有5011det det det ii i A L U u ====∏。

最后，为节省存储量，需对矩阵A 进行压缩，将A 中带内元素存储为数组C [5][501]。

二、源程序代码#include<windows.h>#include<iostream>#include<iomanip>#include<math.h>using namespace std;#define N 501#define K 39#define r 2#define s 2#define EPSI 1.0e-12//求两个整数中的最大值int int_max2(int a, int b){return(a>b ? a : b);}//求两个整数中的最小值int int_min2(int a, int b){return(a<b ? a : b);}//求三个整数中的最大值int int_max3(int a, int b, int c){int t;if (a>b)t = a;else t = b;if (t<c) t = c;return(t);}//定义向量内积double dianji(double x[], double y[]) {double sum = 0;for (int i = 0; i<N; i++)sum = sum + x[i] * y[i];return(sum);}//计算两个数之间的相对误差double erro(double lamd0, double lamd1){double e, d, l;e = fabs(lamd1 - lamd0);d = fabs(lamd1);l = e / d;return(l);}//矩阵A的压缩存储初始化成Cvoid init_c(double c[][N]){int i, j;for (i = 0; i<r + s + 1; i++)for (j = 0; j<N; j++)if (i == 0 || i == 4)c[i][j] = -0.064;else if (i == 1 || i == 3)c[i][j] = 0.16;elsec[i][j] = (1.64 - 0.024*(j + 1))*sin(0.2*(j + 1)) - 0.64*exp(0.1 / (j + 1)); }//矩阵复制void fuzhi_c(double c_const[][N], double c[][N]){int i, j;for (i = 0; i<r + s + 1; i++)for (j = 0; j<N; j++)c[i][j] = c_const[i][j];}//LU三角分解void LUDet_c(double c_const[][N], double c_LU[][N]){double sum;int k, i, j;fuzhi_c(c_const, c_LU);for (k = 1; k <= N; k++){for (j = k; j <= int_min2(k + s, N); j++){sum = 0;for (i = int_max3(1, k - r, j - s); i <= k - 1; i++)sum += c_LU[k - i + s][i - 1] * c_LU[i - j + s][j - 1];c_LU[k - j + s][j - 1] -= sum;}for (j = k + 1; j <= int_min2(k + r, N); j++){sum = 0;for (i = int_max3(1, j - r, k - s); i <= k - 1; i++)sum += c_LU[j - i + s][i - 1] * c_LU[i - k + s][k - 1];c_LU[j - k + s][k - 1] = (c_LU[j - k + s][k - 1] - sum) / c_LU[s][k - 1];}}}//三角分解法解带状线性方程组void jiefc(double c_const[][N], double b_const[], double x[]){int i, j;double b[N], c_LU[r + s + 1][N], sum;for (i = 0; i<N; i++)b[i] = b_const[i];LUDet_c(c_const, c_LU);for (i = 2; i <= N; i++){sum = 0;for (j = int_max2(i - 2, 1); j <= i - 1; j++)sum += c_LU[i - j + 2][j - 1] * b[j - 1];b[i - 1] -= sum;}x[N - 1] = b[N - 1] / c_LU[2][N - 1];for (i = N - 1; i >= 1; i--){sum = 0;for (j = i + 1; j <= int_min2(i + 2, N); j++)sum += c_LU[i - j + 2][j - 1] * x[j - 1];x[i - 1] = (b[i - 1] - sum) / c_LU[2][i - 1];}}//幂法求按模最大特征值double mifa_c(double c_const[][N]){double u[N], y[N];double sum, length_u, beta0, beta1;int i, j;for (i = 0; i<N; i++)//迭代初始向量u[i] = 0.5;length_u = sqrt(dianji(u, u));for (i = 0; i<N; i++)y[i] = u[i] / length_u;for (i = 1; i <= N; i++){sum = 0;for (j = int_max2(i - 2, 1); j <= int_min2(i + 2, N); j++)sum = sum + c_const[i - j + 2][j - 1] * y[j - 1];u[i - 1] = sum;}beta1 = dianji(u, y);do{beta0 = beta1;length_u = sqrt(dianji(u, u));for (i = 0; i<N; i++)y[i] = u[i] / length_u;for (i = 1; i <= N; i++){sum = 0;for (j = int_max2(i - 2, 1); j <= int_min2(i + 2, N); j++)sum = sum + c_const[i - j + 2][j - 1] * y[j - 1];u[i - 1] = sum;}beta1 = dianji(u, y);} while (erro(beta0, beta1) >= EPSI);return(beta1);}//反幂法求按模最小特征值double fmifa_c(double c_const[][N]){double u[N], y[N];double length_u, beta0, beta1;int i;for (i = 0; i<N; i++)//迭代初始向量u[i] = 0.5;length_u = sqrt(dianji(u, u));for (i = 0; i<N; i++)y[i] = u[i] / length_u;jiefc(c_const, y, u);beta1 = dianji(y, u);do{beta0 = beta1;length_u = sqrt(dianji(u, u));for (i = 0; i<N; i++)y[i] = u[i] / length_u;jiefc(c_const, y, u);beta1 = dianji(y, u);} while (erro(beta0, beta1) >= EPSI);beta1 = 1 / beta1;return(beta1);}//计算lamd_1、lamd_501、lamd_svoid calculate1(double c_const[][N], double &lamd_1, double &lamd_501, double &lamd_s) {int i;double lamd_mifa0, lamd_mifa1, c[r + s + 1][N];lamd_mifa0 = mifa_c(c_const);fuzhi_c(c_const, c);for (i = 0; i<N; i++)c[2][i] = c[2][i] - lamd_mifa0;lamd_mifa1 = mifa_c(c) + lamd_mifa0;if (lamd_mifa0<lamd_mifa1){lamd_1 = lamd_mifa0;lamd_501 = lamd_mifa1;}else{lamd_501 = lamd_mifa0;lamd_1 = lamd_mifa1;}lamd_s = fmifa_c(c_const);}//平移+反幂法求最接近u_k的特征值void calculate2(double c_const[][N], double lamd_1, double lamd_501, double lamd_k[]){int i, k;double c[r + s + 1][N], h, temp;temp = (lamd_501 - lamd_1) / 40;for (k = 1; k <= K; k++){h = lamd_1 + k*temp;fuzhi_c(c_const, c);for (i = 0; i<N; i++)c[2][i] = c[2][i] - h;lamd_k[k - 1] = fmifa_c(c) + h;}}//计算cond(A)和det(A)void calculate3(double c_const[][N], double lamd_1, double lamd_501, double lamd_s, double &cond_A, double &det_A){int i;double c_LU[r + s + 1][N];if (fabs(lamd_1)>fabs(lamd_501))cond_A = fabs(lamd_1 / lamd_s);elsecond_A = fabs(lamd_501 / lamd_s);LUDet_c(c_const, c_LU);det_A = 1;for (i = 0; i<N; i++)det_A *= c_LU[2][i];}//*主程序*//int main(){int i, count = 0;double c_const[5][N], lamd_k[K];double lamd_1, lamd_501, lamd_s;double cond_A, det_A;//设置白背景黑字system("Color f0");//矩阵A压缩存储到c[5][501]init_c(c_const);cout << setiosflags(ios::scientific) << setiosflags(ios::right) << setprecision(12) << endl;//计算lamd_1、lamd_501、lamd_scalculate1(c_const, lamd_1, lamd_501, lamd_s);cout << " 矩阵A的最小特征值：λ1 = " << setw(20) << lamd_1 << endl;cout << " 矩阵A的最大特征值：λ501 = " << setw(20) << lamd_501 << endl;cout << " 矩阵A的按模最小的特征值：λs = " << setw(20) << lamd_s << endl;//求最接近u_k的特征值calculate2(c_const, lamd_1, lamd_501, lamd_k);cout << endl << " 与数u_k最接近的特征值：" << endl;for (i = 0; i<K; i++){cout << " λ_ik_" << setw(2) << i + 1 << " = " << setw(20) << lamd_k[i] << " ";count++;if (count == 2){cout << endl;count = 0;}}//计算cond_A和det_Acalculate3(c_const, lamd_1, lamd_501, lamd_s, cond_A, det_A);cout << endl << endl;cout << " 矩阵A的条件数：cond(A) = " << setw(20) << cond_A << endl;cout << " 矩阵A的行列式的值：det(A) = " << setw(20) << det_A << endl << endl;return 0;}三，计算结果四，分析初始向量选择对计算结果的影响当选取初始向量0(1,1,,1)Tu=时，计算的结果如下：此结果即为上文中的正确计算结果。

数值分析实验报告一、 实验3。

1 题目：考虑线性方程组b Ax =，n n R A ⨯∈，n R b ∈,编制一个能自动选取主元,又能手动选取主元的求解线性代数方程组的Gauss 消去过程。

（1）取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=6816816816 A ，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157 b ,则方程有解()T x 1,,1,1*⋯=。

取10=n 计算矩阵的条件数。

分别用顺序Gauss 消元、列主元Gauss 消元和完全选主元Gauss 消元方法求解，结果如何？（2）现选择程序中手动选取主元的功能，每步消去过程都选取模最小或按模尽可能小的元素作为主元进行消元，观察并记录计算结果，若每步消去过程总选取按模最大的元素作为主元,结果又如何？分析实验的结果。

（3）取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异，说明主元素的选取在消去过程中的作用.(4）选取其他你感兴趣的问题或者随机生成的矩阵,计算其条件数，重复上述实验，观察记录并分析实验的结果。

1. 算法介绍首先,分析各种算法消去过程的计算公式， 顺序高斯消去法:第k 步消去中，设增广矩阵B 中的元素()0k kk a ≠(若等于零则可以判定系数矩阵为奇异矩阵，停止计算），则对k 行以下各行计算()(),1,2,,k ikik k kka l i k k n a ==++,分别用ik l -乘以增广矩阵B 的第k 行并加到第1,2,,k k n ++行，则可将增广矩阵B 中第k 列中()k kka 以下的元素消为零；重复此方法，从第1步进行到第n-1步,则可以得到最终的增广矩阵，即()()(),n n n B Ab ⎡⎤=⎣⎦； 列主元高斯消去法：第k 步消去中，在增广矩阵B 中的子方阵()()()()k kkkknk k nknn a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦中,选取()k k i k a 使得()(k)max k k i k ik k i na a ≤≤=，当k i k ≠时，对B 中第k 行与第k i 行交换,然后按照和顺序消去法相同的步骤进行。

一.1.首先构造1000阶正交阵Q 和bB=unidrnd(1000,1000,1000)[Q,R]=qr(B)并且将变量Q 储存为.mat 文件，便于随时调用。

2. A1、A2A1：load('正交Q.mat')N=1000v1=[]v1(1)=10^6v1(2:N-1)=linspace(1000,100,N-2)v1(N)=10^-3A1=Q*diag(v1)*Q'A2:load('正交Q.mat')N=1000v1=[]v1(1:N)=linspace(1000,1,N)A=Q*diag(v1)*Q'A1、A2条件数：9^101=κ、3^102=κ特征值分布：A1：001.01000973.9991000100000>>⋅⋅⋅>>>A2：129989991000>>⋅⋅⋅>>>3. CG 算法：N=1000;x=zeros(N,1);r=[];p=[];r(:,1)=b-A*x;p(:,1)=r(:,1);k=1;for k=1:Nak=r(:,k)'*r(:,k)/(p(:,k)'*(A*p(:,k)));x=x+ak*p(:,k);r(:,k+1)=r(:,k)-ak*(A*p(:,k));bk=r(:,k+1)'*r(:,k+1)/(r(:,k)'*r(:,k));p(:,k+1)=r(:,k+1)+bk*p(:,k);k=k+1;endy=[]for k=1:ky(:,k)=log10(norm(r(:,k),2)/norm(b,2)) %Ïà¶Ô²ÐÁ¿plot(0:k-1,y,'b-')gridendxlabel('step')ylabel('lg(morm(rk))')4.数值性态用A1计算，得到收敛曲线：横坐标是运算步数，纵坐标是对每步的相对残量取对数用A2进行计算，得到收敛曲线：当步数=阶数时，对A1，14010-=e r k ；对A2，8010-=e r k ，但在计算过程中k r 小于机器精度时，计算已经失真，实际在第1000步时对A1，06-7.2689e =k r ，A210-1.8979e =k r 。

1、猜想ln(cond(Hn))与n之间在n较小时满足线性关系，在n较大时则不稳定，因此，设n分别为10,20,50,100，如下图所示，可以看出在n<14时，ln(cond(Hn))呈线性稳定增长，n>14时，函数曲线开始趋于平稳并不断波动，波动幅度较小，并有上升趋势。

程序：N=100;y=zeros(N,1);for n=1:NHn=hilb(n);condn=cond(Hn);y(n)=log(condn);endx=1:N;subplot(224);plot(x,y);xlabel('n');ylabel('ln(cond(Hn))');title('ln(cond(Hn))--n(n=100)');grid ;2、可以看出，log(cond(Hnpre)/cond(Hn))在y=0上下波动。

对比整个曲线图，可以发现，经过预处理，条件数有所下降，但下降值不大。

程序：x=1:100;y=zeros(100,1);y1=zeros(100,1);y2=zeros(100,1);for n=1:100Hn=hilb(n);inv_D=zeros(n);for i=1:ninv_D(i,i)=1/sqrt(Hn(i,i));endHnpre=inv_D*Hn*inv_D;y(n)=log(cond(Hnpre)/cond(Hn));y1(n)=log(cond(Hnpre));y2(n)=log(cond(Hn));end%plot(x,y1);plot(x,y,'r',x,y1,'g',x,y2,'k');legend('y','y1','y2');xlabel('n');ylabel('log(cond(Hnpre)/cond(Hn))');title('log(cond(Hnpre)/cond(Hn))--n(n=100)');grid on;3、设b所有值为1，n x1 x2 x34 -4.0000E+00 -4.0000E+00 -4.0000E+00 6.0000E+01 6.0000E+01 6.0000E+01 -1.8000E+02 -1.8000E+02 -1.8000E+02 1.4000E+02 1.4000E+02 1.4000E+0255.0000E+00 5.0000E+00 5.0000E+00 -1.2000E+02 -1.2000E+02 -1.2000E+026.3000E+02 6.3000E+02 6.3000E+02 -1.1200E+03 -1.1200E+03 -1.1200E+03 6.3000E+02 6.3000E+02 6.3000E+026 -6.0000E+00 -6.0000E+00 -6.0000E+00 2.1000E+02 2.1000E+02 2.1000E+02 -1.6800E+03 -1.6800E+03 -1.6800E+03 5.0400E+03 5.0400E+03 5.0400E+03 -6.3000E+03 -6.3000E+03 -6.3000E+03 2.7720E+03 2.7720E+03 2.7720E+0377.0000E+00 7.0000E+00 7.0000E+00 -3.3600E+02 -3.3600E+02 -3.3600E+02 3.7800E+03 3.7800E+03 3.7800E+03-1.6800E+04 -1.6800E+04 -1.6800E+04 3.4650E+04 3.4650E+04 3.4650E+04 -3.3264E+04 -3.3264E+04 -3.3264E+04 1.2012E+04 1.2012E+04 1.2012E+048 -8.0000E+00 -8.0000E+00 -8.0000E+00 5.0400E+02 5.0400E+02 5.0400E+02 -7.5600E+03 -7.5600E+03 -7.5600E+03 4.6200E+04 4.6200E+04 4.6200E+04 -1.3860E+05 -1.3860E+05 -1.3860E+05 2.1622E+05 2.1622E+05 2.1622E+05 -1.6817E+05 -1.6817E+05 -1.6817E+05 5.1480E+04 5.1480E+04 5.1480E+0499.0000E+00 9.0000E+00 9.0001E+00 -7.2000E+02 -7.2000E+02 -7.2000E+02 1.3860E+04 1.3860E+04 1.3860E+04 -1.1088E+05 -1.1088E+05 -1.1088E+05 4.5045E+05 4.5045E+05 4.5045E+05 -1.0090E+06 -1.0090E+06 -1.0090E+06 1.2613E+06 1.2613E+06 1.2613E+06 -8.2368E+05 -8.2368E+05 -8.2368E+05 2.1879E+05 2.1879E+05 2.1879E+0510 -9.9980E+00 -9.9987E+00 -1.0001E+01 9.8983E+02 9.8989E+02 9.9005E+02 -2.3756E+04 -2.3758E+04 -2.3761E+04 2.4021E+05 2.4022E+05 2.4025E+05 -1.2611E+06 -1.2612E+06 -1.2613E+06 3.7833E+06 3.7835E+06 3.7839E+06 -6.7260E+06 -6.7263E+06 -6.7269E+06 7.0006E+06 7.0008E+06 7.0015E+06 -3.9378E+06 -3.9380E+06 -3.9383E+06 9.2370E+05 9.2373E+05 9.2380E+05111.0927E+01 1.0988E+01 1.0992E+01 -1.3124E+03 -1.3188E+03 -1.3192E+03 3.8410E+04 3.8580E+04 3.8587E+04 -4.7823E+05 -4.8015E+05 -4.8022E+05 3.1396E+06 3.1513E+06 3.1515E+06 -1.2060E+07 -1.2102E+07 -1.2102E+072.8484E+07 2.8575E+07 2.8576E+07 -4.1864E+07 -4.1989E+07 -4.1990E+073.7293E+07 3.7398E+07 3.7398E+07 -1.8420E+07 -1.8469E+07 -1.8469E+07 3.8689E+06 3.8786E+06 3.8785E+0612 -9.6349E+00 -1.2768E+01 -1.1739E+01 1.4311E+03 1.8176E+03 1.6833E+03-5.1063E+04 -6.3363E+04 -5.9039E+047.7783E+05 9.4708E+05 8.8711E+05-6.3022E+06 -7.5528E+06 -7.1069E+063.0320E+07 3.5851E+07 3.3868E+07-9.1788E+07 -1.0728E+08 -1.0171E+081.7935E+082.0753E+08 1.9736E+08-2.2572E+08 -2.5889E+08 -2.4688E+081.7662E+082.0099E+08 1.9214E+08-7.8125E+07 -8.8290E+07 -8.4591E+071.4921E+07 1.6757E+07 1.6087E+07可以看出，当n<9时，三种方法计算出的结果几乎一致，当n>9时，三种方法计算出的结果相差越来越大。

迭代次数l g （|r k |）高等数值分析第一次实验T1. 构造例子说明CG 的数值形态。

当步数 = 阶数时CG 的解如何？当A 的最大特征值远大于第二个最大特征值，最小特征值远小于第二个最小特征值时，方法的收敛性如何？ Answer:对于问题1：当步数 = 阶数时CG 的解如何？ ➢ 在MA TLAB 中构造N 阶对称正定矩阵代码如下：N=1000D = diag(rand(N,1)); U = orth(rand(N,N)); A = U'*D*U;在计算时，取X0=zeros(N,1);b=ones(N,1);自己编写CG 算法，如下： Xk = X0; rk=b-A*Xk; pk=rk; crk_1=rk'*rk; for k=1:N k=k+1; apk=A*pk;ak=crk_1/(pk'*apk); Xk=Xk+ak*pk; rk=rk-ak*apk; crk=rk'*rk; bk_1=crk/crk_1; crk_1=crk; pk=rk+bk_1*pk; m(k)=norm(rk); r(k)=k; endplot(r,m,'r-');Ek=m(k)计算结果如下（绘制出来的log 由上表可以看出对于对称正定矩阵A ，CG 算法还是比较稳定的，但求解步数=阶数时，CG 算法的解即为准确解（误差极小）。

对于问题2：当A 的最大特征值远大于第二个最大特征值，最小特征值远小于第二个最小特征值时，方法的收敛性如何？➢ 构造1000阶的对称正定矩阵如下，收敛准则取为绝对ε<10(-10)： 首先构造一个特征值分别为0.1到1的对称正定矩阵A ，代码如下（算例1）：D = diag(linspace(0.1,1,N)); U = orth(rand(N,N)); A = U'*D*U;在之前的基础上，将最大特征值调为107，最 小特征值为10-5，代码如下（算例2）：DIA=linspace(0.1,1,N); DIA(1)=10^(-5); DIA(N)=10^7; D = diag(DIA); U = orth(rand(N,N)); A = U'*D*U;最后生成一个特征值在10-5到107均匀分布的矩阵 （算例3）:DIA=linspace(10^(-5),10^7,N); D = diag(DIA); U = orth(rand(N,N)); A = U'*D*U;计算结果如右图所示，首先对比可以发现矩阵的收敛速度跟其条件数大小有关，条件数小时，收敛速度快，算例1>2>3，同时，A 的中间特征值分布对CG 的收敛速度有巨大的影响。

数值分析上机实验报告题目：插值法学生姓名学院名称计算机学院专业计算机科学与技术时间一. 实验目的1、掌握三种插值方法：牛顿多项式插值，三次样条插值，拉格朗日插值2、学会matlab提供的插值函数的使用方法二.实验内容1、已知函数在下列各点的值为试用4次牛顿插值多项式P4（x）及三次样条函数S（x）（自然边界条件）对数据进行插值。

用图给出{（x i,y i）,x i=0.2+0.08i,i=0,1,11,10},P4(x)及S（x）。

2、在区间[-1,1]上分别取n=10,20用两组等距节点对龙格函数f(x)=1/(1+25x2)作多项式插值及三次样条插值，对每个n值，分别画出插值函数及f(x)的图形。

3、下列数据点的插值可以得到平方根函数的近似，在区间[0,64]上作图。

（1）用这9个点作8次多项式插值L8（x）（2）用三次样条（第一边界条件）程序求S（x）从得到结果看在[0,64]上，哪个插值更精确，在区间[0,1]上。

两种插值哪个更精确？三.实现方法1. 进入matlab开发环境2. 依据算法编写代码3. 调试程序4. 运行程序5. （1）牛顿插值多项式：P n=f(x0)+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+…+f[x0,x1,…,x n] (x-x0)(x-x n-1)三次样条插值：用三次样条插值函数由题目分析知，要求各点的M值：6.实验代码如下：（1）牛顿插值多项式程序:function varargout=newton(varargin)clear,clcx=[0.2 0.4 0.6 0.8 1.0]; fx=[0.98 0.92 0.81 0.64 0.38]; newtonchzh(x,fx);function newtonchzh(x,fx)n=length(x);FF=ones(n,n); FF(:,1)=fx';for i=2:nfor j=i:nFF(j,i)=(FF(j,i-1)-FF(j-1,i-1))/(x(j)-x(j-i+1));endendfor i=1:nfprintf('%4.2f',x(i)); for j=1:ifprintf('%10.5f',FF(i,j)); endfprintf('\n');end三次样条插值程序:function sanciyangtiao(n,s,t)x=[0.2 0.4 0.6 0.8 1.0];y=[0.98 0.92 0.81 0.64 0.38];n=5for j=1:1:n-1h(j)=x(j+1)-x(j);endfor j=2:1:n-1r(j)=h(j)/(h(j)+h(j-1));endfor j=1:1:n-1u(j)=1-r(j);endfor j=1:1:n-1f(j)=(y(j+1)-y(j))/h(j);endfor j=2:1:n-1d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));endd(1)=0d(n)=0a=zeros(n,n);for j=1:1:na(j,j)=2;endr(1)=0;u(n)=0;for j=1:1:n-1a(j+1,j)=u(j+1);a(j,j+1)=r(j);endb=inv(a)m=b*d'p=zeros(n-1,4);for j=1:1:n-1p(j,1)=m(j)/(6*h(j));p(j,2)=m(j+1)/(6*h(j));p(j,3)=(y(j)-m(j)*(h(j)^2/6))/h(j);p(j,4)=(y(j+1)-m(j+1)*(h(j)^2/6))/h(j);endend图程序：x=[0.2 0.4 0.6 0.8 1.0];y=[0.98 0.92 0.81 0.64 0.38];plot(x,y)hold onfor i=1:1:5y(i)=0.98-0.3*(x(i)-0.2)-0.62500*(x(i)-0.2)*(x(i)-0.4)-0.20833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0.52083*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)*(x(i)-0.8)endk=[0 1 10 11]x0=0.2+0.08*kfor i=1:1:4y0(i)=0.98-0.3*(x(i)-0.2)-0.62500*(x(i)-0.2)*(x(i)-0.4)-0.20833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0.52083*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)*(x(i)-0.8)endplot( x0,y0,'o',x0,y0 )hold ony1=spline(x,y,x0)plot(x0,y1,'o')hold ons=csape(x,y,'variational')fnplt(s,'r')hold ongtext('Èý´ÎÑùÌõ×ÔÈ»±ß½ç')gtext('Ô-ͼÏñ')gtext('4´ÎÅ£¶Ù²åÖµ')(2)多项式插值程序:function [C,D]=longge(X,Y)n=length(X);D=zeros(n,n)D(:,1)=Y'for j=2:nfor k=j:nD(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1));endendC=D(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)))m=length(C);C(m)= C(m)+D(k,k);endend三次样条插值程序：function S=longgesanci(X,Y,dx0,dxn)N=length(X)-1;H=diff(X);D=diff(Y)./H;A=H(2:N-1);B=2*(H(1:N-1)+H(2:N));C=H(2:N);U=6*diff(D);B(1)=B(1)-H(1)/2;U(1)=U(1)-3*(D(1));B(N-1)=B(N-1)-H(N)/2;U(N-1)=U(N-1)-3*(-D(N));for k=2:N-1temp=A(k-1)/B(k-1);B(k)=B(k)-temp*C(k-1);U(k)=U(k)-temp*U(k-1);endM(N)=U(N-1)/B(N-1);for k=N-2:-1:1M(k+1)=(U(k)-C(k)*M(k+2))/B(k);endM(1)=3*(D(1)-dx0)/H(1)-M(2)/2;M(N+1)=3*(dxn-D(N))/H(N)-M(N)/2;for k=0:N-1S(k+1,1)=(M(k+2)-M(k+1))/(6*H(k+1));S(k+1,2)=M(k+1)/2;S(k+1,3)=D(k+1)-H(k+1)*(2*M(k+1)+M(k+2))/6; S(k+1,4)=Y(k+1);endend（3）三次样条函数程序代码：function sanci3(n,s,t)y=[0 1 2 3 4 5 6 7 8];x=[0 1 4 9 16 25 36 49 64];n=9for j=1:1:n-1h(j)=x(j+1)-x(j);endfor j=2:1:n-1r(j)=h(j)/(h(j)+h(j-1));endfor j=1:1:n-1u(j)=1-r(j);endfor j=1:1:n-1f(j)=(y(j+1)-y(j))/h(j);endfor j=2:1:n-1d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));endd(1)=0d(n)=0a=zeros(n,n);for j=1:1:na(j,j)=2;endr(1)=0;u(n)=0;for j=1:1:n-1a(j+1,j)=u(j+1);a(j,j+1)=r(j);endb=inv(a) m=b*d' t=ap=zeros(n-1,4);p(j,1)=m(j)/(6*h(j));p(j,2)=m(j+1)/(6*h(j));p(j,3)=(y(j)-m(j)*(h(j)^2/6))/h(j);p(j,4)=(y(j+1)-m(j+1)*(h(j)^2/6))/h(j); end拉格朗日插值程序：function y=lagrange(x0,y0,x)n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endend四.实验结果1.牛顿插值多项式结果：所以有四次插值牛顿多项式为: P4（x）=0.98-0.3(x-0.2)-0.62500(x-0.2)(x-0.4)-0.20833(x-0.2)(x-0.4)(x-0.6)-0.52083(x-0.2)(x-0.4)(x-0.6)(x-0.8)三次样条插值结果：得到m=(0 -1.6071 -1.0714 -3.1071 0),则可得：图形为：2.多项式插值，n=10时：n=20时:三次样条插值，n=10时：n=20时：3．三次样条插值程序结果：解得:M0=0;M1=-0.5209;M2=0.0558;M3=-0.0261;M4=0.0006;M5=-0.0029;M6=-0.0008;M7=--0.0009;M8=0；则三次样条函数：图形：[0,64]:在区间[0，64]上从图3-2中可以看出蓝色虚线条和绿色线条是几乎重合的，而红色线条在[30，70]之间有很大的起伏，所在在区间[0，64]三次样条插值更精确。

20130917题目求证：在矩阵的LU 分解中，111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明：在高斯消去过程中，假设0jj a ≠ ，若a=0，可以通过列变换使得前面的条件成立，这里不考虑这种情况。

对矩阵A 进行LU 分解，()()()()()1111111L M n M M M n ---=-=∙∙-………… ，其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ，i e 、j e 为n 维线性空间的自然基。

()M j 是通过对单位阵进行初等变换得到，通过逆向的变换则可以得到单位阵，由此很容易得到()M j 的逆矩阵为1n Tn ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。

故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换，从右向左乘，则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。

由于最初的矩阵为单位阵，变换从右向左展开，因而每一次变换不改变已经更新的数据，既该变换是从右向左一列一列更新数据，故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。

数学证明：1nTi j i ji j ee α=+⎛⎫ ⎪⎝⎭∑具有,000n j jA -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式，且有+1,-11,10000=000n j j n j n j AB --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭ 而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式，因此：1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问：能否用逐次householder 相似变换变实矩阵A 为上三角矩阵，为什么？解：不能用逐次householder 相似变换变A 为上三角矩阵，原因如下：A 记作：()12=,,n A a a a ……， ，存在householder 阵1H s.t. 1111H a e α= ，则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数，故无法通过householder 变换实现上三角化。