下载文档原格式
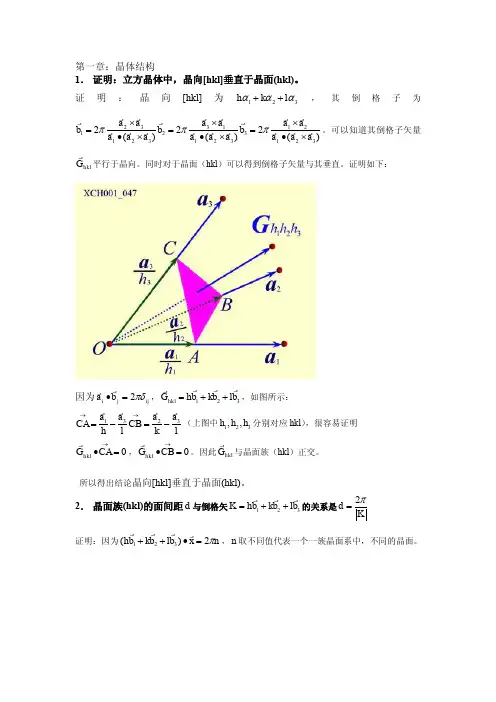
固体物理第一次习题参考答案1．如果将等体积球分别排成下列结构，设x 表示刚球所占体积与总体积之比，证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解：设钢球半径为r ，立方晶系晶格常数为a ，六角密排晶格常数为a,c 钢球体积为V 1，总体积为V 2（1）简单立方单胞含一个原子，a r =2 52.06343321≈==ππa r V V（2）体心立方取惯用单胞，含两个原子，r a 43= 68.0833423321≈=⋅=ππar V V （3）面心立方取惯用单胞，含4个原子，r a =2 74.0623443321≈=⋅=ππar V V （4）六角密排与面心立方同为密堆积结构，可预期二者具有相同的空间占有率 取图示单胞，含两个原子，a r =2 单胞高度a c 38=（见第2题） 74.062233422321≈=⋅⋅=ππc a r V V （5）金刚石取惯用单胞，含8个原子，r a 2341= 34.01633483321≈=⋅=ππar V V2．试证六方密排密堆积结构中128() 1.6333c a =≈解： 六角密排，如图示，4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3．证明：体心立方晶格的倒格子是面心立方，面心立方的倒格子是体心立方。
证：体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢，按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见，体心立方的倒格子是晶格常数为a b π4=的面心立方。
第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的？[解答] 自由电子论只考虑电子的动能。
在绝对零度时，金属中的自由（价）电子，分布在费米能级及其以下的能级上，即分布在一个费米球内。
在常温下，费米球内部离费米面远的状态全被电子占据，这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上，能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说，常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时，费米能级如何变化？[解答] 费米能级3/222)3(2πn mE o F= ， 其中n 单位体积内的价电子数目。
晶体膨胀时，体积变大，电子数目不变，n 变小，费密能级降低。
3． 为什么温度升高，费米能反而降低？[解答] 当K T 0≠时，有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外，温度升高，费米面附近的电子从格波获取的能量就越大，跃迁到费米面以外的电子就越多，原来有一半量子态被电子所占据的能级上的电子就少于一半，有一半量子态被电子所占据的能级必定降低，也就是说，温度生高，费米能反而降低。
4． 为什么价电子的浓度越大，价电子的平均动能就越大？[解答] 由于绝对零度时和常温下电子的平均动能十分相近，我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大，价电子的平均动能就越大，这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时，电子不可能都处于最低能级上，而是在费米球中均匀分布。
由式3/120)3(πn k F =可知，价电子的浓度越大费米球的半径就越大，高能量的电子就越多，价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ，而费米能又正比于电子浓度32l n。
固体物理学考试题及答案一、选择题（每题2分，共20分）1. 固体物理学中，描述晶体中原子排列的周期性规律的数学表达式是（）。
A. 布洛赫定理B. 薛定谔方程C. 泡利不相容原理D. 费米-狄拉克统计答案：A2. 固体中电子的能带结构是由（）决定的。
A. 原子的核外电子B. 晶体的周期性势场C. 原子的核电荷D. 原子的电子云答案：B3. 在固体物理学中，金属导电的原因是（）。
A. 金属中存在自由电子B. 金属原子的电子云重叠C. 金属原子的价电子可以自由移动D. 金属原子的电子云完全重叠答案：C4. 半导体材料的导电性介于导体和绝缘体之间，这是因为（）。
A. 半导体材料中没有自由电子B. 半导体材料的能带结构中存在带隙C. 半导体材料的原子排列无序D. 半导体材料的电子云完全重叠答案：B5. 固体物理学中，描述固体中电子的波动性的数学表达式是（）。
A. 薛定谔方程B. 麦克斯韦方程C. 牛顿第二定律D. 热力学第一定律答案：A6. 固体中声子的概念是由（）提出的。
A. 爱因斯坦B. 德拜C. 玻尔D. 费米答案：B7. 固体中电子的费米能级是指（）。
A. 电子在固体中的最大能量B. 电子在固体中的最小能量C. 电子在固体中的平均水平能量D. 电子在固体中的动能答案：A8. 固体物理学中，描述固体中电子的分布的统计规律是（）。
A. 麦克斯韦-玻尔兹曼统计B. 费米-狄拉克统计C. 玻色-爱因斯坦统计D. 高斯统计答案：B9. 固体中电子的能带理论是由（）提出的。
A. 薛定谔B. 泡利C. 费米D. 索末菲答案：D10. 固体中电子的跃迁导致（）的发射或吸收。
A. 光子B. 声子C. 电子D. 质子答案：A二、填空题（每题2分，共20分）1. 固体物理学中，晶体的周期性势场是由原子的______产生的。
答案：周期性排列2. 固体中电子的能带结构中，导带和价带之间的能量区域称为______。
答案：带隙3. 金属导电的原因是金属原子的价电子可以______。
![《固体物理学》答案[1]](https://img.taocdn.com/s1/m/f8d34b12866fb84ae45c8da9.png)
固体物理试题及参考答案注意：本答案仅供参考作答，名词解释部分有个别题不是很精确，如有自己的想法请自己把握，作图题由于不专业只能表示大概意思，但应该不会有错，一、名词解释1布里渊区：布里渊区是空间中由倒格矢的中垂面所围成的区域，按序号由倒空间的原点逐步向外扩展，可分为第一布里渊区、第二布里渊区、第三布里渊区等等。
2倒格子：晶格经傅里叶变换所得到的几何格子，其倒格子基矢定义：3声子：格波的能量量子，声子的能量为ħω，准动量为4声学波和光学波：声学波是晶格振动中频率比较低的、而且频率随波矢变化较大的那一支格波，描述的是晶体中原胞的整体运动；描述的是晶体中原胞内原子之间的相对运动。
5能带：由于原子之间的相互作用，当若干个原子相互靠近时，由于彼此之间的力的作用，原子原有能级发生分裂，由一条变成多条，形成的众多能级间的间隔很小，故可近似看成连续的，即称之为能带。
6布洛赫函数：当势场具有晶格周期性时，对于含有晶格周期势的薛定谔方程，其解必定具有形式，则晶体中的波函数具有调幅的平面波形式，称其波函数为布洛赫函数。
7电负性：电负性是原子对核外电子束缚能力大小的量度，通常用电离能与亲合能之和表示。
8布拉伐格子：晶体结构中全同原子构成的晶格称为布拉伐格子。
9等效晶面：简单立方晶格中晶面的密勒指数和晶面法线的晶向指数完全相同的面。
10赝势：在离子实内部，用假想的势能取代真实的势能，求解波动方程时，如不改变其能量本征值及离子实之间的区域的波函数，这个假想的势叫做赝势。
二、证明题11证明：体心立方晶格的倒格子是面心立方。
12、证明倒格子原胞的体积为，其中为正格子原胞的体积。
三、作图题13、在面心立方和体心立方的晶胞图上分别画出其原胞。
答：图如下：14、请在下图中标明[110]、[010]、(100)、(111)晶向和晶面。
答：【注意：由于此图没有相应的作图软件，不能画得和老师一样的立体效果，请同学们对照作图】四、简答题15、通过原子电负性的定义及周期分布，说明离子晶体形成的特征。
固体物理经典复习题及答案⼀、简答题1.理想晶体答：内在结构完全规则的固体是理想晶体，它是由全同的结构单元在空间⽆限重复排列⽽构成的。
2.晶体的解理性答：晶体常具有沿某些确定⽅位的晶⾯劈裂的性质，这称为晶体的解理性。
3.配位数答: 晶体中和某⼀粒⼦最近邻的原⼦数。
4.致密度答：晶胞内原⼦所占的体积和晶胞体积之⽐。
5.空间点阵(布喇菲点阵)答：空间点阵(布喇菲点阵)：晶体的内部结构可以概括为是由⼀些相同的点⼦在空间有规则地做周期性⽆限重复排列，这些点⼦的总体称为空间点阵(布喇菲点阵)，即平移⽮量123d 、d 、h h h d 中123,,n n n 取整数时所对应的点的排列。
空间点阵是晶体结构周期性的数学抽象。
6.基元答：组成晶体的最⼩基本单元，它可以由⼏个原⼦(离⼦)组成，整个晶体可以看成是基元的周期性重复排列⽽构成。
7.格点(结点)答: 空间点阵中的点⼦代表着结构中相同的位置，称为结点。
8.固体物理学原胞答：固体物理学原胞是晶格中的最⼩重复单元，它反映了晶格的周期性。
取⼀结点为顶点，由此点向最近邻的三个结点作三个不共⾯的⽮量，以此三个⽮量为边作的平⾏六⾯体即固体物理学原胞。
固体物理学原胞的结点都处在顶⾓位置上，原胞内部及⾯上都没有结点，每个固体物理学原胞平均含有⼀个结点。
9.结晶学原胞答：使三个基⽮的⽅向尽可能的沿空间对称轴的⽅向，以这样三个基⽮为边作的平⾏六⾯体称为结晶学原胞，结晶学原胞反映了晶体的对称性，它的体积是固体物理学原胞体积的整数倍,V=n Ω，其中n 是结晶学原胞所包含的结点数, Ω是固体物理学原胞的体积。
10.布喇菲原胞答：使三个基⽮的⽅向尽可能的沿空间对称轴的⽅向，以这样三个基⽮为边作的平⾏六⾯体称为布喇菲原胞，结晶学原胞反映了晶体的对称性，它的体积是固体物理学原胞体积的整数倍,V=n Ω,其中n 是结晶学原胞所包含的结点数, Ω是固体物理学原胞的体积11.维格纳-赛兹原胞(W-S 原胞)答：以某⼀阵点为原点，原点与其它阵点连线的中垂⾯(或中垂线) 将空间划分成各个区域。
单选题（1）离子性结合是以（）而不是以原子为结合单元，即靠（）间的静电库仑作用相互结合．•A离子，正负离子•B正负离子，离子•C负离子，正离子•D正离子，负离子正确答案:A（2）离子晶体中的长光学波可以与（）发生共振耦合，引起远红外光在共振频率附近的强烈吸收．•A声波•B光波•C声学波•D光学波正确答案:B（3）晶格振动谱中的光学波之所以称为光学波是因为：在长波极限情况，离子晶体的长光学波可以与电磁波发生（），可以引起远红外光在共振频率附近的强烈吸收．•A散射•B共振•C反射•D折射正确答案:B（4）立方晶系中的体心立方晶格的倒格子结构是•A面心立方晶格•B简立方晶格•C六角密排晶格•D金刚石结构正确答案:A（5）在长波极限情况，（）晶体的长光学波可以与电磁波发生共振，引起远红外光在共振频率附近的强烈吸收．•A离子•B分子•C共价•D金属正确答案:A（6）结构介于晶体和非晶体之间，具有准周期结构的称为（）．•A晶体•B非晶体•C准晶体•D固体正确答案:C（7）下面说法正确的是•A同一周期元素自左向右电负性逐渐减弱；•B同一周期元素自上向下电负性逐渐增强；•C某种元素的原子电负性愈小，表示其吸收电子的能力愈强．•D某种元素的原子电负性愈大，表示其吸收电子的能力愈强．正确答案:D（8）对于化合物而言，原子电负性差别小的易于形成（）晶体．•A离子•B金属•C氢•D分子正确答案:D（9）晶体中体积最小的周期性结构单元常称（）•A原胞•B晶胞•C布拉伐格子•D晶格正确答案:A（10）石墨具有层状结构，石墨的层与层之间是靠（）结合的，这种力很弱，所以石墨硬度较金刚石差。
•A库仑引力•B一种强相互作用力•C范德瓦尔斯力•D氢键正确答案:C（11）原子排列具有周期性的称为•A晶体•B非晶体•C准晶体•D固体正确答案:A（12）金刚石结构的最近邻原子数是•A12•B8•C6•D4正确答案:D（13）布里渊区的特征之一是所有布里渊区都是（）对称的．•A轴•B线•C面•D中心正确答案:D（14）贵金属Cu，Ag，Au及Pb，Ni，Al等属于（）结构．•A简立方•B体心立方•C六角密堆•D面心立方正确答案:D（15）晶格振动是指•A晶体中的原子、离子围绕平衡位置作的微振动；•B晶体中的电子围绕平衡位置作的微振动；•C晶体中的原子、离子围绕初始位置作的微振动；•D晶体中的电子围绕初始位置作的微振动；正确答案:A（16）离子晶体的长光学波可以与电磁波发生共振，可以引起远红外光在（）附近的强烈吸收．•A光波频率•B共振频率•C电磁波频率•D晶格振动频率正确答案:B（17）1920年，（）等提出X射线衍射方法，从实验上验证了晶体具有规则几何外形是晶体中原子、分子规则排列结果．•A劳埃•B爱因斯坦•C德拜•D布喇菲正确答案:A（18）共价结合是靠两个原子各贡献一个自旋（）的电子，形成所谓的共价键。
固体物理试题及答案一、选择题（每题2分，共10分）1. 固体物理中，晶体的周期性结构是通过哪种方式描述的？A. 电子云B. 原子轨道C. 布洛赫定理D. 费米面答案：C2. 以下哪种材料不属于半导体材料？A. 硅B. 锗C. 铜D. 砷化镓答案：C3. 在固体物理中，能带理论描述的是：A. 电子在固体中的自由运动B. 电子在固体中的局域化C. 电子在固体中的能级分布D. 电子在固体中的跃迁过程答案：C4. 固体中的声子是：A. 一种基本粒子B. 一种准粒子C. 一种实际存在的粒子D. 一种不存在的粒子答案：B5. 以下哪种效应与超导现象无关？A. 迈斯纳效应B. 约瑟夫森效应C. 霍尔效应D. 量子隧穿效应答案：C二、填空题（每题2分，共20分）1. 固体物理中，描述电子在周期性势场中的运动的定理是______。
答案：布洛赫定理2. 固体中的能带结构是由______决定的。
答案：电子波函数3. 在固体中，电子的费米能级是______。
答案：电子占据的最高能级4. 固体中的电子输运性质可以通过______来描述。
答案：电导率5. 固体中的晶格振动可以用______来描述。
答案：声子6. 固体中的电子-声子相互作用会导致______。
答案：电子散射7. 固体中的能隙是指______。
答案：价带顶部和导带底部之间的能量差8. 超导体的临界温度是指______。
答案：超导相变发生的温度9. 固体中的霍尔效应是由于______。
答案：电子在磁场中的偏转10. 固体中的磁阻效应是由于______。
答案：电子在磁场中的运动受到阻碍1. 简述固体物理中能带理论的基本思想。
答案：能带理论的基本思想是将固体中的电子视为在周期性势场中运动的量子粒子。
由于周期性势场的存在，电子的能级不再是离散的，而是形成了连续的能带。
这些能带决定了固体的电子结构和性质，如导电性、磁性和光学性质等。
2. 描述固体中的声子是如何产生的。
答案：固体中的声子是由于晶格振动的量子化而产生的准粒子。
固体物理试题1答案固体物理试题1——参考答案⼀、填空题（每⼩题2分，共12分）1、体⼼⽴⽅晶格的倒格⼦是⾯⼼⽴⽅点阵，⾯⼼⽴⽅晶格的倒格⼦是体⼼⽴⽅点阵。
2、晶体宏观对称操作的基本元素分别是 1、2、3、4、6、i、m（2）、4等⼋种。
3、N 对钠离⼦与氯离⼦组成的离⼦晶体中，独⽴格波波⽮数为 N ，声学波有 3 ⽀，光学波有 3 ⽀，总模式数为 6N 。
4、晶体的结合类型有⾦属结合、共价结合、离⼦结合、范德⽡⽿斯结合、氢键结合及混合键结合。
5、共价结合的主要特点为⽅向性与饱和性。
6、晶格常数为a的⼀维晶体电⼦势能V(x)的傅⽴叶展开式前⼏项(单位为eV)为:,在近⾃由电⼦近似下, 第⼆个禁带的宽度为 2（eV）。
⼆、单项选择题（每⼩题 2分，共 12 分）1、晶格常数为a的NaCl晶体的原胞体积等于（ D ）.A、B、C、 D、.2、⾦刚⽯晶体的配位数是（ D ）。
A、12B、8C、6D、4.3、⼀个⽴⽅体的点对称操作共有（ C ）。
A、 230个B、320个C、48个D、 32个.4、对于⼀维单原⼦链晶格振动的频带宽度，若最近邻原⼦之间的⼒常数β增⼤为4β，则晶格振动的频带宽度变为原来的（ A ）。
A、 2倍B、4倍C、 16倍D、 1倍.5、晶格振动的能量量⼦称为（ C ）。
A、极化⼦B、激⼦C、声⼦D、光⼦.6、三维⾃由电⼦的能态密度，与能量E的关系是正⽐于（ C ）A 、 12E-B 、0EC 、2/1ED 、E .三、问答题（每⼩题4分，共16分） 1、与晶列垂直的倒格⾯的⾯指数是什么解答正格⼦与倒格⼦互为倒格⼦。
正格⼦晶⾯与倒格⽮垂直,则倒格晶⾯与正格⽮正交。
即晶列与倒格⾯垂直。
2、晶体的结合能、晶体的内能、原⼦间的相互作⽤势能有何区别解答⾃由粒⼦结合成晶体过程中释放出的能量, 或者把晶体拆散成⼀个个⾃由粒⼦所需要的能量, 称为晶体的结合能。
原⼦的动能与原⼦间的相互作⽤势能之和为晶体的内能。
