中考数学压轴题分类汇编：图形变换

中考数学复习《填空压轴题——图形变换综合》专项测试卷(含参考答案)学校:___________班级：___________姓名：___________考号：___________把CD绕点D旋转，点C的对应点为点E，当DE∥AC时，1．如图，AC为矩形ABCD的对角线，AB=5，BC=154CE的长为．2．如图，将线段BC绕点B逆时针旋转120°得到线段BA，点D是平面内一动点，且D、B两点之间的距离为5，连接DA、DC，则DA+DC的最小值为．3．如图，△ABC和△AGF是等腰直角三角形∠BAC=∠G=90°，△AGF的边AF，AG交边BC于点D，E若BD=3，CE=4则AD的值是．4．如图，在四边形ABCD中点E在四边形ABCD的内部，且DE=EC，∠DEC=∠AEB=120∘已知AD= 4，BC=6则AB的长为．5．如图，点D在等边△ABC的BC边上AB=3,BD=1将△ABD绕点A逆时针旋转得到△ACE，其中点B的对应点为点C，点D的对应点为点E,BC的延长线与AE的延长线相交于点F，则cos∠AFB的值为．6．如图，已知△ABC和△ADE为等腰直角三角形∠ACB=∠AED=90°，AC=√10，AE=√2连接CE、BD．在△AED绕点A旋转的过程中当CE所在的直线垂直于AD时BD=．7．如图，在矩形ABCD中AB=4，BC=3，CE=2BE，EF=2连接AF，将线段AF绕着点A顺时针旋转90°得到AP，则线段PE的最小值为．8．如图1的一汤碗，其截面为轴对称图形，碗体ECDF呈半圆形状（碗体厚度不计），直径EF=26cm，碗底AB＝10cm ∠A＝∠B＝90°，AC＝BD＝3cm．（1）如图1，当汤碗平放在桌面MN上时，碗的高度是cm．（2）如图2，将碗放在桌面MN上，绕点B缓缓倾斜倒出部分汤，当碗内汤的深度最小时，tan∠ABM的值是．9．如图．在矩形ABCD中BC=3√3点P在线段BC上运动（含B、C两点），连接AP，以点A为中心，将线段AP逆时针旋转60°到AQ，连接DQ，则线段DQ的最小值为．10．如图，在平面直角坐标系中已知点A(0,2)，点P(a,0)是x轴上一动点，连接P A，在P A右侧作∠PAQ=60°，以P A为半径的⊙P交射线AQ于点B．当−1≤a≤3时，点B移动路径的长为．11．如图，△ABC中∠ACB=90°，AB=3AC=6O是AB边上一点满足CA=CO将△ABC绕点A顺时针旋转至△AB′C′使点C′落在射线CO上连接BB′交CC′的延长线于点F则FB的长为．12．如图在△ABC和△ADE中AB=BC=4√2AD=DE=2∠ABC=∠ADE=90°连接CE CD点O为CE的中点连接OD．将△ADE绕点A在平面内旋转．当∠CDE=90°时OD的长为．13．平面直角坐标系中四边形OABC是正方形点A C在坐标轴上点B(8,8)P是射线OB上一点将△AOP绕点A顺时针旋转90°得到△ABQ Q是点P旋转后的对应点当BP+BQ=10√2时则点Q的坐标为．14．如图在Rt△ABC中∠ABC=90°∠C=30°点D是线段BC上的动点将线段AD绕点A顺时针旋转60°至AD′连接BD′若AB=2cm则BD′的最小值为．15．如图平行四边形ABCD中AB＝16，AD＝12，∠A＝60°E是边AD上一点且AE＝8，F是边AB上的一个动点将线段EF绕点E逆时针旋转60°得到EG连接BG、CG则BG＋CG的最小值是．16．如图在△ABC中∠ACB=90°∠ABC=30°AB=6点P是在△ABC内一点连接AP BP CP 将△APB绕点A逆时针旋转60°得到△AP′B′．若点C P P′B′恰好在同一直线上则PA+PB+PC=．17．如图四边形ABCD为矩形连接BD将矩形ABCD绕点B旋转至矩形A′BC′D′使得边A′D′经过BD中点O 并交BC于点E若D′E=2A′O则AB的值为．AD18．如图在菱形ABCD中AB=2∠BAD=60°将菱形ABCD绕点A逆时针方向旋转对应得到菱形AEFG点E在AC上EF与CD交于点P．（1）EF与DC的关系是（2）DP的长为．19．在Rt△ABC中∠BAC=90°AB=AC D E是斜边BC上两点且∠DAE=45°将△ADC绕点A顺时针旋转90°后得△AFB连接EF下列结论：①△AED≌△AEF；②△AEC的面积等于四边形AFBE的面积；③∠BAD=∠AEC；④BE2+DC2=DE2；其中正确的是．20．如图在平面直角坐标系xOy中把矩形COAB绕点C顺时针旋转α角得到矩形CDEF．设若A(0,3) C(4,0)则BD2+BF2−BC2的最小值为．参考答案1．解：∵ABCD是矩形∵CD=AB=5AD=BC=154当DE∥AC且点E在CD上方时连接CE过点E作EF⊥CD交CD于点F∵DE∥AC∵∠EDF=∠DCA∵tan∠EDF=tan∠DCA即：EFDF =ADCD=1545=34设EF=3x DF=4x根据旋转的性质ED=CD=5在Rt△DEF中DE2=DF2+EF2即：52=(4x)2+(3x)2解得：x=1∵EF=3×1=3DF=4×1=4CF=CD−DF=5−4=1在Rt△FEC中CE=√EF2+CF2=√32+12=√10当DE∥AC且点E在CD下方时连接CE过点E作EF⊥CD交CD延长线于点F∵DE∥AC∵∠EDF=∠DCA∵tan∠EDF=tan∠DCA即：EFDF =ADCD=1545=34设EF=3x DF=4x根据旋转的性质ED=CD=5在Rt△DEF中DE2=DF2+EF2即：52=(4x)2+(3x)2解得：x=1∵EF=3×1=3DF=4×1=4CF=CD+DF=5+4=9在Rt△FEC中CE=√EF2+CF2=√32+92=3√10故答案为：√10或3√10．2．解：如图 把BD 绕点B 顺时针旋转120° 交DC 的延长线于点D` 过点B 作BE ⊥DD ′ 则∠DBD ′=∠ABC =120° DB =D ′B =5∵∠ABD +∠DBC =∠DBC +CBD ′=120°∵∠ABD =∠CBD ′又∵AB =CB DB =D ′B∵△ABD ≌△CBD ′(SAS )∵AD =CD ′∵AD +CD 的最小值为DD ′的值∵BE ⊥DD ′∵∠DBE =12∠DBD ′=60° DE =12DD ′∵∠BDE =30°∵BD =5∵BE =12BD =52∵DE =√52−(52)2=5√32 ∵DD ′=2×5√32=5√3故答案为：5√3．3．解：如图 将△AEC 绕点A 顺时针旋转90°到△AG ′B 位置 连接DG ′∵△ABC 和△AGF 是等腰直角三角形 ∠BAC =∠G =90°∵∠C =∠ABC =∠FAG =45° AB =AC由旋转性质可知：∠ABG′=∠C=45°BG′=CE=4AG′=AE∠BAG′=∠CAE∵∠G′BD=∠ABC+∠ABG′=90°∵DG′=√BG′2+BD2=√32+42=5∵∠BAC=90°∠FAG=45°∵∠BAD+∠CAE=∠BAD+∠G′AB=45°∵∠DAG′=∠DAE=45°又∵AG′=AE AD=AD∵△AG′D≌△AED(SAS)∵DE=DG′=5∵BC=BD+DE+CE=12过点A作AH⊥BC∵AB=AC∠BAC=90°BC=6∵BH=CH=AH=12∵DH=BH−BD=6−3=3∵AD=√DH2+AH2=√32+62=3√5故答案为3√5．4．解：如图将△AED绕点E顺时针旋转120°至△FEC连接BF过点F作FH⊥BC交BC延长线于H则AD=CF=4AE=EF∠ADE=∠FCE∵AD∥BC∴∠ADE+∠EDC+∠ECD+∠ECB=180°∵ED=EC∠CED=120°∴∠EDC=∠ECD=30°∴∠ADE+∠ECB=120°∴∠FCE+∠ECB=120°即∠FCB=120°∵∠FCH=60°∵∠CFH=30°∵CH=12CF=12×4=2FH=√CF2−CH2=2√3∴FB=√BH2+FH2=√(6+2)2+(2√3)2=2√19∵∠AEB=120°∠AEF=120°∴∠FEB=360°−120°−120°=120°∴∠AEB=∠FEB在△ABE和△FBE中{AE=EF ∠AEB=∠FEB BE=BE∴△ABE≌△FBE(SAS)∴AB=FB=2√19．5．解：如图过点A作AH⊥BF于点H过点E作EN⊥BF于点N∵△ABC为等边三角形AH⊥BF∴BH=CH=32,AH=3√32∴DH=BH−BD=12∴AD=√AH2+DH2=√7∵将△ABD绕点A逆时针旋转得到△ACE∴BD=CE=1AD=AE=√7∠B=∠ACF=60°∴∠ECN=180°−∠ACE−∠ACB=60°∵EN⊥CF∴CN=12CE=12EN=√32CN=√32∴HN=HC+CN=2∵∠AHC=∠ENF=90°∴△AHF∽△ENF∴ENAH =EFAF=EFAE+EF∴√323√32=√7+EF解得EF=√72∴NF=√EF2−EN2=1∴cos∠AFB=NFEF =2√77故答案为：2√77．6．解：∵△ABC为等腰直角三角形AC=√10∴AB=√2AC=2√5①当点E在点D上方时如图③过点A作AP⊥BD交BD的延长线于P当CE⊥AD时可证∠AEC=∠ADB=135°∵∠ADE=45°∴∠EDB=90°∴∠PDE=∠AED=∠APD=90°∴四边形APDE是矩形∵AE=DE∴矩形APDE是正方形∴AP=DP=AE=√2在Rt△APB中根据勾股定理得BP=√AB2−AP2=√(2√5)2−(√2)2=3√2∴BD=BP−PD=2√2．②当点E在点D下方时如图④同①的方法得AP=DP=AE=√2BP=3√2∴BD=BP+DP=4√2综上所述BD的长为2√2或4√2．7．解：如图连接AE过点A作AG⊥AE截取AG=AE连接PG，GE ∵将线段AF绕着点A顺时针旋转90°得到AP∵AF=AP,∠PAF=90°∵∠FAE+∠PAE=∠PAE+∠PAG=90°∵∠FAE=∠PAG．又∵AG=AE∵△AEF≌△AGP(SAS)∵PG=EF=2．∵BC=3,CE=2BE∵BE=1．∵在Rt△ABE中AE=√AB2+BE2=√17．∵AG=AE,∠GAE=90°∵GE=√2AE=√34．∵PE≥GE−PG且当点G P E三点共线时取等号∵PE的最小值为GE−PG=√34−2．故答案为：√34−2．8．（1）解：如图设半圆的圆心为O连接OC,OB过点O作直线OP⊥CD于P交AB于Q∵四边形ACPQ是矩形四边形BDPQ是矩形∵AC＝PQ＝3cm PD＝QB∵OP⊥CD∵CP＝DP＝QB＝5cm∵OP＝√OC2−CP2＝√169−25＝12（cm）∵OQ＝OP＋PQ＝15cm．∵碗的高度为15cm；故答案为：15；（2）解：如图1 OB＝√OQ2+QB2＝√225+25＝5√10cm∵将碗放在桌面MN上绕点B缓缓倾斜倒出部分汤∵当半圆O与直线MN相切时碗内汤的深度最小如图2 设半圆O与直线MN相切于点R连接O′R连接OO′O′B过点O作OK⊥O′B于K∵旋转∵OB＝O′B＝5√10cm ∠ABM＝∠OBO′∵半圆O与直线MN相切于点R∵O′R⊥MN∵O′R＝13cm∵BR＝√O′B2−O′R2＝√250−169＝9cm∵S△OO′B＝S﹣S△OBQ﹣S△BRO′梯形OQO′R∵S△OO′B＝12×（5＋9）×（15＋13）﹣12×15×5﹣12×13×9＝100（cm2）∵12×O′B×OK＝100∵12×5√10×OK＝100∵OK＝4√10cm∵BK＝√OB2−OK2＝√250−160＝3√10cm∵tan∠OBO′＝OKBK ＝√103√10＝43∵tan∠MBA＝43故答案为：43．9．解：如图所示以AB为边向右作等边三角形△ABF作射线FQ交AD于点E过点D作DH⊥QE于H连接PQ∵四边形ABCD是矩形∵∠ABP=∠BAD=90°∵△ABF△APQ都是等边三角形∵∠BAF=∠PAQ=60°BA=FA PA=QA∵∠BAP=∠FAQ在△BAP和△FAQ中{BA=FA ∠BAP=∠FAQ PA=QA∵△BAP≌△FAQ（SAS）∵∠ABP=∠AFQ=90°∵∠FAE=∠BAD−∠BAF=90°−60°=30°∵∠AEF=180°−∠AFQ−∠FAE=180°−90°−30°=60°∵AB =AF =3 ∠FAE =30°∵在Rt △AFE 中设FE =x 则AE =2x 根据勾股定理得x 2+32=(2x)23x 2=9x 2=3x =1√3 x 2=−√3（舍）∵FE =√3 AE =2√3∵点Q 在射线FE 上运动∵AD =BC =3√3∵DE =AD −AE =3√3−2√3=√3∵DH ⊥EF ∠DEH =∠AEF =60°∵DH =√DE 2−EH 2=√(√3)2−(√32)2=32∵垂线段最短∵当点Q 与点H 重合时 DQ 的值最小 最小值为32故答案为：32．10．解：连接PB 如图所示∵PA =PB ∠PAQ =60°∵△APB 是等边三角形．当点P 运动到原点O 时 记点B 的位置为M 如图1所示当点P 在x 轴上运动（P 不与O 重合）时∵∠PAB =∠OAM =60°∵∠PAO =∠BAM在△APO 和△ABM 中{AP=AB∠PAO=∠MAB AO=AM∵△APO≌△ABM（SAS）∵∠AMB=∠AOP=90°∵当点P在x轴上运动（P不与O重合）时∠AMB为定值90°∵点B的轨迹为一条经过点M且与AM垂直的线段．当a=−1时点P(−1，0)；当a=3时点P′(3，0)如图2所示∵PP′=3−(−1)=4∵△APB△AP′B′都是等边三角形∵AP=AB AP′=AB′∠PAB=∠P′AB′=60°∵∠PAP′=∠BAB′在△PAP′和△BAB′中{AP=AB∠PAP′=∠BAB′AP′=AB′∵△PAP′≌△BAB′（SAS）∵BB′=PP′=4∵当−1≤a≤3时点B移动路径的长为4故答案为：411．解：过点C作CD⊥AB于点D∵CA=CO CD⊥AB∵AD=OD∵AB=3AC=6∵AC=2∵∠ACB=90°∵在Rt△ABC中cos∠CAB=ACAB =13则在Rt△ACD中AD=AC⋅cos∠CAB=ADAC =13即AD2=13解得：AD=23则AO=2AD=43∵BO=AB−AO=6−43=143∵△AC′B′是由△ACB旋转得到∵AC=AC′,AB=AB′,∠CAC′=∠BAB′∵AC AB =AC′AB′∵△CAC′∽△BAB′∵∠ACO=∠OBF ∵∠BOF=∠COA ∵△ACO∽△FBO∵CA BF =COBO∵CA=CO∵BO=BF=14．3故答案为：14312．解：∵AB=BC=4√2AD=DE=2∠ABC=∠ADE=90°∵AC=√AB2+BC2=8分两种情况讨论：①如下图当点D运动到线段AC上时∵∠ADE=90°∵∠CDE=180°−∠ADE=90°此时CD=AC−AD=8−2=6∵CE=√CD2+DE2=√62+22=2√10∵点O为CE的中点CE=√10；∵OD=12②如下图当点D运动到线段CA的延长线上时此时∠CDE=∠ADE=90°CD=AC+AD=8+2=10∵CE=√CD2+DE2=√102+22=2√26∵点O为CE的中点CE=√26．∵OD=12综上所述OD的长为√10或√26．故答案为：√10或√26．13．解：当点P 在线段OB 上时∵点B 的坐标为(8,8) 四边形OABC 是正方形∵OA =AB =8 ∠OAB =90° ∠AOB =45°在Rt △OAB 中OB =√OA 2+AB 2=√82+82=8√2将△AOP 绕点A 顺时针旋转90°得到△ABQ∵△AOP ≌△ABQ∵OP =BQ∵BP +BQ =BP +OP =OB =8√2与BP +BQ =10√2相矛盾故点P 不在线段OB 上当点P 在线段OB 的延长线上时 如图过点Q 作QF ⊥x 轴于点F由旋转的性质可得OP =BQ ∠AOB =∠ABQ =45°∵BP +BQ =BP +OP =10√2由图可知 OP −BP =8√2解方程组{BP +OP =10√2OP −BP =8√2解得{OP =9√2BP =√2∵BQ =OP =9√2设BQ 与x 轴交于点N∵∠OAB =∠NAB =90° ∠ABQ =45°∵∠ANB =90°−∠ABQ =90°−45°=45°∵△ABN 是等腰直角三角形∵AN =AB =8∵BN =√AB 2+AN 2=√82+82=8√2∵NQ =BQ −BN =9√2−8√2=√2∵∠QFA =90° ∠QNF =∠ANB =45°∵∠NQF =90°−∠QNF =90°−45°=45°∵△QNF 是等腰直角三角形∵QF=NF=NQ⋅sin∠NQF=√2×sin45°=√2×√22=1∵OF=OA+AN+NF=8+8+1=17∵点Q的坐标为(17,−1)故答案为：(17,−1)．14．解：在AC上截取AE=AB=2作EF⊥BC于F如图∵∠ABC=90°∠C=30°∴AC=2AB=4BC=√3AB=2√3∠BAC=60°∴CE=AC−AE=2在Rt△CEF中EF=12CE=1FC=√3EF=√3∵线段AD绕点A顺时针旋转60°至AD′∴AD=AD′∠DAD′=60°∴∠BAD′=∠EAD在△ABD′和△ADE中{AB=AE∠BAD′=∠EAD AD′=AD∴△ABD′∵△AED∴DE=BD′在Rt△DEF中DE2=DF2+EF2=(√3−BD)2+12=(BD−√3)2+1∴当BD=√3时DE2有最小值1∴BD′的最小值为1．15．解：如图取AB的中点N连接EN,EC,GN作EH⊥CD交CD的延长线于H由题意可得：AE=8,DE=4,∵点N是AB的中点∵AN=NB=8,∵AE=AN,∵∠A=60°,∵△AEN是等边三角形∵EA=EN,∠AEN=∠FEG=60°,∠ANE=60°,∵∠AEF=∠NEG,∵EA=EN,EF=EG,∵△AEF≌△NEG(SAS),∵∠ENG=∠A=60°,∵∠GNB=180°−60°−60°=60°,∵点G的运动轨迹是射线NG∵BN=EN,∠BNG=∠ENG=60°，NG=NG,∵△EGN≌△BGN(SAS),∵GB=GE,∵GB+GC=GE+GC≥EC,在Rt△DEH中∠H=90°,DE=4,∠EDH=60°,DE=2,EH=2√3∵DH=12∵在Rt△ECH中EC=√EH²+CH²=√(2√3)2+182=4√21∵GB+GC≥4√21∵GB+GC的最小值为4√21；故答案为4√21．16．解：过点B′作BE′⊥AC交直线AC于点E∵在△ABC中∠ACB=90°∠ABC=30°∴∠BAC=90°−∠ABC=60°AC=12AB=12×6=3∵将△APB绕点A逆时针旋转60°得到△AP′B′∵△APB≌△AP′B′△APP′是等边三角形∵PP′=AP∴AB=AB′=6,∠BAB′=60°∴∠B′AE=180°−∠BAC−∠BAB′=60°在Rt△B′AE中∠AB′E=90°−∠B′AE=30°∴AE=12AB′=3,B′E=√AB′2−AE2=3√3∴CE=AC+AE=3+3=6若点C P P′B′恰好在同一直线上在Rt△B′EC中CB′=√CE2+B′E2=√62+(3√3)2=3√7．∴PA+PB+PC=CB′=3√7．故答案为：3√7．17．解：如图延长D′A′交AD于点F连接BF AC DE∵四边形ABCD为矩形点O是对角线BD的中点∵AC经过点O AD=BC AD∥BC∴OA =OC ∠OAF =∠OCE由旋转的性质可知：AB =A ′B ∠BAF =∠BA ′O =90°在Rt △BAF 和Rt △BA ′F 中{BA =BA ′BF =BF∵Rt △BAF ≌Rt △BA ′F (HL )∵AF =A ′F在△OAF 和△OCE 中{∠OAF =∠OCE OA =OC ∠AOF =∠COE∵△OAF ≌△OCE (ASA )∵AF =CE∵AD =BC AD∥BC∵DF =BE∵四边形BEDF 为平行四边形∵OE =OF设AF =x A ′O =a∵OE =OF =x +a D ′E =2A ′O =2a∵EF =2OF =2x +2a AD =A ′D =x +4a∵DF =BE =AD −AF =4a A ′E =x +2a∵EF 为平行四边形BEDF 的对角线∵S ▱BEDF =2S △BEF∵BE ⋅AB =2×12EF ⋅A ′B∵4a ⋅AB =2×12(2x +2a )⋅A ′B ∵AB =A ′B∵4a =2x +2a∵x =a∵AD =x +4a =5a A ′E =x +2a =3a在Rt △A ′BE 中A ′E =3a BE =4a由勾股定理得：A ′B =√BE 2+A ′E 2=√7a∵AB=A′B=√7a∵AB AD =√7a5a=√75故答案为：√75．18．解：（1）连接BD交AC于O如图所示：∵四边形ABCD是菱形∵CD＝AB＝2，∠BCD＝∠BAD＝60°，∠ACD＝∠BAC＝12∠BAD＝30°，OA＝OC，AC⊥BD∵OB＝12AB＝1∵OA＝√3OB＝√3∵AC＝2√3由旋转的性质得：BC=AD=EF=FG=GA=CD=AE=AB=2∠EAG＝∠BAD＝60°∵CE＝AC−AE＝2√3−2∵四边形AEFG是菱形∵EF∥AG∵∠CEP＝∠EAG＝60°∵∠CEP＋∠ACD＝90°∵∠CPE＝90°∵EF⊥DC∵EF=CD=2∵EF与DC的关系是相等且垂直故答案为：相等且垂直；（2）∵PE＝12CE＝√3−1PC＝√3PE＝3−√3∵DP＝CD−PC＝2−（3−√3）＝√3−1．故答案为：√3−119．解：①根据旋转的性质知∠CAD=∠BAF AD=AF ∵∠BAC=90°∠DAE=45°∵∠CAD+∠BAE=45∘∵∠EAF=∠EAB+∠BAF=45°∵AD=AF AE=AE∵△AEF≌△AED(SAS)故①正确；②根据旋转的性质知△ADC≌△AFB∵△ABC的面积等于四边形AFBD的面积故②错误；③∵∠BAC=90°AB=AC∵∠ABC=∠ACB=45∘∵∠DAE=45°∵∠DAE=∠ABE=45∘∵∠ABE+∠EAB=∠DAE+∠EAB即∠BAD=∠AEC故③正确；④∵∠BAC=90°AB=AC△ADC旋转90°至△AFB∵∠ABC=∠ACB=45∘根据旋转的性质可得△ADC≌△AFB∠ABF=∠ACD=45∘∵∠FBE=45∘+45∘=90∘∵BE2+BF2=EF2∵将△ADC绕点A顺时针旋转90°后得△AFB∵△ADC≌△AFB∵BF=CD∵EF=DE∵BE2+DC2=DE2故④正确；故答案为：①③④．20．解：∵四边形OABC为矩形∵OA∥BC AB∥OC OA=BC AB=OC∠AOC=∠OAB=∠OCB=∠ABC=90°∵A(0 3) C(4 0)∵AO=BC=3 OC=AB=4由旋转可知四边形CDEF为矩形且DE=OA=3 DC=OC=4连CE则在Rt△CDE中CE=√CD2+DE2=√42+32=5过B作BG⊥EF于H且使BG=CF连GF GE则∠BHE=∠CFE=90°∵BG∥CF又∵CF∥DE CF=DE∵BG=CF BG=DE BG∥CF BG∥DE∵四边形CBGF和四边形DBGE均为平行四边形∵BC=FG BD=EG∵BG⊥EF于H∵∠BHF=∠FHG=∠GHE=∠BHE=90°∵BF2=BH2+HF2BD2=EG2=HE2+HG2∵BF2+BD2=BH2+HF2+HE2+HG2又∵BE2=BH2+HE2BC2=GF2=HF2+HG2∵BE2+BC2=BH2+HE2+HE2+HG2∵BF2+BD2=BE2+BC2∵BF2+BD2−BC2=BE2∵当BE最小时BF2+BD2−BC2才最小当C B E三点不共线时在△CBE中BE>CE−CB当C B E三点共线时（点E在CB的延长线上时）BE=CE-CB综上所述BE≥CE-CB=5-3=2即BE≥2∵BE的最小值为2当BE=2时BF2+BD2−BC2=4故答案为：4．。

2023年春九年级数学中考复习《几何图形变换综合压轴题》专题训练（附答案）1．如图，△ABC和△ECD都是等边三角形，直线AE，BD交于点F．（1）如图1，当A，C，D三点在同一直线上时，∠AFB的度数为，线段AE与BD的数量关系为．（2）如图2，当△ECD绕点C顺时针旋转α（0°≤α＜360°）时，（1）中的结论是否还成立？若不成立，请说明理由；若成立，请就图2给予证明．（3）若AC＝4，CD＝3，当△ECD绕点C顺时针旋转一周时，请直接写出BD长的取值范围．2．如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D、E两点分别在AC、BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现：当α＝0°时，的值为；（2）拓展探究：当0°≤α＜360°时，若△EDC旋转到如图2的情况时，求出的值；（3）问题解决：当△EDC旋转至A、B、E三点共线时，若CE＝5，AC＝4，直接写出线段AD的长．3．已知：如图1，线段AD＝5，点B从点A出发沿射线AD方向运动，以AB为底作等腰△ABC，使得AC＝BC＝AB．（1）如图2，当AB＝10时，求证：CD⊥AB；（2）当△BCD是以BC为腰的等腰三角形时，求BC的长；（3）当AB＞5时，在线段BC上是否存在点E，使得△BDE与△ACD全等，若存在，求出BC的长；若不存在，请说明理由；（4）作点A关于直线CD的对称点A′，连接CA′当CA′∥AB时，CA′＝（请直接写出答案）．4．如图1，在△ABC中，AE⊥BC于点E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系是：；数量关系是：；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；（3）如图3，若将（2）中的等腰直角三角形都换成等边三角形，其他条件不变．①试猜想BD与AC的数量关系为：；②你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．5．如图，平面直角坐标系中O为原点，Rt△ABC的直角顶点A在y轴正半轴上，斜边BC 在x轴上，已知B、C两点关于y轴对称，且C（﹣8，0）．（1）请直接写出A、B两点坐标；（2）动点P在线段AB上，横坐标为t，连接OP，请用含t的式子表示△POB的面积；（3）在（2）的条件下，当△POB的面积为24时，延长OP到Q，使得PQ＝OP，在第一象限内是否存在点D，使得△OQD是等腰直角三角形，如果存在，求出D点坐标；如果不存在，请说明理由．6．如图1，已知△ABC中，∠ACB＝90°，AC＝BC＝6，点D在AB边的延长线上，且CD ＝AB．（Ⅰ）求BD的长度；（Ⅱ）如图2，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'．①若α＝30°，A'D'与CD相交于点E，求DE的长度；②连接A'D、BD'，若旋转过程中A'D＝BD'时，求满足条件的α的度数．（Ⅲ）如图3，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'，若点M 为AC的中点，点N为线段A'D'上任意一点，直接写出旋转过程中线段MN长度的取值范围．7．如图①，将两个等腰直角三角形纸片OAB和OCD放置在平面直角坐标系中，点O（0，0），点A（0，+1），点B（+1，0），点C（0，1），点D（1，0）．（Ⅰ）求证：AC＝BD；（Ⅱ）如图②，现将△OCD绕点O顺时针方向旋转，旋转角为α（0°＜α＜180°），连接AC，BD，这一过程中AC和BD是否仍然保持相等？说明理由；当旋转角α的度数为时，AC所在直线能够垂直平分BD；（Ⅲ）在（Ⅱ）的情况下，将旋转角α的范围扩大为0°＜α＜360°，那么在旋转过程中，求△BAD的面积的最大值，并写出此时旋转角α的度数．（直接写出结果即可）8．在△ABC中，AB＝AC，∠BAC＝α，过点A作直线l平行于BC，点D是直线l上一动点，连接CD，射线DC绕点D顺时针旋转α交直线AB于点E．（1）如图1，若α＝60°，当点E在线段AB上时，请直接写出线段AC，AD，AE之间的数量关系，不用证明；（2）如图2，若α＝60°，当点E在线段BA的延长线上时，（1）中的结论是否成立？若成立，请证明；若不成立，请写出正确结论，并证明．（3）如图3，若α＝90°，BC＝6，AD＝，请直接写出AE的长．9．有一根直尺短边长4cm，长边长10cm，还有一块锐角为45°的直角三角形纸板，它的斜边长为16cm，如图甲，将直尺的短边DE与直角三角形纸板的斜边AB重合，且点D 与点A重合．将直尺沿射线AB方向平移，如图乙，设平移的长度为xcm，且满足0≤x ≤12，直尺和三角形纸板重叠部分的面积为Scm2．（1）当x＝0cm时，S＝；当x＝12cm时，S＝．（2）当0＜x＜8（如图乙、图丙），请用含x的代数式表示S．（3）是否存在一个位置，使重叠部分面积为28cm2？若存在求出此时x的值．10．如图①，C为线段BD上的一点，BC≠CD，分别以BC，BD为边在BD的上方作等边△ABC和等边△CDE，连接AE，F，G，H分别是BC，AE，CD的中点，连接FG，GH，FH．（1）△FGH的形状是；（2）将图①中的△CDE绕点C顺时针旋转，其他条件不变，（1）的结论是否成立？结合图②说明理由；（3）若BC＝2，CD＝4，将△CDE绕点C旋转一周，当A，E，D三点共线时，直接写出△FGH的周长．11．已知，射线AB∥CD，P是直线AC右侧一动点，连接AP，CP，E是射线AB上一动点，过点E的直线分别与AP，CP交于点M，N，与射线CD交于点F，设∠BAP＝∠1，∠DCP＝∠2．（1）如图1，当点P在AB，CD之间时，求证：∠P＝∠1+∠2；（2）如图2，在（1）的条件下，作△PMN关于直线EF对称的△P'MN，求证：∠3+∠4＝2（∠1+∠2）；（3）如图3，当点P在AB上方时，作△PMN关于直线EF对称的△P'MN，（1）（2）的结论是否仍然成立，若成立，请说明理由；若不成立，请直接写出∠P，∠1，∠2之间数量关系，以及∠3，∠4与∠1，∠2之间数量关系．12．（1）如图1，平面直角坐标系中A（0，a），B（a，0）（a＞0）．C为线段AB的中点，CD⊥x轴于D，若△AOB的面积为2，则△CDB的面积为．（2）如图2，△AOB为等腰直角三角形，O为直角顶点，点E为线段OB上一点，且OB＝3OE，C与E关于原点对称，线段AB交x轴于点D，连CD，若CD⊥AE，试求的值．（3）如图3，点C、E在x轴上，B在y轴上，OB＝OC，△BDE是以B为直角顶点的等腰直角三角形，直线CB、ED交于点A，CD交y轴于点F，试探究：是否为定值？如果是定值，请求出该定值；如果不是，请求出其取值范围．13．在△ABC中，AB＝AC，∠BAC＝90°．（1）如图1，点P，Q在线段BC上，AP＝AQ，∠BAP＝15°，求∠AQB的度数；（2）点P，Q在线段BC上（不与点B，C重合），AP＝AQ，点Q关于直线AC的对称点为M，连接AM，PM．①依题意将图2补全；②用等式表示线段BP，AP，PC之间的数量关系，并证明．14．【问题背景】如图1，在Rt△ABC中，AB＝AC，D是直线BC上的一点，将线段AD绕点A逆时针旋转90°至AE，连接CE，求证：△ABD≌△ACE；【尝试应用】如图2，在图1的条件下，延长DE，AC交于点G，BF⊥AB交DE于点F，求证：FG＝AE；【拓展创新】如图3，A是△BDC内一点，∠ABC＝∠ADB＝45°，∠BAC＝90°，BD ＝，直接写出△BDC的面积为．15．在平面直角坐标系中，A（a，0），B（0，b）分别是x轴负半轴和y轴正半轴上一点，点C与点A关于y轴对称，点P是x轴正半轴上C点右侧一动点．（1）当2a2+4ab+4b2+2a+1＝0时，求A，B的坐标；（2）当a+b＝0时，①如图1，若D与P关于y轴对称，PE⊥DB并交DB延长线于E，交AB的延长线于F，求证：PB＝PF；②如图2，把射线BP绕点B顺时针旋转45o，交x轴于点Q，当CP＝AQ时，求∠APB的大小．16．已知：在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，左右作平行移动的等边三角形DEF的两个顶点E、F始终在边BC上，DE、DF分别与AB相交于点G、H．（1）如图1，当点F与点C重合时，点D恰好在斜边AB上，求△DEF的周长；（2）如图2，在△DEF作平行移动的过程中，图中是否存在与线段CF始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由；（3）假设C点与F点的距离为x，△DEF与△ABC的重叠部分的面积为y，求y与x的函数关系式，并写出定义域．17．在△ABC中，∠C＝90°，AC＝2，BC＝2，点D为边AC的中点（如图），点P、Q 分别是射线BC、BA上的动点，且BQ＝BP，联结PQ、QD、DP．（1）求证：PQ⊥AB；（2）如果点P在线段BC上，当△PQD是直角三角形时，求BP的长；（3）将△PQD沿直线QP翻折，点D的对应点为点D'，如果点D'位于△ABC内，请直接写出BP的取值范围．18．定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．（1）已知点M，N是线段AB的勾股分割点，若AM＝2，MN＝3，求BN的长．（2）如图2，在等腰直角△ABC中，AC＝BC，∠ACB＝90°，点M，N为边AB上两点满足∠MCN＝45°，求证：点M，N是线段AB的勾股分割点；阳阳同学在解决第（2）小题时遇到了困难，陈老师对阳阳说：要证明勾股分割点，则需设法构造直角三角形，你可以把△CBN绕点C逆时针旋转90°试一试．请根据陈老师的提示完成第（2）小题的证明过程．19．问题背景如图（1），△ABD，△AEC都是等边三角形，△ACD可以由△AEB通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．尝试应用如图（2），在Rt△ABC中，∠ACB＝90°，分别以AC，AB为边，作等边△ACD和等边△ABE，连接ED，并延长交BC于点F，连接BD．若BD⊥BC，求的值．拓展创新如图（3），在Rt△ABC中，∠ACB＝90°，AB＝2，将线段AC绕点A顺时针旋转90°得到线段AP，连接PB，直接写出PB的最大值．20．【教材呈现】如图是苏科版九年级下册数学教材第92页的第17题．一块直角三角形木板，它的一条直角边AC长为1.5m，面积为1.5m2．甲乙两人分别按图1、图2把它加工成一个正方形的桌面，请说明哪个正方形的面积较大．【解决问题】（1）记图1、图2中的正方形面积分别为S1，S2，则S1S2．（填“＞”、“＜”或“＝”）．【问题变式】若木板形状是锐角三角形A1B1C1．某数学兴趣小组继续思考：按图3、图4、图5三种方式加工，分别记所得的正方形面积为S3、S4、S5，哪一个正方形的面积最大呢？（2）若木板的面积S仍为1.5m2．小明：记图3中的正方形为“沿B1C1边的内接正方形”，图4中的正方形为“沿A1C1边的内接正方形”，依此类推．以图3为例，求“沿B1C1边的内接正方形DEFG”的面积．设EF ＝x ，B 1C 1＝a ，B 1C 1边上的高A 1H ＝h ，则S ＝ah ．由“相似三角形对应高的比等于相似比”易得x ＝；同理可得图4、图5中正方形边长，再比较大小即可．小红：若要内接正方形面积最大，则x 最大即可；小莉：同一块木板，面积相同，即S 为定值，本题中S ＝1.5，因此，只需要a +h 最小即可．我们可以借鉴以前研究函数的经验，令y ＝a +h ＝a +＝a +（a ＞0）．下面来探索函数y ＝a +（a ＞0）的图象和性质．①根据如表，画出函数的图象：（如图6）a… 1 2 3 4 … y … 12 9 6 4 3 3 4 4…②观察图象，发现该函数有最小值，此时a 的取值 ；A ．等于2；B ．在1～之间；C ．在～之间；D ．在～2之间．（3）若在△A 1B 1C 1中（如图7），A 1B 1＝5，A 1C 1＝，高A 1H ＝4．①结合你的发现，得到S 3、S 4、S 5的大小关系是 （用“＜”连接）． ②小明不小心打翻了墨水瓶，已画出最大面积的内接正方形的△A 1B 1C 1原图遭到了污损，请用直尺和圆规帮他复原△A 1B 1C 1．（保留作图痕迹，不写作法）参考答案1．解：（1）∵△ABC是等边三角形，∴AC＝BC，∠BAC＝∠ACB＝60°，∵△ECD是等边三角形，∴CE＝CD，∠DCE＝60°，∴∠ACB＝∠DCE＝60°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE＝BD，∠CAE＝∠CBD，在△ABF中，∠AFB＝180°﹣（∠BAF+∠ABF）＝180°﹣（∠BAF+∠CBF+∠ABC）＝180°﹣（∠BAC+∠ABC）＝180°﹣（60°+60°）＝60°，∴∠AFB＝60°，故答案为：∠AFB＝60°，AE＝BD；（2）（1）中结论仍成立，证明：∵△ABC是等边三角形，∴AC＝BC，∠BAC＝∠ACB＝60°，∵△ECD是等边三角形，∴CE＝CD，∠DCE＝60°，∴∠ACB＝∠DCE＝60°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE＝BD，∠CAE＝∠CBD，∵∠AFB+∠CBD＝∠ACB+∠CAE，∴∠AFB＝∠ACB，∵∠ACB＝60°，∴∠AFB＝60°；（3）在△BCD中，BC+CD＞BD，BC﹣CD＜BD，∴点D在BC的延长线上时，BD最大，最大为4+3＝7，当点D在线段BC上时，BD最小，最小为4﹣3＝1，∴1≤BD≤7，即BD长的取值范围为1≤BD≤7．2．解：（1）∵∠BAC＝90°，AB＝AC，∴△ABC为等腰直角三角形，∠B＝45°，∵DE∥AB，∴∠DEC＝∠B＝45°，∠CDE＝∠A＝90°，∴△DEC为等腰直角三角形，∴cos∠C＝＝，∵DE∥AB，∴＝＝，故答案为：；（2）由（1）知，△BAC和△CDE均为等腰直角三角形，∴＝＝，又∠BCE＝∠ACD＝α，∴△BCE∽△ACD，∴＝＝，即＝；（3）①如图3﹣1，当点E在线段BA的延长线上时，∵∠BAC＝90°，∴∠CAE＝90°，∴AE＝＝＝3，∴BE＝BA+AE＝4+3＝7；由（2）知，＝．故AD＝．②如图3﹣2，当点E在线段BA上时，AE＝＝＝3，∴BE＝BA﹣AE＝4﹣3＝1，由（2）知，＝．故AD＝．综上所述，AD的长为或，故答案为：或．3．解：（1）如图2中，∵AB＝10，AD＝5，∴AD＝DB，∵CA＝CB，AD＝DB，∴CD⊥AB．（2）如图1中，当AB＜AD时，BC＝BD．设AB＝10k，则AC＝BC＝6k，∵AD＝5，∴10k+6k＝5，∴k＝，∴BC＝6k＝．如图1﹣1中，当AB＞AD时，BC＝BD，同法可得10k﹣6k＝5，解得k＝，∴BC＝6k＝，综上所述，BC的值为或．（3）如图3﹣1中，当△ADC≌△BED时，BD＝AC＝BC，由（2）可知，BC＝．如图3﹣2中，当△ADC≌△BCE时，点E与C重合，此时AB＝10k＝10，∴k＝1，BC＝6k＝6．综上所述，BC的值为或6．（4）如图3中，当CA′∥AB时，∵CA′∥AB，∴∠ADC＝∠A′CD，由翻折可知，∠A′CD＝∠ACD，∴∠ACD＝∠ADC，∴AC＝AD＝5，∴CA′＝CA＝5．故答案为5．4．解：（1）结论：BD＝AC，BD⊥AC．理由：延长BD交AC于F．∵AE⊥CB，∴∠AEC＝∠BED＝90°．在△AEC和△BED中，，∴△AEC≌△BED（SAS），∴AC＝BD，∠CAE＝∠EBD，∵∠AEC＝90°，∴∠ACB+∠CAE＝90°，∴∠CBF+∠ACB＝90°，∴∠BFC＝90°，∴AC⊥BD，故答案为：BD⊥AC，BD＝AC．（2）如图2中，不发生变化，设DE与AC交于点O，BD与AC交于点F．理由是：∵∠BEA＝∠DEC＝90°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠BDE＝∠ACE，∵∠DEC＝90°，∴∠ACE+∠EOC＝90°，∵∠EOC＝∠DOF，∴∠BDE+∠DOF＝90°，∴∠DFO＝180°﹣90°＝90°，∴BD⊥AC；（3）①如图3中，结论：BD＝AC，理由是：∵△ABE和△DEC是等边三角形，∴AE＝BE，DE＝EC，∠BEA＝∠DEC＝60°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，故答案为：BD＝AC．②能；设BD与AC交于点F，由①知，△BED≌△AEC，∴∠BDE＝∠ACE，∴∠DFC＝180°﹣（∠BDE+∠EDC+∠DCF）＝180°﹣（∠ACE+∠EDC+∠DCF）＝180°﹣（60°+60°）＝60°，即BD与AC的夹角中的锐角的度数为60°．5．解：（1）∵B、C两点关于y轴对称，且C（﹣8，0），∴点B（8，0），BO＝CO，又∵AO⊥BC，∴AC＝AB，∵∠CAB＝90°，AC＝AB，CO＝BO，∴AO＝CO＝BO＝8，∴点A（0，8）；（2）如图1，过点P作PM⊥OB于M，∵点P的横坐标为t，∴OM＝t，∴MB＝8﹣t，∵∠CAB＝90°，AC＝AB，∴∠ABO＝45°，∴∠BPM＝∠ABO＝45°，∴PM＝MB＝8﹣t，∴S△POB＝×OB×PM＝×8×（8﹣t）＝32﹣4t；（3）∵△POB的面积为24，∴32﹣4t＝24，∴t＝2，∴点P（2，6），如图2，当点Q为直角顶点时，过点Q作HG⊥y轴，过点D作DG⊥HG于点G，∵PQ＝OP，点P（2，6），∴点Q（4，12），∵∠OQD＝90°＝∠OHQ＝∠QGD，∴∠OQH+∠DQG＝90°＝∠OQH+∠HOQ，∴∠HOQ＝∠GQD，又∵OQ＝QD，∴△OHQ≌△QGD（AAS），∴OH＝QG＝12，HQ＝GD＝4，∴HG＝16，∴点D（16，8）；当点D为直角顶点时，过点Q作HG⊥y轴，过点D作DG⊥HG于点G，过点D作DN ⊥y轴于N，同理可求△QDG≌△ODN，∴ON＝QG，DN＝DG，∵DN＝QG+HQ＝4+QG，DG＝HN＝12﹣ON，∴ON＝QG＝4，DN＝DG＝8，∴点D（8，4），综上所述：点D（16，8）或（8，4）．6．解：（Ⅰ）如图1，过点C作CH⊥AB于H，∵∠ACB＝90°，AC＝BC＝6，CH⊥AB，∴AB＝CD＝6，CH＝BH＝AB＝3，∠CAB＝∠CBA＝45°，∴DH＝＝＝3，∴BD＝DH﹣BH＝3﹣3；（Ⅱ）①如图2，过点E作EF⊥CD'于F，∵将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A′CD′，∴CD＝CD'＝6，∠DCD'＝30°＝∠CDA＝∠CD'A'，∴CE＝D'E，又∵EF⊥CD'，∴CF＝D'F＝3，EF＝，CE＝2EF＝2，∴DE＝DC﹣CE＝6﹣2；②如图2﹣1，∵∠ABC＝45°，∠ADC＝30°，∴∠BCD＝15°，∴∠ACD＝105°，∵将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A′CD′，∴AC＝A'C，CD＝CD'，∠ACA'＝∠DCD'＝α，∴CB＝CA'，又∵A′D＝BD′，∴△A'CD≌△BCD'（SSS），∴∠A'CD＝∠BCD'，∴105°﹣α＝15°+α，∴α＝45°；如图2﹣2，同理可证：△A'CD≌△BCD'，∴∠A'CD＝∠BCD'，∴α﹣105°＝360°﹣α﹣15°，∴α＝225°，综上所述：满足条件的α的度数为45°或225°；（Ⅲ）如图3，当A'D'⊥AC时，N是AC与A'D'的交点时，MN的长度最小，∵∠A'＝45°，A'D'⊥AC，∴∠A'＝∠NCA'＝45°，∴CN＝A'N＝3，∵点M为AC的中点，∴CM＝AC＝3，∴MN的最小值＝NC﹣CM＝3﹣3；如图4，当点A，点C，点D'共线，且点N与点D'重合时，MN有最大值，此时MN＝CM+CN＝6+3，∴线段MN的取值范围是3﹣3≤MN≤6+3．7．解：（Ⅰ）∵点A（0，+1），点B（+1，0），点C（0，1），点D（1，0），∴OA＝+1，OB＝+1，OC＝1，OD＝1，∴AC＝OA﹣OC＝+1﹣1＝，BD＝+1﹣1＝，∴AC＝BD；（Ⅱ）由题意知，OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，∴∠AOC＝∠AOB﹣∠COB＝90°﹣∠COB，∠BOD＝∠COD﹣∠COB＝90°﹣∠COB，∴∠AOC＝∠BOD，∴△AOC≌△BOD（SAS），∴AC＝BD，∠OAC＝∠OBD，如图1（注：点C在x轴上，为了不要出现误解，点C没画在x轴上），延长AC交BD 于D，连接BC，在Rt△AOB中，OA＝OB，∴∠OAB＝∠OBA＝45°，∴∠CAB+∠ABD＝∠OAB﹣∠OAC+∠ABO+∠BOD＝∠OAB+∠OBA＝90°，∴AC⊥BD，∵AC垂直平分BD，∴CD＝BC，设点C的坐标为（m，n），∴m2+n2＝1①，由旋转知，CD＝＝，∵B（+1，0），[m﹣（+1）]2+n2＝2②，联立①②解得，m＝1，n＝0，∴点C在x轴上，∴旋转角为∠AOC＝90°，故答案为：90°；（Ⅲ）如图2，∵OA＝OB＝+1，∴AB＝OA＝2+，过点O作OH⊥AB于H，∴S△AOB＝OA•OB＝AB•OH，∴OH＝＝＝＝，过点D作DG⊥AB于G，S△ABD＝AB•DG＝（2+）DG，要使△ABD的面积最大，则DG最大，由旋转知，点D是以O为圆心，1为半径的圆上，∴点D在HO的延长线上时，DG最大，即DG的最大值为D'H＝OD'+OH＝1+＝，∴S△ABD最大＝AB•D'H＝（2+）×＝，在Rt△AOB中，OA＝OB，OH⊥AB，∴∠BOH＝45°，∴旋转角∠BOD'＝180°﹣45°＝135°．8．解：（1）AC＝AE+AD．证明：连接CE，∵线段DC绕点D顺时针旋转α交直线AB于点E，α＝60°，∵AB＝AC，∠BAC＝60°，∴CB＝CA＝AB，∠ACB＝60°，∵AD∥BC，∴∠DAF＝∠ACB＝60°，∵∠FDC＝∠EAF＝60°，∠AFE＝∠DFC，∴△AFE∽△DFC，∴，∴，∵∠AFD＝∠EFC，∴△AFD∽△EFC，∴∠DAF＝∠FEC＝60°，∴△DEC是等边三角形，∴CD＝CE，∠ECD＝60°，∴∠BCE＝∠ACD，∴△BCE≌△ACD（SAS），∴BE＝AD，∴AB＝AE+BE＝AE+AD，∴AC＝AE+AD；（2）不成立，AD＝AC+AE．理由如下：在AC的延长线上取点F，使AF＝AD，连接DF，当α＝60°时，∠BAC＝∠EDC＝60°，∵AB＝AC，∴△ABC是等边三角形，∴AB＝AC＝BC∠BCA＝60°，∵l∥BC，∴∠DAC＝∠BCA＝60°，∠EAD＝∠ABC＝60°，∵AF＝AD，∴∠ADF＝∠AFD＝60°，AD＝FD＝AF，∴∠EDC＝∠ADF＝60°，∴∠EDC﹣∠ADC＝∠ADF﹣∠ADC，即∠EDA＝∠CDF，∵AD＝FD，∠EAD＝∠AFD＝60°，∴△EAD≌△CFD（ASA），∴AE＝CF，∴AD＝AF＝AC+CF＝AC+AE；（3）AE的长为或．当点E在线段AB上，过点D作直线l的垂线，交AC于点F，如图3所示．∵△ABC中，∠BAC＝90°，AC＝AB，∴∠ACB＝∠B＝45°．∵直线l∥BC，∴∠DAF＝∠ACB＝45°．∵FD⊥直线l，∴∠DAF＝∠DF A＝45°．∴AD＝FD．∵∠EDC＝∠ADF＝90°，∴∠ADE＝∠FDC．由（1）可知DC＝DE，∴△ADE≌△FDC（SAS），∴AE＝CF．∵AD＝，∴AF＝2，∵BC＝6，∴AC＝AB＝3，∴AE＝AC﹣AF＝3﹣2．当点E在线段AB的延长线上时，如图4所示．过点D作直线l的垂线，交AB于点M，同理可证得△ADC≌△MDE（SAS），∴AC＝EM＝3，∵AD＝，∴AM＝2，∴EM+AM＝3+2．综合以上可得AE的长为3+2或3﹣2．9．解：（1）当x＝0cm时，S＝4×4÷2＝8cm2；当x＝12cm时，S＝4×4÷2＝8cm2．故答案为：8cm2；8cm2．（2）①当0＜x＜4时，∵△CAB为等腰直角三角形，∴∠CAB＝45°，∴△ADG和△AEF都是等腰直角三角形，∴AD＝DG＝x，AE＝EF＝x+4，∴梯形GDEF的面积＝×（GD+EF）×DE＝×（x+x+4）×4＝4x+8．②如图所示：过点C作CM⊥AB于点M．当4＜x＜8时，梯形GDMC的面积＝（GD+CM）×DM＝（x+8）（8﹣x）＝﹣x2+32，梯形CMEF的面积＝（EF+CM）×ME＝[16﹣（x+4）+8][（x+4）﹣8]＝（20﹣x）（x﹣4）＝﹣x2+12x﹣40，S＝梯形GDMC的面积+梯形CMEF的面积＝（﹣x2+32）+（﹣x2+12x﹣40）＝﹣x2+12x ﹣8．综合以上可得，S＝．（3）当0＜x＜4时s最大值小于24，当x＝4时，S＝24cm2，所以当S＝28cm2时，x必然大于4，即﹣x2+12x﹣8＝28，解得x1＝x2＝6，当x＝6cm时，阴影部分面积为28cm2．当8＜≤12时，由对称性可知s的最大值也是小于24，不合题意舍去．∴当x＝6cm时，阴影部分面积为28cm2．10．解：（1）∵△ABC和△CDE都是等边三角形，∴∠B＝∠DCE＝60°，AB＝BC，CE＝CD，∴CE∥AB，∵BC≠CD，∴CE≠AB，∴四边形ABCE是梯形，∵点F，G分别是BC，AE的中点，∴FG是梯形ABCE的中位线，∴FG∥AB，∴∠GFC＝60°，同理：∠GHB＝60°，∴∠FGH＝180°﹣∠GFC﹣∠GHB＝60°＝∠GFC＝∠GHB，∴△FGH是等边三角形，故答案为：等边三角形；（2）成立，理由如下：如图1，取AC的中点P，连接PF，PG，∵△ABC和△CDE都是等边三角形，∴AB＝BC，CE＝CD，∠BAC＝∠ACB＝∠ECD＝∠B＝60°，又F，G，H分别是BC，AE，CD的中点，∴FP＝AB，FC＝BC，CH＝CD，PG＝CE，PG∥CE，PF∥AB，∴FP＝FC，PG＝CH，∠GPC+∠PCE＝180°，∠FPC＝∠BAC＝60°，∠PFC＝∠B＝60°，∴∠FPG＝∠FPC+∠GPC＝60°+∠GPC，∠GPC＝180°﹣∠PCE，∴∠FCH＝360°﹣∠ACB﹣∠ECD﹣∠PCE＝360°﹣60°﹣60°﹣（180°﹣∠GPC）＝60°+∠GPC，∴∠FPG＝∠FCH，∴△FPG≌△FCH（SAS），∴FG＝FH，∠PFG＝∠CFH，∴∠GFH＝∠GFC+∠CFH＝∠GFC+∠PFG＝∠PFC＝60°，∴△FGH为等边三角形；（3）①当点D在AE上时，如图2，∵△ABC是等边三角形，∴∠ACB＝60°，AC＝BC＝2，∵△CDE是等边三角形，∴∠CED＝∠CDE＝60°，CE＝CD＝DE＝4，过点C作CM⊥AE于M，∴DM＝EM＝DE＝2，在Rt△CME中，根据勾股定理得，CM＝＝＝2，在Rt△AMC中，根据勾股定理得，AM＝＝＝4，∴AD＝AM﹣DM＝4﹣2＝2，∵∠ACB＝∠DCE＝60°，∴∠ACB﹣∠DCB＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，连接BE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD＝2，∠ADC＝∠BEC，∵∠ADC＝180°﹣∠CDE＝120°，∴∠BEC＝120°，∴∠BEA＝∠BEC﹣∠CED＝60°，过点B作BN⊥AE于N，∴∠BNE＝90°，在Rt△BNE中，∠EBN＝90°﹣∠BEA＝30°，∴EN＝BE＝1，∴BN＝EN＝，DN＝DE﹣EN＝3，连接BD，根据勾股定理得，BD＝＝＝2，∵点H是CD的中点，点F是BC的中点，∴FH是△BCD的中位线，∴FH＝BD＝，由（2）知，△FGH是等边三角形，∴△FGH的周长为3FH＝3，②当点D在AE的延长线上时，如图3，同①的方法得，FH＝，∴△FGH的周长为3FH＝3，即满足条件的△FGH的周长为3或3．11．（1）证明：如图1中，过点P作PT∥AB．∵AB∥CD，AB∥PT，∴AB∥PT∥CD，∴∠1＝∠APT，∠2＝∠CPT，∴∠APC＝∠APT+∠CPT＝∠1+∠2．（2）证明：如图2中，连接PP′．∵∠3＝∠MPP′+∠MP′P，∠4＝∠NPP′+∠NP′P，∠APC＝∠MP′N，∴∠3+∠4＝2∠APC，∵∠APC＝∠1+∠2，∴∠3+∠4＝2（∠1+∠2）．（3）结论不成立．结论是：∠P＝∠2﹣∠1，∠4﹣∠3＝2（∠2﹣∠1）．理由：如图3中，设PC交AB于E，AP交NP′于F．∵AB∥CD，∴∠PEB＝∠2，∵∠PEB＝∠1+∠P，∴∠2＝∠P+∠1，∴∠P＝∠2﹣∠1．∵∠4＝∠P+∠PFN，∠PFN＝∠3+∠P′，∠P＝∠P′，∴∠4＝∠P+∠3+∠P，∴∠4﹣∠3＝2∠P＝2（∠2﹣∠1），∴∠4﹣∠3＝2（∠2﹣∠1）．12．解：（1）∵A（0，a），B（a，0）（a＞0），∴OA＝a，OB＝a，∵△AOB的面积为2，∴S△AOB＝×a×a＝2，∴a＝2（负值舍去），∴A（0，2），B（2，0），∵C为线段AB的中点，∴C（1，1），∴OD＝BD＝CD＝1，∴S△CDB＝×1×1＝．故答案为：．（2）连AC，过点D作DM⊥BC于M，∵△AOB是等腰直角三角形，∴AO⊥BO，AO＝BO，∠B＝∠OAB＝45°，又CO＝EO，∴AO是CE的垂直平分线，∴AE＝AC，不妨设AE、CD交于F，AO、CD交于G，∴∠CGA＝∠OAE+∠AFC＝∠OCD+∠COA，∵∠AFC＝∠COA＝90°，∴∠OAE＝∠OCD＝∠OAC，又∵∠CAD＝∠CAO+∠OAB＝∠OCD+∠B＝∠CDA，∴CD＝CA＝EA，∴△AOE≌△CMD（AAS），∴OE＝DM，∴＝＝＝3，∴＝2；（3）＝2，理由如下：作点C关于y轴的对称点N，连接BN，作DM∥BC交y轴于M，∵OB＝OC＝ON，∠BON＝90°，∴△BON等腰直角三角形，∴∠BNO＝∠BMD＝45°，∴∠MBD＝∠OBE+∠DBE＝∠OBE+∠BOE＝∠BEN，又∵BD＝BE，∴△BMD≌△ENB（AAS），∴EN＝BM，BN＝DM＝BC，又∵∠BFC＝∠DFM，∠BCF＝∠FDM，∴△BCF≌△MDF（AAS），∴BF＝MF，∴CO﹣EO＝NO﹣EO＝NE＝BM＝2BF，即＝2．13．解：（1）∵在△ABC中，AB＝AC，∠BAC＝90°，∴∠B＝∠C＝45°，∵∠APQ是△ABC的一个外角，∴∠APQ＝∠B+∠BAP，∵∠BAP＝15°，∴∠APQ＝60°，∵AP＝AQ，∴∠APQ＝∠AQB＝60°．（2）①图形如图2所示．②解：结论：PC2+BP2＝2AP2．理由：连接MC．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵AP＝AQ，∴∠APQ＝∠AQP，∴∠BAP＝∠CAQ，∴△ABP≌△ACQ（SAS），∴BP＝CQ，∵点Q关于直线AC的对称点为M，∴AQ＝AM，CQ＝CM，∠CAM＝∠CAQ，∠ACM＝∠ACQ＝45°，∴AP＝AM，∠B＝∠ACM＝45°，∠BAP＝∠CAM，BP＝CM，∴∠BAC＝∠P AM＝90°，在Rt△APM中，AP＝AM，∠P AM＝90°，∴PM＝，∵∠ACQ＝∠ACM＝45°，∴∠PCM＝90°，在Rt△PCM中，∠PCM＝90°，∴PC2+CM2＝PM2，∴PC2+BP2＝2AP2．14．【问题背景】证明：如图1，∵∠BAC＝∠DAE＝90°，∴∠DAB＝∠EAC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）．【尝试应用】证明：如图2，过点D作DK⊥DC交FB的延长线于K．∵DK⊥CD，BF⊥AB，∴∠BDK＝∠ABK＝90°，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∴∠DBK＝∠K＝45°，∴DK＝DB，∵△ABD≌△ACE，∴∠ABD＝∠ACE＝135°，DB＝EC＝DK，∴∠ECG＝45°，∵BF⊥AB，CA⊥AB，∴AG∥BF，∴∠G＝∠DFK，在△ECG和△DKF中，，∴△ECG≌△DKF（AAS），∴DF＝EG，∵DE＝AE，∴DF+EF＝AE，∴EG+EF＝AE，即FG＝AE．【拓展创新】解：如图3中，过点A作AE⊥AD交BD于E，连接CE．．∵∠ADB＝45°，∠DAE＝90°，∴△ADE与△ABC都是等腰直角三角形，同法可证△ABD≌△ACE，∴CE＝BD＝2，∵∠AEC＝∠ADB＝45°，∴∠CED＝∠CEB＝90°，∴S△BDC＝•BD•CE＝×2×2＝6．故答案为：6．15．解：（1）∵2a2+4ab+4b2+2a+1＝0，∴（a+2b）2+（a+1）2＝0，∵（a+2b）2≥0 （a+1）2≥0，∴a+2b＝0，a+1＝0，∴a＝﹣1，b＝，∴A（﹣1，0）B（0，）．（2）①证明：如图1中，∵a+b＝0，∴a＝﹣b，∴OA＝OB，又∵∠AOB＝90°，∴∠BAO＝∠ABO＝45°，∵D与P关于y轴对称，∴BD＝BP，∴∠BDP＝∠BPD，设∠BDP＝∠BPD＝α，则∠PBF＝∠BAP+∠BP A＝45°+α，∵PE⊥DB，∴∠BEF＝90°，∴∠F＝90o﹣∠EBF，又∠EBF＝∠ABD＝∠BAO﹣∠BDP＝45°﹣α，∴∠F＝45o+α，∴∠PBF＝∠F，∴PB＝PF．②解：如图2中，过点Q作QF⊥QB交PB于F，过点F作FH⊥x轴于H．可得等腰直角△BQF，∵∠BOQ＝∠BQF＝∠FHQ＝90°，∴∠BQO+∠FQH＝90°，∠FQH+∠QFH＝90°，∴∠BQO＝∠QFH，∵QB＝QF，∴△FQH≌△QBO（AAS），∴HQ＝OB＝OA，∴HO＝AQ＝PC，∴PH＝OC＝OB＝QH，∴FQ＝FP，又∠BFQ＝45°∴∠APB＝22.5°．16．解：（1）在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，∴AC＝2，∠A＝60°，∵△DEF是等边三角形，∴∠DCE＝60°，∴∠ACD＝30°，∴∠ADC＝90°，∴CD＝AC＝3，∴△DEF的周长＝9；（2）解：结论：CF＝DG．理由：∵BC＝6，EF＝DF＝DE＝3，∴CF+BE＝BC﹣EF＝6﹣3＝3，∵△DEF是等边三角形，∴∠DEF＝60°，∵∠DEF＝∠B+∠EGB，∴∠B＝∠EGB＝∠DGE＝30°，∴EG＝BE，∵EG+DG＝CF+BE＝3，∴CF＝DG；（3）∵S△DEF＝×32＝，S△DGH＝•GH•DH＝•x•x＝x2，y＝S△DFE﹣S△DHG＝﹣x2（0≤x≤3）．17．解：（1）在Rt△ABC中，AC＝2，BC＝2，根据勾股定理得，AB＝＝＝4，∴＝，∵BQ＝BP，∴＝，∴，∵∠QBP＝∠CBA，∴△BPQ∽△BAC，∴∠BQP＝∠ACB＝90°，∴PQ⊥AB；（2）∵点D是AC的中点，∴AD＝CD＝AC＝1，由（1）知，PQ⊥AB，∴∠AQP＝90°，∴∠PQD＜90°，∵△PQD是直角三角形，∴①当∠DPQ＝90°时，如图1，在Rt△ABC中，AC＝2，AB＝4，∴sin∠ABC＝＝，∴∠ABC＝30°，∴∠QPB＝90°﹣∠ABC＝60°，∴∠DPC＝90°﹣∠BPQ＝30°，∴CP＝＝＝，∴BP＝BC﹣CP＝，②当∠PDQ＝90°时，∴∠ADQ+∠PDC＝90°，如图2，过Q作QE⊥AC于E，∴∠DEQ＝90°＝∠ACB，∴∠ADQ+∠DQE＝90°，∴∠DQE＝∠PDC，∴△EQD∽△CDP，∴，∴，设BP＝t，则CP＝BC﹣BP＝2﹣t，在Rt△BQP中，BQ＝BP cos30°＝t，∴AQ＝AB﹣BQ＝4﹣t，在Rt△AEQ中，QE＝AQ cos30°＝（4﹣t）•＝2﹣t，AE＝AQ＝2﹣t，∴DE＝AD﹣AE＝t﹣1，∴，∴t＝或t＝（大于2，舍去）∴BP＝；即BP＝或；（3）；理由：如图3，①当点D'恰好落在边BC上时，由折叠知，PD'＝PD，PQ⊥DD'，由（1）知，PQ⊥AB，∴DD'∥AB，∴∠DD'C＝∠ABC＝30°，∴CD'＝CD＝，设BP＝m，则CP＝BC﹣BP＝2﹣m，∴DP＝D'P＝CD'﹣CP＝m﹣，在Rt△CDP中，根据勾股定理得，DP2＝CP2+CD2，∴（m﹣）2＝（2﹣m）2+1，∴m＝，②当点D'落在D时，即PQ过点D，在Rt△CDP'中，∠P'＝90°﹣∠DD'P'＝30°，∴CP'＝＝＝，∴BP'＝BC+CP'＝，综上：．18．（1）解：当MN最长时，BN＝＝＝；当BN最长时，BN＝＝＝，综合以上可得BN的长为或；（2）证明：如图，把△CBN绕点C逆时针旋转90°，得到△CAN'，连接MN'，∴△AN'C≌△BNC，∴CN'＝CN，∠ACN'＝∠BCN，∠CBN＝∠CAN'，∵∠MCN＝45°，∴∠N'CA+∠ACM＝∠ACM+∠BCN＝45°，∴∠MCN'＝∠BCM，∴△MN'C≌△MNC（SAS），∴MN'＝MN，∵AC＝BC，∠ACB＝90°，∴∠B＝∠CAM＝45°，∴∠CAN'＝45°，∴∠MAN'＝∠CAN'+∠CAM＝45°+45°＝90°，在Rt△MN'A中，AN'2+AM2＝N'M2，∴BN2+AM2＝MN2，∴点M，N是线段AB的勾股分割点．19．问题背景解：∵△ABD，△AEC都是等边三角形，∴∠BAD＝60°，∠CAE＝60°，AD＝AB，AC＝AE，∴∠BAD+∠BAC＝∠CAE+∠BAC，∴∠DAC＝∠BAE，∴△ACD≌△AEB（SAS），∴△ACD可以由△AEB绕点A顺时针旋转60°得到，即旋转中心是点A，旋转方向是顺时针，旋转角是60°；尝试应用∵△ACD和△ABE都是等边三角形，∴AC＝AD，AB＝AE，∠CAD＝∠BAE＝60°，∴∠CAB＝∠DAE，∴△ADE≌△ACB（SAS），∴∠ADE＝∠ACB＝90°，DE＝CB，∵∠ADE＝90°，∴∠ADF＝90°，∵∠ADC＝∠ACD＝60°，∴∠DCF＝∠CDF＝30°，∴CF＝DF，∵BD⊥BC，∴∠BDF＝30°，∴BF＝DF，设BF＝x，则CF＝DF＝2x，DE＝3x，∴；拓展创新∵∠ACB＝90°，∴点C在以AB为直径的圆上运动，取AB的中点D，连接CD，∴CD＝AB＝1，如图，过点A作AE⊥AB，且使AE＝AD，连接PE，BE，∵将线段AC绕点A顺时针旋转90°得到线段AP，∴∠P AC＝90°，P A＝AC，∵∠EAD＝90°，∴∠P AE＝∠CAD，∴△CAD≌△P AE（SAS），∴PE＝CD＝1，∵AB＝2，AE＝AD＝1，∴BE＝＝＝，∴BP≤BE+PE＝+1，当且仅当P、E、B三点共线时取等号，∴BP的最大值为+1．20．解：（1）由AC长为1.5m，△ABC的面积为1.5m2，可得BC＝2m，如图①，设加工桌面的边长为xcm，∵DE∥CB，∴△ADE∽△ACB，∴＝，即＝，解得：x＝；如图②，设加工桌面的边长为ym，过点C作CM⊥AB，分别交DE、AB于点N、M，∵AC＝1.5m，BC＝2m，∴AB＝＝＝2.5（m），∵△ABC的面积为1.5m2，∴CM＝m，∵DE∥AB，∴△CDE∽△CAB，∴＝，即＝，解得：y＝，∴x＞y，即S1＞S2，故答案为：＞．（2）①函数图象如图6所示：②观察图象，发现该函数有最小值，此时a的取值～2之间．故选D．（3）①由（2）可知，S5＜S4＜S3．故答案为：S5＜S4＜S3．②如图7，△A1B1C1即为所求作．。

几何图形变换压轴题中考整理1（黑龙江省哈尔滨市）已知：△ABC的高AD所在直线与高BE所在直线相交于点F．（1）如图l，若△ABC为锐角三角形，且∠ABC＝45°，过点F作FG∥BC，交直线AB于点G，求证：FG＋DC＝AD；（2）如图2，若∠ABC＝135°，过点F作FG∥BC，交直线AB于点G，则FG、DC、AD之间满足的数量关系是____________________________________；（3）在（2）的条件下，若AG＝25，DC＝3，将一个45°角的顶点与点B重合并绕点B旋转，这个角的两边分别交线段FG于M、N两点（如图3），连接CF，线段CF分别3，求线段PQ的长．与线段BM、线段BN相交于P、Q两点，若NG＝2（湖北省随州市）如图①，已知△ABC是等腰三直角角形，∠BAC＝90°，点D是BC 的中点．作正方形DEFG，使点A，C分别在DG和DE上，连接AE，BG．（1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论．（2）将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，小于或等于360°），如图②，通过观察或测量等方法判断（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由．（3）若BC＝DE＝2，在（2）的旋转过程中，当AE为最大值时，求AF的值．3、如图13－1，一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图13－2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 满足的数量关系，并证明你的猜想；（2）若三角尺GEF 旋转到如图13－3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．3．在△ABC 中，点P 为BC 的中点．（1）如图1，求证：AP ＜21（AB +BC ）； （2）延长AB 到D ，使得BD =AC ，延长AC 到E ，使得CE =AB ，连结DE ．①如图2，连结BE ，若∠BAC =60°，请你探究线段BE 与线段AP 之间的数量关系．写出你的结论，并加以证明； ②请在图3中证明：BC ≥21DE ．图13－2图13－3图13－1 A( B ( E )4．我们给出如下定义：有一组相邻内角相等的四边形叫做等邻角四边形．请解答下列问题： （1）写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称；（2）如图1，在ABC △中，AB=AC ，点D 在BC 上，且CD=CA ，点E 、F 分别为BC 、AD 的中点，连接EF 并延长交AB 于点G ．求证：四边形AGEC 是等邻角四边形； （3）如图2，若点D 在ABC △的内部，（2）中的其他条件不变，EF 与CD 交于点H ．图中是否存在等邻角四边形，若存在，指出是哪个四边形，不必证明；若不存在，请说明理由．图2图1H GF DE CBAGFE DCBA5．（1）已知：如图1，Rt △ABC 中，︒=∠90ACB ，︒=∠60BAC ，CD 平分ACB ∠，点E 为AB 中点，AB PE ⊥交CD 的延长线于P ，猜想：PBC PAC ∠+∠= °（直接写出结论，不需证明）.（2）已知：如图2，Rt △ABC 中，︒=∠90ACB ，︒≠∠45BAC ，CD 平分ACB ∠，点E 为AB 中点，AB PE ⊥交CD 的延长线于P ，（1）中结论是否成立，若成立，请证明；若不成立请说明理由．7．如图1，一张三角形纸片ABC ，∠ACB ＝90︒，AC ＝8，BC ＝6．沿斜边AB 的中线CD把这张纸片剪成1122AC D BC D ∆∆和两个三角形(如图2)．将11AC D ∆沿直线2D B （AB ）方向平移（点12,A D D B ，，始终在同一直线上），当点1D 与点B 重合时停止平移．在平移的过程中，112C D BC 与交于点E ，1AC 与222C D C B 、分别交于点F 、P ．（1）当11AC D ∆平移到如图3所示位置时，猜想12D E D F 与的数量关系，并证明你的猜想；（2）设平移距离21D D 为x ，1122AC D BC D ∆∆和重叠（阴影）部分面积为y ，试求yABCD EPPED CBA与x 的函数关系式，并写出自变量x 的取值范围． 10. 如图17、18是两个相似比为1：2的等腰直角△DMN 和△ABC ，将这两个三角形如图19放置，△DMN 的斜边MN 与△ABC 的一直角边AC 重合.⑴ 在图19中，绕点D 旋转△DMN ，使两直角边DM 、DN 分别与BC AC 、交于点F E ,，如图20. 求证：222EF BF AE =+；⑵ 在图19中，绕点C 旋转△DMN ，使它的斜边CM 、直角边CD 的延长线分别与AB 交于点F E 、，如图21，此时结论222EF BF AE =+是否仍然成立？若成立，请给出证明；若不成立，请说明理由.⑶ 如图22，在正方形ABCD 中，F E 、分别是边CD BC 、上的点且满足CEF ∆的周长等于正方形ABCD 的周长的一半，AF AE 、分别与对角线BD 交于点N M 、. 线段BM 、MN 、DN 恰能构成三角形. 请指出线段BM 、MN 、DN 所构成的三角形的形状，并给出证明.11．（1）如图1，BP 为ABC ∆的角平分线，PM AB ⊥于M ，PN BC ⊥于N ，30,23AB BC ==，请补全图形，并求ABP ∆与BPC ∆的面积的比值；（2）如图2，分别以ABC ∆的边AB 、AC 为边向外作等边三角形ABD 和等边三角形ACE ，CD 与BE 相交于点O ，判断AOD ∠与AOE ∠的数量关系，并证明； （3）在四边形ABCD 中，已知BC DC =，且AB AD ≠，对角线AC 平分BAD ∠，请直接写出B ∠和D ∠的数量关系.OABC图1图2PCM EBAD12．如图1，四边形ABCD ，将顶点为A 的角绕着顶点A 顺时针旋转，若角的一条边与DC 的延长线交于点F ，角的另一条边与CB 的延长线交于点E ，连接EF ．（1）若四边形ABCD 为正方形，当∠EAF=45°时，有EF=DF －BE ．请你思考如何证明这个结论（只思考，不必写出证明过程）；（2）如图2，如果在四边形ABCD 中，AB=AD ，∠ABC=∠ADC=90°，当∠EAF=21∠BAD 时，EF 与DF 、BE 之间有怎样的数量关系？请写出它们之间的关系式（只需写出结论）； （3）如图3，如果四边形ABCD 中，AB=AD ，∠ABC 与∠ADC 互补，当∠EAF=21∠BAD 时，EF 与DF 、BE 之间有怎样的数量关系？请写出它们之间的关系式并给予证明． （4）在（3）中，若BC=4，DC=7，CF=2，求△CEF 的周长（直接写出结果即可）．CD 13. （1）如图1，已知矩形ABCD中，点E是BC上的一动点，过点E作EF⊥BD于点F，EG⊥AC于点G，CH⊥BD于点H，试证明CH=EF+EG;图1D(2) 若点E在ＢＣ的延长线上，如图2，过点E作EF⊥BD于点F，EG⊥AC的延长线于点G，CH⊥BD于点H，则EF、EG、ＣH三者之间具有怎样的数量关系，直接写出你的猜想；(3) 如图3，BD是正方形ABCD的对角线,L在BD上，且BL=BC, 连结CL，点E是CL上任一点, EF⊥BD于点F，EG⊥BC于点G，猜想EF、EG、BD之间具有怎样的数量关系，直接写出你的猜想；(4) 观察图1、图2、图3的特性，请你根据这一特性构造一个图形，使它仍然具有EF、EG、ＣH这样的线段，并满足（1）或（2）的结论，写出相关题设的条件和结论.。

14.中考压轴题之图形变换（旋转、翻折、对称、平移）1、（9分）（2012•清远）如图，在矩形纸片ABCD 中，AB = 6，BC = 8。

把△BCD 沿对角线BD 折叠，使点C 落在C '处，C B ' 交AD 于点G ；E 、F 分别是D C '和BD 上的点，线段EF 交AD 于点H ，把△FDE 沿EF 折叠，使点D 落在D '处，点D '恰好与点A 重合。

（1）求证：△ABG ≌△C 'DG ； （2）求tan ∠ABG 的值； （3）求EF 的长。

AB CDE HFG C ' (D ') 题21图OABCDPE FMN 2、（14·珠海）（本题满分9分）如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD ＝AB ＝1，BC ＝2．将点A 折叠到CD 边上，记折叠后A 点对应的点为P （P 与D 点不重合），折痕EF 只与边AD 、BC 相交，交点分别为E 、F ．过点P 作PN ∥BC 交AB 于N 、交EF 于M ，连结PA 、PE 、AM ，EF 与PA 相交于O ． （1）指出四边形PEAM 的形状，并证明；（2）记∠EPM ＝a ，△AOM 、△AMN 的面积分别为S 1、S 2．① 求证：S 1tan a 2＝18 PA 2．② 设AN ＝x ，y ＝S 1－S 2tan a 2，试求出以x 为自变量的函数y 的解析式（不含a ），并确定y 的取值范围．3、（2012山东德州）已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）求证：EG =CG ；（2）将图①中△BEF 绕B 点逆时针旋转45º，如图②所示，取DF 中点G ，连接EG ，CG ．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）将图①中△BEF 绕B 点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）FBACEG图①FBADCEG图②FBACE图③D4、（2014铁岭市）如图所示，已知在直角梯形OABC 中，AB ∥OC ，BC ⊥x 轴于点C ，A （1，1）、B （3，1）．动点P 从O 点出发，沿x 轴正方向以每秒1个单位长度的速度移动．过P 点作PQ 垂直于直线OA ， 垂足为Q ．设P 点移动的时间为t 秒（0＜t ＜4），△OPQ 与直角梯形OABC 重叠部分的面积为S ． （1）求经过O 、A 、B 三点的抛物线解析式； （2）求S 与t 的函数关系式；（3）将△OPQ 绕着点P 顺时针旋转90°，是否存在t ，使得△OPQ 的顶点O 或Q 在抛物线上？若存在，求出t 的值；若不存在，请说明理由．如图，已知正△ABC 的边长为2，E ，F ，G 分别是AB ，BC ，CA 上的点，且AE=BF=CG ，设 △EFG 的面积为y ，AE 的长为x ，则y 关于x 的函数图象大致是（ ）2O A BCxy113PQ。

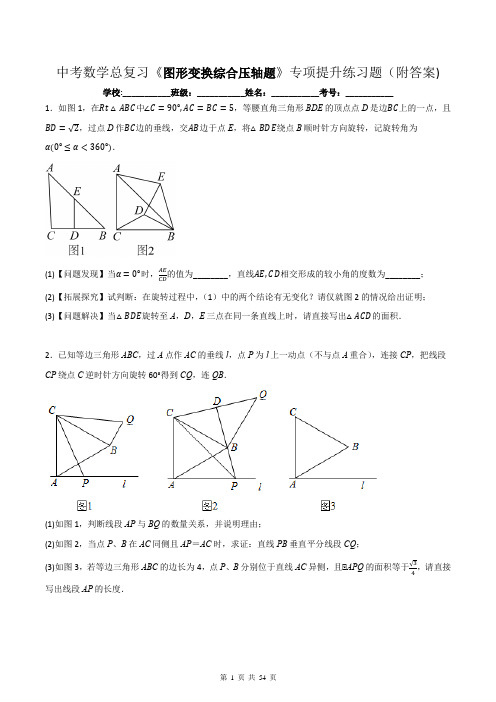
中考数学总复习《图形变换综合压轴题》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________1．如图1，在Rt△ABC中∠C=90°,AC=BC=5，等腰直角三角形BDE的顶点点D是边BC上的一点，且α(0°≤α<360°)．的值为________，直线AE,CD相交形成的较小角的度数为________；(1)【问题发现】当α=0°时，AECD(2)【拓展探究】试判断：在旋转过程中，（1）中的两个结论有无变化？请仅就图2的情况给出证明；(3)【问题解决】当△BDE旋转至A，D，E三点在同一条直线上时，请直接写出△ACD的面积．2．已知等边三角形ABC，过A点作AC的垂线l，点P为l上一动点（不与点A重合），连接CP，把线段CP绕点C逆时针方向旋转60°得到CQ，连QB．(1)如图1，判断线段AP与BQ的数量关系，并说明理由；(2)如图2，当点P、B在AC同侧且AP＝AC时，求证：直线PB垂直平分线段CQ；(3)如图3，若等边三角形ABC的边长为4，点P、B分别位于直线AC异侧，且△APQ的面积等于√3，请直接4写出线段AP的长度．3．在中Rt△ABC中∠ABC=90°，AB=BC点E在射线CB上运动．连接AE，将线段AE绕点E顺时针旋转90°得到EF，连接CF．(1)如图1，点E在点B的左侧运动；①当BE=2，BC=2√3时，则∠EAB=_________°；②猜想线段CA，CF与CE之间的数量关系为_________．(2)如图2，点E在线段CB上运动时，第（1）间中线段CA，CF与CE之间的数量关系是否仍然成立如果成立，请说明理由；如果不成立，请求出它们之间新的数量关系．(3)点E在射线CB上运动BC=√3，设BE=x，以A，E，C，F为顶点的四边形面积为y，请直接写出y与x之间的函数关系式（不用写出x的取值范围）．4．如图1，在矩形ABCD中AB=6，AD=8把AB绕点B顺时针旋转α(0<α<180°)得到，连接，过B点作BE⊥AA′于E点，交矩形ABCD边于F点．(1)求DA′的最小值；(2)若A点所经过的路径长为2π，求点A′到直线AD的距离；(3)如图2，若CF=4，求tan∠ECB的值；(4)当∠A′CB的度数取最大值时，直接写出CF的长．5．【问题探究】（1）如图1锐角△ABC中分别以AB AC为边向外作等腰直角△ABE和等腰直角△ACD 使AE＝AB AD＝AC∠BAE＝∠CAD＝90°连接BD CE试猜想BD与CE的大小关系不需要证明．【深入探究】（2）如图2四边形ABCD中AB＝5BC＝2∠ABC＝∠ACD＝∠ADC＝45°求BD2的值；甲同学受到第一问的启发构造了如图所示的一个和△ABD全等的三角形将BD进行转化再计算请你准确的叙述辅助线的作法再计算；【变式思考】（3）如图3四边形ABCD中AB＝BC∠ABC＝60°∠ADC＝30°AD＝6BD ＝10则CD＝．6．如图1所示在菱形ABCD和菱形AEFG中点A B E在同一条直线上P是线段CF的中点连接PD PG．(1)若∠BAD=∠AEF=120°请直接写出∠DPG的度数及PG的值______．PD(2)若∠BAD=∠AEF=120°将菱形ABCD绕点A顺时针旋转使菱形ABCD的对角线AC恰好与菱形AEFG的边AE在同一直线上如图2 此时（1）中的两个结论是否发生改变？写出你的猜想并加以说明．(3)若∠BAD=∠AEF=180°−2α(0°<α<90°)将菱形ABCD绕点A顺时针旋转到图3的位置求出PGPD 的值．7．如图1 在平面直角坐标系中抛物线y＝ax2+bx+4与x轴交于A（﹣2 0）B两点与y轴交于点C OB＝OC．连接BC点D是BC的中点．(1)求抛物线的表达式；(2)点M在x轴上连接MD将△BDM沿DM翻折得到△DMG当点G落在AC上时求点G的坐标；(3)如图2 E在第二象限的抛物线上连接DE交y轴于点N将线段DE绕点D逆时针旋转45°交ABOM直接写出点E的坐标．与点M若ON＝438．[证明体验]（1）如图1 在△ABC和△BDE中点A B D在同一直线上△A＝△CBE＝△D＝90° 求证：△ABC△△DEB．（2）如图2 图3 AD＝20 点B是线段AD上的点AC△AD AC＝4 连结BC M为BC中点将线段BM绕点B顺时针旋转90°至BE连结DE．ME时求AB的长．[思考探究]（1）如图2 当DE=√22[拓展延伸]（2）如图3 点G过CA延长线上一点且AG＝8 连结GE△G＝△D求ED的长．9．新定义：如图1（图2图3）在△ABC中把AB边绕点A顺时针旋转把AC边绕点A逆时针旋转得到△AB′C′若∠BAC＋∠BA′C′=180°我们称△AB′C′是△ABC的“旋补三角形” △AB′C′的中线AD叫做△ABC的“旋补中线” 点A叫做“旋补中心”(1)【特例感知】①若△ABC是等边三角形（如图2）BC=4则AD=________；②若∠BAC=90°（如图3）BC=6AD=_______；(2)【猜想论证】在图1中当△ABC是任意三角形时猜想AD与BC的数量关系并证明你的猜想；（提示：过点B′作B′E∥AC′且B′E＝AC′连接C′E则四边形AB′EC是平行四边形．）(3)【拓展应用】如图4点A B C D都在半径为5的圆P上且AB与CD不平行AD=6△APD是△BPC的“旋补三角形” 点P是“旋补中心” 求BC的长．10．如图① 抛物线y＝﹣x2+bx+c与x轴交于点A(x10) 点C(x20) 且x1x2满足x1+x2＝2x1•x2＝﹣3 与y轴交于点B E(m0)是x轴上一动点过点E作EP△x轴于点E交抛物线于点P．(1)求抛物线解析式．(2)如图② 直线EP交直线AB于点D连接PB．①点E在线段OA上运动若△PBD是等腰三角形时求点E的坐标；②点E在x轴的正半轴上运动若△PBD+△CBO＝45° 请求出m的值．(3)如图③ 点Q是直线EP上的一动点连接CQ将线段CQ绕点Q逆时针旋转90° 得到线段QF 当m＝1时请直接写出PF的最小值．11．如图△ABC与△DEF都是等腰直角三角形AC=BC DE=DF．边AB EF的中点重合于点O连接BF CD．(1)如图① 当FE△AB时易证BF=CD（不需证明）；(2)当△DEF绕点O旋转到如图②位置时猜想BF与CD之间的数量关系并证明；(3)当△ABC与△DEF均为等边三角形时其他条件不变如图③ 猜想BF与CD之间的数量关系直接写出你的猜想不需证明．12．已知Rt△ABC中AC＝BC△C＝90° D为AB边的中点△EDF＝90° △EDF绕D点旋转它的两边分别交AC CB（或它们的延长线）于E F．(1)如图1 当△EDF绕D点旋转到DE△AC于E时易证S△DEF＋S△CEF与S△ABC的数量关系为__________；(2)如图2 当△EDF绕D点旋转到DE和AC不垂直时上述结论是否成立？若成立请给予证明；(3)如图3 这种情况下请猜想S△DEF S△CEF S△ABC的数量关系不需证明．13．如图① 将一个直角三角形纸片ABC放置在平面直角坐标系中点A(−2,0)点B(6,0)点C在第一象限∠ACB=90°∠CAB=30°．(1)求点C的坐标；(2)以点B为中心顺时针旋转三角形ABC得到三角形BDE点A C的对应点分别为D E．①如图② 当DE∥AB时BD与y轴交于点F求点F的坐标；②如图③ 在（1）的条件下点F不变继续旋转三角形BDE当点D落在射线BC上时求证四边形FDEB为矩形；(3)点F不变记P为线段FD的中点Q为线段ED的中点求PQ的取值范围（直接写出结果即可）．14．如图在Rt△ABC中∠ACB=90∘∠A=30∘点O为AB中点点P为直线BC上的动点（不与点B C重合）连接OC OP将线段OP绕点P逆时针旋转60∘得到线段P Q连接BQ．(1)如图1 当点P在线段BC上时请直接写出线段BQ与CP的数量关系；(2)如图2 当点P在CB长线上时（1）中结论是否成立？若成立请加以证明；若不成立请说明理由；(3)如图3 当点P在BC延长线上时若∠BPO=45∘AC=√6请直接写出BQ的长．15．如图在RtΔABC中∠BAC=90°AB=AC点P是AB边上一动点作PD⊥BC于点D连接AD把AD绕点A逆时针旋转90°得到AE连接CE DE PE．(1)求证：四边形PDCE是矩形；(2)如图2所示当点P运动BA的延长线上时DE与AC交于点F其他条件不变已知BD=2CD的值；求APAF(3)点P在AB边上运动的过程中线段AD上存在一点Q使QA+QB+QC的值最小当QA+QB+QC的值取得最小值时若AQ的长为2 求PD的长．16．感知：如图① △ABC和△ADE都是等腰直角三角形∠BAC=∠DAE=90°点B在线段AD上点C在线段AE上我们很容易得到BD=CE不需要证明；(1)探究：如图② 将△ADE绕点A逆时针旋转α(0<α<90°)连结BD和CE此时BD=CE是否依然成立?若成立写出证明过程；若不成立说明理由；(2)应用：如图③ 当△ADE绕点A逆时针旋转使得点D落在BC的延长线上连接CE；①探究线段BC CD CE之间的数量关系．②若AB=AC=√2CD=1求线段DE的长．17．如图抛物线C：y=ax2+6ax+9a−8与x轴相交于A B两点（点A在点B的左侧）已知点B的横坐标是2 抛物线C的顶点为D．(1)求a的值及顶点D的坐标；(2)点P是x轴正半轴上一点将抛物线C绕点P旋转180°后得到的抛物线C1记抛物线C1的顶点为E抛物线C1与x轴的交点为F G（点F在点G的右侧）．当点P与点B重合时（如图1）求抛物线C1的表达式；(3)如图2 在（2）的条件下从A B D中任取一点E F G中任取两点若以取出的三点为顶点能构成直角三角形我们就称抛物线C1为抛物线C的“勾股伴随同类函数”．当抛物线C1是抛物线C的勾股伴随同类函数时求点P的坐标．18．如图点B坐标为（5 2）过点B作BA△y轴于点A作BC△x轴于点C点D在第一象限内．(1)如图1 反比例函数y1＝mx （x＞0）的图象经过点B点D且直线OD的表达式为y＝52x求线段OD的长；(2)将线段OD从（1）中位置绕点O逆时针旋转得到OD′（如图2）反比例函数y2＝nx（x＞0）的图象过点D' 交AB于点E交BC于点F连接OE OF EF．①若AE+CF＝EF求n的值；②若△OEF＝90°时设D′的坐标为（a b）求（a+b）2的值.19．已知正方形ABCD和等腰直角三角形BEF BE＝EF△BEF＝90° 按图1放置使点F在BC上取DF的中点G连接EG CG．(1)探索EG CG的数量关系和位置关系并证明；(2)将图（1）中△BEF绕点B顺时针旋转45° 再连接DF取DF中点G（见图2）（1）中的结论是否仍然成立？证明你的结论；(3)将图（1）中△BEF绕点B顺时针转动任意角度（旋转角在0°到90°之间）再连接DF取DF中点G（见图3）（1）中的结论是否仍然成立？证明你的结论．20．如图1 已知正方形BEFG点C在BE的延长线上点A在GB的延长线上且AB＝BC过点C作AB的平行线过点A作BC的平行线两条平行线相交于点D．(1)证明：四边形ABCD是正方形；(2)当正方形BEFG绕点B顺时针（或逆时针）旋转一定角度得到图2 使得点G在射线DB上连接BD和DF点Q是线段DF的中点连接CQ和QE猜想线段CQ和线段QE的关系并说明理由；(3)将正方形BEFG绕点B旋转一周时当△CGB等于45°时直线AE交CG于点H探究线段CH EG AH的长度关系．参考答案1．（1）解：Rt△ABC中∵∠C=90°,AC=BC=5∴AB=√AC2+BC2=√52+52=5√2∵ED⊥BC BD=ED=√2∴EB=√DB2+DE2=2,∠B=45°∴AE=AB－EB=5√2−2,CD=BC−DB=5−√2∴AECD =5√2−25−√2=√2故答案为：√2,45°；（2）解：（1）中的两个结论不发生变化理由如下：如图延长AE CD交于F由旋转可得∠CBD=∠ABE∵AB=5√2,BC=5,BE=2,DB=√2∴ABBC =5√25=√2EBDB=2√2=√2∴ABBC=EBDB∴ΔAEB∽ΔCDB∴AECD =ABCB=√2∠EAB=∠DCB∵∠BAC+∠ACB=90°+45°=135°∴∠BAC+∠ACD+∠DCB=∠BAC+∠ACD+∠EAB=135°即∠FAC+∠ACD=135°∴∠F=180°−(∠FAC+∠ACD)=45°∴（1）中的两个结论不发生变化．（3）解：分情况讨论：如图当点D在线段AE上时过点C作CF⊥AD于点F在RtΔABD中AB=5√2,BD=√2∴AD=√AB2−DB2=√(5√2)2−(√2)2=4√3由（2）知ΔEAB∽ΔDCB∠ADC=45°AE=AD+DE=4√3+√2∴CDAE=CBAB∴CD4√3+√2=55√2∴CD=2√6+1在Rt△CDF中CF=CD·sin∠ADC=(2√6+1)·sin45°=2√3+√22∴S△ADC=12AD·CF=12×4√3×(2√3+√22)=12+√6；当点E在线段AD上时如图过点C作CF⊥AD于点F在RtΔADB中AB=5√2,DB=√2∴AD=√AB2−DB2=√(5√2)2−(√2)2=4√3∴AE=AD−DE=4√3−2由（2）知△CDB∽△AEB∴CDAE=BCAB∴CD4√3−2=55√2∴CD=2√6−1由（2）知∠ADC=45°∴CF=CD·sin45°=(2√6−1)×√22=2√3−√22∴SΔACD=12AD·CF=12×4√3×(2√3−√22)=12−√6综上△ADC的面积为12+√6或12−√6．2．（1）解：AP＝BQ．理由如下：在等边△ABC中AC＝BC△ACB＝60°由旋转可得CP＝CQ△PCQ＝60°△△ACB＝△PCQ△△ACB﹣△PCB＝△PCQ﹣△PCB即△ACP＝△BCQ△△ACP△△BCQ（SAS）△AP＝BQ；（2）证明：在等边△ABC中AC＝BC△ACB＝60°由旋转可得CP＝CQ△PCQ＝60°△△ACB＝△PCQ△△ACB﹣△PCB＝△PCQ﹣△PCB即△ACP＝△BCQ△△ACP△△BCQ（SAS）△AP＝BQ△CBQ＝△CAP＝90°；△BQ＝AP＝AC＝BC.△AP＝AC△CAP＝90°△△BAP＝30° △ABP＝△APB＝75°△△CBP＝△ABC+△ABP＝135°△△CBD＝45°△△QBD＝45°△△CBD＝△QBD即BD平分△CBQ△BD△CQ且点D是CQ的中点即直线PB垂直平分线段CQ；（3）解：AP 的长为：√3或√33或2√3+√212． 理由如下：①当点Q 在直线l 上方时 如图所示 延长BQ 交l 于点E 过点Q 作QF ⊥l 于点F由题意可得AC ＝BC PC ＝CQ △PCQ ＝△ACB ＝60°△△ACP ＝△BCQ△△APC △△BCQ （SAS ）△AP ＝BQ △CBQ ＝△CAP ＝90°△△CAB ＝△ABC ＝60°△△BAE ＝△ABE ＝30°△AB ＝AC ＝4△AE ＝BE =4√33△△BEF ＝60°设AP ＝t 则BQ ＝t△EQ =4√23−t在Rt △EFQ 中 QF =√32EQ =√32（4√23−t ） △S △APQ =12AP •QF =√34 即12•t √32（4√23−t ）=√34 解得t =√3或t =√33．即AP 的长为√3或√33．②当点Q 在直线l 下方时 如图所示 设BQ 交l 于点E 过点Q 作QF ⊥l 于点F由题意可得AC ＝BC PC ＝CQ △PCQ ＝△ACB ＝60°△△ACP ＝△BCQ△△APC △△BCQ （SAS ）△AP ＝BQ △CBQ ＝△CAP ＝90°△△CAB ＝△ABC ＝60°△△BAE ＝△ABE ＝30°△△BEF ＝120° △QEF ＝60°△AB ＝AC ＝4△AE ＝BE =4√33设AP ＝m 则BQ ＝m△EQ ＝m −4√33在Rt △EFQ 中 QF =√32EQ =√32（m −4√33） △S △APQ =12AP •QF =√34 即12•m •√32（m −4√33）=√34 解得m =2√3+√213（m =2√3-√213 负值舍去）．综上可得 AP 的长为：√3或√33或2√3+√213． 3．（1）解：①△AB =BC =2√3 BE =2 △ABC =90°△tan∠EAB =BE AB =22√3=√33△△EAB =30°故答案为：30；②过点F 作FD △BC 于D 如图3△△BAE + △AEB = 90° △DEF +△AEB =90°△△BAE = △DEF△AE = EF △ABE =△EDF = 90°△△АВЕ △△ЕDF△AB = ED = BC△FD = DC△CF =√2CD AC =√2AB =√2ED△AC + CF=√2CD +√2ED=√2 (CD + ED )=√2CE ；故答案为：AC +CF =√2CE ；（2）过F 作FH △BC 交BC 的延长线于H 如图4△△AEF =90° AE =EF易证△ABE △△EHF△FH =BE EH =AB =BC△△FHC 是等腰直角三角形△CH =BE =√22FC△EC =BC -BE =√22AC -√22FC 即CA -CF =√2CE ；（3）如图3 当点E在点B左侧运动时y=12×CE×(AB+FD)=12×(√3+x)×(√3+x)=1 2x2+√3x+32；如图4 当点E在点B右侧运动时连接AF 根据勾股定理得AE=√AB2+BE2=√3+x2由旋转得AE=EF△EC=EH-CH=BC-BE=√3−x△y=12×AE×EF+12×EC×FH=1 2x2+32+12(√3−x)x=√3 2x+32综上当点E在点B左侧运动时y=12x2+√3x+32；当点E在点B右侧运动时y=√32x+32．4．（1）解：连接BD DA′ 如图△四边形ABCD是矩形△△BAD=90°△AB=6 AD=8△BD=10由旋转可得BA′=BA=6△BA′+DA′≥BD△当点A′落在BD上时DA′最小最小值为10-6=4△DA′最小值为4；（2）解：由题意得απ×6180=2π解得：α=60°△AB=A′B△△ABA′是等边三角形△△BAA′=60° AB=A′B=AA′=6△△DAA′=30°过点A′作A′M△AD于M点△A′M=12AA′=3△点A′到直线AD的距离为3（3）解：△BC=8 CF=4△BF=4√5△△BAE+△ABE=90° △CBF+△ABE=90°△△BAE=△CBF△△AEB=△BCF=90°△△ABE△△BFC△BE CF =ABBF△BE=6√55过E作EH△BC于H点△EH∥CD△△BEH△△BFC△BE BF =EHCF=BHBC△EH=65BH=125△CH=285△tan∠ECB=EHCH =314；（4）解：当A′C与以B为圆心AB为半径的圆相切时△A′CB最大此时△BA′C=90°分两种情况：当A′在BC的上方时如图1△AB=A′B AE△AA′于E△△ABF=△A′BF△BF=BF△△ABF△△A′BF△△BA′F=△BAF=90°△C A′ F在一条直线上△S△BCF=12BC×AB=12A′B×CF△CF =BC =8如图2当A ′在BC 的下方时连接AF A ′F 则AF =A ′F△A ′B =6 BC =8△A′C =2√7过A ′作A ′P △CD 垂足落在DC 的延长线上△△BCA ′+△A ′CP =90° △A ′CP +△CA ′P =90°△△BCA ′=△CA ′P△△BA ′C =△A ′PC△△A ′BC △△PCA ′△A ′B PC =BC CA ′=A ′CPA ′△A′P =72 PC =32√7△AD 2+DF 2=A ′P 2+PF 2△82+(6−CF )2=(72)2+(32√7+CF)2△CF =83(4−√7)．综上 CF 的长为8或83（4−√7)．5．解：（1）BD ＝CE ．理由是：△△BAE ＝△CAD△△BAE +△BAC ＝△CAD +△BAC 即△EAC ＝△BAD在△EAC 和△BAD 中{AE =AB∠EAC =∠BAD AC =AD△△EAC △△BAD△BD ＝CE ；（2）如图2 在△ABC 的外部 以A 为直角顶点作等腰直角△BAE使△BAE ＝90° AE ＝AB 连接EAEB EC ．△△ACD＝△ADC＝45°△AC＝AD△CAD＝90°△△BAE+△BAC＝△CAD+△BAC即△EAC＝△BAD 在△EAC和△BAD中{AE=AB ∠EAC=∠BAD AC=AD△△EAC△△BAD△BD＝CE．△AE＝AB＝5△BE＝√52+52=5√2△ABE＝△AEB＝45°又△△ABC＝45°△△ABC+△ABE＝45°+45°＝90°△EC2=BE2+BC2=(5√2)2+22=54△BD2=CE2=54．（3）如图△AB＝BC△ABC＝60°△△ABC是等边三角形把△ACD绕点C逆时针旋转60°得到△BCE连接DE 则BE＝AD△CDE是等边三角形△DE＝CD△CED＝60°△△ADC＝30°△△BED＝30°+60°＝90°在Rt△BDE中DE＝√BD2−BE2＝√102−62＝8△CD＝DE＝8．6．解：（1）延长GP交CD于H如图1所示：∵在菱形ABCD和菱形AEFG中AB=CD=AD BE//CD AG=FG FG//BE∴FG//CD∴∠PFG=∠PCH ∵P是线段CF的中点∴PF=PC在△PFG和△PCH中{∠PFG=∠PCHPF=PC∠FPG=∠CPH ∴△PFG≅△PCH(ASA)∴FG=CH PG=PH∴AG=CH∴DG=DH∴DP⊥GH（三线合一）∴∠DPG=90°；∵∠BAD=120°∴∠ADC=60°∴∠PDG=∠PDH=12∠ADC=30°∴PGPD =tan∠PDG=tan30°=√33；（2）（1）中的两个结论不发生改变；理由如下：延长GP交CE于H连接DH DG如图2所示：∵四边形AEFG为菱形∴FG//EC∴∠GFP=∠HCP ∵P是线段CF的中点∴PF=PC在△PFG和△PCH中{∠GFP=∠HCPPF=PC∠FPG=∠CPH ∴△PFG≅△PCH(ASA)∴FG=CH PG=PH∵FG=AG∴AG=CH∵四边形ABCD是菱形∴AC=CD∵∠BAD=∠AEF=120°∴∠ACD=60°∴△ACD是等边三角形∴AD=CD∴∠EAG=∠ADC=60°∠DAC=∠DCA=60°∴∠GAD=180°−∠EAG−∠DAC=60°在△ADG和△CDH中{AD=CD∠GAD=∠DCHAG=CH ∴△ADG≅△CDH(SAS)∴DG=DH∠ADG=∠CDH∴DP⊥GH∴∠DPG=90°∠GDH=∠ADC=60°∴∠GDP=30°∴PGPD =tan30°=√33；（3）延长GP到H使得PH=GP连接CH DG DH延长DC交EA的延长线于点M如图3所示：同（2）可证△PFG≅△PCH∴∠GFC=∠HCF FG=CH∴FG//CH∵FG//AE∴CH//EM∴∠DCH=∠M∵CD//AB∴∠M=∠MAB∴∠DCH=∠MAB∵∠BAD=∠AEF=180°−2α∴∠EAG=∠ADC=2α∴∠GAM=180°−2α∴∠GAD=∠BAM∴∠GAD=∠DCH∵AG=FG∴AG=CH在△ADG和△CDH中{AD=CD∠GAD=∠DCHAG=CH ∴△ADG≅△CDH(SAS)∴∠ADG=∠CDH DG=DH∴∠GDH=∠ADC=2α∴∠DPG =90° ∠GDP =12∠GDH =α∴ PGPD =tanα．7．（1）解：△抛物线y =ax 2+bx +4与y 轴交于点C△点C 的坐标为（0 4）△OC =4△OB=OC =4△B （4 0）将A （-2 0）和B （4 0）的坐标分别代入y =ax 2+bx +4中得：{4a −2b +4=016a +4b +4=0解得：{a =−12b =1△y =−12x 2+x +4（2）解：△A （－2 0） C （0 4）设直线AC 的解析式为y =kx +4将点A （－2 0）代入y =kx +4中 得：−2k +4=0 解得：k =2△直线AC 的解析式为y =2x +4设G （x 2x ＋4）△点D 是BC 的中点△D（2 2）△翻折△△MDB△△MDG△DB=DG△(x−2)2+(2x+4−2)2=(2−4)2+(2−0)2△5x2+4x=0△x1=0，x2=−45△y1=4，y2=125△G（0 4）G（−45125）（3）解：E(2−2√13314−2√139)如图过点D作DP△OC于点P DQ△OB于点Q点D作DH△DN交OB于点H∵∠PDQ=∠NDM=90°∴∠PDQ−∠NDQ=∠NDM−∠NDQ∴∠PDN=∠QDH在ΔDPN和ΔDQH中{DP=DQ∠DON=∠DQH=90°∠PDN=∠QDH∴ΔDPN≅ΔDQH(ASA)∴DN=DH∠NDM=90°−∠PDN−∠QDM=90°−∠QDH−∠QDM=∠HDM 在ΔDMN和ΔDMH中{DN=DH∠NDM=∠HDMDM=DM∴△DMN≌△DMH(SAS)∴MN=MQ+PN△ON =43OM 设OM =x 则ON =43x QM =2－x PN =2－43x △MN =MQ ＋PN =4－73x在Rt △OMN 中 △MON=90°MN 2=ON 2+OM 2即(4−73x)2=(43x)2+(2−x )2△2x 2−x +9=0△x =1 x =92(舍) △N (0 43) △D （2 2）设直线DN 的解析式为y =k 1x +b 1将点N (0 43)和点D （2 2）代入y =k 1x +b 1中 得：{b 1=432k 1+b 1=2 解得：{b 1=43k 1=13△直线DN 的解析式为y =13x +43△y =−12x 2+x +4 △−12x 2+x +4=13x +43△x =2−2√133 x =2+2√133（舍） △y =14−2√139 △E (2−2√133 14−2√139). 8．解：（1）证明 △△A ＝90° △CBE ＝90°△△C ＋△CBA ＝90° △CBA ＋△DBE ＝90°△△C ＝△DBE （同角的余角相等）．又△△A ＝△D ＝90°△△ABC △△DEB ；（2）①△M绕点B顺时针旋转90°至点E M为BC中点△△BME为等腰直角三角形BEBC =BMBC=12△BE=√22ME又△DE=√22ME△BE＝DE．如图过点E作EF△AD垂足为F则BF＝DF △△A＝△CBE＝△BFE＝90°△由（1）得：△ABC△△FEB△BF AC =BEBC=12△AC＝4△BF＝2△AB＝AD－BF－FD＝20－2－2＝16；②如图过点M作AD的垂线交AD于点H过点E作AD的垂线交AD于点F过D作DP△AD过E作NP△DP交AC的延长线于N△M为BC中点MH△AC∴MHAC =BMBC=BHAB=12△MH=12AC=2BH＝AH△△MHB＝△MBE＝△BFE＝90°由（1）得：∠HBM=∠FEB△MB＝EB△△MHB△△BFE△BF＝MH＝2 EF＝BH设EF＝x则DP＝x BH＝AH＝x EP＝FD＝20－2－2x＝18－2x GN＝x＋8 NE＝AF＝2x＋2由(1)得△NGE△△PED△PE NG =PDNE即18−2xx+8=x2x+2解得x1=6x2=−65（舍去）△FD＝18－2x＝6△ED=√EF2+FD2=√62+62=6√2．9．（1）解：①△△ABC是等边三角形BC=4△AB=AC=4∠BAC=60°△AB′=AC′=4∠B′AC′=120°△AD为等腰△AB′C′'的中线△AD⊥B′C′∠C′=30°△∠ADC′=90°在Rt△ADC′'中∠ADC′=90°AC′=4∠C′=30°△AD=12AC′=2；②△∠BAC=90°△∠B′AC′=90°在△ABC和△AB′C′'中{AB=AB′∠BAC=∠B′AC′AC=AC′△△ABC≌△AB′C′（SAS）△B′C′=BC=6△AD=12B′C′=3；故答案为：①2；②3（2）AD＝12BC理由如下：证明：在图1中过点B′作B′E∥AC′且B′E＝AC′连接C′E DE则四边形AB′EC是平行四边形．△∠BAC＋∠B′AC′=180°∠B′AC′+∠AB′E=180°△∠BAC=∠AB′E又△AC＝AC′△CA=EB′在△BAC和△AB′E中{BA=AB′∠BAC=∠AB′E CA=EB′△△BAC≌△AB′E（SAS）△BC=AE又△AD＝12AE△AD＝12BC；（3）如图过点P作PF⊥BC则BF＝CF△PB=PC PF⊥BC△PF为△BC的中线△PF＝12AD=3．在Rt△BPF中∠BFP=90°PB=5PF=3△BF＝√PB2−PF2＝4△BC=2BF=8．10．（1）解：△x 1 x 2满足x 1+x 2＝2 x 1•x 2＝﹣3△b =2 c =3△抛物线的解析式为y ＝﹣x 2+2x +3（2）解：①抛物线y ＝﹣x 2+2x +3与x 轴交于点A (x 1 0) 点C (x 20) 与y 轴交于点B △当y =0时 ﹣x 2+2x +3=0解得x 1=3 x 2=-1当x =0时y ＝3△A (3 0) C (-1 0) B (0 3)△△AOB 为等腰直角三角形△△BAO =45°又EP △x 轴△△ADE 为等腰直角三角形△△ADE =45°又△△PDB =△ADE△△PDB =45°设直线AB 的解析式为y =kx +b则{3k +b =0b =3 解得{k =−1b =3△直线AB 的解析式为y =-x +3△E (m 0) 直线EP 交直线AB 于点D△设点D 为（m -m +3） 点P 为（m ﹣m 2+2m +3）点E 在线段OA 上运动 若△PBD 是等腰三角形 则0＜m ＜3当PD =PB 时△PBD 是以P 为直角顶点的等腰直角三角形△﹣m 2+2m +3-（-m +3）=m解得m=2或m=0（舍去）△点E为（2 0）当BD=BP时△PBD是以B为直角顶点的等腰直角三角形△2 m =﹣m2+2m+3-（-m+3）解得m=1或m=0（舍去）△点E为（1 0）当DB=DP时△PBD是以D为顶点的等腰三角形△△OBD=45°△BD=√2OE=√2m△√2m=﹣m2+2m+3-（-m+3）解得m=3-√2或m=0（舍去）△点E为（3-√20）综上可知点E为（2 0）或（1 0）或（3-√20）②当P在x轴上方时连接BC延长BP交x轴于点F△△BAO=△ABO=45°又△PBD+△CBO＝45°△△CBP=90°△△OBF+△CBO＝90°又△BCO+△CBO＝90°△△OBF=△BCO△△BOC△△FOB△BO FO =OC OB△C(-1 0) B(0 3)△3 FO =1 3△OF=9△点F为（9 0）设直线PB 的解析式为y =mx +n则{9m +n =0n =3解得{m =−13n =3△直线PB 的解析式为y =-13x +3△P B 都在抛物线上△{y =−13x +3y =−x 2+2x +3解得{x =0y =3 （舍去）{x =73y =209△点P 为（73 209）△m =73当P 在x 轴下方时连接BC 设BP 与x 轴交于点H△△PBD +△CBO =45° △OBH +△PBD =45°△△CBO =△OBH又OB =OB △COB =△BOH∴△BOH △△BOC （ASA ）△OC =OH =1△点H （1 0）设直线BH 解析式为：y =kx +b△{k +b =0b =3 解得{k =−3b =3△直线BH 解析式为：y =-3x +3△联立方程组{y =−3x +3y =−x 2+2x +3解得{x =0y =3 （舍去）{x =5y =−12△点P 为（5 -12）△m =5综上可知 m 的值为73或5． （3）解：当m ＝1 得点E （1 0） P （1 4）过点F 作FH △PE又PE △x 轴 △CQF =90°△△CQH +△FQH =90° △CQH +△QCH =90°°△QEC =△QHF =90°△△FQH =△QCH△线段CQ 绕点Q 逆时针旋转90° 得到线段QF△CQ=QF△△QCE △△FQH （AAS ）△CE=QH QE=FH又E （1 0） C （-1 0）△CE=QH =2令Q 为（1 a ）QE=FH=a△点F 的坐标为（1+a a -2）△PF=√(1+a −1)2+(a −2−4)2=√2a 2−12a +36△2＞0△当a =-−122×2=3时 PF 有最小值 且最小值为3√2．11．解：（1）证明：如图① 连接OC∵ΔABC与ΔDEF都是等腰直角三角形AC=BC DE=DF．边AB EF的中点重合于点O∴OC⊥AB OC=12AB=OB OD⊥EF OD=12EF=OF∵FE⊥AB于O∴C F O三点共线在ΔBOF与ΔCOD中{∠OB=OC∠BOF=∠COD=90°OF=OD∴ΔBOF≅ΔCOD(SAS)∴BF=CD；（2）解：猜想BF=CD理由如下：如图② 连接OC OD∵ΔABC与ΔDEF都是等腰直角三角形AC=BC DE=DF．边AB EF的中点重合于点O∴OC⊥AB OC=12AB=OB OD⊥EF OD=12EF=OF∵∠BOF=∠BOC+∠COF=90°+∠COF∠COD=∠DOF+∠COF=90°+∠COF ∴∠BOF=∠COD．在ΔBOF与ΔCOD中{OB=OC∠BOF=∠COD OF=OD∴ΔBOF≅ΔCOD(SAS)∴BF=CD；（3）解：猜想BF=√33CD理由如下：如图③ 连接OC OD．∵ΔABC为等边三角形点O为边AB的中点∴∠BCO=∠ACO=30°∠BOC=90°∴tan∠BCO=OBOC=tan30°=√33∵ΔDEF为等边三角形点O为边EF的中点∴∠FDO=∠EDO=30°∠DOF=90°∴tan∠FDO=OFOD=tan30°=√33∴OBOC =OFOD=√33∵∠BOF=∠BOC+∠COF=90°+∠COF∠COD=∠DOF+∠COF=90°+∠COF∴∠BOF=∠COD∴ΔBOF∽ΔCOD∴BFCD =OBOC=√33∴BF=√33CD．12．解：（1）当△EDF 绕D 点旋转到DE △AC 时 四边形CEDF 是正方形．设△ABC 的边长AC =BC =a 则正方形CEDF 的边长为12a ．△S △ABC =12a 2 S 正方形DECF =（12a ）2=12a 2 即S △DEF +S △CEF =12S △ABC ；故答案为：S △DEF +S △CEF =12S △ABC ； （2）（1）中的结论成立；证明：过点D 作DM △AC DN △BC 则△DME =△DNF =△MDN =90°又△△C =90°△DM △BC DN △AC△D 为AB 边的中点由中位线定理可知：DN =12AC MD =12BC △AC =BC△MD =ND△△EDF =90°△△MDE +△EDN =90° △NDF +△EDN =90°△△MDE=△NDF在△DME 与△DNF 中{∠DME ＝∠DNFMD ＝ND ∠MDE ＝∠NDF△△DME △△DNF （ASA ）△S △DME =S △DNF△S 四边形DMCN =S 四边形DECF =S △DEF +S △CEF由以上可知S 四边形DMCN =12S △ABC △S △DEF +S △CEF =12S △ABC ．（3）连接DC证明：同（2）得：△DEC △△DBF △DCE =△DBF =135°△S △DEF =S 五边形DBFEC=S △CFE +S △DBC=S △CFE +S ΔABC2△S △DEF -S △CFE =S ΔABC2．故S △DEF S △CEF S △ABC 的关系是：S △DEF -S △CEF =12S △ABC ．13．（1）解：如图 过点C 作C G ⊥x 轴∵点A(−2,0)点B(6,0)△AB=8 又∵∠ACB=90°∠CAB=30°△在Rt△ABC中BC=4 在Rt△GBC中BG=2 CG=2√3．又∵点C在第一象限△C(4,2√3)；（2）①∵以点B为中心顺时针旋转三角形ABC得到三角形BDE点A C的对应点分别为D E 且DE//AB△∠FBA=∠EDB=∠CAB=30°．△在Rt△FOB中∵OB=6△OF=2√3．△F(0,2√3)；②△点D落在射线BC上△∠ABD=60°．由①知∠FBA=30°△∠FBD=30°．△∠FBD=∠BDE△DE//FB．又DE=FB=4√3△四边形FDEB是平行四边形.又∠BED=90°△四边形FDEB是矩形.（3）如图连接PQ,FE∵P,Q分别为FD,DE的中点∴PQ=1EF2∵FB=4√3BE=4∵旋转则点E在以B为圆心BE为半径的圆上运动∴FB−BE≤EF≤FB+BE 即4√3−4≤EF≤4√3+4∴2√3−2≤PQ≤2√3+2 14．（1）解：CP=BQ理由：如图1 连接OQ由旋转知PQ=OP△OPQ=60°△△POQ是等边三角形△OP=OQ△POQ=60°在Rt△ABC中O是AB中点△OC=OA=OB△△BOC=2△A=60°=△POQ△△COP=△BOQ在△COP和△BOQ中{OC=OB∠COP=∠BOQOP=OQ△△COP△△BOQ（SAS）；（2）解：CP=BQ理由：如图2 连接OQ由旋转知PQ=OP△OPQ=60°△△POQ是等边三角形△OP=OQ△POQ=60°在Rt△ABC中O是AB中点△OC=OA=OB△△BOC=2△A=60°=△POQ△△COP=△BOQ在△COP和△BOQ中{OC=OB∠COP=∠BOQOP=OQ△△COP△△BOQ（SAS）△CP=BQ；（3）解：BQ＝√6−√22．在Rt△ABC中△A＝30° AC＝√6△BC＝AC·tan A＝√2如图③ 过点O作OH△BC于点H△△OHB＝90°＝△BCA△OH △AC△O 是AB 中点△CH ＝12BC =√22 OH ＝12AC ＝√62△△BPO ＝45° △OHP ＝90°△△BPO ＝△POH△PH ＝OH ＝√62△CP ＝PH －CH ＝√62－√22＝√6−√22连接OQ 同（1）的方法得 BQ ＝CP ＝√6−√22． 15．（1）证明：△AB ＝AC △BAC ＝90°△△B ＝△ACB ＝45°△△DAE ＝△BAC ＝90° AD ＝AE△△BAD ＝△CAE在△BAD 和△CAE 中 {AB =AC∠BAD =∠CAE AD =AE△△BAD △△CAE （SAS ）△△B ＝△ACE ＝45° BD ＝CE△△ECD ＝△ACE +△ACB ＝90°△PD △BC△△BDP ＝△ECD ＝90°△PD △CE△△B ＝△BPD ＝45°△PD ＝BD△PD ＝EC△四边形PDCE 是平行四边形△△PDC ＝90°△四边形PDCE 是矩形；（2）解△如图 过点A 作AM △BC 于点M 过点F 作FN △BC 于点N设CD ＝2m 则BD ＝2CD ＝4m BC ＝6m△AB ＝AC △BAC ＝90° AM △BC△BM ＝MC ＝3m△AM ＝BM ＝3m AB ＝AC ＝3√2m DM =CM -CD =m△BD ＝PD ＝4m△PB ＝4√2m△P A ＝√2m△△ABD △△ACE△BD ＝EC ＝4m设CN ＝FN ＝x△FN △CE△△DFN △△DEC△FN EC ＝DN DC△FNDN ＝EC DC=4m2m =2 △DN ＝12x△12x +x ＝2m△x ＝43m △CF ＝4√23 m△AF ＝AC -CF ＝3√2m －4√23m ＝5√23m △AP AF =√2m 5√23m=35；（3）即：如图 将△BQC 绕点B 顺时针旋转60°得到△BNM 连接QN△BQ＝BN QC＝NM△QBN＝60°△△BQN是等边三角形△BQ＝QN△QA+QB+QC＝AQ+QN+MN△当点A点Q点N点M共线时QA+QB+QC值最小如图连接MC△将△BQC绕点B顺时针旋转60°得到△BNM△BQ＝BN BC＝BM△QBN＝60°＝△CBM△△BQN是等边三角形△CBM是等边三角形△△BQN＝△BNQ＝60° BM＝CM又△AB＝AC△AM垂直平分BC△AD△BC△BQD＝60°△△DBQ=30°BQ△QD=12△BD＝√3QD△AB＝AC△BAC＝90° AD△BC△AD＝BD此时P与A重合设PD＝x则DQ＝x－2△x＝√3（x－2）△x＝3+√3△PD＝3+√3．16．（1）解：成立理由是：△△ABC和△ADE都是等腰直角三角形△AB=AC AD=AE△将△ADE绕点A逆时针旋转α(0<α<90°)连结BD和CE△∠BAD=∠CAE△△ABD≌△ACE(SAS)△BD=CE；（2）解：①△AB=AC∠BAD=∠CAE AD=AE△△ACE≌△ABD(SAS)△BD=CE△BC+CD=BD=CE．②△△ACE≌△ABD△∠ACE=∠ABD=45°又△∠ACB=45°△∠BCE=∠ACB+∠ACE=90°在Rt△BAC中△AB=AC=√2△BC=√AB2+AC2=2又△CD=1CE=BC+CD=3△在Rt△CDE中17．（1）解：△抛物线C：y=ax2+6ax+9a−8与x轴相交于A B两点点B的横坐标是2△B (2,0)△a ×22+6a ×2+9a −8=0解得a =825△抛物线C 的解析式为：y =825x 2+4825x −12825 对称轴：x =−48252×825=−3△当x =−3时 y =825×(−3)2+4825×(−3)−12825=−8 △顶点D 的坐标为(−3,−8)．△a =825 D (−3,−8)．（2）△抛物线C 与x 轴相交于A B 两点△当y =0时 得：825x 2+4825x −12825=0 即(x +8)(x −2)=0解得：x 1=−8 x 2=2△A (−8,0)△点P 与点B 重合△点P 的坐标为(2,0)当抛物线C 绕点P 旋转180°后得到的抛物线C 1 且点P 与点B 重合时△在抛物线C 1中 点B 的坐标仍为(2,0)△点F 与点A 关于点P 对称△点F 的坐标为(12,0)同理点E 与点D 关于点P 对称 设E (m,n ) 则△点P 的坐标为(m−32,n−82) △{m−32=2n−82=0△{m =7n =8△点E 的坐标为(7,8)设抛物线C 1的表达式为：y =a 1(x −12)(x −2)△(7−12)×(7−2)a 1=8△a 1=−825 △y =−825(x −12)(x −2)=−825x 2+11225x −19225 △抛物线C 1的表达式为：y =−825x 2+11225x −19225．（3）根据题意可知 在构成的直角三角形三个顶点中 有两个顶点是从点E F G 中选取 有一个点是从A B D 中任取．由图可知 当点为E G 或F G 时 与A B D 中任意一点构成的三角形是钝角三角形 故只有点E F 为直角三角形其中的两个顶点．设P (m,0)又△抛物线C 绕点P 旋转180°后得到的抛物线C 1 A (−8,0) B (2,0) D (−3,−8)△E (2m +3,8) F (2m +8,0)①当A 为顶点时△在抛物线C 1中 ∠EFO 是一个锐角 点A 在点P 的左侧△∠AEF =90°△AE 2+EF 2=AF 2△(√(2m +11)2+82)2+(√52+(−8)2)2=(2m +16)2解得：m =910；②当B 为顶点时同理可得∠BEF =90°△BE 2+EF 2=BF 2△[√(2m +1)2+82)2+(√52+(−8)2)2=(2m +6)2 解得：m =5910；③当D 为顶点时分两种情况：第一种：∠DEF =90°△DE 2+EF 2=DF 2△(√(2m +6)2+(8+8)2)2+(√52+(−8)2)2=(√(2m +11)2+82)2解得：m =495第二种：∠DFE =90°△DF 2+EF 2=DE 2△(√(2m +11)2+82)2+(√52+(−8)2)2=(√(2m +6)2+(8+8)2)2 解得：m =910．△点P 的坐标为(910,0)或(5910,0)或(495,0)． 18．（1）解：∵D 在直线y =52x 上 ∴设D(t,52t)∵y 1=m x 经过点B (5,2)． ∴m =10．∵D(t,52t)在反比例函数的图象上∴52t 2=10 ∴t =2（负值已舍去）．∴由两点间的距离公式可知：OD =√22+52=√29．（2）解：①∵函数y 2=n x 的图象经过点E ∴OA ⋅AE =OC ⋅CF =n ．∵OC =5 OA =2∴AE =52CF ．∴可设：AE =52t∴EF =AE +CF =72t EB =5−52t在Rt △EBF 由勾股定理得：EF 2=BF 2+BE 2 ∴494t 2=(5−52t)2+(2−t)2． 解得t =7√29−2910∴n =5t =7√29−292． ②∵∠OEF =90°∴∠AEO +∠BEF =90°∵BA ⊥y 轴 BC ⊥x 轴∴∠ABC=90°∴∠BEF+∠BFE=90°∴∠AEE=∠BFE∴△AOE∽△BEF∴OA:AE=BE:BF∵CF=n5,AE=n2,BE=5−n2,BF=2−n5∴2:n2=(5−n2):(2−n5)解得：n=85或n=10（舍）∵D′(a,b)∴ab=8 5由（1）得OD=√29∴OD′=√29∴a2+b2=29∴(a+b)2=29+2×85=1615故(a+b)2的值为1615．19．解：（1）EG＝CG且EG△CG．证明如下：如图① 连接BD．△正方形ABCD和等腰Rt△BEF△△EBF＝△DBC＝45°．△B E D三点共线．△△DEF＝90° G为DF的中点△DCB＝90°△EG＝DG＝GF＝CG．△△EGF＝2△EDG△CGF＝2△CDG．△△EGF＋△CGF＝2△EDC＝90°即△EGC＝90°△EG△CG．（2）仍然成立证明如下：如图② 延长EG交CD于点H．。

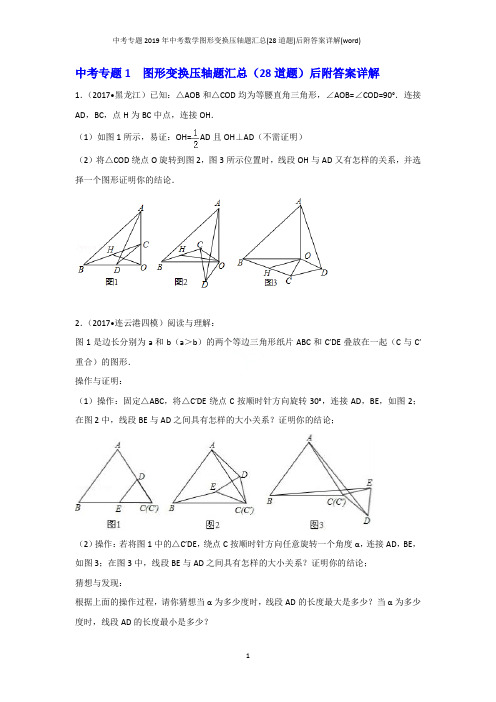
中考专题1 图形变换压轴题汇总（28道题）后附答案详解1．（2017•黑龙江）已知：△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°．连接AD，BC，点H为BC中点，连接OH．（1）如图1所示，易证：OH=AD且OH⊥AD（不需证明）（2）将△COD绕点O旋转到图2，图3所示位置时，线段OH与AD又有怎样的关系，并选择一个图形证明你的结论．2．（2017•连云港四模）阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．操作与证明：（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；猜想与发现：根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？3．（2017•金乡县模拟）请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PC是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为，问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．4．（2017•滦县模拟）两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为和位置关系为；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．5．（2017•路北区三模）如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．（1）求证：△AEC≌△ADB；（2）若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．6．（2017•平房区二模）如图，正方形ABCD，点E在AD上，将△CDE绕点C顺时针旋转90°至△CFG，点F，G分别为点D，E旋转后的对应点，连接EG，DB，DF，DB与CE交于点M，DF与CG交于点N．（1）求证BM=DN；（2）直接写出图中已经存在的所有等腰直角三角形．7．（2017•路南区一模）如图①，△ABC中，AC=BC，∠A=30°，点D在AB边上且∠ADC=45°．（1）求∠BCD的度数；（2）将图①中的△BCD绕点B顺时针旋转得到△BC′D′．当点D′恰好落在BC边上时，如图②所示，连接C′C并延长交AB于点E．①求∠C′CB的度数；②求证：△C′BD'≌△CAE．8．（2017•沙坪坝区一模）已知△ABC和△DEB都是等腰直角三角形，∠BAC=∠EDB=90°．（1）如图1，若点E，B，C在同一直线上，连接AE，当∠AEC=30°，BC=4时，求EB的长；（2）如图2，将图1中的△DEB绕点B顺时针旋转，当点C在ED的延长线上时，EC交AB 于点H，求证：∠EAH=2∠HCB．9．（2017•重庆模拟）已知等腰Rt△ABC与等腰Rt△CDE，∠ACB=∠DCE=90°，把Rt△ABC 绕点C旋转．（1）如图1，当点A旋转到ED的延长线时，若BC=，BE=5，求CD的长；（2）当Rt△ABC旋转到如图2所示的位置时，过点C作BD的垂线交BD于点F，交AE于点G，求证：BD=2CG．10．（2017•河北区模拟）如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．（1）求证：△PMN为等腰直角三角形；（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP，BD 分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．11．（2017•吉安模拟）两块全等的三角板ABC和EDC如图（1）放置，AC=CB，CE=CD，∠ACB=∠ECD=90°，且AB与CE交于F，ED与AB、BC分别交于M、H，△ABC不动，将△EDC 绕点C旋转到如图（2），当∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．12．（2017•江津区校级三模）如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．（1）如图①，当点D在AB上，点E在AC上时，请判断线段CF，DF有怎样的数量关系和位置关系？为什么？（2）如图②，将图①中的△ADE绕点A旋转到图②位置时，请判断（1）中的结论是否仍然成立？并证明你的判断．13．（2017•济宁二模）将两块全等的三角板如图1摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．（1）将图1中△A1B1C绕点C顺时针旋转45°得图2，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；（2）在图2中，若AP1=a，则CQ等于多少？（3）将图2中△A1B1C绕点C顺时针旋转到△A2B2C（如图3），点P2是A2C与AP1的交点．当旋转角为多少度时，有△AP1C∽△CP1P2？这时线段CP1与P1P2之间存在一个怎样的数量关系？．14．（2017•常德）如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．（1）如图1，若BD=BA，求证：△ABE≌△DBE；（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．15．（2017•杭州）如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．（1）求证：△ADE∽△ABC；（2）若AD=3，AB=5，求的值．16．（2017•天水）△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF 的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=2，CQ=9时BC的长．17．（2017•深圳模拟）如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE=AB，点P从点D出发，以每秒1个单位长度沿D→C→B向终点B运动，直线EP交AD于点F，过点F作直线FG⊥DE于点G，交AB于点R．（1）求证：AF=AR；（2）设点P运动的时间为t，①求当t为何值时，四边形PRBC是矩形？②如图2，连接PB．请直接写出使△PRB是等腰三角形时t的值．18．（2017•惠阳区模拟）把Rt△ABC和Rt△DEF按如图（1）摆放（点C与E重合），点B、C（E）、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF 移动的同时，点P从△ABC的顶点A出发，以2cm/s的速度沿AB向点B匀速移动；当点P 移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t（s）．（1）用含t的代数式表示线段AP和AQ的长，并写出t的取值范围；（2）连接PE，设四边形APEQ的面积为y（cm2），试探究y的最大值；（3）当t为何值时，△APQ是等腰三角形．19．（2017•蜀山区二模）如图，在△ABC中，D、E分别为AB、AC上的点，线段BE、CD相交于点O，且∠DCB=∠EBC=∠A．（1）求证：△BOD∽△BAE；（2）求证：BD=CE；（3）若M、N分别是BE、CE的中点，过MN的直线交AB于P，交AC于Q，线段AP、AQ 相等吗？为什么？20．（2017•安徽模拟）如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD 的中点，BF、ED的延长线交于点G，连接GC．（1）求证：AB=GD；（2）如图2，当CG=EG时，求的值．21．（2017•肥城市三模）如图，在锐角△ABC中，D，E分别为AB，BC中点，F为AC上一点，且∠AFE=∠A，DM∥EF交AC于点M．（1）点G在BE上，且∠BDG=∠C，求证：DG•CF=DM•EG；（2）在图中，取CE上一点H，使∠CFH=∠B，若BG=1，求EH的长．22．（2017•石家庄二模）如图，在矩形ABCD和矩形PEFG中，AB=8，BC=6，PE=2，PG=4．PE 与AC交于点M，EF与AC交于点N，动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，伴随点P的运动，矩形PEFG在射线AB上滑动；动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动．点P、K同时开始运动，当点K到达点F时停止运动，点P也随之停止．设点P、K运动的时间是t秒（t＞0）．（1）当t=1时，KE=，EN=；（2）当t为何值时，△APM的面积与△MNE的面积相等？（3）当点K到达点N时，求出t的值；（4）当t为何值时，△PKB是直角三角形？23．（2017•岱岳区二模）如图，C为线段BD上一动点，过B、D分别作BD的垂线，使AB=BC，DE=DB，连接AD、AC、BE，过B作AD的垂线，垂足为F，连接CE、EF．（1）求证：AC•DF=BF•BD；（2）点C运动的过程中，∠CFE的度数保持不变，求出这个度数；（3）当点C运动到什么位置时，CE∥BF？并说明理由．24．（2017•长春模拟）如图，在△ABC中，点D在边AB上（不与A，B重合），DE∥BC交AC于点E，将△ADE沿直线DE翻折，得到△A′DE，直线DA′，EA′分别交直线BC于点M，N．（1）求证：DB=DM．（2）若=2，DE=6，求线段MN的长．（3）若=n（n≠1），DE=a，则线段MN的长为（用含n的代数式表示）．25．（2017•大冶市模拟）如图，△ABC中，点E、F分别在边AB，AC上，BF与CE相交于点P，且∠1=∠2=∠A．（1）如图1，若AB=AC，求证：BE=CF；（2）若图2，若AB≠AC，①（1）中的结论是否成立？请给出你的判断并说明理由；②求证：=．26．（2017•大东区二模）如图1，在锐角△ABC中，D、E分别是AB、BC的中点，点F在AC 上，且满足∠AFE=∠A，DM∥EF交AC于点M．（1）证明：DM=DA；（2）点G在BE上，且∠BDG=∠C，如图2，求证：△DEG∽△ECF；（3）在图2中，取CE上一点H，使得∠CFH=∠B，若BG=5，求EH的长．27．（2017•阳谷县一模）如图，在△ABC中，点D是BA边延长线上一点，过点D作DE∥BC，交CA延长线于点E，点F是DE延长线上一点，连接AF．（1）如果=，DE=6，求边BC的长；（2）如果∠FAE=∠B，FA=6，FE=4，求DF的长．28．（2017•杭州模拟）已知，如图1，点D、E分别在AB，AC上，且=．（1）求证：DE∥BC．（2）已知，如图2，在△ABC中，点D为边AC上任意一点，连结BD，取BD中点E，连结CE并延长CE交边AB于点F，求证：=．（3）在（2）的条件下，若AB=AC，AF=CD，求的值．答案解析1．（2017•黑龙江）已知：△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°．连接AD，BC，点H为BC中点，连接OH．（1）如图1所示，易证：OH=AD且OH⊥AD（不需证明）（2）将△COD绕点O旋转到图2，图3所示位置时，线段OH与AD又有怎样的关系，并选择一个图形证明你的结论．【解答】（1）证明：如图1中，∵△OAB与△OCD为等腰直角三角形，∠AOB=∠COD=90°，∴OC=OD，OA=OB，∵在△AOD与△BOC中，，∴△AOD≌△BOC（SAS），∴∠ADO=∠BCO，∠OAD=∠OBC，∵点H为线段BC的中点，∴OH=HB，∴∠OBH=∠HOB=∠OAD，又因为∠OAD+∠ADO=90°，所以∠ADO+∠BOH=90°，所以OH⊥AD（2）解：①结论：OH=AD，OH⊥AD，如图2中，延长OH到E，使得HE=OH，连接BE，易证△BEO≌△ODA∴OE=AD∴OH=OE=AD由△BEO≌△ODA，知∠EOB=∠DAO∴∠DAO+∠AOH=∠EOB+∠AOH=90°，∴OH⊥AD．②如图3中，结论不变．延长OH到E，使得HE=OH，连接BE，延长EO交AD于G．易证△BEO≌△ODA∴OE=AD∴OH=OE=AD由△BEO≌△ODA，知∠EOB=∠DAO∴∠DAO+∠AOF=∠EOB+∠AOG=90°，∴∠AGO=90°∴OH⊥AD．2．（2017•连云港四模）阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．操作与证明：（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；猜想与发现：根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？【解答】解：操作与证明：（1）BE=AD．∵△C′DE绕点C按顺时针方向旋转30°，∴∠BCE=∠ACD=30度，∵△ABC与△C′DE是等边三角形，∴CA=CB，CE=CD，∴△BCE≌△ACD，∴BE=AD．（2）BE=AD．∵△C′DE绕点C按顺时针方向旋转的角度为α，∴∠BCE=∠ACD=α，∵△ABC与△C′DE是等边三角形，∴CA=CB，CE=CD，∴△BCE≌△ACD，∴BE=AD．猜想与发现：当α为180°时，线段AD的长度最大，等于a+b；当α为0°（或360°）时，线段AD的长度最小，等于a﹣b．3．（2017•金乡县模拟）请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PC是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为，问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．【解答】解：（1）如图，将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A．∴AP′=PC=1，BP=BP′=；连接PP′，在Rt△BP′P中，∵BP=BP′=，∠PBP′=90°，∴PP′=2，∠BP′P=45°；（2分）在△AP′P中，AP′=1，PP′=2，AP=，∵，即AP′2+PP′2=AP2；∴△AP′P是直角三角形，即∠AP′P=90°，∴∠AP′B=135°，∴∠BPC=∠AP′B=135°．（4分）（2）过点B作BE⊥AP′，交AP′的延长线于点E；则△BEP′是等腰直角三角形，∴∠EP′B=45°，∴EP′=BE=1，∴AE=2；∴在Rt△ABE中，由勾股定理，得AB=；（7分）∴∠BPC=135°，正方形边长为．4．（2017•滦县模拟）两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为相等和位置关系为垂直；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．【解答】（1）解：∵CE=CD，AC=BC，∠ECA=∠DCB=90°，∴BE=AD，∵F是DE的中点，H是AE的中点，G是BD的中点，∴FH=AD，FH∥AD，FG=BE，FG∥BE，∴FH=FG，∵AD⊥BE，∴FH⊥FG，故答案为：相等，垂直．（2）答：成立，证明：∵CE=CD，∠ECD=∠ACD=90°，AC=BC，∴△ACD≌△BCE∴AD=BE，由（1）知：FH=AD，FH∥AD，FG=BE，FG∥BE，∴FH=FG，FH⊥FG，∴（1）中的猜想还成立．（3）答：成立，结论是FH=FG，FH⊥FG．连接AD，BE，两线交于Z，AD交BC于X，同（1）可证∴FH=AD，FH∥AD，FG=BE，FG∥BE，∵三角形ECD、ACB是等腰直角三角形，∴CE=CD，AC=BC，∠ECD=∠ACB=90°，∴∠ACD=∠BCE，在△ACD和△BCE中，∴△ACD≌△BCE，∴AD=BE，∠EBC=∠DAC，∵∠DAC+∠CXA=90°，∠CXA=∠DXB，∴∠DXB+∠EBC=90°，∴∠EZA=180°﹣90°=90°，即AD⊥BE，∵FH∥AD，FG∥BE，∴FH⊥FG，即FH=FG，FH⊥FG，结论是FH=FG，FH⊥FG5．（2017•路北区三模）如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．（1）求证：△AEC≌△ADB；（2）若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．【解答】解：（1）由旋转的性质得：△ABC≌△ADE，且AB=AC，∴AE=AD，AC=AB，∠BAC=∠DAE，∴∠BAC+∠BAE=∠DAE+∠BAE，即∠CAE=∠DAB，在△AEC和△ADB中，，∴△AEC≌△ADB（SAS）；（2）∵四边形ADFC是菱形，且∠BAC=45°，∴∠DBA=∠BAC=45°，由（1）得：AB=AD，∴∠DBA=∠BDA=45°，∴△ABD为直角边为2的等腰直角三角形，∴BD2=2AB2，即BD=2，∴AD=DF=FC=AC=AB=2，∴BF=BD﹣DF=2﹣2．6．（2017•平房区二模）如图，正方形ABCD，点E在AD上，将△CDE绕点C顺时针旋转90°至△CFG，点F，G分别为点D，E旋转后的对应点，连接EG，DB，DF，DB与CE交于点M，DF与CG交于点N．（1）求证BM=DN；（2）直接写出图中已经存在的所有等腰直角三角形．【解答】（1）证明：∵四边形ABCD为正方形，∴∠DCB=90°，CD=CB，∵△CDE绕点C顺时针旋转90°至△CFG，∴CF=CD，∠ECG=∠DCF=90°，∴△CDF为等腰直角三角形，∴∠CDF=∠CFD=45°，∵∠BCM+∠DCE=90°，∠DCN+∠DCE=90°，∴∠BCM=∠DCN，∵∠CBM=∠ABC=45°，∴∠CBM=∠CDN，在△BCM和△DCN中，∴△BCM≌△DCN，∴BM=DN；（2）解：∵四边形ABCD为正方形，∴△ABD和△BCD为等腰直角三角形；由（1）得△CDF为等腰三角形；∵△CDE绕点C顺时针旋转90°至△CFG，∴CE=CG，∠ECG=90°，∴△ECG为等腰直角三角形；∵△CBD和△CFD为等腰直角三角形；∴△BDF为等腰直角三角形．7．（2017•路南区一模）如图①，△ABC中，AC=BC，∠A=30°，点D在AB边上且∠ADC=45°．（1）求∠BCD的度数；（2）将图①中的△BCD绕点B顺时针旋转得到△BC′D′．当点D′恰好落在BC边上时，如图②所示，连接C′C并延长交AB于点E．①求∠C′CB的度数；②求证：△C′BD'≌△CAE．【解答】解：（1）∵AC=BC，∠A=30°，∴∠CBA=∠CAB=30°，∵∠ADC=45°，∴∠BCD=∠ADC﹣∠CBA=15°=∠BC'D'；（2）①由旋转可得CB=C'B=AC，∠C'BD'=∠CBD=∠A=30°，∴∠CC'B=∠C'CB=75°；②证明：∵AC=C'B，∠C'BD'=∠A，∴∠CEB=∠C'CB﹣∠CBA=45°，∴∠ACE=∠CEB﹣∠A=15°，∴∠BC'D'=∠BCD=∠ACE，在△C'BD'和△CAE中，，∴△C'BD'≌△CAE（ASA）．8．（2017•沙坪坝区一模）已知△ABC和△DEB都是等腰直角三角形，∠BAC=∠EDB=90°．（1）如图1，若点E，B，C在同一直线上，连接AE，当∠AEC=30°，BC=4时，求EB的长；（2）如图2，将图1中的△DEB绕点B顺时针旋转，当点C在ED的延长线上时，EC交AB 于点H，求证：∠EAH=2∠HCB．【解答】（1）解：如图1中，作AH⊥BC于H．∵AB=AC，∠BAC=90°，AH⊥BC，∴AH=BH=HC=2，在Rt△AEH中，∵∠AHE=90°，AH=2，∠AEH=30°，∴EH==2，∴EB=EH﹣BH=2﹣2．（2）证明：如图2中，连接AD．∵∠BDH=∠HAC，∠BHD=∠CHA，∴△BHD∽△CHA，∴=，∴=，∵∠AHD=∠CHB，∴△AHD∽△CHB，∴∠ADH=∠CBH=45°，∠DAH=∠BCH，∴∠ADB=90°+45°=135°，∴∠ADE=360°﹣90°﹣135°=135°，∴∠ADE=∠ADB，在△ADE和△ADB中，，∴△ADE≌△ADB，∴∠DAE=∠DAB，∵∠DAB=∠BCH，∴∠EAH=2∠HCB．9．（2017•重庆模拟）已知等腰Rt△ABC与等腰Rt△CDE，∠ACB=∠DCE=90°，把Rt△ABC 绕点C旋转．（1）如图1，当点A旋转到ED的延长线时，若BC=，BE=5，求CD的长；（2）当Rt△ABC旋转到如图2所示的位置时，过点C作BD的垂线交BD于点F，交AE于点G，求证：BD=2CG．【解答】解：（1）如图1，∵△ADC是由△BEC绕点C旋转得到的，∴AD=BE=5，∠ADC=∠BEC，∵在等腰Rt△ABC与等腰Rt△CDE中，BC=AC=，∠EDC=∠DEC=45°，∴AB=13，∠ADC=∠BEC=135°，∴∠AEB=90°，∴AE==12，∴DE=7，∴等腰Rt△CDE中，CD=DE=；（2）如图2，过点A作AH∥CE，交CG的延长线于H，连接HE，则∠CAH+∠ACE=180°，∵∠ACB=∠DCE=90°，∴∠BCD+∠ACE=180°，∴∠CAE=∠BCD，∵CF⊥BD，∠ACB=90°，∴∠CBF+∠BCF=∠ACG+∠BCF=90°，∴∠CBF=∠ACG，在△BCD和△CAH中，，∴△BCD≌△CAH（ASA），∴AH=CD=CE，BD=CH，又∵AH∥CE，∴四边形ACEH是平行四边形，∴CH=2CG，∴BD=2CG．10．（2017•河北区模拟）如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．（1）求证：△PMN为等腰直角三角形；（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP，BD 分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．【解答】解：（1）∵△ACB和△ECD是等腰直角三角形，∴AC=BC，EC=CD，∠ACB=∠ECD=90°．在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE=BD，∠EAC=∠CBD，∵∠CBD+∠BDC=90°，∴∠EAC+∠BDC=90°，∵点M、N分别是斜边AB、DE的中点，点P为AD的中点，∴PM=BD，PN=AE，∴PM=PM，∵PM∥BD，PN∥AE，∴∠NPD=∠EAC，∠MPA=∠BDC，∵∠EAC+∠BDC=90°，∴∠MPA+∠NPC=90°，∴∠MPN=90°，即PM⊥PN，∴△PMN为等腰直角三角形；（2）①中的结论成立，理由：设AE与BC交于点O，如图②所示：∵△ACB和△ECD是等腰直角三角形，∴AC=BC，EC=CD，∠ACB=∠ECD=90°．在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE=BD，∠CAE=∠CBD．∵∠AOC=∠BOE，∠CAE=∠CBD，∴∠BHO=∠ACO=90°，∴AE⊥BD，∵点P、M、N分别为AD、AB、DE的中点，∴PM=BD，PM∥BD，PN=AE，PN∥AE，∴PM=PN．∵AE⊥BD，∴PM⊥PN，∴△PMN为等腰直角三角形．11．（2017•吉安模拟）两块全等的三角板ABC和EDC如图（1）放置，AC=CB，CE=CD，∠ACB=∠ECD=90°，且AB与CE交于F，ED与AB、BC分别交于M、H，△ABC不动，将△EDC 绕点C旋转到如图（2），当∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．【解答】解：四边形ACDM是菱形．证明：∵∠ACB=∠DCE=90°，∠BCE=45°，∴∠1=∠2=45°．∵∠E=45°，∴∠1=∠E，∴AC∥DE，∴∠AMH=180°﹣∠A=135°=∠ACD，又∵∠A=∠D=45°，∴四边形ACDM是平行四边形（两组对角分别相等的四边形是平行四边形），∵AC=CD，∴四边形ACDM是菱形．12．（2017•江津区校级三模）如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．（1）如图①，当点D在AB上，点E在AC上时，请判断线段CF，DF有怎样的数量关系和位置关系？为什么？（2）如图②，将图①中的△ADE绕点A旋转到图②位置时，请判断（1）中的结论是否仍然成立？并证明你的判断．【解答】解：（1）CF=DF且CF⊥DF．理由如下：∵∠ADE=90°，∴∠BDE=90°，又∵∠BCE=90°，点F是BE的中点，∴CF=DF=BE=BF，∴∠1=∠3，∠2=∠4，∴∠5=∠1+∠3=2∠1，∠6=∠2+∠4=2∠2，∴∠CFD=∠5+∠6=2（∠1+∠2）=2∠ABC，又∵△ABC是等腰直角三角形，且∠ACB=90°，∴∠ABC=45°，∴∠CFD=90°，∴CF=DF且CF⊥DF．（2）（1）中的结论仍然成立．理由如下：如图，延长DF至G使FG=DF，连接BG，CG，DC，∵F是BE的中点，∴BF=EF，又∵∠BFG=∠EFD，GF=DF，∴△BFG≌△EFD（SAS），∴∠FBG=∠FED，BG=ED，∴BG∥DE，∵△ADE和△ACB都是等腰直角三角形，∴DE=DA，∠DAE=∠DEA=45°，AC=BC，∠CAB=∠CBA=45°，又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣（180°﹣∠AEB﹣∠EAB）﹣45°=∠DEF﹣180°+∠AEB+∠EAB﹣45°=（∠DEF+∠AEB）+∠EAB﹣225°=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°=90°+∠EAB，而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB，∴∠CBG=∠DAC，又∵BG=ED，DE=DA，∴BG=AD，又∵BC=AC，∴△BCG≌△ACD（SAS），∴GC=DC，∠BCG=∠ACD，∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°，∴△DCG是等腰直角三角形，又∵F是DG的中点，∴CF⊥DF且CF=DF．13．（2017•济宁二模）将两块全等的三角板如图1摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．（1）将图1中△A1B1C绕点C顺时针旋转45°得图2，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；（2）在图2中，若AP1=a，则CQ等于多少？（3）将图2中△A1B1C绕点C顺时针旋转到△A2B2C（如图3），点P2是A2C与AP1的交点．当旋转角为多少度时，有△AP1C∽△CP1P2？这时线段CP1与P1P2之间存在一个怎样的数量关系？．【解答】（1）证明：∵∠B1CB=45°，∠B1CA1=90°，∴∠B1CQ=∠BCP1=45°；又B1C=BC，∠B1=∠B，∴△B1CQ≌△BCP1（ASA）∴CQ=CP1；（2）解：如图：作P1D⊥AC于D，∵∠A=30°，∴P1D=AP1；∵∠P1CD=45°，∴=sin45°=，∴CP1=P1D=AP1；又AP1=a，CQ=CP1，∴CQ=a；（3）解：当∠P1CP2=∠P1AC=30°时，由于∠CP1P2=∠AP1C，则△AP1C∽△CP1P2，所以将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C时，有△AP1C∽△CP1P2．这时==，∴P1P2=CP1．14．（2017•常德）如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．（1）如图1，若BD=BA，求证：△ABE≌△DBE；（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．【解答】证明：（1）在Rt△ABE和Rt△DBE中，，∴△ABE≌△DBE；（2）①过G作GH∥AD交BC于H，∵AG=BG，∴BH=DH，∵BD=4DC，设DC=1，BD=4，∴BH=DH=2，∵GH∥AD，∴==，∴GM=2MC；②过C作CN⊥AC交AD的延长线于N，则CN∥AG，∴△AGM∽△NCM，∴=，由①知GM=2MC，∴2NC=AG，∵∠BAC=∠AEB=90°，∴∠ABF=∠CAN=90°﹣∠BAE，∴△ACN∽△BAF，∴=，∵AB=2AG，∴=，∴2CN•AG=AF•AC，∴AG2=AF•AC．15．（2017•杭州）如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．（1）求证：△ADE∽△ABC；（2）若AD=3，AB=5，求的值．【解答】解：（1）∵AG⊥BC，AF⊥DE，∴∠AFE=∠AGC=90°，∵∠EAF=∠GAC，∴∠AED=∠ACB，∵∠EAD=∠BAC，∴△ADE∽△ABC，（2）由（1）可知：△ADE∽△ABC，∴=由（1）可知：∠AFE=∠AGC=90°，∴∠EAF=∠GAC，∴△EAF∽△CAG，∴，∴=16．（2017•天水）△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF 的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=2，CQ=9时BC的长．【解答】（1）证明：∵△ABC是等腰直角三角形，∴∠B=∠C=45°，AB=AC，∵AP=AQ，∴BP=CQ，∵E是BC的中点，∴BE=CE，在△BPE和△CQE中，∵，∴△BPE≌△CQE（SAS）；（2）解：∵△ABC和△DEF是两个全等的等腰直角三角形，∴∠B=∠C=∠DEF=45°，∵∠BEQ=∠EQC+∠C，即∠BEP+∠DEF=∠EQC+∠C，∴∠BEP+45°=∠EQC+45°，∴∠BEP=∠EQC，∴△BPE∽△CEQ，∴=，∵BP=2，CQ=9，BE=CE，∴BE2=18，∴BE=CE=3，∴BC=6．17．（2017•深圳模拟）如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE=AB，点P从点D出发，以每秒1个单位长度沿D→C→B向终点B运动，直线EP交AD于点F，过点F作直线FG⊥DE于点G，交AB于点R．（1）求证：AF=AR；（2）设点P运动的时间为t，①求当t为何值时，四边形PRBC是矩形？②如图2，连接PB．请直接写出使△PRB是等腰三角形时t的值．【解答】（1）证明：如图，在正方形ABCD中，AD=AB=2，∵AE=AB，∴AD=AE，∴∠AED=∠ADE=45°，又∵FG⊥DE，∴在Rt△EGR中，∠GER=∠GRE=45°，∴在Rt△ARF中，∠FRA=∠AFR=45°，∴∠FRA=∠RFA=45°，∴AF=AR；（2）解：①如图，当四边形PRBC是矩形时，则有PR∥BC，∴AF∥PR，∴△EAF∽△ERP，∴，即：由（1）得AF=AR，∴，解得：或（不合题意，舍去），∴，∵点P从点D出发，以每秒1个单位长度沿D→C→B向终点B运动，∴（秒）；②若PR=PB，过点P作PK⊥AB于K，设FA=x，则RK=BR=（2﹣x），∵△EFA∽△EPK，∴，即：=，解得：x=±﹣3（舍去负值）；∴t=（秒）；若PB=RB，则△EFA∽△EPB，∴=，∴，∴BP=AB=×2=∴CP=BC﹣BP=2﹣=，∴（秒）．综上所述，当PR=PB时，t=；当PB=RB时，秒．18．（2017•惠阳区模拟）把Rt△ABC和Rt△DEF按如图（1）摆放（点C与E重合），点B、C（E）、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF 移动的同时，点P从△ABC的顶点A出发，以2cm/s的速度沿AB向点B匀速移动；当点P 移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t（s）．（1）用含t的代数式表示线段AP和AQ的长，并写出t的取值范围；（2）连接PE，设四边形APEQ的面积为y（cm2），试探究y的最大值；（3）当t为何值时，△APQ是等腰三角形．【解答】（1）解：AP=2t∵∠EDF=90°，∠DEF=45°，∴∠CQE=45°=∠DEF，∴CQ=CE=t，∴AQ=8﹣t，t的取值范围是：0≤t≤5；（2）过点P作PG⊥x轴于G，可求得AB=10，SinB=，PB=10﹣2t，EB=6﹣t，∴PG=PBSinB=（10﹣2t）∴y=S△ABC﹣S△PBE﹣S△QCE==∴当（在0≤t≤5内），y有最大值，y最大值=（cm2）（3）若AP=AQ，则有2t=8﹣t解得：（s）若AP=PQ，如图①：过点P作PH⊥AC，则AH=QH=，PH∥BC ∴△APH∽△ABC，∴，即，解得：（s）若AQ=PQ，如图②：过点Q作QI⊥AB，则AI=PI=AP=t∵∠AIQ=∠ACB=90°∠A=∠A，∴△AQI∽△ABC∴即，解得：（s）综上所述，当或或时，△APQ是等腰三角形．19．（2017•蜀山区二模）如图，在△ABC中，D、E分别为AB、AC上的点，线段BE、CD相交于点O，且∠DCB=∠EBC=∠A．（1）求证：△BOD∽△BAE；（2）求证：BD=CE；（3）若M、N分别是BE、CE的中点，过MN的直线交AB于P，交AC于Q，线段AP、AQ 相等吗？为什么？【解答】（1）证明：∵∠BCO=∠CBO，∴∠DOB=∠BCO+CBO=2∠BCO，∵∠A=2∠BCO，∴∠DOB=∠A，∵∠ABE=∠ABE，∴△BOD∽△BAE；（2）解：延长CD，在CD延长线上取一点F，使BF=BD，∴∠BDF=∠BFD，∵∠BDF=∠ABO+∠DOB，∠BEC=∠ABO+∠A，由（1）得∠BOD=∠A，∴∠BDF=∠BEC，∴∠BFD=∠BEC，在△BFC与△CEB中，，∴△BFC≌△CEB，∴BD=BF，∴BD=CE；（3）解：AP=AQ，理由：取BC的中点G，连接GM，GN，∵M，N分别是BE，CD的中点，∴GM，GN是中位线，∴GM∥CE，GM=CE，GN∥BD，GN=BD，∵BD=CE，∴GM=GN，∴∠3=∠4，∵GM∥CE，∴∠2=∠4，∵GN∥BD，∴∠3=∠1，∴∠1=∠2，∴AP=AQ．20．（2017•安徽模拟）如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD 的中点，BF、ED的延长线交于点G，连接GC．（1）求证：AB=GD；（2）如图2，当CG=EG时，求的值．【解答】解：（1）∵D、E分别是线段AC、BC的中点，∴DE为△ABC的中位线，∴DE∥AB，即EG∥AB，∴∠FDG=∠A，∵点F为线段AD的中点，∴AF=DF，在△ABF与△DGF中，∴△ABF≌△DGF（ASA）∴AB=GD（2）∵DE为△ABC的中位线，∴DE=AB，CE=BC=AC∵DG=AB，∴EG=DE+DG∴EG=AB∵DE∥AB，∴∠GEC=∠CBA，∵AC=BC，CG=EG∴△GEC∽△CBA∴，即，∴21．（2017•肥城市三模）如图，在锐角△ABC中，D，E分别为AB，BC中点，F为AC上一点，且∠AFE=∠A，DM∥EF交AC于点M．（1）点G在BE上，且∠BDG=∠C，求证：DG•CF=DM•EG；（2）在图中，取CE上一点H，使∠CFH=∠B，若BG=1，求EH的长．【解答】（1）证明：如图1所示，∴D，E分别为AB，BC中点，∴DE∥AC∵DM∥EF，∴四边形DEFM是平行四边形，∴DM=EF，如图2所示，∵D、E分别是AB、BC的中点，∴DE∥AC，∴∠BDE=∠A，∠DEG=∠C，∵∠AFE=∠A，∴∠BDE=∠AFE，∴∠BDG+∠GDE=∠C+∠FEC，∵∠BDG=∠C，∴∠GDE=∠FEC，∴△DEG∽△ECF；∴，∴，∴，∴DG•CF=DM•EG；（2）解：如图3所示，∵∠BDG=∠C=∠DEB，∠B=∠B，∴△BDG∽△BED，∴，∴BD2=BG•BE，∵∠AFE=∠A，∠CFH=∠B，∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=∠EFH，又∵∠FEH=∠CEF，∴△EFH∽△ECF，∴=，∴EF2=EH•EC，∵DE∥AC，DM∥EF，∴四边形DEFM是平行四边形，∴EF=DM=DA=BD，∴BG•BE=EH•EC，∵BE=EC，∴EH=BG=1．22．（2017•石家庄二模）如图，在矩形ABCD和矩形PEFG中，AB=8，BC=6，PE=2，PG=4．PE 与AC交于点M，EF与AC交于点N，动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，伴随点P的运动，矩形PEFG在射线AB上滑动；动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动．点P、K同时开始运动，当点K到达点F时停止运动，点P也随之停止．设点P、K运动的时间是t秒（t＞0）．（1）当t=1时，KE=1，EN=；（2）当t为何值时，△APM的面积与△MNE的面积相等？（3）当点K到达点N时，求出t的值；（4）当t为何值时，△PKB是直角三角形？【解答】解：（1）当t=1时，根据题意得，AP=1，PK=1，∵PE=2，∴KE=2﹣1=1，∵四边形ABCD和PEFG都是矩形，∴△APM∽△ABC，△APM∽△NEM，∴=，=，∴MP=，ME=，∴NE=；故答案为：1；；（2）由（1）并结合题意可得，AP=t，PM=t，ME=2﹣t，NE=﹣t，∴t×t=（2﹣t）×（﹣t），解得，t=；（3）当点K到达点N时，则PE+NE=AP，由（2）得，﹣t+2=t，解得，t=；（4）①当K在PE边上任意一点时△PKB是直角三角形，即，0＜t≤2；②当点k在EF上时，则KE=t﹣2，BP=8﹣t，∵△BPK∽△PKE，∴PK2=BP×KE，PK2=PE2+KE2，∴4+（t﹣2）2=（8﹣t）（t﹣2），解得t=3，t=4；③当t=5时，点K在BC边上，∠KBP=90°．综上，当0＜t≤2或t=3或t=4或5时，△PKB是直角三角形．23．（2017•岱岳区二模）如图，C为线段BD上一动点，过B、D分别作BD的垂线，使AB=BC，DE=DB，连接AD、AC、BE，过B作AD的垂线，垂足为F，连接CE、EF．（1）求证：AC•DF=BF•BD；（2）点C运动的过程中，∠CFE的度数保持不变，求出这个度数；（3）当点C运动到什么位置时，CE∥BF？并说明理由．【解答】解：（1）∵BF⊥AD，∴∠AFB=∠BFD=90°，∴∠ABF+∠BAF=90°，∵AB⊥BC，∴∠ABF+∠DBF=90°，∴∠BAF=∠DBF，∴△ABF∽△BDF，∴=，即AB•DF=BF•BD，由AB=BC，AB⊥BC，∴AB=AC，∴AC•DF=BF•BD；（2）∵=，AB=BC、BD=DE，∴=，∵∠FBC+∠BDF=90°、∠BDF+∠EDF=90°，∴∠FBC=∠EDF，∴△FBC∽△FDE，∴∠BFC=∠DFE，又∠BFD=∠BFC+∠CFD=90°，∴∠DFE+∠CFD=90°，即∠CFE=90°，故∠CFE的度数保持不变，始终等于90°．（3）当C为BD中点时，CE∥BF，理由如下：∵C为BD中点，∴AB=BC=CD=BD=DE，在△ABD和△CDE中，∵，∴△ABD≌△CDE（SAS），∴∠ADB=∠CED，∵∠CED+∠ECD=90°，∴∠ADB+∠ECD=90°，∴CE⊥AD，∵BF⊥AD，∴CE∥BF．。

九年级中考数学图形变换压轴题专题练习1、在图1-3中，四边形ABCD和CGEF都是正方形，M是AE的中点．（1）如图1，点F在BC延长线上，求证：DM=MG；（2）在图1的基础上，将正方形CGEF绕点C顺时针旋转到图2位置，此时点E在BC延长线上．求证：DM=MG；（3）在图2的基础上，将正方形CGEF绕点C在任一旋转一个角度到如图3位置，此时DM和MG还相等吗？请证明。

2、已知线段AB的长为2a，点P是AB上的动点（P不与A，B重合），分别以AP、PB 为边向线段AB的同一侧作正△APC和正△PBD．（1）连结AD、BC，相交于点Q，设∠AQC=α，那么α的大小是否会随点P的移动而变化？请说明理由；（2）如图2，若点P固定，将△PBD绕点P按顺时针方向旋转（旋转角小于180°），此时α的大小是否发生变化？3、已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且随着点P的运动而运动，PE＝PD总成立．(1)如图(1)，当点P在对角线AC上时，请你通过测量、观察，猜想PE与PB有怎样的关系？(直接写出结论不必证明)；(2)如图(2)，当点P运动到CA的延长线上时，(1)中猜想的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由；(3)如图(3)，当点P运动到CA的反向延长线上时，请你利用图(3)画出满足条件的图形，并判断此时PE与PB有怎样的关系？(直接写出结论不必证明)4、如图（1），Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．AF平分∠CAB，交CD于点E，交CB于点F（1）求证：CE=CF．（2）将图（1）中的△ADE沿AB向右平移到△A′D′E′的位置，使点E′落在BC边上，其它条件不变，如图（2）所示．试猜想：BE′与CF有怎样的数量关系？请证明你的结论．5、如图1，O为正方形ABCD的中心，分别延长OA、OD到点F、E，使OF＝2OA，OE ＝2OD，连接EF．将△EOF绕点O逆时针旋转α角得到△E1OF1(如图2)．(1)探究AE1与BF1的数量关系，并给予证明；(2)当α＝30°时，求证：△AOE1为直角三角形．6、如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．（1）求证：△MDC是等边三角形；（2）将△MDC绕点M旋转，当MD（即MD′）与AB交于一点E，MC（即MC′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值．如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．7、如图(1)，在△ABC中，∠ACB＝90°，AC＝BC＝2，点D在AC上，点E在BC上，且CD＝CE，连接DE.(1)线段BE与AD的数量关系是________，位置关系是________．(2)如图(2)，当△CDE绕点C顺时针旋转一定角度α后，(1)中的结论是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．(3)绕点C继续顺时针旋转△CDE，当90°＜α＜180°时，延长DC交AB于点F，请在图(3)时，旋转角α的度数．中补全图形，并求出当AF＝1＋338、已知菱形ABCD的边长为5，∠DAB＝60°.将菱形ABCD绕着A逆时针旋转得到菱形AEFG，设∠EAB＝α，且0°＜α＜90°，连接DG、BE、CE、CF.(1)如图(1)，求证：△AGD≌△AEB；(2)当α＝60°时，在图(2)中画出图形并求出线段CF的长；(3)若∠CEF＝90°，在图(3)中画出图形并求出△CEF的面积．(1)(2)9、已知，点O为矩形ABCD的对称中心，过O点的直线L交直线AD于M，ON⊥OM交直线DC于N，连MN，现将直线L绕点O顺时针旋转。

中考数学总复习《图形变换综合压轴题》专题测试卷（附答案）1．线段AB与CD的位置关系如图1所示AB=CD=m，AB与CD的交点为O，且∠AOC=60°，分别将AB和AC平移到CE,BE的位置（如图2）．(1)求CE的长和∠DCE的度数；(2)在图2中求证：AC+BD>m．2．如图，在Rt△ABC中∠ACB=90°，∠B=30°将Rt△ABC绕点C顺时针旋转得到Rt△A′B′C，且点B′、A′、B在同一直线上．请仅用无刻度的直尺完成以下作图．(1)在图1中，作出一个以AB为边的等边三角形；(2)在图2中，作出一个菱形．3．如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别A（1，4），B（2，0），C（3，2）（1）画出将△ABC沿AC翻折得到的△AB1C1；（2）画出将△ABC沿x轴翻折得到的△A2BC2；（3）观察发现：△A2BC2可由△AB1C绕点（填写坐标）旋转得到（4）在旋转过程中，点B1经过的路径长为．∠ABC．以点B为旋转中心，4．如图1，在△ABC中BA=BC，D、E是AC边上的两点，且满足∠DBE＝12将△CBE按逆时针方向旋转得到△ABF，连接DF．(1)求证：DF=DE；(2)如图2，若AB⊥BC，其他条件不变．求证：DE2=AD2+EC2．5．如图，将矩形ABCD绕着点B逆时针旋转得到矩形GBEF，使点C恰好落到线段AD上的E点处，连接CE，连接CG交BE于点H．(1)求证：CE平分∠BED；(2)取BC的中点M，连接MH，求证：MH∥BG；(3)若BC=2AB=4，求CG的长．6．已知，△ABC为等边三角形，点D，E为直线BC上两动点，且BD＝CE．点F，点E关于直线AC成轴对称，连接AE，顺次连接A，D，F．（1）如图1，若点D，点E在边BC上，试判断△ADF的形状并说明理由；（2）如图2，若点D，点E在边BC外，求证：∠BAD=∠FDC．7．如图，正方形ABCD中∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交BC、DC（或它们的延长线）于点M、N．(1)如图1，求证：MN=BM+DN；(2)当AB=6，MN=5时，求△CMN的面积；(3)当∠MAN绕点A旋转到如图2位置时线段BM、DN和MN之间有怎样的数量关系？请写出你的猜想并证明．8．如图1 在△ABC中AB=AC点DE、分别在边AB、AC上AD=AE连接DC点P、Q、M分别为DE、BC、DC的中点连接MQ、PM．(1)求证：PM=MQ；(2)当∠A=50°时求 PMQ的度数；(3)将△ADE绕点A沿逆时针方向旋转到图2的位置若∠PMQ=120°判断△ADE的形状并说明理由．9．已知△ABC∠ACB=90°AC=BC=4D是射线CB上一点连接AD将AD绕点A逆时针旋转90°点D落在点E处连接BE交射线AC于点F．(1)如图1当点D与点C重合时求AF的长；(2)如图2当点D在线段BC上时连接CE在点D的运动过程中请问△AEC的面积是否会发生变化？如果不会求出它的面积；如果会请说明理由；(3)当BD=1时求AF的长．10．在等边△BCD中DF⊥BC于点F点A为直线DF上一动点以点B为旋转中心把BA顺时针旋转60°至BE．(1)如图1 点A在线段DF上连接CE求证：CE=DA；(2)如图2 点A在线段FD的延长线上请在图中画出BE并连接CE当∠DEC=45°时连接AC求出∠BAC的度数；(3)在点A的运动过程中若BD=6求EF的最小值11．如图一个含60°角的纸片顶点与等边△ABC的点B重合将该纸片绕点B旋转使纸片60°角的一边交直线AC于点D在另一边上截取点E使BE=BD连接AE．(1)当点D在边AC上时如图① 求证：AC=AD+AE；(2)当点D在边AC所在直线上如图②、如图③时线段AD,AC,AE之间又有怎样的数量关系？请直接写出结论．(3)在图③中AD、BE交于点K若AE=4,BC=6则AD=_______ DK=______．12．已知四边形ABCD中AB⊥AD，BC⊥CD AB=BC,∠ABC=120°∠MBN=60°,∠MBN绕B点旋转它的两边分别交AD，DC（或它们的延长线）于E、F．(1)当∠MBN绕B点旋转到AE=CF时（如图1）求证：AE+CF=EF．(2)当∠MBN绕B点旋转到AE≠CF时在图2种情况下求证：AE+CF=EF．(3)当∠MBN绕B点旋转到AE≠CF时在图3种情况下上述结论是否成立？若成立请给予证明；若不成立线段AE，CF EF又有怎样的数量关系？请写出你的猜想不需证明．13．如图在平行四边形ABCD中AC是对角线AB=AC点E是BC边上一点连接AE将AE绕着点A 顺时针旋转α得到线段AF．(1)如图1 若α=∠BAC=90°连接BF BF=3BC=8求△ABE的面积；(2)如图2 若α=2∠BAC=120°连接CF交AB于H求证：2AH+CE=AD；(3)若在（2）的条件下3CE=BC=9点P为AB边上一动点连接EP将线段EP绕着点E顺时针旋转60°得到线段EQ连接CQ当线段CQ取得最小值时直接写出四边形BHQE的面积．14．已知：正方形ABCD以A为旋转中心旋转AD至AP连接BP、DP．(1)若将AD顺时针旋转30°至AP如图1所示求∠BPD的度数？(2)若将AD顺时针旋转α度(0°<α<90°)至AP求∠BPD的度数？(3)若将AD逆时针旋转α度(0°<α<180°)至AP请分别求出0°<α<90°、α=90°、90°<α<180°三种情况下的∠BPD的度数（图2、图3、图4）．15．已知如图1正方形ABCD的边长为5点E、F分别在边AB、AD的延长线上且BE=DF连接EF．(1)证明：EF⊥AC；(2)将△AEF绕点A顺时针方向旋转当旋转角α满足0°<α<45°时设EF与射线AB交于点G与AC交于点H如图所示试判断线段FH、HG、GE的数量关系并说明理由．(3)若将△AEF绕点A旋转一周连接DF、BE并延长EB交直线DF于点P连接PC试说明点P的运动路径并求线段PC的取值范围．16．【问题思考】如图1 点E是正方形ABCD内的一点过点E的直线AQ以DE为边向右侧作正方形DEFG 连接GC直线GC与直线AQ交于点P则线段AE与GC之间的关系为______．【问题类比】如图2 当点E是正方形ABCD外的一点时【问题思考】中的结论还成立吗？若成立请证明你的结论；若不成立请说明理由；【拓展延伸】如图3 点E是边长为6的正方形ABCD所在平面内一动点【问题思考】中其他条件不变则动点P到边AD的最大距离为______（直接写出结果）．17．（1）【问题发现】如图1 在Rt△ABC中AB=AC∠BAC=90°点D为BC的中点以BD为一边作正方形BDFE点F恰好与点A重合则线段CF与AE的数量关系为_______；（2）【拓展探究】在（1）的条件下如果正方形BDFE绕点B顺时针旋转连接CF AE BF线段CF与AE 的数量关系有无变化？请仅就图2的情形给出证明；（3）【问题解决】当AB=AC=6且（2）中的正方形BDFE绕点B顺时针旋转到E F C三点共线时求出线段AE的长．18．综合与实践：问题情景：如图1、正方形ABCD与正方形AEFG的边AB AE(AB<AE)在一条直线上正方形AEFG以点A为旋转中心逆时针旋转设旋转角为α在旋转过程中两个正方形只有点A重合其它顶点均不重合连接BE DG．(1)操作发现：当正方形AEFG旋转至如图2所示的位置时求证：BE=DG；(2)操作发现：如图3 当点E在BC延长线上时连接FC求∠FCE的度数；(3)问题解决：如图4 如果α=45°AB=2AE=4√2请直接写出点G到BE的距离．19．如图①在正方形ABCD中连接BD点E是边AB上的一点EF⊥AB交BD于点F点P是FD的中点连接EP、CP．(1)如图① 探究EP与CP有何关系并说明理由；(2)若将△BEF绕点B顺时针旋转90° 得到图② 连接FD取FD的中点P连接EP、CP请问在该条件下①中的结论是否成立并说明理由；(3)如果把△BEF绕点B顺时针旋转180° 得到图③ 同样连接FD取FD的中点P连接EP、CP请你直接写出EP与CP的关系．20．综合与实践问题情境：数学活动课上老师向大家展示了一个图形变换的问题．如图1．将正方形纸片ABCD折叠使边AB AD都落在对角线AC上展开得折痕AE AF连接EF．试判断△AEF的形状．独立思考：(1)请解答问题情境提出的问题并写出证明过程．实践探究：(2)如图2．将图1中的∠EAF绕点A旋转使它的两边分别交边BC CD于点P Q连接PQ．请猜想线段BP PQ DQ之间的数量关系并加以证明．问题解决：(3)如图3．连接正方形对角线BD若图2中的∠PAQ的边AP AQ分别交对角线BD于点M N将图3中的正方形纸片沿对角线BD剪开如图4所示．若BM=7DN=24求MN的长．参考答案1．（1）解：∵将AB和AC平移到CE,BE的位置∵AB=CE,AB∥CE∵∠AOC=∠DCE∵∠AOC=60°AB=CD=m∵∠DCE=60°CE=AB=m；（2）证明：如图连接DE由（1）得：∠DCE=60°CE=AB=m∵AB=CD=m∵CD=CE∵△CDE是等边三角形∵DE=CD=m∵将AB和AC平移到CE,BE的位置∵AC=BE在△BDE中BD+BE>DE即AC+BD>m．2．（1）解：△ADB是等边三角形即为所求理由如下：如图延长AC交BB′于一点D∵∠ACB=90°∠CBA=30°将Rt△ABC绕点C顺时针旋转得到Rt△A′B′C ∵∠A=60°，∠B′=30°，BC=B′C∵∠B′BC=30°，∠ABD=60°∵∠BDA=180°−60°−60°=60°∵△ADB是等边三角形；（2）解：四边形ABDE是菱形即为所求理由如下：过点D作DE平行于AB交BC的延长线于一点即为点E连接AE如图：由（1）知△ADB是等边三角形且∠ACB=90°∵BC⊥AD∵DC=AC∵∠DEB =∠ABC∵∠DCE =∠ACB∵△DCE ≌△ACB∵BC =EC∵四边形ABDE 是菱形．3．解：（1）如图：（2）如图：（3）（5 0）（4）B 1经过的路径是以（5 0）为圆心 BB 1为半径的圆弧∵C ＝14×2×π×3＝32π；4．（1）证明：∵∠DBE =12∠ABC∵∠ABD +∠CBE =∠DBE =12∠ABC∵△ABF 由△CBE 旋转而成∵BE =BF ∠ABF =∠CBE∵∠DBF =∠DBE在△DBE 与△DBF 中{BE =BF ∠DBE =∠DBF BD =BD∵△DBE ≌△DBF （SAS ）（2）证明：∵将△CBE按逆时针方向旋转得到△ABF∵BA=BC∠ABC=90°∵∠BAC=∠BCE=45°∵图形旋转后点C与点A重合CE与AF重合∵AF=EC∵∠FAB=∠BCE=45°∵∠DAF=90°在Rt△ADF中DF2=AF2+AD2∵AF=EC∵DF2=EC2+AD2同（1）可得DE=DF∵DE2=AD2+EC2．5．（1）证明：∵将矩形ABCD绕着点B逆时针旋转得到矩形GBEF使点C恰好落到线段AD上的E点处∴BE=BC∴∠BEC=∠BCE∵AD∥BC∴∠BCE=∠DEC∴∠BEC=∠DEC∴CE平分∠BED；（2）证明：过点C作CN⊥BE于N如图：∵CE平分∠BED CD⊥DE CN⊥BE∴CD=CN∴BG=AB=CD=CN∵∠BHG=∠NHC∠GBH=∠CNH=90°BG=CN∴△BHG≌△NHC(AAS)∴GH=CH即点H是CG中点∵点M是BC中点∴MH是△BCG的中位线∵MH∥BG；（3）解：过点C作CN⊥BE于N过G作GR⊥BC于R如图：∵BC=2AB=4∴BG=AB=CD=CN=2∴CN=12 BC∴∠NBC=30°∵∠GBE=90°∴∠GBR=60°∴BR=12BG=1GR=√3BR=√3在Rt△GRC中CG=√GR2+CR2=√(√3)2+(1+4)2=2√7∴CG的长为2√7．6．解：（1）△ADF为等边三角形理由如下：∵△ABC为等边三角形∵AB=AC,∠ABC=∠ACB=60°．在△ABD和△ACE中{AB=AC∠ABC=∠ACBBD=CE∴△ABD≅△ACE(SAS)∴AD=AE,∠BAD=∠CAE．∵点F 点E关于直线AC成轴对称∴AF=AE,∠CAF=∠CAE ∴AD=AF,∠CAF=∠BAD．∵∠BAD+∠DAC=60°∴∠CAF+∠DAC=60°即∠DAF=60°,∵△ADF为等边三角形．（2）∵△ABC为等边三角形∵AB=AC,∠ABC=∠ACB=60°．在△ABD和△ACE中{AB=AC∠ABC=∠ACBBD=CE∴△ABD≅△ACE(SAS)∴AD=AE,∠BAD=∠CAE．∵点F 点E关于直线AC成轴对称∴AF=AE,∠CAF=∠CAE ∴AD=AF,∠CAF=∠BAD．∵∠BAD+∠DAC=60°∴∠CAF+∠DAC=60°∵△ADF为等边三角形．∴∠ADF=∠FDC+∠ADC=60°∵∠BAD+∠ADC=∠ABC=60°∵∠BAD=∠FDC7．（1）解：如图将△ABM绕点A逆时针旋转90°得到△ADM′则：△ABM≌△ADM′∵AM=AM′,BM=DM′,∠BAM=∠DAM′∵四边形ABCD为正方形∵∠BAD=90°∵∠MAN=45°∵∠MAB+∠NAD=45°∵∠M′AD+∠NAD=∠M′AN=45°∵∠MAN=∠M′AN又∵AM=AM′,AN=AN∵△AMN≌△AM′N（SAS）∵MN=M′N=M′D+DN=BM+DN；（2）解：∵四边形ABCD为正方形∵AD=AB=6S正方形=62=36∵△AMN≌△AM′N∵MN′=MN=5∵S△AMN=S△AM′N=12M′N⋅AD=12×5×6=15∵△ABM≌△ADM′∵S△ABM+S△ADN=S△ABM′+S△ADN=S△AM′N=15∵S△CMN=S正方形−S△AMN−S△ADN−S△AMB=36−15−15=6；（3）解：DN=BM+MN理由如下：如图将△ABM绕点A逆时针旋转90°得到△ADM′连接MN 则：∠MAM′=90°△ABM≌△ADM′∵AM=AM′,BM=DM′,∠BAM=∠DAM′∵∠MAN=45°∵∠M′AN=∠M′AM−∠MAN=90°−45°=45°∵∠MAN=∠M′AN又∵AM=AM′,AN=AN∵△AMN≌△AM′N（SAS）∵MN=M′N∵DN=M′D+M′N=BM+MN．8．（1）证明：∵AB=AC AD=AE∵BD=CE∵P M分别为DE DC的中点∵PM=12CE PM∥CE∵M Q分别为DC CB的中点∵MQ=12DB MQ∥OB∵PM=MQ；（2）解：∵点P、Q、M分别为DE、BC、DC的中点∵MQ∥DB PM∥AC∵∠MQC=∠B∵∠PMQ=∠DMP+∠DMQ=∠ACD+∠BCD+∠MQC=∠ACD+∠BCD+∠B =180°−50°=130°；（3）解：∵ADE是等边三角形理由如下：由旋转的性质可知∠BAC=∠DAE∵∠BAD=∠CAE在△BAD和△CAE中{AB=AC ∠BAD=∠CAE AD=AE∵∵BAD∵∵CAE（SAS）∵BD=CE∠ABD=∠ACE ∵P M为DE DC的中点∵PM∥EC∵∠PMD=∠ECD∵M Q为DC BC的中点∵MQ∥DB∵∠MQC=∠DBC∵∠MPQ=∠DMP+∠DMQ=∠DCE+∠MQC+∠MCQ=∠ACD+∠ACE+∠DBC+∠MCQ=∠ACD+∠MCQ+∠DBC+∠ABD=∠ACB+∠ABC=120°∵∠BAC=180°−120°=60°∵∠DAE=∠BAC=60°又∵AD=AE∵∵ADE是等边三角形．9．（1）解：∵将AD绕点A逆时针旋转90°∵AD=AE，∠DAE=90°∵点D与点C重合∵AC=AE∵BC=AC=AE又∵∠AFE=∠BFC∠EAF=∠BCF=90°∵△BCF≌△EAF(AAS)∵AF=CF∵AC=BC=4∵AF=CF=2；（2）解：△AEC的面积不会变化理由如下：如图过点E作EH⊥AC于H∵将AD绕点A逆时针旋转90°∵AD=AE，∠DAE=90°=∠ACB∵∠DAC+∠CAE=90°=∠DAC+∠ADC∵∠ADC=∠CAE∵△ADC≌△EAH(AAS)∵EH =AC =4∵S △ACE =12×AC ⋅EH =8；（3）解：当点D 在线段BC 上时∵BD =1，BC =4∵CD =3∵△ADC ≌△EAH∵CD =AH =3∵CH =1∵∠EHF =∠ACB =90° ∠AFE =∠BFC ，AC =EH =BC∵△EFH ≌△BFC(AAS)∵FH =FC =12 ∵AF =AF +FH =72；当点D 在线段CB 的延长线时 过点E 作EH ⊥直线AC 于H∵BD =1，BC =4∵CD =5同理可证△ACD ≌△EHA∵CD =AH =5∵CH =1同理可证：△BCF ≌△EHF∵FH =FC =12 ∵AF =AC +FC =92综上所述：AF 的长为72或92．10．（1）解：由旋转得 BA =BE ∠ABE =60°∵△BCD 是等边三角形∵BD=BC∠DBC=60°∵∠ABE=∠DBC∵∠DBA+∠ABC=∠ABC+∠CBE ∵∠DBA=∠CBE在△DBA与△CBE中{BD=BC ∠DBA=∠CBE BA=BE∵△DBA≌△CBE（SAS）∵DA=CE．（2）解：如图3由（1）可知△DBA≌△CBE∵DA=CE∠BDA=∠BCE又∵△BCD是等边三角形∵∠BDC=∠BCD=60°DB=DC∵DB=DC∵∵BCD是等腰三角形∵DF⊥BC∵∠BDF=12∠BDC=30°∵∠BDA=180°−∠BDF=150°∵∠BCE=150°∠CDA=360°−∠BDA−∠BDC=150°∵∠DCE=∠BCE−∠BCD=90°∵∠DEC=45°∵∠EDC=45°∵∠DEC=∠EDC ∵CE=CD∵DB=DC=DA∵∠BAD=180°−∠BDA2=15°∠CAD=180°−∠CDA2=15°∵∠BAC=∠BAD+∠CAD=30°．（3）解：∵由图1可知当点A在线段DF上时∠BCE=∠BDA=30°；由图3可知当点A在线段FD的延长线上时∠BCE=∠BDA=150°；由图4可知当点A在线段DF的延长线上时∠BCE=∠BDA=30°；∵综上所述当点A在直线DF上运动时直线CE与直线BC的夹角始终为30°即点E的运动轨迹为一条直线过点F作FE′⊥EC于点E′则当点E运动到点E′时此时EF的长度最短∵BD=CD=BC=6DF⊥BC∵CF=12BC=3又∵FE′⊥EC∠BCE=30°∵FE′=12CF=32∵EF的最小值为32．11．(（1）证明：∵△ABC是等边三角形∵AB=BC∠ABC=60°．∵∠EBD=60°∵∠EBA+∠ABD=∠CBD+∠ABD即：∠ABE=∠CBD∵BD=BE∵△ABE≌△CBD（SAS）∵AE=CD．∵AC=AD+CD∵AC=AD+AE．（2）如图2 当点D在CA的延长线时∵∵DBE=∵ABC=60°∵∵DBE+∵ABD=∵ABC+∵ABD即∵ABE=∵CBD∵AB=BC BE=BD∵∵ABE∵△CBD（SAS）∵AE=CD=AC+AD∵AD=AE-AC；如图3 当点D在AC的延长线上时∵∵ABC=∵DBE=60°∵∵ABC-∵CBE=∵DBE-∵CBE即∵ABE=∵CBD∵AB=BC BD=BE∵△ABE∵△CBD（SAS）∵AE=CD=AD-AC∵AC=AD-AE；综上当点D在CA延长线时AD=AE-AC；当点D在AC的延长线上时AC=AC-AE；（3）解：由（2）得∵ABE∵∵CBD∵CD=AE=4 ∵BAE=∵BCD=180°-∵ACB=120°∵AD=AC+CD=6+4=10 ∵CAE=∵BAE-∵BAC=60°∵∵CAE=∵ACB∵AE∵BC∵∵AKE∵∵CKB∵AK CK =AEBC=46∵AK =23CK又∵AK +CK =AC =BC =6∵53 CK =6∵CK =185∵DK =CK +CD =185+4=385．12．解：（1）∵AB ⊥AD,BC ⊥CD,∵∠A =∠C ,在△ABE 与△CBF 中{AB =BC ∠A =∠C AE =CF ∵△ABE ≅△CBF(SAS),∵∠ABE =∠CBF,BE =BF,∵∠ABC =120°,∠MBN =60°,∵∠ABE =∠CBF =30°,∵AE =12BE,CF =12BF,∵∠MBN =60°，BE =BF∵△BEF 为等边三角形∵BE =BF =EF,∵AE =CF =12EF,∵AE +CF =EF;（2）如图 将Rt △ABE 顺时针旋转120°得△BCG∵BE=BG,AE=CG,∠A=∠BCG,∵AB=BC,∠ABC=120°,∵点A与点C重合∵∠A=∠BCF=90°,∵∠BCG+∠BCF=180°,∵点G、C、F三点共线∵∠ABC=120°,∠MBN=60°,∠ABE=∠CBG,∵∠GBF=60°,在△GBF与△EBF中{BG=BE∠GBF=∠EBFBF=BF∵△GBF≅△EBF(SAS),∵FG=EF,∵EF=AE+CF；（3）不成立EF=AE−CF理由如下：如图将RtΔABE顺时针旋转120° 得ΔBCG∵AE=CG由（2）同理得点C、F、G三点共线∵AB=BC,∠ABC=120°,∵点A与点C重合∵BG=BE,∵∠ABC=∠ABE+∠CBE=120°,∵∠CBG+∠CBE=∠GBE=120°,∵∠MBN=60°,∵∠GBF=60°,在ΔBFG与ΔBFE中{BG=BE∠GBF=∠EBFBF=BF∵△BFG≅△BFE(SAS)∵GF=EF,∵EF=AE−CF.13．（1）解：如图：过点A作BC的垂线交BC于点M∵α=∠BAC=90°∴∠FAB=∠EAC在△FAB和△EAC{FA=EA ∠FAB=∠EAC BA=CA∴△FAB≅△EAC(SAS)∴FB=CE又∵BF=3BC=8∴BE=BC−CE=8−3=5又∵∠BAC=90°AB=AC ∴AM=12BC=4∴S△ABE=12BE×AM=12×5×4=10．（2）解：在BH上截取BP=CE连接CP∵α=2∠BAC=120°∵∠BAC=60°∵AB=AC∵△ABC是等边三角形∵∠B=∠ACB=60°BC=AC 在△CBP和△ACE中{BP=CE∠B=∠ACB=60°BC=AC∴△CBP≅△ACE∴CP=AE=AF∠BPC=∠AEC=60°+∠BAE ∴∠APC=180°−(∠BAE+60°)∵∠FAB=120°−∠BAE∴∠APC=∠FAB在△AHF和△CPH中{∠APC=∠FAB ∠AHF=∠PHC CP=AF∵△AHF≅△PHC(AAS)∴AH=PH∵BP=CE∴AB=BC=AD=AH+PH+CE=2AH+CE．（3）解：如图：∵3CE=BC=9∵CE=3BE=BC−CE=6,连接EH由（2）可知∠BAC=∠ABC=60°∵△BHE是等边三角形∵∠BEH=60°，BE=HE∵将线段EP绕着点E顺时针旋转60°得到线段EP1∵PE=P1E∠PEP1=60°即∠HEP1=∠BEP,在△BPE和△HEP1中{PE=P1E∠HEP1=∠BEPBE=HE,∵△BEP≅△HEP1(SAS),∵∠B=∠EHP1=60°,∵∠BEH=60°∵∠BEH=∠EHP1=60°,∵HP1∥BC点P1的轨迹为过点H且平行BC的直线过H作HP1∥BC其延长线角CD于M过C作CQ⊥BP1于Q由点到直线的距离垂线段最短可知：当CQ⊥MH时即CQ有最小值∵BH∥CM，BC∥HM∵四边形BHMC是平行四边形∵CM=BH=6∠HMC=∠B=60°∵∠QCM=30°∵MQ=12CM=3∵CQ=√CM2−MQ2=3√3∵边形BHQE的面积为BE⋅CQ=6×3√3=18√3．14．（1）解：∵AD顺时针旋转30°至AP∵AD=AP∠PAD=30°∵∠APD=12(180°−30°)=75°∵四边形ABCD为正方形∵AB=AD=AP∠BAD=90°∵∠BAP=90°−30°=60°∵∠BPA=12(180°−60°)=60°∵∠BPD=60°+75°=135°．（2）∵AD顺时针旋转α至AP ∵AD=AP∠PAD=α∵∠APD=12(180°−α)=90°−α2∵四边形ABCD为正方形∵AB=AD=AP∠BAD=90°∵∠BAP=90°−α∵∠BPA=12[180°−(90−α)]=45°+α2∵∠BPD=(90°−α2)+(45°+α2)=135°．（3）①当0°<α<90°时∵AD逆时针旋转α至AP∵AD=AP∠PAD=α∵∠APD=12(180°−α)=90°−α2∵四边形ABCD为正方形∵AB=AD=AP∠BAD=90°∵∠BAP=90°+α∵∠BPA=12[180°−(90+α)]=45°−α2∵∠BPD=(90°−α2)−(45°−α2)=45°．②当α=90°时∵AD逆时针旋转90°至AP∵AD=AP∠PAD=90°∵四边形ABCD为正方形∵AB=AD=AP∠BAD=90°∵∠BAP=90°+90°=180°即点P、A、B三点共线∵∠BPD=∠APD=12(180°−90°)=45°．③当90°<α<180°时∵AD逆时针旋转α至AP∵AD=AP∠PAD=α∵∠APD=12(180°−α)=90°−α2∵四边形ABCD为正方形∵AB=AD=AP∠BAD=90°∵∠BAP=360°−90°+α=270°−α∵∠BPA=12[180°−(270°−α)]=α2−45°∵∠BPD=(90°−α2)+(α2−45°)=45°．15．（1）证明：如图1：∵四边形ABCD是正方形∴AD=AB∠DAC=∠BAC∵BE=DF ∴AD+DF=AB+BE即AF=AE∴AC⊥EF.（2）解：FH2+GE2=HG2理由如下：如图2过A作AK⊥AC截取AK=AH连接GK、EK∵∠CAB=45°∴∠CAB=∠KAB=45°∵AG=AG∴△AGH≅△AGK(SAS)∴GH=GK由旋转得：∠FAE=90°AF=AE∵∠HAK=90°∴∠FAH=∠KAE∴△AFH≅△AEK(SAS)∴∠AEK=∠AFH=45°FH=EK∵∠AEH=45°∴∠KEG=45°+45°=90°Rt△GKE中KG2=EG2+EK2即：FH2+GE2=HG2．（3）解：如图3∵AD=AB∠DAF=∠BAE AE=AF∴△DAF≅△BAE(SAS)∴∠DFA=∠BEA∵∠PNF=∠ANE∴∠FPE=∠FAE=90°∴将△AEF绕点A旋转一周总存在直线EB与直线DF垂直∴点P的运动路径是：以BD为直径的圆如图4当P与C重合时PC最小PC=0当P与A重合时PC最大为5√2．∴线段PC的取值范围是：0≤PC≤5√2．16．解：问题思考：设AQ和BC交于点H∵四边形ABCD和四边形DEFG都为正方形∵∠ADC=∠EDG=90°DA=DC,DE=DG ∵∠ADC−∠EDC=∠EDG−∠EDC即∠ADE=∠CDG∵△DAE≌△DCG(SAS)∵AE=CG∠DAE=∠DCG∵∠DAB=∠DCB=90°∵∠DAE+∠HAB=∠DCG+∠PCH即∠BAH=∠PCH∵∠AHB=∠CHP∵∠B=∠CPA=90°即AE⊥CG故答案为：AE=GC AE⊥GC；问题类比：问题思考中的结论仍然成立理由如下：设AQ和BC交于点H∵四边形ABCD和四边形DEFG都为正方形∵∠ADC=∠EDG=90°DA=DC,DE=DG ∵∠ADC−∠EDC=∠EDG−∠EDC即∠ADE=∠CDG∵△DAE≌△DCG(SAS)∵AE=CG∠DAE=∠DCG∵∠DAB=∠DCB=90°∵∠DAE+∠HAB=∠DCG+∠PCH即∠BAH=∠PCH∵∠AHB=∠CHP∵∠B=∠CPA=90°即AE⊥CG故答案为：AE=GC AE⊥GC；拓展应用：∵∠CPA=90°∵点P的运用轨迹即为以AC为直径的⊙O上如图：当点P位于AD右侧PH⊥AD且经过圆心O时动点P到边AD的距离最大∵正方形的边长为6∵AC=6√2OH=3∵OP=OC=12AC=3√2∵PH=OH+OP=3+3√2即动点P到边AD的最大距离为3+3√2故答案为：3+3√2．17．（1）解：如图1 ∵四边形BDFE是正方形∵FE=BE∠E=90°∵BF=√BE2+FE2=√2FE2=√2FE∵点F与点A重合AB=AC∵CF=AC=AB=BF FE=AE∵CF=√2AE故答案为：CF=√2AE；（2）无变化理由如下：证：如图2 ∵EB=EF∠BEF=90°∵∠EBF=∠EFB=45°BF=√EB2+EF2=√2EB2=√2EB∵AB=AC∠BAC=90°∵∠ABC=∠ACB=45°BC=√AB2+AC2=√2AB2=√2AB∵BF EB =BCAB=√2∠CBF=∠ABE=45°−∠ABF∵△CBF∽△ABE∵CF AE =BCAB=√2∵CF=√2AE；（3）如图2 E F C三点共线且点F在线段CE上∵BC=√2AB AB=AC=6∵BC=√2×6=6√2由（1）得BD=12BC∵BE=EF=BD=12×6√2=3√2∵∠BEC=90°∵CE=√BC2−BE2=√(6√2)2−(3√2)2=3√6∵CF=CE−EF=3√6−3√2∵CF=√2AE∵AE=√22CF=√22×(3√6−3√2)=3√3−3；如图3 E F C三点共线且点F在线段CE的延长线上∵BF EB =BCAB=√2∠CBF=∠ABE=45°+∠CBE∵△CBF∽△ABE∵CF AE =BCAB=√2∵CF=√2AE∵∠BEF=90°∵∠BEC=180°−∠BEF=90°∵CE=√BC2−BE2=√(6√2)2−(3√2)2=3√6∵CF=CE+EF=3√6+3√2∵AE=√22CF=√22×(3√6+3√2)=3√3+3综上所述线段AE的长为3√3−3或3√3+3．18．（1）证明：∵四边形ABCD是正方形∵AB =AD ∠BAE +∠EAD =90°又∵四边形AEFG 是正方形∵AE =AG ∠EAD +∠DAG =90°∵∠BAE =∠DAG ．在△ABE 与△ADG 中{AB =AD,∠BAE =∠DAG AE =AG,∵△ABE ≅△ADG (SAS )∵BE =DG ；（2）解；过F 作FH ⊥BE 垂足为H∵∠AEF =∠ABE =∠EHF =90°∵∠AEB +∠FEH =90° ∠FEH +∠EFH =90°∵∠AEB =∠EFH∵四边形AEFG 是正方形∵AE =EF在△ABE 与△EHF 中{∠ABE =∠EHF ∠AEB =EFH AE =EF∵△ABE≌△EHF (AAS )∵AB =EH BE =FH∵AB =BC =EH∵BC +EC =EH +EC∵BE =CH =FH又∵∠EHF =90°∵∠FCE=45°（3）解：如图连接GB GE过点B作BH⊥AE于点H ∵GE是正方形AEFG的对角线∵∠AEG=45°∵∠EAB=45°∵AB∥GE∵S△BEG=S△AEG=12S正方形AEFG=12×4√2×4√2=16∵AB=2∵BH=AH=√2∵HE=4√2−√2=3√2在Rt△BHE中BE=√(√2)2+(3√2)2=2√5设点G到BE的距离为h∵S△BEG=12×BE×ℎ∵1 2×2√5×ℎ=16解得：ℎ=16√55∵点G到BE的距离为16√55．19．解：（1）EP=CP且EP⊥CP．证明：过PH⊥AB于点H延长HP交CD于点I作PK⊥AD于点K．则四边形PIDK是正方形四边形AKPH是矩形∴AK=HP KD=DI=PI=AH∵AD=CD∴IC=HP ∵AD∥PH∥EF P是DF的中点∴HA=HE∴HE=PI 在Rt△HPE和Rt△ICP中{HE=PI ∠PHE=∠CIP HP=IC∴Rt△HPE≌Rt△ICP(SAS)∴EP=CP∠HPE=∠PCI∠HEP=∠CPI∴∠HPE+∠CPI=90°∴∠EPC=90°∴EP⊥CP；（2）成立．证明：图2中作PH⊥BC则EF∥PH∥CD又∵P是DF的中点∴EH=CH 则PH是EC的中垂线∴PE=CP∵EF=EB∴EF+CD=EC ∵P是DF的中点EH=CH则PH=12(EF+CD)∴PH=12 EC∴△EPC是等腰直角三角形∴EP=CP且EP⊥CP；（3）图3中延长FE交DC延长线于M连MP．∵∠AEM=90°∠EBC=90°∠BCM=90°∴四边形BEMC是矩形．∴BE=CM∠EMC=90°由图（2）可知∵BD平分∠ABC∠ABC=90°∴∠EBF=45°又∵EF⊥AB∴△BEF为等腰直角三角形∴BE=EF∠F=45°．∴EF=CM．∵∠EMC=90°∴MP=12FD=FP．∵BC=EM BC=CD∴EM=CD．∵EF=CM∴EF+EM=CM+DC 即FM=DM又∵FP=DP∠CMP=12∠EMC=45°∴∠F=∠PMC．在△PFE和△PMC中{FP=MP ∠F=∠PMC EF=CM∴△PFE≌△PMC(SAS)．∴EP=CP∠FPE=∠MPC．∵∠FMC=90°MF=MD FP=DP∴MP⊥FD∴∠FPE+∠EPM=90°∴∠MPC+∠EPM=90°即∠EPC=90°∴EP⊥CP．20．（1）解∵ ∵AEF是等腰三角形理由如下∵∵四边形ABCD是正方形∵AB=AD=BC=CD∵BAD=∵B=∵D=90°∵∵ABC∵ADC都是等腰三角形∵∵BAC=∵DAC=45°根据题意得∵∵BAE=∵CAE=22.5° ∵DAF=∵CAF=22.5°(∠BAC+∠DAC)=45°∵BAE=∵DAF=22.5°∵∠EAF=12∵∵B=∵D=90° AB=AD∵∵BAE∵∵DAF（ASA）∵AE=AF∵∵AEF是等腰三角形；（2）解∵ PQ=BP+DQ理由如下∵如图延长CB到T使得BT=DQ．∵AD=AB∵ADQ=∵ABT=90° DQ=BT∵∵ADQ∵∵ABT（SAS）∵AT=AQ∵DAQ=∵BAT由（1）得∵∵P AQ=45°∵∵P AT=∵BAP+∵BAT=∵BAP+∵DAQ=45°∵∵P AT=∵P AQ=45°∵AP=AP∵∵P AT∵∵P AQ（SAS）∵PQ=PT∵PT=PB+BT=PB+DQ∵PQ=BP+DQ；（3）解：如图将∵ADN绕点A顺时针旋转90°得到∵ABR连接RM．∵∵BAD=90° ∵MAN=45°∵∵DAN+∵BAM=45°∵∵DAN=∵BAR∵∵BAM+∵BAR=45°∵∵MAR=∵MAN=45°∵AR=AN AM=AM∵∵AMR∵∵AMN(SAS)∵ RM=MN∵∵D=∵ABR=∵ABD=45°∵∵RBM=90°∵RM2=BR2+BM2∵ DN=BR MN=RM∵BM2+DN2=MN2．∵BM=7DN=24∵MN=√72+242=25．。

专题15 图形变换（平移、旋转、对称）一．选择题1．（2022·山东威海）图1是光的反射规律示意图．其中，PO是入射光线，OQ是反射光线，法线KO⊥MN，∠POK是入射角，∠KOQ是反射角，∠KOQ＝∠POK．图2中，光线自点P射入，经镜面EF反射后经过的点是( )A．A点B．B点C．C点D．D点【答案】B【分析】根据光反射定律可知，反射光线、入射光线分居法线两侧，反射角等于入射角并且关于法线对称，由此推断出结果．【详解】连接EF，延长入射光线交EF于一点N，过点N作EF的垂线NM，如图所示：∠为入射角由图可得MN是法线，PNM因为入射角等于反射角，且关于MN对称∠由此可得反射角为MNB所以光线自点P射入，经镜面EF反射后经过的点是B故选：B．【点睛】本题考查了轴对称中光线反射的问题，根据反射角等于入射角，在图中找出反射角是解题的关键．2．（2022·湖南永州）剪纸是我国具有独特艺术风格的民间艺术，反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中，是中心对称图形的有（ ）① ② ③ ④A ．①②③B ．①②④C ．①③④D ．②③④【答案】A【分析】根据中心对称图形的定义判断即可；【详解】解：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形；∴是中心对称图形的是：①②③；故选：A ．【点睛】本题主要考查中心对称图形的定义，掌握中心对称图形的定义是解题的关键．3．（2022·江苏无锡）雪花、风车…．展示着中心对称的美，利用中心对称，可以探索并证明图形的性质，请思考在下列图形中，是中心对称图形但不一定是轴对称图形的为（ ）A ．扇形B ．平行四边形C ．等边三角形D ．矩形【答案】B【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A 、扇形是轴对称图形，不是中心对称图形，故此选项不合题意；B 、平行四边形不一定是轴对称图形，是中心对称图形，故此选项符合题意；C 、等边三角形是轴对称图形，不是中心对称图形，故此选项不合题意；D 、矩形既是轴对称图形，又是中心对称图形，故此选项不合题意；故选：B ．【点睛】此题主要考查了轴对称图形和中心对称图形的定义，熟练掌握如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心是解题关键．4．（2022·贵州遵义）在平面直角坐标系中，点(),1A a 与点()2,B b -关于原点成中心对称，则a b +的值为（ ）A ．3-B ．1-C ．1D ．3【答案】C【分析】根据关于原点对称的两个点，横坐标、纵坐标分别互为相反数，求得,a b 的值即可求解．【详解】解：∵点(),1A a 与点()2,B b -关于原点成中心对称，∴2,1a b ==-211a b ∴+=-=，故选C ．【点睛】本题考查了关于原点对称的两个点，横坐标、纵坐标分别互为相反数，代数式求值，掌握关于原点对称的两个点，横坐标、纵坐标分别互为相反数是解题的关键．5．（2022·内蒙古赤峰）下列图案中，不是轴对称图形的是（ ）A ．B ．C ．D ．【答案】A【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此判断即可．【详解】A 不是轴对称图形；B 、C 、D 都是轴对称图形；故选：A ．【点睛】本题考查了轴对称图形，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．6．（2022·山东青岛）如图，将ABC 先向右平移3个单位，再绕原点O 旋转180︒，得到A B C ''' ，则点A 的对应点A '的坐标是（ ）A ．(2,0)B ．(2,3)--C ．(1,3)--D ．(3,1)--【答案】C【分析】先画出平移后的图形，再利用旋转的性质画出旋转后的图形即可求解．【详解】解：先画出△ABC平移后的△DEF，再利用旋转得到△A'B'C'，由图像可知A'（-1，-3），故选：C．【点睛】本题考查了图形的平移和旋转，解题关键是掌握绕原点旋转的图形的坐标特点，即对应点的横纵坐标都互为相反数．7．（2022·四川内江）如图，在平面直角坐标系中，点B、C、E在y轴上，点C的坐标为（0，1），AC＝2，Rt△ODE是Rt△ABC经过某些变换得到的，则正确的变换是（ ）A．△ABC绕点C逆时针旋转90°，再向下平移1个单位B．△ABC绕点C顺时针旋转90°，再向下平移1个单位C．△ABC绕点C逆时针旋转90°，再向下平移3个单位D．△ABC绕点C顺时针旋转90°，再向下平移3个单位【答案】D【分析】观察图形可以看出，Rt△ABC通过变换得到Rt△ODE，应先旋转然后平移即可．【详解】解：根据图形可以看出，△ABC绕点C顺时针旋转90°，再向下平移3个单位可以得到△ODE．故选：D．【点睛】本题考查的是坐标与图形变化，旋转和平移的知识，掌握旋转和平移的概念和性质是解题的关键．8．（2022·广西）如图，在△ABC中，点A（3，1），B（1，2），将△ABC向左平移2个单位，再向上平移1个单位，则点B的对应点B′的坐标为（）A．（3，-3）B．（3，3）C．（－1，1）D．（－1，3）【答案】D【分析】根据图形的平移性质求解．【详解】解：根据图形平移的性质，B′（1-2，2+1），即B′（-1，3）；故选：D．【点睛】本题主要考查图形平移的点坐标求解，掌握图形平移的性质是解题的关键．9．（2022·湖南郴州）下列图形既是轴对称图形又是中心对称图形的是（）A．B．C．D．【答案】B【分析】根据轴对称图形和中心对称图形的定义判断即可．【详解】解：A、该图形是轴对称图形，不是中心对称图形，故A选项错误；B、该图形既是轴对称图形，也是中心对称图形，故B选项正确；C、该图形不是轴对称图形，是中心对称图形，故C选项错误；D、该图形既不是轴对称图形，也不是中心对称图形，故D选项错误．故答案为B．【点睛】本题主要考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，中心对称图形是要寻找对称中心旋转180度后与原图重合．10．（2022·广西贵港）若点(,1)A a -与点(2,)B b 关于y 轴对称，则-a b 的值是（ ）A ．1-B ．3-C ．1D ．2【答案】A【分析】根据关于y 轴对称的点，纵坐标相同，横坐标互为相反数解答即可．【详解】∵点(,1)A a -与点(2,)B b 关于y 轴对称，∴a =-2，b =-1，∴a -b =-1，故选A ．【点睛】本题考查了关于y 轴对称的点坐标的关系，代数式求值，解题的关键在于明确关于y 轴对称的点纵坐标相等，横坐标互为相反数．11．（2022·江苏常州）在平面直角坐标系xOy 中，点A 与点1A 关于x 轴对称，点A 与点2A 关于y 轴对称．已知点1(1,2)A ，则点2A 的坐标是（ ）A ．(2,1)-B ．(2,1)--C ．(1,2)-D ．(1,2)--【答案】D【分析】直接利用关于x ，y 轴对称点的性质分别得出A ，2A 点坐标，即可得出答案．【详解】解：∵点1A 的坐标为（1，2），点A 与点1A 关于x 轴对称，∴点A 的坐标为（1，-2），∵点A 与点2A 关于y 轴对称，∴点2A 的坐标是（-1，﹣2）．故选：D ．【点睛】此题主要考查了关于x ，y 轴对称点的坐标，正确掌握关于坐标轴对称点的性质是解题关键．12．（2022·北京）图中的图形为轴对称图形，该图形的对称轴的条数为（ ）A ．1B ．2C ．3D ．5【答案】D 【分析】根据题意，画出该图形的对称轴，即可求解．【详解】解∶如图，一共有5条对称轴．故选：D【点睛】本题主要考查了轴对称图形，熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合，这样的图形就叫做轴对称图形，这条直线叫做对称轴是解题的关键．13．（2022·山东临沂）剪纸艺术是最古老的中国民间艺术之一，先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录．鱼与“余”同音，寓意生活富裕、年年有余，是剪纸艺术中很受喜爱的主题，以下关于鱼的剪纸中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【答案】D【分析】根据轴对称图形和中心对称图形的概念进行判断即可．【详解】A.是轴对称图形，不是中心对称图形，故本选项不合题意；B.不是轴对称图形，是中心对称图形，故本选项不合题意；C.不是轴对称图形，是中心对称图形，故本选项不合题意；D.既是轴对称图形，也是中心对称图形，故本选项符合题意；故选：D．【点睛】本题考查了轴对称图形和中心对称图形的概念，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线(成轴）对称；熟练掌握知识点是解题的关键．14．（2022·山东聊城）如图，在直角坐标系中，线段11A B 是将ABC 绕着点()3,2P 逆时针旋转一定角度后得到的111A B C △的一部分，则点C 的对应点1C 的坐标是（ ）A ．(-2，3)B ．(-3，2)C ．(-2，4)D ．(-3，3)【答案】A 【分析】根据旋转的性质解答即可．【详解】解：∵线段11A B 是将ABC 绕着点()3,2P 逆时针旋转一定角度后得到的111A B C △的一部分，∴A 的对应点为1A ，∴190APA ∠=︒，∴旋转角为90°，∴点C 绕点P 逆时针旋转90°得到的1C 点的坐标为（-2，3），故选：A ．【点睛】本题主要考查了旋转的性质，练掌握对应点与旋转中心的连线是旋转角和旋转角相等是解答本题的关键．15．（2022·湖南）如图，点O 是等边三角形ABC 内一点，2OA =，1OB =，OC =AOB ∆与BOC ∆的面积之和为（ ）AB C D 【答案】C【分析】将AOB ∆绕点B 顺时针旋转60︒得BCD ∆，连接OD ，得到BOD 是等边三角形，再利用勾股定理的逆定理可得90COD ∠=︒，从而求解．【详解】解：将AOB ∆绕点B 顺时针旋转60︒得BCD ∆，连接OD ，OB OD ∴=，60BOD ∠=︒，2CD OA ==，BOD ∴∆是等边三角形，1OD OB ∴==，∵222214OD OC +=+=，2224CD ==，222OD OC CD ∴+=，90DOC ∴∠=︒，AOB ∴∆与BOC ∆的面积之和为21112BOC BCD BOD COD S S S S +=+=+⨯= C ．【点睛】本题主要考查了等边三角形的判定与性质，勾股定理的逆定理，旋转的性质等知识，利用旋转将AOB ∆与BOC ∆的面积之和转化为BOC BCD S S + ，是解题的关键．16．（2022·内蒙古呼和浩特）如图，ABC 中，90ACB ∠=︒，将ABC 绕点C 顺时针旋转得到EDC △，使点B 的对应点D 恰好落在AB 边上，AC 、ED 交于点F ．若BCD α∠=，则EFC ∠的度数是（用含α的代数式表示）（ ）A ．1902α︒+B ．1902α︒-C ．31802α︒-D ．32α【答案】C【分析】根据旋转的性质可得，BC =DC ，∠ACE =α，∠A =∠E ，则∠B =∠BDC ，利用三角形内角和可求得∠B ，进而可求得∠E ，则可求得答案．【详解】解：∵将ABC 绕点C 顺时针旋转得到EDC △，且BCD α∠=∴BC =DC ，∠ACE =α，∠A =∠E ，∴∠B =∠BDC ，∴1809022B BDC αα︒-∠=∠==︒-，∴90909022A E B αα∠=∠=︒-∠=︒-︒+=，∴2A E α∠=∠=，318018018022EFC ACE E ααα∴∠=︒-∠-∠=︒--=︒-，故选：C ．【点睛】本题考查了旋转变换、三角形内角和、等腰三角形的性质，解题的关键是掌握旋转的性质．17．（2022·内蒙古赤峰）如图，点()2,1A ，将线段OA 先向上平移2个单位长度，再向左平移3个单位长度，得到线段''O A ，则点A 的对应点'A 的坐标是（ ）A ．()3,2-B ．()0,4C ．()1,3-D ．()3,1-【答案】C 【分析】根据点向上平移a 个单位，点向左平移b 个单位，坐标P （x ，y ）⇒P （x ，y +a ）⇒P （x +a ，y +b ），进行计算即可．【详解】解：∵点A 坐标为（2，1），∴线段OA 向h 平移2个单位长度，再向左平移3个单位长度，点A 的对应点A ′的坐标为（2-3，1+2），即（-1，3），故选C ．【点睛】此题主要考查了坐标与图形的变化--平移，关键是掌握横坐标，右移加，左移减；纵坐标，上移加，下移减．18．（2022·黑龙江绥化）如图，线段OA 在平面直角坐标系内，A 点坐标为()2,5，线段OA 绕原点O 逆时针旋转90°，得到线段OA '，则点A '的坐标为（ ）A ．()5,2-B ．()5,2C ．()2,5-D ．()5,2-【答案】A 【分析】如图，逆时针旋转90°作出OA '，过A 作AB x ⊥轴，垂足为B ，过A '作A B x ''⊥轴，垂足为B '，证明()A OB BOA AAS '∠ ≌，根据A 点坐标为()2,5，写出5AB =，2OB =，则5OB '=，2A B '=，即可写出点A 的坐标．【详解】解：如图，逆时针旋转90°作出OA '，过A 作AB x ⊥轴，垂足为B ，过A '作A B x ''⊥轴，垂足为B '，∴90A BO ABO ∠'=∠=︒，OA OA '=，∵18090A OB AOB A OA '∠+∠=︒-∠'=︒，90AOB A ∠+∠=︒，∴A OB A ∠'=∠，∴()A OB BOA AAS '∠ ≌，∴OB AB '=，A B OB '=，∵A 点坐标为()2,5，∴5AB =，2OB =，∴5OB '=，2A B '=，∴()5,2A '-，故选：A ．【点睛】本题考查旋转的性质，证明A OB BOA '∠ ≌是解答本题的关键．19．（2022·海南）如图，点(0,3)(1,0)A B 、，将线段AB 平移得到线段DC ，若90,2ABC BC AB ∠=︒=，则点的坐标是（ ）A ．(7,2)B ．(7,5)C ．(5,6)D ．(6,5)【答案】D 【分析】先过点C 做出x 轴垂线段CE ，根据相似三角形找出点C 的坐标，再根据平移的性质计算出对应D 点的坐标．【详解】如图过点C 作x 轴垂线，垂足为点E ，∵90ABC ∠=︒∴90ABO CBE ∠+∠=︒∵90CBE BCE +=︒∠∴ABO BCE Ð=Ð在ABO ∆和BCE ∆中，90ABO BCE AOB BEC =⎧⎨==︒⎩∠∠∠∠ ，∴ABO BCE ∆∆∽，∴12AB AO OB BC BE EC === ，则26BE AO == ,22EC OB ==∵点C 是由点B 向右平移6个单位，向上平移2个单位得到，∴点D 同样是由点A 向右平移6个单位，向上平移2个单位得到，∵点A 坐标为(0，3)，∴点D 坐标为(6，5)，选项D 符合题意，故答案选D【点睛】本题考查了图像的平移、相似三角形的判定与性质，利用相似三角形的判定与性质找出图像左右、上下平移的距离是解题的关键．20．（2022·广西）2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的，展现了运动员不断飞跃，超越自我，奋力拼搏，激励世界的冬残奥精神下列的四个图中，能由如图所示的会徽经过平移得到的是（ ）A ．B ．C ．D ．【答案】D【分析】根据平移的特点分析判断即可．【详解】根据题意，得不能由平移得到，故A 不符合题意；不能由平移得到，故B 不符合题意；不能由平移得到，故C 不符合题意；能由平移得到，故D 符合题意；故选D ．【点睛】本题考查了平移的特点，熟练掌握平移的特点是解题的关键．21．（2022·广西）如图，在ABC 中，4,CA CB BAC α==∠=，将ABC 绕点A 逆时针旋转2α，得到AB C '' ，连接B C '并延长交AB 于点D ，当B D AB '⊥时， 'BB的长是（ ）A B C D 【答案】B【分析】先证'60B AD ∠=︒，再求出AB 的长，最后根据弧长公式求得 'BB．【详解】解：,'CA CB B D AB =⊥ ，12AD DB AB ∴==，AB C '' 是ABC 绕点A 逆时针旋转2α得到，'AB AB ∴=，1'2AD AB =，在'Rt AB D ∆中，1cos ''2AD B AD AB ∠==，'60B AD ∴∠=︒，,'2CAB B AB αα∠=∠= ，11'603022CAB B AB ∴∠=∠=⨯︒=︒，4AC BC == ，cos304AD AC ∴=︒==2AB AD ∴==BB ∴'的长=60180AB π=，故选：B ．【点睛】本题考查了图形的旋转变换，等腰三角形的性质，三角函数定义，弧长公式，正确运算三角函数定义求线段的长度是解本题的关键．22．（2022·内蒙古包头）如图，在Rt ABC 中，90,30,2ACB A BC ∠=︒∠=︒=，将ABC 绕点C 顺时针旋转得到A B C '' ，其中点A '与点A 是对应点，点B '与点B 是对应点．若点B '恰好落在AB 边上，则点A 到直线A C '的距离等于（ ）A ．B ．C ．3D ．2【答案】C【分析】如图，过A 作AQ A C '⊥于,Q 求解4,AB AC == 结合旋转：证明60,,90,B A B C BC B C A CB '''''∠=∠=︒=∠=︒ 可得BB C '△为等边三角形，求解60,A CA '∠=︒ 再应用锐角三角函数可得答案．【详解】解：如图，过A 作AQ A C '⊥于,Q由90,30,2ACB A BC ∠=︒∠=︒=，4,AB AC ∴===结合旋转：60,,90,B A B C BC B C A CB '''''∴∠=∠=︒=∠=︒BB C '∴ 为等边三角形，60,30,BCB ACB ''∴∠=︒∠=︒60,A CA '∴∠=︒sin 60 3.AQ AC ∴=︒== ∴A 到A C '的距离为3．故选C【点睛】本题考查的是旋转的性质，含30︒的直角三角形的性质，勾股定理的应用，等边三角形的判定与性质，锐角三角函数的应用，作出适当的辅助线构建直角三角形是解本题的关键．23．（2022·内蒙古通辽）冬季奥林匹克运动会是世界上规模最大的冬季综合性运动会，下列四个图是历届冬奥会图标中的一部分，其中是轴对称图形的为（ ）A ．B ．C ．D ．【答案】A【分析】根据轴对称图形的定义，即可求解．【详解】解：A 、是轴对称图形，故本选项符合题意；B 、不是轴对称图形，故本选项不符合题意；C 、不是轴对称图形，故本选项不符合题意；D 、不是轴对称图形，故本选项不符合题意；故选：A【点睛】本题主要考查了轴对称图形的定义，熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合，这样的图形就叫做轴对称图形，这条直线叫做对称轴是解题的关键．24．（2022·四川内江）2022年2月第24届冬季奥林匹克运动会在我国北京成功举办，以下是参选的冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是（ ）A ．B ．C ．D ．【答案】C【分析】根据轴对称图形和中心对称图形的定义进行逐一判断即可．【详解】A.不是轴对称图形，也不是中心对称图形，故A 错误；B.不是轴对称图形，也不是中心对称图形，故B 错误；C.既是轴对称图形，也是中心对称图形，故C 正确；D.不是轴对称图形，也不是中心对称图形，故D 错误．故选：C ．【点睛】本题主要考查了中心对称图形和轴对称图形的定义，如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；中心对称图形的定义：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．25．（2022·广西河池）如图，在Rt △ABC 中，90ACB ∠︒＝，6AC ＝，8BC ＝，将Rt ABC 绕点B 顺时针旋转90°得到Rt A B C ''' ．在此旋转过程中Rt ABC 所扫过的面积为( )A ．25π+24B ．5π+24C ．25πD ．5π【答案】A 【分析】根据勾股定理定理求出AB ，然后根据扇形的面积和三角形的面积公式求解．【详解】解：∵90ACB ∠︒＝，6AC ＝，8BC ＝，∴10AB ==，∴Rt ABC 所扫过的面积为2901016825243602ππ⋅⋅+⨯⨯=+．故选：A ．【点睛】本题主要考查了旋转的性质，扇形的面积的计算，勾股定理，熟练掌握扇形的面积公式是解答的关键．26．（2022·上海）有一个正n 边形旋转90 后与自身重合，则n 为（ ）A ．6B ．9C ．12D ．15【答案】C【分析】根据选项求出每个选项对应的正多边形的中心角度数，与90 一致或有倍数关系的则符合题意．【详解】如图所示，计算出每个正多边形的中心角，90 是30 的3倍，则可以旋转得到．A. B. C. D.观察四个正多边形的中心角，可以发现正12边形旋转90°后能与自身重合故选C ．【点睛】本题考查正多边形中心角与旋转的知识，解决本题的关键是求出中心角的度数并与旋转度数建立关系．27．（2022·贵州毕节）矩形纸片ABCD 中，E 为BC 的中点，连接AE ，将ABE △沿AE 折叠得到AFE △，连接CF ．若4AB =，6BC =，则CF 的长是（ ）A ．3B ．175C ．72D ．185【答案】D 【分析】连接BF 交AE 于点G ，根据对称的性质，可得AE 垂直平分BF ，BE =FE ，BG =FG =12BF ，根据E 为BC 中点，可证BE =CE =EF ，通过等边对等角可证明∠BFC =90°，利用勾股定理求出AE ，再利用三角函数（或相似）求出BF ，则根据FC =【详解】连接BF ，与AE 相交于点G ，如图，∵将ABE △沿AE 折叠得到AFE △∴ABE △与AFE △关于AE 对称∴AE 垂直平分BF ，BE =FE ，BG =FG =12BF∵点E 是BC 中点∴BE =CE =DF =132BC =∴5AE ===∵sin BE BG BAE AE AB ∠==∴341255BE AB BG AE ⋅⨯===∴12242225BF BG ==⨯=∵BE =CE =DF ∴∠EBF =∠EFB ，∠EFC =∠ECF∴∠BFC =∠EFB +∠EFC =180902︒=︒∴185FC ==故选 D 【点睛】本题考查了折叠对称的性质，熟练运用对称性质证明相关线段相等是解题的关键．二．填空题28．（2022·山东临沂）如图，在平面直角坐标系中，ABC 的顶点A ，B 的坐标分别是()0,2A ，()2,1B -．平移ABC 得到A B C ''' ，若点A 的对应点A '的坐标为()1,0-，则点B 的对应点B '的坐标是_____________．【答案】()1,3-【分析】根据点A 坐标及其对应点A '的坐标的变化规律可得平移后对应点的横坐标减小1，纵坐标减小2，即可得到答案．【详解】 平移ABC 得到A B C ''' ，点()0,2A 的对应点A '的坐标为()1,0-，∴ABC 向左平移了1个单位长度，向下平移了2个单位长度，即平移后对应点的横坐标减小1，纵坐标减小2，∴()2,1B -的对应点B '的坐标是()1,3-，故答案为：()1,3-．【点睛】本题考查了平移坐标的变化规律，即左减右加，上加下减，熟练掌握知识点是解题的关键．29．（2022·广西贵港）如图，将ABC 绕点A 逆时针旋转角()0180αα︒<<︒得到ADE ，点B 的对应点D 恰好落在BC 边上，若,25DE AC CAD ⊥∠=︒，则旋转角α的度数是______．【答案】50︒【分析】先求出65ADE ∠=︒，由旋转的性质，得到65∠=∠=︒B ADE ，AB AD =，则65ADB ∠=︒，即可求出旋转角α的度数．【详解】解：根据题意，∵,25DE AC CAD ⊥∠=︒，∴902565ADE ∠=︒-︒=︒，由旋转的性质，则65∠=∠=︒B ADE ，AB AD =，∴65ADB B ∠=∠=︒，∴180665550BAD ︒-∠=︒=︒-︒；∴旋转角α的度数是50°；故答案为：50°．【点睛】本题考查了旋转的性质，三角形的内角和定理，解题的关键是熟练掌握旋转的性质进行计算．30.（2022·广西贺州）如图，在平面直角坐标系中，OAB 为等腰三角形，5OA AB ==，点B 到x 轴的距离为4，若将OAB 绕点O 逆时针旋转90︒，得到OA B ''△，则点B '的坐标为__________．【答案】(4,8)-【分析】过B 作BC OA ⊥于C ，过B '作BD x ⊥轴于D ，构建OB D OBC '∆≅∆，即可得出答案．【详解】过B 作BC OA ⊥于C ，过B '作BD x ⊥轴于D ，∴90B DO BCO '∠=∠=︒，∴2390∠+∠= ，由旋转可知90BOB '∠=︒，OB OB '=，∴1290∠+∠=︒，∴13∠=∠，∵OB OB '=，13∠=∠，B DO BCO '∠=∠，∴OB D OBC '∆≅∆，∴B D OC '=，4OD BC ==，∵5AB AO ==，∴3AC ===，∴8OC =，∴8B D '=，∴(4,8)B '-．故答案为：(4,8)-．【点睛】本题考查了旋转的性质以及如何构造全等三角形求得线段的长度，准确构造全等三角形求得线段长度是解题的关键．31．（2022·四川泸州）点()2,3-关于原点的对称点的坐标为________．【答案】()2,3-【分析】根据两个点关于原点对称时，它们的坐标符号相反，可以直接得到答案．【详解】点()2,3-关于原点对称的点的坐标是()2,3-故答案为：()2,3-【点睛】本题主要考查了关于原点对称的点的坐标特点，两个点关于原点对称时，它们的坐标符号相反，即点P （x ，y ）关于原点O 的对称点是P ′（-x ，-y ）．32．（2022·吉林）第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角()0360αα︒<<︒后能够与它本身重合，则角α可以为__________度．（写出一个即可）【答案】60或120或180或240或300（写出一个即可）【分析】如图（见解析），求出图中正六边形的中心角，再根据旋转的定义即可得．【详解】解：这个图案对应着如图所示的一个正六边形，它的中心角3601606︒∠==︒，0360α︒<<︒ ，∴角α可以为60︒或120︒或180︒或240︒或300︒，故答案为：60或120或180或240或300（写出一个即可）．【点睛】本题考查了正多边形的中心角、图形的旋转，熟练掌握正多边形的性质是解题关键．33．（2022·贵州铜仁）如图，在边长为2的正方形ABCD 中，点E 为AD 的中点，将△CDE 沿CE 翻折得△CME ，点M 落在四边形ABCE 内．点N 为线段CE 上的动点，过点N 作NP //EM 交MC 于点P ，则MN +NP 的最小值为________．【答案】8 5【分析】过点M作MF⊥CD于F，推出MN+NP的最小值为MF的长，证明四边形DEMG为菱形，利用相似三角形的判定和性质求解即可．【详解】解：作点P关于CE的对称点P′，由折叠的性质知CE是∠DCM的平分线，∴点P′在CD上，过点M作MF⊥CD于F，交CE于点G，∵MN+NP=MN+NP′≤MF，∴MN+NP的最小值为MF的长，连接DG，DM，由折叠的性质知CE为线段DM的垂直平分线，∵AD=CD=2，DE=1，∴CE∵12CE×DO=12CD×DE，∴DO∴EO∵MF⊥CD，∠EDC=90°，∴DE ∥MF ，∴∠EDO =∠GMO ，∵CE 为线段DM 的垂直平分线，∴DO =OM ，∠DOE =∠MOG =90°，∴△DOE ≌△MOG ，∴DE =GM ，∴四边形DEMG 为平行四边形，∵∠MOG =90°，∴四边形DEMG 为菱形，∴EG =2OE GM = DE =1，∴CG ，∵DE ∥MF ，即DE ∥GF ，∴△CFG ∽△CDE ，∴FG CG DE CE =，即1FG ， ∴FG =35，∴MF =1+35=85，∴MN +NP 的最小值为85．故答案为：85．【点睛】此题主要考查轴对称在解决线段和最小的问题，熟悉对称点的运用和画法，知道何时线段和最小，会运用勾股定理和相似三角形的判定和性质求线段长度是解题的关键．34．（2022·山东潍坊）小莹按照如图所示的步骤折叠A 4纸，折完后，发现折痕AB ′与A 4纸的长边AB 恰好重合，那么A 4纸的长AB 与宽AD 的比值为___________．1【分析】判定△AB ′D ′是等腰直角三角形，即可得出AB AD ，再根据AB ′= AB ，再计算即可得到结论．【详解】解：∵四边形ABCD 是矩形，∴∠D =∠B =∠DAB =90°，由操作一可知：∠DAB ′=∠D ′AB ′=45°，∠AD ′B ′=∠D =90°，AD =AD ′，∴△AB ′D ′是等腰直角三角形，∴AD =AD ′= B ′D ′，由勾股定理得AB ，又由操作二可知：AB ′=AB ，=AB ，∴AB AD ，∴A 4纸的长AB 与宽AD 1：1．【点睛】本题主要考查了矩形的性质以及折叠变换的运用，解题的关键是理解题意，灵活运用所学知识解决问题．35．（2022·山东潍坊）如图，在直角坐标系中，边长为2个单位长度的正方形ABCO 绕原点O 逆时针旋转75︒，再沿y 轴方向向上平移1个单位长度，则点B ''的坐标为___________．【答案】(1)+【分析】连接OB ，OB '由题意可得∠BOB '=75°，可得出∠COB '=30°，可求出B '的坐标，即可得出点B ''的坐标．【详解】解：如图：连接OB ，OB '，作B M '⊥y 轴∵ABCO是正方形，OA=2∴∠COB=45°，OB=∵绕原点O逆时针旋转75︒∴∠BOB'=75°∴∠COB'=30°∵OB'=OB=∴MB'MO∴B'(∵沿y轴方向向上平移1个单位长度∴B''(1)故答案为：(1)【点睛】本题考查了坐标与图形变化﹣旋转，坐标与图形变化﹣平移，熟练掌握网格结构，准确确定出对应点的位置是解题的关键．36．（2022·湖南永州）如图，图中网格由边长为1的小正方形组成，点A为网格线的交点.若线段OA绕原点O顺时针旋转90°后，端点A的坐标变为______．【答案】()2,2-【分析】根据题意作出旋转后的图形，然后读出坐标系中点的坐标即可．【详解】解：线段OA 绕原点O 顺时针旋转90°后的位置如图所示，∴旋转后的点A 的坐标为（2，-2），故答案为：（2，-2）．【点睛】题目主要考查图形的旋转，点的坐标，理解题意，作出旋转后的图形读出点的坐标是解题关键．三．解答题37．（2022·湖南）如图所示的方格纸(1格长为一个单位长度）中，AOB ∆的顶点坐标分别为(3,0)A ，(0,0)O ，(3,4)B ．(1)将AOB ∆沿x 轴向左平移5个单位，画出平移后的△111AO B （不写作法，但要标出顶点字母）；(2)将AOB ∆绕点O 顺时针旋转90︒，画出旋转后的△222A O B （不写作法，但要标出顶点字母）；(3)在（2）的条件下，求点B 绕点O 旋转到点2B 所经过的路径长（结果保留)π．【答案】(1)见解析(2)见解析(3)52π【分析】（1）利用平移变换的性质分别作出A ，O ，B 的对应点1A ，1O ，1B 即可；（2）利用旋转变换的性质分别作出A ，O ，B 的对应点2A ，2O ，2B 即可；（3）利用弧长公式求解即可．(1)解：如图，111A O B ∆即为所求；(2)解：如图，222A O B ∆(即△A 2OB 2）即为所求；(3)解：在Rt AOB ∆中，5OB ==，905253602l ππ∴=⨯⨯=．【点睛】本题考查作图-旋转变换，平移变换，勾股定理、弧长公式等知识，解题的关键是掌握平移变换，旋转变换的性质．38．（2022·湖北荆州）如图，在10×10的正方形网格中，小正方形的顶点称为格点，顶点均在格点上的图形称为格点图形，图中△ABC为格点三角形．请按要求作图，不需证明．(1)在图1中，作出与△ABC全等的所有格点三角形，要求所作格点三角形与△ABC有一条公共边，且不与△ABC重叠；(2)在图2中，作出以BC为对角线的所有格点菱形．【答案】(1)见解析(2)见解析【分析】对于（1），以AC为公共边的有2个，以AB为公共边的有2个，以BC为公共边的有1个，一共有5个，作出图形即可；对于（2），△ABC是等腰直角三角形，以BC为对角线的菱形只有1个，作出图形即可．(1)如图所示．。

2023年春九年级数学中考复习《几何图形变换综合压轴题》专题提升训练（附答案）1．如图，在△ABC中，∠BAC＝90°，AB＝AC，点D为线段AB上一点，线段CD绕点C 逆时针旋转90°能与线段CE重合，点F为AC与BE的交点．（1）若BC＝5，CE＝4，求线段BD的长；（2）猜想BD与AF的数量关系，并证明你猜想的结论；（3）设CA＝3DA＝6，点M在线段CD上运动，点N在线段CA上运动，运动过程中，DN+MN的值是否有最小值，如果有，请直接写出这个最小值；如果没有，请说明理由．2．阅读下列材料，并完成相应的学习任务：图形旋转的应用图形的旋转是全等变换（平移、轴对称、旋转）中重要的变换之一，利用图形旋转中的对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变等性质，可以将一般图形转化成特殊图形，从而达到解决问题的目的．如图1，在Rt△ABC中，∠ACB＝90°，CE平分∠ACB，且AC＝4，BC＝3．过点E作互相垂直的两条直线，即EF⊥ED，EF交AC于点F，ED交BC于点D，求四边形EFCD 的面积．分析：将∠FED以点E为旋转中心顺时针旋转，使得旋转后EF的对应线段所在直线垂直于AC，并且交AC于点M，旋转后ED的对应线段所在直线交BC于点N．则容易证明四边形MENC为正方形．因为∠EMF＝∠END＝90°，ME＝NE，∠MEF＝∠NED，所以△MEF≌△NED，所以S四边形EFCD＝S正方形MENC．学习任务：（1）四边形EFCD的面积等于；（2）如图2，在Rt△ABC中，∠ACB＝90°，①作出△ABC的外接圆O；②作∠ACB的平分线，与⊙O交于点D．要求：尺规作图，不写作法，但保留作图痕迹．（3）在（2）的基础上，若BC+AC＝14，则四边形ACBD的面积等于．3．△ABC为等边三角形，AB＝4，AD⊥BC于点D，点E为AD的中点．（1）如图1，将AE绕点A顺时针旋转60°至AF，连接EF交AB于点G，求证：G为EF中点．（2）如图2，在（1）的条件下，将△AEF绕点A顺时针旋转，旋转角为α，连接BE，H为BE的中点，连接DH，GH．当30°＜α＜120°时，猜想∠DHG的大小是否为定值，并证明你的结论．（3）在△AEF绕点A顺时针旋转过程中，H为BE的中点，连接CH，问线段CH何时取得最大值，请说明理由，并直接写出此时△ADH的面积．4．如图，已知△ABC中，∠ABC＝45°，CD是边AB上的高线，E是AC上一点，连接BE，交CD于点F．（1）如图1，若∠ABE＝15°，BC＝+1，求DF的长；（2）如图2，若BF＝AC，过点D作DG⊥BE于点G，求证：BE＝CE+2DG；（3）如图3，若R为射线BA上的一个动点，以BR为斜边向外作等腰直角△BRH，M 为RH的中点．在（2）的条件下，将△CEF绕点C旋转，得到△CE'F'，E，F的对应点分别为E'，F'，直线MF'与直线AB交于点P，tan∠ACD＝，直接写出当MF'取最小值时的值．5．如图1，已知△ABC中，∠C＝90°，AC＝4，BC＝3，将△ABC绕点B逆时针旋转一定的角度α得到△A1BC1．（1）若α＝90°，则AA1的长为．（2）如图2，若0°＜α＜90°，直线A1C1分别交AB，AC于点G，H，当△AGH为等腰三角形时，求CH的长．（3）如图3，若0°＜α＜360°，M为边A1C1的中点，N为AM的中点，请直接写出CN的最大值．6．问题发现：（1）如图1，在Rt△ABC中，∠ABC＝90°，AB＝6，BC＝8，点D为AB上一点，且AD＝2DB，过点D作DE∥BC，填空：＝，＝；类比探究：（2）如图2，在（1）的条件下将△ADE绕点A逆时针旋转得到△AMN，连接DM，BM，EN，CN，请求出，的值；拓展延伸：（3）如图3，△ABC和△DEF同为等边三角形，且AB＝3EF＝6，连接AD，BE，将△DEF绕AC（DF）的中点O逆时针自由旋转，请直接写出在旋转过程中BE﹣AD的最大值．7．【问题提出】如图1，在等边三角形ABC内部有一点P，P A＝3，PB＝4，PC＝5．求∠APB的度数．【数学思考】当图形中有一组邻边相等时，通过旋转可以将分散的条件集中起来解决问题．【尝试解决】（1）将△APC绕点A逆时针旋转60°，得到△AP'B，连接PP'，则△APP'为等边三角形．∵P'P＝P A＝3，PB＝4，P'B＝PC＝5，∴P'P2+PB2＝P'B2，△BPP'为三角形，∴∠APB的度数为．（2）如图2，在等边三角形ABC外部有一点P，若∠BP A＝30°，求证：P A2+PB2【类比探究】＝PC2．【联想拓展】（3）如图3，在△ABC中，∠BAC＝90°，AB＝AC．点P在直线BC上方且∠APB＝45°，PC＝BC＝2，求P A的长．8．如图（1），已知△ABC中，∠BAC＝90°，AB＝AC；AE是过A的一条直线，且B，C 在AE的异侧，BD⊥AE于D，CE⊥AE于E．（1）求证：BD＝DE+CE；（2）若直线AE绕A点旋转到图（2）位置时（BD＜CE），其余条件不变，问BD与DE，CE的数量关系如何？请给予证明．（3）若直线AE绕A点旋转到图（3）位置时（BD＞CE），其余条件不变，问BD与DE，CE的数量关系如何？请直接写出结果，不需证明；（4）根据以上的讨论，请用简洁的语言表达直线AE在不同位置时BD与DE，CE的数量关系．9．（1）如图1，等腰直角△ABC，∠B＝90°，点D为AC的中点，点E为边AB上的一点，作DE垂直DF交BC于点F，求证：DE＝DF．（2）如图2，等腰直角△ABC，∠B＝90°，点D为AC的中点，点E为边AB上的一点，线段DE绕着点D逆时针旋转90°得到线段DF，求证：点F在线段BC上；（3）如图3，直角△ABC，点D为AC的中点，点E为边AB上的一点，线段DE绕着点D逆时针旋转90°得到线段DF，若AB＝6，BC＝8，①直接写出线段EF＝时，BE的长；②直接写出△ACF是等腰三角形时，BE的长；③直接写出△BEF面积的最大值．10．在平面直角坐标系中，O为原点，点A（﹣4，0），点B（0，3），△ABO绕点B顺时针旋转，得△A'BO'，点A、O旋转后的对应点为A'、O'，记旋转角为α．（1）如图①，α＝90°，边OA上的一点M旋转后的对应点为N，当OM＝1时，点N 的坐标为；（2）在（1）的条件下，当O'M+BN取得最小值时，在图②中画出点M的位置，并求出点N的坐标．（3）如图③，P为AB上一点，且P A：PB＝2：1，连接PO'、P A'，在△ABO绕点B顺时针旋转一周的过程中，△PO'A'的面积是否存在最大值和最小值，若存在，请求出；若不存在，请说明理由．11．如图①，△ABC为直角三角形，∠ACB＝90°，∠BAC＝30°，点D在AB边上，过点D作DE⊥AC于点E，取BC边的中点F，连接DF并延长到点G，使FG＝DF，连接CG．（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答．）问题发现：（1）填空：CE与CG的数量关系是，直线CE与CG所夹的锐角的度数为．探究证明：（2）将△ADE绕点A逆时针旋转，（1）中的结论是否仍然成立，若成立，请仅就图②所示情况给出证明，若不成立，请说明理由；问题解决：（3）若AB＝4，AD＝3，将△ADE由图①位置绕点A逆时针旋转α（0°＜α＜180°），当△ACE是直角三角形时，请直接写出CG的值．12．如图，两直角三角形ABC和DEF有一条边BC与EF在同一直线上，且∠DFE＝∠ACB ＝60°，BC＝1，EF＝2．设EC＝m（0≤m≤4），点M在线段AD上，且∠MEB＝60°．（1）如图1，当点C和点F重合时，＝；（2）如图2，将图1中的△ABC绕点C逆时针旋转，当点A落在DF边上时，求的值；（3）当点C在线段EF上时，△ABC绕点C逆时针旋转α度（0＜α＜90°），原题中其他条件不变，则＝．13．在△ABC中，∠ABC＝45°，AD⊥BC于点D，BE⊥AC于点E，连接DE，将△AED 沿直线AE翻折得到△AEF（点D与点F为对应点），连接DF，过点D作DG⊥DE交BE于点G．（1）如图1，求证：四边形DFEG为平行四边形；（2）如图2，连接CF，若tan∠ABE＝，在不添加任何辅助线与字母的情况下，请直接写出图2中所有正切值等于2的角．14．在△ABC中，∠BAC＝90°，点E为AC上一点，AB＝AE，AG⊥BE，交BE于点H，交BC于点G，点M是BC边上的点．（1）如图1，若点M与点G重合，AH＝2，BC＝，求CE的长；（2）如图2，若AB＝BM，连接MH，∠HMG＝∠MAH，求证：AM＝2HM；（3）如图3，若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN，请直接写出∠AMH、∠NAE、∠MNE之间的角度关系．15．（1）如图1．在Rt△ACB中，∠ACB＝90°，CA＝8，BC＝6，点D、E分别在边CA，CB上，且CD＝3，CE＝4，连接AE，BD，F为AE的中点，连接CF交BD于点G，则线段CG所在直线与线段BD所在直线的位置关系是．（提示：延长CF到点M，使FM＝CF，连接AM）（2）将△DCE绕点C逆时针旋转至图2所示位置时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）将△DCE绕点C逆时针在平面内旋转，在旋转过程中，当B，D，E三点在同一条直线上时，CF的长为．16．在△ABC和△AEF中，∠AFE＝∠ABC＝90°，∠AEF＝∠ACB＝30°，AE＝AC，连接EC，点G是EC中点，将△AEF绕点A顺时针旋转．（1）如图1，若E恰好在线段AC上，AB＝2，连接FG，求FG的长度；（2）如图2，若点F恰好落在射线CE上，连接BG，证明：GB＝AB+GC；（3）如图3，若AB＝3，在△AEF旋转过程中，当GB﹣GC最大时，直接写出直线AB，AC，BG所围成三角形的面积．17．如图，在等腰Rt△ABC中，∠ACB＝90°，点D，E分别在AB，BC上运动，将线段DE绕点E按顺时针方向旋转90°得到线段EF．（1）如图1，若D为AB中点，点E与点C重合，AF与DC相交于点O，求证：OE＝OD；（2）如图2，若点E不与C，B重合，点D为AB中点，点G为AF的中点，连接DG，连接BF，判断线段BF，CE，AD的数量关系并说明理由；（3）如图3，若AB＝4，AD＝3BD，点G为AF的中点，连接CG，∠GDE＝90°，请直接写出CE的长．18．如图，在平面直角坐标系中，点O为坐标原点，点A（x，y）中的横坐标x与纵坐标y 满足+|y﹣8|＝0，过点A作x轴的垂线，垂足为点D，点E在x轴的负半轴上，且满足AD﹣OD＝OE，线段AE与y轴相交于点F，将线段AD向右平移8个单位长度，得到线段BC．（1）直接写出点A和点E的坐标；（2）在线段BC上有一点G，连接DF，FG，DG，若点G的纵坐标为m，三角形DFG 的面积为S，请用含m的式子表示S（不要求写m的取值范围）；（3）在（2）的条件下，当S＝26时，动点P从D出发，以每秒1个单位的速度沿着线段DA向终点A运动，动点Q从A出发，以每秒2个单位的速度沿着折线AB→BC向终点C运动，P，Q两点同时出发，当三角形FGP的面积是三角形AGQ面积的2倍时，求出P点坐标19．如图：直线l1：y＝﹣x+6与x轴交于点A，与y轴交于点B，将△AOB沿直线l1翻折后，设点O的对应点为点C，已知双曲线y＝（x＞0）经过点C．（1）求点A，B的坐标．（2）求k的值．（3）将直线l1绕着点A逆时针旋转得到直线l2．直线l2与y轴交于点B′，将△AOB′沿直线l2翻折得到△AB′C'，当四边形OAC′B′为正方形时停止转动，求转动过程中点C运动到点C′的路径长．20．图形的旋转变换是研究数学相关问题的重要手段之一．小华和小芳对等腰直角三角形的旋转变换进行研究．如图（1），已知△ABC和△ADE均为等腰直角三角形，点D，E分别在线段AB，AC上，且∠C＝∠AED＝90°．（1）观察猜想小华将△ADE绕点A逆时针旋转，连接BD，CE，如图（2），当BD的延长线恰好经过点E时，①的值为；②∠BEC的度数为度；（2）类比探究如图（3），小芳在小华的基础上，继续旋转△ADE，连接BD，CE，设BD的延长线交CE于点F，请求出的值及∠BFC的度数，并说明理由．（3）拓展延伸若AE＝DE＝，AC＝BC＝，当CE所在的直线垂直于AD时，请你直接写出BD 的长．参考答案1．解：（1）在Rt△ABC中，AB＝AC,BC＝5,∴AB＝AC＝BC＝5,由旋转知，CD＝CE＝4,在Rt△ADC中，AD＝＝＝,∴BD＝AB﹣AD＝5﹣；(2)猜想：BD＝2AF,理由：如图1，延长BA至G，使AG＝AB，连接EG，则CG＝CB,∴∠ABC＝∠AGC,在Rt△ABC中，AB＝AC,∴∠ABC＝45°,∴∠AGC＝45°,∴∠BCG＝90°,由旋转知，CD＝CE,∠DCE＝90°＝∠BCG,∴∠BCD＝∠GCE,∴△BCD≌△GCE(SAS),∴BD＝GE,∠CBD＝∠CGE＝45°,∴∠BGE＝∠CGB+∠CGE＝90°＝∠BAC,∴AC∥GE,∴,∴＝,∴EG＝2AF,∴BD＝2AF；(3)存在，如图2，延长DA至P，使AP＝AD，∵∠BAC＝90°,∴点P,点D关于AC对称，∴MN+DN＝MH+PN,过点P作PH⊥CD于H,要使MN+DN最小，则点P,N,M在同一条线上，且PM⊥CD，即MN+DN的最小值为PH，∵CA＝3DA＝6，∴AD＝2,∴DP＝2AD＝4,CD＝＝＝2,连接CP，∴S△CDP＝DP•AC＝CD•PH,∴PH＝＝＝,即DN+MN的最小值为．2．解：（1）如图1中，∵EC平分∠ACB，EM⊥AC，EN⊥BC，∴EM＝EN，∵∠EMC＝∠DNC＝∠MCN＝90°，∴四边形EMCN是矩形，∵EM＝EN，∴四边形EMCN是正方形，设正方形的边长为m，则×AC×BC＝×AC×m+×BC×m，解得m＝，∵EF⊥ED∴∠MEN＝∠FED＝90°，∴∠MEF＝∠NDF，∵∠EMF＝∠END＝90°，∴△EMF≌△END（AAS），∴S四边形EFCD＝S正方形EMCN＝，故答案为：；（2）①如图2中，⊙O即为所求作．②如图2中，射线CD即为所求作．（3）如图2中，过点D作DM⊥CB交CB的延长线于M，DN⊥AC于N．∵∠DMC＝∠DNC＝∠MCN＝90°，∴四边形DMCN是矩形，∵DC平分∠ACB，DM⊥CB，DN⊥AC，∴DM＝DN，∴四边形DMCN是正方形，∴CM＝CN，∵∠ACD＝∠BCD，∴＝，∴DB＝DA，∵DM＝DN，∠DMB＝∠DNA＝90°，∴Rt△DMB≌Rt△DNA（HL），∴BM＝AN，S四边形ACBD＝S正方形DMCN，∴AC+BC＝CM﹣BM+CN﹣AN＝2CM＝14，∴CM＝7，∴S四边形ACBD＝49．故答案为：49．3．（1）证明：∵△ABC是等边三角形，AD⊥BC，∴∠BAD＝∠CAD＝∠BAC＝30°，∵∠EAF＝60°，∴∠GAE＝∠GAF＝30°，∵AE＝AF，∴FG＝EG．（2）解：结论：∠EHD＝120°，是定值．理由：如图2中，连接BF，CE．∵AB＝AC，AD⊥BC，∴BD＝CD，∵BH＝EH，∴DH∥EC，∴∠HDB＝∠ECB，∵FG＝GE，EH＝HB，∴GH∥BF，∴∠EHG＝∠EBF，∵∠EAF＝∠BAC＝60°，∴∠BAF＝∠CAE，∵AF＝AE，AB＝AC，∴△BAF≌△CAE（SAS），∴∠ACE＝∠ABF，∵∠EHD＝∠HDB+∠HBD，∴∠DHG＝∠EHG+∠EHD＝∠EBF+∠HDB+∠HBD＝∠ABF﹣∠ABE+∠ECB+∠ABD+∠ABE＝∠ACE+∠ECB+∠ABD＝∠ACB+∠ABC＝120°．（3）解：如图3中，取AB的中点N，连接AH，HN，CH，CH交AD于M，过点H作HT⊥AD于T．∵EH＝BH，AN＝BN，∴NH为△ABE的中位线，∴HN＝AE＝，∴点H在以N为圆心，为半径的圆上，当C，N，H共线时，CH的值最大，∵△ABC是等边三角形，∴CN⊥AB，∴∠ACM＝∠MCB＝30°，∵AD＝2，∴CN＝AD＝2，在Rt△CMD中，CD＝2，∠MCD＝30°，∴CM＝＝，∴MN＝CN﹣CM＝，∴HM＝HN+MN＝+＝，∴HT＝HM•sin60°＝，∴S△ADH＝•AD•HT＝．4．（1）解：如图1中，过点F作FH⊥BC于H．∵CD⊥AB，∴∠BDC＝90°，∵∠DBC＝45°，∴∠DCB＝90°﹣45°＝45°，∵FH⊥CH，∴∠FHC＝90°，∴∠HFC＝∠HCF＝45°，∴CH＝FH，设FH＝CH＝m，∵∠ABE＝15°，∴∠FBC＝45°﹣15°＝30°，∴BH＝HF＝m，∴m+m＝+1，∴m＝1，∴CF＝CH＝，∵CD＝BC＝，∴DF＝CD﹣CF＝﹣＝．（2）证明：如图2中，连接DE，过点D作DH⊥DE交BE于H．∵∠ADC＝∠FDB＝90°，DB＝DC，BF＝AC，∴Rt△BDF≌Rt△CDA（HL），∴∠DBF＝∠ACD，∵∠BFD＝∠CFE，∴△BFD∽△CFE，∴＝，∴＝，∵∠DFE＝∠BFC，∴△DFE∽△BFC，∴∠DEF＝∠BCF＝45°，∵DH⊥DE，∴∠HDE＝90°，∴∠DHE＝∠DEH＝45°，∴DH＝DE，∵∠BDC＝∠EDH＝90°，∴∠BDH＝∠CDE，∵DB＝DC，DH＝DE，∴△BDH≌△CDE（SAS），∴BH＝EC，∵DH＝DE，DG⊥EH，∴GH＝EG，∴DG＝EH，∴BE＝BH+HE＝EC+2DG．（3）解：如图3中，过点M作MJ⊥BC于J，过点P作PK⊥BC于K．∵△BHR，△DBC都是等腰直角三角形，∴∠DBC＝∠HBR＝45°，∴∠HBC＝90°，∵∠H＝∠HBJ＝∠MJB＝90°，∴四边形BHMJ是矩形，∴BH＝MJ，HM＝BJ，∵BH＝HR，HM＝MR，∴MJ＝2BJ，∴tan∠MBJ＝＝2，∴点M的在射线BM上运动，∴当C，F′，M共线，且CM⊥BM时，F′M的值最小．设AD＝m，∵tan∠ACD＝＝，∴CD＝BD＝3m，DF＝AD＝m，CF＝CF′＝2m，BC＝3m，∵∠CMB＝90°，tan∠CBM＝＝2，∴BM＝m，CM＝m，∴BJ＝HM＝m，JM﹣BH＝HR＝m，∴MR＝m，设BK＝PK＝n，CK＝2n，∴n＝m，∴BK＝PK＝m，CK＝2m，PC＝m，∴PF′＝PC﹣CF′＝m﹣2m，∴＝＝．5．解：（1）∵∠C＝90°，AC＝4，CB＝3，∴AB＝＝＝5，∵α＝90°，∴△ABA1是等腰直角三角形，AA1＝AB＝5．故答案为：5．（2）如图2﹣1中，当AG＝AH时，∵AG＝AH，∴∠AHG＝∠AGH，∵∠A＝∠A1，∠AGH＝∠A1GB，∴∠AHG＝∠A1BG，∴∠A1GB＝∠A1BG，∴AB＝AG＝5，∴GC1＝A1G﹣C1G＝1，∵∠BC1G＝90°，∴BG＝＝＝，∴AH＝AG＝AB﹣BG＝5﹣，∴CH＝AC﹣AH＝4﹣（5﹣）＝﹣1．如图2﹣2中，当GA＝GH时，过点G作GM⊥AH于M．同法可证，GB＝GA1，设GB＝GA1＝x，则有x2＝32+（4﹣x）2，解得x＝，∴BG＝，AG＝5﹣＝，∵GM∥BC，∴＝，∴＝，∴AM＝，∵GA＝GH，GM⊥AH，∴AM＝HM，∴AH＝3，∴CH＝AC﹣AM＝1．综上所述，满足条件的CH的值为﹣1或1．（3）如图3中，取AB的中点J，连接BM，CJ，JN．∵AJ＝BJ，∠ACB＝90°，∴CJ＝AB＝，∵BC1＝BC＝3，MC1＝MA1＝2，∠BC1M＝90°，∴BM＝＝＝，∵AJ＝BJ，AN＝NM，∴JN＝BM＝，∵CN≤CJ+JN，∴CN≤，∴CN的最大值为．6．解：（1）如图1中，在Rt△ABC中，，∵AD＝2DB，∴AB＝AD+DB＝3DB，∵DE∥BC，∴，∵，∴，即，∴，故答案为：，．（2）由旋转性质可知：AD＝AM，AE＝AN，∠BAM＝∠CAN，∵，∠BAM＝∠CAN，∴△ABM∽△ACN，∴，∠ABM＝∠ACN，∵，∠ABM＝∠ACN，∴△DBM∽△ECN，∴．（3）如图3中，连接OB，OE，由三线合一性质可知∠BOC＝∠DOE＝90°，∴∠BOD＝∠COE，∴∠AOB+∠BOD＝∠BOC+∠COE，即∠AOD＝∠BOE，∵，∠AOD＝∠BOE，∴△AOD∽△BOE，∴，∵AB＝3EF＝6，∴，，在△BOE中，由三边关系可得，BE＜BO+OE，当B、O、E三点共线时，BE存在最大值为，∵，∴当BE存在最大值时，BE﹣AD的最大值＝．7．（1）解：如图1，将△APC绕点A逆时针旋转60°，得到△AP′B，连接PP′，则△APP′为等边三角形．∵PP′＝P A＝3，PB＝4，P′B＝PC＝5，∴P′P2+PB2＝P′B2．∴△BPP′为直角三角形．∴∠APB的度数为90°+60°＝150°．故答案为：直角；150°．（2）证明：如图2中，将△P AB绕点B逆时针旋转60°得到△TCB，连接PT．∵BP＝BT，∠PBT＝60°，∴△PBT是等边三角形，∴PT＝PB，∠PTB＝60°，由旋转的性质可知：△P AB≌△TCB，∴∠APB＝∠CTB＝30°，P A＝CT，∴∠PTC＝∠PTB+∠CTB＝60°+30°＝90°，∴PC2＝PT2+CT2，∵PB＝PT，P A＝CT，∴P A2+PB2＝PC2．（3）解：过点C作CT⊥PB于T，连接AT，设CT交AB于O．∵PC＝BC＝2，CT⊥PB，∴PT＝BT，∵∠CAO＝∠BTO＝90°，∠AOC＝∠BOT，∴∠ACT＝∠ABP，∠ATC＝∠ABC＝45°，∵∠CTB＝90°，∴∠ATP＝∠CTA＝∠APT＝45°∵AC＝AB，∴△CAT≌△BAP（AAS），∴CT＝PB＝2PT，∵PC2＝PT2+CT2，∴（2）2＝m2+（2m）2，解得m＝2或﹣2（舍弃），∴PT＝2，∴P A＝PT＝．8．解：（1）∵BD⊥AE，CE⊥AE，∴∠ADB＝∠CEA＝90°，∴∠ABD+∠BAD＝90°，又∵∠BAC＝90°，∴∠EAC+∠BAD＝90°，∴∠ABD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（AAS），∴BD＝AE，AD＝EC，∴BD＝DE+CE．（2）∵BD⊥AE，CE⊥AE，∴∠ADB＝∠CEA＝90°，∴∠ABD+∠BAD＝90°，又∵∠BAC＝90°，∴∠EAC+∠BAD＝90°，∴∠ABD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（AAS），∴BD＝DE﹣CE．（3）同（2）的方法得出，BD＝DE﹣CE．（4）归纳：由（1）（2）（3）可知：当B，C在AE的同侧时，BD＝DE﹣CE．当B，C在AE的异侧时，BD＝DE+CE．9．（1）证明：如图1中，连接BD．∵△ABC是等腰直角三角形，AD＝DC，∴BD⊥AC，BD＝DA＝DC，∴BD⊥AC，∵ED⊥DF，∴∠EDF＝∠BDC＝90°，∴∠EDB＝∠FDC，∵∠DBE＝∠C＝45°，∴△EDB≌△FDC（ASA），∴DE＝DF．（2）证明：如图2中，连接DB，CF．∵∠BDC＝∠EDF＝90°，∴∠BDE＝∠CDF，∵DB＝DC，DE＝DF，∴△EDB≌△FDC（SAS），∴∠DBE＝∠DCF＝45°，∴点F在线段BC上．（3）①如图3﹣1中，过点D作DT⊥AB于T．∵∠ATD＝∠ABC＝90°，∴DT∥CB，∵AD＝DC，∴AT＝TB＝3，∴DT＝BC＝4，∵△DEF是等腰直角三角形，EF＝，∴DE＝DF＝，∴ET＝＝＝1，∴BE＝TB+ET＝3+1＝4，当点E在点T的下方时，BE＝3﹣1＝2，综上所述，满足条件的BE的值为4或2．②如图3﹣2中，∵△ACF是等腰三角形，又∵AD＝DC＝DF，∴∠AFC＝90°，∴△AFC是等腰直角三角形，∴点E与A重合，∴BE＝6．③如图3﹣3中，过点D作DT⊥AB于T，过点F作FR⊥DT于R．∵∠DTE＝∠FRD＝90°，∠EDT＝∠DFR，DE＝DF，∴△DTE≌△FRD（AAS），∴ET＝DR，DT＝FR＝4，设ET＝DR＝m，则RT＝4﹣m，∴S△EFB＝（3+m）（4﹣m）＝（﹣m2+m+12）＝﹣（m﹣）2+，∵﹣＜0，∴△BEF的面积有最大值，最大值为．10．解：（1）∵点A（﹣4，0），点B（0，3），∴OA＝4，OB＝3，由旋转的性质可知，BO＝BO′＝3，OM＝O′N＝1，∠OBO′＝90°，∴N（﹣3，4）．故答案为：（﹣3，4）．（2）如图②中，∵BM＝BN，∴O′M+BN＝O′M+BM，作点B关于OA的对称点B′，连接O′B′交OA于M，连接BM，O′M+BM的值最小．∵O′（﹣3，3），B′（0，﹣3），∴直线O′B′的解析式为y＝﹣2x﹣3，∴M（﹣，0），∴O′N＝OM＝，∴N（﹣3，）．（3）存在．理由：如图③﹣1中，当点O′落在AB的延长线上时，△PO′A′的面积最大．由题意，OA＝4，OB＝3，∴AB＝＝＝5，∴P A：PB＝2：1，∴PB＝，∴PO′＝PB+PO′＝，∴△PO′A′的面积的最大值＝×4×＝．如图③﹣2中，当点O′落在AB上时，△PO′A′的面积最小，最小值为×4×（3﹣）＝．11．解：（1）如图①中，过点D作DT⊥BC于T．∵DE⊥AC，∴∠DEC＝∠ECT＝∠DTC＝90°，∴四边形ECTD是矩形，∴DT＝EC，DT∥AC，∴∠TDB＝∠A＝30°，∴DT＝BD，∵FC＝FB，∠CFG＝∠BFD，FG＝FD，∴△CFG≌△BFD（SAS），∴CG＝BD，∠FCG＝∠B＝60°，∴EC＝CG，∴∠ACG＝90°+60°＝150°，∴直线CE与CG所夹的锐角的度数为30°，故答案为：EC＝CG，30°．（2）成立．理由如下：连接CD，BG，延长BD交CE的延长线于H，设BH交AC于点O．在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝30°，∴cos∠BAC＝＝，cos∠EAD＝＝，∠EAC＝∠DAB，∴＝＝，∴△ACE∽△ABD，∴＝＝，∠ACE＝∠ABD，∵∠HOC＝∠AOB，∴∠H＝∠OAB＝30°，∵CF＝FB，DF＝FG，∴四边形DCGB是平行四边形，∴CG＝BD，CG∥BH，∴∠1＝∠H＝30°，∴EC＝CG，直线CE与CG所夹的锐角的度数为30°．（3）如图③﹣1中，当∠AEC＝90°时，由题意AC＝AB＝2，AE＝AD＝，∴EC＝＝＝，∴CG＝EC＝，如图③﹣2中，当∠EAC＝90°时，可得EC＝＝，∴CG＝EC＝5．综上所述，CG的值为或5．12．解：（1）由题意得，在Rt△ABC中，∠ABC＝90°，∠ACB＝60°，BC＝1，∴AC＝2，BC＝，在Rt△DEC中，∠DEC＝90°，∠DCE＝60°，EF＝2，∴DC＝4，DE＝2，∴∠DCA＝180°﹣∠DCE﹣∠ACB＝60°，∴AC＝EF，∠DCE＝∠DCA，DC＝DC，∴△DEF≌△DAC（SAS），∴AD＝DE＝2，∠EDC＝∠CDA＝30°，∵∠MEC＝60°，∴∠DEM＝30°，∴∠DME＝180°﹣∠DEM﹣∠EDM＝180°﹣∠DEM﹣2∠EDC＝90°，∴DM＝DE＝，∴AM＝AD﹣DM＝，∴＝1，故答案为：1；（2）如图2，连接AE，∵AC＝EF＝2，∠ACE＝60°，∴△AEC是等边三角形，∴AE＝2，∠EAC＝∠AEC＝60°，∴∠AEB+∠BEC＝∠AEC＝60°，∵∠MEB＝60°，∴∠AEB+∠MEA＝60°，∴∠BEC＝∠MEA，∵∠DAE＝∠ECB＝120°，AE＝EC，∴△AME≌△CBE（ASA），∴AM＝BC＝1，∵AD＝DC﹣AC＝2，∴DM＝AD﹣AM＝1，∴＝1；（3）如图3，过点B作BG⊥BE交EM延长线于点G，连接AG，BG，∵∠CBA＝∠EBG＝90°，∴∠EBC＝∠GBA，∵∠MEB＝∠ACB＝60°，∴，∴△ECB∽△GAB，∴，∠AGB＝∠CEB，∴AG＝m，∵∠CEB+∠DEG＝30°，∠AGB+∠EGA＝30°，∴∠AGM＝∠DEM，∴AG∥DE，∴△AGM∽△DEM，∴，∵DE＝EF＝2，∴＝＝．故答案为：．13．（1）证明：如图1中，∵∠ABC＝45°，AD⊥BC于点D，∴∠BAD＝90°﹣∠ABC＝45°，∴△ABD是等腰直角三角形，∴AD＝BD，∵BE⊥AC，∴∠GBD+∠C＝90°，∵∠EAD+∠C＝90°，∴∠GBD＝∠EAD，∵∠ADB＝∠EDG＝90°，∴∠ADB﹣∠ADG＝∠EDG﹣∠ADG，即∠BDG＝∠ADE，∴△BDG≌△ADE（ASA），∴BG＝AE，DG＝DE，∵∠EDG＝90°，∴△EDG为等腰直角三角形，∴∠AED＝∠AEB+∠DEG＝90°+45°＝135°，∵△AED沿直线AE翻折得△AEF，∴△AED≌△AEF，∴∠AED＝∠AEF＝135°，ED＝EF，∴∠DEF＝360°﹣∠AED﹣∠AEF＝90°，∴△DEF为等腰直角三角形，∴∠GDE＝∠DEF＝90°，DG＝DE＝EF，∴DG∥EF，∴四边形DFEG是平行四边形．（2）解：如图2中，设AD交BE于P，过点P作PT⊥AB于T．∵tan∠ABE＝＝，∴可以假设PT＝a，BT＝3a，∵△ABD是等腰直角三角形，∴∠P AT＝45°，∵PT⊥AB，∴∠ATP＝90°，∴∠P AT＝∠APT＝45°，∴AT＝PT＝a，∴P A＝a，AB＝4a，AD＝BD＝2a，∴P A＝PD＝a，∴tan∠BPD＝＝2，∵BE⊥AC，∴∠ADC＝∠PEC＝90°，∴∠EPD+∠ACD＝180°，∵∠EPD+∠BPD＝180°，∴∠BPD＝∠ACD，根据对称性可知，∠ACD＝∠ACF，∠ADF＝∠AFD，AC⊥DF，∴∠ACD＝∠ACF＝∠BPD，∵∠ADF+∠CDF＝90°，∠CDF+∠ACD＝90°，∴∠ADF＝∠ACD，∴∠ACD＝∠ACF＝∠ADF＝∠AFD＝∠BPD，∴正切值等于2的角有：∠ACD，∠ACF，∠ADF，∠AFD．14．解：（1）∵∠BAC＝90°，AB＝AE，∴△BAE为等腰直角三角形，∵AG⊥BE，∴AH是△BAE的中线，∴BE＝2AH＝4，∵∠BEA＝45°，∴∠BEC＝135°，在△BCE中，过点C作CD⊥BE交BE的延长线于点D，如图1，∵∠DEC＝45°，∴△DEC是等腰直角三角形，设ED＝x，则DC＝x，CE＝x，在Rt△BCD中，BC2＝BD2+DC2，即，∴x1＝1或x2＝﹣5（舍去），∴CE＝；（2）如图2，过H作HD⊥HM交AM于点D，连接BD，∵AB＝AE，∠BAC＝90°，∴△ABE是等腰直角三角形，∵AG⊥BE，∴△ABH为等腰直角三角形，∴BH＝AH，∠BAN＝45°，∠BHA＝90°，∵AB＝BM，∴∠BAM＝∠BMA，∵∠HMG＝∠MAH，∴∠BAM﹣∠MAH＝∠BMA﹣∠HMG，即∠BAH＝∠AMH＝45°，∵HD⊥HM，∴△DHM为等腰直角三角形，∴DH＝HM，∠DHM＝90°，∵∠BHD＝∠BHA+∠AHD，∠AHM＝∠DHM+∠AHD，∴∠BHD＝∠AHM，在△BHD与△AHM中，，∴△BHD≌△AHM（SAS），∴∠DBH＝∠MAH，BD＝AM，∴∠BHA＝∠BDA＝90°，∵BA＝BM，∴D是AM的中点，∴AM＝2DM＝2HM，即AM＝2HM；（3）∵H是BE的中点，M是BC的中点，∴MH是△BCE的中位线，∴MH∥CE，∴∠AMH＝∠MAC，∵∠BAC＝90°，∴AM＝BM，∴∠MAB＝∠ABM，∵点B与点N关于线段AM对称，∴∠ABM＝∠ANM，AB＝AN，∴AE＝AN，∴∠AEN＝∠ANE，在△AEN中，∠NAE+2∠ANE＝180°①，∵∠ANE＝∠ANM+∠MNE，∠ABM＝∠ANM＝∠MAB＝90°﹣∠MAC，∴∠ANE＝90°﹣∠MAC+∠MNE，∴∠ANE＝90°﹣∠AMH+∠MNE②，将②代入①，得：∠NAE+2×（90°﹣∠AMH+∠MNE）＝180°，∴∠NAE+180°﹣2∠AMH+2∠MNE＝180°，∴∠NAE+2∠MNE＝2∠AMH．15．解：（1）结论：CG⊥BD．理由：延长CF到点M，使得FM＝CF，连接AM．∵F A＝FE，∠AFM＝∠EFC，FM＝FC，∴△AMF≌△ECF（SAS），∴AM＝CE＝4，∠AMF＝∠ECF，∴AM∥CE，∴∠MAC＝∠DCB＝90°，∵＝＝，∴△MAC∽△DCB，∴∠DBC＝∠ACM，∵∠ACM+∠GCB＝90°，∴∠DBC+∠GCB＝90°，∴∠CGB＝90°，∴CG⊥BD．故答案为：CG⊥BD．（2）结论仍然成立．理由：延长CF到点M，使得FM＝CF，连接AM．∵F A＝FE，∠AFM＝∠EFC，FM＝FC，∴△AMF≌△ECF（SAS），∴AM＝CE＝4，∠AMF＝∠ECF，∴AM∥CE，∴∠MAC+∠ACE＝180°，∴∠MAC＝180°﹣∠ACE，∵∠DCB＝∠DCE+∠ACB﹣∠ACE＝90°+90°﹣∠ACE＝180°﹣∠ACE，∴∠MAC＝∠DCB，∵＝＝，∴△MAC∽△DCB，∴∠DBC＝∠ACM，∵∠ACM+∠GCB＝90°，∴∠DBC+∠GCB＝90°，∴∠CGB＝90°，∴CG⊥BD．（3）如图3中，当点E在线段BD上时，∵△AMC∽△CDB，∴＝＝，在Rt△DCE中，CD＝3，CE＝4，∴DE＝＝＝5，∵CG⊥DE，∴CG＝＝，在Rt△CGB中，CB＝6，CG＝中，∴BG＝＝＝，在Rt△DCG中，DG＝＝＝，∴BD＝BG+DG＝，∴CM＝BD＝，∴CF＝CM＝如图4中，当点E在线段BD的延长线上时，同法可得CF＝CM＝．综上所述，满足条件的CF的值为或．16．（1）解：如图1中，过点F作FH⊥AE于H．在Rt△ABC中，∠ACB＝90°，AB＝2，∠C＝30°，∴AC＝2AB＝4，BC＝AB＝2，∵AE＝EC＝AC＝2，EG＝GC，∴EG＝CG＝1，∵∠AFE＝90°，∠AEF＝30°，∴EF＝AE•cos30°＝，∴FH＝EF＝，HE＝FH＝，∴GH＝HE+EG＝，∴FG＝＝＝．（2）证明：如图2中，取AC的中点M，连接BM，GM，BF．∵AM＝MC，∠ABC＝90°，∴BM＝AM＝CM，∵AC＝2AB，∴AB＝AM＝BM，∴∠BAM＝∠AMB＝∠ABM＝60°，∴∠BMC＝120°，∵AE＝2AF，∠EAF＝60°，∴∠BAF＝120°+∠EAC，∵AM＝MC，EG＝GC，∴GM＝AE＝AF，GM∥AE，∴∠CMG＝∠EAC，∴∠BMG＝120°+∠CMG＝120°+∠EAC＝∠BAF，∴△BAF≌△BMG（SAS），∴∠ABF＝∠MBG，BF＝BG，∴∠FBG＝∠ABM＝60°，∴△BFG是等边三角形，∴BG＝FG，∴BG＝EF+EG＝AE+CG＝AB+CG．（3）解：如图3中，取AC的中点M，连接BM，GM，BF．在MC上取一点D，使得MD＝MG，连接DG，BD．同法可证：△BAF≌△BMG（SAS），∴∠ABF＝∠MBG，BF＝BG，∴∠FBG＝∠ABM＝60°，∴△BFG是等边三角形，∴BG＝FG，∵AM＝CM，EG＝CG，∴MG＝AE，∵AB＝3，∠ABC＝90°，∠ACB＝30°，∴AC＝2AB＝6，AM＝CM＝3，∵AE＝AC＝3，MG＝，∴MD＝MG＝，∵＝＝，∠DMG＝∠GMC，∴△MDG∽△MGC，∴＝＝，∴DG＝CG，∴GB﹣CG＝GB﹣DG≤BD，∴当B，D，G共线时，BG﹣CG的值最大，最大值为BD的长，∴直线AB，AC，BG围成的三角形为△ABD，∵AD＝AM+DM＝3+＝，∴S△ABD＝××＝，∴当GB﹣GC最大时，直线AB，AC，BG所围成三角形的面积为．17．（1）证明：如图1中，∵CA＝CB，∠ACB＝90°，AD＝DB，∴CD⊥AB，CD＝AD＝DB，∵∠DEF＝∠ADC＝90°，DE＝EF，∴AD＝EF，∵∠AOD＝∠EOF，∴△AOD≌△FOE（AAS），∴OE＝OD．（2）解：结论：AD﹣BF＝CE．理由：如图2中，过点E作ET⊥BC交AB于T，过点T作TR⊥AC于R．则四边形ECRT 是矩形，△ART，△EBT都是等腰直角三角形，可得EC＝RT，AT＝RT＝EC．∵∠TEB＝∠DEF＝90°，∴∠TED＝∠BEF，∵ET＝EB，ED＝EF，∴△TED≌△BEF（SAS），∴DT＝BF，∵AD﹣DT＝AT，∴AD﹣BF＝CE．（3）解：如图3中，取AB的中点R，连接GR，BF，过点E作EM⊥AB于M．设GR ＝x，EM＝BM＝y．由（2）可知，△TED≌△BEF（SAS），∴∠ETD＝∠EBF＝45°，∴∠ABC＝45°，∴∠FBA＝90°，∵AG＝GF，AR＝RB＝2，∴GR∥BF，BF＝2GR＝2x，∴∠GRA＝∠FBA＝90°，∵GR⊥AB，∵AB＝4，AD＝3BD，∴AD＝3，BD＝，∴DR＝AD﹣AR＝3﹣2＝，∵∠GRD＝∠EMD＝∠EDG＝90°，∴∠GDR+∠DGR＝90°，∠GDR+∠EDM＝90°，∴∠DGR＝∠EDM，∴△DRG∽△EMD，∴＝，∴＝①又∵AD﹣BF＝CE，∴3﹣2x＝（4﹣y）②，由①②可得y＝（不合题意的解已经舍弃）．∴EC＝4﹣（）＝．18．解：（1）∵+|y﹣8|＝0，又∵≥0，|y﹣8|≥0，∴x＝2，y＝8，∴A（2，8），∵AD⊥x轴，∴OD＝2，AD＝8，∵AD﹣OD＝OE，∴OE＝6，∴E（﹣6，0）．（2）如图1中，连接OG．由题意G（10，m）．∵AD＝DE＝8，∠ADE＝90°，∴∠AED＝45°，∴∠OEF＝∠OFE＝45°，∴OE＝OF＝6，∴F（0，6），∴S＝S△ODG+S△OFG﹣S△OFD＝×2×m+×6×10﹣×2×6＝m+24（0≤m≤8）．（3）如图2中，设FG交AD于J，P（2，t），当点P在DJ上，点Q在AB上时，当S＝26时，m＝2，∴G（10，2），∵F（0，6），∴直线FG的解析式为y＝﹣x+6，∴J（2，），由题意，•（﹣t）×10＝2××2t×6，解得t＝，∴P（2，），当点P在AJ上，点Q在BG上时，同法可得，•（t﹣）×10＝2××（14﹣2t）×8，解得t＝，∴P（2，）．综上所述，满足条件的点P的坐标为（2，）或（2，）．19．解：（1）当x＝0时，y＝6，∴B（0，6），当y＝0时，﹣x+6＝0，∴x＝6，∴A（6，0）；（2）如图1，过点C作CM⊥x轴于M，Rt△ABO中，OA＝6，OB＝6，∴AB＝＝12，∴∠ABO＝30°，由翻折得：∠ABC＝∠ABO＝30°，∠AOB＝∠ACB＝90°，AC＝OA＝6，∴∠CAM＝60°，∴∠ACM＝90°﹣60°＝30°，∴AM＝AC＝3，CM＝3，∴C（9，3），∴k＝9×3＝27；（3）分两种情况：①如图2，当点B'在y轴的负半轴上时，。

中考专题1 图形变换压轴题汇总（28道题）后附答案详解1．（2017•黑龙江）已知：△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°．连接AD，BC，点H为BC中点，连接OH．（1）如图1所示，易证：OH=AD且OH⊥AD（不需证明）（2）将△COD绕点O旋转到图2，图3所示位置时，线段OH与AD又有怎样的关系，并选择一个图形证明你的结论．2．（2017•连云港四模）阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．操作与证明：（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；猜想与发现：根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？3．（2017•金乡县模拟）请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PC是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为，问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．4．（2017•滦县模拟）两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为和位置关系为；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．5．（2017•路北区三模）如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．（1）求证：△AEC≌△ADB；（2）若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．6．（2017•平房区二模）如图，正方形ABCD，点E在AD上，将△CDE绕点C顺时针旋转90°至△CFG，点F，G分别为点D，E旋转后的对应点，连接EG，DB，DF，DB与CE交于点M，DF与CG交于点N．（1）求证BM=DN；（2）直接写出图中已经存在的所有等腰直角三角形．7．（2017•路南区一模）如图①，△ABC中，AC=BC，∠A=30°，点D在AB边上且∠ADC=45°．（1）求∠BCD的度数；（2）将图①中的△BCD绕点B顺时针旋转得到△BC′D′．当点D′恰好落在BC边上时，如图②所示，连接C′C并延长交AB于点E．①求∠C′CB的度数；②求证：△C′BD'≌△CAE．8．（2017•沙坪坝区一模）已知△ABC和△DEB都是等腰直角三角形，∠BAC=∠EDB=90°．（1）如图1，若点E，B，C在同一直线上，连接AE，当∠AEC=30°，BC=4时，求EB的长；（2）如图2，将图1中的△DEB绕点B顺时针旋转，当点C在ED的延长线上时，EC交AB 于点H，求证：∠EAH=2∠HCB．9．（2017•重庆模拟）已知等腰Rt△ABC与等腰Rt△CDE，∠ACB=∠DCE=90°，把Rt△ABC 绕点C旋转．（1）如图1，当点A旋转到ED的延长线时，若BC=，BE=5，求CD的长；（2）当Rt△ABC旋转到如图2所示的位置时，过点C作BD的垂线交BD于点F，交AE于点G，求证：BD=2CG．10．（2017•河北区模拟）如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．（1）求证：△PMN为等腰直角三角形；（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP，BD 分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．11．（2017•吉安模拟）两块全等的三角板ABC和EDC如图（1）放置，AC=CB，CE=CD，∠ACB=∠ECD=90°，且AB与CE交于F，ED与AB、BC分别交于M、H，△ABC不动，将△EDC 绕点C旋转到如图（2），当∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．12．（2017•江津区校级三模）如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．（1）如图①，当点D在AB上，点E在AC上时，请判断线段CF，DF有怎样的数量关系和位置关系？为什么？（2）如图②，将图①中的△ADE绕点A旋转到图②位置时，请判断（1）中的结论是否仍然成立？并证明你的判断．13．（2017•济宁二模）将两块全等的三角板如图1摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．（1）将图1中△A1B1C绕点C顺时针旋转45°得图2，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；（2）在图2中，若AP1=a，则CQ等于多少？（3）将图2中△A1B1C绕点C顺时针旋转到△A2B2C（如图3），点P2是A2C与AP1的交点．当旋转角为多少度时，有△AP1C∽△CP1P2？这时线段CP1与P1P2之间存在一个怎样的数量关系？．14．（2017•常德）如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．（1）如图1，若BD=BA，求证：△ABE≌△DBE；（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．15．（2017•杭州）如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．（1）求证：△ADE∽△ABC；（2）若AD=3，AB=5，求的值．16．（2017•天水）△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF 的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=2，CQ=9时BC的长．17．（2017•深圳模拟）如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE=AB，点P从点D出发，以每秒1个单位长度沿D→C→B向终点B运动，直线EP交AD于点F，过点F作直线FG⊥DE于点G，交AB于点R．（1）求证：AF=AR；（2）设点P运动的时间为t，①求当t为何值时，四边形PRBC是矩形？②如图2，连接PB．请直接写出使△PRB是等腰三角形时t的值．18．（2017•惠阳区模拟）把Rt△ABC和Rt△DEF按如图（1）摆放（点C与E重合），点B、C（E）、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF 移动的同时，点P从△ABC的顶点A出发，以2cm/s的速度沿AB向点B匀速移动；当点P 移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t（s）．（1）用含t的代数式表示线段AP和AQ的长，并写出t的取值范围；（2）连接PE，设四边形APEQ的面积为y（cm2），试探究y的最大值；（3）当t为何值时，△APQ是等腰三角形．19．（2017•蜀山区二模）如图，在△ABC中，D、E分别为AB、AC上的点，线段BE、CD相交于点O，且∠DCB=∠EBC=∠A．（1）求证：△BOD∽△BAE；（2）求证：BD=CE；（3）若M、N分别是BE、CE的中点，过MN的直线交AB于P，交AC于Q，线段AP、AQ 相等吗？为什么？20．（2017•安徽模拟）如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD 的中点，BF、ED的延长线交于点G，连接GC．（1）求证：AB=GD；（2）如图2，当CG=EG时，求的值．21．（2017•肥城市三模）如图，在锐角△ABC中，D，E分别为AB，BC中点，F为AC上一点，且∠AFE=∠A，DM∥EF交AC于点M．（1）点G在BE上，且∠BDG=∠C，求证：DG•CF=DM•EG；（2）在图中，取CE上一点H，使∠CFH=∠B，若BG=1，求EH的长．22．（2017•石家庄二模）如图，在矩形ABCD和矩形PEFG中，AB=8，BC=6，PE=2，PG=4．PE 与AC交于点M，EF与AC交于点N，动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，伴随点P的运动，矩形PEFG在射线AB上滑动；动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动．点P、K同时开始运动，当点K到达点F时停止运动，点P也随之停止．设点P、K运动的时间是t秒（t＞0）．（1）当t=1时，KE=，EN=；（2）当t为何值时，△APM的面积与△MNE的面积相等？（3）当点K到达点N时，求出t的值；（4）当t为何值时，△PKB是直角三角形？23．（2017•岱岳区二模）如图，C为线段BD上一动点，过B、D分别作BD的垂线，使AB=BC，DE=DB，连接AD、AC、BE，过B作AD的垂线，垂足为F，连接CE、EF．（1）求证：AC•DF=BF•BD；（2）点C运动的过程中，∠CFE的度数保持不变，求出这个度数；（3）当点C运动到什么位置时，CE∥BF？并说明理由．24．（2017•长春模拟）如图，在△ABC中，点D在边AB上（不与A，B重合），DE∥BC交AC于点E，将△ADE沿直线DE翻折，得到△A′DE，直线DA′，EA′分别交直线BC于点M，N．（1）求证：DB=DM．（2）若=2，DE=6，求线段MN的长．（3）若=n（n≠1），DE=a，则线段MN的长为（用含n的代数式表示）．25．（2017•大冶市模拟）如图，△ABC中，点E、F分别在边AB，AC上，BF与CE相交于点P，且∠1=∠2=∠A．（1）如图1，若AB=AC，求证：BE=CF；（2）若图2，若AB≠AC，①（1）中的结论是否成立？请给出你的判断并说明理由；②求证：=．26．（2017•大东区二模）如图1，在锐角△ABC中，D、E分别是AB、BC的中点，点F在AC 上，且满足∠AFE=∠A，DM∥EF交AC于点M．（1）证明：DM=DA；（2）点G在BE上，且∠BDG=∠C，如图2，求证：△DEG∽△ECF；（3）在图2中，取CE上一点H，使得∠CFH=∠B，若BG=5，求EH的长．27．（2017•阳谷县一模）如图，在△ABC中，点D是BA边延长线上一点，过点D作DE∥BC，交CA延长线于点E，点F是DE延长线上一点，连接AF．（1）如果=，DE=6，求边BC的长；（2）如果∠FAE=∠B，FA=6，FE=4，求DF的长．28．（2017•杭州模拟）已知，如图1，点D、E分别在AB，AC上，且=．（1）求证：DE∥BC．（2）已知，如图2，在△ABC中，点D为边AC上任意一点，连结BD，取BD中点E，连结CE并延长CE交边AB于点F，求证：=．（3）在（2）的条件下，若AB=AC，AF=CD，求的值．答案解析1．（2017•黑龙江）已知：△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°．连接AD，BC，点H为BC中点，连接OH．（1）如图1所示，易证：OH=AD且OH⊥AD（不需证明）（2）将△COD绕点O旋转到图2，图3所示位置时，线段OH与AD又有怎样的关系，并选择一个图形证明你的结论．【解答】（1）证明：如图1中，∵△OAB与△OCD为等腰直角三角形，∠AOB=∠COD=90°，∴OC=OD，OA=OB，∵在△AOD与△BOC中，，∴△AOD≌△BOC（SAS），∴∠ADO=∠BCO，∠OAD=∠OBC，∵点H为线段BC的中点，∴OH=HB，∴∠OBH=∠HOB=∠OAD，又因为∠OAD+∠ADO=90°，所以∠ADO+∠BOH=90°，所以OH⊥AD（2）解：①结论：OH=AD，OH⊥AD，如图2中，延长OH到E，使得HE=OH，连接BE，易证△BEO≌△ODA∴OE=AD∴OH=OE=AD由△BEO≌△ODA，知∠EOB=∠DAO∴∠DAO+∠AOH=∠EOB+∠AOH=90°，∴OH⊥AD．②如图3中，结论不变．延长OH到E，使得HE=OH，连接BE，延长EO交AD于G．易证△BEO≌△ODA∴OE=AD∴OH=OE=AD由△BEO≌△ODA，知∠EOB=∠DAO∴∠DAO+∠AOF=∠EOB+∠AOG=90°，∴∠AGO=90°∴OH⊥AD．2．（2017•连云港四模）阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．操作与证明：（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；猜想与发现：根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？【解答】解：操作与证明：（1）BE=AD．∵△C′DE绕点C按顺时针方向旋转30°，∴∠BCE=∠ACD=30度，∵△ABC与△C′DE是等边三角形，∴CA=CB，CE=CD，∴△BCE≌△ACD，∴BE=AD．（2）BE=AD．∵△C′DE绕点C按顺时针方向旋转的角度为α，∴∠BCE=∠ACD=α，∵△ABC与△C′DE是等边三角形，∴CA=CB，CE=CD，∴△BCE≌△ACD，∴BE=AD．猜想与发现：当α为180°时，线段AD的长度最大，等于a+b；当α为0°（或360°）时，线段AD的长度最小，等于a﹣b．3．（2017•金乡县模拟）请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PC是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为，问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．【解答】解：（1）如图，将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A．∴AP′=PC=1，BP=BP′=；连接PP′，在Rt△BP′P中，∵BP=BP′=，∠PBP′=90°，∴PP′=2，∠BP′P=45°；（2分）在△AP′P中，AP′=1，PP′=2，AP=，∵，即AP′2+PP′2=AP2；∴△AP′P是直角三角形，即∠AP′P=90°，∴∠AP′B=135°，∴∠BPC=∠AP′B=135°．（4分）（2）过点B作BE⊥AP′，交AP′的延长线于点E；则△BEP′是等腰直角三角形，∴∠EP′B=45°，∴EP′=BE=1，∴AE=2；∴在Rt△ABE中，由勾股定理，得AB=；（7分）∴∠BPC=135°，正方形边长为．4．（2017•滦县模拟）两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为相等和位置关系为垂直；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．【解答】（1）解：∵CE=CD，AC=BC，∠ECA=∠DCB=90°，∴BE=AD，∵F是DE的中点，H是AE的中点，G是BD的中点，∴FH=AD，FH∥AD，FG=BE，FG∥BE，∴FH=FG，∵AD⊥BE，∴FH⊥FG，故答案为：相等，垂直．（2）答：成立，证明：∵CE=CD，∠ECD=∠ACD=90°，AC=BC，∴△ACD≌△BCE∴AD=BE，由（1）知：FH=AD，FH∥AD，FG=BE，FG∥BE，∴FH=FG，FH⊥FG，∴（1）中的猜想还成立．（3）答：成立，结论是FH=FG，FH⊥FG．连接AD，BE，两线交于Z，AD交BC于X，同（1）可证∴FH=AD，FH∥AD，FG=BE，FG∥BE，∵三角形ECD、ACB是等腰直角三角形，∴CE=CD，AC=BC，∠ECD=∠ACB=90°，∴∠ACD=∠BCE，在△ACD和△BCE中，∴△ACD≌△BCE，∴AD=BE，∠EBC=∠DAC，∵∠DAC+∠CXA=90°，∠CXA=∠DXB，∴∠DXB+∠EBC=90°，∴∠EZA=180°﹣90°=90°，即AD⊥BE，∵FH∥AD，FG∥BE，∴FH⊥FG，即FH=FG，FH⊥FG，结论是FH=FG，FH⊥FG5．（2017•路北区三模）如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．（1）求证：△AEC≌△ADB；（2）若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．【解答】解：（1）由旋转的性质得：△ABC≌△ADE，且AB=AC，∴AE=AD，AC=AB，∠BAC=∠DAE，∴∠BAC+∠BAE=∠DAE+∠BAE，即∠CAE=∠DAB，在△AEC和△ADB中，，∴△AEC≌△ADB（SAS）；（2）∵四边形ADFC是菱形，且∠BAC=45°，∴∠DBA=∠BAC=45°，由（1）得：AB=AD，∴∠DBA=∠BDA=45°，∴△ABD为直角边为2的等腰直角三角形，∴BD2=2AB2，即BD=2，∴AD=DF=FC=AC=AB=2，∴BF=BD﹣DF=2﹣2．6．（2017•平房区二模）如图，正方形ABCD，点E在AD上，将△CDE绕点C顺时针旋转90°至△CFG，点F，G分别为点D，E旋转后的对应点，连接EG，DB，DF，DB与CE交于点M，DF与CG交于点N．（1）求证BM=DN；（2）直接写出图中已经存在的所有等腰直角三角形．【解答】（1）证明：∵四边形ABCD为正方形，∴∠DCB=90°，CD=CB，∵△CDE绕点C顺时针旋转90°至△CFG，∴CF=CD，∠ECG=∠DCF=90°，∴△CDF为等腰直角三角形，∴∠CDF=∠CFD=45°，∵∠BCM+∠DCE=90°，∠DCN+∠DCE=90°，∴∠BCM=∠DCN，∵∠CBM=∠ABC=45°，∴∠CBM=∠CDN，在△BCM和△DCN中，∴△BCM≌△DCN，∴BM=DN；（2）解：∵四边形ABCD为正方形，∴△ABD和△BCD为等腰直角三角形；由（1）得△CDF为等腰三角形；∵△CDE绕点C顺时针旋转90°至△CFG，∴CE=CG，∠ECG=90°，∴△ECG为等腰直角三角形；∵△CBD和△CFD为等腰直角三角形；∴△BDF为等腰直角三角形．7．（2017•路南区一模）如图①，△ABC中，AC=BC，∠A=30°，点D在AB边上且∠ADC=45°．（1）求∠BCD的度数；（2）将图①中的△BCD绕点B顺时针旋转得到△BC′D′．当点D′恰好落在BC边上时，如图②所示，连接C′C并延长交AB于点E．①求∠C′CB的度数；②求证：△C′BD'≌△CAE．【解答】解：（1）∵AC=BC，∠A=30°，∴∠CBA=∠CAB=30°，∵∠ADC=45°，∴∠BCD=∠ADC﹣∠CBA=15°=∠BC'D'；（2）①由旋转可得CB=C'B=AC，∠C'BD'=∠CBD=∠A=30°，∴∠CC'B=∠C'CB=75°；②证明：∵AC=C'B，∠C'BD'=∠A，∴∠CEB=∠C'CB﹣∠CBA=45°，∴∠ACE=∠CEB﹣∠A=15°，∴∠BC'D'=∠BCD=∠ACE，在△C'BD'和△CAE中，，∴△C'BD'≌△CAE（ASA）．8．（2017•沙坪坝区一模）已知△ABC和△DEB都是等腰直角三角形，∠BAC=∠EDB=90°．（1）如图1，若点E，B，C在同一直线上，连接AE，当∠AEC=30°，BC=4时，求EB的长；（2）如图2，将图1中的△DEB绕点B顺时针旋转，当点C在ED的延长线上时，EC交AB 于点H，求证：∠EAH=2∠HCB．【解答】（1）解：如图1中，作AH⊥BC于H．∵AB=AC，∠BAC=90°，AH⊥BC，∴AH=BH=HC=2，在Rt△AEH中，∵∠AHE=90°，AH=2，∠AEH=30°，∴EH==2，∴EB=EH﹣BH=2﹣2．（2）证明：如图2中，连接AD．∵∠BDH=∠HAC，∠BHD=∠CHA，∴△BHD∽△CHA，∴=，∴=，∵∠AHD=∠CHB，∴△AHD∽△CHB，∴∠ADH=∠CBH=45°，∠DAH=∠BCH，∴∠ADB=90°+45°=135°，∴∠ADE=360°﹣90°﹣135°=135°，∴∠ADE=∠ADB，在△ADE和△ADB中，，∴△ADE≌△ADB，∴∠DAE=∠DAB，∵∠DAB=∠BCH，∴∠EAH=2∠HCB．9．（2017•重庆模拟）已知等腰Rt△ABC与等腰Rt△CDE，∠ACB=∠DCE=90°，把Rt△ABC 绕点C旋转．（1）如图1，当点A旋转到ED的延长线时，若BC=，BE=5，求CD的长；（2）当Rt△ABC旋转到如图2所示的位置时，过点C作BD的垂线交BD于点F，交AE于点G，求证：BD=2CG．【解答】解：（1）如图1，∵△ADC是由△BEC绕点C旋转得到的，∴AD=BE=5，∠ADC=∠BEC，∵在等腰Rt△ABC与等腰Rt△CDE中，BC=AC=，∠EDC=∠DEC=45°，∴AB=13，∠ADC=∠BEC=135°，∴∠AEB=90°，∴AE==12，∴DE=7，∴等腰Rt△CDE中，CD=DE=；（2）如图2，过点A作AH∥CE，交CG的延长线于H，连接HE，则∠CAH+∠ACE=180°，∵∠ACB=∠DCE=90°，∴∠BCD+∠ACE=180°，∴∠CAE=∠BCD，∵CF⊥BD，∠ACB=90°，∴∠CBF+∠BCF=∠ACG+∠BCF=90°，∴∠CBF=∠ACG，在△BCD和△CAH中，，∴△BCD≌△CAH（ASA），∴AH=CD=CE，BD=CH，又∵AH∥CE，∴四边形ACEH是平行四边形，∴CH=2CG，∴BD=2CG．10．（2017•河北区模拟）如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．（1）求证：△PMN为等腰直角三角形；（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP，BD 分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．【解答】解：（1）∵△ACB和△ECD是等腰直角三角形，∴AC=BC，EC=CD，∠ACB=∠ECD=90°．在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE=BD，∠EAC=∠CBD，∵∠CBD+∠BDC=90°，∴∠EAC+∠BDC=90°，∵点M、N分别是斜边AB、DE的中点，点P为AD的中点，∴PM=BD，PN=AE，∴PM=PM，∵PM∥BD，PN∥AE，∴∠NPD=∠EAC，∠MPA=∠BDC，∵∠EAC+∠BDC=90°，∴∠MPA+∠NPC=90°，∴∠MPN=90°，即PM⊥PN，∴△PMN为等腰直角三角形；（2）①中的结论成立，理由：设AE与BC交于点O，如图②所示：∵△ACB和△ECD是等腰直角三角形，∴AC=BC，EC=CD，∠ACB=∠ECD=90°．在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE=BD，∠CAE=∠CBD．∵∠AOC=∠BOE，∠CAE=∠CBD，∴∠BHO=∠ACO=90°，∴AE⊥BD，∵点P、M、N分别为AD、AB、DE的中点，∴PM=BD，PM∥BD，PN=AE，PN∥AE，∴PM=PN．∵AE⊥BD，∴PM⊥PN，∴△PMN为等腰直角三角形．11．（2017•吉安模拟）两块全等的三角板ABC和EDC如图（1）放置，AC=CB，CE=CD，∠ACB=∠ECD=90°，且AB与CE交于F，ED与AB、BC分别交于M、H，△ABC不动，将△EDC 绕点C旋转到如图（2），当∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．【解答】解：四边形ACDM是菱形．证明：∵∠ACB=∠DCE=90°，∠BCE=45°，∴∠1=∠2=45°．∵∠E=45°，∴∠1=∠E，∴AC∥DE，∴∠AMH=180°﹣∠A=135°=∠ACD，又∵∠A=∠D=45°，∴四边形ACDM是平行四边形（两组对角分别相等的四边形是平行四边形），∵AC=CD，∴四边形ACDM是菱形．12．（2017•江津区校级三模）如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．（1）如图①，当点D在AB上，点E在AC上时，请判断线段CF，DF有怎样的数量关系和位置关系？为什么？（2）如图②，将图①中的△ADE绕点A旋转到图②位置时，请判断（1）中的结论是否仍然成立？并证明你的判断．【解答】解：（1）CF=DF且CF⊥DF．理由如下：∵∠ADE=90°，∴∠BDE=90°，又∵∠BCE=90°，点F是BE的中点，∴CF=DF=BE=BF，∴∠1=∠3，∠2=∠4，∴∠5=∠1+∠3=2∠1，∠6=∠2+∠4=2∠2，∴∠CFD=∠5+∠6=2（∠1+∠2）=2∠ABC，又∵△ABC是等腰直角三角形，且∠ACB=90°，∴∠ABC=45°，∴∠CFD=90°，∴CF=DF且CF⊥DF．（2）（1）中的结论仍然成立．理由如下：如图，延长DF至G使FG=DF，连接BG，CG，DC，∵F是BE的中点，∴BF=EF，又∵∠BFG=∠EFD，GF=DF，∴△BFG≌△EFD（SAS），∴∠FBG=∠FED，BG=ED，∴BG∥DE，∵△ADE和△ACB都是等腰直角三角形，∴DE=DA，∠DAE=∠DEA=45°，AC=BC，∠CAB=∠CBA=45°，又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣（180°﹣∠AEB﹣∠EAB）﹣45°=∠DEF﹣180°+∠AEB+∠EAB﹣45°=（∠DEF+∠AEB）+∠EAB﹣225°=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°=90°+∠EAB，而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB，∴∠CBG=∠DAC，又∵BG=ED，DE=DA，∴BG=AD，又∵BC=AC，∴△BCG≌△ACD（SAS），∴GC=DC，∠BCG=∠ACD，∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°，∴△DCG是等腰直角三角形，又∵F是DG的中点，∴CF⊥DF且CF=DF．13．（2017•济宁二模）将两块全等的三角板如图1摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．（1）将图1中△A1B1C绕点C顺时针旋转45°得图2，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；（2）在图2中，若AP1=a，则CQ等于多少？（3）将图2中△A1B1C绕点C顺时针旋转到△A2B2C（如图3），点P2是A2C与AP1的交点．当旋转角为多少度时，有△AP1C∽△CP1P2？这时线段CP1与P1P2之间存在一个怎样的数量关系？．【解答】（1）证明：∵∠B1CB=45°，∠B1CA1=90°，∴∠B1CQ=∠BCP1=45°；又B1C=BC，∠B1=∠B，∴△B1CQ≌△BCP1（ASA）∴CQ=CP1；（2）解：如图：作P1D⊥AC于D，∵∠A=30°，∴P1D=AP1；∵∠P1CD=45°，∴=sin45°=，∴CP1=P1D=AP1；又AP1=a，CQ=CP1，∴CQ=a；（3）解：当∠P1CP2=∠P1AC=30°时，由于∠CP1P2=∠AP1C，则△AP1C∽△CP1P2，所以将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C时，有△AP1C∽△CP1P2．这时==，∴P1P2=CP1．14．（2017•常德）如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．（1）如图1，若BD=BA，求证：△ABE≌△DBE；（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，求证：①GM=2MC；②AG2=AF•AC．【解答】证明：（1）在Rt△ABE和Rt△DBE中，，∴△ABE≌△DBE；（2）①过G作GH∥AD交BC于H，∵AG=BG，∴BH=DH，∵BD=4DC，设DC=1，BD=4，∴BH=DH=2，∵GH∥AD，∴==，∴GM=2MC；②过C作CN⊥AC交AD的延长线于N，则CN∥AG，∴△AGM∽△NCM，∴=，由①知GM=2MC，∴2NC=AG，∵∠BAC=∠AEB=90°，∴∠ABF=∠CAN=90°﹣∠BAE，∴△ACN∽△BAF，∴=，∵AB=2AG，∴=，∴2CN•AG=AF•AC，∴AG2=AF•AC．15．（2017•杭州）如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．（1）求证：△ADE∽△ABC；（2）若AD=3，AB=5，求的值．【解答】解：（1）∵AG⊥BC，AF⊥DE，∴∠AFE=∠AGC=90°，∵∠EAF=∠GAC，∴∠AED=∠ACB，∵∠EAD=∠BAC，∴△ADE∽△ABC，（2）由（1）可知：△ADE∽△ABC，∴=由（1）可知：∠AFE=∠AGC=90°，∴∠EAF=∠GAC，∴△EAF∽△CAG，∴，∴=16．（2017•天水）△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF 的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=2，CQ=9时BC的长．【解答】（1）证明：∵△ABC是等腰直角三角形，∴∠B=∠C=45°，AB=AC，∵AP=AQ，∴BP=CQ，∵E是BC的中点，∴BE=CE，在△BPE和△CQE中，∵，∴△BPE≌△CQE（SAS）；（2）解：∵△ABC和△DEF是两个全等的等腰直角三角形，∴∠B=∠C=∠DEF=45°，∵∠BEQ=∠EQC+∠C，即∠BEP+∠DEF=∠EQC+∠C，∴∠BEP+45°=∠EQC+45°，∴∠BEP=∠EQC，∴△BPE∽△CEQ，∴=，∵BP=2，CQ=9，BE=CE，∴BE2=18，∴BE=CE=3，∴BC=6．17．（2017•深圳模拟）如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE=AB，点P从点D出发，以每秒1个单位长度沿D→C→B向终点B运动，直线EP交AD于点F，过点F作直线FG⊥DE于点G，交AB于点R．（1）求证：AF=AR；（2）设点P运动的时间为t，①求当t为何值时，四边形PRBC是矩形？②如图2，连接PB．请直接写出使△PRB是等腰三角形时t的值．【解答】（1）证明：如图，在正方形ABCD中，AD=AB=2，∵AE=AB，∴AD=AE，∴∠AED=∠ADE=45°，又∵FG⊥DE，∴在Rt△EGR中，∠GER=∠GRE=45°，∴在Rt△ARF中，∠FRA=∠AFR=45°，∴∠FRA=∠RFA=45°，∴AF=AR；（2）解：①如图，当四边形PRBC是矩形时，则有PR∥BC，∴AF∥PR，∴△EAF∽△ERP，∴，即：由（1）得AF=AR，∴，解得：或（不合题意，舍去），∴，∵点P从点D出发，以每秒1个单位长度沿D→C→B向终点B运动，∴（秒）；②若PR=PB，过点P作PK⊥AB于K，设FA=x，则RK=BR=（2﹣x），∵△EFA∽△EPK，∴，即：=，解得：x=±﹣3（舍去负值）；∴t=（秒）；若PB=RB，则△EFA∽△EPB，∴=，∴，∴BP=AB=×2=∴CP=BC﹣BP=2﹣=，∴（秒）．综上所述，当PR=PB时，t=；当PB=RB时，秒．18．（2017•惠阳区模拟）把Rt△ABC和Rt△DEF按如图（1）摆放（点C与E重合），点B、C（E）、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF 移动的同时，点P从△ABC的顶点A出发，以2cm/s的速度沿AB向点B匀速移动；当点P 移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t（s）．（1）用含t的代数式表示线段AP和AQ的长，并写出t的取值范围；（2）连接PE，设四边形APEQ的面积为y（cm2），试探究y的最大值；（3）当t为何值时，△APQ是等腰三角形．【解答】（1）解：AP=2t∵∠EDF=90°，∠DEF=45°，∴∠CQE=45°=∠DEF，∴CQ=CE=t，∴AQ=8﹣t，t的取值范围是：0≤t≤5；（2）过点P作PG⊥x轴于G，可求得AB=10，SinB=，PB=10﹣2t，EB=6﹣t，∴PG=PBSinB=（10﹣2t）∴y=S△ABC﹣S△PBE﹣S△QCE==∴当（在0≤t≤5内），y有最大值，y最大值=（cm2）（3）若AP=AQ，则有2t=8﹣t解得：（s）若AP=PQ，如图①：过点P作PH⊥AC，则AH=QH=，PH∥BC ∴△APH∽△ABC，∴，即，解得：（s）若AQ=PQ，如图②：过点Q作QI⊥AB，则AI=PI=AP=t∵∠AIQ=∠ACB=90°∠A=∠A，∴△AQI∽△ABC∴即，解得：（s）综上所述，当或或时，△APQ是等腰三角形．19．（2017•蜀山区二模）如图，在△ABC中，D、E分别为AB、AC上的点，线段BE、CD相交于点O，且∠DCB=∠EBC=∠A．（1）求证：△BOD∽△BAE；（2）求证：BD=CE；（3）若M、N分别是BE、CE的中点，过MN的直线交AB于P，交AC于Q，线段AP、AQ 相等吗？为什么？【解答】（1）证明：∵∠BCO=∠CBO，∴∠DOB=∠BCO+CBO=2∠BCO，∵∠A=2∠BCO，∴∠DOB=∠A，∵∠ABE=∠ABE，∴△BOD∽△BAE；（2）解：延长CD，在CD延长线上取一点F，使BF=BD，∴∠BDF=∠BFD，∵∠BDF=∠ABO+∠DOB，∠BEC=∠ABO+∠A，由（1）得∠BOD=∠A，∴∠BDF=∠BEC，∴∠BFD=∠BEC，在△BFC与△CEB中，，∴△BFC≌△CEB，∴BD=BF，∴BD=CE；（3）解：AP=AQ，理由：取BC的中点G，连接GM，GN，∵M，N分别是BE，CD的中点，∴GM，GN是中位线，∴GM∥CE，GM=CE，GN∥BD，GN=BD，∵BD=CE，∴GM=GN，∴∠3=∠4，∵GM∥CE，∴∠2=∠4，∵GN∥BD，∴∠3=∠1，∴∠1=∠2，∴AP=AQ．20．（2017•安徽模拟）如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD 的中点，BF、ED的延长线交于点G，连接GC．（1）求证：AB=GD；（2）如图2，当CG=EG时，求的值．【解答】解：（1）∵D、E分别是线段AC、BC的中点，∴DE为△ABC的中位线，∴DE∥AB，即EG∥AB，∴∠FDG=∠A，∵点F为线段AD的中点，∴AF=DF，在△ABF与△DGF中，∴△ABF≌△DGF（ASA）∴AB=GD（2）∵DE为△ABC的中位线，∴DE=AB，CE=BC=AC∵DG=AB，∴EG=DE+DG∴EG=AB∵DE∥AB，∴∠GEC=∠CBA，∵AC=BC，CG=EG∴△GEC∽△CBA∴，即，∴21．（2017•肥城市三模）如图，在锐角△ABC中，D，E分别为AB，BC中点，F为AC上一点，且∠AFE=∠A，DM∥EF交AC于点M．（1）点G在BE上，且∠BDG=∠C，求证：DG•CF=DM•EG；（2）在图中，取CE上一点H，使∠CFH=∠B，若BG=1，求EH的长．【解答】（1）证明：如图1所示，∴D，E分别为AB，BC中点，∴DE∥AC∵DM∥EF，∴四边形DEFM是平行四边形，∴DM=EF，如图2所示，∵D、E分别是AB、BC的中点，∴DE∥AC，∴∠BDE=∠A，∠DEG=∠C，∵∠AFE=∠A，∴∠BDE=∠AFE，∴∠BDG+∠GDE=∠C+∠FEC，∵∠BDG=∠C，∴∠GDE=∠FEC，∴△DEG∽△ECF；∴，∴，∴，∴DG•CF=DM•EG；（2）解：如图3所示，∵∠BDG=∠C=∠DEB，∠B=∠B，∴△BDG∽△BED，∴，∴BD2=BG•BE，∵∠AFE=∠A，∠CFH=∠B，∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=∠EFH，又∵∠FEH=∠CEF，∴△EFH∽△ECF，∴=，∴EF2=EH•EC，∵DE∥AC，DM∥EF，∴四边形DEFM是平行四边形，∴EF=DM=DA=BD，∴BG•BE=EH•EC，∵BE=EC，∴EH=BG=1．22．（2017•石家庄二模）如图，在矩形ABCD和矩形PEFG中，AB=8，BC=6，PE=2，PG=4．PE 与AC交于点M，EF与AC交于点N，动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，伴随点P的运动，矩形PEFG在射线AB上滑动；动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动．点P、K同时开始运动，当点K到达点F时停止运动，点P也随之停止．设点P、K运动的时间是t秒（t＞0）．（1）当t=1时，KE=1，EN=；（2）当t为何值时，△APM的面积与△MNE的面积相等？（3）当点K到达点N时，求出t的值；（4）当t为何值时，△PKB是直角三角形？【解答】解：（1）当t=1时，根据题意得，AP=1，PK=1，∵PE=2，∴KE=2﹣1=1，∵四边形ABCD和PEFG都是矩形，∴△APM∽△ABC，△APM∽△NEM，∴=，=，∴MP=，ME=，∴NE=；故答案为：1；；（2）由（1）并结合题意可得，AP=t，PM=t，ME=2﹣t，NE=﹣t，∴t×t=（2﹣t）×（﹣t），解得，t=；（3）当点K到达点N时，则PE+NE=AP，由（2）得，﹣t+2=t，解得，t=；（4）①当K在PE边上任意一点时△PKB是直角三角形，即，0＜t≤2；②当点k在EF上时，则KE=t﹣2，BP=8﹣t，∵△BPK∽△PKE，∴PK2=BP×KE，PK2=PE2+KE2，∴4+（t﹣2）2=（8﹣t）（t﹣2），解得t=3，t=4；③当t=5时，点K在BC边上，∠KBP=90°．综上，当0＜t≤2或t=3或t=4或5时，△PKB是直角三角形．23．（2017•岱岳区二模）如图，C为线段BD上一动点，过B、D分别作BD的垂线，使AB=BC，DE=DB，连接AD、AC、BE，过B作AD的垂线，垂足为F，连接CE、EF．（1）求证：AC•DF=BF•BD；（2）点C运动的过程中，∠CFE的度数保持不变，求出这个度数；（3）当点C运动到什么位置时，CE∥BF？并说明理由．【解答】解：（1）∵BF⊥AD，∴∠AFB=∠BFD=90°，∴∠ABF+∠BAF=90°，∵AB⊥BC，∴∠ABF+∠DBF=90°，∴∠BAF=∠DBF，∴△ABF∽△BDF，∴=，即AB•DF=BF•BD，由AB=BC，AB⊥BC，∴AB=AC，∴AC•DF=BF•BD；（2）∵=，AB=BC、BD=DE，∴=，∵∠FBC+∠BDF=90°、∠BDF+∠EDF=90°，∴∠FBC=∠EDF，∴△FBC∽△FDE，∴∠BFC=∠DFE，又∠BFD=∠BFC+∠CFD=90°，∴∠DFE+∠CFD=90°，即∠CFE=90°，故∠CFE的度数保持不变，始终等于90°．（3）当C为BD中点时，CE∥BF，理由如下：∵C为BD中点，∴AB=BC=CD=BD=DE，在△ABD和△CDE中，∵，∴△ABD≌△CDE（SAS），∴∠ADB=∠CED，∵∠CED+∠ECD=90°，∴∠ADB+∠ECD=90°，∴CE⊥AD，∵BF⊥AD，∴CE∥BF．。

教师姓名学生姓名年级初三上课时间学科数学课题名称中考压轴题――图形的变换教学目标图形的三种变换的进一步提高。

教学重难点解题时如何正确把握解题思路，寻找正确的解题方法。

【轴对称】1.如图，Rt△ABC中，∠ACB＝90º，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC 沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为【】A. 35B.45C.23D.322.如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为▲ ．1. 若函数y kx b =-的图像如图所示，则关于x 的不等式()3>0k x b --的解集为【 】A. <2xB. >2xC. <5xD. >5x2.如图，△ABC 和△DBC 是两个具有公共边的全等三角形，AB =AC =3cm ，BC =2cm ，将△DBC 沿射线BC 平移一定的距离得到△D 1B 1C 1，连接AC 1，BD 1．如果四边形ABD 1C 1是矩形，那么平移的距离为 ▲ cm ．1.在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为22的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与A G在同一直线上．（1）小明发现DG⊥BE，请你帮他说明理由．（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，将线段DG与线段BE相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．2.如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ 绕点P旋转，得到△PDE，点D落在线段PQ上．（1）求证：PQ∥AB；（2）若点D在∠BAC的平分线上，求CP的长；（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．【作业】1.如图，在△ABC中，∠BAC=60°，∠ABC=90°，直线l1∥l2∥l3，l1与l2之间距离是1，l2与l3之间距离是2，且l1，l2，l3分别经过点A，B，C，则边AC的长为▲ ．2. 如图，过原点O的直线与反比例函数y1，y2的图象在第一象限内分别交于点A、B，且A为OB的中点，若函数11yx，则y2与x的函数表达式是▲ ．答案：【轴对称】1.如图，Rt △ABC 中，∠ACB ＝90º，AC ＝3，BC ＝4，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B ′处，两条折痕与斜边AB 分别交于点E 、F ，则线段B ′F 的长为【 】A. 35B. 45C. 23D. 32 【答案】B ．【考点】翻折变换（折叠问题）；折叠的性质；等腰直角三角形的判定和性质；勾股定理．【分析】根据折叠的性质可知34CD AC B C BC ACE DCE BCF B CF CE AB =='==∠=∠∠=∠'⊥，，，，，∴431B D DCE B CF ACE BCF '=-=∠+∠'=∠+∠，.∵90ACB ∠=︒，∴45ECF ∠=︒. ∴ECF 是等腰直角三角形. ∴45EF CE EFC =∠=︒，.∴135BFC B FC ∠=∠'=︒. ∴90B FD ∠'=︒.∵1122ABC S AC BC AB CE =⋅⋅=⋅⋅，∴AC BC AB CE ⋅=⋅. 在Rt ABC 中，根据勾股定理，得A B=5，∴123455CE CE ⋅=⋅⇒=.∴125EF CE ==. 在Rt AEC 中，根据勾股定理，得2295AE AC CE =-=，∴95ED AE ==. ∴35DF EF ED =-=. 在Rt B FD '中，根据勾股定理，得222234155B F B D DF ⎛⎫'='-=-= ⎪⎝⎭. 故选B ．2.如图， 矩形ABCD 中，AB =8，BC =6，P 为AD 上一点， 将△ABP 沿BP 翻折至△EBP ， PE 与CD 相交于点O ，且OE =OD ，则AP 的长为 ▲ ．【答案】245. 【考点】翻折变换（折叠问题）；矩形的性质；折叠对称的性质；勾股定理，全等三角形的判定和性质；方程思想的应用.【分析】如答图，∵四边形ABCD 是矩形，∴90,6,8D A C AD BC CD AB ∠=∠=∠=︒==== .根据折叠对称的性质，得ABP EBP ∆∆≌，∴,90,8EP AP E A BE AB =∠=∠=︒== .在ODP ∆和OEG ∆中，∵D E OD OE DOP EOG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ODP ∆≌()OEG ASA ∆.∴,OP OG PG GE == .∴DG EP =.设AP EP x ==，则6,PD GE x DG x ==-= ，∴()8,862CG x BG x x =-=--=+ .在Rt BCG ∆中，根据勾股定理，得222BC CG BG +=，即()()222682x x +-=+.解得245x =. ∴AP 的长为245. 【平移】1. 若函数y kx b =-的图像如图所示，则关于x 的不等式()3>0k x b --的解集为【 】A. <2xB. >2xC. <5xD. >5x【答案】C.【考点】直线的平移；不等式的图象解法；数形结合思想的应用.【分析】如答图，将函数y kx b =-的图像向右平移3 个单位得到函数()3y k x b =--的图象，由图象可知，当<5x 时，函数()3y k x b =--的图象在x 轴上方，即()3>0y k x b =--.∴关于x 的不等式()3>0k x b --的解集为<5x .故选C.2.如图，△ABC 和△DBC 是两个具有公共边的全等三角形，AB =AC =3cm ，BC =2cm ，将△DBC 沿射线BC 平移一定的距离得到△D 1B 1C 1，连接AC 1，BD 1．如果四边形ABD 1C 1是矩形，那么平移的距离为 ▲ cm ．【答案】7．【考点】面动平移问题；相似三角形的判定和性质；等腰三角形的性质；矩形的性质；平移的性质．【分析】如答图，过点A 作AE ⊥BC 于点E ，∵∠AEB =∠AEC 1=90°，∴∠BAE +∠ABC =90°.∵AB =AC ，BC =2，∴BE =CE =12BC =1，∴∠ABC +∠AC 1B =90°. ∴∠BAE =∠AC 1B .∴△ABE ∽△C 1BA . ∴1BE AE AB BC =. ∵AB =3，BE =1，∴1133BC =.∴BC 1=9. ∴CC 1=BC 1﹣BC =9﹣2=7，即平移的距离为7．【旋转】1.在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD 与边长为22的正方形AEFG 按图1位置放置，AD 与AE 在同一直线上，AB 与A G 在同一直线上．（1）小明发现DG ⊥BE ，请你帮他说明理由．（2）如图2，小明将正方形ABCD 绕点A 逆时针旋转，当点B 恰好落在线段DG 上时，请你帮他求出此时BE 的长．（3）如图3，小明将正方形ABCD 绕点A 继续逆时针旋转，将线段DG 与线段BE 相交，交点为H ，写出△GHE 与△BHD 面积之和的最大值，并简要说明理由．【答案】解：（1）∵四边形ABCD 和四边形AEFG 都为正方形，∴AD =AB ，∠DAG =∠BAE =90°，AG =AE ，∴△ADG ≌△ABE （SAS ）.∴∠AGD =∠AEB .如答图1，延长EB 交DG 于点H ，在△ADG 中，∵∠AGD +∠ADG =90°，∴∠AEB +∠ADG =90°.在△EDH 中，∵∠AEB +∠ADG +∠DHE =180°，∴∠DH E=90°. ∴DG ⊥BE .（2）∵四边形ABCD 和四边形AEFG 都为正方形，∴AD =AB ，∠DAB =∠GAE =90°，AG =AE ，∴∠DAB +∠BAG =∠GAE +∠BAG ，即∠DAG =∠BAE ，∴△ADG ≌△ABE （SAS ）.∴DG =BE .如答图2，过点A 作AM ⊥DG 交DG 于点M ，则∠AMD =∠AMG =90°，∵BD 为正方形AB CD 的对角线，∴∠MDA =45°.在Rt △AMD 中，∵∠MDA =45°，AD =2，∴2DM AM ==.在Rt △AMG 中，根据勾股定理得：226GM AG AM =-=，∵26DG DM GM =+=+，∴26BE DG ==+.（3）△GHE 和△BHD 面积之和的最大值为6，理由如下：∵对于△EGH ，点H 在以E G 为直径的圆上，∴当点H 与点A 重合时，△EGH 的高最大；∵对于△BDH ，点H 在以BD 为直径的圆上，∴当点H 与点A 重合时，△BDH 的高最大.∴△GHE 和△BHD 面积之和的最大值为2+4=6．【考点】面动旋转问题；正方形的性质；全等三角形的判定和性质；三角形内角和定理；等腰直角三角形的性质，勾股定理；数形结合思想的应用．【分析】（1）由四边形ABCD 与四边形AEFG 为正方形，利用正方形的性质得到两对边相等，且夹角相等，利用SAS 得到△ADG ≌△ABE ，利用全等三角形对应角相等得∠AGD =∠AEB ，作辅助线“延长EB 交D G 于点H ”，利用等角的余角相等得到∠DHE =90°，从而利用垂直的定义即可得DG ⊥BE .（2）由四边形ABCD 与四边形AEFG 为正方形，利用正方形的性质得到两对边相等，且夹角相等，利用SAS 得到△ADG ≌△ABE ，利用全等三角形对应边相等得到DG =BE ，作辅助线“过点A 作AM ⊥DG 交DG 于点M ”，则∠AMD =∠AMG =90°，在Rt △AMD 中，根据等腰直角三角形的性质求出AM 的长，即为DM 的长，根据勾股定理求出GM 的长，进而确定出DG 的长，即为BE 的长.（3）△GHE 和△BHD 面积之和的最大值为6，理由为：对两个三角形，点H 分别在以EG 为直径的圆上和以BD 为直径的圆上，当点H 与点A 重合时，两个三角形的高最大，即可确定出面积的最大值．2.如图，Rt △ABC 中，∠C =90°，AB =15，BC =9，点P ，Q 分别在BC ，AC 上，CP =3x ，CQ =4x （0＜x ＜3）．把△PCQ 绕点P 旋转，得到△PDE ，点D 落在线段PQ 上．（1）求证：PQ ∥AB ；（2）若点D 在∠BAC 的平分线上，求CP 的长；（3）若△PDE 与△ABC 重叠部分图形的周长为T ，且12≤T ≤16，求x 的取值范围．【答案】解：（1）证明：∵在Rt △ABC 中，AB =15，BC =9，∴222215912AC AB BC =-=-=． ∵34,93123PC x x QC x x BC AC ==== ，∴PC QC BC AC=． 又∵∠C =∠C ，∴△PQC ∽△BAC . ∴∠CPQ =∠B . ∴PQ ∥AB .（2）如答图1，连接AD ，∵PQ ∥AB ，∴∠ADQ =∠DAB ．∵点D 在∠BAC 的平分线上，∴∠DAQ =∠DAB .∴∠ADQ =∠DAQ . ∴AQ =DQ ．在Rt △CPQ 中，∵CP =3x ，CQ =4x ，∴PQ =5x.∵PD =PC =3x ，∴DQ =2x ．∵AQ =12﹣4x ，∴12﹣4x =2x ，解得x =2.∴CP =3x =6．（3）当点E 在AB 上时，∵PQ ∥AB ，∴∠DPE =∠PEB ．∵∠CPQ =∠DPE ，∠CPQ =∠B ，∴∠B =∠PEB . ∴PB =PE =5x .∴3x +5x =9，解得98x =． ①当0＜x ≤98时，34512T PD DE PE x x x x =++=++=，此时0＜T ≤272. ∴当0＜x ≤98时，T 随x 的增大而增大， ∵12≤T ≤16，∴当12≤T ≤272时，1≤x≤98. ②当98＜x ＜3时， 如答图2，设PE 交AB 于点G ，DE 交AB 于F ，作GH ⊥FQ ，垂足为H ，∴HG =DF ，FG =DH ，Rt △PHG ∽Rt △PDE .∵PG =PB =9﹣3x ，∴93453GH x PH x x x-==. ∴()()4393,9355GH x PH x =-=- . ∴()33935FG DH x x ==--， ∴()()()431254933933935555T PG PD DF FG x x x x x x ⎡⎤=+++=-++-+--=+⎢⎥⎣⎦， 此时，272＜T ＜18． ∴当98＜x ＜3时，T 随x 的增大而增大. ∵12≤T ≤16，∴当272＜T ≤16时，98＜x ≤136. 综上所述，当12≤T ≤16时，x 的取值范围是1≤x ≤136． 【考点】面动旋转问题；勾股定理；相似三角形的判定和性质；平行的判定和性质；方程思想、函数思想、分类思想的应用．【分析】（1）先根据勾股定理求出AC 的长，再由相似三角形的判定定理得出△PQC ∽△BAC ，由相似三角形的性质得出∠CPQ =∠B ，由此可得出结论.（2）连接AD ，根据PQ ∥AB 可知∠ADQ =∠DAB ，再由点D 在∠BAC 的平分线上，得出∠DAQ =∠DAB ，故∠ADQ =∠DAQ ，AQ =DQ ．在Rt △CPQ 中根据勾股定理可知，AQ =12﹣4x ，故可得出x 的值，进而得出结论.（3）当点E 在AB 上时，根据等腰三角形的性质求出x 的值，再分0＜x ≤98；98＜x ＜3两种情况进行分类讨论．作业：1.如图，在△ABC 中，∠BAC =60°，∠ABC =90°，直线l 1∥l 2∥l 3，l 1与l 2之间距离是1，l 2与l 3之间距离是2，且l 1，l 2，l 3分别经过点A ，B ，C ，则边AC 的长为 ▲ ．【答案】2213. 【考点】平行线的性质；锐角三角函数定义；特殊角的三角函数值；相似三角形的判定和性质；勾股定理．【分析】如答图，过点B 作EF ⊥l 2，交l 1于E ，交l 3于F ，∵∠BAC =60°，∠ABC =90°，∴3BC tan BAC AB∠==． ∵直线l 1∥l 2∥l 3，∴EF ⊥l 1，EF ⊥l 3. ∴∠AEB =∠BFC =90°．∵∠ABC =90°，∴∠EAB =90°﹣∠ABE =∠FBC .∴△BFC ∽△AEB ，∴3FC BC EB AB==．∵EB =1，∴FC =3．在Rt △BF C 中，()2222237BC BF FC =+=+=． 在Rt △ABC 中，7221332BC AC sin BAC ===∠． 2. 如图，过原点O 的直线与反比例函数y 1，y 2的图象在第一象限内分别交于点A 、B ，且A 为OB 的中点，若函数11y x =，则y 2与x 的函数表达式是 ▲ ．【答案】24y x=. 【考点】反比例函数的图象和性质；曲线上点的坐标与方程的关系；待定系数法的应用. 【分析】设y 2与x 的函数表达式是2k y x =， ∵点B 在反比例函数y 2的图象上，∴可设,k B b b ⎛⎫ ⎪⎝⎭. ∵A 为OB 的中点，∴,22b k A b ⎛⎫ ⎪⎝⎭. ∵点A 在反比例函数11y x =的图象上，∴122k bb =，解得4k =. ∴y 2与x 的函数表达式是24y x =.。