水静力学

第一章 水静力学水静力学的任务是研究液体的平衡规律及其工程应用。

液体的平衡状态有两种：一种是静止状态，即液体相对与地球没有运动，处于静止状态。

另一种是相对平衡，即所研究的整个液体相对于地球在运动，但液体相对于容器或液体质点之间没有相对运动，即处于相对平衡状态。

例如，等速直线行驶或等加速直线行驶小车中所盛的液体，等角速度旋转容器中所盛的液体。

本章的核心问题是根据平衡条件来求解静水压强的分布规律，并根据静水压强的分布规律来确定各种情况下的静水总压力。

即先从点、再到面，最后对整个物体确定静水总压力的大小、方向、作用点。

水静力学是解决水利工程中水力荷载问题的基础，同时也是今后学习水动力学的必要知识。

从后面章节的学习中可以知道，即使水流处于运动状态，在有些情况下，动水压强的分布规律也可认为与静水压强的分布规律相同。

第一节 静止压强及其特性一.静水压强的概念.在静水中有一受压面，其面积为ΔA ，作用其上的压力为ΔP ,则该微小面积上的平均静水压强为A P p ∆∆=，当ΔA →0时，平均压强的极限就是点压强，),,(0lim z y x A P A p p ==∆∆→∆，这也说明了静水压强是关于空间位置坐标的函数。

静水压强的单位有三种表示方法：（1）用应力的单位表示，即N/m 2或kN/m 2；（2）用大气压强的倍数表示；（3）用液柱高度表示。

静水压力并非集中作用于某一点，而是连续地分布在整个受压面上，它是静水压强这一分布荷载的合力。

静水压强反映的是荷载集度。

今后的学习中将重点掌握如何根据静水压强的分布规律推求静水总压力。

由于水利工程中有时习惯将压强称为压力，故水力学中就将静水压力称为静水总压力，以示区别。

游泳胸闷,木桶箍都说明静水压力的存在。

二.静水压强的特性1>方向 垂直指向受压面，用反证法说明。

2>大小 静水中任何一点各个方向的静水压强大小都相等。

n z y x p p p p === 而),,(z y x p p =三.绝对压强 相对压强1> 绝对压强以设想的没有大气压存在的绝对真空状态为零点计量得到的压强称为绝对压强，以p ab 或p ＇来表示。

第二章 水静力学水静力学（Hydrostatics ）是研究液体处于静止状态时的力学规律及其在实际工程中的应用。

“静止”是一个相对的概念。

这里所谓“静止状态”是指液体质点之间不存在相对运动，而处于相对静止或相对平衡状态的液体，作用在每个液体质点上的全部外力之和等于零。

绪论中曾指出，液体质点之间没有相对运动时，液体的粘滞性便不起作用，故静止液体质点间无切应力；又由于液体几乎不能承受拉应力，所以，静止液体质点间以及质点与固壁间的相互作用是通过压应力（称静水压强）形式呈现出来。

水静力学的主要任务是根据力的平衡条件导出静止液体中的压强分布规律，并根据其分布规律，进而确定各种情况下的静水总压力。

因此，水静力学是解决工程中水力荷载问题的基础，同时也是学习水动力学的基础。

§2-1 静水压强及其特性1．静水压强的定义 在静止的液体中，围绕某点取一微小作用面，设其面积为ΔA ，作用在该面积上的压力为ΔP ，则当ΔA 无限缩小到一点时，平均压强A P ∆∆/便趋近于某一极限值，此极限值便定义为该点的静水压强(Hydrostatic Pressure)，通常用符号p 表示，即dA dP A P p A =∆∆=→∆0lim (2-1) 静水压强的单位为2/m N (Pa(帕))，量纲为[][]21--=T ML p 。

2．静水压强的特性静水压强具有两个重要的特性：(1)静水压强方向与作用面的内法线方向重合。

在静止的液体中取出一团液体，用任意平面将其切割成两部分，则切割面上的作用力就是液体之间的相互作用力。

现取下半部分为隔离体，如图2-1所示。

假如切割面上某一点M 处的静水压强p 的方向不是内法线方向而是任意方向，则p 可以分解为切应力τ和法向应力p n 。

从绪论中知道，静止的液体不能承受剪切力也不可能承受拉力，否则将平衡破坏，与静止液体的前提不符。

所以，静水压强唯一可能的方向就是和作用面的内法线方向一致。

(2)静水压强的大小与其作用面的方位无关，亦即任何一点处各方向上的静水压强大小相等。

第二章 水静力学目的要求：掌握静水压强的有关概念；作用在平面、曲面上静水总压力的计算方法。

难点：压力体的绘制 全部内容均为重点水静力学研究液体平衡时的规律及其实际应用，静止时0=τ，只有p 存在。

§2-1 静水压强及其特性 一、定义P ∆—面积ω∆上的静水压力 （N ）平均静水压强ω∆∆=Ppa 点的静水压强)(/lim 20a P m N d dpP p ωωω=∆∆=→∆二、静水压强的特性1、第一特性：静水压强的方向垂直指向被作用面。

2、第二特性：作用于同一点上各方向的静水压强大小相等。

yzp⊿⊿⊿zxxpp ynpxzynACBnzyxpppp,,,，则⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∆∆∆∆∆∆∆spyxpzxpzypnzyx212121⎪⎪⎪⎩⎪⎪⎪⎨⎧∆∆∆∆∆∆∆∆∆zyxZzyxYzyxX616161ρρρ沿x方向力的平衡方程：61),cos(21=∆∆∆+∆-∆∆zyxXxnspzypnxρ612121=∆∆∆+∆∆-∆∆zyxXzypzypnxρ1=∆+-xXppρ取微分四面体无限缩至o 点的极限表面力质量力C pz C z p dz gdz dp =+→'+-=→-=-=γγγρ或 γγ2211p z p z +=+——重力作用下水静力学的基本方程。

对于液面点与液体内任意点h p p pz p h z γγγ+=→+=++00——水静力学基本方程的常用表达式说明：（1）当 2121z z p p >< ，位置较低点压强恒大于位置较高点压强。

液面压强0p 由γh 产生的压强（3） p 随h 作线性增大。

（4）常用a a p h p p ,γ+=为大气压强， 取p a =1个工程大气压=98kN/m 2。

（5）h p p ∆+=γ12二、等压面1、定义：在同一种连续的静止液体中压强相等的点组成的面2、等压面方程：0=dp 0=++Zdz Ydy Xdx3、特性：（1）平衡液体中等压面即是等势面。

第一章 水静力学考点一 静水压强及其特性1、静水压强的定义：静止液体作用在受压面每单位面积上的压力称为静水压强。

2、静水压强的特性：（1）静水压强垂直于作用面，并指向作用面的内部； （2）静止液体中任一点处各个方向的静水压强大小相等。

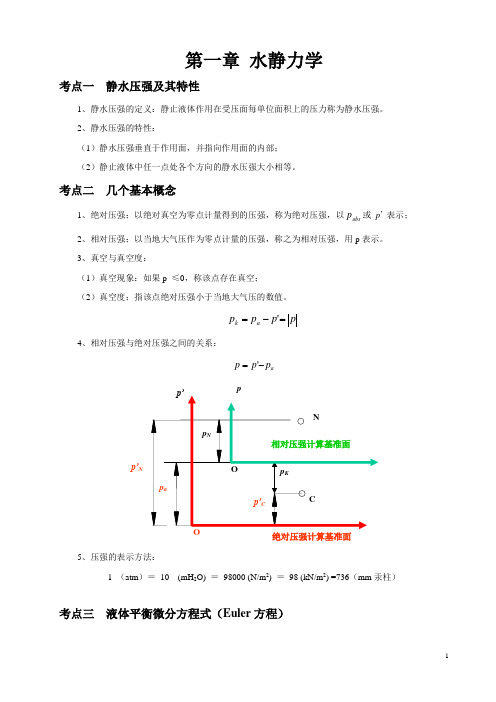
考点二 几个基本概念1、绝对压强：以绝对真空为零点计量得到的压强，称为绝对压强，以abs p 或 p ’ 表示；2、相对压强：以当地大气压作为零点计量的压强，称之为相对压强，用p 表示。

3、真空与真空度：（1）真空现象：如果p ≤0，称该点存在真空； （2）真空度：指该点绝对压强小于当地大气压的数值。

p p p p a k =-='4、相对压强与绝对压强之间的关系：a p p p -='5、压强的表示方法：1 （atm ）＝ 10 (mH 2O) ＝ 98000 (N/m 2) ＝ 98 (kN/m 2) =736（mm 汞柱）考点三 液体平衡微分方程式（Euler 方程）绝对压强计算基准面p’Np1、微分方程：液体平衡微分方程式，是表征液体处于平衡状态时作用于液体上的各种力之间的关系式。

2、综合表达式——压强差公式 ：）＝z Z y Y x X z zpy y p x x p p d d d (d d d d ++=∂∂+∂∂+∂∂ρ ）＝z Z y Y x X p d d d (d ++ρ 3、积分结果 ：若存在一个与坐标有关的力势函数U (x ,y ,z )，使对坐标的偏导数等于单位质量力在坐标投影，即⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂=∂∂=∂∂=z U Z y U Y x UX 可得U z Z y Y x X z zUy y U x x U p d d d d (d d d d ρρ=++=∂∂+∂∂+∂∂）＝U p d d ρ＝积分上式得到： C U p +ρ＝ 或者 )(00U U p p -+ρ＝ 式中， 为自由液面上的压强和力势函数。

考点四 等压面1、定义：静止液体中压强相等的点所组成的面称为等压面。

第3 章水静力学（Hydrostatics)3.1 静止液体中压强的特性3.2 静止液体平衡微分方程3.3 重力作用下静止液体中压强的分布规律3.4 液柱式测压计3.5 液体的相对平衡3.6 液体作用在平面壁上的总压力3.7 液体作用在曲面壁上的总压力第3 章水静力学（Hydrostatics)水静力学是液体在静止或相对静止状态下的力学规律及其应用的科学。

由流动性知，静止状态下，作用在液体上的表面力只有压强。

静止液体中压强的特性3.1 静止液体中压强的特性3.1特性一：静压强的方向与作用面的内法线方向一致，或静压强的方向垂直并指向作用面。

特性二：静止液体中任意点压强的大小与作用面的方向无关。

1707年4月15日出生于瑞士的巴塞尔城 ，1783 年9月18日去逝于俄罗斯的彼得堡，享年76岁。

13岁时入读巴塞尔大学，15岁大学毕业，16岁获硕士学位。

1727年任彼得堡科学院数学教授。

1741年应普鲁士彼德烈大帝的邀请，到柏林担任科学院物理数学所所长。

直到1766年，在沙皇喀德林二世的诚恳敦聘下重回彼得堡。

他从19岁开始发表论文，直到76岁，共写下了886本书籍和论文，涉及到数学分析、代数、数论、几何、物理和力学、天文学、弹道学、航海学、建筑学等。

他的许多著作都是在1766年失明后完成的。

欧 拉 Leonhard Euler3.2.2 等压面等压面—压强相等的空间点构成的面。

在等压面上，p = c ，d p = 0，平衡微分方程的全微分式则可表示为：上式称等压面方程。

根据等压面方程，单位质量力与等压面上任意线段的点0d d d =++z Z y Y x X lf z Z y Y x X d d d d ⋅=++ 等压面方程中，X 、Y 、Z 为单位质量力在三个坐标轴的分力，而 dd x 、d y 、d z 则是等压面上任意线段在三个坐标轴的投影，由矢量代数得：乘积等于乘积等于00，这说明这两个向量相互垂直，即质量力与等压面相互垂直，如重力与水平面。