北师大版八年级数学上册第七章 7.5.2三角形的外角 同步练习题( 教师版)

一．选择题（共2小题）1．（2019•杭州）在ABC ∆中，若一个内角等于另外两个内角的差，则( )A ．必有一个内角等于30︒B ．必有一个内角等于45︒C ．必有一个内角等于60︒D ．必有一个内角等于90︒ 2．（2015秋•西区期中）如图，图中x 的值是( )A ．30︒B ．40︒C ．50︒D ．60︒二．填空题（共1小题）3．（2019•郴州）如图，直线a ，b 被直线c ，d 所截．若//a b ，1130∠=︒，230∠=︒，则3∠的度数为 度．三．解答题（共2小题）4．（2017春•东城区期末）如图，已知在ABC ∆中，//DE CA ，12∠=∠，34∠=∠，84BAC ∠=︒．求EDA ∠的度数．5．（2019秋•南昌县期中）在ABC ∆中，20B A ∠=︒+∠，10C B ∠=∠-︒，求A ∠的度数．参考答案与试题解析一．选择题（共2小题）1．（2019•杭州）在ABC ∆中，若一个内角等于另外两个内角的差，则( )A ．必有一个内角等于30︒B ．必有一个内角等于45︒C ．必有一个内角等于60︒D ．必有一个内角等于90︒ 【解答】解：180A B C ∠+∠+∠=︒，A C B ∠=∠-∠，2180C ∴∠=︒，90C ∴∠=︒，ABC ∴∆是直角三角形，故选：D ．2．（2015秋•西区期中）如图，图中x 的值是( )A ．30︒B ．40︒C ．50︒D ．60︒【解答】解：如图：ACD A B ∠=∠+∠，A x ∠=︒，(10)B x ∠=+︒，(70)ACD x ∠=+︒， 1070x x x ∴++=+，解得：60x =．故选：D ．二．填空题（共1小题）3．（2019•郴州）如图，直线a ，b 被直线c ，d 所截．若//a b ，1130∠=︒，230∠=︒，则3∠的度数为 100 度．【解答】解：//a b ，34∴∠=∠，12423∠=∠+∠=∠+∠，1130∠=︒，230∠=︒， 130303∴︒=︒+∠，解得：3100∠=︒．故答案为：100．三．解答题（共2小题）4．（2017春•东城区期末）如图，已知在ABC ∆中，//DE CA ，12∠=∠，34∠=∠，84BAC ∠=︒．求EDA ∠的度数．【解答】解：4∠是ABD ∆的一个外角，412∴∠=∠+∠，设12x ∠=∠=，则432x ∠=∠=，在ADC ∆中，43180DAC ∠+∠+∠=︒，1804DAC x ∴∠=-，1BAC DAC ∠=∠+∠，841804x x ∴=+-，32x =，180418043252DAC x ∴∠=-=-⨯=︒，//DE CA ，52EDA DAC ∴∠=∠=︒．5．（2019秋•南昌县期中）在ABC ∆中，20B A ∠=︒+∠，10C B ∠=∠-︒，求A ∠的度数．【解答】解：设A x ∠=︒，则20B x ∠=︒+︒，201010C x x ∠=︒+︒-︒=︒+︒， 在ABC ∆中，180A B C ∠+∠+∠=︒，2010180x x x ∴︒+︒+︒+︒+︒=︒，解得50x =︒，即50A ∠=︒。

第2课时三角形的外角【基础练习】知识点1 三角形的外角定理11.如图16,在△ABC中,∠A=70°,∠ABC=60°,那么∠ACB的度数是;与∠ACB相邻的一个外角是,它的度数等于.图162.如果三角形的一个外角等于和它相邻的内角,那么这个三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形3.如图17,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为()图17A.45°B.48°C.50°D.58°4.如图18,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是()图18A.64°B.32°C.30°D.40°5.如图19,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是()图19A.70°B.44°C.34°D.24°6.将一副三角尺按如图20所示的位置放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边放在同一条直线上,则∠α的度数是()图20A.45°B.60°C.75°D.85°7.如图21,D是△ABC的边AC上一点,E是BD上一点,连接EC,若∠A=60°,∠ABD=25°,∠DCE=35°,求∠BEC的度数.图218.一个零件的形状如图22所示,按规定∠A应等于90°,∠B,∠C应分别是21°和32°,现测量得∠BDC=148°,你认为这个零件合格吗?为什么?图22知识点2 三角形的外角定理29.如图23,下列说法中错误的是()图23A.∠1不是△ABC的外角B.∠ACD是△ABC的外角C.∠ACD>∠A+∠BD.∠B<∠1+∠210.如图24,P是△ABC内一点,连接BP并延长交AC于点D,连接PC,则图中∠1,∠2,∠A的大小关系是()图24A.∠A>∠2>∠1B.∠A>∠1>∠2C.∠2>∠1>∠A D ∠1>∠2>∠A11.如图25,已知CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E.求证:∠BAC>∠B.图25【能力提升】12.如图26,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是()图26A.45°B.50°C.55°D.80°13.如图27所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,则下列说法正确的是()图27A.∠2+∠3>∠1B.∠2+∠3<∠1C.∠2+∠3=∠1D.以上均不对14.如图28所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.图2815.如图29所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,连接BE.求证:∠BED>∠C.图2916.已知:如图30,在△ABC中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E 为射线BM上一点.(1)连接CE.①若CE∥AB,求∠BEC的度数;②若CE平分∠ACD,求∠BEC的度数.(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.图30答案1.50°∠BCE130°[解析] 由三角形内角和定理,得∠ACB=180°-70°-60°=50°,则∠BCE=180°-∠ACB=130°.2.A[解析] 三角形的一个外角与和它相邻的内角的度数和为180°.又因为三角形的一个外角等于和它相邻的内角,所以三角形的这个内角为90°,即这个三角形是直角三角形.3.B4.B5.C6.C7.解:∵∠BDC是△ABD的外角,∴∠BDC=∠A+∠ABD=60°+25°=85°.同理∠BEC=∠BDC+∠DCE=85°+35°=120°.8.解:不合格.理由:如图,延长CD与AB相交于点F.若此零件合格,则∠DFB=∠C+∠A=32°+90°=122°,∠BDC=∠DFB+∠B=122°+21°=143°.因为实际量得的∠BDC=148°,143°≠148°,所以这个零件不合格.9.C10.D11.证明:∵CE是∠ACD的平分线,∴∠ACE=∠ECD.∵∠ECD是△BEC的外角,∴∠ECD>∠B.∵∠BAC是△AEC的外角,∴∠BAC>∠ACE,∴∠BAC>∠ECD,∴∠BAC>∠B.12.B[解析] 在△CEF中,∵∠E=80°,∠F=50°,∴∠ECF=50°.如图,延长BC交AD于点M.∵AB∥CF,AD∥CE,∴∠B=∠BCF,∠BMD=∠BCE=50°+∠BCF.又∵∠BMD=∠A+∠B,∴∠A=50°.13.C14.解:设∠1=∠2=x,则∠3=∠4=2x.因为∠BAC=63°,所以∠2+∠4=117°,即x+2x=117°.所以x=39°.所以∠1=39°,所以∠DAC=∠BAC-∠1=63°-39°=24°.15.[解析] 要证明一个角大于另一个角,可用三角形的一个外角大于任何一个和它不相邻的内角,但显然∠BED与∠C之间并不存在外角和内角的关系,所以一定存在一个“中间量”,这个中间量起着桥梁的作用:∠BED>∠BAD=∠C.这种策略是证明角之间不等关系的常用方法.证明:因为∠BAC=90°,所以∠BAD+∠CAD=90°.因为AD⊥BC,所以∠ADC=90°.所以∠C+∠CAD=180°-90°=90°.所以∠BAD=∠C.因为∠BED是△BAE的外角,所以∠BED>∠BAD(三角形的一个外角大于任何一个和它不相邻的内角).所以∠BED>∠C.[点评] 证明两个角的大小关系,一般用到三角形外角与内角之间的关系,这是解题的突破口,但它们之间往往没有直接的联系,这时需要找中间量“过渡”或作辅助线“架桥”,这是解题的关键.16.解:(1)①因为∠A=60°,∠ACB=40°,所以∠ABC=80°.因为BM平分∠ABC,∠ABC=40°.所以∠ABE=12因为CE∥AB,所以∠BEC=∠ABE=40°.②因为∠A=60°,∠ACB=40°,所以∠ABC=80°,∠ACD=180°-∠ACB=180°-40°=140°.因为BM平分∠ABC,CE平分∠ACD,所以∠CBE=1∠ABC=40°,2∠ACD=70°.∠ECD=12所以∠BEC=∠ECD-∠CBE=70°-40°=30°. (2)①若CE⊥BC,则∠ECD=90°.因为∠CBE=40°,所以∠BEC=50°;②若CE⊥AB,因为∠ABE=40°,所以∠BEC=90°+40°=130°;③若CE⊥AC,因为∠CBE=40°,∠ACB=40°,所以∠BEC=180°-40°-40°-90°=10°.综上所述,∠BEC的度数为50°或130°或10°.。

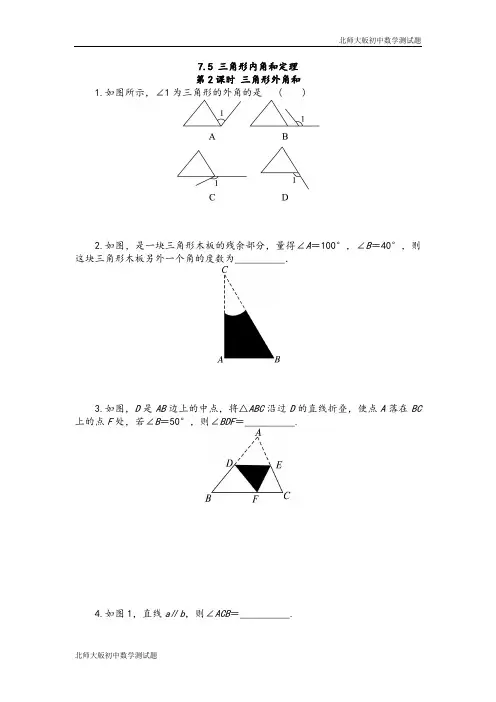
7.5 三角形内角和定理第2课时三角形外角和1.如图所示，∠1为三角形的外角的是 ( )2.如图，是一块三角形木板的残余部分，量得∠A＝100°，∠B＝40°，则这块三角形木板另外一个角的度数为__________．3.如图，D是AB边上的中点，将△ABC沿过D的直线折叠，使点A落在BC 上的点F处，若∠B＝50°，则∠BDF＝__________.4.如图1，直线a∥b，则∠ACB＝__________.5.等腰三角形的一个外角为110°，则这个等腰三角形的三个内角分别为__________．6.已知：如图，在△ABC中，D为BC上一点，∠1＝∠2，∠3＝∠4，∠BAC ＝120°，求∠DAC的度数．掌握的三个数学答题方法树枝答题法关注数学题的解题过程2014年上海市中考状元徐瑜卿认为,数学是一门思维学科,并不是平时做题多就一定会拿高分。

很多同学虽然数学思维很好,但一下笔就丢分,这就要求我们平时练习时一定要注重解题过程。

因此,大家在学习数学时要在立足结论和答案的基础上,仔细深入地了解解题的过程,要求每一步都必须有严谨的推导依据,绝不要想当然。

这样做不仅可以培养我们的逻辑思维能力,而且对于物理、化学的学习也是非常重要的关于这点,徐瑜卿同学还总结出了一个非常实用的解题方法:树枝答题法。

这种方法是用已知条件推导出多个潜在条件,每个潜在条件继续推导出更多潜在条件,如此继续;同时由所求问题或求证的结论逆推所需条件,也是由少到多。

这就像两棵本无关系的树,枝干越伸越多,最终会交织在起,题目最终也就迎刃而解了。

她的这套解题模式针对难题尤其有效,平时多训练,熟练之后往往能一眼看穿关键,能避免走弯路其实,树枝答题法总结一下就是五个字:从条件入手。

在解数学题时,就是要实现“条件”向“结论”转化,由“已知”推出“未知”,因此在般情况下,总是从分析条件入手,看看由条件甲能推出什么?接着又能推出什么?……然后由条件乙能推出什么?当然,如果大家遇到由条件向前推进极其困难的题目,甚至无路可走时,就可以考虑从命题的结论开始往后推,逐步接近命题的条件,用逆推的方法找到解题思路。