单纯形法表的解题步骤

格式：pdf
大小：121.55 KB
文档页数：8

下载文档原格式

第4节单纯形法计算步骤

CB 0 0 0
0 1 0 0 1 -2
cj 基 x1 x4 x5 cj-zj x1 x2 x5
b 2 1 2
4 1 1 6.5 2.5 0.5
0 x1 1 0 0 0 1 0 0
1 -2 x2 x3 -2 1 1 -3 1 -1 1 -2 0 1 0 -5 -3 2
运筹学 0 0 x4 x5 0 0 1 0 0 1 0 2 1 -1 0 0 0 1
（3）求检验数第四步：重复2、3两步，直到计算结束为止。
安徽科技学院例5：用单纯形法求解线性规划问题解：先将其化成标准形式
m a x z 2 x1 x 2 0 x 3 0 x 4 0 x 5 5 x 2 x3 15 x4 24 6 x1 2 x 2 s .t . x5 5 x1 x 2 x ,x ,x ,x ,x 0 1 2 3 4 5
m
bb a b b b1 a . . . bl b ba a . l lk . . a b bb m a
1 l l lk m l
1k lk
mk lk
c … c1 1 … x … x1 1 … … 11 … . .. .. . … 0. 00 … .. .. . … 00 …
… cm clcl … cm … xm xlxal … xm … 0 0 a … 0. . .. . .. . . 1 1 … 0 0 1aa … 0. . lk .. . .. . . a … 1 0a … 1
其他情况转第三步。第三步：从一个可行基解转换到相邻的目标函数值更大的基可行解，列出新的单纯形表
1、确定换入基的变量xk： k m a x j | j 0

单纯形表法详细讲解

单纯形表法详细讲解
单纯形法是一种求解线性规划问题的数学方法。

以下是其详细步骤：
1. 确定初始基可行解：一般采用取松弛变量的方法来获得初始基可行解，从而得到对应的单位矩阵作为基。

2. 判断是否满足最优解条件：单纯形法从可行域中的一个点开始，判断该顶点是否为最优解。

如果不是，就寻找另一个目标函数值更优的顶点。

3. 迭代优化：通过单纯形表判断出顶点是否为最优解，如果线性规划问题没有最优解，则继续迭代优化，直到找到最优解或确定问题无解。

4. 确定最优解：在单纯形表中，理解其系数矩阵、基、基向量、非基向量和基变量等基本概念，从而确定最优解。

5. 确定换入变量和换出变量：在单纯形表中，如果发现非基变量的系数大于零，则可以通过增加这些变量的值来使目标函数增加。

由于每个变量都大于零，对于某个变量增加是有所限制的，如果该变量过大，由于其他限制条件，会导致其他变量小于零。

因此，应该让该变量一直增大，直到有一个其他变量刚好等于0为止，那么这个变量就被换出基。

6. 进行高斯行变换：使用第4行对各行进行高斯行变换，使得二列第四行中的每个x都变成零，也包括c2。

如需更多关于单纯形法的信息，可以咨询数学专家或查阅相关文献资料。

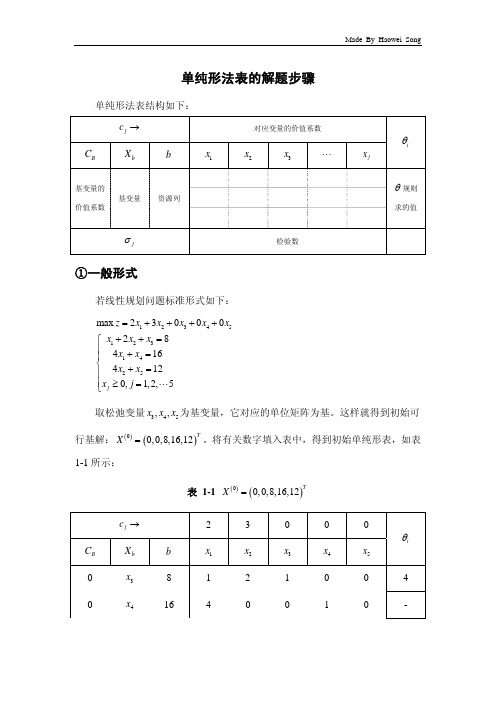
单纯形法表的解题步骤

单纯形法表的解题步骤单纯形法表结构如下：j c →对应变量的价值系数i θB Cb Xb1x 2x 3x " j x基变量的价值系数基变量资源列θ规则求的值j σ检验数①一般形式若线性规划问题标准形式如下：123451231425max 23000284164120,1,2,5j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨+=⎪⎪≥=⎩"取松弛变量345,,x x x 为基变量，它对应的单位矩阵为基。

这样就得到初始可行基解：()()00,0,8,16,12TX =。

将有关数字填入表中，得到初始单纯形表，如表1-1所示：表 1-1 ()()00,0,8,16,12TX =j c →2 3 0 0 0i θB C b X b1x 2x 3x 4x 5x0 3x 8 1 2 1 0 0 4 04x16 4 0 0 1 0 -5x12 0 [4] 0 0 1 3j σ2 3 0 0 0若检验数均未达到小于等于0，则对上表进行调整。

选择上表中检验数最大的列，该列对应的非变量为入基变量；再应用θ规则该列对应的各基变量对应的θ值，选出其中最小的一行，该行对应的基变量为出基变量。

修改单纯形表，对各行进行初等变换，确保基变量组成的矩阵为单为矩阵。

修改后的单纯形表如表1-2所示：表 1-2 ()()10,3,2,16,0TX =检验数12,0σσ>，则进行继续调整，调整后的单纯形法表如表1-3所示：表 1-3 ()()22,3,0,8,0TX =表1-3中， 50σ>，则继续进行调整，调整结果如表1-4所示：表 1-4 ()()34,2,0,0,4TX =检验数0j σ≤，这表示目标函数值已不可能再增大，于是得到最优解：()()3*4,2,0,0,4TX X ==*14z =②带人工变量现有线性规划问题：12312312313123min 321142321,,0z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解，在约束条件中加入松弛变量4x ，剩余变量5x ，人工变量6x ，7x 得到：1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨−++=⎪⎪≥=⎩"其中，M 是一个任意大的正数。

单纯形法的表格解法

1. 最优性检验的依据——检验数σj 一般来说目标函数中既包括基变量，又包括非基变量。现在我们要求
只用非基变量来表示目标函数，这只要在约束等式中通过移项等处理就可以用非基变量来表示基变量，然后用非基变量的表示式代替目标函数中基变量，这样目标函数中只含有非基变量了，或者说目标函数中基变量的系数都为零了。此时目标函数中所有变量的系数即为各变量的检验数，把变量xi的检验数记为σi。显然所有基变量的检验数必为零。在本例题中目标函数为50x1+100x2。由于初始可行解中x1，x2为非基变量，所以此目标函数已经用非基变量表示了，不需要再代换出基变量了。这样我们可知 σ1=50，σ2=100，σ3=0，σ4=0，σ5=0。
向量为 pj j 1, 2,L ,n 则
z j cB1,L , cBm pj cB pj ,
其中，(cB)是由第1列第m行各约束方程中的基变量相应的目标函数依次组成的有序行向量。
单纯形法的表格形式是把用单纯形法求出基本可行解、检验其最优性、
迭代某步骤都用表格的方式来计算求出，其表格的形式有些像增广矩阵，
n
bi aij xj. i 1, 2,L , m
j m1
把以上的表达式带入目标函数，就有
m
n
z c1x1 c2 x2 L cn xn ci xi c j x j
i 1
j m 1
其中：
n
n
z0
c j z j x j z0 j x j
j m 1
j m 1
.
§1 单纯形法的基本思路和原理
非基变量：与非基向量pj相应的变量xj叫非基变量，非基变量有n－m个。由线性代数的知识知道，如果我们在约束方程组系数矩阵中找到一个

第二节单纯形法3.29

单纯形法的进一步讨论
人工变量法：前面讨论了在标准型中系数矩阵有单位矩阵，很容易确定一组基可行解。在实际问题中有些模型并不含有单位矩阵，为了得到一组基向量和初始基可行解，在约束条件的等式左端加一组虚拟变量，得到一组基变量。这种人为加的变量称为人工变量，构成的可行基称为人工基，用大M法或两阶段法求解，这种用人工变量作桥梁的求解方法称为人工变量法。
移项可得： x3 1 x1 x2
显然这是线性规划问题的可行解，此时目标函数值
z 2 x1 2 x2 2M 0 2M
当M无限增大，目标函数值也无限增大。因此此线性规划问题有无界解。不妨令x1 M , x2 0可得一组解
1 x4 2 x1 x2 2
无界解判别方法：
在求解极大化的线性规划问题过程中，若某单纯形表的非基变量的检验数大于0，但是该非基变量的系数列都为负数或零，则该线性规划问题为无界解。
例用单纯形法求解下列LP问题
max z 2 x1 2 x2 x1 x2 1 1 s.t. x1 x2 2 2 x1 , x2 0
max z 2.5x1 x 2
3x1 5 x 2 15 s.t.5 x1 2 x 2 10 x1, x 2 0
例：用单纯形法求解下面的线性规划
max z 2.5x1 x 2
会出现什解：增加松弛变量x , x , 将模型化为标准型：么情况呢 max z 2.5 x1 x 2
3
4
直观上有什么特点？
——目标与某约束斜率相同
2.5
C
X
B b

x
1
x
1
2

单纯形法的计算步骤

变量作为换出变量。
L
min
bi
aik
a ik
0
单纯形法旳计算环节
Page 4
③ 用换入变量xk替代基变量中旳换出变量，得到一种新旳基。相应新旳基能够找出一种新旳基可行解，并相应地能够画出一种新旳单纯形表。
④ 5）反复3）、4）步直到计算结束为止。
单纯形法旳计算环节
将3化为1
换入列
j
乘
,
x2
,
x3
,
x4
0
Page 1
单纯形法旳计算环节
Page 2
2）求出线性规划旳初始基可行解，列出初始单纯形表。
j
检验数
1 c1 (c3a11 c4a21 ) 3 (0 2 0 1) 3
单纯形法旳计算环节
Page 3
3）进行最优性检验
假如表中全部检验数止。不然继续下一步。
，j 则表0中旳基可行解就是问题旳最优解，计算停
单纯形法旳计算环节
例1.8 用单纯形法求下列线性规划旳最优解
max Z 3 x1 4 x2
2 x1 x2 40
x1
3x2
30
x1
,
x2
0
解：1）将问题化为原则型，加入松驰变量x3、x4则原则型为:
max Z 3 x1 4 x2
2 x1 x2 x3 40
x1
3x2
x4
30
x1
以
1/3 后
j
得
到
j
30 5/3 0 10 1/3 1
5/3 0
18 1
0
40
1
0
0
Page 5
bi /ai2，ai2>0

单纯形表例题详解易懂

单纯形法（Simplex Method）是线性规划问题的一种求解方法。

下面我将以一个简单的线性规划问题为例，详细解释如何使用单纯形法求解。

例题：假设我们有一个简单的线性规划问题，目标是最小化目标函数 z = 3x + 2y，约束条件是 x + y <= 10, x >= 0, y >= 0。

首先，我们需要构建问题的数学模型。

数学模型可以表示为以下形式：z = 3x + 2yx + y <= 10x >= 0y >= 0然后，我们可以将这个线性规划问题表示为一个单纯形表。

单纯形表的形式如下：| c | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | ||---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---||x | y | z | u | v | w | x1 | x2 | x3 | ... | xn | s.x | s.y | s.z | c.val | b.x | b.y | b.z | dual.val | dual.x1 | dual.x2 | ... | dual.xn ||在这个表中，c 是目标函数的系数，b 是约束条件的系数，s 是松弛变量的系数，dual 是对偶问题的系数，c.val 是当前解的目标函数值，b.x, b.y, b.z 是约束条件的边界值，s.x, s.y, s.z 是松弛变量的值。

现在，我们可以将例题中的数据填入单纯形表：c = [3, 2, 1]b = [1, 0, -10]s = [1, 1, 0]dual = []然后，我们可以开始迭代求解。

在每一次迭代中，我们首先找到进入变量和离开变量，然后更新单纯形表中的数据。

单纯形法解题步骤

三、单纯形法的解题步骤第一步：作单纯形表.）（1）把原线性规划问题化为标准形式；）（2）找出初始可行基，通常取约束方程组系数矩阵中的单位矩阵；）（3）目标函数非基化；）（4）作初始单纯形表.第二步：最优解的判定.(1) 若所有检验数都是非正数，即，则此时线性规划问题已取得最优解.(2) 若存在某个检验数是正数，即，而所对应的列向量无正分量，则线性规划问题无最优解.如果以上两条都不满足，则进行下一步.第三步：换基迭代.，并确定所在列的非基变量为进基变量.（1）找到最大正检验数，设为（2）对最大正检验数所在列实施最小比值法，确定出主元，并把主元加上小括号.主元是最大正检验数所在列，用常数项与进基变量所对应的列向量中正分量的比值最小者；替换出基变量，从而得到新的基变量.也就是主元所在（3）换基：用进基变量（4）利用矩阵的行初等变换，将主元变为1，其所在列其他元素都变为零，从此得到新的单纯形表；（5）回到第二步，继续判定最优解是否存在，然后进行新一轮换基迭代，直到问题得到解决为止.例3 求.解（1）化标准型：令，引进松弛变量，其标准型为求（2）作单纯形表：在约束方程组系数矩阵中的系数构成单位矩阵，故取为基变量，目标函数已非基化了，作初始单纯形表并“换基迭代”（见表6.8）.表 6.8（3）最终结果：此时检验数均为非正数，线性规划问题取得最优解，最优解为标函数取得最优值.目性规划问题的最优解为：.原线目标函数的最优值为14，即.例4 用单纯形方法解线性规划问题.求.解此数学模型已是标准型了，其中约束方程含有一个二阶单位矩阵（1、2行，3、4列构成），取为基变量，而目标函数没有非基化.从约束方程找出，,代入目标函数, 经整理后，目标函数非基化了.作单纯形表，并进行换基迭代（见表6.9）.最大检验数，由最小比值法知：为主元，对主元所在列施以行初等变换，基变量出基，非基变量进基.表 6.9目前最大检验数，其所在列没有正分量，所以该线性规划问题没有最优解.例5用单纯形方法解线性规划问题.求解此数学模型已是标准型了，其中约束方程含有一个二阶单位矩阵，取为基变量，而目标函数没有非基化.从约束方程找出，,代入目标函数，经整理得,目标函数已非基化.作单纯形表，并进行换基迭代(见表6.10).最大检验数，由最小比值法知：为主元，对主元所在列施以行初等变换，基变量出基，非基变量x2进基，先将主元化为1，然后再将主元所在列的其他元素化为零.表 6.10至此，检验数均为非正数，故得基础可行解.原问题的最优解为：.最优值为6，即.如果我们再迭代一次，将基变量出基，非基变量进基（见表6.11）.表 6.11可得到另一个基础可行解,原问题的最优解为：，最优值仍为6，说明该线性规划问题有无穷多最优解，其最优解均为6.如何知道线性规划问题有无穷多最优解呢？这主要反映在单纯形表中.如果非基变量所对应的检验数为0，我们可对此列继续进行换基迭代，就可以得到另一个基础可行解.以此作下去，可得到许多基础可行解，即相对应的最优解有无穷多个.（4） 011 0。

运筹学1-4单纯形法计算步骤ppt课件

x4
θ
0 x3 21 1 3 1 0 7
0 x4 4 -1 1 0 1 4
cj-zj
3900
0 x3 9 4 0 1 -3
9 x2 4 -1 1 0 1
cj-zj
12 0 0 -9
第19页
cj
3900
CB XB b
x1
x2
x3
x4
θ
0 x3 21 1 3 1 0 7
0 x4 4 -1 1 0 1 4
1 -1 0 1 -
1100
所以把x3换出为非基变量，x2为换入变量即新的基变量。
第29页
cj
CB XB b
0
x3 4
0
x4 2
cj-zj
1
x2 4
1100
x1
x2
x3
x4
θ
-2 1 1 0 4
1 -1 0 1 -
1100
-2 1 1 0
第30页
cj
CB XB b
0
x3 4
0
x4 2
cj-zj
1
θ
0
0 90/1
1
0 75/2
0
1 80/2
0
0
-1/2 0 21
1/2 0 75
-1
1
5
-3 0
2
-5/2
1
-1/2
-1
1
第12页
cj
6
5
0
CB
XB
b
x1
x2
x3
0
x3
90
1
3
1
0
x4
75
2
1
0

单纯形法解题步骤

单纯形法求解全过程详解共9页

（7）接下来，我们的任务就是找另一个基可行解。即转回到步骤（5）。
选择进基变量： max⎨⎧σ1 ⎩
=
5⎫
3
⎬ ⎭
=σk
= σ1 ，即
x1 进基成为基变量。
出基变量：
min
⎧
⎨ ⎩
b1 a11
,
b2 a21
⎫
⎬ ⎭
=
min⎨⎧30 × ⎩
3 5
= 18,10 × 3 = 30⎬⎫ ⎭
=
b1 a11
，即第
3
3
1
0
−
5
5
1
2
1
−
5
5
这时，我们可以得到基 B3 = [P1, P2 ] 对应的基可行解。
即令非基变量 x3 = 0, x4 = 0 ，根据表中的约束条件可得 x1 = 18, x2 = 4 （这两个值正好是表中基变量对应的资源向量 b 对应的分量）那么，第 3 个基可行解为 X 3 = [18,4,0,0]T 。（8）找到了第 3 个基可行解，接下来的任务就是判断该基可行解是否为最优解，检验其是否为最优解的标准前面已经详细讲述，这里就不啰唆了。即转回到步骤（4）。
1
0
1
10 × 3 = 30
3
σ
(2) j
=
cj
−
CB
⋅
Pj
5
0
0
−4
3
3
3
x1
1
0
4
x2
0
1
σ
(3) j
=cj
− CB
⋅ Pj
5
1
先来看主元 a11 所在的行。行的系数表示的是约束条件： 30 = 3 x1 + x3 − 3 x4 ①’。

1.4 单纯形法计算步骤

xB x4 x5
b
19 9 0
m
x1 x2 x3 x4 x5
3 9 10
θ
σj =cj - ci aij
i 1
z= ci bi
i 1
第10页
4.2计算步骤
单纯形法基本步骤
(1) 寻找初始可行基，初始基可行解，建立初始单纯形表。
(2) 对应于所有非基变量检验数σ j 0。若是，停，得到最优解；若否，转(3)。 (3) 若有σ k >0， σ k对应的Pk 0，停，此问题无界；否则转(4)
X *= (4, 2, 0 ,0 , 4)T
最优解
第18页
4.2计算步骤用单纯形法求解线性规划问题
课堂练习
第19页
4.2计算步骤
cj
CB
10 b 19 9 0 3 9 10
3 6 3 3
4 2 1 4
0 1 0 0
0 θ 0 1 0
0 0
xB x4 x5
x1 x2
x3 x4 x5
z
第20页
§1.4 单纯形法计算步骤
1.将非标准型线性规划化为标准型 2.确定初始基可行解：一般设松弛变量为初始基可行解 3.判断：若所有的非基变量的检验数σj≤0，则此解为LP的最优解，若存在某一非基变量的检验数 σj>0，则问题还没有达到最优解，需进行改进 4.迭代：选换入变量max{cj- zj/ cj-zj>0}假设xk为换入变量；选换出变量θ＝min{bi/aik，aik＞0}，假设选取xl为换出变量；然后迭代，使得alk＝1，其余aik为0 m
第11页
4.2计算步骤
单纯形法基本步骤
(4) Max σj =σk→Xk 换入变量 σ >0

第3,4节单纯形法与计算步骤

N =(1 , 2 , 3 ) (3, 0, 4)
（3）基本可行解 X=(0,0,0,8, 7)T 的改进
① 选取换入变量因为max{3，4}=4，取x3为换入变量。 ②
1
选取换出变量
8 1 2 8 7 8 ，且 min B b= , B P3 0 , 2 1 2 7 1
若
-1 -1 (B b) (B b)i min -1 /(B-1Pm+k )i >0,1 i m = -1 l (B Pm+k )l (B Pm+k )i
则选取对应的基变量 xl 为换出变量。
定理3：无最优解判别定理
B1b 若 X= 是一个基本可行解，有一个检验数 m+k 0 -1 但是 B Pm+k 0 ，则该线性规划问题无最优解。
解： (１)确定初始的基本可行解。
C=(5,2,3, 1 ,1)
8 1 2 2 1 0 A= b 7 3 4 1 0 1
1 0 B=(P4 P5 )= ，基变量 0 1
x 4 ,x 5，非基变量 x1 ,x 2 , x 3 。
x1 x4 1 0 1 2 2 CB =(-1,1) 8 X B = ,X N = x 2 ,B= ,N= , C =(5,2,3) ,b= x 0 1 3 4 1 N 7 5 x 3 8 1 X N =0 XB =B b= X=(0,0,0,8, 7)T 7 8 Z=CB B1b=(-1,1) 1 7
因为
m+k 0,
故当λ→+≦时，Z→+≦。

运筹学1-4单纯型法的计算步骤

2 X1 1 3 X2 2
Z8
1 0 -1 4/3 -1/3 0 1 2 -1/3 1/3 0 0 -1 -5/3 -1/3
从最优表可知: 该LP的
最优解是X*=(1, 2, 0, 0, 0)T 相应的目标函数最优值是Zmax=8
表格单纯形法求解步骤
第一步：将LP化为标准型，并加以整理。
引入适当的松驰变量、剩余变量和人工变量，使约束条件化为等式，并且约束方程组的系数阵中有一个单位阵。
（这一步计算机可自动完成）
确定初始可行基，写出初始基本可行解
第二步：最优性检验
计算检验数，检查：所有检验数是否≤ 0？
是——结束，写出最优解和目标函数最优值；还有正检验数——检查相应系数列≤ 0？
是——结束，该LP无“有限最优解”！不属于上述两种情况，转入下一步—基变换。
确定是停止迭代还是转入基变换？
0 1 0
0
0
1
0
0
0
1 c1 c2
0 a1,m1 a1,m2 0 a2,m1 a2,m2
1 a a m,m1 m,m2 cm cm1 cm2
a1,n b1
a2,n
b2
am,n bm
cn 0
-Z，x1，…，xm所对应的系数列向量构成一个基
用矩阵的初等行变换将该基变成单位阵,这时
c1, c2 , , cm 变成0，相应的增广矩
第四步：判断检验数、入基、出基变量。 …….
三、表格单纯形法：
1、初始单纯形表的建立 (1)表格结构：
Cj 2 3 3 0 0
CB
XB
b xj
x1 x2 x3 x4 x5
j
0 X4
3

单纯行法的计算步骤

max c j c j 0 ck ，对应的 xk 为进基变量。选择进基变量：
选择出基变量： min
bi bl ，对应的第 l 个基变量 aik 0 aik alk
为出基变量。
max z 2 x1 x2 5 x2 x3 15 6 x 2 x x 24 2 4 s.t. 1 x1 x2 x5 5 x15 0
max z 3 x1 4 x2 2 x1 x2 x3 40 x1 3 x2 x4 30 x , x , x , x 0 1 2 3 4
alk为主元素
2 1 1 0 A 1 3 0 1
1 0 B1 0 1 a12
4 x2
1
1 2 c2 c3 c4 a13 4 0 0 4 a 0 3 c3 c3 c4 0 0 0 0 a 3 14 22 0 0 0 4 c4 c3 c4 a 0 23 0
x1 x2 X x n
a11 a12 a a22 21 A am1 am 2
b1 b2 b b m

线性规划数学模型的标准型：
C c1, c2 , c3 ,, cn
max z 2 x1 x2 5 x2 x3 15 6 x 2 x x 24 2 4 s.t. 1 x1 x2 x5 5 x15 0

1 1 max z 8 x2 x4 3 3 5 x2 x3 15 1 1 x x x 4 1 3 2 6 4 s.t. 2 1 x2 x4 x5 1 6 3 x1 5 0

1.4单纯形法的计算步骤

−z
x1
x2
L xm
xm+1
L xn L L a1n a2n M
0 1 0 L 0 a1,m+1 1 L 0 a2,m+1 0 0 M M M M 0 0 0 L 1 am,m+1 cm+1 1 c1 c2 L cm … -z+c1x1+c2x2+…+cmxm+cm+1xm+1+ +c
基变量 0
-z
3.确定主元素 3.确定主元素确定 1.计算检验数， 1.计算检验数，由它计算检验数确定为换入变量
计算θ 2. 计算θ，由它确定为换出变量
（2）以[4]为主元素进行旋转运算或迭代运算， [4]为主元素进行旋转运算或迭代运算，为主元素进行旋转运算或迭代运算
c j→ CB 0 0 3 -z XB x3 x4 x2 b 2 16 3 -9 2 x1 1 4 0 2 3 x2 0 0 1 0 0 x3 1 0 0 0 0 x4 0 1 0 0 0 x5 -1/2 0 1/4 -3/4 θ 2 4 -
0 x4 0 1 0 0
0 x5 -1/2 2 1/4 1/4
0 X4 1/4 1/2 -1/8 -1/8 1 0 0
θ 4 12
c j→ CB 2 0 3 -z XB x1 x5 x2
0 x5 0 θ
表 1-5
-3/2
(4) 表1-6最后一行的所有检验数都已为负或零。最后一行的所有检验数都已为负或零。表示目标函数值已不可能再增大，于是得到最优解表示目标函数值已不可能再增大，于是得到最优解
x1 x2
+ a1m+1xm+1 +L+ a1nxn = b1 + a2m+1xm+1 +L+ a2nxn = b2 O xm + amm+1xm+1 +L+ amnxn = bm

线性规划与单纯形法-计算步骤

X * (15, 20, 0, 0) Z* 1350
max Z 3x1 5x2
x1
s.t.
3x1
x1 0
2x2 2 x 2 x2 0
4 12 18
第一次迭代 x2为入基， x4为出基第二次迭代 x1为入基， x5为出基
X * (2, 6, 2, 0, 0) Z* 36
2.4 单纯形法计算步骤
3、确定进基变量（迭代的第一步）
确定进基变量对应于图解法的确定运动方向
x1
x3
8
3x1
2x2 4x2
x4
12
x5 36
3x1 5x2 0x3 0x4 0x5 Z
j
从目标函数-Z+3x1+5 x2 +0x3 +0x4+0x5 =0可知：因为x2的系数大于x1的系数，即生产单位乙产品比甲产品利润更高一些，故应优先多生产乙产品。即x2为进基
5 2
x4
0 x5
Z 30
④
x3
2 3
x4
1 3
x5
4 ①
x2
x1
1 2 x4
2 3 x4
1 3 x5
6 ② 4 ③
3x1 0x2
0 x3
5 2
x4
0 x5
Z 30 ④
④-3×③
x3
2 3
x4
1 3
x5
4 ①
x2
1 2
x4
6 ②
x1
2 3
x4
1 3
x5
4 ③
0
x1
STOP 包括三个步骤： 1、确定进基变量（进基） 2、确定出基变量（出基） 3、对新基可行解的求解（高斯消元）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

单纯形法表的解题步骤
单纯形法表结构如下：
j c →
对应变量的价值系数
i θ
B C
b X
b
1x 2x 3x " j x
基变量的价值系数
基变量资源列
θ规则
求的值
j σ
检验数
①一般形式
若线性规划问题标准形式如下：
123451231425max 23000284164120,1,2,5
j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨
+=⎪⎪≥=⎩"
取松弛变量345,,x x x 为基变量，它对应的单位矩阵为基。

这样就得到初始可
行基解：()()0
0,0,8,16,12T
X =。

将有关数字填入表中，得到初始单纯形表，如表
1-1所示：
表 1-1 ()()00,0,8,16,12T
X =
j c →
2 3 0 0 0
i θ
B C b X b
1x 2x 3x 4x 5x
0 3x 8 1 2 1 0 0 4 0
4x
16 4 0 0 1 0 -
5x
12 0 [4] 0 0 1 3
j σ
2 3 0 0 0
若检验数均未达到小于等于0，则对上表进行调整。

选择上表中检验数最大的列，该列对应的非变量为入基变量；再应用θ规则该列对应的各基变量对应的
θ值，选出其中最小的一行，该行对应的基变量为出基变量。

修改单纯形表，对各行进行初等变换，确保基变量组成的矩阵为单为矩阵。

修改后的单纯形表如表
1-2所示：
表 1-2 ()()10,3,2,16,0T
X =
检验数12,0σσ>，则进行继续调整，调整后的单纯形法表如表1-3所示：
表 1-3 ()()22,3,0,8,0T
X =
表1-3中， 50σ>，则继续进行调整，调整结果如表1-4所示：
表 1-4 ()()34,2,0,0,4T
X =
检验数0j σ≤，这表示目标函数值已不可能再增大，于是得到最优解：
()()3*4,2,0,0,4T
X X ==
*14z =
②带人工变量
现有线性规划问题：
12312312313123min 3211
42321,,0
z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨
−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解，在约束条件中加入松弛变量4x ，剩余变量5x ，人工变量6x ，7x 得到：
1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨
−++=⎪⎪≥=⎩
"
其中，M 是一个任意大的正数。

用单纯形法表进行计算，由于是求MIN ，所以用所有0j σ≥来判别目标函数是否实现了最小化。

初始单纯行表如表2-1所示：
j c →
-3 1 1 0 0 M M
i θ
B C b X b
1x 2x 3x 4x 5x 6x 7x
0 4x 10 3 -2 0 1 0 0 -1 - M 6x 1 0 [1]
0 0 -1 1 -2 1
1
3x
1 -
2 0 1 0 0 0 1 -
j σ
-1 1-M 0 0 M 0 3M-1
j c →
-3 1 1 0 0 M M
i θ
B C b X b
1x 2x 3x 4x 5x 6x 7x
0 4x 12 [3]
0 0 1 -2 2 -5 4
1 2x 1 0 1 0 0 -1 1 -
2 - 1
3x
1 -
2 0 1 0 0 0 1 -
j σ
-1 0 0 0 1 M-1 M+1
上表中得到最优解，12345674,1,9,0,2x x x x x x x z ========−
③两阶段法（含有人工变量的线性规划问题）
下面介绍求解加入人工变量的线性规划问题的两阶段法。

第一阶段：不考虑原问题是否存在基可行解，给原线性规划问题加入人工变量，并构造仅含人工变量的目标函数和要求实现最小化。

如
1111111
21122211
12min 001,,,0n n m n n n n n n n m mn n n m m
n m x x x x a x a x x b a x a x x b
a x a x x b
x x x ω++++++=++++++++=⎧⎪+++=⎪⎪
⎨
⎪+++=⎪≥⎪⎩
"""""""
然后用单纯形法求解上述模型，若得到0ω=,这说明原问题存在基可行解，可以进行第二阶段计算。

否则原问题无可行解，应停止计算。

第二阶段：将第一阶段计算得到的最终表，除去人工变量。

将目标函数行的系数，换成原问题的目标函数系数，作为第二阶段计算的初始表。

各阶段计算方法及步骤与第3节单纯形法相同。

下面举例说明。

例：线性规划问题
12312312313min 3211423211,2,30
z x x x x x x x x x x x x x x =−++++≤⎧⎪−++≥⎪⎨
−+=⎪⎪≥⎩
解：先在上述线性规划问题的约束方程中加入人工变量，给出第一阶段的数学模型为：
67
1234123561374567min 211423211,2,3,,,,0
x x x x x x x x x x x x x x x x x x x x x ω=++++=⎧⎪−++−+=⎪⎨
−++=⎪⎪≥⎩ 这里6x ，7x 是人工变量。

用单纯形法求解，如表3-1所示：
表 3-1 两阶段法求解含人工变量的线性规划问题第一阶段
j c →
0 0 0 0 0 1 1
i θ
B C b X b
1x 2x 3x 4x 5x 6x 7x
0 4x 10 3 -2 0 1 0 0 -1 - 1 6x 1 0 [1]
0 0 -1 1 -2 1
3x
1 -
2 0 1 0 0 0 1 -
j σ
0 -1 0 0 1 0 3
j c →
0 0 0 0 0 1 1
i θ
B C
b X
b
1x 2x 3x 4x 5x 6x 7x
0 4x 12 3 0 0 1 -2 2 -5 0 2x 1 0 [1]
0 0 -1 1 -2
3x
1 -
2 0 1 0 0 0 1
j σ
0 0 0 0 0 1 1
第一阶段求得的结果是0ω=，得到最优解是：
12345670, 1.1,12,0x x x x x x x =======
因为人工变量670x x ==，所以()0,1,1,12,0T
是该线性规划问题的基可行解。

于是可以进行第二阶段运算。

将第一阶段的最终表中的人工变量取消并填入原问题的目标函数的系数。

进行第二阶段的计算，如表3-2所示：
表 3-2两阶段法求解含人工变量的线性规划问题第二阶段
j c →
-3 1 1 0 0
i θ
B C b X b
1x 2x 3x 4x 5x
0 4x 12 [3]
0 0 1 -2 4
1 2x 1 0 1 0 0 -1 - 1
3x
1 -
2 0 1 0 0 -
j σ
-1 0 0 0 1
表3-2中得到最优解为1234,1,9x x x ===，目标函数值2z =−。

④退化情况
单纯形法计算中用θ规则确定换出变量时，有时存在两个以上相同的最小比值，这样在下一次迭代中就有一个或几个基变量等于零，这就出现退化解。

这时换出变量。

尽管计算过程的循环现象极少出现，但还是有可能的。

可利用勃兰特规则解决该问题：
（1）选取0j j c z −>中下标最小的非基变量k x 为换入基变量，即
()min |0j j k j c z =−>
（2）当按θ规则计算存在两个和两个以上最小比值时，选取下标最小的基变量为换出变量。

单纯形法表的解题步骤

合集下载

第4节单纯形法计算步骤

单纯形表法详细讲解

单纯形法表的解题步骤

单纯形法的表格解法

第二节单纯形法3.29

单纯形法的计算步骤

单纯形表例题详解易懂

单纯形法解题步骤

运筹学1-4单纯形法计算步骤ppt课件

单纯形法解题步骤

单纯形法求解全过程详解共9页

1.4 单纯形法计算步骤

第3,4节单纯形法与计算步骤

运筹学1-4单纯型法的计算步骤

单纯行法的计算步骤

1.4单纯形法的计算步骤

线性规划与单纯形法-计算步骤

文档推荐

最新文档

单纯形法表的解题步骤

合集下载

第4节单纯形法计算步骤

单纯形表法详细讲解

单纯形法表的解题步骤

单纯形法的表格解法

第二节单纯形法3.29

单纯形法的计算步骤

单纯形表例题详解易懂

单纯形法解题步骤

运筹学1-4单纯形法计算步骤ppt课件

单纯形法解题步骤

单纯形法求解全过程详解共9页

1.4 单纯形法计算步骤

第3,4节 单纯形法与计算步骤

运筹学1-4单纯型法的计算步骤

单纯行法的计算步骤

1.4单纯形法的计算步骤

线性规划与单纯形法-计算步骤

文档推荐

最新文档

第3,4节单纯形法与计算步骤