大学物理17章答案.docx

大学物理实验智慧树知到课后章节答案2023年下哈尔滨工业大学哈尔滨工业大学第一章测试1.下列四个实验结果的表示方法中，错误的是（）。

A: B: C:D:答案:2.随机误差具有如下所列的哪些特点（）。

A:抵偿性 B:无界性 C:单峰性 D:对称性答案:抵偿性;单峰性;对称性3.在大学物理实验课程中，系统误差的主要来源包括：（）。

A:理论推导中的近似 B:实验仪器或实验装置 C:实验者或环境因素 D:实验方法答案:理论推导中的近似;实验仪器或实验装置;实验者或环境因素;实验方法4.某位同学测量得到某一长度量的测量结果表示为L=10.5680.36 mm。

请判断这个结果表示的对或错。

（）A:对 B:错答案:错第二章测试1.本实验中涉及多个不同量级的长度量的测量，同学们要学会根据测量对象的不同来选择适当的测量仪器。

比如，本实验中用于测量钢丝直径的，用于测量钢丝原长的，用于测量光杠杆臂长的分别是（）。

A:米尺 B:光杠杆 C:钢板尺 D:千分尺答案:米尺;光杠杆;钢板尺2.本实验中，如果初始时望远镜中看到的刻度靠近直尺的下端，则应该调节使之靠近直尺上端。

（）A:对 B:错答案:对第三章测试1.电桥灵敏度越高，待测电阻的测量结果越准确。

提高电桥灵敏度的主要方法有（）。

A:尽量减小导线的接触电阻 B:选用灵敏度高、内阻低的检流计 C:四个桥臂电阻的阻值要尽量均衡配置 D:在桥臂电阻的额定功率容许的情况下，适当提高电源电压答案:尽量减小导线的接触电阻;选用灵敏度高、内阻低的检流计;四个桥臂电阻的阻值要尽量均衡配置;在桥臂电阻的额定功率容许的情况下，适当提高电源电压2.本实验中，要先在低灵敏度下粗调电桥平衡，然后再提高灵敏度细调电桥平衡。

（）A:对 B:错答案:对第四章测试1.本实验中，产生误差的主要原因有（）。

A:温控过程中的波动 B:在本实验的温控范围内，金属或合金材料的电阻阻值不是严格地线性变化 C:测量仪器引起的误差 D:导线的接触电阻答案:温控过程中的波动;测量仪器引起的误差;导线的接触电阻2.本实验中电源使用的是直流稳压电源，不能用干电池代替。

第17章习题解答【17-1】解 首先写出S 点的振动方程若选向上为正方向，则有：－=0 21cos 0-=ϕ 0=－A sin 0>0， sin 0<0即 πϕ320-= 初始位相 πϕ320-= 则 m t y s )32cos(02.0πω-= 再建立如图题17-1（a ）所示坐标系，坐标原点选在S 点，沿x 轴正向取任一P 点，该点振动位相将落后于S 点，滞后时间为：ux t =∆ 则该波的波动方程为：m u x t y ⎥⎦⎤⎢⎣⎡--=πω32)(cos 02.0 若坐标原点不选在S 点，如图题17-1（b ）所示，P 点仍选在S 点右方，则P 点振动落后于S 点的时间为：uL x t -=∆ 则该波的波动方程为：m u L x t y ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0 若P 点选在S 点左侧，如图题17-1（c ）所示，则m u L x t y ⎥⎦⎤⎢⎣⎡--+=πω32)(cos 02.0 【17-2】解（1）由图题17-2可知，波长 =0.8m振幅 A=0.5m频率 Hz Hz u v 1258.0100===λ 周期 s vT 31081-⨯== （2）平面简谐波标准动方程为：⎥⎦⎤⎢⎣⎡+-=ϕω)(cos u x t A y 由图可知，当t=0，x=0时，y=A=，故=0。

将A 、(v)、u 、代入波动方程，得： m x t y ⎥⎦⎤⎢⎣⎡-=)100(250cos 5.0π 【17-3】解 （1）由图题17-3可知，对于O 点，t=0时，y=0，故2πϕ±= 再由该列波的传播方向可知，0<0取 2πϕ= 由图题17-3可知，m OP 40.0==λ，且u=0.08m/s ，则s rrad s rad uv /52/40.008.0222ππλππω==== 可得O 点振动表达式为：m t y )252cos(04.00ππ+= （2）已知该波沿x 轴正方向传播，u=0.08m/s ，以及O 点振动表达式，波动方程为： m x t y ⎥⎦⎤⎢⎣⎡+-=2)08.0(52cos 04.0ππ （3）将x==代入上式，即为P 点振动方程：m t y p ⎥⎦⎤⎢⎣⎡-=ππ3252cos 04.0 （4）图题17-3中虚线为下一时刻波形，由图可知，a 点向下运动，b 点向上运动。

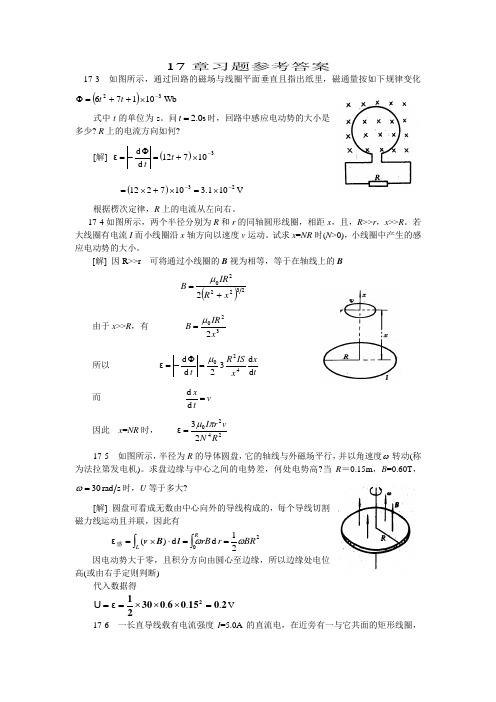
17章习题参考答案17-3 如图所示，通过回路的磁场与线圈平面垂直且指出纸里，磁通量按如下规律变化()Wb 1017632-⨯++=Φt t式中t 的单位为s 。

问s 0.2=t 时，回路中感应电动势的大小是多少? R 上的电流方向如何?[解] ()310712d d -⨯+=Φ-=t tε ()23101.3107212--⨯=⨯+⨯=V根据楞次定律，R 上的电流从左向右。

17-4如图所示，两个半径分别为R 和r 的同轴圆形线圈，相距x ，且，R >>r ，x >>R 。

若大线圈有电流I 而小线圈沿x 轴方向以速度v 运动。

试求x =NR 时(N >0)，小线圈中产生的感应电动势的大小。

[解] 因R>>r 可将通过小线圈的B 视为相等，等于在轴线上的B()2322202xR IR B +=μ由于x >>R ，有 3202x IR B μ=所以 t xxIS R t d d 32d d 420μ=Φ-=ε 而v t x=d d 因此 x =NR 时， 242023R N v r I πμ=ε17-5 如图所示，半径为R 的导体圆盘，它的轴线与外磁场平行，并以角速度ω转动(称为法拉第发电机)。

求盘边缘与中心之间的电势差，何处电势高?当R ＝0.15m ，B =0.60T ，rad 30=ω时，U 等于多大?[解] 圆盘可看成无数由中心向外的导线构成的，每个导线切割磁力线运动且并联，因此有2021d d )(BR r rB R L ωω==⋅⨯=⎰⎰l B v 感ε因电动势大于零，且积分方向由圆心至边缘，所以边缘处电位高(或由右手定则判断)代入数据得201506030212...=⨯⨯⨯==εU V 17-6 一长直导线载有电流强度I =5.0A 的直流电，在近旁有一与它共面的矩形线圈，线圈长l ＝20cm ，宽a =10cm ，共1000匝，如图所示。

[习题解答]17-5 将20g的氦气分别按照下面的过程，从17℃升至27℃，试分别求出在这些过程中气体系统内能的变化、吸收的热量和外界对系统作的功：(1)保持体积不变；(2)保持压强不变；(3)不与外界交换热量。

设氦气可看作理想气体，且。

解(1)保持体积不变：外界对系统不作功,系统内能的变化为,吸收的热量为.这表示，在系统体积不变的情况下，外界对系统不作功，系统从外界获得的热量全部用于内能的增加。

(2)保持压强不变：,系统内能的变化,外界对系统作功.这表示，在系统保持压强不变的情况下，系统从外界获得的热量，一部分用于增加系统的内能，另一部分用于系统对外界作功。

(3)不与外界交换热量，即绝热过程：吸收的热量,系统内能的变化,外界对系统作功.这表示，在绝热条件下，系统与外界无热量交换，外界对系统所作的功全部用于内能的增加。

17-6 把标准状态下的14 g氮气压缩至原来体积的一半，试分别求出在下列过程中气体内能的变化、传递的热量和外界对系统作的功：(2)绝热过程；(3)等压过程。

设氮气可看作为理想气体，且。

解(1)等温压缩过程：外界对系统所作的功;在等温过程中系统内能不变;传递的热量：根据热力学第一定律，有.这表示，在等温过程中，系统内能不变，外界对系统所作的功全部以热量的形式释放到外界。

(2)绝热压缩过程：;,根据绝热方程,,其中,所以;外界对系统所作的功.这表示，在绝热压缩过程中，外界对系统所作的功，全部用于系统内能的增加。

(3)等压过程：根据物态方程，在初态和末态分别有,,两式相除，得或 ,所以.内能的增加为;系统获得的热量为;外界对系统所作的功为.这表示，在等压过程中，系统向外界释放热量，此热量来自于外界对系统所作的功和自身内能的减小。

17-7 在标准状态下的16 g氧气经过一绝热过程对外界作功80 J。

求末态的压强、体积和温度。

设氧气为理想气体，且，。

解系统对外界作功80 J，即,在绝热过程中系统与外界无热量交换，所以,根据热力学第一定律,这表示，在绝热过程中系统降低自身的内能而对外界作功。

第十七章 光的衍射17－1 波长为700nm 的红光正入射到一单缝上，缝后置一透镜，焦距为0.70m ，在透镜焦距处放一屏，若屏上呈现的中央明条纹的宽度为2mm ，问该缝的宽度是多少？假定用另一种光照射后，测得中央明条纹的宽度为1.5mm ，求该光的波长。

解：单缝衍射中央明条纹的宽度为afx λ2=∆m xf a 739109.4102107007.022---⨯=⨯⨯⨯⨯=∆=λfx a2∆=λ代入数据得 nm 5257.02105.1109.437=⨯⨯⨯=--λ17－2一单缝用波长为λ1和λ2的光照明，若λ1的第一级衍射极小与λ2的第二级衍射极小重合。

问（1）这两种波长的关系如何？（2）所形成的衍射图样中是否还有其它极小重合？ 解：（1）单缝衍射极小条件为λθk a =sin依题意有 212λλ= （2）依题意有11sin λθk a = 22sin λθk a =因为212λλ=，所以得所形成的衍射图样中还有其它极小重合的条件为212k k =17－3 有一单缝，缝宽为0.1mm ，在缝后放一焦距为50cm 的汇聚透镜，用波长为546.1nm 的平行光垂直照射单缝，试求位于透镜焦平面处屏上中央明纹的宽度。

解：单缝衍射中央明条纹的宽度为af x λ2=∆代入数据得mm x 461.5101.0101.54610502392=⨯⨯⨯⨯=∆---17－4 用波长为632.8nm 的激光垂直照射单缝时，其夫琅禾费衍射图样第一极小与单缝法线的夹角为50，试求该缝宽。

解：单缝衍射极小的条件λθk a =sin依题意有m a μλ26.70872.0108.6325sin 9=⨯==-17－5 波长为20m 的海面波垂直进入宽50m 的港口。

在港内海面上衍射波的中央波束的角宽是多少？解：单缝衍射极小条件为λθk a =sin依题意有 0115.234.0sin52sin20sin 50===→=--θθ中央波束的角宽为0475.2322=⨯=θ17－6 一单色平行光垂直入射一单缝，其衍射第3级明纹位置恰与波长为600nm 的单色光垂直入射该缝时衍射的第2级明纹位置重合，试求该单色光的波长。

第17章 量子物理基础17.1 根据玻尔理论，计算氢原子在n = 5的轨道上的动量矩与其在第一激发态轨道上的动量矩之比．[解答]玻尔的轨道角动量量子化假设认为电子绕核动转的轨道角动量为2π==n n hL mvr n ，对于第一激发态，n = 2，所以L 5/L 2 = 5/2．17.2设有原子核外的3p 态电子，试列出其可能性的四个量子数．[解答] 对于3p 态电子，主量子数为n = 3，角量子数为 l = 1，磁量子数为 m l = -l , -(l - 1), …, l -1, l ，自旋量子数为 m s = ±1/2．3p 态电子的四个可能的量子数(n ,l ,m l ,m s )为(3,1,1,1/2)，(3,1,1,-1/2)，(3,1,0,1/2)，(3,1,0,-1/2)，(3,1,-1,1/2)，(3,1,-1,-1/2) ．17.3 实验表明，黑体辐射实验曲线的峰值波长λm 和黑体温度的乘积为一常数，即λm T = b = 2.897×10-3m·K ．实验测得太阳辐射波谱的峰值波长λm = 510nm ，设太阳可近似看作黑体，试估算太阳表面的温度．[解答]太阳表面的温度大约为392.8971051010λ--⨯==⨯m b T = 5680(K)．17.4 实验表明，黑体辐射曲线和水平坐标轴所围成的面积M （即单位时间内从黑体单位表面上辐射出去的电磁波总能量，称总辐射度）与温度的4次方成正比，即M = σT 4，其中σ =5.67×10-8W·m -2·K -4．试由此估算太阳单位表面积的辐射功率（太阳表面温度可参见上题）．[解答]太阳单位表面积的辐射功率大约为M = 5.67×10-8×(5680)4 = 5.9×107(W·m -2)．17.5宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于3K 黑体辐射．求：（1）此辐射的单色辐射强度在什么波长下有极大值？（2）地球表面接收此辐射的功率是多少？[解答]（1）根据公式λm T = b ，可得辐射的极值波长为λm = b/T = 2.897×10-3/3 = 9.66×10-4(m)．（2）地球的半径约为R = 6.371×106m ，表面积为 S = 4πR 2．根据公式：黑体表面在单位时间，单位面积上辐射的能量为 M = σT 4，因此地球表面接收此辐射的功率是P = MS = 5.67×10-8×34×4π(6.371×106)2= 2.34×109(W)．17.6 铝表面电子的逸出功为6.72×10-19J，今有波长为λ = 2.0×10-7m 的光投射到铝表面上．试求：（1）由此产生的光电子的最大初动能；（2）遏止电势差；（3）铝的红限波长．[解答]（1）光子的能量为E = hν = hc/λ，根据爱因斯坦光电效应方程hν = E k + A，产生的光电子的最大初动能为E k= hν - A= 6.63×10-34×3×108/2.0×10-7-6.72×10-19= 3.23×10-19(J)．（2）遏止电势差的公式为eU s = E k，遏止电势差为U s = E k/e = 3.23×10-19/1.6×10-19=2.0(V)．（3）铝的红限频率为ν0= A/h，红限波长为λ0= c/ν0= hc/A= 6.63×10-34×3×108/6.72×10-19= 2.96×10-7(m)．17.7 康普顿散射中入射X射线的波长是λ = 0.70×10-10m，散射的X 射线与入射的X射线垂直．求：（1）反冲电子的动能E K ；（2）散射X 射线的波长；（3）反冲电子的运动方向与入射X 射线间的夹角θ．[解答]（1）（2）根据康普顿散射公式得波长变化为21222sin 2 2.42610sin 24ϕπλΛ-∆==⨯⨯= 2.426×10-12(m)，散射线的波长为λ` = λ + Δλ = 0.72426×10-10(m)．反冲电子的动能为`k hchcE λλ=-34834810106.6310310 6.63103100.7100.7242610----⨯⨯⨯⨯⨯⨯=-⨯⨯= 9.52×10-17(J)．（3）由于 /`tan /`hc hc λλθλλ==，0.70.96650.72426==，所以夹角为θ = 44°1`．17.8 求波长分别为λ1 = 7.0×10-7m 的红光；λ2 = 0.25×10-10m 的X 射线的能量、动量和质量．[解答]X 射线的能量为E = h ν = hc/λ，动量为 p = h/λ；由E = hc/λ = mc 2，得其质量为m = h/cλ．对于红光来说，能量为348176.6310310710E --⨯⨯⨯=⨯= 2.84×10-19(J)，动量为34176.6310710p --⨯=⨯= 9.47×10-25(kg·m·s -1)，质量为341876.6310310710m --⨯=⨯⨯⨯= 3.16×10-36(kg)．对于X 射线来说，能量为3482106.63103100.2510E --⨯⨯⨯=⨯= 7.956×10-15(J)，动量为342106.63100.2510p --⨯=⨯= 2.652×10-23(kg·m·s -1)，质量为3428106.63103100.2510m --⨯=⨯⨯⨯= 8.84×10-32(kg)．17.9 处于第四激发态上的大量氢原子，最多可发射几个线系，共几条谱线？那一条波长最长．[解答]第四激发态的氢原子处于第5个能级，最多可发射四个线系．（1）能级5到4，1条谱线；（2）能级5和4到3，2条谱线；（3）能级5、4和3到2，3条谱线；（3）能级5、4、3和2到1，4条谱线．共10条谱线．从能级5跃迁到4发射的光谱频率最小，波长最长．17.10 设氢原子中电子从n = 2的状态被电离出去，需要多少能量．[解答]氢原子能级公式为4222018n me E h n ε=-，当n =1时，基态能级的能量为412208me E h ε=-≈-2.18×10-18(J) = -13.6(eV)，因此 12n E E n =．当电子从n 能级跃迁到m 能级时放出（正）或吸收（负）光子的能量为12211()n m E E E E n m ∆=-=-．电离时，m 趋于无穷大．当电子从n = 2的能级电离时要吸收能量 221113.6()2E ∆=--∞= -3.4(eV)，因此需要3.4eV 的能量．17.11 质量为m 的卫星，在半径为r 的轨道上环绕地球运动，线速度为v ．（1）假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立．证明地球卫星的轨道半径与量子数的平方成正比，即r = Kn 2，（式中K 是比例常数）；（2）应用（1）的结果求卫星轨道和下一个“容许”轨道间的距离，由此进一步说明在宏观问题中轨道半径实验上可认为是连续变化的（利用以下数据作估算：普朗克常数h = 6.63×10-34J·s ，地球质量M = 6×1024kg ，地球半径R = 6.4×103km ，万有引力常数G =6.7×10-11N·m 2·kg -2．[解答]（1）卫星绕地球运动的向心力是万有引力22Mm mv G r r =；根据玻尔理论，角动量为mvr = nh /2π．将前式乘以mr 3得2222()()4nh GMm r mvr π==，所以 222224h n r Kn GMm π==，即：卫星的轨道半径与量子数的平方成正比．（2）假设卫星质量m = 100kg ，比例系数为2224h K GMm π=342211242(6.6310)4 6.710610(100)π--⨯=⨯⨯⨯⨯⨯ = 2.77×10-87．可见：比例系数很小．当r = R 时，地球表面的量子数为460 4.810n ⨯．可见：地球表面处的量子数很大．地面以上的量子数设为n `，(n` = 1,2,3,…)，则总量子数可表示为两个量子数之和：n =n 0 + n`．轨道间的距离为Δr = K [(n 0 + n` + 1)2 - (n 0 + n`)2]= K [2(n 0 + n`) + 1]．由于n 0>>1，所以Δr = 2Kn 0 + 2Kn`．设n` = kn 0，即：取地面以上的量子数为地球表面量子数的倍数，有n = (k + 1)n 0，则r = Kn 02(k + 1)2，Δr = 2Kn 0(k + 1) = 2.66×10-40(k + 1)．这说明：当地面以上的量子数按k + 1成倍地增加时，半径将按k + 1的平方的规律增加，而轨道之间的距离只按k + 1的一次方的规律增加；由于Δr 的系数很小，所以轨道间距是非常非常小的，因此可认为轨道半径是连续变化的．17.12 电子和光子各具有波长2.0×10-10m ，它们的动量和总能量各是多少？[解答]它们的动量都为34106.6310210h p λ--⨯==⨯= 3.315×10-24(kg·m·s -1)．根据公式E 2 = p 2c 2 + m 02c 4，电子的总能量为E ==3×108×[(3.315×10-24)2+ (9.1×10-31×3×108)2]1/2=8.19×10-14(J)．光子的静止质量为零，总能量为E = cp= 3×108×3.315×10-24 = 9.945×10-16(J)．17.13 室温下的中子称为热中子T = 300K ，试计算热中子的平均德布罗意波长．[解答]中子热运动的平均速度为=v其中k为玻尔兹曼常数k= 1.38×10-23J·K-1，m p是电子的质量m p= 1.675×10-27kg，可得平均速度为v= 2.509×104(m·s-1)，平均动量为=np m v= 4.2×10-27(kg·m·s-1)．平均德布罗意波长为/λ=h p= 1.58×10-10(m) = 0.158(nm)．17.14 一束动量是p的电子，通过缝宽为a的狭缝，在距离狭缝为R 处放置一屏，屏上电子衍射图样中央最大的宽度是多少？[解答]根据动量和位置的不确定关系Δp x·Δx≧h，其中位置不确定量为Δx = a，动量的不确定量为Δp x = p sinθ．设电子衍射图样的中央最大半宽度为w，则sinθ = w/R，可得wp a hR⋅≥，宽度为22hRwpa≥．[注意]如果将h改为ћ/2，则宽度为2w≧ћR/pa．两者相差很小．17.15 一宽度为a的一维无限深势阱，试用不确定关系估算阱中质量为m的粒子最低能量为多少？[解答]粒子坐标的不确定范围是Δx ≦a ，动量的不确定范围是Δp ≧h /Δx ≧h /a ．这也就是动量p 的范围．因此能量为E = p 2/2m ≧ h 2/2ma 2，最低能量可估计为E min = h 2/2ma 2．17.16 设有一宽度为a 的一维无限深势阱，粒子处于第一激发态，求在x = 0至x = a /3之间找到粒子的几率？[解答]粒子在一维无限深势阱中的定态波函数为(0)(),(1,2,3,...)πψ≤≤==n x a n x x n a ，Ψ(x ) = 0，(x < 0，x > a )．当粒子处于第一激发态时，n = 2，在x = 0至x = a /3之间被发现的几率为/3220|()|d ψ⎰a x x /32022sin d π=⎰a x x a a23== 0.391．17.17 设粒子在宽度为a 的一维无限深势阱运动时，其德布罗意波在阱内形成驻波，试利用这一关系导出粒子在阱中的能量计算式．[解答]当粒子在势阱中形成稳定驻波时，势阱宽度必然为半波长的整数倍，即n (λ/2) = a ，(n = 1,2,3,…)．根据德布罗意假设 λ = h/p ，可得粒子的动量为2λ==h nhp a 能量为 222228==p h E n m ma ．17.18假定对某个粒子动量的测定可精确到千分之一，试确定这个粒子位置的最小不确定量．（1）该粒子质量为5×10-3kg ，以2m·s -1的速度运动；（2）该粒子是速度为1.8×108m·s -1的电子．[解答]粒子的动量为 p = mv ，动量的不确定量为 Δp = p /1000，根据动量和位置的不确定关系Δp ·Δx ≧ћ/2，位置的不确定量为 Δx = ћ/2Δp ．（1）100024h x p mv π∆≥=∆h3431000 6.631045102-⨯⨯=π⨯⨯⨯= 5.276×10-30(m)．（2）100024h x p mv π∆≥=∆h343181000 6.631049.110 1.810--⨯⨯=π⨯⨯⨯⨯= 3.22×10-10(m)．17.19设有某线性谐振子处于第一激发态，其波函数为2221ψ-=a x ．式中a =，k 为常数，则该谐振子在何处出现的概率最大？[解答]第一激发态的概率为22221||a xw e ψ-==，对x 求导得222222d (2)]d a x a x w xe x a x e t --=+-2222(1)a xx x a e -=-，令d w /d t = 0，得概率最大的位置为x = ±1/a ．17.20一维运动的粒子，处于如下的波函数所描述的状态,(0);()0,(0).x Axe x x x λψ-⎧>=⎨<⎩式中λ > 0，A 为常数．（1）将此波函数归一化；（2）求粒子位置的概率分布函数；（3）粒子在在何处出现的概率最大？[解答]（1）归一化得222201||d d x x A xe x λψ∞∞--∞==⎰⎰ 22201d 2x A x e λλ∞--=⎰2222001{2d }2x x A x e xe x λλλ∞∞---=-⎰222012()d 2xA x e λλ∞--=-⎰ 22220012(){d }2xx A xe e x λλλ∞∞---=--⎰22323012()24xA A e λλλ∞--==，所以A =2λ3/2 ．归一化波函数为3/22,(0);()0,(0).x xe x x x λλψ-⎧>=⎨<⎩（[注]利用Γ函数的性质可简化积分过程．10()d n x n x e x∞--Γ=⎰，当n 为整数时，Γ(n ) = (n - 1)!．设y = 2λx ，则d x = d y /2λ，可得22331001d ()d 2x y x ex y e y λλ∞∞---=⎰⎰ 3311()(3)2()22λλ=Γ=，可以得出同一结果．）（2）粒子坐标的几率分布函数为32224,(0);()|()|0,(0).x x e x w x x x λλψ-⎧>==⎨<⎩（3）利用上一题的方法求导可得几率最大的位置为x = 1/λ．17.21 设有某一维势场如下：0,(0);,(0,).≤≤⎧=⎨<>⎩x LVV x x L该势场可称为有限高势阱，设粒子能量E < V0，求E所满足的关系式．[解答]粒子运动的薛定谔方程为222()0mE Vψψ∇+-=h．在三个区域的方程为210122d2()0,(0);dmE V xxψψ+-=<h22222d20,(0);dmE x Lxψψ+=<<h230322d2()0,().dmE V x Lxψψ+-=>h设1k=h，2k=h，则得221112d0,(0);dk xxψψ-=<（1）222222d0,(0);dk x Lxψψ+=<<（2）223132d0,().dk x Lxψψ-=>（3）方程的通解为ψ1(x) = A1exp(k1x) + B1exp(-k1x),(x<0);（4）ψ2(x ) = A 2cos(k 2x ) + B 2sin(k 2x ),(0<x <L );（5）ψ3(x) = A 3exp(k 1x ) + B 3exp(-k 1x ),(x >L )．（6）当x →-∞时，ψ1有限，所以B 1 = 0；当x →∞时，ψ3有限，所以A 3 = 0．当x = 0时，ψ1(0) = ψ2(0)，可得A 1 = A 2； （7）同时ψ1`(0) = ψ2`(0)，可得k 1A 1 = k 2B 2． （8）当x = L 时，ψ2(L ) = ψ3(L )，ψ2`(L ) = ψ3`(L )，可得A 2cos k 2L +B 2sin k 2L = B 3exp(-k 1L )；（9）-k 2A 2sin k 2L + k 2B 2cos k 2L = -k 1B 3exp(-k 1L )(10)将（9）乘以k 1加（10）得k 1A 2cos k 2L + k 1B 2sin k 2L-k 2A 2sin k 2L + k 2B 2cos k 2L = 0．即 (k 1A 2 + k 2B 2)cos k 2L = (k 2A 2 - k 1B 2)sin k 2L ，亦 122222212t a n k A k B k L k A k B +=-． （11）由（7）和（8）得k 1A 2 = k 2B 2，即 B 2 = k 1A 2/k 2， （12）（12）代入（11）式得12222212tan kk k L k k =-，即0t a n =h （13）这就是总能量满足的关系式．17.22 原子内电子的量子态由n 、l 、m l 、m s 四个量子数表征，当n 、l 、m l 一定时，不同的量子态数目为多少？当n 、l 一定时，不同量子态数目为多少？当n 一定时，不同量子态数目为多少？[解答]当n 、l 、m l 一定时，m s 只取两个值，所以量子态数目为2． 当n 、l 一定时，m l 有(2l + 1)种不同取值，所以量子态数目为2(2l + 1)．当n 一定时，l 从0到(n - 1)共有n 种不同取值，量子态数目为1110002(21)421n n n l l l l l ---===+=+∑∑∑2(1)4222n n n n -=⨯+=．。

习题十二12-1 某单色光从空气射入水中，其频率、波速、波长是否变化?怎样变化?解: υ不变，为波源的振动频率；nn 空λλ=变小；υλn u =变小．12-2 在杨氏双缝实验中，作如下调节时，屏幕上的干涉条纹将如何变化?试说明理由．(1)使两缝之间的距离变小；(2)保持双缝间距不变，使双缝与屏幕间的距离变小； (3)整个装置的结构不变，全部浸入水中； (4)光源作平行于1S ，2S 联线方向上下微小移动； (5)用一块透明的薄云母片盖住下面的一条缝． 解: 由λdD x =∆知，(1)条纹变疏；(2)条纹变密；(3)条纹变密；(4)零级明纹在屏幕上作相反方向的上下移动；(5)零级明纹向下移动．12-3 什么是光程? 在不同的均匀媒质中，若单色光通过的光程相等时，其几何路程是否相同?其所需时间是否相同?在光程差与位相差的关系式∆λπϕ∆2= 中,光波的波长要用真空中波长,为什么?解:nr =∆．不同媒质若光程相等，则其几何路程定不相同；其所需时间相同，为Ct ∆=∆．因为∆中已经将光在介质中的路程折算为光在真空中所走的路程。

12-4 如题12-4图所示，A ，B 两块平板玻璃构成空气劈尖，分析在下列情况中劈尖干涉条纹将如何变化?(1) A 沿垂直于B 的方向向上平移［见图(a)］； (2) A 绕棱边逆时针转动［见图(b)］．题12-4图解: (1)由l2λθ=，2λk e k =知，各级条纹向棱边方向移动，条纹间距不变；(2)各级条纹向棱边方向移动，且条纹变密．12-5 用劈尖干涉来检测工件表面的平整度，当波长为λ的单色光垂直入射时,观察到的干涉条纹如题12-5图所示，每一条纹的弯曲部分的顶点恰与左邻的直线部分的连线相切．试说明工件缺陷是凸还是凹?并估算该缺陷的程度． 解: 工件缺陷是凹的．故各级等厚线(在缺陷附近的)向棱边方向弯曲．按题意，每一条纹弯曲部分的顶点恰与左邻的直线部分连线相切，说明弯曲部分相当于条纹向棱边移动了一条，故相应的空气隙厚度差为2λ=∆e ，这也是工件缺陷的程度．题12-5图 题12-6图12-6 如题12-6图，牛顿环的平凸透镜可以上下移动，若以单色光垂直照射，看见条纹向中心收缩，问透镜是向上还是向下移动?解: 条纹向中心收缩，透镜应向上移动．因相应条纹的膜厚k e 位置向中心移动．12-7 在杨氏双缝实验中，双缝间距d =0.20mm ，缝屏间距D ＝1.0m ，试求： (1)若第二级明条纹离屏中心的距离为6.0mm ，计算此单色光的波长； (2)相邻两明条纹间的距离． 解: (1)由λk dD x =明知，λ22.01010.63⨯⨯=，∴ 3106.0-⨯=λmm oA 6000=(2) 3106.02.010133=⨯⨯⨯==∆-λdD x mm12-8 在双缝装置中，用一很薄的云母片(n=1.58)覆盖其中的一条缝，结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明纹的位置．若入射光的波长为5500oA ，求此云母片的厚度．解: 设云母片厚度为e ，则由云母片引起的光程差为e n e ne )1(-=-=δ按题意 λδ7= ∴ 610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ12-9 洛埃镜干涉装置如题12-9图所示，镜长30cm ，狭缝光源S 在离镜左边20cm 的平面内，与镜面的垂直距离为2.0mm ，光源波长=λ7.2×10-7m ，试求位于镜右边缘的屏幕上第一条明条纹到镜边缘的距离．题12-9图解: 镜面反射光有半波损失，且反射光可视为虚光源S '发出．所以由S 与S '发出的两光束到达屏幕上距镜边缘为x 处的光程差为22)(12λλδ+=+-=Dx d r r第一明纹处，对应λδ= ∴25105.44.0250102.72--⨯=⨯⨯⨯==dD x λmm12-10 一平面单色光波垂直照射在厚度均匀的薄油膜上，油膜覆盖在玻璃板上．油的折射率为1.30，玻璃的折射率为1.50，若单色光的波长可由光源连续可调，可观察到5000 oA 与7000 oA 这两个波长的单色光在反射中消失．试求油膜层的厚度．解: 油膜上、下两表面反射光的光程差为ne 2，由反射相消条件有λλ)21(2)12(2+=+=k kk ne ),2,1,0(⋅⋅⋅=k ①当50001=λoA 时，有2500)21(21111+=+=λλk k ne ②当70002=λoA 时，有3500)21(22222+=+=λλk k ne ③因12λλ>，所以12k k <;又因为1λ与2λ之间不存在3λ满足33)21(2λ+=k ne 式即不存在 132k k k <<的情形，所以2k 、1k 应为连续整数，即 112-=k k ④由②、③、④式可得：51)1(75171000121221+-=+=+=k k k k λλ得 31=k2112=-=k k可由②式求得油膜的厚度为67312250011=+=nk e λoA12-11 白光垂直照射到空气中一厚度为3800 oA 的肥皂膜上，设肥皂膜的折射率为1.33，试问该膜的正面呈现什么颜色?背面呈现什么颜色? 解: 由反射干涉相长公式有λλk ne =+22 ),2,1(⋅⋅⋅=k得 122021612380033.14124-=-⨯⨯=-=k k k ne λ2=k , 67392=λoA (红色)3=k , 40433=λ oA (紫色)所以肥皂膜正面呈现紫红色．由透射干涉相长公式 λk ne =2),2,1(⋅⋅⋅=k 所以 kkne 101082==λ当2=k 时， λ =5054oA (绿色) 故背面呈现绿色．12-12 在折射率1n =1.52的镜头表面涂有一层折射率2n =1.38的Mg 2F 增透膜，如果此膜适用于波长λ=5500 oA 的光，问膜的厚度应取何值? 解: 设光垂直入射增透膜，欲透射增强，则膜上、下两表面反射光应满足干涉相消条件，即λ)21(22+=k e n ),2,1,0(⋅⋅⋅=k∴ 222422)21(n n k n k e λλλ+=+=)9961993(38.14550038.125500+=⨯+⨯=k k oA令0=k ，得膜的最薄厚度为996oA ． 当k 为其他整数倍时，也都满足要求．12-13 如题12-13图，波长为6800oA 的平行光垂直照射到L ＝0.12m 长的两块玻璃片上，两玻璃片一边相互接触，另一边被直径d =0.048mm 的细钢丝隔开．求：(1)两玻璃片间的夹角=θ?(2)相邻两明条纹间空气膜的厚度差是多少? (3)相邻两暗条纹的间距是多少? (4)在这0.12 m 内呈现多少条明条纹?题12-13图解: (1)由图知，d L =θsin ，即d L =θ故 43100.41012.0048.0-⨯=⨯==L d θ(弧度) (2)相邻两明条纹空气膜厚度差为7104.32-⨯==∆λe m(3)相邻两暗纹间距641010850100.421068002---⨯=⨯⨯⨯==θλl m 85.0= mm(4)141≈=∆lL N 条12-14 用=λ 5000oA 的平行光垂直入射劈形薄膜的上表面，从反射光中观察，劈尖的棱边是暗纹．若劈尖上面媒质的折射率1n 大于薄膜的折射率n (n =1.5)．求： (1)膜下面媒质的折射率2n 与n 的大小关系； (2)第10条暗纹处薄膜的厚度；(3)使膜的下表面向下平移一微小距离e ∆，干涉条纹有什么变化?若e ∆=2.0 μm ，原来的第10条暗纹处将被哪级暗纹占据?解: (1)n n >2．因为劈尖的棱边是暗纹，对应光程差2)12(22λλ+=+=∆k ne ，膜厚0=e 处，有0=k ，只能是下面媒质的反射光有半波损失2λ才合题意； (2)3105.15.12500092929-⨯=⨯⨯==⨯=∆ne nλλ mm(因10个条纹只有9个条纹间距)(3)膜的下表面向下平移，各级条纹向棱边方向移动．若0.2=∆e μm ，原来第10条暗纹处现对应的膜厚为)100.2105.1(33--⨯+⨯='∆e mm21100.55.12105.3243=⨯⨯⨯⨯='∆=∆--n e N λ现被第21级暗纹占据．12-15 (1)若用波长不同的光观察牛顿环，1λ＝6000oA ，2λ＝4500oA ，观察到用1λ时的第k 个暗环与用2λ时的第k+1个暗环重合，已知透镜的曲率半径是190cm ．求用1λ时第k 个暗环的半径．(2)又如在牛顿环中用波长为5000oA 的第5个明环与用波长为2λ的第6个明环重合，求未知波长2λ． 解: (1)由牛顿环暗环公式λkR r k =据题意有 21)1(λλR k kR r +==∴212λλλ-=k ，代入上式得2121λλλλ-=R r10101010210450010600010450010600010190-----⨯-⨯⨯⨯⨯⨯⨯=31085.1-⨯=m(2)用A 50001 =λ照射，51=k 级明环与2λ的62=k 级明环重合，则有 2)12(2)12(2211λλR k R k r -=-=∴ 4091500016215212121212=⨯-⨯-⨯=--=λλk k oA12-16 当牛顿环装置中的透镜与玻璃之间的空间充以液体时，第十个亮环的直径由1d ＝1.40×10-2m 变为2d ＝1.27×10-2m ，求液体的折射率． 解: 由牛顿环明环公式2)12(21λR k D r -==空nR k D r 2)12(22λ-==液两式相除得n D D =21，即22.161.196.12221≈==DD n12-17 利用迈克耳逊干涉仪可测量单色光的波长．当1M 移动距离为0.322mm 时，观察到干涉条纹移动数为1024条，求所用单色光的波长．解: 由 2λN d ∆=∆得 102410322.0223-⨯⨯=∆∆=Nd λ710289.6-⨯=m 6289=oA12-18 把折射率为n =1.632的玻璃片放入迈克耳逊干涉仪的一条光路中，观察到有150条干涉条纹向一方移过．若所用单色光的波长为λ= 5000oA ，求此玻璃片的厚度．解: 设插入玻璃片厚度为d ，则相应光程差变化为λN d n ∆=-)1(2∴ )1632.1(2105000150)1(210-⨯⨯=-∆=-n N d λ5109.5-⨯=m 2109.5-⨯=mm习题十三13-1 衍射的本质是什么?衍射和干涉有什么联系和区别?答：波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象．其实质是由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生．而干涉则是由同频率、同方向及位相差恒定的两列波的叠加形成．13-2 在夫琅禾费单缝衍射实验中，如果把单缝沿透镜光轴方向平移时，衍射图样是否会跟着移动?若把单缝沿垂直于光轴方向平移时，衍射图样是否会跟着移动? 答：把单缝沿透镜光轴方向平移时，衍射图样不会跟着移动．单缝沿垂直于光轴方向平移时，衍射图样不会跟着移动．13-3 什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗条纹，单缝处波面各可分成几个半波带?答：半波带由单缝A 、B 首尾两点向ϕ方向发出的衍射线的光程差用2λ来划分．对应于第3级明纹和第4级暗纹，单缝处波面可分成7个和8个半波带．∵由272)132(2)12(sin λλλϕ⨯=+⨯=+=k a284sin λλϕ⨯==a13-4 在单缝衍射中，为什么衍射角ϕ愈大（级数愈大）的那些明条纹的亮度愈小?答：因为衍射角ϕ愈大则ϕsin a 值愈大，分成的半波带数愈多，每个半波带透过的光通量就愈小，而明条纹的亮度是由一个半波带的光能量决定的，所以亮度减小．13-5 若把单缝衍射实验装置全部浸入水中时，衍射图样将发生怎样的变化?如果此时用公式),2,1(2)12(sin =+±=k k a λϕ来测定光的波长，问测出的波长是光在空气中的还是在水中的波长?解：当全部装置浸入水中时，由于水中波长变短，对应='='λϕk a sin nk λ，而空气中为λϕk a =sin ，∴ϕϕ'=sin sin n ，即ϕϕ'=n ，水中同级衍射角变小，条纹变密． 如用)12(sin +±=k a ϕ2λ),2,1(⋅⋅⋅=k 来测光的波长，则应是光在水中的波长．(因ϕsin a 只代表光在水中的波程差)．13-6 在单缝夫琅禾费衍射中，改变下列条件，衍射条纹有何变化?(1)缝宽变窄；(2)入射光波长变长；(3)入射平行光由正入射变为斜入射．解：(1)缝宽变窄，由λϕk a =sin 知，衍射角ϕ变大，条纹变稀； (2)λ变大，保持a ，k 不变，则衍射角ϕ亦变大，条纹变稀；(3)由正入射变为斜入射时，因正入射时λϕk a =sin ；斜入射时，λθϕk a '=-)sin (sin ，保持a ，λ不变，则应有k k >'或k k <'．即原来的k 级条纹现为k '级．13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似，两者是否矛盾?怎样 说明?答：不矛盾．单缝衍射暗纹条件为kk a 2sin ==λϕ2λ，是用半波带法分析(子波叠加问题)．相邻两半波带上对应点向ϕ方向发出的光波在屏上会聚点一一相消，而半波带为偶数，故形成暗纹；而双缝干涉明纹条件为λθk d =s in ，描述的是两路相干波叠加问题，其波程差为波长的整数倍，相干加强为明纹．13-8 光栅衍射与单缝衍射有何区别?为何光栅衍射的明条纹特别明亮而暗区很宽?答：光栅衍射是多光束干涉和单缝衍射的总效果．其明条纹主要取决于多光束干涉．光强与缝数2N 成正比，所以明纹很亮；又因为在相邻明纹间有)1(-N 个暗纹，而一般很大，故实际上在两相邻明纹间形成一片黑暗背景． 13-9 试指出当衍射光栅的光栅常数为下述三种情况时，哪些级次的衍射明条纹缺级?(1)a+b=2a;(2)a+b=3a;(3)a+b=4a.解：由光栅明纹条件和单缝衍射暗纹条件同时满足时，出现缺级．即⎩⎨⎧=''±==±=+)2,1(sin ),2,1,0(sin )( k k a k k b a λϕλϕ可知，当k ab a k '+=时明纹缺级．(1)a b a 2=+时，⋅⋅⋅=,6,4,2k 偶数级缺级； (2)a b a 3=+时，⋅⋅⋅=,9,6,3k 级次缺级； (3)a b a 4=+，⋅⋅⋅=,12,8,4k 级次缺级．13-10 若以白光垂直入射光栅，不同波长的光将会有不同的衍射角．问(1)零级明条纹能否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什么因素有关?解：(1)零级明纹不会分开不同波长的光．因为各种波长的光在零级明纹处均各自相干加强．(2)可见光中红光的衍射角最大，因为由λϕk b a =+sin )(，对同一k 值，衍射角λϕ∞．13-11 一单色平行光垂直照射一单缝，若其第三级明条纹位置正好与6000οA 的单色平行光的第二级明条纹位置重合，求前一种单色光的波长． 解：单缝衍射的明纹公式为)12(sin +=k a ϕ 2λ 当6000=λoA 时，2=kx λλ=时，3=k 重合时ϕ角相同，所以有)132(26000)122(sin +⨯=+⨯=ϕa 2xλ得 4286600075=⨯=x λoA13-12 单缝宽0.10mm ，透镜焦距为50cm ，用5000=λoA 的绿光垂直照射单缝．求：(1)位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少?(2)若把此装置浸入水中(n=1.33)，中央明条纹的半角宽度又为多少? 解：中央明纹的宽度为f nax λ2=∆半角宽度为naλθ1sin-=(1)空气中，1=n ，所以3310100.51010.01050005.02---⨯=⨯⨯⨯⨯=∆x m33101100.51010.0105000sin ----⨯=⨯⨯=θ rad(2)浸入水中，33.1=n ，所以有33101076.31010.033.110500050.02---⨯≈⨯⨯⨯⨯⨯=∆x m331011076.3101.033.1105000sin----⨯≈⨯⨯⨯=θ rad13-13 用橙黄色的平行光垂直照射一宽为a=0.60mm 的单缝，缝后凸透镜的焦距f=40.0cm ，观察屏幕上形成的衍射条纹．若屏上离中央明条纹中心1.40mm 处的P 点为一明条纹；求：(1)入射光的波长；(2)P 点处条纹的级数；(3)从P 点看，对该光波而言，狭缝处的波面可分成几个半波带?解：(1)由于P 点是明纹，故有2)12(sin λϕ+=k a ，⋅⋅⋅=3,2,1k由ϕϕsin tan 105.34004.13≈=⨯==-fx故3105.3126.0212sin 2-⨯⨯+⨯=+=k k a ϕλ3102.4121-⨯⨯+=k mm当 3=k ，得60003=λoA4=k ，得47004=λoA(2)若60003=λoA ，则P 点是第3级明纹；若47004=λoA ，则P 点是第4级明纹． (3)由2)12(sin λϕ+=k a 可知，当3=k 时，单缝处的波面可分成712=+k 个半波带； 当4=k 时，单缝处的波面可分成912=+k 个半波带．13-14 用5900=λoA 的钠黄光垂直入射到每毫米有500条刻痕的光栅上，问最多能看到第几级明条纹? 解：5001=+b a mm 3100.2-⨯= mm 4100.2-⨯=oA由λϕk b a =+sin )(知，最多见到的条纹级数max k 对应的2πϕ=,所以有39.35900100.24max ≈⨯=+=λba k ，即实际见到的最高级次为3max =k .13-15 波长为5000oA 的平行单色光垂直照射到每毫米有200条刻痕的光栅上，光栅后的透镜焦距为60cm ． 求：(1)屏幕上中央明条纹与第一级明条纹的间距；(2)当光线与光栅法线成30°斜入射时，中央明条纹的位移为多少? 解：3100.52001-⨯==+b a mm 6100.5-⨯m(1)由光栅衍射明纹公式λϕk b a =+sin )(，因1=k ,又fx ==ϕϕtan sin所以有λ=+fx b a 1)(即 62101100.51060105000---⨯⨯⨯⨯=+=ba f x λ2100.6-⨯=m 6= cm(2)对应中央明纹，有0=k正入射时，0sin )(=+ϕb a ，所以0sin =≈ϕϕ斜入射时，0)sin )(sin (=±+θϕb a ，即0sin sin =±θϕ因︒=30θ，∴21tan sin ±==≈fx ϕϕ故22103010602121--⨯=⨯⨯==f x m 30= cm这就是中央明条纹的位移值．13-16 波长6000=λoA 的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在 20.0sin =ϕ与30.0sin =ϕ处，第四级缺级．求：(1)光栅常数；(2)光栅上狭缝的宽度；(3)在90°＞ϕ＞-90°范围内，实际呈现的全部级数．解：(1)由λϕk b a =+sin )(式对应于20.0sin 1=ϕ与30.0sin 2=ϕ处满足：101060002)(20.0-⨯⨯=+b a 101060003)(30.0-⨯⨯=+b a得 6100.6-⨯=+b a m(2)因第四级缺级，故此须同时满足λϕk b a =+sin )( λϕk a '=sin解得 k k b a a '⨯='+=-6105.14取1='k ，得光栅狭缝的最小宽度为6105.1-⨯m (3)由λϕk b a =+sin )(λϕsin )(b a k +=当2πϕ=，对应max k k =∴ 10106000100.6106max =⨯⨯=+=--λba k因4±，8±缺级，所以在︒︒<<-9090ϕ范围内实际呈现的全部级数为9,7,6,5,3,2,1,0±±±±±±±=k 共15条明条纹(10±=k 在︒±=90k 处看不到)．13-17 一双缝，两缝间距为0.1mm ，每缝宽为0.02mm ，用波长为4800oA 的平行单色光垂直入射双缝，双缝后放一焦距为50cm 的透镜．试求：(1)透镜焦平面上单缝衍射中央明条纹的宽度；(2)单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹? 解：(1)中央明纹宽度为02.010501048002270⨯⨯⨯⨯==-f al λmm 4.2=cm(2)由缺级条件λϕk a '=sin λϕk b a =+sin )(知k k ab a k k '='=+'=502.01.0 ⋅⋅⋅=',2,1k即⋅⋅⋅=,15,10,5k 缺级．中央明纹的边缘对应1='k ，所以单缝衍射的中央明纹包迹内有4,3,2,1,0±±±±=k 共9条双缝衍射明条纹．13-18 在夫琅禾费圆孔衍射中，设圆孔半径为0.10mm ，透镜焦距为50cm ，所用单色光波长为5000oA ，求在透镜焦平面处屏幕上呈现的爱里斑半径． 解：由爱里斑的半角宽度47105.302.010500022.122.1--⨯=⨯⨯==Dλθ∴ 爱里斑半径5.1105.30500tan 24=⨯⨯=≈=-θθf f d mm13-19 已知天空中两颗星相对于一望远镜的角距离为4.84×10-6rad ，它们都发出波长为5500oA 的光，试问望远镜的口径至少要多大，才能分辨出这两颗星?解：由最小分辨角公式Dλθ22.1= ∴ 86.131084.4105.522.122.165=⨯⨯⨯==--θλD cm13-20 已知入射的X 射线束含有从0.95～1.30oA 范围内的各种波长，晶体的晶格常数为2.75oA ，当X 射线以45°角入射到晶体时，问对哪些波长的X 射线能产生强反射?解：由布喇格公式 λϕk d =sin 2 得kd ϕλsin 2=时满足干涉相长当1=k 时， 89.345sin 75.22=⨯⨯=︒λoA2=k 时，91.1245sin 75.22=⨯⨯=︒λoA3=k 时，30.1389.3==λoA4=k 时， 97.0489.3==λoA故只有30.13=λoA 和97.04=λoA 的X 射线能产生强反射．习题十四14-1 自然光是否一定不是单色光?线偏振光是否一定是单色光?答：自然光不能说一定不是单色光．因为它只强调存在大量的、各个方向的光矢量，并未要求各方向光矢量的频率不一样．线偏振光也不一定是单色光．因为它只要求光的振动方向同一，并未要求各光矢的频率相同．14-2 用哪些方法可以获得线偏振光?怎样用实验来检验线偏振光、部分偏振光和自然光?答：略．14-3 一束光入射到两种透明介质的分界面上时，发现只有透射光而无反射光，试说明这束光是怎样入射的?其偏振状态如何?答：这束光是以布儒斯特角入射的．其偏振态为平行入射面的线偏振光． 14-4 什么是光轴、主截面和主平面?什么是寻常光线和非常光线?它们的振动方向和各自的主平面有何关系? 答：略．14-5 在单轴晶体中，e 光是否总是以e n c /的速率传播?哪个方向以0/n c 的速率传播?答：e 光沿不同方向传播速率不等，并不是以0/n c 的速率传播．沿光轴方向以0/n c 的速率传播．14-6是否只有自然光入射晶体时才能产生O 光和e 光? 答：否．线偏振光不沿光轴入射晶体时，也能产生O 光和e 光．14-7投射到起偏器的自然光强度为0I ，开始时，起偏器和检偏器的透光轴方向平行．然后使检偏器绕入射光的传播方向转过130°，45°，60°，试分别求出在上述三种情况下，透过检偏器后光的强度是0I 的几倍? 解：由马吕斯定律有0o2018330cos 2I I I ==0ο2024145cos 2I I I ==0ο2038160cos 2I I I ==所以透过检偏器后光的强度分别是0I 的83,41,81倍．14-8 使自然光通过两个偏振化方向夹角为60°的偏振片时，透射光强为1I ，今在这两个偏振片之间再插入一偏振片，它的偏振化方向与前两个偏振片均成30°，问此时透射光I 与1I 之比为多少? 解：由马吕斯定律ο20160cos 2I I =80I =32930cos 30cos 20ο2ο20I I I ==∴ 25.2491==I I14-9 自然光入射到两个重叠的偏振片上．如果透射光强为，(1)透射光最大强度的三分之一，(2)入射光强的三分之一，则这两个偏振片透光轴方向间的夹角为多少?解：（1） max 120131cos 2I I I ==α又 20max I I =∴ ,601I I =故 'ο11124454,33cos ,31cos ===ααα.(2) 0220231cos 2I I I ==α∴ 'ο221635,32cos ==αα14-10 一束自然光从空气入射到折射率为1.40的液体表面上，其反射光是完全偏振光．试求：(1)入射角等于多少?(2)折射角为多少? 解：(1),140.1tan 0=i ∴'ο02854=i(2) 'ο0ο323590=-=i y14-11 利用布儒斯特定律怎样测定不透明介质的折射率?若测得釉质在空气中的起偏振角为58°，求釉质的折射率． 解：由158tan οn =,故60.1=n14-12 光由空气射入折射率为n 的玻璃．在题14-12图所示的各种情况中，用黑点和短线把反射光和折射光的振动方向表示出来，并标明是线偏振光还是部分偏振光．图中.arctan ,00n i i i =≠题图14-12 解：见图．题解14-12图题14-13图*14-13如果一个二分之一波片或四分之一波片的光轴与起偏器的偏振化方向成30°角，试问从二分之一波片还是从四分之一波片透射出来的光将是：(1)线偏振光?(2)圆偏振光?(3)椭圆偏振光?为什么?解：从偏振片出射的线偏振光进入晶(波)片后分解为e o ,光，仍沿原方向前进，但振方向相互垂直(o 光矢垂直光轴，e 光矢平行光轴)．设入射波片的线偏振光振幅为A ，则有A.2130sin ,A 2330cos οο====A A A A o e∴ e o A A ≠e o , 光虽沿同一方向前进，但传播速度不同，因此两光通过晶片后有光程差．若为二分之一波片,e o ,光通过它后有光程差2λ=∆，位相差πϕ=∆，所以透射的是线偏振光．因为由相互垂直振动的合成得ϕϕ∆=∆-+22222sincos 2eo eoA A xy A yA x∴ 0)(2=+eoA y A x即 x A A y oe -=若为四分之一波片，则e o ,光的,4λ=∆位相差2πϕ=∆，此时1s i n ,0c o s =∆=∆ϕϕ∴12222=+eoA yA x即透射光是椭圆偏振光．*14-14 将厚度为1mm 且垂直于光轴切出的石英晶片，放在两平行的偏振片之间，对某一波长的光波，经过晶片后振动面旋转了20°．问石英晶片的厚度变为多少时，该波长的光将完全不能通过?解：通过晶片的振动面旋转的角度ϕ与晶片厚度d 成正比．要使该波长的光完全不能通过第二偏振片，必须使通过晶片的光矢量的振动面旋转ο90． ∴ 1212::d d =ϕϕmm 5.412090οο1122=⨯==d d ϕϕ习题十六16-1 将星球看做绝对黑体，利用维恩位移定律测量m λ便可求得T ．这是测量星球表面温度的方法之一．设测得：太阳的m 55.0m μλ=，北极星的m 35.0m μλ=，天狼星的m 29.0m μλ=，试求这些星球的表面温度．解：将这些星球看成绝对黑体，则按维恩位移定律：K m 10897.2,3⋅⨯==-b b T m λ对太阳： K 103.51055.010897.236311⨯=⨯⨯==--mbT λ对北极星：K 103.81035.010897.236322⨯=⨯⨯==--mbT λ对天狼星：K 100.11029.010897.246333⨯=⨯⨯==--mbT λ16-2 用辐射高温计测得炉壁小孔的辐射出射度(总辐射本领)为22.8W ·cm -2，求炉内温度．解：炉壁小孔视为绝对黑体，其辐出度242m W 108.22cm W 8.22)(--⋅⨯=⋅=T M B 按斯特藩-玻尔兹曼定律：=)(T M B 4T σ41844)1067.5108.22()(-⨯⨯==σT M T BK 1042.110)67.58.22(3341⨯=⨯=16-3 从铝中移出一个电子需要4.2 eV 的能量，今有波长为2000οA 的光投射到铝表面．试问：(1)由此发射出来的光电子的最大动能是多少?(2)遏止电势差为多大?(3)铝的截止(红限)波长有多大? 解：(1)已知逸出功eV 2.4=A 据光电效应公式221m mv hv =A +则光电子最大动能：A hcA h mv E m -=-==λυ2max k 21eV 0.2J 1023.3106.12.41020001031063.6191910834=⨯=⨯⨯-⨯⨯⨯⨯=----m2max k 21)2(mvE eUa==∴遏止电势差 V 0.2106.11023.31919=⨯⨯=--a U(3)红限频率0υ,∴000,λυυcA h ==又∴截止波长 1983401060.12.41031063.6--⨯⨯⨯⨯⨯==Ahc λm 0.296m 1096.27μ=⨯=-16-4 在一定条件下，人眼视网膜能够对5个蓝绿光光子(m 105.0-7⨯=λ)产生光的感觉．此时视网膜上接收到光的能量为多少?如果每秒钟都能吸收5个这样的光子，则到 达眼睛的功率为多大? 解：5个兰绿光子的能量J1099.1100.51031063.65187834---⨯=⨯⨯⨯⨯⨯===λυhcn nh E功率 W 1099.118-⨯==tE16-5 设太阳照射到地球上光的强度为8 J ·s -1·m -2，如果平均波长为5000οA ，则每秒钟落到地面上1m 2的光子数量是多少?若人眼瞳孔直径为3mm ，每秒钟进入人眼的光子数是多少?解：一个光子能量 λυhch E ==1秒钟落到2m 1地面上的光子数为21198347ms1001.21031063.6105888----⋅⨯=⨯⨯⨯⨯⨯===hcEn λ每秒进入人眼的光子数为11462192s1042.14/10314.31001.24--⨯=⨯⨯⨯⨯==dnN π16-6若一个光子的能量等于一个电子的静能，试求该光子的频率、波长、动量．解：电子的静止质量S J 1063.6,kg 1011.934310⋅⨯=⨯=--h m 当 20c m h =υ时， 则Hz10236.11063.6)103(1011.92034283120⨯=⨯⨯⨯⨯==--hc m υο12A 02.0m 104271.2=⨯==-υλc122831020122sm kg 1073.21031011.9sm kg 1073.2-----⋅⋅⨯=⨯⨯⨯=====⋅⋅⨯==c m cc m c E p cpE hp 或λ16-7 光电效应和康普顿效应都包含了电子和光子的相互作用，试问这两个过程有什么不同?答：光电效应是指金属中的电子吸收了光子的全部能量而逸出金属表面，是电子处于原子中束缚态时所发生的现象．遵守能量守恒定律．而康普顿效应则是光子与自由电子(或准自由电子)的弹性碰撞，同时遵守能量与动量守恒定律．16-8 在康普顿效应的实验中，若散射光波长是入射光波长的1.2倍，则散射光子的能量ε与反冲电子的动能k E 之比k E /ε等于多少?解：由 2200mc h c m hv +=+υ)(00202υυυυ-=-=-=h h h cm mcE kυεh =∴5)(00=-=-=υυυυυυεh h E k已知2.10=λλ由2.10=∴=υυλυc2.11=υυ则52.0112.110==-=-υυυ16-9 波长ο0A 708.0=λ的X 射线在石腊上受到康普顿散射，求在2π和π方向上所散射的X 射线波长各是多大? 解：在2πϕ=方向上：ο1283134200A0243.0m 1043.24sin1031011.91063.622sin2Δ=⨯=⨯⨯⨯⨯⨯==-=---πϕλλλcm h散射波长ο0A 732.00248.0708.0Δ=+=+=λλλ 在πϕ=方向上ο120200A 0486.0m 1086.422sin2Δ=⨯===-=-cm h cm h ϕλλλ散射波长 ο0A 756.00486.0708.0Δ=+=+=λλλ16-10 已知X 光光子的能量为0.60 MeV ，在康普顿散射之后波长变化了20%，求反冲电子的能量．解：已知X 射线的初能量,MeV 6.00=ε又有00,ελλεhchc =∴=经散射后 000020.1020.0λλλλ∆λλ=+=+=此时能量为 002.112.1ελλε===hc hc反冲电子能量 MeV 10.060.0)2.111(0=⨯-=-=εεE16-11 在康普顿散射中，入射光子的波长为0.030 οA ，反冲电子的速度为0.60c ，求散射光子的波长及散射角． 解：反冲电子的能量增量为202022020225.06.01c m cm cm cm mcE =--=-=∆由能量守恒定律，电子增加的能量等于光子损失的能量， 故有 20025.0c m hchc=-λλ散射光子波长ο121083134103400A043.0m 103.410030.0103101.925.01063.610030.01063.625.0=⨯=⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯=-=------λλλc m h h由康普顿散射公式2sin0243.022sin22200ϕϕλλλ∆⨯==-=cm h可得 2675.00243.02030.0043.02sin2=⨯-=ϕ散射角为 7162'=οϕ16-12 实验发现基态氢原子可吸收能量为12.75eV 的光子．(1)试问氢原子吸收光子后将被激发到哪个能级?(2)受激发的氢原子向低能级跃迁时，可发出哪几条谱线?请将这些跃迁画在能级图上．解：(1)2eV 6.13eV 85.0eV 75.12eV 6.13n-=-=+-解得 4=n或者 )111(22n Rhc E -=∆75.12)11.(1362=-=n解出 4=n题16-12图 题16-13图(2)可发出谱线赖曼系3条，巴尔末系2条，帕邢系1条，共计6条.16-13 以动能12.5eV 的电子通过碰撞使氢原子激发时，最高能激发到哪一能级?当回到基态时能产生哪些谱线?解：设氢原子全部吸收eV 5.12能量后，最高能激发到第n 个能级，则]11[6.135.12,eV 6.13],111[2221nRhc nRhc E E n -==-=-即得5.3=n ，只能取整数，∴ 最高激发到3=n ，当然也能激发到2=n 的能级．于是ο322ο222ο771221A 6563536,3653121~:23A 121634,432111~:12A1026m 10026.110097.18989,983111~:13===⎥⎦⎤⎢⎣⎡-=→===⎥⎦⎤⎢⎣⎡-=→=⨯=⨯⨯===⎥⎦⎤⎢⎣⎡-=→-R R R n R R R n RR R n λυλυλυ从从从可以发出以上三条谱线．题16-14图16-14 处于基态的氢原子被外来单色光激发后发出巴尔末线系中只有两条谱线，试求这两条谱线的波长及外来光的频率．解：巴尔末系是由2>n 的高能级跃迁到2=n 的能级发出的谱线．只有二条谱线说明激发后最高能级是4=n 的激发态．ο1983424ο101983423222324A4872106.1)85.04.3(1031063.6A6573m 1065731060.1)51.14.3(10331063.6e 4.326.13e 51.136.13e 85.046.13=⨯⨯-⨯⨯⨯=-==⨯=⨯⨯-⨯⨯⨯⨯=-=∴-=∴-==-=-=-=-=-=-=-----E E hc E E hcE E hc E E hch VE V E V E a mn mn βλλλλυ基态氢原子吸收一个光子υh 被激发到4=n 的能态 ∴ λυhcE E h =-=14Hz 1008.310626.6106.1)85.06.13(15341914⨯=⨯⨯⨯-=-=--hE E υ16-15 当基态氢原子被12.09eV 的光子激发后，其电子的轨道半径将增加多少倍?解： eV 09.12]11[6.1321=-=-n E E n26.1309.126.13n =-51.16.1309.12.1366.132=-=n , 3=n12r n r n =,92=n,19r r n =轨道半径增加到9倍.16-16德布罗意波的波函数与经典波的波函数的本质区别是什么?答：德布罗意波是概率波，波函数不表示实在的物理量在空间的波动，其振幅无实在的物理意义,2φ仅表示粒子某时刻在空间的概率密度．16-17 为使电子的德布罗意波长为1οA ，需要多大的加速电压? 解： ooA 1A 25.12==uλ 25.12=U∴ 加速电压 150=U 伏16-18 具有能量15eV 的光子，被氢原子中处于第一玻尔轨道的电子所吸收，形成一个光电子．问此光电子远离质子时的速度为多大?它的德布罗意波长是多少? 解：使处于基态的电子电离所需能量为eV 6.13，因此，该电子远离质子时的动能为eV 4.16.13152112=-=+==E E mvE k φ它的速度为31191011.9106.14.122--⨯⨯⨯⨯==mE v k -15s m 100.7⋅⨯=其德布罗意波长为：o953134A 10.4m 1004.1100.71011.91063.6=⨯=⨯⨯⨯⨯==---mvh λ16-19 光子与电子的波长都是2.0οA ，它们的动量和总能量各为多少?解：由德布罗意关系：2mc E =，λhmv p ==波长相同它们的动量相等．1-241034s m kg 103.3100.21063.6⋅⋅⨯=⨯⨯==---λhp光子的能量 eV 102.6J 109.9103103.3316824⨯=⨯=⨯⨯⨯====--pc hch λυε电子的总能量 2202)()(c m cp E +=,eV 102.63⨯=cp而 eV 100.51MeV 51.0620⨯==c m ∴ cp c m >>20 ∴ MeV 51.0)()(202202==+=c m c m cp E16-20 已知中子的质量kg 1067.127n -⨯=m ，当中子的动能等于温度300K 的热平衡中子气体的平均动能时，其德布罗意波长为多少?解：kg 1067.127n -⨯=m ,S J 1063.634⋅⨯=-h ,-123K J 1038.1⋅⨯=-k 中子的平均动能 mpKT E k 2232==德布罗意波长 oA 456.13===mkTh p h λ16-21 一个质量为m 的粒子，约束在长度为L 的一维线段上．试根据测不准关系估算这个粒子所具有的最小能量的值．解：按测不准关系，h p x x ≥∆∆，x x v m p ∆=∆，则h v x m x ≥∆∆,xm h v x ∆≥∆这粒子最小动能应满足222222min 22)(21)(21mLhxm hxm h m v m E x =∆=∆≥∆=16-22 从某激发能级向基态跃迁而产生的谱线波长为4000οA ，测得谱线宽度。

习题十七17-1按照原子核的质子一中子模型,组成原子核；X的质子数和中子数各是多少？核内共有多少个核子？这种原子核的质量数和电荷数各是多少？答：组成原子核；X的质子数是Z,中子数是力-Z・核内共有/个核子.原子核的质量数是核电荷数是Z.17-2原子核的体积与质量数之间有何关系？这关系说明什么？答：实验表明，把原子核看成球体，其半径7?与质量数/的关系为R = R.A\说明原子核的体积与质量数/成正比关系.这一关系说明一切原子核中核物质的密度是一个常数.即单位体积内核子数近似相等，并由此推知核的平均结合能相等.结合能正比于核子数，就表明核力是短程力.如果核力象库仑力那样，按照静电能的公式，结合能与核子数/的平方成正比，而不是与/成正比. 17-3什么叫原子核的质量亏损？如果原子核；X的质量亏损是A加，其平均结合能是多少？解：原子核的质量小于组成原子核的核子的质量之和，它们的差额称为原子核的质量亏损•设原子核的质量为M x,原子核；X的质量亏损为：△刃=[Zm p + (/ - Z)mJ- M x平均结合能为£o= —=0 A A17-4已知％Th的原子质量为232.03821“，计算其原子核的平均结合能.解:结合能为AE = [Zm H + (/ - Z)加”一M] x 931.5 MeV隘Th 原子M = 232.03821 u, Z = 90,力=232,氢原子质量加日=1.007825m n = 1.008665 u:4E = [90x 1.007825 + (232-90)x 1.008665 — 232.0382l]x931.5 MeV= 1.766.56 MeV・・・平均结合能为瓦=乞」766.56= 7 GMA 23217-5什么叫核磁矩？什么叫核磁子(冷)？核磁子冷•和玻尔磁子厶有何相似之处？有何区别？质子的磁矩等于多少核磁子？平常用来衡量核磁矩大小的核磁矩“:的物理意义是什么？它和核的g因子、核自旋量子数的关系是什么？解：原子核自旋运动的磁矩叫核磁矩，核磁子是原子核磁矩的单位，定义为:式中加"是质子的质量.核磁子与玻尔磁子形式上相似，玻尔磁子定义为P B =~^~，式中 4mi e 阻是电子的质量.质子的磁矩不等于冷・质子的磁矩冷=2.79273/Y ・平常用来衡量核 磁矩大小的是核磁矩在外磁场方向分量的最大值“;，它和原子核g 因子、自旋量子数的关系是“；=Sl^N17-6核自旋量子数等于整数或半奇整数是由核的什么性质决定？核磁矩与核自旋角动量有 什么关系？核磁矩的正负是如何规定的？解：原子核是由质子和中子组成.质子和中子的自旋均为丄.因此组成原子核的质子和中子 2数的奇、偶数决定了核自旋量子数为零或丄的奇、偶倍数. 2核磁矩与自旋角动量的关系是：Q 的正负取决于幻的正负.当必与B 平行时必为正，当〃/与E 反平行时，几为负.17-7什么叫核磁共振？怎样利用核磁共振来测量核磁矩？解：原子核置于磁场中，磁场和核磁矩相互作用的附加能量使原子核能级发生分裂.当核在 电磁辐射场中时，辐射场是光子组成的，当光子的能量等于核能级间隔时，原子核便吸 收电磁场的能量，称为共振吸收，这一现象称为核磁共振.在磁场中核能级间隔为：共振吸收时，hv = AE =通常用核磁矩在磁场方向分量的最大值“;来衡量磁矩的大小，//; = g/I^N ,则有 hu 丛B I・・・“；=/罟，已测出/, u,现测得B 就可以算出“；.17-8什么叫核力？核力具有哪些主要性质？答：组成原子核的核子之间的强相互作用力称为核力.核力的主要性质：（1）是强相互作用力，主要是引力・（2）是短程力,作用距离小于10" m , （3）核力与核子的带电状况无关.（4）具有饱和性.17-9什么叫放谢性衰变？ cc, 0,厂射线是什么粒子流？写出鬻U 的©衰变和彳爲Th 的0“N eh 4兀m —^=5.05.xl0-A.^衰变的表示式•写出4衰变和0衰变的位移定则.解：不稳定的原子核都会自发地转变成另一种核而同时放出射线，这种变化叫放射性衰变.6Z 射线是带正电的氮核：He 粒子流，0射线是高速运动的正、负电子流，了射线是光子流.亍 U T 芽 Th+： He芽 Th t 常 pa+「+ QQ 衰变和0衰变的位移定则为：Y+H + q17-10什么叫原子核的稳定性？哪些经验规则可以预测核的稳定性？答：原子核的稳定性是指原子核不会自发地从核中发岀射线而转变成另一种原子核的性质. 以下经验规则可预测核的稳定性：(1) 原子序数大于84的核是不稳定的•(2) 原子序数小于84的核中质子数和中子数都是偶数的核稳定.(3) 质子或中子数等于幻数2、8、20、28、50、82、126的原子核特别稳定.(4) 质子数和中子数之比仝=1的核稳定.比值越大，稳定性越差.P17-11写出放射性衰变定律的公式.衰变常数2的物理意义是什么？什么叫半衰期八？ T x2 2和2有什么关系？什么叫平均寿命厂？它和半衰期片、和2有什么关系？2解：N = N&^ ,衰变常数2 =-理泸 ・的物理意义是表示在某时刻，单位时间内衰变 的原子数与该时刻原子核数的比值.是表征衰变快慢的物理常数.原子核每衰变一半所需的时间叫半衰期.平均寿命r 是每个原子核衰变前存在时间的平均值. 1 T =—7\ = t\n 2 ・217-12测得地壳中铀元素駕U 只点0. 72%,其余为弋U,已知零U 的半衰期为4. 468 X109Q 衰变0衰变的位移定则为:Y+； HeIn 2 T"2年，零u 的半衰期为7. 038X10*年，设地球形成时地壳中的莖U 和莖U 是同样多，试估计 地球的年龄.解：按半衰期r=ln2 = 0：693对繆U ： =2^21 = _ =9.847x10-2 1/年T 、 7.038xl018按衰变定律N =,可得则地球年龄:I 0.72 In ------- = ________ 99.28-(1.551 — 9.847)x10-°= 5.94x109 年17-13放射性同位素主要应用有哪些？答：放射性同位素主要在以下几个方面应用较广泛：医学上用于放射性治疗和诊断；工业上 用于无损检测；农业上用放射性育种；考古学、地质学中用于计算生物或地质年代；生物学 中作示踪原子等等.17-14为什么重核裂变或轻核聚变能够放出原子核能？答：轻核和重核的平均结合能较小，而中等质量（力=40〜60）的核平均结合能较大，因此 将重核裂变成两个中等质量的核或轻核聚变成质量数较大的核时平均结合能升高，从而放出 核能. 17-15原子核裂变的热中子反应堆主要由哪几部分组成？它们各起什么作用？ 答：热中子反应堆的主要组成部份有堆芯、中子反射层、冷却系统、控制系统、防护层.堆芯是放置核燃料和中子减速剂的核心部份，维持可控链式反应，释放原子核能. 冷却系统与换能系统合二为一，再通过冷却系统将堆芯释放出的核能输送到堆芯以外. 控制系统是通过控制棒插入堆芯的长度，控制参加反应的中子数，使反应堆保持稳定的 功率.中子反射层是阻挡中子从反应堆中逸出.防护层是反应堆的安全屏障.17-16试举出在自然界中存在负能态的例子•这些状态与狄拉克真空，结果产生1 MeV 的电 子，此时还将产生什么？它的能量是多少？答：例如物体在引力场中所具有的引力势能；正电荷在负电荷电场中的静电能，都是自然界 中的负能态.这些负能态是能够观测到的，具有可观测效应.狄拉克的负能态是观测不到的, 没有可观测效应.对；；8U ：人0.693 0.693 4.468x10°= 1.551xlO -10 1/年17-17将3MeV能量的了光子引入狄拉克真空，结果产生IMeV的电子，此时还将产生什么？它的能量是多少？答：把能量大于电子静能两倍£>2m o c2 =1.022 MeV的了光子引入真空，它有可能被负能量电子的一个电子所吸收，吸收了这么多能量的电子有可能越过禁区而跃迁到正能量区，并表现为一个正能量的负电子不；同时，留下的空穴表现为一个正能量的正电子，・这一过程称为电子偶的产生，可写为了 T 幺+ +€_按题意，根据能量守恒，正电子的能量为2 MeV17-18试证明任何能量的了光子在真空中都不可能产生正、负电子对.答：证明：设由了光子转化成的一对正负电子其动量分别为卩和卩2,在电子的质心系中应有P1+P2 =0并且正负电子的总能量应大于2加工2.按照相对论，光子动量与能量的关系为E = pc, 动量等于零而能量不等于零的光子是不存在的.显然厂光子转换成正负电子，同时满足能量守恒和动量守恒是不可能的，即在真空中无论7光子能量多大，都不可能产生正负电子对•但是了光子与重原子核作用时便可转化为正负电子对.。

第十七章 电磁振荡和电磁波17-1 若收音机的调谐电路所用线圈的自感系数为41062-⨯.H ，要收听535kHz 到1605kHz 的广播, 问与线圈连接的可变电容的最大值和最小值各为多少?分析 调谐电路是用电感和电容串联而成的振荡电路, 电路的固有频率LC 10=ω．外加电动势的频率ω等于电路固有频率0ω时, 电路中的电流振幅最大，称为电磁共振，0ω为谐振频率．给出电路的自感和谐振频率的最小值、最大值后，只需代入LC10=ω，不难求出电容的最大值和最小值． 解 电容的最大值和最小值分别为37.8pF F 108.37F 106.2)100016052(1)2(1340pF F 10340F 106.2)10005352(1)2(112422221242211=⨯=⨯⨯⨯⨯===⨯=⨯⨯⨯⨯==----ππνππνL C LC 17-2 在LC 电路中, 如果41062-⨯=.L H, F 102110-⨯=.C , 初始时电容器两极板间的电势差V 0=1V , 且电流为零，试求：(1)振荡频率；(2)最大电流；(3)任意时刻电容器两极板间的电场能、自感线圈中的磁场能；(4) 验证在任意时刻电场能和磁场能之和等于初始的电场能．分析 在LC 电路中，如果忽略电路中的电阻，并假设电容器的电场局限在两极板之间，自感线圈中的磁场局限在线圈内部，则振荡电路中无能量损耗，总能量守恒．不过，这只是理想化的结果．解 (1) 5104100.9102.1106.214.32121⨯=⨯⨯⨯⨯⨯==--LC πνHz (2) 4000108.6-⨯====LC CVLCq q I ω A (3) 任意时刻，设两极板间的电势差为)cos(0ϕω+=t V V ，则电容器极板上的电荷为)cos(0ϕω+==t CV CV q ，电路中电流为)sin()sin(d d 00ϕωϕωω+-=+-==t V LC t CV t q I 其中ϕ为初相位．因此，任一时刻电容器两极板间的电场能为)cos 100.6)(cos 21212112202e ϕϕω+⨯=+==-t (ωt CV CV W 自感线圈中的磁场能为)sin 100.6)(sin 21212112202m ϕϕω+⨯==+==-t (ωt CV LI W 任意时刻的总能量为J 100.621211120m e -⨯==+=CV W W W 表明总能量保持不变，并等于初始能量11200100.621-⨯==CV W J ． 17-3 如图17-3所示，将开关K 按下后，电容器即由电池充电，放手后，电容器即经线圈L 放电．不计回路中的电阻，(1)若L =0.01H ，C =1.00μF ，E =1.40V ， 求放手后电容器两极板间的电势差及回路中的电流随时间变化的规律．(2)当分布在电容和电感间的能量相等时，电容器上的电荷为多少?(3)电荷为上述数值时经过了多少时间? 解 (1) t =0时，极板间的电势差为V 0= E = 1.40V 电容器极板上的电荷为)cos(0ϕω+==t CV CV q ，因LC 1=ω，电路中电流为 )sin()sin(d d 00ϕωϕωω+-=+-==t V LC t CV t q I 由初始条件：t =0时，00CV q q ==，得初相0=ϕ，故各量随时间的变化规律为t t CV q 46010cos 1040.1)cos(-⨯=+=ϕωt t V V 4010cos 40.1)cos(=+=ϕωt t V LC I 42010sin 1040.1)sin(-⨯=+-=ϕω (2)t t ωω22cos sin = 时电场能量与磁场能量相等，得22cos =t ω，此时电容器上的电荷为C 1090.9cos 1040.176--⨯=⨯=t q ω (3)由22cos =t ω，取时间的最小可能值，得4πω=t ，即s 1085.745-⨯==ωπt 17-4 一振荡电偶极子辐射电磁波，设电偶极子的电矩振幅为p 0=2.26×10-4C .m ，频率为800kHz ．求：(1)电磁波的波长；(2)在电偶极子赤道圈上距离电偶极子为2km 处电场强度和磁场强度的振幅．分析 本题涉及的概念有：振荡电偶极子、电偶极子的电矩；振荡电偶极子辐射的电磁波在足够远处可视为球面波．解 (1)由波长和频率的关系得m 375m 10810358=⨯⨯==νλc(2)由2/,2πθπνω==，得V/m 285.04sin 200220020===rp r p E v v επνπεθω A/m 1057.74sin 402020-⨯===rp r p H v v πνπθω 17-5 在真空中,一平面电磁波的电场强度由下式给出(式中各量均用国际单位)：)](102cos[6.008=-⨯==z y x E cx t E E π 求：(1)波长和频率；(2)传播方向；(3)磁感强度的大小和方向．分析 因为E 、H 及电磁波的传播方向三者互相垂直构成右手螺旋关系，电场矢量E 在y 方向振动，电磁波以波速c 沿x 正向传播，因此可判定磁场矢量H 在z 方向振动．解 (1) 由电场强度波函数得8102⨯=πω rad/s ，8102==πωνHz ，则 m 31010388=⨯==νλc(2) 由电场强度波函数表示式可知电磁波的传播方向为x 轴正向．(3) 由于H B 0μ=，000000E H B εμμ==，c100=εμ，得 T 100.2900-⨯==cE B )](102cos[100.289cx t B z -⨯⨯=-πB x =B y =017-6 某激光束的直径为0.2cm ，功率为6kW ，求该光束的坡印廷矢量对时间的平均值以及相应的电场强度、磁场强度的振幅．分析 通常激光束的功率实际上是指平均辐射功率，即辐射或接收的激光束的能量对一个周期的平均值．光波是电磁波，光波的能流密度矢量即为电磁波的坡印廷矢量S ．坡印廷矢量定义为单位时间通过垂直于传播方向单位面积的辐射能．所以，坡印廷矢量对时间的平均值应该等于单位面积上的平均辐射功率．解 激光束的平均辐射功率 W 1063⨯=P ，则坡印廷矢量对时间的平均值为2922232 W/m 109.1W/m )101.0(106⨯=⨯⨯⨯==-ππR P S (1) 将激光束视为平面波，坡印廷矢量可写为⎪⎭⎫ ⎝⎛-==v x t H E EH S ω200cos 对一个周期求时间的平均值，得0021H E S = (2) 其中E 0、H 0分别为电振动和磁振动振幅．由电磁波的基本性质0000H E με=，并联立(1)式和(2)式，得V/m 102.126000⨯==εμS E T 100.450000-⨯==E H με 17-7 同轴电缆由半径为r a 的长直导线及包在其外的半径为r b 的导体外壳组成，如图17-7所示．电源电动势为E , 负载电阻为R ，与同轴电缆连成回路．若同轴电缆的电阻很小，电流功率为P ，(1)求证同轴电缆内距轴线r 处一点的电场强度为a br r r E ln E=(r a <r <r b )；(2)求证该处磁感强度Er P B πμ20=(r a <r <r b )；(3)求同轴电缆内的坡印廷矢量S ；(4)对r a <r <r b 的环形面积分坡印廷矢量，证明其结果等于P ．由此我们看到，导线不仅起到引导电流的作用，还起到引导电磁能作用．电源的能量不是通过电流而是通过电磁场传递的．分析 这是一个具有稳恒电流的回路，回路中的电场是稳恒电场．同轴电缆构成一个柱形电容器，考虑到同轴电缆的电阻很小，两极板上的电势分别与电源两极电势相等，于是可以将柱形电容器的两极板就视为电源的两极，并认为电源两极上的正负电荷均匀地分布在柱形电容器的两极板上，因此在同轴电缆两极之间就形成了一个静电场．解 同轴电缆可视为柱形电容器，极板间电压等于电源电动势E ，两极板上的电荷为E E a b r r l C CU q ln 20πε=== 极板间的静电场电场强度方向向下，大小为 E a br r r r l qE ln 120==πε(2)由于同轴电缆的轴对称性，在垂直轴线平面内作半径为r 的圆形安培环路，H 的方向与电流I 形成右手螺旋关系，从左侧观看为逆时针方向．R I r H E ===⋅∑⎰π2d Ll H 电流功率为R P /2E =，则磁感强度为EE r P rR H B πμπμμ22000=== (3) 将能流密度的概念应用于稳恒电流通过的同轴电缆，其内部的坡印廷矢量H E S ⨯=，方向沿同轴电缆向右，大小为ab P r S ln 212π= (4)在同轴电缆内取半径为r , 宽为d r 的细圆环面元，单位时间穿过该面元的能量为r r S P d 2d π⋅=对同轴电缆内截面积分，得P r r ab P r r a br PP b a b a ===⎰⎰⎰d ln d 2ln 2d 2ππ 17-8 对于一个正在充电的平行圆板电容器, 忽略电容器的边缘效应．试证明：(1) 坡印廷矢量S 处处沿半径方向指向电容器内部；(2)电流流进电容器内的功率P 等于储存在该体积中的电场能量的增加率．由此看到, 储存在电容器中的电能并不是通过导线，而是通过导线和电容器极板周围的空间进入电容器的．证 (1) 设圆板电容器半径为R 间距为d , t 时刻两极板间的电场强度为E ,ER图17-7方向垂直板面从左到右．根据例题14-1，半径为r 的圆周上各点磁场强度沿圆周的切线方向，大小为t E r H d d 20ε= 所以圆周上各点坡印廷矢量S 的方向沿半径指向电容器内部，大小为 t E E R EH S d d 20ε== (2) 单位时间内流入电容器内部的功率P 为t EE d R Rd t E E R Rd S P d d 2d d 22020εππεπ==⋅=而电容器储存的电场能量为d R E W 22021πε=所以电场能量的增加率为P t EE d R t W==d d d d 02επ。

第十七 章量子物理题17.1：天狼星的温度大约是11000℃。

试由维思位移定律计算其辐射峰值的波长。

题17.1解：由维思位移定律可得天狼星单色辐出度的峰值所对应的波长该波长nm 257m 1057.27m =⨯==-Tbλ 属紫外区域，所以天狼星呈紫色题17.2：已知地球跟金星的大小差不多，金星的平均温度约为773 K ，地球的平均温度约为293 K 。

若把它们看作是理想黑体，这两个星体向空间辐射的能量之比为多少？题17.2解：由斯特藩一玻耳兹曼定律4)(T T M σ=可知，这两个星体辐射能量之比为4.484=⎪⎪⎭⎫⎝⎛=地金地金T T M M 题17.3：太阳可看作是半径为7.0 ⨯ 108 m 的球形黑体，试计算太阳的温度。

设太阳射到地球表面上的辐射能量为1.4 ⨯ 103W ⋅m －2，地球与太阳间的距离为1.5 ⨯ 1011m 。

题17.3解：以太阳为中心，地球与太阳之间的距离d 为半径作一球面，地球处在该球面的某一位置上。

太阳在单位时间内对外辐射的总能量将均匀地通过该球面，因此有 2244)(R Ed T M ππ=（1）4)(T T M σ= （2）由式（1）、（2）可得K 58004122=⎪⎪⎭⎫⎝⎛=σR E d T题17.4：钨的逸出功是4.52 eV ，钡的选出功是2.50 eV ，分别计算钨和钡的截止频率。

哪一种金属可以用作可见光范围内的光电管阴极材料？题17.4解：钨的截止频率 Hz 1009.115101⨯==hW ν 钡的截止频率Hz 1063.015202⨯==hW ν 对照可见光的频率范围可知，钡的截止频率02ν正好处于该范围内，而钨的截止频率01ν大于可见光的最大频率，因而钡可以用于可见光范围内的光电管材料。

题17.5：钾的截止频率为4.62 ⨯ 1014 Hz ，今以波长为435.8 nm 的光照射，求钾放出的光电子的初速度。

题17.5解：根据光电效应的爱因斯坦方程W mv h +=221ν 其中λνν/0c h W ==，可得电子的初速度15210s m 1074.52-⋅⨯=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=νλc m h v由于选出金属的电子的速度v << c ，故式中m 取电子的静止质量。

习题17-1已知235U原子的质量为235.043 944u，试计算其结合能和比结合能。

解： 235U的结合能为EB(235，92)=(92×1.007 825+143×1.008 665-235.043 944)×931.5 MeV≈1783.87MeV比结合能（平均结合能）为 =ε 1 783.87MeV/235≈7.59MeV17-2试求基态氢原子的质量亏损。

解：由一个静止的自由电子和一个静止的自由质子结合成一个基态的氢原子时，会放出13.6eV的能量，这就是氢原子基态的结合能。

因此，相应的质量亏损为ΔM=ΔE/c2=13.6eV/c2≈1.46×10-8 u17-3一个氢原子的质量为1.6736×10-27kg，一个锂原子的质量为11.6505×10-27kg，一个氦原子的质量为6.6467×10-27kg。

一个锂核受到一个质子轰击变为2个α粒子，⑴写出核反应方程，并计算该反应释放的核能是多少？⑵1mg锂原子发生这样的反应共释放多少核能？解：⑴11H+73Li →242He 反应前一个氢原子和一个锂原子共有8个核外电子，反应后两个氦原子也是共有8个核外电子，因此只要将一个氢原子和一个锂原子的总质量减去两个氦原子的质量，得到的恰好是反应前后核的质量亏损，电子质量自然消掉。

由质能方程ΔE=Δmc2得释放核能ΔE=2.76×10-12J⑵1mg锂原子含锂原子个数为10-6÷11.6505×10-27，每个锂原子对应的释放能量是2.76×10-12J，所以共释放2.37×108J核能。

17-4碘同位素131I样品的半衰期为8.04天。

已知样品发货时，测得其反射性活度为5.0×10-3 Ci，及至样品进入实验室时，测得其放射性活度为4.2×10-3 Ci。

试求两次测量其间经过的时间.解：由t t e I e N N dtdNI λλλλ--===-=00得t e I Iλ-=0可得II t 0ln 1λ= 又因为λλ693.02ln 1==T所以)(0228.2102.4100.5ln 693.004.8ln155天=⨯⨯==--II t λ 17-5在考古工作中，可以从古生物的遗骸中14C 的含量推算古生物到现在的时间t.设ρ是古生物遗骸中14C 和12C 存量之比，ρ0是空气中14C 和12C 存量之比，试推导出下列公式：2ln )/ln(0ρρTt =证明：设古生物中C 12的含量为)(12C N ；刚死时的古生物中C 14的含量为)(140C N ；现在古生物遗骸中C 14的含量为)(14C N ；根据衰变规律，有：t e C N C N λ-=)()(14014由题意可知：)()(1214C N C N =ρ； 古生物刚死时C 14的含量与C 12含量之比与空气二者之比相等，)()(121400C N C N =ρ， 所以te λρρ=0因此得： ρρλ0ln=t2ln )ln(ln1ρρρρλT t ==∴17-6求反应式CHe H N 1264221147+→+的质量亏损.已知N 147的质量为14.00307u, H 21的质量为2.01410u, C 126的质量为12.00000u ，He 42的质量为4.002603u.解：u 014567.04.002603u)12.00000u (2.01410u 14.00307u m =+-+=∆。

第17章 量子物理学基础 参考答案一、选择题1(D)，2(D)，3(C)，4(B)，5(A)，6(C)，7(C)，8(C)，9(D)，10(C) 二、填空题(1)． λ/hc ，λ/h ，)/(λc h . (2)． 2.5，4.0×1014 . (3)． A /h ，))(/(01νν-e h . (4)． π，0 . (5)．3/1 (6)． 1.66×10-33 kg ·m ·s -1 ，0.4 m 或 63.7 mm . (7)． 1， 2. (8)．粒子在t 时刻在(x ，y ，z )处出现的概率密度. 单值、有限、连续.1d d d 2=⎰⎰⎰z y x ψ(9). 2， 2×(2l +1)， 2n 2. (10). 泡利不相容， 能量最小. 三 计算题1. 用辐射高温计测得炼钢炉口的辐射出射度为22.8 W ·cm -2，试求炉内温度．（斯特藩常量σ = 5.67×10-8 W/(m 2·K 4) ）解：炼钢炉口可视作绝对黑体，其辐射出射度为M B (T ) = 22.8 W ·cm -2＝22.8×104 W ·m -2由斯特藩──玻尔兹曼定律 M B (T ) = σT 4 ∴ T = 1.42×103 K2．已知垂直射到地球表面每单位面积的日光功率（称太阳常数）等于1.37×103 W/m 2． (1) 求太阳辐射的总功率． (2) 把太阳看作黑体，试计算太阳表面的温度．（地球与太阳的平均距离为1.5×108 km ，太阳的半径为6.76×105 km ，σ = 5.67×10-8 W/(m 2·K 4)）解： (1) 太阳在单位时间内辐射的总能量 E = 1.37×103×4π(R SE )2 = 3.87×1026 W(2) 太阳的辐射出射度 =π=204Sr EE 0.674×108 W/m 2 由斯特藩－玻尔兹曼定律 40T E σ=可得 5872/40==σE T K3．图中所示为在一次光电效应实验中得出的曲线(1) 求证：对不同材料的金属，AB 线的斜率相同． (2) 由图上数据求出普朗克恒量h ． (基本电荷e =1.60×10-19C)解：(1) 由 A h U e a -=ν 得 e A e h U a //-=ν|14Hz)e h U a /d /d =ν (恒量) 由此可知，对不同金属，曲线的斜率相同． (2) h = e tg θ 1410)0.50.10(00.2⨯--=e= 6.4×10-34J ·s4. 波长为λ的单色光照射某金属M 表面发生光电效应，发射的光电子(电荷绝对值为e ，质量为m )经狭缝S 后垂直进入磁感应强度为B的均匀磁场(如图示)，今已测出电子在该磁场中作圆运动的最大半径为R ．求(1) 金属材料的逸出功A ； (2) 遏止电势差U a ．解：(1) 由 R m eB /2v v = 得 m R e B /)(=v ，代入 A m h +=221v ν 可得 222221mB e mR hc A ⋅-=λ m B e R hc 2222-=λ (2) 221v m U e a =， m eB R e m U a 22222==v .5．光电管的阴极用逸出功为A = 2.2 eV 的金属制成，今用一单色光照射此光电管，阴极发射出光电子，测得遏止电势差为| U a | = 5.0 V ，试求：(1) 光电管阴极金属的光电效应红限波长； (2) 入射光波长．（普朗克常量h = 6.63×10-34 J ·s ， 基本电荷e = 1.6×10-19 C ）解：(1) 由 00/λνhc h A == ==Ahc0λ 5.65×10-7 m = 565 nm(2)a U e m =221v , A U e hc h a +==λν 得 =+=AU e hca λ 1.73×10-7 m = 173 nm6．α粒子在磁感应强度为B = 0.025 T 的均匀磁场中沿半径为R =0.83 cm 的圆形轨道运动． (1) 试计算其德布罗意波长．(2) 若使质量m = 0.1 g 的小球以与α粒子相同的速率运动．则其波长为多少？(α粒子的质量m α =6.64×10-27 kg ，普朗克常量h =6.63×10-34 J ·s ，基本电荷e =1.60×10-19 C)解：(1) 德布罗意公式：)/(v m h =λ由题可知α 粒子受磁场力作用作圆周运动R m B q /2v v α=，qRB m =v α又 e q 2= 则 e R B m 2=v α故 nm 1000.1m 1000.1)2/(211--⨯=⨯==eRB h αλB× × × × ×(2) 由上一问可得 αm eRB /2=v 对于质量为m 的小球 αααλλ⋅=⋅==mm m m eRB hm h 2v =6.64×10-34 m7. 一电子处于原子某能态的时间为10-8 s ，计算该能态的能量的最小不确定量．设电子从上述能态跃迁到基态所对应的光子能量为3.39 eV ，试确定所辐射的光子的波长及此波长的最小不确定量．( h = 6.63×10-34 J ·s )解：根据不确定关系式 ∆E ∆t ≥ 得∆E ≥ /∆t = 0.659×10-7 eV根据光子能量与波长的关系 λν/hc h E ==得光子的波长 ==E hc /λ 3.67×10-7 m波长的最小不确定量为 ∆λ = hc ∆E /E 2 = 7.13×10-15 m8．已知粒子处于宽度为a 的一维无限深方势阱中运动的波函数为 ax n a x n π=sin 2)(ψ ， n = 1, 2, 3, … 试计算n = 1时，在 x 1 = a /4 →x 2 = 3a /4 区间找到粒子的概率．解：找到粒子的概率为⎰4/34/1*1d )()(a a x x x ψψ⎰π=4/34/2d sin 2a a x a x a π+=+ππ=121)12(1＝0.818四 研讨题1. 人体也向外发出热辐射，为什么在黑暗中还是看不见人？参考解答：人体辐射频率太低，远离可见光波段。