2018年高考理科数学平面向量100题(含答案解析)

2018年全国高考数学试题分类汇编——平面向量1.（全国卷Ⅰ理第15题）ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(m ++=，则实数m =2. （全国卷I 文第12题）点O 是三角形ABC 所在平面内的一点，满足OA OC OC OB OB OA ⋅=⋅=⋅，则点O 是ABC ∆的（ ）（A ）三个内角的角平分线的交点（B ）三条边的垂直平分线的交点 （C ）三条中线的交点（D ）三条高的交点3.(湖南卷文第9题)P 是△ABC 所在平面上一点，若PA PC PC PB PB PA ⋅=⋅=⋅，则P 是△ABC 的（ ） A ．外心B ．内心C ．重心D ．垂心4．（全国卷Ⅱ理第8题，文第9题）已知点A （3，1），B （0，0）C （3，0）.设∠BAC 的平分线AE 与BC 相交于E ，那么有λλ其中,CE BC =等于（ ）A ．2B ．21 C ．－3 D ．－315．（全国卷Ⅱ理第10题，文第11题）点P 在平面上作匀速直线运动，速度向量v =（4，－3）（即点P 的运动方向与v 相同，且每秒移动的距离为|v |个单位.设开始时点P 的坐标为（－10，10），则5秒后点P 的坐标为 A ．（－2，4） B ．（－30，25） C ．（10，－5） D ．（5，－10）6. （全国卷III 理第14题，文第14题）已知向量(,12),(4,5),(,10)OA k OB OC k ===-，且A 、B 、C 三点共线，则k=____. 7．（浙江卷理第10题）已知向量a ≠e ，|e |＝1，对任意t ∈R ，恒有|a －t e |≥|a －e |，则（ ） (A) a ⊥e (B) a ⊥(a －e ) (C) e ⊥(a －e ) (D) (a ＋e )⊥(a －e )8．（浙江卷文第8题）已知向量a ＝(x －5，3)，b ＝(2，x )，且a ⊥b ，则由x 的值构成的集合是( ) (A) {2，3} (B) {－1，6} (C) {2} (D) {6}9.（北京卷理第3题，文第4题）若||1,||2,a b c a b ===+，且c a ⊥，则向量a 与b 的夹角为( ) （A ）30° （B ）60° （C ）120° （D ）150°10.（广东卷第12题）已知向量(2,3)a =，(,6)b x =，且a b ，则x 为_________．11.[ 湖北卷理第13题，文第3题（选择题） ]已知向量||).,5(),2,2(k +=-=若不超过5，则k 的取值范围是 12．（重庆卷理第4题）已知A （3，1），B （6，1），C （4，3），D 为线段BC 的中点，则向量AC 与的夹角为（ ）A ．54arccos2-πB ．54arccos C ．)54arccos(-D ．－)54arccos(-13．（重庆卷文第4题）设向量a =（－1，2），b =（2，－1），则（a ·b ）（a +b ）等于 （ ） A ．（1，1） B ．（－4，－4） C ．－4 D ．（－2，－2）14.（福建卷理第3题）在△ABC 中，∠C=90°，),3,2(),1,(==k 则k 的值是 （ ）A ．5B ．－5C ．23D ．23-15．（福建卷文第14题）在△ABC 中，∠A=90°，k AC k AB 则),3,2(),1,(==的值是 .16.（山东卷理第7题，文第8题）已知向量,a b ，且2,56AB a b BC a b =+=-+，72CD a b =-，则一定共线的三点是（ ） （A ）A 、B 、D （B ）A 、B 、C （C ）B 、C 、D （D ）A 、C 、D17.（江苏卷第18题）在ABC ∆中，O 为中线AM 上一个动点，若AM=2，则)(+∙的最小值是________。

母题五 平面向量【母题原题1】【2018上海卷，8】在平面直角坐标系中，已知点A （-1，0），B （2，0），E ，F 是y 轴上的两个动点，且||=2，则⋅的最小值为______.【答案】3-【解析】依题意设(0,),(0,)E a F b 不妨设a b >，则||2,(1,),(2,),2a b AE a BF b a b -===-=+所以22(1,)(2,)22(2)22(1)3AE BF a b ab b b b b b ⋅=⋅-=-+=-++=+-=+-，故所求最小值为3-.【母题原题2】【2017上海卷，7】如图，以长方体的顶点为坐标原点，过的三条棱所在的直线为坐标轴，建立空间直角坐标系，若的坐标为，则的坐标为________【答案】【母题原题3】【2016上海卷，14】如图，在平面直角坐标系中，O 为正八边形的中心，.任取不同的两点，点P 满足0i j OP OA OA ++=，则点P 落在第一象限的概率是_____________.【答案】528【名师点睛】本题主要考查古典概型概率的计算.解答本题时，关键在于能够准确地确定所研究对象的基本事件空间、基本事件个数，利用概率的计算公式求解.本题能较好地考查考生的数学应用意识、基本运算求解能力、数形结合思想等.【命题意图】考查平面向量的基础知识、基本运算、基本应用；考查运算求解能力以及运用数形结合思想分析与解决问题的能力；考查转化与化归思想的应用.【命题规律】平面向量的数量积、模、夹角是高考考查的重点、热点，往往以选择题或填空题的形式出现.常常以平面图形为载体，考查数量积、夹角、垂直的条件等问题；也易同三角函数、解析几何、不等式等知识相结合，以工具的形式出现．浙江卷涉及模的最值问题考查最多.【答题模板】基于平面向量的双重性，解答平面向量最值问题：一般可以从两个角度进行思考：一是利用其“形”的特征，将其转化为平面几何的有关知识进行解决；二是利用其“数”的特征，通过坐标转化为代数中的有关问题进行解决．【方法总结】1.平面向量数量积的计算方法①已知向量a ，b 的模及夹角θ，利用公式a·b ＝|a ||b|cos θ求解； ②已知向量a ，b 的坐标，利用数量积的坐标形式求解．(2)对于向量数量积与线性运算的综合运算问题，可先利用数量积的运算律化简，再进行运算． 2.向量数量积的性质（1）如果e 是单位向量，则a ·e ＝e ·a . （2）a ⊥b ⇔a ·b ＝0.（3）a ·a ＝|a |2，|a （4）cos θ＝||||⋅a ba b .(θ为a 与b 的夹角)（5）|a ·b |≤|a ||b |.3.利用向量夹角公式、模公式，可将有关角度问题、线段长问题转化为向量的数量积来解决．同时应注意： (1)两向量的夹角是指当两向量的起点相同时，表示两向量的有向线段所形成的角，若起点不同，应通过移动，使其起点相同，再观察夹角．(2)两向量夹角的范围为[0，π]，特别当两向量共线且同向时，其夹角为0，共线且反向时，其夹角为π. (3)在利用向量的数量积求两向量的夹角时，一定要注意两向量夹角的范围．1．【上海市虹口区2018届高三下学期教学质量监控（二模）】在中，，点、是线段的三等分点，点在线段上运动且满足k ⋅=，当⋅取得最小值时，实数的值为（ ）A. B. C. D. 【答案】C【解析】2．【上海市黄浦区2018届高三4月模拟（二模）】在给出的下列命题中，是假命题的是（ ） A. 设是同一平面上的四个不同的点，若，则点必共线 B. 若向量是平面上的两个不平行的向量，则平面上的任一向量都可以表示为，且表示方法是唯一的 C. 已知平面向量满足，且，则是等边三角形D. 在平面上的所有向量中，不存在这样的四个互不相等的非零向量，使得其中任意两个向量的和向量与余下两个向量的和向量相互垂直 【答案】D【解析】由 则点必共线，故A正确；由平面向量基本定理可知B 正确；由可知为的外心，由可知为的重心，故为的中心，即是等边三角形，故C 正确；故选D.3．【2017-2018上海市杨浦区高三数学一模】设A 、B 、C 、D 是半径为1的球面上的四个不同点，且满足0AB AC ⋅= ， 0AC AD ⋅= ， 0AD AB ⋅=，用1S 、2S 、3S 分别表示ABC ∆、ACD ∆、ABD ∆的面积，则123S S S ++的最大值是（ ） A.12B. 2C. 4D. 8 【答案】B点睛：本题考查球的内接多面体及基本不等式求最值问题，能够把几何体扩展为长方体，推知多面体的外接球是同一个球，是解答本题的关键．4．【上海市松江、闵行区2018届高三下学期质量监控（二模）】已知向量、的夹角为，，，若，则实数的值为___________.【答案】【解析】由题意可得：，且，则：，据此有：，解得：.5．【上海市普陀区2018届高三下学期质量调研（二模）】点1F ， 2F 分别是椭圆22:12x C y +=的左、右两焦点，点N 为椭圆C 的上顶点，若动点M 满足： 2122MN MF MF =⋅ ，则122MF MF +的最大值为__________.【答案】6【解析】设()00,m x y ，由2212x y +=，得()()()120,1,1,0,1,0N F F -，则由2122MN MF MF =⋅ ，可得()222200001222x y x y +-=-+，化为()2214x y ++=，可设002{ 21x sin y sin αα==-，()()12=2cos 1,21,24cos 2,42MF sin MF sin αααα--=+- ， ()1226cos 1,63MF MF sin αα+=+-，122MF MF +==== 6122MF MF +的最大值为66.【方法点睛】本题主要考查椭圆的简单性质，平面向量的数量积公式，以及三角函数求最值问题，属于难题. 求最值问题常见方法有①配方法：若函数为一元二次函数，常采用配方法求函数求最值；②图象法；③不等式法；④单调性法；⑤换元法：常用代数或三角代换法，用换元法求值域时需认真分析换元参数的范围变化,利用三角换元后往往利用辅助角公式结合三角函数的单调性求解.6．【上海市黄浦区2018届高三4月模拟（二模）】已知向量在向量方向上的投影为，且，则=_______．(结果用数值表示) 【答案】【解析】由题向量在向量方向上的投影为，即即答案为-6.7．【上海市十二校2018届高三联考】在ABC ∆中， 120BAC ︒∠=， 2AB =， 1AC =，D 为线段BC上任一点（包含端点），则AD BC ⋅ 的最大值为________【答案】2∴cos 75AD BC AD BC ADB k ⋅=⨯⨯∠=-，分类讨论：①k =0时,D 与B 重合,由余弦定理得cosABC ∠==， 5AD BC ⋅=- ； ②01k < 时， 5752k -<- ；∴52AD BC -⋅； 则AD BC ⋅的取值范围为[−5,2].其最大值为2.点睛：求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用． 8．【上海市崇明区2018届高三第一次高考模拟考试】在ABC 中,边上的中垂线分别交于点若,则_______【答案】4【解析】设，则，，又，即，故答案为.9．【上海市浦东新区2018届高三数学一模】已知向量()1,2a =-， ()3,4b =，则向量a在向量b的方向上的投影为________ 【答案】-110．【上海市交通大学附属中学2018届高三上学期开学摸底考试】如图，四个棱长为1的正方体排成一个正四棱柱， AB 是一条侧棱， ()1,2,,16i P i =⋯是上、下底面上其余十六个点，则()1,2,,16i AB AP i ⋅=⋯ 的不同值的个数为__________．【答案】2【解析】 由题意得， i i AP AB BP =+,则()2i i i AB AP AB AB BP AB AB BP ⋅=⋅+=+⋅ ,因为i AB BP ⊥ ，所以21i AB APAB ⋅== ， 所以()1,2,,8i AB AP i ⋅=的不同的值的个数为1.11．【2016-2017年上海市闵行区高三4月质量调研考试（二模）】已知定点()1,1A ，动点P 在圆221x y +=上，点P 关于直线y x =的对称点为P '，向量AQ OP O '=，是坐标原点，则PQ 的取值范围是 .【答案】12．【2016-2017年上海市普陀区高三下学期质量调研（二模）】在△ABC 中， D 、E 分别是AB 、AC 的中点， M 是直线DE 上的动点.若△ABC 的面积为1，则2M B M C B C⋅+ 的最小值为 .【解析】因为D、E分别是AB、AC的中点，且M是直线DE上的动点，所以M到直线BC的距离等于A到直线BC的距离的一半，所以1122MBC ABCS S==，则11sin22MBCS MB MC BMC=∠=，所以1sinMB MCBMC=∠，则c o sc o ss i nB M CM B M C M B M C B M CB M C∠⋅=∠=∠，由余弦定理，得当1cos2BMC∠>时，0y'<，当1cos2BMC∠<时，0y'>，即当1cos2BMC∠=时，2cossinBMCyBMC-∠=∠。

第38题 平面向量的线性运算及平面向量的共线问题I ．题源探究·黄金母题【例1】如图，已知四边形ABCD 是等腰梯形，,E F 分别是,AD BC 的中点，,M N 是线段EF 上的两个点，且EM MN NF ==，下底是上底的2倍，若AB a =，BC b =，求AM ．【解析】1122AD AB BC CD a b a a b =++=+-=+， ∴111242AE AD a b ==+． 又1113()()2224EF AB DC a a a =+=+=，∴1134EM EF a ==，所以1111()()4242AM AE EM a b a a b =+=++=+II ．考场精彩·真题回放【例2】【2017课标1理13】已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= .【答案】【解析】分析：222|2|||44||a b a a b b +=+⋅+4421cos60412=+⨯⨯⨯+=所以|2|12a b +==秒杀解析：利用如下图形，可以判断出2a b+的模长是以2为边长的菱形对角线的长度，则为【名师点睛】平面向量中涉及到有关模长的问题，用到的通法是将模长进行平方，利用向量数量积的知识进行解答，很快就能得出答案；另外，向量是一个工具型的知识，具备代数和几何特征，在做这类问题时可以使用数形结合的思想，会加快解题速度.【例3】【2015全国新课标Ⅰ卷】设D 为ABC ∆所在平面内一点3BC CD =，则（ ）A ．1433AD AB AC =-+ B ．1433AD AB AC =-C ．4133AD AB AC =+ D ．4133AD AB AC =-【答案】A【解析】由题知13AD AC CD AC BC =+=+＝1()3AC AC AB +-＝1433AB AC -+，故选A ． 【例4】【2015高考新课标2理13】设向量a ，b 不平行，向量a b λ+与2a b +平行，则实数λ=_________．【答案】12【解析】因为向量a b λ+与2a b +平行，所以2a b k a b λ+=+（），则12,k k λ=⎧⎨=⎩，所以12λ=．【名师点睛】本题考查向量共线，明确平面向量共线定理，利用待定系数法得参数的关系是解题关键，属于基础题．【例5】【2015北京高考卷】在ABC △中，点M ，N 满足2AM MC =，BN NC =．若M N x A B y A =+，则x =______；y =_______．【答案】11,26- 【解析】由题意知无论,AB AC 的位置关系如何，对结果 都没有任何变化，即结论唯一，不妨设AC AB ⊥，4,3AB AC ==，因此以以A 为原点，AB 为x 轴，AC 为y 轴，建立直角坐标系，3(0,0),(0,2),(0,3),(4,0),(2,)2A M CB N ，1(2,),(4,0),(0,3)2MN AB AC =-==，则1(2,)(4,0)(0,3)2x y -=+，42x =，132y =-，所以11,26x y ==-．【例6】【2014福建8】设M 为平行四边形ABCD 对角线的交点，O 为平行四边形ABCD 所在平面内任意一点，则OA OB OC OD +++等于 （ ）..2.3.4A OMB OMC OMD OM【答案】D【解析】由已知得，111,,,222OA OM CA OB OM DB OC OM AC =+=+=+1,2OD OM BD =+而,,CA AC DB BD =-=-所以4OA OB OC OD OM +++=，选D .【名师点睛】本题主要考查向量的加法法则与减法法则及几何意义.解决此类问题时经常出现的错误有：忽视向量的起点与终点，导致加法与减法混淆，对此，要注意三角形法则与平行四边形法则适用的条件.【例7】【2015高考广东卷】设a 是已知的平面向量且0a ≠,关于向量a 的分解,有如下四个命题： ①给定向量b ,总存在向量c ,使=+a b c ； ②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ；③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ；④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c ．上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是（ ） A ．1 B ．2 C ．3 D ．4 【答案】B【解析】利用向量加法的三角形法则，易知①是对的；利用平面向量的基本定理，易知②是对的；以a 的终点作长度为μ的圆，这个圆必须和向量b λ有交点，这个不一定能满足，③是错的；利用向量加法的三角形法则，结合三角形两边的和大于第三边，即必须b c a λμλμ+=+≥，所以④是假命题.综上，选B ．【例8】【2015高考山东理4】已知菱形ABCD 的边长为a ，60ABC ∠= ,则BD CD ⋅=（ ）（A ）232a - （B ）234a - （C ）234a 错误！未找到引用源。

高考真题分类汇编：平面向量1. 【高考真题重庆理6】设,x y ∈R ，向量(,1),(1,),(2,4)a x b y c ===-且//,⊥，则+（A （B （C ） （D ）10 【答案】B【解析】因为c b c a //,⊥，所以有042=-x 且042=+y ，解得2=x ，2-=y ，即)2,1(),1,2(-==b a ，所以)1,3(-=+b a 10=+，选B.2. 【高考真题浙江理5】设a ，b 是两个非零向量。

A. 若|a+b |=|a |-|b |，则a ⊥bB. 若a ⊥b ，则|a +b |=|a |-|b |C. 若|a +b |=|a |-|b |，则存在实数λ，使得b =λaD. 若存在实数λ，使得b =λa ，则|a +b |=|a |-|b | 【答案】C【解析】利用排除法可得选项C 是正确的，∵|a ＋b |＝|a |－|b |，则a ，b 共线，即存在实数λ，使得a ＝λb . 如选项A ：|a ＋b |＝|a |－|b |时，a ，b 可为异向的共线向量；选项B ：若a ⊥b ，由正方形得|a ＋b |＝|a |－|b |不成立；选项D ：若存在实数λ，使得a ＝λb ，a ，b 可为同向的共线向量，此时显然|a ＋b |＝|a |－|b |不成立.3. 【高考真题四川理7】设a 、b 都是非零向量，下列四个条件中，使||||a ba b =成立的充分条件是（ ）A 、a b =-B 、//a bC 、2a b =D 、//a b 且||||a b = 【答案】C【解析】A. =为既不充分也不必要条件；B. 可以推得||||a ba b ==为必要不充分条件；C. 为充分不必要条件；D 同B.4. 【高考真题辽宁理3】已知两个非零向量a ，b 满足|a +b |=|a -b |，则下面结论正确的是(A) a ∥b (B) a ⊥b (C){0,1,3} (D)a +b =a -b 【答案】B【解析】一、由|a +b |=|a -b |，平方可得a ⋅b =0,所以a ⊥b ，故选B二、根据向量加法、减法的几何意义可知|a +b |与|a -b |分别为以向量a ，b 为邻边的平行四边形的两条对角线的长，因为|a +b |=|a -b |，所以该平行四边形为矩形，所以a ⊥b ，故选B 【点评】本题主要考查平面向量的运算、几何意义以及向量的位置关系，属于容易题。

《2018年高考数学分类汇编》第五篇：平面向量一、选择题1．【2018全国一卷6】在ABC △中，AD 为BC 边上的中线，E 为AD 的中点，则EB =uu rA ．3144AB AC -uu u r uuu r B ．1344AB AC -uu u r uuu r C ．3144AB AC +uu u r uuu r D ．1344AB AC +uu u r uuu r 2．【2018全国二卷4】已知向量，满足，，则 A ．4 B ．3 C ．2 D ．03.【2018北京卷6】设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 A 充分而不必要条件B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件4.【2018天津卷8】如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==. 若点E 为边CD 上的动点，则⋅的最小值为 A. 2116 B. 32 C. 2516D. 3 5.【2018浙江卷9】已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为π 3，向量b 满足b 2−4e ·b +3=0，则|a −b |的最小值是 A1BC ．2D ．2二、填空题 1．【2018全国三卷13】已知向量，，．若，则________．2．【2018江苏卷12】在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，(5,0)B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=uu u r uu u r ，则点A 的横坐标为 ．3.【2018上海卷8】在平面直角坐标系中，已知点A （-1，0），B （2，0），E ，F 是y 轴上a b ||1=a 1⋅=-a b (2)⋅-=a a b ()=1,2a ()=2,2-b ()=1,λc ()2∥c a +b λ=的两个动点，且|EF uu v |=2，则AE uu u v ·BF uu v 的最小值为______[参考答案一、选择题1.A2.B3.C4.A5.A二、填空题 1.212.33.3。

第五章 平面向量考点1 平面向量的概念及坐标运算1.(2015·新课标全国Ⅰ，7)设D 为△ABC 所在平面内一点，BC →＝3CD →，则( ) A.AD →＝－13AB →＋43AC → B.AD →＝13AB →－43AC → C.AD →＝43AB →＋13AC → D.AD →＝43AB →－13AC →1.A [∵BC →＝3CD →，∴AC →－AB →＝3(AD →－AC →)，即4AC →－AB →＝3AD →， ∴AD →＝－13AB →＋43AC →.]2.(2015·湖南，8)已知点A ，B ，C 在圆x 2＋y 2＝1上运动，且AB ⊥BC .若点P 的坐标为(2,0)，则|PA →＋PB →＋PC →|的最大值为( ) A.6 B.7 C.8 D.92.B [由A ,B ,C 在圆x 2＋y 2＝1上,且AB ⊥BC ,∴AC 为圆直径,故PA →＋PC →＝2PO →＝(－4，0),设B (x ，y )，则x 2＋y 2＝1且x ∈[-1,1]，PB →＝(x －2，y )，所以PA →＋PB →＋PC →＝(x -6，y ).故|PA →＋PB →＋PC →|＝－12x ＋37，∴x ＝－1时有最大值49＝7，故选B.]3.(2014·福建，8)在下列向量组中，可以把向量a ＝(3,2)表示出来的是( ) A.e 1＝(0,0)，e 2＝(1,2) B.e 1＝(－1,2)，e 2＝(5，－2) C.e 1＝(3,5)，e 2＝(6,10) D.e 1＝(2，－3)，e 2＝(－2,3)3.B [法一 若e 1＝(0，0)，e 2＝(1，2)，则e 1∥e 2，而a 不能由e 1，e 2表示，排除A ；若e 1＝(－1，2)，e 2＝(5，－2)，因为－15≠2－2，所以e 1，e 2不共线，根据共面向量的基本定理，可以把向量a ＝(3，2)表示出来，故选B.法二 因为a ＝(3，2)，若e 1＝(0，0)，e 2＝(1，2)，不存在实数λ，μ，使得a ＝λe 1＋μe 2，排除A ；若e 1＝(－1，2)，e 2＝(5，－2)，设存在实数λ，μ，使得a ＝λe 1＋μe 2，则(3，2)＝(－λ＋5μ，2λ－2μ)，所以⎩⎪⎨⎪⎧3＝－λ＋5μ，2＝2λ－2μ，解得⎩⎪⎨⎪⎧λ＝2，μ＝1.所以a ＝2e 1＋e 2，故选B.]4.(2014·安徽，10)在平面直角坐标系xOy 中，已知向量a ，b ，|a |＝|b |＝1，a ·b ＝0，点Q 满足OQ →＝2(a ＋b ).曲线C ＝{P |OP →＝a cos θ＋b cos θ，0≤θ<2π}，区域Ω＝{P |0<r ≤|PQ →|≤R ，r <R }.若C ∩Ω为两段分离的曲线，则( )A.1<r <R <3B.1<r <3≤RC.r ≤1<R <3D.1<r <3<R4.A [由已知可设OA →＝a ＝(1，0)，OB →＝b ＝(0，1)，P (x ，y )，则OQ →＝(2，2)，曲线C ＝{P |OP →＝(cos θ，sin θ)，0≤θ<2π}，即C ：x 2＋y 2＝1，区域Ω＝{P |0<r ≤|PQ →|≤R ，r <R }表示圆P 1：(x －2)2＋(y －2)2＝r 2与圆P 2：(x －2)2＋(y －2)2＝R 2所形成的圆环，如图所示，要使C ∩Ω为两段分离的曲线，只有1<r <R <3.]5.（2017•浙江,15）已知向量 、 满足| |=1，| |=2，则| + |+| ﹣ |的最小值是________，最大值是________． 5. 4；记∠AOB=α，则0≤α≤π，如图，由余弦定理可得：| + |=，| ﹣ |=，则x 2+y 2=10（x 、y≥1），其图象为一段圆弧MN ，如图，令z=x+y ，则y=﹣x+z ，则直线y=﹣x+z 过M 、N 时z 最小为z min =1+3=3+1=4，当直线y=﹣x+z 与圆弧MN 相切时z 最大，由平面几何知识易知z max 即为原点到切线的距离的倍，也就是圆弧MN 所在圆的半径的倍，所以z max =×=．综上所述，| + |+| ﹣ |的最小值是4，最大值是 ．故答案为：4、．6.（2017•江苏,12）如图，在同一个平面内，向量，，的模分别为1，1，， 与的夹角为α，且tanα=7，与的夹角为45°．若=m+n（m ，n ∈R ），则m+n=________．6. 3 如图所示，建立直角坐标系．A （1，0）．由与的夹角为α，且tanα=7．∴cosα= ，sinα= ．∴C ．cos （α+45°）=（cosα﹣sinα）= ．sin （α+45°）= （sinα+cosα）= ．∴B．∵ =m +n （m ，n ∈R ），∴=m ﹣n ，=0+n ，解得n=，m=．则m+n=3．故答案为：3．7.(2016·全国Ⅰ，13)设向量a ＝(m ，1)，b ＝(1，2)，且|a ＋b |2＝|a |2＋|b |2，则m ＝________. 7.－2[由|a ＋b |2＝|a |2＋|b |2，得a ⊥b ，所以m ×1＋1×2＝0，得m ＝－2.]8.(2015·新课标全国Ⅱ，13)设向量a ，b 不平行，向量λa ＋b 与a ＋2b 平行，则实数λ＝____________.8.12[∵向量a ，b 不平行，∴a ＋2b ≠0，又向量λa ＋b 与a ＋2b 平行，则存在唯一的实数μ，使λa ＋b ＝μ(a ＋2b )成立，即λa ＋b ＝μa ＋2μb ，则得⎩⎪⎨⎪⎧λ＝μ，1＝2μ，解得λ＝μ＝12.]9.(2015·北京，13)在△ABC 中，点M ，N 满足AM →＝2MC →，BN →＝NC →.若MN →＝xAB →＋yAC →，则x ＝________；y ＝________.9.12 －16 [MN →＝MC →＋CN →＝13AC →＋12CB →＝13AC →＋12(AB →－AC →)＝12AB →－16AC →，∴x ＝12，y ＝－16.]10.(2015·江苏，6)已知向量a ＝(2,1)，b ＝(1，－2)，若m a ＋n b ＝(9，－8)(m ，n ∈R )，则m －n 的值为________.10.－3 [∵a ＝(2,1),b ＝(1,-2),∴m a ＋n b ＝(2m ＋n ,m －2n )＝(9,-8)，即⎩⎪⎨⎪⎧2m ＋n ＝9，m －2n ＝－8，解得⎩⎪⎨⎪⎧m ＝2，n ＝5，故m －n ＝2－5＝－3.]11.(2014·新课标全国Ⅰ，15)已知A ，B ，C 为圆O 上的三点，若AO →＝12(AB →＋AC →)，则AB →与AC→的夹角为________.11.90°[由AO →＝12(AB →＋AC →)可知O 为BC 的中点，即BC 为圆O 的直径，又因为直径所对的圆周角为直角，所以∠BAC ＝90°，所以AB →与AC →的夹角为90.]12.(2014·湖南，16)在平面直角坐标系中，O 为原点，A (－1，0)，B (0，3)，C (3,0)，动点D 满足|CD →|＝1，则|OA →＋OB →＋OD →|的最大值是________.12.1＋7 [设D (x ，y )，由|CD →|＝1，得(x －3)2＋y 2＝1，向量OA →＋OB →＋OD →＝(x －1，y ＋3)，故|OA →＋OB →＋OD →|＝（x －1）2＋（y ＋3）2的最大值为圆(x －3)2＋y 2＝1上的动点到点(1，－3)距离的最大值，其最大值为圆(x －3)2＋y 2＝1的圆心(3，0)到点(1，－3)的距离加上圆的半径，即（3－1）2＋（0＋3）2＋1＝1＋7.]考点2 平面向量的数量积及其应用1.（2017•北京,6）设 ， 为非零向量，则“存在负数λ，使得 =λ ”是 • ＜0”的（ ）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件1. A ， 为非零向量，存在负数λ，使得 =λ ，则向量 ， 共线且方向相反，可得 • ＜0．反之不成立，非零向量 ， 的夹角为钝角，满足 • ＜0，而 =λ 不成立．∴ ， 为非零向量，则“存在负数λ，使得 =λ ”是 • ＜0”的充分不必要条件．故选A ．2.（2017•新课标Ⅲ,12）在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若=λ+μ，则λ+μ的最大值为（ ）A.3B.2C.D.22. A 如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，则A（0，0），B（1，0），D（0，2），C（1，2），∵动点P在以点C为圆心且与BD相切的圆上，设圆的半径为r，∵BC=2，CD=1，∴BD= = ,∴BC•CD= BD•r，∴r= ，∴圆的方程为（x﹣1）2+（y﹣2）2= ，设点P的坐标为（cosθ+1，sinθ+2），∵=λ +μ ，∴（cosθ+1，sinθ﹣2）=λ（1，0）+μ（0，2）=（λ，2μ），∴cosθ+1=λ，sinθ+2=2μ，∴λ+μ= cosθ+sinθ+2=sin（θ+φ）+2，其中tanφ=2，∵﹣1≤sin（θ+φ）≤1，∴1≤λ+μ≤3，故λ+μ的最大值为3，故选A.3.（2017•浙江,10）如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD 交于点O，记I1= •，I2= •，I3= •，则（）A.I1＜I2＜I3B.I1＜I3＜I2C.I3＜I1＜I2D.I2＜I1＜I33. C ∵AB⊥BC，AB=BC=AD=2，CD=3，∴AC=2 ，∴∠AOB=∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0＞•＞•，•＞0，即I3＜I1＜I2，故选C．4.（2017•新课标Ⅱ,12）已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则•（+ ）的最小值是（）A.﹣2B.﹣C.﹣D.﹣14. B 建立如图所示的坐标系，以BC 中点为坐标原点，则A （0， ），B （﹣1，0），C（1，0），设P （x ，y ），则=（﹣x ，﹣y ），=（﹣1﹣x ，﹣y ），=（1﹣x ，﹣y ），则 •（ + ）=2x 2﹣2y+2y 2=2[x 2+（y ﹣）2﹣]∴当x=0，y=时，取得最小值2×（﹣ ）=﹣ ，故选B.5.(2016·四川，10)在平面内，定点A ，B ，C ，D 满足|DA →|＝|DB →|＝|DC →|，DA →·DB →＝DB →·DC →＝DC →·DA →＝－2，动点P ，M 满足|AP →|＝1，PM →＝MC →，则|BM →|2的最大值是( ) A.434 B.494 C.37＋634 D.37＋23345.B[由题意,|DA →|＝|DB →|＝|DC →|,所以D 到A ,B ,C 三点的距离相等,D 是△ABC 的外心； DA →·DB →＝DB →·DC →＝DC →·DA →＝-2⇒DA →·DB →－DB →·DC →＝DB →·(DA →－DC →)＝DB →·CA →＝0,所以DB ⊥AC ， 同理可得，DA ⊥BC ，DC ⊥AB ，从而D 是△ABC 的垂心，∴△ABC 的外心与垂心重合，因此△ABC 是正三角形，且D 是△ABC 的中心. DA →·DB →＝|DA →||DB →|cos ∠ADB ＝|DA →||DB →|×⎝ ⎛⎭⎪⎫－12＝－2⇒|DA →|＝2，所以正三角形ABC 的边长为23；我们以A 为原点建立直角坐标系,B ,C ,D 三点坐标分别为B (3,－3)，C (3,3)，D (2,0)，由|AP →|＝1,设P 点的坐标为(cos θ，sin θ)，其中θ∈[0，2π)，而PM →＝MC →，即M 是PC 的中点，可以写出M 的坐标为M ⎝⎛⎭⎪⎫3＋cos θ2，3＋sin θ2 则|BM →|2＝⎝ ⎛⎭⎪⎫cos θ－322＋⎝ ⎛⎭⎪⎫33＋sin θ22＝37＋12sin ⎝ ⎛⎭⎪⎫θ－π64≤37＋124＝494，当θ＝23π时，||2取得最大值494.故选B.6.(2016·山东，8)已知非零向量m ，n 满足4|m |＝3|n |，cos 〈m ，n 〉＝13.若n ⊥(t m ＋n )，则实数t 的值为( )A.4B.－4C.94D.－946.B[∵n ⊥(t m ＋n )，∴n ·(t m ＋n )＝0，即t ·m ·n ＋n 2＝0，∴t |m ||n |cos 〈m ，n 〉＋|n |2＝0，由已知得t ×34|n |2×13＋|n |2＝0，解得t ＝－4，故选B.]7.(2016·全国Ⅲ，3)已知向量BA →＝⎝ ⎛⎭⎪⎫12，32，BC →＝⎝ ⎛⎭⎪⎫32，12，则∠ABC ＝( )A.30°B.45°C.60°D.120°7.A [|BA →|＝1，|BC →|＝1，cos ∠ABC ＝BA →·BC →|BA →|·|BC →|＝32.]8.(2016·全国Ⅱ，3)已知向量a ＝(1，m )，b ＝(3，－2)，且(a ＋b )⊥b ，则m ＝( ) A.－8 B.－6 C.6 D.88.D[由题知a ＋b ＝(4，m －2)，因为(a ＋b )⊥b ，所以(a ＋b )·b ＝0， 即4×3＋(－2)×(m －2)＝0，解之得m ＝8，故选D.]9.(2015·山东，4)已知菱形ABCD 的边长为a ，∠ABC ＝60° ，则BD →·CD →＝( ) A.－32a 2B.－34a 2C.34a 2D.32a29.D [如图所示，由题意，得BC ＝a ，CD ＝a ，∠BCD ＝120°.BD 2＝BC 2＋CD 2－2BC ·CD ·cos 120°＝a 2＋a 2－2a ·a ×⎝ ⎛⎭⎪⎫－12＝3a 2，∴BD ＝3a .∴BD →·CD →＝|BD →|·|CD →|cos 30°＝3a 2×32＝32a 2.]10.(2015·安徽，8)△ABC 是边长为2的等边三角形，已知向量a ，b 满足AB →＝2a ，AC →＝2a ＋b ，则下列结论正确的是( )A.|b |＝1B.a ⊥bC.a ·b ＝1D.(4a ＋b )⊥BC →10.D [由于△ABC 是边长为2的等边三角形；∴(AB →＋AC →)·(AB →－AC →)＝0，即(AB →＋AC →)·CB →＝0，∴(4a ＋b )⊥CB →，即(4a ＋b )⊥BC →，故选D.]11.(2015·四川，7)设四边形ABCD 为平行四边形，|AB →|＝6，|AD →|＝4，若点M ，N 满足BM →＝3MC →，DN →＝2NC →，则AM →·NM →＝( ) A.20 B. 15 C.9 D.611.C[AM →＝AB →＋34AD →，NM →＝CM →－CN →＝－14AD →＋13AB →∴AM →·NM →＝14(4AB →＋3AD →)·112(4AB →－3AD →)＝148(16AB →2－9AD →2)＝148(16×62－9×42)＝9，选C.]12.(2015·福建，9)已知AB →⊥AC →，|AB →|＝1t，|AC →|＝t ，若点P 是△ABC 所在平面内的一点，且AP →＝AB →|AB →|＋4AC →|AC →|，则PB →·PC →的最大值等于( )A.13B.15C.19D.2112.A [建立如图所示坐标系，则B⎝ ⎛⎭⎪⎫1t ，0，C (0，t )，AB →＝⎝ ⎛⎭⎪⎫1t ，0，AC →＝(0，t )，AP →＝AB →|AB →|＋4AC →|AC →|＝t ⎝ ⎛⎭⎪⎫1t ，0＋4t (0，t )＝(1，4)，∴P (1，4)，PB →·PC→＝⎝ ⎛⎭⎪⎫1t－1，－4·(－1，t －4)＝17－⎝ ⎛⎭⎪⎫1t＋4t ≤17－21t·4t ＝13，故选A.]13.(2015·重庆，6)若非零向量a ，b 满足|a |＝223|b |，且(a －b )⊥(3a ＋2b )，则a 与b的夹角为( )A.π4B.π2C.3π4D.π 13.A [由题意(a －b )·(3a ＋2b )＝3a 2－a·b －2b 2＝0，即3|a |2－|a |·|b |cos θ－2|b |2＝0，所以3×⎝ ⎛⎭⎪⎫2232－223cos θ－2＝0，cos θ＝22，θ＝π4，选A.]14.(2015·陕西，7)对任意向量a ，b ，下列关系式中不恒成立的是( )A.|a ·b |≤|a ||b |B.|a －b |≤||a |－|b ||C.(a ＋b )2＝|a ＋b |2D.(a ＋b )(a －b )＝a 2－b214.B [对于A ，由|a ·b |＝||a ||b |cos<a ,b >|≤|a ||b |恒成立；对于B ，当a ，b 均为非零向量且方向相反时不成立；对于C 、D 容易判断恒成立.故选B.]15.(2014·新课标全国Ⅱ，3)设向量a ，b 满足|a ＋b |＝10，|a －b |＝6，则a ·b ＝( ) A.1 B.2 C.3 D.515.A [由向量的数量积运算可知,∵|a ＋b |＝10,∴(a ＋b )2＝10,∴a 2+b 2+2a ·b ＝10,① 同理a 2＋b 2－2a ·b ＝6，② ① －②得4a ·b ＝4，∴a ·b ＝1.]16.(2014·大纲全国，4)若向量a 、b 满足：|a |＝1，(a ＋b )⊥a ，(2a ＋b )⊥b ，则|b |＝( ) A.2 B. 2 C.1 D.2216.B [由题意得⎩⎪⎨⎪⎧（a ＋b ）·a ＝a 2＋a ·b ＝0，（2a ＋b ）·b ＝2a ·b ＋b 2＝0⇒-2a 2+b 2＝0,即－2|a |2＋|b |2＝0,又|a |＝1，∴|b |＝ 2.故选B.]17.(2014·天津，8)已知菱形ABCD 的边长为2，∠BAD ＝120°，点E ，F 分别在边BC ，DC 上，BE ＝λBC ，DF ＝μDC .若AE →·AF →＝1，CE →·CF →＝－23，则λ＋μ＝( )A.12B.23C.56D.71217.C [如图所示,以菱形ABCD 的两条对角线所在直线为坐标轴,建立平面直角坐标系xOy ,不妨设A (0，－1),B (－3，0),C (0，1),D (3，0),由题意得CE →＝(1－λ)·CB →＝(3λ－3，λ－1)，CF →＝(1－μ)CD →＝(3－3μ，μ－1).因为CE →·CF →＝-23，所以3(λ-1)·(1-μ)＋(λ-1)(μ-1)＝－23，即(λ-1)(μ-1)＝13.因为AE →＝AC →＋CE →＝(3λ－3，λ＋1).AF →＝AC →＋CF →＝(3－3μ，μ＋1)，又AE →·AF →＝1，所以(λ＋1)(μ＋1)＝2.由⎩⎪⎨⎪⎧（λ－1）（μ－1）＝13.（λ＋1）（μ＋1）＝2，整理得λ＋μ＝56.选C.]18.（2017•新课标Ⅰ,13）已知向量 ， 的夹角为60°，| |=2，| |=1，则| +2 |=________． 18. ∵向量 ， 的夹角为60°，且| |=2，| |=1，∴=+4 • +4=22+4×2×1×cos60°+4×12=12，∴| +2 |=2 ．故答案为：2．19.（2017•山东,12）已知 ，是互相垂直的单位向量，若﹣与 +λ的夹角为60°，则实数λ的值是________．19. ， 是互相垂直的单位向量，∴| |=||=1，且 • =0； 又 ﹣ 与 +λ 的夹角为60°，∴（﹣）•（ +λ）=| ﹣|×|+λ|×cos60°，即 +（ ﹣1） •﹣λ= ××，化简得﹣λ=×× ，即 ﹣λ= ，解得λ= ．故答案为：． 20.（2017·天津,13）在△ABC 中，∠A=60°，AB=3，AC=2．若 =2，=λ﹣ （λ∈R ），且 =﹣4，则λ的值为________．20.如图所示，△ABC 中，∠A=60°，AB=3，AC=2，=2 ， ∴ = += += + （ ﹣ ）= + ， 又 =λ﹣ （λ∈R ）， ∴ =（ + ）•（λ ﹣ ） =（ λ﹣ ）•﹣+λ=（ λ﹣ ）×3×2×cos60°﹣ ×32+ λ×22=﹣4，∴λ=1，解得λ= ．故答案为：．21.(2016·浙江，15)已知向量a ，b ，|a |＝1，|b |＝2.若对任意单位向量e ，均有|a ·e |＋|b ·e |≤6，则a ·b 的最大值是________.21.12 [由已知可得：6≥|a ·e |＋|b ·e |≥|a ·e ＋b ·e |＝|(a ＋b )·e | 由于上式对任意单位向量e 都成立.∴6≥|a ＋b |成立.∴6≥(a ＋b )2＝a 2＋b 2＋2a ·b ＝12＋22＋2a ·b .即6≥5＋2a ·b ，∴a ·b ≤12.]22.(2015·天津，14)在等腰梯形ABCD 中，已知AB ∥DC ，AB ＝2，BC ＝1，∠ABC ＝60°，动点E 和F 分别在线段BC 和DC 上，且BE →＝λBC →，DF →＝19λDC →，则|AE →|·|AF →|的最小值为________.22.2918 [在梯形ABCD 中，AB ＝2，BC ＝1，∠ABC ＝60°，可得DC ＝1，AE →＝AB →＋λBC →，AF →＝AD →＋19λDC →，∴AE →·AF →＝(AB →＋λBC →)·(AD →＋19λDC →)＝AB →·AD →＋AB →·19λDC →＋λBC →·AD →＋λBC →·19λDC →＝2×1×cos 60°＋2×19λ＋λ×1×cos 60°＋λ19λ×cos 120°＝29λ＋λ2＋1718≥229λ·λ2＋1718＝2918，当且仅当29λ＝λ2，即λ＝23时，取得最小值为2918.]23.(2015·浙江，15)已知e 1,e 2是空间单位向量,e 1·e 2＝12，若空间向量b 满足b ·e 1＝2，b ·e 2＝52，且对于任意x ，y ∈R ，|b －(x e 1＋ye 2)|≥|b －(x 0e 1＋y 0e 2)|＝1(x 0，y 0∈R )，则x 0＝________，y 0＝________，|b |＝________.23.1 2 2 2 [∵e 1·e 2＝|e 1|·|e 2|cos 〈e 1，e 2〉＝12，∴〈e 1，e 2〉＝π3.不妨设e 1＝⎝ ⎛⎭⎪⎫12，32，0，e 2＝(1，0，0)，b ＝(m ，n ，t ). 由题意知⎩⎪⎨⎪⎧b ·e 1＝12m ＋32n ＝2，b ·e 2＝m ＝52，解得n ＝32，m ＝52，∴b ＝⎝ ⎛⎭⎪⎫52，32，t .∵b －(x e 1＋y e 2)＝⎝ ⎛⎭⎪⎫52－12x －y ，32－32x ，t ，∴|b －(x e 1＋y e 2)|2＝⎝ ⎛⎭⎪⎫52－x 2－y 2＋⎝ ⎛⎭⎪⎫32－32x 2＋t 2＝x 2＋xy ＋y 2－4x －5y ＋t 2＋7＝⎝ ⎛⎭⎪⎫x ＋y －422＋34(y －2)2＋t 2.由题意知，当x ＝x 0＝1，y ＝y 0＝2时，⎝⎛⎭⎪⎫x ＋y －422＋34(y －2)2＋t 2取到最小值.此时t 2＝1，故|b |＝⎝ ⎛⎭⎪⎫522＋⎝ ⎛⎭⎪⎫322＋t 2＝2 2.] 24.（2017•江苏,16）已知向量 =（cosx ，sinx ）， =（3，﹣ ），x ∈[0，π]．（Ⅰ）若 ∥ ，求x 的值； （Ⅱ）记f （x ）=，求f （x ）的最大值和最小值以及对应的x 的值．24.（Ⅰ）∵ =（cosx ，sinx ）， =（3，﹣）， ∥ ，∴﹣ cosx+3sinx=0， ∴tanx=，∵x ∈[0，π]， ∴x=，（Ⅱ）f （x ）= =3cosx ﹣ sinx=2 （ cosx ﹣ sinx ）=2 cos （x+ ），∵x ∈[0，π]，∴x+ ∈[ ， ]，∴﹣1≤cos（x+ ）≤ ，当x=0时，f （x ）有最大值，最大值3，当x= 时，f （x ）有最小值，最大值﹣225.(2015·广东，16)在平面直角坐标系xOy 中,已知向量m ＝⎝⎛⎭⎪⎫22，－22,n ＝(sin x ，cosx )，x ∈⎝⎛⎭⎪⎫0，π2.(1)若m ⊥n ，求tan x 的值. (2)若m 与n 的夹角为π3，求x 的值.25.解 (1)因为m ＝⎝ ⎛⎭⎪⎫22，－22，n ＝(sin x ，cos x )，m ⊥n .所以m ·n ＝0，即22sin x －22cos x ＝0，所以sin x ＝cos x ，所以tan x ＝1. (2)因为|m |＝|n |＝1,所以m ·n ＝cos π3＝12，即22sin x －22cos x ＝12，所以sin ⎝ ⎛⎭⎪⎫x －π4＝12， 因为0<x <π2，所以－π4<x －π4<π4，所以x －π4＝π6，即x ＝5π12.26.(2014·北京，10)已知向量a ，b 满足|a |＝1，b ＝(2,1)，且λa ＋b ＝0(λ∈R )，则|λ|＝________.26. 5 [∵|a |＝1，∴可令a ＝(cos θ，sin θ)，∵λa ＋b ＝0，∴⎩⎪⎨⎪⎧λcos θ＋2＝0，λsin θ＋1＝0，即⎩⎪⎨⎪⎧cos θ＝－2λ，sin θ＝－1λ，由sin 2θ＋cos 2θ＝1得λ2＝5，得|λ|＝5.]27.(2014·江西，14)已知单位向量e 1与e 2的夹角为α，且cos α＝13，向量a ＝3e 1－2e 2与b ＝3e 1－e 2的夹角为β，则cos β＝________. 27.223[因为a 2＝(3e 1-2e 2)2＝9-2×3×2×cos α＋4＝9,所以|a |＝3,b 2＝(3e 1-e 2)2＝9-2×3×1×cos α＋1＝8，所以|b |＝22，a ·b ＝(3e 1－2e 2)·(3e 1－e 2)＝9e 21－9e 1·e 2＋2e 22＝9－9×1×1×13＋2＝8，所以cos β＝a ·b |a |·|b |＝83×22＝223.]28.(2014·湖北，11)设向量a ＝(3,3)，b ＝(1，－1).若(a ＋λb )⊥(a －λb )，则实数λ＝________.28.±3 [(a ＋λb )⊥(a －λb )⇒(a ＋λb )·(a －λb )＝a 2－λ2b 2＝0⇒18－2λ2＝0⇒λ＝±3.]29.(2014·江苏，12)如图，在平行四边形ABCD 中，已知AB ＝8，AD ＝5，CP →＝3PD →，AP →·BP →＝2，则AB →·AD →的值是________.29.22 [因为AP →＝AD →＋DP →＝AD →＋14AB →，BP →＝BC →＋CP →＝AD →－34AB →，所以AP →·BP →＝(AD →＋14AB →)·(AD→－34AB →)＝|AD →|2－316|AB →|2－12AD →·AB →＝2，将AB ＝8，AD ＝5代入解得AB →·AD →＝22.]。

2018年高考数学 平面向量基本定理及坐标表示 高考复习题一、选择题：1.已知点A(0,1),B(3,2),向量AB =(-4,-3),则向量BC =( ) A.(-7,-4) B.(7,4) C.(-1,4)D.(1,4)2.设向量a=(2,4)与向量b=(x,6)共线,则实数x=( ) A.2 B.3 C.4 D.63.已知向量a=(5,2),b=(-4,-3),c=(x,y),若3a-2b+c=0,则c=( ) A.(-23,-12) B.(23,12) C.(7,0)D.(-7,0)4.已知在▱ABCD 中,AD =(2,8),AB =(-3,4),对角线AC 与BD 相交于点M,则AM =( ) A.(-21,-6) B.(-21,6) C.(21,-6) D.(21,6) 5.在平面直角坐标系xOy 中,已知A(1,0),B(0,1),C 为坐标平面内第一象限内一点且∠AOC=4,|OC |=2,若OC =λOA +μOB ,则λ+μ=( ) A.22B.2C.2D.426.若α,β是一组基底,向量γ=x α+y β(x,y ∈R),则称(x,y)为向量γ在基底α、β下的坐标.现已知向量a 在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a 在基底m=(-1,1),n=(1,2)下的坐标为( ) A.(2,0) B.(0,-2) C.(-2,0) D.(0,2)7.在△ABC 中,点D 在线段BC 的延长线上,且BC =3CD ,点O 在线段CD 上(与点C 、D 不重合),若=x AB +(1-x)·AC ,则x 的取值范围是( )A.(0,21) B.(0,31) C.(-21,0) D.(-31,0) 二、填空题：8.已知平面向量a=(2,-1),b=(1,1),c=(-5,1).若(a+kb)∥c,则实数k 的值为 . 9.在梯形ABCD 中,已知AB ∥CD,AB=2CD,M,N 分别为CD,BC 的中点.若AB =λAM +μAN ,则λ+μ= .10.向量a,b,c 在正方形网格中的位置如图所示.若c=λa+μb(λ,μ∈R),则μλ= .11.已知向量AC ,AD 和AB 在正方形网格中的位置如图所示,若AC =λAB +μAD ,则λμ= .12.P={a|a=(-1,1)+m(1,2),m ∈R},Q={b|b=(1,-2)+n(2,3),n ∈R}是两个向量集合,则P ∩Q 等于 . 三、解答题：13.已知a=(1,0),b=(2,1).(1)当k 为何值时,ka-b 与a+2b 共线?(2)若AB =2a+3b,BC =a+mb 且A,B,C 三点共线,求m 的值.14.如图,已知点A(1,0),B(0,2),C(-1,-2),求以A,B,C 为顶点的平行四边形的第四个顶点D 的坐标.15.给定两个长度为1的平面向量OA 和OB ,它们的夹角为32,如图所示.点C 在以O 为圆心的圆弧BA 上运动.若OC =x OA +y OB ,其中x,y ∈R,求x+y 的最大值.参考答案1.答案为：A ；解析：根据题意得AB =(3,1),∴BC =AC -AB =(-4,-3)-(3,1)=(-7,-4).故选A.2.答案为：B ；解析：∵a 与b 共线,∴2×6=4x,∴x=3,故选B.3.答案为：A ；解析：由题意可得3a-2b+c=(23+x,12+y)=(0,0),所以23+x=0,12+y=0解得x=-23,y=-12.所以c=(-23,-12).4.答案为：B ；解析：因为在▱ABCD +AD ,AM =所以AM =21(-1,12)=(-2,6).故选B.5.答案为：A ；解析：因为C 为第一象限内一点且|OC |=2,∠AOC=4π,所以C(2,2),又OC =λOA +μOB , 所以(2,2)=λ(1,0)+μ(0,1)=(λ,μ),所以λ=μ=2,λ+μ=22.6.答案为：D ；解析：由已知可得a=-2p+2q=(-2,2)+(4,2)=(2,4).设a=xm+yn,则(2,4)=x(-1,1)+y(1,2)=(-x+y,x+2y),∴-x+y=2,x+2y=4,解得x=0,y=2.故选D. 7.答案为：D ；解析：解法一:依题意,设BO =λBC ,其中1<λ<34,=AB +BO =AB +λBC =AB +λ(AC -AB )=(1-λ)AB +λAC .=x AB +(1-x)·AC ,且AB 、AC 不共线, 于是有x=1-λ∈(-31,0),即x 的取值范围是(-31,0),选D. 解法二:=x AB +AC -x AC ,-AC =x(AB -AC ),即CO =x CB =-3x CD , ∵O 在线段CD(不含C 、D 两点)上,∴0<-3x<1,∴-31<x<0. 8.答案为：21; 解析:由题意知,a+kb=(2,-1)+k(1,1)=(k+2,k-1),由(a+kb)∥c,得-5(k-1)=k+2,解得k=21. 9.答案为:54；解析：解法一:连接AC.由AB =λAM +μAN ,得AB =λ+AB ),则(12-μ)AB +2λ+2μ)AC =0,得(12-μ)AB +得(4341-+μλ2μλ+)AD =0.又因为AB ,AD 不共线,所以由平面向量基本定理得14341-+μλ=0,2μλ+=0， 解得λ=-0.8,μ=1.6所以λ+μ=0.8.解法二:(回路法)连接MN 并延长交AB 的延长线于T,由已知易得AB=0.8AT,∴0.8=AB =λAM +μAN ,即=45λAM +45μAN , ∵T,M,N 三点共线,∴45λ+45μ=1,∴λ+μ=54. 10.答案为：4；解析：以向量a 和b 的交点为坐标原点建立如图所示的坐标系,令每个小正方形的边长为1个单位,则A(1,-1),B(6,2),C(5,-1),所以=(-1,1),b=OB =(6,2),c=BC =(-1,-3).由c=λa+μb 可得-1=-λ+6μ,-3=λ+2μ,解得λ=-2,μ=-0.5所以μλ=4.11.答案为：-3；解析：建立如图所示的平面直角坐标系xAy,则AC =(2,-2),AB =(1,2),AD =(1,0), 由题意可知(2,-2)=λ(1,2)+μ(1,0),即2=λ+μ,-2=2λ,解得λ=-1,μ=3,所以λμ=-3.12.答案为：{(-13,-23)}；解析:P 中,a=(-1+m,1+2m),Q 中,b=(1+2n,-2+3n).令-1+m=1+2n,1+2m=-2+3n,得m=-12,n=-7.此时a=b=(-13,-23),故P ∩Q={(-13,-23)}. 13.解:(1)ka-b=k(1,0)-(2,1)=(k-2,-1).a+2b=(1,0)+2(2,1)=(5,2).∵ka-b 与a+2b 共线,∴2(k-2)-(-1)×5=0,即2k-4+5=0,得k=-21. (2)∵A,B,C 三点共线,∴AB =λBC (λ∈R).即2a+3b=λ(a+mb),∴λ=2,m λ=3,∴m=23.14.解:以A,B,C 为顶点的平行四边形可以有三种情况:▱ABCD;▱ADBC;▱ABDC.设D 的坐标为(x,y). ①若是▱ABCD,则由AB =DC ,得(0,2)-(1,0)=(-1,-2)-(x,y),即(-1,2)=(-1-x,-2-y), ∴-1-x=-1,-2-y=2.∴x=0,y=-4.∴D 点的坐标为(0,-4)(如图中所示的D 1).②若是▱ADBC,则由CB =AD ,得(0,2)-(-1,-2)=(x,y)-(1,0),即(1,4)=(x-1,y),解得x=2,y=4. ∴D 点的坐标为(2,4)(如图中所示的D 2).③若是▱ABDC,则由AB =CD ,得(0,2)-(1,0)=(x,y)-(-1,-2),即(-1,2)=(x+1,y+2),解得x=-2,y=0. ∴D 点的坐标为(-2,0)(如图中所示的D 3).∴以A,B,C 为顶点的平行四边形的第四个顶点D 的坐标为(0,-4)或(2,4)或(-2,0).15.解:解法一:如图,以O 为坐标原点,OA 所在的直线为x 轴,OA 的方向为x 轴的正方向建立平面直角坐标系,则可知A(1,0),B(-21,23),设C(cos α,sin α)(α∈[0,32π]),则有x=cos α+33sin α,y=332sin α,所以x+y=cos α+3sin α=2sin(α+6π),所以当α=3π时,x+y 取得最大值2.解法二:如图,连接AB,记OC 交AB 于D 点.则OC=OD =x OA +y OB ,∵D,A,B 三点共线,∴∴(x+y)max=2.。

2018年全国各地高考数学模拟试题《平面向量》解答题试题汇编（含答案解析）1．（2018•兰州模拟）已知向量，，函数．（1）求f（x）的最小正周期；（2）当时，f（x）的最小值为5，求m的值．2．（2018•海拉尔区校级二模）已知向量（x∈R），设函数f（x）=﹣1．（1）求函数f（x）的单调增区间；（2）已知△ABC的三个内角分别为A，B，C，若∠A为锐角且f（A）=2，B=，边AB=3，求边BC．3．（2018•新疆一模）已知向量=（1，sinx），=（sinx，﹣1），=（1，cosx），x∈（0，π）．（Ⅰ）若（+）∥，求x；（Ⅱ）在△ABC中，角A、B、C的对边分别为a、b、c，且B为（Ⅰ）中的x，2sin2B+2sin2C﹣2sin2A=sinBsinC，求sin（C﹣）的值．4．（2018•咸阳模拟）已知向量=（cosx，﹣1），=（sinx，﹣），函数．（1）求函数f（x）的最小正周期及单调递增区间；（2）在△ABC中，三内角A，B，C的对边分别为a，b，c，已知函数∴的图象经过点，b、a、c成等差数列，且•=9，求a的值．5．（2018•江苏一模）已知向量，．（1）若角α的终边过点（3，4），求•的值；（2）若∥，求锐角α的大小．6．（2018•南京一模）在△ABC中，角A，B，C的对边分别为a，b，c 已知c=．（1）若C=2B，求cosB的值；（2）若=，求cos（B）的值．7．（2018•市中区校级二模）已知函数，其中，，x∈R．（1）求函数y=f（x）的周期和单调递增区间；（2）在△ABC中，角A，B，C所对的边分别为a，b，c，f（A）=2，，且sinB=2sinC，求△ABC的面积．8．（2018•黑龙江模拟）已知向量=（sin，1），=（cos，），f（x）=•．（I）求f（x）的最大值，并求此时x的值；（Ⅱ）在△ABC中，内角A，B，C的对边分别是a，b，c，满足f（B）=，a=2，c=3，求sinA的值．9．（2018•瓦房店市一模）在平面直角坐标系xOy中，已知向量，，．（1）若，求tanx的值；（2）若与的夹角为，求x的值．10．（2018•河南一模）在△ABC中，角A，B，C所对边分别是a，b，c，满足4acosB ﹣bcosC=ccosB．（1）求cosB的值；（2）若，，求a和c的值．11．（2018•玉溪模拟）已知向量=（sinx，cosx），=（cosx，cosx），=（2，1）．（1）若，求的值；（2）若角，求函数f（x）=的值域．12．（2018•黄浦区一模）如图，已知点A是单位圆上一点，且位于第一象限，以x轴的正半轴为始边，OA为终边的角设为α，将OA绕坐标原点逆时针旋转至OB．（1）用α表示A，B两点的坐标；（2）M为x轴上异于O的点，若MA⊥MB，求点M横坐标的取值范围．13．（2018•浙江三模）已知向量=（cosx，sinx），=（﹣，），x∈[0，π]．（Ⅰ）若，求x的值；（Ⅱ）记f（x）=，求f（x）的最大值和最小值以及对应的x的值．14．（2018•雅安模拟）已知函数（x∈R）．（1）求函数f（x）的最小正周期及单调递增区间；（2）在△ABC中，三内角A，B，C的对边分别为a，b，c，已知，若b+c=2a，且，求a的值．15．（2018•盐城三模）在△ABC中，角A，B，C的对边分别为a，b，c，AD为边BC上的中线．（1）若a=4，b=2，AD=1，求边c的长；（2）若，求角B的大小．16．（2018•历城区校级一模）已知曲线C的方程为ax2+ay2﹣2a2x﹣4y=0（a≠0，a为常数）．（1）判断曲线C的形状；（2）设曲线C分别与x轴，y轴交于点A，B（A，B不同于原点O），试判断△AOB的面积S是否为定值？并证明你的判断；（3）设直线l：y=﹣2x+4与曲线C交于不同的两点M，N，且•=﹣，求a 的值．17．（2017•榆林一模）如图，在△ABC中，已知点D，E分别在边AB，BC上，且AB=3AD，BC=2BE．（Ⅰ）用向量，表示．（Ⅱ）设AB=6，AC=4，A=60°，求线段DE的长．18．（2017•海南模拟）在△ABC中，角A，B，C的对边分别是a、b、c，已知，，且．（Ⅰ）求角A的大小；（Ⅱ）若b=3，△ABC的面积，求a的值．19．（2017•阜宁县校级模拟）已知向量=（cosα，﹣1），=（2，sinα），其中，且．（1）求cos2α的值；（2）若sin（α﹣β）=，且，求角β．20．（2017•山东模拟）已知f（x）=，其中．（I）求f（x）在区间[﹣π，π]上的单调递增区间；（Ⅱ）在△ABC中，角A、B、C所对的边分别为a、b、c，f（A）=﹣1，a=，且向量垂直，求边长b和c的值．21．（2017•五模拟）已知向量，函数．（Ⅰ）求函数f（x）的单调递增区间；（Ⅱ）在△ABC中，a，b，c分别为△ABC三个内角A，B，C的对边，若，a=2，求b+c的取值范围．22．（2017•泰州模拟）已知向量=（1，m），=（2，n）．（1）若m=3，n=﹣1，且⊥（+λ），求实数λ的值；（2）若|+|=5，求•的最大值．23．（2017•长春三模）已知点，Q（cosx，sinx），O为坐标原点，函数．（1）求函数f（x）的最小值及此时x的值；（2）若A为△ABC的内角，f（A）=4，BC=3，求△ABC的周长的最大值．24．（2017•江西模拟）已知点P（，﹣1），Q（sin2x，cos2x），O为坐标原点，函数f（x）=．（1）求函数f（x）的对称中心和单调增区间；（2）若A为△ABC的内角，a，b，c分别为角A，B，C的对边，f（A）=2，a=5，求△ABC周长的取值范围．25．（2017•江西模拟）在△ABC中，角A，B，C的对边分别为a，b，c，且（c ﹣2a）=c•（1）求B的大小；（2）已知f（x）=cosx（asinx﹣2cosx）+1，若对任意的x∈R，都有f（x）≤f（B），求函数f（x）的单调递减区间．26．（2017•保定一模）已知=（sinx，﹣cosx），=（cosx，﹣cosx），f（x）=2•．（1）求f（x）的解析式；（2）在△ABC中，a，b，c分别是内角A，B，C的对边，若f（A）=2，b=1，△ABC的面积为，求a的值．27．（2017•菏泽一模）已知向量=（sinx，mcosx），=（3，﹣1）．（1）若∥，且m=1，求2sin2x﹣3cos2x的值；（2）若函数f（x）=•的图象关于直线x=对称，求函数f（2x）在[，]上的值域．28．（2017•山东模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，已知•=，sinA=（1）求sinC的值；（2）设D为AC的中点，若BD的长为，求△ABC的面积．29．（2017•福建模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，且满足sin=，•=6．（1）求△ABC的面积；（2）若c+a=8，求b的值．30．（2017•吉州区校级一模）已知向量=（cosθ，sinθ），=（cosφ，sinφ）（1）若|θ﹣φ|=，求|﹣|的值；（2）若θ+φ=，记f（θ）=•﹣λ|+|，θ∈[0，]．当1≤λ≤2时，求f （θ）的最小值．31．（2017•六安模拟）已知=（3，﹣1），•=﹣5，=x+（1﹣x）．（Ⅰ）若⊥，求实数x的值；（Ⅱ）若||=，求||的最小值．32．（2017•苏州二模）已知向量．（1）当x=时，求的值；（2）若，且，求cos2x的值．33．（2017•张家界一模）在△ABC中，三个内角A，B，C所对的边分别为a，b，c，已知=（sinB﹣sinC，sinC﹣sinA），=（sinB+sinC，sinA），且⊥．（1）求角B的大小；（2）若△ABC的外接圆的半径为1，求△ABC的面积．34．（2017•南通模拟）在平面直角坐标系中，设向量=（cosA，sinA），=（cosB，﹣sinB），其中A，B为△ABC的两个内角．（1）若，求证：C为直角；（2）若，求证：B为锐角．35．（2017•湖北模拟）已知向量，，函数（1）求函数f（x）的最大值及最小正周期；（2）将函数y=f（x）的图象向左平移个单位，得到函数y=g（x）的图象，求g（x）在上的值域．36．（2017•南京三模）已知向量为实数．（1）若，求t的值；（2）若t=1，且，求的值．37．（2017•甘肃模拟）已知△ABC的面积为S，且•=S．（Ⅰ）求tan2B的值；（Ⅱ）若cosA=，且|﹣|=2，求BC边中线AD的长．38．（2017•潍坊三模）已知向量=（sinx，﹣1），=（cosx，），函数f（x）=（+）•．（1）求函数f（x）的单调递增区间；（2）将函数f（x）的图象向左平移个单位得到函数g（x）的图象，在△ABC中，角A，B，C所对边分别a，b，c，若a=3，g（）=，sinB=cosA，求b的值．39．（2017•全国二模）已知点P（，1），Q（cosx，sinx），O为坐标原点，函数f（x）=•．（Ⅰ）求函数f（x）的最小正周期；（Ⅱ）若A为△ABC的内角，f（A）=4，BC=3，△ABC的面积为，求△ABC 的周长．40．（2017•南京一模）如图，在平面直角坐标系xOy上，点A（1，0），点B在单位圆上，∠AOB=θ（0＜θ＜π）．（1）若点B（﹣，），求tan（θ+）的值；（2）若+=，=，求cos（﹣θ）．参考答案与试题解析1．【分析】（1）根据向量的数量积公式和两角和的正弦公式可化简可得f（x）=，再根据周期的定义即可求出，（2）根据正弦函数的性质即可求出m的值．【解答】（1）由题意知：f（x）=cos（2x，sin2x）•（，1）==，所以f（x）的最小正周期为T=π．（2）由（1）知：，当时，．所以当时，f（x）的最小值为．又∵f（x）的最小值为5，∴，即．【点评】本题考查了向量的数量积和三角函数的化简和性质，考查了运算能力，属于基础题．2．【分析】利用向量的数量积求出函数的解析式并化简三角函数式，利用三角函数的性质解得本题．【解答】解：由已知得到函数f（x）=﹣1=2cos2x+2sinxcosx﹣1=cos2x+sin2x=2cos（2x﹣）；所以（1）函数f（x）的单调增区间是（2x﹣）∈[2kπ﹣π，2kπ]，即x∈[kπ﹣，kπ+]，k∈Z；（2）已知△ABC的三个内角分别为A，B，C，f（A）=2，则2cos（2A﹣）=2，因为∠A为锐角，所以A=，又B=，边AB=3，所以由正弦定理得，即，解得BC=．【点评】本题考查了向量的数量积公式、三角函数式的化简以及三角函数性质和解三角形，属于中档题．3．【分析】（Ⅰ）由已知结合向量的坐标加法求得（+），再由（+）∥列式求x；（Ⅱ）由已知等式结合正弦定理及余弦定理求得cosA，进一步得到sinA，由sin （C﹣）=sin（）=sin（），展开两角差的正弦求解．【解答】解：（Ⅰ）∵=（1，sinx），=（sinx，﹣1），=（1，cosx），∴，∵（+）∥，∴（1+sinx）cosx=sinx﹣1，则sinxcosx=sinx﹣cosx﹣1，令sinx﹣cosx=t，得t=，∵x∈（0，π），∴，即．sinxcosx=，t∈（﹣1，]，则t2+2t﹣3=0，解得t=1．∴sinx﹣cosx=1，于是，sin（x﹣）=．可得x=；（Ⅱ）∵2sin2B+2sin2C﹣2sin2A=sinBsinC，∴2b2+2c2﹣2a2=bc，∴，即cosA=，得sinA=．又B=，∴sin（C﹣）=sin（）=sin（）=sin=．【点评】本题考查平面向量共线的坐标表示，考查三角形的解法，是中档题．4．【分析】（1）利用向量的数量积化简函数的解析式，利用函数的周期以及正弦函数的单调区间求解即可．（2）求出A，利用等差数列以及向量的数量积求出bc，通过三角形的面积以及余弦定理求解a即可．【解答】解：==，（1）最小正周期：由得：，所以f（x）的单调递增区间为：；（6分）（2）由可得：所以，又因为b，a，c成等差数列，所以2a=b+c，（8分）而，•=bccosA==9，∴bc=18，，∴．（12分）【点评】本题考查向量以及数列与三角函数相结合，考查数量积的求法，两角和与差的三角函数，三角形的解法，考查计算能力．5．【分析】（1）由三角函数的定义求出sinα、cosα，再根据平面向量数量积的定义计算•的值；（2）根据∥，列方程求出α的三角函数值以及锐角α的值．【解答】解：（1）角α的终边过点（3，4），∴r==5，∴sinα==，cosα==；∴•=sinα+sin（α+）=sinα+sinαcos+cosαsin=×+×+×=；（2）若∥，则，即，∴sin2α+sinαcosα=1，∴sinαcosα=1﹣sin2α=cos2α，对锐角α有cosα≠0，∴tanα=1，∴锐角．【点评】本题考查了三角函数求值与平面向量的数量积计算问题，是中档题．6．【分析】（1）由正弦定理，得sinC=sinB．又C=2B，即2sinBcosB=sinB．cosB=．（2）由=，可得cbcosA=bacosC，b2+c2﹣a2=b2+a2﹣c2，得a=c，求得从而cosB，sinB即可．【解答】解：（1）因为c=，则由正弦定理，得sinC=sinB．…（2分）又C=2B，所以sin2B=sinB，即2sinBcosB=sinB．…（4分）又B是△ABC的内角，所以sinB＞0，故cosB=．…（6分）（2）因为=，所以cbcosA=bacosC，则由余弦定理，得b2+c2﹣a2=b2+a2﹣c2，得a=c．…（10分）从而cosB==，…（12分）又0＜B＜π，所以sinB==．从而cos（B+）=cosBcos﹣sinBsin=．…（14分）【点评】本题主要考查了正弦定理，余弦定理，向量数量积及三角函数恒等变换的应用，属于中档题，7．【分析】（1）利用向量的数量积以及两角和与差化简函数的解析式，通过正弦函数的单调区间求解即可．（2）利用（1）函数的解析式求出A，然后利用余弦定理转化求解即可．【解答】解：（1）=，解得，k∈Z，函数y=f（x）的单调递增区间是（k∈Z）．（2）∵f（A）=2，∴，即，又∵0＜A＜π，∴，∵，由余弦定理得a2=b2+c2﹣2bccosA=（b+c）2﹣3bc=7，①∵sinB=2sinC，∴b=2c，②由①②得，∴．【点评】本题考查余弦定理以及向量的数量积的应用，考查转化思想以及计算能力．8．【分析】（Ⅰ）利用向量数量积的坐标表示结合降幂公式及辅助角公式化简求得f（x），进一步求得函数的最大值，并求得使函数取得最大值的x的值；（Ⅱ）由（Ⅰ）中的解析式结合f（B）=求得B，再由余弦定理求得b，最后由正弦定理得答案．【解答】解：（Ⅰ）由=（sin，1），=（cos，），得f（x）=•===，∴，此时，即．（Ⅱ）在△ABC中，由f（B）=，得，∴，∵0＜B＜π，∴，则，则B=．又a=2，c=3，∴，则b=．由，得．【点评】本题考查平面向量的数量积运算，考查三角函数中的恒等变换应用，训练了正弦定理及余弦定理的应用，是中档题．9．【分析】（1）由已知向量的坐标结合向量垂直的坐标运算可求tanx的值；（2）分别取出||、||，代入数量积公式，结合x的取值范围求解．【解答】解：（1），，若，则，即，得sinx=cosx，∴tanx=1；（2）∵，，∴若与的夹角为，则，即，则，∵，∴，则，即，∴x的值为．【点评】本题考查平面向量的数量积运算，考查三角函数中的恒等变换应用，是中档题．10．【分析】（1）由正弦定理即可由4acosB﹣bccosC=ccosB得到4sinAcosB﹣sinBcosC=sinCcosB，进而得出4sinAcosB=sinA，从而得出cosB的值；（2）由即可得出ac=12，而由余弦定理即可得出a2+c2=24，联立ac=12即可解出a，c的值．【解答】解：（1）由题意得，4sinAcosB﹣sinBcosC=sinCcosB；∴4sinAcosB=sinBcosC+sinCcosB=sin（B+C）=sinA；∵sinA≠0；∴；（2）由得accosB=3，ac=12；由b2=a2+c2﹣2accosB，可得a2+c2=24，所以可得．【点评】考查正弦定理和余弦定理，以及数量积的计算公式，两角和的正弦公式．11．【分析】（1）由求得tanx=2，再利用同角三角函数的基本关系以及两个向量的数量积公式求出的值．（2）利用两个向量的数量积公式以及三角恒等变换求出函数f（x）==sin （2x+）+，再由x的范围，求出f（x）的值域．【解答】解：（1）由可得，∴tanx=2．∴=sinxcosx+cos2x===．（2）∵角，函数f（x）==sinxcosx+cos2x=+=sin（2x+）+，∴2x+∈，sin（2x+）∈[，1]，∴f（x）∈[1，]，即f（x）的值域为[1，]．【点评】本题主要考查两个向量的数量积的运算，三角函数的恒等变换，正弦函数的定义域和值域，属于中档题．12．【分析】（1）利用三角函数的定义直接表示A，B坐标；（2）设出M，利用向量的数量积为0，得到关系式，然后求解点M横坐标的取值范围．【解答】解：（1）点A是单位圆上一点，且位于第一象限，以x轴的正半轴为始边，OA为终边的角设为α，α∈（0，）可得A（cosα，sinα），将OA绕坐标原点逆时针旋转至OB．可得B（cos（），sin（）），即B（﹣sinα，cosα）．（2）设M（x，0），x≠0，=（cosα﹣x，sinα），=（﹣sinα﹣x，cosα）．MA⊥MB，可得（cosα﹣x）（﹣sinα﹣x）+sinαcosα=0．xsinα﹣xcosα+x2=0，可得﹣x=sinα﹣cosα=sin（）∈（﹣1，1）．综上x∈（﹣1，0）∪（0，1）．点M横坐标的取值范围：（﹣1，0）∪（0，1）．【点评】本题考查平面向量的数量积，三角函数定义的应用，考查转化思想以及计算能力．13．【分析】（Ⅰ）根据平面向量时•=0，列方程求得x的值；（Ⅱ）由平面向量的数量积化f（x）为正弦型函数，求出f（x）的最大、最小值以及对应x的值．【解答】解：（Ⅰ）平面向量=（cosx，sinx），=（﹣，），若，则•=0，即﹣cosx+sinx=0，∴tanx=，又x∈[0，π]，∴x=；（Ⅱ）f（x）==﹣cosx+sinx=2（sinx﹣cosx）=2sin（x﹣），又x∈[0，π]，∴x﹣∈[﹣，]；x﹣=，即x=时，f（x）取得最大值为2；x﹣=﹣，即x=0时，f（x）取得最小值为﹣．【点评】本题考查了平面向量的数量积与三角函数的图象和性质的应用问题，是基础题．14．【分析】（1）根据二倍角的余弦公式和两角和差的正弦公式即可得出f（x）=，从而可求出其最小正周期和单调递增区间；（2）根据f（A）=即可求得，由即可求得bc=12，这样由b+c=2a 及即可求出a的值．【解答】解：（1）=；∴f（x）的最小正周期：；由得：；∴f（x）的单调递增区间为：；（2）由可得：，或；而A∈（0，π），所以；又因为2a=b+c；而，∴bc=12；∴=；∴．【点评】考查二倍角的余弦公式，两角和差的正弦公式，以及余弦定理，数量积的计算公式．15．【分析】（1）在△ADC中根据余弦定理计算cosC，再在△ABC中计算c；（2）把代入化简即可得出bcosA=c，故AB⊥BC．【解答】解：（1）在△ADC中，因为，由余弦定理：．故在△ABC中，由余弦定理，得，所以．（2）因为AD为边BC上的中线，所以，所以=，∴c=bcosA．∴AB⊥BC，∴B=90°．【点评】本题考查了余弦定理解三角形，平面向量的应用，属于中档题．16．【分析】（1）把方程化为圆的标准方程，可得结论；（2）求出A，B的坐标，即可得出△AOB的面积S为定值；（3）直线l与曲线C方程联立可得5ax2﹣（2a2+16a﹣8）x+16a﹣16=0，设M（x1，y1），N（x2，y2），利用韦达定理和向量的数量积公式即可求出【解答】解：（1）将曲线C的方程化为x2+y2﹣2ax﹣y=0，∴（x﹣a）2+（y﹣）2=a2+，可知曲线C是以点（a，）为圆心，以为半径的圆．（2）△AOB的面积S为定值．证明如下：在曲线C的方程中令y=0，得ax（x﹣2a）=0，得点A（2a，0），在曲线C方程中令x=0，得y（ay﹣4）=0，得点B（0，），∴S=|OA||OB|=|2a|||=4（为定值），（3）直线l与曲线C方程联立可得5ax2﹣（2a2+16a﹣8）x+16a﹣16=0，设M（x1，y1），N（x2，y2），则x1+x2=，x1x2=，∴•=x1x2+y1y2=5x1x2+8（x1+x2）+16=﹣，即（80a﹣80﹣16a2﹣128a+64+80a）=﹣，即2a2﹣5a+2=0，解得a=2或a=，当a=2或时，都满足△＞0，故a=2或【点评】本题考查圆的方程，考查直线与圆的位置关系，韦达定理，向量的数量积，属于中档题．17．【分析】（Ⅰ）根据平面向量的线性表示与运算法则，用，表示出即可；（Ⅱ）根据平面向量的数量积与模长公式，求出||即可．【解答】解：（Ⅰ）△ABC中，点D，E分别在边AB，BC上，且AB=3AD，BC=2BE；∴=，==（﹣），∴=+=+（﹣）=+；（Ⅱ）设AB=6，AC=4，A=60°，则=+2×ו+=×62+×6×4×cos60°+×42=7，∴||=，即线段DE的长为．【点评】本题考查了平面向量的线性运算以及数量积运算的应用问题，是基础题目．18．【分析】（Ⅰ）利用向量平行，列出方程，通过两角和与差的三角函数，化简求解角A的大小；（Ⅱ）利用三角形的面积，求出c，然后利用余弦定理求解a即可．【解答】解：（Ⅰ）∵，∴（2c﹣b）•cosA﹣a•cosB=0，∴cosA•（2sinC﹣sinB）﹣sinA•cosB=0，即2cosAsinC﹣cosAsinB﹣sinA•cosB=0，∴2cosAsinC=cosAsinB+sinA•cosB，∴2cosAsinC=sin（A+B），即2cosAsinC=sinC，∵sinC≠0∴2cosA=1，即又0＜A＜π∴，（Ⅱ）∵b=3，由（Ⅰ）知∴，，∴c=4，由余弦定理有a2=b2+c2﹣2bccosA=，∴．【点评】本题考查向量与三角函数相结合求解三角形的几何量，考查余弦定理的应用，是基础题．19．【分析】（1）由已知得=2cosα﹣sinα=0，从而sin2α+cos2α=5cos2α=1，进而cos2α=，由此能求出cos2α．（2）由cos2α=，，得cosα=，sinα==，由sin（α﹣β）=，且，得sinβ=2cos，由此能求出β的值．【解答】解：（1）∵向量=（cosα，﹣1），=（2，sinα），其中，且．∴=2cosα﹣sinα=0，∴sin2α+cos2α=5cos2α=1，∴cos2α=，∴cos2α=2cos2α﹣1=﹣．（2）∵cos2α=，，∴cosα=，sinα==，∵sin（α﹣β）=，且，∴sinαcosβ﹣cosαsinβ=，∴2cosβ﹣sinβ=，∴sinβ=2cos，∴sin2β+cos2β=5cos2β﹣2﹣=0，解得cosβ=或cosβ=﹣（舍），∵，∴β=．【点评】本题考查角的余弦值的求法，考查角的求法，是中档题，解题时要认真审题，注意三角函数性质的合理运用．20．【分析】（Ⅰ）根据平面向量的数量积化简f（x）为余弦型函数，求出f（x）在区间[﹣π，π]上的单调递增区间即可；（Ⅱ）根据f（A）=﹣1求出A的值，利用平面向量的数量积和正弦、余弦定理，即可求出b、c的值．【解答】解：（Ⅰ）；∴f（x）==2cos2x﹣sin2x=cos2x﹣sin2x+1=2cos（2x+）+1，令﹣π+2kπ≤2x+≤2kπ，k∈Z，得﹣+kπ≤x≤﹣+kπ，k∈Z，当k=0时，﹣≤x≤﹣，当k=1时，≤x≤，∴f（x）在区间[﹣π，π]上的单调递增区间是[﹣，﹣]和[，]；（Ⅱ）△ABC中，f（A）=﹣1，∴2cos（2A+）+1=﹣1，∴cos（2A+）=﹣1，∴2A+=π，解得A=；又a=，向量垂直，∴•=2sinB﹣3sinC=0，由正弦定理得：2b﹣3c=0，∴b=c；由余弦定理得：a2=b2+c2﹣2bccosA，即=c2+c2﹣2×c2×，解得c=1；∴b=．【点评】本题考查了平面向量的数量积和三角恒等变换以及正弦、余弦定理的应用问题，是综合性题目．21．【分析】（Ⅰ）由已知结合数量积的坐标运算得到f（x），降幂后利用辅助角公式化简，由复合函数的单调性求得函数f（x）的单调递增区间；（Ⅱ）由求得角A，再由余弦定理结合基本不等式求得求b+c的取值范围．【解答】解：（Ⅰ）∵====．∴．由，得，即，∴函数f（x）的单调递增区间为；（Ⅱ）由，得，∴，∴或，即，或A=π+2kπ，k∈Z，∵0＜A＜π，∴．由余弦定理得a2=b2+c2﹣2bccosA，即4=b2+c2﹣bc，∴，即b+c≤4．又∵b+c＞a=2，∴2＜b+c≤4．【点评】本题考查平面向量的数量积运算，考查y=Asin（ωx+φ）型函数的图象和性质，训练了三角形的解法，是中档题．【分析】（1）根据向量的坐标运算和向量的数量积即可求出，（2）根据向量的模求出（m+n）2=16，再根据基本不等式和向量的数量积即可求出【解答】解：（1）m=3，n=﹣1时，=（1，3），=（2，﹣1），∴+λ=（1+2λ，3﹣λ），∵⊥（+λ），∴•（+λ）=1+2λ+3（3﹣λ）=0，解得λ=10，（2）∵=（1，m），=（2，n），∴+=（3，m+n），•=2+mn，∵|+|=5，∴9+（m+n）2=25，∴（m+n）2=16，∴•=2+mn≤2+（m+n）2=6，当且仅当m=n=2或m=n=﹣2时取等号，故•的最大值6．【点评】本题考查了向量的坐标运算，向量的数量积，向量的模和基本不等式，属于基础题23．【分析】（1）利用向量的数量积以及两角和与差的三角函数化简函数的解析式，然后求解最值．（2）利用函数的解析式求解A，然后利用余弦定理求解即可，得到bc的范围，然后利用基本不等式求解最值．【解答】解：（1）∵，∴，∴当时，f（x）取得最小值2．（2）∵f（A）=4，∴，又∵BC=3，∴，∴9=（b+c）2﹣bc．，∴，∴，当且仅当b=c取等号，∴三角形周长最大值为．【点评】本题考查向量的数量积以及两角和与差的三角函数，三角函数的最值，基本不等式以及余弦定理的应用，考查计算能力．24．【分析】（1）利用数量积的坐标运算结合辅助角公式化积，再由y=Asin（ωx+φ）型函数的性质求解；（2）由（1）及f（A）=2求得角A，再由正弦定理把b，c用含有角B的代数式表示，作和后利用三角函数的最值得答案．【解答】解：（1）∵P（，﹣1），Q（sin2x，cos2x），∴f（x）==．由2x﹣，得x=，k∈Z．∴函数f（x）的对称中心为（）；由，得，k∈Z．∴函数f（x）的单调增区间为[﹣，]，k∈Z；（2）由f（A）=2，得，即．又2A∈（），∴，则A=．∵a=5，∴，c=．∴△ABC周长L=5+=5+×=．∵0，∴B+∈（），则sin（B+）∈（，1]．∴L∈（10，15]．【点评】本题考查了平面向量的坐标表示与数量积运算问题，也考查了三角恒等变换与三角函数最值的求法，是中档题．25．【分析】（1）根据向量的数量积定义和三角恒等变换化简即可求出cosB，得出B 的值；（2）化简f（x）的解析式，根据f（B）为f（x）的最大值求出f（x）的解析式，利用正弦函数的单调区间列不等式解出．【解答】解：（1）∵（c﹣2a）=c•，即（c﹣2a）accos（π﹣B）=abccosC，∴2accosB=bcosC+ccosB，∴2sinAcosB=sinBcosC+sinCcosB，∴2sinAcosB=sin（B+C）=sinA，∴cosB=，∴B=．（2）f（x）=cosx（asinx﹣2cosx）+1=sin2x﹣cos2x=sin（2x﹣φ），∵对任意的x∈R，都有f（x）≤f（B）=f（），∴sin（﹣φ）=1，∴φ=，∴f（x）=sin（2x﹣），令，解得≤x≤+kπ，k∈Z．∴函数f（x）的单调递减区间是[，+kπ]，k∈Z．【点评】本题考查了平面向量的数量积，三角函数的恒等变换，正弦函数的性质，属于中档题．26．【分析】（1）根据平面向量的数量积公式和三角恒等变换化简即可；（2）根据f（A）=2计算A，根据面积计算c，再利用余弦定理求出a．【解答】解：（1）f（x）=2sinxcosx+2cos2x=sin2x+cos2x+1=2sin（2x+）+1．（2）∵f（A）=2sin（2A+）+1=2，∴sin（2A+）=，∵A∈（0，π），∴2A+∈（，），∴2A+=，∴A=．=sinA==，∴S△ABC∴c=2，∴a2=b2+c2﹣2bccosA=3，∴a=．【点评】本题考查了三角函数恒等变换，余弦定理解三角形，属于中档题．27．【分析】（1）根据向量平行列出方程，解出sin2x，cos2x即可；（2）化简f（x）解析式，根据对称轴得出m的值，从而得出f（2x）的解析式，利用正弦函数的性质计算f（2x）的值域．【解答】解：（1）当m=1时，=（sinx，cosx），=（3，﹣1）．∵，∴sinx=﹣3cosx．又sin2x+cos2x=1，∴sin2x=，cos2x=．∴2sin2x﹣3cos2x=2×﹣3×=．（2）f（x）==3sinx﹣mcosx=sin（x﹣φ），其中tanφ=．∵函数f（x）=•的图象关于直线x=对称，∴sin（﹣φ）=1或sin（﹣φ）=﹣1．∴φ=+2kπ，或φ=﹣+2kπ．∴m=3tanφ=，①当φ=+2kπ时，f（x）=3sinx﹣cosx=2sin（x﹣），∴f（2x）=2（2x﹣），∵x∈[，]，∴2x﹣∈[，]．∴sin（2x﹣）∈[﹣，1]，∴f（2x）在[，]上的值域为[﹣，2]．②当φ=﹣+2kπ时，f（x）=2sin（x+）=2cos（x+），∴f（2x）=2cos（2x+），∵x∈[，]，∴2x+∈[，]．∴cos（2x+）∈[﹣1，]，∴f（2x）在[，]上的值域为[﹣2，]．【点评】本题考查了平面向量的数量积运算，正弦函数的图象与性质，属于中档题．28．【分析】（1）在△ABC中，•=⇒bccosA=cacosB，即bcosA=acosB，利用正弦定理可得sin（A﹣B）=0，即A=B，再由sinA=，求得cosA=，于是可求sinC的值；（2）D为AC的中点，BD的长为，则由=（+）⇒a2+c2+ac=153①；在△ABD中，利用余弦定理由|BD|2=|AB|2+|AD|2﹣2|AB|•|AD|cosA⇒c2+﹣2c•×=②联立①②，可解得：a=5，c=8，从而可求得△ABC的面积．【解答】解：（1）在△ABC中，∵•=，∴bccosA=cacosB，即bcosA=acosB，由正弦定理得：sinBcosA=sinAcosB，即sin（A﹣B）=0，∴A=B，即△ABC为等腰三角形．又sinA=，∴cosA==，∴sinC=sin（π﹣A﹣B）=sin（π﹣2A）=sin2A=2sinAcosA=2××=；（2）∵D为AC的中点，|BD|=，∴=（+），∴=（+2•+），即=（c2+2accosB+a2），整理得：a2+c2+ac=153①；在△ABD中，由余弦定理得：|BD|2=|AB|2+|AD|2﹣2|AB|•|AD|cosA，即c2+﹣2c•×=②联立①②，解得：a=5，c=8，=acsinB=×5×8×=12．∴△ABC的面积S△ABC【点评】本题考查平面向量数量积的运算，突出考查正弦定理与余弦定理的应用，考查数形结合思想与函数方程思想及综合运算能力，属于难题．【分析】（1）根据二倍角公式求出cosB，再求出sinB，根据向量的数量积和三角形的面积公式即可求出答案；（2）根据余弦定理即可求出答案．【解答】解；（1）∵sin=，∴cosB=1﹣2sin2=1﹣=，∴sinB=，∵•=6，∴•=||•||•cosB=6，∴||•||=10，=||•||•sinB=10×=4；∴S△ABC（2）由（1）可知ac=10，又c+a=8，又余弦定理可得，b2=a2+c2﹣2accosB=（a+c）2﹣2ac﹣2ac×=64﹣×10=32，∴b=4．【点评】本题考查了余弦定理三角形的面积公式和向量的数量积的运算，以及三角函数的化简，属于中档题．30．【分析】（1）根据向量的坐标运算和向量的模以及两角和差即可求出答案，（2）根据向量的数量积和二倍角公式化简得到f（θ）=2cos2（θ﹣）﹣2λcos （θ﹣）﹣1，令t=cos（θ﹣），根据二次函数的性质即可求出．【解答】解：（1）∵向量=（cosθ，sinθ），=（cosφ，sinφ），∴﹣=（cosθ﹣cosφ）+（sinθ﹣sinφ），∴|﹣|2=（cosθ﹣cosφ）2+（sinθ﹣sinφ）2=2﹣2cos（θ﹣φ）=2﹣2cos=2﹣∴|﹣|=1；（2）•=cosθcosφ+sinθsinφ=cos（θ﹣φ）=cos（2θ﹣），∴|+|==2|cos（θ﹣）|=2cos（θ﹣），∴f（θ）=•﹣λ|+|=cos（2θ﹣）﹣2λcos（θ﹣）=2cos2（θ﹣）﹣2λcos （θ﹣）﹣1令t=cos（θ﹣），则t∈[，1]，∴f（t）=2t2﹣2λt﹣1=2（t﹣）2﹣﹣1，又1≤λ≤2，≤≤1∴t=时，f（t）有最小值﹣﹣1，∴f（θ）的最小值为﹣﹣1．【点评】本题考查了向量的坐标运算和向量的数量积以及三角函数的化简，以及二次函数的性质，属于中档题．31．【分析】（Ⅰ）由已知向量的坐标求得||，结合⊥列关于x的方程求得x值；（Ⅱ）求出的最小值，开方得答案．【解答】解：（Ⅰ）∵=（3，﹣1），∴，又•=﹣5，=x+（1﹣x），且⊥，∴，即，解得：x=；（Ⅱ）由=x+（1﹣x），得：==10x2﹣10x（1﹣x）+5（1﹣x）2=5（5x2﹣4x+1）．∴当x=时，，则||的最小值为1．【点评】本题考查平面向量的数量积运算，考查向量垂直与数量积的关系，训练了二次函数最值的求法，是中档题．32．【分析】（1）求出向量的坐标，再计算数量积；（2）化简，得出cos（2x﹣）=，再利用和角公式计算cos2x．【解答】解：（1）当x=时，=（，﹣1），=（，），∴=﹣=．（2）=sinxcosx﹣cos2x=sin2x﹣cos2x﹣=sin（2x﹣）﹣，若=﹣，则sin（2x﹣）=，∵，∴2x﹣∈[﹣，]，∴cos（2x﹣）=．∴cos2x=cos（2x﹣+）=cos（2x﹣）cos﹣sin（2x﹣）sin=﹣=．【点评】本题考查了平面向量的数量积运算，三角函数恒等变换，属于中档题．33．【分析】（1）根据⊥，结合正弦定理和余弦定理求出B的值即可，（2）根据正弦定理以及三角形的面积公式求出即可．【解答】解：（1）∵=（sinB﹣sinC，sinC﹣sinA），=（sinB+sinC，sinA），且⊥，∴（sinB﹣sinC）•（sinB+sinC）+（sinC﹣sinA）•sinA=0，∴b2=a2+c2﹣ac，∴2cosB=1，∴B=；（2）∵⊥，∴△ABC是RT△，而B=，故A=，由==2R，得：==2，解得：a=1，b=，=••1=．故S△ABC【点评】本题考察了向量数量积的运算，考察三角恒等变换，是一道中档题．34．【分析】（1）运用向量垂直的条件：数量积为0，结合两角和的余弦公式和诱导公式即可得证；（2）运用两向量共线的条件和两角和的正弦公式和诱导公式即可得证．【解答】证明：（1）向量=（cosA，sinA），=（cosB，﹣sinB），若，则=0，即cosAcosB﹣sinAsinB=0，即有cos（A+B）=0，即cos（π﹣C）=0，则cosC=0，即有C为直角．（2）若∥，则sinAcosB=﹣3cosAsinB，即sinAcosB+cosAsinB=﹣2cosAsinB，sin（A+B）=﹣2cosAsinB，即sinC=﹣2cosAsinB，由sinB＞0，sinC＞0，则cosA＜0，由sinA＞0，sinB＞0，则cosB＞0，则有B为锐角．【点评】本题考查向量的垂直和共线的条件，主要考查三角函数的化简和两角和差公式的运用和诱导公式的运用，属于中档题和易错题．35．【分析】（1）利用向量的数量积以及两角和与差的三角函数化简函数的解析式，然后求解函数的周期以及最值．（2）利用函数的图象变换求出函数的解析式，然后求解函数的值域．【解答】解：（1）==．所以f（x）的最大值为1，最小正周期为π．（2）由（1）得．将函数y=f（x）的图象向左平移个单位后得到的图象．因此，又，所以，．故g（x）在上的值域为[﹣，1]．【点评】本题考查向量与三角函数相结合，两角和与差的三角函数，考查三角函数的图象与性质以及计算能力．36．【分析】（1）运用向量的加减运算和同角的平方关系，即可求得sinα=，cosα=，进而得到t的值；（2）运用向量的数量积的坐标表示，结合条件的商数关系，求得tanα，再由二倍角的正切公式和和角公式，计算即可得到所求值．【解答】解：（1）向量为实数，若，则（2cosα﹣2sinα，sin2α﹣t）=（，0），可得cosα﹣sinα=，平方可得sin2α+cos2α﹣2cosαsinα=，即为2cosαsinα=1﹣=，（cosα＞0，sinα＞0），由sin2α+cos2α=1，解得cosα+sinα===，即有sinα=，cosα=．则t=sin2α=；（2）若t=1，且，即有4cosαsinα+sin2α=1，即有4cosαsinα=1﹣sin2α=cos2α，由α为锐角，可得cosα∈（0，1），即有tanα==，则tan2α===，===．【点评】本题考查向量的加减运算和数量积的坐标表示，考查同角的基本关系式和二倍角正切公式及和角公式的运用，考查化简整理的运算能力，属于中档题．37．【分析】（Ⅰ）根据△ABC的面积，结合平面向量的数量积求出tanB的值，再求tan2B的值；（Ⅱ）根据tanB的值，求出sinB、cosB，再由cosA的值求出sinA，从而求出sinC=sinB，判断△ABC是等腰三角形，求出底边上的中线AD的长．【解答】解：（Ⅰ）△ABC的面积为S，且•=S；∴accosB=acsinB，解得tanB=2；∴tan2B==﹣；（Ⅱ）∵|﹣|=2，∴||=2，又tanB==2，sin2B+cos2B=1∴sinB=，cosB=；又cosA=，∴sinA=，∴sinC=sin（A+B）=sinAcosB+cosAsinB=；∵sinB=sinC，∴B=C，∴AB=AC=2，∴中线AD也是BC边上的高，∴AD=ABsinB=2×=．【点评】本题考查了平面向量的数量积与三角恒等变换的应用问题，也考查了同角的三角函数关系与应用问题，是综合题．38．【分析】（1）运用向量的加减运算和数量积的坐标表示，以及二倍角公式和正弦公式，由正弦函数的增区间，解不等式即可得到所求；（2）运用图象变换，可得g（x）的解析式，由条件可得sinA，cosA，sinB的值，运用正弦定理计算即可得到所求值．【解答】解：（1）向量=（sinx，﹣1），=（cosx，），函数f（x）=（+）•=（sinx+cosx，）•（sinx，﹣1）=sin2x+sinxcosx﹣=sin2x﹣（1﹣2sin2x）=sin2x﹣cos2x=sin（2x﹣），由2kπ﹣≤2x﹣≤2kπ+，k∈Z，可得kπ﹣≤x≤kπ+，k∈Z，即有函数f（x）的单调递增区间为[kπ﹣，kπ+]，k∈Z；（2）由题意可得g（x）=sin（2（x+）﹣）=sin2x，g（）=sinA=，即sinA=，cosA=±=±，在△ABC中，sinB=cosA＞0，可得sinB=，由正弦定理=，可得b===3．【点评】本题考查向量数量积的坐标表示和三角函数的恒等变换，考查正弦函数的图象和性质，以及图象变换，考查解三角形的正弦定理的运用，以及运算能力，属于中档题．39．【分析】（Ⅰ）根据平面向量的坐标表示与数量积运算求出f（x），即可得出f（x）的最小正周期；（Ⅱ）根据f（A）=4求出A的值，再根据△ABC的面积和余弦定理求出b+c的值，即可求出周长．【解答】解：（Ⅰ）点P（，1），Q（cosx，sinx），∴=（，1），=（﹣cosx，1﹣sinx），函数f（x）=•=（﹣cosx）+（1﹣sinx）=3﹣cosx+1﹣sinx=﹣（sinx+cosx）+4=﹣2sin（x+）+4；∴函数f（x）的最小正周期为T=2π；（Ⅱ）A为△ABC的内角，f（A）=4，∴﹣2sin（A+）+4=4，∴sin（A+）=0，∴A+=π，解得A=；又BC=a=3，∴△ABC的面积为：S=bcsinA=bcsin=，解得bc=3；由余弦定理得：a2=b2+c2﹣2bccosA=b2+c2﹣2bccos=b2+c2+bc=32=9，∴b2+c2=6；∴（b+c）2=b2+c2+2bc=6+6=12，∴b+c=2，∴△ABC的周长为a+b+c=3+2．【点评】本题考查了平面向量的坐标表示与数量积运算问题，也考查了三角恒等变换与余弦定理的应用问题，是综合题．40．【分析】（1）利用三角函数的定义及其和差公式即可得出；（2）利用向量的坐标运算、数量积运算性质、同角三角函数基本关系式、和差公式即可得出．【解答】解：（1）由点B（﹣，），∴sinθ=，，tanθ=﹣．∴tan（θ+）===﹣；（2）∵+=，∴=（1+cosθ，sinθ）．=，∴（cosθ，sinθ）•（1+cosθ，sinθ）=cosθ+cos2θ+sin2θ=cosθ+1=，解得cosθ=，∵0＜θ＜π，∴=．∴cos（﹣θ）==+=．【点评】本题考查了三角函数的定义、向量的坐标运算、数量积运算性质、同角三角函数基本关系式、和差公式，考查了推理能力与计算能力，属于中档题．。

2018年全国各地高考数学试题及解答分类汇编大全（10平面向量）一、选择题1．（2018浙江）已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为π 3，向量b 满足b 2−4e ·b +3=0，则|a −b |的最小值是（ ）A1 BC ．2D ．21.答案：A解答：设(1,0)e =，(,)b x y =，则222430430b e b x y x -⋅+=⇒+-+=22(2)1x y ⇒-+=如图所示，a OA =，b OB =，（其中A 为射线OA 上动点，B 为圆C 上动点，3AOx π∠=.）∴min11a bCD -=-=.（其中CD OA ⊥.）2．（2018天津文）在如图的平面图形中， 已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为（ ）（A ）15- （B ）9- （C ）6- （D ）02．【答案】C【解析】如图所示，连结MN ，由2BM MA =，2CN NA = 可知点M ，N 分别为线段AB ，AC 上靠近点A 的三等分点，则()33BC MN ON OM ==-，由题意可知：2211OM ==，12cos1201OM ON ⋅=⨯⨯︒=-， 结合数量积的运算法则可得：()2333336BC OM ON OM OM ON OM OM ⋅=-⋅=⋅-=--=-．故选C ．3．（2018天津理）如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==. 若点E 为边CD 上的动点，则⋅uu u r uurAE BE 的最小值为 （ ）(A) 2116 (B) 32 (C) 2516(D) 33．【答案】A【解析】建立如图所示的平面直角坐标系，则10,2A ⎛⎫- ⎪⎝⎭，B ⎫⎪⎪⎝⎭，30,2C ⎛⎫⎪⎝⎭，D ⎛⎫ ⎪ ⎪⎝⎭，点E 在CD 上，则()01DE DC λλ=≤≤，设(),E x y ，则：32x y λ⎛⎫⎫+= ⎪⎪ ⎪⎪⎝⎭⎝⎭，即32x y λ⎧⎪=⎨=⎪⎪⎪⎩， 据此可得333,2E λλ⎫- ⎪ ⎪⎝⎭，且3331,22AE λλ⎛⎫=-+ ⎪ ⎪⎝⎭，333,2BE λλ⎛⎫=- ⎪ ⎪⎝⎭，由数量积的坐标运算法则可得：3331222AE BE λλ⎛⎛⎫⋅=+⨯+ ⎪⎝⎭⎝⎭⎝， 整理可得：()()23422014AE BE λλλ⋅=-+≤≤，结合二次函数的性质可知，当14λ=时，AE BE ⋅取得最小值2116，故选A ．4．（2018全国新课标Ⅰ文、理）在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =（）A ．3144AB AC - B ．1344AB AC - C ．3144AB AC+ D ．1344AB AC +4．答案：A解答：由题可知11131[()]22244EB EA AB AD AB AB AC AB AB AC =+=-+=-++=-.5．（2018全国新课标Ⅱ文、理）已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b （ ）A ．4B ．3C ．2D ．0 5．【答案】B 【解析】因为()()222221213⋅-=-⋅=--=+=a a b a a b a ，所以选B ．二、填空1．（2018北京文）设向量()10=,a ，()1,m =-b ，若()m ⊥-a a b ，则m =_________． 1．【答案】1-【解析】()10=Q ,a ，()1m =-,b ，()()()011m m m m m ∴-=--=+-,,,a b ， 由()m ⊥-a a b 得，()0m ⋅-=a a b ，()10m m ∴⋅-=+=a a b ，即1m =-．2. （2018上海）在平面直角坐标系中，已知点A （-1，0），B （2，0），E ，F 是y 轴上的两个动点，且|EF |=2，则AE ·BF 的最小值为______3．（2018江苏）在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，(5,0)B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=，则点A 的横坐标为 ▲ ．3．【答案】3【解析】设()(),20A a a a >，则由圆心C 为AB 中点得5,2a C a +⎛⎫⎪⎝⎭， 易得()()():520C x x a y y a --+-=，与2y x =联立解得点D 的横坐标1D x =，所以()1,2D ．所以()5,2AB a a =--，51,22a CD a +⎛⎫=-- ⎪⎝⎭， 由0AB CD ⋅=得()()()5512202a a a a +⎛⎫--+--= ⎪⎝⎭，2230a a --=，3a =或1a =-，因为0a >，所以3a =．4．（2018全国新课标Ⅲ文、理）已知向量(1,2)=a ，(2,2)=-b ，(1,)λ=c ．若()2+c a b ，则λ=________．4．答案：12解答：2(4,2)a b +=，∵//(2)c a b +，∴1240λ⨯-⨯=，解得12λ=.三、解答题。

1．已知A ，B ，C 为圆O 上的三点，若AO →＝2(AB →＋AC →)，则AB →与AC →的夹角为________．2．设O 在△ABC 的内部，D 为AB 的中点，且OA →＋OB →＋2OC →＝0，则△ABC 的面积与△AOC 的面积的比值为________．3．(2016·南通、连云港、扬州、淮安三模)在平行四边形ABCD 中，若AC →·AD →＝AC →·BD →＝3，则线段AC 的长为________．4．已知向量a ＝⎝⎛⎭⎪⎫sin θ2，cos ⎝ ⎛⎭⎪⎫θ2＋π4，b ＝⎝⎛⎭⎪⎫3sin ⎝ ⎛⎭⎪⎫θ2＋π4，cos θ2，θ∈(0，π)，并且满足a ∥b ，则θ的值为________．5．(2016·安徽六安一中月考)已知△ABC 是边长为1的正三角形，动点M 在平面ABC 内，若AM →·AB →＜0，|CM →|＝1，则CM →·AB →的取值范围是________．6．在平面直角坐标系中，已知A (－2,0)，B (2,0)，C (1,0)，P 是x 轴上任意一点，平面上点M 满足：PM →·PB →≥CM →·CB →对任意P 恒成立，则点M 的轨迹方程为______． 7．在△ABC 中，已知AB →·AC →＝tan A ，则当A ＝π6时，△ABC 的面积为________．8．(2016·南通、扬州、淮安、宿迁、泰州二调)如图，在同一平面内，点A 位于两平行直线m ，n 的同侧，且A 到m ，n 的距离分别为1,3，点B ，C 分别在m ，n 上，|AB →＋AC →|＝5，则AB →·AC →的最大值是________．9．定义一种向量运算“⊗”：a ⊗b ＝⎩⎨⎧a·b ，当a ，b 不共线时，|a －b |，当a ，b 共线时(a ，b 是任意的两个向量)．对于同一平面内的向量a ，b ，c ，e ，给出下列结论： ①a ⊗b ＝b ⊗a ；②λ(a ⊗b )＝(λa )⊗b (λ∈R )； ③(a ＋b )⊗c ＝a ⊗c ＋b ⊗c ；④若e 是单位向量，则|a ⊗e |≤|a |＋1.以上结论一定正确的是________．(填上所有正确结论的序号) 10．已知m ，x ∈R ，向量a ＝(x ，－m )，b ＝((m ＋1)x ，x )． (1)当m ＞0时，若|a |＜|b |，求x 的取值范围；(2)若a ·b ＞1－m 对任意实数x 恒成立，求m 的取值范围．答案精析1．90° 2.4 3. 3 4.π35．－1，－12)解析 如图，以A 为原点，AB 为x 轴建立直角坐标系，则B (1,0)，C (12，32)，设M (x ，y )，AM →·AB →＝(x ，y )·(1,0)＝x ＜0，由|CM →|＝1得(x －12)2＋(y －32)2＝1，所以－12≤x ＜0，所以CM →·AB →＝(x －12，y －32)·(1,0)＝x －12∈－1，－12)．6．x ＝0解析 设P (x 0,0)，M (x ，y )，则由PM →·PB →≥CM →·CB →可得(x －x 0)(2－x 0)≥x －1，x 0∈R 恒成立，即x 20－(x ＋2)x 0＋x ＋1≥0，x 0∈R 恒成立，所以Δ＝(x ＋2)2－4(x＋1)≤0，化简得x 2≤0，则x ＝0，即x ＝0为点M 的轨迹方程． 7.16解析 已知A ＝π6， 由题意得|AB →||AC →|cos π6＝tan π6，则|AB →||AC →|＝23，所以△ABC 的面积S ＝12|AB →||AC →|·sin π6＝12×23×12＝16.8.214解析 设P 为BC 的中点，则AB →＋AC →＝2AP →，从而由|AB →＋AC →|＝5得|AP →|＝52，又AB →·AC →＝(AP →＋PB →)·(AP →＋PC →)＝AP →2－PB →2＝254－PB →2，因为|BC →|≥2，所以PB →2≥1，故AB →·AC →≤254－1＝214，当且仅当|BC →|＝2时等号成立．9．①④解析 当a ，b 共线时，a ⊗b ＝|a －b|＝|b －a|＝b ⊗a ，当a ，b 不共线时，a ⊗b ＝a·b＝b·a＝b ⊗a ，故①是正确的； 当λ＝0，b ≠0时，λ(a ⊗b)＝0，(λa)⊗b ＝|0－b|≠0，故②是错误的； 当a ＋b 与c 共线时，则存在a ，b 与c 不共线，(a ＋b)⊗c ＝|a ＋b －c|，a ⊗c ＋b ⊗c ＝a·c＋b·c，显然|a ＋b －c|≠a·c＋b·c，故③是错误的；当e 与a 不共线时，|a ⊗e|＝|a·e|＜|a|·|e|＜|a|＋1，当e 与a 共线时，设a ＝u e ，u ∈R ，|a ⊗e|＝|a －e|＝|u e －e| ＝|u －1|≤|u |＋1，故④是正确的． 综上，结论一定正确的是①④. 10．解 (1)由题意得|a|2＝x 2＋m 2， |b|2＝(m ＋1)2x 2＋x 2.因为|a|＜|b|，所以|a|2＜|b|2， 从而x 2＋m 2＜(m ＋1)2x 2＋x 2. 因为m ＞0，所以(m m ＋1)2＜x 2，解得x ＜－m m ＋1或x ＞m m ＋1.即x 的取值范围是 (－∞，－mm ＋1)∪(m m ＋1，＋∞)．(2)a·b＝(m ＋1)x 2－mx .由题意，得(m ＋1)x 2－mx ＞1－m 对任意的实数x 恒成立，即(m ＋1)x 2－mx ＋m －1＞0对任意的实数x 恒成立．当m ＋1＝0，即m ＝－1时，显然不成立，所以 ⎩⎨⎧m ＋1＞0，m 2－4(m ＋1)(m －1)＜0，解得⎩⎨⎧m ＞－1，m ＞233或m ＜－233 ，所以m ＞233.23 3，＋∞)．即m的取值范围是(。

2018届高考数学（理）小题精练专题06 平面向量1．已知向量(),3a x =，()2,2b =- ，且a b ⊥，则| a b +=（ ） A ．5 B ．． ． 10 【答案】B【解析】因为a b ⊥所以， 260,3,x x -== | a b+25==+=，故选B ；2．已知2a =，3b=，且两向量夹角为60︒，求()a b b +⋅=（ ） A ． 8 B ． 10 C ． 12 D ． 14 【答案】C3．,AD BE 分别是ABC ∆的中线，若1AD BE ==，且AD 与BE 的夹角为120，则AB AC ⋅=（ ） A ．13 B ． 49 C ． 23 D ． 89【答案】C【解析】由()()1,2{12,2AD AB AC BE AB AC =+=-+解得2233{ ,4233AB AD BE AC AD BE =-=+ 2242233333AB AC AD BE AD BE ⎛⎫⎛⎫⋅=-⋅+= ⎪ ⎪⎝⎭⎝⎭．故选C ．点睛：平面向量的数量积计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用． 利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．列出方程组求解未知数．4．已知等边ABC ∆边长为4， O 为其内一点，且4730OA OB OC ++=，则AOB ∆的面积为 （ ）A ．．C ．D ． 12【答案】B【解析】∵4730OA OB OC ++=，∴7344OA OB CO +=．如图所示，点睛：本题考查了平面向量的应用问题，解题的关键是作出辅助线，根据向量的知识得出各小三角形与原三角形面积之间的关系，是中档题；根据题意，作出图形，利用向量的关系，求出AOB 与ABC 的面积关系，即可得出．5．以原点O 及点()5,2A 为顶点作等腰直角三角形OAB ，使90A =︒，则AB 的坐标为（ ） A ． ()2,5- B ． ()()2,52,5--或 C ． ()2,5- D ． ()()7,33,7-或 【答案】B 【解析】如图设(),B x y ，∵52A（，）， 90A =︒，且OAB 为等腰直角三角形，∴()()(525,20{OA AB x y AB x ⋅=⋅--===，，解得3{ 7x y ==或7{ 3x y ==-，∴()25AB =-，或25-（，），故选B ．6．若，且，，则的取值范围是（ ） A ．B ．C ．D ．【答案】D 【解析】 如图所示：7．已知单位向量,a b 满足a b a b +=-，则a 与b a -夹角为（ ） A ．π6 B ． π3 C ． π4 D ． 3π4【答案】D【解析】因为a b a b +=-，所以a b ⊥ ， ()22cos ,22a b a a b a a b a⋅--===-- ，因此3π,4a b a -=，选D ． 8．已知单位向量1e 与2e 的夹角为3π，向量122e e +与122e e λ+的夹角为23π，则λ=（ ）A ． 23-B ． 3-C ． 3-或23- D ． 1-或3- 【答案】B【解析】由题意可得： 12111cos32e e π⋅=⨯⨯=，且：()()()()()121222112222242152244,22e e e e e e e e λλλλλλ+⋅+=++⋅+=+++=+而()2221222447e e e e e e e e +=+=+⋅+=()22221212112222444e e e e e e e e λλλλ+=+=+⋅+=+利用平面向量夹角公式可得：5421cos32λπ+==-，解得： 3λ=-．本题选择B 选项．9．设向量,a b满足2,3a b a b ==+=，则2a b += ( ) A ． 6 B ． ． 10 D ． 42【答案】D10．已知向量()()1,,3,2a m b ==-，且()//a b b +，则m =（ ） A ．23- B ．23C ．-8D ．8 【答案】A 【解析】考点：向量的坐标运算．11．M 是ABC ∆所在平面内一点，203MB MA MC ++=，D 为AC 中点，则||||MD BM 的值为（ ） A ．12B ．13 C ． 1D ．2【答案】B 【解析】 试题分析：因为203MB MA MC ++=，所以212,33MB MA MC MD MD MB -=+==-，故M 在中线BD 上，且为靠近D 的一个四等分点，故||13||MD BM =．考点：向量运算．12．已知三角形ABC 内的一点D 满足2DA DB DB DC DC DA ===-，且||||||DA DB DC ==．平面ABC 内的动点P ，M 满足||1AP =，PM MC =，则2||BM 的最大值是（ ） A ．494 B ．434 C ． 3763+ D ．372334+ 【答案】A【解析】考点：1、平面向量数量积公式及向量的模；2、平面向量的几何运算及坐标运算．。

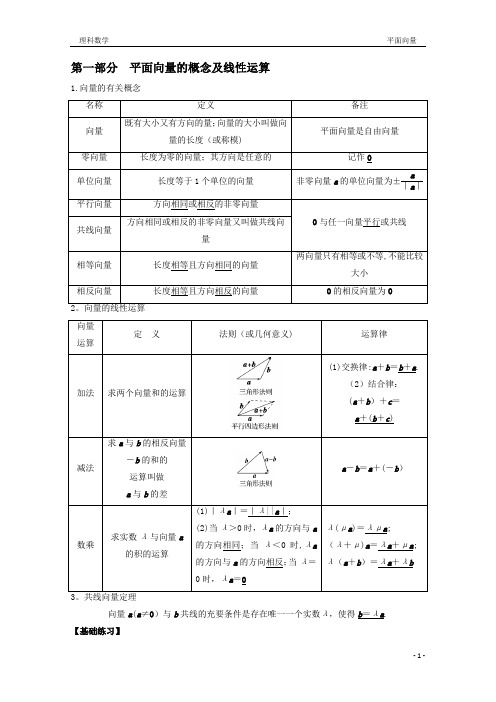
第一部分 平面向量的概念及线性运算1.向量的有关概念名称定义 备注 向量既有大小又有方向的量；向量的大小叫做向量的长度（或称模) 平面向量是自由向量 零向量长度为零的向量；其方向是任意的 记作0 单位向量长度等于1个单位的向量 非零向量a 的单位向量为±a ｜a ｜ 平行向量方向相同或相反的非零向量 0与任一向量平行或共线 共线向量 方向相同或相反的非零向量又叫做共线向量相等向量 长度相等且方向相同的向量两向量只有相等或不等,不能比较大小 相反向量长度相等且方向相反的向量 0的相反向量为0 2。

向量的线性运算向量运算 定 义 法则（或几何意义) 运算律加法 求两个向量和的运算(1)交换律:a ＋b ＝b ＋a .（2）结合律：(a ＋b ）＋c ＝a ＋(b ＋c )减法 求a 与b 的相反向量－b 的和的运算叫做 a 与b 的差a －b ＝a ＋(－b ） 数乘 求实数λ与向量a的积的运算 (1)｜λa ｜＝｜λ||a ｜；(2)当λ＞0时，λa 的方向与a 的方向相同；当λ＜0时,λa的方向与a 的方向相反；当λ＝0时，λa ＝0λ(μa )＝λμa ; （λ＋μ)a ＝λa ＋μa ; λ（a ＋b ）＝λa ＋λb向量a (a ≠0）与b 共线的充要条件是存在唯一一个实数λ，使得b ＝λa .【基础练习】1.判断正误（在括号内打“√"或“×”）(1）零向量与任意向量平行。

( ）(2)若a∥b，b∥c，则a∥c。

（）(3）向量错误!与向量错误!是共线向量，则A，B，C，D四点在一条直线上.( ）(4）当两个非零向量a，b共线时，一定有b＝λa,反之成立.（)(5）在△ABC中，D是BC中点，则错误!＝错误!（错误!＋错误!）.（)2。

给出下列命题：①零向量的长度为零，方向是任意的;②若a，b都是单位向量,则a＝b；③向量错误!与错误!相等.则所有正确命题的序号是（）A。

（安徽）已知向量,a b 满足()()a b a b +2⋅-=-6，且1a =，2b =，则a 与b 的夹角为 . （北京）．已知向量a =（3，1），b =（0，-1），c =（k ，3）。

若a -2b 与c 共线，则k=___________________。

（福建·）已知O 是坐标原点，点A （-1,1）若点M （x,y ）为平面区域，上的一个动点，则OA u u u r ·的取值范围是A.[-1.0]B.[0.1]C.[0.2]D.[-1.2] （广东）若向量a ，b ，c 满足a ∥b 且a ⊥c ，则c ·(a+2b)= A ．4 B ．3 C ．2 D ．0（广东）已知平面直角坐标系xOy 上的区域D 由不等式组02{22x y x y≤≤≤≤给定.若M(x ，y)为D 上动点，点A的坐标为(2，1)．则z OM OA =u u u u r u u u rg的最大值为 A.42 B.32 C.4 D.3（湖北）已知向量a=(x+z,3),b=(2,y-z)，且a ⊥ b.若x,y 满足不等式1x y +≤，则z 的取值范围为A..[-2，2]B.[-2，3]C.[-3，2]D.[-3，3]（辽宁）若a ，b ，c 均为单位向量，且0=⋅b a ，0)()(≤-⋅-c b c a ，则||c b a -+的最大值为A ．12-B ．1C ．2D ．2（全国2）设向量,,a b c r r r 满足1||||1,,,602a b a b a c b c ==⋅=-<-->=or r r r r r r r ，则||c r 的最大值等于(A)2 (B)3 (c)2 (D)1【思路点拨】本题按照题目要求构造出如右图所示的几何图形，然后分析观察不难得到当线段AC 为直径时，||c r最大.【精讲精析】选A .如图，构造,,,120,60,AB a AD b AC c BAD BCD ===∠=∠=o o u u u r r u u u r r u u u r r，所以A 、B 、C 、D 四点共圆，分析可知当线段AC 为直径时，||c r最大，最大值为2.（全国新）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P（山东）设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ=u u u u v u u u u v(λ∈R)，1412A A A A μ=u u u u v u u u u v (μ∈R)，且112λμ+=,则称3A ，4A 调和分割1A ，2A ,已知点C(c ，o),D(d ，O) (c ，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是 （A ）C 可能是线段AB 的中点 （B ）D 可能是线段AB 的中点（C ）C ，D 可能同时在线段AB 上（D ）C ，D 不可能同时在线段AB 的延长线上（陕西）设,a b 是向量，命题“若a b ≠-，则∣a ∣= ∣b ∣”的逆命题是 （ ）（A ）若a b ≠-，则∣a ∣≠∣b ∣ （B ）若a b =，则∣a ∣≠∣b ∣（C ）若∣a ∣≠∣b ∣，则∣a ∣≠∣b ∣ （D ）若∣a ∣=∣b ∣，则a = -b（上海）设12345,,,,A A A A A 是空间中给定的5个不同的点，则使123450MA MA MA MA MA ++++=u u u u r u u u u r u u u u r u u u u r u u u u r r成立的点M 的个数为〖答〗（ ）A 0B 1C 5D 10（四川）如图，正六边形ABCDEF 中，BA CD EF ++u u u r u u u r u u u r =(A)0 (B)BE u u u r (C)AD u u u r (D)CF uuu r（上海）在正三角形ABC 中，D 是BC 上的点，3,1AB BD ==，则AB AD ⋅=u u u r u u u r。

2018届高三理数平面向量高考真题及考点归纳班别： 姓名： 成绩：考点1：平面向量的线性运算、平面向量基本定理1.(2015全国卷I)设D 为ABC 所在平面内一点3BC CD =uu u r uu u r ，则（ ）（A ）1433AD AB AC =-+uuu r uu u r uuu r (B)1433AD AB AC =-uuu r uu u r uuu r （C ）4133AD AB AC =+uuuur uuu r uu u r (D)4133AD AB AC =-uuuuuu r uuu r uu u r 2.(2014全国卷I)已知A ，B ，C 是圆O 上的三点，若1()2AO AB AC =+uuu r uu u r uuu r ，则AB uu u r 与AC uuu r 的夹角为 .3.(2011全国卷)已知a r 与b r 均为单位向量，其夹角为，有下列四个命题其中的真命题是（ ）（以上的a ，b 都是带箭号的）（A ） （B ） （C ） （D ）4.(2015全国卷II) 设向量,a b r r 不平行，向量a b λ+r r 与2a b +r r 平行，则实数_________．考点2：数量积的运算及其模与夹角问题：5.(2014全国卷II)设向量a,b 满足|a+b|a-b|=a ⋅b = ( )A. 1B. 2C. 3D. 5 6.(2017全国卷I) 已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2b |= .7.(2013全国卷II)已知正方形ABCD 的边长为2，E 为CD 的中点，则AE BD uu u r uu u r g =_______. θ12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦14,P P 13,P P 23,P P 24,P P8.(2012全国卷)已知向量,a b r r 夹角为45︒ ，且1,2a a b =-=r r r ；则_____b =r9.(2013全国卷I)1已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t)b ，若b ·c =0，则t =_____.考点3：向量坐标运算：10.(2016全国卷I) 设向量a =(m ，1)，b =(1，2)，且|a +b |2=|a |2+|b |2，则m =11.(2016全国卷II)已知向量(1,)(3,2)a m b ==-r r ，，且()+a b b ⊥r r r ，则m =（ ）（A ）－8 （B ）－6 （C ）6 （D ）812.（2016全国卷III ）（3）已知向量1(2BA =uu v ,1),2BC =uu u v 则∠ABC=（ ） (A)300 (B) 450 (C) 600 (D)1200考点4：关于向量的最值问题：13.(2017全国卷II) 已知ABC △是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+u u r u u r u u u r 的最小是（ ）A ．2-B ．32-C ． 43-D ．1-14．（2015全国卷I ）已知M 00()x y 是双曲线C ：2212x y -=上的一点，F 1、F 2是C 上的两个 焦点，若1MF uuu r ∙2MF uuu u r ＜0，则y 0的取值范围是（ ）（A ）（-3，3） （B ）（-66） （C ）（3-，3） （D ）（ 15．（2017全国卷III ）在矩形ABCD 中，AB =1，AD =2，动点P 在以点C 为圆心且与BD 相切的圆上。

AC DBAD BCAM AOAB ACBC训练目标(1)平面向量数量积的概念；(2)数量积的应用．训练题型(1)向量数量积的运算；(2)求向量的夹角；(3)求向量的模．(1)数量积计算的三种方法：定义、坐标运算、数量积的几何意义；解题策略(2)求两向量的夹角时，要注意夹角θ为锐角和cosθ＞0的区别，不能漏解或增解；(3)求向量的模的基本思想是利用|a|2＝a·a，灵活运用数量积的运算律.1．(2017·玉溪月考)若向量a，b满足|a|＝1，|b|＝2，且a⊥(a＋b)，则a与b的夹角为________．2．(2016·淄博期中)已知矩形ABCD中，AB＝2，BC＝1，则→·→＝________. 3．(2016·镇江模拟)在△ABC中，∠BAC＝90°，D是BC的中点，AB＝4，AC＝3，则→·→＝________.4．(2017·吉林东北师大附中三校联考)如图，已知△ABC外接圆的圆心为O，AB＝23，AC＝22，A为钝角，M是BC边的中点，则→·→＝________.5．已知向量a＝(cosθ，sinθ)，向量b＝(3，－1)，则|2a－b|的最大值与最小值的和为________．6．(2015·安徽改编)△ABC是边长为2的等边三角形，已知向量a，b满足→＝2a，→＝2a＋b，则下列正确结论的个数为________．①|b|＝1；②a⊥b；③a·b＝1；④(4a＋b)⊥→.7．(2015·福建改编)已知→⊥→，|→|＝，|→|＝t，若点P是△ABC所在平面t→＝AB＋4AC，则→·→的最大值等于________．→→|b|＝λBC，DF＝μDC.若→·→＝1，→·→＝－，则λ＋μ＝________.11．(2016·开封冲刺模拟)若等边△ABC的边长为2，平面内一点M满足→＝→＋CA，则→·→＝________.1→OA OB OA OB→→→OPBC AOAM AN14．已知△ABC中，AB＝2，AC＝1，当2x＋y＝t(t＞0)时，|xAB＋yAC|≥→PB PC1AB AC AB AC→→内的一点，且AP PB PC|AB||AC|8．(2016·吉林长春质检)已知向量a＝(1，3)，b＝(0，t2＋1)，则当t∈－3，2]时，|a－tb|的取值范围是________．9．已知菱形ABCD的边长为2，∠BAD＝120°，点E，F分别在边BC，DC上，BE2AE AF CE CF310．(2016·浙江余姚中学期中)已知→与→的夹角为60°，|→|＝2，|→|＝23，OP＝λOA＋μOB，若λ＋3μ＝2，则|→|的最小值为________．1CM CB3MA MB212．(2016·盐城模拟)设O是△ABC的三边中垂线的交点，且AC2－2AC＋AB2＝0，则→·→的取值范围是____________．13．(2016·徐州质检)如图，半径为2的扇形的圆心角为120°，M，N分别为半径OP，OQ的中点，A为弧PQ上任意一点，则→·→的取值范围是________．→→22t恒成立，则△ABC的面积为____，在上述条件下，对于△ABC内一点P，PA·(→＋→)的最小值是________．1.3π 42＝2cos θ＋ ，＝π8－BC AC A B建立如图所示的平面直角坐标系，则 B ，0 ，C (0，t )，→＝tt AB 4→AC 1 4AC ＝(0，t )，AP ＝ ＋ ＝t ，0 ＋ (0，t )＝(1,4)，→| |AC→|t t∴P (1,4)，→·→＝ －1，－4 ·(－1，t －4) tBC BC＝17－ ＋4t ≤17－2 答案精析72.13.－4.55．4解析 由题意可得 a·b ＝ 3cos θ－sin θπ 6则|2a －b|＝ (2a －b)2＝ 4|a|2＋|b|2－4a·b6∈0,4]，所以|2a －b|的最大值与最小值的和为 4.6．1解析 如图，在△ABC 中，由→＝→－→＝2a ＋b －2a ＝b ，得|b|＝2.又|a|＝1，所以 a·b ＝|a||b|cos120°＝－1，所以(4a ＋b)·→＝(4a ＋b)·b ＝4a·b ＋|b|2＝4×(－1)＋4＝0，所以(4a ＋b)⊥→，故正确结论只有④.7．13解析1AB1，0 ，→ → →|AB1PB PC1t1 t·4t ＝13，当且仅当 ＝4t ，即 t ＝ 时取等号．解析由题意， b 即|a －t b9.5BE → DF →CE ·→＝(λ－1， 3(λ－1))·(μ－1， 3(1－μ))＝－2，②AE AF1 1t 28．1， 13]b |b| ＝(0,1)，∴|a －t |b||＝|(1， 3)－t (0,1)|＝|(1， 3－t )|＝ 1＋( 3－t )2＝ (t － 3)2＋1.∵t ∈－ 3，2]，∴ (t － 3)2＋1∈1， 13]，|b||的取值范围是 1， 13]．6解析建立如图所示的平面直角坐标系，则 A (－1,0)，B (0，－ 3)，C (1,0)，D (0， 3)．设 E (x ，y )，11F (x ，y )．由→＝λBC ，得(x ，y ＋ 3)＝λ(1， 3)，解得22 1 1x ＝λ，1 y ＝ 3(λ－1)，1即点 E (λ， 3(λ－1))．由→＝μDC ，得(x ，y － 3)＝μ(1，－ 3)，22解得x ＝μ，2 y ＝ 3(1－μ).2即点 F (μ， 3(1－μ))．又→·→＝(λ＋1， 3(λ－1))·(μ＋1， 3(1－μ))＝1，①35OA OB OP → → OP → → → →→ OBOPOP 9 解析由于→＝→－→＝－ →＋ →，→＝→－→＝ →－ →，故→·→＝ － →＋ → · →－ → ＝－ →2－ →2＋ →·→＝－ ×22－ ×22＋ ×2×2 9 4 BC AO AD DOBC AD BC＝ (→＋→)·(－→＋→) ＝ (|→|2－|→|2)． 设|AC |＝b ，|AB |＝c ，则 b 2－2b ＋c 2＝0， 所以→·→＝ (b 2＋b 2－2b )＝b 2－b .所以→·→∈－ ，2)．2 210．2 3解析 由题意得→·→＝2 3.因为→＝λOA ＋μOB ，所以→2＝(λOA ＋μOB )2＝λ2OA 2＋μ2OB 2＋2λμOA ·→＝4λ2＋12μ2＋4 3λμ.又因为 λ＋ 3μ＝2，所以 λ＝2－ 3μ，所以→2＝4(2－ 3μ)2＋12μ2＋4 3(2－ 3μ)μ＝4( 3μ－1)2＋12，所以当 3μ－1＝0，即 μ＝33 时，|→| ＝2 3. min811．－1 12 1 MA CA CM CB CA MB CB CM CB CA MA MB3 2 3 21 12 1 2 1 1 2 1 1 CB CA CB CA CB CA CB CA3 2 3 2 94 2 9 4 28 ×cos60°＝－ .112．－ ，2)解析如图．设 BC 的中点为 D ，则→·→＝(→＋→)·→＝→·→1AB AC AB AC 21AC AB2→→1 BC AO 2又 b 2－2b ＝－c 2＜0，所以 0＜b ＜2.1BC AO 43 513． ， ]由已知得 M (－ ， 3 则→＝(－ －2cos θ， 3 2 －2sin θ)， 所以→·→＝(－ －2cos θ)(1－2cos θ)＋( 32 －2sin θ)·(－2sin θ)＝ －故 ≤sin(θ＋30°)≤1，所以 ≤→·→≤ . 14．1－5解析 因为|xAB ＋yAC | ＝ x 2→2＋y 2→2＋2xyAB ·→AC AB AC ＝ 4x 2＋y 2＋4xy cos A ≥ 2得 x 2→2＋y 2→2＋2xyAB ·→≥ t 2， → 则 cos A (cos A －1)≤0，则 cos A ≥0，A 的最大值为π→解析 建立如图所示的平面直角坐标系，连结 AO ，设∠AOQ ＝θ，则 A (2cos θ，2sin θ)(0°≤θ≤120°)．12 2 )，N (1,0)，1AM 2AN ＝(1－2cos θ，－2sin θ)，17AM AN 222sin(θ＋30°)，因为 0°≤θ≤120°，所以 30°≤θ＋30°≤150°，123 5AM AN2 28→ →→2 t 恒成立，则由两边平方，1 AB AC AC2又 t ＝2x ＋y ，则 4x 2＋y 2＋4xy (2cos A －1)≥0，则 Δ＝16y 2(2cos A －1)2－16y 2≤0，2 .当 cos A ＝0 时，|xAB ＋yAC |＝ 4x 2＋y 2≥ 当 A ，P ，D 三点共线时，→·→＜0，又此时 AD ＝ BC ＝ ，即有 2→·→＝－2|→PA →|≥－2× |PA |＋|PD | 2＝－5，即有最小值为－5.||PD2PB PC PD PA PB PC PA PD1 2·AB ·AC ＝1； → →2 2(2x ＋y )满足题意，所以此时 △S ABC ＝在 Rt △ABC 中，取 BC 的中点 D ，连结 PD ，则→＋→＝2→，即→·(→＋→)＝2→·→，1 5 PA PD PA PD2 2→ →88。