数据结构英文试题

以下是一份关于数据结构的英文试题，供您参考：1. What is the difference between an array and a linked list?Answer: An array and a linked list are two fundamental data structures used in computer science. An array is a linear data structure that stores elements in a consecutive memory location. It has a fixed size and the elements are accessed by their indices. On the other hand, a linked list is a dynamic data structure that consists of a set of nodes where each node contains the data and a reference (pointer) to the next node. The size of a linked list can vary dynamically and the elements are accessed in the order of their appearance.2. Explain the operation of binary search tree.Answer: A binary search tree is a tree-like data structure in which each node has at most two children, usually referred to as the left child and the right child. The value of each node in the binary search tree is greater than or equal to the value of all nodes in its left subtree and less than or equal to the value of all nodes in its right subtree. This property allows for efficient search, insertion, and deletion operations in the binary search tree. The search operation starts from the root node and compares the value with the target value, following the appropriate branch based on the comparison result until the target value is found or the appropriate action is taken. Insertion and deletion operations also involve maintaining the binary search tree property by adjusting the tree accordingly.3. What is the difference between a stack and a queue?Answer: A stack and a queue are two fundamental data structures used in computer science. A stack is a linear data structure that follows the Last In First Out (LIFO) principle. It allows the addition and removal of elements only at one end, usually referred to as the top of the stack. Elements are added to or removed from the stack using the push and pop operations, respectively. On the other hand, a queue is a linear data structure that follows the First In First Out (FIFO) principle. It allows the addition of elements at one end (rear) and removal of elements at the other end (front). Elements are added to or removed from the queue using the enqueue and dequeue operations, respectively.。

1.Suppose we have a linked list.Eack node has three parts: one data field and twolinked fields.The list has been linked by the first linked field link1,but the list is disorder.Try your best to sort the list with the second linked field into an increasing list.算法:int creasort(struct node &head){if (head.link1 == NULL) //没有结点return ERROR;head.link2 = head.link1; //设排列链表的第一个结点head.link2->link2 = NULL;p = head.link1->link1; //p为链表的第二个结点q = head; //q代表p插入位置的前一个结点if (!p) //只有一个结点return OK;while (p){while ( q->link2 && (q->link2->data < p->data)) //找查找入位置q = q->link2;if (!q->link2) //插在最后{q->link2 = p;}else //插在队列中间{p->link2 = q->link2;q->link2 = p;}p = p->link1;q = head;}return OK;}2.Suppose we have a sequence with the terminal character @.The format of thesequence can be S1&S2,S1 and S2 do not contain ‘&’, S2 is the reverse sequence of S1.Try to write an algorithm to check the sequence if the format of the sequence obeys the above fules then the function return TRUE otherwise FALSE.算法://s为待检查的字符串int checkrules(char *s){len = strlen(s);//用string.h自带函数取字符串s的长度if (len % 2 == 0) //字符串是偶数return FALSE;i = 0; //i指向字符串第一个字符n = len - 1;//n指向字符串最后一个字符while (i < len / 2 && ( s[i] != '&' || s[n] != '&')) //对半劈{if (s[i] == s[n]){i++;n--;}elsebreak;}if (i == len / 2 && s[i] == '&') //i指向中间元素且必须是’&’return TRUE;elsereturn FALSE;}3.Suppose we have a double-linked ciroular list L.Eack node has four fields:twolinked fiels pre and next, one data field data and one frequency field freq.At the beginning the initial value of freq is 0 and after each opeation Locate(L,x),the value in frequency field of x plus 1,and then sort the list according to freq into a non-increasing list.The node which is most frequently accessed is the first node after the head node.算法:void Locate(struct doulin L, int x){struct doulin *; //访问时用到的遍历指针if (x > L.data) //无效的访问return;p = &L; //定位，p指向已经访问的指针while(x--){p = p->next;}p->freq++;//因为形参L不在循环链表里，因此要用L.pre->next表示循环链表的头结点while (p->pre ->freq < p->freq && p->pre != L.pre->next){p->data <-> p->pre->data;p->freq <-> p->pre->freq;}}4.Suppose we have a disordered list of integers.The list has been stored in a stack.You are supposed to sort the list with queue.算法://表示将from队的元素倒到to中void QueToQue(Queue *from, Queue *to, int ns){ tag = 0; //用于标注要排列的数是否进栈while (!QueueEmpty(from)){ DeQueue(from, &nq); //nq用于存取出队元素if ((tag == 0 && nq > ns) || tag == 1) //不能入队EnQueue(to, nq);else //可以入队了{ tag = 1; //设置标志tag为1，表示已经入队了EnQueue(to, ns);EnQueue(to, nq);}}if (tag == 0) //当ns比队中任何数都大时EnQueue(to, ns);}//将队列from中的元素倒到to栈中void QueToStack(Queue *from, Stack *to){ while (!QueueEmpty(from)){ DeQueue(from, &nq);Push(to, nq);}}//排序的本体void sort(Stack *S){ InitQueue(&Q1); InitQueue(&Q2); //初始化两个队列Q1,Q2Pop(S, &ns); EnQueue(&Q1, ns); //先将一个元素出队进栈while (!StackEmpty(S)){ Pop(S,&ns);if (!QueueEmpty(&Q1)) //若Q1队列不空(即Q2队列为空)QueToQue(&Q1, &Q2, ns);else //若Q2队列为空（即Q1队列不为空）QueToQue(&Q2, &Q1, ns);}if (!QueueEmpty(&Q1)) //Q1不为空，也就是要把Q1队载入栈QueToStack(&Q1, S);elseQueToStack(&Q2, S);}5.颜色排列的算法://colors是颜色数组，number是数组大小void colorsort(int *colors, int number){i = 0, j = number – 1;while (colors[i] == 1) //找到第一个非1的单元i++;while (colors[j] == 3) //找到最后一个非3的单元j--;k = i; //遍历指针设为iwhile(k <= j){switch (colors[k]){case 1: colors[k]<->colors[i];i++; k++;break;case 2: k++;break;case 3: colors[k]<->colors[j];j--;break;}}}。

数据结构英⽂试卷A及谜底NEWFinal examination2009 FallData Structure and Algorithm DesignClass:Student Number:Name:TeacherNo.123456789TotalMark1.Single-Choice(20 points)(1) Consider the following definition of a recursive function ff. int ff( int n ) { if( n == 0 ) return 1; return 2 * ff( n - 1 ); }If n > 0, what is returned by ff( n )? (a) log 2 n (b) n 2 (c) 2n (d) 2 * n(2) An input into a stack is like 1,2,3,4,5,6. Which output is impossible? .a. 2,4,3,5,1,6b.3,2,5,6,4,1c.1,5,4,6,2,3d.4,5,3,6,2,1(3) Which of the following data structures uses a "Last-in, First-out" policy for element insertionand removal? (a) Stack (b) Tree (c) Hash table (d) Queue (4) If deleting the i th key from a contiguous list with n keys, keys need to be shifted leftone position.a. n-i b. n-i+1 c. i d. n-i-1(5) Sorting a key sequence （28，84，24，47，18，30，71，35，23）, its status is changed as follows.23，18，24，28，47，30，71，35，8418，23，24，28，35，30，47，71，8418，23，24，28，30，35，47，71，84The sorting method is called (a)．select sorting (b)．Shell sorting (c)．merge sorting (d)．quick sorting(6) The number of keyword in every node except root in a B- tree of order 5 is _ _ at least管路术中要进⾏检查和检测处理。

杭州电子工业学院学生考试卷（A）卷1.(8分) Imagine we have two empty stacks of integers, s1 and s2. draw a picture of each stack after the following operations:PushStack (s1, 3);PushStack (s1, -5);PushStack (s1, 7);PushStack (s1, -9);PushStack (s1, 11);PushStack (s1, -13);while (not emptyStack (s1)) {popStack (s1, x);if (x < 0) {pushStack (s2, x);}} //while2. (8分)Using manual transformation, change the following postfix or prefix expressions to infix form.a. ABC+*D-b. -*A+BCD3. (8分) what would be the contents of queue Q1 after the following code is executed and the following data are entered?Q1 = CreateQueueS1 = CreateStackloop (not end of file)read numberif (number not 0)pushStack (S1, number)elsepopStack (S1, x)popStack (S1, x)loop (not emptyStack (S1))popStack (S1, x)enqueue (Q1, x)end loopend ifend loopThe data are 5, 7, 12, 4, 0, 4, 6, 8, 67, 34, 23 , 5, 0, 44, 33, 22, 6, 0.4. (8分) Create a AVL tree using the following data entered as a sequential set :7, 10, 14, 23, 33, 56, 66, 70, 80, 90.5. (8分)Show the resulting heap after 33, 22, and 8 are added to the following heap :50, 30, 40, 20, 10, 25, 35, 10, 5.6. (8分) After two passes of a sorting algorithm, the follow array :48, 5, 29, 36, 7, 61, 88has been rearranged as shown below :5, 7, 48, 29, 36, 61, 88which sorting algorithm is being used (straight selection, bubble, straight insertion) ? Defend your answer.7.(8分)A graph can be used to show relationships, for example, from the following list of people belonging to the same club (vertices) and their friendships (edges). People = {George, Jim, Jean, Frank, Fred, John, Susan} FriendShip = {(George, Jean), (Frank, Fred), (George, John), (Jim, Fred), (Jim, Frank),(Jim, Susan), (Susan, Frank) }Give the adjacency list representation of this graph.Algorithm Design1.(11分)Write an algorithm that traverses a linked list and deletes all nodes whose keys are negative.2.(11分)Write an algorithm that counts the number of leaves in a binary tree.3.(11分)Write an algorithm called QueueToStack that creates a stack from a queue. At the end of the algorithm, the queue should be unchanged; the front of the queue should be the top of the stack; and the rear of the queue should be the base of the stack.4. (11分) Develop a non-recursive BST (Binary Search Tree) search algorithm SearchBST.。

数据结构期末试卷B3860A book, like a ship, leads us from a narrow place to an infinite sea of life, CalebData structure final paper B1, judge: 10 points, 1 point per question.A full binary tree is also a complete binary treeThe binary tree can be represented by an ordered tree of 0 or less than or equal to 2(a)In the k cross tree where there is only a degree of zero and a degree of k, there are nO of the nodes of 0, and nk for the nodes of k, and nO 二nk + 14,the shortest path to another vertex in a graph with the right connection is not necessarily the only oneIn the undirected graph of n nodes, if the number of edges is less than n minus 1, the graph must be an unconnected graph The binary tree with the shortest path length of the tree must have no node of 1The lookup of the hash table does not need to be compared to the keywordThe binary search method can be used to search for linear linked lists ordered by valueIterating over a heap does not necessarily get an ordered sequenceBecause the last trip of hill sort is the same as the direct insertion sort process, the former must spend more time than the latter2, fill in the blanks: (20 points, 2 points each.)A node with a degree of zero degrees is a node with no subtreesThe son of the same node is called a ____________In a binary linked list with n nodes, there is an empty chainThe adjacency matrix is used for the adjacency matrix storage method, and the adjacency matrix must be a4, a given sequence {100, 86, 4& 73, 35, 39, 42, 57, 66, 21}, as defined by the heap structure, it is an _____________________ heapIn the case of direct insertion sort, the number of data is compared with the initial order of data. In the case of direct selection, the number of data compared with the data is inThe function H, which converts the node keyword to the location of the node, is called __________________ or ____________The sequence of n key words is sorted rapidly, and the space complexity of the average case isChoice: 20 points, 2 points per problem・1, will be a totally has 100 node in the binary tree from top to bottom, from left to right in turn on node number, the serial number of the root node is 1, the number of node，s left child for 49 Numbers forA. 98 b. 99C. 50 d. 48The shape of the heap is aA. AC. complete binary tree d. balance binary treeFor the hash function H (key)二key MOD 13, the keyword that is called a synonym isA. 35 and 41 b. 23 and 39C. 15 and 44 d. 25 and 51Point out how many comparisons are required to find 12 in order tables {2, 5, 5, 7, 10, 14, 15, 1& 23, 35, 41, 52}A, 2, B, 3C, 4, D, 5Suppose a graph with an n vertex and an arc of e is indicatedby the adjacency list, and the time complexity associated with a vertex vi is removed: ___________________A. 0 (n) b. o. (e)C. 0 (n + e)D. 0 (n * e)When looking for dn element in a binary sort tree, its time complexity is approximatelyA, 0 (n) B, 0 (1)C, 0 (log2n) D, 0 (n2)The weight of a tree that has a weight of 3, 8, 6, 2, 5 leaves a Huffman tree with a right path length ofA, 24, B, 48C, 72, D, 53& A character sequence {Q, H, C, Y, P, A, M, S, D, F, R, X}, A trip to the sorting result for {F, H, C, D, P, A, M, Q, R,S, Y, X}, is which of the following sorting algorithmsA, blisters sort B, and the initial step is A sequence of 4 shellsC, 2 merge sort D, and the first element is the quicksort of the boundary elementA tree that is not connected to a connected graph is a.・・that contains all the vertices of the connected graphA: very little connected subgraph BC. greatly connected subgraphD. Large subgraphThe width of the diagram is first traversed by a type similar to the binary treeA. first order traversal B・ Sequence traversalThe post-order traversal of the DFour, answer the question: (total 28 minutes, each question 4)1,the binary tree that is shown in the picture is completed in order traversal, the following sequence traversal, the first sequence traversing, and drawing the binary tree of the middle sequence clues2,please give the adjacency matrix and the adjacency list below, and write the vertex sequence that is the highest priority and breadth of the graph from vertex aFor the diagram below, draw the minimum spanning treeA table 4, known as (49, 66, 73, 52, 40, 37, 65, 43), made according to the order of the elements in the table, in turn, insert a initial empty binary sort tree, draw the binary sort tree elements in the tableA three-order b~tree is shown below, assuming that the key words are removed in sequence, 46, 24, 815, and you can draw the tree after each delete node:6,known as a group of keywords, 14, 23, 01, 68, 20, 84, 27, 55, 11, 10, 79 (19), then the hash function H (key)二key MOD and linear detection method of conflict resolution structure of this group of 13 key hash tableDo you know if the following sequence is a heap? If not, adjust it to heap:(5, 56, 20, 234, 38,29,61,35, 76,28, 100)Program (22 points)Read the following algorithm and answer the following questions: (4)Perfect the program, and answer what the algorithm does? What is the function of r [n + 1] in the algorithm?Void sort (elemtype r [], int n)(int k, I;For (k = n minus 1; k > 二1; k -)・If (r [k] > r [k + 1]){r [n + 1]二r [k];，，For，z (I 二k + 1; r [I] < r [n + 1] ; I + +)R [I - 1] = r [I}}Complete the following program and say what the algorithm does(8)Void weizhisort (struct node r [n], int n)(int low, high, mid, j, I;For (I 二2; I 〈二n; I++){r[0]二r [I];Low 二________ ;High 二...Wh订e (low < = high)Well, it's going to be (1 ow + high) / 2; If (r[0]. Key < r [mid]. Key)Else low 二mid + 1; }For (j 二I - 1).R [j + 1]二T [j]；R [high + 1] = r [0];}The data type is defined as:Struct node(int key：Infotypes otherinfo;3, say what the algorithm does(2 points)Void delete (int a [n], int I){if (I < 0) > =n) printf (〃error 〃);The else (j 二i-1； j 〈n; j + +)A [j]二 a [j + 1];N is equal to n minus 1; } }Improve the program to show its function (8 points)# define NULL 0;Typedef struct Bitnode {Char data;Struct Bitnode * lchild・} Bitreptr;Void inorder_notrecursive (Bitreptr bt, Status (TelemType e)) {InitStack (S):P 二T;While (P | |! StackEmpty (s)){if (P) {Push (S, P);;The else {If (! (p-> data)) return Error;} return OK;A book, like a ship, leads us from a narrow place to an infinite sea of life, caleb。

QuestionsThese questions are intended as a self-test for readers.Answers to the questions may be found in Appendix C.1.In many data structures you can________a single record,_________it,and_______it.2.Rearranging the contents of a data structure into a certain order is called_________.30CHAPTER1Overview3.In a database,a field isa.a specific data item.b.a specific object.c.part of a record.d.part of an algorithm.4.The field used when searching for a particular record is the______________.5.In object-oriented programming,an objecta.is a class.b.may contain data and methods.c.is a program.d.may contain classes.6.A classa.is a blueprint for many objects.b.represents a specific real-world object.c.will hold specific values in its fields.d.specifies the type of a method.7.In Java,a class specificationa.creates objects.b.requires the keyword new.c.creates references.d.none of the above.8.When an object wants to do something,it uses a________.9.In Java,accessing an object’s methods requires the_____operator.10.In Java,boolean and byte are_____________.(There are no experiments or programming projects for Chapter1.)Questions31Chapter1,OverviewAnswers to Questions1.insert,search for,delete2.sorting3.c4.search key5.b6.a7.d8.method9.dot10.data typesQuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.1.Inserting an item into an unordered arraya.takes time proportional to the size of the array.b.requires multiple comparisons.c.requires shifting other items to make room.d.takes the same time no matter how many items there are.2.True or False:When you delete an item from an unordered array,in most cases you shift other items to fill in the gap.3.In an unordered array,allowing duplicatesa.increases times for all operations.b.increases search times in some situations.c.always increases insertion times.d.sometimes decreases insertion times.4.True or False:In an unordered array,it’s generally faster to find out an item is not in the array than to find out it is.5.Creating an array in Java requires using the keyword________.6.If class A is going to use class B for something,thena.class A’s methods should be easy to understand.b.it’s preferable if class B communicates with the program’s user.c.the more complex operations should be placed in class A.d.the more work that class B can do,the better.7.When class A is using class B for something,the methods and fields class A can access in class B are called class B’s__________.74CHAPTER2Arrays8.Ordered arrays,compared with unordered arrays,area.much quicker at deletion.b.quicker at insertion.c.quicker to create.d.quicker at searching.9.A logarithm is the inverse of_____________.10.The base10logarithm of1,000is_____.11.The maximum number of elements that must be examined to complete a binary search in an array of200elements isa.200.b.8.c.1.d.13.12.The base2logarithm of64is______.13.True or False:The base2logarithm of100is2.14.Big O notation tellsa.how the speed of an algorithm relates to the number of items.b.the running time of an algorithm for a given size data structure.c.the running time of an algorithm for a given number of items.d.how the size of a data structure relates to the number of items.15.O(1)means a process operates in_________time.16.Either variables of primitive types or_________can be placed in an array. Chapter2,ArraysAnswers to Questions1.d2.True3.b4.False5.new6.d740APPENDIX C Answers to Questions7.interface8.d9.raising to a power10.311.812.613.False14.a15.constant16.objectsuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.puter sorting algorithms are more limited than humans in thata.humans are better at inventing new algorithms.puters can handle only a fixed amount of data.c.humans know what to sort,whereas computers need to be told.puters can compare only two things at a time.2.The two basic operations in simple sorting are_________items and_________ them(or sometimes_________them).3.True or False:The bubble sort always ends up comparing every item with every other item.4.The bubble sort algorithm alternates betweenparing and swapping.b.moving and copying.c.moving and comparing.d.copying and comparing.5.True or False:If there are N items,the bubble sort makes exactly N*N comparisons.Questions1096.In the selection sort,a.the largest keys accumulate on the left(low indices).b.a minimum key is repeatedly discovered.c.a number of items must be shifted to insert each item in its correctlysorted position.d.the sorted items accumulate on the right.7.True or False:If,in a particular sorting situation,swaps take much longer than comparisons,the selection sort is about twice as fast as the bubble sort.8.A copy is________times as fast as a swap.9.What is the invariant in the selection sort?10.In the insertion sort,the“marked player”described in the text corresponds to which variable in the insertSort.java program?a.inb.outc.tempd.a[out]11.In the insertion sort,“partially sorted”means thata.some items are already sorted,but they may need to be moved.b.most items are in their final sorted positions,but a few still need to be sorted.c.only some of the items are sorted.d.group items are sorted among themselves,but items outside the groupmay need to be inserted in it.12.Shifting a group of items left or right requires repeated__________.13.In the insertion sort,after an item is inserted in the partially sorted group,it willa.never be moved again.b.never be shifted to the left.c.often be moved out of this group.d.find that its group is steadily shrinking.110CHAPTER3Simple Sorting14.The invariant in the insertion sort is that________.15.Stability might refer toa.items with secondary keys being excluded from a sort.b.keeping cities sorted by increasing population within each state,in a sortby state.c.keeping the same first names matched with the same last names.d.items keeping the same order of primary keys without regard to secondary keys.Chapter3,Simple SortingAnswers to Questions1.dparing and swapping(or copying)3.False4.a5.False6.b7.False8.three9.Items with indices less than or equal to outer are sorted.10.c11.d12.copies13.b14.Items with indices less than outer are partially sorted.15.buestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.1.Suppose you push10,20,30,and40onto the stack.Then you pop three items. Which one is left on the stack?2.Which of the following is true?a.The pop operation on a stack is considerably simpler than the remove operation on a queue.b.The contents of a queue can wrap around,while those of a stack cannot.c.The top of a stack corresponds to the front of a queue.d.In both the stack and the queue,items removed in sequence are takenfrom increasingly high index cells in the array.3.What do LIFO and FIFO mean?4.True or False:A stack or a queue often serves as the underlying mechanism on which an ADT array is based.5.Assume an array is numbered with index0on the left.A queue representing a line of movie-goers,with the first to arrive numbered1,has the ticket window on the right.Thena.there is no numerical correspondence between the index numbers andthe movie-goer numbers.b.the array index numbers and the movie-goer numbers increase inopposite left-right directions.c.the array index numbers correspond numerically to the locations in theline of movie-goers.d.the movie-goers and the items in the array move in the same direction.6.As other items are inserted and removed,does a particular item in a queue move along the array from lower to higher indices,or higher to lower?7.Suppose you insert15,25,35,and45into a queue.Then you remove three items.Which one is left?8.True or False:Pushing and popping items on a stack and inserting and removing items in a queue all take O(N)time.174CHAPTER4Stacks and Queues9.A queue might be used to holda.the items to be sorted in an insertion sort.b.reports of a variety of imminent attacks on the star ship Enterprise.c.keystrokes made by a computer user writing a letter.d.symbols in an algebraic expression being evaluated.10.Inserting an item into a typical priority queue takes what big O time?11.The term priority in a priority queue means thata.the highest priority items are inserted first.b.the programmer must prioritize access to the underlying array.c.the underlying array is sorted by the priority of the items.d.the lowest priority items are deleted first.12.True or False:At least one of the methods in the priorityQ.java program (Listing4.6)uses a linear search.13.One difference between a priority queue and an ordered array is thata.the lowest-priority item cannot be extracted easily from the array as it can from the priority queue.b.the array must be ordered while the priority queue need not be.c.the highest priority item can be extracted easily from the priority queue but not from the array.d.All of the above.14.Suppose you based a priority queue class on the OrdArray class in the orderedArray.java program(Listing2.4)in Chapter2,“Arrays.”This will buy you binary search capability.If you wanted the best performance for your priority queue,would you need to modify the OrdArray class?15.A priority queue might be used to holda.passengers to be picked up by a taxi from different parts of the city.b.keystrokes made at a computer keyboard.c.squares on a chessboard in a game program.d.planets in a solar system simulation.Chapter4,Stacks and QueuesAnswers to Questions1.102.bst-In-First-Out;and First-In-First-Out4.False.It’s the other way around.5.b6.It doesn’t move at all.7.458.False.They take O(1)time.9.c10.O(N)11.c12.True13.b14.Yes,you would need a method to find the minimum value.15.aQuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.Questions2451.Which of the following is not true?A reference to a class objecta.can be used to access public methods in the object.b.has a size dependant on its class.c.has the data type of the class.d.does not hold the object itself.2.Access to the links in a linked list is usually through the_________link.3.When you create a reference to a link in a linked list,ita.must refer to the first link.b.must refer to the link pointed to by current.c.must refer to the link pointed to by next.d.can refer to any link you want.4.How many references must you change to insert a link in the middle of a singly linked list?5.How many references must you change to insert a link at the end of a singly linked list?6.In the insertFirst()method in the linkList.java program(Listing5.1),the statement newLink.next=first;means thata.the next new link to be inserted will refer to first.b.first will refer to the new link.c.the next field of the new link will refer to the old first link.d.newLink.next will refer to the new first link in the list.7.Assuming current points to the next-to-last link in a singly linked list,what statement will delete the last link from the list?8.When all references to a link are changed to refer to something else,what happens to the link?9.A double-ended lista.can be accessed from either end.b.is a different name for a doubly linked list.c.has pointers running both forward and backward between links.d.has its first link connected to its last link.246CHAPTER5Linked Lists10.A special case often occurs for insertion and deletion routines when a list is ________.11.Assuming a copy takes longer than a comparison,is it faster to delete an item with a certain key from a linked list or from an unsorted array?12.How many times would you need to traverse a singly linked list to delete the item with the largest key?13.Of the lists discussed in this chapter,which one would be best for implementing a queue?14.Which of the following is not true?Iterators would be useful if you wanted toa.do an insertion sort on a linked list.b.insert a new link at the beginning of a list.c.swap two links at arbitrary locations.d.delete all links with a certain key value.15.Which do you think would be a better choice to implement a stack:a singly linked list or an array?Chapter5,Linked ListsAnswers to Questions1.b2.first3.d4.25.16.c7.current.next=null;8.Java’s garbage collection process destroys it.Chapter5,Linked Lists7419.a10.empty11.a linked list12.once,if the links include a previous reference13.a double-ended list14.bually,the list.They both do push()and pop()in O(1)time,but the list uses memory more efficiently.QuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.1.If the user enters10in the triangle.java program(Listing6.1),what is the maximum number of“copies”of the triangle()method(actually just copies of its argument)that exist at any one time?2.Where are the copies of the argument,mentioned in question1,stored?a.in a variable in the triangle()methodb.in a field of the TriangleApp classc.in a variable of the getString()methodd.on a stack3.Assume the user enters10as in question1.What is the value of n when the triangle()method first returns a value other than1?4.Assume the same situation as in question1.What is the value of n when the triangle()method is about to return to main()?5.True or false:In the triangle()method,the return values are stored on thestack.6.In the anagram.java program(Listing6.2),at a certain depth of recursion,a version of the doAnagram()method is working with the string“led”.When this method calls a new version of itself,what letters will the new version be working with?7.We’ve seen that recursion can take the place of a loop,as in the loop-oriented orderedArray.java program(Listing2.4)and the recursive binarySearch.java program(Listing6.3).Which of the following is not true?a.Both programs divide the range repeatedly in half.b.If the key is not found,the loop version returns because the rangebounds cross,but the recursive version occurs because it reaches thebottom recursion level.c.If the key is found,the loop version returns from the entire method, whereas the recursive version returns from only one level of recursion.d.In the recursive version the range to be searched must be specified in the arguments,while in the loop version it need not be.310CHAPTER6Recursion8.In the recFind()method in the binarySearch.java program(Listing6.3),what takes the place of the loop in the non-recursive version?a.the recFind()methodb.arguments to recFind()c.recursive calls to recFind()d.the call from main()to recFind()9.The binarySearch.java program is an example of the_________approach to solving a problem.10.What gets smaller as you make repeated recursive calls in the redFind() method?11.What becomes smaller with repeated recursive calls in the towers.java program (Listing6.4)?12.The algorithm in the towers.java program involvesa.“trees”that are data storage devices.b.secretly putting small disks under large disks.c.changing which columns are the source and destination.d.moving one small disk and then a stack of larger disks.13.Which is not true about the merge()method in the merge.java program(Listing6.5)?a.Its algorithm can handle arrays of different sizes.b.It must search the target array to find where to put the next item.c.It is not recursive.d.It continuously takes the smallest item irrespective of what array it’s in.14.The disadvantage of mergesort is thata.it is not recursive.b.it uses more memory.c.although faster than the insertion sort,it is much slower than quicksort.d.it is complicated to implement.15.Besides a loop,a___________can often be used instead of recursion. Chapter6,RecursionAnswers to Questions1.102.d3.24.105.false6.“ed”7.b8.c9.divide-and-conquer10.the range of cells to search11.the number of disks to transfer12.c13.b14.b15.stackQuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.1.The Shellsort works bya.partitioning the array.b.swapping adjacent elements.c.dealing with widely separated elements.d.starting with the normal insertion sort.2.If an array has100elements,then Knuth’s algorithm would start with an interval of________.Questions3613.To transform the insertion sort into the Shellsort,which of the following do you not do?a.Substitute h for1.b.Insert an algorithm for creating gaps of decreasing width.c.Enclose the normal insertion sort in a loop.d.Change the direction of the indices in the inner loop.4.True or false:A good interval sequence for the Shellsort is created by repeatedly dividing the array size in half.5.Fill in the big O values:The speed of the Shellsort is more than_______but less than________.6.Partitioning isa.putting all elements larger than a certain value on one end of the array.b.dividing an array in half.c.partially sorting parts of an array.d.sorting each half of an array separately.7.When partitioning,each array element is compared to the_______.8.In partitioning,if an array element is equal to the answer to question7,a.it is passed over.b.it is passed over or not,depending on the other array element.c.it is placed in the pivot position.d.it is swapped.9.True or false:In quicksort,the pivot can be an arbitrary element of the array.10.Assuming larger keys on the right,the partition isa.the element between the left and right subarrays.b.the key value of the element between the left and right subarrays.c.the left element in the right subarray.d.the key value of the left element in the right subarray.11.Quicksort involves partitioning the original array and then_________.362CHAPTER7Advanced Sorting12.After a partition in a simple version of quicksort,the pivot may beed to find the median of the array.b.exchanged with an element of the right subarray.ed as the starting point of the next partition.d.discarded.13.Median-of-three partitioning is a way of choosing the_______.14.In quicksort,for an array of N elements,the partitionIt()method will examine each element approximately______times.15.True or false:You can speed up quicksort if you stop partitioning when the partition size is5and finish by using a different sort.Chapter7,Advanced SortingAnswers to Questions1.c2.403.d4.false5.O(N*logN),O(N2)6.a7.pivot8.d9.true10.c11.partitioning the resulting subarrays12.b13.pivot14.log2N15.trueQuestionsThese questions are intended as a self-test for readers.Answers may be found inAppendix C.1.Insertion and deletion in a tree require what big O time?2.A binary tree is a search tree ifa.every non-leaf node has children whose key values are less than(or equalto)the parent.b.every left child has a key less than the parent and every right child has akey greater than(or equal to)the parent.c.in the path from the root to every leaf node,the key of each node isgreater than(or equal to)the key of its parent.d.a node can have a maximum of two children.3.True or False:Not all trees are binary trees.4.In a complete binary tree with20nodes,and the root considered to be at level 0,how many nodes are there at level4?5.A subtree of a binary tree always hasa.a root that is a child of the main tree’s root.b.a root unconnected to the main tree’s root.c.fewer nodes than the main tree.d.a sibling with the same number of nodes.6.In the Java code for a tree,the______and the_______are generally separate classes.Questions4237.Finding a node in a binary search tree involves going from node to node, askinga.how big the node’s key is in relation to the search key.b.how big the node’s key is compared to its right or left children.c.what leaf node we want to reach.d.what level we are on.8.An unbalanced tree is onea.in which most of the keys have values greater than the average.b.whose behavior is unpredictable.c.in which the root or some other node has many more left children thanright children,or vice versa.d.that is shaped like an umbrella.9.Inserting a node starts with the same steps as_______a node.10.Suppose a node A has a successor node S.Then S must have a key that is larger than_____but smaller than or equal to_______.11.In a binary tree used to represent a mathematical expression,which of the following is not true?a.Both children of an operator node must be operands.b.Following a postorder traversal,no parentheses need to be added.c.Following an inorder traversal,parentheses must be added.d.In pre-order traversal a node is visited before either of its children.12.If a tree is represented by an array,the right child of a node at index n has an index of_______.13.True or False:Deleting a node with one child from a binary search tree involves finding that node’s successor.14.A Huffman tree is typically used to_______text.15.Which of the following is not true about a Huffman tree?a.The most frequently used characters always appear near the top of the tree.b.Normally,decoding a message involves repeatedly following a path fromthe root to a leaf.424CHAPTER8Binary Treesc.In coding a character you typically start at a leaf and work upward.d.The tree can be generated by removal and insertion operations on apriority queue.Chapter8,Binary TreesAnswers to Questions1.O(logN)2.b3.True4.55.c6.node,tree7.a8.cChapter8,Binary Trees7439.finding10.A,A’s left-child descendents11.d12.2*n+113.Falsepress15.cQuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.1.A2-3-4tree is so named because a node can havea.three children and four data items.b.two,three,or four children.c.two parents,three children,and four items.d.two parents,three items,and four children.2.A2-3-4tree is superior to a binary search tree in that it is________.3.Imagine a parent node with data items25,50,and75.If one of its child nodes had items with values60and70,it would be the child numbered__________.4.True or False:Data items are located exclusively in leaf nodes.514CHAPTER102-3-4Trees and External Storage5.Which of the following is not true each time a node is split?a.Exactly one new node is created.b.Exactly one new data item is added to the tree.c.One data item moves from the split node to its parent.d.One data item moves from the split node to its new sibling.6.A2-3-4tree increases its number of levels when________.7.Searching a2-3-4tree does not involvea.splitting nodes on the way down if necessary.b.picking the appropriate child to go to,based on data items in a node.c.ending up at a leaf node if the search key is not found.d.examining at least one data item in any node visited.8.After a non-root node of a2-3-4tree is split,does its new right child contain the item previously numbered0,1,or2?9.A4-node split in a2-3-4tree is equivalent to a_______in a red-black tree.10.Which of the following statements about a node-splitting operation in a2-3 tree(not a2-3-4tree)is not true?a.The parent of a split node must also be split if it is full.b.The smallest item in the node being split always stays in that node.c.When the parent is split,child2must always be disconnected from itsold parent and connected to the new parent.d.The splitting process starts at a leaf and works upward.11.What is the big O efficiency of a2-3tree?12.In accessing data on a disk drive,a.inserting data is slow but finding the place to write data is fast.b.moving data to make room for more data is fast because so many items can be accessed at once.c.deleting data is unusually fast.d.finding the place to write data is comparatively slow but a lot of data can be written quickly.13.In a B-tree each node contains_______data items.Questions51514.True or False:Node splits in a B-tree have similarities to node splits in a2-3 tree.15.In external storage,indexing means keeping a file ofa.keys and their corresponding blocks.b.records and their corresponding blocks.c.keys and their corresponding records.st names and their corresponding keys.Chapter9,Red-Black TreesAnswers to Questions1.in order(or inverse order)2.b3.False4.d5.b6.rotations,changing the colors of nodes7.red8.a9.left child,right child10.d11.a node,its two children12.b13.True14.a15.TrueQuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.574CHAPTER11Hash Tablesing big O notation,say how long it takes(ideally)to find an item in a hash table.2.A__________transforms a range of key values into a range of index values.3.Open addressing refers toa.keeping many of the cells in the array unoccupied.b.keeping an open mind about which address to use.c.probing at cell x+1,x+2,and so on until an empty cell is found.d.looking for another location in the array when the one you want is occupied.ing the next available position after an unsuccessful probe is called_____________.5.What are the first five step sizes in quadratic probing?6.Secondary clustering occurs becausea.many keys hash to the same location.b.the sequence of step lengths is always the same.c.too many items with the same key are inserted.d.the hash function is not perfect.7.Separate chaining involves the use of a_____________at each location.8.A reasonable load factor in separate chaining is________.9.True or False:A possible hash function for strings involves multiplying each character by an ever-increasing power.10.The best technique when the amount of data is not well known isa.linear probing.b.quadratic probing.c.double hashing.d.separate chaining.11.If digit folding is used in a hash function,the number of digits in each group should reflect_____________.12.True or False:In linear probing an unsuccessful search takes longer than a successful search.Questions57513.In separate chaining the time to insert a new itema.increases linearly with the load factor.b.is proportional to the number of items in the table.c.is proportional to the number of lists.d.is proportional to the percentage of full cells in the array.14.True or False:In external hashing,it’s important that the records don’t become full.15.In external hashing,all records with keys that hash to the same value are located in___________.Chapter11,Hash TablesAnswers to Questions1.O(1)2.hash function3.d4.linear probing5.1,4,9,16,256.b7.linked listChapter11,Hash Tables7458.1.09.True10.d11.the array size12.False13.a14.False15.the same blockQuestionsThese questions are intended as a self-test for readers.Answers may be found in Appendix C.1.What does the term complete mean when applied to binary trees?a.All the necessary data has been inserted.b.All the rows are filled with nodes,except possibly the bottom one.c.All existing nodes contain data.d.The node arrangement satisfies the heap condition.2.What does the term weakly ordered mean when applied to heaps?3.A node is always removed from the__________.4.To“trickle up”a node in a descending heap meansa.to repeatedly exchange it with its parent until it’s larger than its parent.b.to repeatedly exchange it with its child until it’s larger than its child.c.to repeatedly exchange it with its child until it’s smaller than its child.d.to repeatedly exchange it with its parent until it’s smaller than its parent.5.A heap can be represented by an array because a heap。

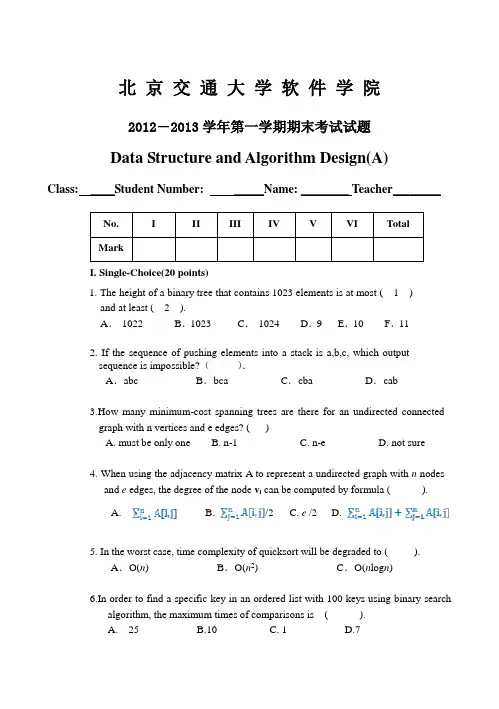
北京交通大学软件学院2012―2013学年第一学期期末考试试题Data Structure and Algorithm Design(A)Class: ____Student Number: _____Name: ________ Teacher________I. Single-Choice(20 points)1. The height of a binary tree that contains 1023 elements is at most ( 1 )and at least ( 2 ).A．1022 B．1023 C．1024 D．9 E．10 F．112. If the sequence of pushing elements into a stack is a,b,c, which outputsequence is impossible?（）．A．abc B．bca C．cba D．cab3.How many minimum-cost spanning trees are there for an undirected connectedgraph with n vertices and e edges? ( )A. must be only oneB. n-1C. n-eD. not sure4. When using the adjacency matrix A to represent a undirected graph with n nodesand e edges, the degree of the node v i can be computed by formula ( ).A. B. /2 C. e /2 D.5. In the worst case, time complexity of quicksort will be degraded to ( ).A．O(n) B．O(n2) C．O(n log n)6.In order to find a specific key in an ordered list with 100 keys using binary searchalgorithm, the maximum times of comparisons is ( ).A. 25B.10C. 1D.77. Consider the following pseudo-code, which indicates part of a standard binary treealgorithm.print( node ){ print data;if( there is a left child ) print( left child );if( there is a right child ) print( right child );}Which of the following is the standard name for this algorithm? ( )A. Inorder traversalB. Preorder traversalC. Postorder traversalD. Binary search8.Which is not the property of a B-tree of order m? ( )A. The root node has m subtree at mostB. All leaf nodes are at the same level.C. The keys in every node are ordered.D. All leaf nodes are connected by links.9. Suppose that we have 1000 distinct integers, which are in the range from 0 to 50. If using Radix Sort according to the Least Significant Digit first, ( ) buckets are needed to constructed.A. 10B. 50C. 51D. 1000II. Fill in the blank (2points * 5)that of___ _ traversal algorithm for a normal tree.2. Here is a hash table, whose size is 18, hashing function isH1(key)=key%17 (% here is the modulus operator), and which usesLinear Probing strategy to cope with the collisions and inserts 26, 25, 72,38, 8, 18, 59 into the hash table in turn. The address of 59 is _ _ _.3. Given a key sequence {2，5，⑤，3}, please write its ascending orderedsequence after being sorted using heap sort. (Note 5=⑤, just 5 is before⑤in original sequence) . Please distinguish 5 and ⑤.4. If a 2-dimensions matrix A[m][n] is stored in an 1-D array withrow-major mapping, then the address of element A[i][j] relative toA[0][0] is ___ ____5. If the in-order and pre-order series of the nodes in a binary tree are“1,2,3,4,5” and “1,2,3,4,5” respectively, the p ostorder sequence shouldbe __________.III. (40 points)1. (8 points) Suppose there is a string abcadececdcdeeeded that comprisesthe characters a, b, c, d and e. We may encode the symbols usingvariable-length codes in order to make the length of string the shortest.Please draw the Huffman tree used to encode the characters, calculatethe weighted path length for the Huffman tree and write the code foreach character.(1)Draw the Huffman tree (3 points)a:2, b:1, c:4, d:5 , e: 6(3 points)(2)Calculate the weighted path length for the Huffman tree (2 points)WPL(T)= 6⨯2+5⨯2+2⨯3+1⨯3+4⨯2 =39(3)write the code for each character. (3 points) 错一个扣一分，扣光为止2. (8 points) Please respectively give two unsorted lists whose length are 4to illustrate that quick sort and selection sort are unstable.(1) An example list for quick sort and the sorting procedure using quicksort. (4 points)（4, 2, ②, 3）-------------------------- (2 points)sorting procedureThe first pass: 3,2,②,4 -------------------------（1point）The second pass: ②,2,3,4 -----------------------（1point）(2) An example list for selection sort and the sorting procedure usingselection sort. (4 points)（2，②，3，1）-------------------------- (1 points)sorting procedureThe first pass: 1,②, 3 , 2------------------------（1point）The second pass: 1,②, 3 , 2----------------------（1point）The third pass: 1,②, 2, 3 ----------------------（1point）3. (8 points) Given the key sequence (331, 166, 367, 236, 268, 137, 337,138), Please give the procedure (distributing and collecting) of sortingusing radix sort method. not necessary to write queue front and rearpointer if queue is null.(1) The first pass (3 points)(2) The second pass (3 points)(3)The third pass (2 points)4.（6 points）There are n1 nodes of degree 1，n2 nodes of degree 2，…，n m nodes of degree m in a tree of degree m，how many leaf nodes there are in the tree? Please give formula and prove your conclusion.Answer：because every node except root has one branch linked, so total nodes are equal to total branches plus one, there are n branches in node of degree n （2points）formula such as （2points）（2points）5. (10 points) Show the result of inserting { 63, 37, 48, 100, 54, 64, 27, 108, 99,42 } into(a) an empty binary search tree（2 points）(b) an initially empty A VL tree（4 points）(c) an initially empty B-tree of order 3（4 points）Answer：(1)（2）A VL （4 points）(3) B-tree （4points）IV. (10 points) Please fill in the blanks in the program which reverses a singly linked list. For example, {1,2,3,4,5,6,7,8,9,10} will become {10,9,8,7,6,5,4,3,2,1} after being reversed.#define list_init_size 100#define n 10#define len sizeof(struct node)typedef struct node{ int num; struct node *next; } lnode,*link;link llist;static int a[]={1,2,3,4,5,6,7,8,9,10};void creat(link *list)//create a singly linked list for key sequence stored in array a[]{ int i=0;lnode *p,*q;q=(struct node*)malloc(len);q->num=a[i]; *list=q;while (i<n-1){ p=(struct node*)malloc(len);i=i+1; （1）;（2）; q=p;}p->next=0;}void reverseList(link *h) // reverse the singly linked list{ lnode *p,*q, *r;p=*h; r=0;while (p){q=p; (3) ;(4) ; r = q;}(5) ;}main(){lnode *l;creat(&l); reverseList(&l);}Answer:(1) __ p->num=a[i];____(2) __ q->next=p;_______(3) __ p=p->next;_________(4) __ q->next =r;________(5) _ _*h=q;_________V.（10 points）Please read the following code, write the functions of programs and write output of the program.#include<stdio.h>#include "malloc.h"#define n 6static char ch[n]={'a','b','c','d','e','f'};static int a[n][n]={0,1,1,0,0,0, 1,0,0,1,1,0, 1,0,0,1,0,1, 0,1,1,0,0,1,0,1,0,0,0,1, 0,0,1,1,1,0};typedef struct node /*邻接表中的边结点*/{ int adjvex; struct node *next; } EdgeNode;typedef struct vnode /*邻接表中的顶点结点*/{ char vertex; EdgeNode *firstedge; } VertexNode[n];typedef struct{ int front,rear; int data[n]; } CirQueue;CirQueue *Q;int path[n],sum=0; int visited[n]; VertexNode G;void createALGraph() /*根据邻接矩阵，建无向网的邻接表表示*/ {int i,j; EdgeNode *s;for(i=0; i<n; i++){ G[i].vertex=ch[i]; G[i].firstedge=0; }for(i=0; i<n; i++){ for(j=0; j<n; j++){ if (a[i][j]==1){ s=(EdgeNode*)malloc(sizeof(EdgeNode));s->adjvex=j; s->next=G[i].firstedge;G[i].firstedge=s;}}}}void print(){ int i; EdgeNode *s;for (i=0; i<n; i++){ s=G[i].firstedge;printf(" %c : ",G[i].vertex);while(s){ printf(" %c",G[s->adjvex].vertex);s=s->next;}printf("\n");}}int ShortestPath(int u,int v)/* 求u和v之间经过的分支数最少的路径*/ { int k,pre[n],spath[n],count=0,found=0;EdgeNode * p;if(u==v) { printf("error\n"); return 0;}Q=(CirQueue*)malloc(sizeof(CirQueue));Q->front=Q->rear=0;for(k=0;k<n;k++) { visited[k]=0; pre[k]=-1;}visited[u]=1; Q->data[Q->rear++]=u;while(!found && Q->front!=Q->rear){ k=Q->data[Q->front++];p=G[k].firstedge;while(p && !found){ if(visited[p->adjvex]==0){ pre[p->adjvex]=k;if(p->adjvex==v) {found=1; break;}visited[p->adjvex]=1;Q->data[Q->rear++]=p->adjvex;}p=p->next;}}if(found){ printf("found: ");spath[count++]=v; k=pre[v];while(k!=u) {spath[count++]=k; k=pre[k];}spath[count]=u;for(k=count;k>=0;k--) printf("%d ", spath[k]);printf("\n"); return 1;}else{printf("There is no path\n"); return 0;}}main(){ int i,j;createALGraph(); print();for(i=0;i<n;i++) { visited[i]=0; path[i]=-1;} printf("\n");printf("The shotest path is "); i=ShortestPath(0,3);}Answer:（1）function of createALGraphCreate linked adjacency list based on adjacency matrix --------------------------------------- (2 points)（2）function of the whole programFind the shortest path which includes the minimum number of branches among all paths from u to v. ---------------------- (3 points)（3）output of the program. ------------------------------- (1+4=5 points)VI. (10 points) Please describe the children-sibling link of a tree in C Language. Write a function to calculate the depth of a normal tree. (10 points)Answer：Typedef struct CSNode （2分）{ char data;struct CSNode *fch, *nsib;} CSNode, *CSTree;int TreeDepth(CSTree T){ if(!T) return 0; （2分）else { h1 = TreeDepth( T->fch ); （2分）h2 = TreeDepth( T->nsib); （2分）if(h1+1> h2) return(h1+1)else return(h2); （2分）}}。

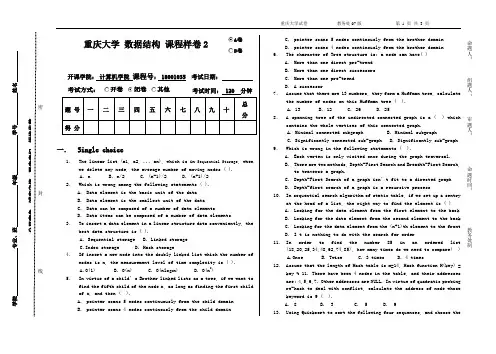
重庆大学 数据结构 课程样卷2开课学院： 计算机学院 课程号： 18001035 考试日期：考试方式：考试时间： 120 分钟一． Single choice1． The linear list (a1, a2, ... an), which is in Sequential Storage , whenwe delete any node, the average number of moving nodes ( ). A. n B. n/2 C. (n-1)/2 D. (n+1)/2 2． Which is wrong among the following statements ( ).A. Data element is the basic unit of the dataB. Data element is the smallest unit of the dataC. Data can be composed of a number of data elementsD. Data items can be composed of a number of data elements3． To insert a data element in a linear structure data conveniently, thebest data structure is ( ).A. Sequential storageB. Linked storageC.Index storageD. Hash storage4． If insert a new node into the doubly linked list which the number ofnodes is n, the measurement level of time complexity is ( ).A.O(1)B. O(n)C. O(nlog 2n)D. O(n 2)5． In virtue of a child’s Brother linked lists as a tree, if we want tofind the fifth child of the node x, as long as finding the first child of x, and then ( ).A. pointer scans 5 nodes continuously from the child domainB. pointer scans 4 nodes continously from the child domainC. pointer scans 5 nodes continously from the brother domainD. pointer scans 4 nodes continously from the brother domain 6． The character of Tree structure is: a node can have( )A. More than one direct pre-trendB. More than one direct successorsC. More than one pre-trendD. A successor7． Assume that there are 13 numbers, they form a Huffman tree, calculatethe number of nodes on this Huffman tree ( ). A. 13 B. 12 C. 26 D. 258． A spanning tree of the undirected connected graph is a ( ) whichcontains the whole vertices of this connected graph.A. Minimal connected subgraphB. Minimal subgraphC. Significantly connected sub-graphD. Significantly sub-graph 9． Which is wrong in the following statements ( ).A. Each vertex is only visited once during the graph traversal.B. There are two methods, Depth-First Search and Breadth-First Search,to traverse a graph.C. Depth-First Search of a graph isn ’t fit to a directed graphD. Depth-first search of a graph is a recursive process10． In sequential search algorithm of static table, if we set up a sentryat the head of a list, the right way to find the element is ( ) A. Looking for the data element from the first element to the back B. Looking for the data element from the second element to the back C. Looking for the data element from the (n+1)th element to the front D. I t is nothing to do with the search for order11． In order to find the number 85 in an ordered list(18,20,25,34,48,62,74,85), how many times do we need to compare( ) A.Once B. Twice C. 3 times D. 4 times12． Assume that the length of Hash table is m=14, Hash function H(key) =key % 11. There have been 4 nodes in the table, and their addresses are: 4,5,6,7. Other addresses are NULL. In virtue of quadratic probing re-hash to deal with conflict, calculate the address of node whose keyword is 9 ( ).A. 8B. 3C. 5D. 913． Using Quicksort to sort the following four sequences, and choose the命题人：组题人：审题人：命题时间：教务处制学院 专业、班 年级 学号 姓名公平竞争、诚实守信、严肃考纪、拒绝作弊封线密first element as the benchmark to divide. During the first division,in the following sequences which need to move the most times ( )A.70,75,82,90,23,16,10,68B.70,75,68,23,10,16,90,82C.82,75,70,16,10,90,68,23D.23,10,16,70,82,75,68,9014．There are 10000 elements in a sequence, the best way to get the very smallest 10 elements in the sequence is ( ).A. QuicksortB. HeapsortC. Insertion sortD. Merge sort15．If the sequence is almost in order, take compare times of key code and move times of key code into account, the best way to sort is( )A. Merge sortB. Insertion sortC. Straight selection sortD.Quicksort二．Fill the blanks1．In order to insert a new node s after the node which pointer q points to in a circular doubly linked list, we need to execute the followingstatements:s->prior=q; s->next=q->next; _____________________;q->next=s;2．In the doubly linked list, if d is a pointer points to a node in the list, then:d->next->__________=d->prior->__________=__________;3．Stack can be considered as an operation restricted linked list ,one end that can insert and remove is called _____________。

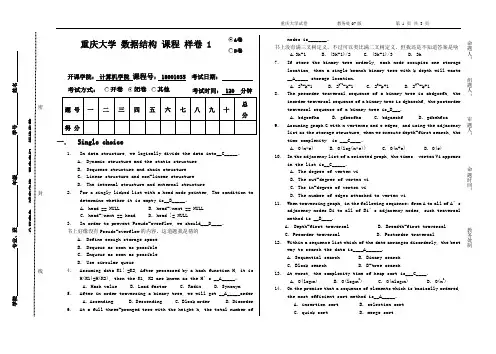
重庆大学 数据结构 课程 样卷1开课学院： 计算机学院 课程号： 18001035 考试日期：考试方式：考试时间： 120 分钟一． Single choice1． In data structure, we logically divide the data into__C_____。

A. Dynamic structure and the static structureB. Sequence structure and chain structureC. Linear structure and non-linear structureD. The internal structure and external structure2． For a singly linked list with a head node pointer, The condition todetermine whether it is empty is__B_____。

A. head == NULLB. head->next == NULLC. head->next == headD. head != NULL3． In order to prevent Pseudo-overflow, we should___D____。

书上好像没有Pseudo-overflow 的内容，这道题我是猜的A. Define enough storage spaceB. Dequeue as soon as possibleC. Enqueue as soon as possibleD. Use circular queue4． Assuming data K1! =K2, After processed by a hash function H, it isH(K1)=H(K2), then the K1, K2 are known as the H’s __A_____。

华东师范大学期中试卷20XX—20xx学年第二学期课程名称：______数据结构_____姓名：___________________ 学号：__________________专业：___________________ 年级/班级：__________________课程性质：专业必修一、单项选择题(共21分，每题3分)1. Stack has the property called last in and first out, then which of the following describes the property of Queue?a) Last in and first outb) First in and last outc) First in and first out2. A list of items from which only the item most recently added can be removed is known as a ( )a) stackb) queuec) circular linked listd) list3. If the following function is called with a value of 2 for n, what is the resultingoutput?void Quiz( int n ){if (n > 0){cout << 0;Quiz(n - 1);cout << 1;Quiz(n - 1);}}a) 00011011b) 11100100c) 10011100d) 01100011e) 0011014. What is the value of the postfix expression ?6?5 * ?4 ?3 ?2 + ?1 - / +a) 19b) 31c) 36d) 635. Given the recursive functionint Func( /* in */ int i,/* in */ int j ){if (i < 11)if (j < 11)return i + j;elsereturn j + Func(i, j - 2);elsereturn i + Func(i - 1, j);}what is the value of the expression Func(12, 15) ?a) 81b) 62c) 19d) 72e) none of the above6. Which one of the following list can use binary search?a) A C E B Db) A B C D Ec) B D A C Fd) E C A B D7. Retrieval from a linked list of length n has running time ( )a) O(1)b) O(lgn)c) O(n)d) O(nlgn)二、填空题（共16分，每空2分）1. If the following function is called with a value of 75 for n, the resulting output is_______【1】_________.void Func( /* in */ int n ){if (n > 0){Func(n / 8);cout << n % 8;}}2. Give the output of the following program. ________【2】__________.template <class List_entry>void print(List_entry &x){cout<<x<<" ";}void main( ){List<int> mylist;for(int i=0;i<5;i++)mylist.insert(i,i);cout<<"Your list have "<<mylist.size()<<" elements:"<<endl;mylist.remove(0,i);mylist.remove(2,i);mylist.insert(i,i);mylist.traverse(print);mylist.clear( );for(i=1;i<3;i++)mylist.insert(i, i);mylist.traverse(print);}3. Read the following program and fill the blank to complete the method.template <class Node_entry>struct Node {// data membersNode_entry entry;Node<Node_entry> *next;Node<Node_entry> *back;// constructorsNode( );Node(Node_entry item, Node<Node_entry> *link_back = NULL, Node<Node_entry>*link_next = NULL);};template <class List_entry>void List<List_entry> :: set_position(int position) const/* Pre: position is a valid position in the List : 0 <=position < count .Post: The current Node pointer references the Node at position . */{if (current_position <= position)for ( ; current_position != position; current_position++)【3】;elsefor ( ; current_position != position; 【4】)current = current->back;}4. Read the following program and fill the blank to complete the method.Error_code recursive_binary_2(const Ordered_list &the_list, const Key &target, int bottom, inttop, int &position)/* Pre: The indices bottom to top define the range in the list to search for the target .Post: If a Record in the range from bottom to top in the list has key equal totarget , then position locates one such entry, and a code of success is returned. Otherwise,not_present is returned, and position is undefined.Uses: recursive_binary_2, together with methods from the classes Ordered_list and Record .*/{Record data;if (bottom <= top) {int mid = 【5】;the_list.retrieve (mid, data);if (data == target) {【6】;return success;}else if (data < target)return recursive_binary_2(the_list, target, 【7】, top, position);elsereturn recursive_binary_2(the_list, target, bottom, 【8】, position);}else return not_present;}三、编程题（共63分）1.（14分）The size of array A is n.If the original array A is (e0, e1, …, e n-2, e n-1).After calling the function inverse, the array A is (e n-1, e n-2, …, e1, e0).Implement the function template:Template <class Type> void inverse( Type A[ ], int n);2.(10分)Write function remove for the implementation of doubly linked list that uses the set_position function.Error_code List<List_entry> :: remove(int position, List_entry &x)3.（16分）Write the following overload operator for stacks:1)bool Stack::operator == (const Stack & s);（8分）2)bool Stack::operator += (const Stack & s);（8分）// pushes the contents of the given stack onto this stack;4.（10分）Write the following function temple:Template <class T> void reverse(Queue <T> & q);// reverses the contents of the given queue;5.（13分）Ackermann’s function is defined as follows,A(0, n) = n+1 for n≥0A(m, 0) = A(m-1, 1) for m>0A(m, n) = A(m-1, A(m, n-1)) for m>0 and n>01)Write a recursive function to calculate Ackermann’s function. (6分)2)Draw the recursion tree of A(2, 1). (7分)数据结构期中考卷参考答案一、单项选择题(3×7＝21)1． c2． a3． e4． b5． a6． b7． c二、填空题(2×8＝16)【1】113【2】Your list have 5 elements:1 2 4 3【3】current = current->next【4】current_position--【5】(bottom + top)/2【6】position = mid【7】mid + 1【8】mid – 1三、编程题(14+16+10+23=63)1.template<class Type> void inverse ( Type A[ ], int n ) {Type tmp;for ( int i = 0; i <= ( n-1 ) / 2; i++ ){tmp = A[i]; A[i] = A[n-i-1]; A[n-i-1] = tmp;}}2.Error_code List<List_entry> :: remove(int position, List_entry &x) {if (position < 0 || position >= count)return range_error;Node<List_entry> *previous, *following;if (position > 0) {set_position(position - 1);previous = current;following = previous->next;previous->next=following->next;if(following->next)following->next->back=previous;}else{following = head;head = head->next;if(head)head->back=NULL;//should be addedcurrent_position = 0;current = head;}delete following;count--;return success;}3.1)bool Stack::operator==(const Stack &s){Stack s1=s, s2=*this;while (!s1.empty( ))if (s1.top( )!= s2.top( )) return false;else { s1.pop( ); s2.pop( );}}2)bool Stack:: operator+=(const Stack &s){Stack ss=s, s2;while (!ss.empty( )){s2.push(ss.top( ));ss.top( );}while (!s2.empty( )){push(s2.top( ));s2.pop( );}}4．Template <class T> void reverse (Queue<T> & q){Stack<T> s ; T data;while ( !q.empty( )){ q.retrieve(data );s.push( data);q.serve( );}while (!s.empty( )){q.append(s.top( ));s.pop( );}}5.1) int akm ( int m, int n ) {if ( m == 0 ) return n+1; // m == 0else if ( n == 0 ) return akm ( m-1, 1 ); // m > 0, n == 0else return akm ( m-1, akm ( m, n-1 ) ); // m > 0, n > 0 }2)v = 2。

2003 Data Structure Test (120 minutes) Class: Student Number: Name:1.Single-Choice(20 points)(1) The Linked List is designed for conveniently b data item.a. gettingb. insertingc. findingd.locating(2) Assume a sequence list as 1,2,3,4,5,6 passes a stack, an impossible output sequence listIs c .a. 2,4,3,5,1,6b.3,2,5,6,4,1c.1,5,4,6,2,3d.4,5,3,6,2,1(3) A queue is a structure not implementing b .a. first-in/first-outb. first-in/last-outc. last-in/last-outd. first-come/first-serve(4) Removing the data item at index i from a sequential list with n items, d items needto be shifted left one position.a. n-ib. n-i+1c. id. n-i-1(5) There is an algorithm with inserting an item to a ordered SeqList and still keeping theSeqList ordered. The computational efficiency of this inserting algorithm is c .a. O(log2n)b. O(1)c. O(n)d.(n2)(6) The addresses which store Linked List d .a. must be sequentialb. must be partly sequentialc. must be no sequentiald. can be sequential or discontiguous(7) According the definition of Binary Tree, there will be b different Binary Treeswith 5 nodes.a. 6b. 5c. 4d. 3(8) In the following 4 Binary Trees, c is not the complete Binary Tree.a b c d(9) A Binary Tree will have a nodes on its level i at most.a.2ib. 2ic.2i+1d.2i-1(10) If the Binary Tree T2 is transformed from the Tree T1, then the postorder of T1 is theb of T2.a. preorderb. inorderc. postorderd. level order(11) In the following sorting algorithm, c is an unstable algorithm.a. the insertion sortb. the bubble sortc. quicksortd. mergesort(12) Assume there is a ordered list consisting of 100 data items, using binary search to find aspecial item, the maximum comparisons is d .a. 25b.1c. 10d.7(13) The result from scanning a Binary Search Tree in inorder traversal is in c order.a. descending or ascendingb. descendingc. ascendingd. out of order(14) The d case is worst for quicksort.a. the data which will be sorted is too larger.b. there are many same item in the data which will be sorted .c. the data will be sorted is out of orderd. the data will be sorted is already in a sequential order.(15) In a Binary Tree with n nodes, there is a non-empty pointers.a. n-1b. n+1c. 2n-1d.2n+1(16) In a undirected graph with n vertexs, the maximum edges is b .a. n(n+1)/2b. n(n-1)/2c. n(n-1)d.n2(17) The priority queue is a structure implementing c .a. inserting item only at the rear of the priority queue.b. inserting item only at the front of the priority queue.c. deleting item according to the priority of the item.d. first in/first out(18) The output from scanning a minimum heap with level traversal algorithm c .a. must be an ascending sequence.b. must be descending sequencec. must have a minimum item at the head position.d. must have a minimum item at the rear position.(19) Assume the preorder of T is ABEGFCDH, the inorder of T is EGBFADHC, then thepostorder of T will be a .a. GEFBHDCAb. EGFBDHCAc. GEFBDHCAd. GEBFDHCA(20) When a recursive algorithm is transformed into a no recursive algorithm, a structureb is generally used.a. SeqListb. Stackc. Queued. Binary Tree2. Please convert the following infix expression (a*(b+c))+(b/d-e)*a into postfix expression,in the converting process, please draw the change of operator stack and the change of the output. (10 points)3. Assume a list is {xal, wan, wil, zol, yo, xul, yum, wen, wim, zi, xem, zom}, please insert these items to an empty Binary Search Tree and then construct the AVL tree. Please draw the whole processes including inserting an item, or rotate nodes to restore height balance.(10 points)4. Assume a list is {48,35,64,92,77,13, 29,44}, firstly insert these items to an empty complete Binary Tree according to the sequence one by one, then please heapify the complete Binary Tree and implement the heap sort. Please draw the whole heapigying process and sorting process. (10 points)5. For the following directed graph, give the adjacency matrix and adjacency list. Then according your adjacency list, please scan the graph using the depth-first search and the breadth-first search and give the corresponding result. (10 points)6. Assume a list is 35,25,47,13,66,41,22,57, please sorting the list with quicksort algorithm. Please write every sorting pass result (no programming).(10 points)7. Assume keys={32,13,49,55,22,39,20}, Hash function is h(key)=key%7. The linear probe open addressing is used to resolve collisions. Please try to calculate the value of Hash for each key and give the final hash table. (10 points)8. Programming (All methods have been declared in textbook can be used directly, or you can rewrite them if they are not same in your answer) (20 points)(1) Assume there are two ascending ordered lists L1 and L2, please merge L1 and L2 into a new list L3. There will be no duplicate items in L3. Then please reverse the L3 into a descending ordered list.(10 points)(2) Please give the complete declaration of Queue in circle model, then write the insert algorithm and delete algorithm. (10 points)。

重庆大学 《数据结构》 课程样卷 3开课学院： 计算机学院 课程号： 18001035 考试日期：考试方式：考试时间： 120 分钟一、 Single choice1． Merge two ordered list, both of them contain n elements, the least timesof comparison is ( ).A. nB. 2n-1C. 2nD. n-12． Sequential stored linear list with the length of 1000, if we insertan element into any position, the possibility is equal, when we insert a new element, the average number of removing elements is ( ). A. 1000 B. 1001 C. 500 D. 4993． Assume that the initial status of stack S and queue Q are both NULL,push elements e1,e2,e3,e4,e5,e6 into the stack S one by one, an element pops from stack, then enter into queue Q. If the sequence which the six elements in the dequeue is e2,e4,e6,e5,e3,e1, the capacity of stack S is at least ( ).A. 6B. 4C. 3D. 24． Two-dimensional array A [10 .. 20,5 .. 10] stores in line sequence,each element occupies 4 storage location, and the memory address of A[10,5] is 1000, then the address of A[20,9] is ( ). A. 1212 B. 1256 C. 1368 D. 13645． A tree with degree 3, it has 2 nodes with the degree 3, one node withthe degree 2, and 2 nodes with the degree 1, so the number of nodes with degree 0 is ( ).A. 4.B. 5.C. 6.D. 76． The inorder sequence of a binary tree is ABCDEFG, and its postordersequence is BDCAFGE, so its pre-order sequence is ( ) A. EGFACDB B. EACBDGF C. EAGCFBD D. EGAFCDB7． A Huffman tree with n leaf nodes, its total number of nodes is ( )A. n-1B. n+1C. 2n-1D. 2n+18． In an adjacency list of undirected graph with n vertexes and e edges,the number of edge node is ( ).A. nB. neC. eD. 2e9． The degree (sum of in-degree and out-degree) of a directed graph isk1, and the number of out-degree is k2. Therefore, in its adjacency list, the number of edge nodes in this singly linked list is ( ). A. k1 B. k2 C. k1-k2 D. k1+k210． If the graph has n vertexes is a circle, so it has ( ) spanning tree.A. nB. 2nC. n-1D.n+111． When look up a sequential list with the length 3, the possibility thatwe find the first element is 1/2, and the possibility that we find the second element is 1/3, the possibility that we find the third element is 1/6, so the average searching length to search any element (find it successfully and the sentry is at the end of the list) is ( ) A. 5/3 B.2 C. 7/3 D.4/312． There is an ordered list {3,5,7,8,11,15,17,22,23,27,29,33}, by binarysearch to search 27, so the number of comparison is ( ) A. 2 B. 3 C. 4 D. 513． Sort the following keyword sequences by using Quicksort, and theslowest one is ( )A. 19,23,3,15,7,21,28B. 23,21,28,15,19,3,7C. 19,7,15,28,23,21,3D. 3,7,15,19,21,23,28 14． Heapsort needs additional storage complexity is ( )A. O(n)B. O(nlog 2n)C. O(n 2) D. O(1)15． If we sort an array within the time complexity of O(nlog2n), needingsort it stably, the way that we can choose is ( )A. Merge sortB. Direct insertion sortC. Heap sortD. Quicksort二、 Fill the blanks1.Assume that the structure of the nodes in doubly circular linked list is (data,llink,rlink), without a head node in the list, if we want命题人：组题人：审题人：命题时间： 教务处制学院 专业、班 年级 学号 姓名公平竞争、诚实守信、严肃考纪、拒绝作弊封线密to insert the node which pointer s points after the node pointer ppoints, then execute as the following statements:; ; ___ _; ;2.Both stack and queue are _______linear structure.3.The four leaf nodes with the weight 9,2,5,7 form a Huffman tree, itsweighted path length is ________.4.In order to ensure that an undirected graph with six vertexes isconnected, need at least ______ edges.5.An n-vertex directed graph, if the sum of all vertices’ out-degreeis s, then the sum of all vertices’ degree is__ ___.6.The Depth-First traversal of a graph is similar to the binarytree_______ traversal; the Breadth-first graph traversal algorithmis similar to the binary tree ______traversal.7. A connected graph with n vertexes and e edges has ____ edges of itsspanning tree.8.The time complexity of binary searching is _____; if there are 100elements, the maximum number of comparisons by binary searching is____.9.Sort n elements by merge sort, the requiring auxiliary space is _____.10.Sort a linear list with 8 elements by Quicksort, at the best, thecomparison time is ______.三、 Application1. Begin from the vertex A, seek the minimum spanning tree by using Primalgorithms2. The following is AOE network:(1) How much time does it take to complete the whole project?(2) Find out all of the critical path.(9 points)3. Assume that a set of keywords is {1，12，5，8，3，10，7，13，97},tryto complete the following questions:(9 points)(1) Choose the keywords in sequence to build a binary sort tree Bt;(2) Draw the structure of the tree after deleting node “12”from thebinary tree Bt.4. The keyword sequence is {503,87,512,61,908,170,897,275,653,462}, usingradix sorting method to sort them in ascending order, try to write every trip results of sort. （9 points）四、 Algorithm1.The following algorithm execute on a singly linked list without headnode, try to analyze and write its function.(5 points)void function(LinkNode *head){LinkNode *p,*q,*r;p=head;q=p->next;while(q!=NULL){r=q->next;q->next=p;p=q;q=r;}head->next=NULL;head=p;}2.Design an algorithm to divide a singly linked list ‘A’ with a headpointer ‘a’ into two singly linked list ‘A’ and ‘B’, whose head pointers are ‘a’and ‘b’, respectively. On the condition that linked list A has all elements of odd serial number in the previous linked listA and linked listB has all elements of even serial number in the previouslinked list A, in addition, the relative order of the original linked list are maintained.(7 points)3. The type of binary tree is defined as follows:typedef struct BiTNode {char data;struct BiTNode *lchild,*rchild;}BiTNode, *BiTree;Please design an algorithm to count how many leaf nodes the binary tree have. （8 points）。

I Single Choice(10 points)1. ( )For the following program fragment the running time(Big-Oh) is .i = 0;s = 0;while(s <( 5*n*n + 2)){ i++;s = s + i;}a. O(n)b. O(n2)c. O(n1/2)d. O(n3)2. ( )Which is non-linear data structure_____.a. queueb.stackc. treed. sequence list3.( )The worst-time for removing an element from a sequence list (Big-Oh) is .a. O(1)b. O(n)c. O(n2)d. O(n3)4.( )In a circular queue we can distinguish(区分) empty queues from full queues by .a. using a gap in the arrayb. incrementing queue positions by 2 instead of 1c.keeping a count of the number of elementsd. a and c5.( )A recursive function can cause an infinite sequence of function calls if .a.the problem size is halved at each stepb.the termination condition is missingc.no useful incremental computation is done in each stepd.the problem size is positive6．( )The full binary tree with height 4 has nodes.a. 15b. 16c.31d.327. ( )Searching in an unsorted list can be made faster by using .a.binary searchb. a sentinel（哨兵）at the end of the listc.linked list to store the elementsd. a and c8.（）Suppose there are 3 edges in an undirected graph G, If we represent graph G with a adjacency matrix, How many “1”s are there in the matrix?a. 3b. 6c. 1d. 99. ( ) Construct a Huffman tree by four leaf whose weights are 9, 2, 5, 7 respectively. The weighted path length is___________.a. 29b. 37c. 46d.4410. Consider the following weighted graph.Consider Dijkstra’s algorithm on this graph to find the shortest paths with s as a starting vertex. Which are the first four vertices extracted from the priority queue by the algorithm (listed in the order they are extracted) ?a. s, y, t, xb. s, y, x, zc. s, t, y, xd. s, y, x, tFig. 111. Here is an array of ten integers:5 3 8 9 1 7 0 26 4Suppose we partition this array using quicksort's partition function and using 5 for the pivot. Which shows the array after partition finishes:a. 5 3 4 2 1 0 7 9 6 8b. 0 3 4 2 1 5 7 9 6 8c. 3 1 0 2 4 5 8 9 6 7d. 3 1 0 2 4 5 8 9 7 6e. None of the aboveII Fill in Blank (10 points)1. For the following program fragment the running time(Big-Oh) is .for ( int i = 0; i < n; i++ )for ( int j = 0; j < =i; j++)s; //s为某种基本操作2. We store a 4×4 symmetric matrix A into an array B with row major order, Store the lower triangle only. the index of element a[2][3] in B is .3．We can use 3 vector type to store value and of non-zero elements in a sparse matrix.4. A______________ is a list where removal and addition occur at the same end . Frequently knowna LIFO (Last-In-First-Out) structure.5.T( n ) = 2T( n/2 )+ cn, T(n) = T( n-1)+cn, T( n ) = O(___________)6. There is a binary tree whose elements are characters. Preorder list of the binary tree is “ABECDFGHIJ” and inorder list of the binary tree is “EBCDAFHIGJ”. Postorder traversal sequence of the binary tree is .7．There are leaf nodes in a full binary tree with n nodes.8．When the input has been sorted ,the running time of insertion sort(Big-Oh) is .9．We sort the sequence（43，02，80，48，26，57，15，73，21，24，66）with shell sort for increment 3, the result is ______ _ .10、In a circular queue, “front” and “rear” are the front pointer and rear pointer respectively. Queue size is “maxsize”. When insert an element in the queue, rear = _________11. A ____________________________________________ is an example of a search tree which is multiway (allows more than two children).12. A tree in which every node is no smaller than its children is termed______________________.III Application of Algorithms（35 points）1.Graph G shown in Fig 2 is a directed graph, please describe G with adjacency matrix and write the orders of breadth first traversal and depth first traversal.Fig.22．The sequence of input keys is shown below:19，1，23，14，55，20，84，27，68，11，10，17A fixed table size of 19 and a hash function H(key)=key%13，with linear probing(线性探测), fill the table below and compute the average length of successful search.3. Show the results of inserting 53,17,78,09,45,65,87 each , one at a time, in a initially empty max heap（大根堆）4. write the sequence of preorder,postorder traversals and add inorder threads in the tree.Fig. 35. Build a Huffman tree and determine Huffman code when the probability distribution(概率分布) over the 8 alphabets ( c1, c2, c3, c4, c5, c6, c7, c8 ) is (0.05, 0.25, 0.03, 0.06, 0.10, 0.11, 0.36, 0.046. Graph G shown in Fig 4 is a directed graph, please describe G with adjacency list and write topological ordering.Fig. 4IV Fill in blank of algorithms.（15）1．Here is single source shortest path algorithm Dijkstra. Fill in blank of the algorithm.class Graph {//图的类定义private:float Edge[NumVertices][NumVertices];float dist[NumVertices];//最短路径长度数组int path[NumVertices];//最短路径数组int S[NumVertices];//最短路径顶点集public:void ShortestPath ( int, int );int choose ( int );};void Graph :: ShortestPath ( int n, int v ){//在具有n 个顶点的带权有向图中, 各边上权值由Edge[i][j]给出。

ONE. Single-Choice1．In the following data structure, ( ) is linear structure.A．Forest B．StackC．Graph D．Binary Tree2．The Linked List is designed for conveniently ( ) data item.A．getting B．insertingC．finding D．locating3．In the four choices, ( ) is not the principles that algorithm designing must obey.A．Correctness(正确性) B．Readability(可读性)C．Robustness(健壮性) D．Cyclicity(周期性)4．Assume a sequence list as 6，5，4，3，2，1 is pushed in a stack, an impossible output sequence list is ( ).A．3，4，6，5，2，1 B．4，5，3，1，2，6C．5，4，3，6，1，2 D．2，3，4，1，5，65．A stack is a structure that follows the principle of ( ).A．First-In/First-Out B．Lirst-In/Last-OutC．Last-In/First-Out D．Random In and Out6．Removing the data item at index i in an array with n items, ( ) items need to be shifted(移动) left one position.A．n-i B．n-i+1C．i D．n-i-17．There is an algorithm with inserting an item to a ordered SeqList(顺序链表) and still keeping the SeqList ordered. The computational efficiency of this inserting algorithm is ( ).A．O(log2n) B．O(1)C．O(n) D．O(n2)8．The addresses which store Linked List ( ).A．must be sequential B．must be partly sequentialC．must be no sequential D．can be sequential or discontinuous 9．According to the definition of Binary Tree, there will be ( ) different Binary Trees with 3 nodes.A．6 B．5C．4 D．310．The depth of a Binary Tree is 5, it will have ( ) nodes at most.A．31 B．32C．16 D．1011．In the following sorting algorithm, ( ) is an unstable algorithm.A．the insertion sort(插入排序) B．the bubble sort(气泡法排序)C．quicksort(快速排序) D．mergesort(归并排序)12．Assume that there is an ordered list consisting of 100 data items, using binary search(二分法查找) to find a special item, the maximum comparisons is ( ).A．25 B．1C．10 D．713．The result from scanning a Binary Search Tree (二叉排序树) in inorder traversal is in ( ) order.A．descending or ascending B．descendingC．ascending D．out of order14．To connect n vertices in an undirected graph, it needs ( ) edges at least.A．n B．n-1C．n+1 D．115．In a directed graph with n vertexes, the maximum edges is ( ).A．n(n+1)/2 B．n(n-1)/2C．n(n-1) D．n216．The output from scanning a minimum heap(小顶堆) with level traversal algorithm ( ).A．must be an ascending sequence.B．must be descending sequence.C．must have a minimum item at the head position.D．must have a minimum item at the rear position.17．When a recursive algorithm (递归算法) is transformed into a no recursive algorithm, a structure ( ) is generally used.A．SeqList B．StackC．Queue D．Binary Tree18．A algorithm is referred to ( ).A．a calculating methodB．a sorting methodC．a sequential set of instructions to solve a problemD．a searching method19．A circular queue(循环队列) is full if ( ).A．(rear+1)% Maxsize == front B．front == rearC．rear+1 == front D．(rear-1)% Maxsize == front20．The difference between static sorting table(静态查找表) and dynamic sorting table(动态查找表) is ( ).A．the difference in logical structureB．the difference in storage structureC．the difference of data typeD．insertion and deletion only can be done in dynamic sorting tableTWO．Blank filling questions1．A connected graph has 【1】component(s).2．In a complete binary tree,the sequence number of node i’s parent ( if exist ) is 【2】the sequence number of node i’s left child ( if exist ) is 【3】the sequence number of node i’s right child ( if exist ) is 【4】3．【5】is the fastest known sorting algorithm in practice.4．A full binary tree of a given height h(h>=1) has 【6】nodes.5．An undirected graph G has N vertices. The number of edges of a MST (最小生成树)of this graph is 【7】.6．Commonly used graph search methods are 【8】and 【9】. 7．Complete the one pass of quicksorting operations. (一趟快速排序算法)int Partition (RedType& R[], int low, int high){ R[0] = R[low] ;pivotkey = R[low].key; // 枢轴while ( low<high ){ while ( low<high && 【10】) 【11】；R[low]=R[high];while ( low<high && R[low].key<=pivotkey ) 【12】；R[high]=R[low] ;}R[low] = R[0] ;return low ; // 返回枢轴所在位置}THREE. Answer True or False for each of the following assertions.( ) 1．The Minimum Spanning Tree of the graph is always unique.( ) 2．In tree structure, there is exactly one path from the root to each node.( ) 3．For every node in an AVL tree(平衡二叉树), the height of the left and right sub-trees can differ by at most 1.( ) 4．Min Heap can locate the current minimum in O(1) time.( ) 5．For any non-empty tree, if n is the number of nodes and e is the numbers of edges then n=e+1.( ) 6．If a binary search tree has l i leaves at hight i(i>=1), then l i /2i<=1( ) 7．The topological sorted order(拓扑排序) of nodes in a graph ( if it exists ) is always unique.( ) 8．A stack is a linear list in which all additions are restrict to one end, called the top. A stack is also called a FIFO list.( ) 9．The array { 23, 17, 14, 6, 13, 10, 1, 5, 7, 12 } is a heap.( ) 10．We can use Time Complexity and Space Complexity to evaluate the efficiency of an algorithm.FOUR.Assume that we are using the hashing function hash( key ) = key mod 11 and the following sequence of keys create a hash table: 12, 44, 13, 88, 23, 94, 11, 39, 20, 16, 5. Show the resulting hash table: Use linear probing(线性探测再散列) with an increment of 1.FIVE. Show the result of inserting {53，68，55，17，82，10，45} into an initially empty binary search tree. Then show the result of deleting root.SIX. The frequency of the symbols { a, b, c, d, e } is { 4, 7, 5, 2, 9 }. Construct the Huffman tree and give the Huffman code of the symbols { a, b, c, d, e }.SEVEN.Suppose the preorder traversal sequences of a binary tree is ABEGFCDH，the inorder traversal sequences is EGBFADHC. Please construct the binary tree，show the final result and write out the postorder traversal sequence of the binary tree.EIGHT. You are given an undirected graph（fig.1）.a. Give adjacency list(邻接表) representation of this graph.b. Construct a minimum spanning tree(最小生成树), using the Prim’s algorithm(普里姆算法). Draw the progress of creation.fig.1NINE. Get the program running results.1．Operation of stack//Suppose Stack and corresponding functions already be corrected defined void main( ){Stack S ;char x, y ;InitStack( S ) ;x=’c’ ; y=’t’ ;Push(S, x) ; Push(S,’u’) ; Push(S, y) ;Pop(S, x) ; Push(S,’r’) ; Push(S, x) ;Push(S, y) ; Pop(S, y) ; Push(S,’s’) ;while( !StackEmpty( S ) ) { Pop( S, y ) ; printf(y) ; }printf( x ) ;}2．Operation of a binary tree.#include <stdio.h>#define LeftChild( i ) ( 2 * ( i ) + 1 )void fun1( int A[ ], int i, int n ){ int Child ;int Tmp ;for( Tmp = A[ i ]; LeftChild( i ) < n; i = Child ){ Child = LeftChild( i ) ;if( Child != n-1 && A[Child+1] > A[Child] ) Child++ ;if( Tmp < A[Child] ) A[i] = A[Child] ;else break ;}A[ i ] = Tmp ;}void fun( int A[ ], int n ){ int i, temp ;for( i = n / 2; i >= 0; i-- )fun1( A, i, n ) ;for( i = n - 1; i > 0; i-- ){ temp = A[0], A[0] = A[i], A[i] = temp ;fun1( A, 0, i ) ;}}#define N 15void main( ){ int a[N]={ 5, 9, 3, 2, 99, 8, 7, 1, 77, 54, 23, 12, 88, -6, -10 } ;int i ;fun( a, N ) ;for( i=0; i<N; i++ )printf( "%d ", a[i] ) ;}TEN.Programming (All methods have been declared in textbook can be used directly, or you can rewrite them if they are not same in your answer)假设以两个元素依值递增有序排列的线性表A和B分别表示两个集合（同一表中的元素值各不相同）。

200X年试题选择题(1)Suppose 1,2,3,4 is the order which these elements push onto a stack. The sequence obtained is(B)A.4.1.2.3B.3.2.4.1C.3.4.1.2D.4.3.1.2(2)Suppose that a linear list contains n=31 nodes, the binary search is applied to the list, the maximum times in searching is (B)A 4B 5C 25-1D 24-1(3)In the following sorting algorithms, which is unstable(A)A Selection sortB Merge sortC Bubble sortD Insertion sort(4)Bubble sort is used for n nodes, the minimum number of comparisons is (A)A n-1B nC n(n-1/2)D n(n+1)/2(5)How many binary trees in different forms can at most be built by three nodes?(B)A 4B 5C 6D 7填空题.(1)The stack takes on character of ___________后进先出____________________(2)The postfix expression is ‘abcdef*/-*+’. Its infix expression is_a+b[c-d/(e*f)]____(3)The advantage of circular queues is _______克服队满溢出_________.(4)If the depth of full binary tree is k, then the number of nodes in the tree at least_2^k+1-1__ (5)The selection sort is used to sort n nodes, the number of its comparisons is __n(n-1)/2____ 三．(1) Write a function Deletion in C for linear list. (5 points)int sq_elete(list,p_n,i)int list[];/*形参数组可不指定大小*/int *p_n,i;{int j;if(i<0||i>=*p_n) return(1);for(j=i+1,j<*p_n;j++) list[j-1]=list[j];(*p_n)--;return(0);}(2)Write a function Pop in C for linked stack. (5 points)(3)Write a function in C for binary search. (10 point )int bisect(a,n,v)int a[],v, n;{ int i,j,m;i=0;j=n-1;while(i<=j){ m=(i+j)/2;if(v==a[m])return(m);if(v<a[m]) j=m-1;else i=m+1;}return(-1);}(4)Write some sentences in C which delete the node b in the following figure. (5 point)(附图)(5)Write some sentences in C which insert the node b in the following figure(5pont)(附图)四．(2)Write a function in C of quick sort. (10 point )Position Partition(List *list, Posotion low, Position high){ ListEntry pivot;Position i, lastsmall, pivotpos;Swap(low,(low+high)/2,list);pivot=list->entry[low];pivotpos=low;for(i=low+1; i<=high;i++)if(LT(list->entry[i].key, pivot.key))Swap(++pivotpos, i, list);Swap(low, pivotpos, list);return pivotpos;}(3)Suppose that a hash table contains 5 entries indexed from 0 through 4 and that the following keys are to be mapped into the table.12,19,17,14,10,24,15Hash function h(k)=k mod 5.(a)Determine the hash addresses and resolute collision by chaining.(b)Write a function in C for search by chaining. (10point)void search2(t,k,p,q)NODE *t[ ];int k;NODE *p,*q;{ *p=NULL;*q=t[h(k)];while(*q!=NULL)if ((*q)->key==k) return;else{*p=*q;*q=(*q)->link;}}五.(1)Write a function in C which will inter change all left and right subtrees in binary tree. (10 point)(2)Write a function in C for linked queue.(10 point)void Append(QueueEntry x,Queue *q){if (QueueFull(q))Error(“cannot append an entry to a full queue.”);else{q->count++;q->rear=(q->rear+1)%MAXQUEUE;q->entry[q->rear]=x;}}选择题(1)In a simple linked list with n nodes, the number of pointer fields with NULL Totals(D).A. nB.2C.n/2D.1(2)In the linear lists, two concepts which are the same as each other is(AB)A node B. record C. field D. type of structure(3)In the binary search tree, for any root of subtree, the keys of all nodes in its left subtree is (D) the keys of all nodes in its right subtree.A less thanB equal toC great thanD less than or equal to(4)For general trees, the correct choice is (B)A it may be emptyB at least one nodeC at least two nodesD A.B and C are incorrect(5)The bubble sort is used to n nodes, least number of comparison is(A)A n-1B nC n(n-1)/2D n(n+1)/2填空题(1)A binary tree with n nodes storaged by standard form, there are ___2n__ pointers where _n-1___pointers are used to point to sub-nodes, and _n+1___ pointers are empty.(2)The postfix expression is abc*+de/f*-, then its infix expression is _a+b*c-d/e*f___(3)The basic operations of linear lists are___插入删除访问______(4)The character of stack is__后进先出__________(5)Hash storage faced with two problems of __Hash函数____ and ____冲突___三．(1)Write a function Pop for stack (5point )V oid Pop(StackEntry *item, Stack *s){if(StackEmpty(s))Error;else*item=S->entry[--s->top] ;}(2)Translate the quadratic formula.(a+b*c)↑d↑(e*f/g)-h*iinto postfix form. (10point)(3)Write a function in C which changes the linked list in Figure 1 to another linked list in Figure2.(10point)(附图)(4)(1).(a)By hand, trace through the steps bubble sort will use on the list. The following seven number to be sorted into increasing order.(b)Write a function of bubble sort. (10point)void bubble_sort(a,n)int a[],n;{ int i,j,t;n ;while(n>0){j=0;for(i=0;i<n;i++)if(a[i]>a[i+1]){t=a[i];a[i]=a[i+1];a[i+1]=t;j=i;}n=j;}}(2)By hand, sort the list 46.26.22.68.48.42.36.84.66 using selection sort.Write a function of selection sort.(10point)void insertion_sort(a, n)int a[ ];int n;{ int i, j;int t;for(i=1;i<n;i++){t=a[i];for(j=i-1;j>=0&&t<a[j];j--)a[j+1]=a[j];a[j+1]=t;}}(3).Suppose that a hash table contains 11 entries from 0 through 10 and that the following keys are to be mapped into the table.(32,75,63,48,94,25,36,18,70)Hash function h(k)=k mod 11(a)Determine the hash addresses and resolute collision by linear probing.(b)Determine the hash addresses and resolute collision by chaining. (10point )(4)For each of the following binary trees, determine the order in which the nodes will be visitedmixed order given by invoking function A(5point)Void A(TreeNode *root, void(*Visit)(TreeEntry x) ){If(root){Visit(root->entry)’B(root->left, Visit);B(root->right, Visit);}}void B(TreeNode *root, void(*Visit)(TreeEbtry x)){If(root){A(root->left, Visit);Visit(root->entry);A(root->right, Visit);}}五.(2)Insert a new node r taken as the right child of node s and draw a threaded-tree.(a) By hand(b) By some sentences in C (10 point)(a)(b)r->rightchild=s->rightchild; // s的右子女指针或后继线索传给rr->rightthread=s->rightthread;//标志一同传送//ar->leftchild=s;r->leftthread=1; // r为leftchild或为s的前驱线索//bs->rightchild=r;s->rightthread=0; //r成为s的右子女//c。

第一章测试1【单选题】(10分) ThealgorithmandflowchartcanhelpustoA.TostorethedataB.ToknowthememorycapacityC.IdentifythedatatypeofavariableD.Specifytheproblemcompletelyandclearly2【单选题】(10分) TherhombusordiamondshapeinflowchartingdenotesA.DecisionB.InputC.InitializationD.Output3【单选题】(10分) Whichofthefollowingisnotanadvantageofaflowchart?A.EfficientcodingB.BettercommunicationC.SystematictestingD.Improperdocumentation4【单选题】(10分) Theflowchartsymbolsusedforstartandstopoperationsarecalledas_______.A.decisionB.processingC.terminalsD.connectors5【单选题】(10分)TheformulaF n=F n-1+F n-2willproduceA.FibonacciNumberB.RamanujanNumberC.PrimeNumberD.EulerNumber6【单选题】(10分) ThemainmeasuresfortheefficiencyofanalgorithmareA.ComplexityandcapacityB.ProcessorandmemoryC.TimeandspaceD.Dataandspace7【单选题】(10分) WhichoneofthefollowingistheconstanttimecomplexityintermsofBig-OhnotationA.O(1)B.O(n2)C.O(n3)D.O(n)8【单选题】(10分)Whatisthetimecomplexityofthefollowingcode?inta=0;for(i=0;i<n;i++){for(j=n;j>i;j--){a=a+i+j;}}A.O(nlog n)B.O(n)C.O(n2)D.O(1)9【单选题】(10分) Whichoneofthefollowingisanexampleforexponentialtimecomplexity?A.O(n2)B.O(2n)C.O(n)D.O(1)10【单选题】(10分)Forlargervaluesof n,whichonerepresentstheslowesttime?A.O(n2)B.O(2n)C.O(n)D.O(n!)第二章测试1【单选题】(10分) Deletionofanelementfromthearrayreducesthesizeofarrayby___________.A.threeB.twoC.zeroD.one2【单选题】(10分)Assumingthatint isof4bytes,whatisthesizeof intarr[10];?A.30B.10C.40D.3【单选题】(10分) Twodimensionalarraysareusefulwhentheelementsbeingprocessedaretobearran gedintheformof___________.A.NoneoftheaboveB.Both(a)and(b)C.rowsD.columns4【单选题】(10分)Inthepolynomial,A(x)=3x2+2x+4,thedegreeofthispolynomialisA.3B.1C.D.5【单选题】(10分)Inthepolynomial,A(x)=3x2+2x+4,coefficientoffirsttermisA.2B.1C.D.36【单选题】(10分) Amatrixhavingalargernumberofelementswithzerovaluesthanthenumberofnon-zeroelem entsissaidtobea_____________.A.triangularmatrixB.zeromatrixC.diagonalmatrixD.sparsematrix7【单选题】(10分)WhilerepresentingthesparsematrixA(m×n)withtnon-zerotermsin3-tuplesform,the sizeofthematrixbecomesA.t×nB.m×nC.3×tD.(t+1)×38【单选题】(10分)Consideringasparseof m×n matrixwith t non-zeroterms,in FAST_TRANSPOSE algorithm,thesi zeofone-dimensionalarray(SorT)isequalto:A.n+tB.mC.nt9【单选题】(10分)Consideringasparseof m×n matrixwith t non-zeroterms,thetimecomplexityof TRANS POSE algorithmis:A.O(n*t)B.O(n+t)C.O(n t)D.O(n-t)10【单选题】(10分)Whichofthefollowingstatementistrueregarding TRANSPOSE and FAST_TRANSPOSE algorit hms.A.NoneoftheaboveB.The TRANSPOSE algorithmisslowerthan FAST_TRANSPOSEC.TheTRANSPOSEalgorithmisfasterthanFAST_TRANSPOSETimecomplexitiesofTRANSPOSEandFAST_TRANSPOSEaresame第三章测试1【单选题】(10分) Theelementisinsertedfirstandwillberemovedlastin_____________.A.queueB.stackC.noneoftheaboveD.linkedlist2【单选题】(10分)Theexpression1*2^3*4^5*6isevaluatedas(^isforpower,asin a^b=a b):A.49152B.173458C.162^30D.32^303【单选题】(10分) Thedatastructurerequiredtocheckwhetheranexpressioncontainsbalancedparenthesisis?A.TreeB.ArrayC.QueueD.Stack4【单选题】(10分)Thepostfixformof A*B+C/D is?A.AB*CD/+B.ABCD+/*C.A*BC+/DD.5【单选题】(10分) Whichdatastructureisneededtoconvertinfixnotationtopostfixnotation?A.StackB.BranchC.QueueD.Tree6【单选题】(10分) Transformthefollowinginfixexpressiontoprefixform.((C*2)+1)/(A+B)A./+*C21+ABB.AB+12C*+/C.NoneoftheaboveD.7【单选题】(10分)Transformthefollowinginfixexpressiontopostfixform.(A+B)*(C-D)/EA.AB+CD-*E/B.AB*C+D/-C.AB+CD*-/ED.ABC*CD/-+8【单选题】(10分) Astackisadatastructureinwhichallinsertionsanddeletionsaremaderespectivelyat:A.atanypositionB.boththeendsC.inthemiddleD.oneend9【单选题】(10分) Whichofthefollowingapplicationsmayuseastack?:A.AlloftheaboveB.SyntaxanalyzerforacompilerC.AparenthesisbalancingprogramD.Keepingtrackoflocalvariablesatruntime10【单选题】(10分) Whichofthefollowingstatementiscorrect.A.NoneoftheaboveB. ApostfixexpressionismerelythereverseoftheprefixexpressionC.PostfixandprefixexpressionsuseparenthesisD. Apostfixexpressionisnotthereverseoftheprefixexpression第四章测试1【单选题】(10分) Aqueueisadatastructureinwhichallinsertionsanddeletionsaremaderespectivelyat:A.rearandfrontB.frontandrearC.rearandrearD.frontandfront2【单选题】(10分) Thefollowingdatastructureisusedforschedulingofjobsduringbatchprocessingincomputer s.A.stackB.queueC.linkedlistD.tree3【单选题】(10分) Inaqueuethedeletionsaretakeplaceat_________.A.NoneoftheaboveB.topC.frontD.rear4【单选题】(10分) Inaqueuetheinsertionsaretakeplaceat_________.A.rearB.topC.NoneoftheaboveD.front5【单选题】(10分)Incircularqueue,thefrontwillalwayspointtooneposition__________fromthefirstelementint hequeue.A.leftB.clockwiseC.counterclockwiseD.right6【单选题】(10分)Whichofthefollowingisnotthetypeofqueue.A.priorityqueueB.doubleendedqueueC.circularqueueD.singleendedqueue7【单选题】(10分)Oneoftheadvantageofcircularqueueis_____________.A.NoneoftheaboveB.effectiveuseofmemoryC.easiercomputationsD.deletingelementsbasedonpriority8【单选题】(10分) Whatisthetimecomplexityofalinearqueuehaving n elements?A.O(nlogn)B.O(logn)C.O(1)D.O(n)9【单选题】(10分)Whatisadequeue?A.AqueueimplementedwithadoublylinkedlistB.Aqueuewithinsert/deletedefinedforfrontendofthequeueC.Aqueuewithinsert/deletedefinedforbothfrontandrearendsofthequeueD. Aqueueimplementedwithbothsinglyanddoublylinkedlist10【单选题】(10分) Onedifferencebetweenaqueueandastackis:A.Queuesrequiredynamicmemory,butstacksdonot.B.Stacksrequiredynamicmemory,butqueuesdonot.C.Stacksusetwoendsforaddinganddeleting,butqueuesuseone.D.Queuesusetwoendsforaddinganddeleting,butstacksuseone.第五章测试1【单选题】(10分) Alinearlistofdataelementswhereeachelementcallednodeisgivenbymeansofpointeriscalle dA.nodelistB.linkedlistC.queueD.stack2【单选题】(10分)Consideranimplementationofunsortedsinglylinkedlist.Supposeithasrepresentationwhich aheadpointeronly.Giventherepresentation,whichofthefollowingoperationcanbeimpleme ntedinO(1)time?(I).Insertionatthefrontofthelinkedlist.(II).Insertionattheendofthelinkedlist.(III).Deletionofthefrontnodeofthelinkedlist.(IV).Deletionofthelastnodeofthelinkedlist.A.IandIIIB.I,II,andIIIC.I,II,andIVD.IandII3【单选题】(10分) Whatisthetimecomplexitytocountthenumberofelementsinthelinkedlist?A.O(1)B.O(n2)C.O(logn)D.O(n)4【单选题】(10分) InwhichofthefollowinglinkedliststherearenoNULLlinks?A.DoublylinkedlistB.NoneoftheaboveC.SinglylinkedlistD.Circularlinkedlist5【单选题】(10分)Indoublylinkedlists,traversalcanbeperformed?A.OnlyinforwarddirectionB.InbothdirectionsC.NoneD.Onlyinreversedirection6【单选题】(10分)Whatkindoflistisbesttoanswerquestionssuchas:“Whatistheitematposition n?”A.Singly-linkedlistsB.NoneoftheaboveC.Doubly-linkedlistsD.Listimplementedwithanarray7【单选题】(10分) Inasinglylinkedlistwhichoperationdependsonthelengthofthelist.A.DeletethelastelementofthelistB.AddanelementbeforethefirstelementofthelistC.DeletethefirstelementofthelistD.Interchangethefirsttwoelementsofthelist8【单选题】(10分)Thelinkfieldinanodecontains:A.dataofcurrentnodeB.addressofthenextnodeC.dataofnextnodeD.dataofpreviousnode9【单选题】(10分)Linkedlistdatastructureoffersconsiderablesavingin:A.SpaceutilizationB.ComputationaltimeC.SpaceutilizationandcomputationaltimeD.Noneoftheabove10【单选题】(10分) Alinearlistinwhicheachnodehaspointerstopointtothepredecessorandsuccessorsnodesis calledas:A.CircularlinkedlistB.Singly-linkedlistsC.Doubly-linkedlistsD.Linearlinkedlist第六章测试1【单选题】(10分) Torepresenthierarchicalrelationshipbetweenelements,whichdatastructureissuitable?A.treeB.arrayC.stackD.queue2【单选题】(10分) Whatisthemaximumnumberchildrenthatabinarytreenodecanhave?A.1B.C.2D.33【单选题】(10分) TheinordertraversaloftreewillyieldasortedlistingofelementsoftreeinA.NoneoftheaboveB.BinarysearchtreesC.BinarytreesD.Heaps4【单选题】(10分) Ifwestorethenodesofabinarytreeinanarraywithindexstartingfromzero,therightchil dofanodehavingindex n canbeobtainedat:A.2n+2B.n+1C.(n-1)/2D.2n+15【单选题】(10分) WhichofthefollowingtraversaloutputsthedatainsortedorderinaBST?A.InorderB.PostorderC.PreorderD.Levelorder6【单选题】(10分)Toobtainaprefixexpression,whichofthefollowingtraversalsisused?A.LevelorderB.InorderC.PostorderD.Preorder7【单选题】(10分) Themaximumnumberofnodesinatreeforwhichpostorderandpreordertraversalsmaybeequ altois_______.A.B.3C.2D.18【单选题】(10分)Supposethenumbers7,5,1,8,3,6,0,9,4,2areinsertedinthatorderintoaninitiallyempty BinarySearchTree.TheBinarySearchTreeusestheusualorderingonnaturalnumbers.What istheinordertraversalsequenceoftheresultanttree?A.024*******B.7510324689C.0123456789D.98642301579【单选题】(10分)Afullbinarytreeisatreewhere________________.A.eachnodehasexactlyzeroortwochildren.B.eachnodehasexactlytwochildrenC.alltheleavesareatthesamelevel.D.eachnodehasexactlyoneortwochildren.10【单选题】(10分) Acompletebinarytreeisatreewhere________________.A. everylevelofthetreeiscompletelyfilledexceptthelastlevelB.eachnodehasexactlytwochildrenC. eachnodehasexactlyzeroortwochildrenD. eachnodehasexactlyoneortwochildren。

Lists and Strings66.1LIST DEFINITIONExercises6.1Given the methods for lists described in this section,write functions to do each of the following tasks.Be sure to specify the preconditions and postconditions for each function.You may use local variablesof types List and List_entry,but do not write any code that depends on the choice of implementation.Include code to detect and report an error if a function cannot complete normally.E1.Error_code insert_first(const List_entry&x,List&a_list)inserts entry x into position0of the List a_list.Answer Error_code insert_first(const List_entry&x,List&a_list)/*Post:Entry x is inserted at position0of List a_list.*/{return a_list.insert(0,x);}E2.Error_code remove_first(List_entry&x,List&a_list)removes thefirst entry of the List a_list,copying it to x.Answer Error_code remove_first(List_entry&x,List&a_list)/*Post:A code of underflow is returned if List a_list is empty.Otherwise,thefirst entry of Lista_list is removed and reported as x.*/{return a_list.remove(0,x);}E3.Error_code insert_last(const List_entry&x,List&a_list)inserts x as the last entry of the List a_list.Answer Error_code insert_last(const List_entry&x,List&a_list)/*Post:Parameter x is inserted as the last entry of the List a_list.*/{return a_list.insert(a_list.size(),x);186Chapter6•Lists and StringsE4.Error_code remove_last(List_entry&x,List&a_list)removes the last entry of a_list,copying it to x.Answer Error_code remove_last(List_entry&x,List&a_list)/*Post:A code of underflow is returned if List a_list is empty.Otherwise,the last entry of Lista_list is removed and reported as x.*/{return a_list.remove(a_list.size()−1,x);}E5.Error_code median_list(List_entry&x,List&a_list)copies the central entry of the List a_list to x if a_list has an odd number of entries;otherwise,it copies the left-central entry of a_list to x.Answer Error_code median_list(List_entry&x,List&a_list)/*Post:A code of underflow is returned if List a_list is empty.Otherwise,the median entry ofList a_list is reported as x.*/{return a_list.retrieve((a_list.size()−1)/2,x);}E6.Error_code interchange(int pos1,int pos2,List&a_list)interchanges the entries at positions pos1and pos2of the List a_list.Answer Error_code interchange(int pos1,int pos2,List&a_list)/*Post:Any entries at positions pos1and pos2of List a_list are interchanged.If either entry ismissing a code of range_error is returned.*/{List_entry entry1,entry2;Error_code outcome=a_list.retrieve(pos1,entry1);if(outcome==success)a_list.retrieve(pos2,entry2);if(outcome==success)a_list.replace(pos1,entry2);if(outcome==success)a_list.replace(pos2,entry1);return outcome;}E7.void reverse_traverse_list(List&a_list,void(*visit)(List_entry&))traverses the List a_list in reverse order(from its last entry to itsfirst).Answer void reverse_traverse_list(List&a_list,void(*visit)(List_entry&))/*Post:The List a_list is traversed,in reverse order,and the function*visit is applied to allentries.*/{List_entry item;for(int i=a_list.size()−1;i>=0;i−−){a_list.retrieve(i,item);(*visit)(item);}}Section6.1•List Definition187 Answer Error_code copy(List&dest,List&source)/*Post:All entries are copied from from source into dest;source remains unchanged.A code of fail is returned if a complete copy cannot be made.*/{List_entry item;Error_code outcome=success;while(!dest.empty())dest.remove(0,item);for(int i=0;i<source.size();i++){if(source.retrieve(i,item)!=success)outcome=fail;if(dest.insert(i,item)!=success)outcome=fail;}return outcome;}E9.Error_code join(List&list1,List&list2)copies all entries from list1onto the end of list2;list1remains unchanged,as do all the entries previously in list2.Answer Error_code join(List&list1,List&list2)/*Post:All entries from list1are copied onto the end of list2.A code of overflow is returned if list2isfilled up before the copying is complete.*/{List_entry item;for(int i=0;i<list1.size();i++){list1.retrieve(i,item);if(list2.insert(list2.size(),item)!=success)return overflow;}return success;}E10.void reverse(List&a_list)reverses the order of all entries in a_list.Answer void reverse(List&a_list)/*Post:Reverses the order of all entries in a_list.A code of fail is returned in case the reversal cannot be completed.*/{List temp;List_entry item;Error_code outcome=success;for(int i=0;i<a_list.size();i++){a_list.retrieve(i,item);if(temp.insert(i,item)!=success)outcome=fail;}for(int j=0;j<a_list.size();j++){temp.retrieve(j,item);a_list.replace(a_list.size()−1−j,item);}}E11.Error_code split(List&source,List&oddlist,List&evenlist)copies all entries from source so that those188Chapter6•Lists and StringsAnswer Error_code split(List&source,List&oddlist,List&evenlist)/*Post:Copies all entries from source so that those in odd-numbered positions make up oddlistand those in even-numbered positions make up evenlist.Returns an error code ofoverflow in case either output listfills before the copy is complete.*/{List_entry item;Error_code outcome=success;for(int i=0;i<source.size();i++){source.retrieve(i,item);if(i%2!=0){if(oddlist.insert(oddlist.size(),item)==overflow)outcome=overflow;}elseif(evenlist.insert(evenlist.size(),item)==overflow)outcome=overflow;}return outcome;}6.2IMPLEMENTATION OF LISTSExercises6.2E1.Write C++functions to implement the remaining operations for the contiguous implementation of a List, as follows:(a)The constructor ListAnswer template<class List_entry>List<List_entry>::List()/*Post:The List is initialized to be empty.*/{count=0;}(b)clearAnswer//clear:clear the List./*Post:The List is cleared.*/template<class List_entry>void List<List_entry>::clear(){count=0;}(c)emptyAnswer//empty:returns non-zero if the List is empty./*Post:The function returns true or false according as the List is empty or not.*/template<class List_entry>bool List<List_entry>::empty()const{return count<=0;Section6.2•Implementation of Lists189(d)fullAnswer//full:returns non-zero if the List is full./*Post:The function returns true or false according as the List is full or not.*/template<class List_entry>bool List<List_entry>::full()const{return count>=max_list;}(e)replaceAnswer template<class List_entry>Error_code List<List_entry>::replace(int position,const List_entry&x)/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds: The entry in position is replaced by x,all other entries remain unchanged.Otherwisethe function fails with an error code of range_error.*/{if(position<0||position>=count)return range_error;entry[position]=x;return success;}(f)retrieveAnswer template<class List_entry>Error_code List<List_entry>::retrieve(int position,List_entry&x)const/*Post:If the List is not full and0≤position<n,where n is the number of entries in the List, the function succeeds:The entry in position is copied to x.Otherwise the function failswith an error code of range_error.*/{if(position<0||position>=count)return range_error;x=entry[position];return success;}(g)removeAnswer/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds: The entry in position is removed from the List,and the entries in all later positions havetheir position numbers decreased by1.The parameter x records a copy of the entryformerly in position.Otherwise the function fails with a diagnostic error code.*/ template<class List_entry>Error_code List<List_entry>::remove(int position,List_entry&x){if(count==0)return underflow;if(position<0||position>=count)return range_error;x=entry[position];count−−;while(position<count){entry[position]=entry[position+1];position++;}return success;190Chapter6•Lists and StringsE2.Write C++functions to implement the constructors(both forms)for singly linked and doubly linked Node objects.Answer The constructors for singly linked nodes are as follows.template<class List_entry>Node<List_entry>::Node(){next=NULL;}template<class List_entry>Node<List_entry>::Node(List_entry data,Node<List_entry>*link=NULL){entry=data;next=link;}The constructors for doubly linked nodes are as follows.template<class List_entry>Node<List_entry>::Node(){next=back=NULL;}template<class List_entry>Node<List_entry>::Node(List_entry data,Node<List_entry>*link_back=NULL,Node<List_entry>*link_next=NULL){entry=data;back=link_back;next=link_next;}E3.Write C++functions to implement the following operations for the(first)simply linked implementation of a list:(a)The constructor ListAnswer template<class List_entry>List<List_entry>::List()/*Post:The List is initialized to be empty.*/{count=0;head=NULL;}(b)The copy constructorAnswer template<class List_entry>List<List_entry>::List(const List<List_entry>&copy)/*Post:The List is initialized to copy the parameter copy.*/{Section6.2•Implementation of Lists191 if(old_node==NULL)head=NULL;else{new_node=head=new Node<List_entry>(old_node->entry);while(old_node->next!=NULL){old_node=old_node->next;new_node->next=new Node<List_entry>(old_node->entry);new_node=new_node->next;}}}(c)The overloaded assignment operatorAnswer template<class List_entry>void List<List_entry>::operator=(const List<List_entry>&copy)/*Post:The List is assigned to copy a parameter*/{List new_copy(copy);clear();count=new_copy.count;head=new_copy.head;new_copy.count=0;new_copy.head=NULL;}(d)The destructor∼ListAnswer template<class List_entry>List<List_entry>::∼List()/*Post:The List is empty:all entries have been removed.*/{clear();}(e)clearAnswer template<class List_entry>void List<List_entry>::clear()/*Post:The List is cleared.*/{Node<List_entry>*p,*q;for(p=head;p;p=q){q=p->next;delete p;}count=0;head=NULL;}(f)sizeAnswer template<class List_entry>int List<List_entry>::size()const/*Post:The function returns the number of entries in the List.*/{return count;192Chapter6•Lists and Strings(g)emptyAnswer template<class List_entry>bool List<List_entry>::empty()const/*Post:The function returns true or false according as the List is empty or not.*/{return count<=0;}(h)fullAnswer template<class List_entry>bool List<List_entry>::full()const/*Post:The function returns1or0according as the List is full or not.*/{return false;}(i)replaceAnswer template<class List_entry>Error_code List<List_entry>::replace(int position,const List_entry&x)/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds:The entry in position is replaced by x,all other entries remain unchanged.Otherwisethe function fails with an error code of range_error.*/{Node<List_entry>*current;if(position<0||position>=count)return range_error;current=set_position(position);current->entry=x;return success;}(j)retrieveAnswer template<class List_entry>Error_code List<List_entry>::retrieve(int position,List_entry&x)const/*Post:If the List is not full and0≤position<n,where n is the number of entries in the List,the function succeeds:The entry in position is copied to x.Otherwise the function failswith an error code of range_error.*/{Node<List_entry>*current;if(position<0||position>=count)return range_error;current=set_position(position);x=current->entry;return success;}(k)removeAnswer/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds:The entry in position is removed from the List,and the entries in all later positions havetheir position numbers decreased by1.The parameter x records a copy of the entryformerly in position.Otherwise the function fails with a diagnostic error code.*/ template<class List_entry>Error_code List<List_entry>::remove(int position,List_entry&x){Node<List_entry>*prior,*current;Section6.2•Implementation of Lists193 if(position>0){prior=set_position(position−1);current=prior->next;prior->next=current->next;}else{current=head;head=head->next;}x=current->entry;delete current;count−−;return success;}(l)traverseAnswer template<class List_entry>void List<List_entry>::traverse(void(*visit)(List_entry&))/*Post:The action specified by function(*visit)has been performed on every entry of the List, beginning at position0and doing each in turn.*/{Node<List_entry>*q;for(q=head;q;q=q->next)(*visit)(q->entry);}E4.Write remove for the(second)implementation of simply linked lists that remembers the last-used position.Answer template<class List_entry>Error_code List<List_entry>::remove(int position,List_entry&x)/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds: The entry at position is removed from the List,and the entries in all later positions havetheir position numbers decreased by1.The parameter x records a copy of the entryformerly at position.Otherwise the function fails with a diagnostic error code.*/ {Node<List_entry>*old_node;if(count==0)return fail;if(position<0||position>=count)return range_error;if(position>0){set_position(position−1);old_node=current->next;current->next=old_node->next;}else{old_node=head;current=head=old_node->next;current_position=0;}x=old_node->entry;delete old_node;count−−;return success;}E5.Indicate which of the following functions are the same for doubly linked lists(as implemented in this194Chapter6•Lists and Strings(a)The constructor List(b)The copy constructor(c)The overloaded assignmentoperator(d)The destructor∼List(e)clear(f)size(g)empty(h)full(i)replace (j)insert (k)retrieve (l)remove (m)traverseAnswer Parts(f)through(h)all remain the same as for simply linked lists.Part(j)appears in the text;parts(a),(b),(c),(d),(e),(i),(k),(l)and(m)are listed here.template<class List_entry>List<List_entry>::List()/*Post:The List is initialized to be empty.*/{count=0;current=NULL;current_position=−1;}//List:a copy constructor/*Post:The List is initialized to copy the parameter copy.*/template<class List_entry>List<List_entry>::List(const List<List_entry>&copy){count=copy.count;current_position=copy.current_position;Node<List_entry>*new_node,*old_node=copy.current;if(old_node==NULL)current=NULL;else{new_node=current=new Node<List_entry>(old_node->entry);while(old_node->next!=NULL){old_node=old_node->next;new_node->next=new Node<List_entry>(old_node->entry,new_node);new_node=new_node->next;}old_node=copy.current;new_node=current;while(old_node->back!=NULL){old_node=old_node->back;new_node->back=new Node<List_entry>(old_node->entry,NULL,new_node);new_node=new_node->back;}}}//List:overloaded assignment/*Post:The List is assigned to copy a parameter*/template<class List_entry>void List<List_entry>::operator=(const List<List_entry>&copy){List new_copy(copy);Section6.2•Implementation of Lists195 current_position=new_copy.current_position;current=new_copy.current;new_copy.count=0;new_copy.current_position=0;new_copy.current=NULL;}//∼List:a destructor to clear the List./*Post:The List is empty:all entries have been removed.*/template<class List_entry>List<List_entry>::∼List(){clear();}template<class List_entry>void List<List_entry>::clear()/*Post:The List is cleared.*/{Node<List_entry>*p,*q;if(current==NULL)return;for(p=current->back;p;p=q){q=p->back;delete p;}for(p=current;p;p=q){q=p->next;delete p;}count=0;current=NULL;current_position=−1;}template<class List_entry>Error_code List<List_entry>::replace(int position,const List_entry&x)/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds: The entry in position is replaced by x,all other entries remain unchanged.Otherwise the function fails with an error code of range_error.*/{if(position<0||position>=count)return range_error;set_position(position);current->entry=x;return success;}template<class List_entry>Error_code List<List_entry>::retrieve(int position,List_entry&x)const/*Post:If the List is not full and0≤position<n,where n is the number of entries in the List, the function succeeds:The entry in position is copied to x.Otherwise the function fails with an error code of range_error.*/{if(position<0||position>=count)return range_error;set_position(position);x=current->entry;196Chapter6•Lists and Stringstemplate<class List_entry>Error_code List<List_entry>::remove(int position,List_entry&x)/*Post:If0≤position<n,where n is the number of entries in the List,the function succeeds:The entry in position is removed from the List,and the entries in all later positions havetheir position numbers decreased by1.The parameter x records a copy of the entryformerly in position.Otherwise the function fails with a diagnostic error code.*/ {Node<List_entry>*old_node,*neighbor;if(count==0)return fail;if(position<0||position>=count)return range_error;set_position(position);old_node=current;if(neighbor=current->back)neighbor->next=current->next;if(neighbor=current->next){neighbor->back=current->back;current=neighbor;}else{current=current->back;current_position−−;}x=old_node->entry;delete old_node;count−−;return success;}template<class List_entry>void List<List_entry>::traverse(void(*visit)(List_entry&))/*Post:The action specified by function*visit has been performed on every entry of the List,beginning at position0and doing each in turn.*/{Node<List_entry>*to_visit=current;if(to_visit!=NULL)//Ignore empty lists.for(;to_visit->back;to_visit=to_visit->back)//Find the beginning of List.;for(;to_visit;to_visit=to_visit->next)(*visit)(to_visit->entry);}Programming Projects6.2P1.Prepare a collection offiles containing the declarations for a contiguous list and all the functions for list processing.Answer Definitionfile:const int max_list=5000;template<class List_entry>class List{Section6.2•Implementation of Lists197 //methods of the List ADTList();int size()const;bool full()const;bool empty()const;void clear();void traverse(void(*visit)(List_entry&));Error_code retrieve(int position,List_entry&x)const;Error_code replace(int position,const List_entry&x);Error_code remove(int position,List_entry&x);Error_code insert(int position,const List_entry&x);protected://data members for a contiguous list implementationint count;List_entry entry[max_list];};Implementationfile:template<class List_entry>List<List_entry>::List()/*Post:The List is initialized to be empty.*/{count=0;}//clear:clear the List./*Post:The List is cleared.*/template<class List_entry>void List<List_entry>::clear(){count=0;}template<class List_entry>int List<List_entry>::size()const/*Post:The function returns the number of entries in the List.*/{return count;}//empty:returns non-zero if the List is empty./*Post:The function returns true or falseaccording as the List is empty or not.*/template<class List_entry>bool List<List_entry>::empty()const{return count<=0;198Chapter6•Lists and Strings//full:returns non-zero if the List is full./*Post:The function returns true or falseaccording as the List is full or not.*/template<class List_entry>bool List<List_entry>::full()const{return count>=max_list;}template<class List_entry>void List<List_entry>::traverse(void(*visit)(List_entry&))/*Post:The action specified by function(*visit)has been performedon every entry of the List,beginning at position0and doingeach in turn.*/{for(int i=0;i<count;i++)(*visit)(entry[i]);}template<class List_entry>Error_code List<List_entry>::insert(int position,const List_entry&x)/*Post:If the List is not full and0<=position<=n,where n is the number of entries in the List,the function succeeds:Any entry formerly atposition and all later entries have theirposition numbers increased by1andx is inserted at position of the List.Else:The function fails with a diagnostic error code.*/{if(full())return overflow;if(position<0||position>count)return range_error;for(int i=count-1;i>=position;i--)entry[i+1]=entry[i];entry[position]=x;count++;return success;}template<class List_entry>Error_code List<List_entry>::retrieve(int position,List_entry&x)const/*Post:If the List is not full and0<=position<n,where n is the number of entries in the List,the function succeeds:The entry in position is copied to x.Otherwise the function fails with an error code of range_error.Section6.2•Implementation of Lists199 {if(position<0||position>=count)return range_error;x=entry[position];return success;}template<class List_entry>Error_code List<List_entry>::replace(int position,const List_entry&x)/*Post:If0<=position<n,where n is the number of entries in the List,the function succeeds:The entry in position is replaced by x,all other entries remain unchanged.Otherwise the function fails with an error code of range_error.*/{if(position<0||position>=count)return range_error;entry[position]=x;return success;}/*Post:If0<=position<n,where n is the number of entries in the List,the function succeeds:The entry in position is removedfrom the List,and the entries in all later positionshave their position numbers decreased by1.The parameter x records a copy ofthe entry formerly in position.Otherwise the function fails with a diagnostic error code.*/template<class List_entry>Error_code List<List_entry>::remove(int position,List_entry&x){if(count==0)return underflow;if(position<0||position>=count)return range_error;x=entry[position];count--;while(position<count){entry[position]=entry[position+1];position++;}return success;}Driver program:#include"../../c/utility.h"#include"list.h"#include"list.cpp"void write_entry(char&c){cout<<c;200Chapter6•Lists and Stringsmain(){char x;List<char>c_list;//a list of characters,initialized emptycout<<"List is empty,it has"<<c_list.size()<<"items.\n"<<"Enter characters and the program adds them to the list.\n"<<"Use Enter key(newline)to terminate the input.\n When"<<"size()is3,the element will be inserted at the front of"<<"the list.\n The other ones will appear at the back.\n";while(!c_list.full()&&(x=cin.get())!=’\n’)if(c_list.size()==3)c_list.insert(0,x);else c_list.insert(c_list.size(),x);cout<<"The list has"<<c_list.size()<<"items.\n";cout<<"The function c_list.full(),got"<<c_list.full();if(c_list.full())cout<<"because the list is full.\n";else cout<<"because the list is NOT full.\n";cout<<"c_list.empty(),expecting0,got"<<c_list.empty()<<".\n";cout<<"c_list.traverse(write_entry)output:";c_list.traverse(write_entry);cout<<"\n";}P2.Write a menu-driven demonstration program for general lists,based on the one in Section3.4.The list entries should be e the declarations and the functions for contiguous lists developed inProject P1.Answer See Project P2for the List class.Menu-driven demonstration program:#include"../../c/utility.h"void introduction()/*POST:An introduction has been written to the terminal.*/{cout<<"\n\nList Demonstration Program.\n\n"<<"This program is intended for verifying list operations.The"<<"\nlists are defined to have single character entries which\n"<<"also act as the keys.\n\n"<<endl;cout<<"This version works with a contiguous list implementation"<<endl;cout<<"\nInsertions and deletions must be specified by list position."<<"\nThe HEAD of the list is located at position0"<<endl;cout<<"Valid commands are shown at the prompt.\n"<<"Both upper and lower case letters can be used.\n";}void help()/*PRE:None.POST:Instructions for the list operations have been printed.Section6.2•Implementation of Lists201 {cout<<"Valid commands are:\n"<<"\tA-Append value to the end of the list.\n"<<"\tI-Insert value into the list.\n"<<"\tD-Delete value from the list.\n"<<"\tR-Replace a value in the list.\n"<<"\tF-Fetch an entry from the list.\n"<<"\tT-Traverse the list and print each entry.\n"<<"\tS-The current size of the list.\n"<<"\t[H]elp[Q]uit."<<endl;}#include<string.h>char get_command()/*PRE:None.POST:A character command belonging to the set of legal commands for the list demonstration has been returned.*/{char c,d;cout<<"Select command and press<Enter>:";while(1){do{cin.get(c);}while(c==’\n’);do{cin.get(d);}while(d!=’\n’);c=tolower(c);if(strchr("aidrftshq",c)!=NULL)return c;cout<<"Please enter a valid command or?for help:"<<endl;help();}}//auxiliary input/output functionsvoid write_ent(char&x){cout<<x;}char get_char(){char c;cin>>c;return c;}//include list data structure#include"../contlist/list.h"。

四川大学期末考试试题（闭卷）A （2013 ——2014 学年第 2 学期）
课程号：课序号：1 课程名称：数据结构(in English ) 任课教师：成绩：
适用专业年级：13电子商务学生人数：159印题份数：160学号：姓名：
2 题间不留空，一般应题卷分开教务处试题编号：
教务处试题编号：
四川大学期末考试试题（闭卷）B （2013 ——2014 学年第 2 学期）
课程号：402079030课序号：0,1 ,2 课程名称：数据结构任课教师：黄勇成绩：
适用专业年级：13电子商务学生人数：159印题份数：160学号：姓名：
注：1试题字迹务必清晰，书写工整。

本题 2 页，本页为第 1 页
2 题间不留空，一般应题卷分开教务处试题编号：
four railway carriages numbered {1,2,3,4 }, which
Programming Questions.（2*10=20）
Write a program that finds the height of a binary tree.
Write an algorithm to delete the i th element in the queue.
本题 2 页，本页为第 2 页
教务处试题编号：。

数据结构考试题（英文版）C++Final Examination Paper On Data Structures(B)I、Fill Vacant Position (1′×10=10′)1、Only ______________________graph has topological order.2、In a______ data structure, all insertions and deletions of entries are madeat one end. It is particularly useful in applications involving______.3、In c++ , we use _______________operator to implement the circularqueues.4、In processing a contiguous list with n entries: insert and remove requiretime approximately to ___. And List, clear, empty, full, size, replace, and retrieve operate in _________ time.5、One of method of searching is ____________________that requiresordered list.6、The time complexity of the insertionsort on average is______________.7、____________is the name for the case when a function invokes itself orinvokes a sequence of other functions,one of which eventually invokes the __________again.II、Multiple choice (2′×10=20′)1、A queue is a version of ( )A. linked listB. LIFO listC. sequential listD. FIFO list2、In a tree, ______are vertices with the same parent. ( )A. childrenB. siblingC. adjacentD. leaf3、How many shapes of binary trees withthree nodes are there ( )A. 12B.15C. 6D. 54、Among sorting algorithms, which kind of algorithm is divide-and-conquer sorting ( ).A. shell sortB. heap sortC. quick sortD. insertionsortIn a binary tree, if the result of traversing under preorder is the same as that under inorder,then ( )A. It is only a binary tree with one nodeB. It is either empty, or the left subtree of any node of the tree is emptyC. It is only an empty binary treeD. It is either empty, or the right subtree of an node of the tree is empty6、For the following graph, one of results ofbreadth-first traversal is ( )A. acbdieghfB. abcideghfC. abcdefghiD. abdeighfc7、The time requirement of retrieving a given target in hash table with n entries is ( )A. O(n)B. O(log2n)C. O(1)D.O(nlog2n)8、Which function is smallest order of magnitude? ( )A. 2 nB. n + lgnC.n 0.1D.100009、There are _______solutions to the problem of placing four queens on a 4×4 board. ( )A. 2B. 3C. 6D. 410、For the following binary tree, the result of traversing under inorder is ( )A. abcdefghiB. dgbechfiaC. dgbaechfiD. gdbehifcaIII、Analyze and Calculate ( 10′×1=10′)1、Let A be a lower triangular matrix andSuppose that (a) Elements of A are stored in row-major ordering(b) Each element occupies k memory locations(c) Indexing begins at 0Please give the calculating formula ofLoc(aij)(address of the element aij) IV、Comprehensive Problem( 8′×5=40′)1、Draw a diagram to illustrate the configuration of linked nodes that iscreated by the following statement.Node *p0=new Node (a);Node *p1=p0→next=new Node(b);Node *p2=p1→next=new Node(c,p1);2、 By hand, trace the action ofquick-sort on the following lists. Given pivot is first entry .35 41 46 38 29 22 3243、Suppose that(a) A hash table contains hash_size=16 position indexed from0 to 15(b) A hash function H(key)=(key*3-2)%13(c) The following keys are to be mapped into the table:10 120 33 45 58 26 3 27 200 400 2Draw the hash table with the collision resolution of chaining.4、Construct a minimal spanning tree of the following connected network.Please give key steps.5、Given a sequence of keys:B , Z,A,Y, C,V, D, W, E,X, FInsert the keys in the order shown above, to build them into an AVL tree (draw the principal AVL tree).V、Develop Algorithm( 10′×2=20′)1、Assume we have the following class specifications:const int maxstack=10;class Stack{public:Stack( );bool empty( )const;Error_code pop( );Error_code top(int &item)const;Error_code push(const int &item);Private:int count;int entry[maxstack]; };Write a program that uses a Stack to read an integer and print all its prime divisors in descending order. For example, with the integer 2100 the output should be 7 5 5 3 2 2 .2、For linked implementation of binary trees, we have the folowing classspecifications:templatestruct Binary_node {Entry data;Binary_node *left;Binary_node *right;};templateclass Binary_tree{protected:Binary_node *root;void recursive_exchange (Binary_node *sub_root);public:void exchange ();};templatevoid Binary_tree:: exchange () {recursive_ exchange (root);}Write the auxiliary function recursive_ exchange to exchange the left subtree and the right subtree of any node ina binary tree.Answer of Final Examination Paper On Data Structures (B)I.1、directed with no cycle(有向无环图) 2、stack栈 reversing 逆序3、 modulus (or i=(i+1)%max)求余、模4、 n constant 常数5、 binary search二分查找6、 0.25n 2 +O(n) 或O(n 2 )7、 Recursion 递归 first function 第一个函数、自身II. 1、D 2、B 3、D 4、C 5、B 6、B 7、C 8、D 9、A10、CIII.：IV．1、2、first pass： 32 29 22 35 41 46 38second pass： 22 29 32 35 38 41 46third pass： 22 29 32 35 38 41 463、 4、5、V. 1、# inlcude# inlcudeVoid main( ){ stack s;int m,n,t;cout<<”please input a number:”;cin>>n；m=n/2;for( i=2; i<=m; i++ )while( n%i==0 ){ s.push(i); n=n/I; }cout<<”descending order is:”<<endl;< p="">while( !s.empty() ) {s.top(t);cout<<t<<="">s.pop(); }cout<<endl;< p="">}3、templatevoidBinary_tree::recursive_exchange(Binary_node*sub_root) { Binary_node *temp;if(sub_root==NULL) return;temp= sub_root->left;sub_root->left=sub_root->right;sub_root->right=temp;recursive_exchange(sub_root->left);recursive_exchange(sub_root->right);}</endl;<></t<</endl;<>。