牛顿迭代法的实验报告

实验报告一：实验题目一、 实验目的掌握求解非线性方程根的二分法、简单迭代法和牛顿迭代法，并通过数值实验比较两种方法的收敛速度。

二、 实验内容1、编写二分法、并使用这两个程序计算02)(=-+=x e x x f 在[0, 1]区间的解，要求误差小于 410- ，比较两种方法收敛速度。

2、在利率问题中，若贷款额为20万元，月还款额为2160元，还期为10年，则年利率为多少？请使用牛顿迭代法求解。

3、由中子迁移理论，燃料棒的临界长度为下面方程的根，用牛顿迭代法求这个方程的最小正根。

4、用牛顿法求方程的根，精确至8位有效数字。

比较牛顿迭代法算单根和重根的收敛速度，并用改进的牛顿迭代法计算重根。

第1题：02)(=-+=x e x x f 区间[0,1] 函数画图可得函数零点约为0.5。

画图函数：function Test1()% f(x) 示意图, f(x) = x + exp(x) - 2; f(x) = 0r = 0:0.01:1;y = r + exp(r) - 2plot(r, y);grid on 二分法程序：计算调用函数：[c,num]=bisect(0,1,1e-4)function [c,num]=bisect(a,b,delta)%Input –a,b 是取值区间范围% -delta 是允许误差%Output -c 牛顿迭代法最后计算所得零点值% -num 是迭代次数ya = a + exp(a) - 2;yb = b + exp(b) - 2;if ya * yb>0return;endfor k=1:100c=(a+b)/2;yc= c + exp(c) - 2;if abs(yc)<=deltaa=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif abs(b-a)<deltanum=k; %num为迭代次数break;endendc=(a+b)/2;err=abs(b-a);yc = c + exp(c) - 2;牛顿迭代法程序：计算调用函数：[c,num]=newton(@func1,0.5,1e-4) 调用函数：function [y] = func1(x)y = x + exp(x) - 2;end迭代算法：function[c,num]=newton(func,p0,delta)%Input -func是运算公式% -p0是零点值% -delta是允许误差%Output -c牛顿迭代法最后计算所得零点值% -num是迭代次数num=-1;for k=1:1000y0=func(p0);dy0=diff(func([p0 p0+1e-8]))/1e-8;p1=p0-y0/dy0;err=abs(p1-p0);p0=p1;if(err<delta)num=k;%num为迭代次数break;endendc=p0;第2题：由题意得到算式：计算调用函数：[c,num]=newton(@func2,0.02,1e-8)程序：先用画图法估计出大概零点位置在0.02附近。

MAAB计算方法迭代法牛顿法二分法实验报告实验目的：比较MAAB计算方法中迭代法、牛顿法和二分法的优缺点，探究它们在求解方程中的应用效果。

实验原理：1、迭代法：将方程转化为x=f(x)的形式，通过不断迭代逼近方程的根。

2、牛顿法：利用函数在特定点的切线逼近根的位置，通过不断迭代找到方程的根。

3、二分法：利用函数值在区间两端的异号性质，通过不断二分缩小区间，最终逼近方程的根。

实验步骤：1、选择一元方程进行求解，并根据方程选择不同的计算方法。

2、在迭代法中，根据给定的初始值和迭代公式，进行迭代计算，直到满足预设的迭代精度要求。

3、在牛顿法中，选择初始点，并根据切线方程进行迭代计算，直到满足预设的迭代精度要求。

4、在二分法中，选择区间，并根据函数值的异号性质进行二分，直到满足预设的迭代精度要求。

5、根据计算结果，比较三种方法的求解效果，包括迭代次数、计算时间、求解精度等指标。

实验结果与分析：通过对多个方程进行测试，得到了以下实验结果：1、迭代法的优点是简单易懂，适用范围广，但当迭代公式不收敛时会导致计算结果不准确。

2、牛顿法的优点是收敛速度较快，但需要计算函数的一阶导数和二阶导数，对于复杂函数较难求解。

3、二分法的优点是收敛性较好，不需要导数信息，但收敛速度较慢。

4、对于线性方程和非线性方程的求解，牛顿法和迭代法通常比二分法更快速收敛。

5、对于多重根的方程，二分法没有明显优势，而牛顿法和迭代法能更好地逼近根的位置。

6、在不同的方程和初值选择下，三种方法的迭代次数和求解精度略有差异。

7、在时间效率方面，二分法在收敛速度较慢的同时，迭代次数较少，牛顿法在收敛速度较快的同时，迭代次数较多，而迭代法对于不同方程有较好的平衡。

结论：1、对于不同类型的方程求解，可以根据具体情况选择合适的计算方法。

2、迭代法、牛顿法和二分法各有优缺点，没有绝对的最优方法，需要权衡各种因素选择最适合的方法。

3、在实际应用中，可以根据方程的特点和精度要求综合考虑不同方法的优劣势，以获得较好的求解效果。

《机器学习》课程实验报告实验：牛顿法的实现姓名：彭文婷专业：生物技术学号：20132123012015年5月5日一、 实验内容1. 构建有效迭代公式求1020x e x +-=的解。

2. 利用牛顿法求上述方程的解。

二、 实验结果及分析1.迭代公式为X=(2-e x )/10由于e^x 大于0，则2-10x 大于0，则x 小于0.2X 小于0时，0小于e^x 小于1， 2-10x 大于2因此【0,0.2】为有根区间取初始值X 0=0X1=0.1X2=0.089482908X3=0.090639136X4=0.090512617X5=0.090526468X6=0.090524952X7=0.090525118X8=0.090525019因为X8-X7≤10-6所以X=0.0905250192.牛顿法函数为f （x) = e x +10x-2一阶导数为f ’（x ）= e x +10Xn+1 = Xn-f(Xn)/f ’(Xn) = Xn-(e Xn +10Xn-2)/(e Xn +10)初始值X0=0X1=0.090909091X2=0.090525108X3=0.090525101因为X3-X2≤10-6所以X=0.090525101分析：迭代法关键在于选取收敛的迭代公式和选取适当的初始值，而牛顿法更为优化，收敛速度快。

但二者都只能得出局部最优解。

三．实验总结通过练习对迭代法和牛顿法有了更深刻的理解，原本使用计算器算的，但输入过于繁琐，后来在Excel中编辑公式计算简便了很多，但要实现计算机自动计算程还是十分困难，在以后的学习中应尽快掌握C语言编程技能。

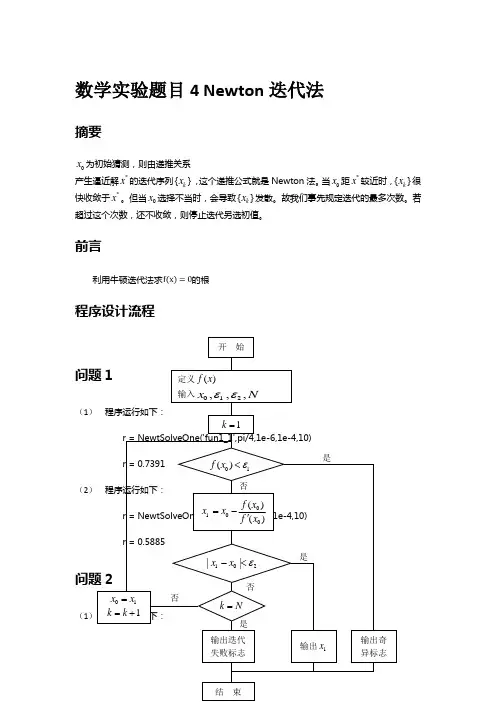
数学实验题目4 Newton 迭代法摘要0x 为初始猜测，则由递推关系产生逼近解*x 的迭代序列{}k x ，这个递推公式就是Newton 法。

当0x 距*x 较近时，{}k x 很快收敛于*x 。

但当0x 选择不当时，会导致{}k x 发散。

故我们事先规定迭代的最多次数。

若超过这个次数，还不收敛，则停止迭代另选初值。

前言利用牛顿迭代法求的根程序设计流程问题1（1 程序运行如下：r = NewtSolveOne('fun1_1',pi/4,1e-6,1e-4,10) r = 0.7391（2 程序运行如下：r = NewtSolveOne('fun1_2',0.6,1e-6,1e-4,10) r = 0.5885问题2（1 程序运行如下：否 是否是是定义()f x输入012,,,x N εε开 始1k =01()f x ε<0100()()f x x x f x =-'102||x x ε-<k N =输出迭代失败标志输出1x输出奇 异标志结 束01x x = 1k k =+ 否r = NewtSolveOne('fun2_1',0.5,1e-6,1e-4,10)r = 0.5671（2）程序运行如下：r = NewtSolveOne('fun2_2',0.5,1e-6,1e-4,20)r = 0.5669问题3（1）程序运行如下：①p = LegendreIter(2)p = 1.0000 0 -0.3333p = LegendreIter(3)p = 1.0000 0 -0.6000 0p = LegendreIter(4)p =1.0000 0 -0.8571 0 0.0857p = LegendreIter(5)p = 1.0000 0 -1.1111 0 0.2381 0②p = LegendreIter(6)p = 1.0000 0 -1.3636 0 0.4545 0 -0.0216r = roots(p)'r= -0.932469514203150 -0.6612 0.9324695142031530.6612 -0.238619186083197 0.238619186083197用二分法求根为：r = BinSolve('LegendreP6',-1,1,1e-6)r = -0.932470204878826 -0.661212531887755 -0.2386200573979590.2386 0.661192602040816 0.932467713647959（2）程序运行如下：①p = ChebyshevIter(2)p = 1.0000 0 -0.5000p = ChebyshevIter(3)p = 1.0000 0 -0.7500 0p = ChebyshevIter(4)p = 1.0000 0 -1.0000 0 0.1250p = ChebyshevIter(5)p = 1.0000 0 -1.2500 0 0.3125 0②p = ChebyshevIter(6)p = 1.0000 0 -1.5000 0 0.5625 0 -0.0313r = roots(p)'r = -0.965925826289067 -0.7548 0.9659258262890680.7547 -0.258819045102521 0.258819045102521用二分法求根为：r = BinSolve('ChebyshevT6',-1,1,1e-6)r = -0.965929926658163 -0.7755 -0.2588289221938780.2588 0.7020 0.965924944196429与下列代码结果基本一致，只是元素顺序稍有不同：j = 0:5;x = cos((2*j+1)*pi/2/(5+1))x =0.965925826289068 0.7548 0.258819045102521-0.258819045102521 -0.7547 -0.965925826289068（3）程序运行如下：①p = LaguerreIter(2)p = 1 -4 2p = LaguerreIter(3)p = 1 -9 18 -6p = LaguerreIter(4)p = 1 -16 72 -96 24p = LaguerreIter(5)p =1.0000 -25.0000 200.0000 -600.0000 600.0000 -120.000②p = LaguerreIter(5)p =1.0000 -25.0000 200.0000 -600.0000 600.0000 -120.000r = roots(p)'r =12.6432 7.8891 3.5964257710407111.4520 0.263560319718141用二分法求根为：r = BinSolve('LaguerreL5',0,13,1e-6)r = 0.263560314567722 1.4789 3.5964257656311507.0720 12.6490（4）程序运行如下：①p = HermiteIter(2)p = 1.0000 0 -0.5000p = HermiteIter(3)p = 1.0000 0 -1.5000 0p = HermiteIter(4)p = 1.0000 0 -3.0000 0 0.7500p = HermiteIter(5)p = 1.0000 0 -5.0000 0 3.7500 0②p = HermiteIter(6)p = 1.0000 0 -7.5000 0 11.2500 0 -1.8750r = roots(p)'r =-2.3587 2.3588 -1.3358490740136961.335849074013698 -0.4367 0.4366用二分法求根为：r = BinSolve('HermiteH6',-3,3,1e-6)r =-2.3516 -1.335849********* -0.43630.4366 1.335848983453244 2.3504所用到的函数function r = NewtSolveOne(fun, x0, ftol, dftol, maxit)% NewtSolveOne 用Newton法解方程f(x)=0在x0附近的一个根%% Synopsis: r = NewtSolveOne(fun, x0)% r = NewtSolveOne(fun, x0, ftol, dftol)%% Input: fun = (string) 需要求根的函数及其导数% x0 = 猜测根，Newton法迭代初始值% ftol = (optional)误差，默认为5e-9% dftol = (optional)导数容忍最小值，小于它表明Newton法失败，默认为5e-9 % maxit = (optional)迭代次数，默认为25%% Output: r = 在寻根区间内的根或奇点if nargin < 3ftol = 5e-9;endif nargin < 4dftol = 5e-9;endif nargin < 5maxit = 25;endx = x0; %设置初始迭代位置为x0k = 0; %初始化迭代次数为0while k <= maxitk = k + 1;[f,dfdx] = feval(fun,x); %fun返回f(x)和f'(x)的值if abs(dfdx) < dftol %如果导数小于dftol，Newton法失败，返回空值r = [];warning('dfdx is too small!');return;enddx = f/dfdx; %x(n+1) = x(n) - f( x(n) )/f'( x(n) )，这里设dx = f( x(n) )/f'( x(n) )x = x - dx;if abs(f) < ftol %如果误差小于ftol，返回当前x为根r = x;return;endendr = []; %如果牛顿法未收敛，返回空值function p = LegendreIter(n)% LegendreIter 用递推的方法计算n次勒让德多项式的系数向量Pn+2(x) = (2*i+3)/(i+2) * x*Pn+1(x) - (i+1)/(i+2) * Pn(x)%% Synopsis: p = LegendreIter(n)%% Input: n = 勒让德多项式的次数%% Output: p = n次勒让德多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %P0(x) = 1p = 1;return;elseif n == 1 %P1(x) = xp = [1 0];return;endpBk = 1; %初始化三项递推公式后项为P0pMid = [1 0]; %初始化三项递推公式中项为P1for i = 0:n-2pMidCal = zeros(1,i+3); %构造用于计算的x*Pn+1pMidCal(1:i+2) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的PnpBkCal(3:i+3) = pBk;pFwd = (2*i+3)/(i+2) * pMidCal - (i+1)/(i+2) * pBkCal; %勒让德多项式三项递推公式Pn+2(x) = (2*i+3)/(i+2) * x*Pn+1(x) - (i+1)/(i+2) * Pn(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把勒让德多项式最高次项系数归一化function p = ChebyshevIter(n)% ChebyshevIter 用递推的方法计算n次勒让德-切比雪夫多项式的系数向量Tn+2(x) = 2*x*Tn+1(x) - Tn(x)%% Synopsis: p = ChebyshevIter(n)%% Input: n = 勒让德-切比雪夫多项式的次数%% Output: p = n次勒让德-切比雪夫多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %T0(x) = 1p = 1;return;elseif n == 1 %T1(x) = xp = [1 0];return;endpBk = 1; %初始化三项递推公式后项为T0pMid = [1 0]; %初始化三项递推公式中项为T1for i = 0:n-2pMidCal = zeros(1,i+3); %构造用于计算的x*Tn+1pMidCal(1:i+2) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的PnpBkCal(3:i+3) = pBk;pFwd = 2*pMidCal - pBkCal; %勒让德-切比雪夫多项式三项递推公式Tn+2(x) = 2*x*Tn+1(x) - Tn(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把勒让德-切比雪夫多项式最高次项系数归一化function p = LaguerreIter(n)% LaguerreIter 用递推的方法计算n次拉盖尔多项式的系数向量Ln+2(x) = (2*n+3-x)*Ln+1(x) - (n+1)*Ln(x)%% Synopsis: p = LaguerreIter(n)%% Input: n = 拉盖尔多项式的次数%% Output: p = n次拉盖尔多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %L0(x) = 1p = 1;return;elseif n == 1 %L1(x) = -x+1p = [-1 1];return;endpBk = 1; %初始化三项递推公式后项为L0pMid = [-1 1]; %初始化三项递推公式中项为L1for i = 0:n-2pMidCal1 = zeros(1,i+3); %构造用于计算的x*Ln+1(x)pMidCal1(1:i+2) = pMid;pMidCal2 = zeros(1,i+3); %构造用于计算的Ln+1(x)pMidCal2(2:i+3) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的Ln(x)pBkCal(3:i+3) = pBk;pFwd =( (2*i+3)*pMidCal2 - pMidCal1 - (i+1)*pBkCal )/ (i+2); %拉盖尔多项式三项递推公式Ln+2(x) = (2*n+3-x)*Ln+1(x) - (n+1)^2*Ln(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把拉盖尔多项式最高次项系数归一化function p = HermiteIter(n)% HermiteIter 用递推的方法计算n次埃尔米特多项式的系数向量Hn+2(x) = 2*x*Hn+1(x) - 2*(n+1)*Hn(x)%% Synopsis: p = HermiteIter(n)%% Input: n = 埃尔米特多项式的次数%% Output: p = n次埃尔米特多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %H0(x) = 1p = 1;return;elseif n == 1 %H1(x) = 2*xp = [2 0];return;endpBk = 1; %初始化三项递推公式后项为L0pMid = [2 0]; %初始化三项递推公式中项为L1for i = 0:n-2pMidCal = zeros(1,i+3); %构造用于计算的x*Hn+1(x)pMidCal(1:i+2) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的Hn(x)pBkCal(3:i+3) = pBk;pFwd =2*pMidCal - 2*(i+1)*pBkCal; %埃尔米特多项式三项递推公式Hn+2(x) = 2*x*Hn+1(x) - 2*(n+1)*Hn(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把拉盖尔多项式最高次项系数归一化function r = BinSolve(fun, a, b, tol)% BinSolve 用二分法解方程f(x)=0在区间[a,b]的根%% Synopsis: r = BinSolve(fun, a, b)% r = BinSolve(fun, a, b, tol)%% Input: fun = (string) 需要求根的函数% a,b = 寻根区间上下限% tol = (optional)误差，默认为5e-9%% Output: r = 在寻根区间内的根if nargin < 4tol = 5e-9;endXb = RootBracket(fun, a, b); %粗略寻找含根区间[m,n] = size(Xb);r = [];nr = 1; %初始化找到的根的个数为1maxit = 50; %最大二分迭代次数为50for i = 1:ma = Xb(i,1); %初始化第i个寻根区间下限b = Xb(i,2); %初始化第i个寻根区间上限err = 1; %初始化误差k = 0;while k < maxitfa = feval(fun, a); %计算下限函数值fb = feval(fun, b); %计算上限函数值m = (a+b)/2;fm = feval(fun, m);err = abs(fm);if sign(fm) == sign(fb) %若中点处与右端点函数值同号，右端点赋值为中点b = m;else %若中点处与左端点函数值同号或为0，左端点赋值为中点a = m;endif err < tol %如果在a处函数值小于tolr(nr) = a; %一般奇点不符合该条件，这样可以去除奇点nr = nr + 1; %找到根的个数递增k = maxit; %改变k值跳出循环endk = k + 1; %二分迭代次数递增endendfunction X = powerX(x,a,b)% powerX 对给定向量(x1, x2,..., xn)返回增幂矩阵(x1^a, x2^a,..., xn^a; x1^a+1, x2^a+1,..., xn^a+1; ...; x1^b, x2^b,..., xn^b;)%% Synopsis: X = powerX(x,a,b)%% Input: x = 需要返回增幂矩阵的向量% a,b = 寻根区间上下限%% Output: X = 增幂矩阵(x1^a, x2^a,..., xn^a; x1^a+1, x2^a+1,..., xn^a+1; ...; x1^b, x2^b,..., xn^b;)if round(a) ~= a | round(b) ~= berror('a,b must be integers');elseif a >= berror('a must be smaller than b!');endx = x(:)';row = b-a+1;col = length(x);X = zeros(row, col);for i = b:-1:aX(b-i+1,:) = x.^i;Endfunction [f, dfdx] = fun1_1(x)f = cos(x) - x;dfdx = -sin(x) - 1;function [f, dfdx] = fun1_2(x)f = exp(-x) - sin(x);dfdx = -exp(-x) - cos(x);function [f, dfdx] = fun2_1(x)f = x - exp(-x);dfdx = 1 + exp(-x);function [f, dfdx] = fun2_2(x)f = x.^2 - 2*x*exp(-x) + exp(-2*x);dfdx = 2*x - 2*exp(-x) + 2*x*exp(-x) - 2*exp(-2*x);function y = LegendreP6(x)p = LegendreIter(6);X = powerX(x,0,6);y = p*X;function y = ChebyshevT6(x)p = ChebyshevIter(6);X = powerX(x,0,6);y = p*X;function y = LaguerreL5(x)p = LaguerreIter(5);X = powerX(x,0,5);y = p*X;function y = HermiteH6(x)p = HermiteIter(6);X = powerX(x,0,6);y = p*X;思考题（1）由于Newton法具有局部收敛性，所以在实际问题中，当实际问题本身能提供接近于根的初始近似值时，就可保证迭代序列收敛，但当初值难以确定时，迭代序列就不一定收敛。

材料科学与工程实验教学中心实验报告课程名称实验名称牛顿迭代法方程求根专业班级学号姓名实验日期材料科学与工程实验教学中心实验报告一．实验目的通过对牛顿迭代法作编程练习与上机运算，进一步体会牛顿迭代法的不同特点二．实验原理（方法）给定初始值x0，ε为根的容许误差，η为｜f(x)｜的容许误差，N为迭代次数的容许值。

①如果f′(x0)=0或迭代次数大于N，则算法失败，结束；否则执行②②计算x1=x0-f(x0)/f′(x0)。

③若｜x1-x0｜<ε或｜f(x1)｜<η，则输出x1，程序结束；否则执行④④令x0=x1，转向①三．实验仪器设备及操作步骤电脑一台操作步骤：打开电脑，打开VB程序，编辑程序四．实验数据及处理（N-S图和程序）f(x)=x³+x²-3x-3结束Private Sub Command1_Click()Dim x0, x!, eps!, kx0 = Val(InputBox("x=0", "ÊäÈë³õÖµ", 0.5))eps = Val(InputBox("eps=", "ÊäÈëepsµÄÖµ", 0.000005)) x = x0 - f(x0) / p(x0)k = 1PrintDo While Abs(x - x0) >= epsPrint "k=" & k, "x=" & x, "f(x)" & f(x)x0 = xk = k + 1x = x0 - f(x0) / p(x0)LoopEnd SubFunction f(ByVal x!) As Singlef = x ^ 3 + x ^ 2 - 3 * x - 3End FunctionFunction p(ByVal x!) As Singlep = 3 * x ^ 2 + 2 * x - 3End Function五．实验结果分析及结论（算例及结果）六．思考题成绩指导教师日期Welcome To Download !!!欢迎您的下载，资料仅供参考！。

MATLAB计算方法迭代法牛顿法二分法实验报告实验报告一、引言计算方法是数学的一门重要应用学科，它研究如何用计算机来解决数学问题。

其中，迭代法、牛顿法和二分法是计算方法中常用的数值计算方法。

本实验通过使用MATLAB软件，对这三种方法进行实验研究，比较它们的收敛速度、计算精度等指标，以及它们在不同类型的问题中的适用性。

二、实验方法1.迭代法迭代法是通过不断逼近解的过程来求得方程的根。

在本实验中，我们选择一个一元方程f(x)=0来测试迭代法的效果。

首先，我们对给定的初始近似解x0进行计算，得到新的近似解x1，然后再以x1为初始近似解进行计算，得到新的近似解x2，以此类推。

直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。

本实验将通过对复杂方程的迭代计算来评估迭代法的性能。

2.牛顿法牛顿法通过使用函数的一阶导数来逼近方程的根。

具体而言，对于给定的初始近似解x0，通过将f(x)在x0处展开成泰勒级数，并保留其中一阶导数的项，得到一个近似线性方程。

然后，通过求解这个近似线性方程的解x1，再以x1为初始近似解进行计算，得到新的近似解x2，以此类推，直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。

本实验将通过对不同类型的方程进行牛顿法的求解，评估它的性能。

3.二分法二分法是通过将给定区间不断二分并判断根是否在区间内来求方程的根。

具体而言，对于给定的初始区间[a,b]，首先计算区间[a,b]的中点c，并判断f(c)与0的大小关系。

如果f(c)大于0，说明解在区间[a,c]内，将新的区间定义为[a,c]，再进行下一轮的计算。

如果f(c)小于0，说明解在区间[c,b]内，将新的区间定义为[c,b]，再进行下一轮的计算。

直到新的区间的长度小于规定的误差阈值为止。

本实验将通过对复杂方程的二分计算来评估二分法的性能。

三、实验结果通过对一系列测试函数的计算，我们得到了迭代法、牛顿法和二分法的计算结果，并进行了比较。

数值分析实验报告x=0.5;y=x-exp(-x);z=x-y/(1+exp(-x));k=1;while abs(z-x)>=1.0e-8 k=k+1;x=z;y=x-exp(-x);z=x-y/(1+exp(-x));endk如图所示结果为下图2、用Newton 切线法求方程310x x --=在1.5附近的一个根.主要代码：clear; x=1.5; y=x^3-x-1; z=x-y/(3*x^2-1); k=1;while abs(z-x)>=1.0e-8 k=k+1; x=z; y=x^3-x-1; z=x-y/(3*x^2-1); end k z 如图所示结果为下图3、用Newton 切线法计算3k =，4k =时，方程2(2)(3)0k x x --=在1.3附近的根(2)以及2.5附近的根(3)K=3时在1.3附近的根主要代码：clear;x=1.3;y=(x-sqrt(2))^3*(x^2-3);m=3*(x^2 - 3)*(x - 2^(1/2))^2 + 2*x*(x - 2^(1/2))^3; z=x-y/m;k=1;while abs(z-x)>=1.0e-8k=k+1;x=z;y=(x-sqrt(2))^3*(x^2-3);m=3*(x^2 - 3)*(x - 2^(1/2))^2 + 2*x*(x - 2^(1/2))^3；z=x-y/m;endk结果为下图K=4时在1.3附近的根主要代码结果为下图K=4时在2.5附近的根主要代码clear;x=2.5;y=(x-sqrt(2))^4*(x^2-3);m= 4*(x^2 - 3)*(x - 2^(1/2))^3 + 2*x*(x - 2^(1/2))^4; z=x-y/m;k=1;while abs(z-x)>=1.0e-5k=k+1;x=z;y=(x-sqrt(2))^4*(x^2-3);m= 4*(x^2 - 3)*(x - 2^(1/2))^3 + 2*x*(x - 2^(1/2))^4; z=x-y/m;endkz结果为下图K=3时在2.5附近的根主要代码结果为下图四、调试和运行程序过程中产生的问题及采取的措施：1、编译时，想用diff求出y的一阶导数，但出现错误，必须把x变成syms形式，编译过程出现错误，就采取把y的一阶导数先算出来，带入newton迭代公式中，程。

实习报告一、实验目的通过上机实习，利用计算机编程进行数值分析课程中关于牛顿迭代法的求解。

由于所需迭代次数较多、数据运算复杂，手工求解非常困难甚至无法进行，通过计算机编程实现相应的算法可以大大提高计算效率和准确率。

二、实验原理牛顿法是求方程f(x)=0近似根的重要方法，是非线性方程线性化的方法。

牛顿迭代法的一般迭代公式:x n+1=x n-f(x n)/f’(x n) n=0,1,2……牛顿迭代法就是用线性的根来逐步逼近方程f(x)=0的跟x*,因而也称为切线法。

三、实验过程1、问题题目：求f（x）=x^3+x^2-3*x-3=0在1.5附近的根，初始值取1.0，1.5，2.5，要求根的精度为0.000001。

2、实验环境本实验在C#环境下进行编程实现。

3、编程思路使用C#建立一个窗体应用程序并进行界面设计，界面包括三个文本框，分别用于输入初始值、输出迭代次数、输出近似值。

同时包括三个按钮，单击按钮时实现的功能分别是进行迭代计算、清空文本框内容以便进行下一次运算、退出程序。

单击Calculate按钮时，首先将初始值输入文本框的值赋给一个double变量，然后设计了一个使用牛顿迭代公式的循环结构，通过判断前每一次迭代后的结果和前一次迭代的值进行比较，当两者相差不超过0.000001时终止循环，并将循环的次数和最后的近似值在下面两个文本框中显示。

设计界面如图所示：所用代码如下：using System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Linq;using System.Text;using System.Windows.Forms;namespace ZUOYE{publicpartialclass Form1 : Form{public Form1(){InitializeComponent();}privatevoid button1_Click(object sender, EventArgs e){double a = double.Parse(txtInput.Text);double b = a - (a * a * a + a * a - 3 * a - 3) / (3 * a * a + 2 * a - 3); int num = 1;for(num=1;System.Math.Abs(a-b)>0.000001;num++){double temp = b;b = temp - (temp * temp * temp + temp * temp - 3 * temp-3) / (3 * temp *temp + 2 * temp - 3);a = temp;}txtNum.Text = num.ToString();txtOutput.Text = Math.Round(b, 6).ToString();}privatevoid button3_Click(object sender, EventArgs e){this.Close();}privatevoid button2_Click(object sender, EventArgs e){txtInput.Clear();txtNum.Clear();txtOutput.Clear();}}}四、实验结果1、当初始值为1.0时：2.初始值为1.5时：3.初始值为2.5时：五、实验总结通过进行上机实习，动手进行相关算法的编程实现，使我对牛顿迭代法的原理有了更加深刻的认识和理解。