波浪理论

波浪理论波浪理论的基本概念和规则波浪理论是描述水波的基本概念和规则的一套理论体系。

它涵盖了波的形成、传播、干涉、衍射和折射等方面的内容，是研究和解释波动现象的重要工具。

波浪是由介质中的微小扰动引起的能量传播现象。

常见的水波是由水面上的微小扰动引起的，这些扰动以波的形式传播到周围的空间中。

波的主要特征有振幅、频率、波长和相速度等。

波浪理论中的基本概念包括：1.波长（λ）：波长是波的长度，定义为两个相邻波峰（或波谷）之间的距离。

波长和波的频率有关，两者之间的关系为v=fλ，其中v是波的速度。

2.频率（f）：频率是波动物体所作往复运动的次数，定义为每秒钟振动的次数。

频率和波长之间的关系为f=v/λ。

3.振幅（A）：振幅是波的最大偏离量，它表示波动的强度和能量的大小。

4.相位（φ）：相位是描述波的位置的物理量，它表示在其中一时刻波的位置相对于特定位置的偏离程度。

5.相速度（v）：相速度是波的传播速度，表示波峰（或波谷）的传播速度。

相速度和频率、波长之间的关系为v=fλ。

波浪理论还有一些重要的规则，例如：1.波动原理：波动原理是指波在传播过程中会继续向前传播，并且传播的速度是固定的。

2.波的干涉：当两个或多个波相遇时，它们会相互作用并产生干涉现象。

干涉可以是构造性的，即波峰和波峰相遇，加强波的振幅；也可以是破坏性的，即波峰和波谷相遇，减小波的振幅。

3.波的衍射：波在遇到障碍物或边缘时会发生弯曲和散射现象，这就是波的衍射。

波的衍射现象表明波动的传播不仅局限于直线传播，其能量也可以传播到遮挡物的后方。

4.波的折射：当波从一种介质传播到另一种介质时，其传播速度和传播方向都会发生变化，这个现象称为波的折射。

波浪理论的应用非常广泛，不仅可以用于研究和理解水波的传播和干涉现象，还可以应用于声波、光波等其他类型的波动现象的研究。

在实际应用中，波浪理论被广泛应用于水利工程、海洋工程、声学和光学等领域，为解决相关问题提供了有效的工具和方法。

波浪理论的原理和应用1. 原理介绍波浪理论是一种描述水波运动的数学理论，通过对水波的传播、干涉和衍射等现象进行研究，来解释波浪的形成和变化。

波浪通常是由风力、地震或潮汐等因素引起的水面运动所产生的，因此波浪理论也广泛应用于海洋工程、航海和天气预报等领域。

2. 波浪类型根据波浪的特征和形成原因，波浪可以分为以下几种类型：•传统波浪：由风力引起，在海洋中传播并最终破碎。

传统波浪的高度和频率取决于风力的强弱和持续时间。

•音速波浪：音速波浪是一种特殊的波浪类型，它的速度接近声速。

•温度波：由温度差异引起的波浪，例如热气球上升时形成的波浪。

3. 波浪的基本参数波浪具有下列基本参数，用于描述波浪的特性：•波长（Wavelength）：波浪的长度，即相邻两个波峰或波谷之间的距离。

•波高（Wave height）：波浪波峰和波谷之间的垂直距离。

•周期（Period）：波浪传播一个波长所需要的时间。

•相速度（Phase velocity）：波浪传播的速度。

4. 波浪的传播波浪的传播是指波浪从产生地传播到目的地的过程。

波浪在传播过程中会遇到折射、反射和衍射等现象，这些现象使得波浪的传播路径发生变化。

•折射：当波浪传播通过介质变化时，波峰和波谷会发生偏折。

•反射：波浪碰到障碍物时，会发生反射现象，即部分波浪被反射回去。

•衍射：波浪遇到障碍物或传播路径发生变化时，会发生衍射现象，即波浪通过障碍物的侧边传播。

5. 波浪的干涉波浪的干涉是指两个或多个波浪相遇并产生干涉现象的过程。

干涉现象会导致波峰和波谷的增强或抵消，从而改变波浪的形状和能量。

•构造性干涉：当两个波浪相遇并位于同相位时，会出现波峰和波峰相加或波谷和波谷相加的情况，使得波浪的振幅增强。

•破坏性干涉：当两个波浪相遇并位于反相位时，会出现波峰和波谷相加的情况，使得波浪的振幅减小甚至消失。

6. 波浪的应用波浪理论除了在理论物理研究中有着重要的地位外，还应用于许多实际领域。

什么是波浪理论？波浪理论，是在1934年山美国一位已退休的会计师艾昭特所建立的专有关股票价格波动和投资技术的理论。

艾略特经过多年对美国道·琼斯工业平均指数运动的形态、调整比率及时间周期的详尽统计，运用数学原理进行分析，力图客观地描述股价运动的基本规则，从而达到预测股市运动趋势的目的。

波浪理论的基本思想是：股价趋势是大众心理的反映。

虽然人的心理活动千变万化，难以捉摸，但大众群体心理活动的总体效应却呈现出某种规则，这种总体效应反映在市场上，就形成了价格的波动。

通过数学与图表的结合，分析这种规则，把握市场的变化，就能做出正确的投资决策。

由于波浪理论主要反映大众心理，因此参与市场的人愈多，其准确性愈高。

波浪理论的基本内容是。

（1）股市波动的基本形态是由一个上升主波和一个调整波所构成。

一个上升主波又由5个浪所组成、调整波则由3个浪所组成，因此，这8个浪便形成一个完整的艾略特周期。

此外，主波的5个浪还可以分出21个小浪，调整波的3个浪也可以分出13个小浪，再细分下去就出现一个由144个小浪构成的完整的大周期。

由此可见。

艾略特波浪可由一个超级大波一级一级分出无数的细微小泊。

（2）股价的一个运动趋势形成后必有相反运动趋势发生，即上升与下跌交替进行。

（3）市场形态并不随时间改变，波浪时而伸展时而压缩，们其基本形态不变。

作为波根理论中的许多方法和结论是以奇异数字组合为依据，奇异数字组合是由1开睛，直至无限，数学组成如下J，1，2J。

5，8，13，21，34，55，89，144……此数学组成具有下列有趣而又重要的特性：（1）任何一个数都是内前两个数之和构成。

（2）除了最初的四个数（1，1，2，3）之外，任何一个数除以其后的一个数，结果都趋向于0．618（即黄金比率）。

（3）除了最初的四个数之外、任何一个数除以其前的一个数，结果都趋向于1.618。

艾略特认为：将奇异数字组合中0.618及1.618的黄金比率应用于波浪分析。

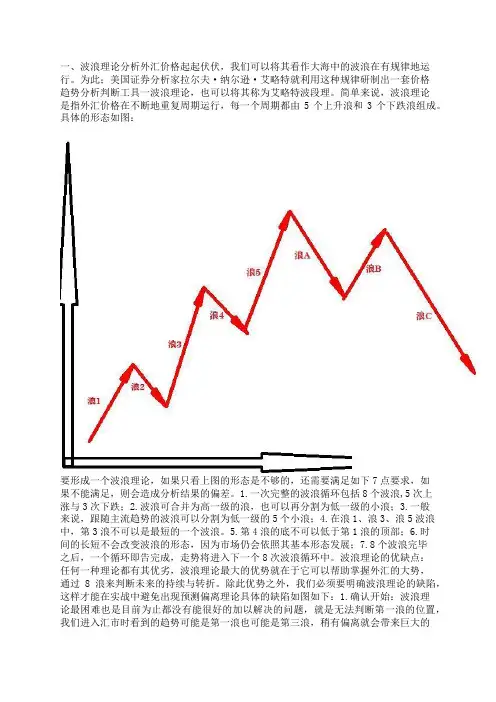
一、波浪理论分析外汇价格起起伏伏，我们可以将其看作大海中的波浪在有规律地运行。

为此；美国证券分析家拉尔夫·纳尔逊·艾略特就利用这种规律研制出一套价格趋势分析判断工具一波浪理论，也可以将其称为艾略特波段理。

简单来说，波浪理论是指外汇价格在不断地重复周期运行，每一个周期都由5个上升浪和3个下跌浪组成。

具体的形态如图：要形成一个波浪理论，如果只看上图的形态是不够的，还需要满足如下7点要求，如果不能满足，则会造成分析结果的偏差。

1.一次完整的波浪循环包括8个波浪,5次上涨与3次下跌；2.波浪可合并为高一级的浪，也可以再分割为低一级的小浪；3.一般来说，跟随主流趋势的波浪可以分割为低一级的5个小浪；4.在浪1、浪3、浪5波浪中，第3浪不可以是最短的一个波浪。

5.第4浪的底不可以低于第1浪的顶部；6.时间的长短不会改变波浪的形态，因为市场仍会依照其基本形态发展；7.8个波浪完毕之后，一个循环即告完成，走势将进入下一个8次波浪循环中。

波浪理论的优缺点：任何一种理论都有其优劣，波浪理论最大的优势就在于它可以帮助掌握外汇的大势，通过8浪来判断未来的持续与转折。

除此优势之外，我们必须要明确波浪理论的缺陷，这样才能在实战中避免出现预测偏离理论具体的缺陷如图如下：1.确认开始：波浪理论最困难也是目前为止都没有能很好的加以解决的问题，就是无法判断第一浪的位置，我们进入汇市时看到的趋势可能是第一浪也可能是第三浪，稍有偏离就会带来巨大的损失。

2.浪中有浪：波浪理论是浪中有浪，可以无限伸延，在一次上升浪中，可以包含无数的上升小浪与下跌小浪跌浪，持续时间可长几年甚至几十年，同时下跌浪也可以包含无数小浪。

3.难以断顶：波浪理论的持续时间非常长許多时候是无法判断是否岀现顶部或者底部，这就很难预测是否开始了新级的波浪；4.主观性强：波浪理论是一套主观分析工具，毫无客观准则，因此它在变化万千的汇市中会十分危险，出错机会也比较大。

波浪理论图解波浪理论是一种技术分析工具，旨在通过观察价格图表中的波浪模式来预测市场走势。

波浪理论由R.N.艾略特于20世纪30年代提出，并在市场分析中得到广泛应用。

本文将详细解释波浪理论的基本原理、应用方法以及注意事项。

波浪理论的基本原理是市场的价格运动可以划分为上升和下降的波浪。

艾略特将市场的价格波动归结为五个上升波浪和三个下降波浪的循环。

这个循环称为“艾略特波动序列”。

具体来说，五个上升波浪被编号为1、2、3、4、5，分别表示远期上涨波浪的五个不同阶段。

然后，三个下降波浪被编号为a、b、c，表示中期/长期下跌波浪。

根据波浪理论，这个序列是构成市场价格走势的基本单位。

波浪理论在市场分析中的应用主要有两个方面。

首先，它可以用来预测市场的未来走势。

根据波浪理论，市场的价格会按照特定的波浪模式进行上涨和下跌。

通过观察和分析当前市场价格图表中的波浪模式，可以推断出接下来市场可能的价格走势。

其次，波浪理论可以用于制定交易策略。

根据波浪理论，市场价格的波浪模式是可以预测的，投资者可以根据这些波浪模式来制定买入和卖出的时机。

在使用波浪理论进行市场分析和交易时，需要注意以下几点。

首先，波浪理论并不是完全准确的预测工具。

市场的价格走势受到各种因素的影响，包括经济、政治、社会等多个方面。

波浪理论只是其中一种技术分析工具，不能完全准确地预测市场走势。

其次，波浪理论需要长时间的观察和实践才能掌握。

艾略特本人在研究和总结波浪理论过程中花费了很多时间和精力，新手投资者需要持续学习和实践才能熟练掌握波浪理论的应用。

再次，波浪理论只是一种辅助工具，不应该是唯一的决策依据。

投资者在做出决策时应该综合考虑多种因素，包括基本面分析、技术分析和风险管理等。

综上所述，波浪理论是一种通过观察价格图表中的波浪模式来预测市场走势的技术分析工具。

它的基本原理是市场价格的波动可以按照特定的波浪模式进行上涨和下跌。

波浪理论可以用于预测市场未来走势和制定交易策略。

波浪理论形态总结归纳波浪理论是由美国分析师艾略特（R.N. Elliott）于20世纪30年代提出的一套股市分析方法。

该理论认为市场价格变动呈现出特定的波浪形态，这些波浪形态可以被用来预测市场走势。

本文将对波浪理论的基本原理及常见的形态进行总结归纳。

一、波浪理论的基本原理波浪理论基于以下三个基本原理：1. 自相似性原理：波浪理论认为市场价格的走势具有自相似性，即在不同的时间尺度上，市场价格的波动会呈现出相似的模式。

2. 原则性原理：波浪理论认为市场价格的变动是有规律可循的，可以按照一定的规则进行分类和预测。

3. 图案原理：波浪理论认为市场价格的波动会形成一系列特定的图案，这些图案反映了市场参与者的心理和行为。

基于以上原理，波浪理论将市场价格的波动划分为上升波段和下降波段，并根据波动的特点和比例建立了一套形态系统。

二、常见的波浪形态1. 五浪上升形态（上涨趋势）：五浪上升形态是由连续的五个上升波段组成的，首先是三浪上涨（1、3、5），然后是两浪回调（2、4）。

通常情况下，第五浪的高点不会超过第三浪的高点。

2. 三浪下降形态（下跌趋势）：三浪下降形态是由连续的三个下降波段组成的，首先是一浪下跌，然后是两浪反弹。

通常情况下，第三浪的低点不会超过第一浪的低点。

3. 扩展形态：扩展形态是指在上升或下降趋势中，波浪的长度超过了正常比例。

例如，五浪上升中的第三浪或第五浪较长，或者三浪下降中的一浪较长。

4. 对称形态：对称形态是指波浪的长度基本相等，没有明显的倾向性。

这种形态表明市场处于盘整或震荡的状态。

5. 异常形态：异常形态是指不符合波浪理论规则的波浪形态，通常是由于市场中的突发事件或其他非正常情况引起的。

这种形态难以预测和分析。

三、波浪理论的应用波浪理论可以应用于各种金融市场，包括股票、期货和外汇市场。

投资者可以通过观察市场价格的波浪形态，来进行市场走势的预测和交易决策。

具体应用波浪理论时，可以结合其他技术指标和交易工具，例如移动平均线、相对强弱指标等，以提高预测准确性和交易效果。

经典波浪理论图解波浪理论波浪理论是由Nalph Nelson Eilliott在1938年所提出的，他将市场上的价格趋势型态，归纳出几个不断反复出现的型态。

Eilliott归纳整个市场的价格波动型态，发现不论趋势的层级大小，均遵循着一种五波上升三波下降的基本节奏，五波的上升趋势可分为三个推动波(impulse wave)以及二个修正波(corrective wave)，三个推动波分别为第1、3及5波，而修正波则为第2及第4波；在三波下降趋势波则分为、b、c三波。

这上升及下降的八波形成一个八个波动的完整周期，而且这样的周期将不断的反覆持续，并且这八个波动的完整周期的现象普遍存在于各种时间刻度，而形成各种大小的波浪，每一个波都可包含了更小规模的波动，并且每一个波也都为另一个更大刻度的波所包含。

波浪理论经典图解几点重要规则：◇正确的波数计算注意, 4的位置高于1的位置,如此第4波与第1波便不会重迭。

◇第三波通常是推动波中最长的一波(即主升段)。

即使不是，也绝不会是推动波中最短的一波。

◇修正波的最大修正幅度为前一波的次级修正波的位置。

例如，第(4)波最大的修正幅度，为第(3)波中的第4波的低点，这是第(4)波的最大修正位置◇交替出现原则--上升波中简单型与横向整理交替出现、修正波中平台整理与三角型态或锯齿型态交替出现--简单型与复杂型交替出现。

波浪理论比较复杂、同一期间可能有多种数浪方式，需要配合其他工具加以排除、选择，因此本人不建议初学者使用。

波浪理论不完全手册波浪理论不完全手册R·E·艾略特（R·E·Elliot）所发明的一种价格趋势分析工具，它是一套完全*而观察得来的规律，可用以分析股市指数、价格的走势，它也是世界股市分析上运用最多，而又最难于了解和精通的分析工具。

艾略特认为，不管是股票还是商品价格的波动，都与大自然的潮汐，波浪一样，一浪跟着一波，周而复始，具有相当程度的规律性，展现出周期循环的特点，任何波动均有迹有循。

波浪理论口诀及图解1. 引言在物理学和工程学中，波浪是一个广泛研究的领域，涉及到波浪的形成、传播、相互作用等方面。

理解波浪理论对于解释海洋、大气中出现的波浪现象以及设计和维护海洋和沿海结构非常重要。

本文将介绍一些波浪理论的口诀，帮助读者快速掌握波浪理论的主要概念。

2. 线性波浪理论2.1 波浪参数线性波浪理论是一种简化的波浪模型，适用于波浪振幅相对较小的情况。

在线性波浪理论中，常用的波浪参数包括：•波高（H）：波浪顶部到波浪底部的垂直距离。

•波长（L）：波浪的水平距离，即两个相邻波峰或波谷之间的距离。

•波周期（T）：波浪从一个波峰到相邻波峰所需时间。

2.2 波浪频率波浪频率是指波浪的周期倒数，通常被表示为 f。

波浪频率与波浪周期的关系为：[ f = ]2.3 波速波速是指波浪峰从一个点传播到相邻点所需的时间，通常被表示为 c。

波速与波长和波周期的关系为：[ c = ]2.4 波浪传播线性波浪理论中，波浪的传播可以通过以下方程来描述：[ + g = 0 ]其中，() 是水面振动的垂直位移，(t) 是时间，(x) 是水平方向的位置，(g) 是重力加速度。

3. 非线性波浪理论3.1 非线性波浪参数非线性波浪理论适用于波浪振幅较大的情况，考虑波浪的非线性效应。

除了线性波浪参数外，非线性波浪理论还引入了以下参数：•波动陡度（S）：波浪高度与波长之比。

•波浪速度（U）：波浪峰的平均速度。

3.2 非线性波浪理论的基本方程非线性波浪理论包括一个非线性波动方程，用于描述非线性波浪的传播。

该方程可以表示为：[ + g + ( U ) = 0 ]3.3 非线性波浪的稳定性非线性波浪可能出现不稳定现象，如波浪破碎、波浪合并等。

非线性波浪的稳定性可以通过波浪理论中的一些数学条件来判断，如雅可比判别式等。

4. 小波理论4.1 小波变换小波理论是一种分析信号的工具，可以分解信号成不同频率和时间范围的成分。

小波变换可以将信号表示为不同尺度和位置的小波基函数的线性组合。

波浪理论原理
波浪理论是一种描述市场波动的技术分析方法，它认为价格的波动并非完全随机，而是有一定的规律可循。

波浪理论的提出者是美国技术分析大师艾略特，他通过对股市长期波动的观察和研究，总结出了波浪理论的基本原理。

波浪理论的核心概念是市场价格的波动是由投资者情绪的波动所驱动的。

艾略
特认为，市场的价格波动呈现出一定的规律性，可以通过波浪理论来进行预测。

波浪理论主要包括了五个基本波动模式，即上升波浪、下降波浪、调整波浪、扩展波浪和三角形波浪。

在波浪理论中，上升波浪和下降波浪是市场价格长期趋势的表现形式，它们分
别代表了市场的牛市和熊市。

而调整波浪则是在上升波浪或下降波浪形成之后，市场价格出现短期回调的现象。

扩展波浪则是指在市场价格出现快速上涨或下跌的情况下，波浪的幅度会超过之前的波浪幅度。

三角形波浪则是指市场价格在形成一定的图表形态后，会出现价格的收敛和波动幅度的缩小。

波浪理论的应用可以帮助投资者更好地把握市场的走势，提高投资的准确性。

通过对市场价格波动的规律性进行分析，投资者可以更好地选择买入和卖出时机，从而获得更好的投资收益。

在实际操作中，投资者可以通过对市场价格波动的观察和分析，结合波浪理论
的基本原理，来制定自己的投资策略。

在进行技术分析时，可以结合波浪理论来进行价格波动的预测，从而更好地把握市场的走势。

总的来说，波浪理论是一种重要的技术分析方法，它通过对市场价格波动的规
律性进行分析，帮助投资者更好地把握市场的走势，提高投资的准确性。

通过对波浪理论的学习和应用，投资者可以更好地进行市场分析，从而获得更好的投资收益。

波浪理论原理
波浪理论是对海洋波浪形成、传播和衰减的原理进行研究的学科。

波浪是由于风的作用而在海洋表面产生的无规则的涨落。

波浪的形成过程主要包括风的作用和海水的相互作用。

首先，风是波浪形成的主要驱动力。

风的吹拂使得海面上的水分子受到扰动，形成一个个起伏的涨落。

当风速增大时，海面上的波浪也会变得更加强烈。

其次，波浪的形成还与海水的密度和深度有关。

在深海区域，波浪会比较大而有规律；而在浅海或者沿海地区，波浪则会变得较小而且更加复杂。

海水的密度差异会导致波浪的传播速度发生改变，同时海底地形的变化也会对波浪形成产生影响。

此外，波浪的衰减和消散也是波浪理论中重要的一部分。

波浪在传播过程中会受到摩擦、消散和干扰等因素的影响而逐渐减弱。

因此，波浪在传播过程中会逐渐失去能量，并最终消散在海洋中。

总的来说，波浪理论通过研究波浪的形成、传播和消散过程，揭示了波浪的物理特性和海洋动力学。

这对于海洋工程、海洋资源开发以及海洋气象等方面具有重要的应用价值。