初二数学经典题练习及答案.docx
- 格式:docx
- 大小:78.27 KB
- 文档页数:7

初二数学试题(考试时间:100分钟 满分:100分)一、选择题(本大题共8题,每题2分,共16分)1.若分式21x -有意义,则x 的取值范围是A .x≠1B .x >1C .x=1D .x <1 2.下列分式中,属于最简分式的是A .42x B .221x x + C .211x x -- D .11x x --3.函数xky =的图象经过点(1,-2),则下列各点中也在该图像上的点是 A .( 1,2 ) B . ( -1,-2 ) C. (-1,2) D .( 2,1) 4.在反比例函数1k y x-=的图象的每个象限内,y 随x 的增大而增大,则k 值可以是 A .-1 B .1 C .2 D .35.函数k kx y +=,xky =(0≠k )在同一坐标系中的图像大致是6.下列式子:(1)y x y x y x -=--122;(2)ca b a a c a b --=--;(3)1-=--b a a b ;(4)y x yx y x y x -+=--+- 中,正确的有A .1个B .2 个C .3 个D .4 个7.两个相似三角形的对应边分别是cm 15和cm 23,它们的周长相差cm 40,则这两个三角 形的周长分别是A .cm 75,cm 115B .cm 60,cm 100C .cm 85,cm 125D .cm 45,cm 85 8.一个铝质三角形框架三条边长分别为24cm 、30cm 、36cm ,要做一个与它相似的铝质三角形框架,现有长为18cm 、40cm 的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有 A .0种 B .1种 C .2种 D .3种二、填空题:本大题共10小题,每小题2分,共20分。
9.21()2- =_______. 10.当x=________,2x -3与543x +的值互为倒数. 11.点C 为线段AB 的黄金分割点且AB = 2,则较小线段BC ≈ (精确到0.01). 12.在比例尺1∶8000000的地图上,量得太原到北京的距离为6.4厘米,则太原到北京的实际距离为 千米.13.现在有3个数:1、2、3请你再添上一个数,使这4个数成比例,你所添的数是 . 14.如图,12∠=∠,添加一个条件 (写出一个即可),使得ADE ∆∽ACB ∆.15.若分式1322+-x x 的值是负数,则x 的取值范围是______________. 16.若分式方程233x mx x -=--有增根,则m 的值为_______________. 17.已知xky =(0<k )的图像上有两点A(1x ,1y ),B(2x ,2y ),且210x x <<,则1y 与2y 的大小关系是________________(用“<”连接). 18.如图,双曲线xy 8-=的图像经过矩形OABC 的顶点B , 两边OA ,OC 在坐标轴上,且OC=2OA ,M ,N 分别为 OA ,OC 的中点,BM 与AN 交于点E ,则四边形EMON 的面积为 . 三、解答题:(本大题共9小题,共64分) 19.(本题8分) (1)21422++--a a a (2)解分式方程: 3233252---=--x x x x20.(本题6分)先化简再求值:⎪⎪⎭⎫⎝⎛++÷--a b ab a ab a b a 22222,其中a=2,1-=b .21EDCBA21.(本题6分)已知121y y y y ,-=与x +2成正比例,2y 与x 成反比例,且当x =1时, y =4;当x =2时,y =7. (1)求y 与x 的函数关系; (2)求x =21时,y 的值.22.(本题6分)如图,在Rt OAB △中,90OAB ∠=o,且点B 的坐标为(4,2). (1)以O 为位似中心,将△OAB 缩小,使得缩小后的△OA 1B 1与△OAB 的相似比为1∶2,画出△OA 1B 1.(所画 △11B OA 与△OAB 在原点两侧).(2分)(2)画出OAB △绕点O 逆时针...旋转90o后的22OA B △, 求△BB 1B 2的面积.(2分+2分)23.(本题6分)在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.在数学课上,老师给出这样一道题:我们知道:2+2=2×2,3+23=3×23,4+34=4×34,…… 请你根据上面的材料归纳出a 、b(a >1,b >1)一个数学关系式. 我们由此得出的结论为:设其中一个数为a ,另一个数为b ,则1-=a ab ; 在数学课上小刚同学又发现了一个新的结论是:;2ab abb a =++ 你认为小刚的结论正确吗?请说明理由.24.(本题6分)甲、乙两公司为“4.20四川芦山地震”灾区捐款300000元.已知乙公司比甲公司人均多捐20元,且甲公司的人数比乙公司的人数多20%,问甲、乙两公司各有多少人?25.(本题8分)如图,在△ABC 中,D 是BC 边上一点,E 是AC 边 上一点.且满足AB=10,AE =2,EC =3, ∠ADE =∠C (1)求证:△ADE ∽△ACD ;(4分) (2)求证:∠CED =∠B .(4分)26.(本题8分)如图,已知线段AB ∥CD,AD 与BC 相交于点K ,E 是线段AD 上的一动点,连接BE ,BE 的延长线交DC 的 延长线交于点F(1)写出图中的所有相似三角形;(2分) (2)若BE 平分∠ABC , ①当CD=1,AB=2, AE=21AD 时,求出BC 的长;(3分) ②当CD=a ,AB=b ,AE=n1AD 时,求出BC 的长.(3分)27.(本题10分)直线y=-x+b 与双曲线xky =相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A 、B 两点,过点C 作直线M N ⊥x 轴于F 点,连接BF . (1)求直线和双曲线的解析式;(4分),垂足为E ,直线PE 与x 轴相交于点H . 点,使以A 、P 、H 为顶点的三角形与△FBC (4分)BDC初二数学试题参考答案一、选择题: ABCA CAAC 二.填空题:9. 4; 10. 3; 11. 0.76; 12. 512; 13.6,23,32中的一个即可; 14.略; 15.x>32; 16.3. 17. 2y <1y ; 18.5819.①22+a ②x=4 20.b a +1,1; 21(1)442+-=xx y .;(2)1.22. (1)略;(2)略;15.23.小刚正确,只要将式子化简得到ab b a =+即可; 24. 甲公司3000人,乙公司2500人;25. 略; 26. (1)略 (2)① 1; ②(n -1)b -a; 27. (1)3--=x y ;x y 4-=; (2)45°; (3)(1,34-) ,(1,8) 初二数学试题参考答案一、选择题: ABCA CAAC二.填空题:9. 4; 10. 3; 11. 0.76; 12. 512; 13.6,23,32中的一个即可; 14.略; 15.x>32; 16.3. 17. 2y <1y ; 18.5819.①22+a ②x=4 20.b a +1,1; 21(1)442+-=xx y .;(2)1.22. (1)略;(2)略;15.23.小刚正确,只要将式子化简得到ab b a =+即可; 24. 甲公司3000人,乙公司2500人;25. 略; 26. (1)略 (2)① 1; ②(n -1)b -a; 27. (1)3--=x y ;x y 4-=; (2)45°; (3)(1,34-) ,(1,8)。
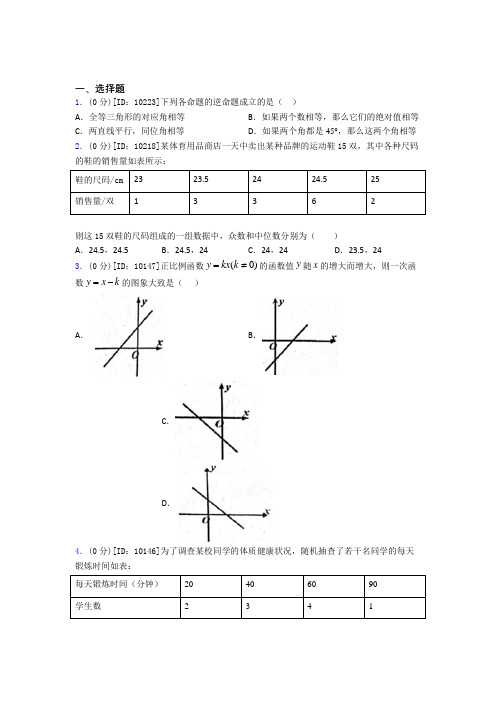
一、选择题1.(0分)[ID :10223]下列各命题的逆命题成立的是( ) A .全等三角形的对应角相等 B .如果两个数相等,那么它们的绝对值相等 C .两直线平行,同位角相等 D .如果两个角都是45°,那么这两个角相等2.(0分)[ID :10218]某体育用品商店一天中卖出某种品牌的运动鞋15双,其中各种尺码的鞋的销售量如表所示: 鞋的尺码/cm 23 23.5 24 24.5 25 销售量/双13362则这15双鞋的尺码组成的一组数据中,众数和中位数分别为( ) A .24.5,24.5B .24.5,24C .24,24D .23.5,243.(0分)[ID :10147]正比例函数(0)y kx k =≠的函数值y 随x 的增大而增大,则一次函数y x k =-的图象大致是( )A .B .C .D .4.(0分)[ID :10146]为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表: 每天锻炼时间(分钟) 20 40 60 90 学生数2341则关于这些同学的每天锻炼时间,下列说法错误的是()A.众数是60B.平均数是21C.抽查了10个同学D.中位数是50 5.(0分)[ID:10144]如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方ab ,形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若8大正方形的面积为25,则小正方形的边长为()A.9B.6C.4D.36.(0分)[ID:10136]已知一次函数y=-0.5x+2,当1≤x≤4时,y的最大值是()A.1.5B.2C.2.5D.-67.(0分)[ID:10187]某单位组织职工开展植树活动,植树量与人数之间关系如图,下列说法不正确的是()A.参加本次植树活动共有30人B.每人植树量的众数是4棵C.每人植树量的中位数是5棵D.每人植树量的平均数是5棵8.(0分)[ID:10181]若一个直角三角形的两边长为12、13,则第三边长为()A.5B.17C.5或17D.5或√3139.(0分)[ID:10177]明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t (单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是()A.300m2B.150m2C.330m2D.450m210.(0分)[ID:10173]如图,长方形纸片ABCD中,AB=4,BC=6,点E在AB边上,将纸片沿CE折叠,点B落在点F处,EF,CF分别交AD于点G,H,且EG=GH,则AE的长为( )A.23B.1C.32D.211.(0分)[ID:10169]直角三角形中,有两条边长分别为3和4,则第三条边长是()A.1B.5C.7D.5或712.(0分)[ID:10168]无论m为任何实数,关于x的一次函数y=x+2m与y=-x+4的图象的交点一定不在()A.第一象限 B.第二象限 C.第三象限 D.第四象限13.(0分)[ID:10167]如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于()A.2B.3C.4D.614.(0分)[ID:10158]下列运算正确的是()A.235+=B.32﹣2=3C.236⨯=D.632÷=15.(0分)[ID:10157]如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑()米A.0.4B.0.6C.0.7D.0.8二、填空题16.(0分)[ID :10331]如图,在ABC 中,AC BC =,点D E ,分别是边AB AC ,的中点,延长DE 到点F ,使DE EF =,得四边形ADCF .若使四边形ADCF 是正方形,则应在ABC 中再添加一个条件为__________.17.(0分)[ID :10325]将一次函数y=3x ﹣1的图象沿y 轴向上平移3个单位后,得到的图象对应的函数关系式为__.18.(0分)[ID :10320]如图所示,BE AC ⊥于点D ,且AB BC =,BD ED =,若54ABC ∠=,则E ∠=___.19.(0分)[ID :10315]计算:182-=______. 20.(0分)[ID :10308]如图,直线l 1:y =x +n –2与直线l 2:y =mx +n 相交于点P (1,2).则不等式mx +n <x +n –2的解集为______.21.(0分)[ID :10304]若x <222)x -(﹣x|的正确结果是__.22.(0分)[ID :10288]某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如表: 候选人甲 乙 测试成绩(百分制)面试8692笔试9083如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权。

初二数学好的试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次根式?A. √2B. 2√3C. √6D. √(-1)2. 一个数的立方等于它本身,这个数是?A. 0B. 1C. -1D. 0, 1, -13. 一个数的相反数是它自己,这个数是?A. 0B. 1C. 2D. -14. 一个数的绝对值是它自己,这个数是?A. 任何数B. 非负数C. 非正数D. 05. 一个数的倒数是它自己,这个数是?A. 0B. 1C. -1D. 1和-16. 一个数的平方等于它本身,这个数是?A. 0B. 1C. -1D. 0, 17. 一个数的平方根是它自己,这个数是?A. 0B. 1C. -1D. 0和18. 一个数的立方根是它自己,这个数是?A. 0B. 1C. -1D. 0, 1, -19. 一个数的四次方等于它本身,这个数是?A. 0B. 1C. -1D. 0, 1, -110. 一个数的五次方等于它本身,这个数是?A. 0B. 1C. -1D. 0, 1, -1二、填空题(每题4分,共20分)1. 一个数的平方是36,这个数是______。
2. 一个数的立方是-27,这个数是______。
3. 一个数的绝对值是5,这个数是______。
4. 一个数的倒数是1/2,这个数是______。
5. 一个数的平方根是4,这个数是______。
三、解答题(每题10分,共50分)1. 计算:(√3 + √2)(√3 - √2)。
2. 计算:(2x - 3)(2x + 3)。
3. 计算:(3x + 2)(3x - 2)。
4. 计算:(2x + 5)(2x - 5)。
5. 已知一个数的平方是25,求这个数。
答案:一、选择题1. A2. D3. A4. B5. D6. D7. D8. D9. D 10. D二、填空题1. ±62. -33. ±54. 25. 16三、解答题1. 3 - 2 = 12. 4x² - 93. 9x² - 44. 4x² - 255. ±5。

初二数学经典试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是无理数?A. 3.14159B. πC. 0.33333...D. √2答案:D2. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是?A. 5B. 6C. 7D. 8答案:A3. 一个数的平方根是4,这个数是?A. 16B. -16C. 4D. 2答案:A4. 一个正数的倒数是1/8,这个正数是?A. 8B. 1/8C. 1/7D. 7答案:A5. 一个二次方程x² - 5x + 6 = 0的解是?A. x = 2, 3B. x = 3, 4C. x = 1, 6D. x = 2, 4答案:A二、填空题(每题2分,共10分)6. 一个数的立方根是2,这个数是______。
答案:87. 一个圆的半径是5厘米,那么它的面积是______平方厘米。
答案:78.58. 如果一个数的绝对值是5,那么这个数可以是______或______。
答案:5,-59. 一个长方体的长、宽、高分别是2米、3米和4米,它的体积是______立方米。
答案:2410. 一个数的平方是25,这个数可以是______或______。
答案:5,-5三、计算题(每题5分,共15分)11. 计算下列表达式的值:(1) (-2)³ + √4 - 2π答案:-7 + 2 - 6.28 = -11.28(2) √(3² + 4²) - 1/2答案:√(9 + 16) - 0.5 = √25 - 0.5 = 5 - 0.5 = 4.5(3) (-3)² ÷ 2 - 1/3答案:9 ÷ 2 - 1/3 = 4.5 - 0.333... = 4.166...四、解答题(每题10分,共20分)12. 解方程:2x - 5 = 3x + 1答案:首先将方程两边的x项聚集在一边,得到2x - 3x = 1 + 5,即-x = 6,解得x = -6。
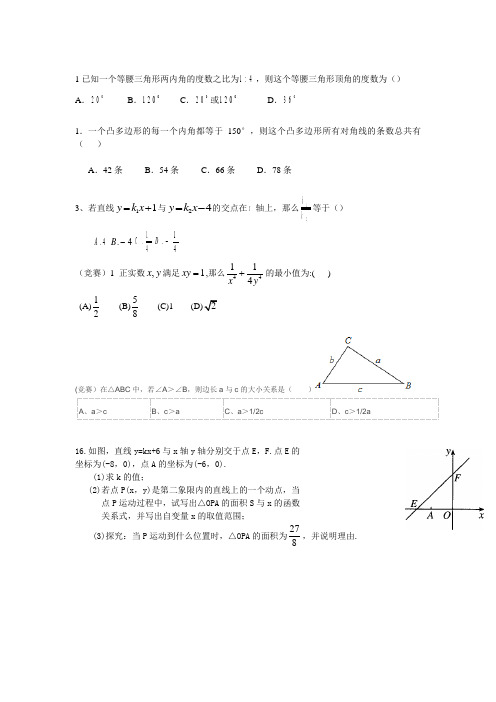
1 已知一个等腰三角形两内角的度数之比为 1 : 4 ,则这个等腰三角形顶角的度数为() A. 2 0 B. 1 2 0 C. 2 0 或 1 2 0 D. 3 61.一个凸多边形的每一个内角都等于 150°,则这个凸多边形所有对角线的条数总共有 ( ) A.42 条 B.54 条 C.66 条 D.78 条3、若直线 y k1x 1 与 y k2x 4 的交点在 x 轴上,那么k1 等于() k2A . 4 B. 4 C .1 1 D . 4 41 1 4 的最小值为:( 4 x 4y)(竞赛)1 正实数 x, y 满足 xy 1 ,那么(A)1 2(B)5 8(C)1(D) 2(竞赛)在△ABC 中,若∠A>∠B,则边长 a 与 c 的大小关系是( A、a>c B、c>a C、a>1/2c) D、c>1/2a16.如图,直线 y=kx+6 与 x 轴 y 轴分别交于点 E,F.点 E 的 坐标为(-8,0),点 A 的坐标为(-6,0). (1)求 k 的值; (2)若点 P(x,y)是第二象限内的直线上的一个动点,当 点 P 运动过程中,试写出△OPA 的面积 S 与 x 的函数 关系式,并写出自变量 x 的取值范围; (3)探究:当 P 运动到什么位置时,△OPA 的面积为27 ,并说明理由. 86 、已知,如图,△ ABC 中,∠ BAC=90 °, AB=AC,D 为 AC 上一点,且∠ BDC=124°,延长 BA 到点 E,使 AE=AD,BD 的延长线交 CE 于点 F,求∠E 的 度数。
7.正方形 ABCD 的边长为 4,将此正方形置于平面直角坐标系中,使 AB 边落在 X 轴的正半 轴上,且 A 点的坐标是(1,0) 。
4 8 ①直线 y= x- 经过点 C,且与 x 轴交与点 E,求四边形 AECD 的面积; 3 3 ②若直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分求直线 l 的解析式, ③若直线 l1 经过点 F 2 3 .0 且与直线 y=3x 平行,将②中直线 l 沿着 y 轴向上平移 个单位 3 2 交 x 轴于点 M ,交直线 l1 于点 N ,求 NMF 的面积.(竞赛奥数)如图,在△ABC 中,已知∠C=60°,AC>BC,又△ABC′、△BCA′、△CAB′ 都是△ABC 形外的等边三角形,而点 D 在 AC 上,且 BC=DC (1)证明:△C′BD≌△B′DC; (2)证明:△AC′D≌△DB′A;9.已知如图,直线 y 3x 4 3 与 x 轴相交于点 A,与直线 y 3x 相交于点 P. ①求点 P 的坐标. ②请判断 OPA 的形状并说明理由. ③动点 E 从原点 O 出发,以每秒 1 个单位的速度沿着 O→P→A 的路线向点 A 匀速运动(E 不与点 O、 A 重合) , 过点 E 分别作 EF⊥x 轴于 F, EB⊥y 轴于 B. 设运动 t 秒时, 矩形 EBOF 与△OPA 重叠部分的面积为 S.求: S 与 t 之间的函数关系式.y PB OEFAx16 多边形内角和公式等于(n - 2)×180 根据题意即(n - 2)×180=150n,求得 n=12, 多边形的对角线的条数公式等于 n(n-3)/2 带入 n=12, 则这个多边形所有对角线 的条数共有 54 条因为两直线交点在 x 轴上,则 k1 和 k2 必然不为 0,且交点处 x=-1/k1=4/k2, 所以 k1:k2=-1:41/x^4+1/4y^4=(y^4+x^4)/x^4y^4 因为 xy=1 所以 x^4y^4=1 所以 原式=y^4+x^4 因为(x^2-y^2)^2>0 且(x^2-y^2)^2=y^4+x^4-x^2y^2 大于或等于 0 所以 y^4+x^4 大于或等于 x^2y^2 即 1 所以 y^4+x^4 的最小值为 1竞赛解:在△ABC 中, ∵∠A>∠B, ∴a>b, ∵a+b>c, ∴2a>a+b>c, ∴a>12c. 故选 C.1、y=kx+6 过点 E(-8,0)则 -8K+6=0 K=3/4 2、 因点 E(-8,0) 则 OE=8 直线解析式 Y=3X/4+6 当 X=0 时,Y=6,则点 F(0,6) 因点 A(0,6),则 A、F 重合 OA=6 设点 P(X,Y) 则点 P 对于 Y 轴的高为|X| 当 P 在第二象限时,|X|=-X S=OA×|X|/2=-6X/2=-3X 3、 S=3|X| 当 S=278 时 278=± 3X X1=278/3,X2=-278/3 Y1=3X1/4+6=3/4×278/3+6=151/2 Y2=3X2/4+6=-3/4×278/3+6=-127/2 点 P1(278/3,151/2),P2(-278/3,-127/2)6 解:在△ABD 和△ACE 中, ∵AB=AC,∠DAB=∠CAE=90° AD=AE, ∴△ABD≌△ACE(SAS) , ∴∠E=∠ADB. ∵∠ADB=180° -∠BDC=180° -124° =56° , ∴∠E=56° .7(1)由题意知边长已经告诉,易求四边形的面积; (2)由第一问求出 E 点的坐标,设出 F 点,根据直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分,其实是两个直角梯形,根据梯形面积公式,可求 出 F 点坐标,从而解出直线 l 的解析式.解:(1)由已知条件正方形 ABCD 的 边长是 4, ∴四边形 ABCD 的面积为:4×4=16; (2)由第一问知直线 y=4/3x-8/3 与 x 轴交于点 E, ∴E(2,0), 设 F(m,4), 直线 l 经过点 E 且将正方形 ABCD 分成面积相等的两部分,由图知是两个直角 梯形, ∴S 梯形 AEFD=S 梯形 EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB) ∴m=4, ∵F(4,4),E(2,0), ∴直线 l 的解析式为:y=2x-4竞赛奥数 (1) 先证△ABC≌△C1BD:∵AB=C1B, ∠ABC=∠C1BD (因为都是 60° +∠ ABD), BD=BC。

一、选择题1. 下列哪个数是无理数?A. 3/4B. √2C. -5D. 0答案:B2. 在直角坐标系中,点A(3, -2)关于x轴对称的点的坐标是?A. (-3, 2)B. (3, 2)C. (-3, -2)D. (2, 3)答案:B3. 若a² + b² = 25,且a + b = 7,则ab的值为?A. 12B. -12C. 6D. -6答案:D4. 下列哪个不等式组的解集是x > 2?A. x > 1 且 x > 3B. x > 1 或 x > 3C. x < 2 或 x > 3D. x > 2 或 x < 1(注:此题选项D虽不完全准确,但相比其他选项,它包含x > 2的部分,若理解为“或”表示至少满足一个条件,则在没有其他更合适选项的情况下,可视为最接近正确答案。
实际教学中应更精确设计选项。
)答案:D5. 一个矩形的周长是20厘米,长是a厘米,则宽是?A. (20 - a)厘米B. (20 - 2a)厘米C. (10 - a)厘米D. 10 - a厘米答案:C二、填空题6. 函数y = 2x + 1与y = 2x - 3的图象关系为____。
答案:平行7. 若等腰三角形的顶角为80°,则它的一个底角为____。
答案:50°8. 已知数据:2,3,x,5,6的平均数为4,则这组数据的中位数是____。
答案:3三、解答题9. 在平行四边形ABCD中,如果∠A = 110°,那么∠C = ?请说明理由。
答案:∠C = 110°。
理由:在平行四边形中,对角相等,即∠A = ∠C。

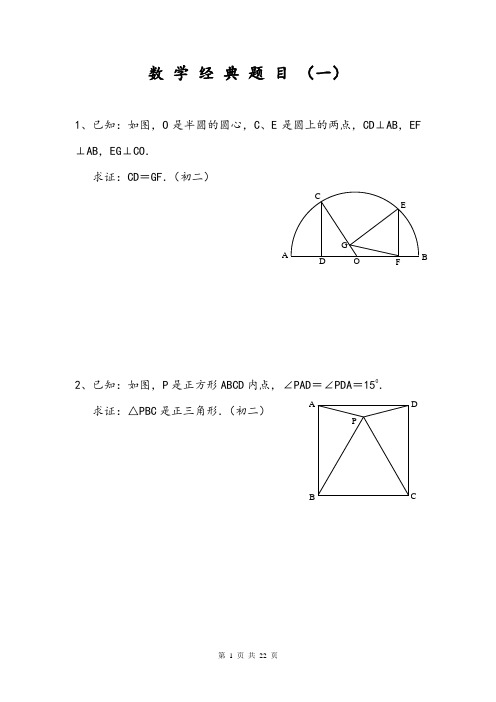
数学经典题目(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)APCDB AFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M中点,AD 、BC 的延长线交MN 于E 、F 求证:∠DEN =∠F .D 2C 2B 2 A 2D 1C 1B 1CBDAA 1B数学经典题目(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM ⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A线,交圆于B、C及D、E,直线EB及CD 求证:AP=AQ.(初二)F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点AEB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 求证:点P 到边AB 的距离等于AB数学经典题目(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.4、如图,PC切圆O于C,AC与直线PO相交于B、D.求证:AB数学经典题目(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC =5.2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)数学经典题目(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.APCBACBPD3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a方形的边长.4、如图,△ABC 中,∠ABC =∠ACB=800,D 、E 分别是点,∠DCA =300,∠EBA =200,求∠BED 的度数.数学经典题目(一)1.如下图做GH ⊥AB,连接EO 。

初二数学经典题型1.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.2.已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .3、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.)4、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC=3a 正方形的边长.6.如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB . (1)求证:① PE=PD ; ② PE ⊥PD ; (2)设AP =x , △PBE 的面积为y . !① 求出y 关于x 的函数关系式,并写出x 的取值范围;ANF E C|MBAP-DB &CGFBQAD#② 当x 取何值时,y 取得最大值,并求出这个最大值.答案1、证明如下。
首先,PA=PD ,∠PAD=∠PDA=(180°-150°)÷2=15°,∠PAB=90°-15°=75°。
在正方形ABCD 之外以AD 为底边作正三角形ADQ , 连接PQ , 则∠PDQ=60°+15°=75°,同样∠PAQ=75°,又AQ=DQ,,PA=PD ,所以△PAQ ≌△PDQ , 那么∠PQA=∠PQD=60°÷2=30°,在△PQA 中,∠APQ=180°-30°-75°=75°=∠PAQ=∠PAB ,于是PQ=AQ=AB , 显然△PAQ ≌△PAB ,得∠PBA=∠PQA=30°,PB=PQ=AB=BC ,∠PBC=90°-30°=60°,所以△ABC 是正三角形。

八年级数学题100道带答案1) 66x+17y=396725x+y=1200答案:x=48 y=47(2) 18x+23y=230374x-y=1998答案:x=27 y=79(3) 44x+90y=779644x+y=3476答案:x=79 y=48(4) 76x-66y=408230x-y=2940答案:x=98 y=51(5) 67x+54y=854671x-y=5680答案:x=80 y=59(6) 42x-95y=-141021x-y=1575答案:x=75 y=48(7) 47x-40y=85334x-y=2006答案:x=59 y=48(8) 19x-32y=-1786 75x+y=4950答案:x=66 y=95 (9) 97x+24y=7202 58x-y=2900答案:x=50 y=98 (10) 42x+85y=6362 63x-y=1638答案:x=26 y=62 (11) 85x-92y=-2518 27x-y=486答案:x=18 y=44 (12) 79x+40y=2419 56x-y=1176答案:x=21 y=19 (13) 80x-87y=2156 22x-y=880答案:x=40 y=12 (14) 32x+62y=5134 57x+y=2850答案:x=50 y=57 (15) 83x-49y=8259x+y=2183答案:x=37 y=61 (16) 91x+70y=5845 95x-y=4275答案:x=45 y=25 (17) 29x+44y=5281 88x-y=3608答案:x=41 y=93 (18) 25x-95y=-4355 40x-y=2000答案:x=50 y=59 (19) 54x+68y=3284 78x+y=1404答案:x=18 y=34 (20) 70x+13y=3520 52x+y=2132答案:x=41 y=50 (21) 48x-54y=-3186 24x+y=1080答案:x=45 y=99 (22) 36x+77y=7619 47x-y=799答案:x=17 y=91 (23) 13x-42y=-2717 31x-y=1333答案:x=43 y=78 (24) 28x+28y=3332 52x-y=4628答案:x=89 y=30 (25) 62x-98y=-2564 46x-y=2024答案:x=44 y=54 (26) 79x-76y=-4388 26x-y=832答案:x=32 y=91 (27) 63x-40y=-821 42x-y=546答案:x=13 y=41 (28) 69x-96y=-1209 42x+y=3822答案:x=91 y=78 (29) 85x+67y=7338 11x+y=308答案:x=28 y=74(30) 78x+74y=12928 14x+y=1218答案:x=87 y=83 (31) 39x+42y=5331 59x-y=5841答案:x=99 y=35 (32) 29x+18y=1916 58x+y=2320答案:x=40 y=42 (33) 40x+31y=6043 45x-y=3555答案:x=79 y=93 (34) 47x+50y=8598 45x+y=3780答案:x=84 y=93 (35) 45x-30y=-1455 29x-y=725答案:x=25 y=86 (36) 11x-43y=-1361 47x+y=799答案:x=17 y=36 (37) 33x+59y=325494x+y=1034答案:x=11 y=49 (38) 89x-74y=-2735 68x+y=1020答案:x=15 y=55 (39) 94x+71y=7517 78x+y=3822答案:x=49 y=41 (40) 28x-62y=-4934 46x+y=552答案:x=12 y=85 (41) 75x+43y=8472 17x-y=1394答案:x=82 y=54 (42) 41x-38y=-1180 29x+y=1450答案:x=50 y=85 (43) 22x-59y=824 63x+y=4725答案:x=75 y=14 (44) 95x-56y=-401 90x+y=1530(45) 93x-52y=-852 29x+y=464答案:x=16 y=45 (46) 93x+12y=8823 54x+y=4914答案:x=91 y=30 (47) 21x-63y=84 20x+y=1880答案:x=94 y=30 (48) 48x+93y=9756 38x-y=950答案:x=25 y=92 (49) 99x-67y=4011 75x-y=5475答案:x=73 y=48 (50) 83x+64y=9291 90x-y=3690答案:x=41 y=92(51) 17x+62y=3216 75x-y=7350(52) 77x+67y=2739 14x-y=364答案:x=26 y=11 (53) 20x-68y=-4596 14x-y=924答案:x=66 y=87 (54) 23x+87y=4110 83x-y=5727答案:x=69 y=29 (55) 22x-38y=804 86x+y=6708答案:x=78 y=24 (56) 20x-45y=-3520 56x+y=728答案:x=13 y=84 (57) 46x+37y=7085 61x-y=4636答案:x=76 y=97 (58) 17x+61y=4088 71x+y=5609答案:x=79 y=45(59) 51x-61y=-1907 89x-y=2314答案:x=26 y=53 (60) 69x-98y=-2404 21x+y=1386答案:x=66 y=71 (61) 15x-41y=754 74x-y=6956答案:x=94 y=16 (62) 78x-55y=656 89x+y=5518答案:x=62 y=76 (63) 29x+21y=1633 31x-y=713答案:x=23 y=46 (64) 58x-28y=2724 35x+y=3080答案:x=88 y=85 (65) 28x-63y=-2254 88x-y=2024答案:x=23 y=46 (66) 43x+50y=706485x+y=8330答案:x=98 y=57 (67) 58x-77y=1170 38x-y=2280答案:x=60 y=30 (68) 92x+83y=11586 43x+y=3010答案:x=70 y=62 (69) 99x+82y=6055 52x-y=1716答案:x=33 y=34 (70) 15x+26y=1729 94x+y=8554答案:x=91 y=14 (71) 64x+32y=3552 56x-y=2296答案:x=41 y=29 (72) 94x+66y=10524 84x-y=7812答案:x=93 y=27 (73) 65x-79y=-5815 89x+y=2314答案:x=26 y=95 (74) 96x+54y=6216 63x-y=1953答案:x=31 y=60 (75) 60x-44y=-352 33x-y=1452答案:x=44 y=68 (76) 79x-45y=510 14x-y=840答案:x=60 y=94 (77) 29x-35y=-218 59x-y=4897答案:x=83 y=75 (78) 33x-24y=1905 30x+y=2670答案:x=89 y=43 (79) 61x+94y=11800 93x+y=5952答案:x=64 y=84 (80) 61x+90y=5001 48x+y=2448答案:x=51 y=21(81) 93x-19y=286x-y=1548答案:x=18 y=88 (82) 19x-96y=-5910 30x-y=2340答案:x=78 y=77 (83) 80x+74y=8088 96x-y=8640答案:x=90 y=12 (84) 53x-94y=1946 45x+y=2610答案:x=58 y=12 (85) 93x+12y=9117 28x-y=2492答案:x=89 y=70 (86) 66x-71y=-1673 99x-y=7821答案:x=79 y=97 (87) 43x-52y=-1742 76x+y=1976答案:x=26 y=55 (88) 70x+35y=829540x+y=2920答案:x=73 y=91 (89) 43x+82y=4757 11x+y=231答案:x=21 y=47 (90) 12x-19y=236 95x-y=7885答案:x=83 y=40 (91) 51x+99y=8031 71x-y=2911答案:x=41 y=60 (92) 37x+74y=4403 69x-y=6003答案:x=87 y=16 (93) 46x+34y=4820 71x-y=5183答案:x=73 y=43 (94) 47x+98y=5861 55x-y=4565答案:x=83 y=20 (95) 30x-17y=239 28x+y=1064答案:x=38 y=53 (96) 55x-12y=4112 79x-y=7268答案:x=92 y=79 (97) 27x-24y=-450 67x-y=3886答案:x=58 y=84 (98) 97x+23y=8119 14x+y=966答案:x=69 y=62 (99) 84x+53y=11275 70x+y=6790答案:x=97 y=59 (100) 51x-97y=297 19x-y=1520答案:x=80 y=39。

初二数学练习题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程x^2 - 5x + 6 = 0的解?A. x = 2B. x = 3C. x = 1 或 x = 6D. x = -2 或 x = -32. 函数y = 2x + 3的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 一个等腰三角形的两边长分别为5cm和10cm,那么它的周长是多少?A. 15cmB. 20cmC. 25cmD. 30cm4. 计算下列表达式的值:(2x - 3)(x + 1) - (x - 2)^2A. x^2 - 2x + 1B. x^2 + 2x - 5C. x^2 - 4x + 5D. x^2 + 4x - 55. 一个数的平方等于该数本身,这个数是?A. 0 或 1B. 0 或 -1C. 1 或 -1D. 0 或 26. 一个圆的半径为5cm,那么它的面积是多少?A. 25π cm^2B. 50π cm^2C. 100π cm^2D. 125π cm^27. 一个等差数列的首项是3,公差是2,那么它的第5项是多少?A. 13B. 15C. 17D. 198. 一个正方体的体积是64立方厘米,那么它的棱长是多少?A. 4cmB. 8cmC. 16cmD. 32cm9. 计算下列表达式的值:(3x^2 - 2x + 1) / (x - 1)A. 3x + 1B. 3x - 1C. 3x + 2D. 3x - 210. 一个二次函数的顶点坐标是(2, -3),且经过点(0, 1),那么它的解析式是?A. y = (x - 2)^2 - 3B. y = -(x - 2)^2 - 3C. y = (x - 2)^2 + 3D. y = -(x - 2)^2 + 3二、填空题(每题2分,共20分)1. 一个直角三角形的两条直角边长分别为3cm和4cm,那么它的斜边长是_________。

初二数学练习题带答案一、选择题(每题4分,共40分)1. 已知两个数的和是8,差是2,则这两个数分别是:A) 3和5B) 4和4C) 2和6D) 1和72. 某笔记本原价600元,现打8折出售,打完折后的价格是多少?A) 480元B) 520元C) 560元D) 600元3. 现在是星期一,过了100天是星期几?A) 星期二B) 星期三C) 星期四D) 星期五4. 如图所示,下面四个角的度数之和是多少?* ** *-----------* ** *A) 90°B) 180°C) 270°D) 360°5. 甲、乙两支队伍进行足球比赛,最终比分为3:1,那么乙队胜甲队的胜率是多少?A) 25%B) 33%C) 50%D) 75%6. 若一个数的平方根是5,那么这个数是多少?A) -5B) 5C) -25D) 257. 有一个长方体箱子,长、宽、高分别是2cm、3cm、4cm,那么它的体积是多少?A) 8cm³B) 12cm³C) 18cm³D) 24cm³8. 早晨7点半,小明从家里出发去上学,他用时25分钟到学校,那么小明是几点出发的?A) 7点B) 7点5分C) 7点10分D) 7点15分9. 若一个数与8的差是5,那么这个数是多少?A) -5B) 3C) 5D) 1310. 一个正方形的周长是32cm,那么它的边长是多少?A) 4cmB) 6cmC) 8cmD) 10cm二、解答题(每题10分,共30分)1. 如图所示,矩形ABCD中,AB = 10cm,BC = 8cm。
若点E在边AD上,且AE = 5cm,求BE的长度。
[插入解答过程和答案的图片]2. 已知两个角的补角之和是160°,求这两个角的度数。
解:设其中一个角的度数为x°,则另一个角的度数为(180° - x°)。

初二数学试题及答案免费一、选择题(每题3分,共30分)1. 下列哪个选项是偶数?A. 1B. 2C. 3D. 4答案:B2. 一个数的平方是36,这个数是:A. 6B. -6C. 6或-6D. 无法确定答案:C3. 一个三角形的三个内角之和是:A. 90°B. 180°C. 360°D. 720°答案:B4. 如果一个数的绝对值是5,那么这个数可以是:A. 5C. 5或-5D. 以上都不是答案:C5. 一个数的倒数是1/2,这个数是:A. 2B. -2C. 1/2D. -1/2答案:A6. 以下哪个选项表示的是不等式?A. 3x + 2 = 7B. 2x - 5 > 0C. 4x = 8D. 3x - 2 ≤ 5答案:B7. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 20厘米D. 2厘米答案:A8. 一个数的立方是-27,这个数是:B. -3C. 3或-3D. 无法确定答案:B9. 以下哪个选项是多项式?A. 5x + 3B. 2x^2 + 5C. 3x/2D. 4x^3 - 2x + 1答案:D10. 如果一个角是直角,那么它的度数是:A. 45°B. 90°C. 180°D. 360°答案:B二、填空题(每题4分,共20分)1. 一个数的平方根是4,那么这个数是______。
答案:162. 一个数的相反数是-8,那么这个数是______。
答案:83. 如果一个三角形的两个内角分别是30°和60°,那么第三个内角是______。
答案:90°4. 一个数的绝对值是其本身,那么这个数是______。
答案:非负数5. 一个数的立方根是2,那么这个数是______。
答案:8三、解答题(每题10分,共50分)1. 计算下列表达式的值:(3x - 2) + (4x + 5),其中x = 2。

初二数学经典几何题型1.已知:如图, P 是正方形ABCD内点,∠ PAD=∠ PDA= 150.求证:△ PBC是正三角形.证明以下。
第一, PA=PD,∠ PAD=∠ PDA=(180° - 150°)÷2=15°,∠PAB=90° - 15°=75°。
A D 在正方形ABCD以外以 AD为底边作正三角形ADQ,连结PQ,则P∠P DQ=60°+15°=75°,相同∠ PAQ=75°,又 AQ=DQ,,PA=PD,因此△PAQ≌△ PDQ,那么∠ PQA=∠PQD=60°÷ 2=30°,在△ PQA中,∠A PQ=180° - 30° - 75°=75°=∠ PAQ=∠ PAB,于是 PQ=AQ=AB,明显△ PAQ≌△ PAB,得∠ PBA=∠PQA=30°,PB=PQ=AB=BC,∠ PBC=90° - 30°=60°,因此△PBC是正三角形。
BC2.已知:如图,在四边形 ABCD中, AD=BC,M、N 分别是 AB、CD的中点, AD、BC的延伸线交 MN于 E、F.求证:∠ DEN=∠ F.F证明 : 连结 AC,并取 AC的中点 G,连结 GF,GM.又点 N为 CD的中点 , 则 GN=AD/2;GN∥ AD,∠GNM=∠ DEM;(1)同理 :GM=BC/2;GM∥ BC,∠ GMN=∠ CFN;(2)又 AD=BC,则 :GN=GM,∠ GNM=∠ GMN故. : ∠ DEM=∠ CFN.3、如图,分别以△ABC的 AC和 BC为一边,在△ ABC的外侧作正方形的中点.求证:点 P 到边 AB的距离等于 AB的一半.EN CDA BMACDE和正方形CBFG,点 P 是 EF证明:分别过 E、 C、 F 作直线 AB 的垂线,垂足分别为 M、 O、 N,在梯形 MEFN中, WE平行 NF由于 P为 EF 中点, PQ平行于两底因此 PQ为梯形 MEFN中位线,因此 PQ=( ME+ NF) /2又由于,角 0CB+角 OBC=90°=角 NBF+角 CBO因此角 OCB=角 NBF而角 C0B=角 Rt=角 BNFCB=BF因此△ OCB全等于△ NBF△MEA全等于△OAC(同理)因此 EM= AO, 0B= NF因此 PQ=AB/2.4、设 P 是平行四边形ABCD内部的一点,且∠PBA=∠ PDA.求证:∠DGCEP FA Q BPAB=∠ PCB.过点 P作 DA的平行线,过点 A 作 DP的平行线,二者订交于点E;连结 BE由于 DP//AE, AD//PE因此,四边形 AEPD为平行四边形A D 因此,∠ PDA=∠AEP已知,∠ PDA=∠PBAP因此,∠ PBA=∠AEP因此, A、 E、 B、 P 四点共圆B C因此,∠ PAB=∠PEB由于四边形 AEPD为平行四边形,因此:PE//AD,且 PE=AD而,四边形 ABCD为平行四边形,因此:AD//BC,且 AD=BC因此, PE//BC ,且 PE=BC即,四边形 EBCP也是平行四边形因此,∠ PEB=∠PCB因此,∠ PAB=∠PCB5.P 为正方形ABCD内的一点,而且PA= a, PB= 2a, PC=3a正方形的边长.解:将△ BAP绕 B 点旋转 90°使 BA 与 BC重合, P 点旋转后到 Q点,连结 PQ 由于△ BAP≌△ BCQ因此 AP= CQ, BP= BQ,∠ ABP=∠ CBQ,∠ BPA=∠BQC 由于四边形 DCBA是正方形因此∠ CBA=90°,因此∠ ABP+∠ CBP=90°,因此∠ CBQ+∠ CBP=90°即∠ PBQ=90°,因此△ BPQ是等腰直角三角形因此 PQ=√ 2*BP,∠ BQP= 45由于 PA=a, PB=2a, PC=3a因此 PQ=2√2a, CQ= a,因此 CP^2= 9a^2, PQ^2+CQ^2= 8a^2+ a^2=9a^2因此 CP^2= PQ^2+ CQ^2,因此△ CPQ是直角三角形且∠ CQA=90°因此∠ BQC=90°+ 45°= 135°,因此∠BPA=∠ BQC=135°作 BM⊥ PQ则△ BPM是等腰直角三角形因此 PM= BM=PB/√2=2a/ √2=√ 2a因此依据勾股定理得:AB^2=AM^2+ BM^2=(√2a+ a)^2 +( √2a)^2=[5 +2√2]a^2A DPBC因此 AB=[ √(5 +2√2)]a6.一个圆柱形容器的容积为 V 立方米,开始用一根小水管向容器内灌水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管灌水。

初二数学练习题带答案
一、选择题
1. 下列哪个选项是正确的?
A. 2x + 3 = 7x - 1
B. 2x + 3 = 7x + 1
C. 2x + 3 = 7x - 2
D. 2x + 3 = 7x + 2
答案:B
2. 哪个方程的解是x = 2?
A. 2x - 4 = 0
B. 3x + 6 = 12
C. 4x - 8 = 0
D. 5x + 10 = 20
答案:B
3. 计算下列哪个表达式的结果为0?
A. 3x - 6x + 2
B. 4x + 2x - 6
C. 5x - 3x + 4
D. 2x + 3x - 5x
答案:D
二、填空题
4. 如果一个数的三倍加上5等于15,那么这个数是______。
答案:2
5. 一个数的两倍减去3等于该数加上4,这个数是______。
答案:7
6. 一个两位数,十位数字比个位数字大3,且这个两位数比由这两个数字交换位置后得到的数大18,这个两位数是______。
答案:54
三、解答题
7. 解方程:3x - 7 = 2x + 8。
答案:x = 15
8. 一个长方形的长是宽的两倍,如果长增加2米,宽增加1米,面积增加10平方米,求原长方形的长和宽。
答案:原长方形的长为8米,宽为4米。
9. 一个工厂生产两种产品,A产品每件利润为20元,B产品每件利润为30元。
如果工厂一天生产A产品x件,B产品y件,且x + y = 100,总利润为3200元,求x和y的值。
答案:x = 40,y = 60。

初二数学精选试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 2B. √2C. 0.5D. 3.14答案:B2. 一个等腰三角形的底边长为6,腰长为5,那么这个三角形的周长是多少?A. 16B. 17C. 18D. 19答案:B3. 下列哪个选项是二次根式?A. √2B. 2√2C. √(-1)D. √(2+3)答案:A4. 一个数的平方是25,这个数是多少?A. 5B. -5C. 5或-5D. 以上都不是答案:C5. 一个二次函数的顶点坐标是(2, -3),那么这个函数的对称轴是?A. x=2B. x=-2C. x=3D. x=-3答案:A6. 一个直角三角形的两个锐角的度数之和是多少?A. 90°B. 180°C. 270°D. 360°答案:A7. 一个圆的半径是5,那么这个圆的面积是多少?A. 25πC. 75πD. 100π答案:B8. 一个正数的算术平方根是3,那么这个数是多少?A. 6B. 9C. 12D. 15答案:B9. 一个数的立方根是2,那么这个数是多少?A. 6B. 8C. 2^3答案:C10. 下列哪个选项是一次函数?A. y=2x+3B. y=x^2+1C. y=√xD. y=1/x答案:A二、填空题(每题4分,共20分)11. 一个等边三角形的边长是8,那么这个三角形的高是________。
答案:4√312. 一个二次函数的图像开口向上,且经过点(1, 0)和(-1, 0),那么这个函数的一般形式是________。
答案:y=a(x-1)(x+1),其中a>013. 一个数的绝对值是5,那么这个数可以是________或________。
答案:5或-514. 一个圆的直径是10,那么这个圆的周长是________。
答案:10π15. 一个直角三角形的两条直角边分别是3和4,那么这个三角形的斜边长是________。

一、选择题1. 选择题答案:C解析:题目中给出的方程为x+3=2x-5,移项得x=8,代入原方程检验,8+3=2×8-5,等式成立,故x=8是方程的解。
2. 选择题答案:B解析:题目中给出的方程为2(x-3)=3(x+2),展开得2x-6=3x+6,移项得x=-12,代入原方程检验,2×(-12-3)=3×(-12+2),等式成立,故x=-12是方程的解。
3. 选择题答案:A解析:题目中给出的方程为x^2-5x+6=0,因式分解得(x-2)(x-3)=0,解得x=2或x=3。
4. 选择题答案:D解析:题目中给出的方程为(x-1)^2=4,开平方得x-1=±2,解得x=3或x=-1。
5. 选择题答案:C解析:题目中给出的方程为(x+2)^2=0,开平方得x+2=0,解得x=-2。
二、填空题1. 填空题答案:x=2解析:题目中给出的方程为x+3=2x-5,移项得x=8,代入原方程检验,8+3=2×8-5,等式成立,故x=8是方程的解。
2. 填空题答案:x=3解析:题目中给出的方程为2(x-3)=3(x+2),展开得2x-6=3x+6,移项得x=-12,代入原方程检验,2×(-12-3)=3×(-12+2),等式成立,故x=-12是方程的解。
3. 填空题答案:x=2解析:题目中给出的方程为x^2-5x+6=0,因式分解得(x-2)(x-3)=0,解得x=2或x=3。
4. 填空题答案:x=3解析:题目中给出的方程为(x-1)^2=4,开平方得x-1=±2,解得x=3或x=-1。
5. 填空题答案:x=-2解析:题目中给出的方程为(x+2)^2=0,开平方得x+2=0,解得x=-2。
三、解答题1. 解答题答案:步骤一:将方程x^2-5x+6=0因式分解得(x-2)(x-3)=0。
步骤二:解得x=2或x=3。
步骤三:代入原方程检验,2^2-5×2+6=0,3^2-5×3+6=0,等式成立。
初二数学经典题型练习1.已知:如图, P 是正方形ABCD内点,∠ PAD=∠ PDA= 150.求证:△ PBC是正三角形.证明如下。
首先, PA=PD,∠ PAD=∠ PDA=(180° - 150°)÷ 2=15°,∠ PAB=90° - 15°=75°。
A D 在正方形 ABCD之外以 AD为底边作正三角形ADQ,连接 PQ,则P∠P DQ=60°+15°=75°,同样∠ PAQ=75°,又 AQ=DQ,,PA=PD,所以△ PAQ≌△ PDQ,那么∠ PQA=∠PQD=60°÷ 2=30°,在△PQA中,B C ∠A PQ=180° - 30° - 75°=75°=∠ PAQ=∠ PAB,于是 PQ=AQ=AB,显然△ PAQ≌△ PAB,得∠ PBA=∠PQA=30°,PB=PQ=AB=BC,∠ PBC=90° - 30°=60°,所以△PBC是正三角形。
2.已知:如图,在四边形 ABCD中, AD= BC,M、N 分别是 AB、CD的中点, AD、 BC的延长线交 MN于 E、F.求证:∠ DEN=∠ F.FE证明 : 连接 AC,并取 AC的中点 G,连接 GF,GM.又点 N为 CD的中点 , 则 GN=AD/2;GN∥ AD,∠GNM=∠ DEM;(1)同理 :GM=BC/2;GM∥ BC,∠ GMN=∠ CFN;(2)又AD=BC,则 :GN=GM,∠ GNM=∠ GMN故. : ∠ DEM=∠ CFN.N CDA BM3、如图,分别以△ABC的 AC和 BC为一边,在△ ABC的外侧作正方形ACDE和正方形CBFG,点 P 是 EF的中点.求证:点P 到边 AB的距离等于AB的一半.证明:分别过E、 C、 F 作直线 AB 的垂线,垂足分别为M、 O、 N,在梯形 MEFN中, WE平行 NF因为 P为 EF 中点, PQ平行于两底所以 PQ为梯形 MEFN中位线,D所以 PQ=( ME+ NF) /2GC又因为,角 0CB+角 OBC=90°=角 NBF+角 CBO E所以角 OCB=角 NBFP F 而角 C0B=角 Rt=角 BNFAQBCB=BF所以△ OCB全等于△ NBF△MEA全等于△OAC(同理)所以 EM= AO, 0B= NF所以 PQ=AB/2.4、设 P 是平行四边形ABCD内部的一点,且∠PBA=∠ PDA.求证:∠ PAB=∠ PCB.过点 P作 DA的平行线,过点 A 作 DP的平行线,两者相交于点E;连接 BE因为 DP2a3a个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高DA A D度一半后,改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间P t 分。
求两P根水管各自注水的速度。
解:设小水管进水速度为x,则大水管进水速度为4x。
B C 由题意得:v v t B C2x 8x解之得: x 5v 8t经检验得:5vx是原方程解。
8t5v,大口径水管速度为5v 。
∴小口径水管速度为8t2t7.如图 11,已知正比例函数和反比例函数的图像都经过点M- 1),且P -1,- 2)为双曲(- 2,(线上的一点, Q为坐标平面上一动点, PA垂直于 x 轴, QB垂直于 y 轴,垂足分别是A、B.( 1)写出正比例函数和反比例函数的关系式;( 2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△ OBQ与△ OAP面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;( 3)如图 12,当点 Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形 OPCQ ,求平行四边形 OPCQ 周长的最小值.yyQB QBAOAOxxMMCPP图图1 解:( 1)设正比例函数解析式为y kx ,将点 ( 2 , 1 )坐标代入得Mk = ,所以正比例函数解1 x2析式为 y =2同样可得,反比例函数解析式为y =2x(2)当点Q 在直线 上运动时,DO1设点 Q 的坐标为 Q (m , m) ,2于是 S △ OBQ = 1OB? BQ1创1mm = 1m 2 ,22241= 1 ,而S △OAP = (- 1)? ( 2)2所以有, 1m 2 = 1 ,解得 m24所以点 Q 的坐标为 Q 1(2 ,1) 和 Q 2 (- 2,- 1)(3)因为四边形是平行四边形,所以 = , = ,OPCQOP CQ OQ PC而点 P ( 1 , 2 )是定点,所以 OP 的长也是定长,所以要求平行四边形OPCQ 周长的最小值就只需求的最小值.OQ因为点 Q 在第一象限中双曲线上,所以可设点Q 的坐标为2Q( n , ) ,n由勾股定理可得 OQ 2 = n 2+ 42 = (n - 2)2+ 4 ,22 n n所以当 ( n - )2 = 0 即 n - = 0 时, OQ 2有最小值 4,n n又因为 OQ 为正值,所以 OQ 与 OQ 2 同时取得最小值,所以 OQ有最小值2.由勾股定理得OP= 5 ,所以平行四边形OPCQ周长的最小值是8.如图, P是边长为1的正方形 ABCD对角线 AC上一动点( P 与 A、 C不重合),点 E 在射线 BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x, △PBE的面积为y.①求出 y 关于 x 的函数关系式,并写出x 的取值范围;②当 x 取何值时, y 取得最大值,并求出这个最大值.解:( 1)证法一:① ∵四边形 ABCD是正方形, AC为对角线,∴BC=DC,∠ BCP=∠ DCP=45°.∵PC=PC,∴ △ PBC≌△ PDC(SAS).A D∴PB= PD,∠PBC=∠ PDC.又∵=,P PB PE1H∴ PE=PD.B2 CE②( i )当点E在线段BC上( E与B、C不重合 ) 时,∵PB=PE,∴ ∠ PBE=∠ PEB,∴ ∠ PEB=∠ PDC,∴ ∠ PEB+∠ PEC=∠ PDC+∠ PEC=180°,∴ ∠ DPE=360°-(∠ BCD+∠ PDC+∠ PEC)=90°,∴ PE⊥ PD.)( ii )当点E与点C重合时,点P 恰好在 AC中点处,此时,PE⊥ PD.( iii)当点E在BC的延长线上时,如图.∵ ∠ PEC =∠ PDC ,∠ 1=∠2,∴ ∠ DPE =∠ DCE =90°,∴⊥ .PE PD综合( i )( ii )( iii ) , PE ⊥ PD .( 2)① 过点P 作 ⊥ ,垂足为 ,则 = .PF BC F BF FE∵ AP =x , AC = 2 ,∴ PC = 2 - x , PF =FC =2( 2 x) 12x .22BF =FE =1- FC =1-( 12 x )=2x .2 2∴△ PBE =· =2( 12 x )1x 22 x .SBFPFx2 222即 y1 x2 2 x (0<x < 2 ).2 2② y1 x2 2 x 1( x2 )2 1 .2222 4∵ a1< 0,2∴ 当 x2 时, y 最大值 1 .24A DPB F E C( 1)证法二:① 过点 P 作 GF ∥ AB ,分别交 AD 、 BC 于 G 、F . 如图所示 . ∵ 四边形 ABCD 是正方形,∴ 四边形 ABFG 和四边形 GFCD 都是矩形,AGD△ AGP 和△ PFC 都是等腰直角三角形 .32P∴ GD=FCFP , GP=AGBF ,∠ PGD =∠ PFE =90° .1又∵ PB =PE ,BF EC∴ BF =FE , ∴ GP =FE ,∴ △ EFP ≌△ PGD ( SAS ) .∴ PE =PD .② ∴ ∠ 1=∠ 2.∴ ∠ 1+∠ 3=∠ 2+∠ 3=90° .∴ ∠ DPE =90° .∴ PE ⊥ PD .( 2)①∵ AP =x ,∴ BF =PG =2x , PF =1-2x .22∴△ PBE =· = 2x ( 1 2 x )1 x2 2 x .SBFPF22 22即 y1 x2 2 x(0<x < 2 ).2 2② y1 x2 2 x 1( x2 )2 1 .2222 4∵ a1< 0,2∴ 当 x2时, y 最大值1 .249、如图,直线 y=k 1x+b 与反比例函数 y=k2x 的图象交于 A ( 1, 6), B (a , 3)两点.( 1)求 k 1、 k 2 的值.( 2)直接写出 k1x+b-k2x > 0 时 x 的取值范围;( 3)如图,等腰梯形 OBCD 中, BC ∥OD ,OB=CD ,OD 边在 x 轴上,过点 C 作 CE ⊥ OD 于点 E ,CE 和反比例函数的图象交于点 P ,当梯形 OBCD 的面积为 12 时,请判断 PC 和 PE 的大小关系,并说明理由.10、如图 12,已知直线1x 与双曲线 yky(k 0) 交于A,B两点,且点 A 的横坐标为 4 .2x( 1)求k的值;( 2)若双曲线y k(k 0) 上一点C的纵坐标为8,求△AOC的面积;x( 3)过原点O的另一条直线l交双曲线y k(k0) 于 P, Q 两点(P点在第一象限),若由点xA, B, P, Q 为顶点组成的四边形面积为24 ,求点 P 的坐标.yAO xB图 12。