九年级数学分式综合练习题

初中数学分式的约分通分综合练习题(附答案)初中数学分式的约分通分综合练题一、单选题1.下列分式中，不论$x$取何值，一定有意义的是（）frac{x-1}{x-1}\cdot\frac{x+1}{x-1}$A。

$\frac{x+1}{x}$B。

$x$C。

$\frac{x^2-1}{x}$D。

$\frac{x^2+1}{x}$2.下列代数式中，是分式的为（）A。

$\frac{1}{2}$B。

$\frac{x}{3}$C。

$\frac{x}{2}-y$D。

$\frac{5}{x^3}$3.下列各式中，是分式的是（）A。

$\frac{2x+1}{x(x-3)}$B。

$2$C。

$\frac{x}{\pi-2}$D。

$\frac{1}{3x^2}$4.当分式$\frac{x}{2x-1}$无意义时，$x$的值是（）A。

$2$B。

$-\frac{1}{2}$C。

$0$D。

$1$5.下列各式正确的是（）A。

$\frac{b+xa}{b+x}=\frac{a}{b+1}$B。

$\frac{y^2n}{n-ax}=\frac{y}{x^2}$C。

$\frac{n}{ma}=\frac{1}{a}$（$a\neq 0$）D。

$m=m-a$6.下列三个分式$\frac{1}{2x^2}$，$\frac{4(m-n)}{3x}$，$\frac{2x+4x^2y}{x^2-1}$，的最简公分母是（）A。

$4(m-n)x$B。

$2(m-n)x^2$C。

$\frac{1}{4}x^2(m-n)$D。

$4(m-n)x^2$7.计算$\frac{(x+y)^2-(x-y)^2}{4xy}$的结果为（）A。

$1$B。

$\frac{1}{2}$C。

$\frac{1}{4}$D。

$0$8.下列分式：$\frac{3x}{-x^2}$，$\frac{x-y}{x^2+y^2}$，$\frac{x+y}{xy+x}$，$\frac{2x+4x^2y}{x^2-1}$，其中是最简分式的有（）A。

计算专题——分式综合 九年级数学中考复习1．阅读下列材料学习“分式方程及其解法”的过程中，老师提出一个问题：若关于x 的分式方程14ax =-的解为正数，求a 的取值范围．经过独立思考与分析后，小明和小聪开始交流解题思路，小明说：解这个关于x 的方程，得到方程的解为4x a =+，由题目可得40a +>，所以4a >-，问题解决．小聪说：你考虑的不全面，还必须0a ≠才行． （1）请回答： 的说法是正确的，正确的理由是 ． 完成下列问题： （2）已知关于x 的方程233m xx x-=--的解为非负数，求m 的取值范围； （3）若关于x 的方程322133x nx x x --+=---无解，求n 的值．2．阅读下列材料：关于x 的方程11x c x c +=+的解是1211,(x c x x c==，2x 表示未知数x 的两个实数解，下同）；22x c x c +=+的解是122,x c x c ==；33x c x c +=+的解是123,x c x c==． 请观察上述方程与解的特征，比较关于x 的方程(0)m mx c m x c+=+≠与它们的关系，猜想它的解是 ．由上述的观察、比较、猜想，可以得出结论：如果方程的左边是未知数与其倒数的倍数的和，方程右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解．请用这个结论解关于x 的方程： （1）1265x x +=； （2）2211x a x a +=+--； （3）2131462a a x x a+++=-．3．我们把形如(mnx m n m x+=+，n 不为零），且两个解分别为1x m =，2x n =的方程称为“十字分式方程”． 例如65x x +=为十字分式方程，可化为2323x x ⨯+=+，12x ∴=，23x =． 再如78x x +=-为十字分式方程，可化为(1)(7)(1)(7)x x-⨯-+=-+-． 11x ∴=-，27x =-．应用上面的结论解答下列问题： （1）若107x x+=-为十字分式方程，则1x = ，2x = ． （2）若十字分式方程45x x -=-的两个解分别为1x a =，2x b =，求1b aa b++的值． （3）若关于x 的十字分式方程232321k k x k x --=--的两个解分别为1x ，212(3,)x k x x >>，求124x x +的值．4．新定义：对非负实数x “四舍五入”到个位数的值记为x <> 即：当n 为非负整数时，如果1122n x n -+，则x n <>=． 反之，当n 为非负整数时，如果x n <>=，则1122n x n -<+ 例如：00.480<>=<>=，0.64 1.491<>=<>=，22<>=， 3.5 4.124<>=<>=，⋯ 试解决下列问题： 填空：①π<>= (π为圆周率）；②如果13x <->=，则实数x 的取值范围为 ；③若关于x 的不等式组24130x x a x -⎧-⎪⎨⎪<>->⎩的整数解恰有4个，求a 的取值范围；④关于x 的分式方程112221m x x x -<>+=--有正整数解，求m 的取值范围； ⑤求满足65x x <>=的所有非负实数x 的值．5．定义：若分式M 与分式N 的和等于它们的积，即M +N ＝MN ，则称分式M 与分式N 互为“关联分式”．如21x x +与21x x -，因为()222422111(1)11x x x x x x x x x x x +==⋅+-+-+-所以21xx +与21xx -互为“关联分式”，其中一个分式是另外一个分式的“关联分式”． （1）分式221a + 分式221a -的“关联分式”（填“是”或“不是”）； （2）求分式()02aab a b≠-的“关联分式”； （3）若分式224ab a b -是分式22aa b+的“关联分式”，ab ≠0，求分式222a b ab -的值．6．阅读材料：对于非零实数a ，b ，若关于x 的分式()()x a x b x--的值为零，则解得1x a =，2x b =．又因为2()()()()x a x b x a b x ab abx a b x x x---++==+-+，所以关于x 的方程()ab x a b x +=+，的解为1x a =，2x b =．（1）理解应用：方程22233x x +=+的解为：1x = ，2x = ；（2）知识迁移：若关于x 的方程35x x+=的解为1x a =，2x b =，求22a b +的值；（3）拓展提升：若关于x 的方程41k x x =--的解为1x ，2x ，且121x x =，求k 的值．7．由完全平方公式222()2a b a ab b -=-+可知，222()2a b a b ab +=-+，而2()0a b -，所以，对所有的实数a ，b 都有：222a b ab +，且只有当a b =时，才有等号成立：222a b ab +=． 应用上面的结论解答下列问题：（1）计算21()x x-= ，由此可知221x x + 2（填不等号）；（2）已知m ，n 为不相等的两正数，试比较：(1%)(1%)m n ++与(1%)(1%)22m n m n++++的大小；（3）试求分式24224x x x -+的最大值．8．如果两个分式M 与N 的和为常数k ，且k 正整数，则称M 与N 互为“和整分式”，常数k 称为“和整值”．如分式1x M x =+，11N x =+，111x M N x ++==+，则M 与N 互为“和整分式”，“和整值” 1k =．（1）已知分式72x A x -=-，22696x x B x x ++=+-，判断A 与B 是否互为“和整分式”，若不是，请说明理由；若是，请求出“和整值” k ； （2）已知分式342x C x -=-，24G D x =-，C 与D 互为“和整分式”，且“和整值” 3k =，若x 为正整数，分式D 的值为正整数t ．①求G 所代表的代数式； ②求x 的值；（3）在（2）的条件下，已知分式353x P x -=-，33mx Q x-=-，且P Q t +=，若该关于x 的方程无解，求实数m 的值．9．我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．如21,11x x x x -+-这样的分式就是假分式；再如：232,11xx x ++这样的分式就是真分式类似的，假分式也可以化为带分式（即:整式与真分式的和的形式）．如：1(1)221111x x x x x -+-==-+++；再如：2211(1)(1)1111111x x x x x x x x x -++-+===++----． 解决下列问题：（1）下列分式中属于“真分式”的有 ；（填序号）①2x ；②211x x -+；③211x x x -+-（2）将假分式22x x +化为带分式的形式；（3）如果211x x -+的值为整数，求x 的整数值．10．对于形如kx m x+=的分式方程，若k ab =，m a b =+，容易检验1x a =，2x b =是分式方程ab x a b x +=+的解，所以称该分式方程为“易解方程”．例如：23x x+=可化为1212x x ⨯+=+，容易检验11x =，22x =是方程的解，∴23x x +=是“易解方程”：又如65x x +=-可化为(2)(3)23x x --+=--，容易检验13x =-，22x =-是方程的解，∴65x x+=-也是“易解方程”．根据上面的学习解答下列问题： （1）判断56x x+=-是不是“易解方程”，若是“易解方程”，求该方程的解1x ，212()x x x <；若不是，说明理由．（2）若1x m =，2x n =是“易解方程” 34x x -=的两个解，求11m n+的值； （3）设n 为自然数，若关于x 的“易解方程” 223352n nx n x ++=+-的两个解分别为1x ，212()x x x <，求211x x -的值．答案版： 1【解答】解：（1）分式方程的解不能是增根，即不能使分式的分母为0，∴小聪说得对，分式的分母不能为0；（2）233m xx x-=--， 233m xx x +=--， 2(3)m x x +=-， 6x m =+，解为非负数，60m ∴+，即6m -，又30x -≠，63m ∴+≠，即3m ≠-，6m ∴-且3m ≠-；（3）322133x nx x x --+=---， 322(3)x nx x -+-=--， (1)2n x -=，原方程无解， 10n ∴-=或3x =，①当10n -=时，解得1n =； ②当3x =时，解得53n =； 综上所述：当1n =或53n =时原方程无解． 2． 【解答】解：11x c x c +=+的解是121,x c x c==； 22x c x c +=+的解是122,x c x c ==； 33x c x c +=+的解是123,x c x c==； ∴(0)m m x c m x c +=+≠的解是1x c =，2mx c=，故答案为：1x c =，2m x c=； （1）1265x x +=， 1155x x ∴+=+， 15x ∴=，215x =； （2）2211x a x a +=+--， 221111x a x a ∴-+=-+--， 11x a ∴-=-或211x a -=- 1x a ∴=，211a x a +=-； （3）2131462a a x x a +++=-， 2131223a a x x a ++∴+=-， 112323x a x a∴+=++-，112323x a x a∴-+=+-， 23x a ∴-=或123x a-=， 132a x +∴=，2312a x a +=．3．【解答】（1）解：方程107x x+=-是十字分式方程，可化为： (2)(5)(2)(5)x x-⨯-+=-+-， 12x ∴=-，25x =-，故答案为：2-，5-． （2）解：十字分式方程45x x-=-的两个解分别为：1x a =，2x b =， 4ab ∴=-，5a b +=-，∴1b a a b++ 221b a ab+=+，2()21a b ab ab +-=+， 2()21a b ab +=-+， 2(5)14-=--， 294=-． （3）解：方程232321k k x k x --=--是十字分式方程，可化为： (23)1(23)1k k x k k x --+=+--， 当3k >时，2330k k k --=->， 关于x 的十字分式方程232321k k x k x --=--的两个解分别为：1x ，212(3,)x k x x >>，1123x k ∴-=-，21x k -=， 122x k ∴=-，21x k =+ ，∴124224222(1)2111x k k k x k k k +-+++====+++． 4． 【解答】解：①由题意可得：3n <>=； 故答案为：3， ②13x <->=， 2.51 3.5x ∴-<， 3.5 4.5x ∴<； 故答案为：3.5 4.5x <； ③解不等式组得：1x a -<<>， 由不等式组整数解恰有4个得，23a <<>， 故2.5 3.5a <； ④解方程得22x m =-<>， 2m -<>是整数，x 是正整数，21m ∴-<>=或2， 21m -<>=时，2x =是增根，舍去． 22m ∴-<>=， 0m ∴<>=， 00.5m ∴<． ⑤0x ，65x 为整数，设65x k =，k 为整数， 则56x k =， 56k k ∴<>=， 151262k k k ∴-+，0k ， 03k ∴， 0k ∴=，1，2，3 则0x =，56，53，52． 5． 【解答】解：（1）+ ＝ ＝ ＝ ＝， ∴分式是分式的“关联分式”；故答案为：是；（2）设分式的“关联分式”为N，则有，∴，∴，∵ab≠0，∴，∴分式的“关联分式”为；（3）∵分式是分式的“关联分式”，∴∵ab≠0，∴b2＝8a2∴，∴．6．【解答】解：（1）abx a bx+=+的解为1x a=，2x b=，∴222233xxx x+=+=+的解为3x=或23x=，故答案为：3，23；（2）35xx+=，5a b∴+=，3ab=，222()225619a b a b ab∴+=+-=-=；（3）41k xx=--可化为2(1)40x k x k-+++=，121x x=，41k∴+=，3k∴=-．7． 【解答】解：（1）4222121()x x x x x -+-=， 2212x x ∴+， 故答案为：42221x x x -+，； （2）(1%)(1%)1%%%%m n m n m n ++=+++⋅， 2(1%)(1%)12%(%)2222m n m n m n m n ++++++=+⋅+，2222()()24242m n m mn n m n mn mn +--=++-=， 又m n ≠， (1%)(1%)(1%)(1%)22m n m n m n ++∴++<++； （3）当0x =时，242024x x x =-+， 当0x ≠时，242222211442422x x x x x x x ==-+-++-，()22242242,x x x x x +==当时等号成立， ∴2421124422x x x =-+-， ∴224212,242x x x x =-+当时的最大值为． 8． 【解答】解：（1）72x A x -=-，22696x x B x x ++=+-， ∴2227697(3)732(2)2262(3)(2)222x x x x x x x x A B x x x x x x x x x -++-+-+-+=+=+=+==-+--+----．A ∴与B 是互为“和整分式”，“和整值” 2k =； （2）①342xC x -=-，24GD x =-， ∴2(34)(2)328(2)(2)(2)(2)(2)(2)x x G x x G C D x x x x x x -++-++=+=-+-+-+， C 与D 互为“和整分式”，且“和整值” 3k =， 223283(2)(2)312x x G x x x ∴+-+=-+=-， 2231232824G x x x x ∴=---+=--；②22(2)24(2)(2)2G x D x x x x -+===--+--，且分式D 的值为正整数t ．x 为正整数， 21x ∴-=-或22x -=-， 1(0x x ∴==舍去）； （3）由题意可得：2212t D ==-=-， ∴353233x mx P Q x x --+=+=--， ∴35323x mx x --+=-， (3)226m x x ∴--=-， 整理得：(1)4m x -=-， 方程无解， 10m ∴-=或方程有增根3x =， 解得：1m =， 当10m -≠，方程有增根3x =， ∴431m -=-， 解得：73m =， 综上：m 的值为：1或73． 9． 【解答】解：（1）由题意可得：①是“真分式”；②③都是“假分式”． 故答案为：①； （2）2244(2)(2)4422222x x x x x x x x x -++-+===-+++++； （3）212(1)332111x x x x x -+-==-+++， 211x x -+的值为整数， ∴31x +的值为整数， 3∴是(1)x +的倍数， x ∴的整数值为4-、2-、0、2． 10．【解答】解：（1）56x x +=-是“易解方程”，理由： 56x x +=-可化为(5)(1)51x x --+=--， 51-<-， ∴56x x +=-是“易解方程”． ∴方程的解为15x =-，21x =-； （2）1x m =，2x n =是“易解方程” 34x x -=的两个解，3mn ∴-=，4m n =+， 则114433n m m n mn ++===--； （3）设2y x =-，方程可化为(23)23n n y n n y ++=++，2232332n n x n x +-+=+-是“易解方程”， n ∴和23n +是这个方程的解， n 为自然数， 23n n ∴<+， ∴必有12x n -=，2223x n -=+， 12x n ∴=+，225x n =+， ∴21125122x n x n -+-==+．。

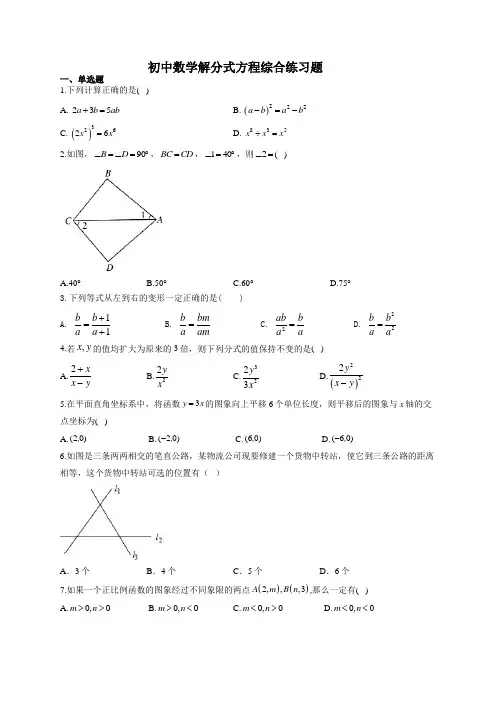
初中数学解分式方程综合练习题一、单选题1.下列计算正确的是( )A. 235a b ab +=B. ()222a b a b -=-C. ()32626x x =D. 835x x x ÷= 2.如图，90B D ∠=∠=︒，BC CD =，140∠=︒，则2∠=( )A.40°B.50°C.60°D.75°3.下列等式从左到右的变形一定正确的是( ) A. 11b b a a +=+ B. b bm a am = C. 2ab b a a= D. 22b b a a = 4.若,x y 的值均扩大为原来的3倍，则下列分式的值保持不变的是( ) A.2x x y +- B.22y x C.3223y x D.()222y x y -5.在平面直角坐标系中，将函数3y x =的图象向上平移6个单位长度，则平移后的图象与x 轴的交点坐标为( )A.(2)0,B.(20)-,C.(6)0,D.(60)-,6.如图是三条两两相交的笔直公路，某物流公司现要修建一个货物中转站，使它到三条公路的距离相等，这个货物中转站可选的位置有（ ）A ．3个B ．4个C ．5个D ．6个7.如果一个正比例函数的图象经过不同象限的两点()()2,,,3A m B n ,那么一定有( )A.0,0m n >>B.0,0m n ><C.0,0m n <>D.0,0m n <<8.关于x 的方程32211x m x x -=+++无解，则m 的值为( ) A.5- B.8-C.2-D.59.下列各分式中,是最简分式的是( ) A.105xy xB. 22x y x y-- C. x y x+ D. 24x 10.若x 为整数，且使分式2123x x ++的值为整数，则满足条件的x 的值有( ) A.5个 B.6个 C.8个 D.7个11.随着时代的进步，人们对 2.5PM （空气中直径小于等于2.5微米的颗粒）的关注日益密切．某市一天中 2.5PM 的值31(ug /m )y 随时间(h)t 的变化如图所示，设2y 表示0时到t 时2.5PM 的值的极差（即0时到t 时 2.5PM 的最大值与最小值的差），则2y 与t 的函数关系大致是（ ）A ．B ．C ．D ．二、解答题12.某商店购进A B 、两种商品，购买1个A 商品比购买1个B 商品多花10元，并且花费300元购买A 商品和花费100元购买B 商品的数量相等．（1）求购买一个A 商品和一个B 商品各需要多少元；（2）商店准备购买A B 、两种商品共80个，若A 商品的数量不少于B 商品数量的4倍，并且购买A B 、商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？13.随着5G 技术的发展，人们对各类5G 产品的使用充满期待，某公司计划在某地区销售一款5G 产品，根据市场分析，该产品的销售价格将随销售周期的变化而变化．设该产品在第x （x 为正整数）个销售周期每台的销售价格为y 元，y 与x 之间满足如图所示的一次函数关系．（1）求y 与x 之间的关系式；（2）设该产品在第x 个销售周期的销售数量为p （万台），p 与x 的关系可以用1122p x =+来描述．根据以上信息，试问：哪个销售周期的销售收入最大？此时该产品每台的销售价格是多少元？14.如图,在ABC △中,90,BAC E ∠=︒为边BC 上的点,且,AB AE D =为线段BE 的中点,过点E 作EF AE ⊥,过点A 作//AF BC ,且,AF EF 相交于点F .(1)求证：C BAD ∠=∠；(2)求证：AC EF =.15.如图, ,60,AB BC ABC BDC =∠=∠=︒求证: AD CD BD +=;三、计算题16.计算： 1.(6)(2)(3)a a a a +--+2.221121x x x x x x--÷+++17.计算：(1)222123234x y x xy --； (2)22y x x xy y x+--. 18.计算:693()(1).x x x x--÷- 19.计算下列小题：（1）计算：20(2)3(6)----；（2）解分式方程：22511x x =--．20.若33m n a a -÷=，且22m n +=，求34m n -21.化简(1)2245a a +--(2)()()22228423xy x y x y xy -+--+-22.对于实数,a b 定义运算：(,0)(,0)b b a a b a a b a a b a -⎧>≠⎪=⎨≤≠⎪⎩▲ 如: 3123=2,8-=▲242416==▲. 照此定义的运算方式计算: [][]2(4)(4)(2)-⨯--▲▲四、填空题23.已知分式2x m x n -+，当2x =时，分式的值为0；当1x =时，分式无意义，则m n += . 24.分式22,b a b a ab a ab ---+的最简公分母是 . 25.一个周长是20cm 的长方形，它的面积()2cm S 与长边()cm x 之间的函数表达式为 ，自变量x 的取值范围是 .26.已知()214k y k x k =-+-是一次函数，则()201932k += .27.如图，在ABC △中,10,12,8,AB AC BC AD AD ====是BAC ∠的平分线.若,P Q 分别是AD 和AC 上的动点，则PC PQ +的最小值是 .28.如图，BD 是ABC △的角平分线，它的垂直平分线分别交AB ，BD ，BC 于点E ，F ，G ，若30ABC ∠=︒，45C ∠=︒，ED =H 是BD 上的一个动点，则HG HC +的最小值为 ．29.分解因式:3x x -=___________.参考答案1.答案：D解析：A 、23a b +，无法计算，故此选项错误；B 、222()2a b a ab b -=-+，故此选项错误；C 、()32628x x =，故此选项错误； D 、835x x x ÷＝，故此选项正确；故选：D ．2.答案：B解析：3.答案：C解析：分式的基本性质是分式的分子、分母同乘(或除以)一个不为零的整式,分式的值不变.选项A,分子、分母同加1,不符合分式的基本性质,故A 错;选项B,分子、分母同乘m ,没有限制m 不等于零,故B 错;选项D,分子乘b ,分母乘a ,故D 错;选项C,分式2ab a中暗含0a ≠这个条件,所以分子、分母同时除以a ,分式值不变,故选C.4.答案：D解析：根据分式的基本性质，可知若,x y 的值均扩大为原来的3倍，选项A 中，23233x x x y x y ++≠-- ，故此选项错误；选项B 中，22629y y x x≠故此选项错误；选项C 中，3322542273y y x x≠ ，故此选项错误；选项D 中22221829()()y y x y x y =--，故此选项正确.5.答案：B解析：根据函数图象的平移规律，可知3y x =向上平移6个单位后得到的函数解析式为36y x =+，令0y =，即360x +=，解得2x =-，∴与x 轴的交点坐标为(20)-,，故选B6.答案：B 解析：利用角平线性质知角平分线上的点到角两边距离相等，通过三角形内心为其内切圆的圆心来解得．解答：根据三条路线构成的三角形知，三角形的内心为三角形内角角平分线的交点． 由三角形内心为该三角形内切圆的圆心，∴所以符合货物中转站到各路的距离相等．这样的点可找到一个．两外角平分线的交点，到三条公路的距离也相等，可找到三个．故答案为：B ．7.答案：D 解析：∵点()2,A m 的横坐标为20>， ∴此点在一、四象限；∵点(),3B n 的纵坐标为30>，∴此点在一、二象限，∴此函数的图象一定经过二、四象限，∴点()2,A m 在第四象限,(),3B n 在第二象限，∴0,0m n <<.故答案为：0,0m n <<.8.答案：A解析：原分式通分得322(1)11x x m x x -++=++ 等式两边同时乘以(1)x +，得322(1)x x m -=++整理得4x m =+因为原分式无解，所以原分式的分母10x +=，即1x =-代入4x m =+中得，14m -=+，解得5m =-，故选A.9.答案：C解析：10.答案：C解析：2122(3)662333x x x x x +++==++++31,2,3,6x ∴+=±±±±，即4,2,1,5,0,6,3,9x =------时，分式的值为整数.故选C.11.答案：B解析：当0t =时，极差285850y -==，当010t <≤时，极差2y 随t 的增大而增大，最大值为43； 当1020t <≤时，极差2y 随t 的增大保持43不变；当2024t <≤时，极差2y 随t 的增大而增大，最大值为98； 故选：B ．12.答案：解：（1）设购买一个B 商品需要x 元，则购买一个A 商品需要(10)x +元， 依题意，得：30010010x x=+， 解得：5x =，经检验，5x =是原方程的解，且符合题意，1015x ∴+=．答：购买一个A 商品需要15元，购买一个B 商品需要5元．（2）设购买B 商品m 个，则购买A 商品(80)m -个，依题意，得：80415(80)5100015(80)51050m m m m m m -≥⎧⎪-+≥⎨⎪-+≤⎩，解得：1516m ≤≤． m 为整数，15m ∴=或16．∴商店有2种购买方案，方案①：购进A 商品65个、B 商品15个；方案②：购进A 商品64个、B 商品16个．解析：13.答案：解：（1）设函数的解析式为：(0)y kx b k =+≠，由图象可得，700055000k b k b +=⎧⎨+=⎩， 解得，5007500k b =-⎧⎨=⎩， ∴y 与x 之间的关系式：5007500y x =-+；（2）设销售收入为w 万元，根据题意得，11(5007500)()22w yp x x ==-++， 即2250(7)16000w x =--+，∴当7x =时，w 有最大值为16000，此时500775004000y =-⨯+=（元）答：第7个销售周期的销售收入最大，此时该产品每台的销售价格是4000元．解析：14.答案：(1),AB AE D =为线段BE 的中点,AD BC ∴⊥, 90C DAC ∴∠+∠=︒,90BAC ∠=︒,90BAD DAC ∴∠+∠=︒,C BAD ∴∠=∠.(2)//AF BC ,FAE AEB ∴∠=∠,AB AE =,B AEB ∴∠=∠B FAE ∴∠=∠,且90,AEF BAC AB AE ∠=∠=︒=.()ABC EAF ASA ∴≌△△,AC EF ∴=.解析：15.答案：证明:如图2中,延长DC 到E,使得DB DE =∵,60DB DE BDC =∠=︒,∴△BDE 是等边三角形,,60,BD BE DBE ABC ∴∠=∠=∠=︒ABD CBE ∴∠=∠,∵AB BC =,∴△ABD ≅ △CBE ,∴AD EC =,∴BD DE DC CE DC AD ==+=+.∴AD CD BD +=.解析：16.答案：1.原式22412312a a a a a =+---=-2.原式21(1)(1)11x x x x x x x -+=⋅=+-+ 解析： 17.答案：解：(1)原式2222222689121212y y x x y x y x y =--222689.12y y x x y--= (2)原式2()y x x x y x y=--- 22()()y x x x y x x y =--- .x y x+=- 解析：18.答案：解：原式22693(3) 3.3x x x x x x x x x x -+--=÷=⋅=-- 解析：19.答案：解：（1）原式43416=-++=；（2）两边都乘以(1)(1)x x +-，得：2(1)5x +=， 解得：32x =， 检验：当32x =时，5(1)(1)04x x +-=≠， ∴原分式方程的解为32x =． 解析：20.答案：解：由1333m n m n a a a ---÷==，得到10m n --=，即1m n =+，代入22m n +=中得：222n n ++=，即0n =，把0n =代入得：1m =，则343m n -=．解析：21.答案：(1)原式3425a a =-+-3a =--(2)原式2222844812xy x y x y xy =-+-+-+225512x y =++ 解析：22.答案：解：根据题意得，412(4)216--==▲，2(4)(2)(4)16--=-=▲， 则[][]12(4)(4)(2)16116-⨯--=⨯=▲▲ 解析：23.答案：3解析：由题意，得402010m n n -=⎧⎪+≠⎨⎪+=⎩，解得41m n =⎧⎨=-⎩，故4(1)3m n +=+-=. 24.答案：()()a a b a b +-解析： 分式22,b a b a ab a ab---+的分母分别是22(),()a ab a a b a ab a a b -=-+=+，故最简公分母是()()a a b a b +-25.答案：210S x x =-+；510x <<解析：长方形的长为cm x ，周长为20cm ，则宽为()10cm x -， 所以它的面积()21010S x x x x =-=-+，易得010010x x x x >⎧⎪->⎨⎪>-⎩，解得510x <<.26.答案：1- 解析：由题意得1k =且10k -≠，解得1k =-，所以()()2019201932321k ++=-=-.27.答案：9.6解析：如图，连接.,BP AB AC AD =是BAC ∠的平分线，AD ∴垂直平分,.BC BP CP ∴=过点B 作BQ AC ⊥于点, Q BQ 交AD 于点P ，则此时PC PQ +取得最小值，最小值为BQ 的长，如图所示.11,22ABC S BC AD AC BQ =⋅=⋅△1289.610BC AD BQ AC ⋅⨯∴===28.答案：解析：29.答案：(1)(1)x x x +-解析：本题考查了分解因式,遵循先提取公因式,再利用平方差公式的顺序,32(1)(1)(1)x x x x x x x -=-=+-．。

分式综合练习题一 选择题1 下列运算正确的是（ ）A -40=1B （-3）-1=31 C （-2m-n ）2=4m-n D （a+b ）-1=a -1+b -12 分式28,9,12zy x xy z x x z y -+-的最简公分母是（ ） A 72xyz 2 B 108xyz C 72xyz D 96xyz 23 用科学计数法表示的树-3.6×10-4写成小数是（ ）A 0.00036B -0.0036C -0.00036D -360004 若分式6522+--x x x 的值为0，则x 的值为（ ）A 2B -2C 2或-2D 2或35计算⎪⎭⎫ ⎝⎛-+÷⎪⎭⎫ ⎝⎛-+1111112x x 的结果是（ ） A 1 B x+1 Cx x 1+ D 11-x 6 工地调来72人参加挖土和运土，已知3人挖出的土1人恰好能全部运走，怎样调动劳动力才能使挖出的土能及时运走，解决此问题，可设派x 人挖土，其它的人运土，列方程 ①3172=-x x ②72-x=3x ③x+3x=72 ④372=-xx 上述所列方程，正确的有（ ）个A 1B 2C 3D 4 7 在ma y x xy x x 1,3,3,21,21,12+++π中，分式的个数是（ ） A 2 B 3 C 4 D 58 若分式方程xa x a x +-=+-321有增根，则a 的值是（ ） A -1 B 0 C 1 D 29 若3,111--+=-ba ab b a b a 则的值是（ ） A -2 B 2 C 3 D -3二 填空1 一组按规律排列的式子：()0,,,,41138252≠--ab a b a b a b a b ，其中第7个式子是第n 个式子是2 7m =3,7n =5,则72m-n =3 ()2312008410-+⎪⎭⎫ ⎝⎛--+-= 4 若2222,2ba b ab a b a ++-=则= 三 化简 1 ()d cd b a c ab 234322222-•-÷ 2 111122----÷-a a a a a a3 ⎪⎭⎫ ⎝⎛---÷--225262x x x x四 解下列各题1 已知b ab a b ab a b a ---+=-2232,311求 的值2 若0<x<1,且xx x x 1,61-=+求 的值五 （5）先化简代数式()()n m n m mn n m n m n m n m -+÷⎪⎪⎭⎫ ⎝⎛+---+222222，然后在取一组m,n 的值代入求值六 解方程 1 12332-=-x x 2 1412112-=-++x x x七 2008年5月12日，四川省发生8.0级地震，我校师生积极捐款，已知第一天捐款4800元，第二天捐款6000元，第二天捐款人数比第一天捐款人数多50人，且两天人均捐款数相等，那么两天共参加捐款的人数是多少？分式练习题参考答案一 CACBC CBBA二 1 -()n n n ab a b 137201,--， 2 9/5， 3 2， 4 53 三 1 ac1 ，2 1-a a ，3 32+-x 四 1 提示：将所求式子的分子、分母同时除以ab 。

（易错题精选）初中数学分式综合训练一、选择题1．下列运算中正确的是（ ）A ．62652()a a a a a== B ．624282()()a a a a == C ．62121022()a a a a a== D ．6212622()a a a a a == 【答案】C【解析】【分析】根据幂的乘方法则、分式的基本性质及同底数幂除法法则计算即可得答案．【详解】 6212122102222()a a a a a a a a a÷===÷， 故选：C ．【点睛】本题考查幂的乘方及分式的基本性质，幂的乘方，底数不变，指数相乘；分式的分子、分母同时乘以（或除以）一个不为0的整式，分式的值不变；同底数幂相除，底数不变，指数相减；熟练掌握分式的基本性质是解题关键．2．若2250(0)a ab b ab ++=≠，则b a a b +=（ ） A ．5B ．-5C ．5±D ．2± 【答案】B【解析】【分析】根据题意，先得到225a b ab +=-，代入计算即可.【详解】解：∵2250(0)a ab b ab ++=≠，∴225a b ab +=-， ∴2255b a a b ab a b ab ab+-+===-； 故选：B.【点睛】本题考查了分式的化简求值，解题的关键是正确得到225a b ab +=-.3．化简21644m m m+--的结果是( ) A ．4m -B ．4m +C ．44m m +-D ．44m m -+ 【答案】B【解析】【分析】根据分式的加减运算法则计算，再化简为最简分式即可.【详解】 21644m m m+-- =2164m m -- =(4)(4)4m m m +-- =m+4.故选B.【点睛】 本题考查分式的加减.同分母分式相加减，分母不变，把分子相加减；异分母分式相加减，先通分，变为同分母的分式，再加减.熟练掌握运算法则是解题关键.4．计算(a 2)3＋a 2·a 3－a 2÷a －3的结果是( )A ．2a 5－aB ．2a 5－1aC ．a 5D ．a 6 【答案】D【解析】【分析】先分别进行幂的乘方、同底数幂的乘法、同底数幂的除法运算，然后再进行合并同类项即可.【详解】原式=a 2×3+a 2+3-a 2-(-3)=a 6+a 5-a 5=a 6，故选D.【点睛】本题考查了有关幂的运算，熟练掌握“幂的乘方，底数不变，指数相乘”、“同底数幂的乘法，底数不变，指数相加”、“同底数幂的除法，底数不变，指数相减”是解题的关键.5．要使分式81x -有意义，x 应满足的条件是（ ） A ．1x ≠-B ．0x ≠C ．1x ≠D ．2x ≠【答案】C【解析】【分析】直接利用分式有意义的条件得出答案．【详解】 要使分式81x -有意义， 则x-1≠0，解得：x≠1．故选：C ．【点睛】此题考查分式有意义的条件，正确把握分式的定义是解题关键．6．x 的取值范围为（ ） A ．5x ≠-B ．0x >C ．5x ≠- 且0x >D ．0x ≥【答案】D【解析】【分析】根据分式有意义的条件可得x+5≠0，再根据二次根式有意义的条件可得x≥0，由此即可求得答案.【详解】由题意得：x+5≠0，且x≥0，解得：x≥0，故选D ．【点睛】本题考查了分式有意义的条件 二次根式有意义的条件，关键是掌握分式有意义的条件是分母不等于零，二次根式中的被开方数是非负数．7．计算()22b a a -⨯的结果为 A ．bB ．b -C ． abD ．b a 【答案】A【解析】【分析】先计算（-a ）2，然后再进行约分即可得.【详解】()22b a a -⨯=22ba a⨯=b ，故选A.【点睛】本题考查了分式的乘法，熟练掌握分式乘法的运算法则是解题的关键.8．若分式12x x +-在实数范围内有意义，则x 的取值范围是（ ） A ．2x >B ．2x <C ．1x ≠-D ．2x ≠【答案】D【解析】【分析】根据分式有意义的条件即可求出答案．【详解】由题意可知：x-2≠0，x≠2，故选：D ．【点睛】本题考查分式的有意义的条件，解题的关键是熟练运用分式有意义的条件，本题属于基础题型．9．一艘轮船往返甲、乙两港之间，第一次往返航行时，水流速度为a 千米时，第二次往返航行时，正遇上发大水，水流速度b 千米时（b a >），已知该船在两次航行中的静水速度相同，则该船这两次往返航行所用时间的关系是（ ）A ．第一次往返航行用的时间少B ．第二次往返航行用的时间少C ．两种情况所用时间相等D ．以上均有可能 【答案】A【解析】【分析】甲乙两港之间的路程一定，可设其为S ，两次航行中的静水速度设为v ，所用时间=顺流时间+逆流时间，注意顺流速度=静水速度+水流速度；逆流速度=静水速度﹣水流速度，把相关数值代入，比较即可.【详解】解：设两次航行的路程都为S ，静水速度设为v ， 第一次所用时间为：222S S vS v a v a v a +=+-- 第二次所用时间为：222S S vS v b v b v b +=+-- ∵b a >，∴22b a >，∴2222v b v a -<-，∴222222vS vS v b v a >-- ∴第一次的时间要短些.故选：A.【点睛】本题主要考查了列代数式，得到两次所用时间的等量关系是解决本题的关键.10．下列计算正确的是（ ）A ．2236a a b b ⎛⎫= ⎪⎝⎭B ．1a b a b b a -=--C ．112a b a b +=+D ．1x y x y --=-+ 【答案】D【解析】【分析】根据分式的乘方、分式的加减运算法则及分式的性质逐一判断即可得答案.【详解】 A.22222()3(3)9a a a b b b ==，故该选项计算错误，不符合题意， B.a b a b a b a b b a a b a b a b +-=+=-----，故该选项计算错误，不符合题意， C.11b a a b a b ab ab ab ++=+=，故该选项计算错误，不符合题意， D.()1x y x y x y x y---+==-++，故该选项计算正确，符合题意， 故选：D.【点睛】本题考查分式的运算，分式的乘方，要把分式的分子、分母分别乘方；同分母分式相加减，分母不变，分子相加减；异分母分式相加减，先通分，变为同分母的分式，再加减；熟练掌握分式的运算法则是解题关键.11．华为Mate20手机搭载了全球首款7纳米制程芯片，7纳米就是0.000000007米．数据0.000000007用科学记数法表示为( )．A ．7710⨯﹣B ．80.710⨯﹣C ．8710⨯﹣D ．9710⨯﹣【答案】D【分析】由科学记数法知90.000000007710-=⨯；【详解】解：90.000000007710-=⨯；故选：D ．【点睛】本题考查科学记数法；熟练掌握科学记数法10n a ⨯中a 与n 的意义是解题的关键．12．生物学家发现某种花粉的直径约为0.0000036毫米，数据0.0000036用科学记数法可表示为（ ）A ．63.610-⨯B ．50.3610-⨯C ．73610-⨯D ．60.3610-⨯【答案】A【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n ，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】13．化简（a ﹣1）÷（1a ﹣1）•a 的结果是（ ） A ．﹣a 2B ．1C ．a 2D ．﹣1 【答案】A【解析】分析：根据分式的混合运算顺序和运算法则计算可得．详解：原式=（a ﹣1）÷1a a-•a =（a ﹣1）•()1a a --•a =﹣a 2，故选：A ．点睛：本题主要考查分式的混合运算，解题的关键是掌握分式的混合运算顺序和运算法则．14．式子()()()()()()a b b c c a b c c a a b c a a b b c ---++------的值不可能等于( )A ．﹣2B ．﹣1C ．0D ．1【解析】【分析】根据分式的加减运算，对式子进行化简，然后根据分式有意义，即可得出答案.【详解】解：()()()()()()-------a b b c c a ++b c c-a a-b b c a b b c=()()()()()()+-+----222a-b b c c a a b b c c a ，分式的值不能为0，因为只有a =b =c 时，分母才为0，此时分式没意义，故选：C ．【点睛】本题主要考察了分式的加减运算以及分式有意义的定义，解题的关键是分式的加减运算要正确进行通分，以及注意分式的分母不能为零.15．计算211a a a -+-的正确结果是（ ） A ．211a a -- B ．211a a --- C ．11a - D ．11a -- 【答案】A【解析】【分析】 先将后两项结合起来，然后再化成同分母分式，按同分母分式加减的法则计算就可以了.【详解】 211a a a -+-， =2(1)1a a a --- =222111a a a a a -+--- =211a a --. 故选：A.【点睛】 本题考查了数学整体思想的运用，分式的通分和约分的运用，解答的过程中注意符号的运用以及完全平方公式的运用.16．化简(1)b b a a a ⎛⎫-÷ ⎪-⎝⎭的结果是（） A ．-a-1B ．–a+1C ．-ab+1D ．-ab+b【答案】B【解析】【分析】 将除法转换为乘法，然后约分即可.【详解】 解：(1)(1)1(1)b b b a a a a a a a a b -⎛⎫⎛⎫-÷=-⨯=--=- ⎪ ⎪-⎝⎭⎝⎭， 故选B.【点睛】本题考查分式的化简，熟练掌握分式的运算法则是解题关键.17．式子2a +有意义，则实数a 的取值范围是（ ） A ．a≥-1B ．a≤1且a≠-2C ．a≥1且a≠2D ．a>2【答案】B【解析】【分析】直接利用二次根式有意义的条件分析得出答案．【详解】1-a≥0且a+2≠0， 解得：a≤1且a≠-2．故选：B ．【点睛】 此题主要考查了二次根式有意义的条件，正确把握二次根式的定义是解题关键．18．下列运算，错误的是（ ）.A ．236()a a =B ．222()x y x y +=+C ．01)1=D ．61200 = 6.12×10 4 【答案】B【解析】【分析】【详解】A. ()326a a =正确，故此选项不合题意；B.()222 x y x 2y xy +=++，故此选项符合题意；C. ()0511-=正确，故此选项不合题意；D. 61200 = 6.12×104正确，故此选项不合题意； 故选B.19．已知1112a b -=，则ab a b -的值是 A ．12 B ．－12 C ．2 D ．－2【答案】D【解析】分析：观察已知和所求的关系，容易发现把已知通分后，再求倒数即可． 解答：解：∵， ∴a ab -=， ∴=， ∴=-2．故选D ．20．如果30x y -= ，那么代数式()2223x y x x y y ⎛⎫+-÷- ⎪⎝⎭的值为（ ） A ．23 B ．2 C ．-2 D ．32【答案】A【解析】【分析】先根据分式的混合运算顺序和运算法则化简原式，再将x ＝3y 代入化简可得．【详解】解：()2223x y x x y y ⎛⎫+-÷- ⎪⎝⎭=()22213xy x y y x y -+-g =()2()13x y y x y --g=3x y y- ∵30x y -=，∴x=3y ， ∴32333x y y y y y --==， 故选：A ．【点睛】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则．。

初三数学下册综合算式专项练习题分式不等式的解法与应用初三数学下册综合算式专项练习题：分式不等式的解法与应用分式不等式是初中数学中的一种重要的题型，它包含了两个部分：分式和不等式。

在解分式不等式时，我们需要分别解分式和不等式两个方面的问题，并且将结果结合起来进行综合分析和应用。

一、分式的解法1. 分式的定义分式是形如$\frac{a}{b}$的数，其中$a$和$b$都是整数，且$b$不为零。

分子$a$表示分式的整体部分，分母$b$表示分式的单位部分。

2. 分式的化简对于分式$\frac{a}{b}$，我们可以进行化简，使分子和分母之间没有公因数。

化简的方法是找到$a$和$b$的最大公因数，然后将分子和分母同时除以最大公因数得到的结果。

例如，对于分式$\frac{4}{6}$，最大公因数是2，因此可以化简为$\frac{2}{3}$。

3. 分式的运算分式之间可以进行加、减、乘、除四种基本运算。

在进行分式的运算时，需要注意分子和分母的处理方法。

加减运算时，要求分母相同，可以通过通分的方式将分母变为相同的值；乘法是将两个分式的分子和分母相乘；除法是将一个分式的分子和分母互换位置，然后与另一个分式相乘。

二、不等式的解法1. 不等式的定义不等式是数之间大小关系的表示形式，包括大于、小于、大于等于、小于等于等几种形式。

例如，$x > 3$表示$x$大于3，$y \leq 2$表示$y$小于等于2。

2. 不等式的性质不等式具有一些性质，例如：- 若$a > b$，则$a + c > b + c$，其中$c$为任意实数。

- 若$a > b$且$b > 0$，则$a \cdot c > b \cdot c$，其中$c$为正实数。

根据这些性质，我们可以在解不等式时进行一些等价变形和推导。

但需要注意，在变形和推导的过程中，不等号的方向不可逆转。

3. 不等式的解集表示不等式的解集一般用数轴上的区间来表示。

初三数学下册综合算式专项练习题含有集合运算分式和绝对值的综合算式在初三数学下册的学习中，综合算式是一个重要的知识点。

综合算式的练习既可以巩固基本的计算能力，又可以培养学生的综合运算思维能力。

本文将分享一些含有集合运算、分式和绝对值的综合算式的专项练习题，希望能够帮助同学们更好地掌握这些知识点。

1. 集合运算综合算式综合运用集合的交、并、差等运算进行计算是初中数学的基本内容。

下面是一些综合运用集合运算的练习题：(1) 设全集为U={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}，A={2, 4, 6, 8}，B={3, 6, 9}，求(A∩B)∪(A∪B)的结果。

解析：首先计算A∩B，即A和B的交集为{6}；然后计算A∪B，即A和B的并集为{2, 3, 4, 6, 8, 9}；最后计算(A∩B)∪(A∪B)，即交集和并集的并集，结果为{2, 3, 4, 6, 8, 9}。

(2) 设全集为U={-3, -2, -1, 0, 1, 2, 3}，A={-2, 0, 2}，B={-3, -1, 1}，求(A-B)∩(A∪B)的结果。

解析：首先计算A-B，即从集合A中去除集合B的元素，结果为{0, 2}；然后计算A∪B，即A和B的并集为{-3, -2, -1, 0, 1, 2}；最后计算(A-B)∩(A∪B)，即差集和并集的交集，结果为{0, 2}。

2. 分式综合算式分式是初中数学中一个重要的概念，具有一定的难度。

下面是一些综合运用分式的练习题：(1) 求下列分式的值：$\frac{5}{\frac{3}{4}}-\frac{\frac{2}{9}-\frac{4}{5}}{1+\frac{1}{2}}$解析：首先计算分式$\frac{3}{4}$的倒数，即$\frac{4}{3}$；然后计算$\frac{2}{9}$和$\frac{4}{5}$的差，即$\frac{2}{9}-\frac{4}{5}=\frac{-14}{45}$；接下来计算分式$1+\frac{1}{2}$的和，即$1+\frac{1}{2}=\frac{3}{2}$；最后计算$\frac{5}{\frac{3}{4}}$和$\frac{\frac{2}{9}-\frac{4}{5}}{1+\frac{1}{2}}$的差，即$\frac{5}{\frac{3}{4}}-\frac{\frac{2}{9}-\frac{4}{5}}{1+\frac{1}{2}}=\frac{20}{3}-\frac{-14}{45}=\frac{610}{45}$。

九年级数学上册综合算式专项练习题分式与根式的除法九年级数学上册综合算式专项练习题：分式与根式的除法在数学学科中，我们学习了很多关于分式和根式的知识，其中包括它们的基本运算。

本文将重点讨论分式与根式的除法，帮助九年级的学生更好地理解和应用相关的概念。

一、分式的除法1. 分式除法的定义分式除法指的是两个分式之间的除法运算。

设有两个分式 a/b 和 c/d，其中 a、b、c、d 均为整数，并且 b 和 d 不为0，那么 a/b 除以 c/d 的结果可以表示为：(a/b) ÷ (c/d) = (a/b) × (d/c)。

2. 分式除法的运算规则（1）将除法转化为乘法：将 a/b 除以 c/d 转化为 a/b 乘以 d/c。

（2）化简分式：将乘法结果化简为最简形式。

（3）避免出现除以0的情况：在进行分式除法时，需要注意除数不为0的限制。

举例来说，假设有分式 3/4 除以 5/6，根据分式除法的定义，可以将除法转化为乘法：(3/4) ÷ (5/6) = (3/4) × (6/5) = 18/20，化简为最简形式即可得到9/10。

二、根式的除法1. 根式除法的定义根式除法指的是根式之间的除法运算。

设有两个根式√a 和√b，其中 a、b 为非负实数，那么√a 除以√b 的结果可以表示为：√a ÷ √b = √(a/b)。

2. 根式除法的运算规则（1）将除法转化为根式：将√a 除以√b 转化为√(a/b)。

（2）化简根式：将结果化简为最简形式。

举例来说，假设有根式√8 除以√2，根据根式除法的定义，可以将除法转化为根式：√8 ÷ √2 = √(8/2) = √4 = 2。

综上所述，九年级数学上册综合算式专项练习题中的分式与根式的除法运算可以根据相应的定义和规则来进行计算。

我们需要将除法转化为乘法（分式除法）或根式（根式除法），然后再化简结果，最终得到最简形式的答案。

1分式与分式方程专题练习（56题）一、单选题1．（2023·甘肃兰州·统考中考真题）方程213x =+的解是（）A ．1x =B ．=1x -C ．5x =D ．5x =-【答案】B【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得解．【详解】解：去分母得：23x =+，解得=1x -，经检验=1x -是分式方程的解．故选：B ．【点睛】本题考查了解分式方程，熟练掌握解分式方程的方法是解题的关键．2．（2023·河北·统考中考真题）化简233y x x ⎛⎫ ⎪⎝⎭的结果是（）A ．6xyB ．5xyC ．25x y D ．26x y 【答案】A【分析】根据分式的乘方和除法的运算法则进行计算即可．【详解】解：2363362y y x x xy x x =⎛⎝⋅⎫= ⎪⎭，故选：A ．【点睛】本题考查分式的乘方，掌握公式准确计算是本题的解题关键．3．（2023·湖南·统考中考真题）下列计算正确的是（）A ．623a a a=B ．()325aa=C ．22()()a ba b a b a b +=+++D ．0113⎛⎫-= ⎪⎝⎭【答案】D【分析】根据分式的约分可判断A ，根据幂的乘方运算可判断B ，根据分式的加法运算可判断C ，根据零指数幂的含义可判断D ，从而可得答案．【详解】解：633a a a=，故A 不符合题意；()326a a =，故B 不符合题意；35二、填空题79三、解答题【答案】原计划平均每天制作【分析】设原计划平均每天制作【详解】解：设原计划平均每天制作3000300051.5x x=+解得：200x=经检验，200x=是原方程的解，且符合题意，答：原计划平均每天制作200【点睛】本题考查了分式方程的应用，根据题意列出方程是解题的关键．25．（2023·湖南岳阳·统考中考真题）水碧万物生，岳阳龙虾好．小龙虾产业已经成为岳阳乡村振兴的名片”．已知翠翠家去年龙虾的总产量是相同，平均亩产量去年比今年少【答案】今年龙虾的平均亩产量【分析】设今年龙虾的平均亩产量是面积相同列出分式方程，解方程并检验即可．【详解】解：设今年龙虾的平均亩产量是由题意得，6000480060 x x=-，解得300x=，经检验，300x=是分式方程的解且符合题意，答：今年龙虾的平均亩产量【点睛】此题考查了分式方程的实际应用，读懂题意，正确列出方程是解题的关键．111315171921232527【答案】甲路线的行驶时间为20min【分析】设甲路线的行驶时间为min x ，则乙路线的行驶事件为()10min x +，根据“甲路线的平均速度为乙路，然后根据题意列二元一次方程组求得零售价为29（万元）313335。

九年级数学下册综合算式专项练习题整式与分式的运算综合综合练习一：整式加减1. 计算：(2x^2 - 3xy + 4) + (4x^2 - 5xy + 1)解析：首先，将同类项进行合并，得到：(2x^2 + 4x^2) + (-3xy - 5xy) + (4 + 1)合并同类项后得：6x^2 - 8xy + 5答案：6x^2 - 8xy + 52. 计算：(3a^3 - 5a^2b + 7ab^2) - (2a^3 - 4a^2b + 3ab^2)解析：同样，合并同类项，得到：(3a^3 - 2a^3) + (-5a^2b - (-4a^2b)) + (7ab^2 - 3ab^2)合并同类项后得：a^3 - a^2b + 4ab^2答案：a^3 - a^2b + 4ab^2综合练习二：整式乘法1. 计算：(2x + 3y)(4x - 5y)解析：将第一个括号中的每一项分别与第二个括号中的每一项相乘，得到：2x * 4x + 2x * (-5y) + 3y * 4x + 3y * (-5y)将结果合并，并合并同类项：8x^2 - 10xy + 12xy - 15y^2得：8x^2 + 2xy - 15y^2答案：8x^2 + 2xy - 15y^22. 计算：(3a + 2b)(a - 4b)解析：同样，将每一项相乘，并进行合并和合并同类项的操作，得到：3a * a + 3a * (-4b) + 2b * a + 2b * (-4b)结果合并并合并同类项：3a^2 - 12ab + 2ab - 8b^2得：3a^2 - 10ab - 8b^2答案：3a^2 - 10ab - 8b^2综合练习三：分式的运算1. 计算：(3/4) + (1/2)解析：由于两个分式的分母不同，我们需要找到它们的最小公倍数，最小公倍数为4，所以分母要通分为4，得到：(3/4) + (2/4)将分子相加，得到：5/4答案：5/42. 计算：(2/3) - (1/4)解析：同样的方法，找到两个分式的最小公倍数，最小公倍数为12，分母通分为12，得到：(8/12) - (3/12)将分子相减，得到：5/12答案：5/12综合练习四：整式与分式的运算1. 计算：(2x^2 - 3xy + 4) + (5/x)解析：由于第一个括号中的表达式是整式，而第二个括号中的表达式是分式，所以我们需要将分式转换为整式。

中考数学复习《分式方程和不等式》单元综合训练题一．选择题（共7小题）1．农户利用“立体大棚种植技术”把毛豆和芹菜进行混种，已知毛豆齐苗后棚湿在18～25℃最适宜，播种芹菜的最适宜温度是15～20℃．农户在毛豆齐苗后在同一大棚播种了芹菜，这时应该把大棚温度设置在下列哪个范围最适宜（）A．15～18℃B．18～20℃C．20～25℃D．20℃以上2．一元一次不等式组解集为（）A．B．C．D．3．若关于x的分式方程有增根，则m的值为（）A．1B．2C．3D．44．分式方程的解是（）A．x＝﹣1B．x＝1C．x＝15D．x＝85．“最是书香能致远，读书之乐乐无穷．”为了传承和发扬中华民族优秀传统文化，丰富校园文化生活，提高全校师生的文化情操和艺术修养，让书香飘逸校园，某校推出“建设书香校园”的活动计划，购买了一批图书．已知购买科普类图书花费30000元，购买文学类图书花费40000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵10元，且购买科普类图书的数量比购买文学类图书的数量少1000本．求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则下列方程正确的是（）A．B．C．D．6．已知关于x的方程的解是负数，则a的取值范围是（）A．a＜1B．a≤1C．a＜1且a≠0D．a≤1或a≠0 7．已知实数a，b，c满足a+2b＝3c，则下列结论不正确的是（）A．a﹣b＝3（c﹣b）B．C．若a＞b，则a＞c＞b D．若a＞c，则二．填空题（共7小题）8．方程的解为．9．不等式3x﹣2＞x的解集为．10．不等式组的整数解有个．11．在平面直角坐标系中，点P（m﹣1，m+2）位于第一象限，则m的取值范围为．12．若关于x的一元一次不等式组的解集为x＞2，且关于y的分式方程＝1的解是整数，则所有满足条件的整数a的值之和是．13．已知关于x的分式方程无解，则a的值为．14．不等式2x﹣6≤5的最大整数解是．三．解答题（共6小题）15．解不等式组：．16．某项电力工程按千米记工作量为1150千米．某工程队承担了此项工程的施工，在完成了100千米工作量后，该工程队改进施工技术和方案，每小时比原来多完成20千米工作量，结果共用了50小时完成了此项工程的施工任务．试问：该工程队改进施工技术和方案后每小时工作量是多少千米？17．某超市用1000元购进一批商品，很快销售完毕，接着又用1100元购进第二批商品，已知两批商品的数量相等，且第一批商品每件的进货价比第二批商品每件进货价少1元．（1）这两批商品进货价每件各是多少元？（2）第一批商品以每件16元全部售出后，若想两批商品所得的利润率不低于50%，则第二批商品每件的售价最少为多少元？18．已知销售1部M型手机和1部N型手机共获利500元，销售2部M型手机和3部N型手机共获利1200元．（1）请问1部M型手机和1部N型手机的利润分别为多少元？（2）若某营业厅计划购进M，N两种型号手机共30部，总利润不超过7000元，问N型手机至少销售多少部？19．经过我市全体市民的不懈努力，2020年娄底市获评“全国文明城市”．为了巩固创文管卫的成果，我市园林部门准备在某路段种植香樟树（娄底市市树）和玉兰树两种树苗．已知购买10棵香樟树和20棵玉兰树共需1100元；购买20棵香樟树和10棵玉兰树共需1000元．（1）求购买1棵香樟树和1棵玉兰树各需多少元？（2）若要购买这两种树苗共600棵，购买经费不超过2万元，问香樟树最少要购买多少棵？20．八年（1）班学生周末乘汽车到抗美援朝纪念馆参观，纪念馆距离学校60km．一部分学生乘慢车先行，出发0.5h后，另一部分学生乘快车前往，结果他们同时到达纪念馆．已知快车的速度是慢车速度的1.5倍，求慢车的速度．。

初中数学第17章《分式》综合练习卷一、填空题1.（－x 2）3÷x 3=_____；6x 2y 3z ÷（－9）xy=_____；（24a 4－16a 3）÷（－8a 2）=_____。

2.在有理式212x +、2y x +、y π、c a b+中分式有_______________________。

3.分式242a b a-约分后的结果为________ 把分式2224x y x y +-变为最简分式为________。

4.已知a=2004,b=2005.则分式()()2244a b a b a b ++-的值为_____________。

5.已知x+y=2、xy=3则______x y y x +=；已知234x y z==、则______25x y x y z +=-+。

6.化简分式22213213143x x x x x x x +-+-•---+得_______________。

7.计算：352______242m m m m -⎛⎫÷+-= ⎪--⎝⎭；计算：422____a b c bc c ab a ⎛⎫⎛⎫⎛⎫•÷= ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭。

8.已知方程()()2815x a a x +=--1的解是x=-5，__________a =那么。

9.x=_____时，211x +-+21的值是零x ；x=_____时，13分式与的值相等x+4x-1。

10.用科学计数法表示0.00000003142：_______；用小数表示：－5.618×10－3=_________。

11.把()23b c-⋅⋅-2a 写成指数不含负数的形式________________。

12.当x=______时，()265x x -+没有意义。

当m=_______时()22101m m x x x-+++的值为1。

13.方程1322k x x x-+=--两边都乘以（x －2），化为整式方程而产生增根，此时k=____。

九年级数学上册综合算式专项练习题分式的除法1. 分式的除法概述在九年级数学上册中，综合算式专项练习题中的一个重要主题是分式的除法。

分式的除法是指在数学运算中，对两个分式进行除法运算，求得它们的商。

本文将介绍分式的除法的概念、步骤和解题技巧。

2. 分式的除法概念分式的除法是指将两个分式相除，得到一个新的分式。

其中，被除数位于除号上方，除数位于除号下方。

例如：2 3───── ÷ ─────5 4首先，我们需要理解分式除法的含义和原理，以便能够正确进行计算。

3. 分式除法的步骤下面是进行分式除法的一般步骤：步骤一：将除法转化为乘法。

2 3───── ÷ ───── = 2 × （1/5） ÷（1/4）5 4步骤二：将乘法转化为分式相乘。

2 ∙ 4 8──────── = ──────── = ──────5 ∙ 3 15 ∙ 2 30步骤三：将得到的乘积化简至最简形式。

8──────30化简后的结果是1/3。

4. 分式除法的解题技巧在解决分式除法问题时，有几个技巧可以帮助我们更好地理解和解决问题：a) 化简分式：在计算过程中，将分式化简至最简形式，可以简化计算过程，得到更清晰的答案。

b) 整体化：将分式中的分子或分母看作整体，有助于更好地理解问题和进行计算。

c) 准确分步：遵循正确的步骤和顺序，逐步进行计算，减少错误的发生。

5. 实例演练为了更好地理解和应用分式的除法，接下来我们来看一个实例演练：题目：计算以下分式的商。

2 6───── ÷ ─────3 4解答：步骤一：将除法转化为乘法。

2 6───── ÷ ───── = 2 × （1/3） ÷（1/4）3 4步骤二：将乘法转化为分式相乘。

2 ∙ 4 8──────── = ──────── = ──────3 ∙ 6 18 9步骤三：将得到的乘积化简至最简形式。

8──────9化简后的结果是8/9。

初三数学上册综合算式专项练习题含有绝对值分式根式的综合运算初三数学上册综合算式专项练习题含有绝对值、分式、根式的综合运算综合算式是初中数学中一个非常重要的概念，它涉及到各种运算符号的组合和运算的优先级。

在初三数学上册中，我们遇到了一些综合算式的专项练习题，其中包含了绝对值、分式和根式。

在本文中，我们将逐一讲解这些题目，并给出解题思路和步骤。

综合算式1：计算绝对值分式的结果题目：计算$\frac{|2x-1|-|x+3|}{2}$，其中$x=-4$。

解析：首先，我们需要计算绝对值。

对于$|2x-1|$，当$x=-4$时，$|2x-1|=|-8-1|=|-9|=9$；对于$|x+3|$，当$x=-4$时，$|x+3|=|-4+3|=|-1|=1$。

将计算结果代入原式，得到$\frac{9-1}{2}=\frac{8}{2}=4$。

因此，该综合算式的结果为4。

综合算式2：分式运算与根式运算结合题目：计算$\sqrt{\frac{3}{2-x}}$，其中$x=1$。

解析：首先，我们需要计算分式。

当$x=1$时，$\frac{3}{2-x}=\frac{3}{2-1}=\frac{3}{1}=3$。

将计算结果代入原式，得到$\sqrt{3}$。

因此，该综合算式的结果为$\sqrt{3}$。

综合算式3：求解含有根式和绝对值的方程题目：求解方程$|x+3|=\sqrt{2x+5}$。

解析：首先，我们需要根据绝对值的定义将方程拆分成两个方程。

当$x+3\geq0$时，$|x+3|=x+3$，方程变为$x+3=\sqrt{2x+5}$；当$x+3<0$时，$|x+3|=-(x+3)$，方程变为$-(x+3)=\sqrt{2x+5}$。

我们先解第一个方程$x+3=\sqrt{2x+5}$：将方程两边平方，得到$(x+3)^2=2x+5$；展开并移项，得到$x^2+6x+9=2x+5$；进一步合并同类项，得到$x^2+6x-2x+9-5=0$；化简后得到$x^2+4x+4=0$；将方程进行因式分解$(x+2)^2=0$；得到方程的解为$x=-2$。