各种力学模型对照表

抗震设防烈度与级数对照表（我们一般讲的6级、7级、8级地震的对应建筑力学上的抗震设防烈度是多少）地震的等级是说遭遇自然灾害地震一次性释放的最大能量相当于世界公认的级别，这与建筑结构没有直接关系。

不论是几级地震，只要建筑结构处于震源中心附近，统统顷刻灰飞湮灭！抗震设防烈度是国家采取抗震设防划分的级别标准来对待，这要依据不同地质构成环境、有史以来震害大小、频率、震害对国民经济危害程度、人口稠密程度、已有工程对国家重要性等等来规定不同标准，以指导预防的投入。

我国GB 50223—2008《建筑工程抗震设防分类标准》有详细的分类，及GB 50011—2010《建筑抗震设计规范》规定。

例如丙类设防中，规定的设防烈度为6度、7度、8度（0.2g）、8度（0.3g）、9度等。

没有对应于地震等级的抗震烈度那种教材！设防烈度不与地震等级发生对应关系！回答你好亲1.一般抗震设防烈度6度是抗震等级为5级。

同一6度区，根据房子高度和结构、重要性等不同，抗震等级也是不同的2.抗震设防烈度和抗震等级是两个不同的概念。

抗震等级一般可分为一、二、三、四个等级更多1条按国家规范，房屋的设防烈度为7度，就是说至少能承受烈度为7度的地震。

抗震度数和地震的里氏级数不一样。

我国抗震设防烈度分6－9度，度数越高要求越严。

根据2002年起实施的《建筑抗震设计规范》，6度及以上地区的建筑必须进行抗震设计，要求做到：当遭受低于本地区抗震设防烈度的多遇地震（50年一遇）影响时，一般不受损坏或不需修理可继续使用。

当遭受相当于本地区抗震设防烈度的地震（475年一遇）时，可能损坏，经一般修理或不需修理仍可继续使用；当遭受高于本地区抗震设防烈度预估的罕遇地震（1641－2475年一遇）时，不致倒塌或发生危及生命的严重破坏。

扩展资料：一、防震缝宽度应分别符合下列要求：1)框架结构(包括设置少量抗震墙的框架结构)房屋的防震缝宽度，当高度不超过15m时不应小于100mm；高度超过15m时，6度、7度、8度和9度分别每增加高度5m、4m、3m和2m，宜加宽20mm；2)框架-抗震墙结构房屋的防震缝宽度不应小于本款1)项规定数值的70%，抗震墙结构房屋的防震缝宽度不应小于本款1)项规定数值的50%；且均不宜小于100mm；3)防震缝两侧结构类型不同时，宜按需要较宽防震缝的结构类型和较低房屋高度确定缝宽。

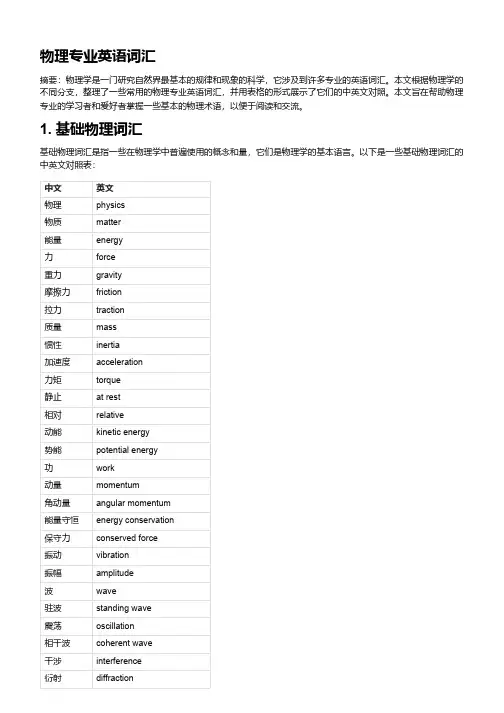
物理专业英语词汇摘要：物理学是一门研究自然界最基本的规律和现象的科学，它涉及到许多专业的英语词汇。

本文根据物理学的不同分支，整理了一些常用的物理专业英语词汇，并用表格的形式展示了它们的中英文对照。

本文旨在帮助物理专业的学习者和爱好者掌握一些基本的物理术语，以便于阅读和交流。

1. 基础物理词汇基础物理词汇是指一些在物理学中普遍使用的概念和量，它们是物理学的基本语言。

以下是一些基础物理词汇的中英文对照表：中文英文物理physics物质matter能量energy力force重力gravity摩擦力friction拉力traction质量mass惯性inertia加速度acceleration力矩torque静止at rest相对relative动能kinetic energy势能potential energy功work动量momentum角动量angular momentum能量守恒energy conservation保守力conserved force振动vibration振幅amplitude波wave驻波standing wave震荡oscillation相干波coherent wave干涉interference衍射diffraction轨道orbit速度velocity速率speed大小magnitude方向direction水平horizontal竖直vertical相互垂直perpendicular坐标coordinate直角坐标系Cartesian coordinate system极坐标系polar coordinate system2. 电学和磁学词汇电学和磁学是研究电荷、电流、电场、磁场等现象和规律的物理学分支，它们与光学、热学、原子物理等有着密切的联系。

以下是一些电学和磁学词汇的中英文对照表：中文英文电子electron电荷charge电流current电场electric field电通量electric flux电势electric potential导体conductor电介质dielectric绝缘体insulator电阻resistor电阻率resistivity电容capacitor3. 物理专业英语词汇物理专业英语词汇是指在物理学的学习和研究中经常使用的一些专业术语，它们涵盖了物理学的各个分支和领域，如力学、电磁学、光学、热学、量子力学等。

饱和温度和饱和压力对照表全文共四篇示例，供读者参考第一篇示例：饱和温度和饱和压力是热力学中常用的两个参数，它们是描述物质相变过程中的重要性质。

在一定条件下，物质将同时存在于液态和气态状态，并且这两个状态之间的平衡是由饱和温度和饱和压力决定的。

饱和温度是指在给定的压力下，物质从液态转变为气态或从气态转变为液态的温度。

饱和压力则是指在给定温度下，物质从液态转变为气态或从气态转变为液态时所处的压力。

这两个参数之间存在着一定的对应关系，通常情况下随着温度的升高，饱和压力也会增加。

为了更直观地了解饱和温度和饱和压力之间的关系，下面将给出一份关于饱和温度和饱和压力的对照表：| 温度(℃) | 压力(kPa) ||---------|----------|| 0 | 611.2 || 5 | 872.7 || 10 | 1238.6 || 15 | 1704.2 || 20 | 2336.1 || 25 | 3176.8 || 30 | 4278.8 || 35 | 5708.9 || 40 | 7550.7 || 45 | 9904.3 || 50 | 12941.0 |从上表中可以看出，随着温度的升高，饱和压力也在不断增加。

这是因为在较高的温度下，分子的热运动增大，从而增加了气体分子与液体分子之间的碰撞频率，导致蒸气压的增加。

饱和温度和饱和压力之间存在着明显的正相关关系。

对于不同的物质，其饱和温度和饱和压力的值也会有所不同。

水在标准大气压下的饱和温度为100℃，饱和压力为101.3kPa；而乙醇在标准大气压下的饱和温度为78.37℃，饱和压力为58.07kPa。

对于不同的物质需要根据其物性参数来确定其饱和温度和饱和压力。

饱和温度和饱和压力是研究物质相变过程不可或缺的重要参数，通过对它们之间的关系进行研究可以更好地理解物质的性质和行为。

希望通过本文的介绍，读者对饱和温度和饱和压力有了更深入的了解。

【说了2000字】第二篇示例：饱和温度和饱和压力是研究物质相变时重要的物理参数。

模型法(1)“对象模型”：即把研究的对象的本身理想化．用来代替由具体物质组成的、代表研究对象的实体系统，称为对象模型（也可称为概念模型）， 实际物体在某种条件下的近似与抽象，如质点、光滑平面、理想气体、理想电表等； 常见的如“力学”中有质点、点电荷、轻绳或杆、轻质弹簧、单摆、弹簧振子、弹性体、绝热物质等；(2)条件模型：把研究对象所处的外部条件理想化.排除外部条件中干扰研究对象运动变化的次要因素，突出外部条件的本质特征或最主要的方面，从而建立的物理模型称为条件模型． (3)过程模型：把具体过理过程纯粹化、理想化后抽象出来的一种物理过程，称过程模型 理想化了的物理现象或过程，如匀速直线运动、自由落体运动、竖直上抛运动、平抛运动、匀速圆周运动、简谐运动等。

有些题目所设物理模型是不清晰的，不宜直接处理，但只要抓住问题的主要因素，忽略次要因素，恰当的将复杂的对象或过程向隐含的理想化模型转化，就能使问题得以解决。

解决物理问题的一般方法可归纳为以下几个环节： 原始的物理模型可分为如下两类：物理解题方法：如整体法、假设法、极限法、逆向思维法、物理模型法、等效法、物理图像法等． 知识分类举要力的瞬时性（产生a ）F=ma 、⇒运动状态发生变化⇒牛顿第二定律 1．力的三种效应：时间积累效应(冲量)I=Ft 、⇒动量发生变化⇒动量定理 空间积累效应(做功)w=Fs ⇒动能发生变化⇒动能定理对象模型（质点、轻杆、轻绳、弹簧振子、单摆、理想气体、点电荷、理想电表、理想变压器、匀强电场、匀强磁场、点光源、光线、原子模型等） 过程模型（匀速直线运动、匀变速直线运动、匀速圆周运动、平抛运动、简谐运动、简谐波、弹性碰撞、自由落体运动、竖直上抛运动等）物理模型2．动量观点：动量(状态量)：p=mv=K mE 2 冲量(过程量)：I = F t动量定理：内容：物体所受合外力的冲量等于它的动量的变化。

公式： F 合t = mv’一mv (解题时受力分析和正方向的规定是关键) I=F 合t=F1t1+F2t2+---=∆p=P 末-P 初=mv 末-mv 初动量守恒定律：内容、守恒条件、不同的表达式及含义：'p p =；0p =∆；21p -p ∆=∆内容：相互作用的物体系统，如果不受外力，或它们所受的外力之和为零，它们的总动量保持不变。

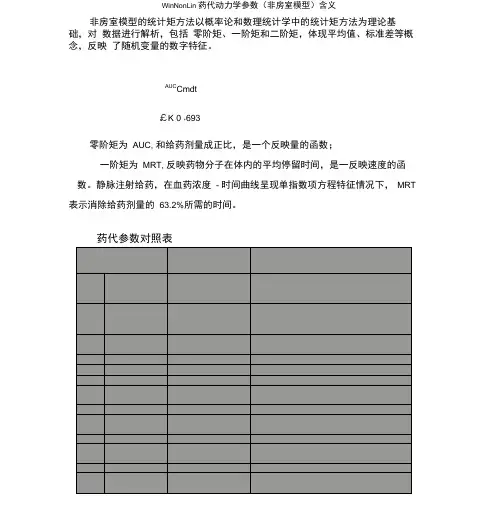
WinNonLin 药代动力学参数（非房室模型）含义
非房室模型的统计矩方法以概率论和数理统计学中的统计矩方法为理论基础，对数据进行解析，包括零阶矩、一阶矩和二阶矩，体现平均值、标准差等概念，反映了随机变量的数字特征。

AUC
Cmdt
￡K 0 +693
零阶矩为AUC, 和给药剂量成正比，是一个反映量的函数；
一阶矩为MRT, 反映药物分子在体内的平均停留时间，是一反映速度的函数。

静脉注射给药，在血药浓度- 时间曲线呈现单指数项方程特征情况下，MRT 表示消除给药剂量的63.2%所需的时间。

药代参数对照表
表1、WinNonLin 药代动力学参数（非房室模型）含义。

纤维增强复合材料宏、细观统一的细观力学模型雷友锋，林宏镇，高德平（空军第八研究所）（南京航空航天大学）摘要：研究了复合材料宏、细观特征之间的联系，将宏观复台材料体中的一点赋予了细观结构特征。

基于细观结构周期性假设．建立了一种数值型细观力学模型，模型中用高阶多项式函数模拟基体和增强相中细观位移场，通过对细观单元力学方程的分析与求解，建立了复合材料宏、细观力学变量之间的联系。

该细观力学模型，不仅能用于复合材料宏观有效性能的预测及细观应力、应变场的分析，而且能够很容易地融入常规有限元法中，实现对复合材料结构的宏、细观一体化分析．以该细观力学模型为基础的计算结果与部分文献中的试验结果及理论计算值具有较好的一致性。

关键词：复合材料，细观力学，有效性能，代表性体积元，细观单元１引言复合材料既表现出宏观特征，又具有明显的细观结构特征，复合材料力学是一种两层次的力学理论”Ｊ。

在宏观尺度上，可以将复合材料当作各向异性的宏观均匀连续体，用连续介质力学理论研究复合材料的力学行为【：】，但是无法研究对宏观行为有重要影响的细观尺度上各组份相的变形及损伤失效行为。

在细观尺度上．复合材料具有包含多种组份相的非均质结构，复合材料细观力学在宏观有效性能预测以及细观应力、应变场分析方面取得了一定的进展。

１。

但是，如果能够将复合材料宏观结构分析与细观结构分析结合起来．在进行宏观结构分析时能够获得细观尺度上的力学参量值．那么将是一种更好的分析方法，１９９７年ＡＳＭＥ／ＡＳＣＥ／ＳＥＳ的复合材料力学专题会特别强调了发展复合材料宏、细观一体化分析技术的迫切性１４Ｊ，近期一些学者在这方面开展了一定的研究工作．提出了一些模型与方法…”１。

本文在分析复合材料宏、细观特征之间联系的基础上，建立联系复合材料宏、细观特征的一种数值型细观力学模型，该模型不仅能够预测复合材料的宏观有效性能以及细观应力、应变场，还能够很容易地融入常规有限元方法中．从而实现对复合材料结构的宏、细观～体化分析。

基于Abaqus的木结构螺栓节点刚度有限元分析孙小鸾; 刘伟庆; 袁盛林; 陆伟东【期刊名称】《《结构工程师》》【年(卷),期】2019(035)004【总页数】9页(P21-29)【关键词】木结构; Abaqus; 螺栓节点; 刚度【作者】孙小鸾; 刘伟庆; 袁盛林; 陆伟东【作者单位】南京工业大学土木工程学院南京210009【正文语种】中文0 引言钢填板螺栓节点作为常见的节点形式,在国内外木结构工程实例中应用广泛,但由于木结构的特殊性,节点因加工精度、安装误差等因素,受力变形往往有滑移现象,达不到完全的刚接,具有明显的半刚性特征。

此类节点在结构整理分析时,常常被简化为铰接,忽略了其在结构中的刚度贡献。

另外,对于类似单层网壳的结构体系,要求连接节点为非铰接,国内多高层木结构规范也要求各层框架承担一部分地震剪力,节点若简化为铰接则无法满足结构受力要求,也限制了此类节点在木结构建筑中的应用。

木结构螺栓节点在有限元模拟领域,Kharouf[1]、Chen[2]以及Santos[3]等人分别建立了二维、三维有限元模型,对单螺栓节点销槽承压开展研究,但忽略了螺栓变形滑移对节点刚度的影响。

He等[4]采用预制裂缝法,通过Abaqus对螺栓节点进行破坏分析,得到的极限承载力与试验结果接近。

Bouchaïr等[5]引入弹簧单元针对群螺栓节点建立二维模型,得出了节点的荷载-位移关系,但未能对节点区域的受力状态得到直观的表达。

王明谦、宋晓滨等[6]基于有限元分析软件建立的节点三维实体模型对于木结构螺栓节点的初始刚度和极限弯矩有较好的模拟精度,在进行模型参数分析时,仅考虑了螺栓直径和边距对节点性能的影响。

张盛东等[7]采用Abaqus对内填三块钢板销式连接胶合木梁的抗弯性能进行了有限元分析,其中胶合木选用弹性阶段正交各向异性以及塑性阶段遵循Hill准则的各向异性模型,模拟结果与试验结果符合较好。

本文采用Abaqus软件对钢填板螺栓节点进行精细化分析,考虑木材的材料非线性、螺栓直径与侧材厚度的比值、螺栓与螺孔间隙、钢填板与侧材间隙、螺栓预紧力以及螺帽接触传力等因素,分析各种因素对螺栓节点的转动刚度与承载力的影响,从而揭示影响节点刚度的关键因素,为螺栓节点更加广泛地应用于木结构实践提供技术参考。

曼宁系数与坡度和土地覆盖的对照表全文共四篇示例，供读者参考第一篇示例：曼宁系数是用于描述河流、河道或水流体系流速和流态特性的参数。

在水文水利领域中，曼宁系数被广泛应用于河流模型中，用来计算水体的流速、流量、水深等水动力学参数。

曼宁系数是一个无量纲的系数，一般取值范围为0.01~0.05，其大小受到地形、土壤类型、植被覆盖和河道形状等因素的影响。

坡度是地表高程的变化率，也是地势倾斜程度的度量。

在自然地理学和水文学中，坡度是一个重要的地形因素，对地表径流和水文过程有着重要的影响。

一般来说，坡度越大，水流速度越快，河道的侵蚀和河岸的崩塌可能会加剧。

土地覆盖是地表被植被、建筑物等物体所覆盖的程度，也是影响水文过程的重要因素之一。

植被覆盖可以减少地表径流速率，减缓水文循环过程，有利于水资源的保护和利用。

曼宁系数、坡度和土地覆盖这三个因素之间存在着密切的关系。

不同的土地覆盖类型和地形条件会影响曼宁系数的取值，进而影响河流的流速和水动力学特性。

下面我们将制作一份关于曼宁系数与坡度和土地覆盖的对照表，以便更好地理解它们之间的关系。

| 土地覆盖类型| 曼宁系数取值范围| 典型坡度范围||---------------|-------------------|--------------|| 草地| 0.02-0.035 | 0-5% || 森林| 0.03-0.045 | 5-15% || 农田| 0.025-0.04 | 0-10% || 城市| 0.03-0.06 | 0-2% || 沙漠| 0.03-0.05 | 0-2% || 水域| 0.02-0.035 | 0-1% |从上表可以看出，不同的土地覆盖类型对曼宁系数的取值范围有着明显的影响。

在同样的坡度条件下，草地的曼宁系数相对较小，而城市和森林的曼宁系数相对较大。

这是因为不同的土地覆盖类型具有不同的粗糙度和阻力，会对水流的摩擦和阻力产生影响。

不同的坡度条件也会对曼宁系数的取值范围产生影响。

结构强度与振动实验技术报告学院：能源与动力学院姓名：学号：SX1导师：指导教师：沈承同组人员：2015年6月实验一 单自由度系统的动力吸振实验一、实验目的通过对单自由度系统施加动力吸振器，减小其振动量，观察实验现象，灵活掌握动力减振实验方法。

二、实验内容基于二自由度反共振原理设计动力吸振的基本理论，测试单自由度系统的固有频率，了解动力吸振器的设计过程，采用动力吸振器后单自由度系统的减振效果。

三、实验原理所谓吸振就是将原系统的振动能量转移到附加系统，从而使原系统的振动减小。

动力吸振器利用联结在振动系统上的附加质量的动力来实现吸振，即将原振动系统的振动能量转移到附加的弹簧质量振动系统上了。

单式动力吸振器是一个单自由度振动系统，与单自由度振动主系统一起构成二自由度系统，力学模型如右图所示。

主系统质量1m ，刚度1k ，位移1y 。

吸振器质量m ，刚度k ，位移y 。

激扰力为sin F t ω。

系统的运动微分方程如下（无阻尼）：()1112122sin m y k k y k y F t ω++-=()122210m y k y y +-=设其稳态响应为11sin y A t ω=22sin y A t ω=代入得到：()()()2221222121222F k m A kk m km kωωω-=+---()()22222121222Fk A k k m k m k ωω=+--- 令111/k m ω=——主系统的固有角频率； 222/k m ω=——动力吸振器的固有角频率； 1/st F k δ=——主系统的静位移；21/m m μ=——质量比值；上式可以改变为无量纲形式：()()()()()22122222122211/1//1//stA ωωδμωωωωωωμωω-=⎡⎤⎡⎤+---⎣⎦⎣⎦()()()()2222221222111//1//stA δμωωωωωωμωω=⎡⎤⎡⎤+---⎣⎦⎣⎦当单式动力吸振器的固有角频率2ω等于外力的角频率ω时，外力正好等于动力吸振器的弹性恢复力22k A ，此时设备不振动，从而达到了减震的目的。

第7章聚合物的粘弹性7.1基本概念 弹：外力T 形变T 应力T 储存能量T 外力撤除T 能量释放T 形变恢复 粘：外力T 形变T 应力T 应力松驰T 能量耗散T 外力撤除T 形变不可恢复理想弹性： 服从虎克定律CT= E •£应力与应变成正比，即应力只取决于应变tot理想粘性：服从牛顿流体定律ds r 一 dt应力与应变速率成正比，即应力只取决于应变速率但是高分子固体的力学行为不服从虎克定律。

当受力时，形变会随时间逐渐发展，因此弹性模量有时总结：理想弹性体 虎克固体 能量储存 形状记忆E = E(「£ .T) E聚合物是典型的粘弹体,E = E( a . £ .T.t)理想粘性体牛顿流体 能量耗散 形状耗散=E( a . £ .T.t)同时具有粘性和弹性。

5间依赖性，而除去外力后，形变是逐渐回复，而且往往残留永久变形 发生。

高分子材料（包括高分子固体，熔体及浓溶液）的力学行为在通常情况下总是或多或少表现为弹性与粘 性相结合的特性，而且弹性与粘性的贡献随外力作用的时间而异，这种特性称之为粘弹性。

粘弹性的本质 是由于聚合物分子运动具有松弛特性。

7.2 聚合物的静态力学松弛现象聚合物的力学性质随时间的变化统称为力学松弛。

高分子材料在固定应力或应变作用下观察到的力学松 弛现象称为静态力学松弛，最基本的有蠕变和应力松弛。

（一）蠕变在一定温度、一定应力的作用下，聚合物的形变随时间的变化称为蠕变。

理想弹性体：a= E- S 应力恒定，故应变恒定，如图7-1理想粘性体，如图7-2，dr cr-ii —dt应力恒定，故应变速率为常数，应变以恒定速率增加（丫^）,说明在弹性变形中有粘流形变n -'E图7-3聚合物 随时间变化图聚合物：粘弹体，形变分为三个部分 ； ① 理想弹性，即瞬时响应：则键长、键角提供;② 推迟弹性形变，即滞弹部分：链段运动护％一严）3E 2③ 粘性流动：整链滑移= —/注：①、②是可逆的，③不可逆。

表8-3 各种力学模型对照表模型名称示意图力学行为模拟对象方程理想弹簧普弹虎克定律εσE=或E/σε=理想粘壶粘流牛顿流体定律dtdεησ=或t⋅=ησεMaxwell 模型(串联模型)应力松弛(线形聚合物)运动方程(应力-应变方程，下同)ησσε+=dtdEdtd1应力松弛方程(运动方程的解，下同))/exp()(τσσtt-=Voigt模型或Kelvin 模型(并联模型)高弹蠕变(交联聚合物)运动方程dtdEεηεσ+=蠕变方程))/exp(1)(()(τεεtt--∞=三元件模型蠕变(交联聚合物)蠕变方程1)(Etσε=))/exp(1(20τσtE--+三元件模型蠕变(线形聚合物)蠕变方程))/exp(1()(20τσεtEt--=t3ησ+四元件模型(Burger 模型)蠕变(线形聚合物)蠕变方程1)(Etσε=))/exp(1(20τσtE--+t3ησ+三元件模型(标准线性固体模型)应力松弛(交联聚合物)蠕变(交联聚合物)运动方程+=+εστσ1EdtddtdEEετ)(21+应力松弛方程+=εσ1E)/exp()(1τεσtE--蠕变方程⎥⎦⎤⎢⎣⎡+--∞=))(exp(1)()(211τεεtEEEt广义Maxwell 模型应力松弛(含多重运动单元的实际聚合物))(ln)/exp()(ln)(τττdtHtE-=⎰∞∞-广义Voigt 模型蠕变(含多重运动单元的实际聚合物))(ln)/exp()(ln)(τττdtLtD-=⎰∞∞-式中：)(τH和)(τL分别为对数应力松弛时间谱和对数蠕变时间谱。