matlab曲柄连杆机构分析讲课讲稿
- 格式:doc
- 大小:605.50 KB
- 文档页数:7





1平面连杆机构的运动分析1。
1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据.机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。
而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时,采用解析法并借助计算机,不仅可获得很高的计算精度及一系列位置的分析结果,并能绘制机构相应的运动线图,同时还可以把机构分析和机构综合问题联系起来,以便于机构的优化设计.1。
2 机构的工作原理在平面四杆机构中,其具有曲柄的条件为:a.各杆的长度应满足杆长条件,即:最短杆长度+最长杆长度≤其余两杆长度之和。
b。
组成该周转副的两杆中必有一杆为最短杆,且其最短杆为连架杆或机架(当最短杆为连架杆时,四杆机构为曲柄摇杆机构;当最短杆为机架时,则为双曲柄机构)。
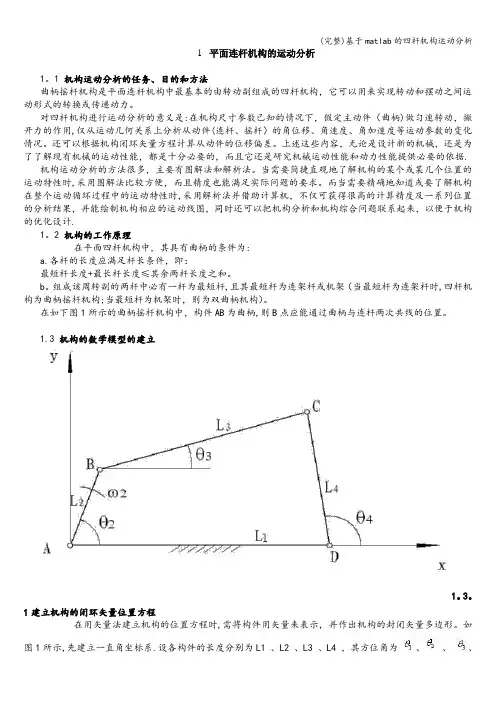
在如下图1所示的曲柄摇杆机构中,构件AB为曲柄,则B点应能通过曲柄与连杆两次共线的位置。
1.3 机构的数学模型的建立1。
3。
1建立机构的闭环矢量位置方程在用矢量法建立机构的位置方程时,需将构件用矢量来表示,并作出机构的封闭矢量多边形。
如图1所示,先建立一直角坐标系.设各构件的长度分别为L1 、L2 、L3 、L4 ,其方位角为、、、.以各杆矢量组成一个封闭矢量多边形,即ABCDA。
其个矢量之和必等于零。





曲柄连杆机构matlab课程设计一、课程目标知识目标:1. 理解曲柄连杆机构的基本原理与运动特性;2. 掌握利用MATLAB软件进行曲柄连杆机构的运动仿真与分析;3. 学会结合实际工程案例,运用所学知识解决曲柄连杆机构的相关问题。
技能目标:1. 能够运用MATLAB软件构建曲柄连杆机构的模型;2. 能够对曲柄连杆机构进行运动分析,并绘制出相应的运动轨迹图;3. 能够根据分析结果,优化曲柄连杆机构的结构参数。
情感态度价值观目标:1. 培养学生对机械原理及MATLAB软件的兴趣,激发学习热情;2. 培养学生严谨的科学态度,注重理论与实践相结合;3. 增强学生的团队协作意识,提高沟通与表达能力。
本课程针对高年级学生,结合学科特点,注重理论知识与实践技能的结合。
通过本课程的学习,使学生能够掌握曲柄连杆机构的基本原理,运用MATLAB软件进行运动仿真与分析,培养解决实际工程问题的能力。
同时,课程强调团队合作,提升学生的综合素质,为将来的学术研究和职业发展打下坚实基础。
二、教学内容1. 曲柄连杆机构基本原理:介绍曲柄连杆机构的类型、特点及其在工程中的应用,重点讲解其运动学及动力学原理。
教材章节:第二章 曲柄连杆机构2. MATLAB软件操作:讲解MATLAB软件的基本操作,包括界面、常用命令、数据类型等,为后续运动仿真打下基础。
教材章节:第一章 MATLAB基础3. 曲柄连杆机构建模与仿真:教授如何使用MATLAB软件构建曲柄连杆机构的模型,进行运动仿真,分析运动特性。
教材章节:第三章 曲柄连杆机构建模与仿真4. 结构参数优化:介绍曲柄连杆机构结构参数对运动性能的影响,教授如何运用MATLAB软件进行参数优化。
教材章节:第四章 曲柄连杆机构优化设计5. 实际工程案例:分析典型曲柄连杆机构在实际工程中的应用,结合MATLAB软件进行案例分析,提高学生解决实际问题的能力。
教材章节:第五章 曲柄连杆机构工程应用案例教学内容安排与进度:共分为五个阶段,每个阶段2学时,共计10学时。
m a t l a b曲柄连杆机构分析clear;clc;n=750;l=0.975;R=0.0381;h=0.2;omiga=n.*pi/30;tmax=2.*pi/omiga;t=0:0.001:tmax; %计算曲柄转一圈的总t值alpha1=atan((h+R.*sin(omiga.*t))./sqrt(l.*l-(h+R.*sin(omiga.*t))))+pi;alpha1p=-(R.*omiga.*cos(omiga.*t))./(l.*cos(alpha1));vb=-R.*omiga.*sin(omiga.*t)+R.*omiga.*cos(omiga.*t).*tan(alpha1);ab=-R.*omiga.^2.*cos(omiga.*t)-(R.*omiga.*cos(omiga.*t)).^2./(l.*(cos(alpha1)).^3)-R.*omiga.^2.*sin(omiga.*t).*tan(alpha1);subplot(1,2,1);plot(t,vb);title('曲柄滑块机构的滑块v-t图');xlabel('时间t(曲柄旋转一周)');ylabel('滑块速度v');grid on;subplot(1,2,2);plot(t,ab);title('曲柄滑块机构的滑块a-t图');xlabel('时间t(曲柄旋转一周)');ylabel('滑块加速度a');grid on;%下面黄金分割法求滑块的速度与加速度最大值epsilon=input('根据曲线初始区间已确定,请输入计算精度epsilon(如输入0.001):');a=0;b=0.04; %初始区间n1=0; %n1用于计算次数a1=b-0.618*(b-a);y1=-R.*omiga.*sin(omiga.*a1)+R.*omiga.*cos(omiga.*a1).*tan(alpha1);a2=a+0.618*(b-a);y2=-R.*omiga.*sin(omiga.*a2)+R.*omiga.*cos(omiga.*a2).*tan(alpha1);while abs(a-b)>=epsilonif y1<=y2b=a2;a2=a1;y2=y1;a1=b-0.618*(b-a);y1=-R.*omiga.*sin(omiga.*a1)+R.*omiga.*cos(omiga.*a1).*tan(alpha1);elsea=a1;a1=a2;y1=y2;a2=a+0.618*(b-a);y2=-R.*omiga.*sin(omiga.*a2)+R.*omiga.*cos(omiga.*a2).*tan(alpha1);endn1=n1+1;endvbm1=omiga*(a+b)/2;disp(['经过',num2str(n1),'次计算,用黄金分割法找到速度最大值对应的wt是:', num2str(vbm1),'弧度。
m a t l a b曲柄连杆机构分析clear;clc;n=750;l=0.975;R=0.0381;h=0.2;omiga=n.*pi/30;tmax=2.*pi/omiga;t=0:0.001:tmax; %计算曲柄转一圈的总t值alpha1=atan((h+R.*sin(omiga.*t))./sqrt(l.*l-(h+R.*sin(omiga.*t))))+pi;alpha1p=-(R.*omiga.*cos(omiga.*t))./(l.*cos(alpha1));vb=-R.*omiga.*sin(omiga.*t)+R.*omiga.*cos(omiga.*t).*tan(alpha1);ab=-R.*omiga.^2.*cos(omiga.*t)-(R.*omiga.*cos(omiga.*t)).^2./(l.*(cos(alpha1)).^3)-R.*omiga.^2.*sin(omiga.*t).*tan(alpha1);subplot(1,2,1);plot(t,vb);title('曲柄滑块机构的滑块v-t图');xlabel('时间t(曲柄旋转一周)');ylabel('滑块速度v');grid on;subplot(1,2,2);plot(t,ab);title('曲柄滑块机构的滑块a-t图');xlabel('时间t(曲柄旋转一周)');ylabel('滑块加速度a');grid on;%下面黄金分割法求滑块的速度与加速度最大值epsilon=input('根据曲线初始区间已确定,请输入计算精度epsilon(如输入0.001):');a=0;b=0.04; %初始区间n1=0; %n1用于计算次数a1=b-0.618*(b-a);y1=-R.*omiga.*sin(omiga.*a1)+R.*omiga.*cos(omiga.*a1).*tan(alpha1);a2=a+0.618*(b-a);y2=-R.*omiga.*sin(omiga.*a2)+R.*omiga.*cos(omiga.*a2).*tan(alpha1);while abs(a-b)>=epsilonif y1<=y2b=a2;a2=a1;y2=y1;a1=b-0.618*(b-a);y1=-R.*omiga.*sin(omiga.*a1)+R.*omiga.*cos(omiga.*a1).*tan(alpha1);elsea=a1;a1=a2;y1=y2;a2=a+0.618*(b-a);y2=-R.*omiga.*sin(omiga.*a2)+R.*omiga.*cos(omiga.*a2).*tan(alpha1);endn1=n1+1;endvbm1=omiga*(a+b)/2;disp(['经过',num2str(n1),'次计算,用黄金分割法找到速度最大值对应的wt是:', num2str(vbm1),'弧度。
'])a=0.04;b=0.08;%初始区间变化,对应的函数取负即可n1=0; %n1用于计算迭代次数a1=b-0.618*(b-a);y1=-(-R.*omiga.*sin(omiga.*a1)+R.*omiga.*cos(omiga.*a1).*tan(alpha1));a2=a+0.618*(b-a);y2=-(-R.*omiga.*sin(omiga.*a2)+R.*omiga.*cos(omiga.*a2).*tan(alpha1));while abs(a-b)>=epsilonif y1<=y2b=a2;a2=a1;y2=y1;a1=b-0.618*(b-a);y1=-(-R.*omiga.*sin(omiga.*a1)+R.*omiga.*cos(omiga.*a1).*tan(alpha1));elsea=a1;a1=a2;y1=y2;a2=a+0.618*(b-a);y2=-(-R.*omiga.*sin(omiga.*a2)+R.*omiga.*cos(omiga.*a2).*tan(alpha1));endn1=n1+1;endvbm2=omiga*(a+b)/2;disp(['经过',num2str(n1),'次计算,找到的另一个速度最大值对应的w是:',num2str(vbm2),'弧度。
'])disp(['两个速度最大值点相差是:',num2str(vbm2-vbm1),'弧度(即',num2str(180*(vbm2- vbm1)/pi),'度)。
'])a=0.02;b=0.06;%对应的函数取负即可n1=0; a1=b-0.618*(b-a);y1=-(-R.*omiga.^2.*cos(omiga.*a1)-(R.*omiga.*cos(omiga.*a1)).^2./(l.*(cos(alpha1)).^3)-R.*omiga.^2.*sin(omiga.*a1).*tan(alpha1));a2=a+0.618*(b-a);y2=-(-R.*omiga.^2.*cos(omiga.*a2)-(R.*omiga.*cos(omiga.*a2)).^2./(l.*(cos(alpha1)).^3)-R.*omiga.^2.*sin(omiga.*a2).*tan(alpha1));while abs(a-b)>=epsilonif y1<=y2b=a2;a2=a1;y2=y1;a1=b-0.618*(b-a);y1=-(-R.*omiga.^2.*cos(omiga.*a1)-(R.*omiga.*cos(omiga.*a1)).^2./ (l.*(cos(alpha1)).^3)-R.*omiga.^2.*sin(omiga.*a1).*tan(alpha1));elsea=a1;a1=a2;y1=y2;a2=a+0.618*(b-a);y2=-(-R.*omiga.^2.*cos(omiga.*a2)-(R.*omiga.*cos(omiga.*a2)).^2./ (l.*(cos(alpha1)).^3)-R.*omiga.^2.*sin(omiga.*a2).*tan(alpha1));endn1=n1+1;enddisp(['经过',num2str(n1),'次计算,找到的加速度最大值对应的w是:',num2str(omiga*(a+b)/2)])disp(['速度最大值点与加速度最大值相差的wt是:',num2str((omiga*(a+b)/2)-vbm1),'弧度。
'])曲柄连杆机构动力学分析图clear;clc;close all;n=750;h=0.2;f=0.15;g=9.8;l=0.975;m2=3.8;R=0.0381;m1=2.1;m3=2.1*2.3;omega=n*pi/30;tmax=2*pi/omega;t=linspace(0,tmax,100);%计算曲柄转一周的总t值for n=1:100alpha1(n)=atan((h+R.*sin(omega.*t(n)))./sqrt(l.*l-(h+R.*sin(omega.*t(n)))))+pi;alpha1p(n)=-(R.*omega.*cos(omega*t(n)))./(l.*cos(alpha1(n)));%alpha1的一阶导数alpha1pp(n)=(R.*omega.^2.*sin(omega.*t(n))+l.*sin(alpha1(n)).*alpha1p(n).^2)./ (l.*cos(alpha1(n)));%alpha1的二阶导数xA=R.*cos(omega*t(n)); yA=R.*sin(omega*t(n));xApp=-R.*omega.^2.*cos(omega.*t(n));yApp=-R.*omega.^2.*sin(omega.*t(n)); %曲柄末端A的加速度x1=xA/2; y1=yA/2;x1pp=xApp./2;y1pp=yApp./2; %曲柄质心的加速度xBpp=xApp-l*(alpha1pp(n).*sin(alpha1(n))+alpha1p(n).^2.*cos(alpha1(n)));yBpp=0; %刀头(滑块)B的加速度x2=xA+l.*cos(alpha1(n))./2;y2=yA+l.*sin(alpha1(n))./2;x2pp=xApp-l*(alpha1pp(n).*sin(alpha1(n))+alpha1p(n).^2.*cos(alpha1(n)))./2;y2pp=yApp+l*(alpha1pp(n).*cos(alpha1(n))-alpha1p(n).^2.*sin(alpha1(n)))./2;%连杆质心的加速度%对于曲柄m1有方程% Ox-m1.*x1pp+Ax=0% Oy-m1.*y1pp+Ay-m1.*g=0% M-Ay.*xA-Ax.*yA+m1.*g.*x1+m1.*y1pp.*x1+m1.*x1pp*y1=0 %对于连杆m2有方程% -Ax+Bn.*cos(alpha1)+Bt.*cos(alpha1+pi/2)-m2.*x2pp=0% -Ay+Bn.*sin(alpha1)+Bt.*sin(alpha1+pi/2)-m2.*y2pp-m2.*g=0 % Bt.*l+m2.*(g+y2pp).*(x2-xA)+m2.*x2pp.*(y2-yA)=0%对于刀头(滑块)m3有方程% -f.*N+Bn.*cos(alpha1-pi)-Bt.*cos(alpha1-pi/2)-m3.*xBpp=0% N-m3.*g+Bn.*sin(alpha1-pi)+Bt.*sin(alpha1-pi/2)=0% 8个方程,未知数也有Ox,Oy,Ax,Ay,Bn,Bt,N,M共8个A=[1,0,1,0,0,0,0,0;0,1,0,1,0,0,0,0;0,0,-yA,-xA,0,0,0,1;0,0,-1,0,cos(alpha1(n)),cos(alpha1(n)+pi/2),0,0;0,0,0,-1,sin(alpha1(n)),sin(alpha1(n)+pi/2),0,0;0,0,0,0,0,l,0,0;0,0,0,0,cos(alpha1(n)-pi),-cos(alpha1(n)-pi/2),-f,0;0,0,0,0,sin(alpha1(n)-pi),sin(alpha1(n)-pi/2),1,0];B=[m1.*x1pp;m1.*y1pp+m1.*g;-m1.*g.*x1-m1.*y1pp.*x1-m1.*x1pp*y1;m2.*x2pp;m2.*y2pp+m2.*g;-m2.*(g+y2pp).*(x2-xA)-m2.*x2pp.*(y2-yA);m3.*xBpp;m3.*g];X=A\B; %X向量的顺序为Ox,Oy,Ax,Ay,Bn,Bt,N,MXT(n,:)=X‘; %将N转置后以行向量形式存入矩阵XT中Bn(n)=X(5);Bt(n)=X(6);N(n)=X(7);%为求滑块最大惯性力Qm从XT中取出的Bn、Bt及N值 Q(n)=Bn(n)*cos(alpha1(n)-pi)-Bt(n)*cos(alpha1(n)-pi/2)-f*N(n);endfor k=1:8subplot(3,3,k);plot(t,XT(:,k));grid on;endsubplot(3,3,9);plot(t,Q);title('Q_B-t曲线');grid on;Qm=max(Q);tm=t(find(Q==Qm));wtm=omega*tm;%找出滑块最大惯性力Qm及对应的时间t和弧度wtdisp([‘当t=’,num2str(tm),‘即wt=’,num2str(wtm),‘时,滑块B达到最大惯性力 Qm=',num2str(Qm),'。