高考数学中利用空间向量解决立体几何的向量方法(二)——解决空间角的问题

立体几何中的向量方法(二)——空间角与距离求解1．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )A ．30°B ．60°C ．120°D ．150°2．若平面α，β的法向量分别为a ＝(－1,2,4)，b ＝(x ，－1，－2)，并且α⊥β，则x 的值为( )A ．10B ．－10 C.12 D ．－123．两平行平面α，β分别经过坐标原点O 和点A (2,1,1)，且两平面的一个法向量n ＝(－1,0,1)，则两平面间的距离是( )A.32B.22C. 3 D ．3 2 4．已知平面α内有一个点A (2，－1,2)，α的一个法向量为n ＝(3,1,2)，则下列点P 中，在平面α内的是( )A ．(1，－1,1) B.⎝ ⎛⎭⎪⎫1，3，32C.⎝ ⎛⎭⎪⎫1，－3，32D.⎝⎛⎭⎪⎫－1，3，325．如图K42－1，长方体ABCD －A 1B 1C 1D 1中，底面是边长为2的正方形，高为1，则异面直线AD 1和C 1D 所成角的余弦值是( )图K42－1 A.55 B ．－55 C.15 D.256．在平行四边形ABCD 中，AB ＝AC ＝1，∠ACD ＝90°，将它沿对角线AC 折起，使AB 和CD 成60°角(如图K43－2)，则B 、D 间的距离为( )图K42－2A．1 B．2 C. 2 D．2或 27．三棱锥的三条侧棱两两互相垂直，长度分别为6,4,4，则其顶点到底面的距离为( )A.143B．217 C.62211D.21738．在棱长为1的正方体ABCD－A1B1C1D1中，E、F分别为棱AA1、BB1的中点，G为棱A1B1上的一点，且A1G＝λ(0≤λ≤1)，则点G到平面D1EF的距离为( )A. 3B.22C.2λ3D.55图K42－39．如图K42－3，四棱锥P－ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD＝AD＝1，AB＝2，点E是AB上一点，当二面角P－EC－D的平面角为π4时，AE＝( )A．1 B.12C．2－ 2 D．2－ 310．已知三棱锥O－ABC的侧棱OA，OB，OC两两垂直，E为OC的中点，且OA＝1，OB＝OC＝2，则平面EAB与平面ABC夹角的余弦值是________．11．如图K42－4，已知四棱柱ABCD－A1B1C1D1中，底面ABCD是边长为a的正方形，侧棱AA1长为b，且AA1与A1B1，A1D1的夹角都是60°，则AC1的长等于________．K42－4图K42－512．如图K42－5，AO⊥平面α，BC⊥OB，BC与平面α的夹角为30°，AO＝BO＝BC＝a，则AC＝________.13．如图K42－6，正方体ABCD－A1B1C1D1的棱长为2，M，N分别是C1D1，CC1的中点，则直线B1N与平面BDM所成角的正弦值为________．图K42－614．(10分)如图K42－7，放置在水平面上的组合体由直三棱柱ABC－A1B1C1与正三棱锥B－ACD组成，其中，AB⊥BC.它的正视图、俯视图、侧视图的面积分别为22＋1,22＋1,1.(1)求直线CA1与平面ACD所成角的正弦值；(2)在线段AC1上是否存在点P，使B1P⊥平面ACD？若存在，确定点P的位置；若不存在，说明理由．图K42－715．(13分) 如图K42－8，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．(1)求证：AF∥平面BCE；(2)求证：平面BCE⊥平面CDE；(3)求直线BF和平面BCE所成角的正弦值．图K42－816．(12分如图K42－9，已知正三棱柱ABC－A1B1C1的各棱长都是4，E是BC的中点，动点F在侧棱CC上，且不与点C重合．1(1)当CF＝1时，求证：EF⊥A1C；(2)设二面角C－AF－E的大小为θ，求tanθ的最小值．图K42－9。

2019-2020年高考数学 7.8 立体几何中的向量方法(二)——求空间角和距离练习——求空间角和距离(25分钟60分)一、选择题(每小题5分,共25分)1.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为()A. B. C. D.【解析】选B.建立空间直角坐标系如图.则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2).=(-1,0,2),=(-1,2,1),cos<,>==.所以异面直线BC1与AE所成角的余弦值为.2.(xx·宁波模拟)已知正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于()A. B. C. D.【解析】选A.以D为原点,建立如图所示的空间直角坐标系,设AB=1,则=(1,1,0),=(0,1,2),=(0,1,0),设平面DBC1的法向量为n=(x,y,z),则取z=1,则y=-2,x=2,所以n=(2,-2,1),所以sinθ====.【一题多解】本题还可以采用如下方法解答.方法一:选A.设AB=1,则AA1=2.设AC∩BD=O,连接C1O,过C作CH⊥C1O于H,连接DH,显然△C1DB是等腰三角形,所以C1O⊥BD,又C1C⊥BD,因为C1O∩C1C=C1,所以BD⊥平面C1CO,CH⊂平面C1CO,所以BD⊥CH,而CH⊥C1O,BD∩C1O=O,所以CH⊥平面C1BD,所以∠CDH是CD与平面C1BD所成的角,在Rt△C1OC中,OC=,C1C=2,所以C1O==,由C1C·OC=C1O·CH知CH==,在Rt△CDH中,sin∠CDH==.方法二:选A.设点C到平面C1BD的距离为h,CD与平面C1BD所成的角为θ,由=知·h=S△CBD·C1C,所以h=,所以sinθ==.3.已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值为()A. B.C. D.【解题提示】以A为原点建立空间直角坐标系,分别求出直线BC1的方向向量与平面DBB1D1的法向量,用空间向量的直线与平面所成角的夹角公式计算得解.【解析】选C.如图建立空间直角坐标系,则B(4,0,0),C(4,4,0),C1(4,4,2),显然AC⊥平面BB1D1D,所以=(4,4,0)为平面BB1D1D的一个法向量.又=(0,4,2).所以cos<,>===.即直线BC1和平面DBB1D1所成角的正弦值为.4.(xx·厦门模拟)二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为()A.150°B.45°C.60°D.120°【解析】选C.由条件知·=0,·=0,因为=++.所以||2=||2+||2+||2+2·+2·+2·=62+42+82+2×6×8cos<,>=(2)2.所以cos<,>=-,则<,>=120°,即<,>=60°.所以二面角的大小为60°.5.(xx·北京模拟)在四面体P-ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为()A. B.a C. D.a【解题提示】以P为原点建立空间直角坐标系,利用空间向量法求解.【解析】选B.根据题意,可建立如图所示的空间直角坐标系Pxyz,则P(0,0,0),A(a,0,0),B(0,a,0),C(0,0,a).所以=(-a,a,0),=(-a,0,a),=(a,0,0).设平面ABC的法向量为n=(x,y,z).由得得令x=1,所以n=(1,1,1),所以P到平面ABC的距离d===a.二、填空题(每小题5分,共15分)6.如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=,M为A1B1的中点,则AM与平面AA1C1C所成角的正切值为.【解析】以C1为原点,C1A1,C1B1,C1C所在直线分别为x,y,z轴建立空间直角坐标系,则平面AA1C1C的法向量为n=(0,1,0),AM=-(1,0,)=,则直线AM与平面AA1C1C所成角θ的正弦值为sinθ=|cos<,n>|==,所以tanθ=.答案:7.已知点E,F分别在正方体ABCD -A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC 所成的二面角的正切值为.【解析】如图,建立空间直角坐标系Dxyz,设DA=1,由已知条件得A(1,0,0),E,F,=,=,设平面AEF的法向量为n=(x,y,z),面AEF与面ABC所成的二面角为θ,由图知θ为锐角,由得令y=1,z=-3,x=-1,则n=(-1,1,-3),平面ABC的法向量为m=(0,0,-1),cosθ=|cos<n,m>|=,tanθ=.答案:8.(xx·石家庄模拟)如图所示,正方体ABCD-A1B1C1D1的棱长为1,E是A1B1上的点,则点E到平面ABC1D1的距离是.【解析】以点D为坐标原点,DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,设点E(1,a,1)(0≤a≤1),连接D1E,则=(1,a,0).连接A1D,易知A1D⊥平面ABC1D1,则=(1,0,1)为平面ABC1D1的一个法向量.所以点E到平面ABC1D1的距离是d==.答案:三、解答题(每小题10分,共20分)9.(xx·湖南高考)如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.(1)证明:O1O⊥底面ABCD.(2)若∠CBA=60°,求二面角C1-OB1-D的余弦值.【解题提示】(1)利用矩形的邻边垂直,及线线平行证明OO1⊥AC,OO1⊥BD.(2)由二面角的定义或者向量法求二面角的余弦值.【解析】(1)因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,因为AC∩BD=O,所以O1O⊥底面ABCD.(2)方法一:如图,过O1作O1H⊥B1O,垂足为H,连接C1H,由(1)可得OO1⊥A1C1,由于A1B1C1D1是菱形,所以B1D1⊥A1C1,所以A1C1⊥平面B1D1DB,所以由三垂线定理得HC1⊥B1O,所以∠O1HC1就是二面角C1-OB1-D的平面角.设棱柱的棱长为2,因为∠CBA=60°,所以OB=,OC=1,OB1=,在直角三角形O1OB1中,O1H==,因为O1C1=1,所以C1H===,所以cos∠C1HO1==,即二面角C1-OB1-D的余弦值为.方法二:因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD,又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.设棱长为2,因为∠CBA=60°,所以OB=,OC=1,所以O,B1,C1,平面BDD1B1的一个法向量为n=,设平面OC1B1的法向量为m=,则由m⊥,m⊥,所以x+2z=0,y+2z=0,取z=-,则x=2,y=2,所以m=,所以cos<m,n>===.由图形可知二面角C1-OB1-D为锐二面角,所以二面角C1-OB1-D的余弦值为.10.(xx·杭州模拟)如图,将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a,(1)若a=2,求证:AB∥平面CDE.(2)求实数a的值,使得二面角A-EC-D的大小为60°.【解析】(1)如图建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(1,1,),D(0,2,0),E(0,0,2),=(2,0,0),=(0,-2,2),=(1,-1,),设平面CDE的一个法向量为n1=(x,y,z),则有-2y+2z=0,x-y+z=0,取z=时,n1=(0,2,),所以·n1=0,又AB不在平面CDE内,所以AB∥平面CDE.(2)如图建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(1,1,),D(0,2,0),E(0,0,a),=(0,-2,a),=(1,-1,),设平面CDE的一个法向量为n2=(x,y,z),则有-2y+az=0,x-y+z=0,取z=2时,n2=(a-2,a,2),又平面AEC的一个法向量为n3=(-1,1,0),因为二面角A-EC-D的大小为60°,所以=,即a2-2a-2=0, 解得a=±2.(20分钟40分)1.(5分)如图,在四面体ABCD中,AB=1,AD=2,BC=3,CD=2,∠ABC=∠DCB=,则二面角A-BC-D的大小为()A. B.C. D.【解析】选 B.二面角A-BC-D的大小等于AB与CD所成角的大小.=++.而=+++2||||·cos<,>,即12=1+9+4+2×1×2cos<,>,所以cos<,>=-,所以AB与CD所成角为,即二面角A-BC-D的大小为.2.(5分)(xx·北京模拟)已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到平面AB1D1的距离是.【解析】如图所示建立空间直角坐标系Dxyz,则A1(2,0,4),A(2,0,0),B1(2,2,4),D1(0,0,4),=(-2,0,4),=(0,2,4),=(0,0,4),设平面AB1D1的法向量为n=(x,y,z),则即解得x=2z且y=-2z,不妨设n=(2,-2,1),设点A1到平面AB1D1的距离为d,则d==.答案:3.(5分)(xx·郑州模拟)正四棱锥S -ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角的大小为.【解析】如图所示,以O为原点建立空间直角坐标系Oxyz.设OD=SO=OA=OB=OC=a,则A(a,0,0),B(0,a,0),C(-a,0,0),P.则=(2a,0,0),=,=(a,a,0).设平面PAC的法向量为n,可求得n=(0,1,1),则cos<,n>===.所以<,n>=60°,所以直线BC与平面PAC的夹角为90°-60°=30°.答案:30°4.(12分)(能力挑战题)如图,在平行四边形ABCD中,AB=2BC=2,∠ABC=120°,M,N分别为线段AB,CD的中点,连接AN,DM交于点O,将△ADM沿直线DM翻折成△A′DM.使平面A′DM⊥平面BCD,F为线段A′C的中点.(1)求证:ON⊥平面A′DM.(2)求证:BF∥平面A′DM.(3)求直线FO与平面A′DM所成的角.【解析】(1)连接MN,由平面几何知四边形AMND是菱形.所以AN⊥DM.因为平面A′DM⊥平面ABCD,DM是交线,AN⊂平面ABCD,所以AN⊥平面A′DM,即ON⊥平面A′DM.(2)取A′D的中点E,连接EF,EM,因为F是A′C中点,所以EFCD.又M是AB中点,所以在平行四边形ABCD中,BMCD,所以EF BM,所以四边形EFBM是平行四边形.所以BF∥EM,因为EM⊂平面A′DM,BF⊄平面A′DM,所以BF∥平面A′DM.(3)因为AB=2BC=2,M是AB中点,所以A′D=A′M=1.因为菱形ADNM中O是DM中点,所以A′O⊥DM,因为平面A′DM⊥平面ABCD,所以A′O⊥平面ABCD.以ON为x轴,OM为y轴,OA′为z轴建立空间直角坐标系,∠ADN=∠ABC=120°,在△ADN中,AD=DN=1,所以AN==.同理求得DM=AD=AM=1,所以N,D,A′,因为N是CD的中点,所以C.因为F是A′C的中点,所以F.因为NO⊥平面A′DM,所以平面A′DM的一个法向量=.因为=,所以||==1.设OF与平面A′DM所成的角为θ,0<θ<,则sinθ=|cos<,>|===,所以θ=.所以直线FO与平面A′DM所成的角为.5.(13分)(xx·江西高考)如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.(1)求证:AB⊥PD.(2)若∠BPC=90°,PB=,PC=2,问AB为何值时,四棱锥P-ABCD的体积最大?并求此时平面PBC与平面DPC 夹角的余弦值.【解题提示】(1)利用面面垂直的性质定理证明AB⊥平面PAD即可.(2)借助两平面垂直的性质,作PO⊥AD,即四棱锥的高找到,过点O作OM⊥BC于点M,连接PM.则四棱锥的体积能用AB的长度表示,即可建立体积与AB的函数,借助二次函数知识求最值;此时可建立空间直角坐标系,利用坐标法求解.【解析】(1)因为ABCD为矩形,所以AB⊥AD,又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以AB⊥平面PAD,又PD⊂平面PAD,所以AB⊥PD.(2)过点P作PO⊥AD于点O,则PO⊥平面ABCD,过点O作OM⊥BC于点M,连接PM.则PM⊥BC,因为∠BPC=90°,PB=,PC=2,所以BC=,PM=,设AB=t,则在Rt△POM中,PO=,所以VP-ABCD=·t··=,所以当t2=,即t=时,VP-ABCD最大为.此时PO=AB=,且PO,OA,OM两两垂直,以OA,OM,OP所在直线为x,y,z轴建立空间直角坐标系Oxyz, 则P,D,C,B.所以=,=,=.设平面PCD的一个法向量m=(x1,y1,z1),则即令x1=1,则m=(1,0,-2),|m|=;同理设平面PBC的一个法向量n=(x2,y2,z2),即令y2=1,则n=(0,1,1),|n|=,设平面PBC与平面DPC夹角为θ,显然θ为锐角,且cosθ===..。

用空间向量法求解立体几何问题典例及解析以多面体为载体，以空间向量为工具，来论证和求解空间角、距离、线线关系以及线面关系相关问题，是近年来高考数学的重点和热点，用空间向量解立体几何问题，极大地降低了求解立几的难度，很大程度上呈现出程序化思想。

更易于学生们所接受，故而执教者应高度重视空间向量的工具性。

首先，梳理一下利用空间向量解决立体几何的知识和基本求解方法 一：利用空间向量求空间角 (1)两条异面直线所成的夹角范围：两条异面直线所成的夹角的取值范围是 。

向量求法：设直线,a b 的方向向量为a,b ，其夹角为θ，则有cos ___________.θ= (2)直线与平面所成的角定义：直线与平面所成的角是指直线与它在这个平面内的射影所成的角。

范围：直线和平面所夹角的取值范围是 。

向量求法：设直线l 的方向向量为a ，平面的法向量为n ，直线与法向量所成角的余弦值为|cos |___________.θ=直线与平面所成的角为ϕ，则有sin ___________.ϕ=或在平面内任取一个向量m ，则|cos |___________.θ=.(3)二面角二面角的取值范围是 . 二面角的向量求法：方法一：在两个半平面内任取两个与棱垂直的向量，则这两个向量所成的 即为所求的二面角的大小；方法二：设1n ，2n 分别是两个面的 ，则向量1n 与2n 的夹角(或其补角)即为所求二面角的平面角的大小。

二：利用空间向量求空间距离 （1）点面距离的向量公式平面α的法向量为n ，点P 是平面α外一点，点M 为平面α内任意一点，则点P 到平面α的距离d 就是 ，即d =||||MP ⋅n n . （2）线面、面面距离的向量公式平面α∥直线l ，平面α的法向量为n ，点M ∈α、P ∈l ，平面α与直线l 间的距离d 就是MP 在向量n 方向射影的绝对值，即d = .平面α∥β，平面α的法向量为n ，点M ∈α、P ∈β，平面α与平面β的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||MP ⋅n n . （3）异面直线的距离的向量公式设向量n 与两异面直线a 、b 都垂直，M ∈a 、P ∈b ，则两异面直线a 、b 间的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||MP ⋅n n .三：利用空间向量解证平行、垂直关系1：①所谓直线的方向向量，就是指 的向量，一条直线的方向向量有 个。

专题8.7 立体几何中的向量方法（二）求空间角与距离一、考纲要求1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题；2.了解向量方法在研究立体几何问题中的应用.二、考点梳理考点一 异面直线所成的角设a ，b 分别是两异面直线l 1，l 2的方向向量，则a 与b 的夹角β l 1与l 2所成的角θ范围 (0，π) ⎝⎛⎦⎤0，π2 求法cos β＝a ·b|a ||b |cos θ＝|cos β|＝|a ·b ||a ||b |考点二 求直线与平面所成的角设直线l 的方向向量为a ，平面α的法向量为n ，直线l 与平面α所成的角为θ，则sin θ＝|cos 〈a ，n 〉|＝|a ·n ||a ||n |.考点三 求二面角的大小(1)如图①，AB ，CD 是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝__〈AB →，CD →〉.(2)如图②③，n 1，n 2 分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|cos 〈n 1，n 2〉|，二面角的平面角大小是向量n 1与n 2的夹角(或其补角). 【特别提醒】1.线面角θ的正弦值等于直线的方向向量a 与平面的法向量n 所成角的余弦值的绝对值，即sin θ＝|cos 〈a ，n 〉|，不要误记为cos θ＝|cos 〈a ，n 〉|.2.二面角与法向量的夹角：利用平面的法向量求二面角的大小时，当求出两半平面α，β的法向量n 1，n 2时，要根据向量坐标在图形中观察法向量的方向，来确定二面角与向量n 1，n 2的夹角是相等，还是互补.三、题型分析例1. （黑龙江鹤岗一中2019届期末）如图，在空间四边形OABC 中，OA ＝8，AB ＝6，AC ＝4，BC ＝5，∠OAC ＝45°，∠OAB ＝60°，则OA 与BC 所成角的余弦值为( )A.3－225B.2－26C.12D.32【答案】A【解析】因为BC →＝AC →－AB →，所以OA →·BC →＝OA →·AC →－OA →·AB →＝|OA →||AC →|cos 〈OA →，AC →〉－|OA →||AB →|cos 〈OA →，AB →〉＝8×4×cos 135°－8×6×cos 120°＝－162＋24. 所以cos 〈OA →，BC →〉＝OA →·BC →|OA →||BC →|＝24－1628×5＝3－225.即OA 与BC 所成角的余弦值为3－225.【变式训练1-1】、（天津新华中学2019届高三质检）如图所示，四棱柱ABCD －A 1B 1C 1D 1中，底面为平行四边形，以顶点A 为端点的三条棱长都为1，且两两夹角为60°.(1)求AC 1的长； (2)求证：AC 1⊥BD ；(3)求BD 1与AC 夹角的余弦值.【解析】(1) 记AB →＝a ，AD →＝b ，AA 1→＝c ，则|a |＝|b |＝|c |＝1，〈a ，b 〉＝〈b ，c 〉＝〈c ，a 〉＝60°， ∴a ·b ＝b ·c ＝c ·a ＝12.|AC 1→|2＝(a ＋b ＋c )2＝a 2＋b 2＋c 2＋2(a ·b ＋b ·c ＋c ·a )＝1＋1＋1＋2×⎝⎛⎭⎫12＋12＋12＝6， ∴|AC →1|＝6，即AC 1的长为 6. (2)证明 ∵AC 1→＝a ＋b ＋c ，BD →＝b －a ，∴AC 1→·BD →＝(a ＋b ＋c )·(b －a )＝a ·b ＋|b |2＋b ·c －|a |2－a ·b －a ·c ＝b ·c －a ·c ＝|b ||c |cos 60°－|a ||c |cos 60°＝0.∴AC 1→⊥BD →，∴AC 1⊥BD .(3)解 BD 1→＝b ＋c －a ，AC →＝a ＋b ，∴|BD 1→|＝2，|AC →|＝3， BD 1→·AC →＝(b ＋c －a )·(a ＋b )＝b 2－a 2＋a ·c ＋b ·c ＝1.∴cos 〈BD 1→，AC →〉＝BD 1→·AC →|BD 1→||AC →|＝66.∴AC 与BD 1夹角的余弦值为66.例2、（2018年天津卷）如图，且AD =2BC ，,且EG =AD ，且CD =2FG ，，DA =DC =DG =2.（I ）若M 为CF 的中点，N 为EG 的中点，求证：；（II ）求二面角的正弦值；（III ）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长.【答案】(Ⅰ)证明见解析；(Ⅱ)；(Ⅲ).【解析】依题意，可以建立以D 为原点， 分别以，，的方向为x 轴，y 轴，z 轴的正方向的空间直角坐标系（如图），可得D （0，0，0），A （2，0，0），B （1，2，0），C （0，2，0），E （2，0，2），F （0，1，2），G （0，0，2），M （0，，1），N （1，0，2）．（Ⅰ）依题意=（0，2，0），=（2，0，2）．设n0=(x，y，z)为平面CDE的法向量，则即不妨令z=–1，可得n0=（1，0，–1）．又=（1，，1），可得，又因为直线MN平面CDE，所以MN∥平面CDE．（Ⅱ）依题意，可得=（–1，0，0），，=（0，–1，2）．设n=（x，y，z）为平面BCE的法向量，则即不妨令z=1，可得n=（0，1，1）．设m=（x，y，z）为平面BCF的法向量，则即不妨令z=1，可得m=（0，2，1）．因此有cos<m，n>=，于是sin<m，n>=．所以，二面角E–BC–F的正弦值为．（Ⅲ）设线段DP的长为h（h∈［0，2］），则点P的坐标为（0，0，h），可得．易知，=（0，2，0）为平面ADGE的一个法向量，故，由题意，可得=sin60°=，解得h=∈［0，2］．所以线段的长为.【变式训练2-1】、（吉林长春市实验中学2019届高三模拟）如图所示，在四棱锥P-ABCD中，底面ABCD 是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，过点E作EF⊥PB于点F.求证：(1)PA ∥平面EDB ； (2)PB ⊥平面EFD .【证明】以D 为坐标原点，射线DA ，DC ，DP 分别为x 轴、y 轴、z 轴的正方向建立如图所示的空间直角坐标系D -xyz .设DC ＝a .(1)连接AC 交BD 于点G ，连接EG .依题意得A (a,0,0)，P (0,0，a )，C (0，a,0)，E ⎝⎛⎭⎫0，a 2，a 2. 因为底面ABCD 是正方形，所以G 为AC 的中点故点G 的坐标为⎝⎛⎭⎫a 2，a 2，0，所以PA ―→＝(a,0，－a )，EG ―→＝⎝⎛⎭⎫a2，0，－a 2， 则PA ―→＝2EG ―→，故PA ∥EG .而EG ⊂平面EDB ，PA ⊄平面EDB ，所以PA ∥平面EDB . (2)依题意得B (a ，a,0)，所以PB ―→＝(a ，a ，－a )．又DE ―→＝⎝⎛⎭⎫0，a 2，a 2， 故PB ―→·DE ―→＝0＋a 22－a 22＝0，所以PB ⊥DE ，所以PB ⊥DE .由题可知EF ⊥PB ，且EF ∩DE ＝E ，所以PB ⊥平面EFD .例3、如图，在四棱锥PABCD 中，底面ABCD 是矩形，PA ⊥底面ABCD ，E 是PC 的中点．已知AB ＝2，AD ＝22，PA ＝2，求异面直线BC 与AE 所成的角的大小．【解析】 建立如图所示的空间直角坐标系，则A(0，0，0)，B(2，0，0)，C(2，22，0)，E(1，2，1)，AE →＝(1，2，1)，BC →＝(0，22，0)．设AE →与BC →的夹角为θ，则cosθ＝AE →·BC →|AE →|·|BC →|＝42×22＝22，所以θ＝π4，所以异面直线BC 与AE 所成的角的大小是π4.【变式训练3-1】、 如图所示，在空间直角坐标系中有直三棱柱ABCA 1B 1C 1，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1夹角的余弦值为________．【答案】55【解析】 不妨令CB ＝1，则CA ＝CC 1＝2，可得C(0，0，0)，B(0，0，1)，C 1(0，2，0)，A(2，0，0)，B 1(0，2，1)，所以BC 1→＝(0，2，－1)，AB 1→＝(－2，2，1)，所以cos 〈BC 1→，AB 1→〉＝BC 1→·AB 1→|BC 1→|·|AB 1→|＝4－15×9＝15＝55＞0，所以BC 1→与AB 1→的夹角即为直线BC 1与直线AB 1的夹角，所以直线BC 1与直线AB 1夹角的余弦值为55.【变式训练3-2】、如图，已知三棱柱ABC -A 1B 1C 1，平面A 1ACC 1⊥平面ABC ，∠ABC ＝90°，∠BAC ＝30°，A 1A ＝A 1C ＝AC ，E ，F 分别是AC ，A 1B 1的中点． (1)证明：EF ⊥BC ；(2)求直线EF 与平面A 1BC 所成角的余弦值．【解析】 (1)证明：连接A 1E ，因为A 1A ＝A 1C ，E 是AC 的中点，所以A 1E ⊥AC . 又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1， 平面A 1ACC 1∩平面ABC ＝AC ，所以A 1E ⊥平面ABC .如图，以点E 为原点，分别以射线EC ，EA 1为y ，z 轴的正半轴，建立空间直角坐标系E -xyz . 不妨设AC ＝4，则A 1(0,0,23)，B (3，1,0)，B 1(3，3,23)，F ⎝⎛⎭⎫32，32，23，C (0,2,0)． 因此，EF ―→＝⎝⎛⎭⎫32，32，23，BC ―→＝(－3，1,0)．由EF ―→·BC ―→＝0得EF ⊥BC .(2)设直线EF 与平面A 1BC 所成角为θ.由(1)可得BC ―→＝(－3，1,0)，A 1C ―→＝(0,2，－23)．设平面A 1BC 的法向量为n ＝(x ，y ，z )．由⎩⎪⎨⎪⎧BC ―→·n ＝0，A 1C ―→·n ＝0，得⎩⎨⎧－3x ＋y ＝0，y －3z ＝0.取n ＝(1, 3，1)，故sin θ＝|cos 〈EF ―→，n 〉|＝|EF ―→·n ||EF ―→|·|n |＝45，∴cos θ＝35.因此，直线EF 与平面A 1BC 所成的角的余弦值为35.。

第九节 利用空间向量求空间角一、基础知识1．异面直线所成角设异面直线a ，b 所成的角为θ，则cos θ＝|a·b||a||b|， 其中a ，b 分别是直线a ，b 的方向向量．2．直线与平面所成角如图所示，设l 为平面α的斜线，l ∩α＝A ，a 为l 的方向向量，n 为平面α的法向量，φ为l 与α所成的角，则sin φ＝|cos 〈a ，n 〉|＝|a ·n||a||n|.3．二面角(1)若AB ，CD 分别是二面角α­l ­β的两个平面内与棱l 垂直的异面直线，则二面角(或其补角)的大小就是向量AB ―→与CD ―→的夹角，如图(1)．(2)平面α与β相交于直线l ，平面α的法向量为n 1，平面β的法向量为n 2，〈n 1，n 2〉＝θ，则二面角α ­l ­β为θ或π－θ.设二面角大小为φ，则|cos φ|＝|cos θ|＝|n 1·n 2||n 1||n 2|，如图(2)(3)． 两异面直线所成的角为锐角或直角，而不共线的向量的夹角为(0，π)，所以公式中要加绝对值．直线与平面所成角的范围为⎣⎡⎦⎤0，π2，而向量之间的夹角的范围为[0，π]，所以公式中要加绝对值．利用公式与二面角的平面角时，要注意〈n 1，n 2〉与二面角大小的关系，是相等还是互补，需要结合图形进行判断．二、常用结论解空间角最值问题时往往会用到最小角定理cos θ＝cos θ1cos θ2.如图，若OA为平面α的一条斜线，O为斜足，OB为OA在平面α内的射影，OC为平面α内的一条直线，其中θ为OA与OC所成的角，θ1为OA与OB所成的角，即线面角，θ2为OB与OC所成的角，那么cos θ＝cos θ1cos θ2.[解题技法]用向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系；(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)两异面直线所成角的余弦等于两向量夹角余弦值的绝对值．[提醒]注意向量的夹角与异面直线所成的角的区别：当异面直线的方向向量的夹角为锐角或直角时，此夹角就是异面直线所成的角；当异面直线的方向向量的夹角为钝角时，其补角才是异面直线所成的角．[解题技法]利用向量求线面角的2种方法(1)分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)．(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线与平面所成的角．[解题技法](1)利用法向量求二面角的大小时，由于法向量的方向不同，两个法向量的夹角与二面角的大小可能相等，也可能互补．所以，两个法向量的夹角的余弦值与二面角的余弦值可能存在正负号的差异．(2)有时用观察法难以判定二面角是钝角还是锐角，为了保证解题结果准确无误，我们给出一种万无一失的方法：就是在两个半平面和二面角的棱上各取1个向量，要求这三个向量必须起点相同，在利用行列式计算法向量时，棱对应的向量必须排前面，即口诀“起点同，棱排前”，这样求出的两个法向量的夹角一定与二面角的大小相等．。

§8.8 立体几何中的向量方法(二)——求空间角距离设a ，b 分别是两异面直线l 1，l 2的方向向量，则2.(1)斜线和它在平面内的射影的所成的角叫做斜线和平面所成的角(或斜线和平面的夹角).(2)斜线和它在平面内的射影所成的角，是斜线和这个平面内所有直线所成角中最小的角.3.二面角(1)从一条直线出发的两个半平面所组成的图形叫做二面角.(2)在二面角α—l —β的棱上任取一点O ，在两半平面内分别作射线OA ⊥l ，OB ⊥l ，则∠AOB 叫做二面角α—l —β的平面角.4.空间向量与空间角的关系(1)设异面直线l 1，l 2的方向向量分别为m 1，m 2，则l 1与l 2所成的角θ满足cos θ＝|cos 〈m 1，m 2〉|.(2)设直线l 的方向向量和平面α的法向量分别为m ，n ，则直线l 与平面α所成角θ满足sin θ＝|cos 〈m ，n 〉|.(3)求二面角的大小1°如图①，AB 、CD 是二面角α—l —β的两个面内与棱l 垂直的直线，则二面角的大小θ＝〈AB →，CD →〉.2°如图②③，n 1，n 2分别是二面角α—l —β的两个半平面α，β的法向量，则二面角的大小θ满足cos θ＝cos 〈n 1，n 2〉或－cos 〈n 1，n 2〉.概念方法微思考1.利用空间向量如何求线段长度？提示 利用|AB →|2＝AB →·AB →可以求空间中有向线段的长度.2.如何求空间点面之间的距离？提示 点面距离的求法：已知AB 为平面α的一条斜线段，n 为平面α的法向量，则点B 到平面α的距离为 |BO →|＝|AB →||cos 〈AB →，n 〉|.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)两直线的方向向量所成的角就是两条直线所成的角.( × )(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角.( × )(3)两个平面的法向量所成的角是这两个平面所成的角.( × )(4)两异面直线夹角的范围是⎝ ⎛⎦⎥⎤0，π2，直线与平面所成角的范围是⎣⎢⎡⎦⎥⎤0，π2，二面角的范围是[0，π].( √ )(5)若二面角α－a －β的两个半平面α，β的法向量n 1，n 2所成角为θ，则二面角α－a －β的大小是π－θ.( × )题组二 教材改编2.已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角为( )A.45°B.135°C.45°或135°D.90° 答案 C解析 cos 〈m ，n 〉＝m·n |m||n |＝11·2＝22，即〈m ，n 〉＝45°. ∴两平面所成二面角为45°或180°－45°＝135°.3.如图，正三棱柱(底面是正三角形的直棱柱)ABC －A 1B 1C 1的底面边长为2，侧棱长为22，则AC 1与侧面ABB 1A 1所成的角为______.答案 π6解析 如图，以A 为原点，以AB →，AE →(AE ⊥AB )，AA 1→所在直线分别为x 轴、y 轴、z 轴(如图)建立空间直角坐标系，设D 为A 1B 1的中点，则A (0,0,0)，C 1(1，3，22)，D (1,0,22)，∴AC 1→＝(1，3，22)，AD →＝(1,0,22).∠C 1AD 为AC 1与平面ABB 1A 1所成的角，cos∠C 1AD ＝AC 1→·AD →|AC 1→||AD →|＝(1，3，22)·(1，0，22)12×9＝32， 又∵∠C 1AD ∈⎣⎢⎡⎦⎥⎤0，π2， ∴∠C 1AD ＝π6. 题组三 易错自纠4.在直三棱柱ABC －A 1B 1C 1中，∠BCA ＝90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC ＝CA ＝CC 1，则BM 与AN 所成角的余弦值为( )A.110B.25C.3010D.22答案 C解析 以点C 为坐标原点，CA ，CB ，CC 1所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系.设BC ＝CA ＝CC 1＝2，则可得A (2,0,0)，B (0,2,0)，M (1,1,2)，N (1，0,2)，∴BM →＝(1，－1,2)，AN →＝(－1,0,2).∴cos〈BM →，AN →〉＝BM →·AN →|BM →||AN →|＝1×(－1)＋(－1)×0＋2×212＋(－1)2＋22×(－1)2＋02＋22＝36×5 ＝3010. 5.已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为________.答案 30°解析 设l 与α所成角为θ，∵cos〈m ，n 〉＝－12， ∴sin θ＝|cos 〈m ，n 〉|＝12，∵0°≤θ≤90°，∴θ＝30°. 题型一 求异面直线所成的角例1 如图，四边形ABCD 为菱形，∠ABC ＝120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE ＝2DF ，AE ⊥EC .(1)证明：平面AEC ⊥平面AFC ；(2)求直线AE 与直线CF 所成角的余弦值.(1)证明 如图所示，连接BD ，设BD ∩AC ＝G ，连接EG ，FG ，EF .在菱形ABCD 中，不妨设GB ＝1.由∠ABC ＝120°，可得AG ＝GC ＝ 3.由BE ⊥平面ABCD ，AB ＝BC ＝2，可知AE ＝EC .又AE ⊥EC ，所以EG ＝3，且EG ⊥AC .在Rt△EBG 中，可得BE ＝2，故DF ＝22. 在Rt△FDG 中，可得FG ＝62. 在直角梯形BDFE 中，由BD ＝2，BE ＝2，DF ＝22，可得EF ＝322，从而EG 2＋FG 2＝EF 2，所以EG ⊥FG .又AC ∩FG ＝G ，AC ，FG ⊂平面AFC ，所以EG ⊥平面AFC .因为EG ⊂平面AEC ，所以平面AEC ⊥平面AFC .(2)解 如图，以G 为坐标原点，分别以GB ，GC 所在直线为x 轴、y 轴，|GB →|为单位长度，建立空间直角坐标系Gxyz ，由(1)可得A (0，－3，0)， E (1,0，2)，F ⎝ ⎛⎭⎪⎫－1，0，22，C (0，3，0)， 所以AE →＝(1，3，2)，CF →＝⎝⎛⎭⎪⎫－1，－3，22. 故cos 〈AE →，CF →〉＝AE →·CF →|AE →||CF →|＝－33. 所以直线AE 与直线CF 所成角的余弦值为33. 思维升华 用向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系；(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.跟踪训练1 三棱柱ABC －A 1B 1C 1中，△ABC 为等边三角形，AA 1⊥平面ABC ，AA 1＝AB ，N ，M 分别是A 1B 1，A 1C 1的中点，则AM 与BN 所成角的余弦值为( )A.110B.35C.710D.45答案 C解析 如图所示，取AC 的中点D ，以D 为原点，BD ，DC ，DM 所在直线分别为x 轴、y 轴、z 轴，建立空间直角坐标系，不妨设AC ＝2，则A (0，－1,0)，M (0,0,2)，B (－3，0,0)，N ⎝ ⎛⎭⎪⎫－32，－12，2， 所以AM →＝(0,1,2)，BN →＝⎝ ⎛⎭⎪⎫32，－12，2， 所以cos 〈AM →，BN →〉＝AM →·BN →|AM →|·|BN →|＝725×5＝710，故选C. 题型二 求直线与平面所成的角例2 (2018·全国Ⅰ)如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF ⊥BF .(1)证明：平面PEF ⊥平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值.(1)证明 由已知可得BF ⊥PF ，BF ⊥EF ，PF ∩EF ＝F ，PF ，EF ⊂平面PEF ，所以BF ⊥平面PEF .又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD .(2)解 如图，作PH ⊥EF ，垂足为H .由(1)得，PH ⊥平面ABFD .以H 为坐标原点，HF →的方向为y 轴正方向，|BF →|为单位长，建立如图所示的空间直角坐标系Hxyz .由(1)可得，DE ⊥PE .又DP ＝2，DE ＝1，所以PE ＝ 3.又PF ＝1，EF ＝2，所以PE ⊥PF .所以PH ＝32，EH ＝32. 则H (0,0,0)，P ⎝ ⎛⎭⎪⎫0，0，32，D ⎝ ⎛⎭⎪⎫－1，－32，0， DP →＝⎝ ⎛⎭⎪⎫1，32，32，HP →＝⎝ ⎛⎭⎪⎫0，0，32. 又HP →为平面ABFD 的法向量，设DP 与平面ABFD 所成的角为θ，则sin θ＝|cos 〈HP →，DP →〉|＝|HP →·DP →||HP →||DP →|＝343＝34. 所以DP 与平面ABFD 所成角的正弦值为34. 思维升华 若直线l 与平面α的夹角为θ，直线l 的方向向量l 与平面α的法向量n 的夹角为β，则θ＝π2－β或θ＝β－π2，故有sin θ＝|cos β|＝|l ·n ||l ||n |. 跟踪训练2 (2018·全国Ⅱ)如图，在三棱锥P －ABC 中，AB ＝BC ＝22，PA ＝PB ＝PC ＝AC ＝4，O 为AC 的中点.(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M －PA －C 为30°，求PC 与平面PAM 所成角的正弦值.(1)证明 因为PA ＝PC ＝AC ＝4，O 为AC 的中点，所以OP ⊥AC ，且OP ＝2 3.如图，连接OB .因为AB ＝BC ＝22AC ， 所以△ABC 为等腰直角三角形，所以OB ⊥AC ，OB ＝12AC ＝2. 由OP 2＋OB 2＝PB 2知PO ⊥OB .因为OP ⊥OB ，OP ⊥AC ，OB ∩AC ＝O ，OB ，AC ⊂平面ABC ，所以PO ⊥平面ABC .(2)解 由(1)知OP ，OB ，OC 两两垂直，则以O 为坐标原点，分别以OB ，OC ，OP 所在直线为x 轴、y 轴、z 轴，建立空间直角坐标系Oxyz ，如图所示.由已知得O (0,0,0)，B (2,0,0)，A (0，－2,0)，C (0,2,0)， P (0,0,23)，AP →＝(0,2,23).由(1)知平面PAC 的一个法向量为OB →＝(2,0,0).设M (a ,2－a ,0)(0≤a ≤2)，则AM →＝(a ,4－a ,0).设平面PAM 的法向量为n ＝(x ，y ，z ).由AP →·n ＝0，AM →·n ＝0，得 ⎩⎨⎧ 2y ＋23z ＝0，ax ＋(4－a )y ＝0，可取y ＝3a ，得平面PAM 的一个法向量为n ＝(3(a －4)，3a ，－a )， 所以cos 〈OB →，n 〉＝OB →·n |OB →||n |＝23(a －4)23(a －4)2＋3a 2＋a 2. 由已知可得|cos 〈OB →，n 〉|＝cos30°＝32， 所以23|a －4|23(a －4)2＋3a 2＋a2＝32， 解得a ＝－4(舍去)或a ＝43.所以n ＝⎝ ⎛⎭⎪⎫－833，433，－43. 又PC →＝(0,2，－23)，所以cos 〈PC →，n 〉＝34. 所以PC 与平面PAM 所成角的正弦值为34. 题型三 求二面角 例3 (2018·锦州模拟)如图，在梯形ABCD 中，AB ∥CD ，AD ＝DC ＝CB ＝2，∠ABC ＝60°，平面ACEF ⊥平面ABCD ，四边形ACEF 是菱形，∠CAF ＝60°.(1)求证：BF ⊥AE ；(2)求二面角B －EF －D 的平面角的正切值.(1)证明 依题意，在等腰梯形ABCD 中，AC ＝23，AB ＝4，∵BC ＝2，∴AC 2＋BC 2＝AB 2，即BC ⊥AC ，又∵平面ACEF ⊥平面ABCD ，平面ACEF ∩平面ABCD ＝AC ，BC ⊂平面ABCD ，∴BC ⊥平面ACEF ，而AE ⊂平面ACEF ，∴AE ⊥BC ，连接CF ，∵四边形ACEF 为菱形，∴AE ⊥FC ，又∵BC ∩CF ＝C ，BC ，CF ⊂平面BCF ，∴AE ⊥平面BCF ，∵BF ⊂平面BCF ，∴BF ⊥AE .(2)解 取EF 的中点M ，连接MC ，∵四边形ACEF 是菱形，且∠CAF ＝60°，∴由平面几何易知MC ⊥AC ，又∵平面ACEF ⊥平面ABCD ，平面ACEF ∩平面ABCD ＝AC ，CM ⊂平面ACEF ，∴MC ⊥平面ABCD .以CA ，CB ，CM 所在直线分别为x ，y ，z 轴建立空间直角坐标系，各点的坐标依次为C (0,0,0)，A (23，0,0)，B (0，2,0)，D (3，－1,0)，E (－3，0,3)，F (3，0,3)，设平面BEF 和平面DEF 的一个法向量分别为n 1＝(a 1，b 1，c 1)，n 2＝(a 2，b 2，c 2)， ∵BF →＝(3，－2,3)，EF →＝(23，0,0)，∴⎩⎪⎨⎪⎧ BF →·n 1＝0，EF →·n 1＝0，即⎩⎨⎧ 3a 1－2b 1＋3c 1＝0，23a 1＝0，即⎩⎪⎨⎪⎧ a 1＝0，2b 1＝3c 1，不妨令b 1＝3，则n 1＝(0,3,2)，同理可求得n 2＝(0,3，－1)，设二面角B －EF －D 的大小为θ，由图易知θ为锐角，∴cos θ＝|cos 〈n 1，n 2〉|＝|n 1·n 2||n 1|·|n 2|＝7130， 故二面角B －EF －D 的平面角的正切值为97. 思维升华 利用向量法求二面角的大小的关键是确定平面的法向量，求法向量的方法主要有两种：①求平面的垂线的方向向量；②利用法向量与平面内两个不共线向量的数量积为零，列方程组求解.跟踪训练3 (2018·全国Ⅲ)如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点.(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M －ABC 体积最大时，求平面MAB 与平面MCD 所成二面角的正弦值.(1)证明 由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，又DM ⊂平面CMD ，故BC ⊥DM .因为M 为CD 上异于C ，D 的点，且DC 为直径，所以DM ⊥CM .又BC ∩CM ＝C ，BC ，CM ⊂平面BMC ，所以DM ⊥平面BMC .又DM ⊂平面AMD ，故平面AMD ⊥平面BMC .(2)解 以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系Dxyz .当三棱锥M －ABC 体积最大时，M 为CD 的中点.由题设得D (0,0,0)，A (2,0,0)，B (2,2,0)，C (0,2,0)，M (0,1,1)，AM →＝(－2,1,1)，AB →＝(0,2,0)，DA →＝(2,0,0)，设n ＝(x ，y ，z )是平面MAB 的法向量，则⎩⎪⎨⎪⎧ n ·AM →＝0，n ·AB →＝0，即⎩⎪⎨⎪⎧ －2x ＋y ＋z ＝0，2y ＝0.可取n ＝(1,0,2)，DA →是平面MCD 的一个法向量，因此cos 〈n ，DA →〉＝n ·DA →|n ||DA →|＝55， sin 〈n ，DA →〉＝255.所以平面MAB 与平面MCD 所成二面角的正弦值是255. 利用空间向量求空间角例 (12分)如图，四棱锥S －ABCD 中，△ABD 为正三角形，∠BCD ＝120°，CB ＝CD ＝CS ＝2，∠BSD ＝90°.(1)求证：AC ⊥平面SBD ；(2)若SC ⊥BD ，求二面角A －SB －C 的余弦值.(1)证明 设AC ∩BD ＝O ，连接SO ，如图①，因为AB ＝AD ，CB ＝CD ，所以AC 是BD 的垂直平分线，即O 为BD 的中点，且AC ⊥BD .[1分]在△BCD 中，因为CB ＝CD ＝2，∠BCD ＝120°，所以BD ＝23，CO ＝1.在Rt△SBD 中，因为∠BSD ＝90°，O 为BD 的中点，所以SO ＝12BD ＝ 3. 在△SOC 中，因为CO ＝1，SO ＝3，CS ＝2，所以SO 2＋CO 2＝CS 2，所以SO ⊥AC .[4分]因为BD ∩SO ＝O ，BD ，SO ⊂平面SBD ，所以AC ⊥平面SBD .[5分](2)解 方法一 过点O 作OK ⊥SB 于点K ，连接AK ，CK ，如图②，由(1)知AC ⊥平面SBD ，所以AO ⊥SB .因为OK ∩AO ＝O ，OK ，AO ⊂平面AOK ，所以SB ⊥平面AOK .[6分]因为AK ⊂平面AOK ，所以AK ⊥SB .同理可证CK ⊥SB .[7分]所以∠AKC 是二面角A －SB －C 的平面角.因为SC ⊥BD ，由(1)知AC ⊥BD ，且AC ∩SC ＝C ，AC ，SC ⊂平面SAC ，所以BD ⊥平面SAC .而SO ⊂平面SAC ，所以SO ⊥BD .在Rt△SOB 中，OK ＝SO ·OB SB ＝62.在Rt△AOK 中，AK ＝AO 2＋OK 2＝422， 同理可求CK ＝102.[10分] 在△AKC 中，cos∠AKC ＝AK 2＋CK 2－AC 22AK ·CK ＝－10535. 所以二面角A －SB －C 的余弦值为－10535.[12分] 方法二 因为SC ⊥BD ，由(1)知，AC ⊥BD ，且AC ∩SC ＝C ，AC ，SC ⊂平面SAC ，所以BD ⊥平面SAC .而SO ⊂平面SAC ，所以SO ⊥BD .[6分]由(1)知，AC ⊥平面SBD ，SO ⊂平面SBD ，所以SO ⊥AC .因为AC ∩BD ＝O ，AC ，BD ⊂平面ABCD ，所以SO ⊥平面ABCD .[7分]以O 为原点，OA →，OB →，OS →的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，如图③，则A (3,0,0)，B (0，3，0)，C (－1,0,0)，S (0,0，3).所以AB →＝(－3，3，0)，CB →＝(1，3，0)，SB →＝(0，3，－3).[8分]设平面SAB 的法向量n ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧ AB →·n ＝－3x 1＋3y 1＝0，SB →·n ＝3y 1－3z 1＝0，令y 1＝3，得平面SAB 的一个法向量为n ＝(1，3，3).同理可得平面SCB 的一个法向量为m ＝(－3，1,1).[10分]所以cos 〈n ，m 〉＝n ·m |n ||m |＝－3＋3＋37×5＝10535. 因为二面角A －SB －C 是钝角，所以二面角A －SB －C 的余弦值为－10535.[12分] 利用向量求空间角的步骤第一步：建立空间直角坐标系，确定点的坐标；第二步：求向量(直线的方向向量、平面的法向量)坐标；第三步：计算向量的夹角(或函数值)，并转化为所求角.1.已知两平面的法向量分别为m ＝(1，－1,0)，n ＝(0,1，－1)，则两平面所成的二面角为( )A.60°B.120°C.60°或120°D.90°答案 C解析 cos 〈m ，n 〉＝m·n |m||n |＝－12·2＝－12， 即〈m ，n 〉＝120°.∴两平面所成二面角为120°或180°－120°＝60°.2.如图，在空间直角坐标系中有直三棱柱ABC －A 1B 1C 1，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1所成角的余弦值为( ) A.55 B.53 C.56 D.54 答案 A解析 设CA ＝2，则C (0,0,0)，A (2,0,0)，B (0,0,1)，C 1(0,2,0)，B 1(0,2,1)，可得向量AB 1→＝(－2,2,1)，BC 1→＝(0,2，－1)，由向量的夹角公式得cos 〈AB 1→，BC 1→〉＝AB 1→·BC 1→|AB 1→||BC 1→|＝0＋4－14＋4＋1×0＋4＋1＝15＝55，故选A. 3.在正方体ABCD －A 1B 1C 1D 1中，点E 为BB 1的中点，则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( )A.12B.23C.33D.22答案 B解析 以A 为原点，AB ，AD ，AA 1所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系Axyz ，设棱长为1，则A 1(0,0,1)，E ⎝⎛⎭⎪⎫1，0，12，D (0,1,0)， ∴A 1D →＝(0,1，－1)，A 1E →＝⎝⎛⎭⎪⎫1，0，－12. 设平面A 1ED 的一个法向量为n 1＝(1，y ，z )，则有⎩⎪⎨⎪⎧ A 1D →·n 1＝0，A 1E →·n 1＝0，即⎩⎪⎨⎪⎧ y －z ＝0，1－12z ＝0，∴⎩⎪⎨⎪⎧ y ＝2，z ＝2，∴n 1＝(1,2,2). ∵平面ABCD 的一个法向量为n 2＝(0,0,1)，∴cos〈n 1，n 2〉＝23×1＝23， 即所成的锐二面角的余弦值为23. 4.在正方体ABCD —A 1B 1C 1D 1中，AC 与B 1D 所成角的大小为( )A.π6B.π4C.π3D.π2答案 D解析 以A 为坐标原点，AB ，AD ，AA 1所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系，设正方体的边长为1，则A (0,0,0)，C (1,1,0)，B 1(1,0,1)，D (0,1,0).∴AC →＝(1,1,0)，B 1D →＝(－1,1，－1)，∵AC →·B 1D →＝1×(－1)＋1×1＋0×(－1)＝0，∴AC →⊥B 1D →，∴AC 与B 1D 所成的角为π2. 5.(2018·包头模拟)已知正三棱柱ABC －A 1B 1C 1，AB ＝AA 1＝2，则异面直线AB 1与CA 1所成角的余弦值为( )A.0B.－14C.14D.12答案 C解析 以A 为原点，在平面ABC 内过A 作AC 的垂线为x 轴，以AC 所在直线为y 轴，以AA 1所在直线为z 轴，建立空间直角坐标系，则A (0,0,0)，B 1(3，1,2)，A 1(0,0,2)，C (0,2,0)，AB 1→＝(3，1,2)，A 1C →＝(0,2，－2)，设异面直线AB 1和A 1C 所成的角为θ，则cos θ＝|AB 1→·A 1C →||AB 1→|·|A 1C →|＝|－2|8·8＝14.46.如图，点A ，B ，C 分别在空间直角坐标系O －xyz 的三条坐标轴上，OC →＝(0,0,2)，平面ABC 的法向量为n ＝(2，1,2)，设二面角C －AB －O 的大小为θ，则cos θ等于( ) A.43B.53C.23D.－23答案 C解析 由题意可知，平面ABO 的一个法向量为OC →＝(0,0，2)，由图可知，二面角C －AB －O 为锐角，由空间向量的结论可知，cos θ＝|OC →·n ||OC →||n |＝|4|2×3＝23. 7.在三棱锥P －ABC 中，PA ⊥平面ABC ，∠BAC ＝90°，D ，E ，F 分别是棱AB ，BC ，CP 的中点，AB ＝AC ＝1，PA ＝2，则直线PA 与平面DEF 所成角的正弦值为________.答案 55解析 以A 为原点，AB ，AC ，AP 所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系，由AB ＝AC ＝1，PA ＝2，得A (0,0,0)，B (1,0,0)，C (0,1,0)，P (0,0,2)，D ⎝ ⎛⎭⎪⎫12，0，0， E ⎝ ⎛⎭⎪⎫12，12，0，F ⎝ ⎛⎭⎪⎫0，12，1. ∴PA →＝(0,0，－2)，DE →＝⎝ ⎛⎭⎪⎫0，12，0， DF →＝⎝ ⎛⎭⎪⎫－12，12，1. 设平面DEF 的法向量为n ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧ n ·DE →＝0，n ·DF →＝0，得⎩⎪⎨⎪⎧ y ＝0，－x ＋y ＋2z ＝0.取z ＝1，则n ＝(2,0,1)，设直线PA 与平面DEF 所成的角为θ，则sin θ＝|cos 〈n ，PA →〉|＝|PA →·n ||PA →||n |＝55，58.如图，在正方形ABCD 中，EF ∥AB ，若沿EF 将正方形折成一个二面角后，AE ∶ED ∶AD ＝1∶1∶2，则AF 与CE 所成角的余弦值为________.答案 45解析 ∵AE ∶ED ∶AD ＝1∶1∶2，∴AE ⊥ED ，即AE ，DE ，EF 两两垂直，所以建立如图所示的空间直角坐标系，设AB ＝EF ＝CD ＝2，则E (0,0,0)，A (1,0,0)，F (0,2,0)，C (0,2,1)，∴AF →＝(－1,2,0)，EC →＝(0,2,1)，∴cos〈AF →，EC →〉＝AF →·EC →|AF →||EC →|＝45， ∴AF 与CE 所成角的余弦值为45. 9.如图所示，在三棱柱ABC —A 1B 1C 1中，AA 1⊥底面ABC ，AB ＝BC ＝AA 1，∠ABC ＝90°，点E ，F 分别是棱AB ，BB 1的中点，则直线EF 和BC 1所成的角是__________.答案 60°解析 以B 点为坐标原点，以BC 所在直线为x 轴，BA 所在直线为y 轴，BB 1所在直线为z 轴，建立空间直角坐标系.设AB ＝BC ＝AA 1＝2，则C 1(2,0,2)，E (0,1,0)，F (0,0,1)，则EF →＝(0，－1,1)，BC 1→＝(2,0,2)，∴EF →·BC 1→＝2，∴cos〈EF →，BC 1→〉＝EF →·BC 1→|EF →||BC 1→|＝22×22＝12， ∵异面直线所成角的范围是(0°，90°]，∴EF 和BC 1所成的角为60°.10.(2019·福州质检)已知点E ，F 分别在正方体ABCD －A 1B 1C 1D 1的棱BB 1，CC 1上，且B 1E ＝2EB ，CF ＝2FC 1，则平面AEF 与平面ABC 所成的锐二面角的正切值为________.答案 23解析 方法一 延长FE ，CB 相交于点G ，连接AG ，如图所示.设正方体的棱长为3，则GB ＝BC ＝3，作BH ⊥AG 于点H ，连接EH ，则∠EHB 为所求锐二面角的平面角.∵BH ＝322，EB ＝1， ∴tan∠EHB ＝EB BH ＝23. 方法二 如图，以点D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴，建立空间直角坐标系Dxyz ，设DA ＝1，由已知条件得A (1,0,0)，E ⎝ ⎛⎭⎪⎫1，1，13， F ⎝ ⎛⎭⎪⎫0，1，23，AE →＝⎝ ⎛⎭⎪⎫0，1，13， AF →＝⎝ ⎛⎭⎪⎫－1，1，23， 设平面AEF 的法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧ n ·AE →＝0，n ·AF →＝0，得⎩⎪⎨⎪⎧ y ＋13z ＝0，－x ＋y ＋23z ＝0.令y ＝1，z ＝－3，x ＝－1，则n ＝(－1,1，－3)，取平面ABC 的法向量为m ＝(0,0，－1)，设平面AEF 与平面ABC 所成的锐二面角为θ，则cos θ＝|cos 〈n ，m 〉|＝31111，tan θ＝23. 11.(2018·鄂尔多斯联考)如图，在几何体ABC －A 1B 1C 1中，平面A 1ACC 1⊥底面ABC ，四边形A 1ACC 1是正方形，B 1C 1∥BC ，Q 是A 1B 的中点，且AC ＝BC ＝2B 1C 1，∠ACB ＝2π3. (1)证明：B 1Q ⊥A 1C ；(2)求直线AC 与平面A 1BB 1所成角的正弦值.(1)证明 如图所示，连接AC 1与A 1C 交于M 点，连接MQ .∵四边形A 1ACC 1是正方形，∴M 是AC 1的中点，又Q 是A 1B 的中点，∴MQ ∥BC ，MQ ＝12BC ， 又∵B 1C 1∥BC 且BC ＝2B 1C 1，∴MQ ∥B 1C 1，MQ ＝B 1C 1，∴四边形B 1C 1MQ 是平行四边形，∴B 1Q ∥C 1M ，∵C 1M ⊥A 1C ，∴B 1Q ⊥A 1C .(2)解 ∵平面A 1ACC 1⊥平面ABC ，平面A 1ACC 1∩平面ABC ＝AC ，CC 1⊥AC ，CC 1⊂平面A 1ACC 1， ∴CC 1⊥平面ABC .如图所示，以C 为原点，CB ，CC 1所在直线分别为y 轴和z 轴建立空间直角坐标系， 令AC ＝BC ＝2B 1C 1＝2，则C (0,0,0)，A (3，－1,0)，A 1(3，－1,2)，B (0,2,0)，B 1(0，1,2)，∴CA →＝(3，－1,0)，B 1A 1—→＝(3，－2,0)，B 1B →＝(0,1，－2)，设平面A 1BB 1的法向量为n ＝(x ，y ，z )，则由n ⊥B 1A 1—→，n ⊥B 1B →，可得⎩⎨⎧ 3x －2y ＝0，y －2z ＝0，可令y ＝23，则x ＝4，z ＝3，∴平面A 1BB 1的一个法向量n ＝(4,23，3)，设直线AC 与平面A 1BB 1所成的角为α，则sin α＝|n ·CA →||n |·|CA →|＝23231＝9331. 12.(2019·盘锦模拟)如图，在四棱锥P －ABCD 中，侧面PAD ⊥底面ABCD ，底面ABCD 为直角梯形，其中AB ∥CD ，∠CDA ＝90°，CD ＝2AB ＝2，AD ＝3，PA ＝5，PD ＝22，点E 在棱AD 上且AE ＝1，点F 为棱PD 的中点.(1)证明：平面BEF ⊥平面PEC ；(2)求二面角A －BF －C 的余弦值.(1)证明 在Rt△ABE 中，由AB ＝AE ＝1，得∠AEB ＝45°，同理在Rt△CDE 中，由CD ＝DE ＝2，得∠DEC ＝45°，所以∠BEC ＝90°，即BE ⊥EC .在△PAD 中，cos∠PAD ＝PA 2＋AD 2－PD 22PA ·AD ＝5＋9－82×3×5＝55， 在△PAE 中，PE 2＝PA 2＋AE 2－2PA ·AE ·cos∠PAE ＝5＋1－2×5×1×55＝4， 所以PE 2＋AE 2＝PA 2，即PE ⊥AD .又平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，PE ⊂平面PAD ，所以PE ⊥平面ABCD ，所以PE ⊥BE .又因为CE ∩PE ＝E ，CE ，PE ⊂平面PEC ，所以BE ⊥平面PEC ，所以平面BEF ⊥平面PEC .(2)解 由(1)知EB ，EC ，EP 两两垂直，故以E 为坐标原点，以射线EB ，EC ，EP 分别为x 轴、y 轴、z 轴的正半轴建立如图所示的空间直角坐标系，则 B (2，0,0)，C (0,22，0)，P (0,0,2)，A ⎝⎛⎭⎪⎫22，－22，0，D (－2，2，0)，F ⎝ ⎛⎭⎪⎫－22，22，1， AB →＝⎝ ⎛⎭⎪⎫22，22，0，BF →＝⎝ ⎛⎭⎪⎫－322，22，1， BC →＝(－2，22，0)，设平面ABF 的法向量为m ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧m ·AB →＝22x 1＋22y 1＝0，m ·BF →＝－322x 1＋22y 1＋z 1＝0， 不妨设x 1＝1，则m ＝(1，－1,22)，设平面BFC 的法向量为n ＝(x 2，y 2，z 2)，则⎩⎨⎧ n ·BC →＝－2x 2＋22y 2＝0，n ·BF →＝－322x 2＋22y 2＋z 2＝0， 不妨设y 2＝2，则n ＝(4,2,52)，记二面角A －BF －C 为θ(由图知应为钝角)，则cos θ＝－|m ·n ||m |·|n |＝－|4－2＋20|10·70＝－11735， 故二面角A －BF －C 的余弦值为－11735. 13.如图，在四棱锥S －ABCD 中，SA ⊥平面ABCD ，底面ABCD 为直角梯形，AD ∥BC ，∠BAD ＝90°，且AB ＝4，SA ＝3.E ，F 分别为线段BC ，SB 上的一点(端点除外)，满足SF BF ＝CE BE＝λ，当实数λ的值为________时，∠AFE 为直角.答案 916解析 因为SA ⊥平面ABCD ，∠BAD ＝90°，以A 为坐标原点，AD ，AB ，AS 所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系Axyz .∵AB ＝4，SA ＝3，∴B (0,4,0)，S (0,0,3).设BC ＝m ，则C (m ,4,0)，∵SF BF ＝CE BE ＝λ，∴SF →＝λFB →.∴AF →－AS →＝λ(AB →－AF →).∴AF →＝11＋λ(AS →＋λAB →)＝11＋λ(0,4λ，3)， ∴F ⎝ ⎛⎭⎪⎫0，4λ1＋λ，31＋λ. 同理可得E ⎝ ⎛⎭⎪⎫m 1＋λ，4，0， ∴FE →＝⎝ ⎛⎭⎪⎫m 1＋λ，41＋λ，－31＋λ. ∵FA →＝⎝ ⎛⎭⎪⎫0，－4λ1＋λ，－31＋λ，要使∠AFE 为直角， 即FA →·FE →＝0，则0·m1＋λ＋－4λ1＋λ·41＋λ＋－31＋λ·－31＋λ＝0， ∴16λ＝9，解得λ＝916. 14.(2018·满洲里模拟)如图，已知直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝AC ＝1，AB ⊥AC ，M ，N ，Q 分别是CC 1，BC ，AC 的中点，点P 在直线A 1B 1上运动，且A 1P →＝λA 1B 1—→(λ∈[0,1]).(1)证明：无论λ取何值，总有AM ⊥平面PNQ ；(2)是否存在点P ，使得平面PMN 与平面ABC 的夹角为60°？若存在，试确定点P 的位置，若不存在，请说明理由.(1)证明 连接A 1Q .∵AA 1＝AC ＝1，M ，Q 分别是CC 1，AC 的中点，∴Rt△AA 1Q ≌Rt△CAM ，∴∠MAC ＝∠QA 1A ，∴∠MAC ＋∠AQA 1＝∠QA 1A ＋∠AQA 1＝90°， ∴AM ⊥A 1Q .∵N ，Q 分别是BC ，AC 的中点，∴NQ ∥AB . 又AB ⊥AC ，∴NQ ⊥AC .在直三棱柱ABC －A 1B 1C 1中，AA 1⊥底面ABC ， ∴NQ ⊥AA 1.又AC ∩AA 1＝A ，AC ，AA 1⊂平面ACC 1A 1， ∴NQ ⊥平面ACC 1A 1，∴NQ ⊥AM .由NQ ∥AB 和AB ∥A 1B 1可得NQ ∥A 1B 1， ∴N ，Q ，A 1，P 四点共面，∴A 1Q ⊂平面PNQ .∵NQ ∩A 1Q ＝Q ，NQ ，A 1Q ⊂平面PNQ ， ∴AM ⊥平面PNQ ，∴无论λ取何值，总有AM ⊥平面PNQ .(2)解 如图，以A 为坐标原点，AB ，AC ，AA 1所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，则A 1(0,0,1)，B 1(1,0,1)，M ⎝⎛⎭⎪⎫0，1，12，N ⎝ ⎛⎭⎪⎫12，12，0， Q ⎝ ⎛⎭⎪⎫0，12，0，NM →＝⎝ ⎛⎭⎪⎫－12，12，12，A 1B 1→＝(1,0,0). 由A 1P →＝λA 1B 1→＝λ(1,0,0)＝(λ，0,0)， 可得点P (λ，0,1)，∴PN →＝⎝ ⎛⎭⎪⎫12－λ，12，－1. 设n ＝(x ，y ，z )是平面PMN 的法向量，则⎩⎪⎨⎪⎧ n ·NM →＝0，n ·PN →＝0，即⎩⎪⎨⎪⎧ －12x ＋12y ＋12z ＝0，⎝ ⎛⎭⎪⎫12－λx ＋12y －z ＝0，得⎩⎪⎨⎪⎧ y ＝1＋2λ3x ，z ＝2－2λ3x ，令x ＝3，得y ＝1＋2λ，z ＝2－2λ，∴n ＝(3,1＋2λ，2－2λ)是平面PMN 的一个法向量.取平面ABC 的一个法向量为m ＝(0,0,1).假设存在符合条件的点P ，则|cos 〈m ，n 〉|＝|2－2λ|9＋(1＋2λ)2＋(2－2λ)2＝12， 化简得4λ2－14λ＋1＝0，解得λ＝7－354或λ＝7＋354(舍去). 综上，存在点P ，且当A 1P ＝7－354时， 满足平面PMN 与平面ABC 的夹角为60°.15.在四棱锥P －ABCD 中，AB →＝(4，－2,3)，AD →＝(－4,1,0)，AP →＝(－6,2，－8)，则这个四棱锥的高h 等于( )A.1B.2C.13D.26 答案 B解析 设平面ABCD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ⊥AB →，n ⊥AD →，即⎩⎪⎨⎪⎧ 4x －2y ＋3z ＝0，－4x ＋y ＝0，令y ＝4，则n ＝⎝⎛⎭⎪⎫1，4，43， 则cos 〈n ，AP →〉＝n ·AP →|n ||AP →|＝－6＋8－323133×226＝－2626， ∴h ＝2626×226＝2. 16.如图所示，在梯形ABCD 中，AB ∥CD ，∠BCD ＝120°，四边形ACFE 为矩形，且CF ⊥平面ABCD ，AD ＝CD ＝BC ＝CF .(1)求证：EF ⊥平面BCF ；(2)点M 在线段EF 上运动，当点M 在什么位置时，平面MAB 与平面FCB 所成的锐二面角最大，并求此时二面角的余弦值.(1)证明 设AD ＝CD ＝BC ＝1，∵AB ∥CD ，∠BCD ＝120°，∴AB ＝2，∴AC 2＝AB 2＋BC 2－2AB ·BC ·cos60°＝3，∴AB 2＝AC 2＋BC 2，则BC ⊥AC .∵CF ⊥平面ABCD ，AC ⊂平面ABCD ，∴AC ⊥CF ，而CF ∩BC ＝C ，CF ，BC ⊂平面BCF ，∴AC ⊥平面BCF .∵EF ∥AC ，∴EF ⊥平面BCF .(2)解 以C 为坐标原点，分别以直线CA ，CB ，CF 为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系，设FM ＝λ(0≤λ≤3)，则C (0,0,0)，A (3，0,0)，B (0，1,0)，M (λ，0,1)，∴AB →＝(－3，1,0)，BM →＝(λ，－1,1).设n ＝(x ，y ，z )为平面MAB 的法向量，由⎩⎪⎨⎪⎧ n ·AB →＝0，n ·BM →＝0，得⎩⎨⎧ －3x ＋y ＝0，λx －y ＋z ＝0，取x ＝1，则n ＝(1，3，3－λ).易知m ＝(1,0,0)是平面FCB 的一个法向量，∴cos〈n ，m 〉＝n ·m |n ||m |＝11＋3＋(3－λ)2×1＝1(λ－3)2＋4. ∵0≤λ≤3，∴当λ＝0时，cos 〈n ，m 〉取得最小值77， ∴当点M 与点F 重合时，平面MAB 与平面FCB 所成的锐二面角最大，此时二面角的余弦值为77.。

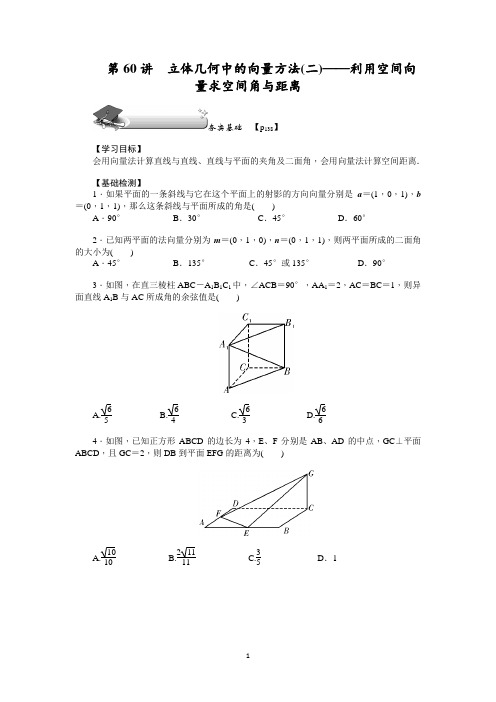
第60讲立体几何中的向量方法(二)——利用空间向量求空间角与距离夯实基础【p138】【学习目标】会用向量法计算直线与直线、直线与平面的夹角及二面角，会用向量法计算空间距离．【基础检测】1．如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a＝(1，0，1)，b ＝(0，1，1)，那么这条斜线与平面所成的角是()A．90°B．30°C．45°D．60°2．已知两平面的法向量分别为m＝(0，1，0)，n＝(0，1，1)，则两平面所成的二面角的大小为()A．45°B．135°C．45°或135°D．90°3．如图，在直三棱柱ABC－A1B1C1中，∠ACB＝90°，AA1＝2，AC＝BC＝1，则异面直线A1B与AC所成角的余弦值是()A.65 B.64 C.63 D.664．如图，已知正方形ABCD的边长为4，E、F分别是AB、AD的中点，GC⊥平面ABCD，且GC＝2，则DB到平面EFG的距离为()A.1010 B.21111 C.35D．1【知识要点】1．空间角和空间距离的向量表示 (1)直线与平面所成的角直线a 的方向向量和平面α的法向量分别为m ，n ，则直线a 与平面α所成的角θ等于向量m ，n 所成的锐角的余角(若所成角为钝角，则取其补角的余角)，即__sin__θ＝|m·n||m|·|n|__．特例：若m ⊥n ，则__a ∥α__或__a α__．若m ∥n ，则a ⊥α.(2)二面角的平面角设二面角α－l －β的两个半平面α和β的法向量分别为m ，n ，二面角α－l －β的大小为θ，则二面角的平面角与两法向量所成的角相等或互补．当二面角为锐角时，cos θ＝|cos〈m ，n 〉|＝|m·n||m||n|；当二面角为钝角时，__cos__θ＝－|cos__〈m ，n 〉|＝－|m·n||m||n|__．特例：若m ∥n ，则__α∥β__，若m ⊥n ，则__α⊥β__．2．点到平面的距离设平面α的法向量为__n __，P 是平面α外一点，Q 是平面α内任一点，则点P 到平面α的距离d 等于PQ →在法向量n 上的投影的绝对值，即d ＝__|n ·PQ →||n|__．典例剖析【p138】考点1求异面直线所成的角例1如图，四边形ABCD为菱形，∠ABC＝120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE＝2DF，AE⊥EC.(1)证明：平面AEC⊥平面AFC；(2)求直线AE与直线CF所成角的余弦值．考点2求直线与平面所成的角例2四棱锥S－ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD.已知∠ABC＝45°，AB＝2，BC＝22，SA＝SB＝ 3.(1)证明：SA⊥BC；(2)求直线SD与平面SAB所成角的正弦值．考点3求二面角例3如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD ＝DC，E是PC的中点，作EF⊥PB交PB于点F.(1)求证：PA∥平面EDB；(2)求二面角F－DE－B的正弦值．考点4求空间距离例4如图，在正四棱柱ABCD－A1B1C1D1中，已知AB＝2，AA1＝5，E，F分别为D1D，B1B上的点，且DE＝B1F＝1.(1)求证：BE⊥平面ACF；(2)求点E到平面ACF的距离；(3)求异面直线AF与BE之间的距离．方法总结【p139】1．利用向量解决几何问题具有快捷、有效的特征．一般方法如下：先将原问题转化为等价的向量问题，即将已知条件的角转化为向量的夹角，线段长度转化为向量的模，并用已知向量表示出未知向量(注意量的集中)，然后利用向量运算解决该向量问题，从而原问题得解．2．利用向量坐标解决立体几何问题的关键在于找准位置，建立恰当、正确的空间坐标系．表示出已知点(或向量)的坐标．难点是通过向量的坐标运算，实现几何问题的代数解法．3．向量法求空间角与距离一般在易建系而又不易直接作出所求角与距离时使用，事半功倍．走进高考【p139】1．(2017·天津)如图，在三棱锥P－ABC中，PA⊥底面ABC，∠BAC＝90°. 点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA＝AC＝4，AB＝2.(1)求证：MN∥平面BDE；(2)求二面角C－EM－N的正弦值；(3)已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为721，求线段AH的长．2．(2017·全国卷Ⅲ)如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD＝∠CBD，AB＝BD.(1)证明：平面ACD⊥平面ABC；(2)过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D－AE－C的余弦值．考 点 集 训 【p 260】A 组题1．长方体ABCD －A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝1，E 为CC 1的中点，则异面直线BC 1与AE 所成角的余弦值为( )A.1010B.3010C.21510D.310102．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )A ．30°B ．60°C ．120°D ．150°3．如图，在三棱锥A －BCD 中，AB ⊥平面BCD ，∠DBC ＝90°，BC ＝BD ＝2，AB ＝1，则BC 和平面ACD 所成角的正弦值为________．4．二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB.已知AB ＝4，AC ＝6，BD ＝8，CD ＝217，则该二面角的大小为________．5．P 是二面角α－AB －β棱上的一点，分别在平面α、β上引射线PM 、PN ，如果∠BPM ＝∠BPN ＝45°，∠MPN ＝60°，那么二面角α－AB －β的大小为________．6．如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E ，F 且EF ＝22，则下列结论中正确的是__________．(填写序号)①AC ⊥BE ；②EF ∥平面ABCD ；③三棱锥A －BEF 的体积为定值； ④异面直线AE ，BF 所成的角为定值．B组题1．已知正方体ABCD－A1B1C1D1的棱长是1，则直线DA1与AC间的距离为________．2．如图，在四棱锥S－ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD＝90°，且AB＝4，SA＝3.E，F分别为线段BC，SB上的点(端点除外)，满足SF BF＝CEBE＝λ，当实数λ的值为________时，∠AFE为直角．3．如图，在直三棱柱ABC－A1B1C1中，AB＝4，AC＝BC＝3，D为AB的中点．(1)求点C到平面A1ABB1的距离；(2)若AB1⊥A1C，求二面角A1－CD－C1的平面角的余弦值．4．在如图所示的几何体中，四边形ABCD为矩形，平面ABEF⊥平面ABCD，EF∥AB，∠BAF＝90°，AD＝2，AB＝AF＝2EF＝1，点P在棱DF上．(1)若P是DF的中点，求异面直线BE与CP所成角的余弦值；(2)若二面角D－AP－C的余弦值为63，求PF的长度．第60讲 立体几何中的向量方法(二)——利用空间向量求空间角与距离夯实基础 【p 138】【学习目标】会用向量法计算直线与直线、直线与平面的夹角及二面角，会用向量法计算空间距离． 【基础检测】1．如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a ＝(1，0，1)，b ＝(0，1，1)，那么这条斜线与平面所成的角是( )A ．90°B ．30°C ．45°D ．60° 【答案】D2．已知两平面的法向量分别为m ＝(0，1，0)，n ＝(0，1，1)，则两平面所成的二面角的大小为( )A ．45°B ．135°C ．45°或135°D ．90° 【答案】C3．如图，在直三棱柱ABC －A 1B 1C 1中，∠ACB ＝90°，AA 1＝2，AC ＝BC ＝1，则异面直线A 1B 与AC 所成角的余弦值是( )A.65 B.64 C.63 D.66【解析】以C 为坐标原点，CA 、CB 、CC 1所在直线分别为x 、y 、z 轴建立空间直角坐标系，则A 1(1，0，2)，B(0，1，0)，A(1，0，0)，C(0，0，0)，则A 1B →＝(－1，1，－2)，AC →＝(－1，0，0)，cos 〈A 1B →，AC →〉＝AC →·A 1B →|AC →|·|A 1B →|＝11＋1＋4＝66.【答案】D4．如图，已知正方形ABCD 的边长为4，E 、F 分别是AB 、AD 的中点，GC ⊥平面ABCD ，且GC ＝2，则DB 到平面EFG 的距离为( )A.1010 B.21111 C.35 D ．1 【解析】以C 为原点，CD 为x 轴，CB 为y 轴，CG 为z 轴建立空间直角坐标系，∴F(4，2，0)，E(2，4，0)，G(0，0，2)，∴FE →＝(－2，2，0)，EG →＝(－2，－4，2)，∴平面EFG 的一个法向量为m ＝(1，1，3)，∵BD ∥平面EFG ，∴直线BD 到平面EFG 的距离即点B到平面EFG 的距离，∴d ＝|BE →·m ||m |＝21111.【答案】B 【知识要点】1．空间角和空间距离的向量表示 (1)直线与平面所成的角直线a 的方向向量和平面α的法向量分别为m ，n ，则直线a 与平面α所成的角θ等于向量m ，n 所成的锐角的余角(若所成角为钝角，则取其补角的余角)，即__sin__θ＝|m·n||m|·|n|__．特例：若m ⊥n ，则__a ∥α__或__a α__．若m ∥n ，则a ⊥α. (2)二面角的平面角设二面角α－l －β的两个半平面α和β的法向量分别为m ，n ，二面角α－l －β的大小为θ，则二面角的平面角与两法向量所成的角相等或互补．当二面角为锐角时，cos θ＝|cos〈m ，n 〉|＝|m·n||m||n|；当二面角为钝角时，__cos__θ＝－|cos__〈m ，n 〉|＝－|m·n||m||n|__．特例：若m ∥n ，则__α∥β__，若m ⊥n ，则__α⊥β__． 2．点到平面的距离设平面α的法向量为__n __，P 是平面α外一点，Q 是平面α内任一点，则点P 到平面α的距离d 等于PQ →在法向量n 上的投影的绝对值，即d ＝__|n ·PQ →||n|__．典 例 剖 析 【p 138】考点1 求异面直线所成的角例1如图，四边形ABCD 为菱形，∠ABC ＝120°，E ，F 是平面ABCD同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE ＝2DF ，AE ⊥EC. (1)证明：平面AEC ⊥平面AFC ；(2)求直线AE 与直线CF 所成角的余弦值．【解析】(1)证明：如图，连接BD ，设BD ∩AC 于点G ，连接EG ，FG ，EF.在菱形ABCD 中，不妨设GB ＝1.由∠ABC ＝120°，可得AG ＝GC ＝ 3.由BE ⊥平面ABCD ，AB ＝BC ，可知AE ＝EC. 又AE ⊥EC ，所以EG ＝3，且EG ⊥AC.在Rt △EBG 中，可得BE ＝2，故DF ＝22.在Rt △FDG 中，可得FG ＝62.在直角梯形BDFE 中，由BD ＝2，BE ＝2，DF ＝22，可得EF ＝322.从而EG 2＋FG 2＝EF 2，所以EG ⊥FG . 又AC ∩FG ＝G ，所以EG ⊥平面AFC.因为EG 平面AEC ，所以平面AEC ⊥平面AFC.(2)以G 为坐标原点，分别以GB →，GC →的方向为x 轴，y 轴正方向，|GB →|为单位长度，建立空间直角坐标系G －xyz.由(1)可得A (0，－3，0)，E (1，0，2)，F ⎝⎛⎭⎫－1，0，22，C (0，3，0)， 所以AE →＝(1，3，2)，CF →＝⎝⎛⎭⎫－1，－3，22.故cos 〈AE →，CF →〉＝AE →·CF →|AE →||CF →|＝－33.所以直线AE 与直线CF 所成角的余弦值为33.考点2 求直线与平面所成的角例2四棱锥S －ABCD 中，底面ABCD 为平行四边形，侧面SBC ⊥底面ABCD.已知∠ABC ＝45°，AB ＝2，BC ＝22，SA ＝SB ＝ 3.(1)证明：SA ⊥BC ；(2)求直线SD 与平面SAB 所成角的正弦值． 【解析】(1)作SO ⊥BC ，垂足为O ，连结AO ， 由侧面SBC ⊥底面ABCD ， 得SO ⊥平面ABCD.因为SA ＝SB ，所以AO ＝BO ，又∠ABC ＝45°，所以△AOB 为等腰直角三角形，AO ⊥OB ，如图，以O 为坐标原点，OA →为x 轴正向，OB →为y 轴正向，OS →为z 轴正向，建立空间直角坐标系O －xyz.A (2，0，0)，B (0，2，0)，C (0，－2，0)，S (0，0，1)，D (2，－22，0)， SA →＝(2，0，－1)，CB →＝(0，22，0)，SA →·CB →＝0， 所以SA ⊥BC.(2)设n ＝(x ，y ，z)为平面SAB 的法向量，则⎩⎪⎨⎪⎧n ·AB →＝0，n ·AS →＝0，得⎩⎨⎧－2x ＋2y ＝0，－2x ＋z ＝0，所以⎩⎨⎧x ＝y ，z ＝2x ，令x ＝1，得n ＝(1，1，2)， |cos 〈n ，SD →〉|＝⎪⎪⎪⎪⎪⎪n ·SD →|n ||SD →|＝2211， SD 与平面SAB 所成的角与SD →与n 所成的角互余．所以，直线SD 与平面SAB 所成角的正弦值为2211.考点3 求二面角例3如图，在四棱锥P －ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD ＝DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F.(1)求证：PA ∥平面EDB ；(2)求二面角F －DE －B 的正弦值．【解析】如图，建立空间直角坐标系，点D 为坐标原点，设DC ＝1.(1)证明：连结AC ，AC 交BD 于点G ，连结EG .依题意得A (1，0，0)，P (0，0，1)，E ⎝⎛⎭⎫0，12，12. 因为底面ABCD 是正方形，所以点G 是此正方形的中心，故点G 的坐标为⎝⎛⎭⎫12，12，0，且PA →＝(1，0，－1)， EG →＝⎝⎛⎭⎫12，0，－12. 所以PA →＝2EG →，即PA ∥EG ，而EG 平面EDB ，且PA 平面EDB ， 因此PA ∥平面EDB.(2)B (1，1，0)，PB →＝(1，1，－1)，又DE →＝⎝⎛⎭⎫0，12，12， 故PB →·DE →＝0，所以PB ⊥DE.由已知EF ⊥PB ，且EF ∩DE ＝E ，所以PB ⊥平面EFD.所以平面EFD 的一个法向量为PB →＝(1，1，－1)．DE →＝⎝⎛⎭⎫0，12，12，DB →＝(1，1，0)， 不妨设平面DEB 的法向量为a ＝(x ，y ，z)，则⎩⎪⎨⎪⎧a ·DE →＝12（y ＋z ）＝0，a ·DB →＝x ＋y ＝0，不妨取x ＝1，则y ＝－1，z ＝1，即a ＝(1，－1，1)， 设二面角F －DE －B 的平面角为θ，则cos θ＝a ·PB →|a ||PB →|＝－13，因为θ∈[0，π]，所以sin θ＝223.即二面角F －DE －B 的正弦值大小为223.考点4 求空间距离例4如图，在正四棱柱ABCD －A 1B 1C 1D 1中，已知AB ＝2，AA 1＝5，E ，F 分别为D 1D ，B 1B 上的点，且DE ＝B 1F ＝1.(1)求证：BE ⊥平面ACF ；(2)求点E 到平面ACF 的距离；(3)求异面直线AF 与BE 之间的距离．【解析】(1)以D 为原点，分别以DA →，DC →，DD 1→的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，则D (0，0，0)，A (2，0，0)，B (2，2，0)，C (0，2，0)，D 1(0，0，5)，E (0，0，1)，F (2，2，4)．于是AC →＝(－2，2，0)，AF →＝(0，2，4)，BE →＝(－2，－2，1)． ∵BE →·AC →＝0，BE →·AF →＝0，∴BE ⊥AC ，BE ⊥AF ，且AC ∩AF ＝A ，∴BE ⊥平面ACF.(2)由(1)知，BE →为平面ACF 的一个法向量，∴向量AE →在BE →上的射影的大小即为E 到平面ACF 的距离，设为d 1，于是d 1＝|AE →|·|cos 〈AE →，BE →〉|＝|AE →|·|AE →·BE →||AE →|·|BE →|＝|（－2，0，1）·（－2，－2，1）|（－2）2＋（－2）2＋12＝53，故点E 到平面ACF 的距离为53.(3)由(1)知AF →＝(0，2，4)，BE →＝(－2，－2，1)， 设AF 与BE 的公垂线的方向向量d ＝(x ，y ，z)，则⎩⎪⎨⎪⎧AF →·d ＝2y ＋4z ＝0，BE →·d ＝－2x －2y ＋z ＝0，得⎩⎪⎨⎪⎧y ＝－2z ，x ＝52z ，取z ＝2，得d ＝(5，－4，2)． 又AB →＝(0，2，0)，设AF 与BE 之间的距离为d 2，则d 2＝|d ·AB →||d |＝|5×0＋（－4）×2＋2×0|35＝8515.【点评】利用向量法求距离关键是应用一个向量在另一个向量上的投影．方 法 总 结 【p 139】1．利用向量解决几何问题具有快捷、有效的特征．一般方法如下：先将原问题转化为等价的向量问题，即将已知条件的角转化为向量的夹角，线段长度转化为向量的模，并用已知向量表示出未知向量(注意量的集中)，然后利用向量运算解决该向量问题，从而原问题得解．2．利用向量坐标解决立体几何问题的关键在于找准位置，建立恰当、正确的空间坐标系．表示出已知点(或向量)的坐标．难点是通过向量的坐标运算，实现几何问题的代数解法．3．向量法求空间角与距离一般在易建系而又不易直接作出所求角与距离时使用，事半功倍．走 进 高 考 【p 139】1．(2017·天津)如图，在三棱锥P －ABC 中，PA ⊥底面ABC ，∠BAC ＝90°. 点D ，E ，N 分别为棱PA ，PC ，BC 的中点，M 是线段AD 的中点，PA ＝AC ＝4，AB ＝2.(1)求证：MN ∥平面BDE ；(2)求二面角C －EM －N 的正弦值；(3)已知点H 在棱PA 上，且直线NH 与直线BE 所成角的余弦值为721，求线段AH 的长． 【解析】如图，以A 为原点，分别以AB →，AC →，AP →方向为x 轴、y 轴、z 轴正方向建立空间直角坐标系．依题意可得A(0，0，0)，B(2，0，0)，C(0，4，0)，P(0，0，4)，D(0，0，2)，E(0，2，2)，M(0，0，1)，N(1，2，0)．(1)DE →＝(0，2，0)，DB →＝(2，0，－2)． 设n ＝(x ，y ，z)为平面BDE 的法向量，则⎩⎪⎨⎪⎧n ·DE →＝0，n ·DB →＝0，即⎩⎪⎨⎪⎧2y ＝0，2x －2z ＝0.不妨设z ＝1，可得n ＝(1，0，1)． 又MN →＝(1，2，－1)，可得MN →·n ＝0.因为MN 平面BDE ，所以MN ∥平面BDE.(2)易知n 1＝(1，0，0)为平面CEM 的一个法向量．设n 2＝(x 1，y 1，z 1)为平面EMN 的法向量，则⎩⎪⎨⎪⎧n 2·EM →＝0，n 2·MN →＝0.因为EM →＝(0，－2，－1)，MN →＝(1，2，－1)，所以⎩⎪⎨⎪⎧－2y 1－z 1＝0.x 1＋2y 1－z 1＝0.不妨设y 1＝1，可得n 2＝(－4，1，－2)．因此有cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝－421，于是sin 〈n 1，n 2〉＝10521.所以，二面角C －EM －N 的正弦值为10521.(3)依题意，设AH ＝h(0≤h ≤4)，则H(0，0，h)，进而可得NH →＝(－1，－2，h)，BE →＝(－2，2，2)．由已知，得|cos 〈NH →·BE →〉|＝|NH →·BE →||NH →||BE →|＝|2h －2|h 2＋5×23＝721，整理得10h 2－21h ＋8＝0，解得h ＝85，或h ＝12.2．(2017·全国卷Ⅲ)如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD ＝∠CBD ，AB ＝BD.(1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D －AE －C 的余弦值．【解析】(1)由题设可得，△ABD ≌△DBC ，从而AD ＝DC. 又△ACD 是直角三角形，所以∠ADC ＝90°.取AC 的中点O ，连接DO ，BO ，则DO ⊥AC ，DO ＝AO. 又由于△ABC 是正三角形，故BO ⊥AC.所以∠DOB 为二面角D －AC －B 的平面角． 在Rt △AOB 中，BO 2＋AO 2＝AB 2. 又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°. 所以平面ACD ⊥平面ABC.(2)由题设及(1)知，OA ，OB ，OD 两两垂直. 以O 为坐标原点，OA →的方向为x 轴正方向，|OA →|为单位长，建立如图所示的空间直角坐标系O －xyz ，则A(1，0，0)，B(0，3，0)，C(－1，0，0)，D(0，0，1)．由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得E ⎝⎛⎭⎫0，32，12. 故AD →＝(－1，0，1)，AC →＝(－2，0，0)，AE →＝⎝⎛⎭⎫－1，32，12.设n ＝(x ，y ，z)是平面DAE 的法向量，则⎩⎪⎨⎪⎧n ·AD →＝0，n ·AE →＝0.即⎩⎪⎨⎪⎧－x ＋z ＝0，－x ＋32y ＋12z ＝0.可取n ＝⎝⎛⎭⎫1，33，1.设m 是平面AEC 的法向量，则⎩⎪⎨⎪⎧m ·AC →＝0，m ·AE →＝0.同理可取m ＝()0，－1，3.则cos 〈n ，m 〉＝n·m|n||m|＝77.所以二面角D －AE －C 的余弦值为77. 考 点 集 训 【p 260】A 组题1．长方体ABCD －A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝1，E 为CC 1的中点，则异面直线BC 1与AE 所成角的余弦值为( )A.1010B.3010C.21510D.31010 【解析】建立坐标系如图所示．则A(1，0，0)，E(0，2，1)，B(1，2，0)，C 1(0，2，2)，BC 1→＝(－1，0，2)，AE →＝(－1，2，1)．cos 〈BC 1→，AE →〉＝AE →·BC 1→|AE →|·|BC 1→|＝3010.所以异面直线BC 1与AE 所成角的余弦值为3010.【答案】B2．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为( )A ．30°B ．60°C ．120°D ．150°【解析】设l 与α所成角为θ，∵cos 〈m ，n 〉＝－12，∴sin θ＝|cos 〈m ，n 〉|＝12，∵0°≤θ≤90°，∴θ＝30°.故选A.【答案】A3．如图，在三棱锥A －BCD 中，AB ⊥平面BCD ，∠DBC ＝90°，BC ＝BD ＝2，AB ＝1，则BC 和平面ACD 所成角的正弦值为________．【解析】以B 为原点，分别以射线BC ，BD ，BA 为x ，y ，z 轴的正半轴建立空间直角坐标系，∵BC ＝BD ＝2，AB ＝1，∴B(0，0，0)，A(0，0，1)，C(2，0，0)，D(0，2，0)， ∴CB →＝(－2，0，0)，CA →＝(－2，0，1)，CD →＝(－2，2，0)， 设平面ACD 的法向量为n ＝(x ，y ，z)．则⎩⎪⎨⎪⎧n ·CA →＝0，n ·CD →＝0，∴⎩⎨⎧－2x ＋z ＝0，－2x ＋2y ＝0，∴可取n ＝(1，1，2)，设直线BC 和平面ACD 所成角为θ，则sin θ＝|cos 〈CB →，n 〉|＝⎪⎪⎪⎪⎪⎪－22×6＝66. 【答案】664．二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB.已知AB ＝4，AC ＝6，BD ＝8，CD ＝217，则该二面角的大小为________．【解析】∵CD →＝CA →＋AB →＋BD →， ∴|CD →|＝（CA →＋AB →＋BD →）2＝36＋16＋64＋2CA →·BD →＝116＋2CA →·BD →＝217. ∴CA →·BD →＝|CA →|·|BD →|·cos 〈CA →，BD →〉＝－24.∴cos 〈CA →，BD →〉＝－12.而二面角与〈CA →，BD →〉互补， ∴所求二面角为60°. 【答案】60° 5．P 是二面角α－AB －β棱上的一点，分别在平面α、β上引射线PM 、PN ，如果∠BPM ＝∠BPN ＝45°，∠MPN ＝60°，那么二面角α－AB －β的大小为________．【解析】不妨设PM ＝a ，PN ＝b ，如图，作ME ⊥AB 于E ，NF ⊥AB 于F ， ∵∠EPM ＝∠FPN ＝45°，∴PE ＝22a ，PF ＝22b ，∴EM →·FN →＝(PM →－PE →)·(PN →－PF →) ＝PM →·PN →－PM →·PF →－PE →·PN →＋PE →·PF →＝abcos 60°－a ×22bcos 45°－22a ×bcos 45°＋22a ×22b＝ab 2－ab 2－ab 2＋ab2＝0， ∴EM →⊥FN →，∴二面角α－AB －β的大小为90°. 【答案】90°6．如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E ，F 且EF ＝22，则下列结论中正确的是__________．(填写序号)①AC ⊥BE ；②EF ∥平面ABCD ；③三棱锥A －BEF 的体积为定值； ④异面直线AE ，BF 所成的角为定值．【解析】∵AC ⊥平面BB 1D 1D ，又BE 平面BB 1D 1D. ∴AC ⊥BE ，故①正确．∵B 1D 1∥平面ABCD ，又E 、F 在直线D 1B 1上运动， ∴EF ∥平面ABCD ，故②正确．③中，由于点B 到直线B 1D 1的距离不变，故△BEF 的面积为定值，又点A 到平面BEF的距离为22，故V A －BEF 为定值，③正确．当点E 在D 1处，点F 为D 1B 1的中点时，建立空间直角坐标系，如图所示，可得A(1，1，0)，B(0，1，0)，E(1，0，1)，F ⎝⎛⎭⎫12，12，1，∴AE →＝(0，－1，1)，BF →＝⎝⎛⎭⎫12，－12，1，∴AE →·BF →＝32. 又|AE →|＝2，|BF →|＝62，∴cos 〈AE →，BF →〉＝AE →·BF →|AE →|·|BF →|＝32.∴此时异面直线AE 与BF 成30°角． 当点E 为D 1B 1的中点，点F 在B 1处时，此时E ⎝⎛⎭⎫12，12，1，F(0，1，1)，∴AE →＝⎝⎛⎭⎫－12，－12，1，BF →＝(0，0，1)， ∴AE →·BF →＝1，|AE →|＝⎝⎛⎭⎫－122＋⎝⎛⎭⎫－122＋12＝62，∴cos 〈AE →，BF →〉＝AE →·BF →|AE →|·|BF →|＝162＝63≠32，故④不正确．【答案】①②③B 组题1．已知正方体ABCD －A 1B 1C 1D 1的棱长是1，则直线DA 1与AC 间的距离为________． 【解析】以A 为原点，分别以射线AB ，AD ，AA 1为x ，y ，z 轴的正半轴建立空间直角坐标系，则A(0，0，0)，C(1，1，0)，D(0，1，0)，A 1(0，0，1)，AC →＝(1，1，0)，DA 1→＝(0，－1，1)， 设MN →＝(x ，y ，z)，MN →⊥AC →，MN →⊥DA 1→，所以x ＋y ＝0，－y ＋z ＝0，令y ＝t ， 则MN →＝(－t ，t ，t)，而另可设M(m ，m ，0)，N(0，a ，b)，MN →＝(－m ，a －m ，b)，则⎩⎨⎧－m ＝－t ，a －m ＝t ，b ＝t ，N(0，2t ，t)，2t ＋t ＝1，t ＝13，|MN →|＝19＋19＋19＝33.【答案】332．如图，在四棱锥S －ABCD 中，SA ⊥平面ABCD ，底面ABCD 为直角梯形，AD ∥BC ，∠BAD ＝90°，且AB ＝4，SA ＝3.E ，F 分别为线段BC ，SB 上的点(端点除外)，满足SF BF ＝CEBE＝λ，当实数λ的值为________时，∠AFE 为直角． 【解析】因为SA ⊥平面ABCD ，∠BAD ＝90°， 故可建立如图所示的空间直角坐标系A －xyz.∵AB ＝4，SA ＝3，∴B(0，4，0)，S(0，0，3)． 设BC ＝m ，则C(m ，4，0)， ∵SF BF ＝CE BE ＝λ，∴SF →＝λFB →. ∴AF →－AS →＝λ(AB →－AF →)．∴AF →＝11＋λ(AS →＋λAB →)＝11＋λ(0，4λ，3)，∴F ⎝ ⎛⎭⎪⎫0，4λ1＋λ，31＋λ. 同理可得E ⎝⎛⎭⎫m1＋λ，4，0，∴FE →＝⎝ ⎛⎭⎪⎫m1＋λ，41＋λ，－31＋λ. ∵FA →＝⎝ ⎛⎭⎪⎫0，－4λ1＋λ，－31＋λ，要使∠AFE 为直角，即FA →·FE →＝0，则0·m1＋λ＋－4λ1＋λ·41＋λ＋－31＋λ·－31＋λ＝0，∴16λ＝9，解得λ＝916.【答案】9163．如图，在直三棱柱ABC －A 1B 1C 1中，AB ＝4，AC ＝BC ＝3，D 为AB 的中点．(1)求点C 到平面A 1ABB 1的距离；(2)若AB 1⊥A 1C ，求二面角A 1－CD －C 1的平面角的余弦值．【解析】(1)由AC ＝BC ，D 为AB 的中点，得CD ⊥AB. 又CD ⊥AA 1，故CD ⊥平面A 1ABB 1，所以点C 到平面A 1ABB 1的距离为CD ＝BC 2－BD 2＝ 5.(2)解法一：如图，取A 1B 1的中点D 1，连接DD 1，则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥平面A 1ABB 1，故CD ⊥A 1D ，CD ⊥DD 1，所以∠A 1DD 1为所求的二面角A 1－CD －C 1的平面角．因为A 1D 为A 1C 在平面A 1ABB 1上的射影，又已知AB 1⊥A 1C ，由三垂线定理的逆定理得AB 1⊥A 1D ，从而∠A 1AB 1，∠A 1DA 都与∠B 1AB 互余，因此∠A 1AB 1＝∠A 1DA ，所以Rt △A 1AD ∽Rt △B 1A 1A ， 因此AA 1AD ＝A 1B 1AA 1，即AA 21＝AD·A 1B 1＝8，得AA 1＝2 2. 从而A 1D ＝AA 21＋AD 2＝2 3.在Rt △A 1DD 1中，cos ∠A 1DD 1＝DD 1A 1D ＝AA 1A 1D ＝63. 解法二：如图，过D 作DD 1∥AA 1交A 1B 1于D 1，在直三棱柱中，易知DB ，DC ，DD 1两两垂直．以D 为原点，射线DB ，DC ，DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D －xyz.设直三棱柱的高为h ，则A(－2，0，0)，A 1(－2，0，h)，B 1(2，0，h)，C(0，5，0)，C 1(0，5，h)，从而AB 1→＝(4，0，h)，A 1C →＝(2，5，－h)．由AB 1→⊥A 1C →，有8－h 2＝0，解得h ＝2 2.故DA 1→＝(－2，0，22)，CC 1→＝(0，0，22)，DC →＝(0，5，0)．设平面A 1CD 的法向量为m ＝(x 1，y 1，z 1)，则m ⊥DC →，m ⊥DA 1→，即⎩⎨⎧5y 1＝0，－2x 1＋22z 1＝0.取z 1＝1，得m ＝(2，0，1)．设平面C 1CD 的法向量为n ＝(x 2，y 2，z 2)，则n ⊥DC →，n ⊥CC 1→，即⎩⎨⎧5y 2＝0，22z 2＝0，取x 2＝1，得n ＝(1，0，0)， 所以cos 〈m ，n 〉＝m ·n |m ||n |＝22＋1·1＝63. 所以二面角A 1－CD －C 1的平面角的余弦值为63. 4．在如图所示的几何体中，四边形ABCD 为矩形，平面ABEF ⊥平面ABCD ，EF ∥AB ，∠BAF ＝90°，AD ＝2，AB ＝AF ＝2EF ＝1，点P 在棱DF 上．(1)若P 是DF 的中点，求异面直线BE 与CP 所成角的余弦值；(2)若二面角D －AP －C 的余弦值为63，求PF 的长度．【解析】(1)因为∠BAF ＝90°，所以AF ⊥AB ，因为平面ABEF ⊥平面ABCD ，且平面ABEF ∩平面ABCD ＝AB ，所以AF ⊥平面ABCD ，因为四边形ABCD 为矩形，所以以A 为坐标原点，AB ，AD ，AF 分别为x ，y ，z 轴，建立如图所示空间直角坐标系A －xyz.所以B(1，0，0)，E ⎝⎛⎭⎫12，0，1，P ⎝⎛⎭⎫0，1，12，C(1，2，0)． 所以BE →＝⎝⎛⎭⎫－12，0，1，CP →＝⎝⎛⎭⎫－1，－1，12， 所以cos 〈BE →，CP →〉＝BE →·CP →|BE →|·|CP →|＝4515， 即异面直线BE 与CP 所成角的余弦值为4515. (2)因为AB ⊥平面ADF ，所以平面APD 的法向量为n 1＝(1，0，0)．设P 点坐标为(0，2－2t ，t)，在平面APC 中，AP →＝(0，2－2t ，t)，AC →＝(1，2，0)，所以平面APC 的法向量为n 2＝⎝⎛⎭⎫－2，1，2t －2t ， 所以，cos 〈n 1，n 2〉＝|n 1·n 2||n 1|·|n 2|＝2（－2）2＋1＋⎝⎛⎭⎫2t －2t 2＝63， 解得t ＝23，或t ＝2(舍)．所以|PF|＝53.。

空间向量求二面角的方法方法一：先作出二面角的平面角，再利用向量的内积公式求解：设∠AOB 是二面角l αβ--的一个平面角,则向量OA 与OB 所成的角就是所求的二面角的大小．例1 正四面体ABCD 中，求相邻两个面所成的二面角．解析：如图1，取BC 边的中点Ｅ,连结AE 、DE ，则AE⊥BC，DE⊥BC，所以∠AED 就是正四面体的两个相邻面ABC 与DBC 所成二面角的平面角,且BC⊥平面ADE ，∴BC⊥AD，∴0EC DA =．设正四面体棱长为1．∵()()ED EA EC CD EC CD DA =+++ =222EC EC CD EC DA CD DA CD ++++ 11121cos120011cos1201424=+⨯⨯⨯++⨯⨯+=． 又在△ABC 与△BCD 中，可求得32ED EA ==, ∴cos ED EAED EA ED EA =，11433322==⨯． 故正四面体的两个相邻面所成的二面角大小为1arccos3．方法二:利用法向量求解:设1n 是平面α的法向量，2n 是平面β的法向量．①若两个平面的二面角如图2所示的示意图,则1n 与2n 之间的夹角θ就是欲求的二面角;②若两个平面的二面角如图3所示的示意图,设1n 与2n 之间的夹角为θ．则两个平面的二面角为πθ-． 例2 如图4，△ABC 是以∠B 为直角的直角三角形,SA⊥平面ABC ，SA=BC=2,AB=4，D 、N 分别是BC 、AB 的中点．求二面角S —ND-A 的余弦值．解析：平面ABC 的法向量是AS ,设平面SND 的法向量为BC AB AS λμ=++n ．∵SA⊥平面ABC ，∴SA⊥BC,SA⊥AB，∴0AS BD =,0AS BN =,0AS BC =，0AS AB = 又AB⊥BC,∴0BC BN =，0AB BD =,0BC NA =． 由()()ND BC AB AS BD BN λμ=++-n 280BC BD AB BN λμλμ=-=+=。

高考理科数学必考——几何证明与利用空间向量求线面角、面
面角
时间过的飞快，距离高考的时间就只剩76天了，同学和老师也越来越紧张了，有些地方欠缺的同学开始寝食难安，老师也赶快奉献点干货来帮助几何证明欠缺的学生。

立体几何其实难度不大，只要你会空间向量，会建系，一切就自然而然水到渠成了。

在这先分析这些立体几何的解题思路。

在立体几何中，第一问一般会让你证明线面平行、线面垂直、面面平行、面面垂直
1、证明线面平行的方法1、平移的方法，找到直线与平面内一条直线平行
2、利用面面平行、证明线面平行
2、证明线面垂直的方法1、证明直线与平面内相交的两直线垂直
3、证明面面平行的方法1、证明一个平面内两相交的直线与另一个平面内两相交的直线互相平行
2、证明平面内两相交的直线分别平行另一个平面
4、证明面面垂直的方法1、先证明一条直线垂直于一个平面，这条直线还在另一个平面内
利用这些方法第一问就可以轻松解决了。

在立体几何第二中，会求线面角、面面角，在第二步中，利用空间向量解决就可以
利用空间向量解决第二问的步骤1、找三垂，建立空间直角坐标系
2、写出各个点的坐标
3、求出直线向量、面的法向量
4、利用夹角公式算出余弦值
下面通过两个例题说明一下这个空间几何。

3.2.3 利用空间向量求空间角、空间距离问题1．空间角及向量求法(1)两异面直线所成的角与两直线的方向向量所成的角相等．( )(2)直线l∥平面α，则直线l到平面α的距离就是直线l上的点到平面α的距离．( )(3)若平面α∥β，则两平面α，β的距离可转化为平面α内某条直线到平面β的距离，也可转化为平面α内某点到平面β的距离．( )答案 (1)× (2)√ (3)√2．做一做(请把正确的答案写在横线上)(1)已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角的大小为________．(2)(教材改编P 111A 组T 11)如图，在正方体ABCD －A 1B 1C 1D 1中，M 是C 1C 的中点，O 是底面ABCD 的中点，P 是A 1B 1上的任意点，则直线BM 与OP 所成的角为________．(3)已知平面α的一个法向量为n ＝(－2，－2,1)，点A (－1,3,0)在平面α内，则点P (－2,1,4)到平面α的距离为________．答案 (1)45°或135° (2)π2 (3)103解析 (2)建立如图所示的空间直角坐标系，设正方体棱长为2 ，则O (1,1,0)，P (2，x,2)，B (2,2,0)，M (0,2,1)，则OP→＝(1，x －1,2)，BM →＝(－2,0,1)．所以OP →·BM →＝0，所以直线BM 与OP 所成角为π2. 探究1 利用空间向量求线线角例1 如图1，已知两个正四棱锥P －ABCD 与Q －ABCD 的高分别为1和2，AB ＝4.求异面直线AQ 与PB 所成角的余弦值．[解] 由题设知，ABCD 是正方形，连接AC ，BD ，交于点O ，则AC ⊥BD .连接PQ ，则PQ 过点O .由正四棱锥的性质知PQ ⊥平面ABCD ，故以O 为坐标原点，以直线CA，DB，QP分别为x轴、y轴、z轴建立空间直角坐标系(如图2)，则P(0,0,1)，A(22，0,0)，Q(0,0，－2)，B(0,22，0)，∴AQ→＝(－22，0，－2)，PB→＝(0,22，－1)．于是cos〈AQ→，PB→〉＝AQ→·PB→|AQ→||PB→|＝39，∴异面直线AQ与PB所成角的余弦值为3 9 .拓展提升两异面直线所成角的求法(1)平移法：即通过平移其中一条(也可两条同时平移)，使它们转化为两条相交直线，然后通过解三角形获解．(2)取定基底法：在一些不适合建立坐标系的题型中，我们经常采用取定基底的方法，这是小技巧．在由公式cos〈a，b〉＝a·b|a||b|求向量a、b的夹角时，关键是求出a·b及|a|与|b|，一般是把a、b用一组基底表示出来，再求有关的量．(3)用坐标法求异面直线的夹角的方法①建立恰当的空间直角坐标系；②找到两条异面直线的方向向量的坐标形式；③利用向量的夹角公式计算两直线的方向向量的夹角；④结合异面直线所成角的范围得到异面直线所成的角．【跟踪训练1】如图，在三棱锥V－ABC中，顶点C在空间直角坐标系的原点处，顶点A，B，V分别在x，y，z轴上，D是线段AB 的中点，且AC ＝BC ＝2，∠VDC ＝θ.当θ＝π3时，求异面直线AC 与VD 所成角的余弦值．解 由于AC ＝BC ＝2，D 是AB 的中点，所以C (0,0,0)，A (2,0,0)，B (0,2,0)，D (1,1,0)．当θ＝π3时，在Rt △VCD 中，CD ＝2，故有V (0,0，6)．所以AC →＝(－2,0,0)，VD →＝(1,1，－6)．所以cos 〈AC →，VD →〉＝AC →·VD→|AC →||VD →|＝－22×22＝－24.所以异面直线AC 与VD 所成角的余弦值为24.探究2 利用空间向量求线面角例2 正三棱柱ABC －A 1B 1C 1的底面边长为a ，侧棱长为2a ，求AC 1与侧面ABB 1A 1所成的角．[解] 建立如下图所示的空间直角坐标系，则A (0,0,0)，B (0，a,0)，A 1(0,0, 2a )，C 1⎝⎛⎭⎪⎪⎫－32a ，a2， 2a ， 取A 1B 1的中点M ，则M ⎝⎛⎭⎪⎫0，a2，2a ，连接AM ，MC 1，有MC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，0，0， AB →＝(0，a,0)，AA1→＝(0,0，2a )．∴MC 1→·AB →＝0，MC 1→·AA 1→＝0， ∴MC 1→⊥AB →，MC1→⊥AA 1→， 即MC 1⊥AB ，MC 1⊥AA 1，又AB ∩AA 1＝A ， ∴MC 1⊥平面ABB 1A 1 .∴∠C 1AM 是AC 1与侧面A 1ABB 1所成的角．由于AC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，a 2，2a ，AM →＝⎝ ⎛⎭⎪⎫0，a 2，2a ，∴AC 1→·AM →＝0＋a 24＋2a 2＝9a 24，|AC 1→|＝3a 24＋a 24＋2a 2＝3a ， |AM →|＝a 24＋2a 2＝32a ， ∴cos 〈AC1→，AM →〉＝9a 243a ×3a 2＝32. ∴〈AC 1→，AM →〉＝30°，即AC 1与侧面ABB 1A 1所成的角为30°. [解法探究] 此题有没有其他解法？解 与原解建立相同的空间直角坐标系，则AB →＝(0，a,0)，AA1→＝(0,0，2a )，AC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，a 2，2a . 设侧面ABB 1A 1的法向量n ＝(λ，x ，y )，∴n ·AB →＝0且n ·AA1→＝0.∴ax ＝0且2ay ＝0.∴x ＝y ＝0.故n ＝(λ，0,0)．∵AC 1→＝⎝ ⎛⎭⎪⎪⎫－32a ，a 2，2a ， ∴cos 〈AC 1→，n 〉＝n ·AC1→|n ||AC 1→|＝－λ2|λ|.∴|cos 〈AC 1→，n 〉|＝12. ∴AC 1与侧面ABB 1A 1所成的角为30°.[条件探究] 此题中增加条件“E ，F ，G 为AB ，AA 1，A 1C 1的中点”，求B 1F 与平面GEF 所成角的正弦值．解 建立如图所示的空间直角坐标系，则B 1(0，a ，2a )，E ⎝ ⎛⎭⎪⎫0，a 2，0，F ⎝ ⎛⎭⎪⎪⎫0，0，22a ，G ⎝⎛⎭⎪⎪⎫－34a ，a 4，2a ， 于是B 1F →＝⎝ ⎛⎭⎪⎪⎫0，－a ，－22a ，EF →＝⎝ ⎛⎭⎪⎪⎫0，－a 2，22a ， EG →＝⎝ ⎛⎭⎪⎪⎫－34a ，－a 4，2a . 设平面GEF 的法向量n ＝(x ，y ，z )，则⎩⎨⎧n ·EF →＝0，n ·EG →＝0，即⎩⎪⎨⎪⎧－a 2y ＋22az ＝0，－34ax －a 4y ＋2az ＝0，所以⎩⎪⎨⎪⎧y ＝2z ，x ＝6z ，令z ＝1，得x ＝6，y ＝2，所以平面GEF 的一个法向量为n ＝(6，2，1)， 所以|cos 〈B 1F →，n 〉|＝|n ·B 1F →||n ||B 1F →|＝⎪⎪⎪⎪⎪⎪⎪⎪－2a －22a 9×a 2＋a 22＝33. 所以B 1F 与平面GEF 所成角的正弦值为33.拓展提升求直线与平面的夹角的方法与步骤思路一：找直线在平面内的射影，充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值)．思路二：用向量法求直线与平面的夹角可利用向量夹角公式或法向量．利用法向量求直线与平面的夹角的基本步骤：(1)建立空间直角坐标系； (2)求直线的方向向量AB →； (3)求平面的法向量n ；(4)计算：设线面角为θ，则sin θ＝|n ·AB→||n ||AB→|.【跟踪训练2】 如图，四棱锥P －ABCD 中，PA ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，PA ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点．(1)证明：MN ∥平面PAB ；(2)求直线AN 与平面PMN 所成角的正弦值．解 (1)证明：由已知得AM ＝23AD ＝2.取BP 的中点T ，连接AT ，TN .由N 为PC 的中点知TN ∥BC ，TN ＝12BC ＝2.又AD ∥BC ，故TN 綊AM ，四边形AMNT 为平行四边形，于是MN ∥AT .因为AT ⊂平面PAB ，MN ⊄平面PAB ，所以MN ∥平面PAB .(2)取BC 的中点E ，连接AE .由AB ＝AC 得AE ⊥BC ，从而AE ⊥AD ，且AE ＝AB 2－BE 2＝AB2－⎝ ⎛⎭⎪⎫BC 22＝ 5.以A 为坐标原点，AE →的方向为x 轴正方向，建立如图所示的空间直角坐标系Axyz .由题意知，P (0,0,4)，M (0,2,0)，C (5，2,0)，N ⎝⎛⎭⎪⎪⎫52，1，2， PM →＝(0,2，－4)，PN →＝⎝ ⎛⎭⎪⎪⎫52，1，－2，AN →＝⎝ ⎛⎭⎪⎪⎫52，1，2. 设n ＝(x ，y ，z )为平面PMN 的法向量，则⎩⎨⎧n ·PM →＝0，n ·PN →＝0，即⎩⎪⎨⎪⎧2y －4z ＝0，52x ＋y －2z ＝0，可取n ＝(0,2,1)．于是|cos 〈n ，AN →〉|＝|n ·AN →||n ||AN →|＝8525，则直线AN 与平面PMN所成角的正弦值为8525.探究3 利用空间向量求二面角例3 如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF ＝2FD ，∠AFD ＝90°，且二面角D －AF －E 与二面角C －BE －F 都是60°.(1)证明：平面ABEF⊥平面EFDC；(2)求二面角E－BC－A的余弦值．[解] (1)证明：由已知可得AF⊥DF，AF⊥FE，所以AF⊥平面EFDC.又AF⊂平面ABEF，故平面ABEF⊥平面EFDC.(2)过D作DG⊥EF，垂足为G，由(1)知DG⊥平面ABEF.以G为坐标原点，GF→的方向为x轴正方向，|GF→|为单位长，建立如图所示的空间直角坐标系Gxyz.由(1)知∠DFE为二面角D－AF－E的平面角，故∠DFE＝60°，则DF＝2，DG＝3，可得A(1,4,0)，B(－3,4,0)，E(－3,0,0)，D(0,0，3)．由已知，AB∥EF，AB⊄平面EFDC，EF⊂平面EFDC，所以AB∥平面EFDC.又平面ABCD∩平面EFDC＝CD，故AB∥CD，CD∥EF.由BE∥AF，可得BE⊥平面EFDC，所以∠CEF为二面角C－BE －F的平面角，∠CEF＝60°.从而可得C(－2,0，3)．连接AC，则EC→＝(1,0，3)，EB→＝(0,4,0)，AC→＝(－3，－4，3)，AB→＝(－4,0,0)．设n＝(x，y，z)是平面BCE的法向量，则⎩⎨⎧n ·EC →＝0，n ·EB →＝0，即⎩⎪⎨⎪⎧x ＋3z ＝0，4y ＝0，所以可取n ＝(3,0，－3)．设m 是平面ABCD 的法向量，则⎩⎨⎧m ·AC →＝0，m ·AB →＝0，同理可取m ＝(0，3，4)．则cos 〈n ，m 〉＝n ·m |n ||m |＝－21919.故二面角E －BC －A 的余弦值为－21919.拓展提升二面角的向量求法(1)若AB ，CD 分别是二面角α－l －β的两个半平面内与棱l 垂直的异面直线，则二面角的大小就是向量AB →与CD →的夹角(如图①)．(2)利用坐标法求二面角的步骤设n 1，n 2分别是平面α，β的法向量，则向量n 1与n 2的夹角(或其补角)就是两个平面夹角的大小，如图②.用坐标法的解题步骤如下：①建系：依据几何条件建立适当的空间直角坐标系． ②求法向量：在建立的坐标系下求两个面的法向量n 1，n 2.③计算：求n1与n2所成锐角θ，cosθ＝|n1·n2| |n1||n2|.④定值：若二面角为锐角，则为θ；若二面角为钝角，则为π－θ.【跟踪训练3】若PA⊥平面ABC，AC⊥BC，PA＝AC＝1，BC ＝2，求二面角A－PB－C的余弦值．解 解法一：如下图所示，取PB 的中点D ，连接CD .∵PC ＝BC ＝2，∴CD ⊥PB .∴作AE ⊥PB 于E ，那么二面角A －PB －C 的大小就等于异面直线DC 与EA 所成的角θ的大小．∵PD ＝1，PE ＝PA 2PB ＝12，∴DE ＝PD －PE ＝12，又∵AE ＝AP ·AB PB ＝32，CD ＝1，AC ＝1，AC →＝AE →＋ED →＋DC →，且AE →⊥ED →，ED →⊥DC→，∴|AC →|2＝|AE →|2＋|ED →|2＋|DC →|2＋2|AE →|·|DC →|·cos(π－θ)， 即1＝34＋14＋1－2×32×1×cos θ，解得cos θ＝33.故二面角A －PB －C 的余弦值为33.解法二：由解法一可知，向量DC →与EA →的夹角的大小就是二面角A －PB －C 的大小，如图，建立空间直角坐标系Cxyz ，则A (1,0,0)，B (0，2，0)，C (0,0,0)，P (1,0,1)，D 为PB的中点，D ⎝⎛⎭⎪⎪⎫12，22，12. ∵PE EB ＝AP 2AB 2＝13，即E 分PB →的比为13，∴E ⎝⎛⎭⎪⎪⎫34，24，34，EA →＝⎝ ⎛⎭⎪⎪⎫14，－24，－34， DC →＝⎝ ⎛⎭⎪⎪⎫－12，－22，－12，|EA →|＝32，|DC →|＝1，EA →·DC →＝14×⎝ ⎛⎭⎪⎫－12＋⎝ ⎛⎭⎪⎪⎫－24×⎝ ⎛⎭⎪⎪⎫－22＋⎝ ⎛⎭⎪⎫－34×⎝ ⎛⎭⎪⎫－12＝12.∴cos 〈EA →，DC →〉＝EA →·DC →|EA →||DC →|＝33. 故二面角A －PB －C 的余弦值为33.解法三：如右图所示，建立空间直角坐标系，则A (0,0,0)，B (2，1,0)，C (0,1,0)，P (0,0,1)，AP →＝(0,0,1)，AB →＝(2，1,0)，CB →＝(2，0,0)，CP →＝(0，－1,1)，设平面PAB 的法向量为m ＝(x ，y ，z )，则⎩⎨⎧m ·AP →＝0，m ·AB →＝0⇒⎩⎪⎨⎪⎧x ，y ，z ·0，0，1＝0，x ，y ，z ·2，1，0＝0⇒⎩⎪⎨⎪⎧y ＝－2x ，z ＝0，令x ＝1，则m ＝(1，－2，0)，设平面PBC 的法向量为n ＝(x ′，y ′，z ′)，则⎩⎨⎧n ·CB →＝0，n ·CP →＝0⇒⎩⎪⎨⎪⎧x ′，y ′，z ′·2，0，0＝0，x ′，y ′，z ′·0，－1，1＝0⇒⎩⎪⎨⎪⎧x ′＝0，y ′＝z ′.令y ′＝－1，则n ＝(0，－1，－1)，∴cos 〈m ，n 〉＝m ·n |m ||n |＝33.∴二面角A －PB －C 的余弦值为33.探究4 利用空间向量求距离例4 已知正方形ABCD 的边长为1，PD ⊥平面ABCD ，且PD ＝1，E ，F 分别为AB ，BC 的中点．(1)求点D 到平面PEF 的距离； (2)求直线AC 到平面PEF 的距离．[解] 解法一：(1)建立如图所示的空间直角坐标系，则D (0,0,0)，P (0，0,1)，A (1,0,0)，C (0,1,0)，E ⎝ ⎛⎭⎪⎫1，12，0，F ⎝ ⎛⎭⎪⎫12，1，0.设DH ⊥平面PEF ，垂足为H ，则DH →＝xDE →＋yDF →＋zDP →＝⎝ ⎛⎭⎪⎫x ＋12y ，12x ＋y ，z ·(x ＋y ＋z ＝1)，PE →＝⎝ ⎛⎭⎪⎫1，12，－1，PF →＝⎝ ⎛⎭⎪⎫12，1，－1.∴DH →·PE →＝x ＋12y ＋12⎝ ⎛⎭⎪⎫12x ＋y －z ＝54x ＋y －z ＝0.同理，DH →·PF →＝x ＋54y －z ＝0，又x ＋y ＋z ＝1，∴可解得x ＝y ＝417，z ＝917.∴DH →＝317(2,2,3)．∴|DH →|＝31717.因此，点D 到平面PEF 的距离为31717.(2)设AH ′⊥平面PEF ，垂足为H ′，则AH ′→∥DH →，设AH ′→＝λ(2,2,3)＝(2λ，2λ，3λ)(λ≠0)，则EH ′→＝EA →＋AH ′→＝⎝ ⎛⎭⎪⎫0，－12，0＋(2λ，2λ，3λ)＝⎝ ⎛⎭⎪⎫2λ，2λ－12，3λ.∴AH ′→·EH ′→＝4λ2＋4λ2－λ＋9λ2＝0，即λ＝117.∴AH ′→＝117(2,2,3)，|AH ′→|＝1717， 又AC ∥平面PEF ，∴AC 到平面PEF 的距离为1717.解法二：(1)由解法一建立的空间直角坐标系知EF →＝⎝ ⎛⎭⎪⎫－12，12，0，PE →＝⎝ ⎛⎭⎪⎫1，12，－1，DE →＝⎝ ⎛⎭⎪⎫1，12，0，设平面PEF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧－12x ＋12y ＝0，x ＋12y －z ＝0，解得⎩⎪⎨⎪⎧y ＝x ，z ＝32x ，令x ＝2，则n ＝(2,2,3)， ∴点D 到平面PEF 的距离d ＝|DE →·n ||n |＝|2＋1|4＋4＋9＝31717.(2)∵AC ∥EF ，∴直线AC 到平面PEF 的距离也即是点A 到平面PEF 的距离．又AE →＝⎝ ⎛⎭⎪⎫0，12，0，∴点A 到平面PEF 的距离为 d ＝|AE →·n ||n |＝117＝1717.拓展提升1.向量法求点到直线的距离的两种思路(1)将求点到直线的距离问题转化为求向量模的问题，即利用待定系数法求出垂足的坐标，然后求出向量的模，这是求各种距离的通法．(2)直接套用点线距公式求解，其步骤为直线的方向向量a →所求点到直线上一点的向量PP ′→及其在直线的方向向量a 上的投影→代入公式．注意平行直线间的距离与点到直线的距离之间的转化． 2．点面距、线面距、面面距的求解方法线面距、面面距实质上都是求点面距，求直线到平面、平面到平面的距离的前提是线面、面面平行．点面距的求解步骤：(1)求出该平面的一个法向量；(2)找出从该点出发的平面的任一条斜线段对应的向量； (3)求出法向量与斜线段对应向量的数量积的绝对值，再除以法向量的模，即可求出点到平面的距离．【跟踪训练4】 正方体ABCD －A 1B 1C 1D 1的棱长为2，E ，F ，G 分别是C 1C ，D 1A 1，AB 的中点，求点A 到平面EFG 的距离．解 如图，建立空间直角坐标系，则A (2,0,0)，E (0,2,1)，F (1,0,2)，G (2,1,0)，∴EF →＝(1，－2,1)，EG →＝(2，－1，－1)，GA →＝(0，－1,0)． 设n ＝(x ，y ，z )是平面EFG 的法向量，则⎩⎨⎧n ·EF →＝0，n ·EG →＝0，∴⎩⎪⎨⎪⎧x －2y ＋z ＝0，2x －y －z ＝0，∴x ＝y ＝z ，可取n ＝(1,1,1)， ∴d ＝|GA →·n ||n |＝13＝33，即点A 到平面EFG 的距离为33.探究5 与空间有关的探索性问题例5 如图，矩形ABCD 和梯形BEFC 所成的平面互相垂直，BE ∥CF ，∠BCF ＝∠CEF ＝90°，AD ＝3，EF ＝2.(1)求证：AE ∥平面DCF ；(2)当AB 的长为何值时，二面角A －EF －C 的大小为60°？[解] 如图，以点C 为坐标原点，以CB ，CF 和CD 所在直线分别作为x 轴、y 轴和z 轴，建立空间直角坐标系Cxyz .设AB ＝a ，BE ＝b ，CF ＝c ，则C (0,0,0)，A (3，0，a )，B (3，0,0)，E (3，b,0)，F (0，c,0)．(1)证明：AE →＝(0，b ，－a )，CB →＝(3，0,0)，BE →＝(0，b,0)，∴CB →·AE →＝0，CB →·BE →＝0， 从而CB ⊥AE ，CB ⊥BE . 又AE ∩BE ＝E ， ∴CB ⊥平面ABE . ∵CB ⊥平面DCF ，∴平面ABE ∥平面DCF .又AE ⊂平面ABE ， 故AE ∥平面DCF .(2)∵EF →＝(－3，c －b,0)，CE →＝(3，b,0)， 且EF →·CE →＝0，|EF→|＝2， ∴⎩⎪⎨⎪⎧－3＋b c －b ＝0，3＋c －b2＝2，解得b ＝3，c ＝4.∴E (3，3,0)，F (0,4,0)．设n ＝(1，y ，z )与平面AEF 垂直， 则n ·AE →＝0，n ·EF →＝0，即⎩⎪⎨⎪⎧1，y ，z ·0，3，－a ＝0，1，y ，z ·－3，1，0＝0，解得n ＝⎝⎛⎭⎪⎪⎫1，3，33a.又∵BA ⊥平面BEFC ，BA →＝(0,0，a )，∴|cos 〈n ，BA →〉|＝|n ·BA →||n ||BA →|＝334a 2＋27＝12， 解得a ＝92或a ＝－92(舍去)．∴当AB ＝92时，二面角A －EF －C 的大小为60°.拓展提升利用向量解决存在性问题的方法策略求解存在性问题的基本策略是：首先，假定题中的数学对象存在；其次，构建空间直角坐标系；再次，利用空间向量法把存在性问题转化为求参数是否有解问题；最后，解方程，下结论．利用上述思维策略，可使此类存在性难题变为常规问题．【跟踪训练5】 在长方体ABCD －A 1B 1C 1D 1中，AD ＝AA 1＝12AB ，点E 是棱AB 上一点，且AEEB＝λ. (1)证明：D 1E ⊥A 1D ；(2)是否存在λ，使得二面角D 1－EC －D 的平面角为π4？并说明理由．解 (1)证明：以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴建立空间直角坐标系，如图所示．不妨设AD ＝AA 1＝1，AB ＝2，则D (0,0,0)，A (1,0,0)，B (1,2,0)，C (0,2,0)，A 1(1,0,1)，B 1(1,2,1)，C 1(0,2,1)，D 1(0,0,1)．因为AEEB ＝λ，所以E ⎝⎛⎭⎪⎫1，2λ1＋λ，0， 于是D 1E →＝⎝ ⎛⎭⎪⎫1，2λ1＋λ，－1，A 1D →＝(－1,0，－1)，所以D 1E →·A 1D →＝⎝ ⎛⎭⎪⎫1，2λ1＋λ，－1·(－1,0，－1)＝－1＋0＋1＝0，故D 1E ⊥A 1D .(2)因为DD 1⊥平面ABCD ，所以平面DEC 的一个法向量为n ＝(0,0,1)，设平面D 1EC 的法向量为n 1＝(x ，y ，z )，又CE →＝⎝ ⎛⎭⎪⎫1，2λ1＋λ－2，0，CD 1→＝(0，－2,1)， 则⎩⎨⎧n 1·CE →＝0，n 1·CD 1→＝0，即⎩⎪⎨⎪⎧n 1·⎝ ⎛⎭⎪⎫1，2λ1＋λ－2，0＝0，n 1·0，－2，1＝0，整理得⎩⎪⎨⎪⎧x －y ·21＋λ＝0，－2y ＋z ＝0，取y ＝1，则n 1＝⎝ ⎛⎭⎪⎫21＋λ，1，2. 因为二面角D 1－EC －D 的平面角为π4，所以22＝|n ·n 1||n ||n 1|，即22＝21＋4＋⎝⎛⎭⎪⎫21＋λ2，解得λ＝233－1. 故存在λ＝233－1，使得二面角D 1－EC －D 的平面角为π4.1.用空间向量解决立体几何问题的“三步曲”(1)建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线，把立体几何问题转化为向量问题.(2)通过向量运算，研究点、直线、平面之间的位置关系以及相应的距离和夹角等问题.(3)把向量的运算结果“翻译”成相应的几何意义. 2.利用法向量求直线AB 与平面α所成的角θ的步骤 (1)求平面α的法向量n .(2)利用公式sin θ＝|cos 〈AB →，n 〉|＝|AB →·n ||AB →||n |，注意直线和平面所成角的取值范围为⎣⎢⎡⎦⎥⎤0，π2.3.利用法向量求二面角的余弦值的步骤 (1)求两平面的法向量.(2)求两法向量的夹角的余弦值.(3)由图判断所求的二面角是锐角、直角，还是钝角，从而下结论.在用法向量求二面角的大小时应注意：平面的法向量有两个相反的方向，取的方向不同求出来的角度当然就不同，所以最后还应该根据这个二面角的实际形态确定其大小.4.点面距的求解步骤(1)求出该平面的一个法向量.(2)找出从该点出发的平面的任一条斜线段对应的向量. (3)求出法向量与斜线段对应向量的数量积的绝对值，再除以法向量的模，即可求出点到平面的距离.1．若两异面直线l 1与l 2的方向向量分别为a ＝(0,4，－3)，b ＝(1,2,0)，则直线l 1与l 2的夹角的余弦值为( )A.32B.8525C.4315D.33答案 B解析 设l 1，l 2的夹角为θ，则cos θ＝|cos 〈a ，b 〉|＝0×1＋4×2＋－3×05×5＝8525.2．直角△ABC 的两条直角边BC ＝3，AC ＝4，PC ⊥平面ABC ，PC ＝95，则点P 到斜边AB 的距离是( )A ．5B ．3C ．3 2 D.125答案 B解析 以C 为坐标原点，CA ，CB ，CP 所在直线为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系．则A (4,0,0)，B (0,3,0)，P ⎝ ⎛⎭⎪⎫0，0，95，所以AB →＝(－4,3,0)，AP →＝⎝⎛⎭⎪⎫－4，0，95， 所以AP →在AB →上的投影长为|AP →·AB →||AB →|＝165，所以点P 到AB 的距离为d ＝|AP →|2－⎝ ⎛⎭⎪⎫1652＝16＋8125－25625＝3.故选B.3．把正方形ABCD 沿对角线AC 折起成直二面角，点E ，F 分别是AD ，BC 的中点，O 是正方形中心，则折起后，∠EOF 的大小为( )A ．(0°，90°)B ．90°C ．120°D ．(60°，120°)答案 C解析 OE →＝12(OA →＋OD →)，OF →＝12(OB →＋OC →)，∴OE →·OF →＝14(OA →·OB →＋OA →·OC →＋OD →·OB →＋OD →·OC →)＝－14|OA →|2.又|OE →|＝|OF →|＝22|OA →|，∴cos 〈OE →，OF →〉＝－14|OA →|212|OA →|2＝－12.∴∠EOF ＝120°.故选C. 4．平面α的法向量n 1＝(1,0，－1)，平面β的法向量n 2＝(0，－1,1)，则平面α与β所成二面角的大小为________．答案π3或2π3解析 设二面角的大小为θ，则cos 〈n 1，n 2〉＝1×0＋0×－1＋－1×12·2＝－12，所以cos θ＝12或－12，∴θ＝π3或2π3.5．如图，在长方体AC 1中，AB ＝BC ＝2，AA 1＝2，点E ，F 分别是平面A 1B 1C 1D 1、平面BCC 1B 1的中心．以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x ，y ，z 轴建立空间直角坐标系．试用向量方法解决下列问题：(1)求异面直线AF 和BE 所成的角；(2)求直线AF 和平面BEC 所成角的正弦值．解 (1)由题意得A (2,0,0)，F ⎝ ⎛⎭⎪⎪⎫1，2，22，B (2,2,0)，E (1，1，2)，C (0,2,0)．∴AF →＝⎝⎛⎭⎪⎪⎫－1，2，22，BE →＝(－1，－1，2)， ∴AF →·BE →＝1－2＋1＝0.∴直线AF 和BE 所成的角为90°.(2)设平面BEC 的法向量为n ＝(x ，y ，z )，又BC→＝(－2,0,0)，BE →＝(－1，－1，2)，则n ·BC →＝－2x ＝0，n ·BE →＝－x －y ＋2z ＝0，∴x ＝0，取z ＝1，则y ＝2，∴平面BEC 的一个法向量为n ＝(0，2，1)．∴cos 〈AF →，n 〉＝AF →·n|AF →||n |＝522222×3＝53333.设直线AF 和平面BEC 所成的角为θ，则sin θ＝53333，即直线AF 和平面BEC 所成角的正弦值为53333.。

高考数学专题——立体几何（空间向量求角与距离）一、空间向量常考形式与计算方法设直线l,m 的方向向量分别为l ⃗,m ⃗⃗⃗⃗，平面α,β的法向量分别为n ⃗⃗1,n 2⃗⃗⃗⃗⃗. （1）线线角：（正负问题）：用向量算取绝对值（因为线线角只能是锐角）直线l,m 所成的角为θ，则0≤θ≤π2，计算方法：cos θ=l⃗⋅m ⃗⃗⃗⃗|l⃗|⋅|m ⃗⃗⃗⃗|； （2）线面角：正常考你正弦值，因为算出来的是角的余角的余弦值 非正常考你余弦值，需要再算一步。

直线l 与平面α所成的角为θ，则0≤θ≤π2，计算方法：sin θ=|l ⃗⋅n 1⃗⃗⃗⃗⃗⃗||l⃗|⋅|n ⃗⃗|； (3)二面角：同进同出为补角；一进一出为原角。

注意：考试从图中观察，若为钝角就取负值，若为锐角就取正值。

平面α,β所成的二面角为θ，则0≤θ≤π，如图①，AB ，CD 是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝⟨AB⃗⃗⃗⃗⃗⃗,CD ⃗⃗⃗⃗⃗⃗⟩．如图②③，n ⃗⃗1,n 2⃗⃗⃗⃗⃗分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|n⃗⃗1⋅n 2⃗⃗⃗⃗⃗⃗|n⃗⃗1|⋅|n2⃗⃗⃗⃗⃗⃗||，二面角的平面角大小是向量n 1与n 2的夹角(或其补角)． (4)空间距离额计算：通常包含点到平面距离，异面直线间距离。

二、空间向量基本步骤空间向量求余弦值或正弦值四步法（1）建系：三垂直，尽量多点在轴上；左右下建系，建成墙角系；锥体顶点在轴上；对称面建系。

一定要注明怎样建成的坐标系（2）写点坐标（3）写向量：向量最好在面上或者轴上（可简化计算量） （4）法向量的简化计算直线的方向向量和平面的法向量（1）直线的方向向量就是指和这条直线平行(或共线)的向量，记作，显然一条直线的方向向量可以有无数个.（2）若直线l ⊥α，则该直线的方向向量即为该平面的法向量，平面的法向量记作，有无数多个，任意两个都是共线向量.平面法向量的求法：设平面的法向量为α⃗=(x,y,z ).在平面内找出（或求出）两个不共线的向量a ⃗=(x 1,y 1,z 1)，b ⃗⃗=(x 2,y 2,z 2)，根据定义建立方程组，得到{α⃗×a ⃗=0α⃗×b ⃗⃗=0，通过赋值，取其中一组解，得到平面的法向量.三、空间向量求距离向量方法求异面直线距离：先求两异面直线的公共法向量，再求两异面直线上任意两点的连结线段在公共法向量上的射影长。

篇一：利用空间向量求立体几何中的角和距离利用空间向量求立体几何中的角和距离四川省宜宾市第一中学校易存新高中数学新教材第二册下（b）中引入空间向量，大大降低了立体几何解题难度，而法向量的引入，对于解决空间的角与距离提供了很大的帮助。

而高考中常以立几知识为载体，以空间向量为工具，常考查空间线、面位置关系的论证和空间距离、空间角的有关计算。

下面举例说明空间向量在求角和距离中的运用。

一.求角1.求异面直线所成的角? (0????2)设异面直线m,n的方向向量分别为m,n，则异面直线m,n所成的角?等于向量m,n所???m?n???成的角或其补角，所以有：cos??cos?m,n??m?n例1．（2006年福建卷)如图，四面体abcd中，o、e分别是bd、bc的中点，ca?cb?cd?bd?2,ab?ad?（i）求证：ao?平面bcd；（ii）求异面直线ab与cd所成角的大小；解：（i）略证。

（ii）∵ao?平面bcd，oc?bd ∴以o为原点，如图建立空间直角坐标系，则b(1,0,0),d(? 1,0,0),1????????0),ba?(?1,0,1),cd?(?1,0).c0),a(0,0,1),e(22????????????????ba.cd?cos?ba,cd?? ?4bacd?异面直线ab与cd所成角的大小为arccos42.求直线与平面所成的角? (0????2)设?为直线l与平面?所成的角，ω为直线l的方向向量v与平面?的法向量n之间的夹角，则有???2??（图1）或???2??（图2）vωn图1 图2即直线l与平面?所成的角?可看成是向量v与平面?的法向量n所成的锐角的余角，所以有sin??cos????cos?v,n???特别地 ??0时，???2，l??；???2时，??0，l??或l//?例2．（2005年浙江卷）．如图，在三棱锥p－abc中，ab⊥bc，ab＝bc＝kpa，点o、d分别是ac、pc的中点，op⊥底面abc．（ⅱ）当k＝12时，求直线pa与平面pbc所成角的大小；解：∵op⊥平面abc，oa=oc，ab=bc，∴oa⊥ob，oa⊥op，ob⊥op。