最新2020年二次函数测试题

二次函数测试题及答案一、选择题（每题3分，共30分）1. 以下哪个选项是二次函数的一般形式？A. y = 2x + 1B. y = x^2 + 3x + 2C. y = 3x^3 - 5D. y = 4/x答案：B2. 二次函数y = ax^2 + bx + c的顶点坐标为（h, k），那么h的值为：A. -b/2aB. -b/aC. b/2aD. b/a答案：C3. 二次函数y = 2x^2 - 4x + 3的对称轴方程是：A. x = 1B. x = -1C. x = 2D. x = -2答案：A4. 如果二次函数y = ax^2 + bx + c的图象开口向上，那么a的值：A. 大于0B. 小于0C. 等于0D. 可以是任意实数答案：A5. 二次函数y = -x^2 + 4x - 3的顶点坐标是：A. (1, 2)B. (2, 1)C. (3, 0)D. (3, 4)答案：C6. 二次函数y = 3x^2 - 6x + 5的图象与x轴的交点个数是：A. 0个B. 1个C. 2个D. 3个答案：C7. 二次函数y = x^2 - 4x + 4的最小值是：A. 0B. 4C. -4D. 1答案：A8. 二次函数y = 2x^2 - 4x + 3的图象开口方向是：A. 向上B. 向下C. 向左D. 向右答案：A9. 二次函数y = -x^2 + 2x + 3的图象与y轴的交点坐标是：A. (0, 3)B. (0, -3)C. (0, 5)D. (0, -5)答案：A10. 二次函数y = 5x^2 - 10x + 8的图象与x轴的交点坐标是：A. (2, 0)B. (-2, 0)C. (1, 0)D. (-1, 0)答案：A二、填空题（每题4分，共20分）1. 二次函数y = ax^2 + bx + c的图象开口向上，且经过点（2, 0），则a的值至少为______。

答案：02. 二次函数y = 2x^2 - 4x + 3的顶点坐标是（______, ______）。

2020年全国各地数学中考试题精选之二次函数一、单选题1.（2020·辽阳模拟）已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）.对于下列命题：①b﹣2a=0；②abc＜0；③4a﹣2b+c＜0；④8a+c＞0.其中正确的有（）A. 4个B. 3个C. 2个D. 1个2.（2020·杭州模拟）在平面直角坐标系中，已知m≠n，函数y=x²+（m+n）x+mn的图象与x轴有a个交点，函数y=mnx²+（m+n）x+1的图象与x轴有b个交点，则a与b的数量关系是（）A. a=bB. a=b-1C. a=b或a=b+1D. a=b或a=b-13.（2020·广西模拟）如图，抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1，与x轴的一个交点坐标为(−1,0)，其部分图象如图所示，下列结论：①2a+b=0；②b2−4ac<0；③当y>0时，x的取值范围是−1<x<3；④当x>0时，y随x增大而增大；⑤若t为任意实数，则有a+b≥at2+ bt，其中结论正确的个数是( )A. 4个B. 3个C. 2个D. 1个4.（2020·铁岭模拟）二次函数y=ax2+bx+c的图象如图所示，在下列说法中：①abc＞0；②a+b+c>0；③4a−2b+c>0；④当x>1时，y随着y的增大而增大.正确的说法个数是（）A. 1B. 2C. 3D. 45.（2020·东城模拟）若点A(1,y1),B(2,y2)在抛物线y=a(x+1)2+2(a<0)上，则下列结论正确的是（）A. 2>y1>y2B. 2>y2>y1C. y1>y2>2D. y2>y1>26.（2020·长丰模拟）若(−2,0)是二次函数y=ax2+bx(a>0)图象上一点，则抛物线y=a(x−2)2+ bx−2b的图象可能是（）A. B.C. D.7.（2020·南山模拟）已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1，其部分图象如图所示，下列说法中：①abc<0；②4a−2b+c<0；③若A（−12，y1）、B（32，y2）、C（−2，y3）是抛物线上的三点，则有y3<y1<y2；④若m，n（m<n）为方程a(x−3)(x+1)−2=0的两个根，则m>−1且n<3，以上说法正确的有（）A. ①②③④B. ②③④C. ①②④D. ①②③8.（2020·萧山模拟）已知二次函数y=a（x-2）2+c，当x=x1时，函数值为y1；当x=x2时，函数值为y2，若|x1-2|>|x2-2|，则下列表达式正确的是（）A. y1+y2>0B. y1-y2>0C. a（y1-y2）>0D. a（y1+y2）>09.（2020·西安模拟）二次函数y＝x2+bx+c的图象经过坐标原点O和点A(7，0)，直线AB交y轴于点B(0，﹣7)，动点C(x，y)在直线AB上，且1＜x＜7，过点C作x轴的垂线交抛物线于点D，则CD的最值情况是( )A. 有最小值9B. 有最大值9C. 有最小值8D. 有最大值810.（2020·广水模拟）二次函数y＝ax2+bx+c（a≠0）图象如图所示，下列结论：①abc＞0；②2a+b＝0；③当m≠1时，a+b＞am2+bm；④a−b+c＞0；⑤若ax12+bx1＝ax22+bx2，且x1≠ x2，则x1+x2＝2.其中正确的有（）A. ①②③B. ②④C. ②⑤D. ②③⑤11.（2020·铜川模拟）若一个二次函数y=ax2−4ax+3(x≠0)的图像经过两点A(m+2,y1)、B(2−m,y2)，则下列关系正确的是（）A. y1=y2B. y1<y2C. y1>y2D. y1≥y212.（2020·连云模拟）竖直向上的小球离地面的高度h（米）与时间t（秒）的关系函数关系式为h=-2t2+mt+25 8，若小球经过74秒落地，则小球在上抛过程中，第（）秒离地面最高.A. 37B. 47C. 34D. 4313.（2020·红花岗模拟）如图，抛物线y＝﹣x2+2x+c+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个命题：①抛物线的对称轴是直线x＝1；②若OC＝OB，则c＝2；③若M（x0，y0）是x轴上方抛物线上一点，则（x0﹣a）（x0﹣b）＜0；④抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2.其中真命题个数是（）A. 1B. 2C. 3D. 414.（2020·柯桥模拟）在同一平面直角坐标系中，先将抛物线A：y＝x2﹣2通过左右平移得到抛物线B，再将抛物线B通过上下平移得到抛物线C：y＝x2﹣2x+2，则抛物线B的顶点坐标为（）A. （﹣1，2）B. （1，2）C. （1，﹣2）D. （﹣1，﹣2）15.（2020·台州模拟）抛物线y＝ax2+bx+c的顶点D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②a+b+c＞0；③c﹣a＝2；④方程ax2+bx+c ﹣2＝0有两个相等的实数根.其中正确的结论是（）A. ③④B. ②④C. ②③D. ①④16.（2020·绍兴模拟）抛物线y＝﹣x2+bx+c与x轴的两个交点坐标如图所示，下列说法中错误的是（）A. 一元二次方程﹣x2+bx+c＝0的解是x1＝﹣2，x2＝1B. 抛物线的对称轴是x=−12C. 当x＞1时，y随x的增大而增大D. 抛物线的顶点坐标是(−12,9 4 )17.（2020·湖州模拟）二次函数y＝ax2+bx+c的部分图象如图所示，有以下结论：①3a﹣b＝0；②b2﹣4ac ＞0；③5a﹣2b+c＞0；④4b+3c＞0，其中错误结论的个数是（）A. 1B. 2C. 3D. 418.（2020·南充模拟）将抛物线y=x(x+2)向左平移1个单位后的解析式为（）A. y=x(x+1)B. y=x(x+3)C. y=(x−1)(x+1)D. y=(x+1)(x+3)19.（2020·沙湾模拟）二次函数y=−x2−1的图象是一条抛物线，下列关于该抛物线的说法正确的是（）A. 开口向上B. 对称轴是x=1C. 当x=0时，函数的最大值是-1D. 抛物线与x轴有两个交点20.（2020·峨眉山模拟）在平面直角坐标系中，已知a≠b，设函数y=(x+a)(x+b)的图像与x轴有M个交点，函数y=(ax+1)(bx+1)的图像与x轴有N个交点，则（）A. M=N−1或M=N+1B. M=N−1或M=N+2C. M=N或M=N+1D. M=N或M=N−121.（2020·峨眉山模拟）如图，二次函数y=ax2+bx+c(a≠0)的图象过点(−2,0)，对称轴为直线x= 1．有以下结论：①abc>0；②8a+c>0；③若A（x1，m），B（x2，m）是抛物线上的两点，当x=x1+x2时，y=c；④点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的取值范围为a≥1；3⑤若方程a(x+2)(4−x)=−2的两根为x1，x2，且x1＜x2，则﹣2≤ x1＜x2＜4．其中正确结论的序号是（）A. ①②④B. ①③④C. ①③⑤D. ①②③⑤22.（2020·旌阳模拟）已知y关于x的函数表达式是y=ax2−4x−a，下列结论错误的是（）A. 若a=−1，函数的最大值是5B. 若a=1，当x≥2时，y随x的增大而增大C. 无论a为何值时，函数图象一定经过点(1,−4)D. 无论a为何值时，函数图象与x轴都有两个交点23.（2020·新都模拟）关于二次函数y=x2−kx+k−1，以下结论：①抛物线交x轴有两个不同的交点；②不论k取何值，抛物线总是经过一个定点；③设抛物线交x轴于A、B两点，若AB=1，则k=4；④抛物线的顶点在y=−(x−1)2图象上；⑤抛物线交y轴于C点，若△ABC是等腰三角形，则k=−√2，0，1．其中正确的序号是（）A. ①②⑤B. ②③④C. ①④⑤D. ②④24.（2020·武侯模拟）如图是二次函数y＝ax2+bx+c的图象，其对称轴为直线x＝1，且与x轴的一个交点为A(3，0)，下列说法错误的是（）A. b2＞4acB. abc＜0C. 4a﹣2b+c＞0D. 当x＜﹣1时，y随x的增大而增大25.（2020·青白江模拟）已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，给出以下结论：①a+ b+c<0；②b2－4ac<0；③b+2a<0；④c<0.其中所有正确结论的序号是( )A. ③④B. ②③C. ①④D. ①②26.（2020·大邑模拟）已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=−2，与x轴的一个交点坐标为(−4,0)，其部分图象如图所示，下列结论：①当x<0时，y随x增大而增大；②抛物线一定过原点；③方程ax2+bx+c=0(a≠0)的解为x=0或x=−4；④当−4<x<0时，ax2+bx+ c>0；⑤a−b+c<0．其中结论错误的．．．个数有（）个A. 1B. 2C. 3D. 427.（2020·永州模拟）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①b2＞4ac；②2a+b＝0；③3a+c＞0；④4a﹣2b+c＜0：⑤9a+3b+c＜0．其中结论正确的个数有（）A. 1个B. 2个C. 3个D. 4个28.（2020·怀化模拟）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=−1，下列结论：①abc＜0；②2a+b=0；③a﹣b+c＞0；④4a﹣2b+c＜0其中正确的是（）A. ①②B. 只有①C. ③④D. ①④29.（2020·黄石模拟）二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（）A. a＞0B. 当﹣1＜x＜3时，y＞0C. c＜0D. 当x≥1时，y随x的增大而增大30.（2020·乾县模拟）已知二次函数y=ax²-8ax（a为常数）的图象不经过第二象限，在自变量x的值满足2≤x≤3时，其对应的函数值y的最大值为3，则a的值为（）A. −14B. 14C. −15D. 15二、填空题31.（2020·海淀模拟）如图，在平面直角坐标系xOy中，有五个点A(2,0),B(0,−2),C(−2,4),D(4,−2),E(7,0)，将二次函数y=a(x−2)2+m(m≠0)的图象记为W．下列的判断中①点A一定不在W上；②点B，C，D可以同时在W上；③点C，E不可能同时在W上．所有正确结论的序号是________．32.（2020·长丰模拟）若抛物线y=x2−2kx+k2+1在−1≤x≤1时，始终在直线y=2的上方，则k的取值范围是________．33.（2020·新疆模拟）如图，二次函数y=ax2+bx+c(a≠0)的图象经过点(−12,0)，对称轴为直线x=1,下列5个结论：①abc<0；②a−2b+4c=0；③2a+b>0；④2c−3b<0；⑤a+b≤m(am+b).其中正确的结论为________. (注：只填写正确结论的序号)34.（2020·昌吉模拟）如图，抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(12,0)，有下列结论：①abc<0；②a﹣2b+4c=0；③25a﹣10b+4c=0；④3b+2c<0；⑤a﹣b≥m（am﹣b）；其中所有正确的结论是________.（填写正确结论的序号）35.（2020·立山模拟）若二次函数y=mx2+(m−2)x+m的顶点在x轴上，则m=________.36.（2020·立山模拟）在同一平面直角坐标系中，若抛物线y=x2+(2m−1)x+2m−4与y=x2−(3m+n)x+n关于y轴对称，则符合条件的m=________；n=________.37.（2020·铁西模拟）二次函数y＝ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：①4a+b＝0；②9a+c＞3b；③,3a+c＞0；④当x＞﹣1时，y的值随x值的增大而增大.⑤4a+2b≥am2−bm（m为任意实数）其中正确的结论有________.（填序号）38.（2020·梧州模拟）已知二次函数y=ax2+bx+c（a≠0）经过点A（1，-1）、B（3，3），且当1≤x≤3时，-1≤y≤3，则a的取值范围是________39.（2020·南充模拟）如图，抛物线y=x2+ax+2经过点P(−2，2)，Q(m，n).若点Q到y轴的距离小于2，则n的取值范围是________.40.（2020·海曙模拟）如图，已知△ABC中，∠ACB＝90°，D是斜边AB上一点，BD＝2AD，CD＝4，则S△ACD 的最大值为________.三、综合题41.如图，已知二次函数y=-x2+bx+c的图像经过点A（4，-5），点B（0，3）。

九年级上册数学《二次函数》单元测试卷【考试时间：90分钟 满分：120分】一．选择题1．（2020•雁塔区校级模拟）已知二次函数2(0)y ax bx c a =++≠的图象如图所示,分析下列四个结论,其中正确结论的个数有( )①0abc <；②30a c +>；③22()a c b +<；④248ac a b -<A ．1个B ．2个C ．3个D ．4个2．（2020•雁塔区校级模拟）已知二次函数2y ax bx c =++的y 与x 的部分对应值如表：下列结论：①抛物线的开口向下；②其图象的对称轴为直线1x =；③当2x <时,函数值y 随x 的增大而增大；④方程20ax bx c ++=有一个根大于4．其中正确的结论有( ) A ．1个B ．2个C ．3个D ．4个3．（2020•碑林区校级二模）如图,抛物线2(0)y ax bx c a =++≠与x 轴交于点(3,0)-,其对称轴为直线12x =-,结合图象分析下列结论：①0abc >；②当0x <时,y 随x 的增大而增大；③30a c +>；④若m ,()n m n <为方程(3)(2)30a x x +-+=的两个根,则3m <-且2n >,其中正确的结论有( )A ．4个B ．3个C ．2个D ．1个4．（2020•滨海新区一模）二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴为直线13x =-,有下列结论：①0abc >； ②20b c +>；③520a b c ++<．其中,正确结论的个数是( )A ．3个B ．2个C ．1个D ．0个5．（2020•泉州二模）已知点1(,)A a m y -,2(,)B a n y -,3(,)C a b y +都在二次函数221y x ax =-+的图象上,若0m b n <<<,则1y 、2y ,3y 的大小关系是( ) A ．123y y y <<B ．132y y y <<C ．312y y y <<D ．231y y y <<6．（2019秋•九龙坡区校级期末）已知二次函数23y x bx a =-+-的图象与x 轴有交点,对称轴位于y 轴左侧,则当关于a ,b 的代数式22(6)a b -+有最小值时,该二次函数的顶点坐标为( ) A ．(1,0)B ．(1,2)C ．(1,0)-D ．(1,2)-7．（2018春•江阴市期中）如图,直线(y kx b k =+、b 为常数）分别与x 轴、y 轴交于点(4,0)A -、(0,3)B ,抛物线221y x x =-++与y 轴交于点C ,点E 在抛物线221y x x =-++的对称轴上移动,点F 在直线AB 上移动,CE EF +的最小值是( )A ．1.4B ．2.5C ．2.8D ．3二．填空题8．（2020•铁西区二模）二次函数2(0)y ax bx c a =++≠的部分图象如图,图象过点(1,0)-,对称轴为直线2x =,下列结论：①40a b +=；②93a c b +>；③,30a c +>；④当1x >-时,y 的值随x 值的增大而增大；⑤242(a b am bm m +-为任意实数）．其中正确的结论有 ．（填序号）9．（2020•镇江模拟）已知二次函数2(21)1y ax a x a =++++与x 轴交于A 、B 两点,(A 点在B 点左侧）C 为二次函数上一点且横坐标为1,已知ABC ∆的面积为72,则a 的值为 ． 10．（2020•肥东县二模）如图,在平面直角坐标系中,正比例函数y kx =的图象与二次函数2142y x x =--+的图象交于P 点(P 在第二象限）,经过P 点与x 轴垂直的直线l 与一次函数4y x =+的图象交于Q 点,当32PQ =时,则k 的值为 ．11．（2019秋•惠城区期末）二次函数2(0)y ax bx c a =++≠的部分图象如图所示,图象过点(4,0)-,对称轴为直线1x =-,下列结论：①0abc >；②20a b -=；③一元二次方程20ax bx c ++=的解是14x =-,21x =；④当0y >时,42x -<<,其中正确的结论有 ．12．（2019秋•娄星区期末）二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴为1x =,给出下列结论：①0abc >； ②当2x >时,0y >；③30a c +>；④30a b +>,其中正确的结论有 ．13．（2019秋•南关区校级月考）抛物线22y x x =++的图象上有三个点(3,)a -、(2,)b -、(3,)c ,则a 、b 、c 的大小关系是 （用“<”连接）．14．（2014秋•金牛区期末）已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列5个结论：①0abc <；②0a b c -+>；③420a b c ++>；④23c b <；⑤()(1a b m am b m +<+≠的实数）,其中正确结论的序号有 ．15．（2008秋•富阳市校级月考）抛物线2(0)y ax bx c a =++≠过点(1,3)A -、(3,3)B -、(1,5)C -,顶点为M 点．在抛物线上是找一点P 使90POM ∠=︒,则P 点的坐标 ． 三．解答题16．（2020春•南岸区校级月考）如图,抛物线223y x x =+-与x 轴交于A 、B 两点（点A 在点B 的左侧）,交y 轴于点C ,抛物线的顶点为点D ． （1）求AB 的长度和点D 的坐标； （2）求直线AC 的函数表达式；（3）点P 是第四象限抛物线上一点,当2PAC PAB S S ∆∆=时,求点P 的坐标．17．（2020•十堰）某企业接到生产一批设备的订单,要求不超过12天完成．这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台．若干天后,每台设备的生产成本将会增加,设第x 天(x 为整数）的生产成本为m （元/台）,m 与x 的关系如图所示．（1）若第x 天可以生产这种设备y 台,则y 与x 的函数关系式为 ,x 的取值范围为 ； （2）第几天时,该企业当天的销售利润最大？最大利润为多少？ （3）求当天销售利润低于10800元的天数．18．（2020•荆门）2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度．某单位的帮扶对象种植的农产品在某月（按30天计）的第x 天(x 为正整数）的销售价格p （元/千克）关于x 的函数关系式为24(020)5112(2030)5x x p x x ⎧+<⎪⎪=⎨⎪-+<⎪⎩,销售量y （千克）与x 之间的关系如图所示．（1）求y 与x 之间的函数关系式,并写出x 的取值范围；（2）当月第几天,该农产品的销售额最大,最大销售额是多少？（销售额=销售量⨯销售价格）19．（2020•沭阳县模拟）如图1,在平面直角坐标系中,已知点A 的坐标是(3,0),并且3OA OC OB ==,动点P 在过A ,B ,C 三点的抛物线上, （1）求抛物线的解析式；（2）是否存在点P ,使得ACP ∆是以AC 为底的等腰三角形？若存在,求出所有符合条件的点P 的坐标；若不存在,说明理由；（3）过动点P 作PE 垂直于y 轴于点E ,交直线AC 于点D ,过点D 作x 轴的垂线,垂足为F ,连接EF ,以线段EF 的中点G 为圆心,以EF 为直径作G ,求G 最小面积．20．（2020•眉山）如图1,抛物线2y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,已知点B 坐标为(3,0),点C 坐标为(0,3)．（1）求抛物线的表达式；∆的面积最大时,求点P的坐标；（2）点P为直线BC上方抛物线上的一个动点,当PBC⊥轴于点D,在直线MD上是否存在点N,使点N到直线（3）如图2,点M为该抛物线的顶点,直线MD xMC的距离等于点N到点A的距离？若存在,求出点N的坐标；若不存在,请说明理由．答案与解析一．选择题1．（2020•雁塔区校级模拟）已知二次函数的图象如图所示,分析下列四个结论,其中正确结论的个数有①；②；③；④A ．1个B ．2个C ．3个D ．4个【解答】解：抛物线开口向下,,对称轴在轴左侧,、同号,,抛物线与轴的交点在上方,,所以,,因此①不正确； 当时,, 当时,, ,即,也就是,因此③正确；抛物线顶点纵坐标,即,又,因此有,所以④正确；对称轴在之间,因此有,又,故有,而,有,即,因此②不正确；综上所述,正确的结论有：③④, 故选：．2．（2020•雁塔区校级模拟）已知二次函数的与的部分对应值如表：2(0)y ax bx c a =++≠()0abc <30a c +>22()a c b +<248ac a b -<0a <y a b 0b <y (0,2)2c >0abc >1x =0y a b c =++<1x =-0y a b c =-+>()()0a b c a b c ∴++-+<22()0a cb +-<22()a c b +<2y >2424ac b a ->0a <248ac a b -<0~1-12ba ->-0a <2b a >0a b c ++<20a a c ++<30a c +<B 2y ax bx c =++y x下列结论：①抛物线的开口向下；②其图象的对称轴为直线；③当时,函数值随的增大而增大；④方程有一个根大于4．其中正确的结论有 A ．1个B ．2个C ．3个D ．4个【解答】解：根据题意：将点、、代入二次函数中, ,解得,所以二次函数,,抛物线的开口向下,所以①正确；,则图象的对称轴为直线,所以②错误；图象的对称轴为直线,当时,函数值随的增大而增大,所以③错误；当时,,解得,,1x =2x <y x 20ax bx c ++=()(1,3)--(0,1)(1,3)2y ax bx c =++313a b c c a b c -+=-⎧⎪=⎨⎪++=⎩131a b c =-⎧⎪=⎨⎪=⎩231y x x =-++10a =-<∴2231331()24y x x x =-++=--+32x =32x =∴32x <y x 0y =2313()024x --+=1x =2x =, ,所以方程有一个根小于4,所以④错误．综上所述：其中正确的结论有①． 故选：．3．（2020•碑林区校级二模）如图,抛物线与轴交于点,其对称轴为直线,结合图象分析下列结论：①；②当时,随的增大而增大；③；④若,为方程的两个根,则且,其中正确的结论有A ．4个B ．3个C ．2个D ．1个【解答】解：抛物线开口向下,,对称轴为,即,因此,与的交点在正半轴,,所以,因此①正确；,对称轴为,当时,随的增大而增大,因此②不正确；3134<<732∴<20ax bx c ++=A 2(0)y ax bx c a =++≠x (3,0)-12x =-0abc >0x <y x 30a c +>m ()n m n <(3)(2)30a x x +-+=3m <-2n >()0a <122b x a =-=-a b =0b <y 0c >0abc >0a <12x =-∴12x <-y x由对称性可知,抛物线与轴的两个交点为,,,,又,, ,,因此③正确；抛物线与轴的两个交点为,,,,为方程的两个根,实际上就是当时,函数相应的自变量的值为、；,根据图象可知,且,因此④正确； 综上所述,正确的结论有：①③④, 故选：．4．（2020•滨海新区一模）二次函数的图象如图所示,对称轴为直线,有下列结论：①； ②；③．其中,正确结论的个数是A ．3个B ．2个C ．1个D ．0个【解答】解：抛物线开口向下,因此,对称轴在轴的左侧,、同号,故,与轴的交点在轴的正半轴,因此, 故,因此①正确,x (3-0)(20)420a b c ∴++=a b =60a c ∴+=0a <30a c ∴+>x (3-0)(20)m ∴()n m n <(3)(2)30a x x +-+=3y =-(3)(2)y a x x =+-x m n 3m <-2n >B 2(0)y ax bx c a =++≠13x =-0abc >20b c +>520a b c ++<()0a <y a b 0b <y y 0c >0abc >对称轴为,即,即,也就是,由图象可知,当时,,即,因此有,所以②正确,当时,,（1） 当时,,（2） （1）（2）得,, 又,则,,因此③正确, 故选：．5．（2020•泉州二模）已知点,,都在二次函数的图象上,若,则、,的大小关系是 A ．B ．C ．D ．【解答】解：抛物线开口向上,对称轴为, 点、的情况：,故点比点离对称轴远,故； 点、的情况：,故点比点离对称轴远,故；点、的情况：,故点比点离对称轴远,故；故,故选：．6．（2019秋•九龙坡区校级期末）已知二次函数的图象与轴有交点,对称轴位于轴左侧,则当关于,的代数式有最小值时,该二次函数的顶点坐标为A ．B ．C ．D ．【解答】解：二次函数的图象与轴有交点,13x =-123b a -=-23a b =32a b =1x =-0y a b c =-+>32b b c -+>20b c +>2x =-420y a b c =-+<1x =0y a b c =++<+520a b c -+<23a b =46a b =5242520a b c a a b c a b c ∴-+=+-+=++<A 1(,)A a m y -2(,)B a n y -3(,)C a b y +221y x ax =-+0m b n <<<1y 2y 3y ()123y y y <<132y y y <<312y y y <<231y y y <<x a =A B n m >B A 21y y >A C m b <C A 31y y >B C b n <B C 23y y >132y y y <<B 23y x bx a =-+-x y a b 22(6)a b -+()(1,0)(1,2)(1,0)-(1,2)-23y x bx a =-+-x△,对称轴位于轴左侧,；,当时,等号成立；,代数式取得最小值时,,此时,解得：（舍去正值）, 故,, 故抛物线的表达式为：,故抛物线的顶点为, 故选：．7．（2018春•江阴市期中）如图,直线、为常数）分别与轴、轴交于点、,抛物线与轴交于点,点在抛物线的对称轴上移动,点在直线上移动,的最小值是A ．1.4B ．2.5C ．2.8D ．3【解答】解：如图,设点关于抛物线对称轴的对称点为,由对称的性质可得,∴24(3)0b a =--y 0b ∴<222(6)(6)4(3)a b a a -+-+-24(3)b a =-22(6)4(3)(4)88a a a -+-=-+4a =24(41)4b =-=2b =±4a =2b =-2221(1)y x x x =++=+(1,0)-C (y kx b k =+b x y (4,0)A -(0,3)B 221y x x =-++y C E 221y x x =-++F AB CE EF +()C C 'CE C E =',当、、三点一线且与垂直时最小,由题意可得,解得,直线解析式为；, ,直线的解析式为, 由,解得, ,,即的最小值为．故选：． 二．填空题CE EF C E EF ∴+='+∴F E C 'C F 'AB CE EF +403k b b -+=⎧⎨=⎩343k b ⎧=⎪⎨⎪=⎩∴334y x =+(0,1)C (2,1)C ∴'∴C F '41133y x =-+41133334y x y x ⎧=-+⎪⎪⎨⎪=+⎪⎩8258125x y ⎧=⎪⎪⎨⎪=⎪⎩8(25F ∴81)25145C F ∴'==CE EF +145C8．（2020•铁西区二模）二次函数的部分图象如图,图象过点,对称轴为直线,下列结论：①；②；③,；④当时,的值随值的增大而增大；⑤为任意实数）．其中正确的结论有 ①③⑤ ．（填序号）【解答】解：抛物线过点,对称轴为直线,因此可得,抛物线与轴的另一个交点为,,,即,因此①正确； 当时,,即,因此②不正确；当时,,又,所以,而,因此有,故③正确； 在对称轴的左侧,即当时,随的增大而增大,因此④不正确；当时,,当时,,因此有,故⑤正确；综上所述,正确的结论有：①③⑤, 故答案为：①③⑤．9．（2020•镇江模拟）已知二次函数与轴交于、两点,点在点左侧）为二次函数上一点且横坐标为1,已知的面积为,则的值为 或 ．【解答】解：,当时,,,二次函数与轴交于、两点点在点左侧）,当时,点,、点；当时,点,点,；为二次函数上一点且横坐标为1,点的纵坐标为,2(0)y ax bx c a =++≠(1,0)-2x =40a b +=93a c b +>30a c +>1x >-y x 242(a b am bm m +-(1,0)-2x =x (5,0)0a b c -+=22bx a=-=40a b +=3x =-930y a b c =-+<93a c b +<5x =2550y a b c =++=4b a =-50a c +=0a <30a c +>2x <y x 2x =42y a b c =++最大x m =2y am bm c =++242a b am bm ++2(21)1y ax a x a =++++x A B (A B C ABC ∆72a 23211-2(21)1(1)(1)y ax a x a ax a x =++++=+++∴0y =11a x a +=-21x =-2(21)1y ax a x a =++++x A B (A B ∴0a >1(a A a +-0)(1,0)B -0a <(1,0)A -1(a B a +-0)C ∴C 21142y a a a a =++++=+的面积为,当时,,得,当时,,得（舍去）,,由上可得,的值是或, 故答案为：或．10．（2020•肥东县二模）如图,在平面直角坐标系中,正比例函数的图象与二次函数的图象交于点在第二象限）,经过点与轴垂直的直线与一次函数的图象交于点,当时,则的值为 或 ．【解答】解：设,则, 由题意：, 解得或,或,点在直线上,或,ABC ∆72∴0a >1(1)()7(42)22a a a +---⨯+=23a =0a <1()(1)7|42|22a a a +---⨯+=123a =2211a =-a 23211-23211-y kx =2142y x x =--+P (P P x l 4y x =+Q 32PQ =k 92-56-21(,4)2P m m m --+(,4)Q m m +2134422m m m --+--=1m =-3-9(1,)2P ∴-5(3,)2-P y kx =92k ∴=-56-故答案为或．11．（2019秋•惠城区期末）二次函数的部分图象如图所示,图象过点,对称轴为直线,下列结论：①；②；③一元二次方程的解是,；④当时,,其中正确的结论有 ①②④ ．【解答】解：二次函数开口向下,,对称轴为直线,即,,,与轴交在正半轴,,,因此①正确；,即,因此②正确；图象过点,对称轴为直线,因此与轴另一个交点,因此一元二次方程的解是,；故③不正确；由图象可得,图象位于轴上方时,即时,相应的自变量的取值范围为,因此④正确； 综上所述,正确的结论有：①②④, 故答案为：①②④．12．（2019秋•娄星区期末）二次函数的图象如图所示,对称轴为,给出下列结论：92-56-2(0)y ax bx c a =++≠(4,0)-1x =-0abc >20a b -=20ax bx c ++=14x =-21x =0y >42x -<<2(0)y ax bx c a =++≠0a <1x =-12ba -=-2b a =0b <y 0c >0abc ∴>2b a =20a b -=(4,0)-1x =-x (2,0)20ax bx c ++=14x =-22x =x 0y >42x -<<2(0)y ax bx c a =++≠1x =①； ②当时,；③；④,其中正确的结论有 ①③④ ．【解答】解：①对称轴在轴右侧,则、异号,,故,正确； ②在函数与轴右侧交点的左侧,故,,错误；③函数对称轴为：,则,时,,即,正确；④,,则,正确； 故答案为：①③④．13．（2019秋•南关区校级月考）抛物线的图象上有三个点、、,则、、的大小关系是 （用“”连接）．【解答】解：把、、分别代入抛物线得,,,；因此有． 故答案为：．14．（2014秋•金牛区期末）已知二次函数的图象如图所示,有下列5个结论：①；②；③；④；⑤的实数）,其中正确结论的序号有 ①③④ ．【解答】解：①由图象可知：,,0abc >2x >0y >30a c +>30a b +>y a b 0c <0abc >2x =x 2x >0y <12b x a =-=2b a =-1x =-0y a b c =-+>30a c +>2b a =-0a >30a b +>22y x x =++(3,)a -(2,)b -(3,)c a b c b a c <<<(3,)a -(2,)b -(3,)c 22y x x =++9328a =-+=4224b =-+=93214c =++=b a c <<b a c <<2(0)y ax bx c a =++≠0abc <0a b c -+>420a b c ++>23c b <()(1a b m am b m +<+≠0a <0c >,,,故此选项正确；②当时,,故,错误；③由对称知,当时,函数值大于0,即,故此选项正确；④当时函数值小于0,,且,即,代入得,得,故此选项正确；⑤当时,的值最大．此时,,而当时,,所以,故,即,故此选项错误．故①③④正确． 故答案为：①③④．15．（2008秋•富阳市校级月考）抛物线过点、、,顶点为点．在抛物线上是找一点使,则点的坐标 , ．【解答】解：抛物线过点、、,所以,解得：,所以抛物线的解析式为：,顶点坐标是,因此直线的解析式为,由于直线与直线垂直,因此直线的解析式为,02b a ->0b ∴>0abc ∴<1x =-0y a b c =-+<0a b c -+>2x =420y a b c =++>3x =930y a b c =++<12bx a =-=2b a =-9()302bb c -++<23c b <1x =y y a b c =++x m =2y am bm c =++2a b c am bm c ++>++2a b am bm +>+()a b m am b +>+2(0)y ax bx c a =++≠(1,3)A -(3,3)B -(1,5)C -MP 90POM ∠=︒P 9(29)42(0)y ax bx c a =++≠(1,3)A -(3,3)B -(1,5)C -39335a b c a b c a b c ++=-⎧⎪++=-⎨⎪-+=⎩140a b c =⎧⎪=-⎨⎪=⎩224(2)4y x x x =-=--M (2,4)-OM 2y x =-PO OM PO 12y x =联立抛物线的解析式有：,解得,, 因此点坐标为,．三．解答题16．（2020春•南岸区校级月考）如图,抛物线与轴交于、两点（点在点的左侧）,交轴于点,抛物线的顶点为点． （1）求的长度和点的坐标； （2）求直线的函数表达式；（3）点是第四象限抛物线上一点,当时,求点的坐标．【解答】解：（1）令,得,解得,或1, ,, ,,；（2）令,得, ,设直线的解析式为,得 ,2124y x y x x ⎧=⎪⎨⎪=-⎩00x y =⎧⎨=⎩9294x y ⎧=⎪⎪⎨⎪=⎪⎩P 9(29)4223y x x =+-x A B A B y C D AB D AC P 2PAC PAB S S ∆∆=P 0y =2230y x x =+-=3x =-(3,0)A ∴-(1,0)B 1(3)4AB ∴=--=2223(1)4y x x x =+-=+-(1,4)D ∴--0x =2233y x x =+-=-(0,3)C ∴-AC (0)y kx b k =+≠303k b b -+=⎧⎨=-⎩解得,,直线的解析式为：；（3）设,,过作轴于点,如下图,则,,,,即,解得,（舍,, ．17．（2020•十堰）某企业接到生产一批设备的订单,要求不超过12天完成．这种设备的出厂价为1200元台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台．若干天后,每台设备的生产成本将会增加,设第天为整数）的生产成本为（元台）,与的关系如图所示．（1）若第天可以生产这种设备台,则与的函数关系式为 ,的取值范围为 ；（2）第几天时,该企业当天的销售利润最大？最大利润为多少？（3）求当天销售利润低于10800元的天数．13k b =-⎧⎨=-⎩∴AC 3y x =--(P m 223)(01)m m m +-<<P PQ x ⊥Q 223PQ m m =--+OQ m =3AQ m =+2PAC PAB S S ∆∆=()2AOC APQ PAB OQPC S S S S ∆∆∆∴+-=梯形22211112[33(323)(3)(23)]4(23)2222m m m m mm m m ⨯⨯+--+-+--+=⨯--+3m =-)25m =∴251(,)525P -/x (x m /m x x y y x 220y x =+x【解答】解：（1）根据题意,得与的解析式为：,故答案为：,；（2）设当天的销售利润为元,则当时,,,随的增大而增大,当时,．当时,设,将和代入得：, 解得：,与的关系式为：,．此时图象开口向下,在对称轴右侧,随的增大而减小,天数为整数,当时,有最大值,为11900元,y x 222(1)220(112)y x x x =+-=+220y x =+112x w 16x (1200800)(220)8008000w x x =-+=+8000>w ∴x ∴6x =8006800012800w =⨯+=最大值612x <m kx b =+(6,800)(10,1000)8006100010k b k b=+⎧⎨=+⎩50500k b =⎧⎨=⎩m ∴x 50500m x =+[1200(50500)](220)w x x ∴=-+⨯+210040014000x x =-++2100(2)14400x =--+w x x ∴7x =w,当时,最大,且元,答：该厂第6天获得的利润最大,最大利润是12800元．（3）由（2）可得,时,,解得：则第天当天利润低于10800元,当时,,解得（舍去）,或,第天当天利润低于10800元,故当天销售利润低于10800元的天数有7天．18．（2020•荆门）2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度．某单位的帮扶对象种植的农产品在某月（按30天计）的第天为正整数）的销售价格（元千克）关于的函数关系式为,销售量（千克）与之间的关系如图所示．（1）求与之间的函数关系式,并写出的取值范围；（2）当月第几天,该农产品的销售额最大,最大销售额是多少？（销售额销售量销售价格）【解答】解：（1）当时,设与的函数关系式为,,1280011900>∴6x =w 12800w =最大值16x 800800010800x +<3.5x <13-612x <2100(2)1440010800x --+<4x <-8x >∴912-x (x p /x 24(020)5112(2030)5x x p x x ⎧+<⎪⎪=⎨⎪-+<⎪⎩y x y x x =⨯020x <y x y ax b =+802040b a b =⎧⎨+=⎩解得,,即当时,与的函数关系式为,当时,设与的函数关系式为,,解得,,即当时,与的函数关系式为,由上可得,与的函数关系式为； （2）设当月第天的销售额为元,当时,,当时,取得最大值,此时,当时,,当时,取得最大值,此时,由上可得,当时,取得最大值,此时,答：当月第15天,该农产品的销售额最大,最大销售额是500元．19．（2020•沭阳县模拟）如图1,在平面直角坐标系中,已知点的坐标是,并且,动点在过,,三点的抛物线上,（1）求抛物线的解析式；（2）是否存在点,使得是以为底的等腰三角形？若存在,求出所有符合条件的点的坐标；若不存在,说明理由；（3）过动点作垂直于轴于点,交直线于点,过点作轴的垂线,垂足为,连接,以线段的中点为圆心,以为直径作,求最小面积．280a b =-⎧⎨=⎩020x <y x 280y x =-+2030x <y x y mx n =+20403080m n m n +=⎧⎨+=⎩440m n =⎧⎨=-⎩2030x <y x 440y x =-y x 280(020)440(2030)x x y x x -+<⎧=⎨-<⎩x w 020x <224(4)(280)(15)50055w x x x =+⨯-+=--+∴15x =w 500w =2030x <214(12)(440)(35)50055w x x x =-+⨯-=--+∴30x =w 480w =15x =w 500w =A (3,0)3OA OC OB ==P A B C P ACP ∆AC P P PE y E AC D D x F EF EF G EF G G【解答】解：（1）点的坐标是,,,,,点,点,设抛物线的解析式为：,,,抛物线解析式为：；（2）是以为底的等腰三角形,,又,是的垂直平分线,,,是的垂直平分线,平分,直线解析式为,联立方程组可得：,A (3,0)3OA ∴=3OA OC OB ==3OC ∴=1OB =∴(0,3)C (1,0)B -(1)(3)y a x x =+-33a ∴=-1a ∴=-∴2(1)(3)23y x x x x =-+-=-++ACP ∆AC AP CP ∴=OA OC =OP ∴AC OA OC =90AOC ∠=︒OP AC OP ∴AOC ∠∴OP y x =223y x y x x =⎧⎨=-++⎩或,点坐标为,或,；（3）如图,点的坐标是,点坐标为,直线解析式为：,设点坐标为,,,,的面积, 当时,最小面积为．20．（2020•眉山）如图1,抛物线与轴交于、两点,与轴交于点,已知点坐标为,点坐标为．∴x y ⎧=⎪⎪⎨⎪=⎪⎩x y ⎧=⎪⎪⎨⎪=⎪⎩∴PA (3,0)C (0,3)∴AC 3y x =-+D (,3)m m -+||DE m ∴=|3|DF m =-+22222(3)EF DE DF m m ∴=+=+-+G 222239[(3)][2()]44422EF m m m πππ=⨯=⨯+-+=⨯-+∴32m =G 98π2y x bx c =-++x A B y C B (3,0)C(0,3)（1）求抛物线的表达式；（2）点为直线上方抛物线上的一个动点,当的面积最大时,求点的坐标；（3）如图2,点为该抛物线的顶点,直线轴于点,在直线上是否存在点,使点到直线的距离等于点到点的距离？若存在,求出点的坐标；若不存在,请说明理由．【解答】解：（1）点,点在抛物线图象上,,解得：,抛物线解析式为：；（2）点,点,直线解析式为：,如图,过点作轴于,交于点,设点,则点,, ,当时,有最大值, 点,；P BC PBC ∆P M MD x ⊥D MD N N MC N A N (3,0)B (0,3)C 2y x bx c =-++∴9303b c c -++=⎧⎨=⎩23b c =⎧⎨=⎩∴223y x x =-++(3,0)B (0,3)C ∴BC 3y x =-+P PH x ⊥H BCG 2(,23)P m m m -++(,3)G m m -+22(23)(3)3PG m m m m m∴=-++--+=-+221133273(3)()22228PBC S PG OB m m m ∆=⨯⨯=⨯⨯-+=--+∴32m =PBC S ∆∴3(2P 15)4（3）存在满足条件,理由如下：抛物线与轴交于、两点,点, ,顶点为, 点为,点,直线的解析式为：,如图,设直线与轴交于点,过点作于,点,,,,,,,设点,点到直线的距离等于点到点的距离, N 223y x x =-++x A B ∴(1,0)A -2223(1)4y x x x =-++=--+∴M(1,4)M (1,4)(0,3)C ∴MC 3y x =-+MC x E N NQ MC ⊥Q ∴(3,0)E -4DE MD ∴==45NMQ ∴∠=︒NQ MC ⊥45NMQ MNQ ∴∠=∠=︒MQ NQ ∴=MQ NQ ∴==(1,)Nn N MC N A,,,, ,,存在点满足要求,点坐标为或． NQ AN ∴=22NQ AN ∴=22)AN ∴=22(|4|)42n n ∴-=+2880n n ∴+-=4n ∴=-±∴NN (1,4-+(1,4--。

人教版2020年九年级数学上册二次函数-函数的性质及几何变换一、选择题1.已知二次函数y=2(x+1)(x﹣a)，其中a＞0，且对称轴为直线x=2，则a的值是( )A.3B.5C.7D.不确定2.点P1(－1，y1)，P2(3，y2)，P3(5，y3)均在二次函数y=－x2＋2x＋c的图象上，则y1，y2，y3的大小关系是( )A.y3＞y2＞y1B.y3＞y1=y2C.y1＞y2＞y3D.y1=y2＞y33.一次函数y=ax＋b(a≠0)与二次函数y=ax2＋bx＋c(a≠0)在同一平面直角坐标系中的图象可能是( )4.函数y=﹣2x2﹣8x+m的图象上有两点A(x1，y1)，B(x2，y2)，若x1＜x2＜﹣2，则( )A.y1＜y2B.y1＞y2C.y1=y2D.y1、y2的大小不确定5.已知二次函数y=3(x-1)2+k的图象上有A(，y1)，B(2，y2)，C(-，y3)三个点，则y1，y2，y3的大小关系是( )A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y3>y2>y16.已知关于x的方程ax2+bx+c=5的一个根是2，且二次函数y=ax2+bx+c的对称轴是直线x=2，则这条抛物线的顶点坐标为（）A.（2,﹣3）B.（2,1）C.（2,5）D.（5,2）7.对于抛物线y=﹣x2+2x+3，有下列四个结论：①它的对称轴为x=1；②它的顶点坐标为（1，4）；③它与y轴的交点坐标为（0，3），与x轴的交点坐标为（﹣1，0）和（3，0）；④当x＞0时，y随x的增大而减小.其中正确的个数为（）A．1 B．2 C．3 D．48.若将抛物线y=5x2先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为( )A.y =5(x-2)2+1B.y =5(x+2)2+1C.y =5(x-2)2-1D.y =5(x+2)2-19.在平面直角坐标系中，将抛物线y＝x2－4先向右平移2个单位，再向上平移2个单位，得到的抛物线解析式为( )A.y=(x＋2)2＋2B.y=(x-2)2-2C.y=(x-2)2＋2D.y=(x＋2)2-210.抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3，则b、c的值为（）A.b=2，c=2B.b=2，c=0C.b=﹣2，c=﹣1D.b=﹣3，c=2二、填空题11.已知A(0，3)，B(2，3)是抛物线y=－x2＋bx＋c上两点，该抛物线的顶点坐标是________.12.二次函数y=x2+6x+5图象的顶点坐标为 ．13.如图，点E是抛物线y=a(x﹣2)2+k的顶点，抛物线与y轴交于点C，过点C作CD∥x轴，与抛物线交于点B，与对称轴交于点D．点A是对称轴上一点，连结AC、AB．若△ABC是等边三角形，则图中阴影部分图形的面积之和是．14.抛物线y=﹣x2+bx+c的部分图象如图所示，若y=0，则x= ．15.如图，抛物线y=ax2＋bx＋c与x轴相交于点A、B(m＋2，0)，与y轴相交于点C，点D在该抛物线上，坐标为(m，c)，则点A的坐标是________.16.把抛物线y=x2-4x+5的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是三、解答题17.已知抛物线y=﹣x2+bx+c经过点A（3，0），B（﹣1，0）．（1）求抛物线的解析式；（2）求抛物线的顶点坐标．18.如图，已知抛物线y=ax2＋bx＋c与x轴交于点A(1，0)，点B(3，0)，且过点C(0，－3).(1)求抛物线的函数表达式和顶点坐标；(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=－x上，并写出平移后抛物线的函数表达式.19.已知二次函数y=ax2＋bx-3的图象经过点A（2,-3）,B（-1,0）.（1）求二次函数的解析式；（2）若把图象沿y轴向下平移5个单位,求该二次函数的图象的顶点坐标.20.如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点．(1)求该抛物线的函数关系式；(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标．21.如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D.（1）请直接写出D点的坐标.（2）求二次函数的解析式.（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围.22.已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9)．(1) 求该二次函数的解析式并写出其对称轴；(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).参考答案1.答案为：B.2.D　3.C4.A5.答案为：C6.C7.C.8.A9.B10.B11.答案为：(1，4)；12.答案为：(﹣3，﹣4)．13.答案为2．14.答案为:﹣3或115.答案为：(－2，0).16.答案为：y=x2-10x+2417.解：（1）∵抛物线y=﹣x2+bx+c经过点A（3，0），B（﹣1，0）．∴抛物线的解析式为；y=﹣（x﹣3）（x+1），即y=﹣x2+2x+3，（2）∵抛物线的解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4，∴抛物线的顶点坐标为：（1，4）．18.解：(1)∵抛物线与x轴交于点A(1，0)，点B(3，0)，∴可设抛物线表达式为y=a(x－1)(x－3)，把C(0，－3)的坐标代入，得3a=－3，解得a=－1，故抛物线表达式为y=－(x－1)(x－3)，即y=－x2＋4x－3.∵y=－x2＋4x－3=－(x－2)2＋1，∴抛物线的顶点坐标为(2，1)；(2)答案不唯一，如：先向左平移2个单位，再向下平移1个单位，得到的抛物线的解析式为y=－x2，平移后抛物线的顶点为(0，0)，落在直线y=－x上.19.解：(1)由已知,有,即,解得∴所求的二次函数的解析式为.(2)（1,）20.解：(1)∵抛物线的顶点D的坐标为(1,﹣4),∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,又∵抛物线过点C(0,﹣3),∴﹣3=a(0﹣1)2﹣4,解得a=1,∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3；(2)∵S△PAB=S△ABD,且点P在抛物线上,∴点P到线段AB的距离一定等于顶点D到AB的距离,∴点P的纵坐标一定为4．令y=4,则x2﹣2x﹣3=4,解得x1=1+2,x2=1﹣2．∴点P的坐标为(1+2,4)或(1﹣2,4)．21.解：（1）∵如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，∴对称轴是x=﹣1.又点C（0，3），点C、D是二次函数图象上的一对对称点，∴D（﹣2，3）；（2）设二次函数的解析式为y=ax2+bx+c（a≠0，a、b、c常数），根据题意得，解得，所以二次函数的解析式为y=﹣x2﹣2x+3；（3）如图，一次函数值大于二次函数值的x的取值范围是x＜﹣2或x＞1.22.解：(1)对称轴是x=2(2)。

2020年中考数学二次函数真题汇编(名师精选全国真题，值得下载练习)一、单选题1.如图，一段抛物线y=﹣x 2+4（﹣2≤x≤2）为C 1 ， 与x 轴交于A 0 ， A 1两点，顶点为D 1；将C 1绕点A 1旋转180°得到C 2 ， 顶点为D 2；C 1与C 2组成一个新的图象，垂直于y 轴的直线l 与新图象交于点P 1（x 1 ， y 1），P 2（x 2 ， y 2），与线段D 1D 2交于点P 3（x 3 ， y 3），设x 1 ， x 2 ， x 3均为正数，t=x 1+x 2+x 3 ， 则t 的取值范围是（ ）A. 6＜t≤8 B. 6≤t≤8 C. 10＜t≤12 D. 10≤t≤12 【答案】D【解析】【解答】解：翻折后的抛物线的解析式为y=（x ﹣4）2﹣4=x 2﹣8x+12， ∵设x 1 ， x 2 ， x 3均为正数，∴点P 1（x 1 ， y 1），P 2（x 2 ， y 2）在第四象限， 根据对称性可知：x 1+x 2=8， ∵2≤x 3≤4，∴10≤x 1+x 2+x 3≤12即10≤t≤12， 故答案为：D ．【分析】根据题意可求出翻折后的抛物线的解析式，设x 1 ， x 2 ， x 3均为正数，可得出点P 1（x 1 ， y 1），P 2（x 2 ， y 2）在第四象限，根据对称性可求出x 1+x 2=8，由2≤x 3≤4，可得出x 1+x 2+x 3的取值范围，从而得出t 的取值范围。

2.已知，平面直角坐标系中，直线y 1=x+3与抛物线y=-x x 的图象如图，点P 是y 2上的一个动点，则点P 到直线y 1的最短距离为（ ）A.B.C. D.【答案】D【解析】【解答】解、∵点P 到直线y 1的距离最短， ∴点P 是直线与抛物线相切时的交点。

设直线y 1平移k 个单位长度，则此时的解析式为 =x+3+k ， 把 =x+3+k 代入y=-x 2+2x 整理得，-x 2+x-3-k=0，△=b 2-4ac=1-4 (-) (-3-k)=0，解得k=-，即直线y 1向下平移个单位长度与抛物线相切， 把k=-代入解析式解方程组可求得点P 的坐标为（1，）；过点P 作PD ⊥直线y 1于点D ，则直线PD 的解析式可设为y 3=-x+b ，把点P （1，）代入可求得b=,即直线PD 的解析式为y 3=-x+，将y 1和y 3的解析式联立解方程组可求得点D 的坐标为（-，）；若直线PD与x轴相较于点C，直线y1=x+3与x、y轴分别相较于点A、B，易得点A （-3,0）、B（0,3），∴∠BAC==∠DCA，由勾股定理可得：CD=，CP=，∴PD=CD-CP=。

二次函数综合题一．二次函数综合题（共50小题）1．（2020•常州）如图，二次函数y＝x2+bx+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，抛物线过点C（1，0），且顶点为D，连接AC、BC、BD、CD．（1）填空：b＝；（2）点P是抛物线上一点，点P的横坐标大于1，直线PC交直线BD于点Q．若∠CQD ＝∠ACB，求点P的坐标；（3）点E在直线AC上，点E关于直线BD对称的点为F，点F关于直线BC对称的点为G，连接AG．当点F在x轴上时，直接写出AG的长．2．（2020•岳阳）如图1所示，在平面直角坐标系中，抛物线F1：y＝a（x−25）2+6415与x轴交于点A（−65，0）和点B，与y轴交于点C．（1）求抛物线F1的表达式；（2）如图2，将抛物线F1先向左平移1个单位，再向下平移3个单位，得到抛物线F2，若抛物线F1与抛物线F2相交于点D，连接BD，CD，BC．①求点D的坐标；②判断△BCD的形状，并说明理由；（3）在（2）的条件下，抛物线F2上是否存在点P，使得△BDP为等腰直角三角形，若存在，求出点P的坐标；若不存在，请说明理由．3．（2020•营口）在平面直角坐标系中，抛物线y＝ax2+bx﹣3过点A（﹣3，0），B（1，0），与y轴交于点C，顶点为点D．（1）求抛物线的解析式；（2）点P为直线CD上的一个动点，连接BC；①如图1，是否存在点P，使∠PBC＝∠BCO？若存在，求出所有满足条件的点P的坐标；若不存在，请说明理由；②如图2，点P在x轴上方，连接P A交抛物线于点N，∠P AB＝∠BCO，点M在第三象限抛物线上，连接MN，当∠ANM＝45°时，请直接写出点M的坐标．4．（2020•通辽）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A，B，与y轴交于点C．且直线y＝x﹣6过点B，与y轴交于点D，点C与点D关于x轴对称，点P是线段OB上一动点，过点P作x轴的垂线交抛物线于点M，交直线BD于点N．（1）求抛物线的函数解析式；（2）当△MDB的面积最大时，求点P的坐标；（3）在（2）的条件下，在y轴上是否存在点Q，使得以Q，M，N三点为顶点的三角形是直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由．5．（2020•咸宁）如图，在平面直角坐标系中，直线y=−12x+2与x轴交于点A，与y轴交于点B，抛物线y=−23x2+bx+c过点B且与直线相交于另一点C（52，34）．（1）求抛物线的解析式；（2）点P是抛物线上的一动点，当∠P AO＝∠BAO时，求点P的坐标；（3）点N（n，0）（0＜n＜52）在x轴的正半轴上，点M（0，m）是y轴正半轴上的一动点，且满足∠MNC＝90°．①求m与n之间的函数关系式；②当m在什么范围时，符合条件的N点的个数有2个？6．（2020•深圳）如图1，抛物线y＝ax2+bx+3（a≠0）与x轴的交点A（﹣3，0）和B（1，0），与y轴交于点C，顶点为D．（1）求该抛物线的解析式；（2）连接AD，DC，CB，将△OBC沿x轴以每秒1个单位长度的速度向左平移，得到△O 'B 'C '，点O 、B 、C 的对应点分别为点O '、B '、C '，设平移时间为t 秒，当点O '与点A 重合时停止移动．记△O 'B 'C '与四边形AOCD 重合部分的面积为S ，请直接写出S 与t 之间的函数关系式；（3）如图2，过该抛物线上任意一点M （m ，n ）向直线l ：y =92作垂线，垂足为E ，试问在该抛物线的对称轴上是否存在一点F ，使得ME ﹣MF =14？若存在，请求出F 的坐标；若不存在，请说明理由．7．（2020•天水）如图所示，拋物线y ＝ax 2+bx +c （a ≠0）与x 轴交于A 、B 两点，与y 轴交于点C ，且点A 的坐标为A （﹣2，0），点C 的坐标为C （0，6），对称轴为直线x ＝1．点D 是抛物线上一个动点，设点D 的横坐标为m （1＜m ＜4），连接AC ，BC ，DC ，DB ．（1）求抛物线的函数表达式；（2）当△BCD 的面积等于△AOC 的面积的34时，求m 的值； （3）在（2）的条件下，若点M 是x 轴上一动点，点N 是抛物线上一动点，试判断是否存在这样的点M ，使得以点B ，D ，M ，N 为顶点的四边形是平行四边形．若存在，请直接写出点M 的坐标；若不存在，请说明理由．8．（2020•辽阳）如图，抛物线y ＝ax 2﹣2√3x +c （a ≠0）过点O （0，0）和A （6，0）．点B 是抛物线的顶点，点D 是x 轴下方抛物线上的一点，连接OB ，OD ．（1）求抛物线的解析式；（2）如图①，当∠BOD＝30°时，求点D的坐标；（3）如图②，在（2）的条件下，抛物线的对称轴交x轴于点C，交线段OD于点E，点F是线段OB上的动点（点F不与点O和点B重合），连接EF，将△BEF沿EF折叠，点B的对应点为点B'，△EFB'与△OBE的重叠部分为△EFG，在坐标平面内是否存在一点H，使以点E，F，G，H为顶点的四边形是矩形？若存在，请直接写出点H的坐标，若不存在，请说明理由．9．（2020•烟台）如图，抛物线y＝ax2+bx+2与x轴交于A，B两点，且OA＝2OB，与y轴交于点C，连接BC，抛物线对称轴为直线x=12，D为第一象限内抛物线上一动点，过点D作DE⊥OA于点E，与AC交于点F，设点D的横坐标为m．（1）求抛物线的表达式；（2）当线段DF的长度最大时，求D点的坐标；（3）抛物线上是否存在点D，使得以点O，D，E为顶点的三角形与△BOC相似？若存在，求出m的值；若不存在，请说明理由．10．（2020•宜宾）如图，已知二次函数的图象顶点在原点，且点（2，1）在二次函数的图象上，过点F（0，1）作x轴的平行线交二次函数的图象于M、N两点．（1）求二次函数的表达式；（2）P为平面内一点，当△PMN是等边三角形时，求点P的坐标；（3）在二次函数的图象上是否存在一点E，使得以点E为圆心的圆过点F和点N，且与直线y＝﹣1相切．若存在，求出点E的坐标，并求⊙E的半径；若不存在，说明理由．11．（2020•潍坊）如图，抛物线y＝ax2+bx+8（a≠0）与x轴交于点A（﹣2，0）和点B（8，0），与y轴交于点C，顶点为D，连接AC，BC，BC与抛物线的对称轴l交于点E．（1）求抛物线的表达式；（2）点P是第一象限内抛物线上的动点，连接PB，PC，当S△PBC=35S△ABC时，求点P的坐标；（3）点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M，使得以点M，N，E为顶点的三角形与△OBC相似？若存在，求点M的坐标；若不存在，请说明理由．12．（2020•株洲）如图所示，二次函数y＝ax2+bx+c（a＞0）的图象（记为抛物线L）与y 轴交于点C，与x轴分别交于点A、B，点A、B的横坐标分别记为x1，x2，且0＜x1＜x2．（1）若a＝c，b＝﹣3，且过点（1，﹣1），求该二次函数的表达式；（2）若关于x的一元二次方程ax2+bx+c＝0的判别式△＝4．求证：当b＜−52时，二次函数y1＝ax2+（b+1）x+c的图象与x轴没有交点．（3）若AB2=c2−2c+6c，点P的坐标为（−√x0，﹣1），过点P作直线l垂直于y轴，且抛物线的L的顶点在直线l上，连接OP、AP、BP，P A的延长线与抛物线L交于点D，若∠OPB＝∠DAB，求x0的最小值．13．（2020•怀化）如图所示，抛物线y＝x2﹣2x﹣3与x轴相交于A、B两点，与y轴相交于点C，点M为抛物线的顶点．（1）求点C及顶点M的坐标．（2）若点N是第四象限内抛物线上的一个动点，连接BN、CN，求△BCN面积的最大值及此时点N的坐标．（3）若点D是抛物线对称轴上的动点，点G是抛物线上的动点，是否存在以点B、C、D、G为顶点的四边形是平行四边形．若存在，求出点G的坐标；若不存在，试说明理由．（4）直线CM交x轴于点E，若点P是线段EM上的一个动点，是否存在以点P、E、O 为顶点的三角形与△ABC相似．若存在，求出点P的坐标；若不存在，请说明理由．14．（2020•张家界）如图，抛物线y＝ax2﹣6x+c交x轴于A，B两点，交y轴于点C．直线y ＝﹣x +5经过点B ，C ．（1）求抛物线的解析式；（2）抛物线的对称轴l 与直线BC 相交于点P ，连接AC ，AP ，判定△APC 的形状，并说明理由；（3）在直线BC 上是否存在点M ，使AM 与直线BC 的夹角等于∠ACB 的2倍？若存在，请求出点M 的坐标；若不存在，请说明理由．15．（2020•广元）如图，直线y ＝﹣2x +10分别与x 轴，y 轴交于A ，B 两点，点C 为OB 的中点，抛物线y ＝x 2+bx +c 经过A ，C 两点．（1）求抛物线的函数表达式；（2）点D 是直线AB 下方的抛物线上的一点，且△ABD 的面积为452，求点D 的坐标；（3）点P 为抛物线上一点，若△APB 是以AB 为直角边的直角三角形，求点P 到抛物线的对称轴的距离．16．（2020•孝感）在平面直角坐标系中，已知抛物线y ＝ax 2+4ax +4a ﹣6（a ＞0）与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，顶点为点D ．（1）当a ＝6时，直接写出点A ，B ，C ，D 的坐标：A ，B ，C ，D ；（2）如图1，直线DC 交x 轴于点E ，若tan ∠AED =43，求a 的值和CE 的长；（3）如图2，在（2）的条件下，若点N为OC的中点，动点P在第三象限的抛物线上，过点P作x轴的垂线，垂足为Q，交AN于点F；过点F作FH⊥DE，垂足为H．设点P 的横坐标为t，记f＝FP+FH．①用含t的代数式表示f；②设﹣5＜t≤m（m＜0），求f的最大值．17．（2020•绥化）如图1，抛物线y=−12（x+2）2+6与抛物线y1＝﹣x2+12tx+t﹣2相交y轴于点C，抛物线y1与x轴交于A、B两点（点B在点A的右侧），直线y2＝kx+3交x轴负半轴于点N，交y轴于点M，且OC＝ON．（1）求抛物线y1的解析式与k的值；（2）抛物线y1的对称轴交x轴于点D，连接AC，在x轴上方的对称轴上找一点E，使以点A，D，E为顶点的三角形与△AOC相似，求出DE的长；（3）如图2，过抛物线y1上的动点G作GH⊥x轴于点H，交直线y2＝kx+3于点Q，若点Q'是点Q关于直线MG的对称点，是否存在点G（不与点C重合），使点Q'落在y轴上？若存在，请直接写出点G的横坐标，若不存在，请说明理由．18．（2020•福建）已知直线l1：y＝﹣2x+10交y轴于点A，交x轴于点B，二次函数的图象过A，B两点，交x轴于另一点C，BC＝4，且对于该二次函数图象上的任意两点P1（x1，y1），P2（x2，y2），当x1＞x2≥5时，总有y1＞y2．（1）求二次函数的表达式；（2）若直线l2：y＝mx+n（n≠10），求证：当m＝﹣2时，l2∥l1；（3）E为线段BC上不与端点重合的点，直线l3：y＝﹣2x+q过点C且交直线AE于点F，求△ABE与△CEF面积之和的最小值．19．（2020•菏泽）如图，抛物线y＝ax2+bx﹣6与x轴相交于A，B两点，与y轴相交于点C，OA＝2，OB＝4，直线l是抛物线的对称轴，在直线l右侧的抛物线上有一动点D，连接AD，BD，BC，CD．（1）求抛物线的函数表达式；（2）若点D在x轴的下方，当△BCD的面积是92时，求△ABD的面积；（3）在（2）的条件下，点M是x轴上一点，点N是抛物线上一动点，是否存在点N，使得以点B，D，M，N为顶点，以BD为一边的四边形是平行四边形，若存在，求出点N的坐标；若不存在，请说明理由．20．（2020•湘潭）如图，抛物线y＝﹣x2+bx+5与x轴交于A，B两点．（1）若过点C的直线x＝2是抛物线的对称轴．①求抛物线的解析式；②对称轴上是否存在一点P，使点B关于直线OP的对称点B'恰好落在对称轴上．若存在，请求出点P的坐标；若不存在，请说明理由．（2）当b≥4，0≤x≤2时，函数值y的最大值满足3≤y≤15，求b的取值范围．21．（2020•内江）如图，抛物线y＝ax2+bx+c经过A（﹣1，0）、B（4，0）、C（0，2）三点，点D（x，y）为抛物线上第一象限内的一个动点．（1）求抛物线所对应的函数表达式；（2）当△BCD的面积为3时，求点D的坐标；（3）过点D作DE⊥BC，垂足为点E，是否存在点D，使得△CDE中的某个角等于∠ABC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．22．（2020•黑龙江）如图，已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣1，0），B（3，0），与y轴交于点C．（1）求抛物线的解析式；（2）抛物线上是否存在点P，使∠P AB＝∠ABC，若存在请直接写出点P的坐标．若不存在，请说明理由．23．（2020•武汉）将抛物线C：y＝（x﹣2）2向下平移6个单位长度得到抛物线C1，再将抛物线C1向左平移2个单位长度得到抛物线C2．（1）直接写出抛物线C1，C2的解析式；（2）如图（1），点A在抛物线C1（对称轴l右侧）上，点B在对称轴l上，△OAB是以OB为斜边的等腰直角三角形，求点A的坐标；（3）如图（2），直线y＝kx（k≠0，k为常数）与抛物线C2交于E，F两点，M为线段EF的中点；直线y=−4k x与抛物线C2交于G，H两点，N为线段GH的中点．求证：直线MN经过一个定点．24．（2020•襄阳）如图，直线y=−12x+2交y轴于点A，交x轴于点C，抛物线y=−14x2+bx+c经过点A，点C，且交x轴于另一点B．（1）直接写出点A，点B，点C的坐标及拋物线的解析式；（2）在直线AC上方的抛物线上有一点M，求四边形ABCM面积的最大值及此时点M 的坐标；（3）将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O′A′，若线段O′A′与抛物线只有一个公共点，请结合函数图象，求m的取值范围．25．（2020•陕西）如图，抛物线y＝x2+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标．26．（2020•金昌）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣2交x轴于A，B两点，交y轴于点C，且OA＝2OC＝8OB．点P是第三象限内抛物线上的一动点．（1）求此抛物线的表达式；（2）若PC∥AB，求点P的坐标；（3）连接AC，求△P AC面积的最大值及此时点P的坐标．27．（2020•泸州）如图，已知抛物线y＝ax2+bx+c经过A（﹣2，0），B（4，0），C（0，4）三点．（1）求该抛物线的解析式；（2）经过点B的直线交y轴于点D，交线段AC于点E，若BD＝5DE．①求直线BD的解析式；②已知点Q在该抛物线的对称轴l上，且纵坐标为1，点P是该抛物线上位于第一象限的动点，且在l右侧，点R是直线BD上的动点，若△PQR是以点Q为直角顶点的等腰直角三角形，求点P的坐标．28．（2020•泰州）如图，二次函数y1＝a（x﹣m）2+n，y2＝6ax2+n（a＜0，m＞0，n＞0）的图象分别为C1、C2，C1交y轴于点P，点A在C1上，且位于y轴右侧，直线P A与C2在y轴左侧的交点为B．（1）若P点的坐标为（0，2），C1的顶点坐标为（2，4），求a的值；（2）设直线P A与y轴所夹的角为α．①当α＝45°，且A为C1的顶点时，求am的值；②若α＝90°，试说明：当a、m、n各自取不同的值时，PAPB的值不变；（3）若P A＝2PB，试判断点A是否为C1的顶点？请说明理由．29．（2020•齐齐哈尔）综合与探究在平面直角坐标系中，抛物线y=12x2+bx+c经过点A（﹣4，0），点M为抛物线的顶点，点B在y轴上，且OA＝OB，直线AB与抛物线在第一象限交于点C（2，6），如图①．（1）求抛物线的解析式；（2）直线AB的函数解析式为，点M的坐标为，cos∠ABO＝；连接OC，若过点O的直线交线段AC于点P，将△AOC的面积分成1：2的两部分，则点P的坐标为；（3）在y轴上找一点Q，使得△AMQ的周长最小．具体作法如图②，作点A关于y轴的对称点A'，连接MA'交y轴于点Q，连接AM、AQ，此时△AMQ的周长最小．请求出点Q的坐标；（4）在坐标平面内是否存在点N，使以点A、O、C、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．30．（2020•天津）已知点A（1，0）是抛物线y＝ax2+bx+m（a，b，m为常数，a≠0，m＜0）与x轴的一个交点．（Ⅰ）当a＝1，m＝﹣3时，求该抛物线的顶点坐标；（Ⅱ）若抛物线与x轴的另一个交点为M（m，0），与y轴的交点为C，过点C作直线l 平行于x轴，E是直线l上的动点，F是y轴上的动点，EF＝2√2．①当点E落在抛物线上（不与点C重合），且AE＝EF时，求点F的坐标；②取EF的中点N，当m为何值时，MN的最小值是√2 2？31．（2020•泰安）若一次函数y＝﹣3x﹣3的图象与x轴，y轴分别交于A，C两点，点B的坐标为（3，0），二次函数y＝ax2+bx+c的图象过A，B，C三点，如图（1）．（1）求二次函数的表达式；（2）如图（1），过点C作CD∥x轴交抛物线于点D，点E在抛物线上（y轴左侧），若BC恰好平分∠DBE．求直线BE的表达式；（3）如图（2），若点P在抛物线上（点P在y轴右侧），连接AP交BC于点F，连接BP，S△BFP＝mS△BAF．①当m=12时，求点P的坐标；②求m的最大值．32．（2020•德州）如图1，在平面直角坐标系中，点A 的坐标是（0，﹣2），在x 轴上任取一点M ，连接AM ，分别以点A 和点M 为圆心，大于12AM 的长为半径作弧，两弧相交于G ，H 两点，作直线GH ，过点M 作x 轴的垂线l 交直线GH 于点P ．根据以上操作，完成下列问题．探究：（1）线段P A 与PM 的数量关系为 ，其理由为： ．（2）在x 轴上多次改变点M 的位置，按上述作图方法得到相应点P 的坐标，并完成下列表格：M 的坐标… （﹣2，0） （0，0） （2，0） （4，0） … P 的坐标… （0，﹣1） （2，﹣2） …猜想：（3）请根据上述表格中P 点的坐标，把这些点用平滑的曲线在图2中连接起来；观察画出的曲线L ，猜想曲线L 的形状是 ．验证：（4）设点P 的坐标是（x ，y ），根据图1中线段P A 与PM 的关系，求出y 关于x 的函数解析式．应用：（5）如图3，点B （﹣1，√3），C （1，√3），点D 为曲线L 上任意一点，且∠BDC ＜30°，求点D 的纵坐标y D 的取值范围．33．（2020•连云港）在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y=12x2−32x﹣2的顶点为D，交x轴于点A、B（点A在点B左侧），交y轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P．（1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；（2）当BP﹣CP的值最大时，求点P的坐标；（3）设点Q是抛物线L1上的一个动点，且位于其对称轴的右侧．若△DPQ与△ABC相似，求其“共根抛物线”L2的顶点P的坐标．34．（2020•枣庄）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y 轴交于点C，连接AC，BC．M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q．（1）求抛物线的表达式；（2）过点P作PN⊥BC，垂足为点N．设M点的坐标为M（m，0），请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．35．（2020•凉山州）如图，二次函数y ＝ax 2+bx +c 的图象过O （0，0）、A （1，0）、B （32，√32）三点．（1）求二次函数的解析式；（2）若线段OB 的垂直平分线与y 轴交于点C ，与二次函数的图象在x 轴上方的部分相交于点D ，求直线CD 的解析式；（3）在直线CD 下方的二次函数的图象上有一动点P ，过点P 作PQ ⊥x 轴，交直线CD 于Q ，当线段PQ 的长最大时，求点P 的坐标．36．（2020•达州）如图，在平面直角坐标系xOy 中，已知直线y =12x ﹣2与x 轴交于点A ，与y 轴交于点B ，过A 、B 两点的抛物线y ＝ax 2+bx +c 与x 轴交于另一点C （﹣1，0）．（1）求抛物线的解析式；（2）在抛物线上是否存在一点P ，使S △P AB ＝S △OAB ？若存在，请求出点P 的坐标，若不存在，请说明理由；（3）点M 为直线AB 下方抛物线上一点，点N 为y 轴上一点，当△MAB 的面积最大时，求MN +12ON 的最小值．37．（2020•成都）在平面直角坐标系xOy 中，已知抛物线y ＝ax 2+bx +c 与x 轴交于A （﹣1，0），B （4，0）两点，与y 轴交于点C （0，﹣2）．（1）求抛物线的函数表达式；（2）如图1，点D 为第四象限抛物线上一点，连接AD ，BC 交于点E ，连接BD ，记△BDE 的面积为S 1，△ABE 的面积为S 2，求S 1S 2的最大值； （3）如图2，连接AC ，BC ，过点O 作直线l ∥BC ，点P ，Q 分别为直线l 和抛物线上的点．试探究：在第一象限是否存在这样的点P ，Q ，使△PQB ∽△CAB ．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．38．（2020•滨州）如图，抛物线的顶点为A （h ，﹣1），与y 轴交于点B （0，−12），点F （2，1）为其对称轴上的一个定点．（1）求这条抛物线的函数解析式；（2）已知直线l 是过点C （0，﹣3）且垂直于y 轴的定直线，若抛物线上的任意一点P （m ，n ）到直线l 的距离为d ，求证：PF ＝d ；（3）已知坐标平面内的点D （4，3），请在抛物线上找一点Q ，使△DFQ 的周长最小，并求此时△DFQ 周长的最小值及点Q 的坐标．39．（2020•济宁）我们把方程（x﹣m）2+（y﹣n）2＝r2称为圆心为（m，n）、半径长为r 的圆的标准方程．例如，圆心为（1，﹣2）、半径长为3的圆的标准方程是（x﹣1）2+（y+2）2＝9．在平面直角坐标系中，⊙C与x轴交于点A，B，且点B的坐标为（8，0），与y 轴相切于点D（0，4），过点A，B，D的抛物线的顶点为E．（1）求⊙C的标准方程；（2）试判断直线AE与⊙C的位置关系，并说明理由．40．（2020•聊城）如图，二次函数y＝ax2+bx+4的图象与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C，抛物线的顶点为D，其对称轴与线段BC交于点E，垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F，动直线l在抛物线的对称轴的右侧（不含对称轴）沿x轴正方向移动到B点．（1）求出二次函数y＝ax2+bx+4和BC所在直线的表达式；（2）在动直线l移动的过程中，试求使四边形DEFP为平行四边形的点P的坐标；（3）连接CP，CD，在动直线l移动的过程中，抛物线上是否存在点P，使得以点P，C，F为顶点的三角形与△DCE相似？如果存在，求出点P的坐标；如果不存在，请说明理由．41．（2020•乐山）已知抛物线y ＝ax 2+bx +c 与x 轴交于A （﹣1，0），B （5，0）两点，C 为抛物线的顶点，抛物线的对称轴交x 轴于点D ，连结BC ，且tan ∠CBD =43，如图所示．（1）求抛物线的解析式；（2）设P 是抛物线的对称轴上的一个动点．①过点P 作x 轴的平行线交线段BC 于点E ，过点E 作EF ⊥PE 交抛物线于点F ，连结FB 、FC ，求△BCF 的面积的最大值；②连结PB ，求35PC +PB 的最小值．42．（2020•甘孜州）如图，在平面直角坐标系xOy 中，直线y ＝kx +3分别交x 轴、y 轴于A ，B 两点，经过A ，B 两点的抛物线y ＝﹣x 2+bx +c 与x 轴的正半轴相交于点C （1，0）．（1）求抛物线的解析式；（2）若P 为线段AB 上一点，∠APO ＝∠ACB ，求AP 的长；（3）在（2）的条件下，设M 是y 轴上一点，试问：抛物线上是否存在点N ，使得以A ，P ，M ，N 为顶点的四边形为平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．43．（2020•自贡）在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A（﹣3，0）、B （1，0），交y轴于点N，点M为抛物线的顶点，对称轴与x轴交于点C．（1）求抛物线的解析式；（2）如图1，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E 作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：①求PD+PC的最小值；②如图2，Q点为y轴上一动点，请直接写出DQ+14OQ的最小值．44．（2020•重庆）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与y轴交于点C，与x轴交于A，B两点（点A在点B的左侧），且A点坐标为（−√2，0），直线BC的解析式为y=−√23x+2．（1）求抛物线的解析式；（2）过点A作AD∥BC，交抛物线于点D，点E为直线BC上方抛物线上一动点，连接CE，EB，BD，DC．求四边形BECD面积的最大值及相应点E的坐标；（3）将抛物线y＝ax2+bx+2（a≠0）向左平移√2个单位，已知点M为抛物线y＝ax2+bx+2（a≠0）的对称轴上一动点，点N为平移后的抛物线上一动点．在（2）中，当四边形BECD的面积最大时，是否存在以A，E，M，N为顶点的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．45．（2020•无锡）在平面直角坐标系中，O为坐标原点，直线OA交二次函数y=14x2的图象于点A，∠AOB＝90°，点B在该二次函数的图象上，设过点（0，m）（其中m＞0）且平行于x轴的直线交直线OA于点M，交直线OB于点N，以线段OM、ON为邻边作矩形OMPN．（1）若点A的横坐标为8．①用含m的代数式表示M的坐标；②点P能否落在该二次函数的图象上？若能，求出m的值；若不能，请说明理由．（2）当m＝2时，若点P恰好落在该二次函数的图象上，请直接写出此时满足条件的所有直线OA的函数表达式．46．（2020•重庆）如图，在平面直角坐标系中，已知抛物线y＝x2+bx+c与直线AB相交于A，B两点，其中A（﹣3，﹣4），B（0，﹣1）．（1）求该抛物线的函数表达式；（2）点P为直线AB下方抛物线上的任意一点，连接P A，PB，求△P AB面积的最大值；（3）将该抛物线向右平移2个单位长度得到抛物线y＝a1x2+b1x+c1（a1≠0），平移后的抛物线与原抛物线相交于点C，点D为原抛物线对称轴上的一点，在平面直角坐标系中是否存在点E，使以点B，C，D，E为顶点的四边形为菱形，若存在，请直接写出点E 的坐标；若不存在，请说明理由．47．（2020•遂宁）如图，抛物线y＝ax2+bx+c（a≠0）的图象经过A（1，0），B（3，0），C （0，6）三点．（1）求抛物线的解析式．（2）抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D，直线BE交AD于点E，若直线BE将△ABD的面积分为1：2两部分，求点E的坐标．（3）P为抛物线上的一动点，Q为对称轴上动点，抛物线上是否存在一点P，使A、D、P、Q为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．48．（2020•南充）已知二次函数图象过点A（﹣2，0），B（4，0），C（0，4）．（1）求二次函数的解析式．（2）如图，当点P为AC的中点时，在线段PB上是否存在点M，使得∠BMC＝90°？若存在，求出点M的坐标；若不存在，请说明理由．（3）点K在抛物线上，点D为AB的中点，直线KD与直线BC的夹角为锐角θ，且tanθ= 53，求点K的坐标．49．（2020•上海）在平面直角坐标系xOy 中，直线y =−12x +5与x 轴、y 轴分别交于点A 、B （如图）．抛物线y ＝ax 2+bx （a ≠0）经过点A ．（1）求线段AB 的长；（2）如果抛物线y ＝ax 2+bx 经过线段AB 上的另一点C ，且BC =√5，求这条抛物线的表达式；（3）如果抛物线y ＝ax 2+bx 的顶点D 位于△AOB 内，求a 的取值范围．50．（2020•常德）如图，已知抛物线y ＝ax 2过点A （﹣3，94）． （1）求抛物线的解析式；（2）已知直线l 过点A ，M （32，0）且与抛物线交于另一点B ，与y 轴交于点C ，求证：MC 2＝MA •MB ；（3）若点P ，D 分别是抛物线与直线l 上的动点，以OC 为一边且顶点为O ，C ，P ，D 的四边形是平行四边形，求所有符合条件的P 点坐标．一．二次函数综合题（共9小题）1．（2020•衢州）如图1，在平面直角坐标系中，△ABC 的顶点A ，C 分别是直线y =−83x +4与坐标轴的交点，点B的坐标为（﹣2，0），点D是边AC上的一点，DE⊥BC于点E，点F在边AB上，且D，F两点关于y轴上的某点成中心对称，连结DF，EF．设点D的横坐标为m，EF2为l，请探究：①线段EF长度是否有最小值．②△BEF能否成为直角三角形．小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究，请你一起来解决问题．（1）小明利用“几何画板”软件进行观察，测量，得到l随m变化的一组对应值，并在平面直角坐标系中以各对应值为坐标描点（如图2）．请你在图2中连线，观察图象特征并猜想l与m可能满足的函数类别．（2）小明结合图1，发现应用三角形和函数知识能验证（1）中的猜想，请你求出l关于m的函数表达式及自变量的取值范围，并求出线段EF长度的最小值．（3）小明通过观察，推理，发现△BEF能成为直角三角形，请你求出当△BEF为直角三角形时m的值．2．（2020•黔东南州）已知抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点（点A在点B 的左边），与y轴交于点C（0，﹣3），顶点D的坐标为（1，﹣4）．（1）求抛物线的解析式．（2）在y轴上找一点E，使得△EAC为等腰三角形，请直接写出点E的坐标．（3）点P是x轴上的动点，点Q是抛物线上的动点，是否存在点P、Q，使得以点P、Q、B、D为顶点，BD为一边的四边形是平行四边形？若存在，请求出点P、Q坐标；若不存在，请说明理由．3．（2020•湖州）如图，已知在平面直角坐标系xOy 中，抛物线y ＝﹣x 2+bx +c （c ＞0）的顶点为D ，与y 轴的交点为C ．过点C 的直线CA 与抛物线交于另一点A （点A 在对称轴左侧），点B 在AC 的延长线上，连结OA ，OB ，DA 和DB ．（1）如图1，当AC ∥x 轴时，①已知点A 的坐标是（﹣2，1），求抛物线的解析式；②若四边形AOBD 是平行四边形，求证：b 2＝4c ．（2）如图2，若b ＝﹣2，BC AC =35，是否存在这样的点A ，使四边形AOBD 是平行四边形？若存在，求出点A 的坐标；若不存在，请说明理由．4．（2020•嘉兴）在篮球比赛中，东东投出的球在点A 处反弹，反弹后球运动的路线为抛物线的一部分（如图1所示建立直角坐标系），抛物线顶点为点B ．（1）求该抛物线的函数表达式．（2）当球运动到点C 时被东东抢到，CD ⊥x 轴于点D ，CD ＝2.6m ．①求OD 的长．②东东抢到球后，因遭对方防守无法投篮，他在点D 处垂直起跳传球，想将球沿直线快速传给队友华华，目标为华华的接球点E （4，1.3）．东东起跳后所持球离地面高度h 1（m ）（传球前）与东东起跳后时间t （s ）满足函数关系式h 1＝﹣2（t ﹣0.5）2+2.7（0≤t ≤1）；小戴在点F （1.5，0）处拦截，他比东东晚0.3s 垂直起跳，其拦截高度h 2（m ）与东东起。

二次函数测试题及答案一、选择题1. 下列哪个选项不是二次函数的一般形式？A. y = ax^2 + bx + cB. y = 3x^2 - 2x + 1C. y = 5x^2 + 3D. y = 2x答案：D2. 二次函数y = ax^2 + bx + c的顶点坐标是：A. (-b, c)B. (-b/2a, c)C. (-b/2a, 4ac - b^2 / 4a)D. (-b/a, 4ac - b^2 / 4a)答案：C3. 若二次函数y = ax^2 + bx + c的图象开口向上，则a的取值范围是：A. a > 0B. a < 0C. a = 0D. a ≠ 0答案：A二、填空题4. 二次函数y = x^2 - 2x + 1的顶点坐标是_________。

答案：(1, 0)5. 当a > 0时，二次函数y = ax^2 + bx + c的图象与x轴的交点个数最多为_______。

答案：2三、解答题6. 已知二次函数y = 2x^2 - 4x + 3，求其顶点坐标。

解：首先，我们可以将二次函数写成顶点形式：y = 2(x - 1)^2 + 1。

因此，顶点坐标为(1, 1)。

7. 某二次函数的图象经过点(1, 1)和(2, 4)，且对称轴为直线x = 2。

求该二次函数的解析式。

解：设二次函数的解析式为y = a(x - 2)^2 + k。

将点(1, 1)代入得：1 = a(1 - 2)^2 + k1 = a + k将点(2, 4)代入得：4 = a(2 - 2)^2 + k4 = k由上述两个方程组可得a = -3，k = 4。

因此，该二次函数的解析式为y = -3(x - 2)^2 + 4。

四、应用题8. 某工厂生产一种产品，其成本函数为C(x) = 0.5x^2 - 10x + 100，其中x表示产品数量。

求该工厂生产多少件产品时，平均成本最低。

解：平均成本为C(x)/x = 0.5x - 10 + 100/x。

二次函数的练习题及答案一、选择题：1. 若二次函数y=ax^2+bx+c的图像开口向上，且与x轴有交点，则a 和b应满足的条件是（）。

A. a>0, b>0B. a<0, b<0C. a>0, b^2>4acD. a<0, b^2>4ac2. 二次函数y=-x^2+4x-1的顶点坐标是（）。

A. (1,4)B. (2,3)C. (-2,3)D. (2,-3)3. 对于二次函数y=ax^2+bx+c，当x=-1时，函数值最大，那么a的取值范围是（）。

A. a>0B. a<0C. a=0D. 无法确定二、填空题：1. 已知二次函数y=2x^2-8x+3，当x=______时，函数值最小。

2. 若二次函数y=-3x^2-6x+5的图像与x轴的交点坐标为（x1，0），（x2，0），则x1+x2=______。

三、解答题：1. 已知二次函数y=-2x^2+4x+1，求出当x取何值时，函数值y最大，并求出最大值。

2. 已知二次函数y=3x^2-6x+2，求出函数与x轴的交点坐标。

四、应用题：1. 某工厂生产一种产品，其生产成本与产品数量的关系可以近似为二次函数：C(x)=0.5x^2-100x+3000，其中x代表产品数量，C(x)代表成本。

求出当生产多少件产品时，成本最低，并求出最低成本。

2. 某公司计划在一块长为60米的空地上建一个矩形花园，花园的长和宽之和为30米。

设花园的长为x米，求出花园的面积最大时的长和宽，并求出最大面积。

答案：一、选择题：1. C2. B3. B二、填空题：1. 22. -2三、解答题：1. 当x=1时，函数值y最大，最大值为3。

2. 函数与x轴的交点坐标为（1，0）和（2，0）。

四、应用题：1. 当生产200件产品时，成本最低，最低成本为2000元。

2. 花园的长为15米，宽为15米时，面积最大，最大面积为225平方米。

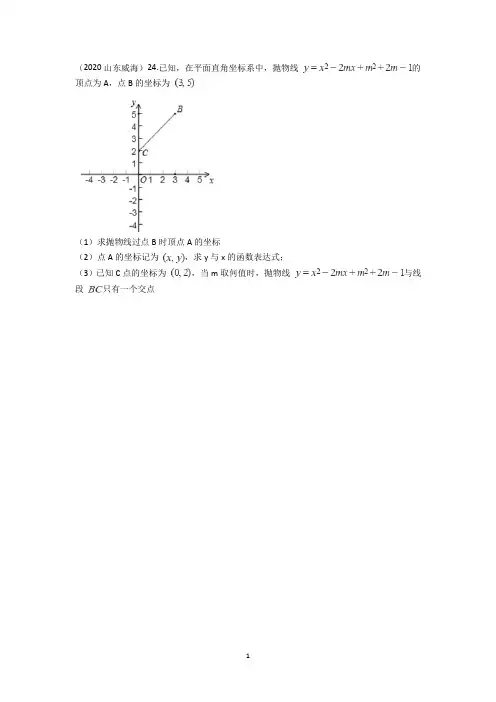
（2020山东威海）24.已知，在平面直角坐标系中，抛物线的顶点为A，点B的坐标为（1）求抛物线过点B时顶点A的坐标（2）点A的坐标记为，求y与x的函数表达式；（3）已知C点的坐标为，当m取何值时，抛物线与线段只有一个交点（2020山东淄博）24. ( 15分) 如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax2+bx+ （a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．（1）求这条抛物线对应的函数表达式；（2）已知R是抛物线上的点，使得△ADR的面积是平行四边形OABC的面积的，求点R 的坐标；（3）已知P是抛物线对称轴上的点，满足在直线MD上存在唯一的点Q，使得∠PQE＝45°，求点P的坐标．（2020山东烟台）25.如图，抛物线y＝ax2+bx+2与x轴交于A，B两点，且OA＝2OB，与y 轴交于点C，连接BC，抛物线对称轴为直线x＝，D为第一象限内抛物线上一动点，过点D作DE⊥OA于点E，与AC交于点F，设点D的横坐标为m．（1）求抛物线的表达式；（2）当线段DF的长度最大时，求D点的坐标；（3）抛物线上是否存在点D，使得以点O，D，E为顶点的三角形与相似？若存在，求出m的值；若不存在，请说明理由．（2020山东滨州）26. ( 15分) 如图，抛物线的顶点为A(h，－1)，与y轴交于点B ，点F(2，1)为其对称轴上的一个定点．（1）求这条抛物线的函数解析式；（2）已知直线l是过点C(0，－3)且垂直于y轴的定直线，若抛物线上的任意一点P(m，n)到直线l的距离为d，求证：PF＝d；（3）已知坐标平面内的点D(4，3)，请在抛物线上找一点Q，使△DFQ的周长最小，并求此时DFQ周长的最小值及点Q的坐标．（2020山东东营）24. ( 10分) 如图，抛物线的图象经过点，交x轴于点(点A在点B左侧)，连接直线与轴交于点D,与上方的抛物线交于点E,与交于点F．（1）求抛物线的解析式及点的坐标；（2）是否存在最大值？若存在，请求出其最大值及此时点E的坐标；若不存在，请说明理由．（山东潍坊）25.如图，抛物线与x轴交于点和点，与y轴交于点C，顶点为D，连接与抛物线的对称轴l交于点E．（1）求抛物线的表达式；（2）点P是第一象限内抛物线上的动点，连接，当时，求点P的坐标；（3）点N是对称轴l右侧抛物线上的动点，在射线上是否存在点M，使得以点M，N，E为顶点的三角形与相似？若存在，求点M的坐标；若不存在，请说明理由．（2020山东菏泽）24.如图，抛物线与轴相交于A，B两点，与y轴相交于点C，，，直线l是抛物线的对称轴，在直线l右侧的抛物线上有一动点D，连接，，，．（1）求抛物线的函数表达式；（2）若点D在x轴的下方，当的面积是时，求的面积；（3）在（2）的条件下，点M是x轴上一点，点N是抛物线上一动点，是否存在点N，使得以点B，D，M，N为顶点，以为一边的四边形是平行四边形，若存在，求出点N的坐标；若不存在，请说明理由．（2020山东枣庄）25.如图，抛物线交x轴于，两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作轴，交抛物线于点P，交BC于点Q．（1）求抛物线的表达式；（2）过点P作，垂足为点N．设M点的坐标为，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．（2020山东青岛）22.某公司生产A型活动板房成本是每个425元．图①表示A型活动板房的一面墙，它由长方形和抛物线构成，长方形的长，宽，抛物线的最高点E到的距离为．（1）按如图①所示的直角坐标系，抛物线可以用表示，求该抛物线的函数表达式；（2）现将A型活动板房改造为B型活动板房．如图②，在抛物线与之间的区域内加装一扇长方形窗户，点G，M在上，点N，F在抛物线上，窗户的成本为50元．已知，求每个型活动板房的成本是多少？（每个B型活动板房的成本＝每个A型活动板房的成本+一扇窗户的成本）（3）根据市场调查，以单价650元销售（2）中的型活动板房，每月能售出100个，而单价每降低10元，每月能多售出20个．公司每月最多能生产160个型活动板房．不考虑其他因素，公司将销售单价（元）定为多少时，每月销售型活动板房所获利润（元）最大？最大利润是多少？（2020山东泰安）25.若一次函数的图象与x轴，y轴分别交于A，C两点，点B的坐标为，二次函数的图象过A，B，C三点，如图（1）．（1）求二次函数的表达式；（2）如图（1），过点C作轴交抛物线于点D，点E在抛物线上（轴左侧），若恰好平分．求直线的表达式；（3）如图（2），若点P在抛物线上（点P在轴右侧），连接交于点F，连接，．①当时，求点P的坐标；②求的最大值．（2020山东临沂）25.已知抛物线．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；（3）设点，在抛物线上，若，求m的取值范围．（2020山东济宁）21.我们把方程(x- m)2+(y-n)2=r2称为圆心为(m，n)、半径长为r的圆的标准方程．例如，圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9．在平面直角坐标系中,圆C与轴交于点A．B．且点B的坐标为(8．0),与y轴相切于点D(0, 4)，过点A,B,D 的抛物线的顶点为E．（1）求圆C的标准方程；（2）试判断直线AE与圆C的位置关系，并说明理由．答案解析◆（2020山东威海）24.【答案】（1）解：∵抛物线y＝x2−2mx＋m2＋2m−1过点B（3，5），∴把B（3，5）代入y＝x2−2mx＋m2＋2m−1，整理得，m2−4m＋3＝0，解得m1＝1，m2＝3，当m＝1时，y＝x2−2x＋2＝（x−1）2＋1，其顶点A的坐标为（1，1）；当m＝3时，y＝x2−6x＋m2＋14＝（x−3）2＋5，其顶点A的坐标为（3，5）；综上，顶点A的坐标为（1，1）或（3，5）；（2）解：∵y＝x2−2mx＋m2＋2m−1＝（x−m）2＋2m−1，∴顶点A的坐标为（m，2m−1），∵点A的坐标记为（x，y），∴x＝m，∴y＝2x−1；（3）解：由（2）可知，抛物线的顶点在直线y＝2x−1上运动，且形状不变，由（1）知，当m＝1或3时，抛物线过B（3，5），把C（0，2）代入y＝x2−2mx＋m2＋2m−1，得m2＋2m−1＝2，解得m＝1或−3，所以当m＝1或−3时，抛物线经过点C（0，2），如图所示，当m＝−3或3时，抛物线与线段BC只有一个交点（即线段CB的端点），当m＝1时，抛物线同时过点B、C，不合题意，所以m的取值范围是−3≤m≤3且m≠1．【解析】【分析】（1）根据待定系数法求得解析式，然后把解析式化成顶点式即可求得；（2）化成顶点式，求得顶点坐标，即可得出y与x的函数表达式；（3）把C（0，2）代入y＝x2−2mx＋m2＋2m−1，求得m＝1或−3，结合（1）根据图象即可求得．◆（2020山东淄博）24.【答案】（1）解：OA＝2＝BC，故函数的对称轴为x＝1，则x＝﹣＝1①，将点A的坐标代入抛物线表达式得：0＝4a﹣2b+ ②，联立①②并解得，故抛物线的表达式为：y＝﹣x2+ x+ ③；（2）解：由抛物线的表达式得，点M（1，3）、点D（4，0）；∵△ADR的面积是▱OABC的面积的，∴×AD×|y R|＝×OA×OB，则×6×|y R|＝×2× ，解得：y R＝± ④，联立④③并解得，或故点R的坐标为（1+ ，4）或（1﹣，4）或（1+ ，﹣4）或（1﹣，﹣4）；（3）解：作△PEQ的外接圆R，∵∠PQE＝45°，故∠PRE＝90°，则△PRE为等腰直角三角形，当直线MD上存在唯一的点Q，则RQ⊥MD，点M、D的坐标分别为（1，4）、（4，0），则ME＝4，ED＝4﹣1＝3，则MD＝5，过点R作RH⊥ME于点H，设点P（1，2m），则PH＝HE＝HR＝m，则圆R的半径为m，则点R（1+m，m），S△MED＝S△MRD+S△MRE+S△DRE，即×EM•ED＝×MD×RQ+ ×ED•y R+ ×ME•RH，∴×4×3＝×5× m+ ×4×m+ ×3×m，解得m＝60 ﹣84，故点P（1，120 ﹣168）．◆（2020山东烟台）25.【答案】（1）解：设OB＝t，则OA＝2t，则点A、B的坐标分别为（2t，0）、（﹣t，0），则x＝＝（2t﹣t），解得：t＝1，故点A、B的坐标分别为（2，0）、（﹣1，0），则抛物线的表达式为：y＝a（x﹣2）（x+1）＝ax2+bx+2，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+x+2；（2）解：对于y＝﹣x2+x+2，令x＝0，则y＝2，故点C（0，2），由点A、C的坐标得，直线AC的表达式为：y＝﹣x+2，设点D的横坐标为m，则点D（m，﹣m2+m+2），则点F（m，﹣m+2），则DF＝﹣m2+m+2﹣（﹣m+2）＝﹣m2+2m，∵﹣1＜0，故DF有最大值，此时m＝1，点D（1，2）；（3）解：存在，理由：点D（m，﹣m2+m+2）（m＞0），则OD＝m，DE＝﹣m2+m+2，以点O，D，E为顶点的三角形与△BOC相似，则或，即＝2或，即＝2或，解得：m＝1或﹣2（舍去）或或（舍去），故m＝1或．【解析】【分析】（1）点A、B的坐标分别为（2t，0）、（﹣t，0），则x＝＝（2t﹣t），即可求解；（2）点D（m，﹣m2+m+2），则点F（m，﹣m+2），则DF＝﹣m2+m+2﹣（﹣m+2）＝﹣m2+2m，即可求解；（3）以点O，D，E为顶点的三角形与△BOC相似，则或，即＝2或，即可求解．◆（2020山东滨州）26.【答案】（1）解：设抛物线的函数解析式为由题意,抛物线的顶点为又抛物线与y轴交于点抛物线的函数解析式为（2）证明：∵P（m，n），∴，∴P（m，），∴，∵F（2，1），∴，∵，，∴d2=PF2，∴PF=d．（3）解：如图，过点Q作QH⊥直线l于H，过点D作DN⊥直线l于N．∵△DFQ的周长=DF+DQ+FQ，DF是定值= ，∴DQ+QF的值最小时，△DFQ的周长最小，∵QF=QH，∴DQ+DF=DQ+QH，根据垂线段最短可知，当D，Q，H共线时，DQ+QH的值最小，此时点H与N重合，点Q在线段DN上，∴DQ+QH的最小值为6，∴△DFQ的周长的最小值为，此时Q（4，- ）．◆（2020山东东营）24.【答案】（1）解：把代入，即，解得∴抛物线的解析式为令可得:∴；（2）解：存在，如图，由题意，点E在y轴的右侧，作轴，交于点G直线与轴交于点∴，设所在直线的解析式为，将代入上述解析式得：解得:的解析式为设则，其中.∴抛物线开口方向朝下∴当时，有最大值，最大值为.将t=2代入=-2+3+2=3∴点的坐标为．（2020山东潍坊）25.【答案】（1）解：抛物线过点和点抛物线解析式为：（2）解：当时，直线BC解析式为：过点P作PG 轴，交轴于点G，交BC于点F设即（3）解：为等腰直角三角形抛物线的对称轴为点E的横坐标为3又点E在直线BC上点E的纵坐标为5设①当MN=EM，, 时解得或（舍去）此时点M的坐标为②当ME=EN，时解得：或（舍去）此时点M的坐标为③当MN=EN，时连接CM，易知当N为C关于对称轴l的对称点时，，此时四边形CMNE为正方形解得：（舍去）此时点M的坐标为在射线上存在点M，使得以点M，N，E为顶点的三角形与相似，点M的坐标为：，或．【解析】【分析】（1）直接将和点代入，解出a，b的值即可得出答案；（2）先求出点C的坐标及直线BC的解析式，再根据图及题意得出三角形PBC的面积；过点P作PG 轴，交轴于点G，交BC于点F，设，根据三角形PBC的面积列关于t的方程，解出t的值，即可得出点P 的坐标；（3）由题意得出三角形BOC为等腰直角三角形，然后分MN=EM，MN=NE，NE=EM 三种情况讨论结合图形得出边之间的关系，即可得出答案．◆（2020山东菏泽）24.【答案】（1）解：∵OA=2，OB=4，∴A（-2，0），B（4，0），将A（-2，0），B（4，0）代入得：，解得：∴抛物线的函数表达式为：（2）解：由（1）可得抛物线的对称轴l：，，设直线BC：，可得：解得，∴直线BC的函数表达式为：，如图1，过D作DE⊥OB交OB于点F,交BC于点E，设，则，∴，由题意可得整理得解得（舍去），∴，∴∴；（3）解：存在由（1）可得抛物线的对称轴l：，由（2）知，①如图2当时，四边形BDNM即为平行四边形，此时MB=ND=4，点M与点O重合，四边形BDNM即为平行四边形，∴由对称性可知N点横坐标为-1，将x=-1代入解得∴此时，四边形BDNM即为平行四边形．②如图3当时，四边形BDMN为平行四边形，过点N做NP⊥x轴，过点D做DF⊥x轴，由题意可得NP=DF∴此时N点纵坐标为将y= 代入，得，解得：∴此时或，四边形BDMN为平行四边形．综上所述，或或．【解析】【分析】（1）直接利用待定系数法可求得函数解析式；（2）先求出函数的对称轴和直线BC的函数表达式，过D作DE⊥OB交OB于点F,交BC于点E，用式子表示出的面积从而求出D的坐标，进一步可得的面积；（3）根据平行四边形的性质得到，结合对称轴和点D坐标易得点N的坐标．◆（2020山东枣庄）25.【答案】（1）解：将，代入，得，解之，得．所以，抛物线的表达式为．（2）解：由，得．将点、代入，得，解之，得．所以，直线BC的表达式为：．由，得，．∴∵，∴．∴．∴．．∵∴当时，PN有最大值，最大值为．（3）解：存在，理由如下：由点，，知．①当时，过Q作轴于点E，易得，由，得，（舍）此时，点；②当时，则．在中，由勾股定理，得．解之，得或（舍）此时，点；③当时，由，得（舍）．综上知所述，可知满足条件的点Q有两个，坐标分别为：，．【解析】【分析】（1）将点A、B的坐标代入解析式中求解即可；（2）由(1)求得点C坐标，利用待定系数法求得直线BC的解析式，然后用m表示出PN，再利用二次函数的性质即可求解；（3）分三种情况：①AC=CQ；②AC=AQ；③CQ=AQ，分别求解即可．◆（2020山东青岛）22.【答案】（1）解：由题可知D（2,0），E（0,1）代入到得解得∴抛物线的函数表达式为；（2）解：由题意可知N点与M点的横坐标相同，把x=1代入，得y=∴N（1，）∴MN= m，∴S四边形FGMN=GM×MN=2× = ，则一扇窗户的价格为×50=75元因此每个B型活动板的成本为425+75=500元；（3）解：根据题意可得w=(n-500)（100+20× ）=-2（n-600）2+20000,∵一个月最多生产160个，∴100+20× ≤160解得n≥620∵-2＜0∴n≥620时，w随n的增大而减小∴当n=620时，w最大=19200元．【解析】【分析】（1）根据图形及直角坐标系可得到D,E的坐标，代入即可求解；（2）根据N点与M点的横坐标相同，求出N点坐标，再求出矩形FGMN的面积，故可求解；（3）根据题意得到w关于n的二次函数，根据二次函数的性质即可求解．◆（2020山东泰安）25.【答案】（1）解：令，得．令时，．∴．∵抛物线过点，∴．则，将代入得解得∴二次函数表达式为．（2）解：设交于点M．∵，∴，．∵，∴．∴．∵平分，∴．又∵，∴．∴．由条件得：．∴．∴．∴．∵，∴直线解析式为．（3）解：① ，∴．过点P作交于点N，则．∴．∵，∴．∵直线的表达式为，设，∴．∴．∴，则，解得．∴点或．②由①得：．∴．∴有最大值，．【解析】【分析】（1）先求的点A、C的坐标，再用待定系数法求二次函数的解析式即可；（2）设交于点M．由可得，．再由，根据平行线的性质可得，所以．已知平分，根据角平分线的定义可得．利用AAS证得．由全等三角形的性质可得．由此即可求得点M的坐标为（0，-1）．再由，即可求得直线解析式为；（3）①由可得．过点P作交于点N，则．根据相似三角形的性质可得．由此即可求得．设，可得．所以．由此即可得=2，解得．即可求得点或；②由①得．即．再根据二次函数的性质即可得．◆（2020山东临沂）25.【答案】（1）解：∵，∴，∴其对称轴为：．（2）解：由（1）知抛物线的顶点坐标为：，∵抛物线顶点在轴上，∴，解得：或，当时，其解析式为：，当时，其解析式为：，综上，二次函数解析式为：或．（3）解：由（1）知，抛物线的对称轴为，∴关于的对称点为，当函数解析式为时，其开口方向向上，∵且，∴；当函数解析式为时，其开口方向向下，∵且，∴或．【解析】【分析】（1）将二次函数化为顶点式，即可得到对称轴；（2）根据（1）中的顶点式，得到顶点坐标，令顶点纵坐标等于0，解一元二次方程，即可得到的值，进而得到其解析式；（3）根据抛物线的对称性求得点Q关于对称轴的对称点，再结合二次函数的图象与性质，即可得到的取值范围．◆（2020山东济宁）21.【答案】（1）解：连接CD，CB，过C作CF⊥AB，∵点D（0，4），B（8，0），设圆C半径为r，圆C与y轴切于点D，则CD=BC=OF=r，CF=4，∵CF⊥AB，∴AF=BF=8-r，在△BCF中，，即，解得：r=5，∴CD=OF=5，即C（5，4），∴圆C的标准方程为：；（2）解：由（1）可得：BF=3=AF，则OA=OB-AB=2，即A（2，0），设抛物线表达式为：，将A，B，D坐标代入，，解得：，∴抛物线表达式为：，∴可得点E（5，），设直线AE表达式为：y=mx+n，将A和E代入，可得：，解得：，∴直线AE的表达式为：，∵圆C的标准方程为，联立，解得：x=2，故圆C与直线AE只有一个交点，横坐标为2，即圆C与直线AE相切.【解析】【分析】（1）连接CD，CB，过C作CF⊥AB，分别表示出BF和CF，再在△BCF 中利用勾股定理构造方程求解即可得到圆C半径以及点C坐标，从而得到标准方程；（2）由（1）可得点A坐标，求出抛物线表达式，得到点E坐标，再求出直线AE的表达式，联立直线AE和圆C的表达式，通过判断方程根的个数即可得到两者交点个数，从而判断位置关系.。

二次函数50题一、选择题：1.若二次函数y=(m＋1)x2-mx＋m2-2m-3的图象经过原点，则m的值必为( )A.-1或3B.-1C.3D.-3或12.若为二次函数的图象上的三点，则的大小关系是（）A. B. C. D.3.如图，抛物线y=﹣x2+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列三个判断中，①当x＞0时，y＞0；②若a=﹣1，则b=4；③抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2；正确的是（）A．①B．②C．③D．①②③都不对4.已知一条抛物线经过E（0,10）,F（2,2）,G（4,2）,H（3,1）四点,选择其中两点用待定系数法能求出抛物线解析式的为（）A.E，FB.E，GC.E，HD.F，G5.已知二次函数y=ax2-1的图象开口向下，则直线y=ax-1经过的象限是( )A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限6.生产季节性产品的企业，当它的产品无利润时就会及时停产.现有一生产季节性产品的企业，其一年中获得的利润y和月份n之间函数关系式为y=-n2+14n-24，则该企业一年中利润最高的月份是( )A.5月B.6月C.7月D.8月7.已知抛物线y=x2﹣x，它与x轴的两个交点间的距离为（）A．0 B．1 C．2 D．48.一次函数y=ax+b（a≠0）与二次函数y=ax2+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（）A． B． C． D．9.二次函数y=x2+2x-7的函数值是8，那么对应的x的值是( )A.5B.3C.3或-5D.-3或510.抛物线y=3x2向下平移3个单位,再向左平移2个单位,得到的抛物线解析式为（）A.y=3(x+2)2+3B.y=3(x-2)2+3C.y=3(x+2)2﹣3D.y=3(x-2)2﹣311.已知二次函数y=x2+2x﹣3,当自变量x取m时,对应的函数值小于0,设自变量分别取m﹣4，m+4时对应的函数值为y1，y2，则下列判断正确的是（）A.y1＜0，y2＜0B.y1＜0，y2＞0C.y1＞0，y2＜0D.y1＞0，y2＞012.把抛物线y=(x+1)2向下平移2个单位,再向右平移1个单位,所得到抛物线是( )A.y=(x+2)2+2B.y=(x+2)2-2C.y=x2+2D.y=x2-213.生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业，其一年中获得的利润y和月份n之间函数关系式为y=﹣n2+14n﹣24，则该企业一年中应停产的月份是（）A.1月、2月、3月B.2月、3月、4月C.1月、2月、12月D.1月、11月、12月14.二次函数y=-x2+bx+c的图象如图所示:若点A(x1,y1),B(x2,y2)在此函数图象上,且x1<x2<1,则y1与y2的大小关系是( )A.y1≤y2B.y1<y2C.y1≥y2D.y1>y215.二次函数y=x2﹣4x+5的最小值是( )A.﹣1B.1C.3D.516.在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A（x1，y1），B（x2，y2）是该二次函数图象上的两点,其中﹣3≤x1＜x2≤0,则下列结论正确的是（）A.y1＜y2B.y1＞y2C.y的最小值是﹣3D.y的最小值是﹣417.二次函数y=ax2＋bx＋c(a下列结论：①ac＜0；②当x＞1时，y的值随x的增大而减小；③3是方程ax2＋(b-1)x+c=0的一个根；④当-1＜x＜3时，ax2＋(b-1)x＋c＞0.其中正确的个数为( )A．4个 B．3个 C．2个 D．1个18.如图,直线y=0.5x+2与y轴交于点A,与直线y=﹣0.5x交于点B，以AB为边向右作菱形ABCD，点C恰与原点O重合，抛物线y=(x﹣h)2+k的顶点在直线y=-0.5x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是（）A.﹣2≤h≤0.5B.﹣2≤h≤1C.﹣1≤h≤1.5D.﹣1≤h≤0.519.下列函数是二次函数的是( )A.y=2x+1B.y=-2x+1C.y=x2+2D.y=0.5x-220.抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到抛物线是（）A.y=3(x﹣1)2﹣2B.y=3(x+1)2﹣2C.y=3(x+1)2+2D.y=3(x﹣1)2+2二、填空题：21.已知点(2,5),(4,5)是抛物线y=ax2+bx+c上的两点, 则这条抛物线的对称轴是22.二次函数y=x2-3x+2的图像与x轴的交点坐标是 ,与y轴的交点坐标为23.对于二次函数，有下列说法：①如果当x≤1时随的增大而减小，则m≥1；②如果它的图象与x轴的两交点的距离是4，则；③如果将它的图象向左平移3个单位后的函数的最小值是-4，则m=－1；④如果当x=1时的函数值与x=2013时的函数值相等，则当x=2014时的函数值为－3．其中正确的说法是．24.如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何？25.如图，在Rt△ABC中，∠C=90°，AB= 5，AC= 4，则cos A= ．A B C26.抛物线y=2（x﹣3）2+3的顶点在象限．27.某种商品每件进价为20元，调查表明：在某段时间内若以每件x元（20≤x≤30，且x为整数）出售，可卖出（30﹣x）件．若使利润最大，每件的售价应为元．28.如图,点A是抛物线y=x2﹣4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为．29.如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°，按以下步骤作图：①以点B为圆心，小于AB的长为半径画弧，分别交AB、BC于点M、N；②分别以点M、N为圆心，大于0.5MN的长为半径画弧，两弧相交于点G；③连结BG交AC边于点E，交⊙O于点D，连接CD.则△ABE与△CDE的面积之比为．30.将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是 cm2．31.如图，二次函数y1＝ax2＋bx＋c(a≠0)与一次函数y2＝kx＋m(k≠0)的图象相交于点A(－2，4)，B(8，2)，则使y1＞y2成立的x的取值范围是__ _．32.如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1，将C1向右平移得C2，C2与x轴交于点B，D，若直线y=x+m与C1，C2共有3个不同的交点，则m的取值范围是．33.如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（0.5，2.5）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．当△PAC为直角三角形时, 点P的坐标是____________________．34.如图,已知函数y=与y=ax2+bx（a＞0，b＞0）的图象交于点P,点P的纵坐标为1.则关于x的方程ax2+bx+=0的解为．35.二次函数y=2（x﹣3）2﹣4的最小值为．36.如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x=2，且OA=OC，则下列结论：①abc＞0；②9a+3b+c＜0；③c＞﹣1；④关于x的方程ax2+bx+c=0（a≠0）有一个根为 -a-1.其中正确的结论个数有（填序号）37.已知二次函数y=﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m=0的解为．38.如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为米.39.若抛物线y1=a1x2+b1x+c1与y2=a2x2+b2x+c2满足=k（k≠0,1）,则称y1，y2互为“相关抛物线”.给出如下结论：①y1与y2的开口方向，开口大小不一定相同；②y1与y2的对称轴相同；③若y2的最值为m，则y1的最值为k2m；④若y2与x轴的两交点间距离为d，则y1与x轴的两交点间距离也为d．其中正确的结论的序号是（把所有正确结论的序号都填在横线上）．40.如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是．三、解答题：41.已知二次函数y=x2+bx+c的图象经过点（0，2）和（1，﹣1），求图象的顶点坐标和对称轴．42.一元二次方程x2+2x-3=0的二根x1,x2(x1< x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标，且此抛物线过点A(3,6)．（1）求此二次函数的解析式．（2）用配方法求此抛物线的顶点为P对称轴（3）当x取什么值时，y随x增大而减小？43.某水渠的横截面呈抛物线形,水面的宽为AB（单位：米）,现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4.（1）求a的值；（2）点C（-1，m）是抛物线上一点，点C关于原点O的对称点为点D，连接CD,BC,BD，求△BCD的面积.44.某公司销售A，B两种产品，根据市场调研，确定两条信息：信息1：销售A种产品所获利润y：（万元）与销售产品x（吨）之间存在二次函数关系，如图所示：信息2：销售B种产品所获利润y（万元）与销售产品x（吨）之间存在正比例函数关系y2=0.3x．根据以上信息，解答下列问题；（1）求二次函数解析式；（2）该公司准备购进A、B两种产品共10吨，求销售A、B两种产品获得的利润之和最大是多少万元．45.已知抛物线y=x2﹣2x+1．（1）求它的对称轴和顶点坐标；（2）根据图象，确定当x＞2时，y的取值范围．46. 某种商品的进价为每件50元，售价为每件60元，每个月可卖出200件；如果每件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于72元），设每件商品的售价上涨x元（x为整数），每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少时每个月可获得最大利润?最大利润是多少?47.如图，二次函数y=﹣x2+bx+c图象（抛物线）与x轴交于A（1,0）,且当x=0和x=﹣2时所对应函数值相等．（1）求此二次函数的表达式；（2）设抛物线与x轴的另一交点为点B，与y轴交于点C，在这条抛物线的对称轴上是否存在点D，使得△DAC 的周长最小？如果存在，求出D点的坐标；如果不存在，请说明理由．（3）设点M在第二象限，且在抛物线上，如果△MBC的面积最大，求此时点M的坐标及△MBC的面积．48.如图,已知二次函数的图象经过点A（6,0）、B（﹣2,0）和点C（0,﹣8）．（1）求该二次函数的解析式；（2）设该二次函数图象的顶点为M，若点K为x轴上的动点，当△KCM的周长最小时，点K的坐标为；（3）连接AC，有两动点P、Q同时从点O出发，其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动，点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动，当P、Q两点相遇时，它们都停止运动，设P、Q同时从点O出发t秒时，△OPQ的面积为S．①请问P、Q两点在运动过程中，是否存在PQ∥OC？若存在，请求出此时t的值；若不存在，请说明理由；②请求出S关于t的函数关系式，并写出自变量t的取值范围；③设S0是②中函数S的最大值，直接写出S0的值．49.如图，直线y=0.5x﹣2与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx﹣2经过A，B，C，点B坐标为（﹣1，0）．（1）求抛物线的解析式；（2）若点D是线段AC上一个动点，DE⊥AC，交直线AC下方的抛物线于点E，EG⊥x轴于点G，交AC于点F，请求出DF长的最大值；（3）设抛物线对称轴与x轴相交于点H，点P是射线CH上的一个动点，当△ABP是直角三角形时，请直接写出点P的坐标．50.如图,在平面直角坐标系中,点A的坐标为（m，m）,点B的坐标为（n，-n）,抛物线经过A、O、B三点,连结OA、OB、AB，线段AB交y轴于点C．已知实数m、n（m＜n）分别是方程x2-2x-3=0的两根.（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E两点（点D在y轴右侧），连结OD、BD.①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标.参考答案1.C2.D3.C4.C5.D6.C7.C8.C9.C10.C11.D12.D13.C14.B15.B16.D17.B18.A19.C20.A21.答案为：(0,6) ； (2,0),(3,0)22.答案为：（1,0），（2,0）、（0,2），23.答案为：①②④．24.答案为：0.8．25.答案为：0.826.答案为：第一．27.答案为：2528.答案为：（2，﹣1）或（2，2）．29.答案为0.5．30.答案为:12.5;31.答案为：x＜－2或x＞832.解：令y=﹣2x2+8x﹣6=0，即x2﹣4x+3=0，解得x=1或3，则点A（1，0），B（3，0），由于将C1向右平移2个长度单位得C2，则C2解析式为y=﹣2（x﹣4）2+2（3≤x≤5），当y=x+m1与C2相切时，令y=x+m1=y=﹣2（x﹣4）2+2，即2x2﹣15x+30+m1=0，△=﹣8m1﹣15=0，解得m1=﹣，当y=x+m2过点B时，即0=3+m2，m2=﹣3，当﹣3＜m＜﹣时直线y=x+m与C1、C2共有3个不同的交点，故答案是：﹣3＜m＜﹣．33.答案为：（3，5）或（3.5，5.5）33.答案为：x=﹣3．34.答案为：﹣4．35.答案为：①③④；36.答案为：x1=4，x2=﹣237.答案为:0.538.答案为：①②④．39.答案为：-1＜x＜3．40.解：把点（0，2）和（1，﹣1）代入y=x2+bx+c得，解这个方程组得，所以所求二次函数的解析式是y=x2﹣4x+2；因为y=x2﹣4x+2=（x﹣2）2﹣2，所以顶点坐标是（2，﹣2），对称轴是直线x=2．y=0.5(x+1)2 -2 ∴它的顶点坐标为（-1，-2）对称轴为直线x=-1.当y=0时，即0.5(x+3)(x-1)=0解得x1=-3，x2=1.∴x＜-3时…当x取什么值时， y随x增大而减小.41.解：（1）∵ ,由抛物线的对称性可知,∴（4,0）.∴ 0＝16a-4.∴ a.（2）如图所示，过点C作于点E，过点D作于点F.∵ a=,∴ -4.当-1时，m=×-4=-,∴ C（-1,-）.∵点C关于原点O的对称点为点D，∴ D（1,）.∴ .∴△BCD的面积为15平方米.42.解：（1）根据题意，设销售A种产品所获利润y与销售产品x之间的函数关系式为y=ax2+bx，将（1，1.4）、（3，3.6）代入解析式，得：a+b=1.4,9a+3b=3.6，解得：a=-0.1,b=1.5，∴销售A种产品所获利润y与销售产品x之间的函数关系式为y=﹣0.1x2+1.5x；（2）设购进A产品m吨，购进B产品（10﹣m）吨，销售A、B两种产品获得的利润之和为W元，则W=﹣0.1m2+1.5m+0.3（10﹣m）=﹣0.1m2+1.2m+3=﹣0.1（m﹣6）2+6.6，∵﹣0.1＜0，∴当m=6时，W取得最大值，最大值为6.6万元，答：购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元．44.【解答】解：（1）y=x2﹣2x+1=（x﹣1）2，对称轴为直线x=1，顶点坐标为（1，0）；（2）抛物线图象如下图所示：由图象可知当x＞2时，y的取值范围是y＞1．45.解答：解：（1）y=（30－20+x）（180－10x）=－10x2+80x+1800（0≤x≤5，且x为整数）；（2）当x=时，y最大=1960元；∴每件商品的售价为34元．答：每件商品的售价为34元时，商品的利润最大，为1960元；（3））1920=－10x2+80x+1800 ， x2－8x+12=0，即（x－2）（x－6）=0，解得x=2或x=6，∵0≤x≤5，∴x=2，∴售价为32元时，利润为1920元．46.【解答】解：（1）∵当x=0和x=﹣2时所对应的函数值相等，∴抛物线的对称轴为直线x=﹣1，∴抛物线与x轴的另一个交点坐标为（﹣3，0），∴抛物线解析式为y=﹣（x+3）（x﹣1），即y=﹣x2﹣2x+3；（2存在．连结BC交直线x=﹣1于点D，则DB=DA，∴DC+DA=DC+DB=BC，∴此时DA+DC最小，△ADC的周长最小，当x=0时，y=﹣x2﹣2x+3=3，则C（0，3），设直线BC的解析式为y=kx+m，把B（﹣3，0），C（0，3）代入得，解得，∴直线BC的解析式为y=x+3，当x=﹣1时，y=x+3=2，∴D点坐标为（﹣1，2）；（3）作MN∥y轴交BC于N，如图，设M（t，﹣t2﹣2t+3）（﹣3＜x＜0），则N（t，t+3），S△BCM=S△MNB+S△NMC=•3•MN=（﹣t2﹣2t+3﹣t﹣3）=﹣t2﹣t=﹣（t+）2+，∴当t=﹣时，△MBC的面积的最大值为，此时M点坐标为（﹣，）．47.解：（1）设二次函数的解析式为y=a（x+2）（x﹣6）∵图象过点（0，﹣8）∴a=∴二次函数的解析式为y=x2﹣x﹣8；（2）∵y=x2﹣x﹣8=（x2﹣4x+4﹣4）﹣8=（x﹣2）2﹣∴点M的坐标为（2，﹣）∵点C的坐标为（0，﹣8），∴点C关于x轴对称的点C′的坐标为（0，8）∴直线C′M的解析式为：y=﹣x+8令y=0得﹣x+8=0解得：x=∴点K的坐标为（，0）；（3）①不存在PQ∥OC，若PQ∥OC，则点P，Q分别在线段OA，CA上，此时，1＜t＜2∵PQ∥OC，∴△APQ∽△AOC∴∵AP=6﹣3tAQ=18﹣8t，∴∴t=∵t=＞2不满足1＜t＜2；∴不存在PQ∥OC；②分情况讨论如下，情况1：0≤t≤1S=OP•OQ=×3t×8t=12t2；情况2：1＜t≤2作QE⊥OA，垂足为E，S=OP•EQ=×3t×=﹣+情况3：2＜t＜作OF⊥AC,垂足为F,则OF=S=QP•OF=×(24-11t)×=-+；③当0≤t≤1时，S=12t2，函数的最大值是12；当1＜t≤2时，S=﹣+，函数的最大值是；当2＜t＜，S=QP•OF=﹣+，函数的最大值为；∴S0的值为．49.50.解（1）解方程，得，.∵，∴，∴A（-1，-1），B（3，-3）.∵抛物线过原点，设抛物线的解析式为.∴解得，.∴抛物线的解析式为.（2）①设直线AB的解析式为.∴解得，. ∴直线AB的解析式为.∴C点坐标为（0，）.∵直线OB过点O（0，0），B（3，-3），∴直线OB的解析式为.∵△OPC为等腰三角形，∴OC=OP或OP=PC或OC=PC.设，，（i）当OC=OP时, .解得，（舍去）. ∴ P（,）.（ii）当OP=PC时，点P在线段OC的中垂线上，∴ (,.（iii）当OC=PC时，由，解得，（舍去）. ∴ P(.∴P点坐标为P1（,）或(,或P(.②过点D作DG⊥x轴，垂足为G，交OB于Q，过B作BH⊥x轴，垂足为H.设Q（，），D(，).===，∵0＜＜3，∴当时，S取得最大值为，此时D（，.。

二次函数单元测试题及答案一、选择题1. 二次函数y = ax^2 + bx + c中，当a的值变为原来的2倍时，函数图像如何变化？A. 向上平移B. 向下平移C. 向左平移D. 向右平移答案：B2. 下列哪个选项是二次函数的标准形式？A. y = x^2 + 2x + 1B. y = 2x^2 - 3x + 4C. y = 3x + 4D. y = x - 2答案：B3. 若二次函数y = -2x^2 + 3x + 1的顶点坐标为(1, 2)，则下列哪个选项是正确的？A. a = -2, b = 3, c = 1B. a = 2, b = -3, c = -1C. a = -2, b = -3, c = -1D. a = 2, b = 3, c = 1答案：A4. 二次函数y = 3x^2 - 6x + 9的最小值是多少？A. 0B. 3C. 9D. 无法确定答案：C5. 如果二次函数y = x^2 + 4x + 4的图像与x轴相交于两点A和B，那么线段AB的长度是多少？A. 2B. 4C. 6D. 8答案：C二、填空题6. 已知二次函数y = 2x^2 - 5x + 3，其顶点坐标为__________。

答案：(1, -1)7. 函数y = -x^2 + 4x - 3的最大值是__________。

答案：18. 若二次函数y = 3x^2 - 2x - 5的图像关于y轴对称，则新的函数表达式为y = __________。

答案：y = 3x^2 + 2x - 5三、解答题9. 已知二次函数y = -2x^2 + 6x + 3，求该函数在x = -1时的函数值。

答案：当x = -1时，y = -2*(-1)^2 + 6*(-1) + 3 = -2 - 6 + 3 =-5。

10. 给定二次函数y = x^2 - 6x + 9，求该函数的对称轴方程。

答案：对称轴为x = -b/(2a) = -(-6)/(2*1) = 3。

二次函数单元测试题姓名： 班级： 学号： 成绩： .一、选择题（共10小题；共30分） 1. 下列函数中不是二次函数的是A.B.C.D.2. 下列各点中，在函数 的图象上的点是A.C.D.3.对于函数 的图象，下列说法不正确的是A. 开口向下B. 对称轴是C. 最大值为D. 与轴不相交4. 已知函数 ，下列结论正确的是A. 当 时， 随的增大而减小 B. 当 时， 随 的增大而增大 C. 当时， 随的增大而减小 D. 当 时， 随的增大而增大5. 如图在同一个坐标系中函数和的图象可能的是A.B.C.D.6. 关于抛物线；下列说法正确的是A. 顶点是坐标原点B. 对称轴是直线C. 有最高点D. 经过坐标原点7. 将抛物线 向左平移 个单位，再向上平移 个单位，平移后所得抛物线的解析式为A. B.C.D.8. 将二次函数，化为的形式，结果为A. B.C. D.9. 某畅销书的售价为每本元，每星期可卖出本．书城准备开展“读书节活动”，决定降价促销．经调研，如果调整书籍的售价，每降价元，每星期可多卖出本．设每件商品降价元后，每星期售出此畅销书的总销售额为元，则与之间的函数关系式为A. B.C. D.10. 如图，抛物线和直线都经过点，抛物线的对称轴为，那么下列说法正确的是A.B.C.D. 是的解二、填空题（共6小题；共18分）11. 已知二次函数，当时，随的增大而（填“增大”或“减小”）．12. 抛物线的顶点坐标为；当时，随的增大而减少．13.已知，是抛物线上的两点，则（填，，）．14. 函数的图象的对称轴是，顶点坐标是．15. 若把函数化为的形式，其中，为常数，则．16. 二次函数的图象如图所示，下列结论：①；②；③一元二次方程有两个不相等的实数根；④当或时，．上述结论中正确的是（填所有正确结论的序号）．三、解答题（共4小题；共52分）17. 已知关于的二次函数的图象经过，两点，求这个二次函数的解析式．18. 已知抛物线．（1）写出抛物线的开口方向、对称轴和顶点坐标；（2）当随的增大而增大时，求的取值范围．19. 某童装专卖店在销售中发现，一款童装每件进价为元，若销售价为元，每天可售出件，为迎接“双十一”，专卖店决定采取适当的降价措施，以扩大销售量，经市场调查发现，如果毎件童装降价元，那么平均每天可多售出件，设每件降价元，平均每天可盈利元．（1）写出与的函数关系式；（2）当该专卖店每件童装降价多少元时，平均每天盈利元?（3）该专卖店要想平均每天盈利元，可能吗?请说明理由．20. 如图，已知抛物线与轴交于，两点，与轴交于点，点的坐标为．（1）求的值及抛物线的顶点坐标；（2）点是抛物线对称轴上的一个动点，当的值最小时，求点的坐标．答案第一部分1. D2. B 【解析】A，把代入函数关系式：，故此点不在函数图象上；B，把代入函数关系式：，故此点在函数图象上；C，把代入函数关系式：，故此点不在函数图象上；D，把代入函数关系式：，故此点不在函数图象上；故选：B．3. D4. C 【解析】函数，对称轴为直线，开口方向上，故当时，随的增大而减小．5. C【解析】当时，函数的图象经过一、三、四象限；函数的开口向上，对称轴在轴上；当时，函数的图象经过二、三、四象限；函数的开口向下，对称轴在轴上，故C正确．6. D7. A 【解析】，原抛物线顶点坐标为，向左平移个单位，再向上平移个单位，平移后的抛物线顶点坐标为，所得抛物线解析式为，故选A．8. D9. B10. D【解析】由图象可知，，，故A错误；由图象得知抛物线与轴有两个不同的交点，，故B错误；过点，．过点，．，故C错误；对称轴为，．．．当时，，由图象可知，，，即；故D正确．第二部分11. 增大12. ，13.【解析】，是抛物线上的两点，，，．14. 直线，16. ②③④第三部分17. ．18. （1）．所以抛物线的开口向下，抛物线的对称轴为直线，顶点坐标为；（2）抛物线开口向下，在对称轴的右侧随的增大而增大，抛物线的对称轴，当时随的增大而增大．19. （1）根据题意，．（2）当时，，解得，（舍）．答：当每件童装降价元时平均每天盈利元．（3）不可能盈利元．当时，，，．方程无实数根．答：不可能盈利元．20. （1）把代入得：，解得：．，，顶点坐标为．（2）连接并交抛物线对称轴于点，连接，此时的值最小．设是直线上任意一点，连接，，，则，，，，即．设直线的解析式为，把，代入，得直线的解析式为．当时，．当的值最小时，点的坐标为．。

2020年初中数学二次函数综合题及答案(经典题型)启东教育精心教学启东教育提供了一份学科教师辅导讲义，其中包括了二次函数试题。

以下是其中的选择题和填空题：选择题：1.若y=(m-2)x^2-m是关于x的二次函数，则m=（）A。

-1B。

2C。

-1或2D。

m不存在2.下列函数关系中，可以看作二次函数y=ax^2+bx+c(a≠0)模型的是（）A。

在一定距离内，汽车行驶的速度与行驶的时间的关系B。

我国人口自然增长率为1%，这样我国总人口数随年份变化的关系C。

矩形周长一定时，矩形面积和矩形边长之间的关系D。

圆的周长与半径之间的关系4.将一抛物线向下向右各平移2个单位得到的抛物线是y=-x^2，则抛物线的解析式是（）A。

y=-(x-2)^2+2B。

y=-(x+2)^2+2C。

y=-(x+2)^2+2D。

y=-(x-2)^2-25.抛物线y=x^2-6x+24的顶点坐标是（）A。

(-6,-6)B。

(-6,6)C。

(6,6)D。

(6,-6)6.已知函数y=ax^2+bx+c，图象如图所示，则下列结论中正确的有（）个A。

-1B。

2C。

3D。

47.函数y=ax^2-bx+c（a≠0）的图象过点（-1，），则y=abc的值是（）A。

-1B。

1C。

2D。

-28.已知一次函数y=ax+c与二次函数y=ax^2+bx+c（a≠0），它们在同一坐标系内的大致图象如图所示：其中，A、B、C、D分别表示以下哪个函数？A。

y=ax+c，y=ax^2+bx+cB。

y=ax+c，y=-ax^2+bx+cC。

y=-ax+c，y=ax^2+bx+cD。

y=-ax+c，y=-ax^2+bx+c填空题：13.无论m为任何实数，总在抛物线y=x^2+2mx+m上的点的坐标是（）。

答案：（m,m）16.若抛物线y=ax^2+bx+c（a≠0）的对称轴为直线x=2，最小值为-2，则关于方程ax^2+bx+c=-2的根为（）。

答案：（3,0）和（1,0）17.抛物线y=(k+1)x^2+k^2-9开口向下，且经过原点，则k=（）。

《二次函数》单元测试卷 (含答案)考生姓名：______________ 考号：______________时间限制：90分钟一、选择题（每小题2分，共30分）（每小题2分，共30分）1. 下列函数中，是二次函数的是（）A. y = x + 2B. y = 2x^2 + 3x + 1C. y = 1/xD. y = √x2. 设二次函数 f(x) = 2x^2 + 5x - 3，那么它的判别式为（）A. -13B. 17C. 29D. -393. 若二次函数的图象与x轴有两个交点，则该二次函数的判别式必须为（）A. 大于0B. 等于0C. 小于0D. 无法确定4. 已知二次函数 f(x) = 3x^2 + 4x + 2，那么它的对称轴为（）A. x = -2/3B. x = -4/3C. x = 4/3D. x = 2/35. 设函数 f(x) = ax^2 + bx + c，若a > 0，则函数图象开口向（）A. 上B. 下C. 左D. 右...二、填空题（每小题3分，共30分）（每小题3分，共30分）1. 设二次函数 f(x) = 2x^2 - 5x + 3，那么它的顶点坐标为（）答案：(5/4, 37/8)2. 若二次函数 y = ax^2 + bx + c 的顶点坐标为 (2, -3)，则 a + b+ c 的值为（）答案：-53. 设二次函数 f(x) = -x^2 + 4x + 5，那么它的对称轴的方程为（）答案：x = 24. 若二次函数的图象与y轴相交于点 (0, 6)，则该二次函数必定为（）答案：f(x) = 2x^2 + 35. 设二次函数 f(x) = ax^2 + bx + c，若a > 0，则函数的值域为（）答案：( -∞, f(c) ]...三、解答题（共40分）（共40分）1. 解方程 3x^2 - 2x - 1 = 0解答：首先，我们可以求出这个二次方程的判别式：Δ = b^2 - 4ac = (-2)^2 - 4*3*(-1) = 4 + 12 = 16因为判别式大于0，所以方程有两个不相等的实根。

2020苏科版九下第五章《二次函数》（难题）单元测试（一）班级：___________姓名：___________得分：___________一、选择题（本大题共10小题，共30分）1.已知二次函数y=ax2+bx+c(a≠0)图象如图所示，下列结论：①abc<0；②2a−b<0；③b2>(a+c)2；④点(−3,y1)，(1,y2)都在抛物线上，则有y1>y2．其中正确的结论有()A. 4个B. 3个C. 2个D. 1个2.已知二次函数y=−14x2+bx+c的图象如下，则一次函数y=−14x−2b与反比例函数y=cx在同一平面直角坐标系中的图象大致是()A. B.C. D.3.二次函数y=ax2+bx+c(a≠0)的图象如图所示，下列结论：①ac>0；②当x≥1时，y随x的增大而减小；③2a+b=0；④b2−4ac<0；⑤4a−2b+c>0，其中正确的个数是()A. 1B. 2C. 3D. 44.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示，与x轴的一个交点坐标为(4,0)，抛物线的对称轴是x=1.下列结论中：①abc>0；②2a+b=0；③方程ax2+bx+c=2有两个不相等的实数根；④4a−2b+c=0；⑤若点A(m,n)在该抛物线上，则am2+bm+c≤a+b+c，其中正确的个数有()A. 1个B. 2个C. 3个D. 4个5.如图，一条抛物线与x轴相交于M、N两点(点M在点N的左侧)，其顶点P在线段AB上移动．若点A、B的坐标分别为(−2,3)、(1,3)，点N的横坐标的最大值为4，则点M的横坐标的最小值为()A. −1B. −3C. −5D. −76.关于x的二次函数y=x2+bx+b2在b≤x≤b+3范围内，函数值有最小值21，则b的值是()A. ±√7或2√7B. √7或±2√7C. −4或√7D. 1或−4或√77.如图，垂直于x轴的直线AB分别与抛物线C1：y=x2(x≥0)和抛物线C2：y=x24(x≥0)交于A，B两点，过点A作CD//x轴分别与y轴和抛物线C2交于点C，D，过点B作EF//x轴分别与y轴和抛物线C1交于点E，F，则S△OFBS△EAD的值为()A. √26B. √24C. 14D. 168.如图，抛物线y=14x2−4与x轴交于A、B两点，P是以点C(0,3)为圆心，2为半径的圆上的动点，Q是线段PA的中点，连结OQ.则线段OQ的最大值是()A. 3B. √412C. 72D. 49.如图，二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A，B两点，与y轴交于点C，且OA=OC.则下列结论：①abc<0；②b2−4ac4a>0；③ac−b+1=0；④OA·OB=−ca.其中正确结论的个数是()A. 4B. 3C. 2D. 110.如图，抛物线y=12(x−5)(x−9)与x轴交于点A、B，把抛物线在x轴及其下方的部分记作C1，将C1向左平移得到C2，C2与x轴交于B、D，若直线y=12x+m与C1、C2共有三个不同的交点，则m的取值范围是()A. −298<m<−52B. −298<m<−12C. −72<m<−52D. −72<m<−12二、填空题（本大题共8小题，共24分）11.如图，已知⊙P的半径为2，圆心P在抛物线y=12x2−3上运动，当⊙P与x轴相切时，圆心P的坐标为______．12.二次函数y=ax2+bx+c的图象如图所示，以下结论：①abc>0；②4ac<b2；③2a+b>0；④其顶点坐标为(12,−2)；⑤当x<12时，y随x的增大而减小；⑥a+b+c>0中，正确的有______.(只填序号)13.如图是二次函数y=ax2+bx+c的部分图象，由图象可知方程ax2+bx+c=0的解是______，______．14.已知：二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示，那么它的图象与x轴的另一个交点坐标是______．x…−1012…y…0343…15.已知二次函数y=ax2+bx−6(a>0)的图象与x轴的交点A坐标为(n,0)，顶点D的坐标为(m,t)，若m+n=0，则t=______16.已知当−1<x<0时，二次函数y=x2−3mx+2的值恒大于1，则m的取值范围为______．17.抛物线y=ax2+bx+c经过点A(−3,0)、B(4,0)两点，则关于x的一元二次方程a(x−1)2+c=b−bx的解是___________．18. 如图，在平面直角坐标系中，点O 为原点，平行于x 轴的直线与抛物线L 1：y =a 1x 2 相交于A ，B (点B 在第一象限)，点D 在AB 的延长线上，且BD =AB ，过O ，B ，D 三点的抛物线L 2，顶点为P ，对应函数的二次项系数为a 2，过点P 作PE //x 轴，交抛物线L 1于E 、F 两点，则a 1a 2的值为_____，ABEF 的值为_____．三、解答题（本大题共6小题，共66分） 19. 已知抛物线C 1:y =ax 2−4ax −5(a >0)．(1)当a =1时，求抛物线与x 轴的交点坐标及对称轴．(2)①试说明无论a 为何值，抛物线C 1一定经过两个定点，并求出这两个定点的坐标;②将抛物线C 1沿这两个定点所在直线翻折，得到抛物线C 2，请直接写出抛物线C 2对应的函数表达式．(3)若(2)中抛物线C 2的顶点到x 轴的距离为2，求a 的值．20. 已知函数y =mx 2−6x −7(m 是常数)．(1)当m =−1时，该函数的图象与直线y =2有几个公共点？说明理由； (2)若该函数的图象与x 轴只有一个公共点，求m 的值．21.某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，某村组织村民加工包装土特产销售给游客，以增加村民收入．已知某种土特产每袋成本10元．试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如表：若日销售量y是销售价x的一次函数，试求：(1)日销售量y(袋)与销售价x(元)的函数关系式；(2)假设后续销售情况与试销阶段效果相同，要使这种土特产每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？22.在平面直角坐标系中，已知抛物线y=−x2+4x．(1)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“方点”.试求拋物线y=−x2+4x的“方点”的坐标；(2)如图，若将该抛物线向左平移1个单位长度，新抛物线与x轴相交于A、B两点(A在B左侧)，与y轴相交于点C，连接BC.若点P是直线BC上方抛物线上的一点，求△PBC的面积的最大值；(3)第(2)问中平移后的抛物线上是否存在点Q，使△QBC是以BC为直角边的直角三角形？若存在，直接写出所有符合条件的点Q的坐标；若不存在，说明理由．23. 数学兴趣小组的同学们对函数y 1={ax 2+bx +c(x ≤1)2x−1(x >1)的图象和性质进行了探究．已知x ≤1时，函数y =ax 2+bx +c 的图象的对称轴为直线x =−2，顶点在x 轴上，与y 轴的交点坐标为(0,2)，探究过程如下，请补充过程： (1)a =______，b =______，c =______；(2)在给出的平面直角坐标系中，画出函数图象，并写出这个函数的一条性质：______；(3)进一步探究函数图象并解决问题：①若y 1=m 有三个实数解，则m 的取值范围为：______；②若函数y 2=x +n 的图象与该函数有三个交点，则n 的取值范围为：______．24. 如图，抛物线过点A(0,1)和C ，顶点为D ，直线AC 与抛物线的对称轴BD 的交点为B(√3,0)，平行于y 轴的直线EF 与抛物线交于点E ，与直线AC 交于点F ，点F的横坐标为4√3，四边形BDEF为平行四边形．3(1)求点F的坐标及抛物线的解析式；(2)若点P为抛物线上的动点，且在直线AC上方，当△PAB面积最大时，求点P 的坐标及△PAB面积的最大值；(3)在抛物线的对称轴上取一点Q，同时在抛物线上取一点R，使以AC为一边且以A，C，Q，R为顶点的四边形为平行四边形，求点Q和点R的坐标．答案和解析1.B解：∵抛物线开口向上，∴a>0，∵−b<0，2a∴b>0，∵抛物线交y轴于负半轴，∴c<0，∴abc<0，故①正确，>−1，a>0，∵−b2a∴b<2a，∴2a−b>0，故②错误，∵x=1时，y>0，∴a+b+c>0，∵x=−1时，y<0，∴a−b+c<0，∴(a+c)2−b2=(a+b+c)(a−b+c)<0，∴b2>(a+c)2，故③正确，∵点(−3,y1)，(1,y2)都在抛物线上，观察图象可知y1>y2，故④正确．2.Cx2+bx+c，解：二次函数y=−14二次函数图象的对称轴位于y轴左侧，a、b同号，即b<0，进一步，由对称轴为x=−1，，得出b=2a=−12二次函数图象经过y轴正半轴可知c>0，进一步，二次函数图象经过(−3,0)，将b=−12代入，求出c=34；联立一次函数y=−14x−2b与反比例函数y=cx得到：cx=−14x−2b，即x2−4x+3=0．则Δ=16−12=4>0，所以，可以确定一次函数和反比例函数的图象有2个交点；由b<0可知，直线y=−14x−2b经过一、二、四象限，由c>0可知，反比例函数y=cx的图象经过第一、三象限，3.B解：①∵抛物线开口向上，且与y轴交于负半轴，∴a>0，c<0，∴ac<0，结论①错误；②∵抛物线开口向上，且抛物线对称轴为直线x=1，∴当x≥1时，y随x的增大而增大，结论②错误；③∵抛物线对称轴为直线x=1，∴−b2a=1，∴b=−2a，∴2a+b=0，结论③正确；④∵a>0，c<0，b=−2a，∴b2−3ac=4a2−3ac=a(4a−3c)>0，结论④错误；⑤∵当x=−2时，y>0，∴4a−2b+c>0，结论⑤正确．4.D解：由图象可得，a<0，b>0，c>0，∴abc<0，故①错误，−b2a=1，则b=−2a，故2a+b=0，故②正确；由图象可知，抛物线与直线y=2有两个交点，故方程ax2+bx+c=2有两个不相等的实数根，故③正确；∵抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(4,0)，抛物线的对称轴是x= 1，∴该抛物线与x轴的另一个交点为(−2,0)，∴当x=−2时，y=4a−2b+c=0，故④正确；∵当x=1时，该函数取得最大值，此时y=a+b+c，∴点A(m,n)在该抛物线上，则am2+bm+c≤a+b+c，故⑤正确；5.C解：根据题意知，点N的横坐标的最大值为4，此时对称轴过B点，点N的横坐标最大，此时的M点坐标为(−2,0)，当对称轴过A点时，点M的横坐标最小，此时的N点坐标为(1,0)，M点的坐标为(−5,0)，故点M的横坐标的最小值为−5，6.C解：y=x2+bx+b2的图象开口向上，对称轴为直线x=−b2，①当−b2<b，即b>0时，在自变量x的值满足b≤x≤b+3的情况下，y随x的增大而增大，∴当x=b时，y=b2+b⋅b+b2=3b2为最小值，∴3b2=21，解得，b1=−√7(舍去)，b2=√7；②当b≤−b2≤b+3时，即−2≤b≤0，∴x=−b2，y=34b2为最小值，∴34b2=21，解得，b1=−2√7(舍去)，b2=2√7(舍去)；③当−b2>b+3，即b<−2时，在自变量x的值满足b≤x≤b+3的情况下，y随x的增大而减小，故当x=b+3时，y=(b+3)2+b(b+3)+b2=3b2+9b+9为最小值，∴3b2+9b+9=21.解得，b1=1(舍去)，b2=−4；故b的值为√7或−4．7.D解：设点A、B横坐标为a，则点A纵坐标为a2，点B的纵坐标为a24，∵BE//x轴，∴点F纵坐标为a24，∵点F是抛物线y=x2上的点，∴点F横坐标为x=√y=12a，∵CD//x轴，∴点D纵坐标为a2，∵点D是抛物线y=x24上的点，∴点D横坐标为x=√4y=2a，∴AD=a，BF=12a，CE=34a2，OE=14a2，∴S△OFBS△EAD =12BF⋅OE12AD⋅CE=18×43=16．8.C解：连接BP，如图，当y=0时，14x2−4=0，解得x1=4，x2=−4，则A(−4,0)，B(4,0)，∵Q是线段PA的中点，∴OQ为△ABP的中位线，∴OQ=12BP，当BP最大时，OQ最大，而BP过圆心C时，PB最大，如图，点P运动到P′位置时，BP最大，∵BC=√32+42=5，∴BP′=5+2=7，∴线段OQ的最大值是72．9.B解：∵抛物线开口向下，∴a<0，∵抛物线的对称轴在y轴的右侧，∴b>0，∵抛物线与y轴的交点在x轴上方，∴c>0，∴abc<0，所以①正确；∵抛物线与x轴有2个交点，∴△=b2−4ac>0，而a<0，<0，所以②错误；∴b2−4ac4a∵C(0,c)，OA=OC，∴A(−c,0)，把A(−c,0)代入y=ax2+bx+c得ac2−bc+c=0，∴ac−b+1=0，所以③正确；设A(x1,0)，B(x2,0)，∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A，B两点，∴x1和x2是方程ax2+bx+c=0(a≠0)的两根，∴x1⋅x2=c，a∴OA⋅OB=−c，所以④正确．a10.A(x−5)(x−9)与x轴交于点A、B，解：∵抛物线y=12∴B(5,0)，A(9,0)，∴抛物线向左平移4个单位长度，(x−3)2−2，∴平移后解析式y=12当直线y=12x+m过B点，有2个交点，∴0=52+m，m=−52，当直线y=12x+m与抛物线C2相切时，有2个交点，∴12x+m=12(x−3)2−2，即x2−7x+5−2m=0，∵相切，∴△=49−20+8m=0，∴m=−298，如图∵若直线y=12x+m与C1、C2共有3个不同的交点，∴−298<m<−52，11.(−√10,2)或(√10,2)或(−√2,−2)或(√2,−2)解：∵⊙P与x轴相切，∴点P到x轴的距离为2，即P点的纵坐标为2或−2，当y=2时，12x2−3=2，解得x1=−√10，x2=√10，则P点坐标为(−√10,2)或(√10,2)；当y=−2时，12x2−3=−2，解得x1=−√2，x2=√2，则P点坐标为(−√2,−2)或(√2,−2)，综上所述，圆心P的坐标为(−√10,2)或(√10,2)或(−√2,−2)或(√2,−2)．故答案为(−√10,2)或(√10,2)或(−√2,−2)或(√2,−2)．12.①②③⑤解由图象可得，a>0，c<0，b<0，△=b2−4ac>0，对称轴为x=12∴abc>0，4ac<b2，当x<12时，y随x的增大而减小．故①②⑤正确∵−b2a =12<1∴2a+b>0故③正确由图象可得顶点纵坐标小于−2，则④错误当x=1时，y=a+b+c<0故⑥错误13.x1=−1x2=5解：由图象可知对称轴x=2，与x轴的一个交点横坐标是5，它到直线x=2的距离是3个单位长度，所以另外一个交点横坐标是−1．所以x1=−1，x2=5．14.(3,0)解：∵抛物线y=ax2+bx+c经过(0,3)、(2,3)两点，∴对称轴x=0+22=1；点(−1,0)关于对称轴对称点为(3,0)，因此它的图象与x轴的另一个交点坐标是(3,0)．15.−8．解：函数的对称轴为直线x=m=−n，由中点公式得，函数与x轴另外一个交点的坐标为(−3n,0)，则设抛物线的表达式为：y=a(x−n)(x+3n)=a(x2+2nx−3n2)=ax2+bx−6即：−3an2=−6，解得：an2=2，当x=m=−n时，y=a(x2+2nx−3n2)=−4an2=−8=t，16.m≥−23解：二次函数y=x2−3mx+2的图象是一条开口向上的抛物线，(1)当抛物线的对称轴x=32m≤−1时，即m≤−23，要使二次函数解析式的值−1<x<0时恒大于1，只要x=−1，y=1+3m+2=3m+ 3≥1，解得：m≥−23，∴m=−23，(2)当抛物线的对称轴x=32m≥0时，即m≥0时，要使二次函数解析式的值−1<x<0时恒大于1，只要m≥0即可；(3)当抛物线的对称轴x=32m在区间−1<x<0时，∵−1<32m<0，∴−23<m<0，综上所述：m的取值范围是：m≥−23．17.x1=−2，x2=5解：关于x的一元二次方程a(x−1)2+c=b−bx变形为a(x−1)2+b(x−1)+c=0，把抛物线y=ax2+bx+c沿x轴向右平移1个单位得到y=a(x−1)2+b(x−1)+c，因为抛物线y=ax2+bx+c经过点A(−3,0)、B(4,0)，所以抛物线y=a(x−1)2+b(x−1)+c与x轴的两交点坐标为(−2,0)，(5,0)，所以一元二次方程a(x−1)2+b(x−1)+c=0的解为x1=−2，x2=5．18.−3；2√33如图3，抛物线L3与x轴交于点G，其对称轴与x轴交于点Q，过点B作BK⊥x轴于点K，设OK=t，则AB=BD=2t，点B的坐标为(t,a1t2)，根据抛物线的轴对称性，得OQ=2t，OG=2OQ=4t．设抛物线L3的函数表达式为y=a2x(x−4t)，∵该抛物线过点B(t,a1t2)，∴a1t2=a2t(t−4t)，∵t≠0，∴a1a2=−3，由题意得，点P的坐标为(2t,−4a2t2)，则−4a2t2=a1x2，解得，x1=−2√33t，x2=2√33t，∴EF=2|x1|=4√33t，∵AB=2t，∴ABEF =4√33t×12t=2√3319.解：(1)当a=1时，抛物线为y=x2−4x−5，即y=(x−2)2−9.∴对称轴为直线x=2．令y=0，得(x−2)2−9=0，解得x1=−1，x2=5．∴抛物线与x轴的交点坐标为(−1,0)和(5,0)；(2) ①抛物线C1对应的函数表达式为y=ax2−4ax−5，即y=ax(x−4)−5．∵当ax(x−4)=0时，y恒为−5，∴抛物线C1一定经过两个定点(0,−5)、(4,−5)； ②抛物线C 1:y =ax 2−4ax −5=a(x −2)2−4a −5，它的顶点坐标为(2,−4a −5).过两个定点的直线为直线y =−5．将抛物线C 1沿上述直线翻折，得到抛物线C 2，开口大小不变、方向相反， 易得顶点坐标为(2,4a −5)．∴抛物线C 2对应的函数表达式为y =−a(x −2)2+4a −5，即y =−ax 2+4ax −5；(3)∵抛物线 C 2的顶点(2,4a −5)到x 轴的距离为2，∴|4a −5|=2，4a −5=2，解得a =74;或4a −5=−2，解得a =34．综上所述，a =74或34．20. 解：(1)m =−1时，{y =2y =−x 2−6x −7，解得{x =−3y =2， ∴该函数的图象与直线y =2有1个公共点．(2)①当m =0时，函数y =−4x +1的图象与x 轴只有一个交点；②当m ≠0时，若函数y =mx 2−6x −7的图象与x 轴只有一个交点，则方程mx 2−6x −7=0有两个相等的实数根，所以△=(−6)2−4m ⋅(−7)=0，m =−97．综上，若函数y =mx 2−4x +1的图象与x 轴只有一个交点，则m 的值为0或−97．21. 解：(1)依题意，根据表格的数据，设日销售量y(袋)与销售价x(元)的函数关系式为y =kx +b 得{25=15k +b 20=20k +b ，解得{k =−1b =40故日销售量y(袋)与销售价x(元)的函数关系式为：y =−x +40(2)依题意，设利润为w 元，得w =(x −10)(−x +40)=−x 2+50x +400整理得w =−(x −25)2+225∵−1<0∴当x =25时，w 取得最大值，最大值为225故要使这种土特产每日销售的利润最大，每袋的销售价应定为25元，每日销售的最大利润是225元．22.解：(1)由题意得：x=y，∴−x2+4x=x，解得，x1=0，x2=3，∴抛物线的方点坐标是(0,0)，(3,3)；(2)如图1，过P点作y轴的平行线交BC于点D，∵y=−x2+4x=−(x−2)2+4，∴向左平移1个单位长度后抛物线的表达式为y=−(x−1)2+4=−x2+2x+3，在y=−x2+2x+3中，当x=0时，y=3；当y=0时，x1=−1，x2=3，∴C(0,3)，A(−1,0)，B(3,0)，设直线BC的解析式为y=kx+3，将点B(3,0)代入，得，k=−1，∴直线BC的解析式为y=−x+3，设P(m,−m2+2m+3)，则D(m,−m+3)，∴PD=−m2+2m+3−(−m+3)=−m2+3m(0<m<3)，∴S△PBC=12(−m2+3m)×3=−32(m−32)2+278(0<m<3)，∴当m=32时，△PBC的面积最大，最大值为278；(3)存在，理由如下：∵C(0,3)，B(3,0)，∴OB=OC=3，∴△OBC为等腰直角三角形，∴∠CBO=45°，①当点B为直角顶点时，如图2，过点B作直线BC的垂线，交y轴于点M，交抛物线于点Q，则∠OBM =45°，∴△OBM 为等腰直角三角形，∴OB =OM =3，∴M(0,−3)，设直线BM 的解析式为y =kx −3，将点B(3,0)代入，得，k =1，∴直线BM 的解析式为y =x −3，联立，得{y =−x 2+2x +3y =x −3， 解得，x 1=−2，x 2=3，∴Q 1(−2,−5)；②当点C 为直角顶点时，如图2，过点C 作直线BC 的垂线，交抛物线于点Q ， 则QC//BM ，则直线QC 的解析式为y =x +3，联立，得{y =−x 2+2x +3y =x +3， 解得，x 1=0，x 2=1，∴Q 2(1,4)，综上所述，点Q 的坐标为(−2,−5)或(1,4)．23. 12 2 2 当x =−2时，函数有最小值0 0<m ≤92 32<n ≤72．解：(1)∵函数y =ax 2+bx +c 的图象的对称轴为直线x =−2，过(0,2)，(−2,0)，则：{−b 2a =−2c =24a −2b +c =0， 解得：{a =12b =2c =2；(2)由(1)知，y 1={12x 2+2x +2(x ≤1)2x−1(x >1)， 图象如图所示：根据图象，可知当x =−2时，函数有最小值0；(3)①由图可知，当0<y 1≤92时，y 1=m 有三个实数解， 即若y 1=m 有三个实数解，则m 的取值范围为：0<m ≤92；②由图可知，当y 2=x +n 与y =12x 2+2x +2相切时，两个函数图象恰好有两个交点，把y =x +n 代入y =12x 2+2x +2，得12x 2+2x +2=x +n ， ∴12x 2+x +2−n =0，∴△=1−4×12(2−n)=0， 解得n =32．当y 2=x +n 过点(1,92)时，两个函数图象恰好有三个交点， ∴1+n =92，解得n =72， 所以满足条件的n 的取值范围是32<n ≤72．故答案为：12，2，2；当x =−2时，函数有最小值0；0<m ≤92；32<n ≤72．24. 解：(1)设抛物线的解析式为y =ax 2+bx +c(a ≠0)， ∵A(0,1)，B(√3,0)，设直线AB 的解析式为y =kx +m ，∴{√3k +m =0m =1， 解得{k =−√33m =1， ∴直线AB 的解析式为y =−√33x +1， ∵点F 的横坐标为4√33， ∴F 点纵坐标为−√33×4√33+1=−13，∴F点的坐标为(43√3,−13)，又∵点A在抛物线上，∴c=1，对称轴为：x=−b2a=√3，∴b=−2√3a，∴解析式化为：y=ax2−2√3ax+1，∵四边形DBFE为平行四边形．∴BD=EF，∴−3a+1=163a−8a+1−(−13)，解得a=−1，∴抛物线的解析式为y=−x2+2√3x+1；(2)设P(n,−n2+2√3n+1)，作PP′⊥x轴交AC于点P′，则P′(n,−√33n+1)，∴PP′=−n2+73√3n，S△ABP=12OB⋅PP′=−√32n2+72n=−√32(n−76√3)2+4924√3，∴当n=76√3时，△ABP的面积最大为4924√3，此时P(76√3,4712).(3)∵{y=−√33x+1y=−x2+2√3x+1，∴x=0或x=73√3，∴C(73√3,−43)，设Q(√3,m)，①当AQ为对角线时，∴R(−43√3,m +73)，∵R 在抛物线y =−(x −√3)2+4上， ∴m +73=−(−43√3−√3)2+4， 解得m =−443，∴Q(√3,−443)，R(−43√3,−373)；②当AR 为对角线时，∴R(103√3,m −73)， ∵R 在抛物线y =−(x −√3)2+4上， ∴m −73=−(103√3−√3)2+4， 解得m =−10，∴Q(√3,−10)，R(103√3,−373).综上所述，Q(√3,−443)，R(−43√3,−373)；或Q(√3,−10)，R(103√3,−373).。

二次函数试题及答案一、选择题1. 已知二次函数y=ax^2+bx+c（a≠0）的图象开口向上，且与x轴有两个交点，则a、b、c之间的关系是（）。

A. b^2-4ac>0B. b^2-4ac=0C. b^2-4ac<0D. b^2-4ac≤0答案：A2. 若二次函数y=ax^2+bx+c的图象与y轴的交点为（0，3），则c的值为（）。

A. 3B. -3C. 0D. 1答案：A二、填空题1. 若二次函数y=ax^2+bx+c的图象的顶点坐标为（2，-1），则b=______。

答案：-4a-42. 已知抛物线y=ax^2+bx+c与x轴的交点为（-1，0）和（3，0），则b=______。

答案：-2a三、解答题1. 已知二次函数y=ax^2+bx+c（a≠0）的图象经过点（1，2）和（-1，0），求该二次函数的解析式。

答案：将点（1，2）和（-1，0）代入二次函数的解析式，得到方程组：\begin{cases}a+b+c=2 \\9a-3b+c=0\end{cases}解得a=1，b=-2，c=1，所以二次函数的解析式为y=x^2-2x+1。

2. 已知抛物线y=ax^2+bx+c（a≠0）的对称轴为直线x=1，且抛物线经过点（0，3），求抛物线的解析式。

答案：由对称轴为直线x=1，可知-b/2a=1，即b=-2a。

又抛物线经过点（0，3），代入解析式得c=3。

设a=1，则b=-2，c=3，所以抛物线的解析式为y=x^2-2x+3。

四、综合题1. 已知二次函数y=ax^2+bx+c（a≠0）的图象与x轴的交点为（2，0）和（-3，0），且抛物线的顶点坐标为（-1，-4），求该二次函数的解析式。

答案：由抛物线与x轴的交点可知，2和-3是方程ax^2+bx+c=0的两个根，所以有：\begin{cases}4a+2b+c=0 \\9a-3b+c=0\end{cases}又因为顶点坐标为（-1，-4），所以有：\begin{cases}-\frac{b}{2a}=-1 \\\frac{4ac-b^2}{4a}=-4\end{cases}解得a=1，b=4，c=-6，所以二次函数的解析式为y=x^2+4x-6。

二次函数综合题一．二次函数综合题（共50小题）1．（2020•西藏）在平面直角坐标系中，二次函数y=12x2+bx+c的图象与x轴交于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是第四象限内抛物线上的一个动点．（1）求二次函数的解析式；（2）如图甲，连接AC，P A，PC，若S△P AC=152，求点P的坐标；（3）如图乙，过A，B，P三点作⊙M，过点P作PE⊥x轴，垂足为D，交⊙M于点E．点P在运动过程中线段DE的长是否变化，若有变化，求出DE的取值范围；若不变，求DE的长．2．（2020•德阳）如图1，抛物线y＝ax2﹣2ax﹣3a（a≠0）与x轴交于点A，B．与y轴交于点C．连接AC，BC．已知△ABC的面积为2．（1）求抛物线的解析式；（2）平行于x轴的直线与抛物线从左到右依次交于P，Q两点．过P，Q向x轴作垂线，垂足分别为G，H．若四边形PGHQ为正方形，求正方形的边长；（3）如图2，平行于y轴的直线交抛物线于点M，交x轴于点N（2，0）．点D是抛物线上A，M之间的一动点，且点D不与A，M重合，连接DB交MN于点E．连接AD并延长交MN于点F．在点D运动过程中，3NE+NF是否为定值？若是，求出这个定值；若不是，请说明理由．3．（2020•锦州）在平面直角坐标系中，抛物线y=−13x2+bx+c交x轴于A（﹣3，0），B（4，0）两点，交y轴于点C．（1）求抛物线的表达式；（2）如图，直线y=34x+94与抛物线交于A，D两点，与直线BC交于点E．若M（m，0）是线段AB上的动点，过点M作x轴的垂线，交抛物线于点F，交直线AD于点G，交直线BC于点H．①当点F在直线AD上方的抛物线上，且S△EFG=59S△OEG时，求m的值；②在平面内是否存在点P，使四边形EFHP为正方形？若存在，请直接写出点P的坐标；若不存在，请说明理由．4．（2020•朝阳）如图，抛物线y=−12x2+bx+c与x轴交于点A，点B，与y轴交于点C，抛物线的对称轴为直线x＝﹣1，点C坐标为（0，4）．（1）求抛物线表达式；（2）在抛物线上是否存在点P，使∠ABP＝∠BCO，如果存在，求出点P坐标；如果不存在，请说明理由；（3）在（2）的条件下，若点P在x轴上方，点M是直线BP上方抛物线上的一个动点，求点M到直线BP的最大距离；（4）点G是线段AC上的动点，点H是线段BC上的动点，点Q是线段AB上的动点，三个动点都不与点A，B，C重合，连接GH，GQ，HQ，得到△GHQ，直接写出△GHQ 周长的最小值．5．（2020•鞍山）在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）经过点A（﹣2，﹣4）和点C（2，0），与y轴交于点D，与x轴的另一交点为点B．（1）求抛物线的解析式；（2）如图1，连接BD，在抛物线上是否存在点P，使得∠PBC＝2∠BDO？若存在，请求出点P的坐标；若不存在，请说明理由；（3）如图2，连接AC，交y轴于点E，点M是线段AD上的动点（不与点A，点D重合），将△CME 沿ME 所在直线翻折，得到△FME ，当△FME 与△AME 重叠部分的面积是△AMC 面积的14时，请直接写出线段AM 的长． 6．（2020•赤峰）如图，已知二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴交于A （1，0），B （4，0）两点，与y 轴交于点C ，直线y =−12x +2经过B ，C 两点．（1）直接写出二次函数的解析式 ；（2）平移直线BC ，当直线BC 与抛物线有唯一公共点Q 时，求此时点Q 的坐标；（3）过（2）中的点Q 作QE ∥y 轴，交x 轴于点E ．若点M 是抛物线上一个动点，点N 是x 轴上一个动点，是否存在以E ，M ，N 三点为顶点的直角三角形（其中M 为直角顶点）与△BOC 相似？如果存在，请直接写出满足条件的点M 的个数和其中一个符合条件的点M 的坐标；如果不存在，请说明理由．7．（2020•大连）在平面直角坐标系xOy 中，函数F 1和F 2的图象关于y 轴对称，它们与直线x ＝t （t ＞0）分别相交于点P ，Q ．（1）如图，函数F 1为y ＝x +1，当t ＝2时，PQ 的长为 ；（2）函数F 1为y =3x ，当PQ ＝6时，t 的值为 ；（3）函数F 1为y ＝ax 2+bx +c （a ≠0），①当t =√b b 时，求△OPQ 的面积；②若c ＞0，函数F 1和F 2的图象与x 轴正半轴分别交于点A （5，0），B （1，0），当c ≤x ≤c +1时，设函数F 1的最大值和函数F 2的最小值的差为h ，求h 关于c 的函数解析式，并直接写出自变量c 的取值范围．8．（2020•桂林）如图，已知抛物线y ＝a （x +6）（x ﹣2）过点C （0，2），交x 轴于点A 和点B （点A 在点B 的左侧），抛物线的顶点为D ，对称轴DE 交x 轴于点E ，连接EC ．（1）直接写出a 的值，点A 的坐标和抛物线对称轴的表达式；（2）若点M 是抛物线对称轴DE 上的点，当△MCE 是等腰三角形时，求点M 的坐标；（3）点P 是抛物线上的动点，连接PC ，PE ，将△PCE 沿CE 所在的直线对折，点P 落在坐标平面内的点P ′处．求当点P ′恰好落在直线AD 上时点P 的横坐标．9．（2020•葫芦岛）如图，抛物线y ＝ax 2+94x +c （a ≠0）与x 轴相交于点A （﹣1，0）和点B ，与y 轴相交于点C （0，3），作直线BC ．（1）求抛物线的解析式；（2）在直线BC 上方的抛物线上存在点D ，使∠DCB ＝2∠ABC ，求点D 的坐标；（3）在（2）的条件下，点F 的坐标为（0，72），点M 在抛物线上，点N 在直线BC 上．当以D，F，M，N为顶点的四边形是平行四边形时，请直接写出点N的坐标．10．（2020•呼伦贝尔）如图，抛物线y=−12x2+bx+c与x轴交于点A（﹣1，0）和点B（4，0），与y轴交于点C，连接BC，点P是线段BC上的动点（与点B，C不重合），连接AP并延长AP交抛物线于点Q，连接CQ，BQ，设点Q的横坐标为m．（1）求抛物线的解析式和点C的坐标；（2）当△BCQ的面积等于2时，求m的值；（3）在点P运动过程中，PQAP是否存在最大值？若存在，求出最大值；若不存在，请说明理由．11．（2020•沈阳）如图1，在平面直角坐标系中，O是坐标原点，抛物线y=12x2+bx+c经过点B（6，0）和点C（0，﹣3）．（1）求抛物线的表达式；（2）如图2，线段OC绕原点O逆时针旋转30°得到线段OD．过点B作射线BD，点M是射线BD上一点（不与点B重合），点M关于x轴的对称点为点N，连接NM，NB．①直接写出△MBN的形状为；②设△MBN的面积为S1，△ODB的面积为是S2．当S1=23S2时，求点M的坐标；（3）如图3，在（2）的结论下，过点B作BE⊥BN，交NM的延长线于点E，线段BE 绕点B逆时针旋转，旋转角为α（0°＜α＜120°）得到线段BF，过点F作FK∥x轴，交射线BE于点K，∠KBF的角平分线和∠KFB的角平分线相交于点G，当BG＝2√3时，请直接写出点G的坐标为．12．（2020•大庆）如图，抛物线y＝ax2+bx+12与x轴交于A，B两点（B在A的右侧），且经过点C（﹣1，7）和点D（5，7）．（1）求抛物线的函数表达式；（2）连接AD，经过点B的直线l与线段AD交于点E，与抛物线交于另一点F．连接CA，CE，CD，△CED的面积与△CAD的面积之比为1：7，点P为直线l上方抛物线上的一个动点，设点P的横坐标为t．当t为何值时，△PFB的面积最大？并求出最大值；（3）在抛物线y＝ax2+bx+12上，当m≤x≤n时，y的取值范围是12≤y≤16，求m﹣n 的取值范围．（直接写出结果即可）13．（2020•镇江）如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c （a、c是常数，a＜0）的图象经过点M（﹣1，1），交直线l于点N，图象的顶点为D，它的对称轴与x 轴交于点C ，直线DM 、DN 分别与x 轴相交于A 、B 两点．（1）当a ＝﹣1时，求点N 的坐标及AC BC 的值；（2）随着a 的变化，AC BC 的值是否发生变化？请说明理由；（3）如图②，E 是x 轴上位于点B 右侧的点，BC ＝2BE ，DE 交抛物线于点F ．若FB ＝FE ，求此时的二次函数表达式．14．（2020•眉山）如图1，抛物线y ＝﹣x 2+bx +c 与x 轴交于A 、B 两点，与y 轴交于点C ，已知点B 坐标为（3，0），点C 坐标为（0，3）．（1）求抛物线的表达式；（2）点P 为直线BC 上方抛物线上的一个动点，当△PBC 的面积最大时，求点P 的坐标；（3）如图2，点M 为该抛物线的顶点，直线MD ⊥x 轴于点D ，在直线MD 上是否存在点N ，使点N 到直线MC 的距离等于点N 到点A 的距离？若存在，求出点N 的坐标；若不存在，请说明理由．15．（2020•河池）在平面直角坐标系xOy 中，抛物线与x 轴交于（p ，0），（q ，0），则该抛物线的解析式可以表示为：y ＝a （x ﹣p ）（x ﹣q ）＝ax 2﹣a （p +q ）x +apq ．（1）若a ＝1，抛物线与x 轴交于（1，0），（5，0），直接写出该抛物线的解析式和顶点坐标；（2）若a ＝﹣1，如图（1），A （﹣1，0），B （3，0），点M （m ，0）在线段AB 上，抛物线C 1与x 轴交于A ，M ，顶点为C ；抛物线C 2与x 轴交于B ，M ，顶点为D ．当A ，C ，D 三点在同一条直线上时，求m 的值；（3）已知抛物线C 3与x 轴交于A （﹣1，0），B （3，0），线段EF 的端点E （0，3），F （4，3）．若抛物线C 3与线段EF 有公共点，结合图象，在图（2）中探究a 的取值范围．16．（2020•雅安）已知二次函数y ＝ax 2+2x +c （a ≠0）的图象与x 轴交于A 、B （1，0）两点，与y 轴交于点C （0，﹣3），（1）求二次函数的表达式及A 点坐标；（2）D 是二次函数图象上位于第三象限内的点，求点D 到直线AC 的距离取得最大值时点D 的坐标；（3）M 是二次函数图象对称轴上的点，在二次函数图象上是否存在点N ，使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请写出点N 的坐标（不写求解过程）．17．（2020•绵阳）如图，抛物线过点A （0，1）和C ，顶点为D ，直线AC 与抛物线的对称轴BD 的交点为B （√3，0），平行于y 轴的直线EF 与抛物线交于点E ，与直线AC 交于点F ，点F 的横坐标为4√33，四边形BDEF 为平行四边形． （1）求点F 的坐标及抛物线的解析式；（2）若点P 为抛物线上的动点，且在直线AC 上方，当△P AB 面积最大时，求点P 的坐标及△P AB面积的最大值；（3）在抛物线的对称轴上取一点Q，同时在抛物线上取一点R，使以AC为一边且以A，C，Q，R为顶点的四边形为平行四边形，求点Q和点R的坐标．18．（2020•长春）在平面直角坐标系中，函数y＝x2﹣2ax﹣1（a为常数）的图象与y轴交于点A．（1）求点A的坐标．（2）当此函数图象经过点（1，2）时，求此函数的表达式，并写出函数值y随x的增大而增大时x的取值范围．（3）当x≤0时，若函数y＝x2﹣2ax﹣1（a为常数）的图象的最低点到直线y＝2a的距离为2，求a的值．（4）设a＜0，Rt△EFG三个顶点的坐标分别为E（﹣1，﹣1）、F（﹣1，a﹣1）、G（0，a﹣1）．当函数y＝x2﹣2ax﹣1（a为常数）的图象与△EFG的直角边有交点时，交点记为点P．过点P作y轴的垂线，与此函数图象的另一个交点为P′（P′与P不重合），过点A作y轴的垂线，与此函数图象的另一个交点为A′．若AA′＝2PP′，直接写出a的值．19．（2020•海南）抛物线y＝x2+bx+c经过点A（﹣3，0）和点B（2，0），与y轴交于点C．（1）求该抛物线的函数表达式；（2）点P是该抛物线上的动点，且位于y轴的左侧．①如图1，过点P作PD⊥x轴于点D，作PE⊥y轴于点E，当PD＝2PE时，求PE的长；②如图2，该抛物线上是否存在点P，使得∠ACP＝∠OCB？若存在，请求出所有点P 的坐标：若不存在，请说明理由．20．（2020•丹东）如图1，在平面直角坐标系中，抛物线y=−12x2+bx+c与x轴交于A，B两点，A点坐标为（﹣2，0），与y轴交于点C（0，4），直线y=−12x+m与抛物线交于B，D两点．（1）求抛物线的函数表达式．（2）求m的值和D点坐标．（3）点P是直线BD上方抛物线上的动点，过点P作x轴的垂线，垂足为H，交直线BD于点F，过点D作x轴的平行线，交PH于点N，当N是线段PF的三等分点时，求P点坐标．（4）如图2，Q是x轴上一点，其坐标为（−45，0）．动点M从A出发，沿x轴正方向以每秒5个单位的速度运动，设M的运动时间为t（t＞0），连接AD，过M作MG⊥AD 于点G，以MG所在直线为对称轴，线段AQ经轴对称变换后的图形为A′Q′，点M在运动过程中，线段A′Q′的位置也随之变化，请直接写出运动过程中线段A′Q′与抛物线有公共点时t的取值范围．21．（2020•益阳）如图，在平面直角坐标系中，点F的坐标是（4，2），点P为一个动点，过点P作x轴的垂线PH，垂足为H，点P在运动过程中始终满足PF＝PH．【提示：平面直角坐标系内点M、N的坐标分别为（x1，y1）、（x2，y2），则MN2＝（x2﹣x1）2+（y2﹣y1）2】（1）判断点P在运动过程中是否经过点C（0，5）；（2）设动点P的坐标为（x，y），求y关于x的函数表达式；填写下表，并在给定坐标系中画出该函数的图象；x…02468…y……（3）点C关于x轴的对称点为C'，点P在直线C'F的下方时，求线段PF长度的取值范围．22．（2020•吉林）如图，在平面直角坐标系中，抛物线y=−12x2+bx+32与x轴正半轴交于点A，且点A的坐标为（3，0），过点A作垂直于x轴的直线l．P是该抛物线上的任意一点，其横坐标为m，过点P作PQ⊥l于点Q，M是直线l上的一点，其纵坐标为﹣m+3 2．以PQ，QM为边作矩形PQMN．（1）求b的值．（2）当点Q与点M重合时，求m的值．（3）当矩形PQMN是正方形，且抛物线的顶点在该正方形内部时，求m的值．（4）当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时，直接写出m的取值范围．23．（2020•永州）在平面直角坐标系xOy中，等腰直角△ABC的直角顶点C在y轴上，另两个顶点A，B在x轴上，且AB＝4，抛物线经过A，B，C三点，如图1所示．（1）求抛物线所表示的二次函数表达式．（2）过原点任作直线l交抛物线于M，N两点，如图2所示．①求△CMN面积的最小值．②已知Q（1，−32）是抛物线上一定点，问抛物线上是否存在点P，使得点P与点Q关于直线l对称，若存在，求出点P的坐标及直线l的一次函数表达式；若不存在，请说明理由．24．（2020•宿迁）二次函数y＝ax2+bx+3的图象与x轴交于A（2，0），B（6，0）两点，与y轴交于点C，顶点为E．．（1）求这个二次函数的表达式，并写出点E的坐标；（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标；（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标．25．（2020•毕节市）如图（1），在平面直角坐标系中，抛物线y＝ax2+bx+4（a≠0）与y轴交于点A，与x轴交于点C（﹣2，0），且经过点B（8，4），连接AB，BO，作AM⊥OB 于点M，将Rt△OMA沿y轴翻折，点M的对应点为点N．解答下列问题：（1）抛物线的解析式为，顶点坐标为；（2）判断点N是否在直线AC上，并说明理由；（3）如图（2），将图（1）中Rt△OMA沿着OB平移后，得到Rt△DEF．若DE边在线段OB上，点F在抛物线上，连接AF，求四边形AMEF的面积．26．（2020•鄂尔多斯）如图1，抛物线y ＝x 2+bx +c 交x 轴于A ，B 两点，其中点A 的坐标为（1，0），与y 轴交于点C （0，﹣3）．（1）求抛物线的函数解析式；（2）点D 为y 轴上一点，如果直线BD 与直线BC 的夹角为15°，求线段CD 的长度；（3）如图2，连接AC ，点P 在抛物线上，且满足∠P AB ＝2∠ACO ，求点P 的坐标．27．（2020•鸡西）已知抛物线y ＝a （x ﹣2）2+c 经过点A （﹣2，0）和点C （0，94），与x 轴交于另一点B ，顶点为D ．（1）求抛物线的解析式，并写出顶点D 的坐标；（2）如图，点E ，F 分别在线段AB ，BD 上（点E 不与点A ，B 重合），且∠DEF ＝∠DAB ，DE ＝EF ，直接写出线段BE 的长．28．（2020•随州）如图，在平面直角坐标系中，抛物线y＝ax2+bx+1的对称轴为直线x=3 2，其图象与x轴交于点A和点B（4，0），与y轴交于点C．（1）直接写出抛物线的解析式和∠CAO的度数；（2）动点M，N同时从A点出发，点M以每秒3个单位的速度在线段AB上运动，点N 以每秒√2个单位的速度在线段AC上运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动的时间为t（t＞0）秒，连接MN，再将线段MN绕点M顺时针旋转90°，设点N落在点D的位置，若点D恰好落在抛物线上，求t的值及此时点D的坐标；（3）在（2）的条件下，设P为抛物线上一动点，Q为y轴上一动点，当以点C，P，Q 为顶点的三角形与△MDB相似时，请直接写出点P及其对应的点Q的坐标．（每写出一组正确的结果得1分，至多得4分）29．（2020•黄石）在平面直角坐标系中，抛物线y＝﹣x2+kx﹣2k的顶点为N．（1）若此抛物线过点A（﹣3，1），求抛物线的解析式；（2）在（1）的条件下，若抛物线与y轴交于点B，连接AB，C为抛物线上一点，且位于线段AB的上方，过C作CD垂直x轴于点D，CD交AB于点E，若CE＝ED，求点C 坐标；（3）已知点M（2−4√33，0），且无论k取何值，抛物线都经过定点H，当∠MHN＝60°时，求抛物线的解析式．30．如图1，在平面直角坐标系中，A（﹣2，﹣1），B（3，﹣1），以O为圆心，OA的长为半径的半圆O交AO延长线于C，连接AB，BC，过O作ED∥BC分别交AB和半圆O 于E，D，连接OB，CD．（1）求证：BC是半圆O的切线；（2）试判断四边形OBCD的形状，并说明理由；（3）如图2，若抛物线经过点D且顶点为E．①求此抛物线的解析式；②点P是此抛物线对称轴上的一个动点，以E，D，P为顶点的三角形与△OAB相似，问抛物线上是否存在一点Q．使S△EPQ＝S△OAB？若存在，请直接写出Q点的横坐标；若不存在，说明理由．31．（2020•娄底）如图，抛物线经过点A（﹣3，0）、B（1，0）、C（0，3）．（1）求抛物线的解析式；（2）点P（m，n）是抛物线上的动点，当﹣3＜m＜0时，试确定m的值，使得△P AC 的面积最大；（3）抛物线上是否存在不同于点B的点D，满足DA2﹣DC2＝6，若存在，请求出点D 的坐标；若不存在，请说明理由．32．（2020•郴州）如图1，抛物线y ＝ax 2+bx +3（a ≠0）与x 轴交于A （﹣1，0），B （3，0），与y 轴交于点C ．已知直线y ＝kx +n 过B ，C 两点．（1）求抛物线和直线BC 的表达式；（2）点P 是抛物线上的一个动点．①如图1，若点P 在第一象限内，连接P A ，交直线BC 于点D ．设△PDC 的面积为S 1，△ADC 的面积为S 2，求S 1S 2的最大值； ②如图2，抛物线的对称轴l 与x 轴交于点E ，过点E 作EF ⊥BC ，垂足为F ．点Q 是对称轴l 上的一个动点，是否存在以点E ，F ，P ，Q 为顶点的四边形是平行四边形？若存在，求出点P ，Q 的坐标；若不存在，请说明理由．33．（2020•鄂州）如图，抛物线y =12x 2+bx +c 与x 轴交于A 、B 两点（点A 在点B 左边），与y 轴交于点C ．直线y =12x ﹣2经过B 、C 两点．（1）求抛物线的解析式；（2）点P 是抛物线上的一动点，过点P 且垂直于x 轴的直线与直线BC 及x 轴分别交于点D 、M ．PN ⊥BC ，垂足为N ．设M （m ，0）．①点P 在抛物线上运动，若P 、D 、M 三点中恰有一点是其它两点所连线段的中点（三点重合除外）．请直接写出符合条件的m 的值；②当点P 在直线BC 下方的抛物线上运动时，是否存在一点P ，使△PNC 与△AOC 相似．若存在，求出点P的坐标；若不存在，请说明理由．34．（2020•包头）如图，在平面直角坐标系中，抛物线y=13x2﹣2x经过坐标原点，与x轴正半轴交于点A，该抛物线的顶点为M，直线y=−12x+b经过点A，与y轴交于点B，连接OM．（1）求b的值及点M的坐标；（2）将直线AB向下平移，得到过点M的直线y＝mx+n，且与x轴负半轴交于点C，取点D（2，0），连接DM，求证：∠ADM﹣∠ACM＝45°；（3）点E是线段AB上一动点，点F是线段OA上一动点，连接EF，线段EF的延长线与线段OM交于点G．当∠BEF＝2∠BAO时，是否存在点E，使得3GF＝4EF？若存在，求出点E的坐标；若不存在，请说明理由．35．（2020•玉林）如图，已知抛物线：y1＝﹣x2﹣2x+3与x轴交于A，B两点（A在B的左侧），与y轴交于点C．（1）直接写出点A，B，C的坐标；（2）将抛物线y1经过向右与向下平移，使得到的抛物线y2与x轴交于B，B'两点（B'在B的右侧），顶点D的对应点为点D'，若∠BD'B'＝90°，求点B'的坐标及抛物线y2的解析式；（3）在（2）的条件下，若点Q在x轴上，则在抛物线y1或y2上是否存在点P，使以B′，C，Q，P为顶点的四边形是平行四边形？如果存在，求出所有符合条件的点P的坐标；如果不存在，请说明理由．36．（2020•云南）抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A的坐标为（﹣1，0），点C的坐标为（0，﹣3）．点P为抛物线y＝x2+bx+c上的一个动点．过点P作PD⊥x轴于点D，交直线BC于点E．（1）求b、c的值；（2）设点F在抛物线y＝x2+bx+c的对称轴上，当△ACF的周长最小时，直接写出点F 的坐标；（3）在第一象限，是否存在点P，使点P到直线BC的距离是点D到直线BC的距离的5倍？若存在，求出点P所有的坐标；若不存在，请说明理由．37．（2020•湘西州）已知直线y＝kx﹣2与抛物线y＝x2﹣bx+c（b，c为常数，b＞0）的一个交点为A（﹣1，0），点M（m，0）是x轴正半轴上的动点．（1）当直线y＝kx﹣2与抛物线y＝x2﹣bx+c（b，c为常数，b＞0）的另一个交点为该抛物线的顶点E时，求k，b，c的值及抛物线顶点E的坐标；（2）在（1）的条件下，设该抛物线与y轴的交点为C，若点Q在抛物线上，且点Q的横坐标为b，当S△EQM=12S△ACE时，求m的值；（3）点D在抛物线上，且点D的横坐标为b+12，当√2AM+2DM的最小值为27√24时，求b的值．38．（2020•广州）平面直角坐标系xOy中，抛物线G：y＝ax2+bx+c（0＜a＜12）过点A（1，c﹣5a），B（x1，3），C（x2，3）．顶点D不在第一象限，线段BC上有一点E，设△OBE的面积为S1，△OCE的面积为S2，S1＝S2+3 2．（1）用含a的式子表示b；（2）求点E的坐标：（3）若直线DE与抛物线G的另一个交点F的横坐标为6a+3，求y＝ax2+bx+c在1＜x ＜6时的取值范围（用含a的式子表示）．39．（2020•徐州）如图，在平面直角坐标系中，函数y＝﹣ax2+2ax+3a（a＞0）的图象交x 轴于点A、B，交y轴于点C，它的对称轴交x轴于点E．过点C作CD∥x轴交抛物线于点D，连接DE并延长交y轴于点F，交抛物线于点G．直线AF交CD于点H，交抛物线于点K，连接HE、GK．（1）点E的坐标为：；（2）当△HEF是直角三角形时，求a的值；（3）HE与GK有怎样的位置关系？请说明理由．40．（2020•恩施州）如图1，抛物线y=−14x2+bx+c经过点C（6，0），顶点为B，对称轴x＝2与x轴相交于点A，D为线段BC的中点．（1）求抛物线的解析式；（2）P 为线段BC 上任意一点，M 为x 轴上一动点，连接MP ，以点M 为中心，将△MPC 逆时针旋转90°，记点P 的对应点为E ，点C 的对应点为F ．当直线EF 与抛物线y =−14x 2+bx +c 只有一个交点时，求点M 的坐标．（3）△MPC 在（2）的旋转变换下，若PC =√2（如图2）．①求证：EA ＝ED ．②当点E 在（1）所求的抛物线上时，求线段CM 的长．41．（2020•黄冈）已知抛物线y ＝ax 2+bx +c 与x 轴交于点A （﹣1，0），点B （3，0），与y 轴交于点C （0，3）．顶点为点D ．（1）求抛物线的解析式；（2）若过点C 的直线交线段AB 于点E ，且S △ACE ：S △CEB ＝3：5，求直线CE 的解析式；（3）若点P 在抛物线上，点Q 在x 轴上，当以点D ，C ，P ，Q 为顶点的四边形是平行四边形时，求点P 的坐标；（4）已知点H （0，458），G （2，0），在抛物线对称轴上找一点F ，使HF +AF 的值最小．此时，在抛物线上是否存在一点K ，使KF +KG 的值最小？若存在，求出点K 的坐标；若不存在，请说明理由．42．（2020•十堰）已知抛物线y＝ax2﹣2ax+c过点A（﹣1，0）和C（0，3），与x轴交于另一点B，顶点为D．（1）求抛物线的解析式，并写出D点的坐标；（2）如图1，E为线段BC上方的抛物线上一点，EF⊥BC，垂足为F，EM⊥x轴，垂足为M，交BC于点G．当BG＝CF时，求△EFG的面积；（3）如图2，AC与BD的延长线交于点H，在x轴上方的抛物线上是否存在点P，使∠OPB＝∠AHB？若存在，求出点P的坐标；若不存在，请说明理由．43．（2020•淮安）如图①，二次函数y＝﹣x2+bx+4的图象与直线l交于A（﹣1，2）、B（3，n）两点．点P是x轴上的一个动点，过点P作x轴的垂线交直线l于点M，交该二次函数的图象于点N，设点P的横坐标为m．（1）b＝，n＝；（2）若点N在点M的上方，且MN＝3，求m的值；（3）将直线AB向上平移4个单位长度，分别与x轴、y轴交于点C、D（如图②）．①记△NBC的面积为S1，△NAC的面积为S2，是否存在m，使得点N在直线AC的上方，且满足S1﹣S2＝6？若存在，求出m及相应的S1，S2的值；若不存在，请说明理由．②当m＞﹣1时，将线段MA绕点M顺时针旋转90°得到线段MF，连接FB、FC、OA．若∠FBA+∠AOD﹣∠BFC＝45°，直接写出直线OF与该二次函数图象交点的横坐标．44．（2020•长沙）我们不妨约定：若某函数图象上至少存在不同的两点关于原点对称，则把该函数称之为“H函数”，其图象上关于原点对称的两点叫做一对“H点”．根据该约定，完成下列各题．（1）在下列关于x的函数中，是“H函数”的，请在相应题目后面的括号中打“√”，不是“H函数”的打“×”．①y＝2x（）；②y=m x（m≠0）（）；③y＝3x﹣1（）．（2）若点A（1，m）与点B（n，﹣4）是关于x的“H函数”y＝ax2+bx+c（a≠0）的一对“H点”，且该函数的对称轴始终位于直线x＝2的右侧，求a，b，c的值或取值范围．（3）若关于x的“H函数”y＝ax2+2bx+3c（a，b，c是常数）同时满足下列两个条件：①a+b+c＝0，②（2c+b﹣a）（2c+b+3a）＜0，求该“H函数”截x轴得到的线段长度的取值范围．45．（2020•邵阳）如图，在平面直角坐标系中，矩形ABCD的边BC与x轴、y轴的交点分别为C（8，0），B（0，6），CD＝5，抛物线y＝ax2−154x+c（a≠0）过B，C两点，动点M从点D开始以每秒5个单位长度的速度沿D→A→B→C的方向运动到达C点后停止运动．动点N从点O以每秒4个单位长度的速度沿OC方向运动，到达C点后，立即返回，向CO方向运动，到达O点后，又立即返回，依此在线段OC上反复运动，当点M停止运动时，点N也停止运动，设运动时间为t．（1）求抛物线的解析式；（2）求点D的坐标；（3）当点M，N同时开始运动时，若以点M，D，C为顶点的三角形与以点B，O，N 为顶点的三角形相似，求t的值；（4）过点D与x轴平行的直线，交抛物线的对称轴于点Q，将线段BA沿过点B的直线翻折，点A的对称点为A'，求A'Q+QN+DN的最小值．46．（2020•青海）如图1（注：与图2完全相同）所示，抛物线y=−12x2+bx+c经过B、D两点，与x轴的另一个交点为A，与y轴相交于点C．（1）求抛物线的解析式．（2）设抛物线的顶点为M，求四边形ABMC的面积．（请在图1中探索）（3）设点Q在y轴上，点P在抛物线上．要使以点A、B、P、Q为顶点的四边形是平行四边形，求所有满足条件的点P的坐标．（请在图2中探索）47．（2020•山西）综合与探究如图，抛物线y=14x2﹣x﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．直线l与抛物线交于A，D两点，与y轴交于点E，点D的坐标为（4，﹣3）．（1）请直接写出A，B两点的坐标及直线l的函数表达式；（2）若点P是抛物线上的点，点P的横坐标为m（m≥0），过点P作PM⊥x轴，垂足为M．PM与直线l交于点N，当点N是线段PM的三等分点时，求点P的坐标；（3）若点Q是y轴上的点，且∠ADQ＝45°，求点Q的坐标．48．（2020•广东）如图，抛物线y=3+√36x2+bx+c与x轴交于A，B两点，点A，B分别位于原点的左、右两侧，BO＝3AO＝3，过点B的直线与y轴正半轴和抛物线的交点分别为C，D，BC=√3CD．（1）求b，c的值；（2）求直线BD的函数解析式；（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ 相似时，请直接写出所有满足条件的点Q的坐标．49．（2020•荆门）如图，抛物线L：y=12x2−54x﹣3与x轴正半轴交于点A，与y轴交于点B．（1）求直线AB的解析式及抛物线顶点坐标；（2）如图1，点P为第四象限且在对称轴右侧抛物线上一动点，过点P作PC⊥x轴，垂足为C，PC交AB于点D，求PD+BD的最大值，并求出此时点P的坐标；（3）如图2，将抛物线L：y=12x2−54x﹣3向右平移得到抛物线L'，直线AB与抛物线L'交于M，N两点，若点A是线段MN的中点，求抛物线L'的解析式．50．如图，在直角坐标系中，四边形OABC 是平行四边形，经过A （﹣2，0），B ，C 三点的抛物线y ＝ax 2+bx +83（a ＜0）与x 轴的另一个交点为D ，其顶点为M ，对称轴与x 轴交于点E ．（1）求这条抛物线对应的函数表达式；（2）已知R 是抛物线上的点，使得△ADR 的面积是▱OABC 的面积的34，求点R 的坐标； （3）已知P 是抛物线对称轴上的点，满足在直线MD 上存在唯一的点Q ，使得∠PQE ＝45°，求点P 的坐标．。