数值分析上机第四次作业
- 格式:docx
- 大小:172.62 KB
- 文档页数:9

数值分析大作业三四五六七数值分析大作业三四五六七Document number【SA80SAB-SAA9SYT-SAATC-SA6UT-SA18】大作业三1. 给定初值0x 及容许误差,编制牛顿法解方程f (x )=0的通用程序. 解:Matlab 程序如下:函数m 文件:fu.mfunction Fu=fu(x)Fu=x^3/3-x;end函数m 文件:dfu.mfunction Fu=dfu(x)Fu=x^2-1;end用Newton 法求根的通用程序Newton.mclear;x0=input('请输入初值x0:');ep=input('请输入容许误差:');flag=1;while flag==1x1=x0-fu(x0)/dfu(x0);if abs(x1-x0)<ep< p="">flag=0;endx0=x1;endfprintf('方程的一个近似解为:%f\n',x0);寻找最大δ值的程序:Find.mcleareps=input('请输入搜索精度:');ep=input('请输入容许误差:');flag=1;k=0;x0=0;while flag==1sigma=k*eps;x0=sigma;k=k+1;m=0;flag1=1;while flag1==1 && m<=10^3x1=x0-fu(x0)/dfu(x0);if abs(x1-x0)endm=m+1;x0=x1;endif flag1==1||abs(x0)>=epflag=0;endendfprintf('最大的sigma 值为:%f\n',sigma);2.求下列方程的非零根5130.6651()ln 05130.665114000.0918x x f x x +??=-= ?-解:Matlab 程序为:(1)主程序clearclcformat longx0=765;N=100;errorlim=10^(-5);x=x0-f(x0)/subs(df(),x0);n=1;while n<n< p="">x=x0-f(x0)/subs(df(),x0);if abs(x-x0)>errorlimn=n+1;elsebreak;endx0=x;enddisp(['迭代次数: n=',num2str(n)])disp(['所求非零根: 正根x1=',num2str(x),' 负根x2=',num2str(-x)])(2)子函数非线性函数ffunction y=f(x)y=log((513+0.6651*x)/(513-0.6651*x))-x/(1400*0.0918);end(3)子函数非线性函数的一阶导数dffunction y=df()syms x1y=log((513+0.6651*x1)/(513-0.6651*x1))-x1/(1400*0.0918);y=diff(y);end运行结果如下:迭代次数: n=5所求非零根: 正根x1=767.3861 负根x2=-767.3861大作业四试编写MATLAB 函数实现Newton 插值,要求能输出插值多项式. 对函数21()14f x x=+在区间[-5,5]上实现10次多项式插值.分析:(1)输出插值多项式。

数值分析上机作业(四)常微分方程数值解一、问题描述考虑以下问题2000()999.75()1000.25()()du u t v t dtdv u t v t dt=−++=−初始条件为(0)0,(0)2u v ==−。
其精确解为0.52000.50.52000.5() 1.4998750.4998751() 2.999750.000251t t t t u t e e v t e e −−−−=−++=−−+请分别用古典四级四阶显式Runge-Kutta 方法和隐式二级四阶Runge-Kutta 方法计算,计算区间取成[0,20],并与精确解比较。
二、方法描述2.1古典四级四阶显式Runge-Kutta 方法考虑一阶常微分方程的初值问题000'(,),[,]()y f x y x x b y x y =∈=(1)经典四级四阶Runge-Kutta 方法的计算公式为112341213243(22)6(,)(,)22(,)22(,)n n n n n n n n n n h y y K K K K K f x y h h K f x y K h h K f x y K K f x h y hK +=++++==++=++=++四阶Runge-Kutta 方法的每一步需要计算四次函数值f ,可以证明其阶段误差为5()O h 。
再考虑一阶常微分方程组的初值问题0000'(,(),())'(,(),())()()x f t x t y t y g t x t y t x t x y t y ====(2)四阶Runge-Kutta 公式为1123411234(22)6(22)6n n n n h x x f f f f h y y g g g g ++=++++=++++其中11211211322322433433(,,)(,,)(,,)222(,,)222(,,)222(,,)222(,,)(,,)n n n n n n n n n n n n n n n n n n n n n n n n f f t x y g g t x y h h h f f t x f y g h h h g g t x f y g h h h f f t x f y g h h h g g t x f y g f f t h x hf y hg g g t h x hf y hg ===+++=+++=+++=+++=+++=+++2.2隐式二级四阶Runge-Kutta 方法考虑一阶常微分方程的初值问题(1),其计算公式为112112212()2111((,()244111((,()244m m m m m m h y y K K K f x h y hK hK K f x h y hK hK +=++=+++=++++再考虑一阶常微分方程组的初值问题(2),其计算公式为112112()2()2n n n n h x x f f h y y g g ++=++=++112121121221212211111((,(,()2444411111((,(,()2444411111((,(,()2444411((,(24m m m m m m m m m m m f f t h x hf hf y hg hg g g t h x hf hf y hg hg f f t h x hf hf y hg hg g g t h x hf =+++++−=+++++−=++++++=+++1212111,()444m hf y hg hg +++三、方案设计3.1给定函数将给定的初值问题写成通用形式,即编写函数将这个函数保存为f.m。

实验一实验项目:共轭梯度法求解对称正定的线性方程组实验内容:用共轭梯度法求解下面方程组(1) 123421003131020141100155x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪= ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 迭代20次或满足()(1)1110k k x x --∞-<时停止计算。
编制程序:储存m 文件function [x,k]=CGmethod(A,b)n=length(A);x=2*ones(n,1);r=b-A*x;rho=r'*r;k=0;while rho>10^(-11) & k<1000k=k+1;if k==1p=r;elsebeta=rho/rho1;p=r+beta*p;endw=A*p;alpha=rho/(p'*w);x=x+alpha*p;r=r-alpha*w;rho1=rho;rho=r'*r;end运行程序:clear,clcA=[2 -1 0 0;-1 3 -1 0;0 -1 4 -1;0 0 -1 5];b=[3 -2 1 5]';[x,k]=CGmethod(A,b)运行结果:x =1.5058823529411760.0117647058823530.5294117647058821.105882352941177(2) Ax b =,A 是1000阶的Hilbert 矩阵或如下的三对角矩阵,A[i,i]=4,A[i,i-1]=A[i-1,i]=-1,i=2,3,..,nb[1]=3, b[n]=3, b[i]=2,i=2,3,…,n-1迭代10000次或满足()()710k k r b Ax -=-≤时停止计算。
编制程序:储存m 文件function [x,k]=CGmethod_1(A,b)n=length(A);x(1:n,1)=0;r=b-A*x;r1=r;k=0;while norm(r1,1)>10^(-7)&k<10^4k=k+1;if k==1p=r;elsebeta=(r1'*r1)/(r'*r);p=r1+beta*p;endr=r1;w=A*p;alpha=(r'*r)/(p'*w);x=x+alpha*p;r1=r-alpha*w;end运行程序:clear,clcn=1000;A=hilb(n);b=sum(A')';[x,k]=CGmethod(A,b)实验二1、 实验目的:用复化Simpson 方法、自适应复化梯形方法和Romberg 方法求数值积分。

第一章第二题(1) 截断误差为104-时:k=1;n=0;m=0;x=0;e=1e-4;while k==1x1=x+(-1)^n/(2*n+1);if abs(x-x1)<ey=4*x1;m=n+1;break;endx=x1;k=1;n=n+1;endformat longy,my =3.141792613595791m =5001(2)截断误差为108-时:k=1;n=0;m=0;x=0;e=1e-8;while k==1x1=x+(-1)^n/(2*n+1);if abs(x-x1)<ey=4*x1;m=n+1;break;endx=x1;k=1;n=n+1;endformat longy,my =3.141592673590250m =50000001由以上计算可知,截断误差小于104-时,应取5001项求和,π=3.141792613595791;截断误差小于108-时,应取50000001项求和,π=3.141592673590250。
第二章第二题a=[0 -2 -2 -2 -2 -2 -2 -2];b=[2 5 5 5 5 5 5 5];c=[-2 -2 -2 -2 -2 -2 -2 0];v=220;r=27;d=[v/r 0 0 0 0 0 0 0];n=8;for i=2:na(i)=a(i)/b(i-1);b(i)=b(i)-c(n-1)*a(i);d(i)=d(i)-a(i)*d(i-1);end;d(n)=d(n)/b(n);for i=n-1:-1:1d(i)=(d(i)-c(i)*d(i+1));end;I=d'I =1.0e+002 *1.490717294184090.704617906351300.311568212434910.128623612390290.049496991380330.017168822994210.004772412363470.00047741598598第三章第一题(1)Jacobi迭代法:b=[12;-27;14;-17;12]x = [0;0;0;0;0;]k = 0;r = 1;e=0.000001A=[10,1,2,3,4;1,9,-1,2,-3;2,-1,7,3,-5;3,2,3,12,-1;4,-3,-5,-1,15;] D = diag(diag(A));B = inv(D)*(D-A);f = inv(D)*b;p = max(abs(eig(B)));if p >= 1'迭代法不收敛'returnendwhile r >ex0 = x;x = B*x0 + f;k = k + 1;r = norm (x-x0,inf);endxk计算结果:x =1.0000-2.00003.0000-2.00001.0000k =65(2) 高斯赛德尔迭代:A=[10,1,2,3,4;1,9,-1,2,-3;2,-1,7,3,-5;3,2,3,12,-1;4,-3,-5,-1,15;]x=[0;0;0;0;0];b=[12;-27;14;-17;12]c=0.000001L=-tril(A,-1)U=-triu(A,1)D=(diag(diag(A)))X=inv(D-L)*U*x+inv(D-L)*b;k=1;while norm(X-x,inf)>= cx=X;X=inv(D-L)*U*x+inv(D-L)*b;k=k+1;endXk计算结果:X =1.0000-2.00003.0000-2.00001.0000k =37(3) SOR:A=[10,1,2,3,4;1,9,-1,2,-3;2,-1,7,3,-5;3,2,3,12,-1;4,-3,-5,-1,15] x=[0;0;0;0;0];b=[12;-27;14;-17;12]e=0.000001w=1.44;L=-tril(A,-1)U=-triu(A,1)D=(diag(diag(A)))X=inv(D-w*L)*((1-w)*D+w*U)*x+w*inv(D-w*L)*bn=1;while norm(X-x,inf)>=ex=X;X=inv(D-w*L)*((1-w)*D+w*U)*x+w*inv(D-w*L)*b;n=n+1;endXn计算结果:X =1.0000-2.00003.0000-2.00001.0000n =22由以上可知,共轭梯度法收敛速度明显快于Jacobi法和G-S法。


第一章(1)按从大到小的顺序计算S的程序为:N#include<stdio.h>void main(){float n,j,s=0;printf("请输入n:");scanf("%f",&n);for(j=2;j<=n;j++)s=s+1/(j*j-1);printf("s=%f\n",s);}(2)按从小到大的顺序计算S的程序为:N#include<stdio.h>void main(){float n,j,s=0;printf("请输入n:");scanf("%f",&n);for(j=n;j>=2;j--)s=s+1/(j*j-1);printf("s=%f\n",s);}(3)精确值,从大到小,从小到大的计算程序为:#include<stdio.h>void main(){float n,j,s1,s2=0,s3=0;printf("请输入n:");scanf("%f",&n);s1=(3.0/2-1/n-1/(n+1))/2;for(j=2;j<=n;j++)s2=s2+1/(j*j-1);for(j=n;j>=2;j--)s3=s3+1/(j*j-1);printf("精确算法的结果为:%f\n",s1);printf("从大到小顺序的结果为:%f\n",s2); printf("从小到大顺序的结果为:%f\n",s3); }结果如下:精确值从大到小的值从小到大的值有效位数从大到小从小到大210S0.740049 0.740049 0.74005 6 5410S0.7499 0.749852 0.7499 4 4610S0.749999 0.749852 0.749999 3 6(4)通过本上机题,我们可以看出:当n较小时,两种算法的结果都很接近精确值,而当n较大时,两种算法的结果差别较大,按从大到小的顺序计算的值与精确值有较大的误差,而按从小到大的顺序计算的值与精确值吻合。

数值分析上机作业(1、2、3、4、6章)第一章17. 舍入误差与有效数设2211NN j S j ==-∑,其精确值为1311221N N ⎛⎫-- ⎪+⎝⎭。
(1)编制按从大到小的顺序22211121311N S N =+++---,计算N S 的通用程序; (2)编制按从小到大的顺序2221111(1)121N S N N =+++----,计算N S 的通用程序;(3)按两种顺序分别计算210S ,410S ,610S ,并指出有效位数(编制程序时使用单精度);(4)通过本上机题你明白了什么?运行结果:按从大到小的顺序计算得:N N S误差e有效位数2⨯8 100.7400495 94.95049501392230710-4⨯ 4 100.7498521 54.79049995000258010-6⨯ 3 100.7498521 41.46900000499994310-按从小到大的顺序计算得:N N S误差e有效位数2⨯84.95049501392230710-100.7400495 944.99950003618465610-⨯8 100.7499000 965.00044450291170510-⨯11 100.7499990 13(4)通过本题可以看出,不同算法造成的误差是不同的,好的算法可以让计算结果精度更高。
对于本题,当采用从大到小的顺序累加计算时,计算误差随着N的增大而增大;当采用从小到大的顺序累加计算时,计算误差随着N的增大而减小。
因此在N比较大时宜采用从小到达的顺序累加计算。
第二章20.Newton 迭代法(1)给定初值0x 及容许误差ε,编制Newton 法解方程()0f x =根的通用程序;(2)给定方程3()03x f x x =-=,易知其有三个根*1x =,*20x =,*3x =①由Newton 方法的局部收敛性可知存在0δ>,当0(,)x δδ∈-时Newton 迭代序列收敛于根*2x ,试确定尽可能大的δ;②试取若干初始值,观察当0(,1)x ∈-∞-,(1,)δ--,(,)δδ-,(,1)δ,(1,)+∞时Newton 序列是否收敛以及收敛于哪一个根;(3)通过本上机题,你明白了什么?本实验取610ε-=,找到的最大的0.774597δ=②当0(,1)x ∈-∞-时,计算结果如下:x0 xend -1000 -1.732051 -500 -1.732051 -100 -1.732051 -10 -1.732051 -1.5-1.732051Newton 序列收敛于-1.732051当0(1,)xδ∈--时,计算结果如下:x0 xend-0.95 1.732051-0.90 1.732051-0.85 1.732051-0.80 -1.732051-0.78 -1.732051 Newton序列收敛于1.732051或-1.732051当0(,)xδδ∈-时,计算结果如下:x0 xend-0.77 0.000000-0.5 0.000000-0.1 0.0000000.3 0.0000000.77 0.000000 Newton序列收敛于0当0(,1)xδ∈时,计算结果如下:x0 xend0.78 1.7320510.80 1.7320510.85 -1.7320510.90 -1.7320510.95 -1.732051 Newton序列收敛于1.732051或-1.732051当0(1,)x∈+∞时,计算结果如下:x0 xend1.5 1.73205110 1.732051100 1.732051500 1.7320511000 1.732051Newton序列收敛于1.732051(3)通过本题发现,Newton迭代法解方程初始值的选取非常重要,不同的初始值会收敛于方程不同的根,且有些区间是全局收敛,有些区间是局部收敛。

数值分析上机实验报告选题:曲线拟合的最小二乘法指导老师:专业:学号:姓名:课题八 曲线拟合的最小二乘法一、问题提出从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。
在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量y 与时间t 的拟合曲线。
二、要求1、用最小二乘法进行曲线拟合;2、近似解析表达式为()33221t a t a t a t ++=ϕ;3、打印出拟合函数()t ϕ,并打印出()j t ϕ与()j t y 的误差,12,,2,1Λ=j ;4、另外选取一个近似表达式,尝试拟合效果的比较;5、*绘制出曲线拟合图*。
三、目的和意义1、掌握曲线拟合的最小二乘法;2、最小二乘法亦可用于解超定线代数方程组;3、探索拟合函数的选择与拟合精度间的关系。
四、计算公式对于给定的测量数据(x i ,f i )(i=1,2,…,n ),设函数分布为 特别的,取)(x j ϕ为多项式j j x x =)(ϕ (j=0, 1,…,m )则根据最小二乘法原理,可以构造泛函令0=∂∂ka H (k=0, 1,…,m ) 则可以得到法方程求该解方程组,则可以得到解m a a a ,,,10Λ,因此可得到数据的最小二乘解曲线拟合:实际工作中,变量间未必都有线性关系,如服药后血药浓度与时间的关系;疾病疗效与疗程长短的关系;毒物剂量与致死率的关系等常呈曲线关系。
曲线拟合是指选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。
五、结构程序设计在程序结构方面主要是按照顺序结构进行设计,在进行曲线的拟合时,为了进行比较,在程序设计中,直接调用了最小二乘法的拟合函数polyfit ,并且依次调用了plot 、figure 、hold on 函数进行图象的绘制,最后调用了一个绝对值函数abs 用于计算拟合函数与原有数据的误差,进行拟合效果的比较。

《数值分析》上机习题1.用Newton法求方程X7 - 28X4 + 14=0在(0.1,1.9)中的近似根(初始近似值取为区间端点,迭代6次或误差小于0.00001)。
#include<stdio.h>#include<math.h>int main(){ float x1,x,f1,f2;static int count=0;x1=0.1 ;//定义初始值do{x=x1;f1=x*(x*x*x*x*x*x-28*x*x*x)+14;f2=7*x*x*x*x*x*x-4*28*x*x*x;//对函数f1求导x1=x-f1/f2; count++; }while(fabs(x1-x)>=1e-5);printf("%8.7f\n",x1); printf("%d\n",count);return 0;}2.已知函数值如下表:试用三次样条插值求f(4.563)及f’(4.563)的近似值。
include <stdio.h>#include <math.h>#define N 11main(){double B[N+1][N+1],m,x,u[N+1],y[N+1],c[N+1],d[N+1];double e[N+1]={2,0,4.15888308,6.5916738,8.3177664,9.6566268,10.750557,11.675460 6,12.47667,13.1833476,13.8155106,14.0155106};int i;x=4.563;B[0][0]=-2;B[0][1]=-4;B[N][N-1]=4;B[N][N]=2;for(i=1;i<N;i++){B[i][i-1]=1;B[i][i]=4;B[i][i+1]=1;}u[0]=B[0][0];y[0]=e[0];for(i=1;i<N;i++){m=B[i][i-1]/u[i-1];u[i]=B[i][i]-m*B[i-1][i];y[i]=e[i]-m*y[i-1];}c[N]=y[N]/u[N];for(i=N-1;i>=0;i--)c[i]=(y[i]-B[i][i+1]*c[i+1])/u[i];for(i=0;i<12;i++){m=fabs(x-i);if(m>=2)d[i]=0;else if(m<=1)d[i]=0.5*fabs(pow(m,3))-m*m+2.0/3;elsed[i]=(-1.0/6.0)*fabs(pow(m,3))+m*m-2*fabs(m)+4/3.0;} m=0;for(i=0;i<12;i++) m=m+c[i]*d[i];printf("f(%4.3f)=%f\n",x,m);printf("f'(4.563)=%lf\n",(c[4]-c[2])/2); }3.用Romberg 算法求)00001.0(sin )75(32314.1=+⎰ε允许误差dx x x x x . #include "stdafx.h" #include<stdio.h> #include<math.h> float f(float x) {float f=0.0;f=pow(3.0,x)*pow(x,1.4)*(5*x+7)*sin(x*x); return (f); } main() {int i=1,j,k,n=12;float T[12],a=1.0,b=3.0,s=0.0; T[0]=0.5*(b-a)*(f(a)+f(b));for(j=1;j<n-1;j++){ for(k=1;k<=pow(2,j-1);k++) s+=f(a+(2*k-1)*(b-a)/pow(2,j)); T[j]=0.5*(T[j-1]+(b-a)*s/pow(2,j-1)); s=0.0; }T[11]=(4*T[1]-T[0])/(float)3;for(;fabs(T[11]-T[0])>0.00001;i++) {T[0]=T[11];for(j=1;j<n-1-i;j++) T[j]=(pow(4,i)*T[j+1]-T[j])/(pow(4,i)-1); T[11]=(pow(4,i+1)*T[1]-T[0])/(pow(4,i+1)-1); }printf("%f\n",T[11]); }4. 用定步长四阶Runge-Kutta 求解一、程序要求用定步长四阶法求解 y1’=1y2’=y3 y3’=1000-1000y2-100y3(y1(0)=y2(0)=y3(0)=0) h=0.0005,打印yi(0.025),yi(0.045),yi(0.085),yi(0.1),(i=1,2,3)h =0.0005,打印y i (0.025) ,⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧===--===0)0(0)0(0)0(10010001000//1/321323321y y y y y dt dy ydt dy dt dyy i(0.045) ,y i(0.085) ,y i(0.1) ,(i=1,2,3)#include "stdafx.h"#include <stdio.h>#include <math.h>double F(double x,double y[4],double f[4]){f[1]=0*x+0*y[1]+0*y[2]+0*y[3]+1;f[2]=0*x+0*y[1]+0*y[2]+1*y[3]+0;f[3]=0*x+0*y[1]-1000*y[2]-100*y[3]+1000;return(1);}void main(){double F(double x,double y[4],double f[4]);doubleh=0.0005,x=0,Y[4],k[5][4],s[4],f[4],det,m[4]={0.025,0.045,0.085,0.1};int i,j,t; for(t=0;t<=3;t++)/*龙格-库塔算法*/{for(j=0;j<=3;j++)Y[j]=0; //每求一组值后将初值条件还原为0 for(i=1;i<=int(m[t]/h);i++){for(j=1;j<=3;j++)s[j]=Y[j];det=F(x,s,f);for(j=1;j<=3;j++)k[1][j]=h*f[j]; /*四阶古典公式中的k值和求和的计算*/ for(j=1;j<=3;j++)s[j]=Y[j]+0.5*k[1][j];det=F(x+0.5*h,s,f);for(j=1;j<=3;j++)k[2][j]=h*f[j];for(j=1;j<=3;j++)s[j]=Y[j]+0.5*k[2][j];det=F(x+0.5*h,s,f);for(j=1;j<=3;j++)k[3][j]=h*f[j];for(j=1;j<=3;j++)s[j]=Y[j]+k[3][j];det=F(x+h,s,f);for(j=1;j<=3;j++)k[4][j]=h*f[j];for(j=1;j<=3;j++)Y[j]=Y[j]+(k[1][j]+2*k[2][j]+2*k[3][j]+k[4][j])/6;x+=h;} for(j=1;j<=3;j++)printf("y[%d](%f)=%f ",j,m[t],Y[j]); printf("\n"); } } 5.⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=40.00001 4.446782 2.213474- 0.238417 1.784317 0.037585- 1.010103- 3.123124 2.031743- 4.446782 30.719334 3.123789 1.103456- 2.121314 0.71828- 0.336993 1.112348 3.067813 2.213474- 3.123789 14.7138465 0.103458- 3.111223- 2.101023 1.056781- 0.784165- 1.7423820.238417 1.103456- 0.103458- 9.789365 0.431637 3.741856- 1.836742 1.563849 0.718719 1.7843172.1213143.111223- 0.431637 19.8979184.101011 2.031454 2.189736 0.113584-0.037585- 0.71828- 2.101023 3.741856- 4.101011 27.108437 3.123848 1.012345- 1.112336 1.010103- 0.336993 1.056781- 1.836742 2.031454 3.123848 15.567914 3.125432- 1.061074- 3.123124 1.112348 0.784165- 1.563849 2.189736 1.012345- 3.125432- 19.141823 2.115237 2.031743- 3.067813 1.742382 0.718719 0.113584- 1.112336 1.061074- 2.115237 12.38412A Tb )5.6784392- 4.719345 1.1101230 86.612343- 1.784317 0.84671695 25.173417- 33.992318 2.1874369(= 用列主元消去法求解Ax=b 。
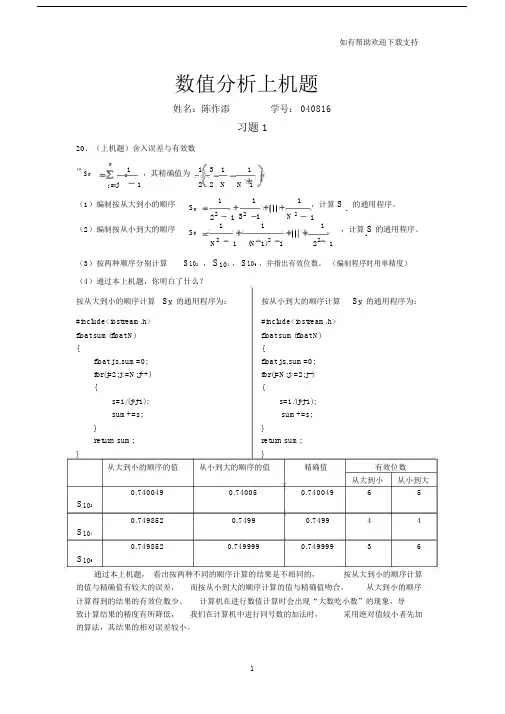
如有帮助欢迎下载支持数值分析上机题姓名:陈作添学号: 040816习题 120.(上机题)舍入误差与有效数N11 3 1 1设S N,其精确值为 。
22 2 NN 1j 2j1(1)编制按从大到小的顺序111 ,计算 S 的通用程序。
S N1 321N 21 N22(2)编制按从小到大的顺序111,计算 S 的通用程序。
S N1(N 1)2 122 1NN 2(3)按两种顺序分别计算S 102 , S 104 , S 106 ,并指出有效位数。
(编制程序时用单精度)(4)通过本上机题,你明白了什么?按从大到小的顺序计算 S N 的通用程序为: 按从小到大的顺序计算 S N 的通用程序为:#include<iostream.h> #include<iostream.h> float sum(float N) float sum(float N) {{float j,s,sum=0; float j,s,sum=0; for(j=2;j<=N;j++) for(j=N;j>=2;j--) {{s=1/(j*j-1); s=1/(j*j-1); sum+=s;sum+=s;}}return sum;return sum;}}从大到小的顺序的值从小到大的顺序的值精确值有效位数从大到小从小到大0.7400490.740050.74004965 S 1020.7498520.74990.74994 4S 1040.7498520.7499990.74999936S 106通过本上机题, 看出按两种不同的顺序计算的结果是不相同的,按从大到小的顺序计算的值与精确值有较大的误差, 而按从小到大的顺序计算的值与精确值吻合。
从大到小的顺序计算得到的结果的有效位数少。
计算机在进行数值计算时会出现“大数吃小数”的现象,导致计算结果的精度有所降低,我们在计算机中进行同号数的加法时,采用绝对值较小者先加的算法,其结果的相对误差较小。

《数值分析》大作业四一、算法设计方案:复化梯形积分法,选取步长为1/500=0.002,迭代误差控制在E ≤1.0e-10①复化梯形积分法:11()[()()2()]2n b ak h f x dx f a f b f a kh -=⎰≈+++∑,截断误差为:322()''()''(),[,]1212Tb a b a R f h f a b nηηη--=-=-∈其中。
复化Simpson 积分法,选取步长为1/50=0.02,迭代误差控制在E ≤1.0e-10②Simpson 积分法:121211()[()()4()2()]3m m bi i ai i h f x dx f a f b f x f x --==≈+++∑∑⎰,截断误差为:4(4)(),[,]180sb a R h fa b ηη-=-∈。
③Guass 积分法选用Gauss-Legendre 求积公式:111()()ni i i f x dx A f x -=≈∑⎰截断误差为:R=()()n 2n 422n !2×(2[2!]2n 1fn n ⨯(2)η())+ η∈(1,1)。
选择9个节点:-0.9681602395,-0.8360311073,-0.6133714327,-0.3242534234,0,0.3242534234,0.6133714327,0.8360311073,0.9681602395, 对应的求积系数依次为:0.0812743884,0.1806481607,0.2606106964,0.3123470770,0.3302393550,0.3123470770,0.2606106964,0.1806481607,0.0812743884。
二、程序源代码:#include<stdio.h>#include<math.h>#include<stdlib.h>#define E 1.0e-10/****定义函数g和K*****/double g(double a){double b;b=exp(4*a)+(exp(a+4)-exp(-a-4))/(a+4);return b;}double K(double a,double b){double c;c=exp(a*b);return c;}/******复化梯形法******/void Tixing( ){double u[1001],x[1001],h,c[1001],e;int i,j,k;FILE *fp;fp=fopen("f:/result0. xls ","w");h=1.0/1500;for(i=0;i<3001;i++){x[i]=i*h-1;u[i]=g(x[i]);}for(k=0;k<100;k++){e=0;for(i=0;i<1001;i++){for(j=1,c[i]=0;j<N-1;j++)c[i]+=K(x[i],x[j])*u[j];u[i]=g(x[i])-h*c[i]-h/2*(K(x[i],x[0])*u[0]+K(x[i],x[N-1])*u[N-1]);e+=h*(exp(4*x[i])-u[i])*(exp(4*x[i])-u[i]);}if(e<=E) break;}for(i=0;i<1001;i++)fprintf(fp,"%.12lf,%.12lf\n",x[i],u[i]);fclose(fp);}/******复化Simpson法******/void simpson( ){double u[101],x[101],h,c[101],d[101],e;int i,j,k;FILE *fp;fp=fopen("f:/result1.xls","w");h=1.0/50;for(i=0;i<101;i++){x[i]=i*h-1;u[i]=g(x[i]);}for(k=0;k<50;k++){e=0;for(i=0;i<101;i++){for(j=1,c[i]=0,d[i]=0;j<51;j++){c[i]+=K(x[i],x[2*j-1])*u[2*j-1];if(j<50)d[i]+=K(x[i],x[2*j])*u[2*j];}u[i]=g(x[i])-4*h/3*c[i]-2*h/3*d[i]-h/3*(K(x[i],x[0])*u[0]+K(x[i],x[M-1])*u[M-1]);e+=h*(exp(4*x[i])-u[i])*(exp(4*x[i])-u[i]);}if(e<=E) break;}for(i=0;i<101;i++)fprintf(fp,"%.12lf,%.12lf\n",x[i],u[i]);fclose(fp);}/******Gauss积分法******/void gauss( ){double x[9]={-0.9681602395,-0.8360311073,-0.6133714327,-0.3242534234,0,\0.3242534234,0.6133714327,0.8360311073,0.9681602395},A[9]={0.0812743884,0.1806481607,0.2606106964,0.3123470770,0.3302393550,\0.3123470770,0.2606106964,0.1806481607,0.0812743884},u[9],c[9],e;int i,j,k;FILE *fp;fp=fopen("f:/result2. xls ","w");for(i=0;i<9;i++)u[i]=g(x[i]);for(k=0;k<50;k++){e=0;for(i=0;i<9;i++){for(j=0,c[i]=0;j<9;j++)c[i]+=A[j]*K(x[i],x[j])*u[j];u[i]=g(x[i])-c[i];e+=A[i]*(exp(4*x[i])-u[i])*(exp(4*x[i])-u[i]);}if(e<=E) break;}for(i=0;i<9;i++)fprintf(fp,"%.12lf,%.12lf\n",x[i],u[i]);fclose(fp);}/******主函数******/main(){Tixing ( );Simpson( );Gauss( );return 0;}三、运算结果复化梯形数据-10.018323-0.920.02523-0.9980.018471-0.9180.025433-0.9960.018619-0.9160.025637-0.9940.018768-0.9140.025843-0.9920.018919-0.9120.026051-0.990.019071-0.910.02626-0.9880.019224-0.9080.026471-0.9860.019378-0.9060.026683-0.9840.019534-0.9040.026897-0.9820.019691-0.9020.027113-0.980.019849-0.90.027331-0.9780.020008-0.8980.02755-0.9760.020169-0.8960.027772-0.9740.020331-0.8940.027995-0.9720.020494-0.8920.028219-0.970.020658-0.890.028446-0.9680.020824-0.8880.028674-0.9660.020992-0.8860.028905-0.9640.02116-0.8840.029137-0.9620.02133-0.8820.029371-0.960.021501-0.880.029607-0.9580.021674-0.8780.029844-0.9560.021848-0.8760.030084-0.9540.022023-0.8740.030326-0.9520.0222-0.8720.030569-0.950.022378-0.870.030815-0.9480.022558-0.8680.031062-0.9460.022739-0.8660.031311-0.9440.022922-0.8640.031563-0.9420.023106-0.8620.031816-0.940.023291-0.860.032072-0.9380.023478-0.8580.032329-0.9360.023667-0.8560.032589-0.9340.023857-0.8540.032851-0.9320.024048-0.8520.033114-0.930.024241-0.850.03338-0.9280.024436-0.8480.033648-0.9260.024632-0.8460.033918-0.9240.02483-0.8440.034191-0.9220.025029-0.8420.034465-0.840.034742-0.760.047841-0.8380.035021-0.7580.048225-0.8360.035302-0.7560.048613 -0.8340.035586-0.7540.049003 -0.8320.035872-0.7520.049396 -0.830.03616-0.750.049793 -0.8280.03645-0.7480.050193 -0.8260.036743-0.7460.050596 -0.8240.037038-0.7440.051002 -0.8220.037335-0.7420.051412 -0.820.037635-0.740.051825 -0.8180.037937-0.7380.052241 -0.8160.038242-0.7360.052661 -0.8140.038549-0.7340.053084 -0.8120.038858-0.7320.05351 -0.810.039171-0.730.05394 -0.8080.039485-0.7280.054373 -0.8060.039802-0.7260.054809 -0.8040.040122-0.7240.05525 -0.8020.040444-0.7220.055693 -0.80.040769-0.720.056141 -0.7980.041096-0.7180.056591 -0.7960.041426-0.7160.057046 -0.7940.041759-0.7140.057504 -0.7920.042094-0.7120.057966 -0.790.042432-0.710.058431 -0.7880.042773-0.7080.058901 -0.7860.043116-0.7060.059374 -0.7840.043463-0.7040.05985 -0.7820.043812-0.7020.060331 -0.780.044164-0.70.060816 -0.7780.044518-0.6980.061304 -0.7760.044876-0.6960.061796 -0.7740.045236-0.6940.062293 -0.7720.045599-0.6920.062793 -0.770.045966-0.690.063297 -0.7680.046335-0.6880.063805 -0.7660.046707-0.6860.064318 -0.7640.047082-0.6840.064834 -0.7620.04746-0.6820.065355-0.680.06588-0.60.090722 -0.6780.066409-0.5980.091451-0.6760.066942-0.5960.092185 -0.6740.06748-0.5940.092926 -0.6720.068022-0.5920.093672 -0.670.068568-0.590.094424 -0.6680.069119-0.5880.095183 -0.6660.069674-0.5860.095947 -0.6640.070234-0.5840.096718 -0.6620.070798-0.5820.097494 -0.660.071366-0.580.098277 -0.6580.071939-0.5780.099067 -0.6560.072517-0.5760.099862 -0.6540.0731-0.5740.100664 -0.6520.073687-0.5720.101473 -0.650.074278-0.570.102288 -0.6480.074875-0.5680.103109 -0.6460.075476-0.5660.103937 -0.6440.076082-0.5640.104772 -0.6420.076694-0.5620.105614 -0.640.077309-0.560.106462 -0.6380.07793-0.5580.107317 -0.6360.078556-0.5560.108179 -0.6340.079187-0.5540.109048 -0.6320.079823-0.5520.109924 -0.630.080464-0.550.110806 -0.6280.08111-0.5480.111696 -0.6260.081762-0.5460.112593 -0.6240.082418-0.5440.113498 -0.6220.08308-0.5420.114409 -0.620.083748-0.540.115328 -0.6180.08442-0.5380.116254 -0.6160.085098-0.5360.117188 -0.6140.085782-0.5340.118129 -0.6120.086471-0.5320.119078 -0.610.087165-0.530.120035 -0.6080.087865-0.5280.120999 -0.6060.088571-0.5260.12197 -0.6040.089282-0.5240.12295 -0.6020.089999-0.5220.123938-0.550.110806-0.470.152592 -0.5480.111696-0.4680.153817-0.5460.112593-0.4660.155053-0.5440.113498-0.4640.156298-0.5420.114409-0.4620.157553-0.540.115328-0.460.158819-0.5380.116254-0.4580.160095-0.5360.117188-0.4560.16138-0.5340.118129-0.4540.162677-0.5320.119078-0.4520.163983-0.530.120035-0.450.1653-0.5280.120999-0.4480.166628-0.5260.12197-0.4460.167966-0.5240.12295-0.4440.169315-0.5220.123938-0.4420.170675-0.520.124933-0.440.172046-0.5180.125936-0.4380.173428-0.5160.126948-0.4360.174821-0.5140.127967-0.4340.176225-0.5120.128995-0.4320.17764-0.510.130031-0.430.179067-0.5080.131076-0.4280.180505-0.5060.132128-0.4260.181955-0.5040.13319-0.4240.183416-0.5020.134259-0.4220.18489-0.50.135338-0.420.186375-0.4980.136425-0.4180.187871-0.4960.13752-0.4160.18938-0.4940.138625-0.4140.190901-0.4920.139738-0.4120.192435-0.490.140861-0.410.19398-0.4880.141992-0.4080.195538-0.4860.143132-0.4060.197109-0.4840.144282-0.4040.198692-0.4820.145441-0.4020.200288-0.480.146609-0.40.201897-0.4780.147786-0.3980.203518-0.4760.148973-0.3960.205153-0.4740.15017-0.3940.206801-0.4720.151376-0.3920.208462-0.390.210136-0.310.289382 -0.3880.211824-0.3080.291706-0.3860.213525-0.3060.294049 -0.3840.21524-0.3040.296411 -0.3820.216969-0.3020.298792 -0.380.218711-0.30.301192 -0.3780.220468-0.2980.303611 -0.3760.222239-0.2960.306049 -0.3740.224024-0.2940.308508 -0.3720.225823-0.2920.310985 -0.370.227637-0.290.313483 -0.3680.229465-0.2880.316001 -0.3660.231308-0.2860.318539 -0.3640.233166-0.2840.321098 -0.3620.235039-0.2820.323677 -0.360.236927-0.280.326277 -0.3580.23883-0.2780.328897 -0.3560.240748-0.2760.331539 -0.3540.242682-0.2740.334202 -0.3520.244631-0.2720.336886 -0.350.246596-0.270.339592 -0.3480.248576-0.2680.34232 -0.3460.250573-0.2660.345069 -0.3440.252586-0.2640.347841 -0.3420.254614-0.2620.350635 -0.340.256659-0.260.353451 -0.3380.258721-0.2580.35629 -0.3360.260799-0.2560.359151 -0.3340.262894-0.2540.362036 -0.3320.265005-0.2520.364944 -0.330.267134-0.250.367875 -0.3280.269279-0.2480.37083 -0.3260.271442-0.2460.373809 -0.3240.273622-0.2440.376811 -0.3220.27582-0.2420.379838 -0.320.278035-0.240.382888 -0.3180.280268-0.2380.385964 -0.3160.28252-0.2360.389064 -0.3140.284789-0.2340.392189 -0.3120.287076-0.2320.395339-0.230.398514-0.150.548804-0.2280.401715-0.1480.553212-0.2260.404942-0.1460.557655 -0.2240.408194-0.1440.562134 -0.2220.411473-0.1420.56665 -0.220.414778-0.140.571201 -0.2180.418109-0.1380.575789 -0.2160.421467-0.1360.580414 -0.2140.424853-0.1340.585076 -0.2120.428265-0.1320.589775 -0.210.431705-0.130.594512 -0.2080.435172-0.1280.599287 -0.2060.438668-0.1260.604101 -0.2040.442191-0.1240.608953 -0.2020.445743-0.1220.613844 -0.20.449323-0.120.618774 -0.1980.452932-0.1180.623744 -0.1960.45657-0.1160.628754 -0.1940.460237-0.1140.633805 -0.1920.463934-0.1120.638895 -0.190.46766-0.110.644027 -0.1880.471416-0.1080.6492 -0.1860.475203-0.1060.654414 -0.1840.47902-0.1040.659671 -0.1820.482867-0.1020.664969 -0.180.486746-0.10.67031 -0.1780.490655-0.0980.675694 -0.1760.494596-0.0960.681121 -0.1740.498569-0.0940.686592 -0.1720.502573-0.0920.692107 -0.170.50661-0.090.697666 -0.1680.510679-0.0880.70327 -0.1660.514781-0.0860.708919 -0.1640.518916-0.0840.714613 -0.1620.523084-0.0820.720352 -0.160.527285-0.080.726138 -0.1580.53152-0.0780.731971 -0.1560.535789-0.0760.73785 -0.1540.540093-0.0740.743776 -0.1520.544431-0.0720.749751-0.070.7557730.01 1.040796 -0.0680.7618430.012 1.049156-0.0660.7679620.014 1.057583 -0.0640.7741310.016 1.066077 -0.0620.7803480.018 1.07464 -0.060.7866160.02 1.083272 -0.0580.7929340.022 1.091973 -0.0560.7993030.024 1.100743 -0.0540.8057230.026 1.109585 -0.0520.8121950.028 1.118497 -0.050.8187190.03 1.127481 -0.0480.8252950.032 1.136537 -0.0460.8319240.034 1.145666 -0.0440.8386060.036 1.154868 -0.0420.8453410.038 1.164144 -0.040.8521310.04 1.173494 -0.0380.8589760.042 1.18292 -0.0360.8658750.044 1.192421 -0.0340.872830.046 1.201999 -0.0320.879840.048 1.211654 -0.030.8869070.05 1.221386 -0.0280.8940310.052 1.231196 -0.0260.9012120.054 1.241085 -0.0240.9084510.056 1.251054 -0.0220.9157480.058 1.261102 -0.020.9231030.06 1.271232 -0.0180.9305170.062 1.281442 -0.0160.9379910.064 1.291735 -0.0140.9455250.066 1.30211 -0.0120.953120.068 1.312569 -0.010.9607750.07 1.323112 -0.0080.9684930.072 1.333739 -0.0060.9762720.074 1.344452 -0.0040.9841130.076 1.355251 -0.0020.9920180.078 1.366136 00.9999860.08 1.377109 0.002 1.0080180.082 1.38817 0.004 1.0161140.084 1.39932 0.006 1.0242760.086 1.41056 0.008 1.0325030.088 1.4218890.09 1.433310.17 1.973853 0.092 1.4448230.172 1.9897080.094 1.4564280.174 2.005689 0.096 1.4681260.176 2.021799 0.098 1.4799180.178 2.038039 0.1 1.4918050.18 2.054408 0.102 1.5037870.182 2.07091 0.104 1.5158660.184 2.087543 0.106 1.5280410.186 2.104311 0.108 1.5403150.188 2.121213 0.11 1.5526870.19 2.138251 0.112 1.5651580.192 2.155425 0.114 1.577730.194 2.172738 0.116 1.5904020.196 2.19019 0.118 1.6031760.198 2.207781 0.12 1.6160530.2 2.225515 0.122 1.6290340.202 2.24339 0.124 1.6421180.204 2.261409 0.126 1.6553080.206 2.279573 0.128 1.6686040.208 2.297883 0.13 1.6820060.21 2.31634 0.132 1.6955160.212 2.334945 0.134 1.7091350.214 2.3537 0.136 1.7228630.216 2.372605 0.138 1.7367010.218 2.391662 0.14 1.750650.22 2.410872 0.142 1.7647120.222 2.430236 0.144 1.7788860.224 2.449756 0.146 1.7931740.226 2.469433 0.148 1.8075770.228 2.489268 0.15 1.8220960.23 2.509262 0.152 1.8367310.232 2.529417 0.154 1.8514840.234 2.549733 0.156 1.8663550.236 2.570213 0.158 1.8813460.238 2.590857 0.16 1.8964570.24 2.611667 0.162 1.911690.242 2.632645 0.164 1.9270450.244 2.65379 0.166 1.9425230.246 2.675106 0.168 1.9581260.248 2.6965930.25 2.7182520.33 3.743385 0.252 2.7400850.332 3.7734530.254 2.7620940.334 3.803761 0.256 2.7842790.336 3.834314 0.258 2.8066430.338 3.865111 0.26 2.8291860.34 3.896156 0.262 2.8519110.342 3.927451 0.264 2.8748180.344 3.958996 0.266 2.8979090.346 3.990796 0.268 2.9211850.348 4.02285 0.27 2.9446480.35 4.055162 0.272 2.96830.352 4.087734 0.274 2.9921420.354 4.120567 0.276 3.0161750.356 4.153664 0.278 3.0404010.358 4.187026 0.28 3.0648220.36 4.220657 0.282 3.0894390.362 4.254558 0.284 3.1142540.364 4.288731 0.286 3.1392680.366 4.323179 0.288 3.1644830.368 4.357903 0.29 3.18990.37 4.392906 0.292 3.2155220.372 4.42819 0.294 3.2413490.374 4.463758 0.296 3.2673840.376 4.499612 0.298 3.2936280.378 4.535753 0.3 3.3200830.38 4.572185 0.302 3.346750.382 4.608909 0.304 3.3736320.384 4.645928 0.306 3.4007290.386 4.683245 0.308 3.4280440.388 4.720861 0.31 3.4555790.39 4.75878 0.312 3.4833350.392 4.797003 0.314 3.5113130.394 4.835533 0.316 3.5395160.396 4.874373 0.318 3.5679460.398 4.913524 0.32 3.5966040.4 4.95299 0.322 3.6254930.402 4.992773 0.324 3.6546130.404 5.032876 0.326 3.6839670.406 5.0733 0.328 3.7135570.408 5.114050.41 5.1551260.497.099276 0.412 5.1965330.4927.1562980.414 5.2382720.4947.213778 0.416 5.2803460.4967.27172 0.418 5.3227590.4987.330127 0.42 5.3655120.57.389004 0.422 5.4086080.5027.448353 0.424 5.4520510.5047.508179 0.426 5.4958420.5067.568486 0.428 5.5399850.5087.629277 0.43 5.5844830.517.690556 0.432 5.6293380.5127.752327 0.434 5.6745540.5147.814595 0.436 5.7201330.5167.877362 0.438 5.7660770.5187.940634 0.44 5.8123910.528.004414 0.442 5.8590770.5228.068707 0.444 5.9061380.5248.133516 0.446 5.9535770.5268.198845 0.448 6.0013960.5288.264699 0.45 6.04960.538.331082 0.452 6.0981910.5328.397998 0.454 6.1471730.5348.465452 0.456 6.1965480.5368.533447 0.458 6.2463190.5388.601989 0.46 6.296490.548.671081 0.462 6.3470640.5428.740728 0.464 6.3980450.5448.810935 0.466 6.4494340.5468.881705 0.468 6.5012370.5488.953044 0.47 6.5534560.559.024956 0.472 6.6060940.5529.097445 0.474 6.6591550.5549.170517 0.476 6.7126420.5569.244175 0.478 6.7665580.5589.318426 0.48 6.8209080.569.393272 0.482 6.8756950.5629.46872 0.484 6.9309210.5649.544774 0.486 6.9865910.5669.621439 0.4887.0427080.5689.6987190.579.776620.6513.46367 0.5729.8551470.65213.571810.5749.9343050.65413.68082 0.57610.01410.65613.79071 0.57810.094530.65813.90147 0.5810.175610.6614.01313 0.58210.257340.66214.12569 0.58410.339730.66414.23915 0.58610.422780.66614.35352 0.58810.50650.66814.46881 0.5910.590890.6714.58502 0.59210.675960.67214.70217 0.59410.761710.67414.82026 0.59610.848150.67614.9393 0.59810.935280.67815.05929 0.611.023110.6815.18025 0.60211.111650.68215.30218 0.60411.20090.68415.42509 0.60611.290870.68615.54898 0.60811.381560.68815.67387 0.6111.472980.6915.79977 0.61211.565130.69215.92667 0.61411.658020.69416.0546 0.61611.751660.69616.18355 0.61811.846050.69816.31354 0.6211.94120.716.44457 0.62212.037110.70216.57665 0.62412.133790.70416.7098 0.62612.231250.70616.84401 0.62812.32950.70816.97931 0.6312.428530.7117.11569 0.63212.528360.71217.25316 0.63412.628990.71417.39174 0.63612.730420.71617.53143 0.63812.832680.71817.67225 0.6412.935750.7217.81419 0.64213.039650.72217.95728 0.64413.144390.72418.10151 0.64613.249960.72618.24691 0.64813.356390.72818.393470.7318.541210.8125.53363 0.73218.690130.81225.738720.73418.840250.81425.94545 0.73618.991580.81626.15385 0.73819.144120.81826.36392 0.7419.297890.8226.57568 0.74219.452890.82226.78914 0.74419.609140.82427.00431 0.74619.766640.82627.22121 0.74819.925410.82827.43985 0.7520.085450.8327.66025 0.75220.246780.83227.88242 0.75420.409410.83428.10638 0.75620.573340.83628.33213 0.75820.738580.83828.5597 0.7620.905160.8428.78909 0.76221.073070.84229.02033 0.76421.242330.84429.25342 0.76621.412950.84629.48839 0.76821.584940.84829.72524 0.7721.758310.8529.964 0.77221.933080.85230.20467 0.77422.109250.85430.44728 0.77622.286830.85630.69184 0.77822.465840.85830.93836 0.7822.646290.8631.18686 0.78222.828190.86231.43735 0.78423.011550.86431.68986 0.78623.196380.86631.9444 0.78823.382690.86832.20098 0.7923.570510.8732.45962 0.79223.759830.87232.72034 0.79423.950670.87432.98315 0.79624.143040.87633.24807 0.79824.336960.87833.51513 0.824.532440.8833.78432 0.80224.729490.88234.05568 0.80424.928110.88434.32922 0.80625.128340.88634.60496 0.80825.330170.88834.882910.8935.163090.94643.99154 0.89235.445520.94844.344880.89435.730220.9544.701070.89636.017210.95245.060110.89836.306510.95445.422040.936.598120.95645.786870.90236.892080.95846.154630.90437.188410.9646.525350.90637.487110.96246.899050.90837.788210.96447.275750.9138.091730.96647.655470.91238.397680.96848.038240.91438.70610.9748.424090.91639.016990.97248.813040.91839.330380.97449.205110.9239.646280.97649.600330.92239.964720.97849.998720.92440.285720.9850.400320.92640.60930.98250.805140.92840.935480.98451.213210.9341.264280.98651.624560.93241.595720.98852.039210.93441.929820.9952.45720.93642.26660.99252.878540.93842.606090.99453.303270.9442.948310.99653.73140.94243.293270.99854.162980.94443.64101154.59802复化Simpson数据:-1 0.018319929 -0.34 0.256658088 0.32 3.596641805 -0.98 0.0198445 -0.32 0.278035042 0.34 3.896195298-0.96 0.021494322 -0.3 0.301192133 0.36 4.220697765-0.94 0.023283225 -0.28 0.326278124 0.38 4.572227037-0.92 0.025220379 -0.26 0.353453177 0.4 4.95303418-0.9 0.027320224 -0.24 0.382891765 0.42 5.365557596-0.88 0.029594431 -0.22 0.41478194 0.44 5.812438891-0.86 0.032059069 -0.16 0.527292277 0.54 8.671138204-0.84 0.034728638 -0.14 0.571209036 0.56 9.39333156-0.82 0.037621263 -0.12 0.61878367 0.58 10.17567433-0.8 0.040754615 -0.1 0.670320427 0.6 11.02317608-0.78 0.044149394 -0.08 0.726149698 0.62 11.94126383-0.76 0.047826844 -0.06 0.78662861 0.64 12.93581634-0.74 0.051810827 -0.04 0.85214479 0.66 14.01320231-0.72 0.056126648 -0.02 0.92311742 0.68 15.1803205-0.7 0.060802006 0 1.0000013 0.7 16.44464467 -0.68 0.065866854 0.02 1.083288424 0.72 17.81427057 -0.66 0.071353499 0.04 1.173512427 0.74 19.29796874 -0.64 0.077297255 0.06 1.271250748 0.76 20.90523965 -0.62 0.083735917 0.08 1.377129533 0.78 22.64637562 -0.6 0.090711017 0.1 1.491826493 0.8 24.53252554 -0.58 0.098266855 0.12 1.616076341 0.82 26.57576756 -0.56 0.106452202 0.14 1.750674449 0.84 28.78918506 -0.54 0.11531904 0.16 1.896482943 0.86 31.18695183 -0.52 0.12492459 0.18 2.054435268 0.88 33.78442141 -0.5 0.135329888 0.2 2.225543071 0.9 36.59822683 -0.48 0.14660204 0.22 2.410901825 0.92 39.64638571 -0.46 0.158812728 0.24 2.611698647 0.94 42.94841704 -0.44 0.17204064 0.26 2.829219145 0.96 46.52546475 -0.42 0.18636997 0.28 3.064856356 0.98 50.40043451 -0.4 0.201892977 0.3 3.320119013 1 54.59813904 -0.38 0.218708553 0.46 6.296539601-0.36 0.236924875 0.48 6.820959636-0.2 0.449328351 0.5 7.389057081-0.18 0.486751777 0.52 8.004469675Gauss积分数据:0102030405060四、讨论①在满足相同精度要求的情况下复化梯形积分法比复化Simpson 积分法计算所需节点数多,计算量大。
1.用两种方法解sin 5cos 20.31x x +=-,如何一次求出此方程的四个根。
解:方法一:在Matlab 命令窗口输入命令x=solve('sin(5*x)+cos(2*x)=-0.31')运行后输出结果:x =- 0.36685340479904406504913603551901 - 0.089925518994485866153169602644131*i 方法二:在Matlab 命令窗口输入命令E1=sym('sin(5*x)+cos(2*x)=-0.31');[x1]=solve(E1)运行后输出结果:x1 =- 0.36685340479904406504913603551901 - 0.089925518994485866153169602644131*i 2.用三种方法解方程11852912312x x x x -+-=。
解:方法一:在Matlab 命令窗口输入命令x=solve('9*x^11-12*x^8+x^5-3*x^2=12')运行后输出结果:x =1.1945355092112803561808169303487 - 0.25878939596021341127295614138703 + 0.98996423045277565907337492165509*i - 0.91081125361412082546165956220494 + 0.34557668006489020731472236114125*i - 0.6567748898900820562684890790666 - 0.94093805304063227438930031737768*i - 0.6567748898900820562684890790666 + 0.94093805304063227438930031737768*i 0.34695114229720670305614226506505 + 0.85428006847946699100354057810685*i - 0.25878939596021341127295614138703 - 0.98996423045277565907337492165509*i 0.88215664256156941185655405241917 + 0.47468310614563172153151897912015*i 0.34695114229720670305614226506505 - 0.85428006847946699100354057810685*i 0.88215664256156941185655405241917 - 0.47468310614563172153151897912015*i - 0.91081125361412082546165956220494 - 0.34557668006489020731472236114125*i 方法二:在Matlab 命令窗口输入命令fa=[9,0,0,-12,0,0,1,0,0,-3,0,-12];xk=roots(fa)运行后输出结果:xk =-0.9108 + 0.3456i-0.9108 - 0.3456i-0.6568 + 0.9409i-0.6568 - 0.9409i-0.2588 + 0.9900i-0.2588 - 0.9900i1.1945 + 0.0000i0.8822 + 0.4747i0.8822 - 0.4747i0.3470 + 0.8543i0.3470 - 0.8543i方法三:在Matlab命令窗口输入命令E1=sym('9*x^11-12*x^8+x^5-3*x^2-12=0'); [x1]=solve(E1)运行后输出结果:x1 =1.1945355092112803561808169303487 - 0.25878939596021341127295614138703 + 0.98996423045277565907337492165509*i - 0.91081125361412082546165956220494 + 0.34557668006489020731472236114125*i - 0.6567748898900820562684890790666 - 0.94093805304063227438930031737768*i - 0.6567748898900820562684890790666 + 0.94093805304063227438930031737768*i 0.34695114229720670305614226506505 + 0.85428006847946699100354057810685*i - 0.25878939596021341127295614138703 - 0.98996423045277565907337492165509*i 0.88215664256156941185655405241917 + 0.47468310614563172153151897912015*i 0.34695114229720670305614226506505 - 0.85428006847946699100354057810685*i 0.88215664256156941185655405241917 - 0.47468310614563172153151897912015*i - 0.91081125361412082546165956220494 - 0.34557668006489020731472236114125*3 用MATLAB 方法求函数11852()912312f x x x x x =-+--的导数'()f x 。
20130917题目求证:在矩阵的LU 分解中,111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明:在高斯消去过程中,假设0jj a ≠ ,若a=0,可以通过列变换使得前面的条件成立,这里不考虑这种情况。
对矩阵A 进行LU 分解,()()()()()1111111L M n M M M n ---=-=∙∙-………… ,其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ,i e 、j e 为n 维线性空间的自然基。
()M j 是通过对单位阵进行初等变换得到,通过逆向的变换则可以得到单位阵,由此很容易得到()M j 的逆矩阵为1n Tn ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。
故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换,从右向左乘,则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。
由于最初的矩阵为单位阵,变换从右向左展开,因而每一次变换不改变已经更新的数据,既该变换是从右向左一列一列更新数据,故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。
数学证明:1nTi j i ji j ee α=+⎛⎫ ⎪⎝⎭∑具有,000n j jA -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式,且有+1,-11,10000=000n j j n j n j AB --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭ 而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式,因此:1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问:能否用逐次householder 相似变换变实矩阵A 为上三角矩阵,为什么?解:不能用逐次householder 相似变换变A 为上三角矩阵,原因如下:A 记作:()12=,,n A a a a ……, ,存在householder 阵1H s.t. 1111H a e α= ,则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数,故无法通过householder 变换实现上三角化。
数值分析上机题答案【篇一:数值分析上机试题对应参考答案】么是近似值x* 有效数字?若近似值x*的误差限是某一位的半个单位,该位到x*的第一位非零数字共有n位,就说x*有n位有效数字。
它可表示为2、数值计算应该避免采用不稳定的算法,防止有效数字的损失. 因此,在进行数值运算算法设计过程中主要注意什么?(1)简化计算过程,减少运算次数;(2)避免两个相近的数相减;(3)避免除数的绝对值远小于被除数的绝对值;(4)防止大数“吃掉”小数的现象;(5)使用数值稳定的算法,设法控制误差的传播。
3、写出“n 阶阵a 具有n 个不相等的特征值”的等价条件(至少写3 个)(1)|a|不为零(2)n阶矩阵a的列或行向量组线性无关(3)矩阵a为满秩矩阵(4)n阶矩阵a与n阶可逆矩阵b等价4、迭代法的基本思想是什么?就是用某种极限过程去逐步逼近线性方程组精确解得方法。
其基本思想为:先任取一组近似解初值x0,然后按照某种迭代原则,由x0计算新的近似解x1,以此类推,可计算出x2,x3,…xk,。
,如果{x}收敛,则取为原方程组的解。
5、病态线性方程组的主要判断方法有哪些?(1)系数矩阵的某两行(列)几乎近似相关(2)系数矩阵的行列式的值很小(3)用主元消去法解线性方程组时出现小主元(4)近似解x*已使残差向量r=b-ax*的范数很小,但该近似解仍不符合问题要求。
6、lagrange 插值的前提条件是什么?并写出二次lagrange 插值的基函数。
1,j?i?(x)? 前提条件是:l i ,j?0,1,2?,n.?ij0,j?i?二次lagrange 插值的基函数: (x?x)(x?x)12??lx0(xx)(xx) 0?10?2 (x?x)(x?x)02?? lx1(xx)(xx)1?01?2(x?x)(x?x)01?? lx2(x?x)(x?x)20217、什么是数值积分的代数精度?如果某一个求积公式对于次数不超过m的多项式均能准确地成立,但对于m+1次多项式就不准确成立,则称该求积公式具有m次代数精度(或代数精确度)。
数值分析上机题目4 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN实验一实验项目:共轭梯度法求解对称正定的线性方程组 实验内容:用共轭梯度法求解下面方程组(1) 123421003131020141100155x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪=⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 迭代20次或满足()(1)1110k k x x --∞-<时停止计算。
编制程序:储存m 文件function [x,k]=CGmethod(A,b)n=length(A);x=2*ones(n,1);r=b-A*x;rho=r'*r; k=0;while rho>10^(-11) & k<1000 k=k+1; if k==1 p=r; elsebeta=rho/rho1; p=r+beta*p; end w=A*p;alpha=rho/(p'*w); x=x+alpha*p; r=r-alpha*w; rho1=rho; rho=r'*r; end运行程序:clear,clcA=[2 -1 0 0;-1 3 -1 0;0 -1 4 -1;0 0 -1 5]; b=[3 -2 1 5]'; [x,k]=CGmethod(A,b)运行结果: x =(2) Ax b =,A 是1000阶的Hilbert 矩阵或如下的三对角矩阵, A[i,i]=4,A[i,i-1]=A[i-1,i]=-1,i=2,3,..,n b[1]=3, b[n]=3, b[i]=2,i=2,3,…,n-1迭代10000次或满足()()710k k r b Ax -=-≤时停止计算。
编制程序:储存m 文件function [x,k]=CGmethod_1(A,b) n=length(A);x(1:n,1)=0;r=b-A*x;r1=r; k=0;while norm(r1,1)>10^(-7)&k<10^4 k=k+1; if k==1 p=r; elsebeta=(r1'*r1)/(r'*r);p=r1+beta*p; end r=r1; w=A*p;alpha=(r'*r)/(p'*w); x=x+alpha*p; r1=r-alpha*w; end运行程序: clear,clc n=1000; A=hilb(n); b=sum(A')';[x,k]=CGmethod(A,b)实验二1、 实验目的:用复化Simpson 方法、自适应复化梯形方法和Romberg 方法求数值积分。
一. 上机作业任务一: 用五点差分格式求解Poisson 方程边值问题,P124-------3、4(任选一题)。
二. 上机作业任务二:用Simpson 求积法计算定积分()baf x dx ⎰。
下面两种方法任选一。
(1)变步长复化Simpson 求积法。
(2)自适应Simpson 求积法三. 上机作业任务三:用MATLAB 语言编写连续函数最佳平方逼近的算法程序(函数式M 文件)。
要求算法程序可以适应不同的具体函数,具有一定的通用性。
并用此程序进行数值试验,写出计算实习报告。
所编程序具有以下功能:1. 用Lengendre 多项式做基,并适合于构造任意次数的最佳平方逼近多项式。
可利用递推关系 0112()1,()()(21)()(1)()/2,3,.....n n n P x P x xP x n xP x n P x n n --===---⎡⎤⎣⎦=2. 被逼近函数f(x)用M 文件建立数学函数。
这样,此程序可通过修改建立数学函数的M 文件以适用不同的被逼近函数(要学会用函数句柄)。
3. 要考虑一般的情况]1,1[],[)(+-≠∈b a x f 。
因此,程序中要有变量代换的功能。
4. 计算组合系数时,计算函数的积分采用数值积分的方法。
5. 程序中应包括帮助文本和必要的注释语句。
另外,程序中也要有必要的反馈信息。
6. 程序输入:(1)待求的被逼近函数值的数据点0x (可以是一个数值或向量)(2)区间端点:a,b 。
7. 程序输出:(1)拟合系数:012,,,...,n c c c c(2)待求的被逼近函数值00001102200()()()()()n n s x c P x c P x c P x c P x =++++ 8. 试验函数:()cos ,[0,4]f x x x x =∈+;也可自选其它的试验函数。
9. 用所编程序直接进行计算,检测程序的正确性,并理解算法。
10. 分别求二次、三次、。
数值分析上机第四次作业实验项目:共轭梯度法求解对称正定的线性方程组实验内容:用共轭梯度法求解下面方程组(1) 123421003131020141100155x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪= ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 迭代20次或满足()(1)1110k k x x --∞-<时停止计算。
(2) Ax b =,A 是1000阶的Hilbert 矩阵或如下的三对角矩阵,A[i,i]=4,A[i,i-1]=A[i-1,i]=-1,i=2,3,..,nb[1]=3, b[n]=3, b[i]=2,i=2,3,…,n-1迭代10000次或满足()()710k k r b Ax -=-≤时停止计算。
(3)*考虑模型问题,方程为 222222(),(,)(0,1)(0,1)(0,)1,(1,),01(,0)1,(,1),01xy y x u u x y e x y D x yu y u y e y u x u x e x ∂∂+=+∈=⨯∂∂==≤≤==≤≤用正方形网格离散化,若取1/,10h N N ==,得到100n =的线性方程组,并用共轭梯度法(CG 法)求解,并对解作图。
实验要求:迭代初值可以取01(,1,...,)ij u i j N ==,计算到32||||10k r -≤停止.本题有精确解(,)xy u x y e =,这里k u 表示以k ij u 为分量的向量,u 表示在相应点(,)i j 上取值作为分量的向量.实验一:(1)编制函数子程序CGmethod 。
function [x,k]=CGmethod(A,b)n=length(A);x=zeros(n,1);r=b-A*x;rho=r'*r;k=0;while rho>10^(-12) & k<20k=k+1;if k==1p=r;elsebeta=rho/rho1;p=r+beta*p;endw=A*p;alpha=rho/(p'*w);x=x+alpha*p;r=r-alpha*w;rho1=rho;rho=r'*r;end编制主程序shiyan1_1:clear,clcA=[2,-1,0,0;-1,3,-1,0;0,-1,4,1;0,0,-1,5]; b=[3,-2,1,5]';[x,k]=CGmethod(A,b)运行结果为:x =1.3882-0.2855-0.02220.9367k =20(2)编制函数子程序CGmethod_1function [x,k]=CGmethod_1(A,b)n=length(A);x(1:n,1)=0;r=b-A*x;r1=r;k=0;while norm(r1,1)>=10^(-7)&k<10^4k=k+1;if k==1p=r;elsebeta=(r1'*r1)/(r'*r);p=r1+beta*p;endr=r1;w=A*p;alpha=(r'*r)/(p'*w);x=x+alpha*p;r1=r-alpha*w;end编制主程序shiyan1_2:clear,clcn=1000;A=hilb(n);b=sum(A')';[x,k]=CGmethod_1(A,b)运行结果为:x 的值,均接近1,迭代次数k=32实验二实验目的:用复化Simpson 方法、自适应复化梯形方法和Romberg 方法求数值积分。
实验内容:计算下列定积分 (1) dx x x x ⎰⎪⎪⎭⎫ ⎝⎛+-202610 (2)⎰10dx x x (3) ⎰20051dx x 实验要求:(1)分别用复化Simpson 公式、自适应复化梯形公式计算要求绝对误差限为71021-⨯=ε,输出每种方法所需的节点数和积分近似值,对于自适应方法,显示实际计算节点上离散函数值的分布图;(2)分析比较计算结果。
2、实验目的:高斯数值积分方法用于积分方程求解。
实验内容:线性的积分方程的数值求解,可以被转化为线性代数方程组的求解问题。
而线性代数方程组所含未知数的个数,与用来离散积分的数值方法的节点个数相同。
在节点数相同的前提下,高斯数值积分方法有较高的代数精度,用它通常会得到较好的结果。
对第二类Fredholm 积分方程b t a t f ds s y s t k t y ba ≤≤+=⎰),()(),()( 首先将积分区间[a,b]等分成n 份,在每个子区间上离散方程中的积分就得到线性代数方程组。
实验要求:分别使用如下方法,离散积分方程中的积分1.复化梯形方法;2.复化辛甫森方法;3.复化高斯方法。
求解如下的积分方程t t e ds s y e e t y --=⎰10)(12)(,方程的准确解为t e , 并比较各算法的优劣。
实验二1、复化Simpson 方法)输入积分区间下限0输入积分区间上限2输入等分份数20输入被积函数(以x 为自变量)x^6/10-x^2+xS =1.1619输入积分区间下限0输入积分区间上限1输入等分份数20输入被积函数(以x为自变量)x*sqrt(x)S =0.4000输入积分区间下限5输入积分区间上限200输入等分份数20输入被积函数(以x为自变量)1/sqrt(x)S =23.82182、自动变步长Simpson方法函数1:输入积分区间下限0输入积分区间上限2输入为课本的第几个函数(第一个这输入1):1S =1.619(过程省略)i =19函数2:输入积分区间下限0输入积分区间上限1输入为课本的第几个函数(第一个这输入1):2S =0.4(过程省略)i =17函数3:输入积分区间下限5输入积分区间上限200输入为课本的第几个函数(第一个这输入1):3S=23.8121(过程省略)i =111编制程序如下:Clear,clcsyms xa=input('输入积分区间下限');b=input('输入积分区间上限');n=input('输入等分份数');ff=input('输入被积函数(以x为自变量)');h=(b-a)/n;f=inline(ff,'x');sum1=0;for i=0:n-1sum1=sum1+f(a+i*h+0.5*h);endfor i=1:n-1sum2=sum2+f(a+i*h);endfor i=0:2*nX(i+1,1)=f((b-a)*i/(n*2)+a); endS=h/6*(f(a)+4*sum1+2*sum2+f(b))function S = zdsps( n )a=0;b=1;h=(b-a)/4;f=inline('x^(3/2)','x');sum1=0;sum2=0;for i=0:n-1sum1=sum1+f(a+i*h+0.5*h);endfor i=1:n-1sum2=sum2+f(a+i*h);endfor i=0:2*nx(i+1,1)=f((b-a)*i/(n*2)+a); endS=h/6*(f(a)+4*sum1+2*sum2+f(b)); endfunction S = zpsgs(a,b,n,ff )h=(b-a)/n;sum1=0;sum2=0;sum3=0;sum4=0;if ff==1f=inline('x^6/10-x^2+x','x'); endif ff==2f=inline('x^(3/2)','x');endif ff==3f=inline('1/sqrt(x)','x');for i=0:n-1sum1=sum1+f(a+i*h+0.25*h);sum2=sum2+f(a+i*h+0.75*h);sum4=sum4+f(a+i*h+0.5*h);endfor i=1:n-1sum3=sum3+f(a+i*h);endfor i=0:4*nx(i+1,1)=f((b-a)*i/(n*4)+a);endS=h/(6*2)*(f(a)+4*sum1+4*sum2+2*(sum3+sum4)+f(b));endclear , clca=input('输入积分区间下限');b=input('输入积分区间上限');ff=input('输入为课本的第几个函数(第一个这输入1):');for i=2:300S(i)=zpsgs(a,b,(i),ff);S(i+1)=zpsgs(a,b,(i+1),ff);if abs(S(i+1)-S(i))<0.5*10^(-7)breakendendS %所求积分值i %所分份数实验三1、对常微分方程初值问题2cos (0)1y y x y '=-+⎧⎨=⎩(0)x π<< 分别使用Euler 显示方法、改进的Euler 方法和经典RK 法和四阶Adams 预测-校正算法,求解常微分方程数值解,并与其精确解cos sin y x x =+进行作图比较。
其中多步法需要的初值由经典RK 法提供。
2、实验目的:Lorenz 问题与混沌实验内容:考虑著名的Lorenz 方程⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=-=)1.8()(bz xy dtdz xz y rx dtdy x y s dt dx其中s, r, b 为变化区域有一定限制的实参数。
该方程形式简单,表面上看并无惊人之处,但由该方程揭示出的许多现象,促使“混沌”成为数学研究的崭新领域,在实际应用中也产生了巨大的影响。
实验方法:先取定初值Y0=(x, y, z)=(0, 0, 0),参数s=10, r=28, b=8/3,用MATLAB 编程数值求解,并与MATLAB 函数ods45的计算结果进行对比。
实验要求:(1)对目前取定的参数值s, r 和b ,选取不同的初值Y0进行运算,观察计算的结果有什么特点?解的曲线是否有界?解的曲线是不是周期的或趋于某个固定点?(2)在问题允许的范围内适当改变其中的参数值s, r, b ,再选取不同的初始值Y0进行试算,观察并记录计算的结果有什么特点?是否发现什么不同的现象?3、定义函数子程序为:function z=f(x,y)z=-y+2*cos(x);return主程序为:clear,clcb=pi;a=0;n=100;y(1)=1;h=(b-a)/n;x=a:h:b;for i=1:ny(i+1)=y(i)+h*f(x(i),y(i));endt1=plot(x,y,'r-')hold onfor i=1:nK1=f(x(i),y(i));K2=f(x(i+1),y(i)+h*K1);y(i+1)=y(i)+h*(K1+K2)/2;endt2=plot(x,y,'b+')for i=1:nK1=f(x(i),y(i));K2=f(x(i)+0.5*h,y(i)+0.5*h*K1);K3=f(x(i)+0.5*h,y(i)+0.5*h*K2);K4=f(x(i),y(i)+h*K3);y(i+1)=y(i)+h*(K1+2*K2+2*K3+K4)/6;endt3=plot(x,y,'ko')for i=1:3K1=f(x(i),y(i));K2=f(x(i)+0.5*h,y(i)+0.5*h*K1);K3=f(x(i)+0.5*h,y(i)+0.5*h*K2);K4=f(x(i),y(i)+h*K3);y(i+1)=y(i)+h*(K1+2*K2+2*K3+K4)/6;endfor i=4:nz=y(i)+h/24*(55*f(x(i),y(i))-59*f(x(i-1),y(i-1))...+37*f(x(i-2),y(i-2))-9*f(x(i-3),y(i-3)));y(i+1)=y(i)+h/24*(9*f(x(i+1),z)+19*f(x(i),y(i))...-5*f(x(i-1),y(i-1))+f(x(i-2),y(i-2)));endt4=plot(x,y,'g*')t5=ezplot('sin(x)+cos(x)',[0,pi])xlabel('x轴','FontWeight','bold')ylabel('y轴', 'FontWeight','bold')legend([t1,t2,t3,t4,t5],'向前Euler法','¸改进的Euler法','经典四阶Runge-Kutta法','四阶Adams公式','精确解')原图为:局部放大图为:由图可得:四阶Adams公式及改进的欧拉法将为精确。