机械优化设计实例(人字架优化)

机械优化设计实例(人字架优化)第1页共5页人字架的优化设计一、问题描述如图1所示的人字架由两个钢管组成，其顶点受外力2F=3×105N 。

已知人字架跨度2B=152 cm,钢管壁厚T=0.25cm,钢管材料的弹性模量E=2.1510? MPa ，材料密度p=7．8×103 kg ／m ，许用压应力δy =420 MPa 。

求钢管压应力δ不超过许用压应力δy 和失稳临界应力δc 的条件下，人字架的高h 和钢管平均直径D 使钢管总质量m 为最小。

二、分析设计变量：平均直径D 、高度h三、数学建模所设计的空心传动轴应满足以下条件：（1）强度约束条件即δ≤??????y δ 经整理得()[]y hTDhB F δπ≤+2122（2）稳定性约束条件：[]c δδ≤()()()***-*****28h B D T E hTDhB F ++≤+ππ （3）取值范围：第2页共5页*****≤≤D ***-*****≤≤h则目标函数为：()2*****__.122min x x xf +?=-约束条件为：***-*****00106)(212241≤-+?=x Tx x X g π()***-*****5.*****.***-********-*****)(2 221212242≤++-+?=X x x x Tx x g π010)(13≤-=x X g0120)(14≤-=x X g 0200)(25≤-=x X g01000)(26≤-=x X g四、优化方法、编程及结果分析1优化方法综合上述分析可得优化数学模型为：()Tx x X 21,=；)(min x f ；()0..≤x g t s i 。

考察该模型，它是一个具有2个设计变量，6个约束条件的有约束非线性的单目标最优化问题，属于小型优化设计，故采用SUMT 惩罚函数内点法求解。

2方法原理内点惩罚函数法简称内点法，这种方法将新目标函数定义于可行域内，序列迭代点在可行域内逐步逼近约束边界上的最优点。

机械优化设计经典实例机械优化设计是指通过对机械结构和工艺的改进，提高机械产品的性能和技术指标的一种设计方法。

机械优化设计可以在保持原产品功能和形式不变的前提下，提高产品的可靠性、工作效率、耐久性和经济性。

本文将介绍几个经典的机械优化设计实例。

第一个实例是汽车发动机的优化设计。

汽车发动机是汽车的核心部件，其性能的提升对汽车整体性能有着重要影响。

一种常见的汽车发动机优化设计方法是通过提高燃烧效率来提高功率和燃油经济性。

例如，通过优化进气和排气系统设计，改善燃烧室结构，提高燃烧效率和燃油的利用率。

此外，采用新材料和制造工艺，减轻发动机重量，提高动力性能和燃油经济性也是重要的优化方向。

第二个实例是飞机机翼的优化设计。

飞机机翼是飞机气动设计中的关键部件，直接影响飞机的飞行性能、起降性能和燃油经济性。

机翼的优化设计中，常采用的方法是通过减小机翼的阻力和提高升力来提高飞机性能。

例如，优化机翼的气动外形，减小阻力和气动失速的风险；采用新材料和结构设计，降低机翼重量，提高飞机的载重能力和燃油经济性；优化翼尖设计，减小湍流损失，提高升力系数。

第三个实例是电机的优化设计。

电机是广泛应用于各种机械设备和电子产品中的核心动力装置。

电机的性能优化设计可以通过提高效率、减小体积、降低噪音等方面来实现。

例如，采用优化电磁设计和轴承设计，减小电机的损耗和噪音，提高效率；通过采用新材料和工艺，减小电机的尺寸和重量，实现体积紧凑和轻量化设计。

总之，机械优化设计在提高机械产品性能和技术指标方面有着重要应用。

通过针对不同机械产品的特点和需求，优化设计可以提高机械产品的可靠性、工作效率、耐久性和经济性。

这些经典实例为我们提供了有效的设计思路和方法，帮助我们在实际设计中充分发挥机械优化设计的优势和潜力。

机械最优化设计及应用实例
机械最优化设计是指基于数学模型和优化算法，通过对机械系统的设计参数进行优化，以使系统满足一定的性能指标或者达到最优的设计目标。

以下是机械最优化设计的一些应用实例：
1. 汽车设计：汽车是一个复杂的机械系统，涉及到多个设计参数，如引擎排量、车身重量、气动设计等。

通过机械最优化设计，可以优化汽车的燃料效率、行驶稳定性等性能指标。

2. 飞机设计：飞机的设计涉及到多个参数，如机翼形状、机身结构等。

通过机械最优化设计，可以优化飞机的升力、阻力等性能指标，提高飞机的飞行效率和安全性。

3. 增材制造：增材制造是一种先进的制造技术，通过逐层加工材料来制造复杂的结构。

机械最优化设计可以用来优化增材制造的工艺参数，如激光功率、扫描速度等，以实现高质量、高效率的制造过程。

4. 结构优化：机械系统的结构设计是一个关键的环节，通过机械最优化设计，可以优化结构的刚度、强度、耐久性等性能指标，提高系统的工作性能和使用寿命。

5. 机器人设计：机器人是一种复杂的机械系统，涉及到多个参数，如关节结构、连杆长度等。

通过机械最优化设计，可以优化机器人的运动性能、负载能力等指标，提高机器人的工作效
率和精度。

总之，机械最优化设计在各个领域具有广泛的应用，可以提高机械系统的性能和效率，推动科技进步和工业发展。

关于MATLAB的机械优化设计综述摘要：机械优化设计是以数学规划理论为基础，以计算机为工具，一种自动寻优、先进的、现代的设计方法。

MATLAB作为一种集计算功能、符号运算功能和图形处理功能于一身的科学计算语言，其中的优化工具箱，可为线性、非线性最小化、非线性最小二乘、二次规划、方程求解、多目标优化等问题提供求解方法。

运用MATLAB解决机械设计的优化问题不仅方便实用，且编程简单，效率高。

关键词：机械优化，MATLAB正文：线性规划在机械设计中应用非常少，主要是因其要求目标函数、约束条件都是线性的，而机械设计问题一般都是非线性的。

目前，线性规划在一维下料问题中应用比较多。

求解线性规划问题常用的方法有单纯形法、大M法等。

在MATLAB中由linprog函数来求解线性规划问题。

二次规划在机械设计中的应用比较少，在MATLAB中求解二次规划问题可用quadprog函数。

无约束优化有很多种算法，如最速下降法、Newton法、拟Newton 法、共轭梯度法、信赖域法等。

其中，拟Newton法利用了Newton 法的二次收敛性使得可靠性更高，同时这种算法收敛速度也很快，所以在目前应用得相当广泛。

而拟Newton法中应用比较多的主要有BFGS算法和DFP变尺度法。

在ＭＡＴＬＡＢ优化工具箱中求解无约束优化问题采用fminbnd函数、fminunc函数和fminsearch函数，其中默认的算法就是BFGS算法。

fminunc函数和fminbnd函数要求目标函数必须连续，而函数fminsearch常用来处理不连续的函数。

fminbnd 函数可以求解区间［*1，*2］内单变量非线性函数的最小值。

在机械优化设计中大多数问题是有约束优化问题。

为了保证设计的机械零件安全可靠，设计时必须确定相应的设计准则，而这些设计准则就成了目标函数的约束条件。

这些设计准则包括强度准则、刚度准则、寿命准则、振动稳定性准则和可靠性准则，大多数是非线性的。

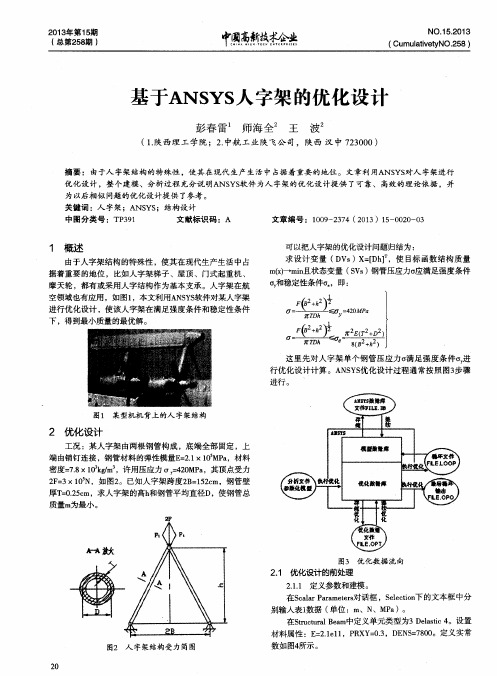
% 人字架结构尺寸优化设计% 1-主程序% 人字架优化调用两级减速器目标函数文件与非线性约束文件% 设计变量(钢管平均直径D和人字架高度H)的初始值x0=[100;800];% 设计变量(钢管平均直径D和人字架高度H)的下界与上界Lb=[20;200];Ub=[140;1200];% 调用多维约束优化函数% 线性不等式约束放入约束函数文件，参数A,b定义为空矩阵% 没有线性等式约束，参数Aeq,beq定义为空矩阵options=optimset('largescale','off','display','iter');% 'largescale','off'关闭了大规模方式；% 'display'用来控制计算过程的显示；% 'iter'表示显示优化过程的每次计算结果。

[x,fn,exitflag,output]=fmincon(@rzjyh_f,x0,[],[],[],[],Lb,Ub,@rzjyh_g,options);% 返回值exitflag：>0表示计算收敛，=0表示超过了最大的迭代次数，<0表示计算不收敛；% 返回值output有3个分量，其中：% iterations是优化过程中迭代次数，funcCount是代入函数值的次数，algorithm是优化所采用的算法disp ' ******** 人字架结构尺寸优化设计最优解********'fprintf(' 钢管平均直径 D = %3.4f mm \n',x(1))fprintf(' 人字架高度H = %3.4f mm \n',x(2))fprintf(' 人字架体积V = %3.4f mm^3 \n',fn)% 调用多维约束优化非线性约束函数(jsqyh_g)计算最优点x*的性能约束函数值g=rzjyh_g(x);disp ' ======== 最优点的性能约束函数值========'fprintf(' 人字架钢管压缩强度g1 = %3.4f MPa \n',g(1))fprintf(' 人字架钢管稳定性g2 = %3.4f MPa \n',g(2))% 2-目标函数(rzjyh_f)function f=rzjyh_f(x);% 人字架跨距B;钢管厚度T;B=1520;T=2.5;f=2*pi*x(1)*T*sqrt((B/2)^2+x(2)^2);% 3-约束函数(rzjyh_g)function [g,ceq]=rzjyh_g(x);% 人字架跨距B;钢管厚度T;载荷P;弹性模量E;许用压应力Cy;B=1520;T=2.5;P=294300;E=2.119e5;sigma_y=690;% 钢管压缩强度条件Q=0.5*P*sqrt((B/2)^2+x(2)^2)/x(2); % 钢管轴向压力sigma=Q/(pi*T*x(1)); % 钢管压应力g(1)=sigma-sigma_y;% 钢管稳定性条件sigma_c=0.125*pi^2*E*(x(1)^2+T^2)/((B/2)^2+x(2)^2); % 稳定临界应力g(2)=sigma-sigma_c;% 钢管平均直径边界条件g(3)=200-x(2);g(4)=x(1)-140;% 人字架高度边界条件g(5)=20-x(1);g(6)=x(2)-1200;% 没有非线性等式约束ceq=[];% 4-人字架结构尺寸优化设计的几何描述% 按等间隔矢量产生二维网格矩阵xx1=linspace(20,140,20); % D取值范围20- 140 xx2=linspace(200,1200,200); % H取值范围200-1200 [x1,x2]=meshgrid(xx1,xx2);% 数学模型% 人字架跨距B;钢管厚度T;载荷P;弹性模量E;许用压应力sigma_y;B=1520;T=2.5;P=294300;E=2.119e5;sigma_y=690;f=2*pi.*x1*T.*sqrt((B/2)^2+x2.^2); % 目标函数f% 目标函数值几何描述fh=contour(x1,x2,f); % 目标函数等高线clabel(fh); % 标注目标函数值title('\rm 人字架结构尺寸优化的设计平面');xlabel('钢管平均直径\rm D / mm ');ylabel('人字架高度\rm H / mm ');% 钢管压缩强度条件Q=0.5*P*sqrt((B/2)^2+x2.^2)./x2; % 钢管轴向力sigma=Q./(pi.*x1*T); % 钢管压应力g1=sigma-sigma_y; % 约束函数g1% 钢管稳定性条件sigma_c=0.125*pi^2*E.*(x1.^2+T^2)./((B/2)^2+x2.^2); % 稳定临界应力g2=sigma-sigma_c; % 约束函数g2% 约束函数几何描述hold on;g1h=contour(x1,x2,g1);g2h=contour(x1,x2,g2);% 标注图形gtext('X*');gtext('g_1(X)=0');gtext('g_2(X)=0');计算结果：max Directional First-orderIter F-count f(x) constraint Step-size derivative optimality Procedure0 3 1.73329e+006 -401 7 880958 -41.65 0.5 -1.42e+006 4.65e+0052 11 778317 -34.75 0.5 -2.04e+005 5.46e+0043 15 733855 -27.57 0.5 -8.95e+004 2.8e+0044 19 712302 -13.03 0.5 -4.34e+004 1.35e+0045 23 701688 -6.281 0.5 -2.13e+004 7.36e+0036 27 696432 -3.074 0.5 -1.05e+004 3.72e+0037 31 693820 -1.519 0.5 -5.23e+003 1.87e+0038 35 692519 -0.7551 0.5 -2.61e+003 9359 38 691219 0.004675 1 -1.3e+003 2.2510 41 691220 9.639e-008 1 1.27 0.18111 44 691220 1.137e-013 1 5.35e-005 5.88e-005 Hessian modifiedOptimization terminated: first-order optimality measure less than options.TolFunand maximum constraint violation is less than options.TolCon.Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin12******** 人字架结构尺寸优化设计最优解********钢管平均直径 D = 47.5144 mm人字架高度H = 529.2580 mm人字架体积V = 691219.9363 mm^3======== 最优点的性能约束函数值========人字架钢管压缩强度g1 = 0.0000 MPa人字架钢管稳定性g2 = 0.0000 MPa。

机械优化设计案例11.题目对一对单级圆柱齿轮减速器，以体积最小为目标进行优化设计。

2■已知条件已知数输入功p=58kw，输入转速n i=1000r/min，齿数比u=5, 齿轮的许用应力［、：］H=550Mpa，许用弯曲应力［:］F=400Mpa。

3■建立优化模型3.1问题分析及设计变量的确定由已知条件得求在满足零件刚度和强度条件下，使减速器体积最小的各项设计参数。

由于齿轮和轴的尺寸(即壳体内的零件) 是决定减速器体积的依据，故可按它们的体积之和最小的原则建立目标函数。

单机圆柱齿轮减速器的齿轮和轴的体积可近似的表示为：2 2 2 2 2 2v =0.25*0 -d z1) 0.25二b(d2 -d z2) -0.25(b -c)(D g2 -d g2)-d0c 0.25二l(d； d；2) 7二d； 8：d；22 2 2 2 2 2 2 2= 0.25叫m z b _d z初+m z u b _d z2b-0.8b(mzu—10m) +2 2 2 22.05bd Z2 -0.05b(mzu -10m -1.6d z2)+d zd + 28d z1 +32d z2】式中符号意义由结构图给出，其计算公式为d1= mz, d2= mz2D g2二u m1z10md g2=1.6d z2,d0=0.25(u m1z10m-1.6d z2)c =0.2b由上式知，齿数比给定之后，体积取决于b、Z1、m、l、d z1和d z2六个参数，则设计变量可取为x 二［X1 X2 X3 X4 X冷］丁=［b 乙m I d z1 d z2〕T3.2目标函数为2 2 2 2 2 2 f (x^ 0.785398(4.75X1X2X385X1X2X3-85X1X30.92X1X^X1X52 2 2 2 2 20.8x1x2x3x^ -1.6x1x3x6x4x5x4x628x532x6)—；min3.3约束条件的建立1)为避免发生根切，应有乙-為山=17，得g i（x） =17 _X2 乞0:? .：■■ b.■:min 二—T max m CO CD 2 ）齿宽应满足 d , Fin和Fax为齿宽系数'd的最大值和最小值，一般取；：min =0.9, max=1.4,得g2（x） =0.9 -为（X2X3） _0g3（x） =x1;（X2X3） -1.4 乞03）动力传递的齿轮模数应大于2mm,得g4（x）=2-X3 乞04）为了限制大齿轮的直径不至过大，小齿轮的直径不能大于d1 max 彳得g5（x） 7x3 -3 0 005）齿轮轴直径的范围：dzmin - dz "/x得g6（x）=1 0 0X5 _0g7（x） =X5 -1 5 00g8（x） =1 3 0X6 岂0g9（x）=冷一2 0 0 06）轴的支撑距离1按结构关系，应满足条件：1 - b • 2：伽• 0.5dz2（可取比min =20），得g10 （x）二X1 0.5x6 - X4 - 40 _ 0 7）齿轮的接触应力和弯曲应力应不大于许用值，得g11（x） =1468250. （x2x3 _ % ） -550 - 0q12（x）=7098 2 Q-4 2 一400 —0 12X1X2X3 （0.169 0.6666 10 x^ 0.854 10 X2）g13（x）=70982 2 4 2 -400 空01X1X2X3 （0.2824 0.177 10 x^0.394 10 X2）8）齿轮轴的最大挠度；max 不大于许用值，得g 14（x ） =117.04x ；.（X 2X 3X 4） -0.003x 4 乞 09）齿轮轴的弯曲应力；w 不大于许用值［'」w ，得 g i5（x ）=厶］（2.85"0 生）2 +2.4X101'-5.5 兰0X 5 V X 2X 3 | 61 J 2.85^ 10 沧\2 丄c 12g i6（x ）=p 1（ -------------- ） +6X10 —5.5 兰 0X 6 t X 2X 34■优化方法的选择由于该问题有6个设计变量，16个约束条件的优化设计问题， 采用传统的优化设计方法比较繁琐，比较复杂，所以选用 Matlab 优化工具箱中的fmincon 函数来求解此非线性优化问题，避免了 较为繁重的计算过程。

1 MATLAB优化工具箱简介MATLAB 是由美国MathWorks 公司发布的主要面向科学计算、数据可视化及数值计算的高级技术计算语言和交互式环境，简称矩阵实验室[1]。

MATLAB 是一个集强大的科学计算、完美的可视化功能、完善的自我帮助系统的开放式交互的大型软件，现已广泛应用于数学物理、材料化工、机电自动化、管理金融、生物医药、海洋科学、航天军工、语音处理以及社会科学等各个领域，种类繁多且不断拓展的工具箱使MATLAB 软件深受科研工作者的青睐。

MATLAB 优化工具箱（optimization toolbox）是基于MATLAB 的面向最优化求解的专用工具箱[2]，其主界面如图1所示。

MATLAB 优化工具箱几乎可以完美求解各类优化问题。

其高效简洁的函数表达和对算法参数的自由设置便于用户调用各类优化函数，利用MATLAB 优化工具箱可以求解线性规划、非线性规划和多目标规划问题。

此外，该优化工具箱还提供了线性、非线性最小化、方程求解、曲线拟合、最大最小问题和半无限问题等的求解方法，为优化方法在实际工摘 要 首先对MATLAB优化工具箱进行了简要介绍，并归纳了其常用优化函数进行。

然后利用MATLAB优化工具箱，以人字架的高h 和人字架的钢管平均直径D 为优化变量，在保证刚度和失稳的条件下，以人字架质量最小为目标函数进行了优化。

优化结果表明：MATLAB 优化工具箱对于解决非线性约束问题十分有效。

关键词 MATLAB优化工具箱 人字架 非线性约束 目标函数中图分类号 TH 122DOI：10.16759/ki.issn.1007-7251.2020.06.008Optimized Design of Herringbone Frame Based on MATLABHANG Liyan WANG YanweiAbstract: First, the MATLAB optimization toolbox was briefly introduced, and its commonly used optimization functions were summarized. Then using MATLAB optimization toolbox, the height h of the herringbone frame and the average diameter D of the steel tube of the herringbone frame were used as the optimization variables. Under the condition of ensuring the rigidity and instability, the optimization was carried out with the minimum quality of the herringbone frame as the objective function. The optimization results showed that the MATLAB optimization toolbox was very effective for solving nonlinear constrained problems.Key words: MATLAB optimization toolbox; Herringbone Frame; Nonlinear constraint problem; Objective function黄立言* 王彦伟（武汉工程大学 机电工程学院）基于MATLAB的人字架优化设计* 黄立言，男，1993年生，硕士研究生在读。