事件的关系与运算
- 格式:ppt
- 大小:895.00 KB
- 文档页数:22




事件的关系和运算事件的关系常用的有包含关系、互斥关系和独立关系。
事件的运算常用的有并运算、交运算、差运算和补运算。
1. 包含关系:如果事件A发生必然导致事件B发生,则称事件B包含事件A,记作A⊆B。
例如,事件A为"今天下雨",事件B为"今天有降水",则A⊆B,因为当今天下雨时,当然也说明今天有降水。
2. 互斥关系:如果事件A和事件B不能同时发生,则称事件A和事件B互斥,记作A∩B=Ø。
例如,事件A为"掷一次骰子,结果为奇数",事件B为"掷一次骰子,结果为偶数",则A∩B=Ø,因为掷一次骰子的结果不可能既是奇数又是偶数。
3. 独立关系:如果事件A的发生与发生或不发生事件B无关,则称事件A和事件B独立,记作P(A|B) = P(A),其中P(A|B)表示在事件B发生的条件下事件A发生的概率。
例如,事件A为"掷一次骰子,结果为1",事件B为"抽一张牌,结果为红心",则A和B是独立事件,因为掷骰子的结果不会受到抽牌的影响。
事件的运算包括:1. 并运算:事件A∪B表示事件A和事件B中至少一个事件发生的情况。
例如,事件A为"今天下雨",事件B为"今天有降雨",则A∪B表示今天下雨或者今天有降雨。
2. 交运算:事件A∩B表示事件A和事件B同时发生的情况。
例如,事件A为"掷一次骰子,结果为奇数",事件B为"掷一次骰子,结果为3",则A∩B表示掷一次骰子的结果既是奇数又是3。
3. 差运算:事件A-B表示事件A发生但事件B不发生的情况。
例如,事件A为"今天下雨",事件B为"今天有降雨",则A-B表示今天下雨但今天没有降雨。
4. 补运算:事件A的补事件表示事件A不发生的情况,记作A'或Ac。




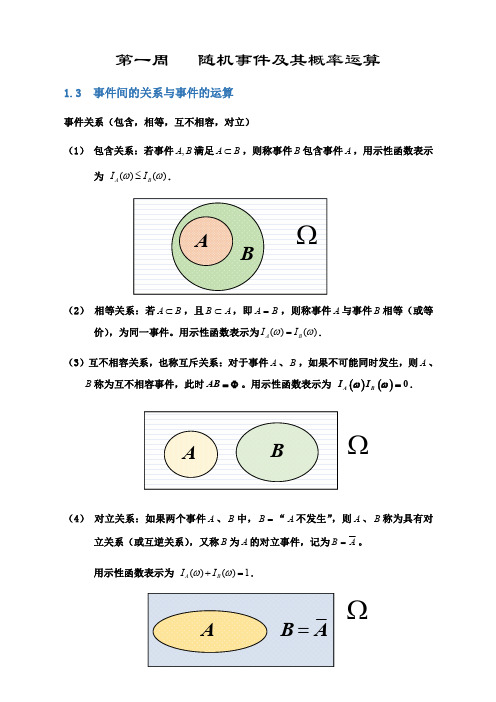
第一周随机事件及其概率运算1.3事件间的关系与事件的运算事件关系(包含,相等,互不相容,对立)(1)包含关系:若事件,A B 满足A B⊂,则称事件B 包含事件A ,用示性函数表示为()()ωω≤A B I I .(2)相等关系:若A B ⊂,且A B ⊂,即B A =,则称事件A 与事件B 相等(或等价),为同一事件。
用示性函数表示为()()A B I I ωω=.(3)互不相容关系,也称互斥关系:对于事件A 、B ,如果不可能同时发生,则A 、B 称为互不相容事件,此时AB =Φ。
用示性函数表示为()()0A B I I ωω=.(4)对立关系:如果两个事件A 、B 中,=B “A 不发生”,则A 、B 称为具有对立关系(或互逆关系),又称B 为A 的对立事件,记为A B =。
用示性函数表示为()()1ωω+=A B I I .ΩΩ*********************************************************事件运算(和,积,差,交换律,结合律,分配律,结合律,对偶律)(1)事件的和:事件A 与事件B 的并集构成的事件称为事件A 与事件B 的和事件,记为A B 或A B +,即{}|A B x x A x B =∈∈ 或,如图所示的阴影部分.显然,当且仅当事件A 与事件B 至少有一个发生时,事件A B 才发生。
n 个事件n A A A ,,,21 的和事件,即为n 个集合的并集 n k k A 1=。
(2)事件的积(或交):事件A 与事件B 的交集构成的事件称为事件A 与事件B 的积(或交)事件,事件A 与事件B 同时发生。
记为A B 或AB 。
n 个事件n A A A ,,,21 的积事件,即为n 个集合的交集 nk k A 1=。
(3)事件的差:事件A 与事件B 的差集所构成的事件称为事件A 与事件B 的差事件,记为B A -。
{}|A B x x A x B AB -=∈∉=且。





第一章
随机事件及其概率主讲教师胡发胜
教授
第二讲事件的关系及其运算
事件的关系与运算与集合的关系与运算是完全事件是样本空间的子集,因此,. 这里需要强调的是,要学会利用概率论的语言来解释这些关系及相似的其运算.
在一般情况下,事件的关系是怎样的呢?
.
—.—本讲小结:
这一讲我们学习了事件的关系及其运算,利用这些关系及其运算,我们可以用简单的事件去表示复杂的事件,这下一讲样便于我们利用简单事件的概率去求复杂事件的概率 我们讲一类简单概率模型古典概型。


10.1.2事件的关系和运算一、教材分析事件的关系与运算是继随机事件的后续部分,本节课提出了事件的关系、事件的运算等两部分学生将通过新旧知识的对比学习来进行自主学习,同时通过共同探讨来理解和掌握新知识的实际含义。
二、教学目标与核心素养课程目标1.理解并掌握时间的关系和运算.2.能够将事件的运算关系知识灵活运用到实际事件中数学学科素养数学抽象:事件的关系和运算三、教学重难点重点:事件运算关系的实际含义难点:事件运算关系的应用四、课前准备教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
五、教学环境教学场所:教室(含多媒体);教学用具:计算机多媒体六、教学过程(含设计意图)为不可能事件,A(三)、当堂检测例1如图,由甲、乙两个元件组成一个并联电路,每个元件可能正常或失效.设事件A=“甲元件正常”,B=“乙元件正常”.(1)写出表示两个元件工作状态的样本空间;(2)用集合的形式表示事件A,B 以及它们的对立事件;(3)用集合的形式表示事件A∪B和事件A∩B,并说明它们的含义及关系.【答案】(1)样本空间为Ω={(0,0),(0,1),(1,0),(1,1)}.(2)A={(1,0),(1,1)},B={(0,1),(1,1)},A={(0,0),(0,1)},B={(0,0),(1,0)}.(3)A ∪B={(0,1),(1,0),(1,1)},A∩B={(0,0)};A∪B表示电路工作正常,A∩B 表示电路工作不正常;A∪B和A∩B互为对立事件.[跟踪训练1] 某人打靶时连续射击两次,下列事件中与事件“至少一次中靶”互为对立的是( ).(A)至多一次中靶(B)两次都中靶(C)只有一次中靶(D)两次都没有中靶(2)C10.1.2 事件的关系和运算1.事件的关系和运算例1 例2。
