小学五年级平面图形面积
- 格式:doc
- 大小:336.00 KB
- 文档页数:5
平行图形的面积
一、练习题
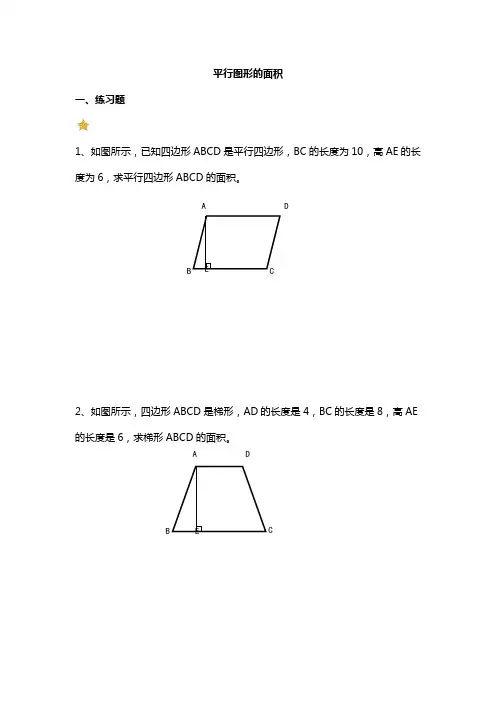
1、如图所示,已知四边形ABCD 是平行四边形,BC 的长度为10,高AE 的长度为6,求平行四边形ABCD 的面积。
2、如图所示,四边形ABCD 是梯形,AD 的长度是4,BC 的长度是8,高AE 的长度是6,求梯形ABCD 的面积。
A B D C E A B D E C
3、如图所示,已知平行四边形ABCD 的面积是24,CD 边上的高AE 的长度是3,求AB 的长度。
4、如图所示,已知长方形的周长是18,宽是4,求长方形的面积。
A B C D E
5、如下图,已知AC=10,BD=6,BE=6,求AD 的长度。
B A D
C E
二、答案
1、答案解析:因为平行四边形面积=底×高,所以平行四边形ABCD的面积=10×6=60。
2、答案解析:因为梯形面积=(上底+下底)×高÷2,所以梯形ABCD的面积=(4+8)×6÷2=36。
3、答案解析:平行四边形面积=底×高,即3×CD=24,则CD=24÷3=8,AB=CD=8。
4、答案解析:因为长方形周长=(长+宽)×2,所以长+宽=18÷2=9,宽=4,长=9-4=5,长方形面积=长×宽=5×4=20。
5、答案解析:三角形ABD面积=BD×AC÷2=6×10÷2=30,三角形ABD面积=AD×BE÷2=30,所以AD=30×2÷6=10。

平面几何图形的面积板块一:基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是(24 )平方分米,三角形的面积是(12 )平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?上底+下底=20.5-8.5=12(米)梯形面积=12×8.5÷2=51(平方米)3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?32原长方形的长:24÷2=12(米)原长方形的宽:24÷3=8(米)原来长方形的面积:12×8=96(平方米)4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
方法一:可以分割成两个钝角三角形第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)方法二:两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
方法一:可以分割成三个钝角三角形第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)一共的面积:8+16+24=48(平方厘米)方法二:把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)板块二:拓展提高【例题1】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15(厘米)(15+20)×8÷2=140(平方厘米)【例题2】右图中甲的面积比乙的面积大__________平方厘米.乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8(平方厘米)【例3】右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积,则:长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24(平方厘米)则三角形BCE 的面积=24-9=15(平方厘米)EC=15×2÷6=5(厘米)ED=5-4=1(厘米)【巩固】如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积,则:三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8(平方厘米)则三角形BCD 的面积=8+2=10(平方厘米)CD=10×2÷4=5(厘米)【例4】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?1215222原来的面积=15×12=180(平方分米)现在的的面积=(15-2)×(12-2)=130(平方厘米)减少的面积:180-130=50(平方厘米)【巩固】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?5×22566-2×5=56(平方厘米)设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长:8+5=13(厘米)原来长方形的宽:8+2=10(厘米)原来长方形的面积:13×10=130(平方厘米)【例5】下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。



五年级数学教案——《图形的面积》【教学内容】北师大版小学数学五年级上册P16-17 “比较图形的面积”。
【教学目标】1、借助方格纸,能直接判断图形面积的大小。
2、通过交流,知道比较图形面积大小的基本方法。
3、体验图形形状的变化与面积大小变化的关系。
【教学重点】掌握比较图形面积大小的方法。
会用不同的方法去比较图形的面积大小【教具准备】课件、方格纸、直尺、各种平面图形的硬纸板、七巧板等【教学设计】教学过程教学过程说明一、复习旧知,揭示新课。
1、课件播放已经学过的各种平面图形(长方形、正方形、三角形、梯形等),让学生说出图形的名称以及特征。
2、让学生拿出准备的长方形的硬纸板。
跟同桌说说哪儿是它的周长,哪儿是它的面积。
并且用手比划一下这个长方形的周长有多长?用手摸一摸它的面积有多大?(注:明确图形的周长是指绕图形一周的长度;图形的面积是指所占平面的大小。
)3、师:任意拿出两个图形纸板,说说哪个面积大?哪个面积小?让学生进行直观判断。
如果两个形状不同,大小很难区分时,你有什么办法?--揭示课题:我们今天来探讨图形面积的比较。
二、自主探究:比较图形面积的大小。
1、出示课本16页网格中的13个图形。
2、自主探究活动:这些图形的面积之间有什么关系呢?请同学们先仔细观观察、比较,看谁的发现最多多!3、小组交流:在小组里交流你的发现。
①全班交流,归纳比较图形面积的方法:各组派代表说说你们组找到了哪些图形之间的面积大小关系?是怎么知道的?依据同学的回答,归纳学生所使用的比较方法如下:②板书:A、数方格的方法;(重点说明这个方法,为今后学习面积公式的推导作好铺垫。
)B、重叠法;(通过旋转、平移、翻转等操作方法,使两个图形重叠,再观察比较出图形面积的大小)C、转化法;(通过割补、拼合转化为规则的图形后,再做比较)三、实践活动:比较图形面积的大小。
1、活动一:课件出示课本17页1题:师:同学们观察得很仔细,总结了这么多的比较图形面积大小的方法,那我要考考大家的眼力,下列图形中哪些与图1的面积一样?为什么?你用的是什么方法得到的?(注:重点要引导学生怎样对图形进行平移和分割,让学生体会形状变化而面积不变的事实,培养学生图形的转化思想,为后续运用转化思想学习面积公式的推导打下基础。

姓名:1、求下面图形的面积。
3、量出所需要的数据,再求图形的面积。
面积公式在生活中的运用。
1、有一块平行四边形菜地,底是240m,宽是125m,在这块地里共收油菜7.38吨。
这块菜地有多少公顷?平均每公顷收油菜多少吨?2、有一块麦田的形状是平行四边形。
它的底是250m,高是84m,共收小麦14.7吨。
这块菜地平均每公顷收小麦多少吨?3、一块玻璃的形状是一个三角形,它的底是12.5dm,高是7.8dm。
每平方米玻璃的价格是68元,买这块玻璃要用多少钱?4、小雨的书房需要用一些同样大小的平行四边形地砖铺地,每块砖的第是7dm,高是4dm,每平方米地砖的价格是0.25元,小雨带了200元钱去建材城买地砖,他最多能买多少块这样的地砖?5、一架滑翔机模型的尾翼是由两个完全相同的梯形组成的。
它的面积是多少?6、一个果园的形状是梯形。
它的上底是160米,下底是180米,高是50米。
如果每棵果树占地10平方米,这个果园共有多少棵果树?7、如图,靠墙围成一个花坛,围成花坛的篱笆长46米,求这个花坛的面积?8、有一块梯形地,上底长64米,比下底短16米,高50米。
平均每15平方米种一棵果树,这块地共种多少棵果树?基础题型三、已知周长,求平面图形的面积。
注:“已知周长,求图形的面积这一类题型”,我们先要根据“周长”,求出计算“面积”所需要的条件,再代入面积公式计算。
另外,在求计算面积所需要的条件时,列方程来求解可以降低出错率。
【例题】已知一个等边三角形的周长是15cm,高约是4.3cm。
求三角形的面积。
分析与解:等边三角形的周长是其边长的3倍,所以等边三角形的边长是:15÷3=5(cm),所以三角形的面积是:S=ah÷2=5×÷2=10.75(2cm)1、一个等腰直角三角形的两条直角边的和是8.4dm,求三角形的面积?2、一个等腰梯形的周长是34cm,一腰长度是5cm,等腰梯形的高是3cm。

五年级数学面积求解技巧五年级数学面积求解技巧在五年级的数学学习中,面积是一个重要的概念。
从求解简单的平面图形面积到复杂的立体图形面积,都需要掌握一些基本的技巧。
本文将介绍五年级数学面积求解的一些技巧。
一、平面图形面积的求解1. 长方形和正方形面积的求解长方形的面积等于长度乘以宽度,即面积=长×宽。
正方形的面积等于边长的平方,即面积=边长×边长。
2. 三角形面积的求解三角形的面积等于底边长度乘以高的一半,即面积=底边×高÷2。
当底边和高的长度已知时,直接代入公式即可求得面积。
当底边和顶点的坐标已知时,可以通过计算底边和高的长度来求得面积。
可以利用勾股定理或者直角三角形的特性来计算。
当三角形的三个顶点的坐标已知时,可以利用向量运算来求解。
可以通过顶点坐标的向量表示来计算面积。
3. 梯形面积的求解梯形的面积等于上底加下底的平均值乘以高,即面积=(上底+下底)×高÷2。
当上底和下底的长度已知时,直接代入公式即可求得面积。
当上底、下底和高的长度已知时,可以直接代入公式求得面积。
4. 长度单位的转换在求解面积时,有时需要将图形的尺寸从一种单位转换为另一种单位。
例如,将图形的尺寸从厘米转换为米,或者从毫米转换为厘米。
转换单位时,需要根据单位之间的比例关系来计算。
例如,1米=100厘米,1厘米=10毫米,根据这些比例可以进行单位的转换。
二、立体图形面积的求解1. 立方体面积的求解立方体的表面积等于6个面的面积之和。
每个面的面积可以根据上述的平面图形面积求解方法来计算。
2. 矩形长方体面积的求解矩形长方体的表面积等于底面的面积加上四个侧面的面积。
可以通过计算底面的面积和四个侧面的面积来求解总面积。
3. 圆柱体面积的求解圆柱体的表面积等于底面圆的周长乘以高,再加上两个底面的面积。
可以通过计算底面圆的周长和两个底面的面积来求解总面积。
4. 球体面积的求解球体的表面积等于4πr²,其中π是圆周率,r是球的半径。



平面图形面积练习题一、填空。
1、一个平行四边形的底长8厘米,是高的2倍,它的面积是(),与它等底等高的三角形面积是()。
2、一堆钢管,最上层有3根,最下层有13根,每相邻两层相差1根,这堆钢管一共有()根。
3、一个直角三角形,三条边分别是10厘米、8厘米、6厘米,它的面积是(),用两个这样的三角形拼成的长方形面积是()。
4、一个三角形和一个平行四边形的底相等,面积也相等,已知三角形的高是32厘米,那么平行四边形的高是()厘米。
5、一个平行四边形的面积是8平方分米,高是2分米,它的底是()分米。
6、一个近似梯形的花坛,高10米,上下底之和是16米,面积是()。
7、一个三角形的面积是6平方分米,底3分米,高是()。
8、用四根硬纸条钉成一个长方形框架,将它拉成一个平行四边形后,周长(),面积()。
------(填“不变”或“变大”、“变小”)9、三角形的底扩大3倍,高不变,面积会()。
10、0.45公顷=()平方米。
11、两个完全一样的梯形可以拼成一个()形。
12、一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是()平方厘米。
13、平行四边形的底是2分米5厘米,高是底的1.2倍,它的面积是()平方厘米。
14、梯形的上底增加3厘米,下底减少3厘米,高不变,面积()。
一、判断。
1、三角形面积是平行四边形的一半。
()2、两个面积相等的三角形一定能拼成一个平行四边形。
()3、面积相等的两个梯形,形状不一定相等。
()4、下面的图1中,长方形和平行四边形面积相等。
()图1 图25、上面的图2中,阴影部分面积比空白部分面积大。
()6、梯形的上底下底越长,面积越大。
()7、任何一个梯形都可以分成两个等高的三角形。
()三、知识应用1、两个同样的梯形,上底长23厘米,下底长27厘米,高20厘米。
如果把这两个梯形拼成一个平行四边形,这个平行四边形的面积是多少?2、在方格纸上画出面积相等的三角形和梯形。
四、面积计算。
人教版五年级下册《平面图形面积》小学数学-有答案-单元测试卷一、填空(每题3分)1. 一个平行四边形的底长8厘米,是高的2倍,它的面积是________,与它等底等高的三角形面积是________.2. 一个梯形的上底是16米,下底是24米,高30米,它的面积是________平方米。
3. 一堆钢管,最上层有3根,最下层有13根,每相邻两层相差1根,这堆钢管一共有________根。
4. 一个直角三角形,三条边分别是10厘米、8厘米、6厘米,它的面积是________,用两个这样的三角形拼成的长方形面积是________.5. 一个三角形和一个平行四边形的底相等,面积也相等,已知三角形的高是32厘米,那么平行四边形的高是________厘米。
6. 一个平行四边形的面积是8平方分米,高是2分米,它的底是________分米。
7. 一个近似梯形的花坛,高10米,上下底之和是16米,面积是________.8. 一个三角形的面积是6平方分米,底3分米,高是________.9. 用四根硬纸条钉成一个长方形框架,将它拉成一个平行四边形后,周长________,面积________A.不变B.变大C.变小。
10. 三角形的底扩大3倍,高不变,面积会________.二、判断(每题3分)三角形面积是平行四边形的一半。
________(判断对错)两个面积相等的三角形一定可以拼成一个平行四边形。
________.(判断对错)面积相等的两个梯形,形状不一定相等。
________(判断对错)三、知识应用(每题5分)一个梯形广告牌,它的上底是8米,下底是12米,高是6米。
如果要给这个广告牌涂上油漆,按每平方米花费15元来计算,共要花多少元?张大伯靠一面墙用篱笆围成一个面积是72平方米的梯形养鸡场,至少需要多少米的篱笆?一种等腰直角三角形小旗,直角边长4分米。
现在有一块长12分米,宽6分米的长方形布料,用它最多可以剪成多少块这样的小旗?(小旗不能用边角料拼合)参考答案与试题解析人教版五年级下册《平面图形面积》小学数学-有答案-单元测试卷一、填空(每题3分)1.【答案】32平方厘米,16平方厘米【考点】平行四边形的面积三角形的周长和面积【解析】先求平行四边形的高是多少,再根据平行四边形的面积S=aℎ,三角形的面积S=aℎ÷2,据此代入数据即可求解。
五年级下册数学面积公式
在数学中,面积是一个非常重要的概念。
它表示一个平面图形所占的范围。
在学习五年级下册数学时,我们需要掌握一些常见的面积公式。
1. 矩形面积公式
矩形是我们日常生活中常见的图形。
矩形的面积可以通过长乘以宽来计算。
假设矩形的长为a,宽为b,则矩形的面积A=a×b。
2. 三角形面积公式
三角形的面积可以通过底乘以高再除以2来计算。
假设三角形的底为b,高为h,则三角形的面积A=1/2×b×h。
3. 圆形面积公式
圆形是一个非常常见的几何图形,它的面积可以通过π乘以半径的平方来计算。
假设圆的半径为r,则圆形的面积A=π×r^2。
4. 扇形面积公式
扇形是圆的一部分,它的面积可以通过圆的面积除以角度再乘以角度的弧度数来计算。
假设扇形的中心角为θ,则扇形的面积A=θ/360°×π×r^2。
5. 梯形面积公式
梯形是一个四边形,它的面积可以通过两个平行边的长度和高度来计算。
假设梯形的上底为a,下底为b,高为h,则梯形的面积A=(a+b)×h/2。
平面图形面积
练习1:
例二:
图中正方形的边长为10cm,ED=8cm,△EFC 的面积是45平方厘米,求梯形BCDF的面积。
练习2:
练习3:
例四:
长方形ABCD的长为5厘米、宽为3厘米,设其对角线BD对折后得到的图形如下所示:则图中阴影部分的周长是_______厘米。
练习4:
如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为()cm。
图中,E、F分别为AD、BC边上一点,连接AF和BE,相交于P;连接CE和DF,相交于Q。
已知三角形ABP的面积是20平方厘米,三角形CDQ的面积是35平方厘米。
求阴影部分EPFQ 的面积。
练习5:
如图: ABCD是平行四边形,三角形EBC是直角三角形,EC长8厘米,BC长10厘米,阴影部分的面积比三角形EFG的面积大10平方厘米。
平行四边形的面积是多少平方厘米
例六:
已知长方形的长是15厘米,宽是8厘米,四边形EFGH的面积是12平方厘米,求空白部分的面积
如图,ABCD为平行四边形,三角形DCE的面积是97平方厘米,阴影部分的面积是多少平方厘米
当堂检测
一.如图,在四边形ABCD中,DCFG为正方形,ADEB为梯形,DE=30厘米,DG=24厘米,AB=39厘米,求梯形ABED的面积
二.在四边形ABCD中,AB=BC=10厘米,BE=8厘米,AD的长是______厘米。
三.一个长方形被两条直线分成四个长方形,其中三个的面积分别是20亩,25亩,30亩,另一个长方形的面积是多少亩。
四.如图所示,梯形中的两个小三角形的面积为3、9平方厘米,梯形ABCD的面积是 ___.
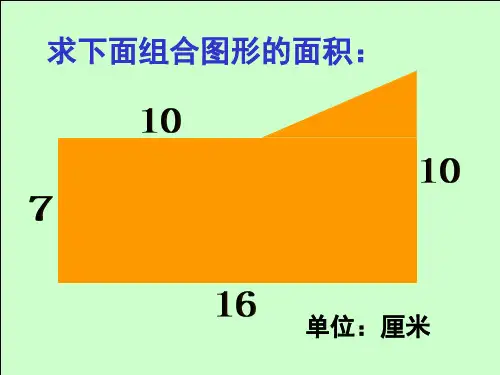
面积计算:
如图7—;11,正方形abcd的边长是4厘米,cg=3厘米求长方形defg的面积。