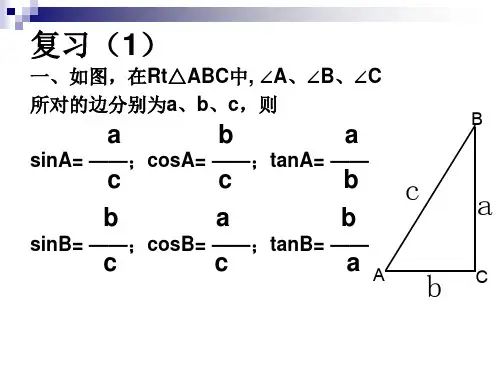
2、已知 0, ,且sin ,cos
是方程5x2 -x- 12 =0的两个根,求 5
sin 3 + cos 3 、tan +cot
以及tan -cot的值
例3、若sin
=
m-3 m+5
,cos
=
4-2m m+5
,
2
,
,则m的取值范围?
45
44
45
cos( ) 5 ,且 (0, ),sin( ) 12
4 13
4
4 13
上式 ( 4 5 3 12) 56 5 13 5 13 65
应用:找出已知角与未知角之间的关系
例4:已知
tan 2 2
2,2
(
2
,
),求
45
4 13
44
4
求sin( )
解:
sin(
)
cos[
2
[cos(
()cos)(]co) s[s(in(4))(sin(4)]
)]
4
4
4
4
sin( ) 3 ,且 ( , 3 )cos( ) 4
关键:弦
切
练习:
1、已知tan =2,求值:
1 sin cos 2sin cos
sin cos
(3) sin 2 2cos 2 1
注:公式的正用、反用、变形、“1”的变通。
例2、已知sin
+cos
=
1, 5
0, ,求cot的值
y=tanx, x ( , ) 的反函数y=arctanx, x R