下载文档原格式
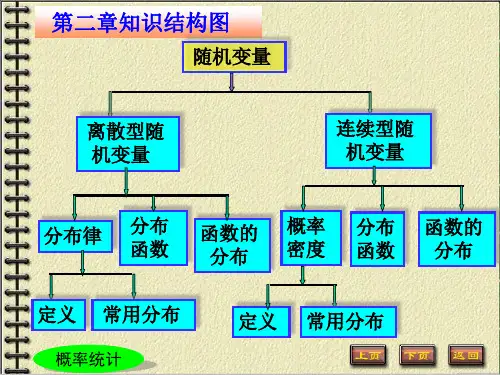
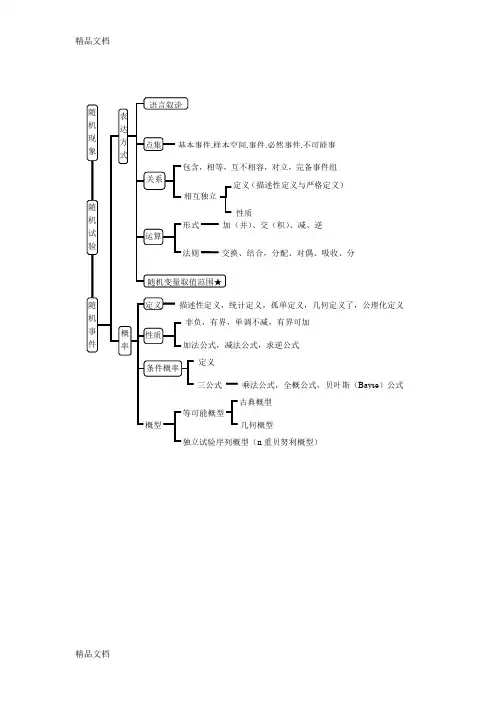
概率论与数理统计知识点的细分目录引言概率统计漫谈第一章概率论基础0101 随机事件※010101 随机试验，样本空间，事件010102 事件间关系与运算※0102 古典概型与概率010 古典概型，随机抽球问题010202 随机分球问题0103 概率的定义及性质010301 概率的定义（包括频率与概率，概率的公理化定义）010302 概率的性质0104 条件概率010401 条件概率的定义010402 乘法公式※010403 全概率公式※010404 贝叶斯公式0105 事件的独立性※010501 事件的独立性0106 单元小结0107 简单综合题选解0108 综合提高题选解第二章随机变量及其分布0 离散型随机变量※01 随机变量的概念，离散型随机变量※02 几个常用的离散型分布( 两点分布，贝努里试验，二项分布，泊松定理，泊松分布)03 几何分布与超几何分布0202 随机变量的分布函数0203 连续型随机变量※020301 连续型随机变量，概率密度020302 均匀分布与指数分布020303 正态分布0204 随机变量函数的分布020401 离散型随机变量函数的分布律020402 连续型随机变量函数的分布(分布函数法）4020403 连续型随机变量函数的分布（公式法）0205 单元小结0206 简单综合题选解0207 综合提高题选解第三章多维随机变量及其分布0301 二维随机变量030101 二维随机变量的分布函数030102 二维随机变量的分布律030103 二维随机变量的概率密度030104 二维均匀分布，二维正态分布0302 边缘分布030 边缘分布函数，边缘分布律030202 边缘概率密度0303 条件分布030301 离散型随机变量的条件分布律030302 条件分布函数，连续型随机变量的条件概率密度0304 随机变量的独立性030401 两个随机变量的独立性030402 多个随机变量的独立性0305 二维随机变量函数的分布030501 二维离散型随机变量函数的分布030502 和的分布030503 最大与最小值的分布0306 单元小结0307 简单综合题选解0308 综合提高题选解第四章数字特征和极限理论0401 随机变量的数学期望※040101 期望的概念040102 几种常用离散型随机变量期望的计算040103 几种常用连续型随机变量期望的计算040104 随机变量函数的期望040105 数学期望的性质0402 随机变量的方差※040 方差的定义及性质040202 几种常用离散型随机变量期望的计算040203 几种常用连续型随机变量方差的计算040204 切比雪夫不等式0403 随机变量的协方差与相关系数040301 协方差与相关系数的概念040302 相关系数的性质040303 协方差的性质040304 矩、协方差矩阵040305 多维正态分布简介0404 大数定律与中心极限定理※040401 三个大数定律※040402 Levy-Lindeberg中心极限定理040403 De Moivre-Laplace中心极限定理0405 单元小结0406 简单综合题选解※0407 综合提高题选解第五章数理统计初步0501 数理统计的基本概念050101 总体、样本、统计量050102 分布及其性质050103 t分布与F分布050104 单正态总体抽样分布定理050105 双正态总体抽样分布定理0502 点估计050 矩估计法※050202 极大似然估计的概念050203 极大似然估计的计算050204 估计量的相合性与无偏性050205 估计量的有效性0503 区间估计050301 区间估计概念050302 单正态总体均值的区间估计050303 单正态总体方差的区间估计050304 双正态总体均值差的区间估计050305 双正态总体方差比的区间估计0504 假设检验050401 假设检验原理050402 单正态总体参数的双边检验050403 单正态总体参数的单边检验（U检验法）050404 单正态总体参数的单边检验（t检验法）050505 单正态总体参数的单边检验（检验法）050406 双正态总体均值差的检验050407 双正态总体方差比的检验0505 单元小结0506 简单综合题选解0507 综合提高题选解。
附加知识：排列组合知识小结：一、计数原理1•加法原理：分类计数。
2•乘法原理：分步计数。
二、排列组合1 •排列数(与顺序有关):A"' = n(ti—1)(/1 —2)…(“—m + l),(/n M ii)A：二〃!，=女口：4^ = 7x6x5x4x3=2520, 5!= 5x 4x 3x2x 1= 1202•组合数(与顺序无关)：如：C4=< = 7x6x5x4 = 3 C S=C；.5= C；=Z X6=214! 4x3x2xl 2x13•例题：(1)从1, 2, 3, 4, 5这五个数字中，任取3个数字，组成一个没有重复的3位数，共有_^ = 5x4x3 = 60_种取法。
(2)从0, 1, 2, 3, 4这五个数字中，任取3个数字，组成一个没有重复的3位数，共有_AX = 4x4x3 = 48_种取法。
(3)有5名同学照毕业照，共有_^ = 5x4x3x2xl=120—种排法。
(4)有5名同学照毕业照，其中有两人要排在一起，那么共有—A2^ = (2xl)x(4x 3x2x1)= 48 种排法。
(5)袋子里有8个球，从中任意取出3个，共有_C；—种取法。
(6)袋子里有8个球，5个白球，3个红球。
从中任意取岀3个，取到2个白球1个红球的方法有_ __________ 种。
8x7x63x2x1第一章、基础知识小结一、随机事件的关系与运算1•事件的包含设A, B为两个事件，若A发生必然导致B发生，则称事件B 包含于A,记作Bu4。
2.和事件事件=A,B中至少有一个发生“为事件A与B的和事件，记作AUB 或A+B。
性质：（1） AuAUBEuAUE；（2）若Ac B,则AUB = B3•积事件：事件A,B同时发生，为事件A与事件B的积事件，记作AQB 或AB。
性质：（1）AB CZ A9AB CZ B；（2）若AuB,则AB= A4•差事件：書件A发生而B不发生为事件A与B事件的差事件，记作A-B（AB）O性质：（1） A—BuA；（2）若AuB,则A—B = 05•互不相容事件：若事件A与事件B不能同时发生，即AB = <P,则称事件A与事件B是互不相容的两个事件，简称A与B互不相容（或互斥）。
概率论与数理统计知识点总结(免费超详细版) 题目：概率论与数理统计知识点总结摘要本文总结了概率论和数理统计方面的基础知识，涉及概率分布、参数估计、假设检验、卡方检验、多元分析等。
对这些知识点的理解和了解可以帮助人们更好地分析和利用数据，促进数据分析的发展。
关键词：概率论，数理统计，概率分布，参数估计，假设检验，卡方检验，多元分析正文1.概率论概率论是数理统计中一门重要科学，它是一门数学研究现实世界事件发生的规律性、可预测性及不确定性的学科。
在概率论中，我们引入了诸如概率、期望和方差等概念，用来描述和推断某种随机现象的发生。
2.概率分布概率分布是在给定的实际情况下随机变量取值的概率分布。
典型的概率分布包括正态分布、泊松分布和二项分布。
此外，也有一些联合分布，例如协方差、共轭先验、贝叶斯估计等。
3.参数估计参数估计是根据样本数据估计总体参数的统计方法。
它涉及到将总体参数估计为样本参数的过程，通常使用最大似然估计、贝叶斯估计和假定测试等方法。
4.假设检验假设检验是基于统计学原理，用来评估某一假设是否真实存在的方法。
其中包括t检验、F检验、Z检验等，它们之间的区别在于所使用的抽样分布不同。
5.卡方检验卡方检验是一种统计检验，用于直接检验某个抽样值是否遵循某种理论分布。
卡方检验可以根据观察到的抽样数据和理论分布之间的差异来衡量分布概率值的有效性。
6.多元分析多元分析是一种分析不同变量之间交互影响的统计方法。
它包括多元回归分析、多元判别分析、因子分析等，能够帮助我们了解多个变量之间的关系。
结论本文总结了概率论和数理统计方面的基础知识，包括概率分布、参数估计、假设检验、卡方检验和多元分析等。
了解这些知识点可以帮助人们更好地分析和利用数据，促进数据分析的发展。
概率论和数理统计方面的知识点在实际应用中有着重要作用。
概率论可以帮助研究人员对随机现象进行建模、分析和推断，其中包括使用概率分布建立统计模型和估计参数，并使用假设检验和卡方检验来检验假设，以及用多元分析来推断不同变量之间的关系。
