第六章计算方法
- 格式:pdf
- 大小:492.53 KB
- 文档页数:8

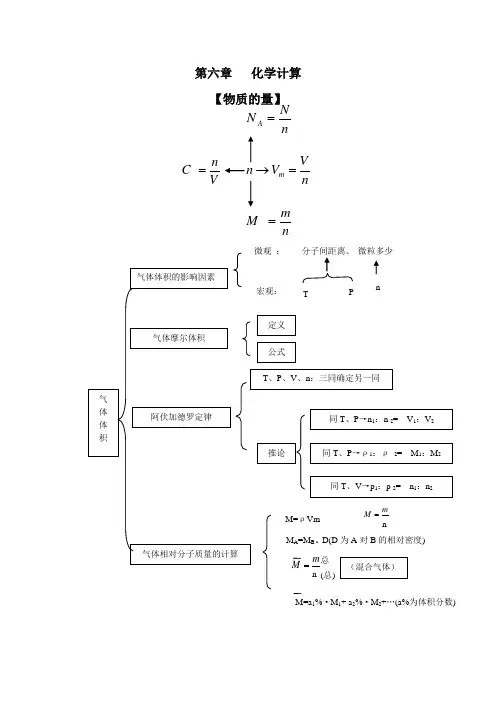
第六章 化学计算 【物质的量】nVV n m =→nm M =V n C =nN N A =M=a 1%·M 1+ a 2%·M 2+…(a%为体积分数)知识点1:有关物质的量、气体摩尔体积、阿伏加德罗常数、物质的量浓度等基本量的计算。
1、下列说法正确的是A.6.02×1023个12C 原子数,就是阿伏加德罗常数B.1摩尔原子的质量等于它的原子量C.氢原子的摩尔质量为1.008gD.1摩尔12C 原子的质量是12g 答案:D2、下列结论正确的是A.摩尔是七个基本物理量之一B.每摩尔物质含有1mol 即N A 个指定微粒C.1molCl就是指1mol氯D.氢氧化钠的摩尔质量为40g答案:B3、某中性溶液中含有0.2molNa+、0.25molMg2+、0.4molCl-,则SO42-为A. 0.1molB. 0.3molC. 0.5molD. 0.15mol答案:D4、下列各组物质物质的量相同的是A.标准状况下11.2升CO和7gN2B.1molCO2和非标准状况下32克氧气C.在标准状况下22.4升水和1molHCl D.6.02×1022个CO2分子和32克O2答案:B5、下列说法错误的是A.1mol任何物质都含有约6.02×1023个原子B.0.012kg碳-12含有约6.02×1023个碳原子C.阿伏加德罗常数的数值约等于6.02×1023D.使用摩尔时必须指明微粒的名称答案:A6、对相同质量的SO2和SO3来说,下列关系正确的是A.含氧原子个数比为2:3B.含硫元素质量比为5:4C.含氧元素质量比为6:5D.含硫原子个数比为1:1答案:B7、下列数量的物质中含原子个数最多的是A.0.4mol氧气 B.4℃时5.4mLH2O C.标况下5.6L二氧化碳 D.10 g氖答案:B8、在相同的条件下,两种物质的量相同的气体必然A.体积均为22.4LB.具有相同的体积C.是双原子分子D.具有相同的原子数目答案:B9、同温、同压下,H2和He两种气体单质的,如果质量相同,下列说法错误的是A.体积比为2 :1B.原子个数之比为2 :1C.密度之比为1 :2D.质子数之比为1 :1答案:BD10、下列叙述正确的是A.在标准状况下,2mol氧所占的体积为22.4LB.0.5mol H2和1mol Cl2光照条件下,完全化合生成的物质中约有6.02×1023个HCl分子C.若两种物质的物质的量相同,则所含的微粒数相同,在同温同压下,所占的体积也相同D.在标准状况下,4.48L HCl溶解于100mL水里,所得溶液的物质的量浓度为2mol· L-1 答案:B11、若N A表示阿伏加德罗常数,下列说法正确的是A.1molCl2作为氧化剂得到电子数为N AB.在0℃,101KPa时,22.4L氢气中含有N A个氢原子C.14g氮气含有7N A个电子D.N A个一氧化碳分子和0.5mol甲烷的质量比为7:4答案:C12、.某500mL溶液中含0.1molFe2+、0.2molFe3+,加入0.2mol铁粉,待Fe3+完全还原后,溶液中Fe2+的物质的量浓度为(假设反应前后体积不变)A.0.4mol/L B.0.6mol/L C.0.8mol/L D.1.0mol/L答案:C13、将20gNaOH溶于水后,制成100mL的碱溶液,则此溶液的物质的量浓度为A.0.5mol/L B.5mol/L C.1mol/L D.10mol/L答案:B14、在标准状况下,将VLA气体(摩尔质量为Mg/mol)溶于0.1L水中,所得溶液的密度为dg/cm3,则此溶液的物质的量浓度为答案:B15、在标准状况下,用一充满氯化氢气体的烧瓶做喷泉实验,当水充满整个烧瓶后,烧瓶内盐酸溶液的物质的量浓度是()A.0.045mol/L B.1mol/LC.0.1mol/L D.缺少数据无法计算答案:A16、把70%HNO3(密度为1.40g/cm3)加到等体积的水中,稀释后硝酸溶液中溶质的质量分数是A 0.35B <0.35C >0.35D ≤0.35答案:C17、把一定质量的10%的NaOH溶液250mL,加热蒸发掉8g水后,浓度为12%,则浓缩前NaOH溶液的物质的量浓度为A.1.2 B.3 C.0.48 D.4.8答案:C18、VL硫酸钠溶液中含mgNa+离子,则溶液中SO42-的物质的量浓度为()答案:C19、有K2SO4和Al2(SO4)3的混合溶液,已知其中Al3+的物质的量浓度为0.4mol·L-1,SO42-的物质的量浓度为0.7 mol·L-1,则此溶液中K+的物质的量浓度为A.0.1 mol·L-1B.0.15 mol·L-1C.0.2 mol·L-1D.0.3 mol·L-1答案:C20、在三个密闭容器中分别充入N e、H2、O2三种气体,当它们的温度和密度都相同时,这三种气体的压强(p)从大到小的顺序是A.P(N e)>P(H2)>P(O2) B.P(O2)>P(N e)>P(H2)C.P(H2) >P(O2)>P(N e) D.P(H2)>P(N e)>P(O2)答案:D21、下列叙述正确的是A.相同条件下,N2和O3的混合气体与等体积的N2所含原子数相等B.等物质的量的甲基(-CH3)与羟基(-OH)所含电子数相等C.常温常压下28 g CO与22.4 L O2所含分子数相等D.16 g CH4与18 g NH4+所含质子数相等答案:B22、下列叙述正确的是A.48 g O3气体含有6.02×1023个O3分子B.常温常压下,4.6g NO2气体含有1.81×1023个NO2分子C.0.5mol/LCuCl2溶液中含有3.01×1023个Cu2+D.标准状况下,33.6L 水含有9.03×1023个H2O分子答案:A23、用N A代表阿伏加德罗常数,下列说法正确的是A.标准状况下,22.4LCHCl3中含有的氯原子数目为3N AB.7gC n H2n中含有的氢原子数目为N AC.18gD2O中含有的质子数目为10N AD.1L 0.5 mol/L Na2CO3溶液中含有的CO32-数目为0.5N A答案:B24、设N A为阿伏加德罗常数,下列叙述中正确的是A.常温下,11.2L甲烷气体含有甲烷分子数为0.5N AB.14g乙烯和丙烯的混合物中总原子数为3N AC.0.1mol/L的氢氧化钠溶液含钠离子数为0.1N A个D.5.6g 铁与足量稀硫酸失去电子数为0.3N A答案:B25、阿伏加德罗常数约为6.02×1023,下列叙述正确的是A.2.24LCO2中含有的原子数为0.3×6.02×1023B.0.1L 3 mol/L NH4NO3溶液中含有的NH4+数目为0.3×6.02×1023C.5.6g 铁粉与硝酸反应失去电子数一定为0.3×6.02×1023D.4.5 g二氧化硅晶体中含有的硅氧键数目为0.3×6.02×1023答案:D26、对相同状况下的12C18O和14N2两种气体,下列说法正确的是A.若质量相等,则质子数相等B.若原子数相等,则中子数相等C.若分子数相等,则体积相等D.若体积相等,则密度相等答案:C27、设NA表示阿伏加德罗常数,下列叙述中正确的是A.常温常压下,11.2L氧气所含的原子数为N AB.1.8g的NH4+离子中含有的电子数为N AC.常温常压下,48gO3含有的氧原子数为3N AD.2.4g金属镁变为镁离子时失去的电子数为0.1N A答案:C28、(2001-16)设N A为阿佛加德罗常数,下列说法不正确的是A.标准状况下的22.4L辛烷完全燃烧,生成二氧化碳分子数为8N AB.18g水中含有的电子数为10N AC.46g 二氧化氮和46g四氧化二氮含有的原子数均为3N AD.在1L2mol/L的硝酸镁溶液中含有的硝酸根离子数为4N A答案:A29、(2002-8)N A为阿佛加德罗常数,下述正确的是A.80g硝酸铵含有氮原子数为2N AB.1L 1mol/L的盐酸溶液中,所含氯化氢分子数为N AC.标准状况下,11.2L四氯化碳所含分子数为0.5 N AD.在铜与硫的反应中,1mol铜失去的电子数为2 N A答案:A30、(2003-3)以N A表示阿佛加德罗常数,下列说法中正确的是A.53g碳酸钠中含N A个CO32-B.0.1molOH-含N A个电子C.1.8g重水(D2O)中含N A个中子D.标准状况下11.2L臭氧中含N A个氧原子答案:B31、设NA为阿佛加德罗常数,下列叙述中正确的是A.46 g NO2和N2O4混合气体中含有原子数为3N AB.标准状况下22.4 L H2中含中子数为2N AC.1L 1mol/L醋酸溶液中离子总数为2N AD.1molMg与足量O2或N2反应生成MgO或Mg3N2均失去2N A个电子答案:AD32、N A代表阿伏加德罗常数,下列说法正确的是A.9gD2O中含有的电子数为5N AB.1molMgCl2中含有的离子数为2N AC.1molCH4分子中共价键总数为4N AD.7.1g C12与足量NaOH溶液反应转移的电子数为0.2N A答案:C33、设阿伏加德常数为N A。





第六章习题答案1.用二分法求方程在区间[1内的根,要求其绝对误差不超 32()330f x x x x =+−−=,2]过210.−解: 由于(1)113340,f =+−−=−<32(2)2232330,f =+−×−=>且当时,[1,2]x ∈22110()3233()033f x x x x ′=+−=+−> 所以方程在区间[1内仅有一个实根。
,2] 由2111(21)10,22k −+−≤×解得2ln10 6.64385.ln 2k ≥≥所以需要二分7次,才能得到满足精度要求的根。
取[1区间的中点将区间二等分,求得,2]1 1.5,x =(1.5) 1.8750,f =−<与(1)f 同号,因此得到下一区间[1如此继续下去,即得计算结果。
.5,2];计算结果如下表:k(())f k k a a 的符号(())x f x k k 的符号(())b f b k k 的符号0 1(-) 1.5(-) 2(+) 1 1.5(-) 1.75(+) 2(+) 2 1.5(-) 1.625(-) 1.75(+) 3 1.625(-) 1.6875(-) 1.75(+) 4 1.6875(-) 1.71875(-) 1.75(+) 5 1.71875(-) 1.734375(+) 1.75(+) 6 1.71875(-) 1.7265625(-) 1.734375(+) 7 1.7265625(-) 1.73046875(-) 1.734375(+)7()1.73046875 1.73a b x +==≈77取即满足精度要求2。
2.证明1s 在[0内有一个根,使用二分法求误差不大于in 0x x −−=,1]41102−×的根要迭代多少次?证明: 设()1sin ,f x x =−−x由于(0)10sin 010,f =−−=>(1)11sin1sin10,f =−−=−<且当时,[0,1]x ∈()1cos 0.f x x ′=−−< 因此方程在区间[0内有一个根。

计算方法第六章迭代法迭代法是一种重要的数值计算方法,在数学和计算机科学中有广泛的应用。
本章将介绍迭代法的基本概念、原理和应用,以及相关的数学原理和计算技巧。
首先,我们来了解迭代法的基本概念。
迭代法是通过逐步逼近的方式得到一个问题的解。
迭代法的基本思路是从一个初始值开始,通过重复计算和更新,得到更加接近最终解的近似值。
迭代法的优点是简单和灵活,但需要注意选择合适的迭代公式和初始值,以及控制迭代的停止条件。
迭代法的原理可以用以下的一般形式表示:```x_(n+1)=f(x_n)```其中,x_n表示第n次迭代得到的近似值,x_(n+1)表示第(n+1)次迭代的近似值,f是一个函数,表示迭代公式。
迭代法的思想是通过不断迭代更新x的值,直到满足一些停止条件为止。
迭代法的应用非常广泛,特别是在求解非线性方程和优化问题方面有重要的应用。
在求解非线性方程时,我们可以将方程转化为形式为f(x)=0的等式,然后通过迭代法逼近方程的根。
在优化问题中,我们可以通过最小化或最大化一个函数来寻找最优解,也可以使用迭代法逐步逼近最优解。
在迭代法的实际应用中,我们需要注意一些数学原理和计算技巧。
首先,迭代法的收敛性是关键的,即通过迭代公式逐步逼近的值是否趋于问题的解。
在评估迭代法的收敛性时,常用的方法有判断迭代序列的极限是否存在和是否满足一些收敛条件。
其次,选择合适的迭代公式和初始值对于迭代法的成功应用非常重要。
迭代公式应该是简单和有效的,能够在迭代过程中逐步逼近问题的解。
初始值的选择也会直接影响迭代的结果,通常需要根据问题的特点和经验进行选择。
另外,迭代法的计算精度和计算效率也是需要考虑的问题。
在迭代过程中,我们需要根据问题的要求不断调整迭代的次数和迭代的停止条件,以达到较高的计算精度。
同时,我们也需要通过优化迭代公式和使用更加高效的计算技巧来提高计算的效率。
最后,迭代法的应用还可以进一步扩展到其他领域。
例如,在图像处理中,我们可以使用迭代法逐步改进图像的质量;在机器学习中,我们可以使用迭代法来调整模型的参数,以求得更好的拟合效果。