结构方程模型估计案例

结构方程模型案例结构方程模型（Structural Equation Modeling, SEM）是一种用于建立和验证研究假设的统计分析方法。

它结合了因果关系和测量模型，可以用来探索变量之间的关系以及对研究模型进行验证。

在本文中，我们将介绍一个结构方程模型的案例，以展示其在实际应用中的作用和价值。

假设我们想研究人们对环境保护的态度对其环保行为的影响。

为了建立一个结构方程模型，我们需要明确我们的研究假设和测量指标。

在这个案例中，我们假设人们对环境保护的态度会对其环保行为产生积极的影响。

首先，我们需要选择合适的测量指标来度量人们对环境保护的态度和环保行为。

在这个案例中，我们选择了以下指标：1. 人们对环境保护的态度：我们采用了一个问卷调查，包括了一系列与环境保护相关的问题，例如“您认为环境保护对社会的重要性是？”和“您是否愿意为环境保护做出自己的贡献？”等。

每一个问题都使用了一个5点量表来度量人们的态度，从彻底不允许到彻底允许。

2. 环保行为：我们通过观察人们在日常生活中的实际行为来度量环保行为。

例如，我们可以观察他们是否进行垃圾分类、是否使用可再生能源等。

接下来，我们需要建立一个结构方程模型来分析这些指标之间的关系。

我们假设人们对环境保护的态度会对其环保行为产生积极的影响。

因此，我们将人们对环境保护的态度作为自变量，环保行为作为因变量。

在结构方程模型中，我们需要考虑到测量误差的影响。

因此，我们引入了一个潜在变量——人们对环境保护的態度。

这个潜在变量可以通过测量指标来进行估计。

为了验证我们的模型，我们需要采集一些数据。

我们可以通过随机抽样的方式选择一定数量的参预者，并要求他们填写我们设计的问卷。

此外，我们还可以观察他们的实际行为来采集环保行为的数据。

采集到数据后，我们可以使用结构方程模型来进行分析。

通过计算测量指标和潜在变量之间的关系，以及潜在变量和因变量之间的关系，我们可以得出结论。

如果我们的模型能够很好地拟合数据，并且相关系数达到统计显著水平，那末我们的研究假设就得到了支持。

结构方程模型案例结构方程模型 (Structural Equation Modeling, SEM) 是一种统计分析方法，用于建立和检验变量之间的因果关系模型。

这种模型可以用于解决许多复杂的研究问题，如预测变量之间的关系、检验理论模型以及估计和测试不同截面之间的因果关系。

本文将通过一个实际案例来说明如何使用结构方程模型。

案例背景：公司想要了解员工满意度对工作绩效的影响，以及工作环境对员工满意度和工作绩效的影响。

公司采集了员工的满意度、工作绩效和工作环境的数据，并希望通过结构方程模型来分析这些变量之间的关系。

理论模型：基于现有研究和理论，研究者提出了以下理论模型：工作环境->员工满意度->工作绩效变量测量：为了构建结构方程模型，首先需要测量各个变量。

在这个案例中，工作环境通过一个问卷调查来测量，员工满意度通过一个满意度调查来测量，工作绩效通过员工的绩效评价来测量。

每个变量通过多个观测指标来测量，例如，工作环境包括工作安全、工作福利、工作周围环境等指标。

模型估计：模型分析：经过模型估计后，可以进行模型分析来检验理论模型的拟合度。

在这个案例中，我们可以使用路径系数(standardized path coefficients)来解释变量之间的因果关系。

例如，路径系数的大小表示一个变量对另一个变量的直接影响程度，路径系数的方向则表示两个变量之间的关系是正向还是负向。

结果解释：通过模型分析，研究者可以得到一个具有统计显著性的结构方程模型。

然后，研究者可以通过路径系数解释变量之间的关系。

在这个案例中，结果可能显示工作环境对员工满意度有正向影响，员工满意度对工作绩效有正向影响。

这意味着改善工作环境可能会提高员工满意度，从而提高工作绩效。

结论与建议：最后，研究者可以根据结构方程模型的结果提出结论和建议。

在这个案例中，研究者可以建议公司改善工作环境，以提高员工满意度和工作绩效。

此外，研究者还可以进一步研究其他影响员工满意度和工作绩效的因素，以完善这个模型。

结构方程模型--- Lisre啲初级应用• 一、为何要用结构方程模型？•二、模型原理简介•三、模型建模•四、例子：员工流失动因模型・很多社会、心理研究中所涉及到的变量，都不能准确、直接地测量，这种变量称为潜变量，如工作自主权、工作满意度等。

・这时，只能退而求其次，用一些外显指标，去间接测量这些潜变量。

如用工作方式选择、工作目标调整作为工作自主权（潜变量）的指标，以目前工作满意度、工作兴趣、工作乐趣、一工作厌恶程度（外显指标）作为工作满意度的指*示。

・传统的统计分析方法不能妥善处理这些潜变量，而结构方程模型则能同时处理潜变量及其指标。

一个回归分析和结构方程比较的例子：•假如有五道题目来测量外向型性格，还有四道题目来测量自信。

研究自信与外向型性格的关系。

假如是你，你将怎样来进行研究？・回归分析的做法：先分别计算外向题目的总分（或平均分）和自信题目的总分（或平均分），在计算两个总分的相关。

・这样的计算所得的两个潜变量（性格与自信）的关系，恰当吗？y =方0 + b{x{ + b2x2 + s・1）无法处理因变量（Y）多于一个的情况；・2）无法处理自变量（X）之间的多重共线性；・3）无法对一些不可直接测量的变量进行处理，主要是一些主观性较强的变量进行测量。

如幸福感、组织认同感、学习能力等；・4）没有考虑变量（自变量、因变量）的测量误差, 以及测量误差之间的关系•针对1):路径分析(Path Analysis)-缺点：分开考察不同的因变量，无法考察因变量之间的关系且缺少整体的视角・针对2):偏最小二乘法(PLS)-缺点：相关理论尚不完善，解释力较弱。

-《王惠文，偏最小二乘法理论与应用，国防工业出版社》•针对3):指标赋予权重，进行综合评价，得岀一个量化的指标-缺点：权重设计，需要相当的技巧，通常的方法，如AHP,模糊综合评判等方法缺少信度与效度•针对4):没有办法解决・同时处理多个因变量・容许自变量和因变量含测量［误差传统方法（如回归）假设自变量没有误差］・同时估计因子结构和因子关系・容许更大弹性的测量模型・估计整个模型的拟合程度［用以比较不同模型］・SEM包括:回归分析、因子分析（验证性因子分析、探索性因子分析）、t检验、方差分析、比较各组因子均值、交互作用模型、实验设计•Structural Equation Modeh SEM•Covarianee Structure Modeling，CSM•Lin ear Structural Rela 廿on ship , LISREL从上述名称中可以看岀，结构方程模型的几个本质特征是：结构、协方差、线性二、结构方程简介工作厌恶程度•简单来说，结构方程模型分 另： •测量方程(measurement equation)测量方程描述潜变量与指标之间的关系，如工 作方式选择等指标与工作自 主权的关系； •纟吉构方程(structural equation), 描述潜变量之间的关系，女口工作 自主权与工作满意度的关系。

结构方程模型在抽样检验中的应用及案例介绍引言结构方程模型（Structural Equation Modeling，简称SEM）是一种统计方法，用于估计和验证变量之间的关系以及模型的适配度。

它将测量模型和结构模型相结合，既可以分析变量之间的因果关系，也可以评估模型的适配度。

在抽样检验中，结构方程模型广泛应用于不同领域，如社会科学、教育研究、生物医学等。

本文将介绍结构方程模型在抽样检验中的应用，并通过案例分析加深理解。

结构方程模型结构方程模型是一种基于协方差矩阵的多变量分析方法，用于测量和估计潜变量之间的关系。

它包括两个部分：测量模型和结构模型。

测量模型是用于测量潜变量的可观测指标的模型。

它采用观测数据，并根据潜在的隐变量构建指标。

测量模型通过指标的共变异来估计潜变量的值，并为结构模型提供输入。

结构模型用于描述潜变量之间的关系。

它通过路径系数表示变量之间的直接或间接影响关系，并可以通过模型拟合指标（如χ^2拟合度检验、RMSEA）评估模型的适配度。

结构方程模型在抽样检验中的优势相比传统的统计方法，结构方程模型在抽样检验中具有以下优势：1.模型估计和测试：结构方程模型能够同时估计和测试测量模型和结构模型，提供对模型的全面评估。

2.潜变量的估计和解释：结构方程模型能够估计潜变量的值，并探索潜变量之间的关系，从而更全面地理解研究对象。

3.模型适应度评估：结构方程模型提供了多种指标用于评估模型的适应度，包括χ^2拟合度检验、比较拟合指数（CFI）、根均方误差估计（RMSEA）等。

4.变量的建模：结构方程模型能够处理多变量的复杂关系，并提供灵活的变量建模方法。

案例介绍：教育领域中的结构方程模型应用在教育研究中，结构方程模型被广泛应用于理解学生学业成绩的影响因素。

以下是一个关于学业成绩的结构方程模型案例。

研究研究目的是探索学生的学业成绩与多个影响因素之间的关系。

研究假设包括学习动机、学习时间、学习策略和社会支持对学业成绩有直接或间接的影响。

结构方程模型估计案例
一、案例背景
本案例涉及一所位于美国的研究型大学，本案例旨在通过结构方程模
型估计学生参与大学课程的因素。

为此，本案例采用了一份包含180个受
访者的调查数据，每个受访者均为本校大学生。

二、研究假设
●学生投入的时间越多，他们的学习成绩就会越高。

●当学生有充足的资源可用时，他们的学习成绩会更高。

●学生对学习任务的兴趣和动机越高，他们的学习成绩也会越高。

●学生的学习成绩受到家庭背景和家庭环境的影响。

三、研究模型
本案例选择结构方程模型（SEM）进行模型估计，此模型包含四个变量，即学习时间（T）、学习资源（R）、兴趣/动机（I）和家庭环境（E）。

根据协方差矩阵，这四个变量都会对学生学习成绩（O）产生影响。

四、数据收集
本案例的数据收集工作包括：
1.对学生进行面对面访谈，收集学生投入课程的时间、学习资源、兴
趣/动机和家庭环境的信息，以及他们的学习成绩。

2.使用定量数据分析方法（如SPSS和AMOS）进行数据分析，以获得
研究要求的结果。

三、结构方程模型。

结构方程模型原理以及经典案例研究结构方程模型（Structural Equation Modeling, SEM）是一种统计分析方法，主要用于建立和检验复杂的因果关系模型。

该模型可以同时考虑多个观测变量和潜在变量之间的关系，从而更准确地评估变量之间的关联性和因果性。

SEM的基本原理是基于路径分析和因子分析的组合。

路径分析可以用来建立变量之间的因果关系模型，并通过评估路径系数来分析变量之间的直接和间接影响。

因子分析用于构建潜在变量，并通过潜在变量与观测变量之间的关系来解释观测变量的变异。

经典的SEM案例研究可以帮助我们更好地理解SEM的应用和优势。

以下是一个经典的SEM案例研究：假设研究者想要探究家庭背景对学生学业成绩的影响。

研究者收集了500名学生的数据，包括学业成绩、家庭背景因素（例如家庭收入、父母教育水平）、自我效能感和学习动机等变量。

首先，研究者使用因子分析方法构建潜在变量模型。

他们将家庭收入、父母教育水平等观测变量组合起来，构建了一个“家庭背景”潜在变量，用以测量学生的家庭背景因素。

同样地，他们根据相关的观测变量构建了“自我效能感”和“学习动机”两个潜在变量。

接下来，研究者使用路径分析方法建立因果关系模型。

他们假设家庭背景对学生学业成绩有直接和间接的影响。

间接影响通过自我效能感和学习动机来实现。

路径分析模型将家庭背景作为独立变量，学业成绩作为因变量，自我效能感和学习动机作为中介变量。

研究者在模型中还考虑了其他潜在变量（例如学习时间、学校环境），以控制其他可能的影响因素。

最后，研究者使用SEM方法对模型进行参数估计和假设检验。

他们通过评估路径系数来确定各个变量之间的直接和间接关系。

如果路径系数显著不为零，则可以断定两个变量之间存在关系。

通过SEM方法，研究者可以对研究模型进行全面的分析，包括直接和间接关系、回归系数、误差方差等。

通过以上案例，我们可以看到SEM的优势在于可以同时处理多个因素的复杂关系。

结构方程模型自由度计算举例
这里以一个简单的结构方程模型为例,讲解结构方程模型自由度的计算方法:
结构方程模型自由度计算举例
我们设计一个简单的结构方程模型,包含3个潜在变量1、2、3,它们之间没有方向关系,只考虑方差协方差矩阵中的元素。

对于这个模型:
1. 每个潜在变量有1个方差待估计,因此方差数字是3。

2. 每两个潜在变量之间有1个协方差待估计。

三个变量之间有(3,2)=3个二元组合。

3. 总的待估计参数数为:方差数字3 + 协方差数字3 = 6
4. 每个观测值都会提供1个信息。

假设我们有100个观测样本,则数据能提供的信息量是100。

5. 结构方程模型自由度 = 信息量 - 待估计参数数
= 100 - 6
= 94
所以这个简单模型的自由度是94。

自由度较大表明模型还可以增加更多结构关系形成更复杂的模型结构。

以上是一个简单结构方程模型自由度计算的实例,希望能帮助大家初步了解结构方程模型分析中的这个重要概念。

AMOS结构方程模型修正经典案例第一节模型设定结构方程模型分析过程可以分为模型构建、模型运算、模型修正以及模型解释四个步骤。

下面以一个研究实例作为说明，使用Amos7软件1进行计算，阐述在实际应用中结构方程模型的构建、运算、修正与模型解释过程。

一、模型构建的思路本案例在著名的美国顾客满意度指数模型(ASCI)的基础上，提出了一个新的模型，并以此构建潜变量并建立模型结构。

根据构建的理论模型，通过设计问卷对某超市顾客购物服务满意度调查得到实际数据，然后利用对缺失值进行处理后的数据2进行分析，并对文中提出的模型进行拟合、修正和解释。

二、潜变量和可测变量的设定本文在继承ASCI模型核心概念的基础上，对模型作了一些改进，在模型中增加超市形象。

它包括顾客对超市总体形象及与其他超市相比的知名度。

它与顾客期望，感知价格和顾客满意有关，设计的模型见表7-1。

模型中共包含七个因素(潜变量)：超市形象、质量期望、质量感知、感知价值、顾客满意、顾客抱怨、顾客忠诚，其中前四个要素是前提变量，后三个因素是结果变量，前提变量综合决定并影响着结果变量(Eugene W. Anderson & Claes Fornell，2000;殷荣伍，2000)。

2.1、顾客满意模型中各因素的具体范畴1本案例是在Amos7中完成的。

2见spss数据文件“处理后的数据.sav”。

参考前面模型的总体构建情况、国外研究理论和其他行业实证结论，以及小范围甄别调查的结果，模型中各要素需要观测的具体范畴，见表7-2。

三、关于顾客满意调查数据的收集本次问卷调研的对象为居住在某大学校内的各类学生（包括全日制本科生、全日制硕士和博士研究生），并且近一个月内在校内某超市有购物体验的学生。

调查采用随机拦访的方式，并且为避免样本的同质性和重复填写，按照性别和被访者经常光顾的超市进行控制。

问卷内容包括7个潜变量因子，24项可测指标，3正向的，采用Likert10级量度从“非常低”到“非常高”本次调查共发放问卷500份，收回有效样本436份。

结构方程模型中调节效应的标准化估计一、本文概述1、结构方程模型（SEM）简介结构方程模型（Structural Equation Modeling，简称SEM）是一种广泛应用于社会科学研究中的统计技术，它结合了路径分析和多元回归分析，使得研究者能够同时检验多个变量间的因果关系。

SEM不仅允许研究者估计直接效应，还能探索间接效应和总效应，从而提供一个全面、整合的视角来理解变量之间的关系。

SEM还能够处理测量误差，并通过拟合指数来评估模型的拟合程度。

在SEM中，研究者首先需要根据理论或先前的研究来构建一个假设模型，该模型包括一系列的观察变量（也称为指标或测量项）和潜在变量（也称为构念或因子）。

观察变量是可以直接测量的变量，如问卷中的项目得分；而潜在变量则是无法直接测量的抽象概念，需要通过一组观察变量来间接测量。

一旦模型建立，研究者就可以使用统计软件（如AMOS、Mplus、EQS 等）来估计模型的参数，并检验模型的拟合度。

模型的参数估计通常基于最大似然法或其他优化算法。

通过这些参数估计，研究者可以了解变量之间的因果关系强度、方向以及显著性水平。

结构方程模型是一种强大而灵活的工具，它能够帮助研究者更深入地理解变量之间的关系，并为理论发展提供实证支持。

在社会科学、心理学、教育学、管理学等领域，SEM已经成为了一种广泛使用的分析方法。

2、调节效应在SEM中的重要性在结构方程模型（SEM）中，调节效应的重要性不容忽视。

调节效应，也称为中介效应或调节路径，它描述了一个或多个变量如何影响两个主要变量之间的关系强度或方向。

在SEM的框架内，这种效应是通过在路径模型中引入一个或多个中介变量来考察的，这些中介变量在自变量和因变量之间起到了“桥梁”或“调节器”的作用。

调节效应有助于深化我们对变量间关系的理解。

通过探究中介变量对自变量和因变量关系的调节作用，我们可以更准确地理解这些关系的本质和动态过程。

这不仅有助于理论的发展和完善，也为实践中的决策和干预提供了更有力的依据。

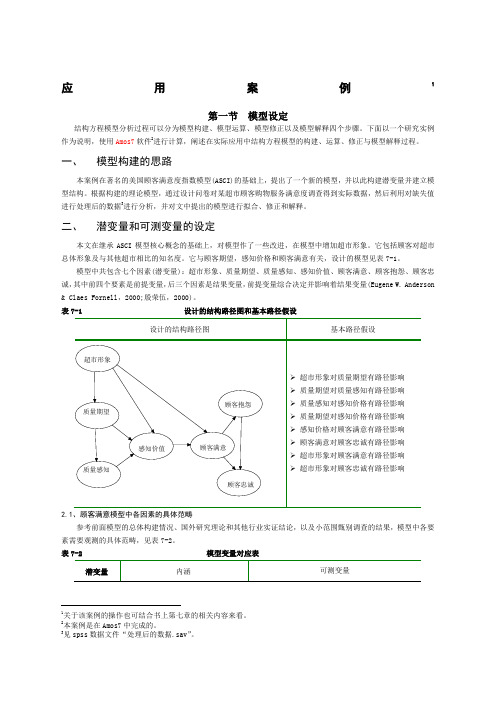
应用案例1第一节模型设定结构方程模型分析过程可以分为模型构建、模型运算、模型修正以及模型解释四个步骤。

下面以一个研究实例作为说明，使用Amos7软件2进行计算，阐述在实际应用中结构方程模型的构建、运算、修正与模型解释过程。

一、模型构建的思路本案例在著名的美国顾客满意度指数模型(ASCI)的基础上，提出了一个新的模型，并以此构建潜变量并建立模型结构。

根据构建的理论模型，通过设计问卷对某超市顾客购物服务满意度调查得到实际数据，然后利用对缺失值进行处理后的数据3进行分析，并对文中提出的模型进行拟合、修正和解释。

二、潜变量和可测变量的设定本文在继承ASCI模型核心概念的基础上，对模型作了一些改进，在模型中增加超市形象。

它包括顾客对超市总体形象及与其他超市相比的知名度。

它与顾客期望，感知价格和顾客满意有关，设计的模型见表7-1。

模型中共包含七个因素(潜变量)：超市形象、质量期望、质量感知、感知价值、顾客满意、顾客抱怨、顾客忠诚，其中前四个要素是前提变量，后三个因素是结果变量，前提变量综合决定并影响着结果变量(Eugene W. Anderson & Claes Fornell，2000;殷荣伍，2000)。

表7-1 设计的结构路径图和基本路径假设2.1、顾客满意模型中各因素的具体范畴参考前面模型的总体构建情况、国外研究理论和其他行业实证结论，以及小范围甄别调查的结果，模型中各要素需要观测的具体范畴，见表7-2。

表7-2 模型变量对应表1关于该案例的操作也可结合书上第七章的相关内容来看。

2本案例是在Amos7中完成的。

3见spss数据文件“处理后的数据.sav”。

4正向的，采用Likert10级量度从“非常低”到“非常高”三、关于顾客满意调查数据的收集本次问卷调研的对象为居住在某大学校内的各类学生（包括全日制本科生、全日制硕士和博士研究生），并且近一个月内在校内某超市有购物体验的学生。

调查采用随机拦访的方式，并且为避免样本的同质性和重复填写，按照性别和被访者经常光顾的超市进行控制。

结构方程模型及其应用举例结构方程模型（Structural Equation Modeling，简称SEM）是一种统计分析方法，用于评估和验证复杂的因果关系模型。

它结合了因子分析、路径分析和回归分析等多种分析方法，可以用来研究多个变量之间的因果关系，提供一种统一的框架来检验理论假设。

SEM的核心思想是将观察到的变量分为显性变量和潜变量，并构建一个模型来描述它们之间的关系。

潜变量是无法直接观察到的变量，通常用多个测量指标来衡量。

显性变量则是直接观察到的变量。

SEM的模型可以包括多个潜变量和显性变量之间的因果关系。

SEM的应用范围很广泛，以下是一些常见的应用举例：1.人力资源管理研究：SEM可以用于分析员工的工作满意度和组织绩效之间的关系。

研究者可以通过测量员工的满意度和组织绩效，并构建一个SEM模型来测试员工满意度对组织绩效的影响程度。

2.教育研究：SEM可以用于研究教育政策对学生学业成绩的影响。

研究者可以测量学生的学业成绩、家庭背景、教育政策等变量，并构建一个SEM模型来评估这些变量之间的关系。

3.社会科学研究：SEM可以用于研究社会现象和心理健康之间的关系。

研究者可以测量社交支持、心理健康等变量，并构建一个SEM模型来评估这些变量之间的因果关系。

4.金融研究：SEM可以用于分析股价和财务指标之间的关系。

研究者可以测量公司的财务指标和股价，并构建一个SEM模型来测试财务指标对股价的影响程度。

除了上述应用举例，SEM还可以用于医学研究、市场研究、环境科学研究等领域。

SEM具有很多优点，例如可以处理多变量系统、可以估计测量误差、可以同时考虑观察变量和潜变量等。

然而，使用SEM也存在一些挑战，例如需要大样本和复杂计算等。

在实际应用中，研究者需要根据自己的研究问题和数据情况，选择合适的SEM模型和估计方法。

然后，他们需要通过模型拟合度指标（如卡方拟合度检验、均方根误差、比较拟合指数等）来评估模型的拟合度。

结构方程模型案例汇总-共18页结构方程模型( Structural Equation，SEM)Modeling20 世纪——主流统计方法技术：因素分析回归分析20 世纪70 年代：结构方程模型时代正式来临结构方程模型是一门基于统计分析技术的研究方法学，它主要用于解决社会科学研究中的多变量问题，用来处理复杂的多变量研究数据的探究与分析。

在社会科学及经济、市场、管理等研究领域，有时需处理多个原因、多个结果的关系，或者会碰到不可直接观测的变量（即潜变量），这些都是传统的统计方法不能很好解决的问题。

SEM能够对抽象的概念进行估计与检定，而且能够同时进行潜在变量的估计与复杂自变量/ 因变量预测模型的参数估计。

结构方程模型是一种非常通用的、主要的线形统计建模技术，广泛应用于心理学、经济学、社会学、行为科学等领域的研究。

实际上，它是计量经济学、计量社会学与计量心理学等领域的统计分析方法的综合。

多元回归、因子分析和通径分析等方法都只是结构方程模型中的一种特例。

结构方程模型是利用联立方程组求解，它没有很严格的假定限制条件，同时允许自变量和因变量存在测量误差。

在许多科学领域的研究中，有些变量并不能直接测量。

实际上，这些变量基本上是人们为了理解和研究某类目的而建立的假设概念，对于它们并不存在直接测量的操作方法。

人们可以找到一些可观察的变量作为这些潜在变量的“标识”，然而这些潜在变量的观察标识总是包含了大量的测量误差。

在统计分析中，即使是对那些可以测量的变量，也总是不断受到测量误差问题的侵扰。

自变量测量误差的发生会导致常规回归模型参数估计产生偏差。

虽然传统的因子分析允许对潜在变量设立多元标识，也可处理测量误差，但是，它不能分析因子之间的关系。

只有结构方程模型即能够使研究人员在分析中处理测量误差，又可分析潜在变量之间的结构关系。

简单而言，与传统的回归分析不同，结构方程分析能同时处理多个因变量，并可比较及评价不同的理论模型。

多层结构方程模型贝叶斯估计下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!多层结构方程模型（MSEM）是一种结合了结构方程模型（SEM）和层次模型的统计分析方法，可以同时考虑不同层次的变量之间的关系。

结构方程模型案例一、引言结构方程模型（Structural Equation Modeling, SEM）是一种统计分析方法，用于研究变量之间的关系和模型的适配度。

它可以同时考虑观测变量和潜在变量之间的关系，适用于各种研究领域，如社会科学、教育学、心理学等。

本文将介绍一个关于教育质量的结构方程模型案例。

二、研究背景教育质量是一个重要的社会指标，对社会经济发展和个人成长具有重要影响。

本研究旨在探究教育质量的影响因素和作用机制，以提供改善教育质量的参考。

三、研究目的本研究的目的是构建一个结构方程模型，分析教育质量与学生学业成绩、教师素质、学校资源等变量之间的关系，并评估模型的适配度。

四、研究变量和假设1. 自变量：a. 学生学业成绩b. 教师素质c. 学校资源2. 因变量：教育质量3. 假设：a. 学生学业成绩对教育质量有正向影响b. 教师素质对教育质量有正向影响c. 学校资源对教育质量有正向影响五、研究方法1. 数据收集：通过问卷调查的方式收集学生学业成绩、教师素质、学校资源和教育质量的数据。

2. 数据分析：使用结构方程模型进行数据分析，包括模型拟合度检验、参数估计和路径分析等。

六、数据分析结果1. 模型拟合度检验：通过比较实际观测数据和模型预测数据的差异，评估模型的适配度。

适配度指标包括χ^2值、自由度、标准化拟合指数（CFI）、均方根误差逼近指数（RMSEA）等。

2. 参数估计：通过估计结构方程模型中的路径系数，判断变量之间的关系强度和方向。

3. 路径分析：根据参数估计结果，分析学生学业成绩、教师素质、学校资源对教育质量的直接和间接影响。

七、讨论与结论根据数据分析结果，我们得出以下结论：1. 学生学业成绩对教育质量有显著正向影响；2. 教师素质对教育质量有显著正向影响；3. 学校资源对教育质量有显著正向影响；4. 教师素质在学生学业成绩和教育质量之间起到中介作用。

八、研究局限性和建议本研究存在以下局限性：1. 样本选择有限，可能不具有代表性；2. 数据收集方式可能存在主观性和记忆偏差；3. 变量的测量可能存在误差。

结构方程模型估计案例结构方程模型（Structural Equation Modeling，SEM）是一种常用的多变量统计分析方法，可以用来建立因果关系模型，并对模型中的参数进行估计。

以下是一个使用结构方程模型进行估计的案例。

假设我们要研究一些城市中大学生的幸福感，该模型包含三个潜在变量：经济条件（Economic Conditions）、社交支持（Social Support）和幸福感（Well-being）。

经济条件和社交支持通过各自的指标变量进行测量，幸福感由经济条件和社交支持两个潜在变量作为预测变量进行建模。

首先，我们需要收集一些数据来进行分析。

假设我们随机选择了1000名大学生，并针对每个大学生进行问卷调查，获取以下数据：1.经济条件指标变量的测量方法：- 房产数量（Property）：测量每个大学生拥有的房产数量。

- 家庭资产（Wealth）：测量每个大学生家庭的总资产。

2.社交支持指标变量的测量方法：- 朋友数量（Friends）：测量每个大学生拥有的朋友数量。

- 亲友支持（Support）：测量每个大学生从亲友那里获得的支持程度。

- 社交活动（Activities）：测量每个大学生参与的社交活动的频率。

3.幸福感指标变量的测量方法：- 主观幸福感（Subjective Well-being）：通过问卷让每个大学生评估自己的主观幸福感程度。

- 心理健康（Mental Health）：通过问卷让每个大学生评估自己的心理健康状况。

接下来，我们可以使用结构方程模型对这些数据进行分析和估计。

首先，我们需要建立模型。

可以采用如下模型：-经济条件→幸福感-社交支持→幸福感然后，我们需要根据数据对模型中的参数进行估计。

可以使用最小二乘法来估计参数。

在估计过程中，我们还可以考虑一些控制变量，如性别、年龄等，以控制其他可能影响幸福感的因素。

最后，我们可以进行模型拟合度检验，检查模型是否与实际数据拟合得好。