第二节 二重积分的计算法

第二节_二重积分的计算法二重积分：在平面上规定一个有界闭合区域D，对于D上的每一点P(x,y)，都有一个标量函数f(x,y)与之对应。

则二重积分的数值就是由函数f(x,y)在区域D上所有点处的函数值决定的。

二重积分一般可以表示为∬Df(x,y)dA。

计算二重积分的方法主要有以下几种：直角坐标法、极坐标法、换元积分法和累次积分法。

1.直角坐标法：针对矩形、直角三角形、抛物线和折线边界的区域，可以直接使用直角坐标法来计算二重积分。

具体步骤如下：(1)写出二重积分的累加和形式：I=ΣΣf(x,y)ΔA。

(2)将区域D分成若干小矩形，计算每个小矩形的面积ΔA。

(3)在每个小矩形上选择代表点(x,y)，计算f(x,y)的函数值。

(4)将函数值与相应小矩形的面积相乘，加和求和即可得到二重积分的数值。

2.极坐标法：当具有极坐标对称性的区域时，采用极坐标法可以简化计算。

具体步骤如下：(1) 确定极坐标变换：x=r*cosθ，y=r*sinθ。

(2) 根据变换的雅可比矩阵计算面积元素dA的极坐标形式：dA=rdrdθ。

(3) 将二重积分转化为极坐标下的累次积分：I=∫∫Df(x,y)dxdy=∫∫Df(r*cosθ,r*sinθ)rdrdθ。

(4)将极坐标下的积分区域和积分限进行变换，然后按照累次积分进行计算。

3.换元积分法：当二重积分区域D的边界方程比较复杂时，可以使用换元积分法来简化计算。

具体步骤如下：(1)根据边界方程对二重积分区域D进行变换，将原来的二重积分区域映射到一个新的坐标系中的区域G。

(2)根据变换的雅可比矩阵，计算新坐标系下的面积元素dA'。

(3) 将二重积分转化为新坐标系下的累次积分：I=∫∫Df(x,y)dxdy=∫∫Gf(x(u,v),y(u,v))，J(u,v)，dudv，其中J(u,v)为雅可比行列式。

(4)对新坐标系下的累次积分按照直角坐标法或极坐标法进行计算。

4.累次积分法：当二重积分区域D可以通过垂直于坐标轴的直线进行划分时，可以使用累次积分法进行计算。

第二节 二重积分的计算方法教学目的：利用直角坐标系把二重积分化为二次积分 教学重难点：将积分区域用不等式组表示 教 法:讲授 课 时:4仅仅依靠二重积分的定义及其性质，不可能对一般的二重积分进行计算。

本节介绍一种二重积分的计算方法，这种方法是把二重积分化为两次单积分（即两次定积分）来计算。

一、利用直角坐标系计算二重积分我们首先来考虑直角坐标系下面积元素σd 的表达形式。

在二重积分的定义中对区域D 的分割是任意的，极限∑=→∆ni i i i f 10),(lim σηξλ都存在，那么对于区域进行特殊分割该极限也应该存在。

因此，在直角坐标系下，我们用平行于x 轴和y 轴的两族直线把区域D 分割成许多小区域（图10—4）。

除靠区域D 边界曲线的一些小区域外，其余的都是小矩形区域。

当这些小区域的直径的最大者λ→0时，这些靠区域D 边界的不规则的小区域的面积之和趋于0。

因此，第i 个小矩形区域i σ∆的面积k j i y x ∆⋅∆=∆σ。

因此，直角坐标系下面积元素dxdy d =σ。

于是二重积分的直角坐标形式为⎰⎰⎰⎰=DDdxdy y x f d y x f ),(),(σ。

由二重积分的几何意义知道，如果0),(≥y x f ，⎰⎰Dd y x f σ),(的值等于一个以D 为底、以曲面),(y x f z =为顶的曲顶柱体的体积。

下面我们用定积分的微元法来推导二重积分的计算公式。

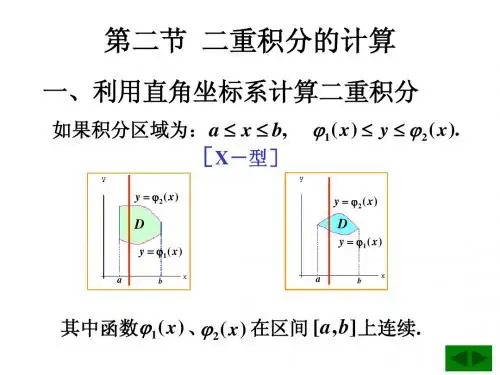
若积分区域D 可用不等式组表示为⎩⎨⎧≤≤≤≤)()(21x y x b x a ϕϕ 如图10—5，选x 为积分变量，x ∈[a ，b]，任取小区间[x ，dx x +]⊂ [a ，b]。

在x 轴上分别过点x 、dx x +作垂直于x 轴的平面，设)(x A 表示过点x 垂直x 轴的平面与曲顶柱体相交的截面的面积，则小薄片的体积近似等于以)(x A 为底、dx 为高的柱体的体积，即体积元素 dx x A dV )(=该截面是一个以区间)](),([21x x ϕϕ为底边、以曲线),(y x f z =（x 固定）为曲边的曲边梯形，因此⎰=)()(21),()(x x dy y x f x A ϕϕ所以⎰⎰⎰=ba Ddx x A d y x f )(),(σ=dx dy y x f x x ba ]),([)()(21⎰⎰ϕϕ，即dx dy y x f d y x f x x b a D]),([),()()(21⎰⎰⎰⎰=ϕϕσ。

第二节二重积分的计算法第二节学习的是二重积分的计算法。

二重积分的计算法可以通过分别采用直角坐标系和极坐标系进行求解。

本文将详细介绍这两种方法的具体步骤。

在直角坐标系中，假设被积函数为f(x,y)，要计算其在D上的二重积分，其中D是一个有界区域，可以采用以下步骤进行求解：1.将区域D进行划分，然后选择该划分的一个子区域Di，其面积为ΔA。

2. 在子区域Di内任选一个点(xi, yi)，将该点作为积分的取值点。

3. 将函数值f(xi, yi)与子区域的面积ΔA相乘，得到局部的积分量f(xi, yi)ΔA。

4.将所有子区域的局部积分量相加，得到近似的二重积分。

5.使用极限的思想，当划分的子区域趋近无穷小时，近似的二重积分趋近于准确的二重积分。

6.对于具体的函数形式，可以通过积分的性质进行变换，求解更为简便。

在计算二重积分时，需要注意以下几点：1.对于非均匀分布的划分，可以通过增加划分数量来提高近似的准确度。

2.划分的子区域大小越小，计算结果越准确，但也会增加计算的复杂度。

3.当函数比较复杂时，可以选择适当的数值计算方法来求解。

接下来，我们将介绍使用极坐标系进行二重积分的计算方法。

极坐标系中的二重积分采用极坐标系下的面积元素dA=rdrdθ。

具体步骤如下：1.将被积函数f(x,y)转换为极坐标下的形式f(r,θ)。

2.将被积区域D在极坐标系下的范围确定，也即确定r的取值范围和θ的取值范围。

3. 计算面积元素dA，即dA=rdrdθ。

4.将被积函数f(r,θ)与面积元素dA相乘，得到局部的积分量f(r,θ)dA。

5.将所有局部积分量相加，得到近似的二重积分。

6.使用极限的思想，当面积元素dA趋近无穷小时，近似的二重积分趋近于准确的二重积分。

极坐标系的二重积分计算方法可以简化计算过程，特别适用于对称性较强的函数和区域。

在实际应用中，二重积分的计算方法可以进一步推广到多重积分的计算。

多重积分的计算涉及到更高维度的坐标系和更复杂的积分区域，但基本的思想和步骤与二重积分类似。

第二节 二重积分的计算法 一．本课的基本要求掌握在直角坐标系、极坐标系中二重积分的计算． 二．本课的重点、难点二重积分的计算为重点、积分限的确定为难点． 三．教学内容由⎰⎰∑→→∆=Dni iif d y x f 10),(),(lim σηξσλ；引入本次课题． 一． 直角坐标系中的累次积分法假定0),(≥y x f ，按照二重积分的几何意义⎰⎰Dd y x f σ),(的值等于以D 为底、以曲面),(y x f Z =为顶的曲顶柱体的体积．在上一章第一节我们知道区域D 的不等式组表示法通常有两种：1．⎩⎨⎧≤≤≤≤)()(21x y x bx a ϕϕ 或2．⎩⎨⎧≤≤≤≤)()(21y x y d y c ψψ 图1为方便，不妨以表示法1为例讨论．设⎰⎰Dd y x f σ),(所表示图形为图1．思路：⑴ 曲顶柱体的体积V 等于二重积分的值A ．⑵ 能否找到另一种计算曲顶柱体体积V 的方法；如能找到，设其表达式为B ． ⑶ 由传递关系可得到二重积分的计算方法，即A=B ．在定积分的应用中我们已讨论过“平行截面面积为已知的立体的体积” 的求法．下面我们就利用其求法之一的切片法来计算二重积分⎰⎰Dd y x f σ),(所表示的柱体的体积．在区间[a,b]上任意取定一点0x ，作平行于yoz 面的平面0x x =，它与曲顶柱体相截所得截面是一个以区间[])(),(0201x x ϕϕ为底、曲线),(0y x f Z =为曲边的曲边梯形（图1中阴影部分）．所以，这载面的面积为：⎰=)()(000201),()(x x dy y x f x A ϕϕ．由0x 的任意性，过区间[a,b]上任一点x 且平等yoz 面的平面截曲顶柱体所得截面的面积为：⎰=)()(21),()(x x dy y x f x A ϕϕ应用平行截面面积为已知的立体体积的求法，得曲顶柱体体积为：⎰⎰⎰==bax x badx dy y x f dx x A V )()(21]),([)(ϕϕ即⎰⎰⎰⎰=bax x Ddx dy y x f d y x f )()(21]),([),(ϕϕσ ⑴同理由表示法2可得：⎰⎰⎰⎰=dcy y Ddy dx y x f d y x f )()(21]),([),(ϕϕσ ⑵由此看到，二重积分的计算可化为两次定积分来计算．把二重积分化为两次定积分的方法称为累次积分法．在上述讨论中，我们假定0),(≥y x f ，但实际上述公式的成立并不受此条件限制． 以后我们称图1所示的积分区域为X ─型区域，后者为Y ─型区域。