回溯算法的一些例题
- 格式:doc
- 大小:55.00 KB
- 文档页数:11

回溯法典型例题一、回溯法是啥呢?哎呀,回溯法就像是在一个迷宫里找路一样。
想象一下,你走进了一个超级复杂的迷宫,有好多岔路口。
回溯法就是当你走到一个岔路口发现不对的时候,就退回来,再试试其他的路。
它就像是你脑袋里的一个小导航,在你走错路的时候提醒你“哎呀,这条路不对,咱得回去重新选”。
比如说,在解决一些组合问题的时候,就像从一堆数字里选出满足某个条件的组合。
如果随便乱选,可能永远也找不到答案。
这时候回溯法就登场啦,它会有条理地去尝试各种可能的组合,一旦发现这个组合不行,就回到上一步,再换一种选法。
这就像是你在玩拼图,发现这块拼图放不进去,就换一块试试。
二、典型例题来喽1. 八皇后问题这可是回溯法里的经典呢。
在一个8×8的棋盘上放8个皇后,要求任何两个皇后都不能在同一行、同一列或者同一对角线上。
怎么用回溯法解决呢?我们就从第一行开始,试着放一个皇后,然后到第二行再放,但是要保证和前面放的皇后不冲突。
如果到某一行发现没有地方可以放了,那就回到上一行,重新调整上一行皇后的位置,再接着往下放。
这个过程就像是走迷宫的时候,发现前面是死胡同,就退回来换条路走。
2. 数独问题数独大家都玩过吧。
每个小九宫格、每行、每列都要填上 1 - 9这9个数字,而且不能重复。
用回溯法解决的时候,我们就从第一个空格开始,试着填一个数字,然后看这个数字是不是满足规则。
如果不满足,就换一个数字试试。
如果这个空格试遍了所有数字都不行,那就回到上一个空格,重新调整那个空格的数字,再接着往下填。
这就像我们在搭积木,发现这块积木放上去不稳,就换一块试试。
3. 全排列问题比如说给你几个数字,让你求出它们的全排列。
用回溯法的话,我们就从第一个数字开始,固定它,然后对剩下的数字求全排列。
当对剩下数字求全排列的时候,又可以把第二个数字固定,对后面的数字求全排列,这样一层一层下去。
如果发现排列不符合要求,就回溯到上一层,换一种排列方式。
这就像是在给小朋友排队,这个小朋友站这里不合适,就换个位置,然后重新给后面的小朋友排队。

回溯算法原理和几个常用的算法实例回溯算法是一种基于深度优先的算法,用于解决在一组可能的解中找到满足特定条件的解的问题。
其核心思想是按照特定的顺序逐步构造解空间,并通过剪枝策略来避免不必要的。
回溯算法的实现通常通过递归函数来进行,每次递归都尝试一种可能的选择,并在达到目标条件或无法继续时进行回溯。
下面介绍几个常用的回溯算法实例:1.八皇后问题:八皇后问题是一个经典的回溯问题,要求在一个8×8的棋盘上放置8个皇后,使得每个皇后都不能相互攻击。
即每行、每列和对角线上都不能有两个皇后。
通过在每一列中逐行选择合适的位置,并进行剪枝,可以找到所有满足条件的解。
2.0-1背包问题:0-1背包问题是一个经典的组合优化问题,要求在一组物品中选择一些物品放入背包,使得其总重量不超过背包容量,同时价值最大化。
该问题可以通过回溯算法进行求解,每次选择放入或不放入当前物品,并根据剩余物品和背包容量进行递归。
3.数独问题:数独问题是一个经典的逻辑推理问题,要求在一个9×9的网格中填入数字1-9,使得每行、每列和每个3×3的子网格中都没有重复数字。
该问题可以通过回溯算法进行求解,每次选择一个空格,并依次尝试1-9的数字,然后递归地进行。
4.字符串的全排列:给定一个字符串,要求输出其所有可能的排列。
例如,对于字符串"abc",其所有可能的排列为"abc"、"acb"、"bac"、"bca"、"cab"和"cba"。
可以通过回溯算法进行求解,每次选择一个字符,并递归地求解剩余字符的全排列。
回溯算法的时间复杂度通常比较高,因为其需要遍历所有可能的解空间。
但是通过合理的剪枝策略,可以减少的次数,提高算法效率。
在实际应用中,可以根据具体问题的特点来设计合适的剪枝策略,从而降低算法的时间复杂度。


1.跳马问题:在n*m,棋盘上有一中国象棋中的马:1.马走日字;
2.马只能往右走。
请你找出一条可行路径,使得马可以从期盼的左下角(1,1)走到右上角(n,m)。
2.任何一个自然数x都可以被写成若干自然数之和的形式,如5=1+4;5=2+3;5=1+1+1+1+1;……现请你编写一个程序,给出自然数X的所有拆分等式(2+3和3+2视为相同形式)。
3.有形如下图形的地图,图中每一块区域
代表一个省份,现请你用红(1)、蓝(2)、黄(3)、
绿(4)四种颜色给这些省份填上颜色,要求每
一省份用一种颜色,且任意两个相邻省份的
颜色不能相同,请给出一种符合条件的填色
方案。
地图用无向图的形式给出,每个省份
代表图上的一个顶点,边代表两个省份是相
邻的。

火柴游戏• 有红,绿,蓝三种颜色的火柴,所有火柴长度一样。
用它们可以组成一些数字, 如下图所示:•• 为了让组成的火柴好看一些,我们规定:有公共点的火柴必须不同色。
例如,用红火柴4根和蓝火柴3根可以组成数12,21,7等。
而且有些方案虽然数字和它们的排列顺序都相同,但是有颜色之分。
问:一共可以组成多少个数(可以包含多个数字,但至少包含一个数字)?同一个数用不同颜色表示算作不同的数,火柴可以有剩余。
• 输入• 三个整数n1, n2, n3 (0 ≤ n1,n2,n3 ≤ 15),即三种颜色的火柴的数目。
• 输出• 仅一个数,即可以组成的数的数目。
结果保证不超过1016。
骑士游历问题设有一个n*m 的棋盘(2≤n ≤50,2≤m ≤50),如下图。
在棋盘上任一点有一个中国象棋马,马走的规则为:1.马走日字2.马只能向右走。
即左图所示:当n ,m 给出之后,同时给出马起始的位置和终点的位置,试找出从起点到终点的所有路径的数目。
例如:(n=10,m=10),(1,5)(起点),(3,5)(终点)。
应输出2(即由(1,5)到(3,5)共有2条路径,如下图):输入:n ,m ,x1,y1,x2,y2(分别表示n ,m ,起点坐标,终点坐标) 输出:路径数目(若不存在从起点到终点的路径,输出0)过河卒如图,A点有一个过河卒,需要走到目标B点。
卒行走的规则:可以向下、或者向右。
••同时在棋盘上的任一点有一个对方的马(如上图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。
例如上图C点上的马可以控制8个点(图中的P1,P2….P8)。
卒不能通过对方马的控制点。
•棋盘用坐标表示,A点(0,0)、B点(n,m)(n,m为不超过20的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定:C≠A,同时C≠B)。
现在要求你计算出卒从A点能够到达B点的路径的条数。
•输入:•键盘输入B点的坐标(n,m)以及对方马的坐标(X,Y)输出:•屏幕输出一个整数(路径的条数)。


洛谷回溯题目回溯法是一种常用的算法思想,它可以用于解决一些求解所有可能解的问题。
在计算机领域,回溯法通常用于解决一些组合、排列、子集、图的遍历等问题。
洛谷是一个在线的题库和评测系统,提供了众多回溯题目。
下面将介绍一些常见的洛谷回溯题目,并提供一些参考内容。
1. P1601 A + B Problem【标准题】:该题目要求计算两个非负整数的和,并输出结果。
可以使用回溯法解决,通过遍历所有可能的进位方式,逐位进行求和。
2. P1142 回文串:该题目要求判断一个字符串是否为回文串。
可以使用回溯法解决,通过遍历所有可能的子串,判断其是否为回文串。
3. P1980 数字统计:该题目要求计算从 1 到 n 的所有数字中,出现了多少次数字 d。
可以使用回溯法解决,通过遍历所有可能的数字,统计出现次数。
4. P1088 火星人:该题目要求给定一组数字,将其重新排序,使得相邻数字之间的差的绝对值之和最小。
可以使用回溯法解决,通过遍历所有可能的排列方式,计算差的绝对值之和。
5. P1726 送水问题:该题目要求计算一个地图上送水的最短路径,给定起点和终点。
可以使用回溯法解决,通过遍历所有可能的路径,找到最短路径。
6. P1303 硬币问题:该题目要求计算使用最少的硬币组合成给定的金额。
可以使用回溯法解决,通过遍历所有可能的硬币组合方式,找到最少的硬币数量。
以上是一些常见的洛谷回溯题目,针对每个题目,可以使用不同的回溯法思路进行解决。
回溯法常常使用递归的方式实现,通过不断地尝试每一种可能的选择,找到满足条件的解。
在编写回溯算法时,需要注意设置递归终止条件,避免出现无限递归的情况。
在解决回溯问题时,可以参考以下内容:1. 回溯法的基本原理和思路2. 如何设置递归终止条件以及如何进行剪枝操作3. 如何进行状态的保存和恢复4. 如何利用递归进行循环的优化5. 如何通过合理的设计递归函数参数,进行状态的传递和更新6. 如何实现题目所需的具体功能,例如判断回文串、计算路径长度、统计出现次数等。

回溯算法在生活中案例
回溯算法是一种通过探索所有可能的解来解决问题的算法,当发现当前解不满足条件时,它会回溯到上一步,重新尝试其他可能的解。
以下是一些回溯算法在生活中的实际应用案例:
1. 组合优化问题:在日常生活中,很多问题可以通过组合优化问题来求解。
例如,旅行商问题(Traveling Salesman Problem),该问题是一个著名的组合优化问题,通过回溯算法可以找到最短路径或最优解。
2. 游戏AI:在游戏中,AI常常需要做出决策,而回溯算法可以帮助AI在游戏中进行决策。
例如,在棋类游戏中,AI可以使用回溯算法来分析游戏局面,预测游戏的胜负结果。
3. 数据库查询优化:在数据库查询中,回溯算法可以用于优化查询。
例如,在关系型数据库中,查询优化器可以使用回溯算法来选择最优的查询计划。
4. 编译器设计:在编译器的设计中,回溯算法可以用于语法分析。
编译器通过语法分析将源代码转化为机器代码,而回溯算法可以帮助编译器检查源代码是否符合语法规则。
5. 图像处理:在图像处理中,回溯算法可以用于图像修复、去噪等任务。
通过回溯算法可以找到最优的修复方案或去噪参数。
6. 决策支持系统:在决策支持系统中,回溯算法可以帮助决策者进行决策。
例如,在医疗诊断中,医生可以使用回溯算法来分析病人的病情,并给出最佳的治疗方案。
总之,回溯算法在许多领域都有广泛的应用,可以帮助人们解决复杂的问题。


典型的回溯算法问题一、购票问题有2n个人排队购一件价为0.5元的商品,其中一半人拿一张1元人民币,另一半人拿一张0.5元的人民币,要使售货员在售货中,不发生找钱困难,问这2n个人应该如何排队?找出所有排队的方案。
(售货员一开始就没有准备零钱)分析:(1)根据题意可以看出,要使售货员在售货中,不发生找钱困难,则在排队中,应该是任何情况下,持0.5元的排在前面的人数多于持1元的人数。
(2)该问题可以用二进制数表示:用0表示持0.5元的人,用1表示持1元的人,那么2n个人排队问题化为2n个0、1的排列问题。
这里我们用数组B[1..2n ] 存放持币情况。
(3)设k是B数组下标指针,B[K]=0或B[K]=1,另用数组d[0]、d[1]记录0与1的个数,且必须满足:n >d[0]>=d[1]。
(4)算法:回溯搜索。
(a)先将B[1]、B[2]、……B[2n]置-1,从第一个元素开始搜索,每个元素先取0,再取1,即B[K]+1→B[K],试探新的值,若符合规则,增加一个新元素;(b)若k<2n,则k+1→k,试探下一个元素,若k=2n则输出B[1]、B[2] ……,B[2n]。
(c)如果B[K]的值不符合要求,则B[K]再加1,试探新的值,若B[K]=2,表示第k 个元素的所有值都搜索过,均不符合条件,只能返回到上一个元素B[K-1],即回溯。
(d)返回到上一个元素k:=k-1 ,并修改D[0]、D[1]。
(5)直到求出所有解。
二、骑士游历问题在n×n的国际象棋上的某一位置上放置一个马,然后采用象棋中“马走日字”的规则,要求这个马能不重复地走完 n×n个格子,试用计算机解决这个问题。
分析:本题是典型的回溯算法问题,设骑士在某一位置,设(X,Y ),按规则走,下一步可以是如图 ( n=5 ) 所示的8个位置之一。
我们将重点考虑前进的方向:如果某一步可继续走下去,就试探着走下去且考虑下一步的走法,若走不通则返回,考虑另选一个位置。
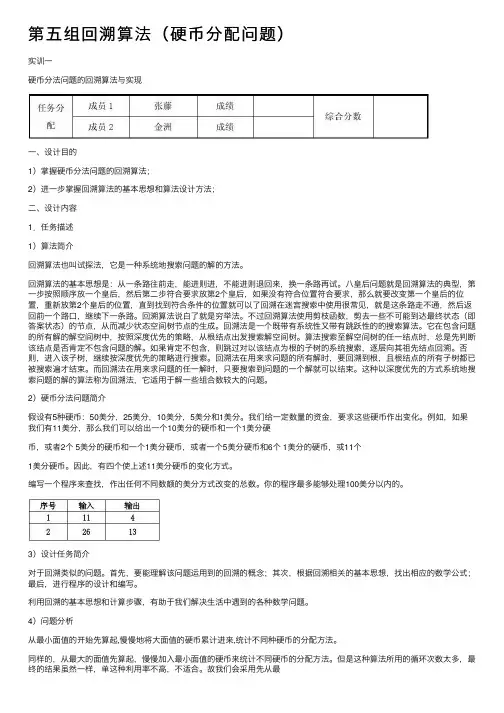
第五组回溯算法(硬币分配问题)实训⼀硬币分法问题的回溯算法与实现⼀、设计⽬的1)掌握硬币分法问题的回溯算法;2)进⼀步掌握回溯算法的基本思想和算法设计⽅法;⼆、设计内容1.任务描述1)算法简介回溯算法也叫试探法,它是⼀种系统地搜索问题的解的⽅法。
回溯算法的基本思想是:从⼀条路往前⾛,能进则进,不能进则退回来,换⼀条路再试。
⼋皇后问题就是回溯算法的典型,第⼀步按照顺序放⼀个皇后,然后第⼆步符合要求放第2个皇后,如果没有符合位置符合要求,那么就要改变第⼀个皇后的位置,重新放第2个皇后的位置,直到找到符合条件的位置就可以了回溯在迷宫搜索中使⽤很常见,就是这条路⾛不通,然后返回前⼀个路⼝,继续下⼀条路。
回溯算法说⽩了就是穷举法。
不过回溯算法使⽤剪枝函数,剪去⼀些不可能到达最终状态(即答案状态)的节点,从⽽减少状态空间树节点的⽣成。
回溯法是⼀个既带有系统性⼜带有跳跃性的的搜索算法。
它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。
算法搜索⾄解空间树的任⼀结点时,总是先判断该结点是否肯定不包含问题的解。
如果肯定不包含,则跳过对以该结点为根的⼦树的系统搜索,逐层向其祖先结点回溯。
否则,进⼊该⼦树,继续按深度优先的策略进⾏搜索。
回溯法在⽤来求问题的所有解时,要回溯到根,且根结点的所有⼦树都已被搜索遍才结束。
⽽回溯法在⽤来求问题的任⼀解时,只要搜索到问题的⼀个解就可以结束。
这种以深度优先的⽅式系统地搜索问题的解的算法称为回溯法,它适⽤于解⼀些组合数较⼤的问题。
2)硬币分法问题简介假设有5种硬币:50美分,25美分,10美分,5美分和1美分。
我们给⼀定数量的资⾦,要求这些硬币作出变化。
例如,如果我们有11美分,那么我们可以给出⼀个10美分的硬币和⼀个1美分硬币,或者2个 5美分的硬币和⼀个1美分硬币,或者⼀个5美分硬币和6个 1美分的硬币,或11个1美分硬币。
因此,有四个使上述11美分硬币的变化⽅式。
回溯法(⼆)——0-1背包问题 问题1、给定背包容量w,物品数量n,以及每个物品的重量wi,求背包最多能装多少多重的物品。
问题2、给定背包容量w,物品数量n,以及每个物品的重量wi、价值vi,求背包最多能装多少价值的物品。
这是⼀个基本的0-1背包问题,每个物品有两种状态(0:不装、1:装),总共有n步,所以可以⽤回溯法来解决,复杂度是O(2^n)。
C++版代码如下#include <iostream>#include <math.h>#include <cstring>using namespace std;#define MAXSIZE 256int maxWeight = -9999;// 回溯法解决0-1背包问题(其实可以暴⼒(n层for循环),回溯法也是n层for循环,即复杂度是O(2^n))void basePackage(int stuff[], int curState, int state, int curWeight, int weight){// 如果装满了(其实应该是接近装满了)或者已经“⾛完”所有物品if(curState == state || curWeight == weight){if(curWeight > maxWeight)maxWeight = curWeight;return ;}// 不装basePackage(stuff, curState + 1, state, curWeight + 0, weight);// 装if(curWeight + stuff[curState] <= weight)basePackage(stuff, curState + 1, state, curWeight + stuff[curState], weight);}// 回溯法解决0-1背包问题(其实可以暴⼒(n层for循环),回溯法也是n层for循环,即复杂度是O(2^n))// 背包升级问题回溯法解决(加⼊背包的价值)void secPackage(int weight[], int value[], int curV, int curW, int weightLimit, int curS, int n){// 如果背包总重量等于背包限制if(curW == weightLimit || curS == n){if(curV > maxWeight)maxWeight = curV;return ;}// 不装secPackage(weight, value, curV, curW, weightLimit, curS + 1, n);if(curW + weight[curS] <= weightLimit)// 装secPackage(weight, value, curV + value[curS], curW + weight[curS], weightLimit, curS + 1, n);}int main(int argc, char* argv[]){// 总重量,物品个数int w, n;cin>>w>>n;int a[MAXSIZE + 1];for(int i = 0; i < n; i++)cin>>a[i];basePackage(a, 0, n, 0, w);cout<<maxWeight<<endl;return 0;}。
回溯法N皇后问题例如:8皇后问题:要在8×8的国际象棋棋盘中放8个皇后,使任意两个皇后都不能互相吃掉。
规则是皇后能吃掉同一行、同一列、同一对角线的任意棋子。
下图为一种方案,求所有的解。
模型建立:不妨设8个皇后为x i,他们分别在第i行(i=1,2,3,4,5,6,7,8),这个问题的解空间,就是一个8个皇后所在的序号,为n元一维向量(x1,x2,x3,x4,x5,x6,x7,x8),搜索空间是1<=xi<=8(i=1,2,3,4,5,6,7,8),共88个状态。
约束条件是8个点(1,x1),(2,x2),(3,x3),(4,x4),(5,x5),(6,x6),(7,x7),(8,x8)不在同一列和同一对角线上。
算法设计:用回溯法从开始结点出发,以深度优先的方式搜索整个解空间。
这个开始结点就成为一个活结点,同时也成为当前的扩展结点。
在当前的扩展结点出,搜索向纵深方向移动至一个活结点。
这个新结点就成为一个新的活结点,并成为当前扩展结点。
如果在当前的扩展结点出不能再向纵深方向移动,则当前扩展结点就成为死结点。
此时,应往回移动(回溯)至最近的一个活结点处,病史这个活结点成为当前的扩展结点。
回溯法即以这种工作方式递归的在解空间中搜索,直至找到所要求的解或解空间中已没有活结点时为止。
程序设计:#include <stdio.h>#include <math.h>void backdate(int n);int check(int k);int a[20],n;void main(){printf("Please input a number N>3:\n");scanf("%d",&n);backdate(n);}void backdate(int n){int k;a[1]=0;k=1;while(k>0){a[k]=a[k]+1;while((a[k]<=n)&&(check(k)==0))a[k]=a[k]+1;if(a[k]<=n)if(k==n){ int i;printf("%d皇后的解为:\n",n);for(i=1;i<=n;i++)printf("%d\n",a[i]);}else{k++;a[k]=0;}elsek--;}}int check(int k){int i;for(i=1;i<=k-1;i++)if((abs(a[i]-a[k])==abs(i-k))||(a[i]==a[k])) return(0);return(1);}运行结果:。
跳马问题回溯法全文共四篇示例,供读者参考第一篇示例:跳马问题是一个经典的数学问题,也是一个很好的回溯法的练习题。
跳马问题是指在一个棋盘上,给定一个起始位置和一个目标位置,棋盘上只能按照马跳的规则(即按照国际象棋中马的行走规则)进行移动,问是否能够从起始位置跳到目标位置。
这个问题看似简单,但实际上需要一定的技巧和思考。
回溯法是一种解决问题的方法,它通过逐步构建解空间树并在搜索过程中剪枝,从而找到问题的解。
在解决跳马问题时,回溯法可以帮助我们搜索所有可能的跳法,找到可以到达目标位置的路径。
我们需要定义一些重要的概念。
在国际象棋中,马可以按照以下规则进行移动:以当前位置为中心,向八个方向中的一个方向跳两步,再沿着90度角的一个方向跳一步,即“日”字形。
在跳马问题中,我们可以用一个二维数组来表示棋盘,每个位置用一个数字来表示,表示该位置被访问的次序;用一个二维数组来存储马的移动规则;用一个二维数组来存储每一步的移动路径。
接下来,我们可以编写一个函数来实现跳马的逻辑。
我们需要判断当前位置是否合法,即在棋盘范围内且未被访问过;然后,我们需要判断是否已经到达目标位置,如果是,则返回true;否则,我们尝试按照马的移动规则进行递归搜索。
在搜索的过程中,我们可以记录已经访问过的位置,并在遇到无法移动的情况下进行回溯。
通过不断递归搜索,我们可以找到所有可能的路径,并判断是否存在一条路径能够到达目标位置。
这就是回溯法在解决跳马问题中的应用。
跳马问题是一个经典的数学问题,通过回溯法可以很好地解决。
回溯法是一种非常重要的解决问题的方法,可以帮助我们在搜索过程中不断调整搜索空间,并找到问题的最优解。
希望通过这篇文章的介绍,你能更好地理解跳马问题和回溯法的应用。
愿你在学习和探索中不断进步,解决更多有趣的问题!第二篇示例:跳马问题是一个经典的数学问题,它需要运用回溯法来解决。
跳马问题源于国际象棋中的一种走法,即马的走法。
马每次走日字形,即向前走两步,然后向左或向右一步,或者向前走一步,然后向左或向右两步。
回溯算法经典问题请设计⼀个函数,⽤来判断在⼀个矩阵中是否存在⼀条包含某字符串所有字符的路径。
路径可以从矩阵中的任意⼀个格⼦开始,每⼀步可以在矩阵中向左,向右,向上,向下移动⼀个格⼦。
如果⼀条路径经过了矩阵中的某⼀个格⼦,则该路径不能再进⼊该格⼦。
分析:回溯算法这是⼀个可以⽤回朔法解决的典型题。
⾸先,在矩阵中任选⼀个格⼦作为路径的起点。
如果路径上的第i个字符不是ch,那么这个格⼦不可能处在路径上的第i个位置。
如果路径上的第i个字符正好是ch,那么往相邻的格⼦寻找路径上的第i+1个字符。
除在矩阵边界上的格⼦之外,其他格⼦都有4个相邻的格⼦。
重复这个过程直到路径上的所有字符都在矩阵中找到相应的位置。
由于回朔法的递归特性,路径可以被开成⼀个栈。
当在矩阵中定位了路径中前n个字符的位置之后,在与第n个字符对应的格⼦的周围都没有找到第n+1个字符,这个时候只要在路径上回到第n-1个字符,重新定位第n个字符。
由于路径不能重复进⼊矩阵的格⼦,还需要定义和字符矩阵⼤⼩⼀样的布尔值矩阵,⽤来标识路径是否已经进⼊每个格⼦。
当矩阵中坐标为(row,col)的格⼦和路径字符串中相应的字符⼀样时,从4个相邻的格⼦(row,col-1),(row-1,col),(row,col+1)以及(row+1,col)中去定位路径字符串中下⼀个字符如果4个相邻的格⼦都没有匹配字符串中下⼀个的字符,表明当前路径字符串中字符在矩阵中的定位不正确,我们需要回到前⼀个,然后重新定位。
⼀直重复这个过程,直到路径字符串上所有字符都在矩阵中找到合适的位置class Solution {public:bool hasPath(char* matrix, int rows, int cols, char* str){if(str==NULL||rows<=0||cols<=0)return false;bool *isOk=new bool[rows*cols]();for(int i=0;i<rows;i++){for(int j=0;j<cols;j++)if(isHsaPath(matrix,rows,cols,str,isOk,i,j))return true;}return false;}bool isHsaPath(char *matrix,int rows,int cols,char *str,bool *isOk,int curx,int cury){if(*str=='\0')return true;if(cury==cols){curx++;cury=0;}if(cury==-1){curx--;cury=cols-1;}if(curx<0||curx>=rows)return false;if(isOk[curx*cols+cury]||*str!=matrix[curx*cols+cury])return false;isOk[curx*cols+cury]=true;bool sign=isHsaPath(matrix,rows,cols,str+1,isOk,curx-1,cury)||isHsaPath(matrix,rows,cols,str+1,isOk,curx+1,cury)||isHsaPath(matrix,rows,cols,str+1,isOk,curx,cury-1)||isHsaPath(matrix,rows,cols,str+1,isOk,curx,cury+1);isOk[curx*cols+cury]=false;return sign;}};。
回溯算法原理和几个常用的算法实例回溯算法是一种通过不断尝试和回退的方式来进行问题求解的算法。
它的基本思想是在过程中,当发现当前的选择并不符合要求时,就进行回退,尝试其他的选择,直到找到符合要求的解或者遍历完所有可能的选择。
回溯算法通常用于问题求解中的和排列组合问题,比如求解八皇后问题、0-1背包问题、数独等。
下面将介绍几个常用的回溯算法实例。
1.八皇后问题:八皇后问题是指在一个8×8的国际象棋棋盘上,放置八个皇后,使得任意两个皇后都不在同一行、同一列或同一斜线上。
可以通过递归的方式依次尝试每一行的位置,并判断当前位置是否满足条件。
如果满足条件,则进入下一行尝试;否则回溯到上一行,并尝试其他的位置,直到找到解或遍历完所有的可能。
2.0-1背包问题:0-1背包问题是指在给定一组物品和一个容量为C的背包,每个物品都有自己的重量和价值,求解在不超过背包容量时,如何选择物品使得背包中物品的总价值最大。
可以通过递归的方式依次考察每个物品,并判断是否选择当前物品放入背包。
如果放入当前物品,则背包容量减小,继续递归考察下一个物品;如果不放入当前物品,则直接递归考察下一个物品。
直到遍历完所有物品或背包容量为0时,返回当前总价值。
3.数独问题:数独是一种通过填充数字的方式使得每一行、每一列和每一个九宫格内的数字都满足一定条件的谜题。
可以通过递归的方式依次尝试填充每一个空格,并判断当前填充是否符合条件。
如果符合条件,则继续递归填充下一个空格;如果不符合条件,则回溯到上一个空格,并尝试其他的数字,直到找到解或遍历完所有的可能。
回溯算法的时间复杂度一般较高,通常为指数级别。
因此,在实际应用中,可以结合剪枝等优化策略来提高算法的效率。
此外,回溯算法也可以通过非递归的方式进行实现,使用栈来存储当前的状态,从而避免递归带来的额外开销。
总之,回溯算法是一种非常有效的问题求解方法,通过不断尝试和回退,可以在复杂的空间中找到符合要求的解。
回溯算法经典例题回溯算法是一种解决问题的方法,其核心思想是通过深度优先搜索来寻找解决方案。
回溯算法通常用于解决需要重复操作的问题,例如迷宫问题、图论问题等。
以下是回溯算法的经典例题:1. 八皇后问题八皇后问题是一个经典的回溯算法例题,它要求在 8×8 的国际象棋棋盘上放置八个皇后,使得它们无法相互攻击。
回溯算法的核心思想是,不断尝试每个皇后的位置,直到找到合法的位置为止。
具体实现如下:```cpp#include <iostream>using namespace std;int queen_board[8][8] = {{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0}}};int main(){int n = 8;int queen = 0;for (int i = 0; i < 8; i++){for (int j = 0; j < 8; j++){if (queen_board[i][j] == 0){queen_board[i][j] = queen++;cout << "Queen placed on " << i << ", " << j << endl;}}}return 0;}```在这个实现中,我们首先初始化一个 8×8 的矩阵来表示皇后可以放置的位置,如果当前位置已经放置了一个皇后,则将该位置标记为已经放置,并重新搜索下一个位置。
回溯算法搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。
回溯是搜索算法中的一种控制策略。
它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。
如迷宫问题:进入迷宫后,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已无路可走,这时,首先看其它方向是否还有路可走,如果有路可走,则沿该方向再向前试探;如果已无路可走,则返回一步,再看其它方向是否还有路可走;如果有路可走,则沿该方向再向前试探。
按此原则不断搜索回溯再搜索,直到找到新的出路或从原路返回入口处无解为止。
递归回溯法算法框架[一]procedure Try(k:integer);beginfor i:=1 to 算符种数 Doif 满足条件 thenbegin保存结果if 到目的地 then 输出解else Try(k+1);恢复:保存结果之前的状态{回溯一步}end;end;递归回溯法算法框架[二]procedure Try(k:integer);beginif 到目的地 then 输出解elsefor i:=1 to 算符种数 Doif 满足条件 thenbegin保存结果Try(k+1);end;end;例 1:素数环:把从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。
【算法分析】非常明显,这是一道回溯的题目。
从1 开始,每个空位有 20(19)种可能,只要填进去的数合法:与前面的数不相同;与左边相邻的数的和是一个素数。
第 20个数还要判断和第1个数的和是否素数。
〖算法流程〗1、数据初始化; 2、递归填数:判断第J种可能是否合法;A、如果合法:填数;判断是否到达目标(20个已填完):是,打印结果;不是,递归填下一个;B、如果不合法:选择下一种可能;【参考程序】program z74;框架[一]var a:array[0..20]of byte;b:array[0..20]of boolean;total:integer;function pd(x,y:byte):boolean;var k,i:byte;begink:=2; i:=x+y; pd:=false;while (k<=trunc(sqrt(i)))and(i mod k<>0) do inc(k);if k>trunc(sqrt(i)) then pd:=true;end;procedure print;var j:byte;begininc(total);write('<',total,'>:');for j:=1 to 20 do write(a[j],' ');writeln;end;procedure try(t:byte);var i:byte;beginfor i:=1 to 20 doif pd(a[t-1],i)and b[i] thenbegina[t]:=i; b[i]:=false;if t=20 then begin if pd(a[20],a[1]) then print;endb[i]:=true;end;end;BEGINfillchar(b,sizeof(b),#1);total:=0;try(1);write('total:',total);END.通过观察,我们可以发现实现回溯算法的特性:在解决过程中首先必须要先为问题定义一个解的空间.这个空间必须包含问题的一个解。
在搜索路的同时也就产生了新的解空间。
在搜索期间的任何时刻.仅保留从起始点到当前点的路径。
例 2:设有 n 个整数的集合{1,2,…,n},从中取出任意 r 个数进行排列(r<n),试列出所有的排列。
解法一:program it15; 框架[一]type se=set of 1..100;VAR s:se;n,r,num:integer;b:array [1..100] of integer;PROCEDURE print;var i:integer;beginnum:=num+1;for i:=1 to r dowrite(b[i]:3);writeln;end;PROCEDURE try(k:integer);VAR i:integer;beginfor i:=1 to n doif i in s thenbeginb[k]:=i;s:=s-[i];if k=r then prints:=s+[i];end;end;BEGINwrite('Input n,r:');readln(n,r); s:=[1..n];num:=0;try(1);writeln('number=',num);END.解法二:program it15; 框架[二]type se=set of 1..100;VARs:se;n,r,num,k:integer;b:array [1..100] of integer;PROCEDURE print;var i:integer;beginnum:=num+1;for i:=1 to r dowrite(b[i]:3);writeln;end;PROCEDURE try(s:se;k:integer); VAR i:integer;beginif k>r then printelsefor i:=1 to n doif i in s thenbeginb[k]:=i;end;end;BEGINwrite('Input n,r:');readln(n,r);s:=[1..n];num:=0;try(s,1);writeln('number=',num);readln;END.例3、任何一个大于1的自然数n,总可以拆分成若干个小于n 的自然数之和. 当n=7共14种拆分方法:7=1+1+1+1+1+1+17=1+1+1+1+1+27=1+1+1+1+37=1+1+1+2+27=1+1+1+47=1+1+2+37=1+1+57=1+2+2+27=1+2+47=1+3+37=1+67=2+2+37=2+57=3+4total=14{参考程序}program jjj;var a:array[0..100]of integer;n,t,total:integer;procedure print(t:integer);var i:integer;beginwrite(n,'=');for i:=1 to t-1 do write(a[i],'+');writeln(a[t]);total:=total+1;end;procedure try(s,t:integer);var i:integer;beginfor i:=1 to s doif (a[t-1]<=i)and(i<n) thenbegina[t]:=i;s:=s-a[t];if s=0 then print(t)else try(s,t+1);s:=s+a[t];end;end;beginreadln(n);try(n,1);writeln('total=',total);readln;end.例 4、八皇后问题:要在国际象棋棋盘中放八个皇后,使任意两个皇后都不能互相吃。
(提示:皇后能吃同一行、同一列、同一对角线的任意棋子。
)放置第i个皇后的算法为:procedure Try(i);beginfor 第i 个皇后的位置=1 to 8 do;if 安全 thenbegin放置第 i个皇后;对放置皇后的位置进行标记;if i=8 then 输出else Try(i+1);{放置第 i+1个皇后}对放置皇后的位置释放标记,尝试下一个位置是否可行;end;end;【算法分析】显然问题的键在于如何判定某个皇后所在的行、列、斜线上是否有别的皇后;可以从矩阵的特点上找到规律,如果在同一行,则行号相同;如果在同一列上,则列号相同;如果同在/斜线上的行列值之和相同;如果同在\斜线上的行列值之差相同;如果斜线不分方向,则同一斜线上两皇后的行号之差的绝对值与列号之差的绝对值相同。
从下图可验证:对于一组布局我们可以用一个一维数组来表示:A:ARRAY [1..8] OF INTEGER;A[I]的下标I 表示第I个皇后在棋盘的第I行,A[I]的内容表示在第 I行的第 A[I]列,例如:A[3]=5就表示第3个皇后在第3行的第5列。
在这种方式下,要表示两个皇后 I和 J不在同一列或斜线上的条件可以描述为:A[I]<>A[J] AND ABS(I-J)<>ABS(A[I]-A[J]){I和 J分别表示两个皇后的行号}考虑每行有且仅有一个皇后,设一维数组A[1..8]表示皇后的放置:第i行皇后放在第j列,用A[i]=j来表示,即下标是行数,内容是列数。
判断皇后是否安全,即检查同一列、同一对角线是否已有皇后,建立标志数组b[1..8]控制同一列只能有一个皇后,若两皇后在同一对角线上,则其行列坐标之和或行列坐标之差相等,故亦可建立标志数组c[1..16]、d[-7..7]控制同一对角线上只能有一个皇后。
从分析中,我们不难看出,搜索前进过程实际上是不断递归调用的过程,当递归返回时即为回溯的过程。
program ex1;var a:array[1..8] of byte;b:array[1..8] of boolean;c:array[1..16] of boolean;d:array[-7..7] of boolean;sum:byte;procedure pr;var i:byte;beginfor i:=1 to 8 do write(a[i]:4);inc(sum);writeln(' sum=',sum);end;procedure try(t:byte);var j:byte;beginfor j:=1 to 8 do{每个皇后都有8种可能位置}if b[j] and c[t+j] and d[t-j] then {寻找放置皇后的位置}begin {放置皇后,建立相应标志值}a[t]:=j;{摆放皇后}b[j]:=false;{宣布占领第j列}c[t+j]:=false;{占领两个对角线}d[t-j]:=false;if t=8 then pr {8个皇后都放置好,输出}else try(t+1);{继续递归放置下一个皇后}b[j]:=true; {递归返回即为回溯一步,当前皇后退出}c[t+j]:=true;d[t-j]:=true;end;end;BEGINfillchar(b,sizeof(b),#1);fillchar(c,sizeof(c),#1);fillchar(d,sizeof(d),#1);sum:=0;try(1);{从第1个皇后开始放置}END.例 5:马的遍历中国象棋半张棋盘如图 4(a)所示。